 Open Access
Open Access
ARTICLE
The Behavior of a Gas Bubble in a Square Cavity Filled with a Viscous Liquid Undergoing Vibrations
1 Computational Fluid Dynamics Lab, Institute of Continuous Media Mechanics, Ural Branch of the Russian Academy of Sciences, Perm, 614013, Russia
2 Theoretical Physics Department, Perm State University, Perm, 614990, Russia
* Corresponding Author: Tatyana Lyubimova. Email:
(This article belongs to the Special Issue: Advanced Problems in Fluid Mechanics)
Fluid Dynamics & Materials Processing 2024, 20(11), 2417-2429. https://doi.org/10.32604/fdmp.2024.052391
Received 31 March 2024; Accepted 22 July 2024; Issue published 28 October 2024
Abstract
External vibrations are known to be one of the promising ways to control the behavior of multiphase systems. The computational modeling of the behavior of a gas bubble in a viscous liquid in a horizontal cylinder of square cross-section, which undergoes linearly polarized translational oscillations in weightless conditions, has been carried out. Under vibrations, the bubble moves towards the wall of the vessel with acceleration determined by the amplitudes and frequency of vibrations. Near the wall, at a distance of the order of the thickness of the viscous Stokes boundary layer, the effects of viscosity become more important and, as a result, the bubble is repelled from the wall. After some oscillations, equilibrium conditions are attained where the attractive force balances the repulsive force; accordingly, the average position of the bubble ceases to change. The numerical modelling shows that the average behaviors of a deformable bubble near a wall under normal and tangential vibration are similar.Keywords
Nomenclature
| φ | Marker function |
| α | Surface tension coefficient |
| a | Dimensionless vibration amplitude |
| ω | Angular frequency of vibration |
| l | Cavity length |
| ε | Half-thickness of the transition layer |
| λ | Density |
| μ | Viscosity |
| | Bubble Radius |
| Re | Reynolds number |
| Fr | Froude number |
| We | Weber number |
| σ | Viscous stress tensor |
| p | Pressure |
| γ | Unit vector |
| ν | Velocity |
| n | Interface normal vector |
| | Liquid density |
| | Vapor density |
| | Volume force |
| ρ (φ) | Density field |
| η (φ) | Viscosity field |
| H (φ) | Heaviside function |
| δ (φ) | Dirac delta function |
| k (φ) | Interface curvature |
Multiphase systems are widespread in nature and technology. For instance, during the crystal growth process, bubbles may form in a melt caused by gas emission, which dramatically affects the structure of the crystal [1–3]. In selective laser melting applications, gas bubbles that can appear when metallic powder melts [4] should be moved close to the melt-free surface to increase the coalescence rate. In these examples, the bubbles change the structure of the final product, resulting in rejects. On the other hand, in many processes, bubbles are intentionally generated. For example, in flotation, bubbles are used to collect target components at the liquid-gas interface [5–8]. Thus, it is important to understand and manage the dynamics of such systems. One of the ways to control the behavior of multiphase systems is the impact of external vibration. The possibilities for the intensification of the flotation efficiency by ultrasound vibrations is discussed in [9,10]. Vibrations are known to cause unusual behavior of mechanical systems [11–14], and can be used to impose required motion, stabilization or shape change [15–18].
This work deals with the investigation of the dynamics of a gas bubble in a viscous liquid in a vessel performing linearly polarized translational vibrations. The behavior of a solid in a liquid undergoing high-frequency translational vibrations was considered using the inviscid approach in [19–21]. The study showed that an average vibration force acts on a solid from the vibrating liquid, as a result of which the solid is attracted to the closest wall. This force decreases rapidly with increasing distance from the solid to the wall. Both in the case when the wall vibrates parallel to itself, and in the case when the wall vibrates perpendicular to itself, the force of interaction between the inclusion and the wall in an inviscid fluid is an attractive force.
The influence of periodical external forcing on submerged solid bodies has been experimentally studied by many authors. The dynamics of a solid body in a liquid under high-frequency rotational vibration was studied in [22]. The behavior of a heavy cylinder in a horizontal cylindrical cavity at modulated rotation is considered in [23]. Lift force acting on a heavy solid in a rotating cavity under conditions of time-dependent rotation rate is experimentally investigated in [24]. The dynamics of a solid of nearly neutral buoyancy in a cavity subjected to rotational vibrations is studied in [25]. An analytical model for the periodic motion of a small particle in a viscous fluid was developed in [26] in Stokes flow approximation, taking into account virtual mass, Stokes drag, and introducing history forces. Later, the analysis was confirmed experimentally in [27].
In [28], resonance oscillations of a drop (bubble) subjected to small amplitude vibrations in zero gravity conditions within a container filled with a fluid of varying densities are examined. The resonance frequency shift caused by viscosity is determined. It is shown that the resonant oscillation is possible if the frequency of the forced vibrations coincides with the sum of eigen-oscillations frequencies. Oscillations of a clamped liquid drop surrounded by an incompressible fluid of a different density are studied in [29]. It is shown that the fundamental frequency of free oscillations can vanish in a certain interval of values of the Hocking parameter. The length of this interval depends on the aspect ratio of the drop.
The existence of the attraction force for a particle vibrating parallel to the closest wall was experimentally studied in [30]. The velocity of a steel ball hung in a liquid by a thin wire has been measured experimentally to confirm the strength of this attractive force. High-frequency experiments revealed that the average particle location shifts towards the same wall when the particle is brought close to it. This shift is dependent on the liquid and particle densities as well as on the vibration parameters.
Experimental and numerical investigation of the interaction of two solid particles in an oscillating viscous liquid was carried out in [31,32]. It has been demonstrated that the viscosity’s braking effect increases to such an extent at distances below a threshold value that the interaction force reverses sign, exhibiting repulsion as opposed to attraction. It is observed that this critical distance grows with rising viscosity and/or decreasing frequency. Recently, in [33], a numerical analysis of two spheres in a viscous fluid-filled oscillating box was carried out. The simulation demonstrates that the particles oscillate over extended trajectories that are both parallel and perpendicular to the oscillating flow. The influence of a magnetic field on two solid particles is considered in [34].
In [35], the effect of viscosity on a gas bubble’s mobility in close proximity to a wall was examined. It was discovered that in high-viscosity liquids, a bubble’s attraction to the closest wall is replaced by repulsion. The explanation for the bubble’s repulsion from the wall was a drop in flow intensity brought on by the viscosity between the bubble and the wall. This behavior was investigated experimentally in [36–38]. The study examined the relationship between a solid spherical particle strung on a wire and the wall of a rectangular cell that was filled with liquid and exposed to varying frequencies and amplitudes of horizontal vibrations. To investigate the attracting or repelling force produced in the normal direction, the fluid’s viscosity was changed.
The purpose of the current work is to numerically study the dynamics of a gas bubble in a square-shaped cavity filled with a viscous incompressible liquid under linearly polarized translational vibrations of finite amplitude and frequency.
Let us consider the behavior of a cylindrical gas bubble in a viscous liquid filling a long horizontal cylinder with a square cross-section under conditions of weightlessness. A vessel with liquid undergoes linearly polarized translational vibrations of finite amplitude and frequency. The geometry of the problem is presented in Fig. 1. Note, that the origin of the axis corresponds to x0 and y0, i.e., the center of the cavity. The problem is considered in a two-dimensional formulation that substantially reduces computation costs of the modelling under the high frequency vibration while allows to capture relevant phenomena.
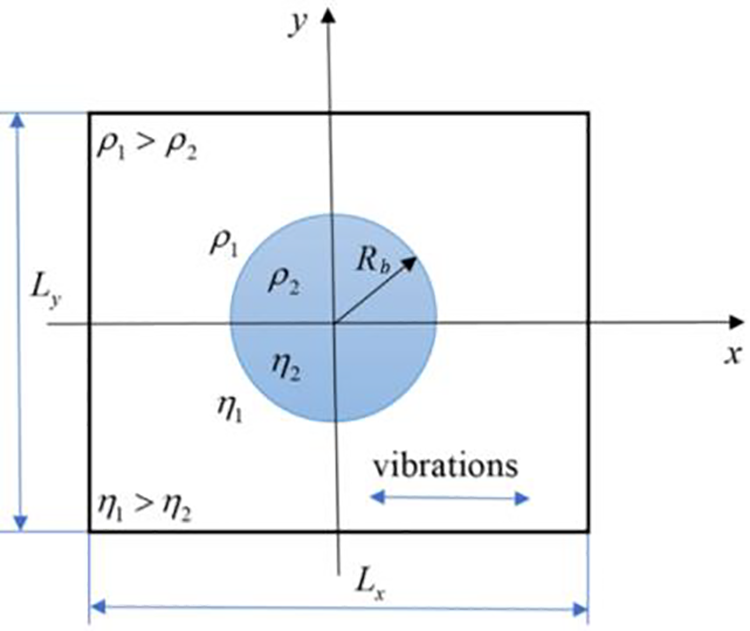
Figure 1: Problem geometry
Ansys Fluent, the industry-leading fluid simulation software [39], was used for the modelling. Calculations were carried out for long horizontal cylinders of square cross-section in a two-dimensional formulation. In the reference frame of oscillating container, the system of equations is:
where
Here
In this work, the Volume of Fluid method [40,41] was used which is based on tracking the volume of each phase in computational cells close to the boundary of the media. Using this method, one can simulate the behavior of a system of two or more immiscible liquids. To determine the shape of the interface, a geometric reconstruction scheme (“The Geometric Reconstruction Scheme”) is used.
According to the Volume of Fluid method, the volume fraction of a phase,
Here H (φ) is continuous Heaviside function that reads:
where ε is half-thickness of the transition layer.
The following continuity equation was solved for the volume fraction of the phases to track the interface between the phases:
The volume fraction of the primary phase can be found by:
Tracing the interface between phases is accomplished by solving the continuity equation for the volume fraction of one (or more) phases. Volume force is written as:
where φ is the marker function, δ(φ) is the Dirac delta function, α is the surface tension coefficient,
The numerical modelling was performed for parameters of experimental work [45]. At walls of the cavity, a sticking condition is imposed. Initially the bubble is located near the center of the cavity with a shift along X of 0.1 mm from the center, the velocities of the liquid and the bubble are equal to zero. The distance between the center of mass of the bubble and the walls: lower and upper: 1.5 mm, right: 1.4 mm, left: 1.6 mm. The displacement of the bubble is necessary to ensure that the bubble will always move towards the same wall (the nearest one). If one place the bubble in the center, it will be attracted to either the right or left wall depending on initial disturbance.
Calculations were carried out at fixed values of the following parameters:
• Square area with sides 3 mm.
• Bubble radius,
• Densities of liquid and gas in the bubble: 44.4 and 18.4 kg/m3, respectively.
• Dynamic viscosity of liquid is 4.75−6 kg/(m s), gas in a bubble is 1.97−6 kg/(m s).
The ratio of the bubble diameter to the side of the area is 1/2. It was chosen in accordance to the experiment [45]. The frequency and amplitude of vibrations varied. Most calculations were carried out for a time interval of 5 s. Modelling of a high frequency vibration effect requires limits time step of numerical iteration because it has to be much less that the period of vibration. For all calculations, a time step of
The spatial discretization is performed using the third-order MUSCL scheme (Monotone Upstream-Centered Schemes for Conservation Laws). The grid is rectangular and consists of

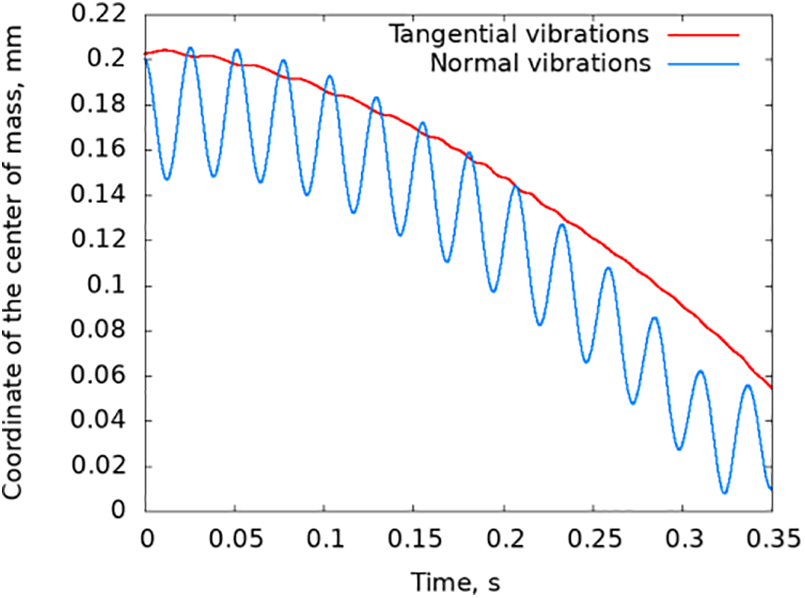
Figure 2: Comparison of the dependences of distance from the bubble to the wall on time for different directions of vibrations at f = 38.5 Hz, a = 0.1 mm, Rb = 0.2 mm
The average vibration force acting on a rigid cylinder suspended in a vibrating liquid of different density was calculated analytically in [20,21] for the case of viscosity neglection. This force per unit length of the cylinder is:
where the dimensionless distance between the wall and the cylinder is expressed as h/l. The force is caused by the fact that the growth of the pulsating flow velocity between the wall and the cylinder results in a decrease in pressure there, which causes the attraction of the cylinder to the wall (Bernoulli effect). In [32,35], it was found that at small distance from a wall, comparable to the thickness of viscous boundary layer, the force changes sign and the inclusion starts to repel from the wall. The origin of this phenomenon is in the suppression of the flow near the wall by viscosity [32,35].
As shown in [21], the inclusion suspended in low viscous fluid is attracted to the wall both in the cases of normal and tangential vibrations. Our numerical modelling performed for the vibration tangential to the wall confirms that average motions of deformable bubble near the wall under normal and tangential vibration are similar. The bubble moves towards the wall with nearly the same acceleration (see Fig. 2, where the evolution of the distance between the bubble with radius 0.2 mm and the wall is shown for both cases).
3.2 Dynamics of Bubble under Vibrations Normal to the Boundary
Let us first consider the dynamics of a gas bubble in a liquid with a viscosity comparable to water (kinematic viscosity: 1.07 × 10−6 m3/s), in a vessel with solid walls, which is subjected to linearly polarized translational vibrations with an amplitude of 0.2 mm and frequency 20 Hz. Fig. 3 shows the dependence of the coordinates of the center of mass on time. As can be seen, under the influence of vibrations the bubble performs forced oscillations with a frequency equal to the vibration frequency. An accelerated average movement of the bubble towards the nearest wall of the vessel is also observed. This movement is associated with the action of an average vibrational force acting on the bubble from the vibrating liquid.
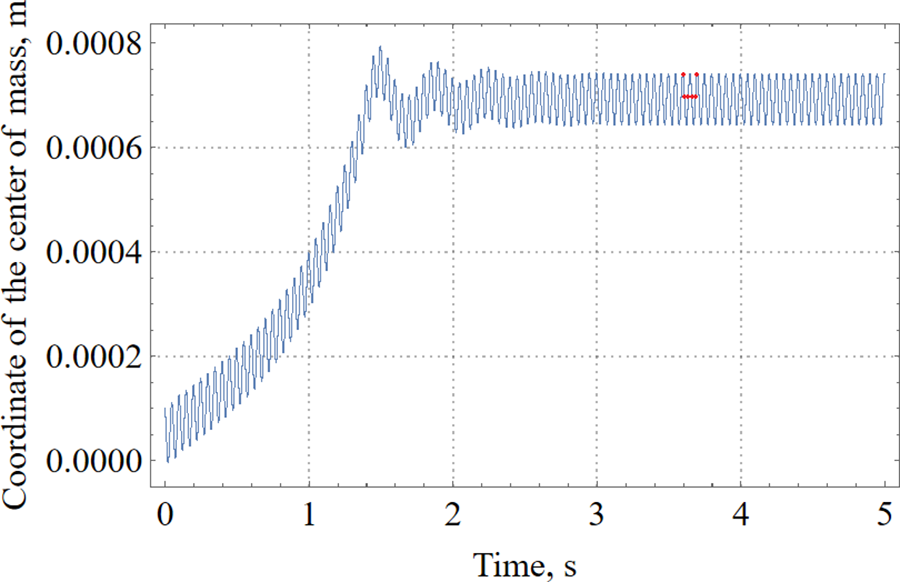
Figure 3: Temporal evolution of the bubble center mass at amplitude 0.2 mm and frequency 20 Hz
In a time of about 1.5 s, the bubble reaches the wall, then, for about 0.5 s, it performs damped oscillations around a certain position near the wall. Subsequently, the average position of the bubble does not change; it performs only forced oscillations at this distance from the wall.
Fig. 4 shows data on the movement and change in the instantaneous shape of a bubble over two periods of forced oscillations for a bubble located near the wall (the period is 0.05 s). In Figs. 3 and 4, the red dots indicate where the bubble frames were taken from.
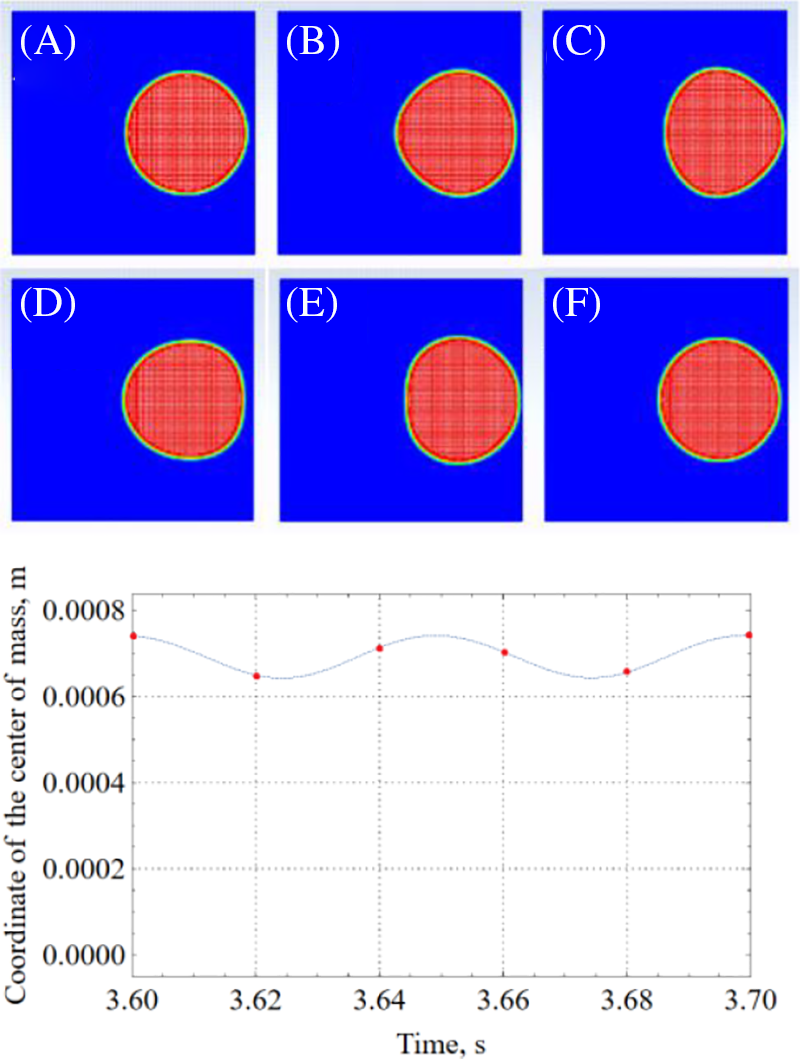
Figure 4: Evolution of the instantaneous position and shape of the bubble with time ((A): 3.60 s, (B): 3.62 s, (C): 3.64 s, (D): 3.66 s, (E): 3.68 s, (F): 3,70 s) and the dependence of the bubble center mass coordinate on time
3.3 Effect of Vibration Frequency on Bubble Dynamics
Let us discuss the influence of vibration frequency on the dynamics of a bubble. To study the vibration frequency influence, the calculations were carried out at fixed vibration amplitude equal to 0.2 mm for several vibration frequency values: 15, 20, 38.5, 45 Hz. Fig. 5 shows the coordinates of the center of mass vs. time for different frequencies. As can be seen, under the influence of vibrations the bubble moves on average to the wall of the container with an acceleration determined by the frequency of vibrations. This movement is associated with the action of an average vibration force, which, as can be seen from the formula (6), is proportional to the squared frequency of vibration, therefore, the higher the frequency, the faster the bubble reaches the wall. When approaching the wall, the bubble performs forced oscillations near the wall at a small distance from the wall.
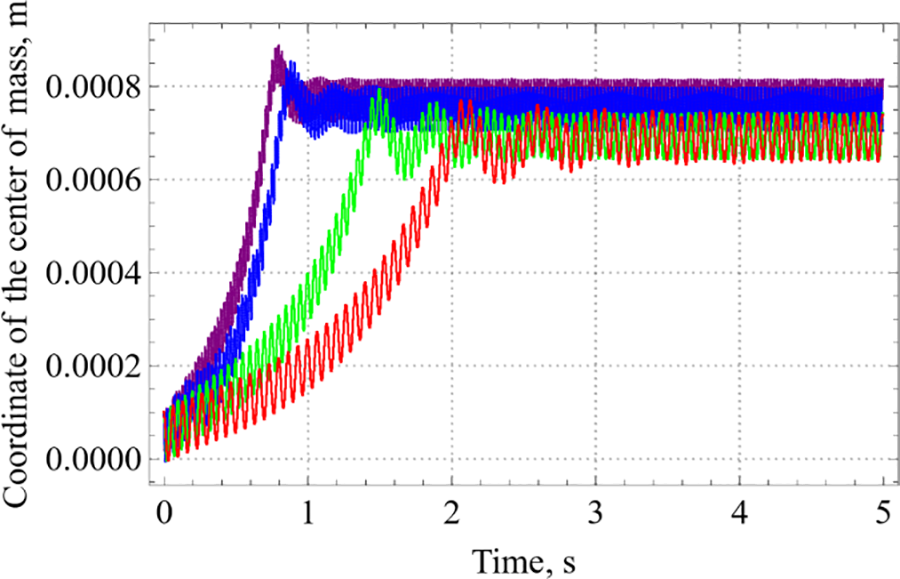
Figure 5: Dependences of the coordinates of the center of mass of the bubble on time for the vibration amplitude 0.2 mm and different vibration frequencies (violet: 45 Hz, blue: 38.5 Hz, green: 20 Hz, red: 15 Hz)
Near the wall, at a distance of the order of the thickness of the viscous boundary layer, the decelerating effect of viscosity starts to work. As a result, after some oscillations, the average location of the bubble ceases to change; the bubble makes only forced oscillations around the position determined by the balance of the attractive and repulsive forces. The thickness of the viscous Stokes layer becomes smaller with increasing vibration frequency, therefore the quasi-equilibrium distance at which forced oscillations of the bubble occur near the wall decreases with increasing vibration frequency (see Fig. 6). As can be seen from the graph, the average distance between the bubble centroid and the wall progressively decreases with the increase of frequency.
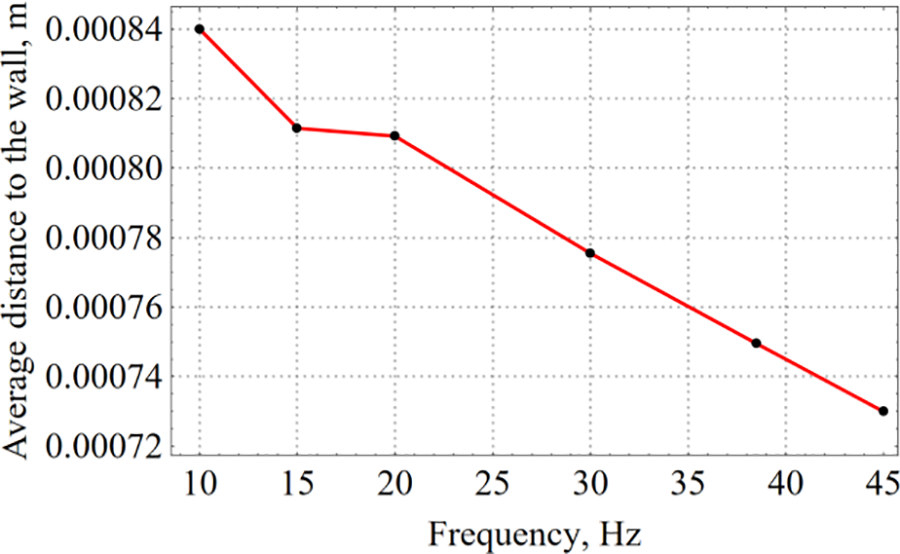
Figure 6: Dependence of the quasi-equilibrium (average) distance between the center of mass of the bubble and the wall on the vibration frequency at a fixed vibration amplitude equal to 0.2 mm
Fig. 7 shows the instantaneous shapes of the bubble at various time moments under vibrations with frequencies of 15 and 45 Hz. It can be seen that at a higher frequency the bubble reaches the wall faster and its shape changes more strongly. Fig. 8 shows the dependences of the coordinate of the center of mass on time for frequencies 15 and 45 Hz. One can see that the bubble performs forced oscillations with the imposed vibration frequency; the average distance from the wall is smaller for higher frequency.
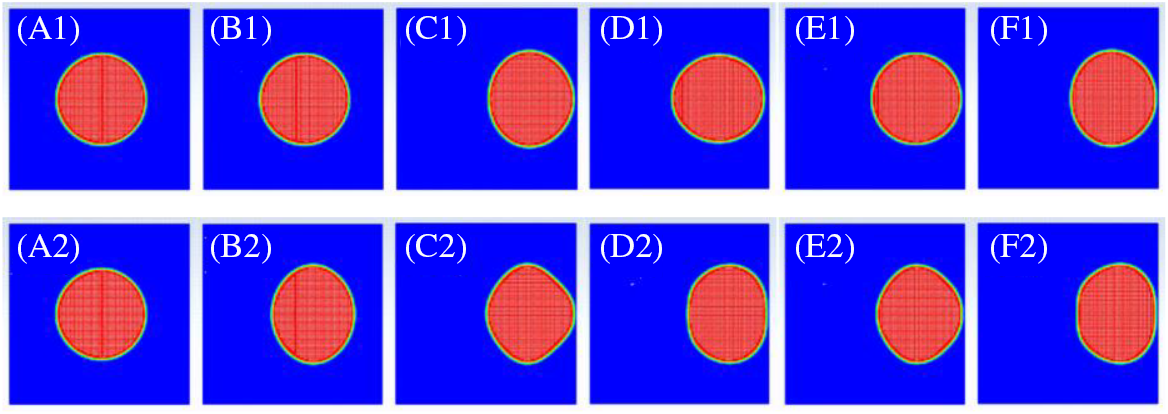
Figure 7: Comparison of instantaneous bubble shapes at different time moments for the vibration frequencies 15 Hz (A1–F1) and 45 Hz (A2–F2): A1, A2–0 s, B1, B2–1 s, C1, C2–2 s, D1, D2–3 s, E1, E2–4 s, F1, F2–5 s
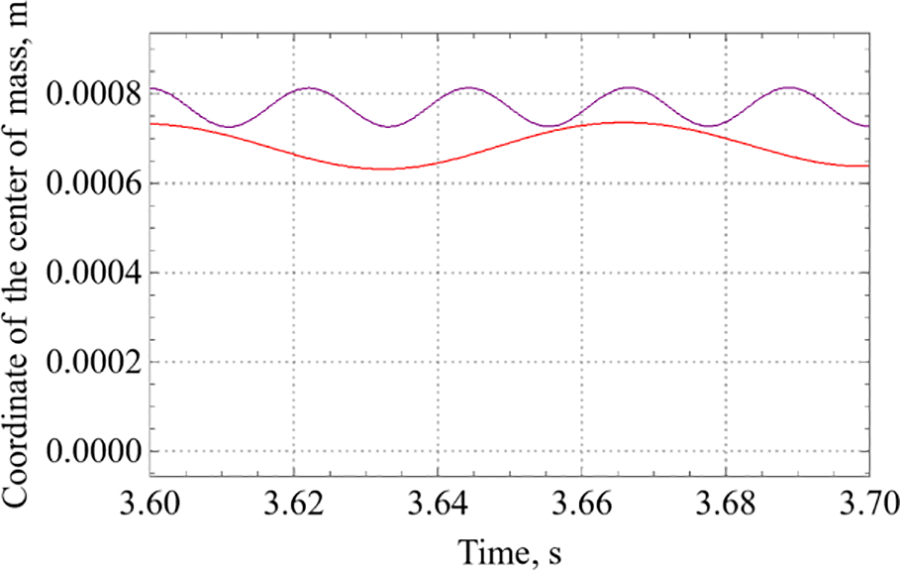
Figure 8: Comparison of the dependences of the coordinate of the center of mass on time for a bubble under vibrations with frequencies 15 and 45 Hz (red: 15 Hz, purple: 45 Hz)
3.4 Effect of Vibration Amplitude on Bubble Dynamics
Let us consider the influence of the vibration amplitude on the dynamics of the bubble. To study the effect of vibration amplitude, the computations were conducted at a fixed vibration frequency 38.5 Hz for several vibration amplitude values: 0.10, 0.15, 0.20 mm.
Fig. 9 shows the dependences of the coordinates of the center of mass on time for different vibration amplitudes. It can be seen that the greater the amplitude, the faster the bubble gets to the wall, this corresponds to the formula (6) for the average vibration force, from which it follows that the average vibration force is proportional to the squared vibration amplitude. The quasi-equilibrium distance at which the bubble performs forced vibrations in the vicinity of the wall at the last stage decreases with increasing vibration amplitude (see Fig. 10). As can be seen from the graph, the average distance from the center of mass of the bubble to the wall progressively decreases with the increase of amplitude.
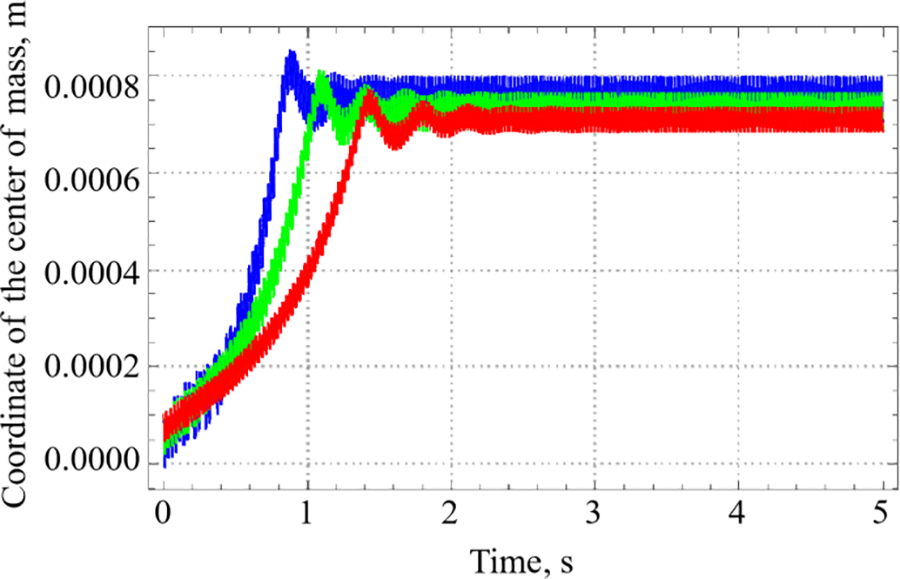
Figure 9: Dependences of the coordinates of the center of mass on time at frequency 38.5 Hz and various vibration amplitudes (blue: 0.20 mm, green: 0.15 mm, red: 0.10 mm)
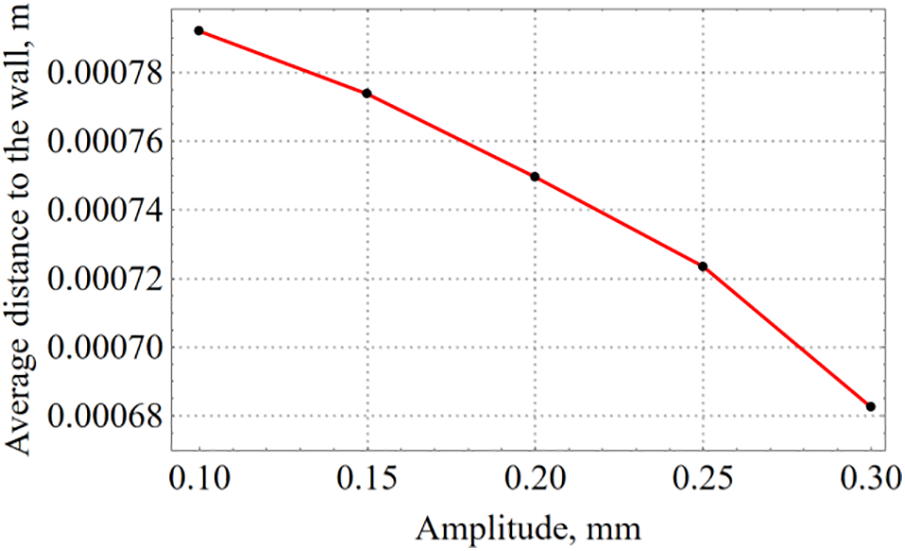
Figure 10: Dependence of the quasi-equilibrium (average) distance between the center of mass of the bubble and the wall on the vibration amplitude at a fixed vibration frequency equal to 38.5 Hz
Fig. 11 presents the instantaneous shapes of the bubble at various time moments under vibrations with frequency 45 Hz and amplitudes 0.10 and 0.20 mm. As can be seen, at larger amplitude the bubble is more deformed and reaches the wall faster. Fig. 12 shows a comparison of the dependences of the coordinate of the center of mass on time over 4 periods of vibrations for amplitudes 0.10 and 0.20 mm. You can see that the bubble performs forced oscillations with the imposed vibration frequency. The average distance from the wall is smaller for larger amplitude.
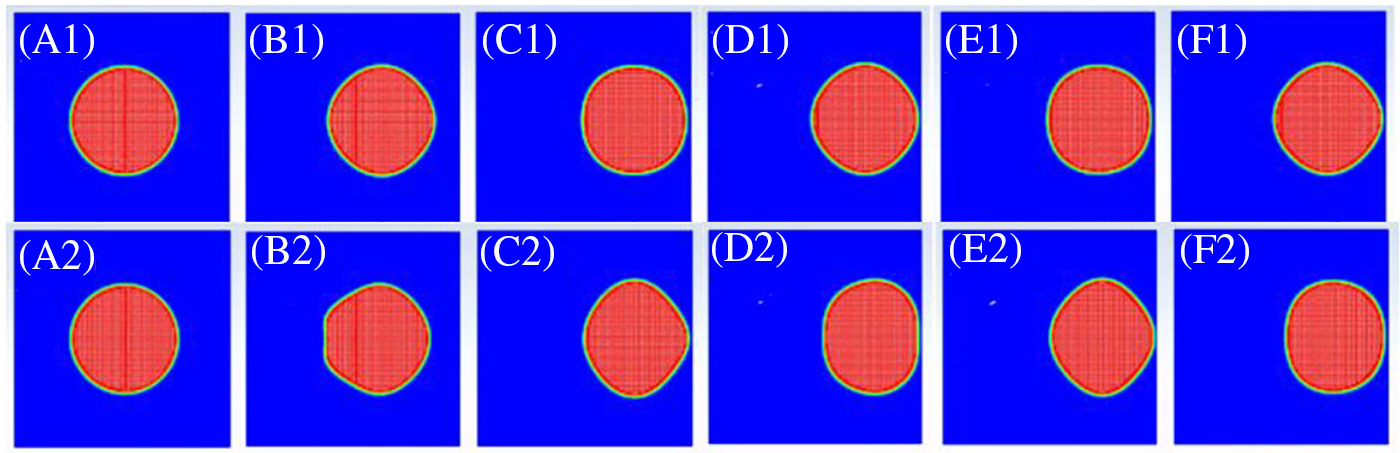
Figure 11: Instantaneous bubble shapes at different times for amplitudes 0.1 mm (A1–F1) and 0.2 mm (A2–F2): A1, A2–0 s, B1, B2–1 s, C1, C2–2 s, D1, D2–3 s, E1, D2–4 s, F1, F2–5 s
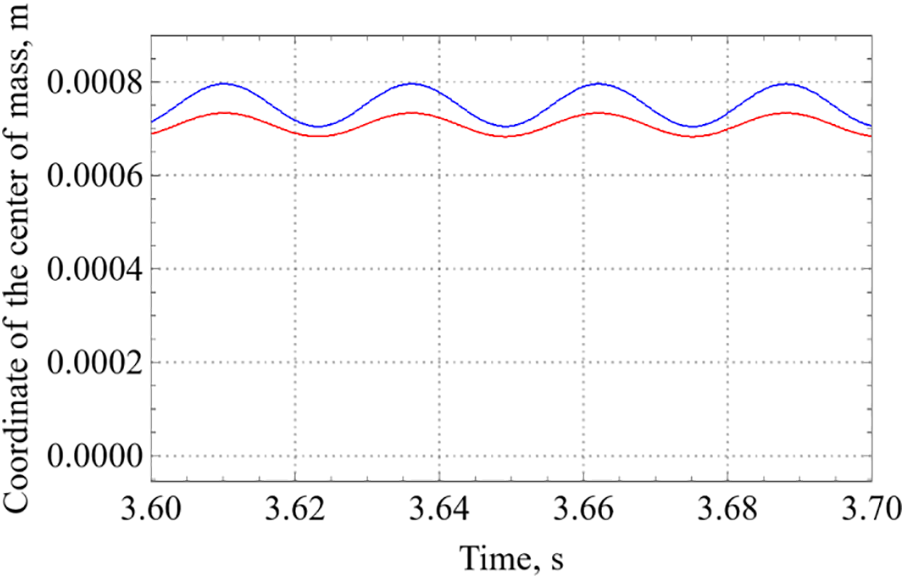
Figure 12: Comparison of the dependences of the coordinate of the center of mass on time at the vibration frequency 45 Hz and different vibration amplitudes (red: 0.1 mm, blue: 0.2 mm)
Numerical modeling of the behavior of a gas bubble in a viscous liquid in a horizontal cylinder of square cross-section, undergoing linearly polarized translational vibrations under weightless conditions, was carried out. The calculations have shown that, under the influence of an average force of vibrational attraction to the nearest wall, for all considered parameter values, the bubble demonstrates acceleratory average displacement from the center of the container to the wall. Upon reaching the wall, after several oscillations, the average position of the bubble ceases to change and then, it performs only forced oscillations with a frequency equal to the vibration frequency, around a certain quasi-equilibrium average position, depending on the amplitude and frequency of vibrations.
Acknowledgement: Computations were performed on the Uran supercomputer at Institute of Mathematics and Mechanics of the Ural Branch of the Russian Academy of Sciences.
Funding Statement: The research was supported by the Ministry of Science and High Education of Russia (Theme No. 121031700169-1).
Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Tatyana Lyubimova; software: Yulia Garicheva, Andrey Ivantsov; data collection: Yulia Garicheva; analysis and interpretation of results: Tatyana Lyubimova; draft manuscript preparation: Yulia Garicheva, Tatyana Lyubimova, Andrey Ivantsov. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data presented in this study are available on request from the corresponding author.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Hirscha A, Trempa M, Kupka I, Schmidtner L, Kranert Ch, Reimann Ch, et al. Investigation of gas bubble growth in fused silica crucibles for silicon Czochralski crystal growth. J Cryst Growth. 2020;533:1254. doi:10.1016/j.jcrysgro.2019.125470. [Google Scholar] [CrossRef]
2. Klimm D, Wolff N. On thermodynamic aspects of oxide crystal growth. Appl Sci. 2022;12(6):2774. doi:10.3390/app12062774. [Google Scholar] [CrossRef]
3. Shi Q, Tao J, Zhang J, Su Y, Cai T. Crack- and bubble-induced fast crystal growth of amorphous griseofulvin. Cryst Growth Des. 2020;20(1):24–8. doi:10.1021/acs.cgd.9b01292. [Google Scholar] [CrossRef]
4. Ivanov IA, Dub VS, Karabutov AA, Cherepetskaya EB, Bychkov AS, Kudinov IA, et al. Effect of laser-induced ultrasound treatment on material structure in laser surface treatment for selective laser melting applications. Sci Rep. 2021;11(1):23501. doi:10.1038/s41598-021-02895-8. [Google Scholar] [PubMed] [CrossRef]
5. Nguyen AV. Particle-bubble interaction in flotation. Particle-bubble interaction in flotation. In: Bubble drop interfaces; 2011. p. 351–84. doi:10.1163/ej.9789004174955.i-558. [Google Scholar] [CrossRef]
6. Brabcova Z, Karapantsios T, Kostoglou M, Basarova P, Matis K. Bubble-particle collision interaction in flotation systems. Colloids Surf A: Physicochem Eng Aspects. 2014;473:95–103. doi:10.1016/j.colsurfa.2014.11.040. [Google Scholar] [CrossRef]
7. Cheng G, Shi C, Yan X, Zhang Z, Xu H, Lu Y. A study of bubble-particle interactions in a column flotation process. Physicochem Probl Miner Process. 2017;53(1):17–33. doi:10.5277/ppmp170102. [Google Scholar] [CrossRef]
8. Zhou Y, Albijanic B, Tadesse B, Wanga Y, Yang J. Investigation of bubble-particle attachment interaction during flotation. Miner Eng. 2019;133:91–4. doi:10.1016/j.mineng.2018.12.023. [Google Scholar] [CrossRef]
9. Lyubimov DV, Klimenko LS, Lyubimova TP, Filippov LO. The interaction of a rising bubble and a particle in oscillating fluid. J Fluid Mech. 2016;807:205–20. doi:10.1017/jfm.2016.608. [Google Scholar] [CrossRef]
10. Chen Y, Truong VNT, Bu X, Xie G. A review of effects and applications of ultrasound in mineral flotation. Ultrason Sonochem. 2020;60:104739. doi:10.1016/j.ultsonch.2019.104739. [Google Scholar] [PubMed] [CrossRef]
11. Chelomey VN. Paradoxes in mechanics caused by vibrations. Acta Astronaut. 1984;11(5):269–73. doi:10.1016/0094-5765(84)90010-9. [Google Scholar] [CrossRef]
12. Sorokin VS, Blekhman II, Vasilkov VB. Motion of a gas bubble in fluid under vibration. Nonlinear Dyn. 2012;67(1):147–58. doi:10.1007/s11071-011-9966-9. [Google Scholar] [CrossRef]
13. Kong G, Mirsandi H, Buist KA, Peters EAJF, Baltussen MW, Kuipers JAM. Oscillation dynamics of a bubble rising in viscous liquid. Exp Fluids. 2019;60(8):130. doi:10.1007/s00348-019-2779-1. [Google Scholar] [CrossRef]
14. Li Z, Zhou Y, Xu L. Sinking bubbles in a fluid under vertical vibration. Sinking bubbles in a fluid under vertical vibration. Phys Fluids. 2021;33(3):037130. doi:10.1063/5.0040493. [Google Scholar] [CrossRef]
15. Lyubimov DV, Lyubimova TP, Cherepanov AA. Dynamics of fluid interfaces in vibrational fields. Moscow: PhysMathLit; 2003. p. 216. [Google Scholar]
16. Fedyushkin A, Bourago N, Polezhaev V, Zharikov E. The influence of vibration on hydrodynamics and heat-mass transfer during crystal growth. J Cryst Growth. 2005;275(1–2):e1557–63. doi:10.1016/j.jcrysgro.2004.11.220. [Google Scholar] [CrossRef]
17. Zhang H, Du M, Hu H, Zhang H, Song N. Review of ultrasonic treatment in mineral flotation: mechanism and recent development. Molecules. 2024;29(9):1984. doi:10.3390/molecules29091984. [Google Scholar] [PubMed] [CrossRef]
18. Ivantsov A, Lyubimova T, Khilko G, Lyubimov D. The shape of a compressible drop on a vibrating solid plate. Mathematics. 2023;11(21):4527. doi:10.3390/math11214527. [Google Scholar] [CrossRef]
19. Lugovtsov BA, Sennitskiy VL. Motion of body in vibrating fluid. USSR Rept Eng Equipment Transl into English from Doklady Akademii Nauk SSSR. 1987;289(2):68. [Google Scholar]
20. Lyubimov D, Lyubimova T, Cherepanov A. On a motion of solid body in a vibrating fluid. Convective Flows. Collect Perm State Univ. 1987;61–70. [Google Scholar]
21. Lyubimov D, Cherepanov A, Lyubimova T. The motion of solid body in a liquid under the influence of a vibrational field. In: Reviewed Proceedings of the First International Symposium on Hydromechanics and Heat/Mass Transfer in Microgravity; 1992; Perm, Moscow, Russia. p. 247–51. [Google Scholar]
22. Kozlov VG. Solid-body dynamics in cavity with liquid under high-frequency rotational vibration. EPL. 1996;36(9):651–656. doi:10.1209/epl/i1996-00282-0. [Google Scholar] [CrossRef]
23. Kozlov NV, Vlasova OA. Behavior of a heavy cylinder in a horizontal cylindrical liquid-filled cavity at modulated rotation. Fluid Dyn Res. 2016;48(5):055503. doi:10.1088/0169-5983/48/5/055503. [Google Scholar] [CrossRef]
24. Vlasova OA, Kozlov VG, Kozlov NV. Lift force acting on a heavy solid in a rotating liquid-filled cavity with a time-varying rotation rate. J Appl Mech Tech Phys. 2018;59(2):219–28. doi:10.1134/S0021894418020050. [Google Scholar] [CrossRef]
25. Schipitsyn V, Kozlov V. Dynamics of a solid of nearly neutral buoyancy in cavity subjected to rotational vibrations. Phys Fluids. 2020;32(4):044102. doi:10.1063/1.5145095. [Google Scholar] [CrossRef]
26. Coimbra CFM, Rangel RH. Spherical particle motion in harmonic stokes flows. AIAA J. 2001;39(9):1673–82. doi:10.2514/2.1524. [Google Scholar] [CrossRef]
27. Lesperance D, Coimbra CFM, Trolinger JD, Rangel RH. Experimental verification of fractional history effects on the viscous dynamics of small spherical particles. Exp Fluids. 2005;38(1):112–6. doi:10.1007/s00348-004-0905-0. [Google Scholar] [CrossRef]
28. Lyubimov DV, Lyubimova TP, Cherepanov AA. Resonance oscillations of a drop (bubble) in a vibrating fluid. J Fluid Mech. 2021;909:A18. doi:10.1017/jfm.2020.949. [Google Scholar] [CrossRef]
29. Pyankova MA, Alabuzhev AA. Influence of the properties of the plate surface on the oscillations of the cramped drop. Phys Fluids. 2022;34(9):092015. doi:10.1063/5.0101011. [Google Scholar] [CrossRef]
30. Hassan S, Lyubimova TP, Lyubimov DV, Kawaji M. Effects of vibrations on particle motion near a wall: existence of attraction force. Int J Multiphase Flow. 2006;32(9):1037–54. doi:10.1016/j.ijmultiphaseflow.2006.05.008. [Google Scholar] [CrossRef]
31. Klotsa D, Swift MR, Bowley RM, King PJ. Interaction of spheres in oscillatory fluid flows. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76(5):056314. doi:10.1103/PhysRevE.76.056314. [Google Scholar] [PubMed] [CrossRef]
32. Lyubimova TP, Lyubimov DV, Shardin M. The interaction of rigid cylinders in a low reynolds number pulsational flow. Microgravity Sci Technol. 2011;23(3):305–9. doi:10.1007/s12217-010-9252-3. [Google Scholar] [CrossRef]
33. Overveld TJJM, Shajahan MT, Breugem WP, Clercx HJH, Duran-Matute M. Numerical study of a pair of spheres in an oscillating box filled with viscous fluid. Phys Rev Fluids. 2022;7(1):014308. doi:10.1103/PhysRevFluids.7.014308. [Google Scholar] [CrossRef]
34. El-Sapa S, Albalawi W. Interaction of two rigid spheres oscillating in an infinite liquid under the control of a magnetic field. J Applied Math. 2023;1:1146872–13. doi:10.1155/2023/1146872. [Google Scholar] [CrossRef]
35. Lyubimova TP, Cherepanova A. Vibrational dynamics of bubbles suspended in a viscous liquid. In: Proceedings of the Third International Symposium on Physical Sciences in Space; 2007 Oct 22–26; Nara, Japan: Nihon Maikurogurabiti Oyo Gakkai. p. 234–5. [Google Scholar]
36. Saadatmand M, Kawaji M. Effect of viscosity on vibration-induced motion of a spherical particle suspended in a fluid cell. Microgravity Sci Technol. 2010;22(3):433–40. doi:10.1007/s12217-010-9189-6. [Google Scholar] [CrossRef]
37. Saadatmand M, Kawaji M, Hu HH. Vibration-induced attraction of a particle towards a wall in microgravity—the mechanism of attraction force. Microgravity Sci Technol. 2012;24(1):53–64. doi:10.1007/s12217-011-9291-4. [Google Scholar] [CrossRef]
38. Liang R, Liang D, Yan F. Bubble motion near a wall under microgravity: existence of attractive and repulsive forces. Microgravity Sci Technol. 2011;23(1):79–88. doi:10.1007/s12217-010-9238-1. [Google Scholar] [CrossRef]
39. Matsson JE. An introduction to ANSYS FLUENT 2023. USA: SDC Publications; 2023. [Google Scholar]
40. Sharma P, Chandra L, Ghoshdastidar PS, Shekhar R. A novel approach for modelling fluid flow and heat transfer in an open volumetric air receiver using ANSYS-FLUENT. Sol Energy. 2020;204:246–55. doi:10.1016/j.solener.2020.04.031. [Google Scholar] [CrossRef]
41. Boudreaux JM. Exploration of segmented flow in microchannels using the volume of fluid method in ANSYS fluent. Louisiana State University and Agricultural and Mechanical College: USA; 2015. [Google Scholar]
42. Osher S, Sethian JA. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations. J Comput Phys. 1988;79(1):12–49. doi:10.1016/0021-9991(88)90002-2. [Google Scholar] [CrossRef]
43. Frank T, Jain S, Matyushenko AA, Garbaruk AV. The OECD/NEA MATIS-H benchmark—CFD analysis of water flow through a 5x5 rod bundle with spacer grids using ANSYS FLUENT and ANSYS CFX. In: Conference on Experimental Validation and Application of CFD and CMFD Codes in Nuclear Reactor Technology; 2012 Sep 10–12; Daejeon, Republic of Korea. [Google Scholar]
44. Brackbill JU, Kothe DB, Zemach C. A continuum method for modeling surface tension. J Comput Phys. 1992;100(2):335–54. doi:10.1016/0021-9991(92)90240-Y. [Google Scholar] [CrossRef]
45. Beysens D. The effect of vibrations on inhomogeneous matter: some studies in weightlessness. Mechanical Reports. 2004;332(5-6):457–65. doi:10.1016/j.crme.2004.02.016. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools