 Open Access
Open Access
ARTICLE
Experimental Study of Thermal Convection and Heat Transfer in Rotating Horizontal Annulus
Laboratory of Vibrational Hydromechanics, Perm State Humanitarian Pedagogical University, Perm, 614990, Russia
* Corresponding Author: Alexei Vjatkin. Email:
(This article belongs to the Special Issue: Advanced Problems in Fluid Mechanics)
Fluid Dynamics & Materials Processing 2024, 20(11), 2475-2488. https://doi.org/10.32604/fdmp.2024.052377
Received 31 March 2024; Accepted 24 June 2024; Issue published 28 October 2024
Abstract
A genuine technological issue–the thermal convection of liquid in a rotating cavity–is investigated experimentally. The experiments are conducted within a horizontal annulus with isothermal boundaries. The inner boundary of the annulus has a higher temperature, thus exerting a stabilising influence on the system. It is shown that when the layer rotation velocity diminishes, two-dimensional azimuthally periodic convective rolls, rotating together with the cavity, emerge in a threshold manner. The development of convection is accompanied by a significant intensification of heat transfer through the layer. It is shown that the averaged thermal convection excitation in the form of a system of two-dimensional rolls occurs against the background of oscillations of a non-isothermal fluid in the cavity reference frame caused by the gravity field. The excitation threshold and the structure of convective rolls are consistent with the results of the earlier theoretical studies by the authors performed using the equations of “vibrational” convection obtained by the averaging method. Furthermore, the experiments have revealed a new type of averaged flow in the form of a spatially periodic system of toroidal vortices. It is shown that a steady streaming, excited by the inertial oscillations of the fluid, is responsible for the generation of the toroidal vortices. These flows develop in a non-threshold manner and are most clearly manifested in a case of resonant excitation of one of the inertial modes.Graphic Abstract
Keywords
Nomenclature
| a | Amplitude of the oscillating force field modulation, m s−2 |
| b | The amplitude of vibrations, m |
| C | Mass concentration of the aqueous solution of glycerol, % |
| D | Outer diameter of the layer, m |
| d | Inner diameter of the layer, m |
| g | Gravity acceleration, m s−2 |
| h | Thickness of the layer, m |
| L | Length of the layer, m |
| m | Wave number |
| Nu | Nusselt number |
| Pr | Prandtl number |
| Q | Heat release capacity, W |
| ˉR | Average radius of the cylindrical layer, m |
| Ra | Centrifugal Rayleigh number |
| Rag | Gravitational Rayleigh number |
| Rv | Vibrational parameter |
| T1 | Temperature of the inner boundary of the layer, °C |
| T2 | Temperature of the outer boundary of the layer, °C |
| T3 | Temperature in the water jacket, °C |
| Ta | Taylor number |
| β | Thermal expansion coefficient, К−1 |
| χ | Thermal diffusivity, m2 sc1 |
| φ | Angular distance between temperature sensors, deg |
| ν | Kinematical viscosity, m2 s−1 |
| Θ0 | Temperature difference at the layer boundaries in the absence of convection, °C |
| Θ | Temperature difference at the layer boundaries, °C |
| ρ | Relative thickness |
| τ | Period of temperature oscillations |
| Ωrot | Angular velocity of rotation, rad s−1 |
| Ω | The radian frequency of vibrations, rad s−1 |
| Ωd | The angular velocity of the drift, rad s−1 |
| ωr | Dimensionless rotation velocity |
Thermal convection in rotating systems is a fundamental problem of current interest and importance for various technological processes [1–4]. One of the examples is thermal convection in rotating stars and planets [5–7]. Fluid oscillations can have a strong effect on convection. In the case of stars and planets, oscillations of liquid cores and atmospheres can be caused by various reasons. These could be tidal oscillations caused by the gravitational interaction with satellites or inertial oscillations associated with the action of the Coriolis force [8,9]; oscillations can also be excited by vibrations of solids (cores) inside the rotating liquid [10] and uneven rotation of the shell [11,12]. It is known that high-frequency oscillations of a non-isothermal fluid generate an averaged mass force that can both suppress thermal convection and cause it. This independent mechanism of averaged thermal convection is usually called a “thermovibrational” one [13].
In a uniform oscillating force field acosΩtn , for example, the inertial one, caused by high-frequency translational vibrations of the cavity with an amplitude b and radian frequency Ω , the averaged effect on a non-isothermal fluid is determined by the vibrational parameter [13].
Rv≡(aβΘh/Ω)2/2νχ. (1)
Here a≡bΩ2 is the amplitude of the oscillating force field modulation.
Different aspects of “Vibrational thermal convection” is being intensively researched nowadays [14–18] both experimentally and theoretically. In technological terms, vibrations are an effective way of controlling various fluid processes. A horizontal fluid layer with a vertical temperature gradient under the action of longitudinal vibrations of finite frequency is considered in [14]. The simulation results showed that the effect of vibration on the stability threshold is complex: vibration can both stabilise and destabilise the ground state depending on the values of the parameters. The effect of vibration on silicon melt in the crucible to further control the crystallisation process is theoretically and numerically studied in [15]. In [16], a model of vibrational convection in a heterogeneous mixture of two liquids separated by diffusion boundaries is obtained. Another direction of research is related to the manifestation of thermovibrational convection in microgravity conditions. Thus, in the case when vibration and temperature gradient are parallel, a series of new convection modes are found for the cubic cavity geometry [17]. The researches are not limited to single-phase systems. In [18], the regularities of clustering of non-isodense particles of finite mass and finite size induced by turbulent thermovibrational flow are presented. A large number of studies devoted to the manifestation of thermovibrational convection in various technological applications (multiphase media, porous media, liquid mixtures, microgravity) indicate the relevance of this scientific direction.
Averaged thermal convection in cavities rotating around a horizontal axis represents a special class of problems in which the “thermovibrational mechanism” is manifested. In this case, there is no vibration effect on the cavity, and the role of the periodic forcing is played by gravity oscillating in the cavity reference frame with a frequency equal to Ωrot , the cavity rotation velocity. A theoretical description of the averaged (vibrational) thermal convection in rotating systems is given in [19]. The averaged action of the non-isothermal fluid oscillations is described by a term analogous to that of classical thermal vibration convection with translational vibrations of the cavity [13]. The qualitative difference is associated with the action of the Coriolis force, which affects the oscillations of non-isothermal fluid and the structure of convective flows. Experimental confirmation for the excitation of steady convective currents of a “vibrational” nature in rotating cavities of various configurations was obtained in the works [20,21]. The studies [21] were carried out in thin cylindrical layers rotating around a horizontal axis. Using the equations of vibrational convection obtained by the averaging method [22,23], a two-dimensional averaged convection in cylindrical layers was simulated numerically. In such a two-dimensional formulation, in the limiting case of high rotation frequencies, the averaged effect is determined by the vibration parameter.
Rv≡(gβΘh/Ωrot)2/2νχ. (2)
It is clear that in (2) the gravity acceleration g plays the role of the inertial acceleration a in (1). The theoretical analysis shows that in addition to the Prandtl number, the stability of a liquid layer rotating around a horizontal axis with boundaries of different temperatures is determined by two parameters, vibrational parameter (2) and centrifugal Rayleigh number Ra≡Ω2rotˉRβΘh3/νχ . Here, the centrifugal acceleration acts as a static force field Ω2rotˉR (gravity as a source of buoyancy is replaced by centrifugal force), where ˉR is the average radius of the cylindrical layer, and h is the layer thickness. Note that these two mechanisms, centrifugal convection and averaged convection, appear independently. As a result, thermal convection can develop in both cases Ra>0 and Ra<0 when the inner boundary of the rotating layer has a higher temperature. The results of the experimental studies performed in thin layers are in good agreement with the theoretical ones [23]. From an applied and fundamental perspective, the experimental study of the averaged thermal convection features depending on the relative thickness of the rotating cylindrical layer represents a significant problem.
The purpose of this work is to experimentally study the features of averaged thermal convection in a uniformly rotating horizontal cylinder of an average thickness h/ˉR= 0.55. Previously, experiments have been carried out for the cases of h/ˉR= 0.21 [23] and 0.92 [22]. The experiments indicated the important role of the Coriolis force, which manifests itself in the excitation of the fluid inertial oscillations and generation of the average three-dimensional convective flows. The results of this research are pertinent to the consideration of the influence of external force fields on convection in rotating systems in technological processes occurring in both gravitational and microgravity conditions [24,25].
2 Experimental Setup and Techniques
The paper examines thermal convection in a rotating cylindrical layer with boundaries of different temperatures. The working cavity is a system of coaxially arranged cylinders (Fig. 1a): 1–internal aluminum cylinder, 2 and 3–transparent plexiglass pipes of different diameters. The cylinders 1–3 are sealed in flanges that define a coaxial arrangement and solid rotation around the horizontal axis. The working layer is enclosed between an aluminum heat exchanger 1 and the pipe 2. Parameters of the formed gap are the inner diameter d=42.0 mm, the outer one D=74.0 mm, average radius of the cylindrical layer ˉR=(d+D)/4=29 mm, length L=182 mm. High value of the aspect ratio L/h=11.4 eliminates the influence of the end effects. The relative thickness is ρ=d/D=0.57 . Previously, the results of the experiments with the layers ρ=0.8 [23] and 0.3 [22] were presented. The change in the relative layer thickness is achieved by reducing the diameter of the inner cylinder.
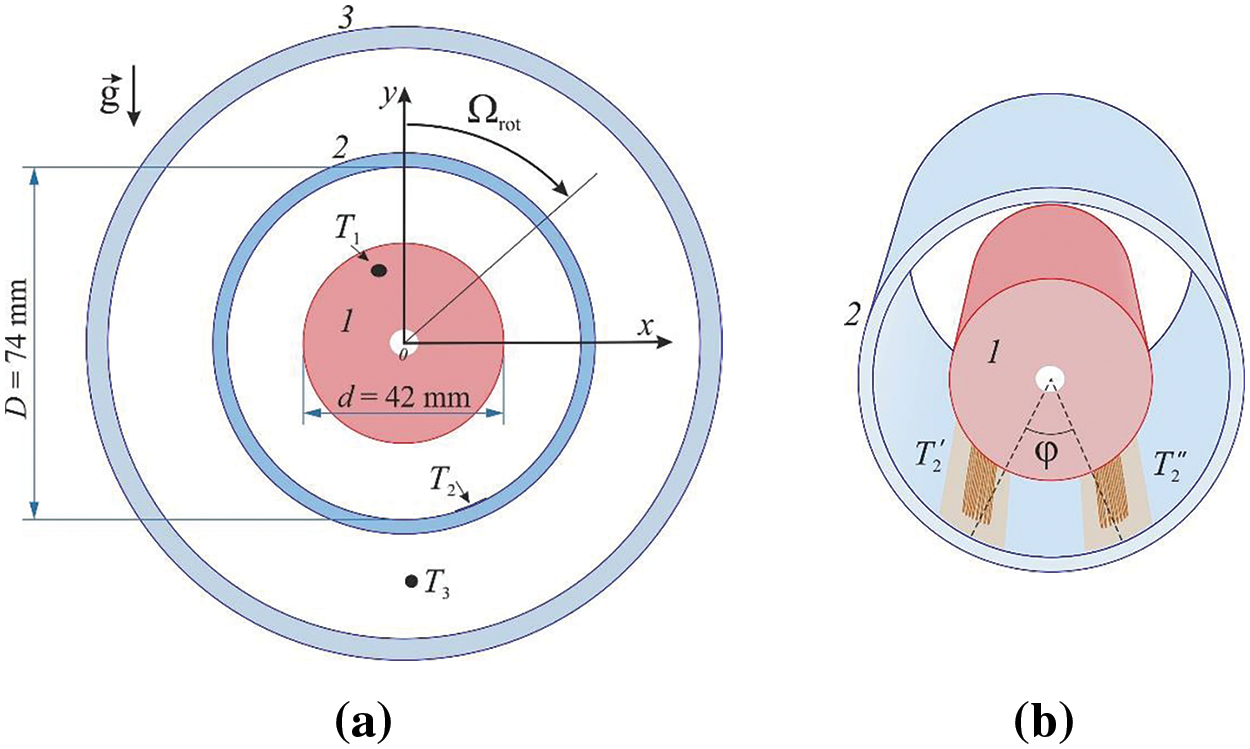
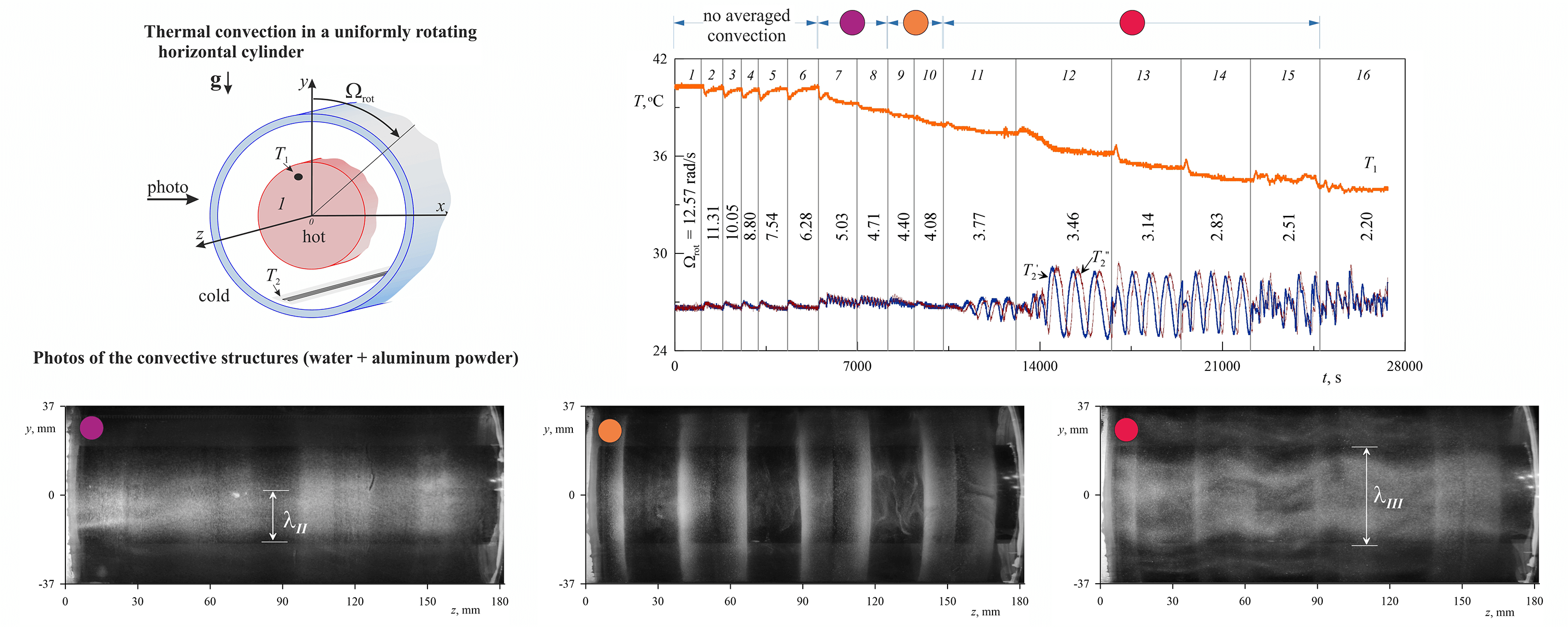
Figure 1: Working cavity scheme (a) and temperature sensors location scheme (b)
The inner boundary of the layer is heated by an electric wire heater installed in the centre of the aluminium heat exchanger along its entire length. A coolant of a constant temperature of 20°C is pumped between pipes 2 and 3 (referred to as the “jacket”) to ensure the cooling of the layer through the outer cylindrical boundary. A powerful jet thermostat LIOP LT-400 is used to circulate the coolant. The large volume of pumped liquid allows to ensure the constancy of its temperature regardless of the realised mode of convection in the layer. The temperature sensors are copper resistance thermometers. The temperatures T1 of the internal heat exchanger and the coolant T2 are measured by sensors with sensitive elements made of copper wire wound around a dielectric core and placed in a protective sealed casing. The sensor diameter is 4 mm and the length is 40 mm. The sensor that measures temperature T1 , is glued into an aluminum heat exchanger. The coolant temperature is controlled at the outlet of the “jacket”. In order to achieve this, the sensor is positioned within the installation housing in such a way that the liquid is able to wash over the sensitive part.
The sensors that measure the temperature T2 of the outer layer boundary have a specific configuration: copper wire with a thickness of 0.02 mm is located along the layer generatrix in the form of several loops and is fixed to the wall using self-adhesive film. Along the azimuth of the layer, the width of the sensor is 5 mm. Temperature T2 measurements are integral over the cavity length. The configuration of the resistance thermometers is determined by the structure of convective flows, which mainly have the form of two-dimensional rolls extended along the rotation axis. As shown in the work [23] convection in cylindrical layers rotating around the horizontal axis is accompanied by an azimuthal drift of the whole system of convective flows. The direction of the drift is opposite to the direction of the cavity rotation. The drift of the convective structures allows to identify the peculiarities of the convective modes, for this purpose two temperature sensors are located with a given angular shift φ=0.68 rad relative to each other (Fig. 1b). Analysis of the time dependences of the temperature T2′ and T2″ of sensors spaced in azimuth at a known angle makes it possible to determine both the azimuthal drift velocity and the wavelength of convective structures.
The experimental procedure is as follows. At the beginning of the experiment, the power on the electric heater is set. Using a jet thermostat LIOP LT-400, cooling water at a temperature of 20°C is supplied into the “jacket”. The working cavity is rotated at a relatively high angular velocity Ωrot . As a result of the stabilizing effect of the centrifugal force of inertia, an equilibrium temperature distribution is established in the liquid layer with a maximum at the inner boundary. The time to reach an equilibrium state ranges from 1 to 3 h. Next, the angular velocity of rotation is reduced step by step (Fig. 2). At each step, the time to reach the stationary flow mode is waited. Throughout the experiment, the power of the electric heater Q and the temperature T3 of the coolant remain constant. Distilled water is used as the working fluid.
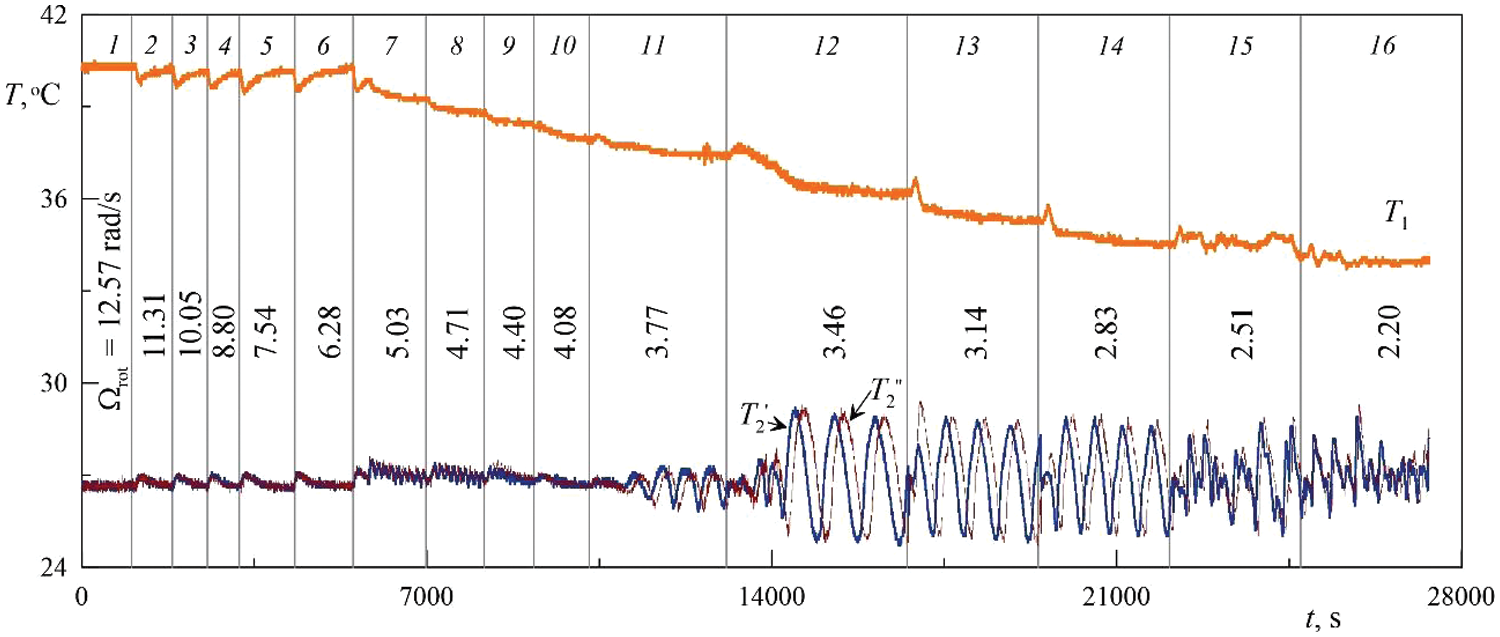
Figure 2: Typical view of the temperature recording during stepwise reduction angular velocity of rotation Ωrot . The heater power is Q=23.3 W
After the experiment, the average temperature values T1 , T2 and T3 are calculated at each step of the experiment. The calculations take into account only stationary modes, transient processes are not considered. When the temperature fluctuations occur (Fig. 2, steps 11–16) the time-averaged temperature value for the full period of oscillations is calculated. Average temperature values according to the results of the experiment Fig. 2 are shown in Fig. 3. The state of quasi-equilibrium corresponds to area I (Fig. 3). The appearance of the convective flows is registered by the decrease in temperature T1 in area II. Dashed line on the border of areas I and II corresponds to the critical value of the angular velocity of rotation Ω∗rot 1 , at which the threshold excitation of convection is observed. The convective mode in area III (Fig. 2, steps 12–14) is characterized by regular temperature fluctuations. The change of the convective modes is again accompanied by a characteristic change of dependence T1(Ωrot) , which makes it possible to determine the critical value of angular velocity of rotation Ω∗rot 2 (dashed line on the border of areas II and III). Along with the average temperature in areas II and III, the crosses in Fig. 3 show the amplitude values of temperature T2 during regular oscillations.
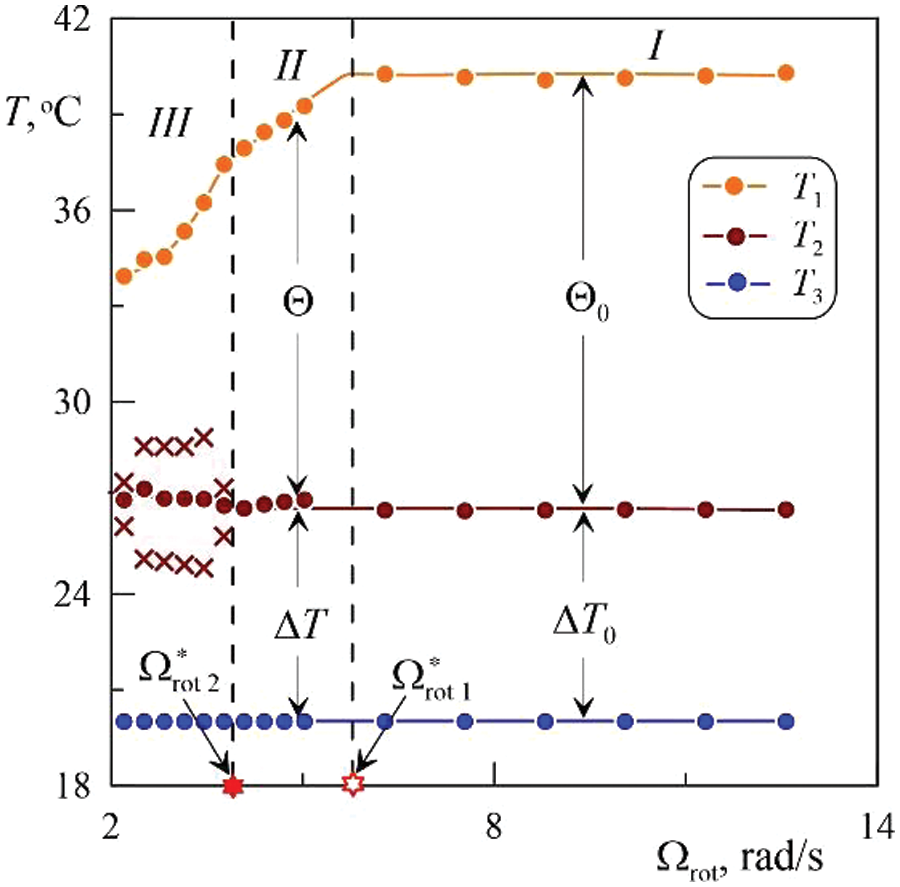
Figure 3: Temperatures T1 , T2 and T3 vs. angular velocity of rotation Ωrot . The experimental conditions correspond to Fig. 2
As already noted, the power Q of the electric heater mounted on the axis of the internal heat exchanger does not vary within one experiment (for example, in Figs. 2 and 3). Constant value of Q defines the equilibrium temperature distribution characterised by the temperature difference Θ0 . The following experiments are carried out at other constant values of Q . Variation of the power Q of the electric heater in the range Q=5−37 W provides the series of equilibrium temperature differences within Θ0=7−28 °C.
Temperature measurements. The experiments have shown that the sequence of changes in the convective modes with a decreased cavity angular velocity of rotation depends on the power of heat release in the inner cylinder, which is characterized by the temperature difference between the layer boundaries Θ0 . The sequence shown in Figs. 2 and 3 corresponds to the relatively large temperature differences Θ0 > 11 °С (Fig. 4a, curves 2 and 3). The equilibrium state (area I) is disrupted in a threshold manner with the appearance of convective flows (Fig. 4a, dashed line, points 4). When the angular velocity of rotation is less than critical, the temperature drop at the layer boundaries Θ turns out to be less than Θ0 (recall that the heat flux in each experiment is maintained constant). Note that in this case, the crisis of quasi-equilibrium stability (dashed line, points 4) is not accompanied by low-frequency fluctuations of temperature T2 near the outer boundary of the layer (Fig. 2, steps 7–10). The next threshold decrease in temperature drop Θ occurs on the border of areas II and III (Fig. 4, dashed line, points 5) and is accompanied by the development of regular temperature fluctuations near the outer boundary (Fig. 2, steps 11–14).
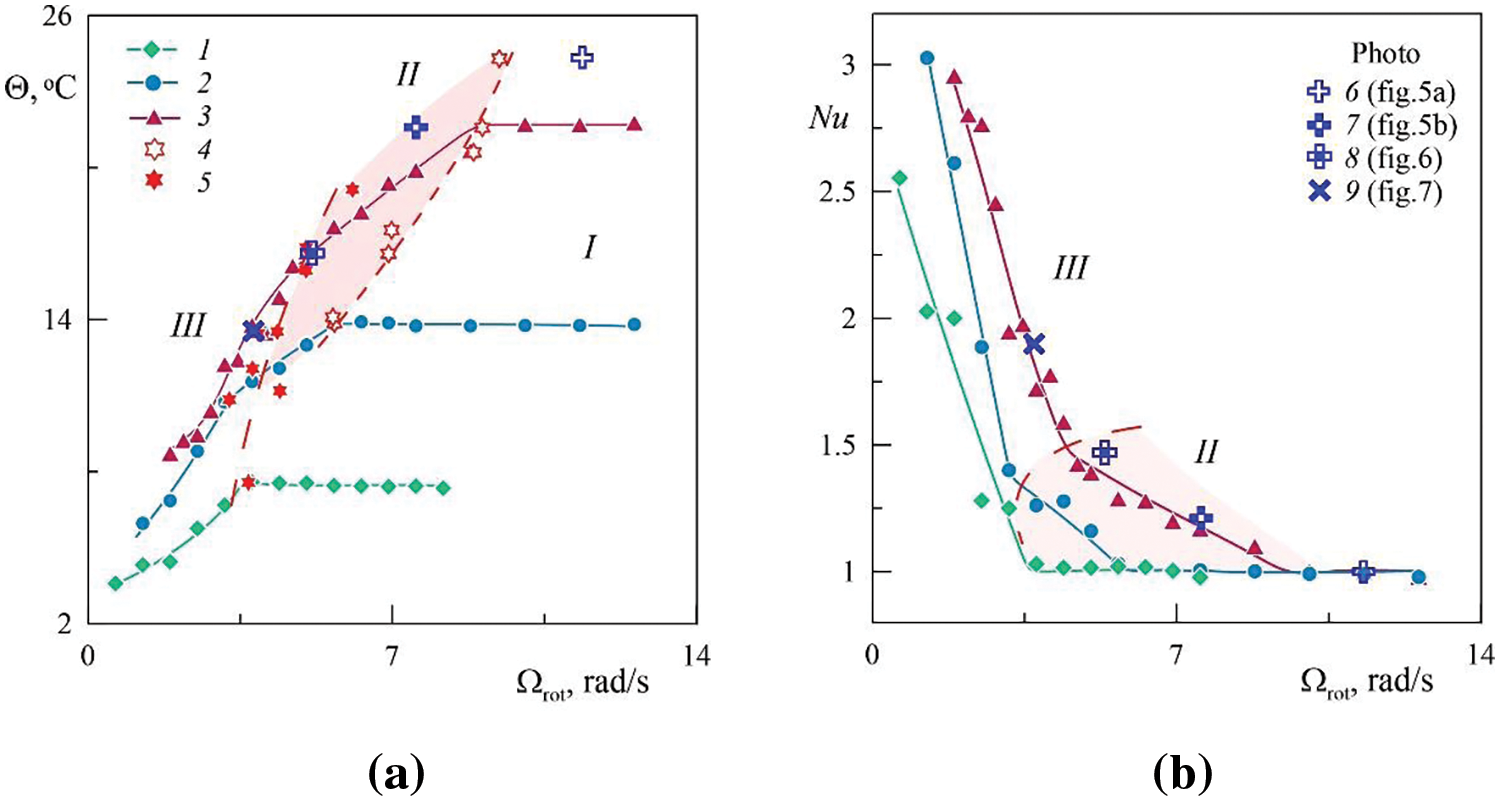
Figure 4: Dependence of the temperature difference Θ (a) and the Nusselt number Nu (b) angular velocity of rotation Ωrot ; Θ0=7.3 (1), 13.8 (2) and 21.7°С (3)
For small temperature changes (Fig. 4a, curve 1) disruption of the equilibrium of a non-isothermal fluid in a centrifugal field with a decrease of the angular velocity of rotation occurs according to a different scenario. It is observed on the border of areas I and III (Fig. 4, dashed line, points 5) and is accompanied by the appearance of regular temperature fluctuations recorded by a sensor at the outer boundary of the layer. As will be shown below, the dashed line (points 5) corresponds to the threshold of vibrational thermal convection excitation, accompanied by the appearance of large-scale 2D vortices, the slow azimuthal drift of which leads to the temperature fluctuations at the outer boundary of the layer.
At large temperature differences Θ0 , the threshold development of thermal vibrational convection, accompanied by an increase in heat transfer and amplitude of low-frequency temperature fluctuations at the outer boundary (area III in Fig. 3), is preceded by a threshold increase in heat transfer in the absence of the described temperature fluctuations in the layer (area II in Figs. 3 and 4).
With an increase in the equilibrium temperature difference between the layer boundaries Θ0 , the critical values of the angular velocity of rotation corresponding to the threshold curves 4 and 5 monotonically increase. A range of the angular velocity of rotation corresponding to the convective mode II increases (Fig. 4a).
Let us dwell on heat transfer through the layer during rotation. To do this, introduce the Nusselt number, which characterizes the ratio of heat transport through the layer to conductive heat transport at the same power of heat release, Nu≡Q/Qmol . The Nusselt number takes the form Nu≡(ΔT/Θ)/(ΔT0/Θ0) . This follows from the fact that the molecular heat flux is proportional to the temperature difference Qmol=KΘ , and the total heat flux could be characterized by the equilibrium temperature difference, Q=KΘ0(ΔT/ΔT0) . Here K is heat flux sensor coefficient.
At rapid rotation Nu=1 , which corresponds to the conductive regime. With a decrease in the cavity rotation velocity, heat transport increases in a threshold manner, which is caused by the appearance of convective flows in the layer (Fig. 4b).
The heat transfer curves have a characteristic form for each convective mode: with a decrease in the rotation velocity, heat transport in the area II increases less intensively than that in the area III. The break in the heat transport curves corresponds to the threshold of the convective regimes change (border of areas II and III).
Photo registration. Photo recording is carried out using aluminum powder added to a liquid using a small amount of surfactant. The powder, which has a density higher than the density of the liquid, is distributed under the centrifugal force of inertia on the inner wall of the cavity (the outer boundary of the working layer). The surfactant is necessary to ensure the mobility of the powder and prevent it from sticking to the cavity boundaries. The photo in Fig. 5a shows the distribution of powder on the outer boundary of the working layer. In the central part of the frame, one can see an aluminum heat exchanger covered with black film for better visualization. For the observer (the camera is immovable in the laboratory reference frame), the lower boundary of the layer rises.

Figure 5: Photos of the convective structures (a, b) and the flow pattern (c). The experimental conditions correspond to the points 6 and 7 in Fig. 4: (a) Ωrot=11.31 rad/s, Θ0=24.4 °С; (b, c) Ωrot=7.54 rad/s, Θ=21.6 °C
At rapid rotation, heavy particles of the visualizer are distributed on the outer wall of the layer, while remaining mobile. The powder is concentrated in the form of rings (light stripes in Fig. 5a), periodically located along the cavity axis. In the center of each ring, there is a dark stripe where there is practically no aluminum powder, and the contours of the rings are blurred. The rings of aluminum powder indicate the existence of a system of weak toroidal vortices periodically located along the layer. It should be noted that the existence of toroidal vortices, arising in a non-threshold way, in this range of experimental parameters has virtually no effect on heat transfer–photo in Fig. 5a corresponds to the thermal conductivity regime (area I in Fig. 4a).
The first heat transport crisis (the border of areas I and II in Fig. 4a) is accompanied by the appearance of the longitudinal convective rolls located along the axis of rotation (Fig. 5b). Adjacent rolls rotate in concert in opposite directions. These longitudinal convective structures are poorly expressed in the photo due to the fact that the visualizer is heavy aluminum powder, most of which is concentrated on the wall, while the rolls are localized in the bulk of the layer. The longitudinal rolls wavelength λII commensurates with the layer thickness; 10 pairs of the longitudinal rolls are laid on the perimeter of the layer (the flow pattern in the perpendicular cross section is presented in Fig. 5c). In a certain range of rotation velocities, two-dimensional and three-dimensional toroidal rolls coexist (area II in Fig. 4a). The appearance of the longitudinal convective rolls does not affect the location of the rings.
With further decrease in the angular velocity of rotation near the transition of modes II and III the position of the rings changes (Fig. 6a), and the edges of the rings become more pronounced. Two-dimensional convective rolls do not manifest themselves, while three-dimensional toroidal structures provide a relatively large heat transport. According to the observations, we can conclude that the intensity of toroidal vortexes grows with a decrease in rotation rate, which results in the blurring of relatively weak longitudinal rolls, near the threshold curve III. The scheme of the toroidal vortices in the axial cross-section of the upper part of the layer is shown in Fig. 6b. The absence of temperature fluctuations recorded by a longitudinal integral sensor at the outer boundary of the layer proves that the toroidal vortices do not have azimuthal periodicity.

Figure 6: Photographs of the aluminum powder distribution on the cavity wall (a) and the schema of the steady flows in the layer (b). The experimental conditions correspond to the mark 8 in Fig. 4: Ωrot=5.02 rad/s, Θ=16.6 °C
With a further decrease in the angular velocity of rotation there again observed a threshold manner appearance of the longitudinal rolls in the layer (Fig. 7). The wavelength λIII significantly exceeds the wavelength λII of two-dimensional structures in mode II. The appearance of the rolls is accompanied by temperature fluctuations recorded by the longitudinal integral sensor at the outer boundary of the layer. As it had been shown in the work [23] the regular temperature fluctuations are caused by the slow azimuthal retrograde drift of the entire liquid layer in the direction opposite to the cavity rotation. Relative to the observer, the lower boundary in the photo rises, while the structures drift from top to bottom. The intensity of these convective structures is high enough; the flows pick up particles of aluminum powder, carrying them into the middle of the layer. The longitudinal rolls are characterized by the presence of a bend associated with toroidal vortex structures responsible for the formation of the periodic structure in Figs. 5 and 6. In the dark areas between the light rings, the shape of the rolls allows us to conclude that in this area, there is a retrograde movement caused by the radial flow of fluid from the inner cylinder to the outer boundary in a system of toroidal vortices. The scheme of the toroidal vortices in Fig. 6b is built, taking this observation into account.
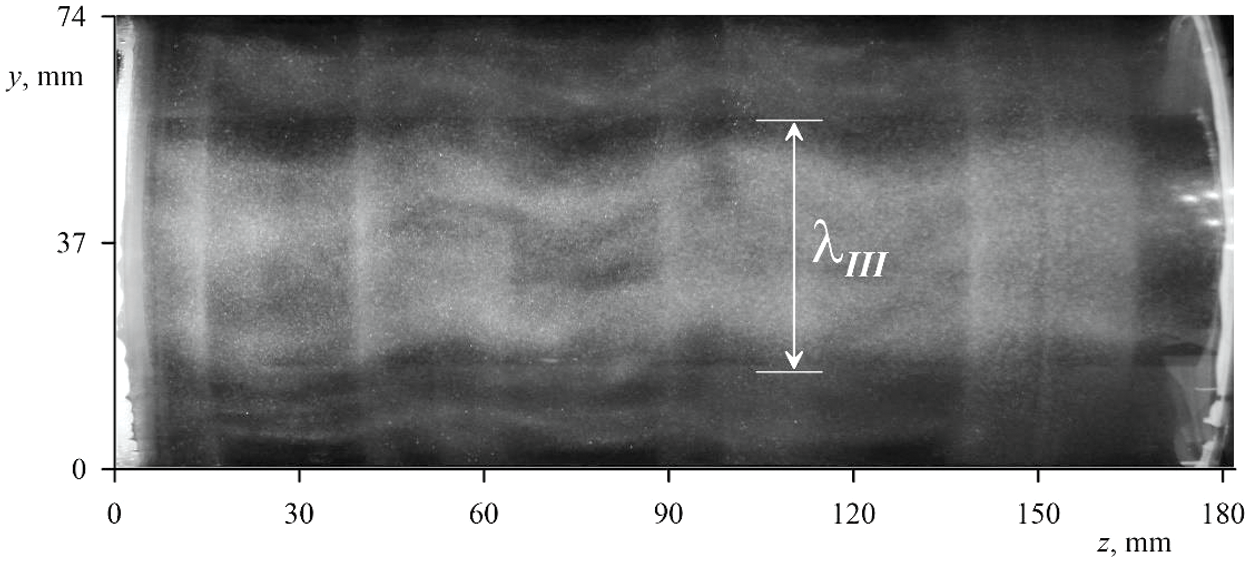
Figure 7: Photos of the convective structures. The experimental conditions correspond to the mark 9 in Fig. 4: Ωrot=3.77 rad/s, Θ=13.5 °C
Drift of the convective structures. Earlier, in it was found that the longitudinal rolls in this range of experimental parameters are excited due to the dominant action of the thermovibrational mechanism. In experiments with thin layers, the drift of large-scale two-dimensional convective rolls was discovered and described in [23]. To study the phenomenon of the supercritical dynamics of convective flows in the form of two-dimensional rolls, a technique was proposed using several longitudinal integral temperature sensors located at a given distance from each other. The drift of the liquid layer is recorded by the sensors in the form of temperature fluctuations shifted in time (Fig. 8). The information about the time shift and the oscillation period allows one to calculate the drift velocity and the convective structures wavelength.
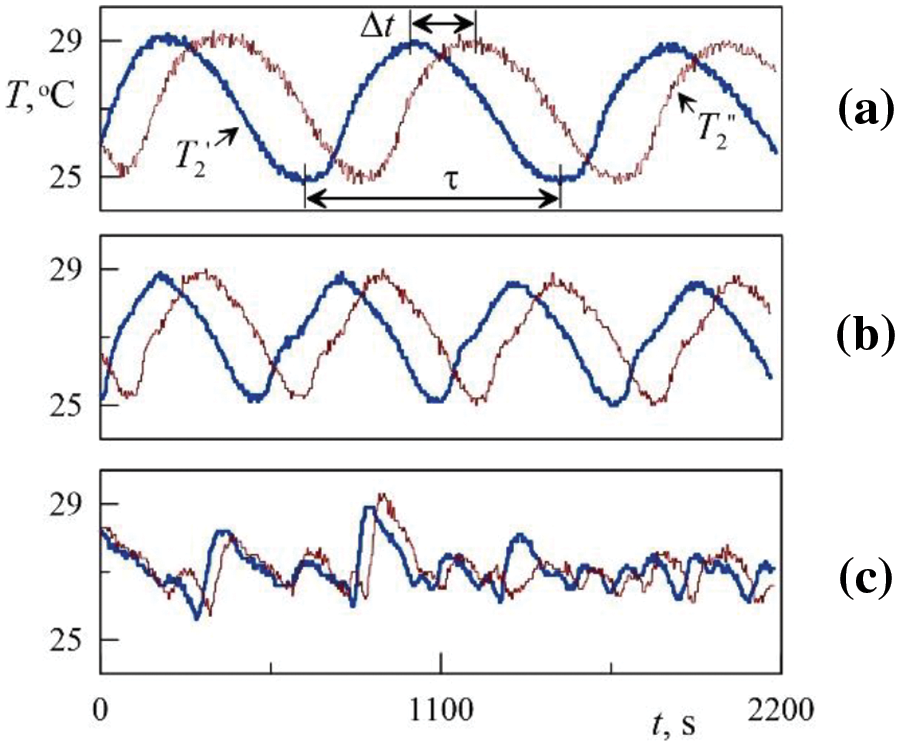
Figure 8: Temperature fluctuations recorded by two temperature sensors spaced apart in azimuth at the outer boundary of the layer (corresponding to steps 11 (a), 13 (b) and 15 (c) in Fig. 2)
Let us calculate the drift velocity and wavelength from the temperature fluctuations recording in Fig. 8a. Temperature fluctuation shift Δt allows one to calculate the angular velocity of the drift using the formula Ωd=φ/Δt , where φ is the angular distance between the longitudinal integral sensors, the layout of which is shown in Fig. 1b. For the case shown in Fig. 8a the angular velocity of the drift is 0.003 rad/s. The value of the oscillation period τ equals the time of a pair of rolls passage in the vicinity of the sensor. The wave number is calculated using the formula m=Ωdτ/2π . For the experimental conditions in Fig. 8a,b the wave number is 3, which agrees satisfactorily with the results of a numerical study [22,23] and a direct observation from the photo in Fig. 7. It should be noted that the results of the wavelengths and wave numbers measuring based on the temperature fluctuations are greatly influenced by the irregular rearrangement of the longitudinal rolls and their deviation from the horizontal position. For example, Fig. 8c shows the temperature fluctuations with the regularity violation associated with a high intensity of convective heat transport and, as a consequence, active restructuring of the convective flows.
Thermal convection in a thin cylindrical layer located horizontally and uniformly rotating around a horizontal axis was experimentally studied in [22,23]. It was shown that in the case of the layer heated from the internal boundary, the convection has a thermal vibrational nature and manifests itself in the threshold development of the rolls elongated along the axis of rotation. The control parameters are the centrifugal Rayleigh number Ra=Ω2rotˉRβΘh3/νχ and the vibrational parameter Rv=(gβΘh)2/2νχΩ2rot . The experimental technique involves a stepwise decrease in the cavity rotation velocity, which leads to a simultaneous decrease of Ra and increase of Rv . In Fig. 9a,b, points 1–3 show the experimental steps corresponding to the results in Fig. 4, while points 6–9–the values of the dimensionless parameters corresponding to the experimental conditions under which the photographs in Figs. 5–7 were obtained. At rapid rotation the quasi-equilibrium state is observed in the layer, there is no thermal convection (region I in Fig. 9). The stability of the equilibrium is disrupted by the toroidal structures localized near the outer boundary of the layer (Fig. 5a), which have virtually no effect on heat transfer Nu=1 (Fig. 9b).
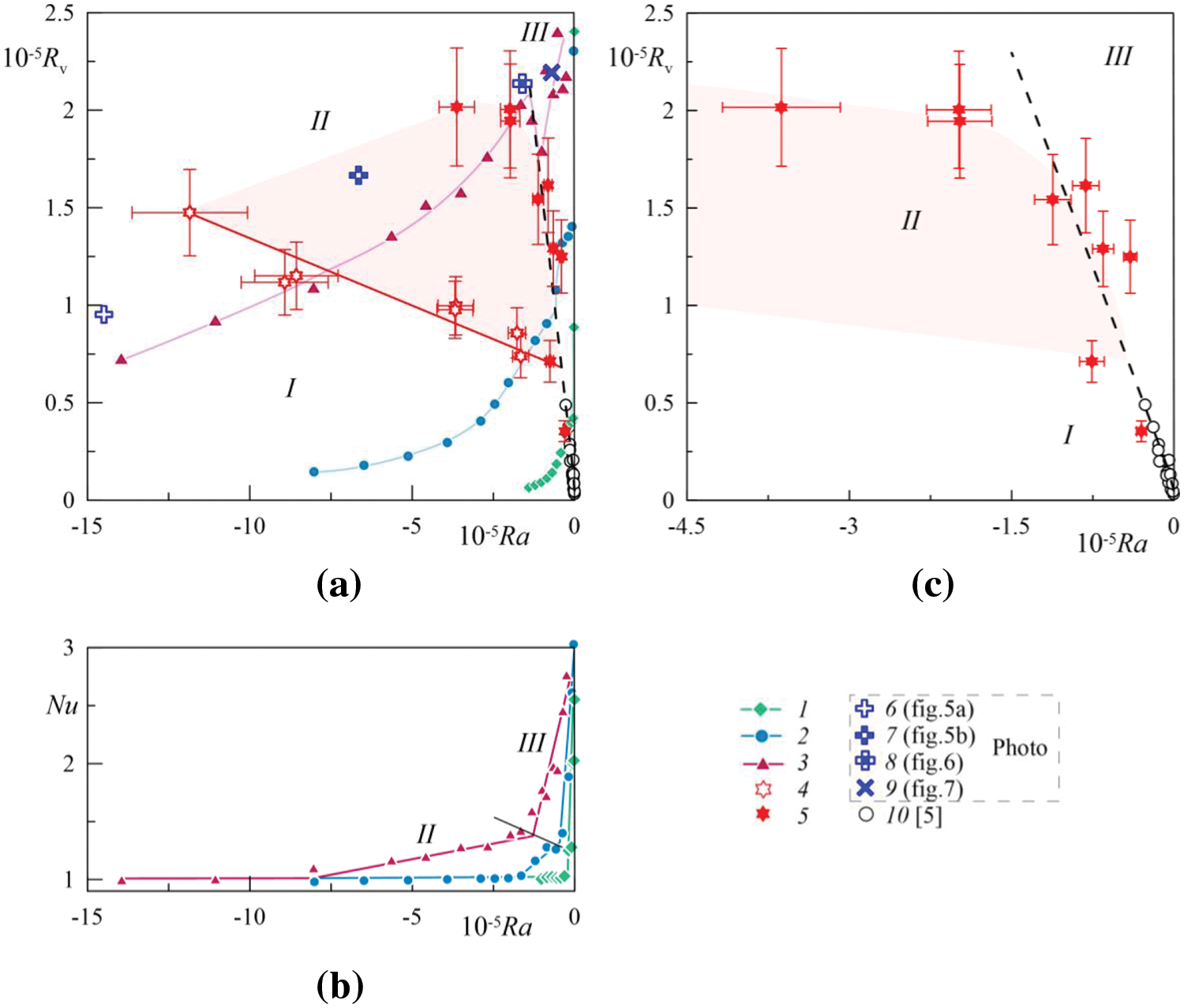
Figure 9: Experimental results on the plane of control parameters: vibration parameter Rv (a, с) and the Nusselt number Nu (b) vs. centrifugal Rayleigh number Ra
With decreasing the centrifugal Rayleigh number Ra (with a decrease in the cavity rotation velocity), heat transport in the layer experiences the crises associated with the threshold appearance of the convective flows (Fig. 9b). At large temperature differences, the first critical increase in heat transport is associated with the appearance of the longitudinal rolls against the background of weak toroidal vortices (Fig. 5b). Points 4 in Fig. 9 marks the appearance threshold of the two-dimensional structures existing in area II. With further decrease of Ra the Nusselt number increases, which indicates an increase in the intensity of the convective flows, especially the toroidal vortices. As it follows from the observations, the longitudinal rolls are not recorded near the area III boundary. It can be assumed that this is explained by an increase in the intensity of the toroidal vortices (Fig. 6), which play a decisive role in heat transport. The physical mechanism for the generation of the three-dimensional (toroidal) convective structures is presumably associated with the resonant excitation of the inertial mode [11] in the process of the liquid inertial oscillations. In the problems of thermal convection in the layers rotating around a horizontal axis this regime is observed for the first time and requires further detailed study.
Points 5 in Fig. 9 marks the excitation threshold of thermal vibrational convection, manifested in the form of longitudinal rolls of large transverse size (Fig. 7). The dashed line shows the theoretical threshold curve obtained in [22]. Threshold points 10 were obtained in the experiments with thin layers in the same formulation of the problem [23]. Fig. 9c separately shows the excitation thresholds of thermovibrational convection with an enlarged scale along the horizontal axis. In [23], the analysis of experimental and theoretical research results shows that one more important parameter describing thermovibrational convection is the dimensionless rotation velocity ωr≡Ωroth2/ν . The parameter characterizes the ratio of the boundary layers thickness to the working layer thickness. In the case of small ωr (relatively thick boundary layers) the thermovibrational mechanism does not play an important role. In the experiments with middle layers in the areas of convective regimes changing ωr exceeds 1000. Thus, the thermovibrational mechanism is clearly manifested under these experimental conditions. Note that the experimental threshold of the thermovibrational convection development (the boundary of areas II and III) is in satisfactory agreement with the theoretical threshold of linear stability, despite the presence of intense convective flows. The exception is the points obtained at large values of Rv . The discrepancy between the experimental threshold points and the linear theory curve in this case is associated with the emergence of a new convection mechanism associated with the inertial oscillations of the liquid and the excitation of resonance effects.
The structure of convective flows in a rotating horizontal cylindrical layer of moderate thickness h/ˉR= 0.55 with isothermal boundaries was studied experimentally. The case of stable stratification of a liquid in a centrifugal force field was considered. The inner boundary of the layer had a higher temperature, and at rapid rotation, the liquid was in equilibrium. It was found that as the angular velocity of rotation decreases, the various convective structures develop in the layer. The first type in the form of toroidal vortex flows develops in a non-threshold manner and at high rotation velocities has virtually no effect on heat transfer. As the angular velocity of rotation decreases, the intensity of the toroidal vortices increases. The experiments indicated that these convective structures are the result of steady streaming generated in the boundary layers because of the fluid inertial oscillations. The intensity of averaged toroidal flows increases noticeably if the geometry of the cavity (aspect ratio) meets the conditions for one of the inertial modes excitation.
Regardless of the toroidal structures, two threshold transitions were discovered as the angular velocity of rotation decreased. The first of the transitions manifests itself in a relatively small but threshold, intensification of heat transport. The convective structure observed in the layer was a system of azimuthally periodic two-dimensional convective rolls with the size consistent with the thickness of the layer. The nature and the generation mechanism of these rolls, which were observed simultaneously with toroidal structures, are not fully understood and need to be studied.
The second threshold transition and the third type of averaged convective structures were associated with the development of “vibrational” thermal convection in the form of two-dimensional vortex structures with a greater wavelength. Their development leads to a significant threshold intensification of heat transport. The research results are presented on the plane of the control dimensionless parameters, the centrifugal Rayleigh number and the vibrational parameter. It was shown that the wavelength of the thermovibrational vortex system and its excitation threshold are consistent with the results of linear theoretical stability analysis based on the thermovibrational convection equations obtained by the averaging method.
Acknowledgement: The authors thank A.S. Selyanin for his help in experimental setup production.
Funding Statement: This work was supported by the Ministry of Education of the Russian Federation (Project KPZU-2023-0002).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Alexei Vjatkin and Victor Kozlov; data collection: Alexei Vjatkin and Svyatoslav Petukhov; analysis and interpretation of results: Alexei Vjatkin and Victor Kozlov; draft manuscript preparation: Alexei Vjatkin, Victor Kozlov and Svyatoslav Petukhov. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Lappa M. Thermal convection: patterns, evolution and stability. Nashville, TN: John Wiley & Sons; 2009. [Google Scholar]
2. Lappa M. Rotating thermal flows in natural and industrial processes. Nashville, TN: John Wiley & Sons; 2012. [Google Scholar]
3. Vadasz P. Natural convection in rotating flows. In: Handbook of thermal science and engineering. Cham: Springer International Publishing; 2018. p. 691–758. [Google Scholar]
4. Song JJ, Li PX, Chen L, Li CH, Li BW, Huang LY. A review on Rayleigh-Bénard convection influenced by the complicating factors. Int Commun Heat Mass Transf. 2023;144:106784. [Google Scholar]
5. Rodda C, Harlander U. Transition from geostrophic flows to Inertia–gravity waves in the spectrum of a differentially heated rotating annulus experiment. J Atmos Sci. 2020;77(8):2793–806. [Google Scholar]
6. Gizon L, Cameron RH, Bekki Y, Birch AC, Bogart RS, Sacha Brun A, et al. Solar inertial modes: observations, identification, and diagnostic promise. Astron Astrophys. 2021;652:L6. [Google Scholar]
7. Adriani A, Bracco A, Grassi D, Moriconi ML, Mura A, Orton G, et al. Two-year observations of the Jupiter polar regions by JIRAM on board Juno. J Geophys Res Planets. 2020;125(6):e2019JE006098. [Google Scholar]
8. Le Bars M, Cébron D, Le Gal P. Flows driven by libration, precession, and tides. Annu Rev Fluid Mech. 2015;47(1):163–93. [Google Scholar]
9. Le Bars M, Barik A, Burmann F, Lathrop DP, Noir J, Schaeffer N, et al. Fluid dynamics experiments for planetary interiors. Surv Geophys. 2022;43(1):229–61. doi:10.1007/s10712-021-09681-1. [Google Scholar] [PubMed] [CrossRef]
10. Kozlov N. Theory of the vibrational hydrodynamic top. Acta Astronaut. 2015;114(1):123–9. doi:10.1016/j.actaastro.2015.04.010. [Google Scholar] [CrossRef]
11. Subbotin S, Dyakova V. Inertial waves and steady flows in a liquid filled librating cylinder. Microgravity Sci Technol. 2018;30(4):383–92. doi:10.1007/s12217-018-9621-x. [Google Scholar] [CrossRef]
12. Shiryaeva M, Subbotina M, Subbotin S. Linear and non-linear dynamics of inertial waves in a rotating cylinder with antiparallel inclined ends. Fluid Dyn Mater Process. 2024;20(4):787–802. doi:10.32604/fdmp.2024.048165. [Google Scholar] [CrossRef]
13. Gershuni GZ, Lyubimov AV. Thermal vibrational convection. Chichester, England: John Wiley & Sons; 1998. [Google Scholar]
14. Smorodin BL, Myznikova BI, Keller IO. Asymptotic laws of thermovibrational convecton in a horizontal fluid layer. Microgravity Sci Technol. 2017;29(1–2):19–28. doi:10.1007/s12217-016-9522-9. [Google Scholar] [CrossRef]
15. Bouarab S, Mokhtari F, Kaddeche S, Henry D, Botton V, Medelfef A. Theoretical and numerical study on high frequency vibrational convection: influence of the vibration direction on the flow structure. Phys Fluids. 2019;31(4):043605. [Google Scholar]
16. Vorobev A, Lyubimova T. Vibrational convection in a heterogeneous binary mixture. Part 1. Time-averaged equations. J Fluid Mech. 2019;870:543–62. [Google Scholar]
17. Crewdson G, Lappa M. The zoo of modes of convection in liquids vibrated along the direction of the temperature gradient. Fluids. 2021;6(1):30. [Google Scholar]
18. Crewdson G, Lappa M. An investigation into the behavior of non-isodense particles in chaotic thermovibrational flow. Fluid Dyn Mater Process. 2022;18(3):497–510. doi:10.32604/fdmp.2022.020248. [Google Scholar] [CrossRef]
19. Kozlov VG. Thermal vibrational convection in rotating cavities. Fluid Dyn. 2004;39(1):3–11. [Google Scholar]
20. Kozlov V, Vjatkin A, Sabirov R. Convection of liquid with internal heat release in a rotating container. Acta Astronaut. 2013;89(1):99–106. doi:10.1016/j.actaastro.2013.04.001. [Google Scholar] [CrossRef]
21. Vjatkin AA, Ivanova AA, Kozlov VG, Rysin KY. Effect of the tangential component of a force field on convection in a rotating plane layer. Izv Atmos Ocean Phys. 2017;53(2):187–94. doi:10.1134/S000143381702013X. [Google Scholar] [CrossRef]
22. Vyatkin AA, Kozlov VG, Siraev RR. Convective stability of fluid in a rotating horizontal annulus. Fluid Dyn. 2017;52(4):526–35. doi:10.1134/S001546281704007X. [Google Scholar] [CrossRef]
23. Vjatkin A, Siraev R, Kozlov V. Theoretical and experimental study of thermal convection in rotating horizontal annulus. Microgravity Sci Technol. 2020;32(6):1133–45. doi:10.1007/s12217-020-09827-7. [Google Scholar] [CrossRef]
24. Porter J, Salgado Sánchez P, Shevtsova V, Yasnou V. A review of fluid instabilities and control strategies with applications in microgravity. Math Model Nat Phenom. 2021;16(207):24. doi:10.1051/mmnp/2021020. [Google Scholar] [CrossRef]
25. Shevtsova V, Ryzhkov II, Melnikov DE, Gaponenko YA, Mialdun A. Experimental and theoretical study of vibration-induced thermal convection in low gravity. J Fluid Mech. 2010;648:53–82. doi:10.1017/S0022112009993442. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
