Stability of the Liquid-Vapor Interface under the Combined Influence of Normal Vibrations and an Electric Field

Nomenclature

1  Introduction

In various materials processing technologies, it is common for a heated sample to contact a cold liquid. The best-known example is the hardening process, in which hot metal, as a result of such contact, acquires new useful properties. Here, the key factor is the amount of heat transfer, which decreases significantly during film boiling when the hot surface is covered with a more or less stable film of vapor. For instance, achieving stability at the liquid-vapor boundary is anticipated under microgravity conditions while undergoing subcooling [1], where the temperature within the liquid medium remains distinct from the saturation temperature. Consequently, the interface moves towards full stability in scenarios devoid of phase transitions, with all the heat absorbed being dissipated through thermal conductivity within the liquid. Such a process of subcooled film boiling should be avoided if possible, and the resulting vapor layer must be destroyed.

Vibrations, which, as we know, always exist on orbital stations, can change the average shape of an interface [2,3], induce a parametric resonance [4], stabilize the interface or destroy it [5]. For example, the effect of vibrations on the heat flux of the second boiling crisis, leading in general to its increase, is described in [6]. Note that the result of many recent works is the intensification of heat and mass transfer processes associated with various boiling regimes by vibration [7–10] or acoustic [11–13] influence. In general, the behavior of the liquid-vapor interface and liquid microlayers plays an important role in nucleate boiling and boiling crisis triggering [14,15].

Previously, in article [16], the influence of the electric field on the minimum heat flux of film boiling, which to some extent can replace the force of gravity under terrestrial conditions (see [17,18]), was studied within the framework of the hydrodynamic theory of boiling crises. The development of modern numerical methods makes it possible to supplement the data of simplified theoretical models (see [19,20]).

Experimental research [21] indicated that the stability of the interface under subcooling conditions can be maintained even in the presence of a gravitational field directed towards the heating surface. This occurs when the Rayleigh-Taylor instability is completely suppressed due to a phase transition at a critical subcooling heat flux value. This phenomenon is observed only in the case of sufficiently thin vapor films, which in [22] allowed the authors to construct a theory using the long-wave approximation. A more comprehensive study based on the long-wave approximation was carried out in [23], which, in addition to linear stability analysis, presents the results of weakly nonlinear analysis and numerical modeling of the dynamics of the interface of subcooled or saturated film boiling phases. For stability under subcooling conditions, stable nonlinear regimes have been found.

The problem under consideration belongs to the class of stability problems for two-layer, two-phase systems in a gravity field. It is assumed that there is a base state in which these layers are in mechanical equilibrium, and the heat fluxes in the media caused by heating on the side of one of the phases are balanced at their interface at the saturation temperature, so that the phase transition does not occur. The linear stability of such a base state was studied in [24–26]. It is shown that the phase transition not only reduces the disturbance growth rate in the region of Rayleigh-Taylor instability but also shifts the boundary of this region towards long-wave disturbances. This shift is determined by the combined effect of phase transition and the viscosity of the media. A strictly linear theory that does not use a quasi-equilibrium approximation for heat transfer (see [24]) was developed in [27,28], where, as in [22,23], the existence of a completely stable configuration of media was confirmed and conditions for its implementation were specified.

The effect of vertical vibrations of finite frequencies, when the type of disturbances at the interface is determined by the Floquet theory, was considered in [29] in the absence of a phase transition. The study revealed the onset of parametric instability, the excitation threshold of which is determined by viscous dissipation. Here, a phase transition can be considered an additional inhibiting factor for instability.

The purpose of this study is to construct a linear theory of the stability of a vapor film under the condition of subcooled film boiling, taking into account the combined effect of vertical vibrations and an electric field.

2  Statement of the Problem

Let us consider a layer of liquid, the lower boundary of which is separated from the solid flat surface of a horizontal heater by a layer of vapor (see Fig. 1). In this work, we do not study the influence of boundary effects associated with the finite sizes of the examined system, and therefore we proceeded from the assumption that the surface of the heater, as well as the layers of liquid and its vapor, extend infinitely in the horizontal plane. For the same reason, the upper boundary of the liquid volume is supposed to be sufficiently distant from the interface, which minimizes its effect on the phase boundary, and the thickness of the heater is not limited.

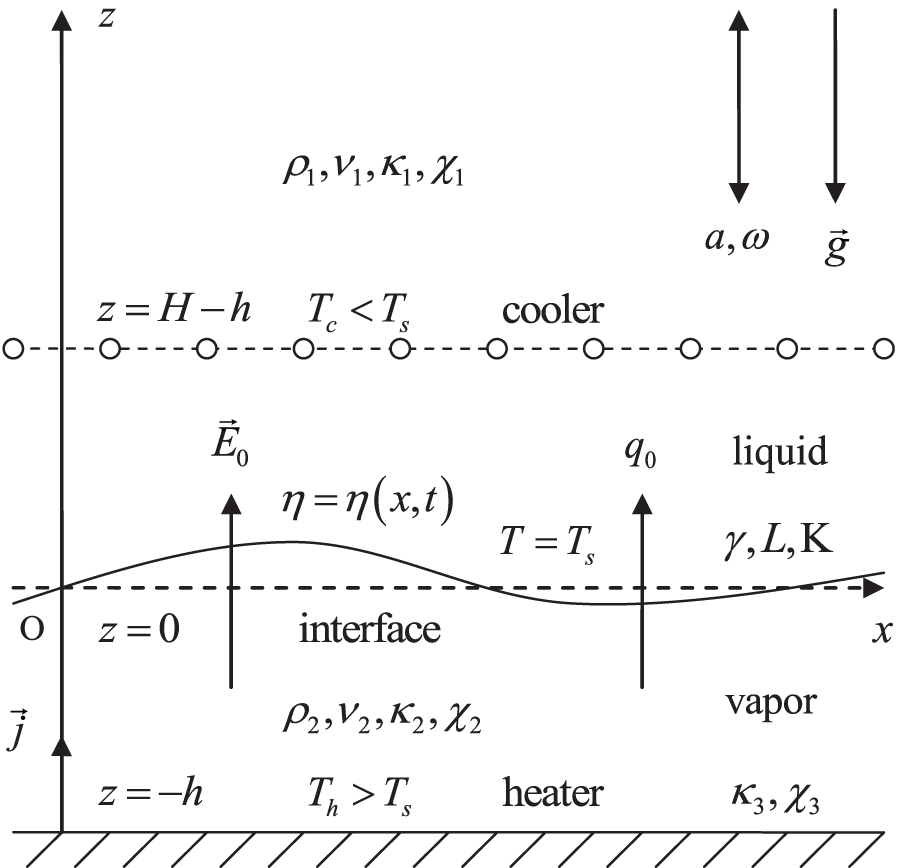
Figure 1: Configuration and system parameters: a vapor film of the thickness h is located on the surface of a horizontal heater and is exposed to vibrations with the amplitude a and frequency ω and an electric field with the intensity E0

We consider the problem in a two-dimensional formulation, which, due to the homogeneity of the system relative to the horizontal plane, is sufficient to study the linear stability of the possible base state in the system. It is convenient to locate the origin of the Cartesian coordinate system {x,z} at a certain point O on the interface between the media, corresponding to the base state, at which the vapor film of thickness h (defined below) is formed on the surface of the heater. The vertical axis z extending from the point O into the liquid layer is normal to the surface of the heater. The horizontal axis x lies in the plane parallel to the surface of the heater, which corresponds to the coordinate surface z=−h .

The dependences of all fields of physical quantities considered below, such as velocity, pressure and temperature, as well as the electric field potential, are specified in terms of the two spatial coordinates x and z and time t , and the flow velocity vectors of both the liquid and its vapor lie in the plane formed by the coordinate axes x and z .

The force of gravity with the acceleration vector g→ is directed downward along the vertical z -axis. Vertical harmonic vibrations with the amplitude a and frequency ω are excited in the same direction. They are created by the translational movement of the heater according to the following law:

r→=r→0+j→acos⁡ωt, (1)

where r→ is the radius vector of a certain point of the heater in the laboratory reference frame at time t , r→0 is its time-average value, and j→ is the unit vector of the normal to the heater surface.

The vibration frequency is considered an arbitrary variable, but the velocity amplitude of vibrations, aω , is taken to be much less than the speed of sound, c (generally speaking, it is different in a liquid and its vapor), which makes it possible to consider vibrations as non-acoustic and to neglect the effect of the compressibility of the medium under consideration:

aω≪c. (2)

Since the system is studied in the reference frame associated with the heater, the acceleration of the modulated gravity field takes the following form:

g→m=g→−j→aω2cos⁡ωt. (3)

Due to the difference in densities between the liquid and its vapor, such modulation can dramatically affect the stability and dynamics of the interface.

The surface of the heater is kept at a constant temperature Th , which is higher than the saturation temperature of the liquid, Ts (depending, generally speaking, on the total hydrostatic pressure existing near the lower boundary of the liquid layer) and causes part of the liquid to turn into vapor. The vaporization process is limited by subcooling, which is provided by a cooling system located at a distance H from the heater (for example, in the form of thin metal tubes used to pump cold water). Due to subcooling, the liquid being in contact with the heater is kept at a constant temperature equal to Tc , which is lower than Ts . This results in the thermally conductive and convective removal of a greater or lesser part of the heat from the phase boundary, which would otherwise be involved in the formation of vapor.

In this study, we proceed from the assumption that the temperature difference in the system is not large enough to cause noticeable inhomogeneity between the liquid and its vapor. In what follows, they are considered homogeneous viscous incompressible heat-conducting media in the state that is far below their critical point, the criteria of which are determined by the following conditions:

Th−TsTs≪1,   Ts−TcTs≪1. (4)

The implementation of these conditions allows us to further specify the material parameters of the phases that do not depend on temperature and, what is more important, to exclude from consideration the convective instability that can arise in the layers of the above media due to the non-isothermal inhomogeneity of their densities. This study also excludes thermocapillary effects and the effect of radiation from the heater surface.

The vapor in the film is considered an ideal dielectric, and the liquid and heater material are considered ideal conductors of electricity, so in this we follow paper [30]. As will be discussed below, in the base state, when the surface of the heater is covered with a layer of vapor of constant thickness, the potential difference between two conductors generates in the layer a uniform electric field of intensity equal to E0 .

3  Equations and Boundary Conditions

The movement of the liquid and its vapor in the non-inertial reference frame associated with the heater and the transfer of heat are controlled by the Navier-Stokes equation for an incompressible medium written for each phase:

∂u→j∂t+(u→j∇)u→j=−1ρj∇pj+νjΔu→j, (5)

the continuity equation

divu→j=0, (6)

and the heat transfer equation

∂Tj∂t+u→j∇Tj=χjΔTj. (7)

Here u→j , pj and Tj are the fields of velocity, pressure and temperature in the media, respectively, ρj , νj and χj are the density, coefficients of kinematic viscosity and thermal diffusivity of the phases, respectively. The index j indicates either the liquid ( j=1 ), or its vapor ( j=2 ), or the solid material of the heater ( j=3 ), inside which the movement is absent ( u→3=0 ), and the heat transfer equation has the following form:

∂T3∂t=χ3ΔT3. (8)

Note that the modulated gravity field in the reference frame associated with the heater has a gradient form and can be compensated by the media pressure field. Then, Eq. (5) retains the same form as in the laboratory reference frame.

The electric field potential in the vapor layer, Ψ2 , due to its divergence-free nature associated with the absence of free charges in a dielectric medium [31], obeys the Laplace equation

ΔΨ2=0. (9)

On the solid heater surface at z=−h , we apply no-slip condition for the vapor velocity (10), temperature continuity condition (11) and heat flux balance condition (12). In addition, for the conductive surface of the heater, we assume the condition of zero electric field potential (13) and specify the heater surface temperature (14):

u→2=0, (10)

[T]{2,3}=0, (11)

[κ∂T∂z]{2,3}=0, (12)

Ψ2=0, (13)

T3=Th, (14)

where κj is the thermal conductivity coefficient of the phases, and hereinafter the square brackets []{i,j} indicate a jump in the corresponding value when passing through the interface from the j -th to the i -th phase.

In the liquid layer at z=H−h , corresponding to the location of the refrigerator, the condition of constant temperature (15) is satisfied. Also, on the basis of the model used in this study, we assume that the velocity of the liquid vanishes (16):

T1=Tc, (15)

u→1=0. (16)

The liquid-vapor interface, characterized by the equation

G(x,z,t)=z−η(x,t)=0, (17)

is expected to satisfy the following criteria: kinematic condition (18), mass flow balance (19), continuity of tangential velocity components (20), continuity of tangential stresses (21), equilibrium of normal stresses (22), temperature continuity (23), heat flux equilibrium (24) and the constancy of electric field potential on the liquid’s conducting surface (25):

∂G∂t=u→1∇G+ξρ1, (18)

[u→∇G+ξρ]{1,2}=0, (19)

[uτ]{1,2}=0, (20)

[σnτ]{1,2}=0, (21)

[−p+σnn+ρ(g−aω2cos⁡ωt)z]{1,2}=γdivn→+ε0ε2(∇Ψ2)22, (22)

[T]{1,2}=0, (23)

[κ∂T∂n]{1,2}=Lξ, (24)

Ψ2=const. (25)

Here η represents the interface position, γ denotes the surface tension coefficient, L stands for the latent heat of vaporization, ε0 represents the electrical constant, ε2 is the dielectric constant of the vapor, σ¯¯ symbolizes the viscous stress tensor, while n→ and τ→ are the unit vectors pointing outward normal and tangent to the interface, respectively.

It is important to note that terms in boundary conditions (21), (22) and (24) related to energy and momentum transfer during phase transition (see [32]) are disregarded in the linear stability theory as secondary effects. In addition, the normal stress balance condition (22)contains the inertial-gravitational term, including vibrations due to the redefinition of pressure (see above). On the right-hand side of the condition, we take into account the electric force [31]

fe=ε0ε2(∇Ψ2)22. (26)

The rate of phase transition, ξ , is associated both with the deviation of the liquid-vapor interface temperature from the liquid saturation temperature Ts and with pressure disturbances at the interface (see [33]):

Kξ=T2−Ts+TsL(p1ρ1−p2ρ2), (27)

where the value of the nonequilibrium number K can be estimated based on the kinetic theory of an ideal gas (see [34]) as

K=8Rg3Ts5/8Rg3Ts5πM3πM3Lps. (28)

Here Rg is the universal gas constant, M is the molar mass of the liquid substance, and ps is the pressure corresponding to the saturation temperature Ts .

4  Base State and Perturbation Problem

The Eqs. (5)–(9) and boundary conditions (10)–(16), (18)–(25) and (27) are solved to find a stable state of a liquid and its vapor ( u→j=0 , pj=const ; j=1,2 ) with a flat phase boundary ( η=0 ) maintained at the saturation temperature of the liquid, Ts , without undergoing phase change ( ξ=0 ).

For the layers of liquid and its vapor, as well as for the heater material, the linear temperature profiles are determined by

T¯j=Ts−q0κjz   (j=1,2), (29)

T¯3=Th−q0κ3(z+h), (30)

where the thickness of the vapor film in the base state, h , and the equilibrium heat flux of subcooling, q0 , are found from the following expressions:

h=Hκ1(Ts−Tc)κ2(Th−Ts)+1, (31)

q0=κ1(Ts−Tc)+κ2(Th−Ts)H. (32)

In addition, we obtain a linear electric field potential profile, corresponding to a given uniform electric field strength E0 , for the vapor layer:

Ψ¯2=E0(z+h). (33)

It is known that the thermal conductivity coefficient of a subcritical liquid, κ1 , is much larger than the thermal conductivity coefficient of its vapor, κ2 , and therefore, when the heating temperature (Th−Ts) is less than or comparable to the subcooling temperature (Ts−Tc) , the thickness of the vapor film, h, determined from (31) is much less than the distance between the heater and the refrigerator, H . Taking this fact into account, we assume, for the sake of simplicity, that H→∞ . In order to completely exclude H from consideration, the prescribed subcooling heat flux q0 associated with the thickness of the vapor film, h , is used in the following as a controlling parameter:

h=κ2(Th−Ts)q0. (34)

Next, we consider a perturbed state characterized by

ujx=υjx(z,t)cos⁡kx, (35)

ujz=υjz(z,t)sin⁡kx, (36)

pj=πj(z,t)sin⁡kx, (37)

Tj=T¯j+θj(z,t)sin⁡kx, (38)

Ψ2=Ψ¯2+ϕ2(z,t)sin⁡kx, (39)

η=f(t)sin⁡kx, (40)

ξ=ζ(t)sin⁡kx, (41)

where the temperatures of the media in the base state, T¯j , are determined from expressions (29) and (30), the electric field potential in the vapor layer in the base state, Ψ¯2 , is found from expression (33), the amplitudes υjx , υjz , πj , θj , ϕ2 , f and ζ specify small deviations from the base state, and k is the wavenumber of disturbances.

Let’s adjust the problem formulation for the perturbed state by considering a scenario where the temperature of the heater surface may vary from the previously defined value Th , which now serves solely as a parameter defining the base state. Additionally, the condition of constant temperature (14) is replaced by the condition of attenuation of its disturbances in the heater at a distance from its surface at z→∞ :

T3→T¯3. (42)

Pressure disturbances created by the flow of the media under consideration ( j=1,2 ), corresponding to Eq. (5), which is linearized over small disturbances, and Eq. (6) satisfy the Laplace equation

Δpj=0. (43)

From Eq. (6), upon substituting fields (35) and (36), the following relationship between the amplitudes υjx and υjz is derived:

υjx=1k∂υjz∂z. (44)

This is the standard technique, which will be used further to write no-slip condition (59) and continuity condition (67) for the x -component of velocity.

To represent the stability problem in a dimensionless form, we use the gravitational-capillary length dγg=γ/γ(ρ1−ρ2)g(ρ1−ρ2)g as a unit of length. Such a choice is justified by the fact that the specified length scale is the only acceptable option for a thick vapor layer, when kh≫1 , and also by the fact that this unit, unlike the thickness of the vapor film, h , does not depend on the thermal conditions in the system. As a unit of time, we use the gravitational-capillary time tγg=(ρ1+ρ2)dγg3/(ρ1+ρ2)dγg3γγ , dγg/dγgtγgtγg as a unit of flow velocity, (ρ1+ρ2)dγg2/(ρ1+ρ2)dγg2tγg2tγg2 as a unit of pressure, q0dγg/q0dγg(κ1+κ2)(κ1+κ2) as a unit of temperature, ρ1+ρ2dγg/ρ1+ρ2dγgε0ε2tγgε0ε2tγg as a unit of electric field strength, and (ρ1+ρ2)dγg/(ρ1+ρ2)dγgtγgtγg as a unit of phase transition rate.

The problem is characterized by the following dimensionless parameters for the liquid and its vapor ( j=1,2 ):

ρ~j=ρjρ1+ρ2,   κ~j=κjκ1+κ2,   Rej=1νjdγg2tγg,   Pej=1χjdγg2tγg (45)

and for the heater material ( j=3 ):

δ=κ2κ3,   Pe3=1χ3dγg2tγg. (46)

The Bond number is determined by the thickness of the vapor film as

Bo=hdγg, (47)

the dimensionless phase transition parameters are

Λ=L(ρ1+ρ2)q0dγgtγg,   J=(κ1+κ2)KL1dγg,   Π=(κ1+κ2)Ts(ρ1+ρ2)L21tγg, (48)

the dimensionless electric field strength is

Z=ε0ε2E0ρ1+ρ2tγgdγg, (49)

and the dimensionless frequency and amplitudes of acceleration and vibration velocity are

Ω=ωtγg,   A=aω2g,   B=AΩ. (50)

The relative densities and thermal conductivities of the liquid and its vapor are related by the following relationships: ρ~1+ρ~2=1 and κ~1+κ~2=1 . The Reynolds, Rej , and Peclet, Pej , numbers are determined based on the coefficients of kinematic viscosity, νj , and thermal diffusivity, χj , of the respective media.

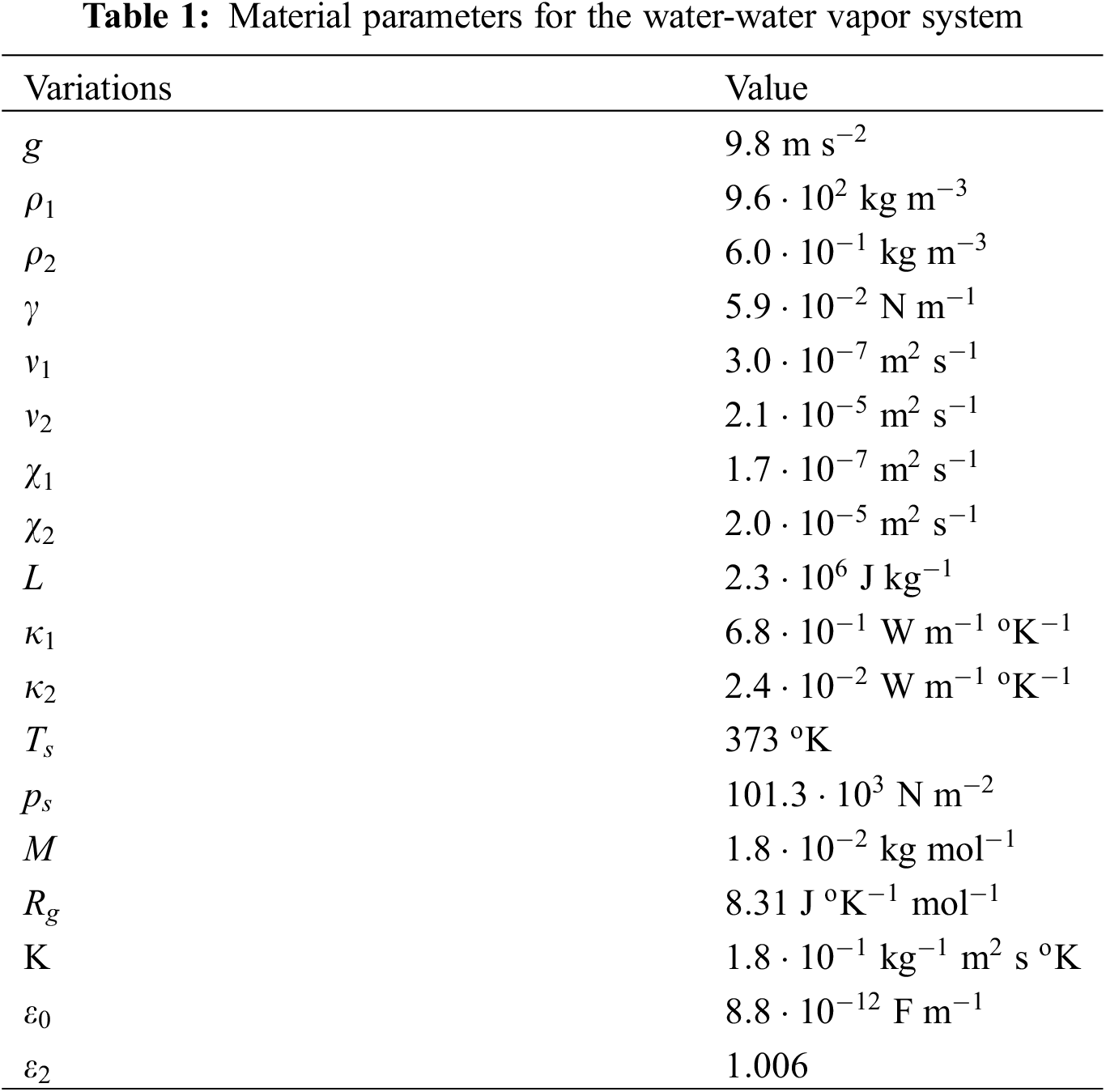
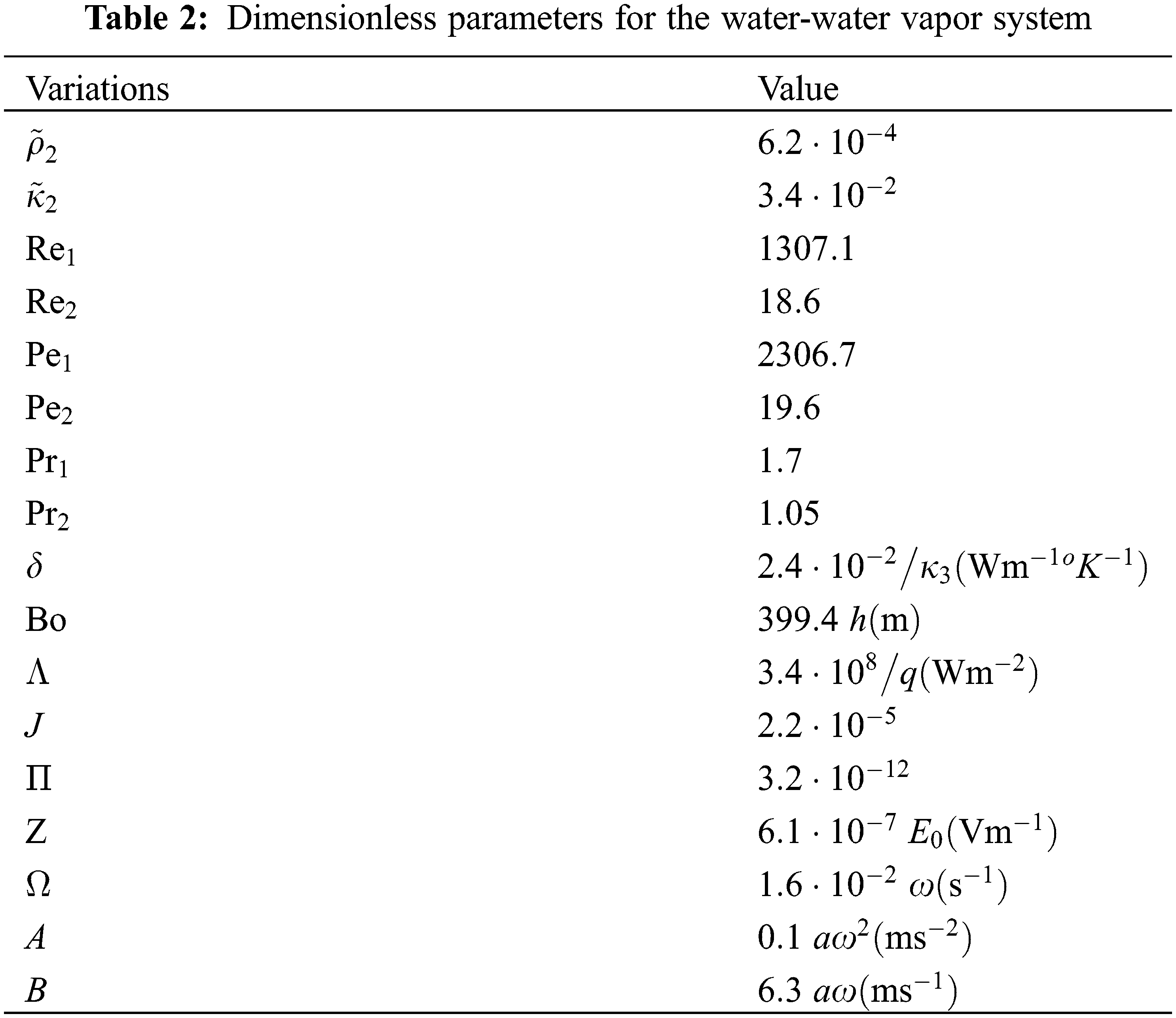
Table 1 shows the dimensional material parameters for a water-water vapor system under the atmospheric pressure and at the water saturation temperature corresponding to this pressure, which is equal to 100°C. Table 2 shows the values of dimensionless parameters, which are calculated using the values from Table 1.

For the dimensionless amplitudes υjz , πj , θj , ϕ2 , f , ζ , coordinate z , time t and wavenumber k , we use the same notation. Substituting fields of the perturbed state (35)–(41) into Eq. (5) linearized over small perturbations and projected onto the axis z , linearized Eqs. (7)–(9), as well as Eq. (43), and applying the nondimensionalization procedure, we obtain the following equations for disturbances of velocity, pressure and temperature in the liquid and its vapor ( j=1,2 ):

Dπj=0, (51)

(∂∂t−1RejD)υjz=−1ρ~j∂πj∂z, (52)

(∂∂t−1PejD)θj=υjzκ~j, (53)

electric field potential in the vapor layer:

Dϕ2=0, (54)

and temperature in the heater material:

(∂∂t−1Pe3D)θ3=0. (55)

Hereinafter, the following operator is used:

D≡∂2∂z2−k2. (56)

Substituting fields (35)–(41) into boundary conditions (10)–(13), (15), (16) and (42), and conditions (18)–(25) and (27), which are previously transferred to the coordinate surface z=0 and linearized, we obtain after performing nondimensionalization the following boundary conditions in the heater at z→−∞ :

θ3=0, (57)

on the solid surface of the heater at z=−Bo :

υ2z=0, (58)

∂υ2z∂z=0, (59)

[θ]{2,3}=0, (60)

[κ~∂θ∂z]{2,3}=0, (61)

ϕ2=0, (62)

in the liquid layer at z→∞ :

υ1z=0, (63)

θ1=0, (64)

on the undisturbed liquid-vapor interface at z=0 :

∂f∂t=υ1z+ζρ~1, (65)

[υz+ζρ~]{1,2}=0, (66)

[∂υz∂z]{1,2}=0, (67)

[ρ~Re(D+2k2)υz]{1,2}=0, (68)

[−π+2ρ~Re∂υz∂z]{1,2}+(1−k2−Acos⁡Ωt)f−Z∂ϕ2∂z|z=0=0, (69)

[θ−fκ~]{1,2}=0, (70)

[κ~∂θ∂z]{1,2}=Λζ, (71)

ΛJζ=θ2−fκ~2+ΛΠ(π1ρ~1−π2ρ~2), (72)

ϕ2+Zf=0. (73)

It is important to highlight that the departure of the interface temperature from the equilibrium temperature, leading to a phase transition, is a result of both local temperature disturbances concerning the base state and the displacement of the interface in regions where the base temperature differs from the initial temperature. This is reflected in boundary conditions (70)and (72), which contain both the amplitudes θj and amplitude f .

From Eq. (54) and boundary conditions (62) and (73), the following solution can be obtained for the perturbed electric field potential in the vapor layer:

ϕ2=−Zsh k(z+Bo)sh kBof, (74)

which allows us to determine the magnitude of the electric force acting under condition (69),

Z∂ϕ2∂z|z=0=−Z2kth kBof. (75)

In the next section of this work, disturbances of physical fields are expanded into series according to Floquet modes (78)–(83). From Eq. (55), the following solution is found for the n -th mode of temperature disturbances in the heater material with the Floquet index μ+iα , decaying at z→−∞ according to boundary condition (57):

θ3(n)∼exp⁡[k2+Pe3{μ+i(α+nΩ)}⋅z]. (76)

After substituting into boundary conditions (60) and (61), it allows us to write the condition (fulfilled at z=−Bo ) for the n -th mode of temperature disturbances in the vapor layer, which no longer contains θ3(n) :

δdθ2(n)dz−k2+Pe3{μ+i(α+nΩ)}⋅θ2(n)=0. (77)

Then, we consider the limiting case of an ideal heat-conducting boundary ( δ→0 ), when θ2(n)=0 at z=−Bo .

5  Floquet Theory

Due to the fact that the inertial-gravitational acceleration in boundary condition (69) is a time-periodic function with a period of 2π/2πΩΩ , the problem of linear stability (51)–(55), (57)–(73), (75) and (77) should be studied within the framework of Floquet theory, as was done earlier for the configuration of two viscous incompressible liquids in a modulated gravity field in the absence of a phase transition [29]. Based on this theory, we present the disturbance amplitudes υjz , πj , θj , ϕ2 , f and ζ in the form of the following series expansions in Floquet modes:

υjz(z,t)=exp⁡(μ+iα)t⋅∑n=−∞∞υjz(n)(z)exp⁡inΩt, (78)

πj(z,t)=exp⁡(μ+iα)t⋅∑n=−∞∞πj(n)(z)exp⁡inΩt, (79)

θj(z,t)=exp⁡(μ+iα)t⋅∑n=−∞∞θj(n)(z)exp⁡inΩt, (80)

ϕ2(z,t)=exp⁡(μ+iα)t⋅∑n=−∞∞ϕ2(n)(z)exp⁡inΩt, (81)

f(t)=exp⁡(μ+iα)t⋅∑n=−∞∞f(n)exp⁡inΩt, (82)

ζ(t)=exp⁡(μ+iα)t⋅∑n=−∞∞ζ(n)exp⁡inΩt. (83)

Here μ and α are the real and imaginary parts of the Floquet exponent, and exp⁡(μ+iα)2π/2πΩΩ is the Floquet multiplier. The Fourier series represent time-periodic functions with a period of 2π/2πΩΩ .

The Floquet multiplier is an eigenvalue of a real transformation, which means that it is either real or always has a complex conjugate pair. In addition, α is defined only by the modulo Ω , and we can always assume that 0≤α≤Ω/Ω22 . Two cases, α=0 and α=Ω/Ω22 , are of special interest. In the case called harmonic, when α=0 , the Floquet multiplier has a positive value. Whereas in the subharmonic case at α=Ω/Ω22 , this multiplier has a negative value. When 0 < α < Ω/Ω22 , the Floquet multiplier is a complex quantity.

The relationship between positive and negative Floquet modes depends on the magnitude of α . In the harmonic and subharmonic cases, the following conditions must be fulfilled, respectively: x(−n)=x(n)∗ or x(−n)=x(n−1)∗ , where x(n) needs to be substituted for one of the amplitudes υjz(n) , πj(n) , θj(n) , ϕ2(n) , f(n) and ζ(n) . Thus, expansions (78)–(83) can be written only in terms of non-negative mode numbers. On the other hand, when 0 < α < Ω/Ω22 , the Floquet coefficients with positive and negative n are linearly independent. The complex conjugate parts must be added to expansions (78)–(83) to form real fields.

Disturbances either increase with time at μ > 0 , or decay at μ < 0 , or remain neutral at μ=0 . It can be shown that disturbances with 0 < α < Ω/Ω22 always decay with time. Since we are only interested in disturbances that increase with time or remain neutral, the objective of our further discussion will be harmonic and subharmonic cases.

Solutions for υjz(n) , πj(n) and θj(n) , which we do not present here because of their cumbersome derivation, can be obtained from Eqs. (51)–(53). Substituting expansions (78)–(83) into boundary conditions (57)–(73) and (77), we arrive at a system of linear algebraic equations written for each of the modes. Moreover, the neighboring modes are “engaged” in condition (69) through the factor cos⁡Ωt . By transferring the term describing such “engagement” to the right side of the system and resolving it relative to the amplitude f(n) , we can obtain the following set of relations for the amplitudes of disturbances of the media interface:

f(n)=R(n)A(f(n+1)+f(n−1)), (84)

which need to be supplemented with the reality conditions

f(−1)=f(1)∗(harmoniccase) (85)

f(−1)=f(0)∗(subharmoniccase) (86)

In this case, the coefficients R(n) specify a kind of the f(n) -amplitude response to the two neighboring modes.

By limiting the number of modes under consideration to a certain considerable number and separating the real and imaginary parts from relations (84), we arrive at the problem of eigenvalues for the vibration amplitude A (or rather, the inverse amplitude A−1 ). Mathematically, the problem reduces to finding an eigenvalue for the vibration amplitude with other prescribed parameters: the vibration frequency, wavenumber and Floquet exponent. By setting such an indicator, corresponding to a neutral disturbance (harmonic or subharmonic), it is possible to determine the boundaries of instability regions.

6  Results

Calculations were carried out in a program written in Fortran using procedures from the IMSL mathematic library, based on the data from Tables 1 and 2 for the water-vapor system. The number of base functions in expressions (78)–(83) was taken to be equal to fifty. The model was restricted to the limiting case of an ideal heat-conducting boundary, when δ→0 . First, let us consider the case of a thick vapor layer, when Bo∼1 .

As it follows from Fig. 2, two types of instability are possible in the system. First, there is a non-parametric instability, which can be either the Rayleigh-Taylor instability or a combination of the Rayleigh-Taylor and the Tonks-Frenkel instabilities. The latter is similar to the Rayleigh-Taylor instability but is caused by an electric field. These types of instability exist in the range of wavenumbers from zero to a certain critical value, which decreases with the increasing intensity of the vibration effect.

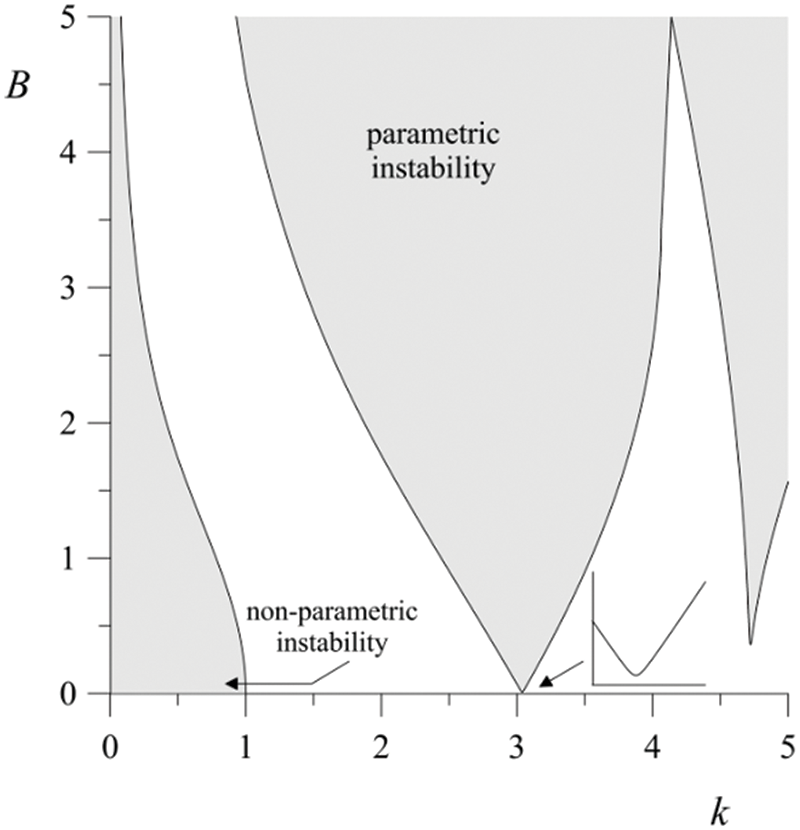
Figure 2: Regions of instability in the space of parameters “wavenumber–amplitude of vibration velocity” for the dimensionless frequency Ω=10 . The phase transition parameter is Λ=1010 ; the electric field parameter is Z=0

The vibrations themselves are capable of causing parametric instability, which is characterized by the excitation threshold, which depends on the dissipative factors of the system: the viscosity of the liquid and its vapor, as well as the phase transition. With a further increase in the vibration intensity, the parametric instability becomes the most dangerous. It can be shown that this occurs at such a vibration amplitude when, at a certain Floquet exponent (which we find in an iterative process), the appearance of the regions of disturbances with such an exponent (parametric and non-parametric) is directly associated with the indicated vibration amplitude (Fig. 3).

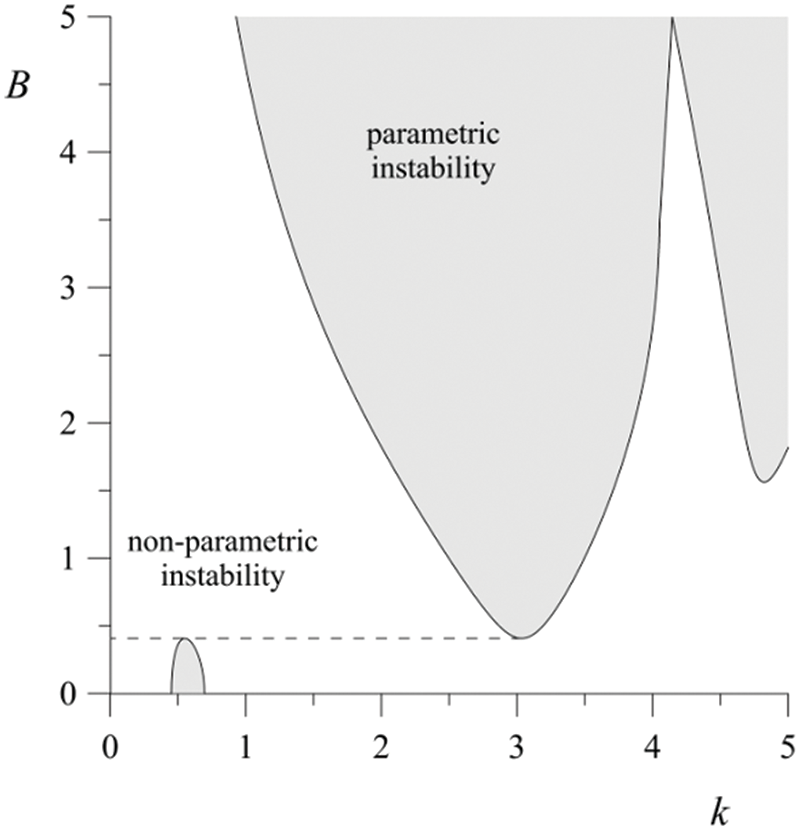
Figure 3: Illustration of a situation where parametric instability becomes most dangerous at B=0.406 . The boundaries of the regions in the space of parameters “wavenumber–amplitude of vibration velocity” are constructed for the dimensionless frequency Ω=10 and Floquet exponent μ=0.597 . The phase transition parameter is Λ=1010 ; the electric field parameter is Z=0

Fig. 4 shows the threshold for the occurrence of parametric instability and the threshold for its transformation into the most dangerous one versus the frequency of vibrations. It is assumed that there is no electric field and that the subcooling heat flux through the system is small. Thus, this figure illustrates the situation when the Rayleigh-Taylor instability and parametric instability appear in the system in the absence of such complicating factors as a phase transition and an electric field. It can be seen that at a very high vibration frequency, these two thresholds practically coincide. Data on the threshold for the occurrence of parametric instability and its becoming the most dangerous (see Fig. 4) for a high dimensionless vibration frequency were compared with the results of the high-frequency approximation without a phase transfer (see [5]). An excellent match was obtained.

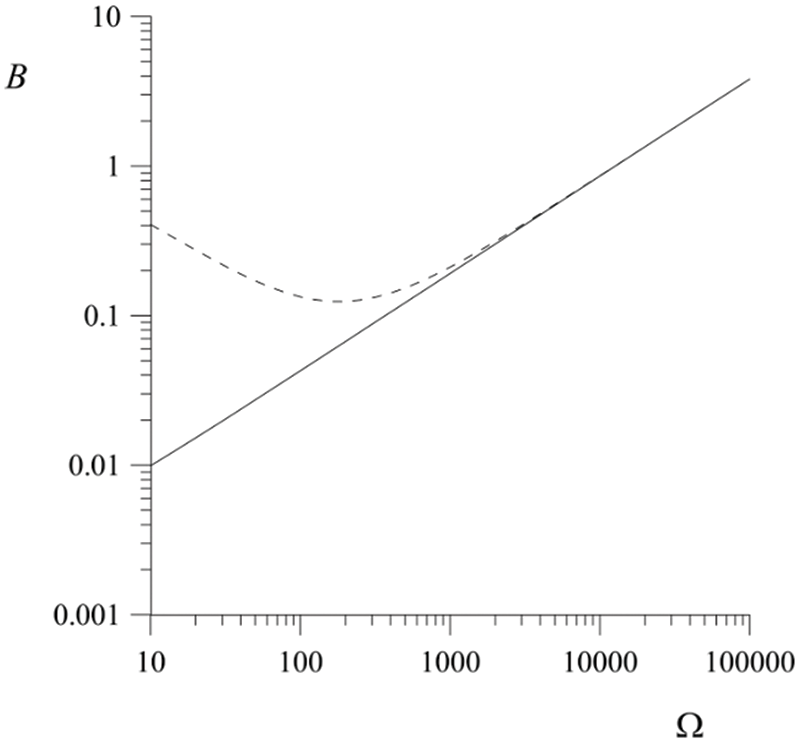
Figure 4: Dependence of the threshold for the occurrence of parametric instability (solid line) and its becoming the most dangerous (dashed line) on the vibration frequency. The phase transition parameter is Λ=1010 ; the electric field parameter is Z=0

As it follows from Fig. 5, the effect of phase transition, even in the limit of strong subcooling at Λ=0 , weakly affects the threshold for excitation of parametric instability in the system in the case of a thick vapor layer. In general, the same observation also applies to the threshold for the formation of the most dangerous parametric instability.

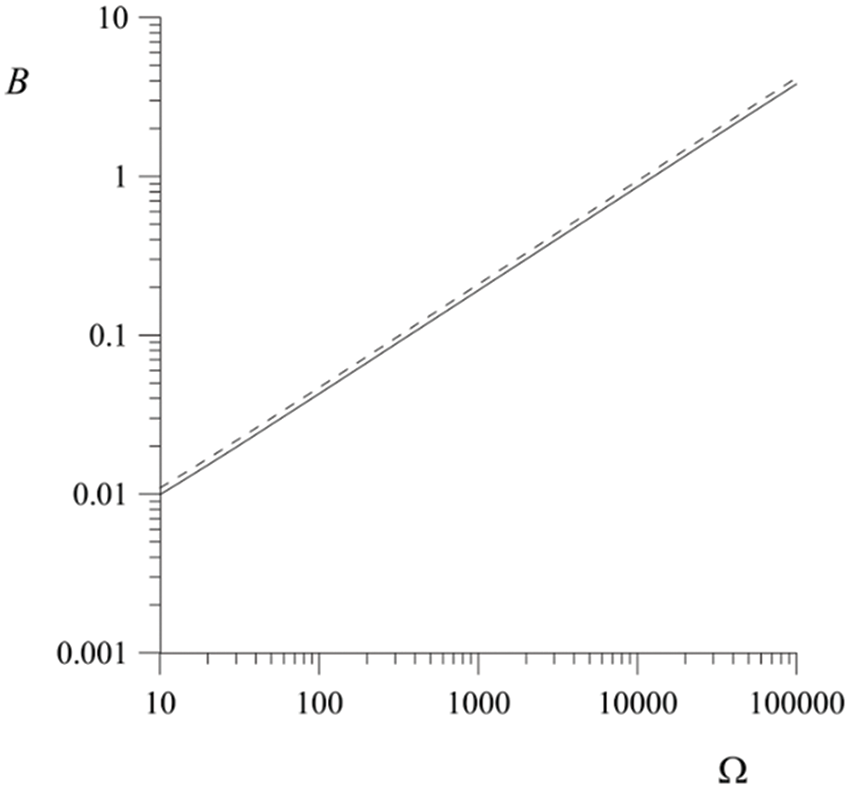
Figure 5: Dependence of the threshold for the occurrence of parametric instability on the vibration frequency. The phase transition parameter is Λ=1010 (solid line) and Λ=0 (dashed line). The electric field parameter is Z=0

From Figs. 6 and 7, it is seen that the electric field is capable of influencing the thresholds for the occurrence of parametric instability and its transformation into the most dangerous disturbances in the direction of their increase. The effect is most pronounced at low and moderate vibration frequencies.

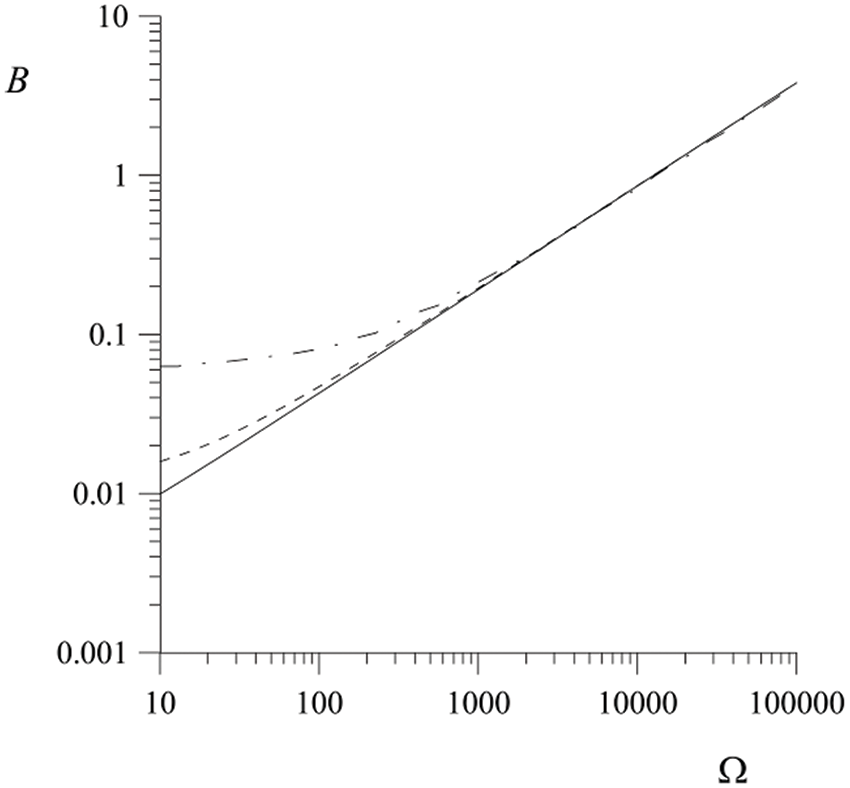
Figure 6: Dependence of the threshold for the occurrence of parametric instability on the vibration frequency. The electric field parameter is Z=0 (solid line), Z=2 (dashed line) and Z=5 (dash-dotted line). The phase transition parameter is Λ=1010

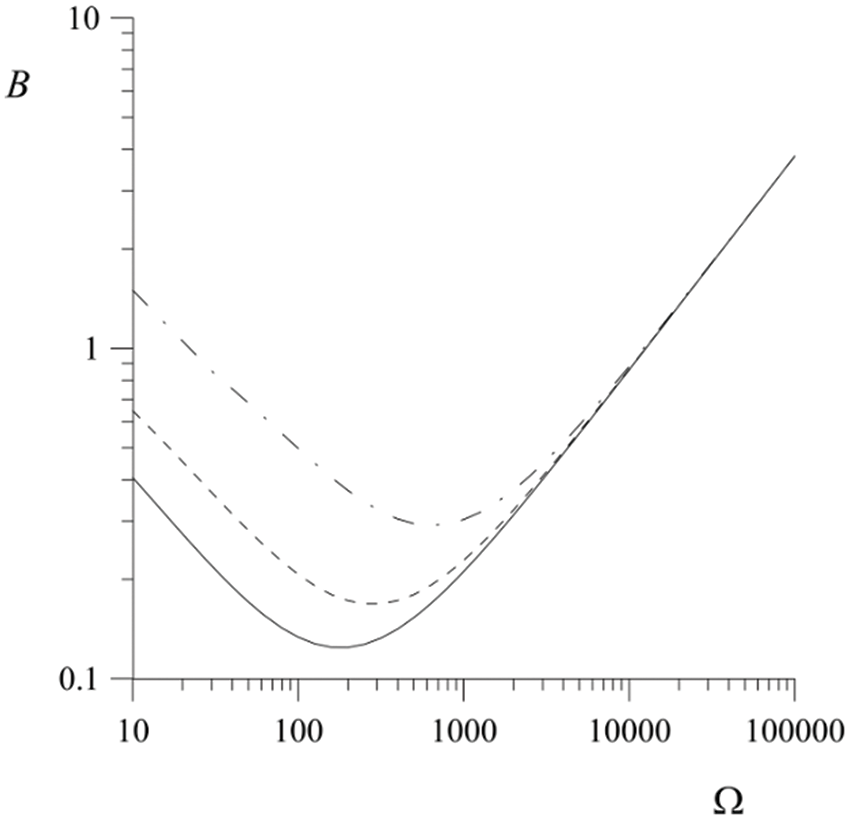
Figure 7: Dependence of the threshold for the formation of parametric instability as the most dangerous on the vibration frequency. The electric field parameter is Z=0 (solid line), Z=1 (dashed line) and Z=2 (dash-dotted line). The phase transition parameter is Λ=1010

It is known [22,23] that the pressure of viscous vapor in a sufficiently thin vapor film, caused by its influx from the liquid side as a result of the phase transition effect, stabilizes the long-wave disturbances, leading to the appearance of another region of stability in addition to the region of short-wave disturbances associated with the influence of surface tension. The region of instability caused by the medium-wave disturbances separating the above two regions is getting narrower with increasing subcooling heat flux until it disappears completely at a certain critical value.

Consideration of the linear stability of the system in the absence of vibrations and electric fields allowed us to construct the stability map presented in Fig. 8. It is seen that vibrations do not shift the boundary of region I, where stabilization of the non-parametric instability by a phase transition is impossible. The influence of vibrations on stabilization is possible only in region II, where long-wave damped disturbances exist, as shown in Fig. 9 for a point in this area. In addition, the electric field acts in the direction of increasing the stabilization threshold of instability.

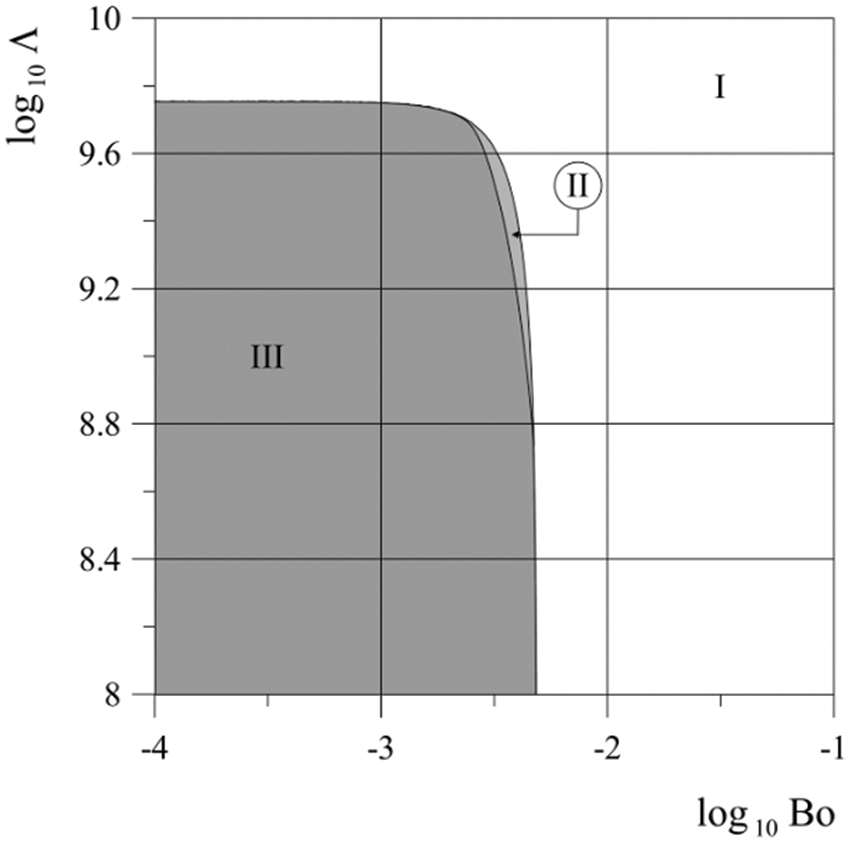
Figure 8: System stability map in the absence of vibrations and electric field. I: region where the effect of the phase transition is to reduce the critical wavenumber; II: region where damped long-wave disturbances appear; III: region where instability is completely suppressed by the phase transition effect

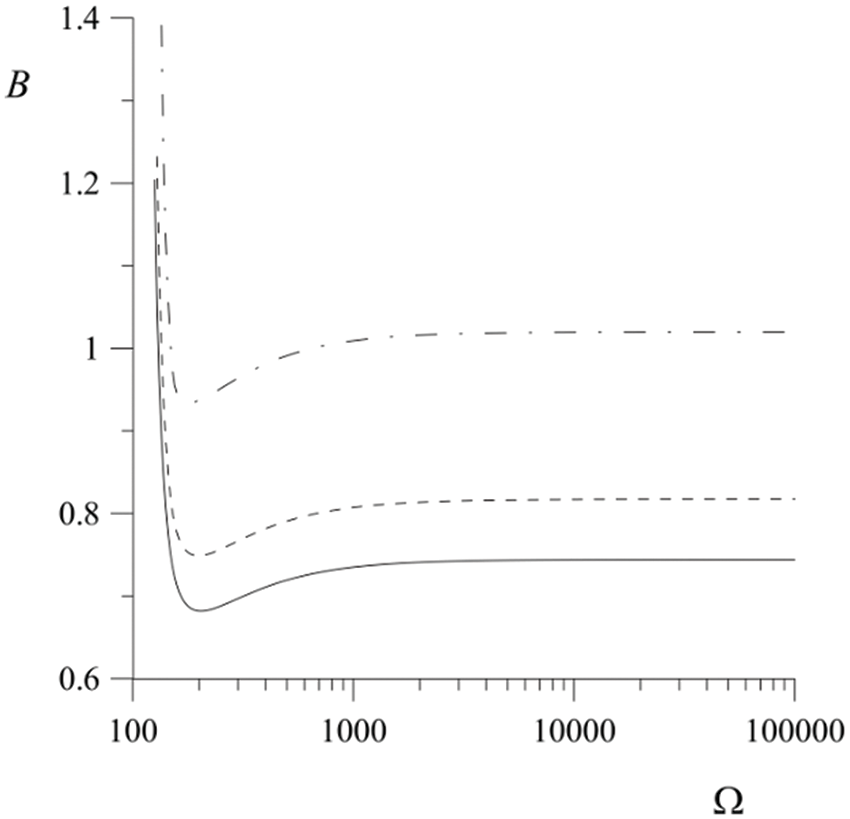
Figure 9: Dependence of the stabilization threshold of non-parametric instability on vibration frequency. The electric field parameter is Z=0 (solid line), Z=0.01 (dashed line) and Z=0.02 (dash-dotted line). The phase transition parameter is Λ=2⋅109 ; the Bond number is Bo=0.004

The size of region II on the instability map is small, and we can conclude that vibrations have virtually no effect on the phenomenon of stabilization of nonparametric instability. A stable vapor film, however, can be destroyed by the parametric instability. The intensity of the vibrations required to produce such an effect can be determined from Figs. 10 and 11. The phase transition, as a dissipative factor, contributes to an increase in the threshold, and the electric field contributes to its decrease.

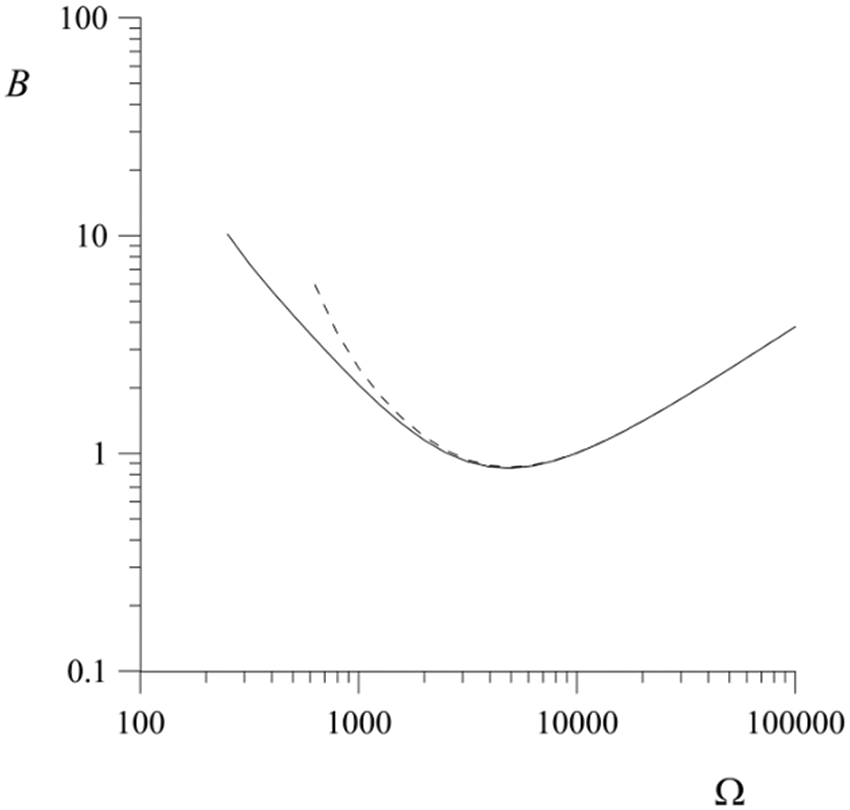
Figure 10: Dependence of the excitation threshold of parametric instability on vibration frequency. The phase transition parameter is Λ=1010 (solid line) and Λ=103 (dashed line). The electric field parameter is Z=0 ; the Bond number is Bo=0.004

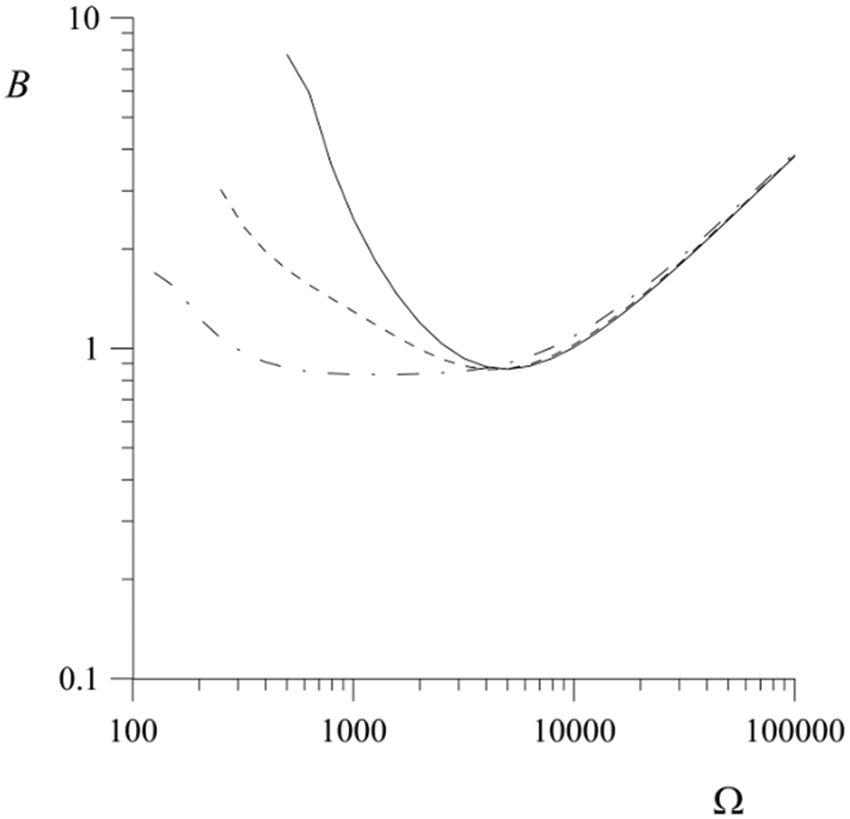
Figure 11: Dependence of the excitation threshold of parametric instability on vibration frequency. The electric field parameter is Z=0 (solid line), Z=2 (dashed line) and Z=5 (dash-dotted line). The phase transition parameter is Λ=103 ; the Bond number is Bo=0.004

7  Conclusion

Based on the complete equations of heat and mass transfer, we analyzed the linear stability of the base state of the liquid-vapor interface in conditions of subcooled film boiling, taking into account the modulation of the gravity field caused by vertical vibrations of the heater and the additional influence of the electric field. The solution for disturbances developed in the framework of the Floquet theory with a lower-limited number of harmonics and a given disturbance multiplier was used to obtain a matrix, whose eigenvalues indicate the required amplitude of the vibration effect. This allowed us to construct resonant “bags” on the stability map for the harmonic and subharmonic cases. The minimum amplitude determines the threshold for the occurrence of parametric instability in the system.

In a certain range of wavenumbers (the boundaries of the range are determined by the condition that the determinant of a certain matrix for a system of amplitude equations is equal to zero), the instability occurs as a combination of the Rayleigh-Taylor and Tonks-Frenkel instabilities. The narrowing of this range to zero provides a condition for suppressing this instability. There may also be a situation where this instability disappears due to the action of vibrations and heat flux through the interface, and the parametric instability has not yet been excited. In this case, which has to be avoided, the liquid-vapor interface is stable at any wavenumber of disturbances.

It is shown that in thin vapor films with a thickness of the order of tens of microns, the electric field acts as a factor that partially complicates the stabilization of the Rayleigh-Taylor instability by a phase transfer and at the same time facilitates the excitation of parametric instability at vibration frequencies of the order of tens of kilohertz. The threshold for excitation of parametric instability in terms of vibration amplitude can be reduced by three times by applying an electric field with a strength of about three million volts per meter.

Acknowledgement: The authors would like to thank the anonymous reviewers for the helpful suggestion.

Funding Statement: The research was supported by the Ministry of Science and High Education of Russia (Theme No. 121031700169-1).

Availability of Data and Materials: The data presented in this study are available on request from the corresponding author.

Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.

References

1. Oka T, Abe Y, Mori YH, Nagashima A. Pool boiling of n-pentane, CFC-113 and water under reduced gravity: parabolic flight experiments with a transparent heater. J Heat Transf Trans ASME. 1995;117(2):408–17. doi:10.1115/1.2822537. [Google Scholar] [CrossRef]

2. Ivantsov A, Lyubimova T, Khilko G, Lyubimov D. The shape of a compressible drop on a vibrating solid plate. Mathematics. 2023;11(21):4527. doi:10.3390/math11214527. [Google Scholar] [CrossRef]

3. Lyubimova TP, Fomicheva AA, Ivantsov AO. Dynamics of a bubble in oscillating viscous liquid. Philos Trans R Soc A Math Phys Eng Sci. 2023;381(2245):68. doi:10.1098/rsta.2022.0085. [Google Scholar] [PubMed] [CrossRef]

4. Konovalov VV, Lyubimov DV, Lyubimova TP. Resonance oscillations of a drop or bubble in a viscous vibrating fluid. Phys Fluids. 2021;33(9):344. doi:10.1063/5.0061979. [Google Scholar] [CrossRef]

5. Briskman VA. Parametric stabilization of the interface between liquids. Dokl Akad Nauk SSSR. 1976;226(5):1041–4 (In Russian). [Google Scholar]

6. Konovalov VV, Lyubimova TP, Lyubimov DV. Effect of normal vibrations of a flat horizontal heater on the second boiling crisis. J Appl Mech Tech Phys. 2006;47(4):534–41. doi:10.1007/s10808-006-0086-0. [Google Scholar] [CrossRef]

7. Staszel C, Sinha-Ray S, Yarin AL. Forced vibration of a heated wire subjected to nucleate boiling. Int J Heat Mass Transf. 2019;135:44–51. doi:10.1016/j.ijheatmasstransfer.2019.01.101. [Google Scholar] [PubMed] [CrossRef]

8. Unno N, Yuki K, Taniguchi J, Satake S. Boiling heat transfer enhancement by self-excited vibration. Int J Heat Mass Transf. 2020;153(2–4):119588. doi:10.1016/j.ijheatmasstransfer.2020.119588. [Google Scholar] [CrossRef]

9. Fedyushkin AI. Numerical simulation of gas-liquid flows and boiling under effect of vibrations and gravity. J Phys Conf Series. 2020;1479:012094. doi:10.1088/1742-6596/1479/1/012094. [Google Scholar] [CrossRef]

10. Mondal K, Bhattacharya A. Pool boiling enhancement through induced vibrations in the liquid pool due to moving solid bodies—a numerical study using lattice Boltzmann method (LBM). Phys Fluids. 2021;33(9):1419. doi:10.1063/5.0057637. [Google Scholar] [CrossRef]

11. Tang J, Sun L, Wu D, Du M, Xie G, Yang K. Effects of ultrasonic waves on subcooled pool boiling on a small plain heating surface. Chem Eng Sci. 2019;201:274–87. doi:10.1016/j.ces.2019.03.009. [Google Scholar] [CrossRef]

12. Li X, Tang J, Sun L, Li J, Bao J, Liu H. Enhancement of subcooled boiling in confined space using ultrasonic waves. Chem Eng Sci. 2020;223:115751. doi:10.1016/j.ces.2020.115751. [Google Scholar] [CrossRef]

13. Wan Z, Duan J, Wang X, Zheng M. Saturated boiling heat transfer under ultrasound. Int Commun Heat Mass Transf. 2020;115(1):104511. doi:10.1016/j.icheatmasstransfer.2020.104511. [Google Scholar] [CrossRef]

14. Liu H, Liu W, Yan P, Chen D, Dong K, Qin J, et al. The role mechanism of vapor-liquid behavior on boiling crisis triggering. Int J Heat Mass Transf. 2022;196(4):123248. doi:10.1016/j.ijheatmasstransfer.2022.123248. [Google Scholar] [CrossRef]

15. Chen J, Liu H, Dong K. Experimental and LBM simulation study on the bubble dynamic behaviors in subcooled flow boiling. Int J Heat Mass Transf. 2023;206(4):123947. doi:10.1016/j.ijheatmasstransfer.2023.123947. [Google Scholar] [CrossRef]

16. Johnson RL. Effect of an electric field on boiling heat transfer. AIAA J. 1968;6(8):1456–60. doi:10.2514/3.4788. [Google Scholar] [CrossRef]

17. Di Marco P, Grassi W. Effects of external electric field on pool boiling: comparison of terrestrial and microgravity data in the ARIEL experiment. Exp Therm Fluid Sci. 2011;35(5):780–7. [Google Scholar]

18. Ahangar Zonouzi S, Aminfar H, Mohammadpourfard M. A review on effects of magnetic fields and electric fields on boiling heat transfer and CHF. Appl Therm Eng. 2019;151:11–25. [Google Scholar]

19. Feng Y, Li H, Guo K, Lei X, Zhao J. Numerical study on saturated pool boiling heat transfer in presence of a uniform electric field using lattice Boltzmann method. Int J Heat Mass Transf. 2019;135:885–96. [Google Scholar]

20. Feng Y, Li H, Guo K, Lei X, Zhao J. Numerical investigation on bubble dynamics during pool nucleate boiling in presence of a non-uniform electric field by LBM. Appl Therm Eng. 2019;155:637–49. [Google Scholar]

21. Abbassi A, Winterton RHS. The non-boiling vapour film. Int J Heat Mass Transf. 1989;32:1649–55. [Google Scholar]

22. Tanaka H. On the stability of vapour film in pool film boiling. Int J Heat Mass Transf. 1988;31(1):129–34. doi:10.1016/0017-9310(88)90229-3. [Google Scholar] [CrossRef]

23. Panzarella CH, Davis SH, Bankoff SG. Nonlinear dynamics in horizontal film boiling. J Fluid Mech. 2000;402:163–94. doi:10.1017/S0022112099006801. [Google Scholar] [CrossRef]

24. Hsieh DY. Interfacial stability with mass and heat transfer. Phys Fluids. 1978;21(5):745–8. doi:10.1063/1.862292. [Google Scholar] [CrossRef]

25. Ho S-P. Linear Rayleigh-Taylor stability of viscous fluids with mass and heat transfer. J Fluid Mech. 1980;101(1):111–27. doi:10.1017/S0022112080001565. [Google Scholar] [CrossRef]

26. Adham-Khodaparast K, Kawaji M, Antar BN. The Rayleigh-Taylor and Kelvin-Helmholtz stability of a viscous liquid-vapor interface with heat and mass transfer. Phys Fluids. 1995;7(2):359–64. doi:10.1063/1.868633. [Google Scholar] [CrossRef]

27. Konovalov VV, Lyubimov DV, Lyubimova TP. The Rayleigh-Taylor instability of the externally cooled liquid lying over a thin vapor film coating the wall of a horizontal plane heater. Phys Fluids. 2016;28(6):064102. doi:10.1063/1.4952998. [Google Scholar] [CrossRef]

28. Konovalov VV, Lyubimova TP. The effect of natural convection in a liquid layer and the thermal inhomogeneity of vapor on the stability of a vapor film on a flat horizontal heater. Int J Heat Mass Transf. 2018;117(3–4):107–18. doi:10.1016/j.ijheatmasstransfer.2017.09.120. [Google Scholar] [CrossRef]

29. Kumar K, Tuckerman LS. Parametric instability of the interface between two fluids. J Fluid Mech. 1994;279:49–68. doi:10.1017/S0022112094003812. [Google Scholar] [CrossRef]

30. Berghmans J. Electrostatic fields and the maximum heat flux. Int J Heat Mass Transf. 1976;19(7):791–7. doi:10.1016/0017-9310(76)90133-2. [Google Scholar] [CrossRef]

31. Landau LD, Pitaevskii LP, Lifshitz EM. Electrodynamics of continuous media. Oxford: Butterworth-Heinemann; 1984. vol. 8. [Google Scholar]

32. Burelbach JP, Bankoff SG, Davis SH. Nonlinear stability of evaporating/condensing liquid films. J Fluid Mech. 1988;195:463–94. doi:10.1017/S0022112088002484. [Google Scholar] [CrossRef]

33. Kanatani K. Interfacial instability induced by lateral vapor pressure fluctuation in bounded thin liquid-vapor layers. Phys Fluids. 2010;22(1):012101. doi:10.1063/1.3275854. [Google Scholar] [CrossRef]

34. Palmer HJ. The hydrodynamic stability of rapidly evaporating liquids at reduced pressure. J Fluid Mech. 1976;75(03):487–511. doi:10.1017/S0022112076000347. [Google Scholar] [CrossRef]