 Open Access
Open Access
ARTICLE
Experimental Investigation of Particles Dynamics and Solid-Liquid Mixing Uniformity in a Stirred Tank
1 State Key Laboratory of Complex Nonferrous Metal Resources Clean Utilization, Kunming University of Science and Technology, Kunming, 650093, China
2 Faculty of Metallurgical and Energy Engineering, Kunming University of Science and Technology, Kunming, 650093, China
3 Department of Mechanical Engineering, Faculty of Engineering, Urmia University of Technology, Urmia, 5756151818, Iran
4 State Environmental Protection Key Laboratory of Mineral Metallurgical Resources Utilization and Pollution Control, Ministry of Ecology and Environment, Wuhan, 430081, China
* Corresponding Author: Qingtai Xiao. Email:
Fluid Dynamics & Materials Processing 2024, 20(11), 2585-2602. https://doi.org/10.32604/fdmp.2024.050704
Received 14 February 2024; Accepted 01 August 2024; Issue published 28 October 2024
Abstract
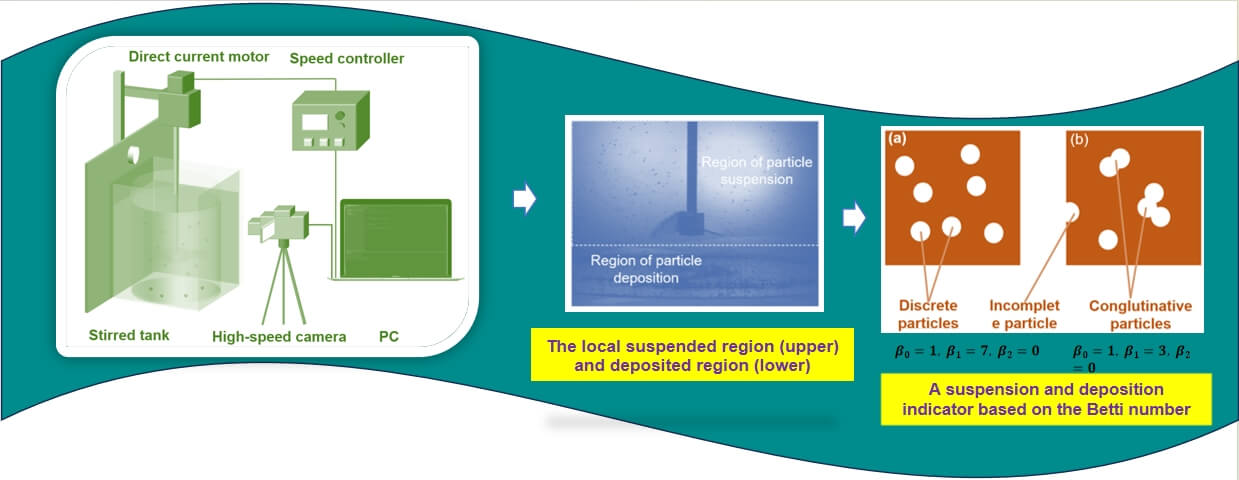
Particle suspension and deposition dynamics are significant factors affecting the level of mixing quality in solid-liquid two-phase stirring processes. In general, the ability to increase the suspension rate and minimize deposition effects is instrumental in improving the uniformity of particle mixing, accelerating the reaction of involved solid-liquid two-phase, and improving the efficiency of production operations. In this work, suspension and deposition indicator based on the Betti number and a uniformity indicator are introduced and obtained by means of image analysis. The influence of the blade type, rotation speed, blade diameter and blade bottom height on the particle suspension/deposition characteristics and mixing uniformity are carefully investigated. The experimental results show that the two-phase motion region can be divided into three local regions, including a bottom motion along the wall, a low-degree suspension region under the blade and a high suspension region above the blade. The best degree of particle suspension is attained by the double-inclined blade paddle at a speed of 270 r/min, a paddle diameter ratio of 0.414, and a height-diameter ratio of 0.086. The double-inclined blade paddle has a better effect on promoting particle suspension and solid-liquid two-phase mixing uniformity.Graphic Abstract
Keywords
Nomenclature
| CHomP | Computational homology program |
| Coefficient of variation | |
| Local discrepancy function of temperature field | |
| Paddle diameter/cm | |
| Inner diameter of the stirred tank/cm | |
| Particle immersion degree | |
| Grayscale at the position in the particle suspension region | |
| Spatial distance between the paddles and the bottom/cm | |
| Image entropy | |
| Single non-uniformity coefficient, | |
| Quantity of rows of the grayscale matrix | |
| Quantity of columns of the grayscale matrix | |
| Height-diameter ratio | |
| Paddle diameter ratio | |
| Agitating speed/r/min | |
| Particle suspension degree | |
| Uniformity coefficient | |
| The zeroth dimension Betti number | |
| The first dimension Betti number | |
| The second dimension Betti number | |
| Local region of grayscale matrix | |
| Length of local rectangular region in particle suspension region/cm | |
| Width of local rectangular region in particle suspension region/cm | |
| L1, L2, L3, L4, L5, L6 and L7 | Working conditions |
Mixing is one of the most common operations in process engineering [1–3] and has been widely used to prepare composite materials [4], promote heat and mass transfer [5], improve the chemical reaction of two-phase or multiphase systems [6], and so on [7–10]. Solid-liquid two-phase mixing is a popular operation in various mixing processes [11], and stirring is one of the most significant operations to enhance the mixing performance of solid-liquid two-phase mixtures [12]. Due to the advantages of flexible operation, high mixing state quality, large contact area, and strong applicability, stirring has been successfully used in machinery equipment [13,14], the chemical industry [15] and other process industries [16–19] since the 1940s. It is accepted that the type, size, quantity, and revolutions per minute of impellers significantly influence the flow field structure in stirred tanks. Hence, for the analogy from the convective heat transfer enhancement [20], the solid-liquid two-phase mixture can improve its mixing state quality, mass and heat transfer, and reaction yields by increasing its particle suspension degree and mixing uniformity [21]. Enhancement of the particle suspension degree and mixing uniformity is primarily related to the design of impellers, geometric configuration of the stirred tank, fluid properties, and operation conditions [22,23]. In fact, failing to account for such variations of above various influence factors would be undesirable in terms of both precise regulation of the solid-liquid two-phase mixing process and the intelligent management of the product quality of metallurgical industries.
In general, mechanical agitation injects energy into the solid-liquid two-phase mixing system through paddle rotation that generates turbulence, so that the solid phase can be suspended [24]. In the 1950s, Zwietering [25] proposed the concept of a critical state of off-bottom suspension in which no particles stayed more than 1–2 s at the bottom of the stirred tank and used it as a criterion for solid phase suspension. Based on energy balance, Baldi et al. [26] proposed a new model to explain the suspension mechanism of the solid phase in a cylindrical stirred tank. Mishra et al. [27] investigated the solid suspension performance under the stirring of a Maxblend impeller by electrical resistance tomography and computational fluid dynamics techniques. They found that the maximum homogeneity of the solid phase stirred by the Maxblend impeller was higher compared to that of the A200 and Rushton impellers. Moreover, the increase in impeller speed is detrimental to the mixing state quality after reaching the peak homogeneity [28]. Liu et al. [29] investigated and compared the just-suspended impeller speeds and just-suspended power consumption of three coaxial mixers and one single-impeller mixer in a viscous system. Giuseppina et al. [30] investigated the application of the Maxblend impeller stirring in turbulent single-phase and two-phase mixing systems using stereoscopic particle image velocimetry and electrical resistance tomography. From the work from Mirfasihi et al. [31], a set of experiments were undertaken in a benchtop baffled vessel using electrical resistance tomography to characterize blending times and mixing behaviors of miscible liquids with a range of viscosity contrasts. Yang et al. [32] investigated the effects of coaxial mixer rotation mode, impeller inner diameter, gas flow rate, and viscosity on the flow regime. These works explored the characteristics of the solid-liquid two-phase mixing process by various methods and impeller, among which the electrical tomography technique was a widely used non-invasive technique. However, if the diameter of the solid phase was too small, it would be difficult to identify small particles in the liquid phase, Maxblend impellers and coaxial mixers are very effective at mixing viscous fluids, the mixing state quality in low-viscosity fluids is poor.
Direct imaging is a low-cost non-invasive technology that enables flexible detection. From open literature, Yang et al. [33] used visual methods to conduct a detailed experimental investigation on the suspension characteristics of a solid-liquid two-phase system with a solid phase volume fraction of 1% to 40%. Sutkar et al. [34] used Fourier transform and digital image processing technology to explore the hydrodynamic characteristics of a jet flow fluidized bed with a guide plate. Juez et al. [35] used inline digital image processing technology to study the texture evolution of pictures taken at the surface of a stirring bed. Teoman et al. [36] processed images of a vessel bottom at various stirring speeds by image processing techniques to quantify the area covered by the solid phase. Table 1 shows a comparison of electrical resistance tomography and direct imaging technology. Direct imaging technology has the following limitations. (1) It is difficult to observe the solid phase through a stirred tank, especially for industrial metal stirred tanks. (2) The solid phase overlapping is unavoidable when acquiring flow images, which leads to errors in the extracted flow features. However, the direct imaging technology has high detection accuracy, and the extracted image features can reflect the solid-liquid two-phase suspension law within a certain error range.
Furthermore, there is a need to quantitatively characterize the dynamics of the solid phase during enhanced solid-liquid two-phase mixing using mechanical agitation. For instance, Behnia et al. [37] used the Lyapunov exponent spectrum, bifurcation diagram, time series, and phase diagram to study the dynamic characteristics of the radial response of bubbles. Tchakui et al. [38] characterized the chaos of the dynamic process of a piezoelectric microelectromechanical system (MEMS) by using detection methods such as the maximum Lyapunov exponent, Poincare surface of section, and small alignment index. However, the phase space in the above methods needed to be reconstructed, and it was easy to produce certain errors due to the interference of delay time and embedding dimension. The Betti number is one of the most valuable methods to quantify the mixing time and uniformity of a multiphase flow mixing process [39], and it has been widely used to quantify the characteristics of multiphase flow mixing processes. For instance, Liao et al. [40] introduced the Betti number to evaluate the mixing state quality and the suspension effect of the solid-liquid two-phase system. In addition, the distribution uniformity of the solid-liquid two-phase mixing process, that is, the dispersion uniformity of the solid phase in the liquid phase, should also be known.
This paper aimed to study particle suspension and mixing homogeneity in stirred tanks using algebraic topology theory and image analysis. Specifically, the effects of propeller type, rotation speed, propeller diameter, and paddle height on the particle suspension and mixing uniformity of the solid-liquid two-phase mixing process were investigated. Firstly, we proposed to estimate the suspension degree of the solid phase more accurately with the help of the relationship between the Betti number and the number of particles in the local flow region. In addition, the local discrepancy function, image entropy, and coefficient of variation were introduced to evaluate the mixing uniformity of the solid and liquid mixture. This work would be helpful to expand the insights in the field of solid-liquid two-phase mixing, improve the technical accuracy of measuring the quality of solid-liquid two-phase mixing, and increase the efficiency of industrial production.
The rest of the article is structured as follows. Section 2 describes the experiment related to the solid-liquid two-phase mixing process and related methods. Section 3 discusses the effects of experimental parameters, such as the propeller type, rotation speed, propeller diameter, and paddle height, on particle suspension and solid-liquid two-phase mixing uniformity. Finally, Section 4 presents the conclusions drawn from this work.
2.1 Solid-Liquid Two-Phase Mixing Setup and Materials
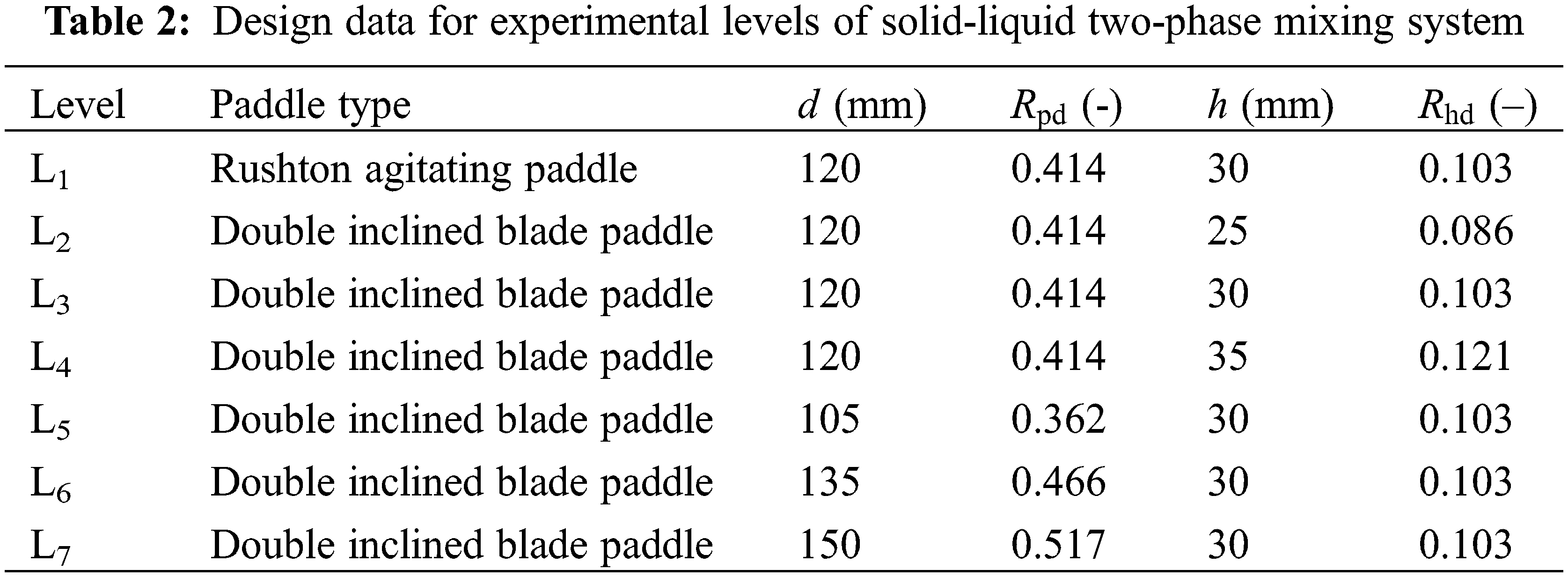
Various kinds of stirred tanks for solid-liquid two-phase mixing have been widely used in the mineral industry, metallurgical engineering, and chemical engineering for reactions, leaching, digestion, precipitation, adsorption, heat transfer, and mass transfer operations. Here, the schematic diagram of the solid-liquid two-phase mixing system is shown in Fig. 1. According to this figure, the present mixing system included the direct current motor, speed controller, stirred tank, high-speed camera, mixing paddle, and personal computer. The stirred tank was divided into two: an inner round tank and an outer square tank, both made of plexiglass. The outer diameter of the stirred tank was 300 mm, the wall thickness of the stirred tank was 5 mm, the height was 300 mm, and the filling volume of the liquid phase was 19.5 dm3. In solid-liquid two-phase mixing systems, axial impellers are critical for the mixing performance, especially to improve the suspension of particles at the bottom of the stirred tank and reduce the sedimentation of the solid phase. The mixing paddle was made of stainless steel, which had smooth surfaces, sufficient hardness, and good wear and corrosion resistance. The paddle types used in this work included a paddle with double inclined blades and a Rushton agitating paddle. The Rushton turbine is one of the most extensively studied radial pumping impellers in single-phase and multiphase operations due to its outstanding dispersion performance.
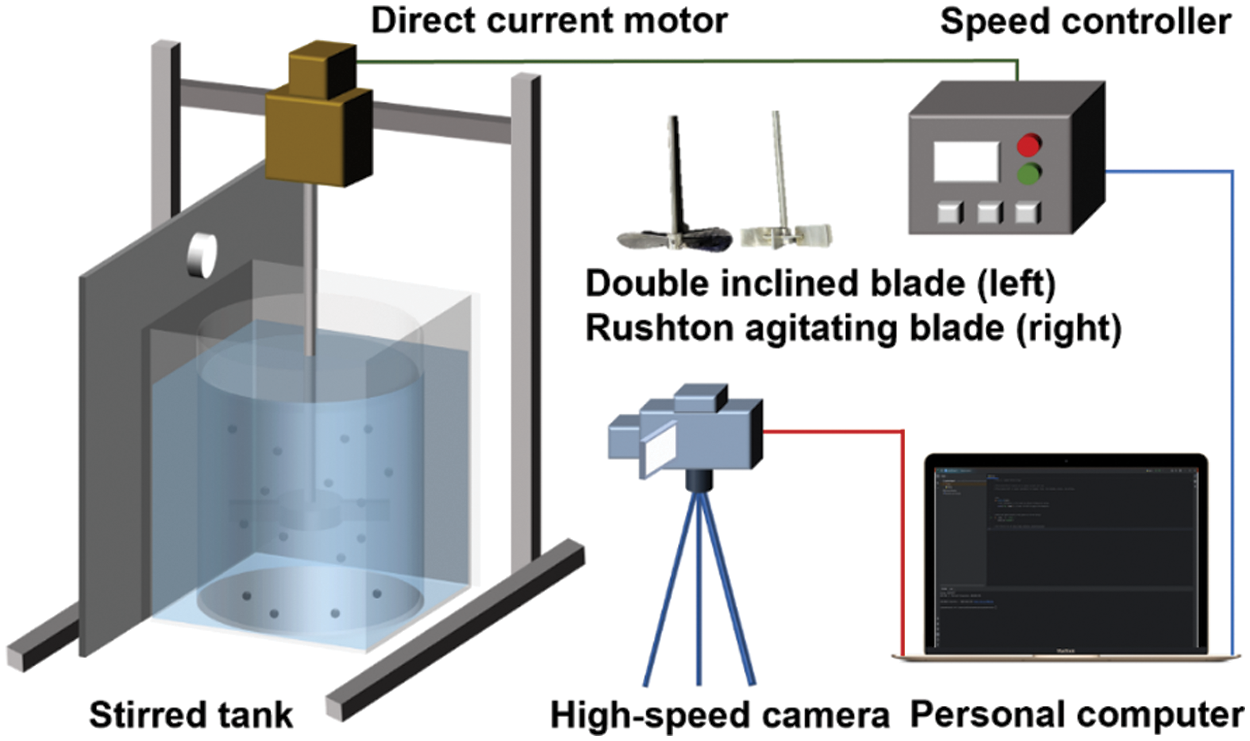
Figure 1: Schematic diagram of the custom-made solid-liquid two-phase mixing system
The designed operation factors and experimental setup are shown in Table 2. In this table, the paddle diameter ratio was obtained by comparing the paddle diameter with the inner diameter D of the stirred tank. The height-diameter ratio was obtained by comparing the spacing between the paddle and bottom with the inner diameter D of the stirred tank. For each case of the various mixing process experiments, the agitating speed was increased from 200 to 270 r/min, and the agitating or mixing time to reach a stable state (i.e., when sedimentary particles were no longer suspended) at each speed was controlled within 5 s. During the experimental mixing procedure, 5 g of glass microbeads (the number was approximately 10,000) were added to the inner stirred tank, and then 14.5 kg of water was injected to achieve a water surface height of 22 cm for the inner stirred tank. Subsequently, the agitating began and the fixed high-speed camera was used to record the mixing state quality of the solid-liquid two-phase mixture continuously. Next, the flow images of the stable mixing state quality for the mixture were obtained under the agitating condition. After obtaining the recorded video of the solid-liquid two-phase mixing process of all cases, digital image processing technology was employed to obtain the solid-liquid two-phase flow images of each case at every second of the mixing process experiments within steady-state conditions.
2.2 Indicators of Particle Suspension and Mixing Uniformity
Theoretically, homology analysis is developed as an advanced form of topology that deals not with measurable features such as lengths and/or angles but mostly with the connectivity of given objects. In the field of algebraic topology theory, the topological space, , includes a significant set of invariants, all of which take a value of a non-negative integer or infinity. The invariant represents the number of connected components in the space, and the invariant represents the change of channels in the structure. In a two-dimensional space, general channels are reduced into circles. In short, is the number of blocks in the pattern, and is the number of holes in the area. If the number of blocks in the pattern is sufficiently large, the effect of phase mixing is good enough.
In this work, the instantaneous flow images of the solid-liquid two-phase mixing process were recorded by the high-speed camera. Then, these captured flow images were converted into grayscale patterns, as shown in Fig. 2. The local upper region in a typical flow image was defined as the particle suspension region. In the lower part of a typical flow image, the local region of which the top line was approximately 10 mm away from the bottom of the stirred tank was defined as the particle deposition region. Therefore, the first dimension Betti number was used to characterize the topological distribution of the suspended solid phase, which had a value of assuming that all particles were suspended and did not block each other. From this, the particle suspension degree could be estimated by
(1)
and
(2)
where represents the particle suspension degree, represents the particle immersion degree, and the invariant represents the first dimension Betti number related to the number of suspended particles in the solid-liquid two-phase mixing process. The topology of structures in various fields has been quantified with the Betti numbers that are topological invariant quantities. It is found that Betti numbers remain unchanged under transformations including translation, rotation, and deformation. As mentioned above, , , and are defined as the number of one-dimensional, two-dimensional, and three-dimensional holes in the structure. If the data sets are three-dimensional, the topology can be defined with three Betti numbers, each having a simple and intuitive meaning. Specifically, the zeroth Betti number ( ), first Betti number ( ), and second Betti number ( ) probe the number of isolated objects, tunnels, and cavities, respectively. Computational Homology Project (CHomP) was adopted to calculate the Betti numbers of the binarized images for free.

Figure 2: Schematic diagram of the region of particle suspension (upper) and region of particle deposition (lower) of the solid particles in solid-liquid two-phase mixing process
Digital image processing technology is favorable for describing images or physical fields. Mathematically, a digital image can be converted into a digital matrix composed of various pixels. Here, the grayscale flow image of the solid-liquid two-phase mixing process could be regarded as a digital matrix. In addition, experiments are essential to industrial and scientific areas. In statistical experiment design theory, the uniform (low-discrepancy) design seeks its design points to be uniformly scattered on the experimental domain by minimizing a given discrepancy. The introduced concept (i.e., discrepancy) characterizes the deviation between the empirical distribution of the design points and the theoretical uniform distribution of the design points. Some bias-correction techniques are commonly adopted to improve the finite-sample performance of these estimators [41]. For , , , , and , the local discrepancy function of the particle suspension region in the digital matrix is given by [42]
(3)
where denotes the grayscale value at position of the particle suspension region , , and and refer to the quantities of the rows and columns of the grayscale digital matrix, respectively. Each element in the matrix refers to a grayscale value. It is worth mentioning that the grayscale values of the particles and the liquid phase in the image are different, and the grayscale values of the four corners of the matrix vary. It can be seen immediately that depends on the direction of the first calculated position. To address this issue, from the left-upper, left-lower, right-lower, and right-upper directions of the flow image are respectively calculated. Besides, is related to the values of and . Specifically, the areas of the four directions corresponding to the four areas increase as and increase. Finally, the areas can cover the whole flow image. Thereby, the single of the grayscale matrix is given by
(4)
where refers to the absolute value of , and ( ) refers to the nonuniformity degree of the grayscale value distribution in the local particle suspension region. Parameter refers to the upper-left, lower-left, lower-right, and upper-right directions respectively. To be conservative in this work, the uniformity coefficient of the particle suspension region is given by
(5)
where refers to the mixing uniformity of the local region in terms of particle deposition. To be brief, a higher uniformity coefficient indicates more uniformly distributed particle mixing.
A quantitative measure of mixing uniformity is essential to enable accurate recognition of uniformly distributed points by computers without human intervention. A good mathematical measure of mixing uniformity must also agree with the human perception of mixing uniformity. The coefficient of variation (denoted hereinafter by ) [43] and image entropy (denoted hereinafter by ) [44] are favorable for describing the distribution uniformity of objectives in flow images and physical fields. Specifically, is a statistic that measures the variation degree of each observed value in a grayscale digital matrix, whereas of an image can represent the aggregation characteristics of the grayscale distribution of the image. From the one-dimensional entropy, the two-dimensional entropy of the image can be formed by introducing the feature quantity that reflects the spatial characteristics of the grayscale distribution. Here, these two methods of image analysis were also introduced and used to calculate and compare the uniformity degree of solid-liquid two-phase mixing in instantaneous images.
Direct imaging methods also have their limitations. For a comprehensive error analysis, Fig. 3 shows a simplified error analysis model based on the topology of the multi-dimensional Betti number structure. In Fig. 3a the independent distribution of the solid phase in the local imaging region is shown with several topologically invariant Betti numbers: the zeroth Betti number = 1, first Betti number = 7, and second Betti number = 0. Fig. 3b shows the case of the connected solid phase in the imaging region with = 1, = 3, and = 0. Although the degree of solid particle suspension was the same in the imaging region, the solid phase was connected or incomplete at the edges of the particles, which led to errors arising from the various topologically invariant Betti numbers that were prevalent in this experimental process, although it was not possible to precisely characterize the degree of particle suspension during solid-liquid two-phase mixing. The Betti numbers associated with the suspended particles in the solid-liquid two-phase mixing process could well explain the general law of particle suspension in the solid-liquid two-phase mixing process. Besides, to discuss the reproducibility of this technique, some tests were performed by other operators independently on the same day using the same experimental system. The results they obtained differed from each other by less than 5% and were also consistent with other results [30].
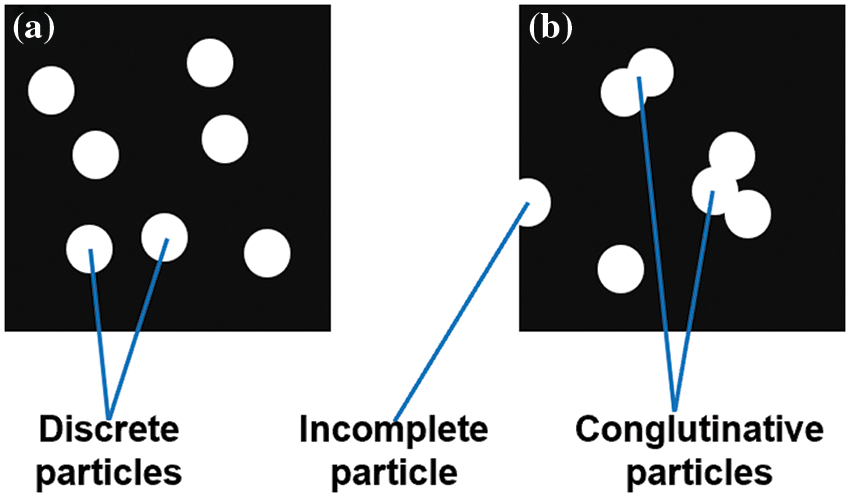
Figure 3: Case of independent distribution of solid phase in the local imaging region (a) and case of connected solid phase in the local imaging region (b)
3.1 Effect of Paddle Shape on Particle Suspension and Mixing Uniformity
Uniform mixing of solid-liquid two-phase is desired to avoid the deposition of the solid phase (i.e., particles), enhance the contact area between the solid and liquid phases, improve the reaction rates between reactants, and ensure uniform reaction progress in the whole stirred tank. It is well known that an appropriate selection of design variables and operating parameters including the impeller speed, impeller clearance, and number of impellers could enhance the suspension quality of solid-liquid two-phase mixtures. Fig. 4 shows the first dimension Betti number and the corresponding particle suspension degree under stirring of the Rushton agitating paddle and paddle with double inclined blades. Fig. 4a,b shows the variations of particle suspension degree with the stirring speed under the agitation of the Rushton agitating paddle and the paddle with double inclined blades, respectively. It could be observed that the particle suspension degree increased with the increase in agitating speed from 200 to 270 r/min. However, there was an obvious difference between these two stirring strategies. Specifically, at lower speeds ranging from 200 to 220 r/min, the uplift force on the solid phase generated by the paddle with double inclined blades on the fluid was greater than that generated by the Rushton paddle, which promoted particle levitation. At higher speeds ranging from 240 to 270 r/min, a chaotic segregation zone was formed around the paddles, resulting in reduced mixing performance and particle suspension. The particle suspension degree in Fig. 4b was significantly higher than that in Fig. 4a when the impeller speed ranged from 200 to 220 r/min. As shown in Fig. 4b, the particle suspension degree decreased at higher stirring speeds from 240 to 270 r/min.
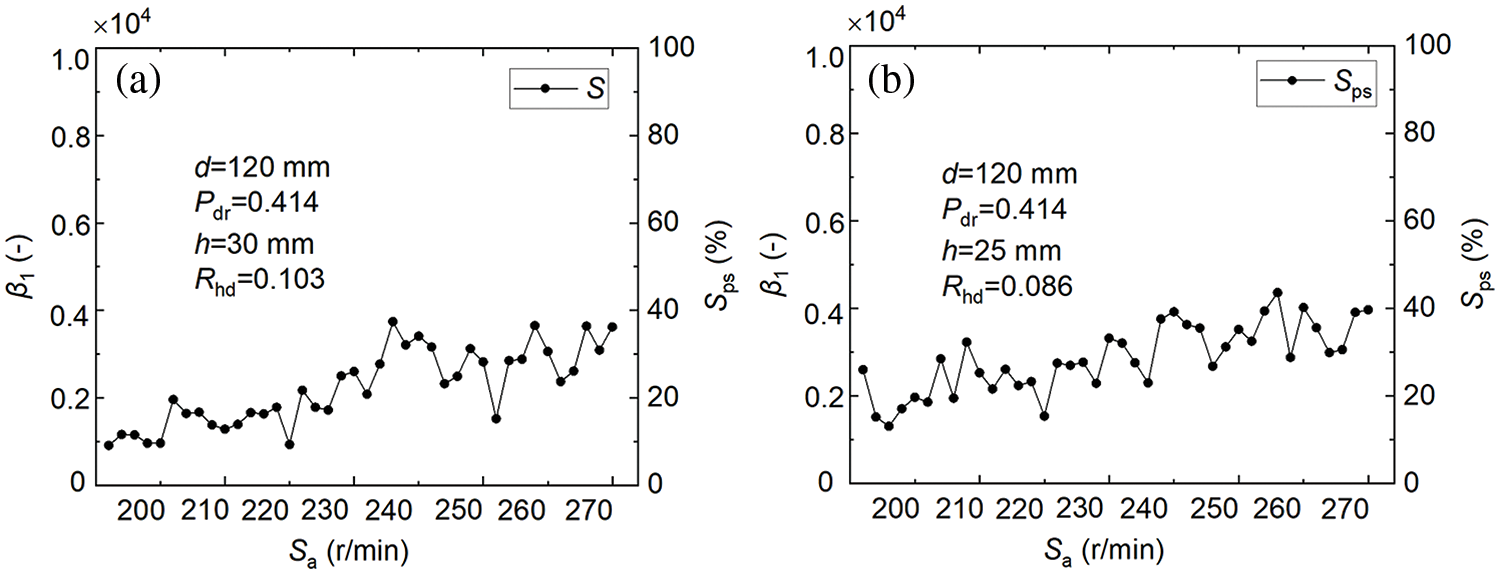
Figure 4: Relation between Rushton agitating paddle and particle suspension degree (a); relation between paddle with double inclined blades and particle suspension degree (b)
Solid-liquid two-phase mixing systems have been popular in industrial production and scientific experiments related to suspension. The change in concentration and the fluctuation of uniformity directly determine the physical and chemical properties and service stability of the final product. Therefore, real-time, in-situ, and precise measurements are critical. As shown in Table 3, Case #1 used the Rushton agitating paddle, and Case #2 employed the paddle with double inclined blades. Under the stirring of the Rushton agitating paddle, the average particle suspension degree corresponding to the eight rotational speeds was 10.28%, 15.86%, , and 30.66%, respectively. Under the stirring of the paddle with double inclined blades, the average particle suspension degree corresponding to the eight rotational speeds was 20.66%, 16.52%, , and 31.86%, respectively. It was found that the suspension degree of particles increased with the increase in rotational speed, and the levitation gap between the two paddle types narrowed at high speeds. However, the mixing state quality from the paddle with double inclined blades was still better than that of the Rushton agitating paddle. At the maximum rotational speed of 270 r/min in this work, the suspension degree reached 30.66% when the Rushton agitating paddle was used, while the highest suspension degree reached 31.86% when the paddle with double inclined blades was used, under which it was easier to lift solid phase with more suspended particles and better mixing process quality.

The distribution of a finite number of points (e.g., particles or solid phase) is referred to as a pattern in this work. Uniformity and aggregation of particles or solid phase are considered as two typical opposite features of a pattern. The uniformity indicator is used to describe the uniformity of a finite point set (e.g., particles, bubbles, or droplets). However, aggregation may increase solid-solid interfaces between particles, bubbles, or droplets. In the following text, therefore, some experimental results related to the mixing uniformity of the solid-liquid two-phase mixture in the stirred tank are illustrated, where the two paddles (i.e., the Rushton agitating paddle and paddle with double inclined blades) are considered.
The two panels of Fig. 5 show the uniformity coefficient (denoted hereinafter by ), , and under working conditions and . It could be observed from Fig. 5a that the change in the three uniformity indicators was not obvious. Especially, the values of under various values of agitating speed ( ) were all close to . It could be preliminarily concluded that the Rushton agitating paddle could make solid-liquid two-phase mixing evenly at various speeds. The finding obtained from Fig. 5b was consistent with that from Fig. 5a. For instance, the average uniformity indicators under the eight cases of were approximatively , , and , respectively. However, the values of from Fig. 5b were markedly lower than those in Fig. 5a. In addition, the values of in Fig. 5b were slightly greater than those in Fig. 5a. It could be concluded that the paddle with double inclined blades was more beneficial to promoting the mixing uniformity of the solid-liquid two-phase mixture when the other parameters were kept the same. The satisfactory performance of the paddle with double inclined blades also preliminarily confirmed its superiority in promoting mixing uniformity and improving particle suspension.
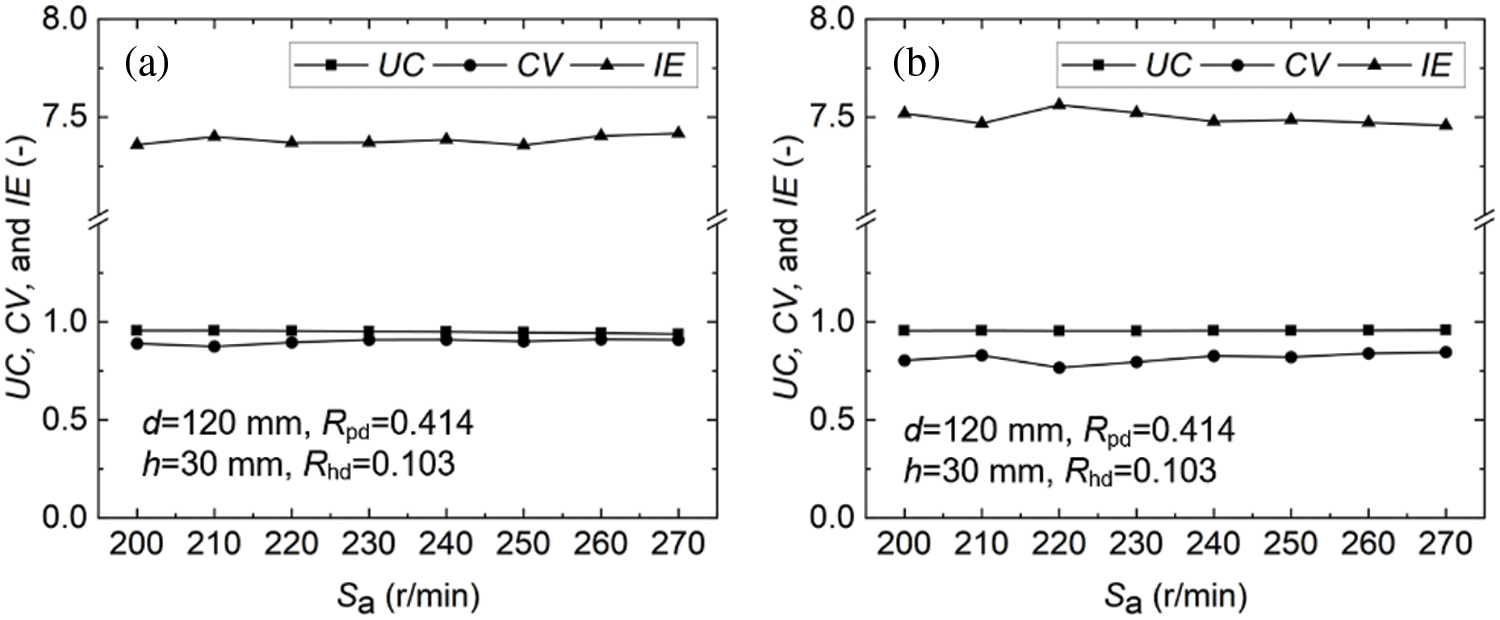
Figure 5: , , and for Rushton paddle (a) and paddle with double inclined blades (b)
3.2 Effect of Rotational Speed on Particle Suspension and Mixing Uniformity
Another factor essential for the solid-liquid two-phase mixing process is the agitation speed. For generalization, the key is to convert the stirring speed to the Reynolds number. The solid-liquid two-phase mixing process at various agitation speeds was successfully conducted and the experimental data are shown in Fig. 6. According to this figure, the agitation speed was varied as follows: , , , , , , , and r/min. Fig. 6a shows the relationship between the agitating speed and the particle suspension degree. Here, in experimental case L2, the paddle diameter was mm, the paddle diameter ratio was , the spatial distance between the paddle and the bottom was mm, and the height-diameter ratio was . The particle suspension degree fluctuated slightly under the various rotational speeds from to r/min by an interval of 10 r/min. In addition, the average particle suspension degrees corresponding to the eight rotational speeds were respectively 20.66%, 16.52%, 20.90%, 25.82%, 26.18%, 31.06%, 29.62%, and 31.86% under the stirring of the paddle with double inclined blades. It was found that the suspension degree of particles increased with the increase in rotational speed. Therefore, it could be believed that the mixing state quality of the solid-liquid two-phase mixing system in the stirred tank could be improved by increasing the agitating speed. Naturally, the solid phase might be completely suspended at the bottom, and the mixing state quality of a solid-liquid two-phase mixing system might be optimized if the mixing speed reached a critical value at which the solid phase was completely suspended at the bottom of the stirred tank. Fig. 6b shows the levels of , , and with stirring of the paddle with double inclined blades. From the present results, the average , , and levels of the eight observations of did not change much with the varying agitation speed. The experimental results led to a conclusion similar to that from the discussion related to agitation speed above. In addition, an interesting phenomenon could be observed in this subfigure. Under the same experimental conditions, Fig. 6a shows that the particle suspension increased with an increasing stirring speed, while Fig. 6b shows that remained constant with the increasing stirring speed. The paddle with double inclined blades promoted the suspension of particles, though not significantly affecting the mixing uniformity of the solid-liquid two-phase mixing system. This shows that with the increase in rotational speed, the paddle with double inclined blades could not only improve the suspension degree of particles in the stirred tank but also ensure the mixing uniformity of the solid-liquid two-phase mixing system.
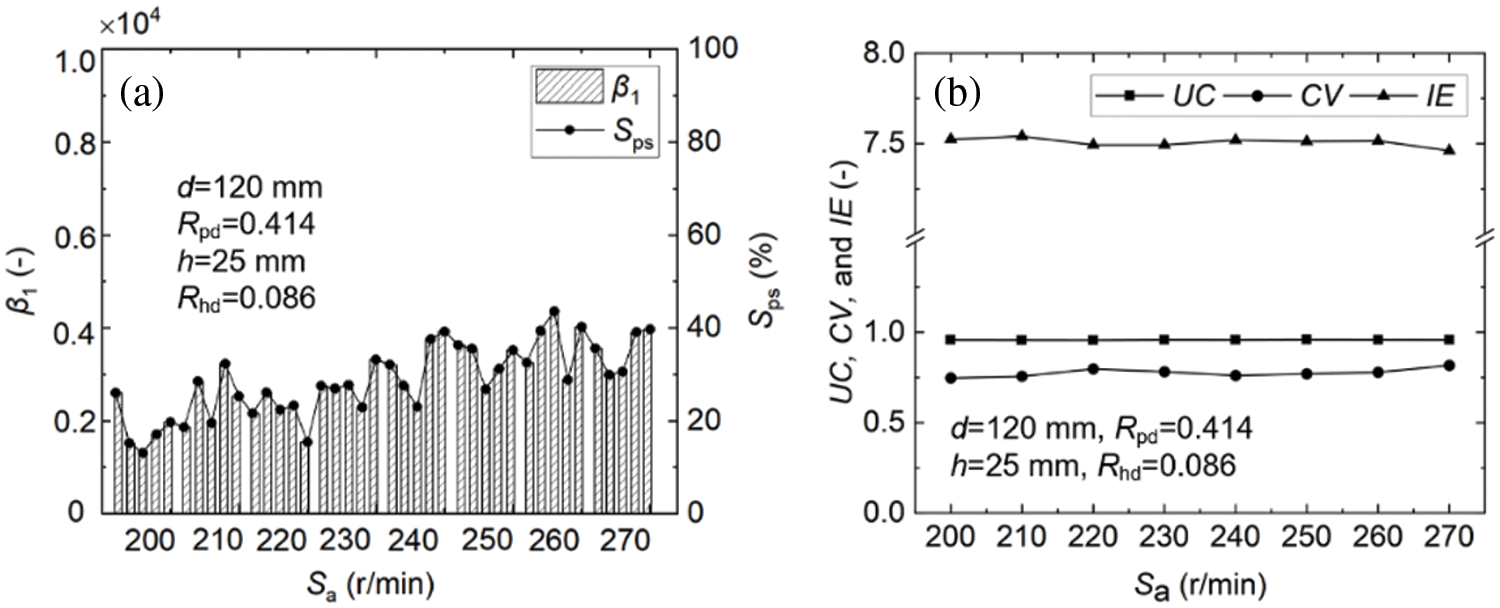
Figure 6: Relation between and (a); relation between and , and (b)
3.3 Effect of Propeller Diameter on Particle Suspension and Mixing Uniformity
Another popular variation among design variables and operation parameters is the paddle wheel diameter. Experiments were conducted in the tanks with four paddle wheel diameters. Fig. 7 shows the relationship between paddle diameter and particle suspension degree. The paddle diameter ratio in this figure was , , , and , respectively. As could be seen from this figure, the particle suspension gradually increased as the rotational speed increased. However, the particle suspension degree did not increase with the increase of the paddle diameter ratio . Within the speed range considered in this work, the particles mostly moved along the wall at the tank bottom when the propeller diameter was small. Some particles began to converge to the center below the paddle and most of them showed a low suspension state as the paddle diameter ratio increased.
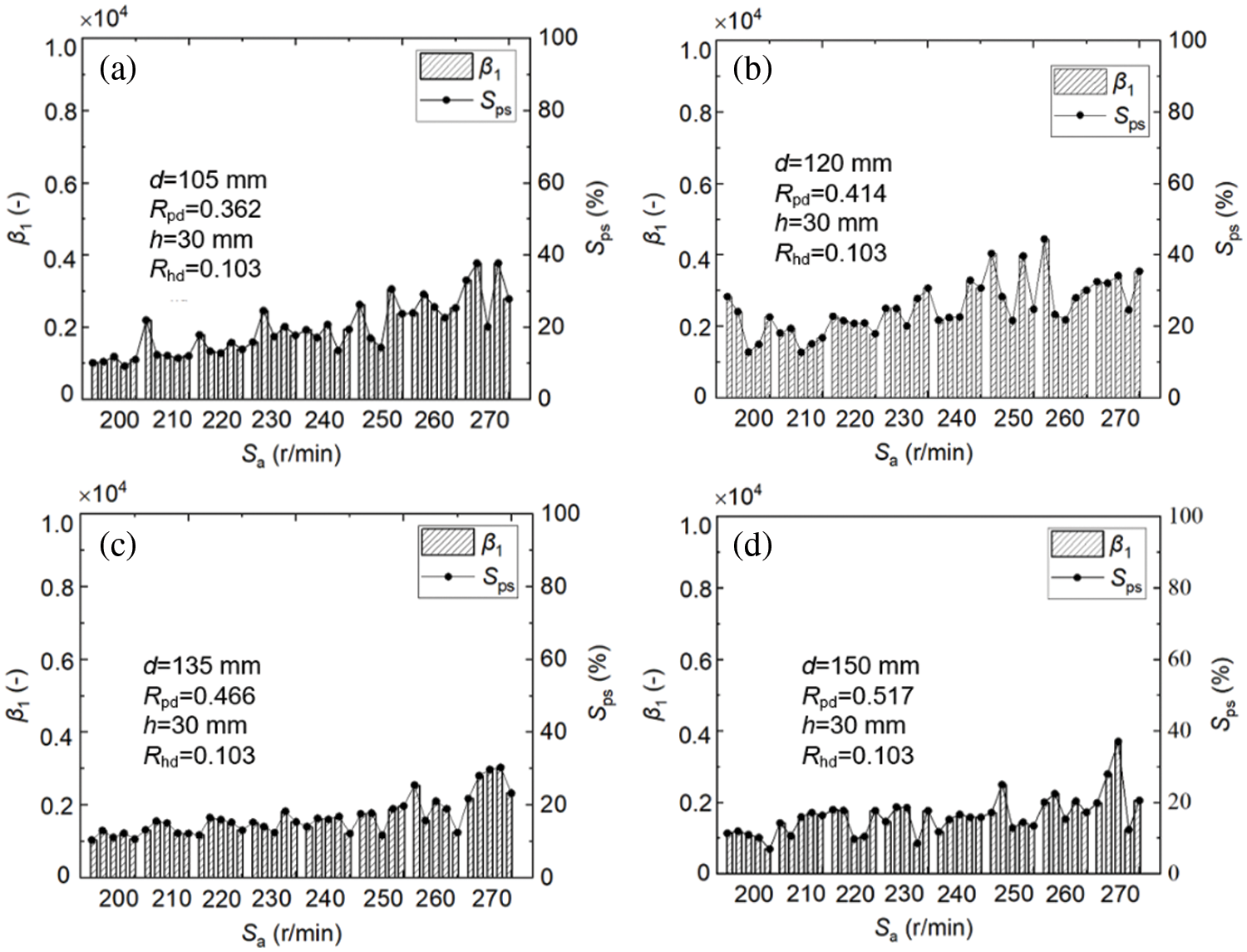
Figure 7: (a) Relationship between Sa and β1 for paddle diameter d = 105 mm, (b) Relationship between Sa and β1 for paddle diameter d = 120 mm, (c) Relationship between Sa and β1 for paddle diameter d = 135 mm, (d) Relationship between Sa and β1 for paddle diameter d = 150 mm
As shown in Fig. 8, the solid phase moved in low suspension below the paddle and near the middle of the tank bottom when the paddle diameter ratio was large enough. The reason might be that the state dominated by the bottom motion near the wall became the state dominated by the low-degree suspension motion below the paddle. Therefore, for the solid-liquid two-phase agitation, there would be an optimal propeller diameter or propeller diameter ratio. Under this condition, a relatively optimal mixing state quality could be obtained for the solid-liquid two-phase system. However, the mixing state quality of the solid-liquid two-phase mixture would be reduced if the propeller diameter was less than or exceeded this level.

Figure 8: Instantaneous image of solid-liquid two-phase mixing process from the case L7
In addition, the stirring performance analysis is of great research significance, and a vast number of flow visualization tests have been undertaken before assessing the mixing performance to identify the mixing behavior. Hence, several data were combined to check the stirring performance and obtain the working environment for better stirring performance. The fluctuations of , , and under stirring of the paddle with double inclined blades under various propeller diameters were not obvious, as shown in Fig. 9. It indicated that the paddle diameter ratio might not be the main factor affecting the mixing uniformity. In general, the stirring performance would be better when the paddle diameter was 120 mm in this work. The results might provide new insights for optimizing the stirrer design and identifying simulation obstacles and future simulation scopes for programmers undertaking the mixing performance simulation. However, it still faced certain challenges before optimizing its performance.
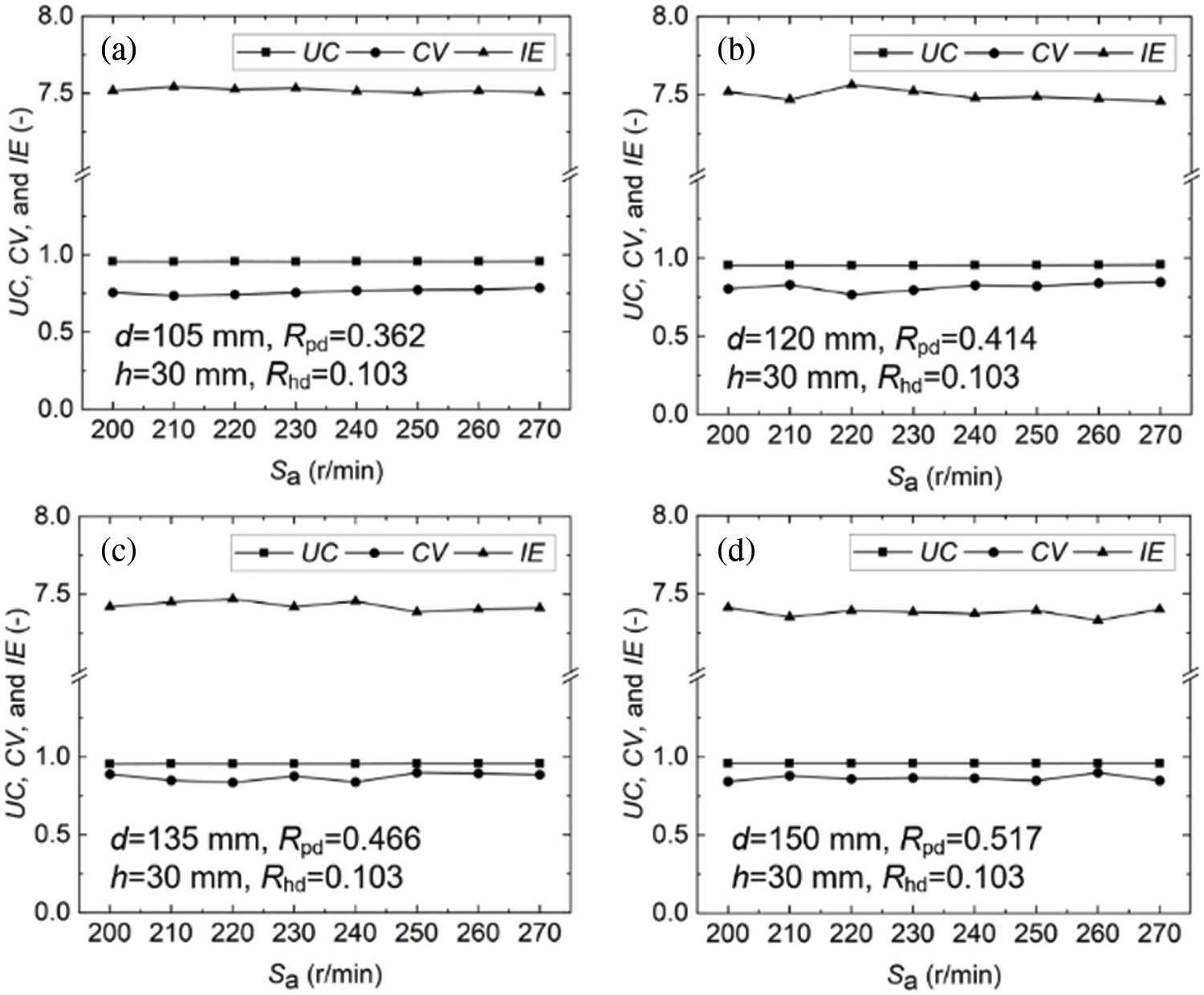
Figure 9: The uniformity coefficient ( ), coefficient of variation ( ) and image entropy ( ) with stirring of paddle with double inclined blades and various propeller diameter d = 105 mm (a), d = 12 mm (b), d = 135 mm (c) and d = 150 mm (d)
3.4 Effect of Paddle Height off the Bottom on Mixing State Quality
Fig. 10 shows the relationship between the height of the paddle off the bottom and the particle suspension degree. It could be seen from this figure that the particle suspension degree showed a decreasing trend with the increase in height-diameter ratio. The solid phase tended to deposit at the bottom of the stirred tank and move along the wall during mixing when the height-diameter ratio of the paddle was small. The solid phase in low suspension under the paddle at high rotational speeds seemed to be less. Fig. 11 shows the flow images of the solid-liquid two-phase mixing process of L2, L3, and L4. The solid phase under the paddle was more likely to show the state of the bottom near the wall. The solid phase began to gather toward the center and showed a low suspension state when the height-diameter ratio increased. The solid phase at the tank bottom converged toward the center, and most of them showed a low suspension state under the paddle. Almost no particles moved along the wall, and high rotational speed could further promote the solid phase below the paddle to show a low suspension state. It also increased the motion range of the solid phase in low suspension. Therefore, the decrease of the height of the paddle off the bottom could promote the mixing state quality of the solid-liquid two-phase mixture, but when the height was too small, its effect on the mixing state quality was also diminished.
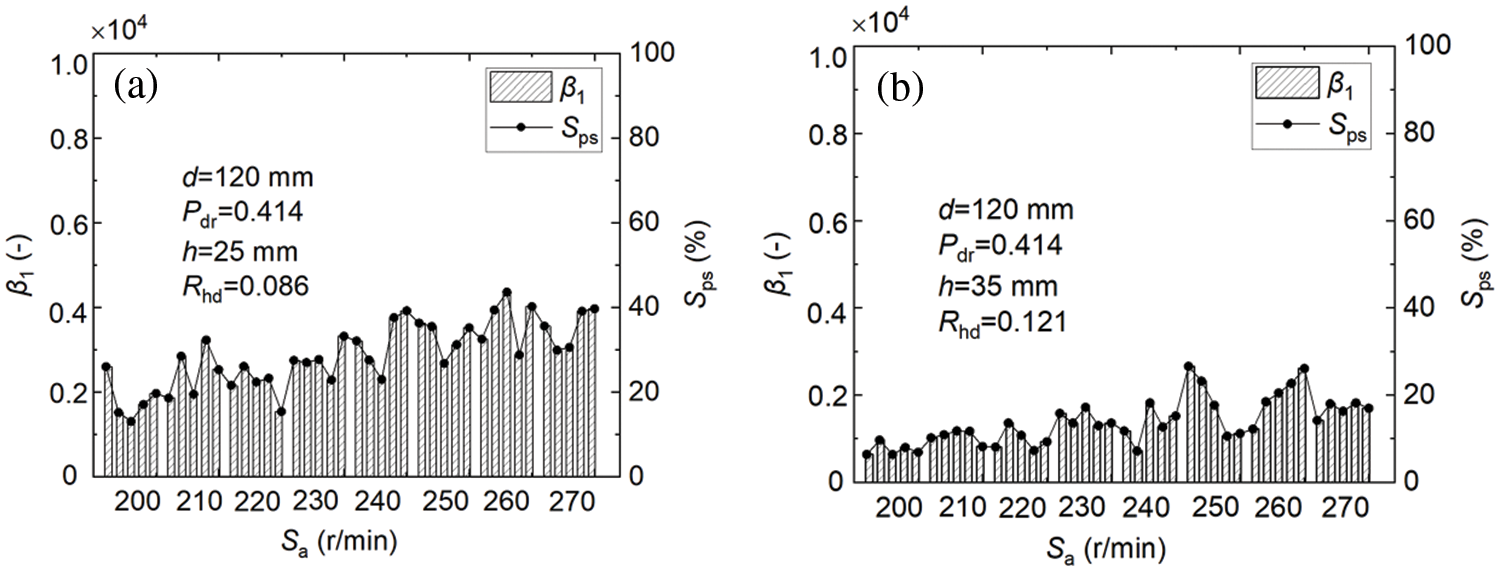
Figure 10: Relationship between Sa and β1 for the height of the paddle off the bottom h = 0.25 mm (a) and h = 0.35 mm (b)

Figure 11: Flow images from solid-liquid two-phase mixing process of L2, L3, and L4
On the one hand, a high height-diameter ratio of the stirred tank was usually believed to be beneficial due to improved selection pressure on particles with better settling ability. On the other hand, some operations needed to be carried out at appropriate blade speeds to obtain the necessary quality and maximum throughput. However, a change in the blade speed would bring about changes to the mixing process in several approaches. For instance, there would be changes in the particle flow patterns, particle structure, and force imparted to the particles in the mixture. Knowledge of these matters is still in its infancy. In addition, investigations of the effect of blade speed would also become critical when scaling up a solid-liquid two-phase stirred tank to a full-scale mixer. Fig. 12 shows , , and vs. rotational speed for mixing with various heights of the paddle with double inclined blades. Under the same rotational speed, decreased slightly with the increase of the height-diameter ratio, and the solid-liquid two-phase mixing uniformity had a slightly decreasing trend. However, with the increase in blade speed, the mixing uniformity between the solid phase and liquid phase showed an obvious decreasing trend. On the one hand, it might be due to reduced particle suspension. On the other hand, it was probably due to the high position of the blade causing eddy currents in the center of the liquid surface. It was found that the stirring performance was better when the height of the blade from the bottom was 25 mm. Generally, the most significant design parameter for the stirred tank was the height-diameter ratio, which can be very flexible in practice. When designing a stirred tank, various parameters need to be fully considered and comprehensively optimized according to the specific reaction process requirements and process conditions to ensure the desired reaction process in the stirred tank.
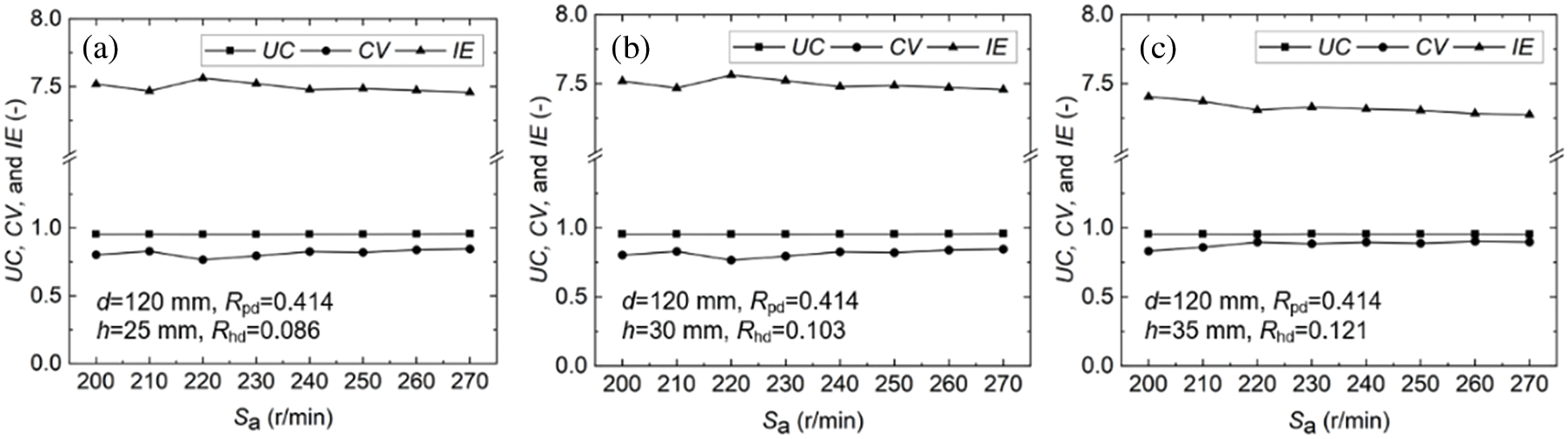
Figure 12: The uniformity coefficient (UC), coefficient of variation (CV) and image entropy (IE) with stirring of paddle with double inclined blades and paddle height h = 25 mm (a), h = 30 mm (b) and h = 35 mm (c).
In this work, the experiment for measuring the mixing state quality of the solid-liquid two-phase mixture was designed, and the flow images of the solid-liquid two-phase mixing process were obtained and processed. Specifically, the suspension indicators of the solid phase and mixing uniformity of the solid-liquid two-phase mixture were obtained by algebraic topology theory and digital image processing technology. The relationships between the mixing state quality and the propeller type, rotating speed, propeller diameter, and distance between the paddle and bottom were analyzed. The increase in agitating speed could promote the particle suspension degree, and the higher the agitating speed, the greater the effect on the mixing state quality. The decrease of the spacing between the paddle and the bottom could also improve the particle suspension degree, but the effect on the mixing state quality of the solid phase and liquid phase was diminished if the spacing was too small. The influence of paddle diameter on the mixing state quality of the solid-liquid two-phase mixture was also large and differed from the previous two. For agitating solid-liquid two-phase mixing, an optimal paddle diameter or paddle diameter ratio existed, under which the optimum mixing state quality of the solid-liquid two-phase mixture could be obtained. The solid phase motion could be divided into three parts: bottom motion along the wall, low suspension under the blade, and high suspension above the blade. The best particle suspension degree could be achieved at an agitating speed of 270 r/min, a paddle diameter ratio of 0.414, and a height diameter ratio of 0.086 by the paddle with double inclined blades.
Acknowledgement: The authors wish, especially, to thank the referees for numerous detailed questions and comments that greatly improved the presentation.
Funding Statement: The authors acknowledge the financial support from the Yunnan Fundamental Research Project, China (No. 202201BE070001-026), Interdisciplinary Research Project of Kunming University of Science and Technology (No. KUST-xk2022001), Yunnan Major Scientific and Technological Projects (No. 202302AQ370001-4), Open Foundation of State Environmental Protection Key Laboratory of Mineral Metallurgical Resources Utilization and Pollution Control (No. HB202204), and Young Elite Scientist Sponsorship Program by China Association for Science and Technology, China (No. YESS20210106).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Kai Yang, Hua Wang, Qingtai Xiao; data collection: Kai Yang, Qinwen Yao, Qingtai Xiao, Yingshan Li; analysis and interpretation of results: Kai Yang, Qinwen Yao, Saleh Khorasani, Qingtai Xiao; draft manuscript preparation: Kai Yang, Wanchang Chen, Qingtai Xiao. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Yang K, Liu J, Wang M, Wang H, Xiao Q. Identifying flow patterns in a narrow channel via feature extraction of conductivity measurements with a support vector machine. Sensors. 2023;23(4):1907. doi:10.3390/s23041907. [Google Scholar] [PubMed] [CrossRef]
2. Kress P, Nägele H-J, Oechsner H, Ruile S. Effect of agitation time on nutrient distribution in full-scale CSTR biogas digesters. Bioresour Technol. 2018;247:1–6. doi:10.1016/j.biortech.2017.09.054. [Google Scholar] [PubMed] [CrossRef]
3. Jadidi B, Ebrahimi M, Ein-Mozaffari F, Lohi A. Analysis of cohesive particles mixing behavior in a twin-paddle blender: DEM and machine learning applications. Particuology. 2024;90:350–63. doi:10.1016/j.partic.2023.12.010. [Google Scholar] [CrossRef]
4. Wu W, Chen K, Tsotsas E. Prediction of particle mixing in rotary drums by a DEM data-driven PSO-SVR model. Powder Technol. 2024;434:119365. doi:10.1016/j.powtec.2024.119365. [Google Scholar] [CrossRef]
5. Bowler AL, Bakalis S, Watson NJ. A review of in-line and on-line measurement techniques to monitor industrial mixing processes. Chem Eng Res Des. 2020;153:463–95. doi:10.1016/j.cherd.2019.10.045. [Google Scholar] [CrossRef]
6. Deng T, Fisonga M, Ke H, Li L, Wang J, Deng Y. Mixing uniformity effect on leaching behaviour of cement-based solidified contaminated clay. Sci Total Environ. 2024;908:167957. doi:10.1016/j.scitotenv.2023.167957. [Google Scholar] [PubMed] [CrossRef]
7. Yang K, Wang Y, Li M, Li X, Wang H, Xiao Q. Modeling topological nature of gas-liquid mixing process inside rectangular channel using RBF-NN combined with CEEMDAN-VMD. Chem Eng Sci. 2023;267:118353. doi:10.1016/j.ces.2022.118353. [Google Scholar] [CrossRef]
8. Mishra P, Ein-Mozaffari F. Critical review of different aspects of liquid-solid mixing operations. Rev Chem Eng. 2020;36(5):555–92. doi:10.1515/revce-2018-0017. [Google Scholar] [CrossRef]
9. Mao C, Hou Y, Wang Y. Research on the effects of slurry uniformity and mixing power of continuous cementing slurry mixers based on statistical and CFD methods. Geoenergy Sci Eng. 2024;233:212574. doi:10.1016/j.geoen.2023.212574. [Google Scholar] [CrossRef]
10. Yang K, Wang Y, Wang M, Pan J, Wang H, Xiao Q. A unified heat transfer model for gas-liquid two-phase mixing process in a rectangular channel based on steady status identification. Appl Therm Eng. 2024;236:121612. doi:10.1016/j.applthermaleng.2023.121612. [Google Scholar] [CrossRef]
11. Yang Z, Holemans T, Lagrain B, Sels B, Vanierschot M. A solid-liquid mixing reactor based on swirling flow technology. Chem Eng Sci. 2023;280:119054. doi:10.1016/j.ces.2023.119054. [Google Scholar] [CrossRef]
12. Kajiwara S, Sakai M. Numerical investigation on a bimodal mixing system of solid-liquid mixture in an industrial mixing cooker. Adv Powder Technol. 2024;35(1):104300. doi:10.1016/j.apt.2023.104300. [Google Scholar] [CrossRef]
13. Sandhanshiv RD, Patel DM. Design and fabrication of an adjustable stirring and degassing system for synthesis of metal matrix composite material. Mater Today Proc. 2022;59:974–8. [Google Scholar]
14. Yamazaki T, Kitamura S, Matsumiya T. Effect of liquid phase in flux on hot metal desulfurization by mechanical stirring process. Tetsu Hagane-J Iron Steel Inst Jpn. 2019;105(1):1–9. doi:10.2355/tetsutohagane.TETSU-2018-123. [Google Scholar] [CrossRef]
15. Li D, Lu T, Yu Z, Song W, Ding Y. Experimental investigation on the promotion of CO2 hydrate formation for cold thermal energy storage-effect of gas-inducing stirring under different agitation speeds. Green Energy Resour. 2023;1(4):100047. doi:10.1016/j.gerr.2024.100047. [Google Scholar] [CrossRef]
16. Yulianingsih R, Gohtani S. The influence of stirring speed and type of oil on the performance of pregelatinized waxy rice starch emulsifier in stabilizing oil-in-water emulsions. J Food Eng. 2020;280:109920. [Google Scholar]
17. Lee Y, Lee S, Cui M, Kim J, Ma J, Han Z, et al. Improving sono-activated persulfate oxidation using mechanical mixing in a 35-kHz ultrasonic reactor: persulfate activation mechanism and its application. Ultrason Sonochem. 2021;72:105412. doi:10.1016/j.ultsonch.2020.105412. [Google Scholar] [PubMed] [CrossRef]
18. Jin X, Chandratilleke RG, Wang S, Shen Y. DEM investigation of mixing indices in a ribbon mixer. Particuology. 2022;60:37–47. doi:10.1016/j.partic.2021.03.005. [Google Scholar] [CrossRef]
19. Adibi M, Mirkazemi SM, Alamolhoda S. The comparative study on microstructure and magnetic properties of cobalt ferrite/MWCNTs nanocomposite prepared using mechanical mixing and hydrothermal routs. J Magn Magn Mater. 2023;586:171187. doi:10.1016/j.jmmm.2023.171187. [Google Scholar] [CrossRef]
20. Zhang M, Gao Q, Zhao Z, Guo L, Li X, Zhang C, et al. Liquid metal manifold microchannel heat sink for ultra-high heat flux cooling. Appl Therm Eng. 2024;248:123117. doi:10.1016/j.applthermaleng.2024.123117. [Google Scholar] [CrossRef]
21. Kolano M, Danke J, Kraume M. Using thrust to control the mixing process in stirred tanks with side-entering agitators and viscoelastic fluids. Biomass Bioenergy. 2021;152:106180. doi:10.1016/j.biombioe.2021.106180. [Google Scholar] [CrossRef]
22. Li A, Yao Y, Tang X, Liu P, Zhang Q, Li Q, et al. Experimental and computational investigation of chaotic advection mixing in laminar rectangular stirred tanks. Chem Eng J. 2024;485:149956. doi:10.1016/j.cej.2024.149956. [Google Scholar] [CrossRef]
23. Meng T, Wang Y, Wang S, Qin S, Zhang Q, Wang Y, et al. Exploration of multishafts stirred reactors: an investigation on experiments and large eddy simulations for turbulent chaos and mixing characteristics. Ind Eng Chem Res. 2024;63(5):2441–56. doi:10.1021/acs.iecr.3c04042. [Google Scholar] [CrossRef]
24. Wu J, Nguyen B, Graham L, Hurley M, Harris D, Short G, et al. Increased agitation reliability for slurry suspension in mineral processing. Miner Eng. 2021;170:107008. doi:10.1016/j.mineng.2021.107008. [Google Scholar] [CrossRef]
25. Zwietering TN. Suspending of solid particles in liquid by agitators. Chem Eng Sci. 1958;8(3–4):244–53. doi:10.1016/0009-2509(58)85031-9. [Google Scholar] [CrossRef]
26. Baldi G, Conti R, Alaria E. Complete suspension of particles in mechanically agitated vessels. Chem Eng Sci. 1978;33(1):21–5. doi:10.1016/0009-2509(78)85063-5. [Google Scholar] [CrossRef]
27. Mishra P, Ein-Mozaffari F. Using tomograms to assess the local solid concentrations in a slurry reactor equipped with a Maxblend impeller. Powder Technol. 2016;301:701–12. doi:10.1016/j.powtec.2016.07.007. [Google Scholar] [CrossRef]
28. Mishra P, Ein-Mozaffari F. Using computational fluid dynamics to analyze the performance of the Maxblend impeller in solid-liquid mixing operations. Internal J Multiphase Flow. 2017;91:194–207. doi:10.1016/j.ijmultiphaseflow.2017.01.009. [Google Scholar] [CrossRef]
29. Liu B, Xu Z, Fan F, Huang B. Experimental study on the solid suspension characteristics of coaxial mixers. Chem Eng Res Des. 2018;133:335–46. doi:10.1016/j.cherd.2018.03.035. [Google Scholar] [CrossRef]
30. Giuseppina M, Francesco M, Federico A, Suzuka I, Katsuhide T, Alessandro P. Large blade impeller application for turbulent liquid-liquid and solid-liquid mixing. Can J Chem Eng. 2022;100(9):2230–44. doi:10.1002/cjce.24483. [Google Scholar] [CrossRef]
31. Mirfasihi S, Basu W, Martin P, Kowalski A, Fonte CP, Keshmiri A. Investigation of mixing miscible liquids with high viscosity contrasts in turbulently stirred vessels using electrical resistance tomography. Chem Eng J. 2024;486:149712. doi:10.1016/j.cej.2024.149712. [Google Scholar] [CrossRef]
32. Yang C, Yao J, Chen X, Xu Z, Zhou G, Xu Z, et al. Experimental study on gas-liquid flow regimes of coaxial mixers equipped with a Rushton/pitched blade turbine and anchor. Chem Eng Res Des. 2024;202:377–89. doi:10.1016/j.cherd.2023.12.040. [Google Scholar] [CrossRef]
33. Yang M, Lai Y. Experimental study on solid-liquid suspension characteristics in a mixing tank. Chin J Mech Eng. 2011;47(6):186–92 (In Chinese). doi:10.3901/JME.2011.06.186. [Google Scholar] [CrossRef]
34. Sutkar VS, Deen NG, Salikov V, Antonyuk S, Heinrich S, Kuipers JAM. Experimental and numerical investigations of a pseudo-2D spout fluidized bed with draft plates. Powder Technol. 2015;270:537–47. doi:10.1016/j.powtec.2013.11.030. [Google Scholar] [CrossRef]
35. Juez JM, Artoni R, Cazacliu B. Monitoring of concrete mixing evolution using image analysis. Powder Technol. 2017;305:477–87. doi:10.1016/j.powtec.2016.10.008. [Google Scholar] [CrossRef]
36. Teoman B, Shastry S, Abdelhamid S, Armenante PM. Imaging method for the determination of the minimum agitation speed, Njs, for solids suspension in stirred vessels and reactors. Chem Eng Sci. 2021;231:116263. doi:10.1016/j.ces.2020.116263. [Google Scholar] [CrossRef]
37. Behnia S, Mobadersani F, Yahyavi M, Rezavand A. Chaotic behavior of gas bubble in non-Newtonian fluid: a numerical study. Nonlinear Dyn. 2013;74:559–70. doi:10.1007/s11071-013-0988-3. [Google Scholar] [CrossRef]
38. Tchakui MV, Woafo P, Skokos C. Chaotic dynamics of piezoelectric mems based on maximal Lyapunov exponent and Smaller Alignment Index computations. Int J Bifurcat Chaos. 2019;30:09. [Google Scholar]
39. Gameiro M, Singh A, Kondic L, Mischaikow K, Morris JF. Interaction network analysis in shear thickening suspensions. Phys Rev Fluids. 2020;5(3):034307. doi:10.1103/PhysRevFluids.5.034307. [Google Scholar] [CrossRef]
40. Liao Y, Wei N, Liu J, Wang H, Xiao Q. Enhancement of solid-liquid mixing state quality in a mechanical stirred reactor with serial-chaotic rotation generated by basic speed method. Chemosphere. 2024;349:140804. doi:10.1016/j.chemosphere.2023.140804. [Google Scholar] [PubMed] [CrossRef]
41. Park C, Kim H, Wang M. Investigation of finite-sample properties of robust location and scale estimators. Commun Stat Simul Comput. 2022;51(5):2619–45. doi:10.1080/03610918.2019.1699114. [Google Scholar] [CrossRef]
42. Wang Z, Zhu N, Wang W, Chao X. Y-Net: a dual-branch deep learning network for nonlinear absorption tomography with wavelength modulation spectroscopy. Opt Express. 2022;30(2):2156–72. doi:10.1364/OE.448916. [Google Scholar] [PubMed] [CrossRef]
43. Amdouni A, Castagliola P, Taleb H, Celano G. One-sided run rules control charts for monitoring the coefficient of variation in short production runs. Eur J Ind Eng. 2016;10(5):639–63. doi:10.1504/EJIE.2016.078804. [Google Scholar] [PubMed] [CrossRef]
44. Rodriguez G, Anderlei T, Micheletti M, Yianneskis M, Ducci A. On the measurement and scaling of mixing time in orbitally shaken bioreactors. Biochem Eng J. 2014;82:10–21. doi:10.1016/j.bej.2013.10.021. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools
