 Open Access
Open Access
ARTICLE
Impact of the Inlet Flow Angle and Outlet Placement on the Indoor Air Quality
1 Laboratoire des Sciences et Ingénierie Maritimes, Faculté de Génie Mécanique. Université des Sciences et de la Technologie d’Oran Mohammed Boudiaf, BP 1505 El M’Naouer, Oran, 31000, Algérie
2 Laboratoire LERMAB IUT Longwy, Université de Lorraine, Nancy, 54000, France
* Corresponding Author: Ikram Mostefa Tounsi. Email:
(This article belongs to the Special Issue: Materials and Energy an Updated Image for 2023)
Fluid Dynamics & Materials Processing 2024, 20(11), 2603-2616. https://doi.org/10.32604/fdmp.2024.050641
Received 12 February 2024; Accepted 11 July 2024; Issue published 28 October 2024
Abstract
This study aims to optimize the influence of the inlet inclination angle on the Indoor Air Quality (IAQ), heat, and temperature distribution in mixed convection within a two-dimensional square cavity filled with an air-CO2 mixture. The air-CO2 mixture enters the cavity through two inlet openings positioned at the top wall, which is set at the ambient temperature (TC). Three values of the Reynolds numbers, ranging from 1000 to 2000, are considered, while the Prandtl number is kept constant (Pr = 0.71). The temperature distribution and streamlines are shown for Rayleigh number (Ra) equal to 104, three inlet inclination angles ϕ (0, π/6 and π/4) and three CO2 concentrations values (1500, 2500, 3500 ppm) applied at both hot vertical walls (maintained at a constant temperature TH). A finite volume method is used under the assumption of two-dimensional laminar flow to solve the Navier-Stokes and energy equations. The results indicate that inlet inclination angle has an impact on the indoor air quality (IAQ), which, in turn, affects the heat transfer distribution and thermal comfort within the cavity.Keywords
Nomenclature
| C0 | Reference concentration (ppm) |
| CH | Hot concentration (ppm) |
| Cin | Concentration at the inlet port (ppm) |
| Cm | Mean concentration at the middle of the cavity (ppm) |
| CO | Carbone monoxide |
| Cout | Concentration at the outlet sort (ppm) |
| CTh | Threshold concentration (ppm) |
| CO2 | Carbone dioxide |
| H | Height of the cavity (m) |
| IIAQ | Indoor air quality index |
| L | Width of the inlet sort (m) |
| L | Width of the cavity (m) |
| NO2 | Nitrogen dioxide |
| P | Pressure (pa) |
| P | Dimensionless pressure |
| Pr | Prandtl number (-) |
| Ra | Rayleigh number (-) |
| Re | Reynolds number (-) |
| Ri | Richardson number (-) |
| TC | Cold temperature (K) |
| TH | Hot temperature (K) |
| Tin | Temperature at the inlet port (K) |
| Tm | Mean temperature at the middle of the cavity (K) |
| Tout | Temperature at the outlet sort (K) |
| ui | Initial inlet velocity (m.s−1) |
| U | Velocity component for x direction (m.s−1) |
| V | Velocity component for y direction (m.s−1) |
| W | Width of the outlet sort (m) |
| x,y | Cartesian coordinates (m) |
| X,Y | Dimensionless coordinates |
| Abbreviations | |
| CFD | Computational Fluid Dynamic |
| EFCS | Efficiency factor contaminant source |
| EPA | Environmental Protection Agency |
| IAQ | Indoor Air Quality |
| OH | Over Head system |
| PM | Particulate matter |
| PV | Personal ventilation |
| UFAD | Under Floor Air Distribution |
| VOCs | Volatile Organic Compounds |
| VRF-SV | Variable Refrigerant Flow integrated Stratum Ventilation |
| WHO | World Health Organization |
| Greek Symbols | |
| φ | Inlet inclination angle (°) |
| Β | Volumetric expansion coefficient (1/K) |
| φ | Dimensionless species’ concentration |
| βS | Concentration expansion coefficient (βS = Co−1) (m3.kg−1) |
| α | Thermal diffusivity (m2.s−1) |
| μ | Dynamic viscosity (kg.m−1.s−1) |
| ν | Kinematic viscosity (m2.s−1) |
| Θ | Dimensionless temperature |
| εT | Temperature distribution effectiveness |
| εC | Contaminant removal effectiveness |
The World Health Organization (WHO) characterizes air quality as the threshold of air purity necessary to uphold environmental balance and human well-being [1]. As per data provided by the Environmental Protection Agency (EPA), people usually allocate about 93% of their time indoors, with 87% of their existence occurring within built environments, 6% in transit, and a mere 7% outdoors [2]. Consequently, the increasing prevalence of indoor activities compared to outdoor pursuits underscores the critical importance of indoor air quality. This became a big concern starting in the late 1960s due to issues such as radon dispersion, house dust, and formaldehyde exposure in the late 1970s. Various studies have delved into the effects of COVID-19 on indoor air quality and thermal comfort in different environments. Sloan Wood et al. [3] identified several strategies aimed at enhancing indoor air quality and mitigating the transmission of airborne syndromes. These strategies encompass installing air filtration systems, controlling temperature, managing humidity levels, and ensuring proper ventilation. In a review by Lipinski et al. [4], the focus was on assessing the effectiveness of current ventilation and air conditioning systems during the COVID-19 pandemic, particularly in buildings with high occupancy rates. Tzoutzas et al. [5], in their study on healthcare clinics in Athens during the COVID-19 pandemic, evaluated the performance of mechanical ventilation systems (air purifiers). The study specifically examined their impact on reducing concentrations of Volatile Organic Compounds (VOCs), particulate matters (PM2.5, PM10), and CO2. The results indicated the efficacy of air purifiers in reducing contaminants and improving indoor air quality. Alicia et al. [6] conducted an analysis on the impact of the COVID-19 pandemic on indoor air quality and thermal comfort in Spain during the winter season. Their study focused on classrooms equipped with mechanical ventilation. Results revealed a reduction in CO2 concentration to 300 ppm when employing a hybrid system during the pandemic. In naturally ventilated schools, a decrease to 400 ppm of CO2 concentration was observed throughout all teaching hours. In another study, Rodriguez et al. [7] assessed the risks of COVID-19 and indoor CO2 levels in two educational areas in central Spain by examining the ventilation conditions. Mechanical ventilation demonstrated positive outcomes, particularly in reducing CO2 levels in university settings when compared to secondary schools. Lovec et al. [8] conducted an assessment of the COVID-19 pandemic impact on thermal comfort and indoor air quality in kindergarten classrooms in Slovenia. The study spanned 125 days, covering both the period before and during the pandemic. Notably, a significant reduction in CO2 concentration was observed when children spent only 30% of their time in the classroom during the pandemic, indicating an improvement in indoor air quality facilitated by ventilation protocols. In a separate study, Pietrogrande et al. [9] monitored Indoor Air Quality (IAQ) in two dwellings over a two-week period. Their investigation included the kitchen and bedrooms during three seasons: spring, summer, and winter. The findings indicated variations in mean indoor concentrations depending on the season. Furthermore, an increase in the number of occupants, whether human or animal, correlated with higher concentrations of Volatile Organic Compounds (VOCs). Additionally, elevated CO2 levels, exceeding 1000 ppm, were detected during the spring season. In a post COVID-19 pandemic, Buonomano et al. [10] proposed specific ventilation standards and demonstrated the effects of various ventilation configurations that were studied to reduce the likelihood of indoor contagion.
Moreover, recent studies have shifted their focus towards reducing CO2 emissions by presenting various solutions to enhance occupants’ well-being. This includes the utilization of environmentally friendly construction materials such as fiber concrete, dried fibers of Luffa, recycled ceramic tiles, and the incorporation of wood and bamboo. Himes et al. [11] conducted a comparison between a mass timber and a conventional concrete-steel mid-rise building, revealing a unanimous reduction in emissions of 216 kg CO2 e/m2 (floor area). Consequently, substituting mass timber for conventional building materials could potentially yield a 9% reduction in emissions by the year 2030 if implemented in half of the buildings. Brandner et al. [12] employed mass timber as the primary construction material in mid and high-rise buildings, concluding that an adequate mass timber capacity can meet the demands of the built environment. In a study by Xu et al. [13], the CO2 reduction rate was analyzed by utilizing bamboo as an ideal building material. When compared to cement, steel, timber, and engineered lumber, one cubic meter of bamboo-assembled components was found to reduce 249.92 kg of CO2 emissions from the atmosphere. Additionally, Belatrache et al. [14] investigated the impact of date palm waste in building thermal insulation, revealing favorable results in terms of thermal comfort associated with date palm fiber.
Varied inlet and outlet positions serve as solutions to improve indoor air quality and achieve efficient ventilation. To investigate this, Griffiths et al. [15] conducted a one-week study on the ventilation performance in a classroom with natural ventilation during the summer season. They found that purge ventilation proved to be a beneficial solution, leading to a reduction in CO2 concentration by 1000 ppm. Lopez et al. [16,17] emphasized the advantages of the UFAD (Under Floor Air Distribution) ventilation system in improving indoor air quality. A comparison with the traditional over head system (OH) led to the conclusion that, for optimal thermal comfort and a cooler environment, it is advisable to position return vents on both sides of the room. Jaszczur et al. [18] analyzed experimentally and numerically in the occupied zone the impact of ceiling diffuser on air temperature distribution. In conclusion, the ceiling diffuser performance was depending on the airflow rate as well as the geometrical construction of diffuser. Abanto et al. [19] studied in computer room, the ceiling diffuser airflow distribution using CFD model. Appropriate results were found in term of temperature and relative humidity inside the room model. While Li et al. [20] investigated numerically the indoor air distribution for new ceiling diffuser model. They found out that the improved model gave a less time-consuming and energy-saving than the first model.
In Andalusia, Fernández-Agüera et al. [21] measured CO2 concentrations in 42 classrooms during winter and midseason. Their study investigated the impact of trickle ventilation and open windows on the health of 917 students. In cases where windows were closed, 42% of the study cases exhibited high CO2 concentrations (above 2000 ppm). Laaroussi et al. [22] conducted a numerical analysis of heat transfer in a hall building, incorporating a heating and air conditioning system with two heat sources in the hall. The study observed the effective efficiency of the air conditioning system in maintaining a low-temperature level. In a simulation by Kong et al. [23] using computational fluid dynamics (CFD), a cubicle office with and without personal ventilation (PV) was investigated. The study demonstrated the favorable performance of personal ventilation (PV) systems under various airflow rates. Furthermore, Cai et al. [24], utilizing the Efficiency Factor of Contaminant Source (EFCS), examined the performance of ventilation systems, considering the influence of source position and evacuation modes. Their study concluded by evaluating the impact of EFCS on emergency ventilation behavior. Yau et al. [25] examined the variable refrigerant flow integrated stratum ventilation (VRF-SV) system on tropical building. They concluded that, the supply air temperature has no impact on the VRF-SV system used with/without the integrated approach. Thus, the system was fitting for this type of building (tropical application). Singh et al. [26], investigating different inlet and outlet locations, altered these positions for six configurations in a two-dimensional rectangular cavity under varying Reynolds (Re) and Richardson numbers (Ri). Notably, the study revealed that for optimal cooling effectiveness, it is preferable to position the inlet at the bottom of the cold wall and the outlet at the top of the hot wall. Koufi et al. [27] conducted a numerical examination of mixed convection in a ventilated cavity filled with an air-CO2 mixture in a low turbulent regime. The study considered three different CO2 concentrations (1000, 2000, and 3000 ppm) and four configurations. The researchers concluded that one of the configurations was particularly effective in removing CO2 contaminants, ensuring adequate temperature control within the cavity, and exhibiting superior ventilation effectiveness compared to the other configurations. Similarly, Mostefa Tounsi et al. [28] conducted a numerical investigation, exploring the impact of inlet position on indoor air quality and thermal comfort within a ventilated cavity filled with a mixture of air and CO2, considering different CO2 concentrations and Reynolds numbers. The study highlighted the significant effect of the inlet position on both temperature distribution and the indoor air quality index. Serrano-Arellano et al. [29] conducted a study in a cavity filled with an air-CO2 mixture, examining various outlet configurations (A, B, C, and D) with a constant air inlet opening across different Reynolds numbers (Re) ranging from 5 × 102 to 4 × 104. At Re = 1 × 104, a significant removal of contaminants was observed for case A compared to the other configurations. In another study, Xamán et al. [30] explored laminar flow regimes within a ventilated cavity filled with an air-CO2 mixture. The investigation considered three different CO2 concentration values and various configurations. For optimal thermal comfort and air quality, the latest configuration demonstrated the most favorable performance. Gijon-Rivera et al. [31] conducted a numerical study in a rectangular ventilated cavity filled with an air-CO2 mixture, analyzing conjugate heat and mass transfer with ten configurations, considering various Reynolds numbers (Re), contaminant sources, and Richardson numbers (Ri). The results indicated that the position and number of outlet types have a notable impact on both heat and contaminant distribution. In addition, Carli et al. [32] investigated the impact of inlet and outlet positions on contaminant distribution in an office room equipped with a ceiling cooling system. The study observed a significant influence of the outlet position, particularly in the context of variable displacement ventilation.
The previous literature review has consistently affirmed the significance of varied inlet and outlet positions in influencing indoor air quality and thermal comfort in enclosed spaces. However, none of the preceding studies have specifically investigated the impact of the inclination of the inlet angle on indoor air quality. This paper presents three inclination angles, 0, π/6 and π/4, corresponding to the two inlet air openings. The study considers variable Reynolds numbers (Re) ranging from 1000 to 2000 and three different hot CO2 concentrations (1500, 2500, 3500 ppm) applied on both hot vertical walls. The two inlet air gaps are positioned on the top wall of the cavity, while the two outlet configurations are located at the bottom of the right and left walls. The main objective of this study is to evaluate the impact of the inclination angle on temperature, and heat distribution as well as its influence on the removal of CO2 contaminants inside the cavity. Various characteristic parameters are calculated with the aim of illustrating the effect of inlet inclination angle on enhancing optimal thermal comfort and air quality within the cavity.
2 Numerical Analysis and Modeling
Fig. 1 depicts a two-dimensional square cavity (L = H), within this cavity, fluid flow is introduced from three distinct angles (φ): 0, π/6, and π/4. The ambient temperature (TC), Prandtl number (Pr) of 0.71, and various Reynolds numbers (Re) ranging from 1000 to 2000 characterize the scenario. Both horizontal walls exhibit zero heat flux, while the vertical walls maintain a constant hot temperature (TH) along with three distinct CO2 concentrations (1500, 2500, and 3500). The outlet ports are positioned at the bottom of both the right and left walls, with the inlet port size being expressed as half of the outlet size (l = 0.5 × w) and as 0.02 of the full cavity width (l = 0.02 × L). The flow is assumed to be laminar, employing the Boussinesq approximation. The non-dimensional governing equations, species conservation equations along with dimensionless parameters, are presented, including the expression for the inlet flow velocity in terms of x and y components. The three characteristic parameters (εT, εC and IIAQ) are also defined in the following equations:
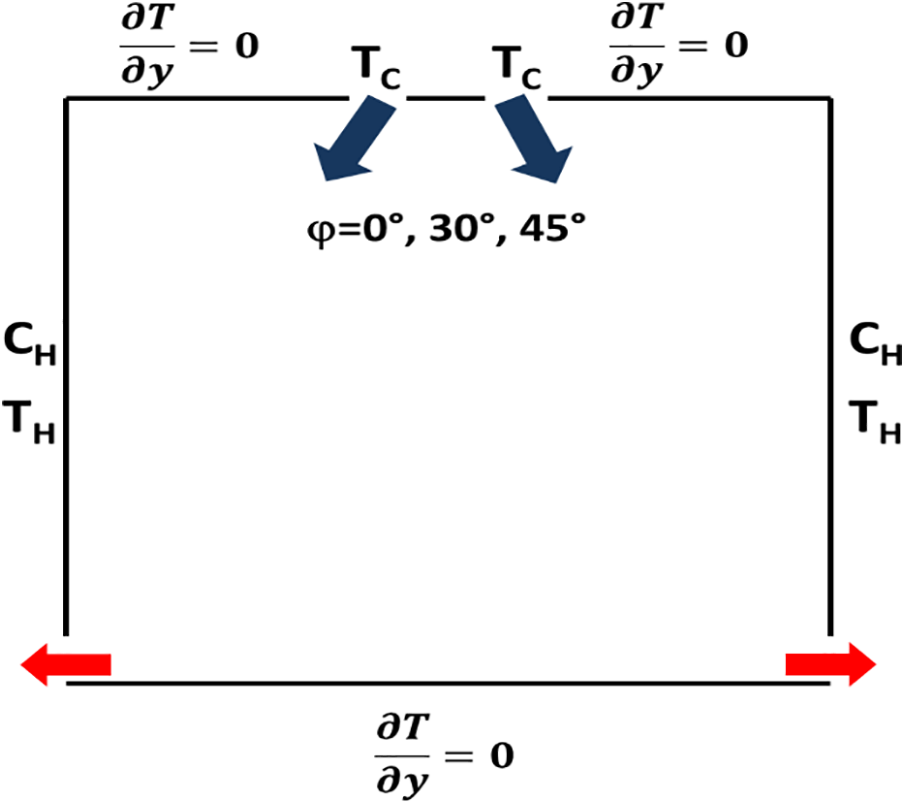
Figure 1: The model geometry
To validate the obtained results, it is imperative to compare and verify them against existing data. De Vahl Davis [33] conducted an analysis on natural convection in a dimensionless cavity with a varying Rayleigh number within the range of 103 ≤ Ra ≤ 106. The study considered a Prandtl number (Pr) of 0.71 and a heat wall on one side of the cavity. The results of Numin and Numax, obtained using different Rayleigh numbers (Ra) and various grid meshes (123 * 123, 223 * 223, 323 * 323, 370 * 370), were meticulously compared with the values derived from De Vahl Davis’s benchmark as it illustrated in Table 1.
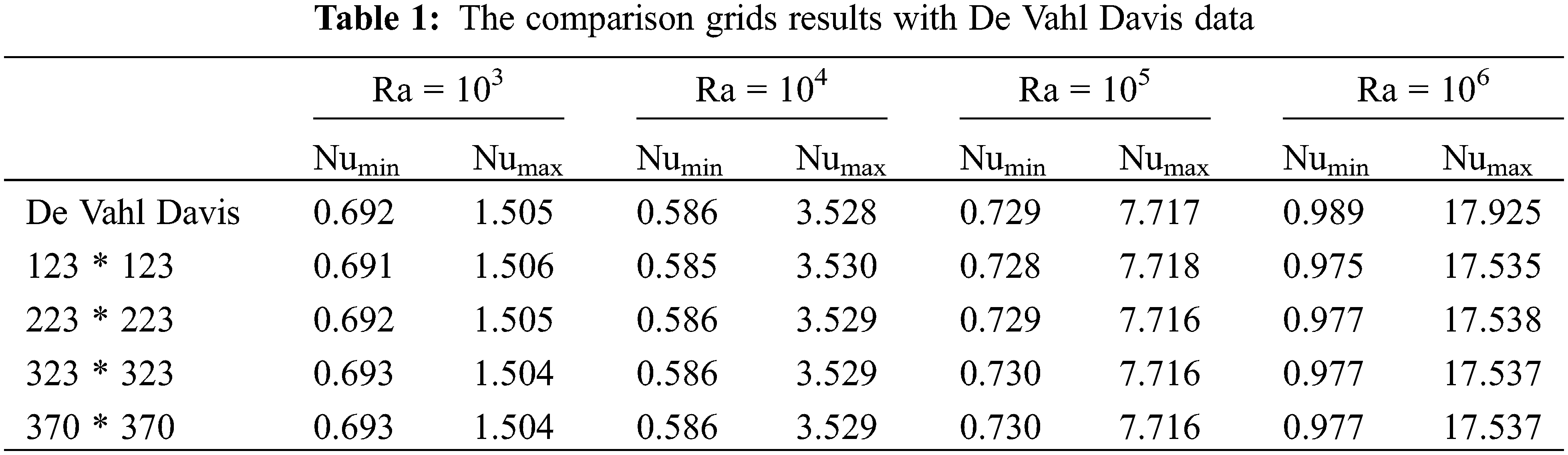
It was observed from Table 1 that the values of Numin and Numax stabilized and remained constant after using a grid of 323 * 323. As a result, this mesh grid (323 * 323) was selected for the simulations due to its consistency and agreement with the data presented in De Vahl Davis’s benchmark.
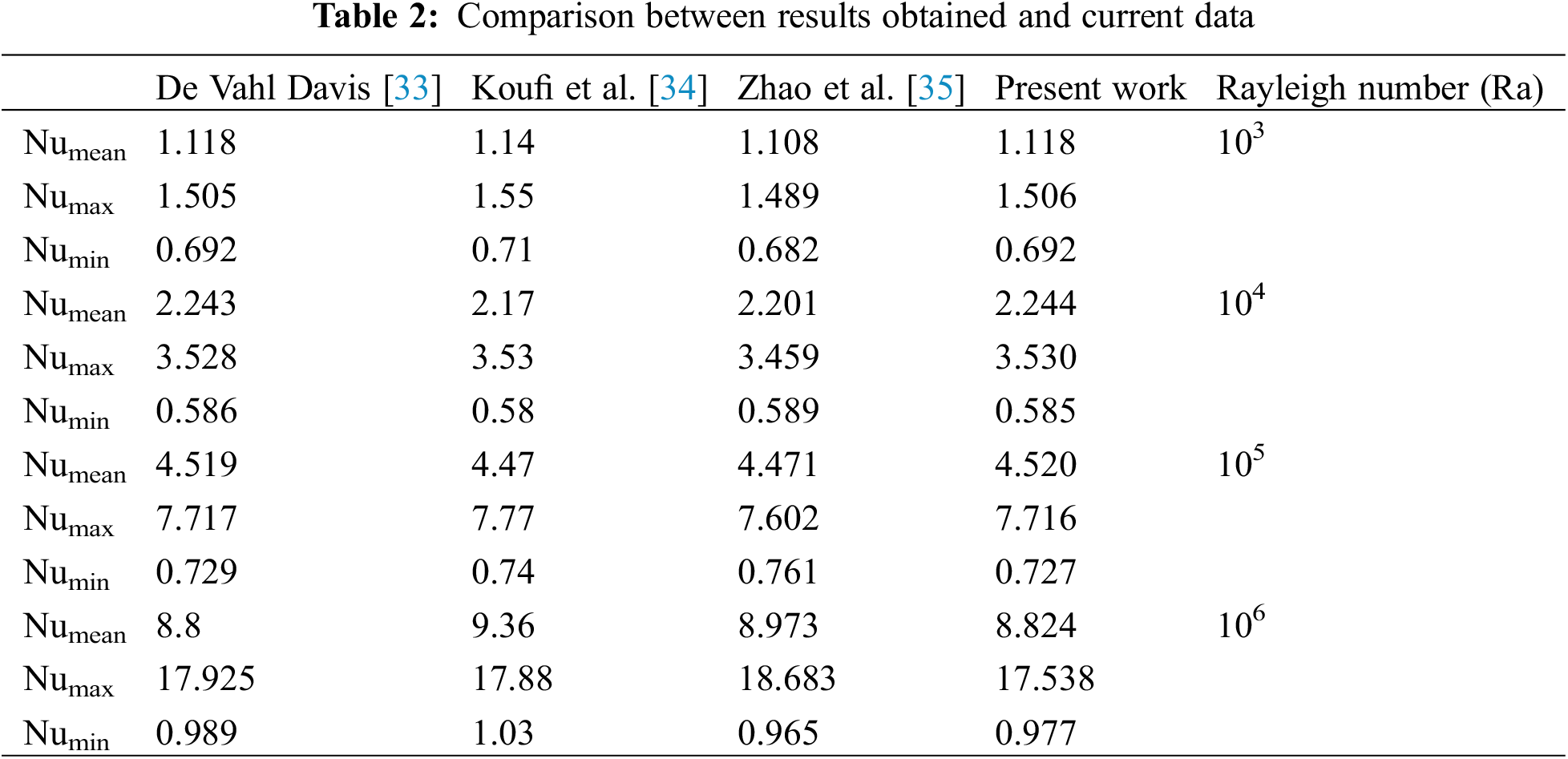
The present study was subjected to comparison with findings from De Vahl Davis [33], Koufi et al. [34], and Zhao et al. [35], with a focus on parameters such as Numean, Numax, and Numin. The results obtained as it shown in Table 2, for each Rayleigh number (Ra) within the range of 103 to 106 exhibited consistent agreement between the present work and the referenced data. Identical Nu values were observed across all categories, reaffirming the reliability and alignment of the outcomes from the current investigation with the existing literature.
3.1 The Characteristic Parameters (εT, εC, IIAQ)
Table 3 illustrates three key parameters effectiveness (εT, εC, and IIAQ) across different Reynolds numbers (Re) and CH concentrations (1500, 2500, and 3500 ppm), considering three distinct inlet flow inclinations (φ) of 0, π/6, and π/4. Notably, a marginal impact of the flow inclination angle (φ) is observed on ventilation and temperature effectiveness as Reynolds numbers (Re) and CH concentrations increase. Importantly, effective ventilation, denoted by a value of εC exceeding unity, is particularly notable for the inclination angle φ = π/4. This finding suggests that at this specific inclination angle, the ventilation system demonstrates enhanced performance, facilitating better air circulation within the cavity. Additionally, it’s essential to highlight that the indoor air quality index (IIAQ) exhibits sensitivity to both the inclination angle φ and the variation in Reynolds numbers (Re), as evident from the data presented in Table 3. This observation underscores the intricate interplay between flow dynamics, ventilation efficacy, and indoor air quality, necessitating a nuanced understanding for optimal system design and operation.
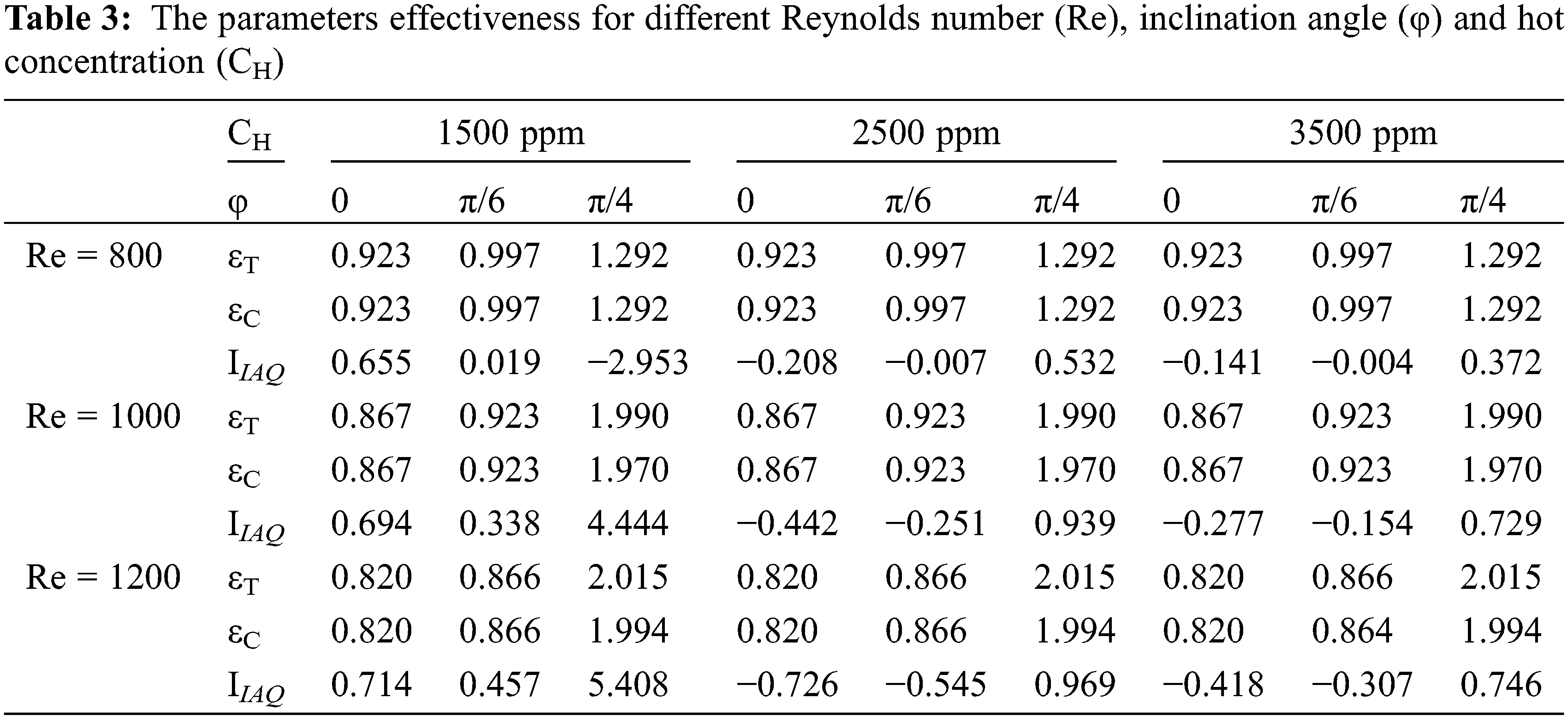
Referring to the Environmental Protection Agency’s (EPA) air quality guide for particle pollution [36], a suitable indoor air quality index falls between 0 and 50, as depicted in Fig. 2. Therefore, Table 3 indicates satisfactory indoor air quality across various Reynolds numbers for all inlet flow angles (0°, 30°, and 45°). The most favorable indoor air quality values are observed for the angle φ = 30°, attributed to the creation of jets that assist in expelling the hot concentration outward from the cavity. The negative sign in some instances indicates that the CO2 contaminant’s concentration near the outlet port exceeds that in the middle of the cavity.
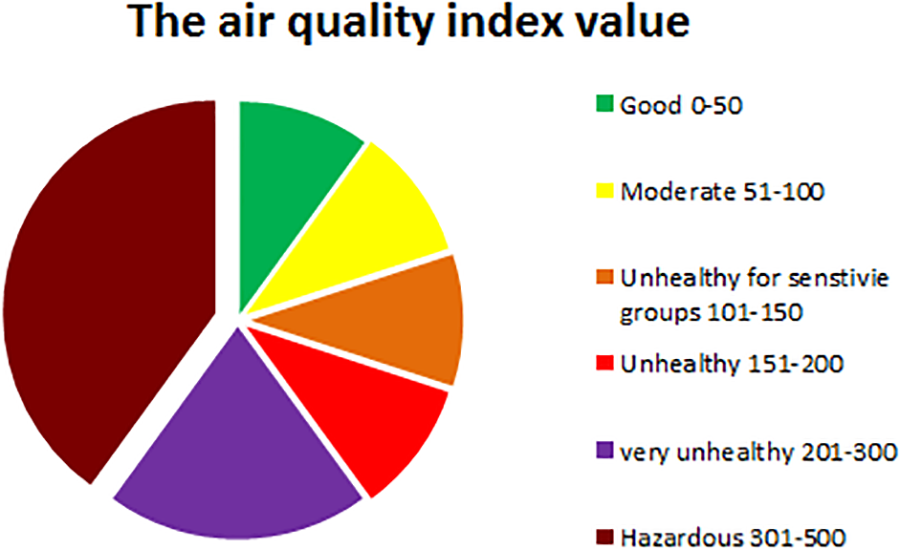
Figure 2: The air quality index value signification
The results from Table 3 highlight that an inlet inclination angle of 0° is deemed inappropriate when compared to the other angles (30°, 45°) in terms of ventilation and contaminant removal parameters (εT and εC). This suggests that an angle of 0° may not be the most effective approach to achieve suitable ventilation and cooling for the vertical walls of the cavity, thereby impacting thermal comfort. Consequently, the subsequent analysis and findings will concentrate on the two inlet angles, φ = 30° and φ = 45°, to gain a deeper understanding of their influence on heat transfer and thermal comfort.
3.2 Local Nusselt Number on the Hot Wall (Vertical Walls)
Fig. 3 provides a visual representation of the local Nusselt number (NuL) distribution along the hot vertical walls (both left and right sides), taking into account two distinct inlet flow angles (φ) at 30° and 45°, coupled with three different Reynolds number (Re) values, while maintaining a constant carbon dioxide concentration (CH) of 2500 ppm. This specific configuration is selected to align with real-world indoor air quality standards. The graph vividly illustrates the direct correlation between the Reynolds number (Re) and the local Nusselt number, showcasing an increase in NuL with escalating Re values. Notably, at Re = 1200, there is a marked surge in NuL, accompanied by a significant reduction in the vicinity of the outlet port. This phenomenon results in the expulsion of elevated heat transfer magnitudes from the cavity, thereby effectively dissipating heat and cooling both hot walls.
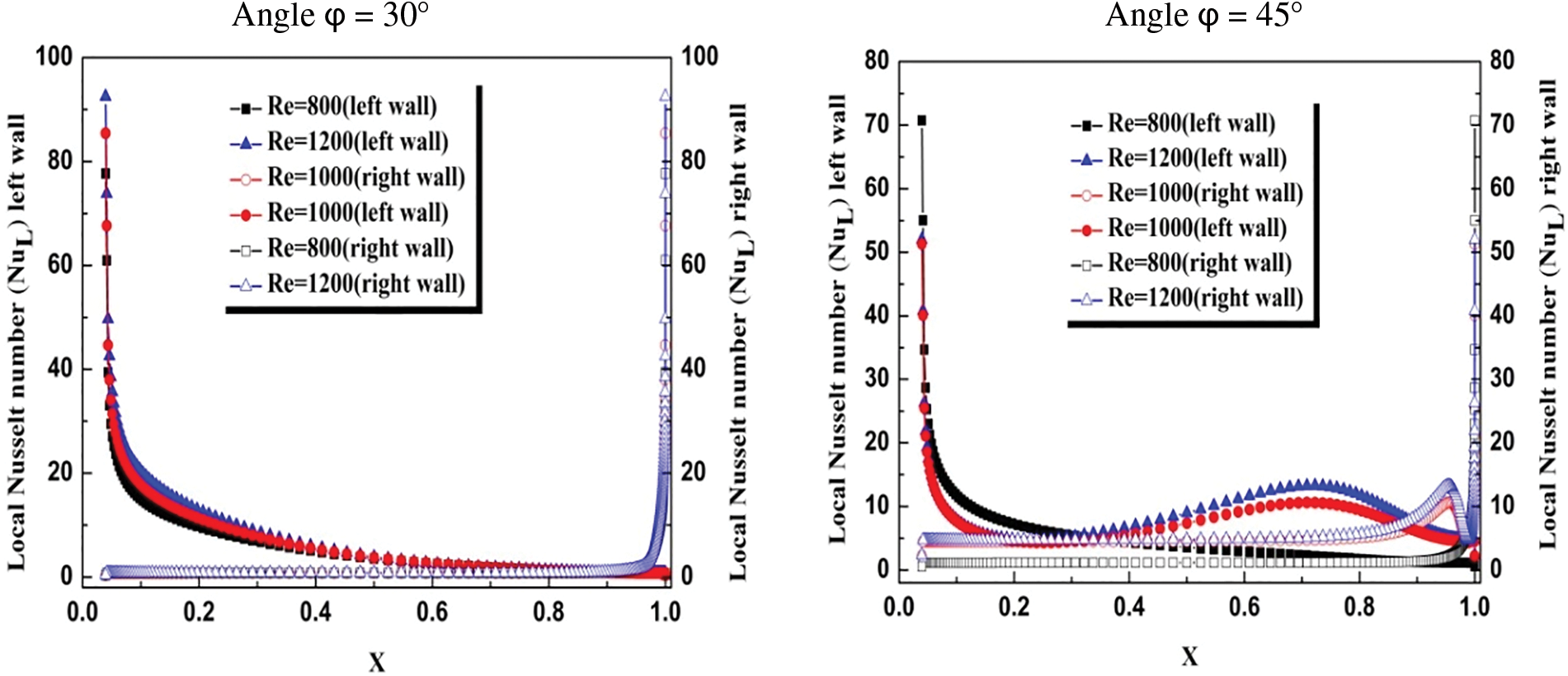
Figure 3: Local Nusselt number for both vertical sides with different Reynolds number (Re) at CH = 2500 ppm
The consistent nature of these findings across both the left and right walls emphasizes the reliability of the analysis. Furthermore, the impact of the inlet flow angle (φ) on the Nusselt number is distinctly apparent. There’s a noticeable reduction in NuL at the upper sections of both vertical walls as the inlet flow angle increases. Specifically, when φ = 45°, there’s a palpable decrease in heat transfer, signifying efficient cooling of the hot vertical walls compared to other angles. Conversely, around the outlet port, there’s an observed increase in the local Nusselt number at φ = 45° compared to other angles, attributed to the heightened convection values in this setup. These trends hold true across various scenarios, showcasing the consistent physical phenomena governing heat transfer dynamics in the system.
The Nusselt number at the both sides is obtained with the following equations:
Fig. 4 presents comprehensive visualizations of iso-concentration, streamlines, and temperature profiles at the midpoint of the cavity (Y = H/2). The graphs depict variations in Reynolds number (Re = 800, 1000, 1200), CH concentration set at 2500 ppm, and two different inclination angles (φ) of π/6 and π/4. Observations reveal a subtle influence of increasing Reynolds number on iso-concentration, particularly notable at an angle of 30° where the impact is more pronounced. The direct relationship between velocity and Reynolds number implies that elevated air-CO2 flow velocity leads to a deficiency in CO2 concentration, resulting in a decrease in indoor contaminants. The distinct peak noted at φ = 30° is attributed to the presence of jet flow phenomena, gradually diminishing as the inclination angle increases. Furthermore, higher inclination angles consistently correspond to elevated iso-concentration values, a consistent trend observed across all cases examined within this study, highlighting the physical implications of flow dynamics on indoor air quality.
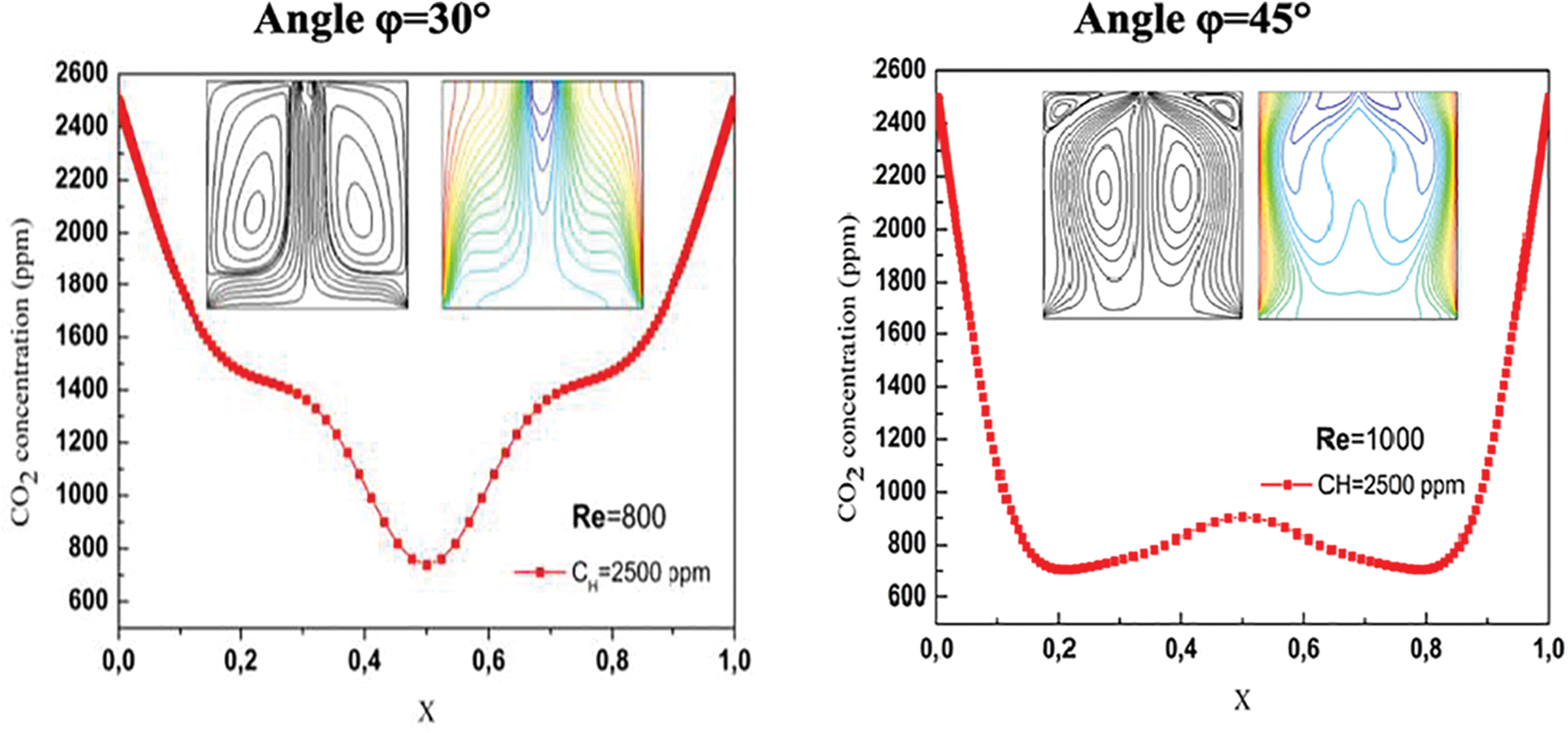
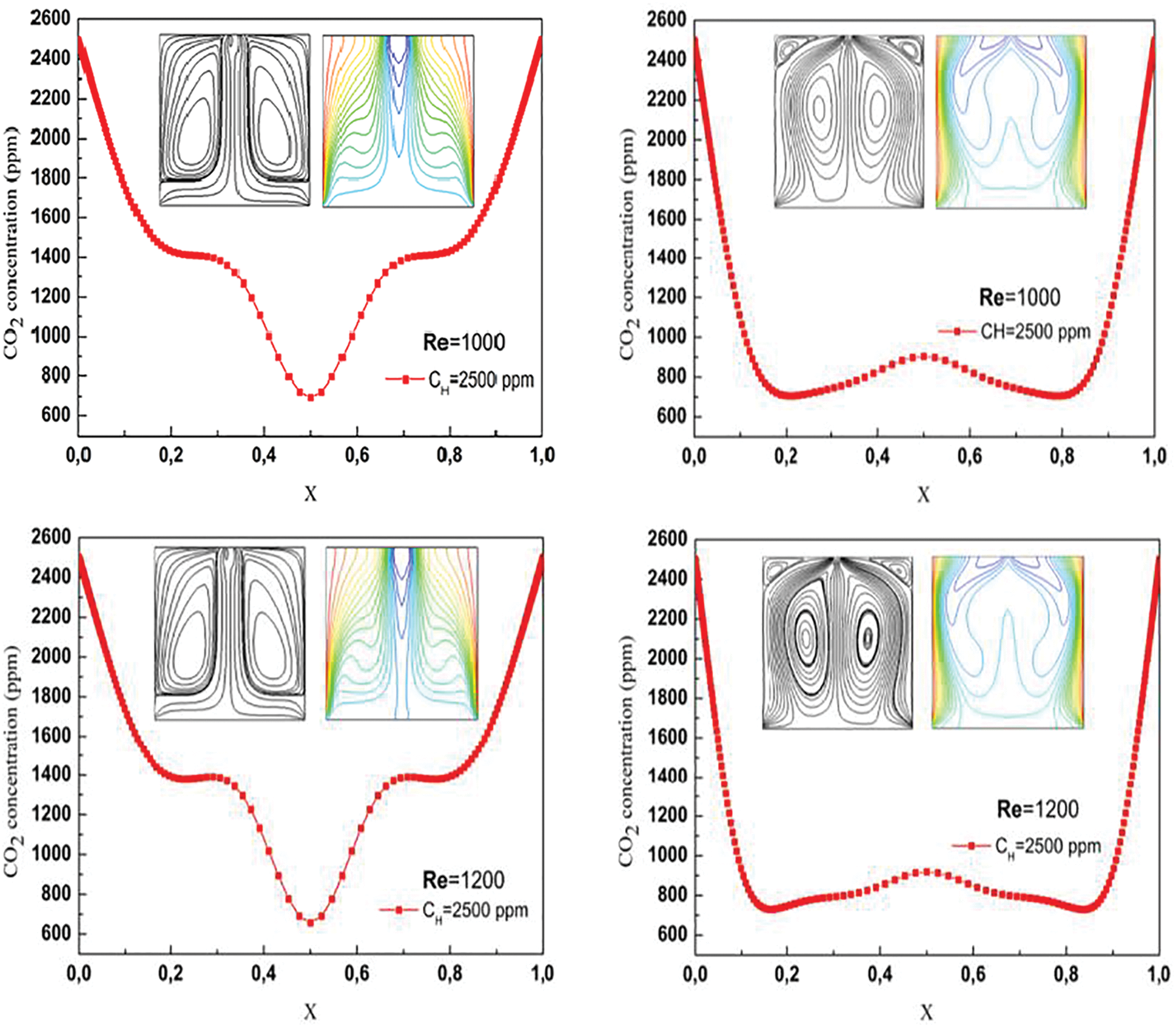
Figure 4: The iso-concentration, streamlines, temperature for CH = 2500, φ = π/6, π/4, Re = 800, 1000, 1200
Fig. 4 provides additional insights into the system by including streamlines and temperature contours (isotherms), showcasing the impact of varying Reynolds numbers (800, 1000, and 1200), with a fixed CH concentration of 2500 ppm, and considering both inlet flow angles (φ) at 30° and 45°. Both aspects aim to elucidate the impact of the inclination angle on the cooling of the vertical walls. The effect of increasing Reynolds number (Re) is evident in both isotherms and streamlines. In the case of streamlines, vortexes are more pronounced for the angle φ = 45° compared to the other inlet flow angle, potentially leading to compromised indoor air quality in those regions. Regarding isotherms, the rise in Reynolds number correlates with a decrease in temperature in the middle of the cavity. This influence is particularly notable in the temperature distribution, especially for the angle φ = 45°.
This paper presents a numerical study of a two-dimensional square cavity filled with an air-CO2 mixture, heated from both vertical walls. The investigation considers three different Reynolds numbers (800, 1000, 1200), varying CO2 concentrations (1500, 2500, 3500 ppm), and three inlet inclination angles (φ) of 0, π/6, π/4. These parameters are applied to both inlet ports at the top wall under laminar flow conditions.
The key findings of this study can be summarized as follows:
• The inclination angle (φ) significantly influences the indoor air quality index, local Nusselt number, streamlines, and temperature contours.
• The best indoor air quality index is achieved at an inclination angle of φ = 30°. φ = 45° is preferable for effectively cooling the hot vertical walls, as indicated by the temperature distribution results.
• The variation in the local Nusselt number between the left and right sides of the cavity (hot vertical walls) is minor across different Reynolds numbers (Re).
• In cases where φ > 30°, notable vortex formations occur in the corners, particularly pronounced at larger angles.
In conclusion, this study highlights the impact of top inclination inlet angles in cooling vertical walls and influencing indoor air quality, thereby contributing to the thermal comfort of indoor spaces across various Reynolds numbers (Re) and CO2 concentrations. As a future avenue of research, exploring turbulent flow regimes, especially for φ > 45°, could provide insights into achieving higher and more suitable indoor air quality conditions.
Acknowledgement: An acknowledgement filled with gratitude to the “PHC TASSILI Project” from all authors for the huge support to realize this work.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Mustapha Boussoufi, Ikram Mostefa tounsi; data collection: Ikram Mostefa Tounsi; analysis and interpretation of results: Ikram Mostefa Tounsi, Amina Sabeur; draft manuscript preparation: Ikram Mostefa Tounsi. Amina Sabeur, Mohammed El Ganaoui. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data acquired and assessed as part of this research can be accessed on request from the corresponding author.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. World Health Organization (WHO). Coronavirus; 2020 Apr 19. Available from: www.who.int. [Accessed 2023]. [Google Scholar]
2. Environmental Protection Agency (EPA). Indoor air quality; 2022. Available from: www.epa.gov/indoor-air-quality-iaq. [Accessed 2023]. [Google Scholar]
3. Sloan Wood O, Sloan Wood H, Kumar P. Prioritising indoor air quality in building design can mitigate future airborne viral outbreaks. Cities Health. 2021;5(1):162–5. doi:10.1080/23748834.2020.1786652. [Google Scholar] [CrossRef]
4. Lipinski T, Ahmad D, Serey N, Jouhara H. Review of ventilation strategies to reduce the risk of disease transmission in high occupancy buildings. Int J Thermofluids. 2020;7–8:100045. doi:10.1016/j.ijft.2020.100045. [Google Scholar] [CrossRef]
5. Tzoutzas I, Maltezou HC, Barmparesos N, Tasios P, Efthymiou C, Assimakopoulos MN, et al. Indoor air quality evaluation using mechanical ventilation and portable air purifiers in an academic dentistry clinic during the COVID-19 pandemic in Greece. Int J Environ Res Public Health. 2021;18(16):8886. doi:10.3390/ijerph18168886. [Google Scholar] [PubMed] [CrossRef]
6. Alicia A, Llanos J, Escandón R, Sendra J. Effects of the COVID-19 Pandemic on indoor air quality and thermal comfort of primary schools in winter in a mediterranean climate. Sustainability. 2021;13(5):2699. doi:10.3390/su13052699. [Google Scholar] [CrossRef]
7. Rodríguez D, Urbieta IR, Velasco A, Laborda MAC, Jiménez E. Assessment of indoor air quality and risk of COVID-19 infection in Spanish secondary school and university classrooms. Build Environ. 2022;226(3):109717. doi:10.1016/j.buildenv.2022.109717. [Google Scholar] [PubMed] [CrossRef]
8. Lovec V, Premrov M, Leskovar VŽ. Practical impact of the COVID-19 pandemic on indoor air quality and thermal comfort in kindergartens: a case study of Slovenia. Int J Environ Res Public Health. 2021;18:9712. [Google Scholar] [PubMed]
9. Pietrogrande MC, Casari L, Demaria G, Russo M. Indoor air quality in domestic environments during periods close to Italian COVID-19 lockdown. Int J Environ Res Public Health. 2021;18:4060. [Google Scholar] [PubMed]
10. Buonomano A, Forzano C, Giuzio GF, Palombo A. New ventilation design criteria for energy sustainability and indoor air quality in a post COVID-19 scenario. Renew Sustain Energ Rev. 2023;182(2):113378. doi:10.1016/j.rser.2023.113378. [Google Scholar] [PubMed] [CrossRef]
11. Himes A, Busby G. Wood buildings as a climate solution. Dev Built Environ. 2020;4(3):100030. doi:10.1016/j.dibe.2020.100030. [Google Scholar] [CrossRef]
12. Brandner R, Flatscher G, Ringhofer A, Schickhofer G, Thiel A. Cross laminated timber (CLT): overview and development. Eur J Wood Wood Prod. 2016;74(3):331–51. doi:10.1007/s00107-015-0999-5. [Google Scholar] [CrossRef]
13. Xu X, Xu P, Zhu J, Li H, Xiong Z. Bamboo construction materials: carbon storage and potential to reduce associated CO2 emissions. Sci Total Environ. 2022;814:152697. doi:10.1016/j.scitotenv.2021.152697. [Google Scholar] [PubMed] [CrossRef]
14. Belatrache D, Bentouba S, Zioui N, Bourouis M. Energy efficiency and thermal comfort of buildings in arid climates employing insulating material produced from date palm waste matter. Energy. 2023;283(19):128453. doi:10.1016/j.energy.2023.128453. [Google Scholar] [CrossRef]
15. Griffiths M, Eftekhari M. Control of CO2 in a naturally ventilated classroom. Energy Build. 2008;40(4):556–60. doi:10.1016/j.enbuild.2007.04.013. [Google Scholar] [CrossRef]
16. Lopez NS, Galeos SK, Calderon BR, Dominguez DR, Uy BJ, Iyengar R. Computational fluid dynamics simulation of indoor air quality and thermal stratification of an underfloor air distribution system (UFAD) with various vent layouts. Fluid Dynam Mater Process. 2021;17(2):333347. doi:10.32604/fdmp.2021.011213. [Google Scholar] [CrossRef]
17. Lopez NS, Galeos SK, Calderon BR, Dominguez DR, Uy BJ, Iyengar R. Numerical simulation of thermal stratification and air quality in an underfloor air distribution system (UFAD). In: Proceedings of International Conference on Sustainable Energy and Green Technology; 2019–2020; Bangkok, Thailand. [Google Scholar]
18. Jaszczur M, Madejski P, Borowski M, Karch M. Experimental analysis of the air stream generated by square ceiling diffusers to reduce energy consumption and improve thermal comfort. Heat Transf Eng. 2022;43(3–5):463–73. doi:10.1080/01457632.2021.1875169. [Google Scholar] [CrossRef]
19. Abanto J, Barrero D, Reggio M, Ozell B. Airflow modelling in a computer room. Build Environ. 2004;39(12):1393–402. doi:10.1016/j.buildenv.2004.03.011. [Google Scholar] [CrossRef]
20. Li X, Zhao B, Guan P, Ren H. Air supply opening model of ceiling diffusers for numerical simulation of indoor air distribution under actual connected conditions, part II: application of the model. Numer Heat Transf Appl. 2006;49(8):821–30. doi:10.1080/10407780500506915. [Google Scholar] [CrossRef]
21. Fernández-Agüera J, Campano MA, Domínguez-Amarillo S, Acosta I, Sendra JJ. CO2 concentration and occupants’ symptoms in naturally ventilated schools in mediterranean climate. Buildings. 2019;9(9):197. doi:10.3390/buildings9090197. [Google Scholar] [CrossRef]
22. Laaroussi N, Chihab Y, Garoum M, Bénet LV, Lacroux F. Study of the aeraulic flows in a building including heating and air conditioning systems. Fluid Dynam Mater Process. 2015;11(4):354365. doi:10.3970/fdmp.2015.011.354. [Google Scholar] [CrossRef]
23. Kong M, Zhang Z, Wang J. Air and air contaminant flows in office cubicles with and without personal ventilation: a CFD modeling and simulation study. Build Simul. 2015;8(4):381–92. doi:10.1007/s12273-015-0219-6. [Google Scholar] [CrossRef]
24. Cai H, Long W, Li X, Barker D. Evaluating emergency ventilation strategies under different contaminant source locations and evacuation modes by efficiency factor of contaminant source (EFCS). Build Environ. 2010;45(2):485–97. doi:10.1016/j.buildenv.2009.07.005. [Google Scholar] [CrossRef]
25. Yau YH, Rajput UA. Thermal comfort assessment and design guidelines of a VRF-integrated stratum ventilation system for a large tropical building. Arab J Sci Eng. 2022;47(12):16149–70. doi:10.1007/s13369-022-06823-4. [Google Scholar] [CrossRef]
26. Singh S, Sharif MAR. Mixed convective cooling of a rectangular cavity with inlet and exit openings on differentially heated side walls. Numer Heat Transf A: Appl. 2003;44(3):233–53. doi:10.1080/716100509. [Google Scholar] [CrossRef]
27. Koufi L, Younsi Z, Naji H. Numerical simulation of the CO2 diffusion effect on low turbulent mixed convection in a ventilated room heated by the bottom. Therm Sci. 2021;25(6B):4783–96. doi:10.2298/TSCI200116291K. [Google Scholar] [CrossRef]
28. Mostefa Tounsi I, Boussoufi M, Sabeur A, El Ganaoui M. Numerical analysis of indoor air quality in an open room: effect of the outlet opening. Int J Thermofluids. 2023;18(5):100356. doi:10.1016/j.ijft.2023.100356. [Google Scholar] [CrossRef]
29. Serrano-Arellano J, Gijon-Rivera M, Riesco-Avila JM, Xaman J, Alvarez G. Indoor air quality analysis based on the ventilation effectiveness for CO2 contaminant removal in ventilated cavities. Revista Mexicana Física. 2014;60(4):309–17. [Google Scholar]
30. Xaman J, Ortiz A, Álvarez G, Chávez Y. Effect of a contaminant source (CO2) on the air quality in a ventilated room. Energy. 2011;36(5):3302–18. doi:10.1016/j.energy.2011.03.026. [Google Scholar] [CrossRef]
31. Gijon-Rivera M, Serrano-Arellano J. Thermal comfort and air quality analysis of a ventilated cavity: a single or multiple air outlets. In: First Thermal and Fluids Engineering Summer Conference, 2016; New York, NY, USA. doi:10.1615/TFESC1.cmd.013234. [Google Scholar] [CrossRef]
32. Carli M, Tomasi R, Zecchin R, Villi G. Comparison of displacement ventilation and mixing ventilation systems with regard to ventilation effectiveness in offices. In: Proceedings Air Infiltration and Ventilation Centre TightVent Conference; 2012; Copenhagen, Denmark. [Google Scholar]
33. De Vahl Davis G. Natural convection of air in a square cavity a bench mark numerical solution. Int J Numer Methods Fluids. 1983;3:249–64. [Google Scholar]
34. Koufi L, Younsi Z, Cherif Y, Naji H. Numerical investigation of turbulent mixed convection in an open cavity: effect of inlet and outlet openings. Int J Thermal Sci. 2017;116:103–17. doi:10.1016/j.ijthermalsci.2017.02.007. [Google Scholar] [CrossRef]
35. Zhao M, Yang M, Lu M, Zhang Y. Evolution to chaotic mixed convection in a multiple ventilated cavity. Int J Therm Sci. 2011;50:2464–72. doi:10.1016/j.ijthermalsci.2011.07.001. [Google Scholar] [CrossRef]
36. United States Environment Protection Agency (US EPA). Indoor air quality and climate change; 2022. Available from: www.epa.gov. [Accessed 2023]. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools