 Open Access
Open Access
ARTICLE
Numerical Simulations of Snow Accumulation in the Bogie Region of a Train Considering Snow Particle Rotation
1 State Key Laboratory of Rail Transit Vehicle System, Southwest Jiaotong University, Chengdu, 610031, China
2 College of Railway Transportation, Hunan University of Technology, Zhuzhou, 412000, China
3 GD Midea Air-Conditioning Equipment Co., Ltd., Foshan, 528311, China
* Corresponding Author: Jiye Zhang. Email:
(This article belongs to the Special Issue: Computational Fluid Dynamics: Two- and Three-dimensional fluid flow analysis over a body using commercial software)
Fluid Dynamics & Materials Processing 2024, 20(10), 2337-2352. https://doi.org/10.32604/fdmp.2024.052609
Received 08 April 2024; Accepted 11 June 2024; Issue published 23 September 2024
Abstract
To investigate the influence of snow particle rotational motion on the accumulation of snow in the bogie region of high-speed trains, an Euler‒Lagrange numerical approach is adopted. The study examines the effects of snow particle diameter and train speed on the ensuing dynamics. It is shown that considering snow particle rotational motion causes significant deviation in the particle trajectories with respect to non-rotating particles. Such a deviation increases with larger snow particle diameters and higher train speeds. The snow accumulation on the overall surface of the bogie increases, and the amount of snow on the vibration reduction device varies greatly. In certain conditions, the amount of accumulated snow can increase by several orders of magnitudes.Keywords
Nomenclature
| u | Air flow velocity (m/s) |
| up | Particle velocity (m/s) |
| | Particle Reynolds number |
| | Aerodynamic viscosity (Pa∙s) |
| | Drag coefficient |
| g | Gravitational acceleration (m/s2) |
| | Fluid density (kg/m3) |
| | Particle density (kg/m3) |
| | Rotational moment of inertia of the particles (kg∙m2) |
| | Diameter of the particles (m) |
| | Particle’s relative angular velocity with respect to the fluid |
| | Coefficient of rotational resistance |
| T | Moment of the force of the fluid on the snow particles (N∙m) |
| | Magnus force (N) |
| | Projected area of the particle (N) |
| | Rotational lift coefficient |
| | Particle mass (kg) |
| | Relative angular velocity between the particle and the fluid (rad/s) |
| w | Relative velocity between particles and air (m/s) |
When high-speed trains operate in high-cold regions, snow accumulates on the tracks and forms snow smoke around the train due to the train’s wind [1]. Due to the exposed and complex nature of the bogie and its proximity to the ground, snow particles carried by the train wind easily adhere to the bogie surface. Snow mainly accumulates in tiny gaps on the bogie surface and upper surfaces of the components. Most scholars use unsteady Reynolds-averaged algorithms to determine the flow field characteristics around trains and bogies and DPM (discrete phase models) to simulate the movement of snow particles at the bottom of the trains. Considering the worst-case scenario, Gao et al. [2,3] assumed that snow particles adhered to the bogie surface upon collision. They conducted a simulation analysis of the movement and deposition of snow particles on the bottom of a train using the discrete phase method, and the simulation results were consistent with the wind tunnel test results. This method was also applied to calculate the snow accumulation characteristics under different skirt configurations in crosswind environments [4]. Wang et al. [5,6] explored the impact of the wheel rotation and bogie cavity shape on the snow accumulation on a bogie surface. Allian [7] performed numerical simulations based on several experiments to verify the snow accumulation mechanism at the bottom of high-speed trains. Cai et al. [8] studied the snow and wind flow characteristics around a train, analyzed the reasons for bogie snow formation from the flow field at the bottom of a train, and established a set of snow particle capture criteria. Different deposition characteristics of wet snow and dry snow were considered to determine the wet snow adhesion state based on the angle of collision between snow particles and the bogie and the critical shear rate on the bogie surface. The adhesion state of dry snow was determined based on the speed of motion of snow particles and critical shear rate on the bogie surface [9,10], which provide a more practical simulation of snow particle deposition on the bogie. Considering the irregularity of the shape of snow particles, according to the shape correction coefficient proposed by Leith [11], List et al. [12], Lan et al. [13,14] calculated the drag coefficient of particles of different shapes using a user-defined function (UDF), studied the movement characteristics of snow particles in the bogie region, and analyzed anti-snow measures in the bogie region through active blowing. However, these studies did not consider the rotational motion of snow particles, which can alter their trajectory and present different movement and deposition characteristics.
The flow field beneath a high-speed train becomes extremely complex due to the influence of the bogie, which causes flow deviations, an uneven velocity distribution and an uneven pressure distribution in the bogie region. In gas-solid two-phase flows, nonconcentric particle collisions and velocity gradients cause particle rotation [15]. Parsa et al. [16] indicated that the particle rotation was controlled by small-scale characteristics of turbulence and was nearly a universal phenomenon. When particles are small, and the concentration is low, their rotation is determined by the velocity gradient along their trajectory. Liu et al. [17] analyzed particle erosion in seawater pipelines and found that rotating particles significantly altered their trajectories with increased collisions against the pipe walls in curved sections. Hao et al. [18] studied the gas-solid two-phase flow in risers and concluded that the particle rotation affected the flow characteristics. Zhang et al. [19] investigated the Magnus force that acted on individual spherical sand particles under different Reynolds numbers and proposed modifications to the Magnus force equation based on their calculations. Adedeji et al. [20] used an erosion-coupled dynamic mesh method to predict the real surface deformation of a standard 90° bend. They found that the particle rotation significantly influenced the shape and size of the surface deformation, and the simulation results better matched experimental results when the particle rotation was considered. Triesch et al. [21] applied FLUENT to simulate gas-solid flow in pipes and diffusers, considering the effects of the wall roughness on the particle–wall collisions, Magnus force, Saffman lift force, and interparticle collisions. Their computational results were consistent with experimental data. These studies indicate that the Magnus force caused by particle rotation alters the trajectory of snow particles and should not be directly ignored. Therefore, this study considers the influence of the Magnus effect induced by snow particle rotation on the motion and deposition of snow particles in the bogie region by comparing the results obtained with and without particle rotation and analyzing the differences.
The flow field in the bogie region of a high-speed train is mainly obtained by solving the continuity equation and momentum equation as follows:
where
where μ is the aerodynamic viscosity; ρp and dp are the particle velocity and particle density, respectively; CD is the drag coefficient, whose values are provided in the literature [22]; Rep is the relative Reynolds number; up is the particle velocity;
When snow particles rotate in the flow field, they change the velocity of the fluid near the particle surfaces. This change increases the velocity on the side where the airflow direction is the same as the particle rotation direction and decreases the velocity on the opposite side. At this point, the snow particle experiences a force perpendicular to its direction of motion, which makes it flow toward the side with a higher velocity. This force is known as the Magnus force [15]. Assuming that the snow particle is a regular sphere and considering the gravity, air drag on the particle, and Magnus force, the equations that govern the snow particle trajectory, momentum conservation, and angular momentum conservation are:
where
where
To save computational resources, a trailer bogie and a simplified vehicle body model were established, as shown in Fig. 1a. Fig. 1b shows the size of the computational domain. The fluid domain was discretized using a hybrid grid approach involving tetrahedral, prismatic, and hexahedral grids. Eight layers of prism grids were allocated on the bogie surface and simplified vehicle body, the first-layer grid height was 0.001 m, and the boundary layer growth rate was 1.2. Fig. 1c shows the computational grid.

Figure 1: Computational model
2.3 Boundary Conditions and Solution Settings
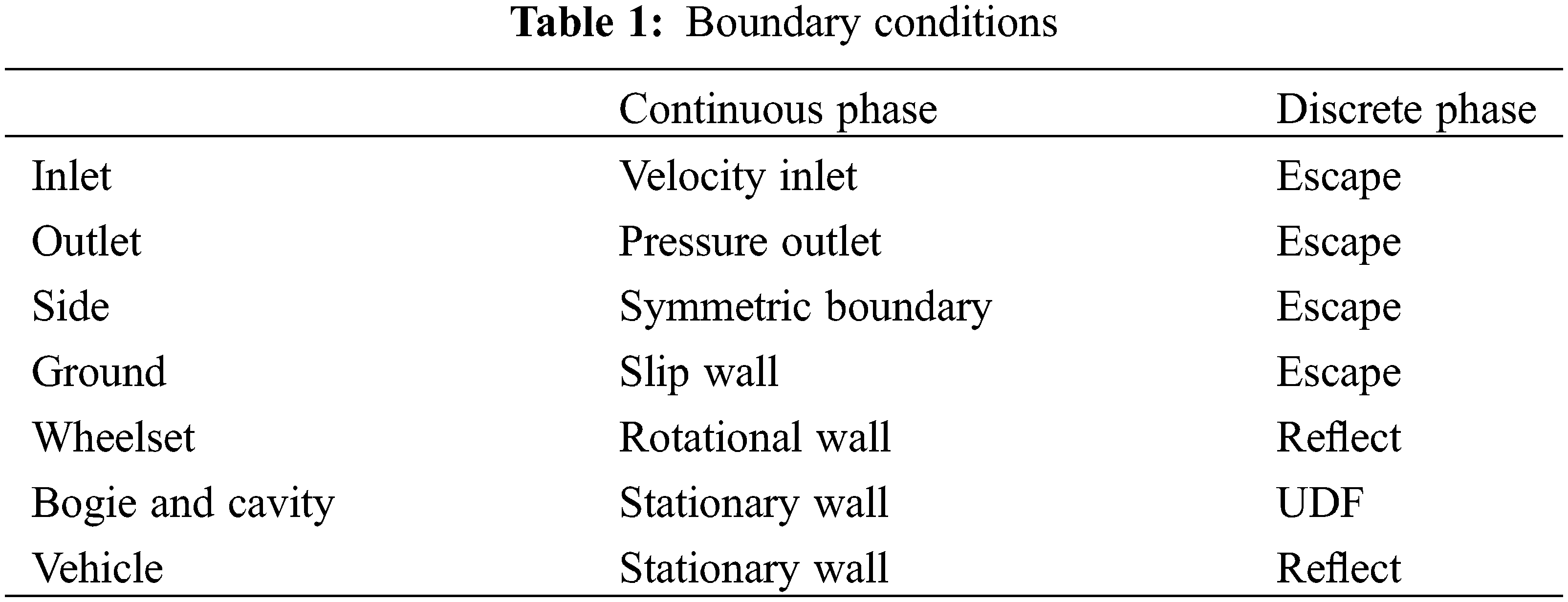
The unsteady RANS equations coupled with a realizable k-ε turbulence model were used in the continuous phase, and the DPM was used for the snow particles. The SIMPLE algorithm was used to determine the flow field using a pressure-based solver technique based on the coupled pressure-velocity method. In the spatial discretization, the least-square cell-based scheme was used for the gradient term, the second-order upwind scheme was used for the pressure term, and the momentum term was used to solve the k and ε equations. The first-order implicit scheme was used in the transient simulation. Table 1 lists the boundary conditions for the calculation, and the UDF was written based on reference [25]. Specifically, snow particles were considered to be in a stable deposition state when the incident angle was less than 60 degrees and the friction speed at the collision point was less than 1 m/s. Otherwise, the snow particles would return to the flow field for a new round of calculations.
After achieving stability in the continuous phase solution, the wall y+ values are primarily 30–300, as depicted in Fig. 2, which validates the accuracy of the selected turbulence model. Subsequently, the discrete phase model was activated for the transient analysis. Following the method in reference [13], a severe snowfall environment was simulated for the bottom of the train. Snow particles were introduced 1 m ahead of the bogie cavity, as shown in Fig. 3. Considering the increase in train speed, the number of snow particles released per unit time from the snow release surface was correspondingly increased to maintain the train in the same snowfall environment for controlled variable comparison.

Figure 2: y+ values on the walls of the vehicle body and bogie

Figure 3: Relative positions of snow particle emission surface
Train speeds of 200, 250, and 300 km/h were selected for the motion analysis of snow particles around the bogie. The diameter of the snow particles was 150 µm, assuming that their initial rotational speed was 0 rad/s. For a transient solution, the time step should satisfy a Courant number (CFL) below 1 [13]. CFL is defined as follows:
where Δt and Δx are the time step and mesh size, respectively.
In the unsteady state calculation of this manuscript, particles and gases belong to two-way coupling, and the calculation process is as follows:
(1) Solve the continuous phase flow field (prior to introduction of the discrete phase).
(2) Introduce the discrete phase by calculating the particle trajectories for each discrete phase injection.
(3) Recalculate the continuous phase flow, using the interphase exchange of momentum, heat, and mass determined during the previous particle calculation. Due to the lack of consideration of temperature and particle mass changes in this study, particles are mainly affected by air resistance and Magnus force, the momentum source term for their impact on gas has been added to Eq. (3).
(4) Recalculate the discrete phase trajectories in the modified continuous phase flow field.
(5) Repeat the previous two steps until a converged solution is achieved in which both the continuous phase flow field and the discrete phase particle trajectories are unchanged with each additional calculation.
The transient solution time steps for different train speeds were determined based on the Courant number, mass flow rate of snow particles, wheel rotation speed, and calculation time step for each speed level, as listed in Table 2.

2.4 Grid Sensitivity Analysis and Verification
To ensure the feasibility of the calculation method, three sets of sparse and dense grids were divided to check the grid independence. Table 3 shows the average resolution of the three sets of grids and number of grids, where

A monitoring line was arranged on the center symmetric surface at 0.2 m from the undercarriage, and Fig. 3 shows the relative position. Fig. 4a–c shows the pressure coefficient Cp (

Figure 4: Mesh sensitivity analysis
Because of the lack of experimental equipment, the simulation results of this study could not be compared with experimental data; hence, the DPM was not validated. However, various scholars conducted wind tunnel experiments and successfully simulated the test results using computational fluid dynamics. To ensure the reliability of the computational approach, we used the computational methods of Wang et al. [5,6] in this study.
3 Calculation Results and Analysis
3.1 Snow Particle Motion and Deposition Characteristics at Different Operating Speeds
3.1.1 Flow Field Characteristics around the Bogie
Fig. 5 shows the streamline and velocity plots on the cross-sections of the wheel at y = 0.7475 m (Plane 1) and the symmetric plane of the bogie at y = 0 m (Plane 2). The rotation of the brake discs and wheels causes a significant upward flow of streamlines, and the velocity distribution in the bogie region generally exhibits a higher velocity at the rear and a lower velocity at the front.

Figure 5: Flow characteristics in the bogie region
Between the front wheel and the bogie cavity, there is a low-speed vortex region due to the opposing motion because an airflow rotates with the wheelset and another airflow separates upward from the front edge of the wheel. Streamlines between the rear wheel and bogie cavity are drawn into the interior of the bogie by the rotating components and subsequently flow toward the front of the bogie. When the train speed increases, the velocity distribution in the bogie region also increases, mainly around the rotating components, but the changes in velocity gradient are less pronounced elsewhere.
3.1.2 The Trajectory of Snow Particles
To observe the trajectory of snow particles, particles released from coordinates near the brake disc (point P1 (19, 0, 0)) and near the wheelset (point P2 (19, 0.7475, 0)) were selected as tracking objects, as shown in Fig. 6a. Fig. 6b–d shows the trajectories of snow particles at different speed levels, where “R” represents the trajectory considering the rotational motion of the snow particles. When the rotational motion of the snow particles is considered, their trajectories significantly change, which raise their positions and change the snow accumulation locations. Furthermore, when the train speed increases, the trajectory changes caused by the snow particle rotation become more pronounced. After colliding with the brake disc or wheelset, snow particles rebound and move rearward along the airflow underneath the bogie. Since the brake disc has a smaller diameter than the wheel, the snow particles released from point P1 generally have a greater trajectory than those from point P2.

Figure 6: Snow particle spatial trajectories at different train speeds
3.1.3 Snow Particle Deposition Characteristics
(1) Incident mass of snow particles
Fig. 7 compares the distribution of the snow particle incident mass (mass of snow particles that collide with the surface) on the bogie surface at different speeds. Taking 200 km/h as an example, the dashed box indicates the snow particle rotation. Since the wheelset and brake disc are high-speed rotating components, their surfaces have no snow deposition; thus, they are hidden to observe the distribution of snow particles on components such as the brake caliper. Snow particles are more likely to impact the rear of the bogie, with particularly noticeable differences in snow particle incident mass on the brake calipers and lateral dampers at the front and rear of the bogie. When the operating speed increases, the snow particle incident mass on the bogie surface also increases with significant variations in areas such as the bolster, anti-roll bar, traction rod, and top of the brake calipers. The changes in the distribution of snow particle incident mass also become more pronounced due to the snow particle rotation, particularly at areas such as the top of the bolster, the top of the frame, and the ends of the frame.

Figure 7: Distribution of the snow particle incident mass on the bogie at different speeds (t = 1 s)
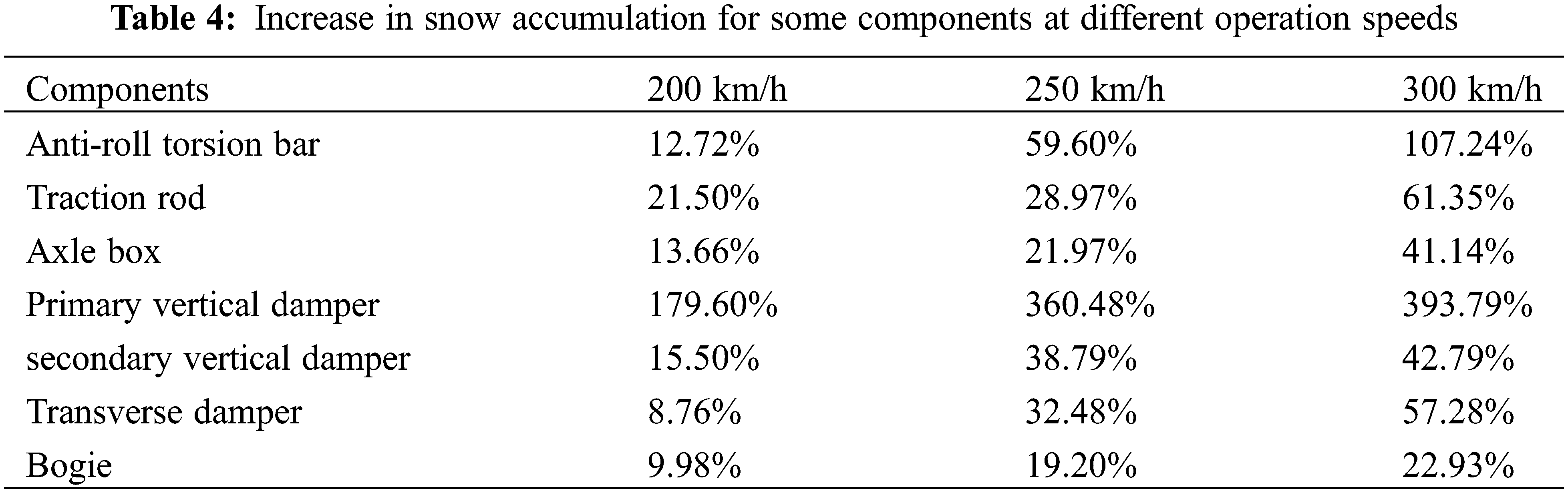
(2) Snow accumulation in various components of the bogie
Fig. 8 compares the snow accumulation on various components of the bogie at different operating speeds. Table 4 presents the snow growth ratio for selected components after considering the snow particle rotation. The results indicate that when the snow particle rotation is considered, the snow accumulation on each component increases, and a higher operating speed corresponds to more pronounced snow accumulation variation. Without considering the snow particle rotation, the snow accumulation on the bogie at various operating speeds is 0.316, 0.384, and 0.450 g, respectively. However, considering the snow particle rotation, the snow accumulation is 0.347, 0.458, and 0.553 g, i.e., increases of 9.98%, 19.20%, and 22.93%, respectively. When the operating speed of the train is 300 km/h, the snow accumulation on each component increases by more than 40%, and the snow accumulation on the primary vertical dampers even increases by 393.79%. The damping components are most significantly affected by snow accumulation, which threatens the safety of the train operation.

Figure 8: Comparison of snow accumulation in bogie components
3.2 Snow Particle Movement and Deposition Characteristics at Different Snow Particle Diameters
One of the factors that affect the Magnus force is the diameter of snow particles. This section will explore the effect of the snow particle diameter on the motion and deposition characteristics of snow particles. To control the variables, the train operating speed was fixed at 200 km/h, and snow particle diameters of 150, 200, and 300 µm were selected for calculation and analysis.
3.2.1 The Trajectory of Snow Particles
Fig. 9 shows the motion trajectories of snow particles with different diameters. When the diameter is 200 µm and snow particle rotation is considered, the snow particles that are released from point P2 are in a shearing state at the leading edge of the wheelset, hover there and cannot continue moving backward. When the diameter is 300 µm, the snow particles released from point P2 in a rotating state first collide and rebound with the front wheel, closely follow the motion of the wheelset, significantly uplift, and finally leave the bogie region after colliding with the rear wheel. In contrast, snow particles in a nonrotating state collide with the front wheel under the influence of gravity eventually reach the ground.

Figure 9: Snow particle spatial trajectories for different diameters
3.2.2 Snow Particle Deposition Characteristics
(1) Incident mass of snow particles
Fig. 10 shows the incident masses of snow particles on the bogie surface at different diameters. Since the mass of a snow particle is proportional to the cube of its diameter, an increase in diameter causes a significant increase in particle mass. Consequently, the airflow cannot carry as many snow particles into the bogie region, and the frequency of collisions between snow particles and the bogie surface significantly decreases. When the rotation of snow particles is considered, more snow particles reach the top of the bogie. For example, when the snow particle diameter is 300 µm, the average snow particle incidence masses on the anti-rollover torsion bar, rear lateral damper, and traction rod surfaces are 9.68 × 10−5, 2.49 × 10−5, and 5.23 × 10−6 kg/m2, respectively. When the snow particle rotation is not considered, the average snow particle incidence masses on these surfaces are 3.71 × 10−6, 1.63 × 10−6, and 8.28 × 10−7 kg/m2, which show significant differences.

Figure 10: Incident mass distribution of snow particles on the bogie at different diameters (t = 1 s)
(2) Snow accumulation in various components of the bogie
Fig. 11 compares the snow accumulation on various components of the bogie at different snow particle diameters. Table 5 shows the increase in the snow accumulation ratio for some components after considering the snow particle rotation. A comparison with Table 4 reveals that when the snow particle rotation is considered, the snow particle diameter causes a significantly difference change in snow accumulation from the train operating speed. When the snow particle diameter increases, the overall snow accumulation on the bogie decreases. The reason is that with increased mass, the number of snow particles that the airflow can carry decreases, so fewer snow particles come into contact with the bogie surface.

Figure 11: Comparison of the snow accumulation on bogie components

Without considering the snow particle rotation, the deposition amounts of snow particles with different diameters on the bogie are 0.316, 0.201, and 0.108 g. With the snow particle rotation, the deposition amounts are 0.347, 0.239, and 0.126 g, i.e., increases of 9.81%, 19.11%, and 17.26%, respectively. When the snow particle diameter is 300 µm, the snow accumulation on the primary vertical damper and anti-roll torsion bar increases by 310.94 times and 9.70 times, respectively, and the snow accumulation on most components increases by more than 100%.
Fig. 12 shows the distribution of snow accumulation on the bogie surface in comparison cases 1 (Uref = 200 km/h, dp = 150 µm), 2 (Uref = 200 km/h, dp = 300 µm) and 3 (Uref = 300 km/h, dp = 150 µm). Compared to case 2, the variation in snow distribution on the bogie surface due to snow particle rotation is particularly significant. This is most noticeable for components such as the anti-roll torsion bar, lateral damper, brake caliper top surface, and bolster, as highlighted by the purple box in the figure. In cases 1 and 3, the difference in snow accumulation at the rear of the bolster and frame is more pronounced.

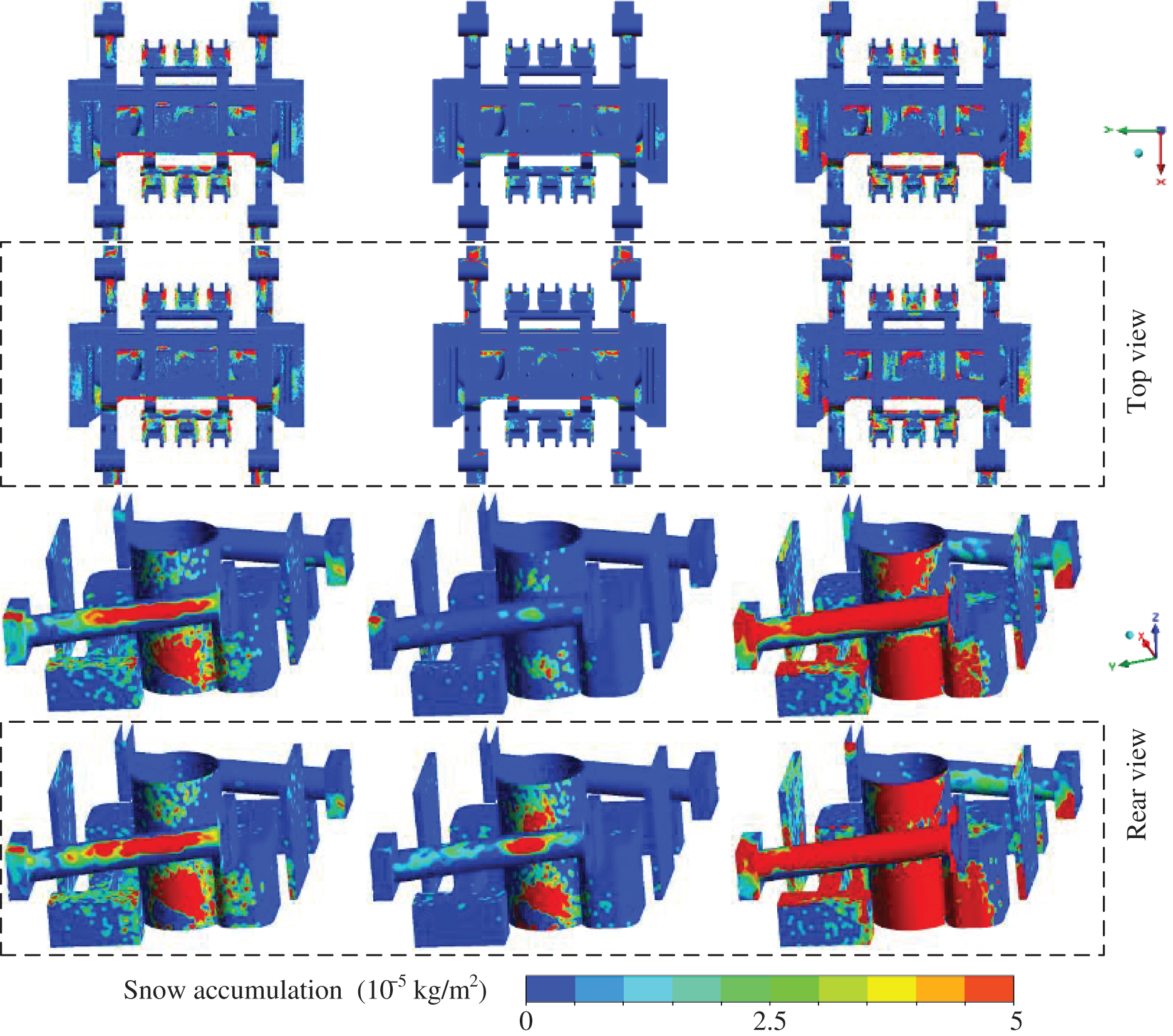
Figure 12: Snow distribution on the bogie surface (t = 1 s)
Regardless of whether the snow particle diameter or operating speed changes, the snow accumulation on various components of the bogie does not necessarily increase when the snow particle rotation is considered. For example, the snow accumulation on the anti-hunting damper and steel spring at a diameter of 300 µm decreases by 15.98% and 41.5%, respectively. The Magnus force caused by the snow particle rotation can lift more snow particles into the interior of the bogie. However, it also changes the lateral trajectory of the snow particles, which changes the snow accumulation position and decreases the snow accumulation on some components.
In addressing the rotational equilibrium equation for spherical snow particles and considering the Magnus effect of snow particles, we conducted calculations using a discrete phase model to study the motion and deposition of snow particles in the bogie region, where different snow particle diameters and train speeds were used as the variables. The main conclusions are as follows:
(1) The Magnus force induced by the snow particle rotation alters the trajectory of snow particles. Areas with greater velocity gradients in the bogie region, such as that near the wheelsets, experience larger changes in snow particle trajectories. The change in snow particle trajectory changes the collision position with the bogie, which affects the deposition location.
(2) When the train speed increases, more snow accumulates on the bogie surface. However, an increase in snow particle diameter decreases the snow accumulation on the bogie surface. The overall snow accumulation on the bogie caused by the snow particle rotation increases, and the snow particle diameter more significantly changes the snow accumulation than the train speed.
(3) When the snow particle rotation is considered, the increase in snow accumulation on components such as the vertical damper exceeds 20%. In the most severe cases, there is an order of magnitude change in snow accumulation, which threatens the safety of the train operation. Analyzing the snow accumulation on various components can provide a reference for implementing localized anti-snow measures on components that tend to accumulate snow.
Acknowledgement: The authors acknowledge the computing resources provided by the State Key Laboratory of Rail Transit Vehicle System, Southwest Jiaotong University, China.
Funding Statement: This research was funded by The National Natural Science Foundation of China (Grant No. 12172308), and the Provincial Natural Science Foundation of Hunan (Grant No. 2023JJ40260).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Hong Lan; data collection: Jiye Zhang; analysis and interpretation of results: Hong Lan, Yao Zhang, Lu Cai; draft manuscript preparation: Hong Lan, Yao Zhang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this paper are available from the corresponding author upon reasonable request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Kloow L, Jenstav M. High-speed train operation in winter climate. Stockholm, Sweden: KTH Railway Group and Transrail; 2011. [Google Scholar]
2. Gao GJ, Zhang Y, Xie F, Zhang J, He K, Wang JB, et al. Numerical study on the anti-snow performance of deflectors in the bogie region of a high-speed train using the discrete phase model. Proc IMechE, Part F: J Rail and Rapid Transit. 2019;233(2):141–59. doi:10.1177/0954409718785290. [Google Scholar] [CrossRef]
3. Gao GJ, Zhang Y, Wang JB. Numerical and experimental investigation on snow accumulation on bogies of high-speed trains. J Cent South Univ Sci Tech Mining Metall. 2020;27(6):1039–53. doi:10.1007/s11771-020-4350-x. [Google Scholar] [CrossRef]
4. Gao GJ, Zhang Y, Miao XJ, Wang JB, Zhang J, Jiang C. Influence of bogie fairing configurations on the snow accretion around bogie regions of a high-speed train under crosswind conditions. J Mech Based Des Struct Mach. 2023;51(10):5452–69. doi:10.1080/15397734.2021.2003711. [Google Scholar] [CrossRef]
5. Wang JB, Zhang J, Zhang Y, Liang XF, Krajnovic S, Gao GJ. Impact of rotation of wheels and bogie cavity shapes on snow accumulating on the bogies of high-speed trains. J Cold Regions Sci Tech. 2019;159(6):58–70. doi:10.1016/j.coldregions.2018.12.003. [Google Scholar] [CrossRef]
6. Wang JB, Zhang J, Zhang Y, Xie F, Krajnovic S, Gao GJ. Impact of bogie cavity shapes and operational environment on snow accumulating on the bogies of high-speed trains. J Wind Eng Ind Aerodyn. 2018;176(9):211–24. doi:10.1016/j.jweia.2018.03.027. [Google Scholar] [CrossRef]
7. Allain E. Experimental and numerical study of snow accumulationon a high-speed train. In: 24th Applied Aerodynamic Conference; 2006; San Francisco, CA: American Institude of Aeronautic and Astronautics. p. 2006–3648. [Google Scholar]
8. Cai L, Li T, Zhang JY. Numerical study on deposition characteristics of snow particle on bogie of high-speed train. J Zhejiang Univ (Eng Sci). 2020;54(4):804–15 (In Chinese). [Google Scholar]
9. Cai L, Lou Z, Li T, Zhang JY. Numerical study of dry snow accretion characteristics on the bogie surfaces of a high-speed train based on the snow deposition model. Int J Rail Transp. 2022;10(3):393–411. doi:10.1080/23248378.2021.1918589. [Google Scholar] [CrossRef]
10. Cai L, Lou Z, Liu N, An C, Zhang JY. Numerical investigation of the deposition characteristics of snow on the bogie of a high-speed train. Fluid Dyn Mater Process. 2020;16(1):41–53. doi:10.32604/fdmp.2020.07731. [Google Scholar] [CrossRef]
11. Leith D. Drag on non-spherical objects. J Aerosol Sci Tech. 1987;6:153–61. doi:10.1080/02786828708959128. [Google Scholar] [CrossRef]
12. List R, Schemenauer RS. Free-fall behavior of planar snow crystals, conical graupel and small hail. J Am Meteorol Soc. 1971;28:110–5. doi:10.1175/1520-0469(1971)028<0110:FFBOPS>2.0.CO;2. [Google Scholar] [CrossRef]
13. Lan H, Cai L, Zhang JY, He PH. Research on movement and deposition of snow particles with different shapes in the bogie region. Proc IMechE, Part F: J Rail and Rapid Transit. 2023;237(5):669–79. doi:10.1177/09544097221129730. [Google Scholar] [CrossRef]
14. Lan H, Zhang JY, Xu GF, Cai L. Research on snow prevention in the bogie region based on active blowing method. Proc IMechE, Part C: J Mech Eng Sci. 2024;238(12):5597–609. doi:10.1177/09544062231207700. [Google Scholar] [CrossRef]
15. Yuan ZL, Zhu LF, Gen F. Gas solid two phase flow and numerical simulation. Nanjing, China: Southeast University Press; 2013 (In Chinese). [Google Scholar]
16. Parsa S, Calzavarini E, Toschi F, Voth GA. Rotation rate of rods in turbulent fluid flow. Phys Rev Lett. 2012;109(13):134501. doi:10.1103/PhysRevLett.109.134501. [Google Scholar] [PubMed] [CrossRef]
17. Liu HQ, Liu AH, Fan SD, Wu Y, Pei J. Analysis of the erosive wear process of seawater pipes by particle rotation under turbulence. Ship Eng. 2019;41(5):128–34 (In Chinese). [Google Scholar]
18. Hao ZH, Chen JH, Bai YH, Wang S, Xu PF, Lu HL. Numerical study on gas-solid flow in a riser using dynamic theory with consideration of particle rotation. J Chem Eng Chin Univ. 2010;24(5):776–82 (In Chinese). [Google Scholar]
19. Zhang S, Hu ZY, Lu ZY. Numerical study of MAGNUS effect in wind-sand movement. J Desert Res. 2010;30(3):498–504 (In Chinese). [Google Scholar]
20. Adedeji OE, Duarte CAR. Prediction of thickness loss in a standard 90 elbow using erosion-coupled dynamic mesh. Wear. 2020;460:203400. doi:10.1016/j.wear.2020.203400. [Google Scholar] [CrossRef]
21. Triesch O, Bohnet M. Measurement and CFD prediction of velocity and concentration profiles in a decelerated gas-solids flow. Powder Tech. 2001;115(2):101–13. doi:10.1016/S0032-5910(00)00337-5. [Google Scholar] [CrossRef]
22. Morsi SAJ, Alexander AJ. An investigation of particle trajectories in two-phase flow systems. J Fluid Mech. 1972;55(2):193–208. doi:10.1017/S0022112072001806. [Google Scholar] [CrossRef]
23. Dennis SCR, Singh SN, Ingham DB. The steady flow due to a rotating sphere at low and moderate Reynolds numbers. J Fluid Mech. 1980;101(2):257–79. doi:10.1017/S0022112080001656. [Google Scholar] [CrossRef]
24. Oesterlé B, Dinh TB. Experiments on the lift of a spinning sphere in a range of intermediate Reynolds numbers. Exp Fluids. 1998;25(1):16–22. doi:10.1007/s003480050203. [Google Scholar] [CrossRef]
25. Tao Y, Zhang BR, Xu L, Tian HL, Zhang YP, Zhang QW. Simulation of snow accumulation on high-speed train bogies based on snow-wall bonding criteria validation. J Zhejiang Univ (Eng Sci). 2022;56(4):674–82 (In Chinese). [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools