 Open Access
Open Access
ARTICLE
High-Precision Flow Numerical Simulation and Productivity Evaluation of Shale Oil Considering Stress Sensitivity
1 Petroleum Engineering Technology Research Institute of Shengli Oilfield, SINOPEC, Dongying, 257000, China
2 Postdoctoral Scientific Research Working Station of Shengli Oilfield, SINOPEC, Dongying, 257000, China
* Corresponding Author: Mingjing Lu. Email:
(This article belongs to the Special Issue: Fluid and Thermal Dynamics in the Development of Unconventional Resources II)
Fluid Dynamics & Materials Processing 2024, 20(10), 2281-2300. https://doi.org/10.32604/fdmp.2024.051594
Received 09 March 2024; Accepted 23 May 2024; Issue published 23 September 2024
Abstract
Continental shale oil reservoirs, characterized by numerous bedding planes and micro-nano scale pores, feature significantly higher stress sensitivity compared to other types of reservoirs. However, research on suitable stress sensitivity characterization models is still limited. In this study, three commonly used stress sensitivity models for shale oil reservoirs were considered, and experiments on representative core samples were conducted. By fitting and comparing the data, the “exponential model” was identified as a characterization model that accurately represents stress sensitivity in continental shale oil reservoirs. To validate the accuracy of the model, a two-phase seepage mathematical model for shale oil reservoirs coupled with the exponential model was introduced. The model was discretely solved using the finite volume method, and its accuracy was verified through the commercial simulator CMG. The study evaluated the productivity of a typical horizontal well under different engineering, geological, and fracture conditions. The results indicate that considering stress sensitivity leads to a 13.57% reduction in production for the same matrix permeability. Additionally, as the fracture half-length and the number of fractures increase, and the bottomhole flowing pressure decreases, the reservoir stress sensitivity becomes higher.Keywords
Nomenclature
| K | Permeability |
| Ki | Permeability at Pi |
| m | Stress sensitivity coefficient |
| P | Reservoir pressure |
| Pi | Reservoir pressure at i time |
| Fs | Permeability influence factor |
| ϕ | Porosity |
| ϕm | Matrix porosity |
| ϕf | Fracture porosity |
| λα | The flow coefficient of the α phase |
| λm,α | Flow coefficient of α phase in matrix |
| λf,α | Flow coefficient of α phase in fracture |
| α | Different phase states, including oil and water |
| bα | Proportion of oil and water |
| Sα | Saturation of oil and water |
| vα | Flow velocity of oil and water |
| qα | Source and sinks of oil and water |
| S | Skin factor |
| DZ | Formation thickness, m |
| ψf−m | Coupling Term in Flow between Fractures and Matrix in Shale Reservoirs |
| V | Mesh element volume |
| Aik | Intersection area fraction between the fracture plane and the grid block |
| Af,m | The cross-sectional area of the fracture surface |
| hf,m | The length of the fracture unit |
| grad | Gradient |
| div | Divergence |
The stress sensitivity of rocks refers to the deformation and subsequent reduction or closure of rock pores caused by the action of effective stress, ultimately leading to a decrease in reservoir permeability. Shale, compared to other rocks, has a higher content of shale clay, making it more compressible [1]. Therefore, shale is more susceptible to the influence of effective stress, resulting in significant pore shrinkage and exhibiting a higher degree of stress sensitivity compared to other rock types. Additionally, shale reservoirs have well-developed bedding planes [2], which are easily deformed under stress. Thus, when subjected to external forces, the bedding planes in shale are prone to deformation. Given the extensive development of bedding planes in shale, the impact of effective stress on shale is more pronounced. Shale oil reservoirs exhibit a high degree of fracture development, including natural fractures and microfractures. Moreover, during the extraction process, hydraulic fracturing techniques are employed to create hydraulic fractures in shale, enhancing the reservoir’s effective permeability and increasing shale oil production [3]. Since the volume of fractures is much larger than that of other pores, fractures experience a greater impact from effective stress compared to other types of pores. Therefore, shale exhibits stronger stress sensitivity than other rock types [4–7].
Gangi [8] developed a model to elucidate the variation of fracture permeability with pressure and confining stress, utilizing a conceptual nail-bed representation to consider the roughness of fracture surfaces. Pedrosa [9] conducted stress sensitivity experiments on shale oil cores in 1986. They observed that the stress sensitivity coefficients were all less than 1 and followed an exponential relationship, indicating an exponential model. Bernabe [10] proposed a power-law evaluation model in the same year. Fan et al. [11] introduced a quadratic cubic stress sensitivity model in 2002. Chen et al. [12] proposed a cubic quartic stress sensitivity model in 2000.
Based on the aforementioned mathematical models for stress sensitivity, it is necessary to select an appropriate stress sensitivity model applicable to shale formations. In 2019, Geng et al. [13] conducted stress sensitivity experiments on fractured shale samples from the Longmaxi Formation in the Fuling area, China. The experimental results indicated that the stress sensitivity of fractured shale samples followed an exponential model. In 2018, Zhu et al. [14] used variable pore pressure experiments to fit the permeability data obtained under different effective stresses and found that an exponential fit provided a good representation. Rosalind [15] conducted stress sensitivity experiments on shale cores over a wide stress range, and the experimental results demonstrated that the stress sensitivity variation in shale cores followed an exponential model. Furthermore, Duan et al. [16] conducted experiments on shale samples from the Longmaxi Formation in the Sichuan Basin. They compared the fitting and correction results of various models, including the exponential model, Gangi model, and Walsh model, for the permeability of natural fractures. The results revealed a significant stress sensitivity between microfractures and artificial fractures, and the trend was consistent with the exponential model [17–19].
Based on the general and open source numerical simulation framework MRST (MATLAB Reservoir Simulation Toolbox) [20], this study investigated the stress sensitivity of shale reservoir matrix and fractures by investigating the latest mathematical characterization models of shale reservoirs. As a result, a novel mathematical model is developed to consider the stress sensitivity of shale in multiphase and multiscale conditions, leading to the establishment of a numerical simulation framework for shale oil reservoirs. This framework provides a new technological approach for the evaluation of shale oil reservoirs and offers a simulation platform specifically tailored for the development of terrestrial shale oil in our country [21–24]. The integration of this framework enables a comprehensive understanding of the dynamic characteristics of shale oil reservoirs, facilitates optimization of development strategies, and enhances overall development efficiency. Consequently, this research carries significant implications for the rational exploitation and utilization of shale oil resources in our country [25–28].
2 The Establishment and Solution of a Stress-Sensitive Mathematical Model for Shale Oil Considering Stress Sensitivity
2.1 Stress-Sensitive Mathematical Representation Model
To determine the most suitable stress sensitivity model for shale oil reservoirs and improve the precision of numerical simulations, stress sensitivity experiments were conducted on core samples extracted from a representative well in the X shale oil field in China. Through the literature review in Section 1, we discovered that the current mainstream mathematical models for characterizing stress sensitivity in shale reservoirs include the exponential model, Gangi model, and power-law model. We fitted these models to experimental data separately, and the fitting results are depicted in Fig. 1.
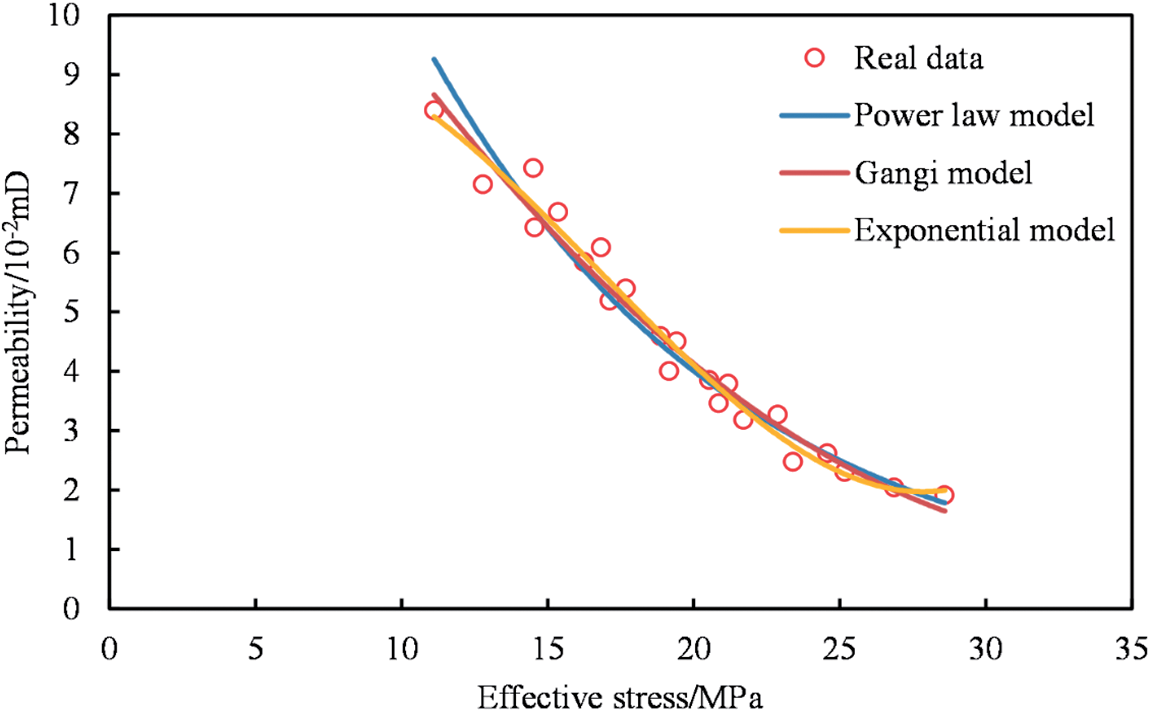
Figure 1: Fitting experimental data of rock core stress sensitivity using different models
A total of three core samples were chosen for experimentation, and the correlation coefficients (R²) resulting from fitting these samples with various stress sensitivity models are presented in Table 1. The fitting outcomes indicate that, among the three frequently employed stress sensitivity representation models, the exponential model demonstrates the most favorable fit with the experimental data from shale cores. All correlation coefficients for the fits surpass 0.9. Consequently, in contrast to the commonly used stress sensitivity representation models, the exponential model stands out as a more accurate mathematical representation of stress sensitivity in shale oil. This choice enables a more precise simulation of fluid flow processes in shale reservoirs.
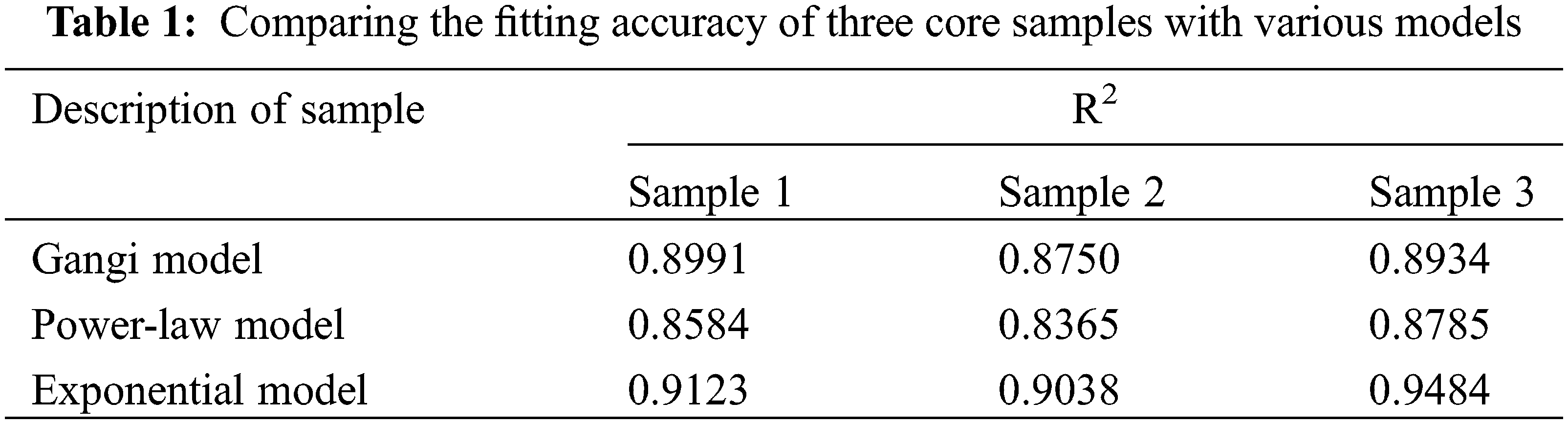
2.2 Establishment of Shale Oil Matrix and Fracture Models
After comparing the fitting outcomes of various stress sensitivity mathematical representation models with stress sensitivity experiments on shale cores, the exponential model was ultimately chosen as the mathematical representation for stress sensitivity in shale. The expression for the exponential model is presented in Eq. (1):
K=Kiexp(−m(Pi−P)) (1)
In this section, for the high-precision simulation of the oil-water flow process in the pore-fracture media of shale reservoirs, we first utilize mathematical representation models to depict the stress sensitivity of both the matrix and fractures. Striving for minimal error, we accomplish macroscopic flow simulation for shale reservoirs. The fundamental see page mathematical model is expressed as Eq. (2):
∂t[ϕ∑α=o,wραSα]+∑α=o,w∇(ραvα)−∑α=o,w∇(ραqα)=0 (2)
As we are investigating two-phase flow equations, the gravitational term can be neglected. The expression for velocity v is given by Eq. (3):
vα=−λα∇pα (3)
Stress sensitivity, depicting the correlation between the permeability of the matrix and fractures and the effective stress in the formation, is quantified through a dimensionless parameter-the permeability influence factor Fs . Its expression is defined by Eq. (4):
Fs=em(p−pi) (4)
By integrating the shale permeability influence factor Fs with the velocity equation and substituting the coupled velocity equation into the fundamental seepage mathematical model, we derive the mathematical representation model for shale oil seepage that incorporates stress sensitivity. This is expressed in Eq. (5):
∂t[ϕ∑α=o,wSα]+∑α=o,w∇(vαFs)−∑α=o,w∇(qα)=0 (5)
By substituting Eq. (3) into Eq. (5), we derive the mathematical seepage model for the matrix and fractures, as depicted in Eqs. (6) and (7):
∂t[ϕm∑α=o,wSα]−∑α=o,w∇(λm,α∇pαFs)−∑α=o,w∇(qα)=0,Ωm (6)
∂t[ϕf∑α=o,wSα]−∑α=o,w∇(λf,α∇pαFs)−∑α=o,w∇(qα)=0,Ωf (7)
In the formulas, Ωm represents the matrix grid, and Ωf represents the fracture grid. The expressions for λm,α and λf,α are provided by Eqs. (8) and (9):
λm,α=kmkrαBαμα (8)
λf,α=kfkrαBαμα (9)
2.3 Discretization and Solution of the Shale Oil Flow Model
Common discrete methods in reservoir simulation encompass the Finite Difference Method (FDM), Finite Volume Method (FVM), and Finite Element Method (FEM). Each method possesses its unique advantages and drawbacks in numerical simulations. The Finite Difference Method is extensively used in reservoir simulation and is considered the foundational method; however, it exhibits limitations in handling complex boundary conditions. Although the Finite Element Method resolves complex boundary issues, it may lack clear physical interpretations and can lead to numerical oscillations during calculations. Conversely, the Finite Volume Method not only tackles complex boundary issues but also guarantees local mass conservation. Thus, the Finite Volume Method offers a distinct advantage in discrete algorithms for reservoir numerical simulation.
To achieve a more precise depiction of fluid transport in reservoirs, scholars have proposed various numerical discretization methods such as Two-Point Flux Approximation (TPFA), Mixed Finite Element Method (MFE), Multipoint Flux Approximation (MPFA), and Approximate Finite Difference Method (MFD). This paper adopts the Two-Point Flux Approximation Finite Volume Method (TPFA-FVM) for the discretization of control equations and a fully implicit first-order backward Euler scheme for time discretization, aiming to enhance the accuracy of fluid flow representation in the reservoir. The discretization of control equations for both matrix and fracture grids results in the following discrete equations, as shown in Eqs. (10) and (11):
ϕmV△t((Sαn+1)−(Sαn))−div{λm,α(pn+1)Fs(Pn+1)μα(Pn+1)T⋅grad(Pn+1)}−V(Pn+1)qα(Pn+1)−V(Pn+1)ψf−m(Pn+1)=0 (10)
ϕfV△t((Sαn+1)−(Sαn))−div{λf,α(pn+1)Fs(Pn+1)μα(Pn+1)T⋅grad(Pn+1)}−V(Pn+1)qα(Pn+1)−V(Pn+1)ψm−f(Pn+1)=0 (11)
In this study, the numerical solution of the model considering stress sensitivity in shale oil reservoirs is investigated. The accurate and efficient solution of the governing equations plays a vital role in obtaining reliable predictions of fluid flow behavior and understanding the complex mechanisms in shale formations. To address this, the NonlinearSolver, an existing nonlinear solver available in the MRST framework, is employed for solving the nonlinear equations. The nonlinear Jacobian matrix is computed using automatic differentiation techniques, ensuring accurate and efficient computation of the model solution.
The dual-porosity model treats fractures and reservoir matrix as overlapping media where fluids flow relatively independently in each medium while also exchanging mass flux. However, this model is only suitable for densely distributed interconnected fractures and is challenging to apply to numerical simulations of large-scale conduit fractures. The Discrete Fracture Model (DFM) simplifies fractures through dimensional reduction. However, when fractures are complexly distributed, a significant amount of irregular meshing is necessary near fractures, greatly increasing workload and severely impacting computational efficiency. The Embedded Fracture Model improves simulation efficiency by efficiently dividing fractured reservoirs using orthogonal grids based on the Discrete Fracture Model (DFM). This significantly enhances simulation efficiency.
In this context, the fractures are represented using the Embedded Discrete Fracture Model (EDFM). EDFM directly incorporates a structured matrix grid, reducing the dimensionality of the fractures, and treats them as source-sink terms. To establish connections between the matrix, fractures, and wellbore, EDFM introduces Non-Neighboring Connections (NNC). The precision of EDFM surpasses that of equivalent continuous medium models. Its advantage lies in avoiding the intricate, unstructured grids associated with discrete fracture networks, thereby reducing computational complexity. This technology demonstrates significant prowess in accurately predicting production capacities in hydraulic fracturing wells.
EDFM adopts the concept of a double-porosity fracture model, incorporating a flow coupling term ψf−m to couple the matrix and the fractures. Consequently, the matrix grid does not necessarily align with the fracture plane [29–31]. The EDFM formulation includes three types of Non-Neighboring Connections (NNC): (1) Fracture-Matrix, (2) Fracture-Fracture, and (3) Fracture-Wellbore. The general NNC model can be expressed as follows:
ψNNCf−m=TNNCf−m(Pn+1f−Pn+1m) (12)
ψNNCf−m=−ψNNCm−f (13)
Fracture-matrix NNC: Fracture-matrix conductivity Tf−m can be expressed as:
TNNCik=K0,ikμα,ikAikdik (14)
dik denotes the average normal distance from the matrix to the fracture surface, as depicted in Eq. (15):
dik=∫dikdvVi (15)
Fracture-Fracture NNC: The calculation of the conductivity between intersecting fractures is given by:
TNNCjk=tjtk∑Nintsm=1tm ,tm=Af,m0.5hf,mk0,mμα,m (16)
Fracture-Well NNC: If the well intersects with the fracture unit, the effective wellbore index WI and the equivalent radius re can be expressed as:
WIf=2πKfwfln(rerw)+s ,re=0.14√h2f+DZ2 (17)
3 Evaluation of Productivity in Stress-Sensitive Shale Oil Horizontal Wells
3.1 Overview of Shale Oil in X Oilfield
In this study, we present a case study utilizing production data from the X Oilfield to conduct analysis and simulation. The parameters used in the analysis and simulation are based on the values provided in Table 2. The data presented in this paper is sourced from actual data obtained from shale oil reservoirs in our country. However, due to confidentiality constraints, we are unable to provide detailed data.
The objective of this study is to analyze the variation in shale oil reservoir productivity, considering stress sensitivity, under the influence of different geological parameters, fracture parameters, and production parameters. This research delves into the reservoir behavior and performance of continental shale oil fields. The oil-water relative permeability curve is depicted in Fig. 2.
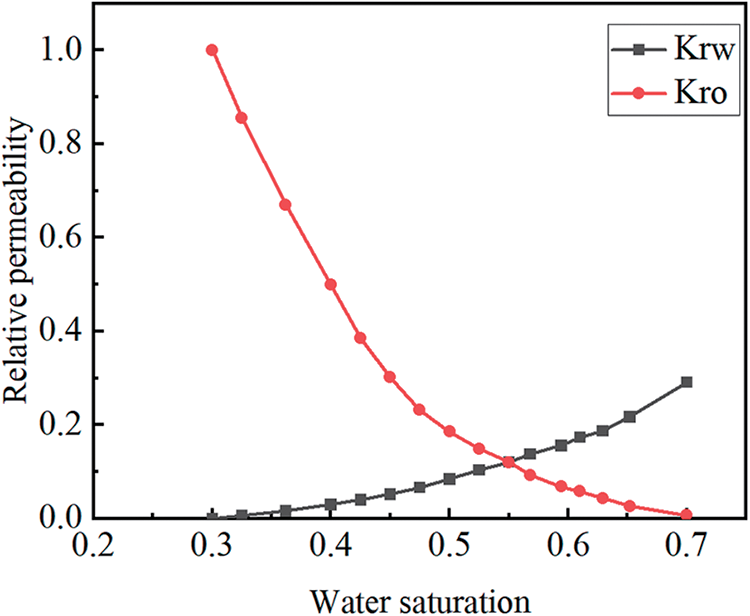
Figure 2: Oil-water relative permeability curve
3.2 Verification of Shale Oil Mathematical Model Considering Stress Sensitivity
Conceptual models for shale oil reservoirs with dimensions of 61 × 17, 11 × 22, and 5 × 10 were established using the data provided in Table 2. Based on the established matrix grid and fracture data, along with user-defined grid partition parameters, a mesh data structure describing the entire model is generated. This includes information such as the coordinates of grid elements, connectivity, boundary conditions, etc. Simultaneously, the imported attributes of fracture elements are assigned to the respective fracture element grids. The mesh is then subjected to visualization processing to ensure its correctness and consistency. The partitioning of the fracture grid is depicted in the left part of Fig. 3, while the non-neighboring connections (NNC) between fractures and matrix are displayed in the right part of Fig. 3.
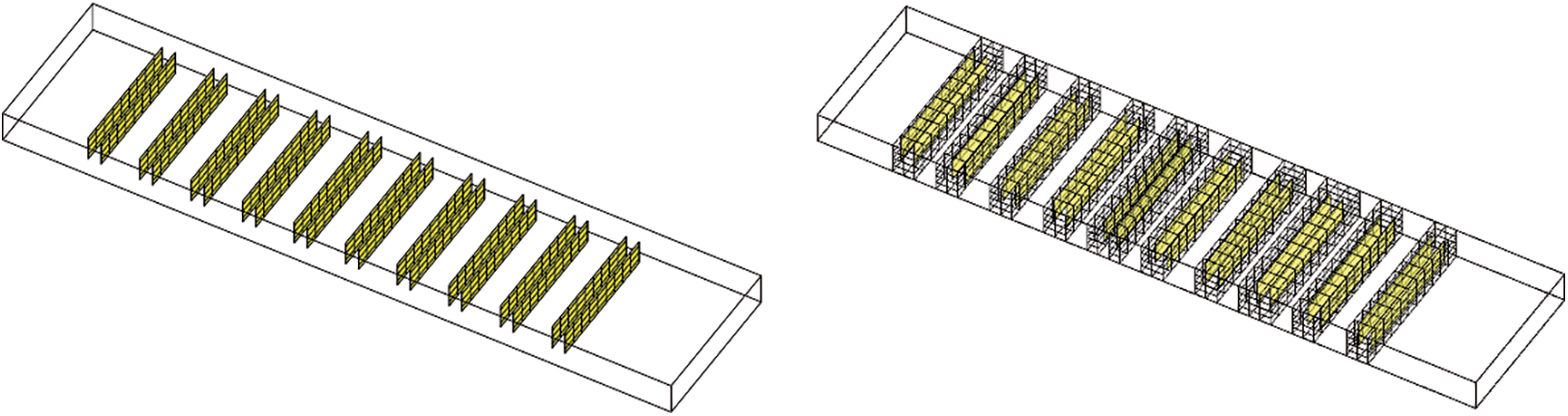
Figure 3: Fracture grid (left) and non-adjacent connection between matrix and fracture (right)
The constructed models were supplemented with reservoir and fluid data from Table 2. Simulations were performed for a horizontal well with specific parameters: a length of 1000 m, inter-stage spacing of 60 m, inter-cluster spacing of 20 m, and a fracturing pattern consisting of one stage with two clusters and 20 fractures. Simulations were conducted to estimate the cumulative oil production over a 5-year period, both considering and not considering stress sensitivity. The relationship between production time and cumulative oil production was derived, and these results were then compared with the predictive outcomes generated by the commercial CMG model. Fig. 4 illustrates the fitting results.
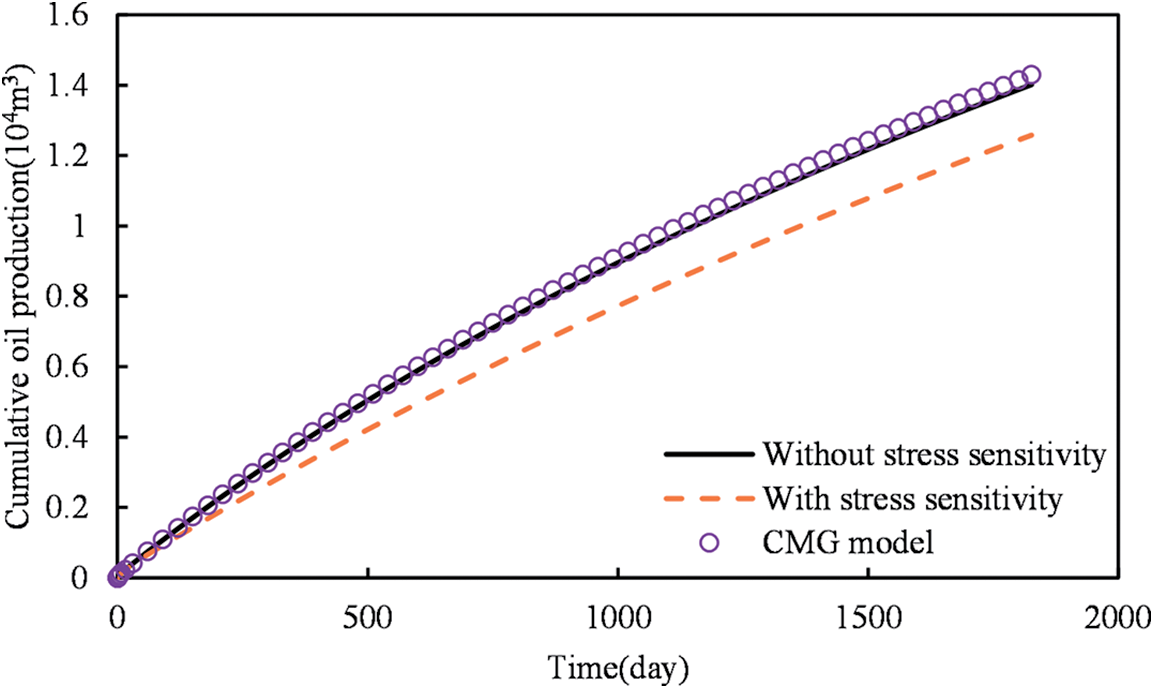
Figure 4: Validation of a stress-sensitive shale oil numerical model
The results indicate that the cumulative oil production curve predicted by the CMG commercial simulator closely aligns with the simulation results of the shale oil numerical model constructed in this paper when stress sensitivity is not considered. This demonstrates the accuracy of the model established in this study.
3.3 Sensitivity Analysis of a Stress-Sensitive Shale Oil Productivity Model
In this section, we conduct a sensitivity analysis using the numerical simulation model established in Section 2, taking into account stress sensitivity. The sensitivity analysis primarily focuses on four aspects: the impact of considering stress sensitivity on production, the influence of matrix permeability on production, the effect of fracture parameters on production, and the influence of bottomhole flowing pressure on production.
3.3.1 The Influence of Stress Sensitivity Coefficient on Production Capacity
According to the fitting outcomes obtained from three sets of core stress sensitivity experimental data and exponential models, the stress sensitivity coefficients for core samples 1, 2, and 3 were determined to be 0.045, 0.094, and 0.113, respectively. The stress sensitivity coefficients obtained from fitting the samples in Section 2.1 were subsequently incorporated into a numerically simulated model of stress-sensitive shale oil. The simulation calculations yielded results depicted in Fig. 5.

Figure 5: Comparison of cumulative oil production under different stress sensitivity coefficients
Based on Fig. 5, it is evident that considering stress sensitivity significantly reduces the cumulative oil production within a span of 15 years compared to the scenario where stress sensitivity is not taken into account. This phenomenon can be attributed to the decrease in permeability of the matrix and fractures due to stress sensitivity. Consequently, fluid flow capacity within the pore network is enhanced, leading to a narrower pressure drop range around the fractures when stress sensitivity is considered.
Simulation analysis of three stress sensitivity coefficients shows a clear trend, as shown in Fig. 6: higher coefficients correspond to lower oil production. The exponential model attributes this to greater damage to reservoir permeability under the same effective stress. For instance, at 20 MPa effective stress and 0.16 mD permeability, a curve illustrates matrix and fracture permeability variations with the stress sensitivity coefficient. When the coefficient is 0.045, matrix permeability is 0.065 mD and fracture permeability is 12.197 D. With a coefficient of 0.113, matrix permeability decreases to 0.0166 mD and fracture permeability to 3.13 D, indicating a 30% increase in damage. Thus, higher coefficients lead to more extensive damage, resulting in stronger stress sensitivity and lower oil production.
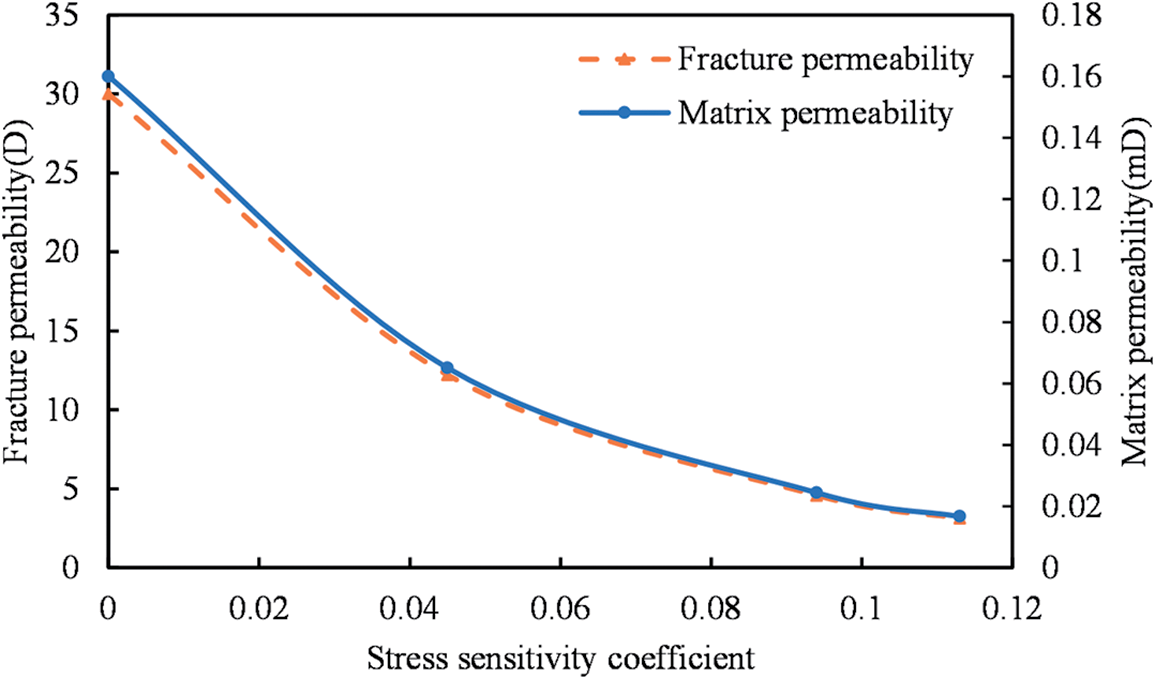
Figure 6: Permeability variation curves of matrix and fractures with stress sensitivity coefficient in shale reservoirs
3.3.2 The Influence of Matrix Permeability on Production Capacity under Stress Sensitivity
The study investigates the variation in shale oil productivity over a 15-year period for matrix permeabilities of 0.05, 0.1, 0.15, 0.2, 0.25, and 0.3 mD. Curves illustrating the relationship between cumulative oil production over time and matrix permeability are plotted for scenarios considering and not considering stress sensitivity.
Analysis of Fig. 7 reveals a gradual increase in cumulative oil production with higher matrix permeabilities. When the matrix permeability is 0.3 mD, the productivity increases by 57.52% compared to a matrix permeability of 0.05 mD. This is attributed to the enhanced flow capacity of shale oil in matrix pores as matrix permeability increases, making it easier for shale oil in the reservoir to accumulate in fractures.
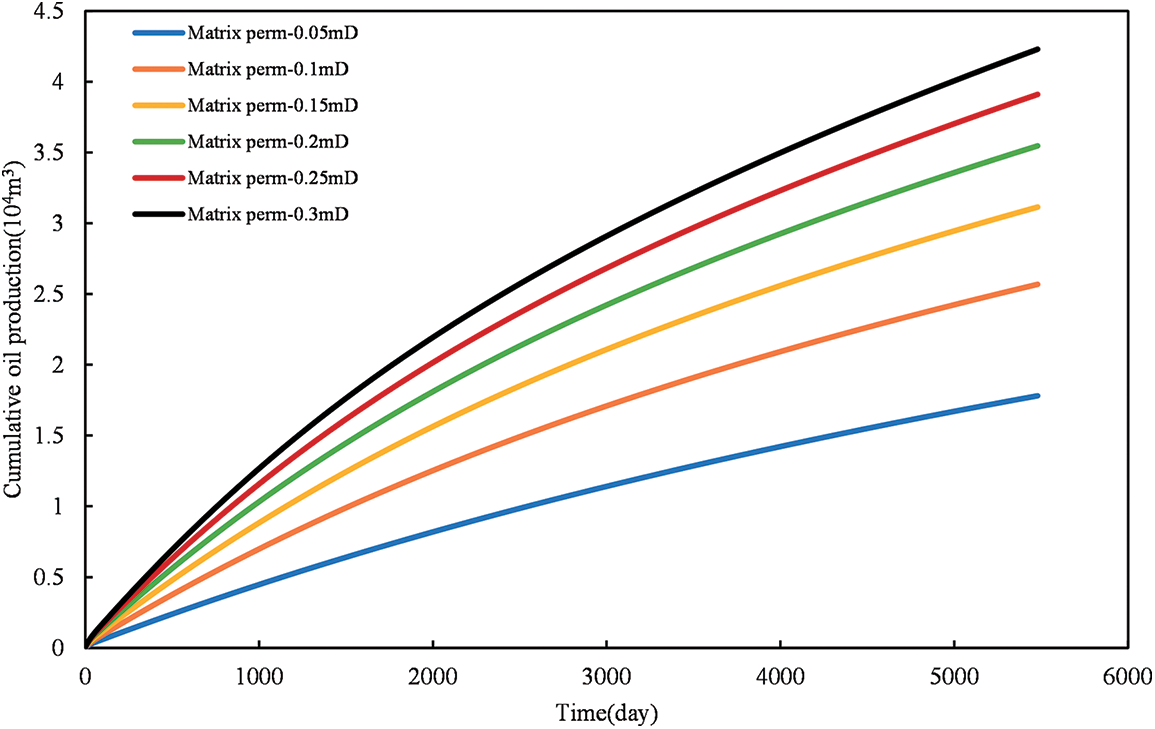
Figure 7: The effect of matrix permeability on cumulative oil production after considering stress sensitivity
As matrix permeability rises, the influence zone of fractures expands, and the pressure drop near the fractures increases. To understand the impact of stress sensitivity on the reservoir due to changes in matrix permeability, a comparative analysis of the relationship between cumulative oil production and matrix permeability is presented for scenarios with and without stress sensitivity, as illustrated in Fig. 8.
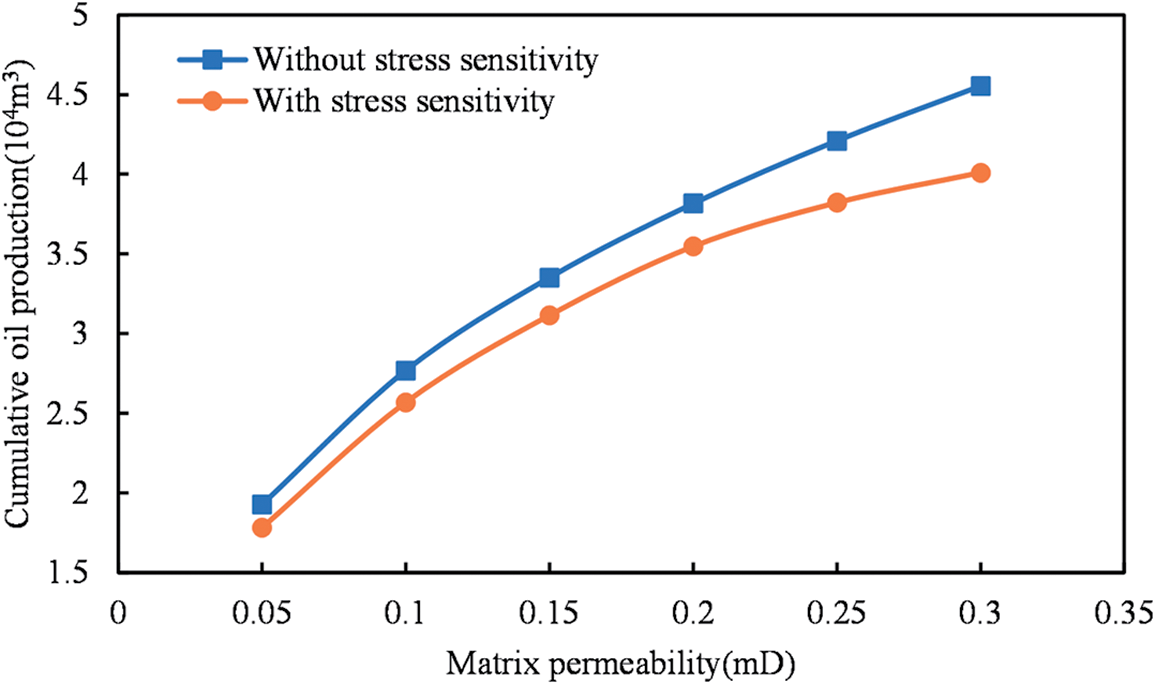
Figure 8: Impact of stress sensitivity on cumulative oil production across various matrix permeabilities in shale reservoirs
Based on the analysis of Fig. 8, it is observed that regardless of considering stress sensitivity, the relationship between cumulative oil production and matrix permeability exhibits a gradually diminishing trend. However, when stress sensitivity is taken into account, the curve demonstrates a more pronounced flattening trend. This can be attributed to the fact that as matrix permeability increases, the oil production rate accelerates, causing a more rapid decline in reservoir pressure. Additionally, the enhanced stress sensitivity effect amplifies the damage to the reservoir. Consequently, the upward trend of cumulative oil production becomes less steep as the increase in matrix permeability progresses.
3.3.3 The Influence of Fracture Parameters on Production Capacity under Stress Sensitivity
Due to the considerably larger scale of fractures in shale compared to its pores, stress sensitivity exerts a much more substantial influence on fractures than on matrix pores. Therefore, it is crucial to consider fracture parameters when evaluating their impact on production yield. This section will analyze the effects of fracture parameters on production capacity, with a focus on three key aspects: fracture half-length, number of fractures, and fracture flow capacity. Through the examination of these parameters, our aim is to gain insights into how fracture characteristics influence production capacity, considering the significant role of stress sensitivity in shale reservoirs.
The Impact of Fracture Half-Length on Production Capacity under Stress Sensitivity
In this study, we conduct an analysis of the influence of fracture half-length on the productivity of shale oil, focusing on a range of fracture half-lengths between 50 and 100 meters. The fracture pattern employed is a one-stage, two-cluster configuration consisting of a total of 20 stages, with an inter-stage spacing of 60 meters and an inter-cluster spacing of 20 meters. To investigate the impact of stress sensitivity, we plot the curves depicting the cumulative oil production over time for both stress-sensitive and non-stress-sensitive scenarios, while considering variations in fracture half-length.
Analysis of Fig. 9 indicates that the longer the half-length of the fracture, the higher the cumulative oil production. When the half-length of the fracture is 100 m, the productivity increases by 36.12% compared to a half-length of 50 m. This is attributed to the increased volume of the fracture with a longer half-length, leading to an expanded influence zone. This, in turn, results in a higher effective volume, allowing a larger area of shale oil from matrix pores to enter the fracture. For a clearer comparison of the impact of stress sensitivity on cumulative reservoir production with varying fracture half-lengths, the relationship between cumulative oil production and fracture half-length is presented for scenarios with and without stress sensitivity in Fig. 10.
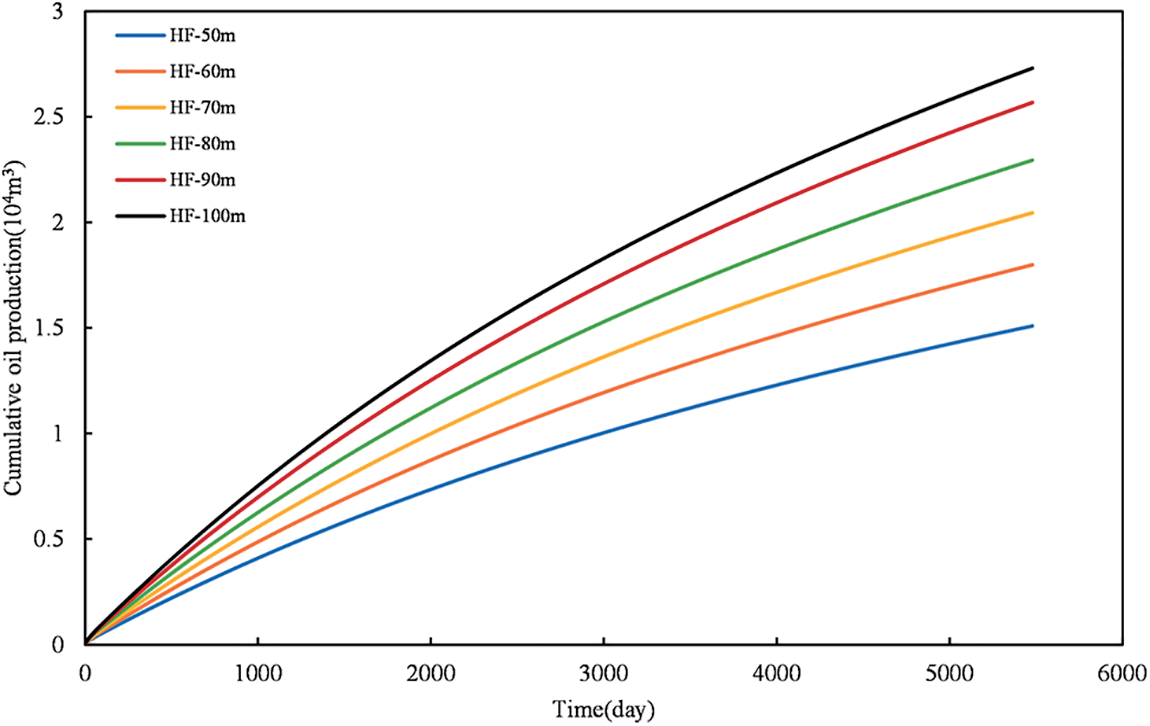
Figure 9: The effect of fracture half-length on cumulative oil production after considering stress sensitivity
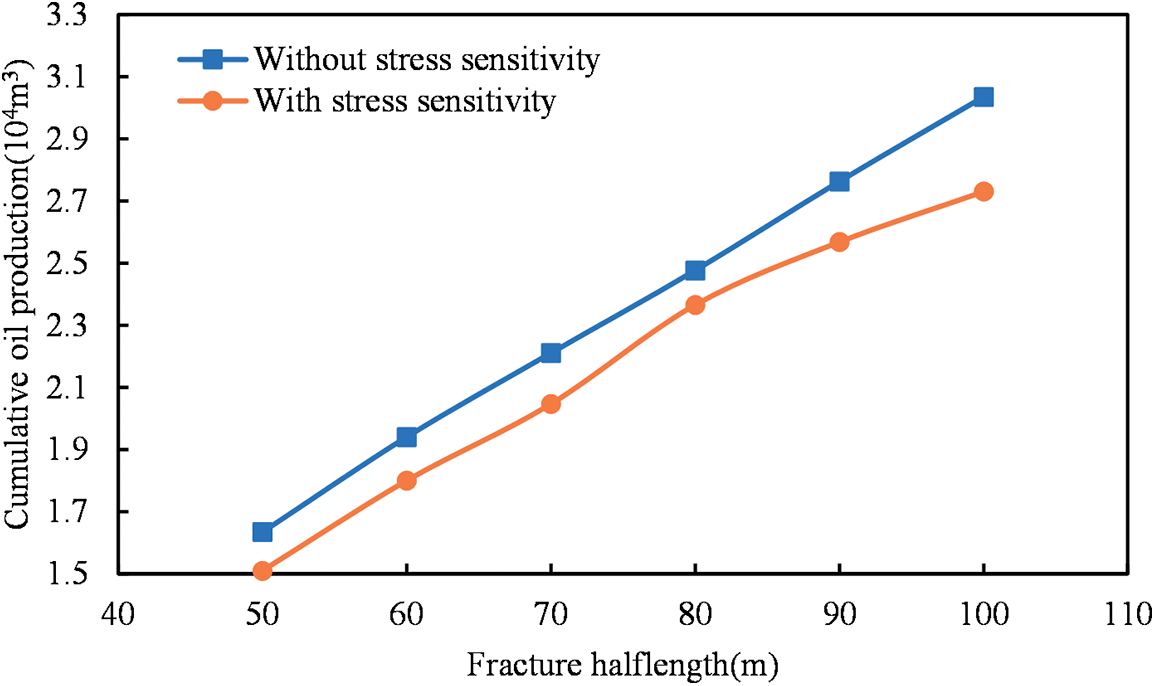
Figure 10: Impact of stress sensitivity on cumulative oil production across various fracture half-length in shale reservoirs
Examination of Fig. 10 clearly demonstrates that accounting for stress sensitivity leads to a slower increase in cumulative oil production with the elevation of fracture half-length, in contrast to scenarios excluding stress sensitivity. This phenomenon is attributed to the elongation of the fracture half-length, resulting in an elevated rate of pressure drop within the reservoir. Additionally, as the fracture volume expands under consistent external forces, the fracture becomes more susceptible to contraction or complete closure, exacerbating the extent of permeability damage. Fig. 11 provides a schematic illustration of this concept.
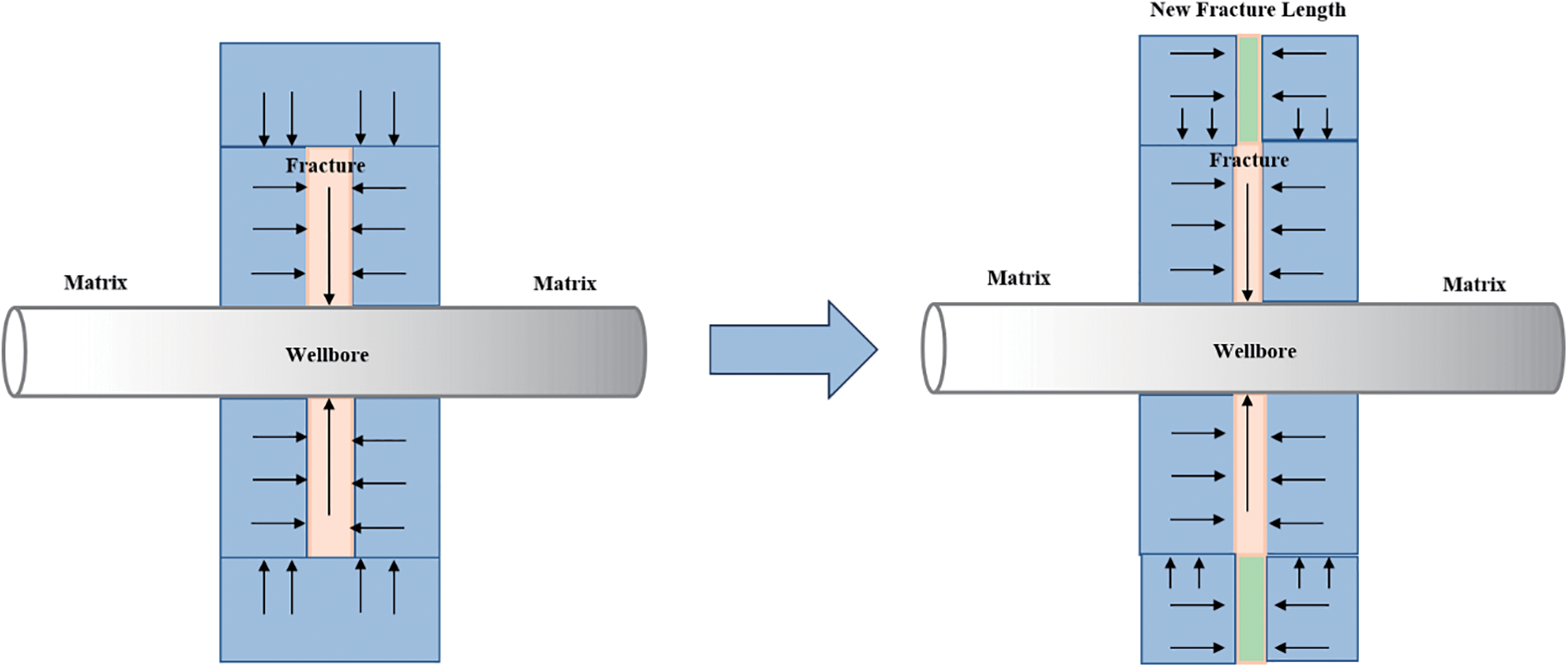
Figure 11: Schematic diagram of fracture half-length influence on productivity after considering stress sensitivity
The Influence of Fracture Count on Productivity under Stress Sensitivity
Analysis was conducted on horizontally drilled wells with stitching patterns consisting of one cluster per section, two clusters per section, and three clusters per section. The horizontal section length was set to 1000 m, with a spacing of 30 m between sections and 20 m between clusters. Subsequently, curves illustrating the relationship between cumulative oil production over time, fracture count, and the consideration of stress sensitivity were plotted.
Based on Fig. 12, it can be observed that under the stitching patterns of one cluster per section, two clusters per section, and three clusters per section, the cumulative oil production increases with an increasing number of fractures. This can be attributed to the fact that with a fixed spacing, a higher number of fractures results in a larger effective drainage volume, allowing more shale oil to flow into the fractures and consequently increasing the production rate. In order to analyze the impact of different fracture counts on productivity considering stress sensitivity, a comparative analysis was conducted by contrasting the curves depicting the relationship between cumulative oil production, fracture count, and the consideration of stress sensitivity vs. no consideration of stress sensitivity.
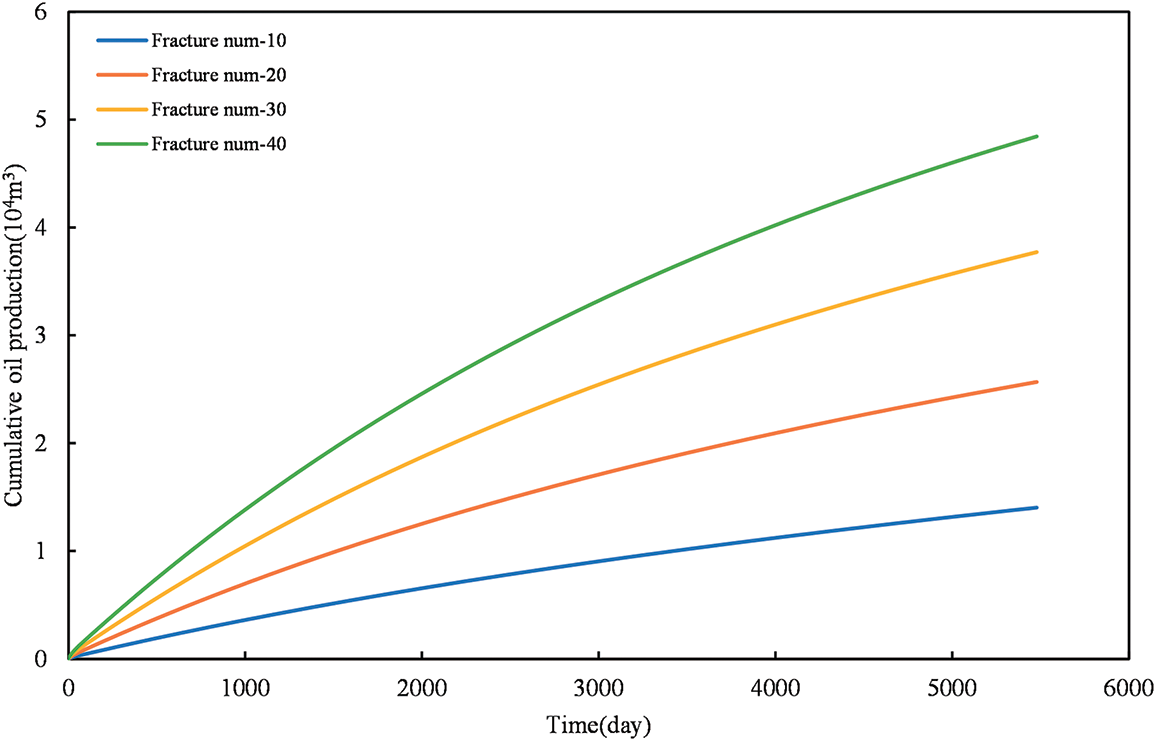
Figure 12: The effect of fracture number on cumulative oil production after considering stress sensitivity
Examination of Fig. 13 indicates that, when accounting for stress sensitivity, the upward trend of cumulative oil production with the number of fractures becomes considerably more gradual. This phenomenon arises from the increased number of fractures, leading to a larger oil drainage area under identical bottom-hole flowing pressure conditions. Consequently, the pressure drop per individual fracture increases, resulting in the accumulation of stress sensitivity within the fractures. As a result, a smoother upward trend in cumulative oil production occurs when stress sensitivity is considered, in contrast to scenarios where stress sensitivity is disregarded, as depicted in Fig. 14.
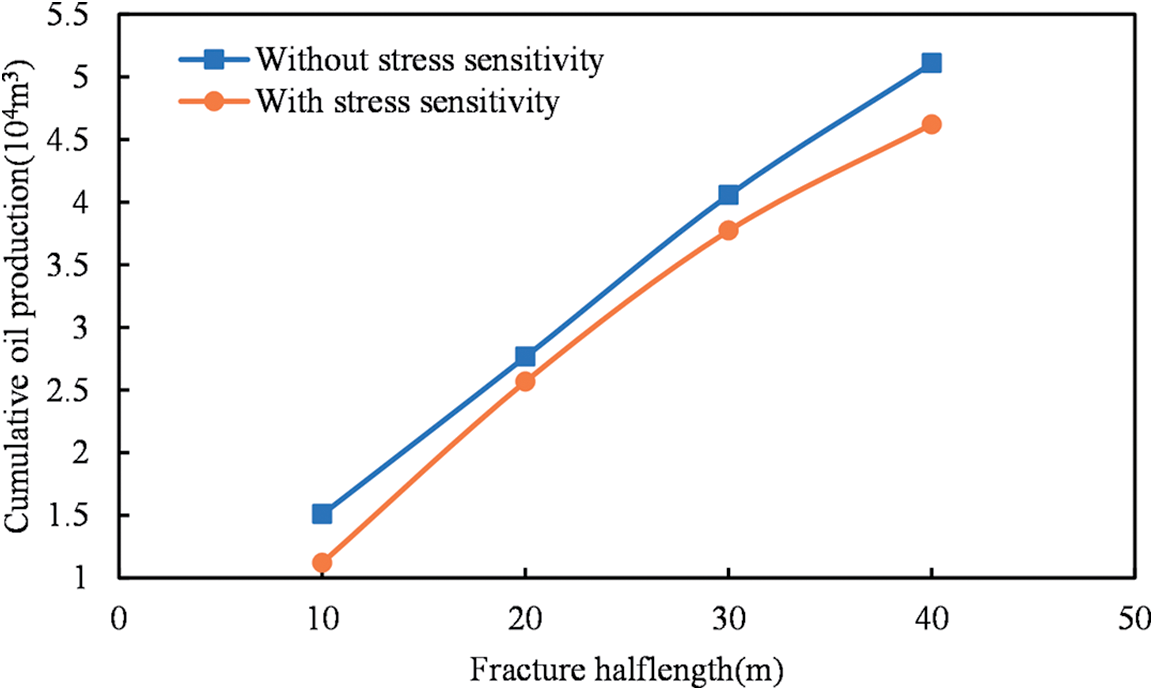
Figure 13: Impact of stress sensitivity on cumulative oil production across various fracture number in shale reservoirs
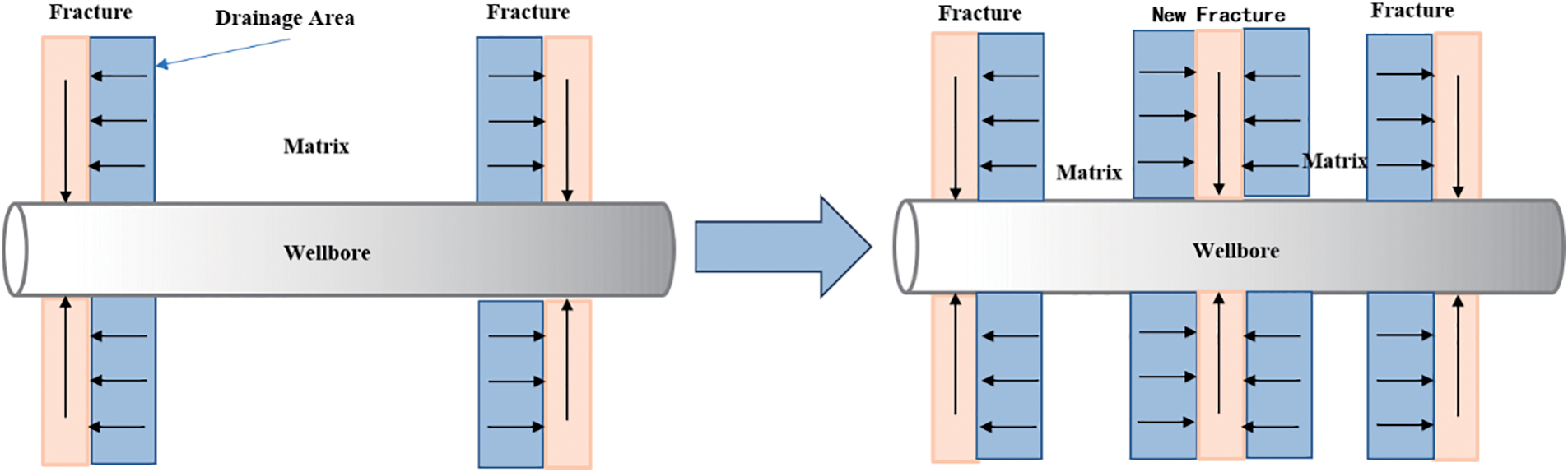
Figure 14: Schematic diagram of influence of fracture number on productivity after considering stress sensitivity
The Impact of Fracture Flow Capacity on Productivity under Stress Sensitivity
Analyzing the impact of fracture flow capacity on productivity, the range of fracture flow capacity is set between 100 and 600 mD·m. The horizontal well is designed with a seam pattern of one segment and two clusters, divided into a total of 10 segments, with a segment spacing of 60 m and a cluster spacing of 20 m. Two sets of graphs are plotted to depict the relationship between cumulative oil production over 15 years and time, as well as the relationship between cumulative oil production and fracture flow capacity. The analysis is conducted for scenarios considering and not considering stress sensitivity.
Fig. 15 analysis demonstrates a continuous increase in cumulative oil production within the reservoir as fracture flow capacity increases. At a fracture flow capacity of 600 mD·m, productivity rises by roughly 6.1% in comparison to that at 100 mD·m. This phenomenon is attributed to shale oil flowing from the matrix through fractures into the wellbore, then being produced to the surface. Therefore, increased fracture flow capacity facilitates fluid flow toward the wellbore, resulting in a continuous rise in cumulative oil production in the reservoir.
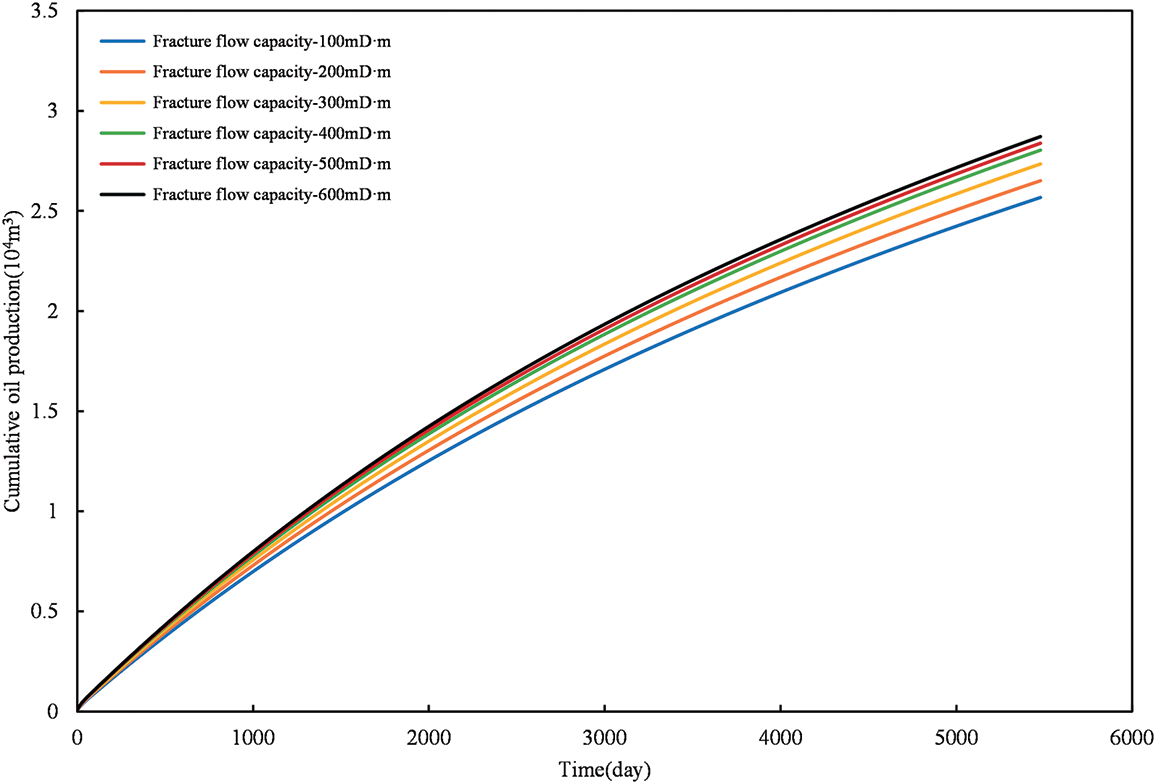
Figure 15: The effect of fracture flow capacity on cumulative oil production after considering stress sensitivity
To further analyze the impact of fracture flow capacity on cumulative production with and without stress sensitivity, a comparative analysis is conducted. The relationship between cumulative oil production over 15 years and fracture flow capacity is presented for scenarios considering and not considering stress sensitivity in Fig. 16.
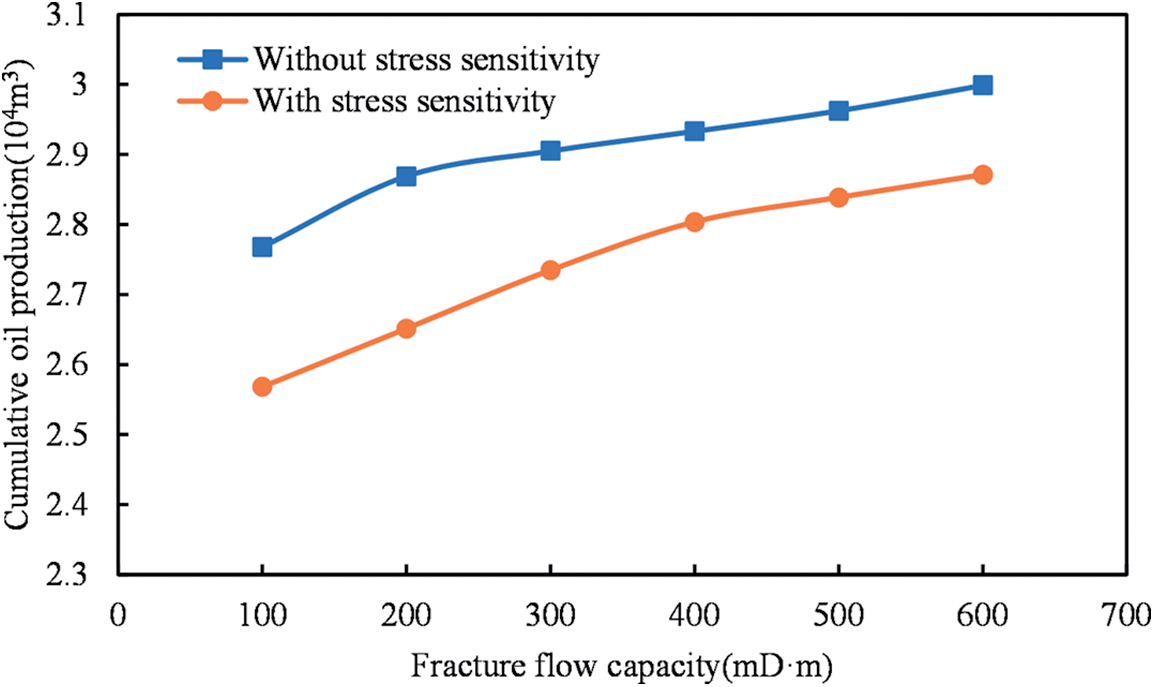
Figure 16: Impact of stress sensitivity on cumulative oil production across various fracture flow capacity in shale reservoirs
Analysis of Fig. 16 indicates that considering stress sensitivity, the cumulative oil production increases with higher fracture flow capacity. As the fracture flow capacity increases, the pressure drop around the fracture expands, leading to a slower upward trend in cumulative oil production. This contrast is more pronounced when compared to the influence of matrix permeability. This phenomenon is attributed to fractures being the primary conduits for fluid flow in the reservoir. In comparison to matrix pores, fractures are more sensitive to stress. With increasing fracture flow capacity, the rate of pressure drop in the reservoir accelerates, thereby enhancing the effect of stress sensitivity.
3.3.4 The Influence of Bottomhole Flow Pressure on Productivity under Stress Sensitivity Effects
In practical production processes, the effective stress on reservoir pores is determined by the difference between the overlying rock pressure and the pore pressure within the formation. Recent investigations have revealed that a decrease in bottom hole flowing pressure results in a decline in pore pressure, consequently leading to an increase in the effective stress exerted on reservoir pores (see Fig. 17).

Figure 17: Analysis of factors leading to increased stress sensitivity due to reduced bottom hole flow pressure
We conducted an analysis to evaluate the cumulative oil production under various bottomhole pressures. Bottom hole flowing pressures were varied between 20 and 50 MPa. The well completion design comprised two clusters per segment, totaling 20 segments. Inter-segment spacing was 60 m, and inter-cluster spacing was 20 m. We plotted a relationship curve illustrating the cumulative oil production over a 15-year period under various bottom hole pressures and corresponding time intervals.
Analysis of Fig. 18 reveals that as the bottom-hole flowing pressure decreases, the cumulative oil production continuously increases. This is attributed to the larger production pressure differential and the resulting increase in oil production rate when the bottom-hole flowing pressure decreases. To facilitate the analysis of the impact of bottom-hole flowing pressure on cumulative oil production in the presence of stress sensitivity, the above curves are organized to obtain the relationship curves between different bottom-hole pressures and cumulative oil production.
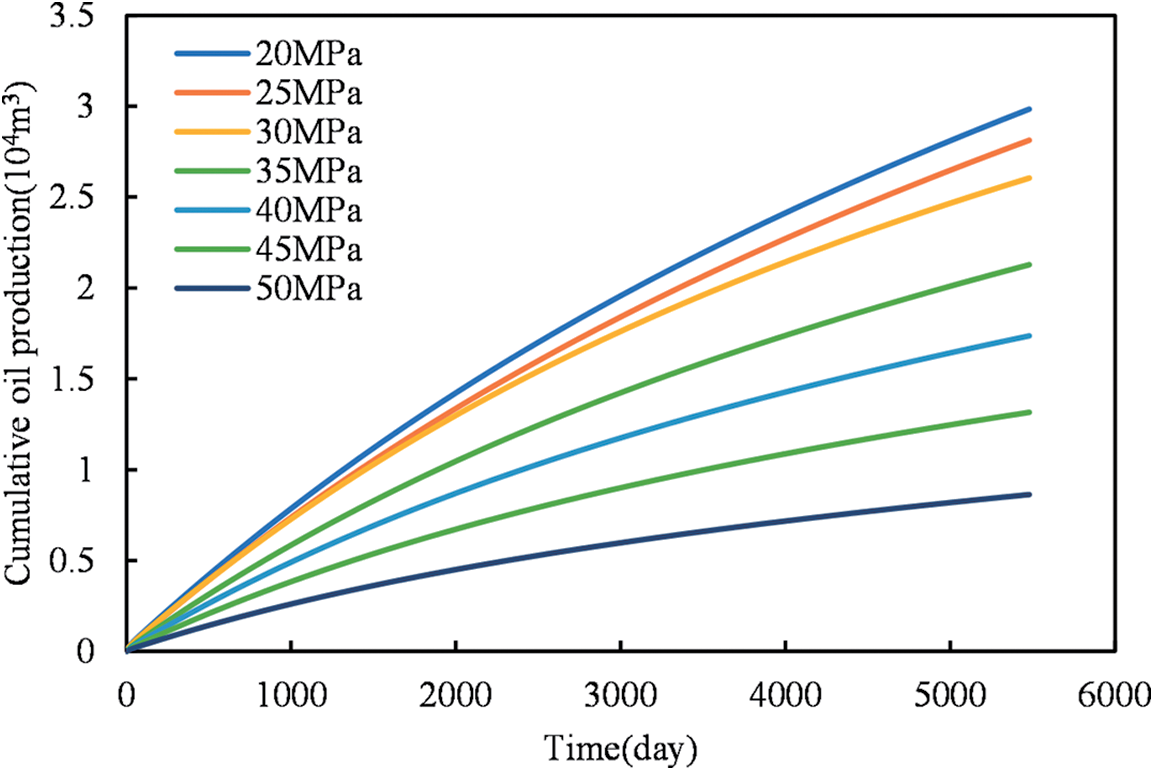
Figure 18: The effect of bottom hole flowing pressure on cumulative oil production after considering stress sensitivity
Lower bottom hole pressure during shale oil extraction and production leads to a greater production pressure differential, thereby enhancing shale oil production. As shown in Fig. 19, the curve has an obvious inflection point when the bottom hole flow pressure is 30 MPa. This inflection point arises due to the decrease in bottom hole pressure, which augments the effective stress on reservoir pores, thereby amplifying stress sensitivity’s impact. Thus, a decrease in bottom hole pressure amplifies the influence of stress sensitivity.
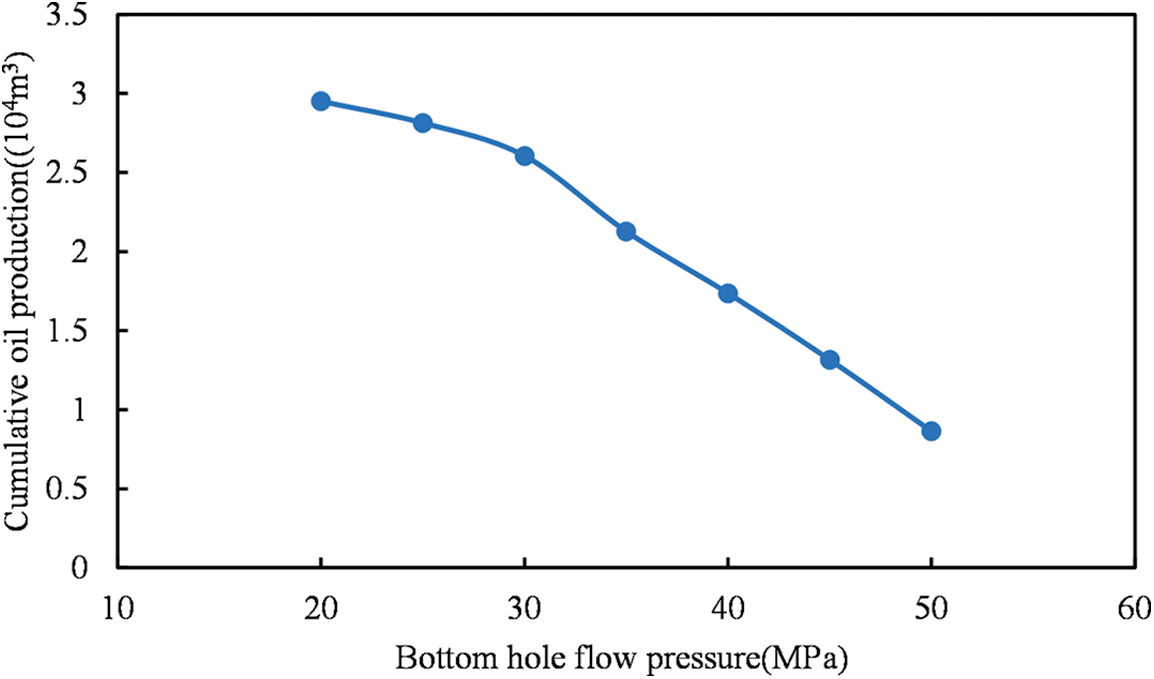
Figure 19: Impact of stress sensitivity on cumulative oil production across various bottom hole flowing pressure in shale reservoirs
When effective stress is low, permeability is highly sensitive to changes. A slight increase can significantly decrease permeability. However, at high effective stress, permeability variations are minimal. In oil and gas field development, during initial production, pore pressure is high and effective stress is low, causing reduced permeability primarily at this stage. Thus, stress sensitivity impacts production mainly in the early stages. In shale oil reservoir development, attention is needed to avoid reducing bottom hole pressure rapidly for short-term high production rates, which may cause irreversible reservoir damage.
(1) After a comprehensive investigation of stress sensitivity mathematical models, the exponential model is chosen to characterize stress sensitivity in continental shale oil reservoirs. This selection is based on fitting and comparison with experimental data obtained from a shale reservoir in China. To account for shale stress sensitivity, a permeability correction factor (Fs) was introduced. Subsequently, an accurate two-phase flow mathematical model, which considers stress sensitivity in continental shale oil reservoirs, is established by integrating this factor with the flow model.
(2) The two-point flux approximation finite volume method (TPFA-FVM) was employed to discretize the governing equations, and the non-linear solver available in the MRST software was utilized to solve the equations. Additionally, an Embedded Discrete Fracture Model (EDFM) was employed to model larger fractures, such as hydraulic and natural fractures. Consequently, a numerical model considering stress sensitivity in shale oil reservoirs was developed.
(3) The modeling was performed on a representative well from onshore continental shale oil fields in China, and the model’s accuracy was validated using the commercial simulator CMG. Subsequently, the model was utilized to analyze the productivity of horizontal wells under various engineering, geological, and fracture factors, taking stress sensitivity into account. The following conclusions were drawn:
When stress sensitivity is taken into account, there is a significant decrease in cumulative oil production in the reservoir. Additionally, as the stress sensitivity coefficient increases, the extent of permeability damage becomes more pronounced. The cumulative oil production from horizontal wells decreases, experiencing a 16.5% reduction when the stress sensitivity coefficient is 0.113 compared to when it is 0.045.
Comparing permeability damage and cumulative oil production under different fracture flow capacities and matrix permeabilities reveals that as both matrix permeability and fracture flow capacity increase, the oil production rate rises. However, reservoir pressure drops, stress sensitivity intensifies, permeability damage increases, and the upward trend in cumulative oil production gradually slows. When stress sensitivity is considered, the cumulative oil production change for matrix permeability in the range of 0.05~0.3 mD is about 82% of that without stress sensitivity. Similarly, when fracture conductivity is 100~600 mD·m, the cumulative oil production change is about 74% of that without stress sensitivity.
Analyzing the impact of stress sensitivity on fracture parameters in horizontal well productivity reveals that with an increase in fracture half-length, the rate of reservoir pressure drop accelerates. Larger fracture volumes make them more susceptible to deformation and closure under external forces, leading to more severe stress sensitivity effects. When stress sensitivity is considered, cumulative oil production increases by 36.12% when the fracture half-length is 100 m compared to when it is 50 m. Moreover, with an increase in the number of fractures, the pressure drop per individual fracture rises, causing more extensive permeability damage. In scenarios considering stress sensitivity, a one-segment-four-cluster seam pattern results in a 71.07% increase in cumulative oil production compared to a one-segment-one-cluster pattern.
Analyzing the impact of bottom-hole flowing pressure on horizontal well productivity, considering stress sensitivity reveals that a decrease in bottom-hole flowing pressure leads to reduced pore pressure, an increase in effective stress on reservoir pores, and more pronounced stress sensitivity effects.
Acknowledgement: None.
Funding Statement: This work was supported by the China Postdoctoral Science Foundation (2021M702304) and Natural Science Foundation of Shandong Province (ZR2021QE260).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Mingjing Lu, Qin Qian; data collection: Anhai Zhong; analysis and interpretation of results: Feng Yang, Wenjun He, Min Li; draft manuscript preparation: Mingjing Lu, Anhai Zhong. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The datasets generated and analyzed during the current study are not publicly available due to confidentiality request by the party providing the data but are available from the corresponding author on reasonable request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Javadpour F, Fisher D, Unsworth M. Nanoscale gas flow in shale gas sediments. J Can Pet Technol. 2007;46(10):53–61. doi:10.2118/07-10-06. [Google Scholar] [CrossRef]
2. Chalmers G, Ross D, Bustin R. Geological control on matrix permeability of Devonian Gas Shale in the Horn River and Liard Basin, northeastern British Columbia, Canada. Int J Coal Geol. 2012;103(6):120–31. doi:10.1016/j.coal.2012.05.006. [Google Scholar] [CrossRef]
3. Fu YG, Ma F, Zeng LX, She CY, Chen Y. Key techniques of experimental evaluation in the fracturing treatment for shale gas reservoirs. Nat Gas Ind. 2011;31(4):51–4. [Google Scholar]
4. Nie XR, Chen JB, Yuan SM. Experimental study on stress sensitivity considering time effect for tight gas reservoirs. Mechanics. 2018;24(6):784–9. doi:10.5755/j01.mech.24.6.22462. [Google Scholar] [CrossRef]
5. Wijaya N, Sheng JJ. Shut-in effect in removing water blockage in shale-oil reservoirs with stress-dependent permeability considered. SPE Reserv Eval Eng. 2020;23(1):81–94. doi:10.2118/195696-PA. [Google Scholar] [CrossRef]
6. Peng Y, Zhao JZ, Kamy S, Li ZL. Fractional model for simulating the viscoelastic behavior of artificial fracture in shale gas. Eng Fract Mech. 2020;228:106892. doi:10.1016/j.engfracmech.2020.106892. [Google Scholar] [CrossRef]
7. Kelly M, Akkutlu IY. Fracture closure effects on producing gas-oil ratio of hydraulically-fractured shale oil wells. In: SPE Hydraulic Fracturing Technology Conference and Exhibition; 2024; The Woodlands, Texas, USA. doi:10.2118/217791-MS. [Google Scholar] [CrossRef]
8. Gangi AF. Variation of whole and fractured porous rock permeability with confining pressure. Int J Rock Mech Min Sci Geomech Abstr. Pergamon. 1978;15(5):249–57. doi:10.1016/0148-9062(78)90957-9. [Google Scholar] [CrossRef]
9. Pedrosa OA. Pressure transient response in stress-sensitive formations. In: SPE Western Regional Meeting; 1986. SPE15115. [Google Scholar]
10. Bernabe Y. The effective pressure law for permeability in Chelmsford granite and Barre granite. Int J Rock Mech Min Sci Geomech Abstr. 1986;23(3):267–75. doi:10.1016/0148-9062(86)90972-1. [Google Scholar] [CrossRef]
11. Fan XP, Xu XR. Experimental and mechanism research about permeability damage with the change of stress. Pet Explor Dev. 2002;29(2):444. [Google Scholar]
12. Chen D, Chen H, Zhang W, Lou J, Shan B. An analytical solution of equivalent elastic modulus considering confining stress and its variables sensitivity analysis for fractured rock masses. J Rock Mech Geotech Eng. 2022;14(3):825–36. doi:10.1016/j.jrmge.2021.08.007. [Google Scholar] [CrossRef]
13. Geng Y, Tang D, Xu H, Tao S, Ma L, Zhu X. Experimental study on permeability stress sensitivity of reconstituted granular coal with different lithotypes. Fuel. 2017;202(1):12–22. doi:10.1016/j.fuel.2017.03.093. [Google Scholar] [CrossRef]
14. Zhu PX, Zhong JW. Experimental study on stress sensitivity of fractured shale reservoir. Petrochem Ind Technol. 2018;25(10):146–75. [Google Scholar]
15. Rosalind AA. Impact of stress sensitive permeability on production data analysis. In: SPE Unconventional Reservoirs Conference; 2008. SPE114166. [Google Scholar]
16. Duan XG, An WG, Hu ZM, Gao SS, Ye LY, Chang J. Experimental study on fracture stress sensitivity of Silurian Longmaxi shale formation, Sichuan Basin. Nat Gas Geosci. 2017;28(9):1416–24. [Google Scholar]
17. Crawford B, Homburg J, Fernandez-Ibanez F, Myers RD, Gao B. Predicting pore volume and transmissibility multipliers for simulating geomechanical effects in naturally fractured reservoirs using stress-sensitive discrete fracture network modeling. In: 2nd International Discrete Fracture Network Engineering Conference; 2018; Seattle, Washington, USA. p. D033S015R003. [Google Scholar]
18. Sikiru S, Soleimani H, Rostami A, Hamza MF, Afolabi LO. Analysis of CH4 and H2 adsorption on heterogeneous shale surfaces using a molecular dynamics approach. Fluid Dyn Mater Process. 2024;20(1):31–44. doi:10.32604/fdmp.2023.029281. [Google Scholar] [CrossRef]
19. Wang W, Xie Q, Wang H, Su YL, Gomari SR. Pseudopotential-based multiple-relaxation-time lattice Boltzmann model for multicomponent and multiphase slip flow. Adv Geo-Energy Res. 2023;9(2):106–16. doi:10.46690/ager.2023.08.04. [Google Scholar] [CrossRef]
20. Wang B. MRST-shale: an open-source framework for generic numerical modeling of unconventional shale and tight gas reservoirs. Geosciences. 2021;11(2):106. doi:10.3390/geosciences11020106. [Google Scholar] [CrossRef]
21. Grasso S, Tuero F, Downey RA, Martinez A, Downey M, Olmos M, et al. A novel shale oil enhanced recovery method for the Vaca Muerta shale. In: SPE/AAPG/SEG Latin America Unconventional Resources Technology Conference; 2023; Buenos Aires, Argentina. [Google Scholar]
22. Daniel B, Martin P, Simon F, Florian E, Kai Z. Stress sensitivity of porosity and permeability under varying hydrostatic stress conditions for different carbonate rock types of the geothermal Malm reservoir in Southern Germany. Geotherm Energy. 2021;9(1):15–74. [Google Scholar]
23. Tutuncu AN. Coupled geomechanical modeling and microseismic monitoring for environmental safety and risk evaluation in unconventional shale reservoirs. In: SEG technical program expanded abstracts. 2013. p. 4500–1. [Google Scholar]
24. El Sgher M, Aminian K, Matey-Korley V, Ameri S. Impact of different fracture fluid and stress shadow on productivity of the multi-stage fractured marcellus shale horizontal wells. In: SPE Canadian Energy Technology Conference and Exhibition; 2024; Calgary, Alberta, Canada. doi:10.2118/218094-MS. [Google Scholar] [CrossRef]
25. Yu G, Liu C, Zhang L, Fang L. Parameter sensitivity and economic analyses of an interchange-fracture enhanced geothermal system. Adv Geo-Energy Res. 2021;5(2):166–80. doi:10.46690/ager.2021.02.06. [Google Scholar] [CrossRef]
26. Aguilera R. Effect of fracture compressibility on gas-in-place calculations of stress-sensitive naturally fractured reservoirs. SPE Reserv Eval Eng. 2008;11(2):307–10. doi:10.2118/100451-PA. [Google Scholar] [CrossRef]
27. Ru Z, An K, Hu J. The impact of sulfur precipitation in developing a sour gas reservoir with pressure-sensitive effects. Adv Geo-Energy Res. 2019;3(3):268–76. doi:10.26804/ager.2019.03.05. [Google Scholar] [CrossRef]
28. Deng Y, Wang W, Su Y, Sun S, Zhuang X. An unsupervised machine learning based double sweet spots classification and evaluation method for tight reservoirs. J Energy Resour Technol. 2023;145(7):072602. doi:10.1115/1.4056727. [Google Scholar] [CrossRef]
29. Zhang Q, Wang WD, Su YL, Chen W, Lei ZD, Li L, et al. A semi-analytical model for coupled flow in stress-sensitive multi-scale shale reservoirs with fractal characteristics. Petrol Sci. 2024;21(1):327–42. doi:10.1016/j.petsci.2023.10.003. [Google Scholar] [CrossRef]
30. Zhuang X, Wang W, Su Y, Yan B, Li Y, Li L, et al. Multi-objective optimization of reservoir development strategy with hybrid artificial intelligence method. Expert Syst Appl. 2024;241(3):122707. doi:10.1016/j.eswa.2023.122707. [Google Scholar] [CrossRef]
31. Fernandes FB, Braga A.M. B. Poroelastic-flow model for permeability loss management in biot’s stress-sensitive oil reservoirs with finite extent hydraulic fractures during well-reservoir drawdown. SPE Prod Oper. 2023;38(4):603–26. doi:10.2118/215809-PA. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
