 Open Access
Open Access
REVIEW
Fluidization and Transport of Vibrated Granular Matter: A Review of Landmark and Recent Contributions
1
Department of Mechanical and Aerospace Engineering, University of Strathclyde, Glasgow, UK
2
European Space Agency, European Space Research and Technology Centre, Noordwijk, Netherland
* Corresponding Author: Marcello Lappa. Email:
Fluid Dynamics & Materials Processing 2024, 20(1), 1-29. https://doi.org/10.32604/fdmp.2023.029280
Received 13 February 2023; Accepted 20 April 2023; Issue published 08 November 2023
Abstract
We present a short retrospective review of the existing literature about the dynamics of (dry) granular matter under the effect of vibrations. The main objective is the development of an integrated resource where vital information about past findings and recent discoveries is provided in a single treatment. Special attention is paid to those works where successful synthetic routes to as-yet unknown phenomena were identified. Such landmark results are analyzed, while smoothly blending them with a history of the field and introducing possible categorizations of the prevalent dynamics. Although no classification is perfect, and it is hard to distillate general properties out of specific observations or realizations, two possible ways to interpret the existing results are defined according to the type of forcing or the emerging (ensuing) regime of motion. In particular, first results concerning the case where vibrations and gravity are concurrent (vertical shaking) are examined, then the companion situation with vibrations perpendicular to gravity (horizontal shaking) is described. Universality classes are introduced as follows: (1) Regimes where sand self-organizes leading to highly regular geometrical “pulsating” patterns (thin layer case); (2) Regimes where the material undergoes “fluidization” and develops an internal multicellular convective state (tick layers case); (3) Regimes where the free interface separating the sand from the overlying gas changes inclination or develops a kind a patterned configuration consisting of stable valleys and mountains or travelling waves; (4) Regimes where segregation is produced, i.e., particles of a given size tend to be separated from the other grains (deep containers). Where possible, an analogy or parallelism is drawn with respect to the companion field of fluid-dynamics for which the assumption of “continuum” can be applied.Keywords
Nomenclature
| b | Vibration amplitude [m] |
| d | Characteristic particle size [m] |
| f | Shaking frequency [Hz] |
| h | Depth of granular material [m] |
| H | Thickness of the fluidized layer [m] |
| i | Unit vector along the direction of gravity |
| N | Number of particle layers [-] |
| n | Unit vector along the direction of vibrations |
| s | Displacement [m] |
| φ | Angle between the direction of vibrations and gravity [rad] |
| ζ | Characteristic particle size to amplitude of vibrations ratio [-] |
| θ | Inclination with respect to the horizontal direction [rad] |
| λ | Pattern wavelength |
| Φ | Phase shift [rad] |
| Γ | Reduced dimensionless acceleration [-] |
| ω | Angular frequency of vibrations [rad/s] |
| Subscripts | |
| cr | critical |
| g | gravity |
| h | horizontal |
| v | vertical |
Bulk granular solids are widespread in nature and technology. Gravel and common sand are just examples of such materials on the surface of our planet. Despite their apparent “simplicity” and great availability, they play a strategic role in a number of areas, e.g., in delivering ecosystem services, vital infrastructure for economic development, providing livelihoods within communities and maintaining biodiversity [1]. Instances of relevant applications can be found in oil refineries and platforms [2], pharmaceutical processes [3], civil engineering [4], and even in agriculture (for plant growth [5]). Yet importantly, notable links also exist with soft matter physics [6], materials science [7], geophysics [8]) and even space exploration [9].
From a physical point of view, i.e., at a more fundamental level, granular materials can be regarded as collections of solid particles, which, in the absence of cohesive forces, are held together only by gravity. This seemingly innocuous definition, however, should not be misread as implying that the microscopic characterization of these media is simple. Although some relevant microphysical reasoning has often been used to elaborate a specific mathematical formalism for the real physical contents of such systems [10–12], a comprehensive understanding of their behaviors at small scales has not been attained yet. An important gap of knowledge, in particular, still concerns the elaboration of models able to predict the “ensemble” dynamics of these collections of particles at several scales when they are subjected to external mechanical stimuli (i.e., energy is somehow injected into them).
Under a certain perspective, granular media may be regarded as a kind of fluid (just as gases or liquids can be regarded as a collection of molecules); nevertheless, unlike fluid dynamics, there is no reliable continuum description of these systems. Despite some interesting advancements in translating ideas conceived for fluids to this field have been elaborated over the years (see, e.g., Nicot et al. [13]; Lappa [14]), the very complex rheology of granular materials often prevents the application of such models to practical circumstances.
In particular, most of problems stem from the nature of the interaction among particles. The main reason for the consumption at small scales (i.e., dissipation) of energy injected into a collection of grains (at large scales) is the essentially inelastic nature of the collisions among them. This intrinsic (fundamental) feature essentially makes all paradigms based on purely elastic interactions (such as those valid for ideal gases, see again Lappa [14], scarcely relevant or completely inapplicable). The energy dissipation taking place at the level of granular contact effectively sets these media into a new class of physical behavior for which continuum equations analogous to the Navier-Stokes equations for fluids have not been defined yet (and it is even not clear whether such an attempt would make sense or not). Although phenomenological models can be constructed, their connection with reality is still unclear as the physics of a granular medium itself is still unknown at a more microscopic level.
Although the boundary between the physics of fluids or solids on the one hand and granular materials on the other hand is subtle and elusive, in a quite surprising way, however, the analogies between these distinct states of matter still keep attracting the attention of researchers. It is a well-known fact that granular media can undergo phenomena that closely mimic those occurring in fluids or solids. Under the effect of an external (mechanical) stimulus, the material keeps behaving as a solid until the applied shear stress exceeds a threshold that depends on the material itself. As soon as this limiting value is overcome, the material “fails” and begins to “flow” [15].
The “differences” with respect to “standard” solids or fluids, however, start to show up as soon as some specific aspects are considered. Although, an analogy may be drawn between the aforementioned ability to depart from a static condition and the abrupt failure of a conventional solid (e.g., a piece of metal or glass), the hallmark of this phenomenon when it happens in a granular medium is the dependence of the threshold shear stress (also known as the “failure shear” or “critical stress”) on the intrinsic level of compressive stress inside the material itself. Another distinguishing mark can be put in relation with the ensuing hysteretic behavior, i.e., the ability of granular media to keep flowing even in the applied shear stress becomes smaller than the abovementioned threshold value [15]. As the reader might have realized at this stage, this specific aspect, in turn, connects to another very important question or issue, that is, the non-trivial dynamics of these media at the macroscopic scale.
Given their abovementioned dissipative nature, just like fluids, granular media are able to behave as pattern-forming systems of exceptional complexity as a result of the equilibrium established between the energy injected into them at large scale and the dissipation occurring due to inelastic collisions and other frictional effects on small scales.
For the specific case in which the aforementioned external stimuli correspond to the application of “vibrations” (this being the most common processes used to fluidize and obtain transport of granular materials in the industrial world [16], the possible outcomes in term of macrophysical behavior are extremely rich and include different dynamical states such as “clustering”, the spontaneous formation of stable arches, cellular patterns, standing waves of various types (featuring stripes, squares, hexagons and localized objects such as particle-like “oscillons” or one-dimensional “worms”), traveling waves, “heaping”, stick-slip motion during avalanches, segregation, liquefaction, Non-Newtonian shearing, thixotropy and, last but not least, vibrationally-induced bulk convection and even turbulent-like states [17].
This phenomenological variety may be regarded as another important factor hindering the possibility to place these materials in a well-defined category (such as ordinary liquids and solids). It also affects in a detrimental way the possibility to use them as convenient prototypes or test-beds to clarify further the general principles governing the dynamics of “complex systems” (i.e., systems where “complexity” emerges as a consequence of the interplay of parts or constitutive elements that would behave in a relatively simple way if separated [18]).
Given these premises, the main objective of this review is placing all this knowledge in a well-defined and structured theoretical context to be used as a basis for further exploration of this field.
As several aspects are embedded in this specific subject, we follow a logical approach where an attempt is made to present the different phenomena in a segregated way. The related governing parameters are introduced in Section 2. In line with the existing literature, where a sort of dichotomy has been created between the dynamics with vibrations parallel and perpendicular to gravity, such cases are treated separately in Sections 3.1 and 3.2, respectively. Since such circumstances are just realizations of more complex situations where vibrations can have an arbitrary direction, the case with oblique shaking is finally examined in Section 3.3. Whenever possible, landmark studies appearing in the literature are presented in a chronological order. Special attention, however, is paid to creating the required links among the different contributions and “distilling” general trends and relevant physical interpretations for the phenomena under discussion.
Vibrations acting on a granular material can be conveniently modeled as a sinusoidal displacement in time, characterized by an amplitude b (m) and an angular frequency ω (rad/s), where ω = 2πf and f is the frequency (in Hz). From a purely mathematical point of view, this can be expressed as:
where
In turn, this simple kinematic law of motion serves as a basis to derive the related dynamic effects or forces. In practice, these can be obtained in a natural way by taking the second time derivative of Eq. (1) with respect to time. By doing so, indeed, one gets the vibration-induced acceleration, namely:
where obviously
which indicates that the dynamic effect corresponding to vibrations with amplitude b and frequency f, is a time-varying acceleration with amplitude given by the product of b and the square of the angular frequency ω = 2πf (i.e., the strength of the resulting force acting on grains grows linearly with the amplitude of vibrations and quadratically with the related frequency).
The total acceleration acting on the granular material (including the gravity effect) can therefore be cast in compact form as:
where g accounts for the constant gravity acceleration (9.81 ms−2 on the surface of Earth) and ig is the related unit vector oriented vertically (towards the center of Earth).
Notably, the vibrations do not contribute to any time-averaged acceleration or force. This can be easily demonstrated by taking the integral of Eq. (4) over the vibration period P = 2π/ω:
from which the reader will easily infer that aaverage = g.
This explains why the constant gravity acceleration g is generally used as a reference quantity to translate the considered problem into a non-dimensional space of parameters. This is typically achieved by defining the nondimensional vibration acceleration acting on grains (also known as “reduced dimensionless acceleration”) as:
Similarly, the non-dimensional vibration frequency is defined as:
where h is the depth of the granular material. Another characteristic non-dimensional parameter traditionally used in the literature to characterize these systems relates to their inherent geometrical properties, namely, the aforementioned depth h and the characteristic particle size d. Their ratio simply reads:
often also simply referred to as “number of particle layers”.
The particle size and the amplitude of vibrations are dimensionally homogeneous; this leads to the possibility to introduce another non-dimensional group formally defined as:
We will consider the related physical meaning (changes induced in the dynamics by variations of this parameter) later in this work.
The relative inclination of the vibrations with respect to gravity does also play a role. The simplest way to account for this effect is to consider as “input parameter” the angle (φ) between the directions of the two unit vectors
Additional influence factors naturally stem from the consideration of other relatively logical arguments.
As already discussed to a certain extent in the introduction, a vibrated granular material may be regarded as the locus of permanent and individual agitation of solid particles. In practice, this relative motion is induced by the momentum transferred to grains by the edges of the container, which hit them repetitively. Such a motion is transferred to the bulk of the medium as grains are mostly in contact with each other, and, accordingly, they undergo unlimited series of solid frictions and inelastic collisions. This simple realization leads to the conclusion that the electrostatic and frictional effects related to the involved particle materials and surface roughness should be regarded as additional relevant degrees of freedom.
A synthetic account of their impact and related mechanisms will be provided directly in the next section together with an illustration of related historical developments. In general, their role is much more elusive (i.e., less quantifiable) as other concurrent factors can contribute to determine the final outcomes in terms of system behavior (these being, e.g., the presence or absence of an interstitial gas, the humidity level and, last but not least, the initial level of material compaction or porosity).
3 Granular Materials under the Influence of Vibrations
In line with what we have anticipated in the introduction, in this section (where the case of parallel gravity and vibration is considered, i.e., φ = 0) we essentially follow a chronological order, i.e., landmark results appearing in the literature are presented before contributions that are more recent. The sequence being implemented also obeys another criterion, that is, an attempt is made to present phenomena of increasing complexity as the discussion progresses. Along these lines, first we concentrate on the dynamics of vibrated “layers”, i.e., collection of particles whose depth is relatively small with respect to the transverse extension; then “deep” systems, where “bulk” effects are enabled, are considered.
3.1 Vertical Shaking (Thin Layers)
In such a context, a first work deserving attention is that by Thomas et al. [19], who investigated the effect of vertical vibration on shallow layers of granular materials with increasing layer heights. Most interestingly, these authors developed a classification of the possible system behaviors articulated in four types of ‘response’. In order to do so, a variety of different granular materials were considered, namely, soda-lime glass beads (density = 2500 kg/m3) and barium-titanate glass beads (density = 4490 kg/m3). For each type of glass, three particle sizes were examined: 74–105 μm (geometric mean, 88 μm), 149– 210 μm (mean, 177 μm) and 595.841 μm (mean, 707 μm). Experiments were conducted at 25 Hz in a relatively narrow rectangular container, 162 mm × 25 mm. First, the critical value of vibrational acceleration needed to mobilize the layer was determined, and then the bed height was increased by adding more material in the attempt to discern the effect of this change on the dynamic response of the bed itself.
Transitions from static bed to mobile vibrated layer was detected for Γcr ≅ 1 for particle sizes above 100 μm. Below 100 μm, Γcr was seen to increase monotonically with decreasing particle size, this relationship, however, being also strongly affected by the considered powder’s cohesiveness.
We describe the abovementioned four states (or vibration modes) in the following in order of appearance due to increasing bed height, i.e., the first state corresponds to the lowest layer depth.
In particular, Thomas et al. [19] called the first two modes “Newtonian States” given their apparent property of producing trajectories of the individual grains obeying Newtonian Mechanics only, i.e., trajectories determined solely by inertial and aerodynamic drag effects.
As revealed by the experiments conducted by these authors, put simply, the general trend of the Newtonian states is that a dense band of material is generated near the base of the vibrated container in conjunction with a scattered distribution of particles throughout the top of the container, which move “in an independent, random fashion”. The difference between the “Newtonian-I” and “Newtonian-II” regimes is simply due to the particles in the upper region of the vessel being more uniformly scattered than in the “Newtonian-I” regime (this being due to the increased number of particles present in the Newtonian-II case caused by the increased layer depth, compare Figs. 1a and 1b).

Figure 1: Four characteristic states identified in the study by Thomas et al. [19]: (a) Newtonian I state, (b) Newtonian II state, (c) Coherent-Expanded state, (d) Coherent-Condensed state
Thomas et al. [19] also reported on two other regimes with “particles acting in concert” referred to as the “C-E Coherent-expanded state” and the “C-C Coherent Condensed State”, characterized by a stronger sensitivity to aerodynamic effects and the existence of regions of particles responding as more of a single entity. In particular, the “Coherent Expanded” was depicted as a regime with the granular bed moving as a bulk mass, thereby causing the formation of gaps between the solid and the vessel floor in the upward part of the vibrational cycle (free flight stage).
Thomas et al. [19] argued that this gap, in turn, is responsible for an upward flow of gas through the medium as it approaches the vessel bed during the downward part of the vibration cycle (causing expansion in the bulk medium). The “Coherent Condensed” State finally corresponds to a suppression of the abovementioned expansion mechanism, i.e., this regime is characterized by the medium moving as a cohesive (condensed) solid like structure throughout the vibration cycle (more specifically, as shown in Figs. 1c and 1d, in this regime the degree of compaction tends to be greater in the parts of the bulk closer to the vessel floor and more scattered towards the surface of the structure as the bulk moves away from the vessel floor in the upward part of the vibration cycle).
In both cases when the effective acceleration experienced by the grains becomes negative, the layer of granular material loses contact, leaving a small gap between the bottom of the layer and the container bottom wall. As time passes, the gap first increases, and then it shrinks until the layer hits the bottom wall. However, the layer does not bounce after the collision with the base because, owing to the inelastic nature of this interaction, the collisions between individual grains and the aerodynamic drag (if a gas is present), its kinetic energy is essentially dissipated and a compaction of the layer is produced.
These authors were also the first to report on interesting symmetry breaking phenomena showing up for values of Γ slightly larger than those required to produce a Coherent-Condensed state (the case shown in Fig. 1d, in particular, corresponds to what they defined as “hill-and-dale” surface behavior).
This was one of the earliest realizations that granular materials can produce instabilities just as fluids can do when the amount of available energy increases to a certain extent. Other investigators soon confirmed this idea through other dedicated experiments where such behaviors were referred to as “arching phenomena” (see, e.g., Douady et al. [20]; Hsiau et al. [21]).
As an example, Douady et al. [20] considered glass spheres with diameter dispersion 0.63–0.80 mm, and number of particle layers in the range 10 ≤ N ≤ 100 in a rectangular container with base 100 mm × 12 mm (i.e., relatively small horizontal width as compared to the other horizontal dimension), and found that such arching phenomena reflect the existence of clusters of particles in the bed, which move at different rates with respect to each other and become interlocked during the downward part of the vibration cycle (as they fall towards the vessel floor disorderedly). They introduced the concept of a “node” accordingly as the locus of the vibrated material grains that have limited mobility.
In practice, as confirmed by other studies where the underlying mechanisms have been placed in a relevant theoretical context, the onset of the arch feature can be ascribed to a “period doubling instability”, which for a fixed depth of the layer is excited when Γ exceeds a given threshold. This instability causes clusters of particles to move “out of phase” with respect to each other. In other words, before the period-doubling bifurcation, the layer apparently bounces at the excitation frequency (as described in the preceding text, in this case, the free surface is nearly horizontal and the free space between the bottom surface and the container bottom wall displays a uniform thickness, Fig. 1c). As the period-doubling bifurcation is produced, however, two limit cycles with opposite phases are excited and different regions of the layer can therefore oscillate out of phase. Typically, the peak positions alternate i.e., a minimum corresponds to a maximum in the next period. A further increase in the parameter Γ typically leads to a decrease in the wavelength associated to these dynamics (the distance between two peaks or valleys).
Notably, Douady et al. [20] could observe such phenomena also in experiments with irregular grains.
Remarkably, other similar analyses have shown that these peaks or valleys (as observed ‘locally’) may even reflect the existence of more complex fascinating patterns or ‘waveforms’ if they are considered ‘collectively’ (i.e., if an “ensemble view” of the considered system is considered). Relevant and valuable examples of this line of inquiry are the works by Melo et al. [22,23], Umbanhowar et al. [24], Tsimring et al. [25] and Bizon et al. [26], where, in particular, the constraint of two-dimensional (i.e., narrow) container was removed by allowing the vessels to be cylindrical or have comparable length and width.
In particular, by means of dedicated experiments conducted in a 76 mm diameter container (with the size of glass spheres in the range between 200 and 400 μm and 3 ≤ N ≤ 100), Melo et al. [22] confirmed that as a second critical threshold is exceeded (Γ ≅ 2.2), a well-defined transition occurs from a flat surface to standing wave patterns oscillating at half the excitation frequency (yet reflecting the existence of a “period-doubling bifurcation”). The following patterns were observed: “stripes” (formally corresponding to the reverberation along a given direction of the purely two-dimensional arching phenomena detected by other authors in narrow containers) or “squares”, where valleys and peaks self-organize in order to give an external observer the illusion of a waveform with the square topology.
Interestingly, it was also confirmed that a continuous transition between these states can be enabled by varying the vibration frequency at constant Γ. More precisely, for a small frequency, on increasing Γ the flat surface undergoes a transition to a square pattern consisting of two standing waves with perpendicular wave vectors oscillating at half the driving frequency. However, if the frequency becomes larger than a given threshold value, stripes reflecting a single parametric standing wave are obtained [22]. Interestingly, the unique behavior of these stripes led these authors to introduce an analogy with the well-known dynamics of the convective rolls produced by Rayleigh-Bénard (RB) convection in fluids. Indeed, the observed stripes were closely mimicking the well-known tendency of RB rolls to orient their axis in a direction perpendicular to the sidewalls of the container, thereby giving rise to defects in the center of domains with curved sidewalls (see, e.g., Lappa [18]).
In this regard, it is also worth citing the later study by Clément et al. [27], who using aluminum spheres of diameter 1.5 mm in containers with horizontal width 150 and 300 mm (6 ≤ f ≤ 25 Hz) and small width (leading again to a quasi-two-dimensional behavior), clarified the relationship between the wavelength and the frequency of vibrations (the reader being referred to the decreasing trend shown in Fig. 2). In these experiments, the larger the layer free flight (the amplitude of vibrations), the larger the vertical deformation of the layer (the amplitude of the pattern) and the larger the wavelength selected. Moreover, they reported that for frequencies larger than a crossover value (which is relatively large), the wavelength saturates at a value independent of the excitation frequency. Later, yet for a two-dimensional vibrated layer, Clément et al. [28] confirmed that there are two regimes for the wavelength selection: a dispersive regime where the wavelength decreases with increasing frequency and a saturation regime where the wavelength depends on the number of granular layers in vertical direction (N).

Figure 2: Surface instability for increasing values of the frequency (larger in the lower panel)
Similar information about the trends displayed by the wavelength in the square pattern case, as a function of the layer depth h, the particle size and the vibration frequency, can be found in the aforementioned study by Melo et al. [22]. In particular, these authors reported that, in analogy with known properties of the Faraday waves in fluids, the mean wavelength λ of the square pattern (close to the onset) first increases with h but then saturates at a constant value (that is even almost independent of the particle size). Moreover, the location of the saturation point increases with d, but it always corresponds to a specific number of particle layers, i.e., N = 7, and for this value of N, the wavelength is inversely proportional to the frequency of vibrations for different particle diameters [22] could show that, in line with this trend, λ attains a minimum in the limit as the frequency tends to infinite.
The most interesting outcome of the study by Melo et al. [22], however, concerns the insights provided into the unique features that distinguish the observed standing waves from the equivalent Faraday waves in fluids. Indeed, it was clarified that, as witnessed by their quick suppression as soon as the forcing is stopped, such oscillatory dynamics do not represent a parametric excitation of known intrinsic collective modes of the granular layer. They should rather be regarded as collective modes strongly damped by internal granular friction where spatial coupling is essentially due to the lateral momentum transfer induced by the multiple collisions among the grains. Another factor contributing to setting them apart from analogous behaviors in fluids is the essentially hysteretic nature of the related primary bifurcation, i.e., the patterns disappear at less magnitude of the plate vibrations than they first appear.
Yet for the case N = 7 (in a subsequent work, based on 150–180 μm diameter bronze spheres in a container with diameter 127 mm), Melo et al. [23] found that the hexagonal topology can enter the dynamics if specific conditions are considered. More precisely, hexagonal patterns arise spontaneously from squares or stripes when the vertical motion of the layer undergoes a second period doubling bifurcation for Γ ≅ 3.9. Like squares and stripes, the hexagons also recover their initial configuration after two periods, however, there is an important distinguishing feature: In this case, by translating in time by one period, one does not obtain a pattern spatially shifted of one-half wavelength. Rather, two distinct patterns show up in alternate cycles; these consist of a set of isolated peaks on a triangular lattice, which is turned during the next oscillation into hexagonal cells, each one centered on a former peak location (Melo et al. [23]).
On further increasing Γ, the hexagonal pattern is taken over by more complicated states composed of distinct spatial domains of different relative phase separated by “kinks” (phase discontinuities). Although, as illustrated above, the experimental studies by Melo et al. [22,23] might be regarded as a complete characterization of all the emerging patterns in the Γ-f space for a fixed depth h of the layer, the interested reader may also consider the similar investigation by Bizon et al. [26], where it was shown that Γ ≅ 5.5 can cause the recovery of the squares and stripes pattern, while a further increase to ≅7 leads to the reformation of the hexagon pattern (see, e.g., Fig. 3 for a qualitative sketch of such a series of transitions).

Figure 3: Qualitative map of the spatio-temporal states in the Γ, f* plane for a vertically vibrated layer, where
Even more exotic phenomena have been detected in the frame of other valuable studies. As an example, Umbanhowar et al. [24] revealed that conditions exist for which in place of the collective behaviors leading to patterns with a pervasive distribution of stripes, squares or hexagons, vibrated grains can give rise to “localized features” or “excitations”, generally known as “oscillons”. These authors defined an oscillon as “a small, circularly symmetric excitation which oscillates at frequency f/2, i.e., during one cycle of the container, it is a peak; on the next cycle it is a crater”.
The diameter of these features was typically 30 particles and they were typically found in a range of Γ below the lower stability boundary of the standing-wave patterns for frequencies in the transition region between squares and stripes. Interestingly, these states were obtained by locally perturbing the layer or by decreasing Γ from an already established patterned state.
Their unique dynamics can be described as follows. In the range of parameters for which oscillons are formed, the granular layer undergoes a free flight (starting as soon as the container acceleration drops below– g), followed by an impulsive acceleration produced by the impact of the layer with the base of the container. Accordingly, oscillons that have the shape of craters are turned into peaks (and vice versa) during the collision portion of the cycle. When an oscillon with the crater morphology hits the container, its grains are accelerated towards the centre; accordingly, a peak is formed during the subsequent free flight. At the next impact, particles are spread radially outwards and the crater morphology is recovered. Furthermore, oscillons do not travel in the horizontal direction, rather they do drift about slowly, and randomly (the time required to displace them by a distance equal to their diameter taking about 103 cycles of vibrations).
Most importantly, these phenomena have a propensity to assemble into ‘molecular’ and ‘crystalline’ structures. More precisely, oscillons of like phase can display a short-range, repulsive interaction, while oscillons of opposite phase tend to attract and ‘bind’, thereby leading to the formation of stable dipoles, longer chains or even fascinating triangular tetramer structures, as shown in Fig. 4 [24].
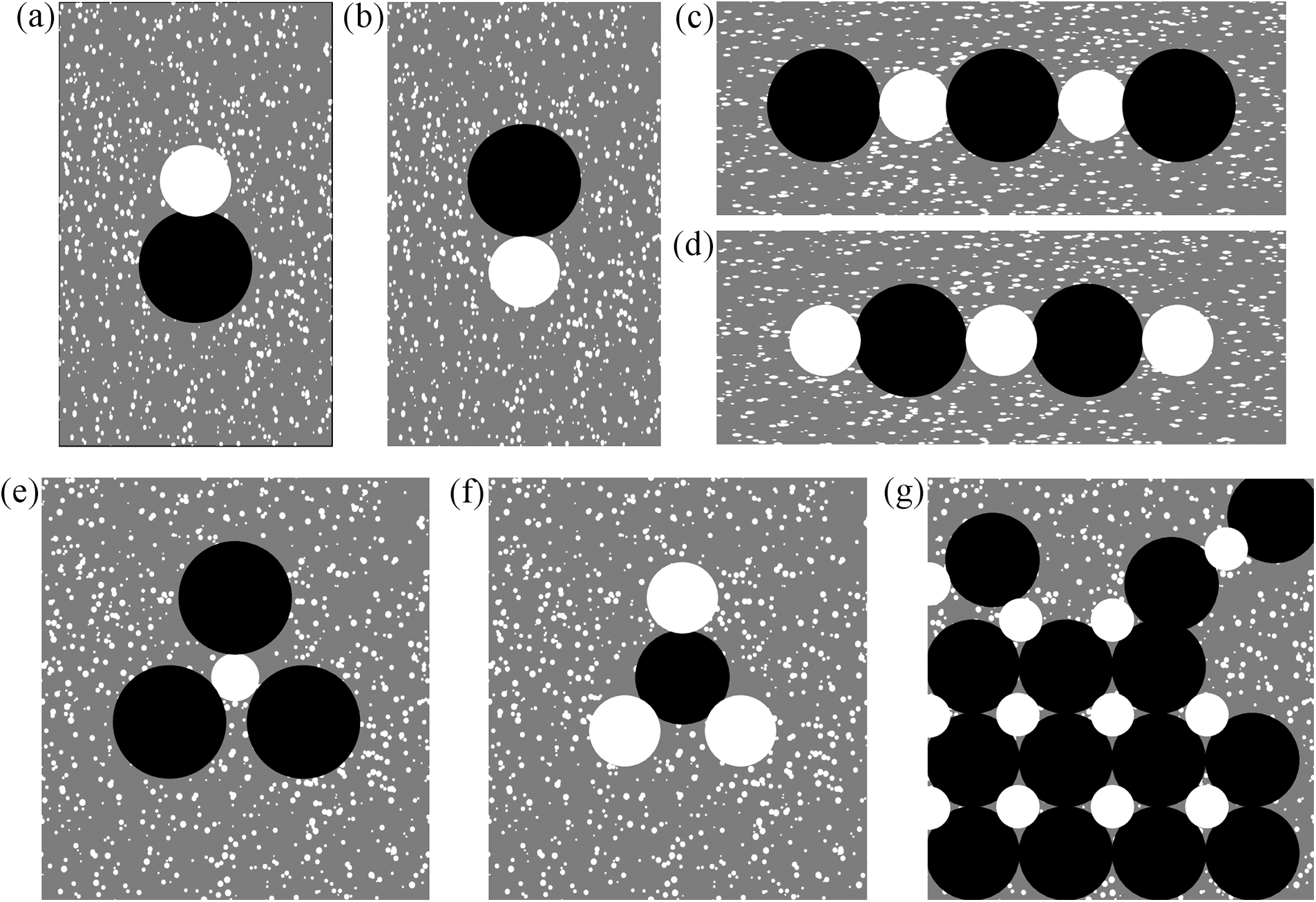
Figure 4: Sketch of oscillon types and related crystalline structures (black regions correspond to craters and white regions correspond to oscillon peaks): (a) peak-crater dipole, (b) crater-peak dipole (corresponding to the configuration shown in panel (a) after one period), (c) polymeric chain (3 craters, 2 peaks), (d) polymeric chain (2 craters, 3 peaks) (corresponding to panel (c) after one period), (e) triangular tetramer (3 craters, one peak), (f) triangular tetramer (3 peaks, one crater) (corresponding to panel (e) after one period), (g) “crystal”
3.2 Vertical Shaking (Thick Layers)
New behaviors are enabled in vibrated granular materials as their depth is increased significantly (thick layer case). These concern material ‘fluidization’, the onset of ‘convection’ and ‘surface instabilities’ (these leading to the formation of ‘heaps’ on the surface of the bed). As these phenomena are not independent from each other, we will treat them simultaneously in the present section, in conjunction with an effort to highlight the related interconnections and cause-and-effect relationships in the light of existing interpretations or theories.
Seminal experiments about the ability of granular materials to enter a “fluidized” state date back to Faraday, who used the following statement to describe it: “the particles rise up at the centre, overflow, fall down upon all sides and disappear at the bottom apparently proceeding inwards” [29].
An interesting (more quantitative) characterization of such a scenario is available in the more recent study by Laroche et al. [30], where the experimental set-up consisted of vertically vibrating vessels with different horizontal sections (rectangular 100 mm × 12 mm, square 75 mm × 75 mm, cylindrical with diameter 90 mm and toroidal with diameters 80–90 mm) filled with particles of different sizes (0.63 to 0.8 mm), different shapes (spherical or irregular), made of different substances (various types of salt, glass spheres and fillite). The experiments were conducted by increasing the acceleration at a fixed value of the frequency, mostly in the range 10–100 Hz and it was observed that the convective regime can be generated by applying sufficient vibrational acceleration.
In particular, as shown by these experiments in the range 10 < N < 140, as soon as a critical acceleration Γcr ≅ 1 is exceeded, the particles begin to move and the horizontal free surface of the granular material becomes unstable. Owing to this instability, “disturbances” appear in proximity to the lateral boundaries of the container (the vertical sidewalls), which force particles to migrate toward the center of the cell and form a heap on the surface of the bed. In a large container, the heap is a cone; in a narrow (two-dimensional) cell, a slice of this cone is obtained. This process continues until an equilibrium condition is attained where the tendency of particles to accumulate in the center is balanced by the avalanching of particles down the slopes of the formed heap. This typically happens once the heap reaches a certain height and the corresponding slope angle is greater than the materials angle of repose. In this condition, the avalanching mechanism transports particles down the free surface from the top of the heap back to the boundaries where the aforementioned disturbances were originally produced. In practice, as time passes, a unique circulation mechanism is established in the bulk of the material by which grains move downward along the vertical sidewalls and upward in the middle of the container (thereby contributing to keep the height of the heap constant in time).
Laroche et al. [30] provided an interesting interpretation of this behavior based on the existence of regions with “different packing structure”. They argued that the packing of the granular material determines if it will respond with solid or fluid like characteristics because, in practice, the relative compaction of clusters of granular materials defines how easily particles can move. In particular, the least compact regions of the heap, i.e., the free surface of the slope where avalanching occurs, allows the granular particles to flow freely down the heap until they reach the sidewalls where they interact with the boundaries and ‘sink’ (while being compacted as they move toward the vessel floor). This mechanism is shown in Fig. 5. As the bed oscillates these compact regions leave the floor and, restricted from easily moving upward by the compaction caused by the material above, they relocate to the center of the cell where the local vertical compaction is lower and allows the material to move upward forming the heap.
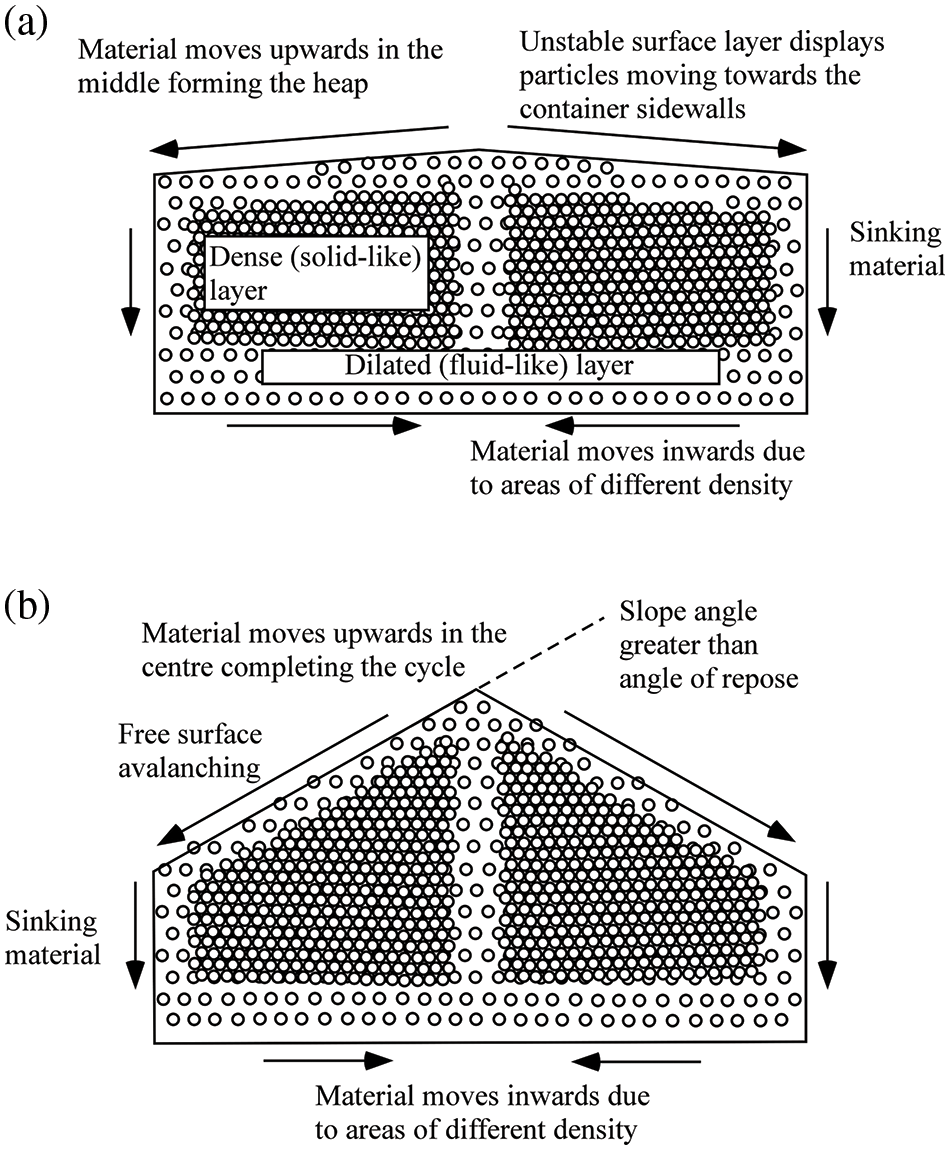
Figure 5: Heap formation mechanism: (a) Heap formation, (b) Self-sustaining heap
In line with this interpretation, Laroche et al. [30] could not observe this convective phenomenon when the layer was too thin, i.e., N too small. Moreover, they noticed a dependence of the slope of the stationary heap on the acceleration. With glass spheres, on increasing Γ just above Γcr, a plateau was attained with the surface inclination nearly equal to the angle of repose; when Γ ≅ 1.5, the angle was seen to decrease until an almost horizontal layer was obtained for Γ ≅ 5, which they ascribed to the corresponding increase in the flight time and the ability of the material to skip/mitigate the solidification (compression) effect induced by its interaction/impact with the bottom wall before being lifted again (thereby allowing the upper part of the layer to remain fluidized, and induce a decrease in the angle of the heap accordingly). Yet in line with these arguments, these authors inferred that the presence of an interstitial gas can plays a significant role in such dynamics as during the free flight timeframe, due to the variation of the gap width, air flows through the layer, thereby contributing to fluidize the granular material and allowing it to behave as a deformable porous medium.
Later studies have clarified that although the presence of gas can somehow support these phenomena, it is not strictly necessary, as another important factor contributing to their genesis, namely the frictional effects produced by the interaction of the grains with the sidewalls, can be effective also in vacuum.
A relevant example of this line of inquiry is represented by the experimental investigation conducted by Clement et al. [31]. They restricted their work to a container with the front and back (transparent) walls kept apart at a distance of one particle diameter only (two-dimensional dynamics) with aluminum (d = 1.5 mm) or stainless-steel (d =1 mm) particles subjected to a frequency in the range 8 to 30 Hz. It was shown that convective motion and associated heaping can occur in such a cell essentially because of sidewall generated shearing and inter-particle frictional effects. This was indirectly demonstrated by performing an experiment with particles contained in the toroidal space between two concentric cylinders (mimicking an infinite system in the horizontal direction given the absence of sidewalls perpendicular to the circumferential direction). No convection or surface instability was observed in this case. A boundary was then introduced into the middle of this annular container (thereby breaking is translational invariance in the azimuthal direction), which caused heap formation and the associated convection to occur (with the material returning to the previous state of surface stability and lack of mobility when the boundary was removed). In order to clarify the influential role played by the inter-particle friction, additional tests were conducted by altering the walls to generate maximal friction while using granular material that provided minimal inter particle friction. It was observed that in this test case no convective motion or heaping was generated thus highlighting the need for both wall and inter-particle friction.
In line with these observations (see, e.g., Medved et al. [32]), notably, alternative interpretations have been appearing in the literature where the fluidization of the material has been explained directly in terms of ‘net’ frictional forces acting on the system rather than in terms of relative compaction and expansion of the material. According to these ‘views’, the key ingredient needed to justify such dynamics should rather be sought in the ability of gravity to break the symmetry of the excitation, i.e., in the realization that the frictional forces that the sidewalls exert on the particles during the up- and down-stroke portions of a vibration cycle are not equivalent. We have seen before that the compression stage in which all particles are compacted, is followed by a shear-induced dilation and fluidization process as the layer detaches from the bottom wall (see again Fig. 5). One may therefore argue that the frictional drag acting on the particles near the wall when they rise is larger than that effective in the fall stage and that, accordingly, a net downward frictional force per cycle is produced (by which the particles located in proximity to the sidewalls are forced to sink).
Other authors have shed additional light on the distribution of velocities that are established in the material as a result of such mechanisms. As an example, using a cylindrical container, Knight et al. [33] could show that the upward grain velocity along the cylinder axis decays exponentially from the top free surface into the bulk of the material. Then, this flow changes direction in proximity to the inner container walls, displaying a radial dependence resembling that of either a hyperbolic cosine or a modified Bessel function of order zero.
Other interesting contributions for two-dimensional and cylindrical containers are due to Hsiau et al. [34] and Aoki et al. [35], respectively. In particular, the latter authors reported on a novel convective state, termed as "upward" mode convection, characterized by the existence of multi-pairs of convection rolls and the formation of a valley and arching structures in the centre of the container. For values of Γ < 4 the previously described “downward” mode of convection (shown in Fig. 5) was obtained with the formation of a heap, while the mechanism by which the upward mode of convection is generated was observed for Γ ≅ 6. This was ascribed to a period-doubling bifurcation, which causes the areas of the granular bed closest to the sidewalls to impact the container walls at an earlier phase and with greater intensity than the middle of the bed with the container floor. This can result in the formation of a valley structure with height highest at the walls and lowest in the container centre.
It has also been shown that at higher values of vibrational acceleration (Γ ≅ 8 or 9) a further transition to a state with multiple pairs of convection rolls can occur, provided the container horizontal dimension is sufficiently high.
As a final example of this specific series of studies, here, we consider the experiments in a rectangular container that Evesque and Rajchenbach [36] conducted using a parallelepipedic container (100 mm × 55 mm × 20 mm) partially filled up with monodisperse glass spheres, the diameter of which varied from 0.2 to 2 mm, vertically shaken, in the range of frequencies 10–1000 Hz. As a distinguishing mark with respect to other results in the literature, these experiments have shown that in place of a heap or a valley located in the center of the container, the entire free surface of the grains can become inclined at an angle θ to the horizontal; simultaneously, there is a continuous surface flow, rolling down the free surface and a convective transport of matter from the bottom to the top along one of the sidewalls, which continuously refills the top of the heap with new particles. These authors ascribed the choice of the direction of the slope to a spontaneous breaking of symmetry in the convective system (although this specific asymmetry might also be explained according to the presence of spurious vibrations in the horizontal direction, the interested reader being referred to Section 3.4 for additional information in this regard).
Notably, Evesque et al. [36] observed no difference for the value of the instability threshold when repeating the experiments in vacuum. Also, no modification of the dynamics was reported when changing the size of particles for a fixed amplitude of the vibrations, i.e., on changing ζ for a fixed b. Interestingly, for much larger amplitude of vibrations, they reported on another permanent state, characterized by the temporal and spatial intermittencies of jets of particles at the free surface.
As a concluding remark for this section, we wish to highlight that another fascinating phenomenon that vertically vibrated thick layers of granular materials can exhibit is a form of surface wave motion that causes the movement of particle upwards against gravity along the free surface of a heap. This is only observed for granular materials that can sustain a high angle of repose and is typical of non-spherical particles. These surface waves are different from those described on Section 3.1 as they only show up in thick layers, display an essentially ‘traveling’ nature and move upward against gravity beneath the free surface of the heap; moreover, the critical value of Γ at which they occur is dependent on the non-dimensional kinetic energy of the system and, most importantly (their hallmark with respect to the dynamics described in Section 3.1), the related Γcr also scales with the aspect ratio of the cell.
Pak et al. [37] (who considered particles with diameter in the range 0.2 ≤ d ≤ 2 mm, 0 ≤ f ≤ 30 Hz, amplitude 0.3 ≤ b ≤ 6 mm and depths 30 ≤ h ≤ 50 mm) reported these novel surface waves most prominently in annular concentric cylindrical containers, but they can also occur in rectangular enclosures. These surface waves begin at the point where the avalanching free surfaces of multiple heaps meet causing a small heap to form at the slope base. This smaller heap breaks into two parts (Fig. 6a) and travels up the larger heap under the free surface at a greater velocity than the avalanching material flowing down the free surface above. As it travels upward, the wave extends and decreases in size until it dissipates (Figs. 6b–6d).

Figure 6: Sketch showing a side view near the origin of the waves at the lowest point of the heap: (a) Pulse formation and split, (b) Pulse begins to move up the slope, (c) Pulse continues to move up the slope, (d) Pulse dissipates into the slope
Pak et al. [37] argued that an explanation for the appearance of such waves should be sought in the existence of “shear bands” within the vibrated medium. These shear bands were defined as regions within the granular material of higher shearing relative to the rest of the medium. According to their interpretation, these bands dilate during the upward part of the vibration cycle, which allows free particles to join the band. When the surface waves are generated at the bottom of the avalanching heap an accompanying shear band is produced also, which travels upward with the wave, becoming disjointed from it as it rises and eventually moving towards the inside of the heap and finally dissipating.
Interestingly, these authors could show that if the height of the layer is gradually reduced, the traveling waves are suppressed, and the standing waves due to a period-doubling bifurcation, originally described by Douady et al. [20], are recovered (see Section 3.1).
As already discussed to a certain extent in Section 2, the response of granular materials to shaking can depend sensitively on the angle φ between the direction of gravity and vibrations. Indeed, studies in the past three decades have conclusively established that a variation of this angle from φ = 0 (parallel case treated in Sections 3.1 and 3.2) to φ = 90° (subject treated in this section) can induce remarkable changes in the emerging dynamics and the underlying mechanisms.
Some of these modifications might be anticipated on the basis of logical arguments stemming from proper consideration of the phenomena described in Section 3.2 and related interpretations.
We have illustrated there that, because of fluidization induced by vertical vibrations in relatively thick (deep) layers, convective states emerge where the material is recirculated from the top surface to the bottom of the container and then back again to the top (and, unless a symmetry breaking phenomenon is enabled, grains move upwards in the center of the container and downwards along its sidewalls). Moreover, if the walls are sufficiently smooth, the strength of such a convective flow can be significantly mitigated or even be completely suppressed (and this is due to the significant role played in such processes by the friction between the grains and the (vertical) sidewalls).
As elucidated in the earlier section, a possible key to understanding these behaviors lies in considering that in the φ = 0° case, gravity breaks the symmetry of the excitation. In other words, it causes a difference in the magnitude of the frictional forces that the sidewalls exert on the particles during the up- and down-stroke portions of a vibration cycle, and, accordingly, a net frictional force per cycle directed downward.
If the direction of vibrations is rotated by 90°, obviously, gravity can no longer break the symmetry as it does in the vertical case and, therefore, such a net force per cycle cannot be produced; rather, the motion eventually induced in the bulk of the granular material is perpendicular to the direction of gravity, i.e., it is parallel to the top free surface of the material, which can be therefore perturbed, respond and expand with mechanisms that are fundamentally different from those responsible for the convective behavior in vertically vibrated systems [32].
A first milestone work, on which several other investigators would successively rely, was the experimental study by Evesque [38] where the ability of horizontal vibrations to cause fluidization and ensuing convective states was verified for both cylindrical and rectangular containers (using Fontainebleau sand and horizontal vibration in the range 80–170 Hz).
Subsequent efforts have clarified that, unlike vertical vibrations, horizontal shaking generally causes a decoupling of the granular material into two horizontal layers, which display distinct behaviors, namely, an upper highly fluidized region and a lower region that essentially follows the motion of the container like a solid body would do (Fig. 7).
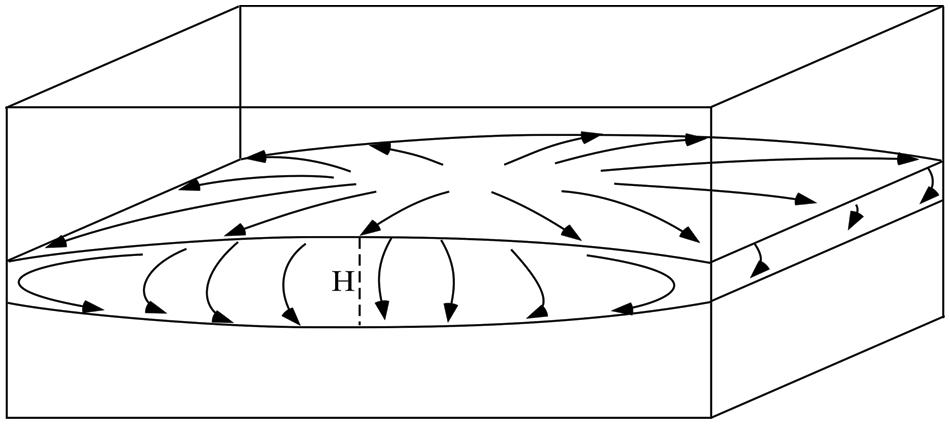
Figure 7: Sketch of time-averaged convection flow lines in the liquefied layer
A quantitative analysis of this effect can be found in the work by Tennakoon et al. [39]. Using a 121 mm × 19.3 mm rectangular section cell horizontally vibrated at frequencies 3 ≤ f ≤ 15 Hz and at amplitudes 0 ≤ b ≤ 15 mm, with spherical glass beads, smooth Ottawa sand, and sieved rough sand having diameters of 0.2 ≤ d ≤ 1 mm and N ≅ 40, these authors studied the dependence of the liquefied layer thickness on the other system parameters. It was clarified that the dominant flow is in the direction of shaking with grains rising up in the center of the cell and flowing transversely along the surface towards the side walls and finally sinking at the wall boundaries. As sketched in Fig. 7, typically, the top surface of the liquefied layer displays a dome shape that is concave down, while the bottom surface of this layer is concave upwards near the side walls, thereby giving rise to a fluidized layer with a non-constant thickness, which attains its maximum value H in the center of the container.
Tennakoon et al. [39] could clearly show that, as Γ grows, a well-defined transition occurs to a convective state inside the mobilized layer with thickness Hcr at a specific value Γcr (solid line in Fig. 8). On increasing further, Γ, more of the layer becomes liquefied, i.e., H becomes larger. Moreover, this process is affected by hysteresis (see Fig. 8 for a qualitative representation of this behavior), i.e., if Γ is decreased below Γcr once flow has begun, H decreases accordingly, but it does not vanish until Γ reaches a
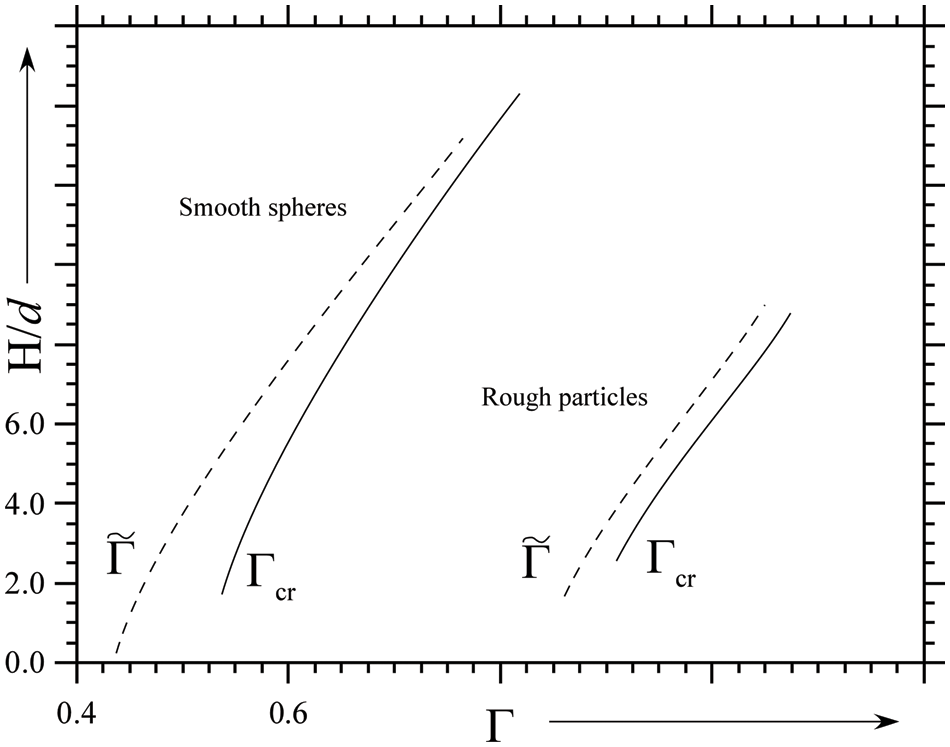
Figure 8: Qualitative sketch showing the dependence of the mobilized layer thickness on the acceleration for the horizontal vibrations case; Γcr and
Yet following Tennakoon et al. [39], an explanation/justification for this trend can be elaborated in its simplest form on the basis of the argument that, as also illustrated in Section 1, the material starts to flow due to the breaking of static friction, whereas once flow has begun, the less demanding (in terms of forces required to maintain it) dynamical friction becomes the governing physical mechanism. In addition, the grains must dilate in order to flow, but once dilated, the flow is more easily sustained [39]. Notably, these authors found both
Other works appearing in the literature have essentially focused on the patterning behavior associated to the convective state established in the material once it enters the fluidized state.
In this regard, it is worth citing Medved et al. [32], who, using poppy seeds (average size ≅ 0.8 mm) in a container with extension along the direction of vibrations 200 mm, width ranging between 11 and 25 mm and a filling height of 62 mm, vibrated at 33 Hz, clarified that the roughness of the boundaries and the container dimensions do exert an influence on the shape and number of emerging convective rolls. More precisely, the typical outcome is given by four counter-rotating rolls arranged in two pairs on top of each other when the container bottom and lateral walls are relatively rough (Fig. 9), whereas, in agreement with the earlier findings of Evesque [38] and Tennakoon et al. [39] (see also Hsiau et al. [40]), only a single pair of counter-rotating convection rolls is obtained for smooth walls if the filling height is relatively small (the situation with four rolls being recovered when the filling height is increased to a level that depends on the container width).
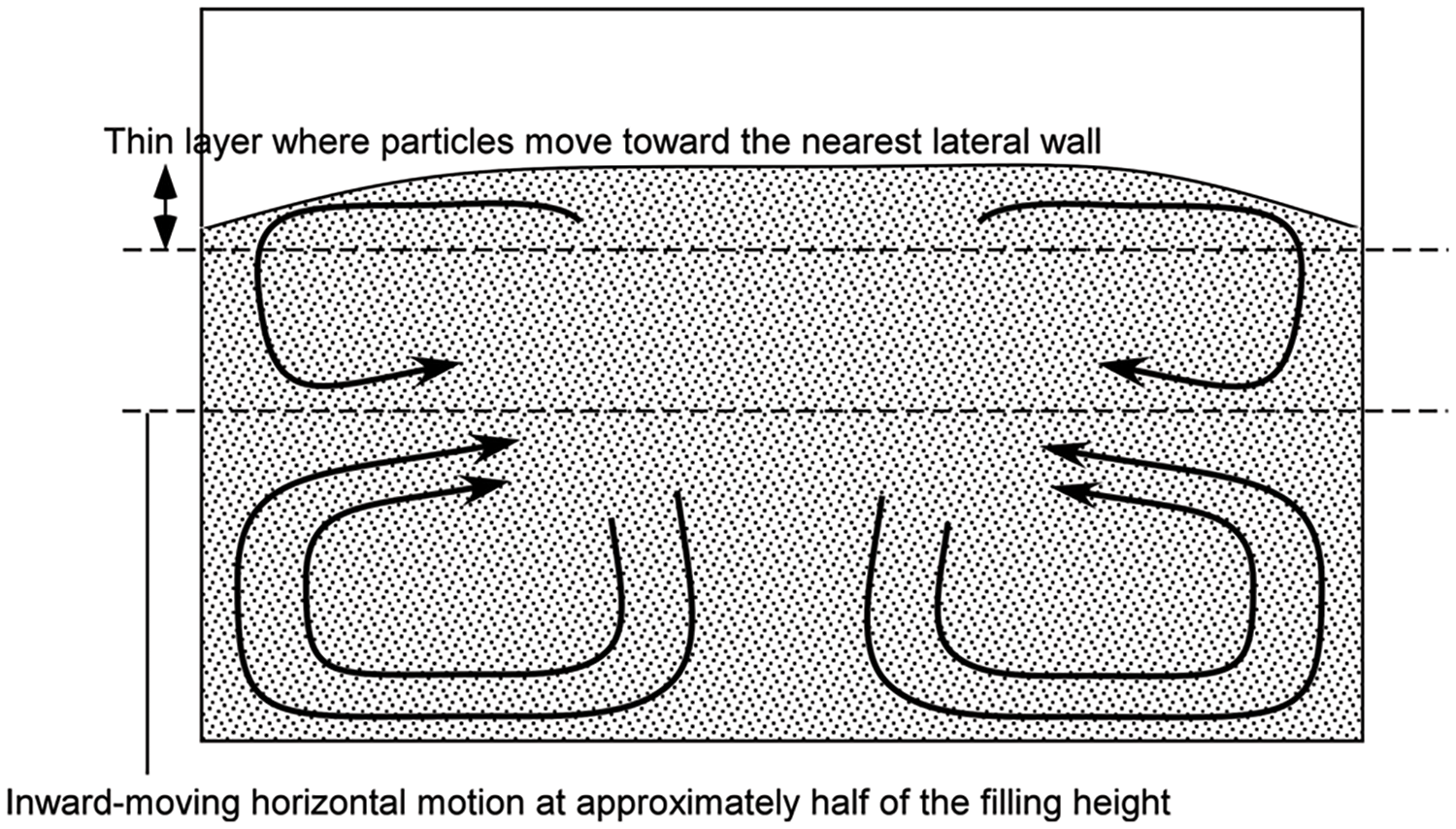
Figure 9: Sketch of the four-roll state. Along the free surface, particles move in a thin layer toward the nearest lateral wall; then they sink along the wall until are captured by in an inward-moving horizontal motion at approximately half of the filling height; in the lower portion of the container, the second pair of rolls rotates in the opposite direction, i.e., particles move downward near the center of the container and up in proximity to the lateral walls
In another study, Medved et al. [41] further explored the dynamics of this system for increasing values of Γ revealing the existence of novel behaviors not observed in the case of vertical vibrations, namely a harmonic response in the bulk with a depth-dependent phase lag and amplitude (such that regions of the granular material can actually move in opposite directions at any instant) and a subharmonic mechanism affecting an inclined portion of the shear zone.
The sequence was found to be the following: Γ = 0.5, fluidization occurs; then H grows linearly from zero below Γ = 0.5 (fluidization onset) to a maximum value corresponding to N = 16 at Γ = 3, after which point it levels off and becomes independent of Γ.
In this range, owing to the horizontal shaking, the sidewalls periodically push the granular material towards the center of the container, which then is allowed to re-expand. During the re-expansion, however, it lags behind the walls owing to its inertia and other dissipative effects. This results in the emergence of a gap between the granular material and the sidewall itself into which particles can avalanche. The depth, δg, of this gap is a function of Γ roughly following the same evolution law of H for 0.5 ≤ Γ ≤ 2.5. At a certain acceleration value, however, Γg, the gap abruptly extends to the bottom of the cell. After this event, the system undergoes a period-doubling bifurcation at Γ = 3.7 and a second, period-quadrupling bifurcation at Γ = 5.9 (these being largely frequency-independent over the range 18 < f < 50 Hz).
3.4 Cases with Inclined Vibrations
This section is devoted to a discussion of the more general case in which vibrations form an arbitrary angle with the direction of gravity or with the considered layer of granular material itself. As developed in the following, in particular, an interesting line of research exists where it has been demonstrated that inclined vibrations can be used to induce a net transport of grains or particles in a certain direction even if gravity would tend to displace them in the opposite direction.
Before starting to deal with this specific aspect, however, it is worth recalling the extension by Shi et al. [42] to the findings yielded by Clément et al. [27] and Clément et al. [28] for the case of a 2D thin layer vibrated vertically (discussed in Section 3.1).
Yet considering a 2D layer (for which the width is limited in comparison to the other horizontal extension), Shi et al. [42] found that when it is inclined with respect to the horizontal direction (i.e., it is not exactly perpendicular to gravity), the amplitudes of the peaks emerging as a result of the shaking process are non-uniform along the layer. Moreover, for different inclinations, the maximum amplitudes and the number of the peaks change. More precisely, the maximum amplitude grows while the average wavelength varies non-monotonically.
These authors considered particles with an average size d = 1 mm, Γ = 3.6, 8 ≤ f ≤ 12 Hz. It was shown that the average wavelength also depends on the frequency (the larger the frequency, the smaller the wavelength).
Along these lines, additional interesting information can be found in the study by Tennakoon and Behringer [43], where inclined shaking resulting from the combination of vertical and horizontal vibrations was applied to a granular material in a non-inclined rectangular container (with size 120 mm along the horizontal shaking direction, width ranging from 5 to 20 mm in a direction perpendicular to shaking, filled with glass spheres having diameter 0.2 ≤ d ≤ 1 mm, layer depth 60 mm, subjected to vibrations with frequency 3 ≤ f ≤ 15 Hz and amplitude 0 < b ≤ 20 mm).
Different acceleration amplitudes and angular frequencies (Γ, ω) were considered for the horizontal and vertical vibrations, respectively (hereafter simply referred to as Γv, ωv and Γh, ωh for φ = 0 and 90°, respectively).
In line with the phenomenology already described in Sections 3.2 and 3.3, respectively, these authors found that when only vertical or horizontal vibrations are applied, the response of the system is markedly different. For purely vertical shaking, when Γv < Γvcr ≅ 1, the steady state is a flat layer. When Γv > Γvcr, convection is enabled and this typically results in a single heap. By contrast, for purely horizontal shaking, when Γh > Γ hcr, grains near the top surface of a flat layer dilate and begin to flow, while the rest of the layer follows the solid body motion of the shaker; moreover, this initial transition is essentially hysteretic.
These authors reported several novel flow dynamics for the case in which both Γv and Γh are ≠ 0 as a function of their ratio, the related angular frequency ratio ωv/ωh and the phase shift Φ. In the following, for the sake of brevity, we limit ourselves to discussing the case with ωv/ωh = 1 and Φ = 0.
For this specific condition, Tennakoon et al. [43] described the following dynamics:
If Γv < Γvcr, on increasing Γh while keeping fixed Γv, starting from the situation with a flat free surface of the material, as soon as Γh exceeds a given value Γhs that depends on Γv (Γhs ≅ 0.39 for Γv = 0.68) a new state emerges, where a static heap is formed in proximity to the right wall of the container. This heap is the result of convective motion. Such a motion however stops when the increased slope attains a certain value. Only if Γh is increased beyond Γhcr (≅0.6), the top layer along the slope liquefies and starts to oscillate in a permanent way under the effect of the imposed shaking. On increasing further Γh, the thickness of the liquefied layer grows, while its average slope becomes smaller.
Having completed a description of the emerging patterns in “closed systems” (containers and enclosures), we turn now to considering the case of “open system”. As already outlined at the beginning of this section, this may be regarded as a case of “special interest”, given the ability of inclined vibrations to induce peculiar convective states in very thin layers by which particles are continuously transported along a given direction.
The principles associated to this transport process are synthetically illustrated in the following. They essentially rely on the interplay among the different forces acting on particles, namely, gravity (that tends to keep particles in contact with the bottom of the considered container or plate), the vertical component of vibrations (by which particles experience a time-varying force in the vertical direction), the horizontal component of vibrations (by which particles are displaced horizontally), friction forces (if particles are in contact with the bottom wall) and inertia. In practice, different conditions are possible depending on the relative importance of these effects.
For simplicity, first we consider the case of a perfectly horizontal plate subjected to horizontal vibrations (Fig. 10).
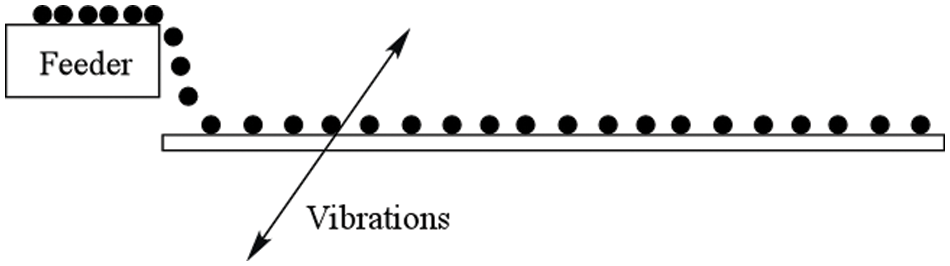
Figure 10: Horizontal plate with particles subjected to inclined vibrations
A trivial state in this case is obviously represented by the situation in which particles experience no net motion in the horizontal direction (Fig. 11a). This happens when the particle remains in contact with the plate (the vertical acceleration induced by vibrations not being sufficient to lift the particle) and due to the friction and other adhesion effects it moves back and forth in the horizontal direction in a perfectly synchronous way with the plate itself (in other words, the inertial and frictional forces acting on the particle balance exactly the motion of the vibrating plate in the horizontal direction, i.e., the time-averaged displacement of the particle in the horizontal direction is exactly zero).
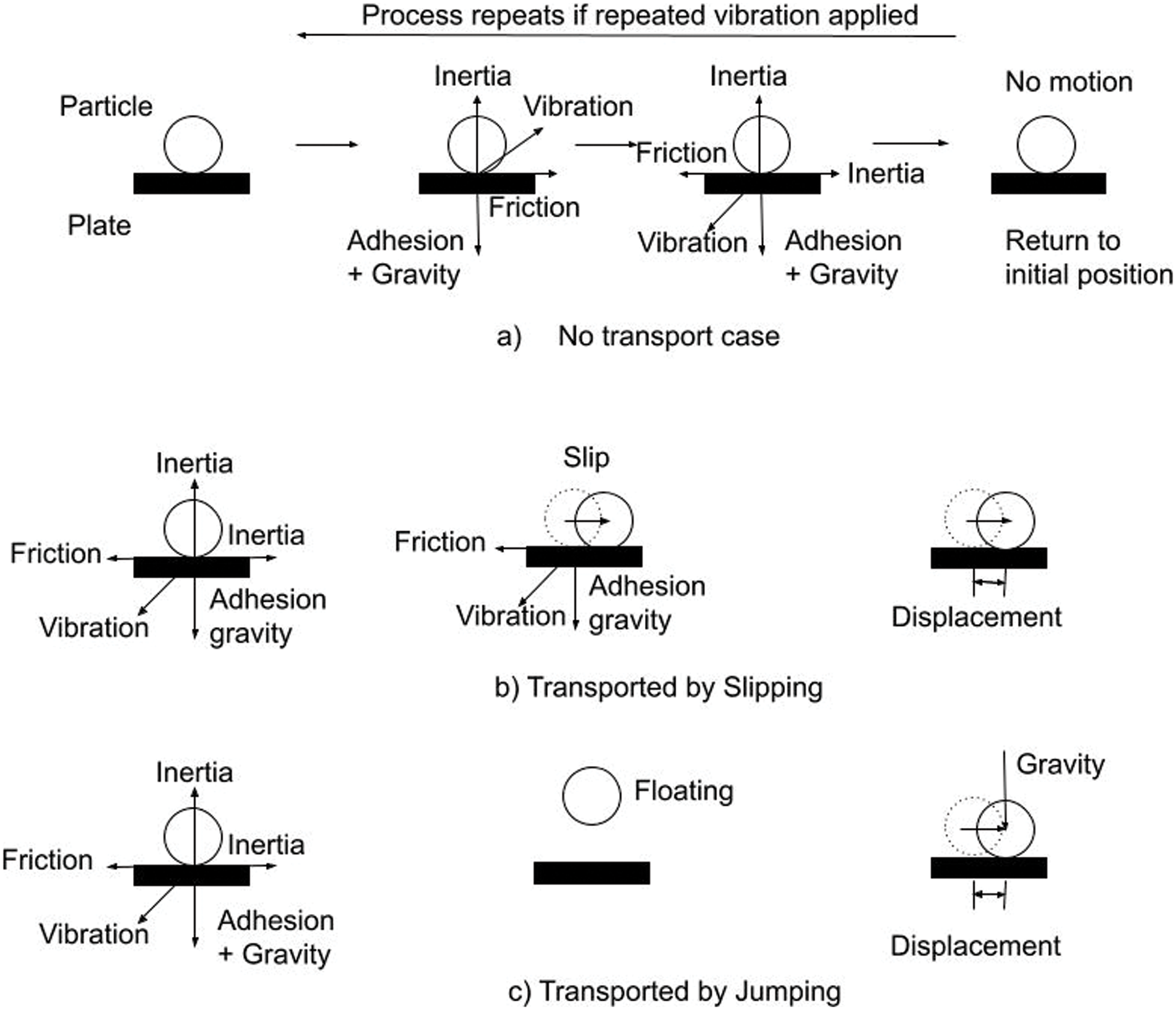
Figure 11: Sketch of the possible regimes of particle transport on horizontal plate subjected to inclined vibrations: (a) particle is not transported, (b) particle is transported by slipping on the plate, (c) particle is transported by jumping on the plate
Another possible condition is represented by the so-called “slipping regime” (Fig. 11b). In this case, although the acceleration induced by the vertical component of vibrations is still not enough to allow the particle to detach from the underlying plate, the particles inertia can overcome friction, causing the particle to “slip” along the plate in the horizontal direction (resulting in it being transported a small distance along the plate). In this case, the frictional force acting on the particle is affected by the position of the plate in the vibration cycle, specifically when the plate is at the highest vertical point in one oscillation the friction is minimal, whereas when the plate is at the lowest vertical point in the oscillation the friction is maximized which results in the particle tending to be transported in one direction. Transport of the particle for greater distances can be caused by the repetition of the process described above (i.e., particle displacement is merely due to the accumulation of small slipping motions).
The third possible condition, i.e., the “jumping regime” is fundamentally similar to the “slipping” state with the added condition that the particle now detaches from the plate as the vibration is enough to cause the particles inertia to overcome both the adhesion force between the particle and the plate and the force of gravity (Fig. 11c). This detachment from the plate results in the particle to falling back towards the plate caused by the effects of gravity, however, landing at a different point in the plates vibration cycle with respect to that which it initially detached; this effect, coupled with the horizontal motion seen in the slipping case, causes the particle to be repeatedly transported a small distance along the plate.
Relevant experiments along these lines can be found in the study by Adachi et al. [44], who investigated the effective realization of the three above-mentioned regimes of particle motion using a mixture of non-spherical particles (which therefore cannot rotate along the plate) with different sizes (lunar and Martian regolith simulants, FJS-1 and JSC Mars-1, respectively). Allowing the parameter Γ to vary in the range 1 ≤ Γ ≤ 2.7 with the vibrations angle spanning the interval 45 ≤ φ ≤ 75°, these authors measured the net transport velocity of the particles in the different conditions. Most interestingly, it was found that such a velocity is affected not only by Γ and the inclination angle, but it also depends on the average size of the particles. In particular, while the velocity grows with Γ, it has a non-monotonic dependence on φ, with the best performances being achieved for φ = 60°. It was also observed that large particles can be transported more easily than small particles, which Adachi et al. [44] ascribed to the higher inertia of particles with a larger diameter.
These authors also evaluated the transport performances in terms of the amount of particles being displaced in time with respect to the mass “supply rate”. Similarly to the velocity performance, the mass transport rate was also higher at φ = 60°. In all cases, however, it was observed to first increase with the mass supply rate and then decrease (Fig. 12). In order to justify this trend, Adachi et al. [44] argued that at a certain stage, the mass transport rate is detrimentally affected by the too large number of particles being present in the system at the same time, which disturb each other and cause disruption and other blockage effects.

Figure 12: Qualitative representation of the vibrationally-induced mass transport rate as a function of the mass supply rate for a horizontal plate obliquely vibrated
In subsequent works, still using the same granular materials, Kawamoto [45] and Kawamoto et al. [46] have verified the ability of these physical mechanisms to cause a continuous displacement of particles even in the condition for which particles acquire potential energy, i.e., the move upwards along an inclined path (inclined with respect to the horizontal direction by an angle θ > 0, see Fig. 13).
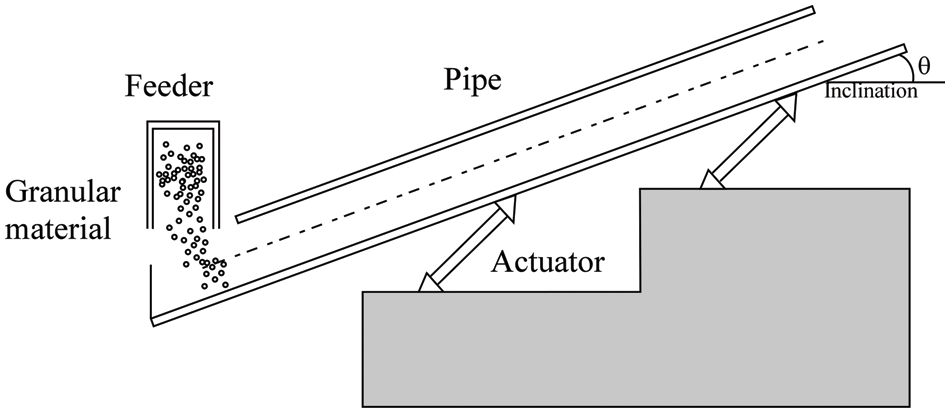
Figure 13: Sketch of the inclined pipe
It was shown that particles can be transported against gravity essentially by means of the jumping effect described before, which is enabled when the acceleration induced by vibrations exceeds gravity. In particular, the mass transport rate attains a maximum when θ=0 and then it decreases until a given threshold (limiting) angle is exceeded (θ ≅ 24° according to Kawamoto [45]).
Another interesting observation reported by this author concerns the ability of this system to cause a separation of particles with larger size from those with smaller size due to a unique process in which while some of them move upwards, others are transported downwards. Observed was the tendency of large particles to rise to the top of the vibrated granular material due to the so-called Brazil nut effect [47]. Originally identified in 1976, this process refers to the ability of the larger balls contained in a can (which also includes smaller balls), to rise to the top when the can is shaken (even though the larger balls are more dense than the others, see Rosato et al. [48], and references therein). Its name derives from the example of a typical container of mixed nuts, in which the largest are just the Brazil nuts. In a similar vein, Kawamoto [45] observed larger particles to rise and then to roll and slip down the surface of the vibrated layer, thereby being accumulated at the bottom of the tube. This tendency was reported for particles larger than 100 µm in the θ ≅ 15° case. Kawamoto [45] also investigated these fascinating dynamics in a more extreme case where particles substantially larger than the average grain size were introduced into the bulk material and submitted to the vibrational transport process. This resulted in the clear segregation of all these large particles to the bottom of the tube with only relatively small particles being transported upwards (see Fig. 14).
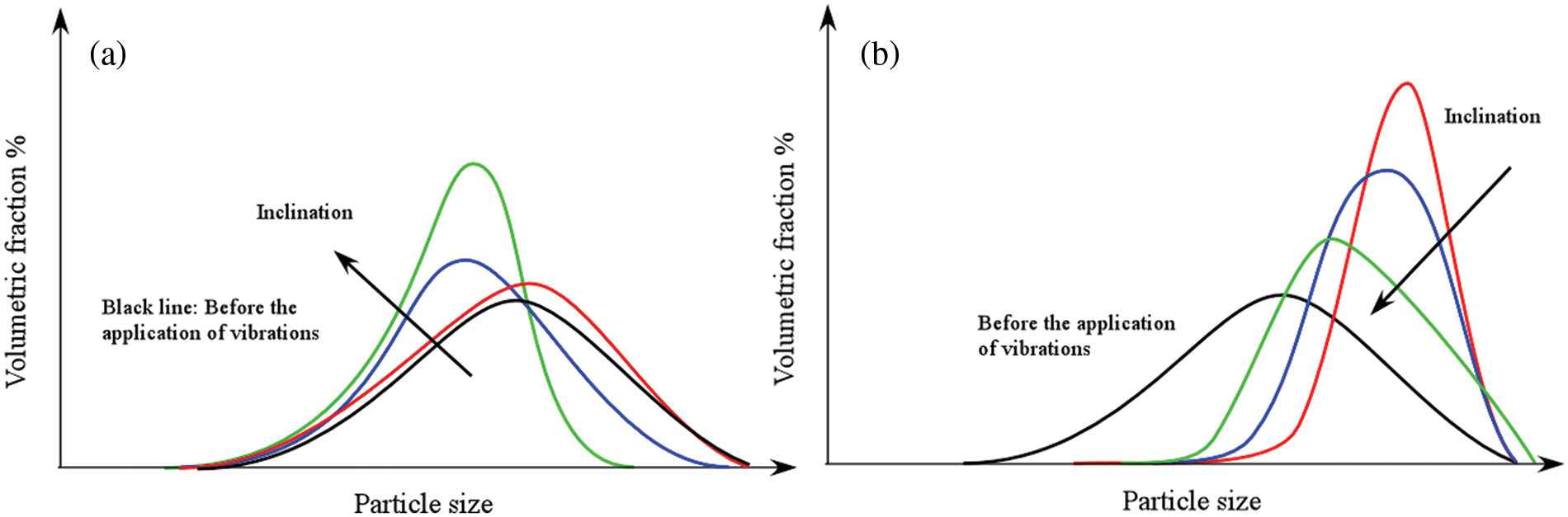
Figure 14: Qualitative sketch of the particle size distribution for upward transported (a) and downward transported (b) particles after vibration transport in an inclined tube for different inclinations θ
Kawamoto et al. [46] further explored how the inclination of the system can alter the effectiveness of such a size-segregation effect in terms of the involved particle sizes. Their interesting results can be summarized as follows. For the case of small inclinations such as θ ≅ 10° the segregation of particles larger than 100 µm occurs, which indicates that low inclinations are effective in removing large particles from a bulk of granular material. When the inclination of the system is around 20° the size segregation effectiveness is more moderate in the sense that particles slightly smaller than the average particle size are predominantly transported to the top of the tube whereas particles slightly larger than the average particle size are predominantly moved towards the bottom of the system.
For an inclination of 30° particles smaller than 100 µm were observed to be transported to the top of the system. When it exceeded 30°, almost no particles were collected at the upper outlet, and almost all particles fell downward. These results highlight that the size segregation properties can be altered by changing the inclination of the system, for example, low inclinations can be used to remove large particles from a bulk whereas high inclinations can be used to collect small particles from the bulk (Fig. 14).
3.5 Cases with Vibrations in a Low Gravity Environment
For the sake of completeness, a final case is treated in the present section, namely, that of particles in microgravity, a condition in which the parameter Γ defined through Eq. (6) ideally tends to infinite. Indeed, a few experiments have been conducted in this unique environment to overcome some of the typical effects induced by gravity. As extensively illustrated in the preceding sections, gravity should be regarded as a significant source of anisotropy (always pulling particles towards the bottom of the considered container) and the main reason forcing them to experience friction (as a result of the gravity-induced material compaction or of the interaction with the container bottom and/or sidewalls). Dedicated experiments in a low-gravity environment have therefore been conducted to filter out such effects and explore the sensitivity of these systems to conditions where inelastic collisions are the only interaction mechanism. Most interestingly, it has been found that in such unique conditions, particles can give rise to additional fascinating phenomena, which are not possible in normal gravity conditions.
A landmark study in this regard is that by Falcon et al. [49], where microgravity conditions were obtained through a Mini-Texus 5 space probe launched from Esrange (Northern Sweden) on a Nike-Improved Orion rocket. Three cubic containers were used for the experiments (1 cm3 in inner volume). These cells were filled with 0.281, 0.562, and 0.8915 g of 0.3–0.4 mm in diameter bronze spheres, respectively (solid fractions: 3.2%, 6.4%, and 10.1%), with the total number of particles in each cell being therefore ≅ 1420, 2840, and 4510, respectively (corresponding to roughly 1, 2, and 3 particle layers at rest). A shaking frequency f and maximal displacement amplitude b in the ranges 1 to 60 Hz and 0.1 to 2.5 mm, respectively, were considered.
Interestingly, these authors reported that when dilute conditions are established, particles essentially behave as the molecules of a gas, i.e., they undergo erratic motions in space. Unlike molecular gases, however, (as expected) these media are characterized by inelastic collisions, which result in a continuous loss of kinetic energy over time (from which the denomination of “granular gas” to distinguish them from the classical “molecular gases”). Moreover, most importantly, if the initial density of the medium is increased, for a fixed frequency and amplitude of vibrations, particle clusters start to show up at a certain stage (this happens when the initial density of the granular gas exceeds a given value, known as the gas-liquid transition threshold). The emerging clusters are generally referred to as “granular liquid droplets”, and coexist with the granular gas (see Fig. 15).

Figure 15: Qualitative sketch of particle clusters formed in air in microgravity conditions under the effect of vibrations
Falcon et al. [49] found the gas-liquid transition to depend on the collision rate in the system. Noirhomme et al. [50,51] conducted additional experiments in the framework of the 66th and 69th ESA parabolic flight campaigns. These have revealed that, by forcing the system with vibrations along a given direction, the onset of the gas-liquid granular transition (for which local clusters show up) essentially corresponds to a condition where the translational energy provided to the system through unidirectional vibrations is finally converted into kinetic energy of the particles and equally divided among their (3) translational degrees of freedom (which corresponds to how classical monoatomic molecular gases behave when they are in equilibrium conditions).
This important realization has led to introduce another interesting analogy between these vibrated systems and “fluids” undergoing thermal convection. It is well known that the patterning behavior associated to thermal convection in fluids subjected to a unidirectional temperature gradient (heated from below and cooled from above) in normal gravity conditions should be regarded as the natural outcome of the equilibrium established between the energy that is injected into the fluid at a relatively large scale and the dissipation that takes place on smaller scales due to viscous effects (see, e.g., Lappa [18]). Similarly, the patterns displayed by dense granular gases should be seen as the natural effect or consequence of the equilibrium attained between the energy continuously injected into the system (by means of unidirectional vibrations) and the dissipation produced on small scales because of the aforementioned inelastic collisions (occurring among the particles along the 3 dimensions of the physical space).
Yet for the sake of completeness and as a very concluding remark for this review, we wish to highlight that particle clustering in microgravity can also be induced by another effect, that is, the interplay of particle “inertia” and convective thermovibrational effects when the particles are immersed in a viscous liquid that is subjected to a temperature gradient and vibrations at the same time (this theme is no longer discussed here as it is beyond the scope of the present survey, the interested reader will find additional details in the works by Lappa [52–56], Lappa et al. [57], Crewdson et al. [58,59].
Conditions exist for which vibrated granular materials can exhibit fascinating (in some cases exotic or counter-intuitive) phenomena. These depend on a variety of factors, which include, but are not limited to, the relative importance of gravity with respect to the amplitude of the acceleration induced by vibrations (the case in which their ratio is zero representing a limiting condition known as “microgravity”), the direction of vibrations, their frequency and the geometrical (in terms of particle shape and size) and physical (elastic and frictional) properties of the considered granular materials. The relative direction of gravity and vibrations can break the symmetry of the excitation, thereby leading to different categories of mechanisms. In practical applications or experiments, on changing the frequency and amplitude of vibrations, the emerging behaviors typically consist of ‘phase’ transitions (from an apparent solid to a fluid-like state or vice versa) and ‘textural’ transformations when the material is in a state for which the spontaneous formation of “patterns” is allowed. Although the presence of an interstitial gas may somehow play a more or less negligible role in such dynamics, “universality classes” can be identified, that is, the emerging trends or mechanisms always reflect the balance that is established on certain scales between the (vibrational) energy injected into these system at a large scale and the dissipation occurring as a result of particle-to-particle, or particle-to-container frictional or inelastic collisional effects. This equilibrium often evolves through a series or a “hierarchy” of bifurcations by which these systems find new ways to redistribute and dissipate the available energy on small scales.
As most of the existing experimental results relate to cases where particles are spherical, have a uniform diameter distribution, and the same density, an exciting prospect for the future is the extension of these fascinating lines of inquiry to more realistic cases where grains have an arbitrary shape, are present with a variety of possible sizes and/or are made of different substances.
Acknowledgement: None.
Funding Statement: This work has been supported by the European Space Agency (ESA Contract 4000138607/22/NL/GLC/my, grant recipient: M.L., https://www.esa.int/Enabling_Support/Preparing_for_the_Future/Discovery_and_Preparation/Implemented_OSIP_ideas_June_2022).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: M.L and P.W; data collection: P.W, M.L and S.V.B; analysis and interpretation of results: P.W and M.L; draft manuscript preparation: P.W and M.L. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All the data used in the study are included in the manuscript.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. UNEP (2019). Sand and sustainability: Finding new solutions for environmental governance of global sand resources. GRID-Geneva, United Nations Environment Programme, Geneva, Switzerland. http://www.unepgrid.ch/ [Google Scholar]
2. Grieves, C. G., Crame, L. W., Venardos, D. G., Ying, W. C. (1980). Powdered versus granular carbon for oil refinery wastewater treatment. Journal (Water Pollution Control Federation), 52(3), 483–497. [Google Scholar]
3. Sonnergaard, J. M. (2006). Quantification of the compactibility of pharmaceutical powders. European Journal of Pharmaceutics and Biopharmaceutics, 63(3), 270–277. [Google Scholar] [PubMed]
4. Santoni, R. L., Tingle, J. S., Webster, S. L. (2001). Engineering properties of sand-fiber mixtures for road construction. Journal of Geotechnical and Geoenvironmental Engineering, 127(3), 203–295. [Google Scholar]
5. Horabik, J., Molenda, M. (2016). Parameters and contact models for DEM simulations of agricultural granular materials: A review. Biosystems Engineering, 147(2), 206–225. [Google Scholar]
6. Hogan, S. A., O’Loughlin, I. B., Kelly, P. M. (2016). Soft matter characterisation of whey protein powder systems. International Dairy Journal, 52, 1–9. [Google Scholar]
7. El-Eskandarany, M. S. (2015). Mechanical alloying: Nanotechnology, materials science and powder metallurgy, 2nd edition Oxford, UK: Elsevier. [Google Scholar]
8. Jefferies, M., Been, K. (2016). Soil liquefaction: A critical state approach, 2nd edition New York, USA: CRC Press. [Google Scholar]
9. Walton, O. (2012). Challenges in transporting, handling and processing regolith in the lunar environment. In: Badescu, V. (Ed.Moon, prospective energy and material resources. New York: Springer. [Google Scholar]
10. Herrmann, H. J. (1995). Simulating granular media on the computer. In: Garrido, P. L., Marro, J. (Eds.Third granada lectures in computational physics. Lecture notes in physics, vol. 448. Berlin, Heidelberg: Springer. https://doi.org/10.1007/3-540-59178-8_28 [Google Scholar] [CrossRef]
11. Shäfer, J., Dippel, S., Wolf, D. E. (1996). Force schemes in simulations of granular materials. Journal de Physique I, 6(1), 5–20. [Google Scholar]
12. Hodgson D. J. M., Hermes M., Blanco E., Poon W. C. K. (2022). Granulation and suspension rheology: A unified treatment featured. Journal of Rheology, 66(5), 853–858. https://doi.org/10.1122/8.0000515 [Google Scholar] [CrossRef]
13. Nicot, F., Hadda, N., Guessasma, M., Fortin, J., Millet, O. (2013). On the definition of the stress tensor in granular media. International Journal of Solids and Structures, 50(14–15), 2508–2517. [Google Scholar]
14. Lappa, M. (2019). Chapter 1. On the nature of fluid-dynamics. In: Patrick, L. (Ed.Understanding the nature of science, pp. 1–64. Hauppauge: Nova Science Publishers Inc.https://novapublishers.com/shop/understanding-the-nature-of-science/ [Google Scholar]
15. Levy, A., Kalman, H. (2001). Handbook of conveying and handling of particulate solids, 1st edition Amsterdam, The Netherland: Elsevier Science. [Google Scholar]
16. Brown, R. L., Richards, J. C. (1966). Principles of powder mechanics. Oxford: Pergamon Press. [Google Scholar]
17. Radjai, F., Roux, S. (2002). Turbulent-like fluctuations in quasistatic flow of granular media. Physical review letters, 89(6), 064302. [Google Scholar] [PubMed]
18. Lappa, M. (2009). Thermal convection: Patterns, evolution and stability. Chichester, England: John Wiley & Sons. [Google Scholar]
19. Thomas B., Mason M. O., Liu Y. A., Squires A. M. (1989). Identifying states in shallow vibrated beds. Powder Technology, 57(4), 267–280. [Google Scholar]
20. Douady, S., Fauve, S., Laroche, C. (1989). Subharmonic instabilities and defects in a granular layer under vertical vibrations. Europhysics Letters, 8(7), 621–627. [Google Scholar]
21. Hsiau, S. S., Wu, M. H., Chen, C. H. (1998). Arching phenomena in a vibrated granular bed. Powder technology, 99(2), 185–193. [Google Scholar]
22. Melo, F., Umbanhowar, P., Swinney, H. L. (1994). Transition to parametric wave patterns in a vertically oscillated granular layer. Physical Review Letters, 72(1), 172–175. [Google Scholar] [PubMed]
23. Melo, F., Umbanhowar, P., Swinney, H. L. (1995). Hexagons, kinks, and disorder in oscillated granular layers. Physical Review Letters, 75(21), 3838–3841. [Google Scholar] [PubMed]
24. Umbanhowar, P. B., Melo, F., Swinney, H. L. (1996). Localised excitations in a vertically vibrated granular layer. Nature, 382(6594), 793–796. [Google Scholar]
25. Tsimring, L. S., Aranson, I. S. (1997). Localised and cellular patterns in a vibrated granular layer. Physical Review Letters, 79(2), 213–216. [Google Scholar]
26. Bizon, C., Shattuck, M. D., Swift, J. B., McCormick, W. D., Swineey, H. L. (1998). Pattern in 3D vertically oscillated granular layers: Simulation and experiment. Physical Review Letters, 80(1), 57–60. [Google Scholar]
27. Clément, E., Vanel, L., Rajchenbach, J., Duran, J. (1996). Pattern formation in a vibrated granular layer. Physical Review E, 53(3), 2972–2975. [Google Scholar]
28. Clément, E., Labous, L. (2000). Pattern formation in a vibrated granular layer: The pattern selection issue. Physical Review E, 62(6), 8314–8323. [Google Scholar]
29. Faraday, M. (1831). On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Philosophical Transactions of the Royal Society of London, 52, 299–339. [Google Scholar]
30. Laroche, C., Douady, S., Fauve, S. (1989). Convective flow of granular masses under vertical vibrations. Journal de Physique, 50(7), 699–706. [Google Scholar]
31. Clément, E., Duran, J., Rajchenbach, J. (1992). Experimental study of heaping in a two-dimensional “sandpile”. Physical Review Letters, 69(8), 1189–1192. [Google Scholar]
32. Medved, M., Dawson, D., Jaeger, H. M., Nagel, S. R. (1999). Convection in horizontally vibrated granular material. Chaos, 9(3), 691– 696. [Google Scholar] [PubMed]
33. Knight, J. B., Ehrichs, E. E., Kuperman, V. Y., Flint, J. K., Jaeger, H. M. et al. (1996). Experimental study of granular convection. Physical Review E, 54(5), 5726–5738. [Google Scholar]
34. Hsiau, S. S., Chen, C. H. (2000). Granular convection in a vertical shaker. Powder Technology, 111(3), 210–217. [Google Scholar]
35. Aoki, K. M., Akiyama, T., Yamamoto, K., Yoshikawa, T. (1997). Experimental study on the mechanism of convection modes in vibrated granular beds. Europhysics Letters, 40(2), 159–164. [Google Scholar]
36. Evesque, P., Rajchenbach, J. (1989). Instability in a sand heap. Physical Review Letters, 62(1), 44–46. [Google Scholar] [PubMed]
37. Pak, H., Behringer, R. (1993). Surface waves in vertically vibrated granular materials. Physical Review Letters, 71(12), 1832–1835. [Google Scholar] [PubMed]
38. Evesque, P. (1992). Shaking dry powders and grains. Contemporary Physics, 33(4), 245–261. [Google Scholar]
39. Tennakoon, S. G. K., Kondic, L., Behringer, R. P. (1999). Onset of flow in a horizontally vibrated granular bed: Convection by horizontal shearing. Europhysics Letters, 45(4), 470–475. https://doi.org/10.1209/epl/i1999-00190-3 [Google Scholar] [CrossRef]
40. Hsiau, S. S., Ou, M. Y., Tai, C. H. (2002). The flow behavior of granular material due to horizontal shaking. Advanced Powder Technology, 13(2), 167–180. [Google Scholar]
41. Medved, M., Dawson, D., Jaeger, H. M., Nagel, S. R. (2000). Modes of response in horizontally vibrated granular matter. Europhysics Letters, 52(1), 66–72. [Google Scholar]
42. Shi, X. D., Miao, G. Q. (2008). Pattern formation in a vibrated granular layer on an inclined base. Chinese Physics Letters, 25(5), 1727–1730. [Google Scholar]
43. Tennakoon, S. G. K., Behringer, R. P. (1997). Vertical and horizontal vibration of granular materials: Coulomb friction and a novel switching state. Physical Review Letters, 81(4), 794–797. [Google Scholar]
44. Adachi, M., Hamazawa, K., Mimuro, Y., Kawamoto, H. (2017). Vibration transport system for lunar and Martian regolith using dielectric elastomer actuator. Journal of Electrostatics, 89(1), 88–98. [Google Scholar]
45. Kawamoto, H. (2020). Vibration Transport of lunar regolith for in situ resource utilization using piezoelectric actuators with displacement-amplifying mechanism. Journal of Aerospace Engineering, 33(3), 04020014. [Google Scholar]
46. Kawamoto, H., Chin, K. (2021). Particle-size classification of lunar regolith through inclined vibrating tube. Journal of Aerospace Engineering, 34(3), 06021003. [Google Scholar]
47. Scröter, M., Ulich, S., Kreft, J., Swift, J. B., Swinney, H. L. (2006). Mechanisms in the size segregation of a binary granular mixture. Physical Review E, 74(1), 001307. [Google Scholar]
48. Rosato, A., Strandburg, K. J., Prinz, F., Swendsen, R. H. (1987). Why the brazil nuts are on top. Physical Review Letters, 58(10), 1038–1041. https://doi.org/10.1103/PhysRevLett.58.1038 [Google Scholar] [PubMed] [CrossRef]
49. Falcon, E., Wunenburger, R., Évesque, P., Fauve, S., Chabot, C. et al. (1999). Cluster formation in a granular medium fluidized by vibrations in low gravity. Physical Review Letters, 83(2), 440–443. https://doi.org/10.1103/PhysRevLett.83.440 [Google Scholar] [CrossRef]
50. Noirhomme, M., Cazaubiel, A., Darras, A., Falcon, E., Fischer, D. et al. (2018). Threshold of gas-like to clustering transition in driven granular media in low-gravity environment. Europhysics Letters, 123(1), 14003. [Google Scholar]
51. Noirhomme, M., Cazaubiel, A., Falcon, E., Fischer, D., Garrabos, Y. et al. (2021). Particle dynamics at the onset of the granular gas-liquid transition. Physical Review Letters, 126(12), 128002. [Google Scholar] [PubMed]
52. Lappa, M. (2014). The patterning behavior and accumulation of spherical particles in a vibrated non-isothermal liquid. Physics of Fluids, 26(9), 093301. https://doi.org/10.1063/1.4893078 [Google Scholar] [CrossRef]
53. Lappa, M. (2016a). Numerical study into the morphology and formation mechanisms of three-dimensional particle structures in vibrated cylindrical cavities with various heating conditions. Physical Review Fluids, 1(6), 064203. https://doi.org/10.1103/PhysRevFluids.1.064203 [Google Scholar] [CrossRef]
54. Lappa, M. (2016b). On the nature, formation and diversity of particulate coherent structures in microgravity conditions and their relevance to materials science and problems of astrophysical interest. Geophysical & Astrophysical Fluid Dynamics, 110(4), 348–386. https://doi.org/10.1080/03091929.2016.1194410 [Google Scholar] [CrossRef]
55. Lappa, M. (2017). On the multiplicity and symmetry of particle attractors in confined non-isothermal fluids subjected to inclined vibrations. International Journal of Multiphase Flow, 93(1), 71–83. https://doi.org/10.1016/j.ijmultiphaseflow.2017.03.015 [Google Scholar] [CrossRef]
56. Lappa, M. (2022). Characterization of two-way coupled thermovibrationally driven particle attractee. Physics of Fluids, 34(5), 053109. https://doi.org/10.1063/5.0091520 [Google Scholar] [CrossRef]
57. Lappa, M., Burel, T. (2020). Symmetry breaking phenomena in thermovibrationally driven particle accumulation structures. Physics of Fluids, 32(5), 053314. https://doi.org/10.1063/5.0007472 [Google Scholar] [CrossRef]
58. Crewdson, G., Lappa, M. (2022a). An investigation into the behavior of non-isodense particles in chaotic thermovibrational flow. Fluid Dynamics & Materials Processing, 18(3), 497–510. https://doi.org/10.32604/fdmp.2022.020248 [Google Scholar] [CrossRef]
59. Crewdson, G., Evans, M., Lappa, M. (2022b). Two-dimensional vibrationally-driven solid particle structures in non-uniformly heated fluid containers. Chaos, 32(10), 103119. https://doi.org/10.1063/5.0104680 [Google Scholar] [PubMed] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools