 Open Access
Open Access
ARTICLE
Prediction and Optimization of the Thermal Properties of TiO2/Water Nanofluids in the Framework of a Machine Learning Approach
1 Sate Key Laboratory of Complex Nonferrous Clean Utilization, Kunming University of Science and Technology, Kunming, 650093, China
2 Faculty of Metallurgical and Energy Engineering, Kunming University of Science and Technology, Kunming, 650093, China
3 Jiangxi Guoxing Intelligent Energy Co., Ganzhou, 330300, China
4 Faculty of Media and Information Engineering, Yunnan Open University, Kunming, 650500, China
* Corresponding Author: Shan Qing. Email:
Fluid Dynamics & Materials Processing 2023, 19(8), 2181-2200. https://doi.org/10.32604/fdmp.2023.027299
Received 24 October 2022; Accepted 14 December 2022; Issue published 04 April 2023
Abstract
In this study, comparing multiple models of machine learning, a multiple linear regression (MLP), multilayer feed-forward artificial neural network (BP) model, and a radial-basis feed-forward artificial neural network (RBF-BP) model are selected for the optimization of the thermal properties of TiO2/water nanofluids. In particular, the least squares support vector machine (LS-SVM) method and radial basis support vector machine (RB-SVM) method are implemented. First, curve fitting is performed by means of multiple linear regression in order to obtain bivariate correlation functions for thermal conductivity and viscosity of the nanofluid. Then the aforementioned models are used for a predictive analysis of the dependence of its thermal conductivity and viscosity on temperature and volume fraction. The results show that the least squares support vector machine (LS-SVM) has a prediction accuracy higher than the other models. The model predicts the thermal conductivity of TiO2/water MSE = 1.0853 × 10−6, R2 = 0.99864, MAE = 0.00092, RMSE = 0.00104, and the viscosity of TiO2/water MSE = 8.1397 × 10−6, R2 = 0.99995, MAE = 0.00074, RMSE = 0.0009.Keywords
Nomenclature
| ANN | Artificial neural network |
| MLR | Multiple linear regression |
| BP | Multilayer feedforward artificial neural network |
| RBF-BP | Radial basis feedforward artificial neural network |
| SVM | Support vector machines |
| RB-SVM | Radial basis support vector machine |
| LS-SVM | Least squares support vector machine |
| MSE | Mean square error |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| R2 | Regression coefficient |
| T | Temperature ( |
| φ | Volume fraction (vol%) |
| xi | Related variables |
| ωT | Variable coefficient |
| x | Estimate |
| xs | Actual value |
| c | Regularization parameter |
| σ2 | Nuclear parameter |
| | Experimental data |
| | Forecast data |
| | Dynamic viscosity |
| W/(m⋅K) | Thermal conductivity |
Scholars and researchers have proposed several methods to improve the heat transfer of fluids [1–4]. One method proposed is to use fluids with better heat transfer properties. Nanomaterials have promising applications in different engineering fields. Incorporating nanomaterials into fluids, thus preparing nanofluids, was proposed [5–7]. Nanofluids are relatively new-generation fluids with better thermal properties than conventional fluids [8–10]. These fluids consist of a primary fluid and particles of 1–100 nm in size. Nanofluids, suspensions, or colloids consist of particles much smaller than 100 nm, which increase the total heat transfer coefficient between the These fluids consist of a primary fluid and particles of 1–100 nm in size. And the surrounding surface. This phenomenon gives nanofluids higher thermal conductivity than the base fluid [11–14]. Additionally, nanofluids can decrease operating costs, improve energy efficiency, and create a cleaner environment. The effects of different nanoparticle types and parameters (e.g., temperature, volume fraction, particle shape, and particle size) on nanofluids’ thermal conductivity and viscosity have been studied and discussed in many articles [15–23].
Forecasting is a method of predicting the future based on existing information. In recent decades, artificial intelligence has advanced with the times due to the rapid development of computers. Machine learning has been widely used in engineering research, especially in predicting systems with nonlinear behavior. Several artificial intelligence-based model prediction methods exist, including artificial neural networks (ANN) [24], genetic algorithms (GA), pion swarm optimization (PSO), response surface methodologic (RSM) [25,26], support vector machine (SVM), and other swarm optimization methods to process data [27–29]. Artificial intelligence, as a trusted algorithm at this stage, is also used to predict nanofluid behavior and reduce laboratory costs by building models to predict the behavior of nanofluids [30–33].
Moreover, the large amount of data generated by experimental studies are also challenging to model with conventional techniques. In a generalized scheme of model prediction, the relationship between control factors and response variables is established. Traditional analytical methods have poor predictive power and poor coupling ability. Artificial neural networks to predict the behavior of nanofluids predicting thermal conductivity and viscosity have been the subject of several studies [34–37]. The designed artificial neural networks can predict the behavior of nanofluids, but the details of the learning algorithm are not described in their studies.
Ahammed et al. [38] investigated the effect of volume concentration and temperature on graphene-water nanofluids’ viscosity and surface tension. Harandi et al. [39] investigated how temperature and volume fraction affected the thermal conductivity of EG/multi-walled carbon nanotube iron oxide liquids. Measure the data at 0–2.3 vol% and . According to the predicted results, the thermal conductivity increased by 50% in most cases compared to the base fluid. Toghraie et al. [40] investigated the effect of nanoparticle volume fraction and temperature on the thermal conductivity of ZnO/EG nanofluids. and volume fraction of 0.1%–3.5% experiments showed that the thermal conductivity increased with increasing volume fraction and temperature. Also, high-temperature thermal conductivity was higher than low-temperature thermal conductivity. Soylu et al. [41] studied the influence of the doping rate of Ag/Cu doped TiO2 nanofluid on thermal properties. As the doping rates and concentrations of different materials were investigated in the temperature range of , the thermal conductivity increased with increasing doping levels. Alirezaei et al. [42] investigated the rheological behavior of MWCNT-MgO (10%–90%) hybrid nanofluid (oil-based) at different volume fractions, temperatures, and shear rates. The results showed that the dynamic viscosity of the nanofluid decreased with increasing temperature.
In some studies, researchers have used artificial neural network methods and described the details of the algorithms. Sharma et al. [43] studied the progress of machine learning in nanofluids and the advantages and disadvantages of various machine learning. This review mainly introduces the factors affecting the thermophysical properties of nanofluids, the application scenarios of nanofluids, and the application of various machine learning methods in predicting the properties of nanofluids. Esfahani et al. [44] predicted the thermal conductivity of water/silver oxide nanofluids. They used a two-stage approach combining ultrasonic devices, magnetic mixing, and acidity control methods to prepare water/silver oxide nanofluid. They examined the thermal conductivity of the nanofluid at a volume fraction of 0.125%–2% and
According to the above literature review, the majority of studies at present have high costs and little experimental data. Secondly, all machine learning methods are used to study the single thermal properties of a particular nanofluid. This method cannot compare the advantages of different machine learning methods in predicting the thermal properties of nanofluid, and it may have a different excellent effect in predicting other thermal properties. With this in mind, this paper investigates the accuracy of different machine-learning models in predicting nanofluids’ thermal conductivity and viscosity based on a small amount of data. The highlight of this study lies in designing various optimized machine learning methods to predict the two thermal properties and compare their effects. Secondly, the neural network selected in many studies can only be applied to predicting large data volumes. This study uses a small data volume model to predict nanofluids. This paper uses several machine learning models to predict the thermal conductivity and viscosity of TiO2/water nanofluids with 0.25–2 vol%. In this study, the grid search algorithm and cross-validation are applied to the machine learning model selected in this paper. The model is optimized to ensure its high accuracy and wide application.
The experimental preparation of TiO2/water nanofluids in the laboratory was chosen as the material for study in the paper [58]. It shows that titanium dioxide (TiO2) has excellent optical and electronic properties, low cost, high photocatalytic activity, chemically stable lines, non-toxicity, antibacterial properties, UV protection, and environmental cleanliness. Moreover, the thermal conductivity of TiO2/water nanofluid was increased by 22% compared to other essential fluids [59]. The TiO2/water nanofluid was prepared by selecting spherical TiO2 with a diameter of 20 nm and using deionized water as the base fluid. Choose spherical TiO2 particles with a diameter of 20 nm, use deionized water as the base solution, and add TiO2 in different proportions. Then put the liquid into the ultrasonic cell and vibrate to ensure that the nanoparticles are fully dispersed in the base liquid to prepare TiO2/water nanofluids. Forty sets of TiO2/water nanofluid thermal conductivity and viscosity data are shown in Fig. 1. The data were divided into 80% as the training set and 20% as the test set. According to the data plots, it was found that the thermal conductivity of the nanofluid increased and viscosity decreased as the temperature increased; as the concentration of nanoparticles increased, the thermal conductivity and viscosity increased.
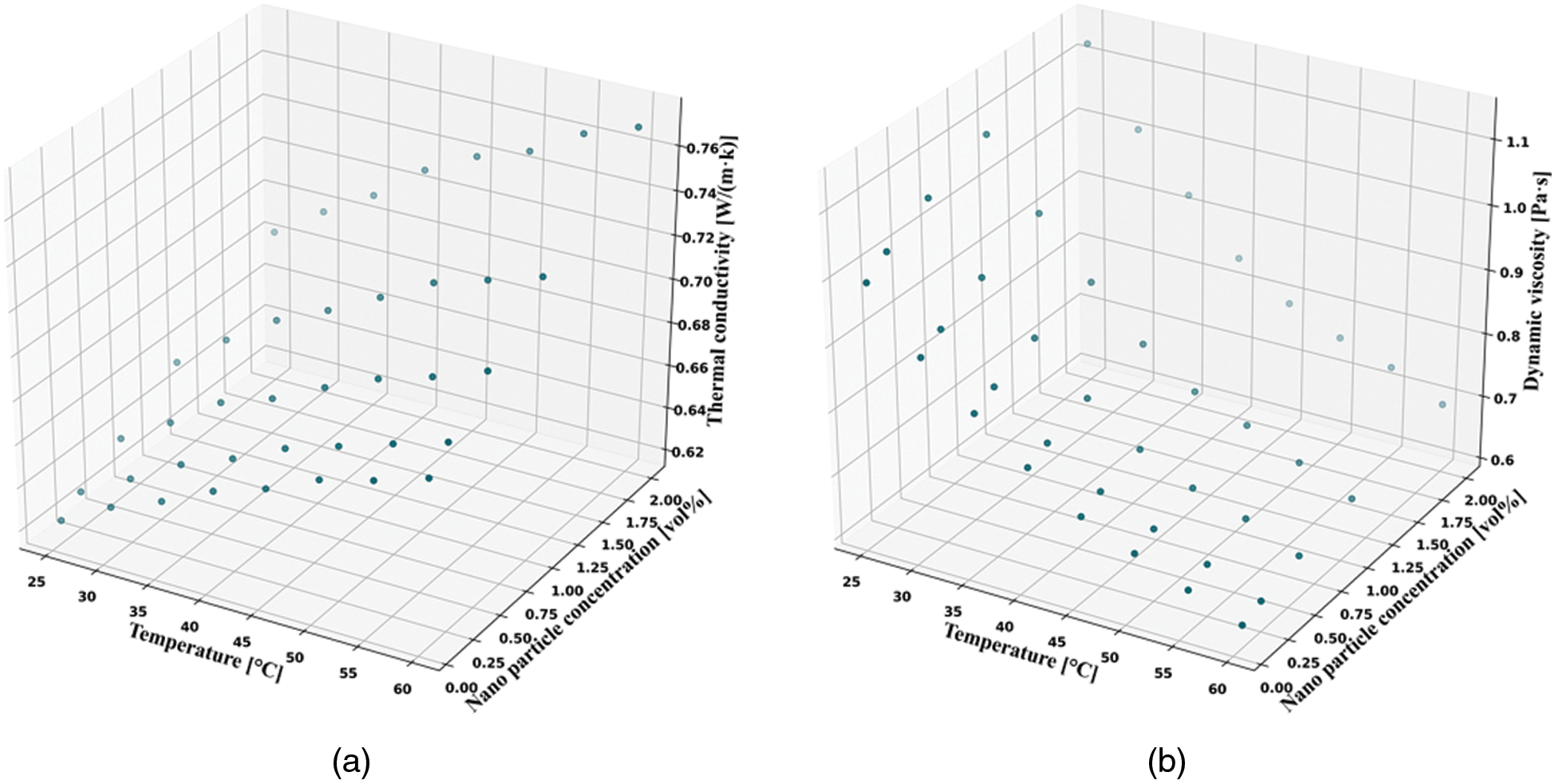
Figure 1: Thermal conductivity (a) and viscosity (b) data of TiO2/water nanofluid
In this section, we briefly introduce the selected machine learning models and the model accuracy evaluation criteria and highlight their advantages and disadvantages from a practical point of view. In this paper, we program the models using python and choose the most adaptable version3.6. The sklearn library is called to write five machine-learning models and evaluation metrics, and the matplotlib library is used to plot the images.
Artificial intelligence-based multiple linear regression and artificial neural networks are models for testing a single nanofluid’s thermal conductivity and viscosity. Therefore, in this paper, the most widely used multiple linear regression (MLR) model, the multilayer feedforward artificial neural network (BP) model, and the radial basis feedforward artificial neural network (RBF-BP) model of artificial neural networks are selected. Subsequently, two models, the Radial Basis Support Vector Machine (RB-SVM) and Least Squares Support Vector Machine (LS-SVM), which are more popular and have high accuracy at this stage, are developed.
In real-world problems, changes in the dependent variable are often influenced by several important factors when it is necessary to use two or more influencing factors as independent variables to explain the changes in the dependent variable. If this relationship is linear, the linear multiple regression model can be used to describe it. The mathematical model of linear regression is Eq. (1).
BP model is a kind of artificial neural network multilayer perceptron, which was proposed by a scientific group headed by Rumelhart and Hinton in 1986 [60]. BP neural networks can classify arbitrarily complex patterns and have excellent multi-dimensional function mapping. It can solve heterogeneous and other problems that simple perceptions cannot fight. Structurally, the BP model has three layers: an input layer, an implicit layer, and an output layer. In essence, it uses the grid error squared as the objective function and the gradient descent method to calculate the minimum value of the objective function. The primary process is as follows: first, the working signal is propagated forward, then the error signal is propagated backward to update the weights according to the error.
The BP neural network is improved by combining the BP neural network, which can better predict the unknown samples, and the RBF neural network, which can nonlinearly approximate any data set. RBF-BP composite neural network algorithm is a two-layer implicit layer neural network system. The RBF neural network is the first-level hidden layer, and the BP neural network is the second-level hidden layer.
Support vector machine is a supervised learning binary classification model that maps the feature vectors of the training set to some points in space, which the neural network classifies in an optimal line. Vapnik and Chervonenkis first proposed SVM in 1963, and the current version was modified by Hearst et al. [61]. RB-SVM uses kernel functions to replace the inner product, mapping the input data to higher space and thus solving for the best value. In this implementation, the radial basis function is utilized as the kernel function in the SVM, as shown in Eq. (2) [61].
The least squares support vector machine is a refinement and modification of the support vector machine that simplifies the solution process by solving a linear system of equations instead of the quadratic optimization problem in the SVM. The LS-SVM model consists of a regularization parameter (c) and a kernel parameter (σ^2). The kernel function defines the magnitude of the impact of a single training sample, with smaller values having a more significant impact and larger values having a minor impact.
3.2 Evaluation Metrics of Machine Learning Models
This study uses a total of four evaluation metrics, including mean square error (MSE), root means square error (RMSE), mean absolute error (MAE), and regression coefficient (R2), to evaluate the models [62–64]. Evaluation metrics are available to predict two nanofluids’ thermal conductivity and viscosity and find the most accurate model. The MSE, RMSE, MAE, and R2 are mathematically by Eqs. (3) to (6) [62–64].
where
It is worth mentioning that when the MSE, RMSE, and MAE values converge to 0, and the model with R2 is close to 1, it is considered the most accurate model. The RMSE is mainly for outliers with large deviations, while the MAE is for all individual differences for the mean. In addition to these metrics, it is sometimes necessary to consider the model’s size when searching for the best machine-learning model.
In machine learning models, hyperparameters are the parameters that must perform well. These include the number of neurons per layer and the number of hidden layers in the artificial neural network. If the hyperparameters are not selected correctly, the models will not perform well. Therefore, there are two ways to select hyperparameters: one is to fine-tune them empirically, and the other is to select different size parameters to bring into the model and pick the best ones. However, the above method requires manual debugging, which wastes much time and leads to failure to find the optimal hyperparameters. So cross-validation using grid search is the best method. The grid search is a parameter search. It is to adjust the parameters sequentially according to the set steps within the specified parameter range, train the model with the adjusted parameters, and compare the accuracy to find the best parameters.
3.4 Min-Max Normalized Data Set Preprocessing
Normalization refers to a linear variation of the initial data set, which results in a result mapped between 0 and 1. Data normalization speeds up gradient descent to find the optimal solution and improves accuracy using Eq. (7).
Data normalization where
This section summarizes and compares the machine learning models for the selected area. It compares the accuracy of various models with different parameters, selects the most accurate model from them, and analyzes the results.
4.1 Grid Search Cross-Validation to Select the Best Parameters
The evaluation metrics are filtered and validated by training and test set data using grid search CV to select the optimal number of neurons and parameters. All models are trained with 20 iterations and report only the best-selected model result, thus eliminating the effect of randomness on the performance of the developed models.
Fig. 2 shows a roughly linear relationship between thermal conductivity and viscosity of TiO2/water, according to the MLR sub-correlation. Hence, the design of a one-time multiple linear regression model was more suitable for predicting the thermal conductivity model.
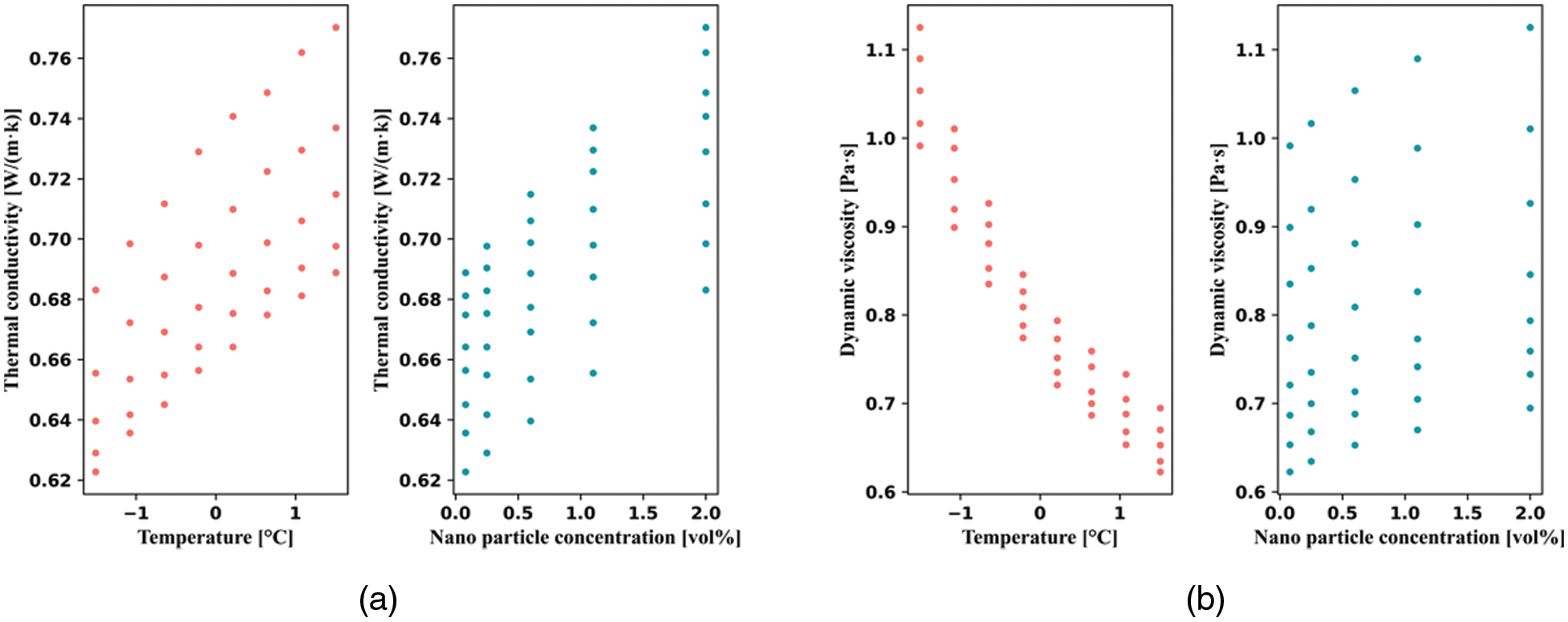
Figure 2: Correlation plot of MLR sub-analysis of thermal conductivity (a) and viscosity (b) of TiO2/water nanofluid
A curve-fitting model function Eq. (8) for the thermal conductivity of TiO2/water, a function of temperature and particle ratio, was fitted using a linear regression method. Eq. (9) is a linear relationship function of the viscosity of TiO2/water. T is the nanofluid temperature in °C and
Fig. 3 shows the number of neurons in the BP neural network corresponding to the best MSE value according to grid search cross-validation. Based on the comprehensive comparison of multiple parameters (MSE, R2, MAE, RMSE) in Table 2. The TiO2/water thermal conductivity model is the most suitable model when the number of neurons in the hidden layer is up to 66. The TiO2/water viscosity model is the best model when the number of neurons in the hidden layer is up to 45. Fig. 4 shows the predicted data of the BP best-fit model compared with the actual data.
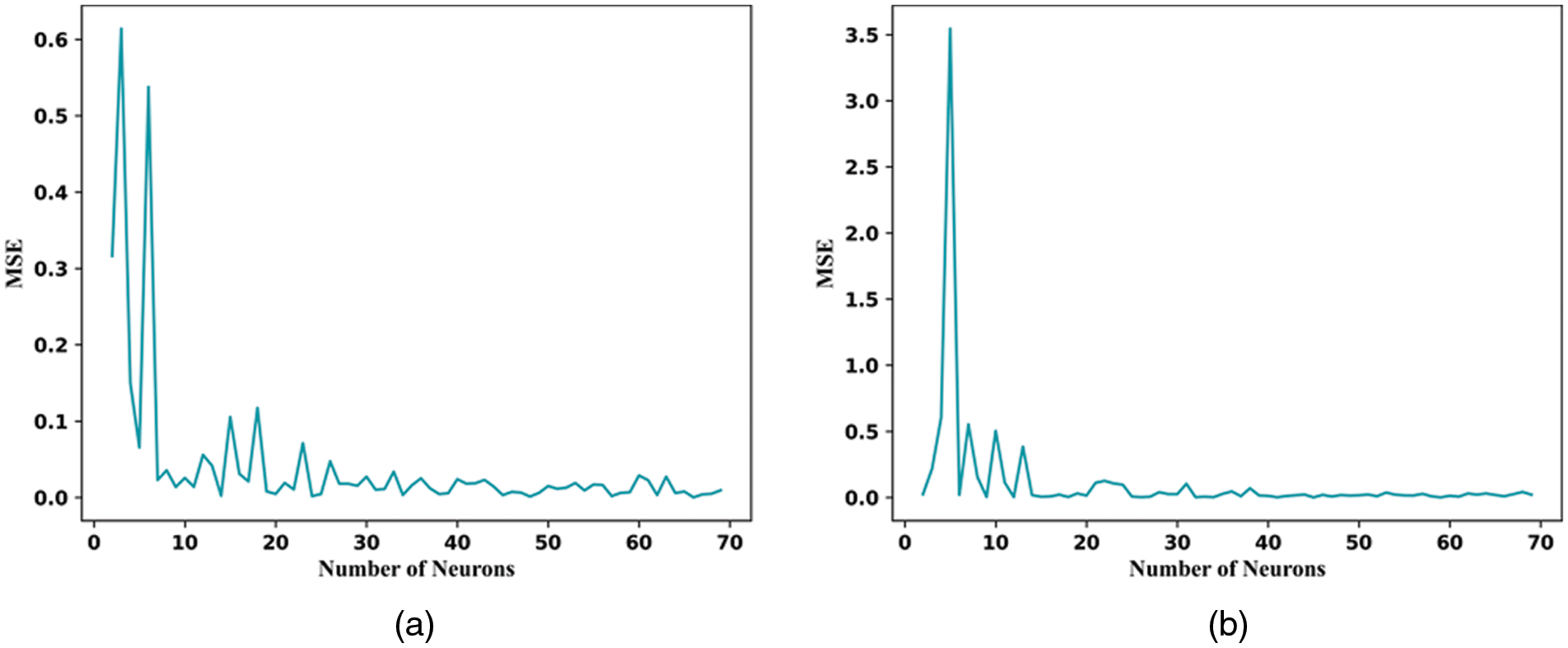
Figure 3: BP model MSE of thermal conductivity (a) and viscosity (b) of TiO2/water nanofluid vs. the number of hidden layer neurons
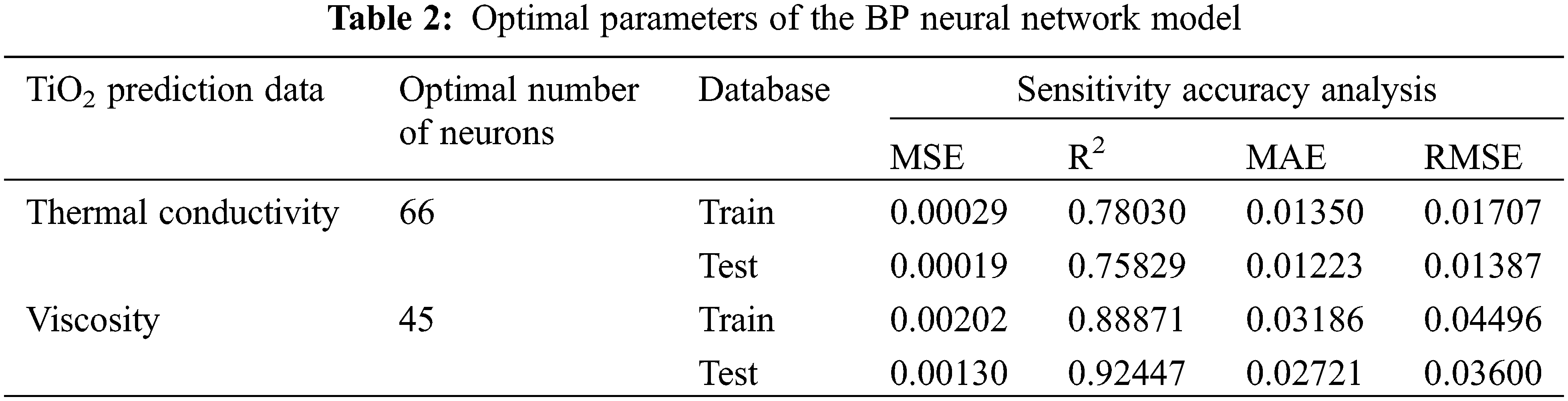
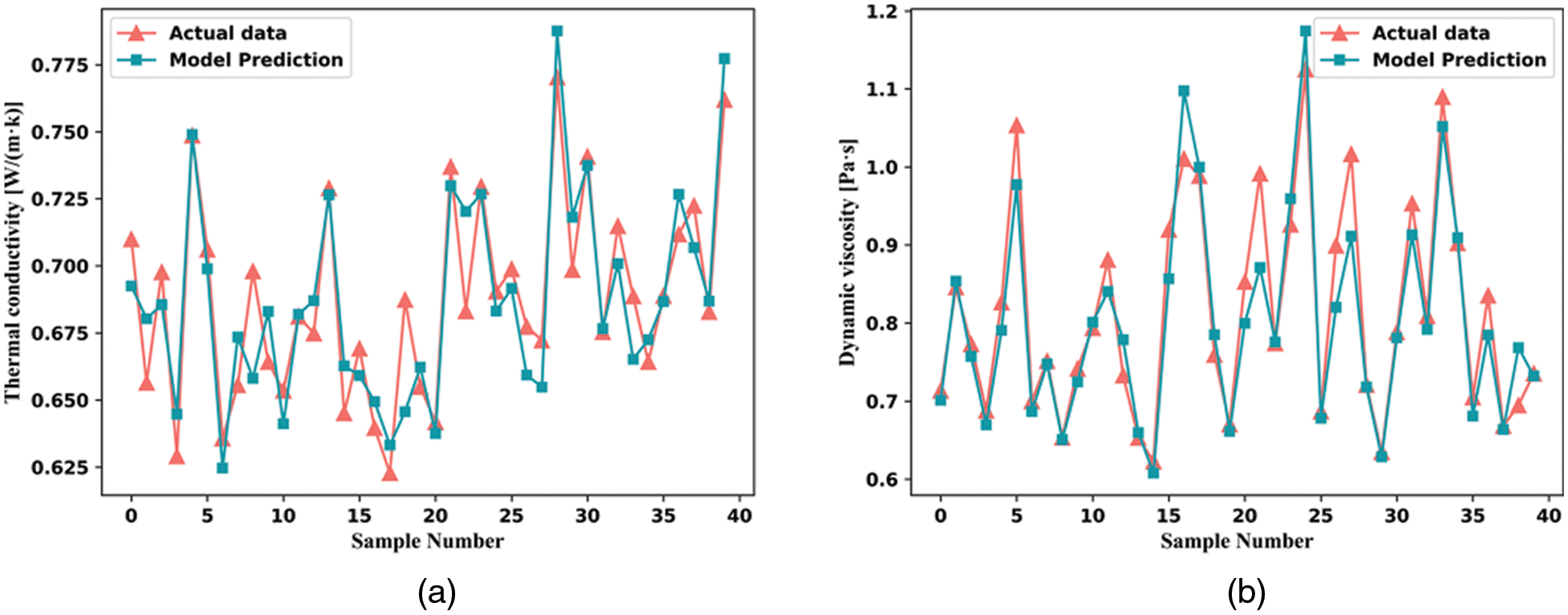
Figure 4: TiO2/water nanofluid thermal conductivity (a) and viscosity (b) BP model actual data vs. predicted data
Based on the grid search CV, Fig. 5 shows the most suitable MSE model for selecting TiO2/water thermal conductivity and viscosity. Table 3 summarizes the results for the best parameters of the RBF-BP model. As can be seen, the RBF-BP model with 10 and 7 hidden neurons is the best model for this structure. Fig. 6 compares the predicted and actual data for the selected RBF-BP best model.
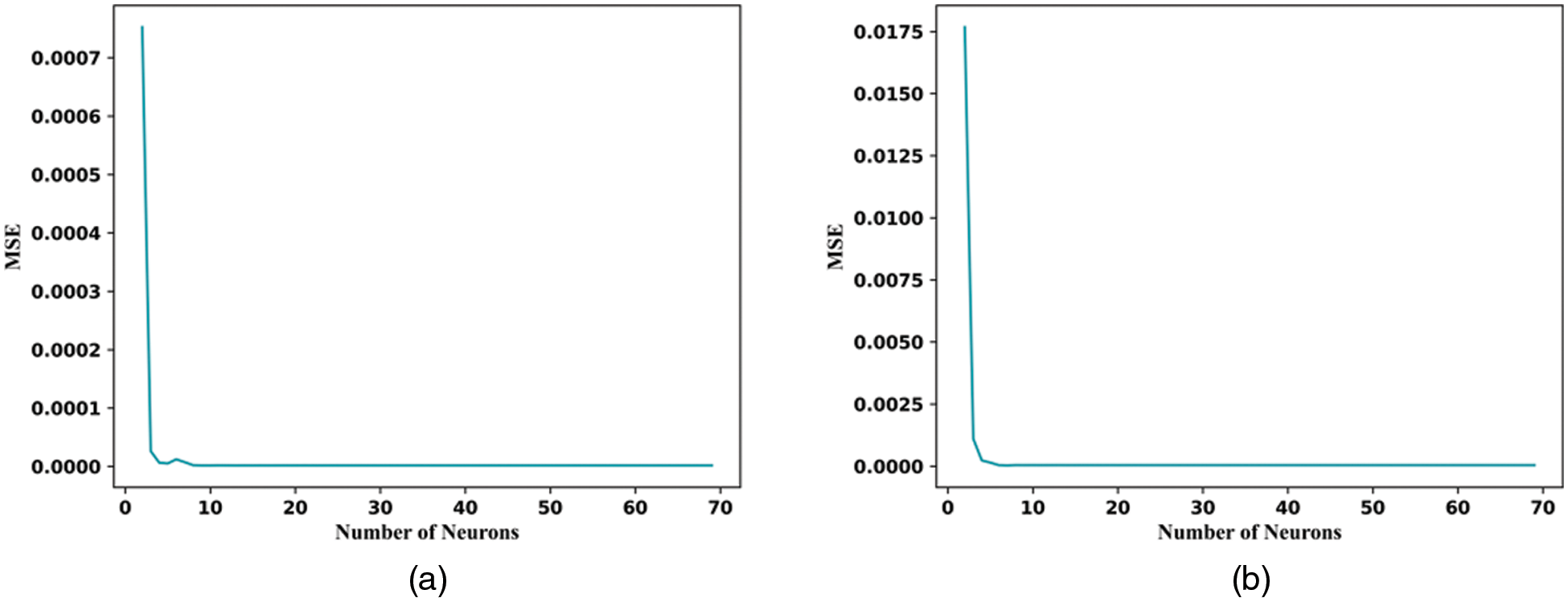
Figure 5: MSE of TiO2/water nanofluid thermal conductivity (a) and viscosity (b) of RBF-BP model vs. number of hidden layer neurons
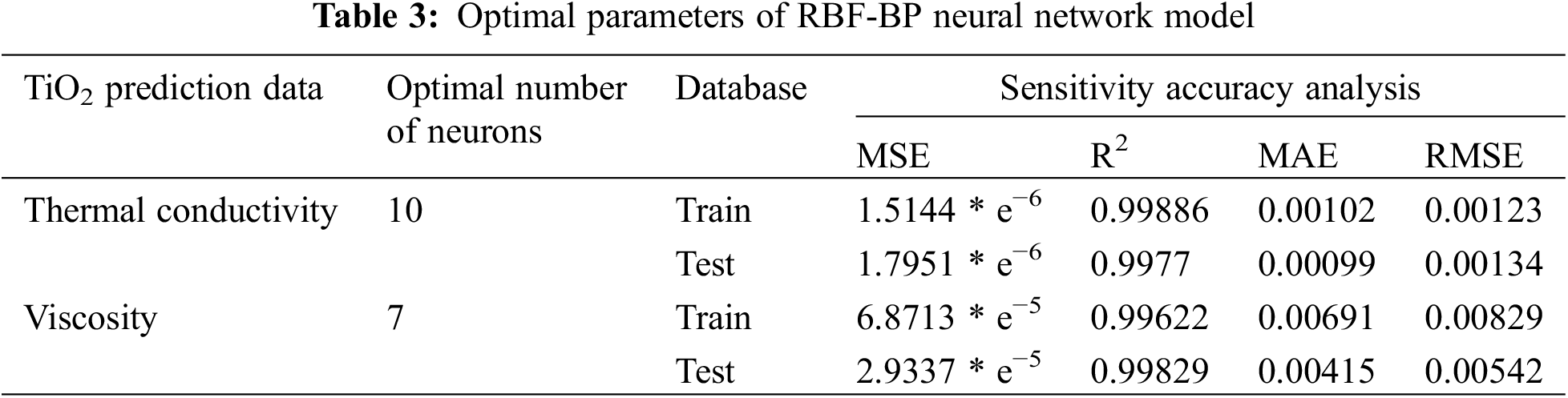
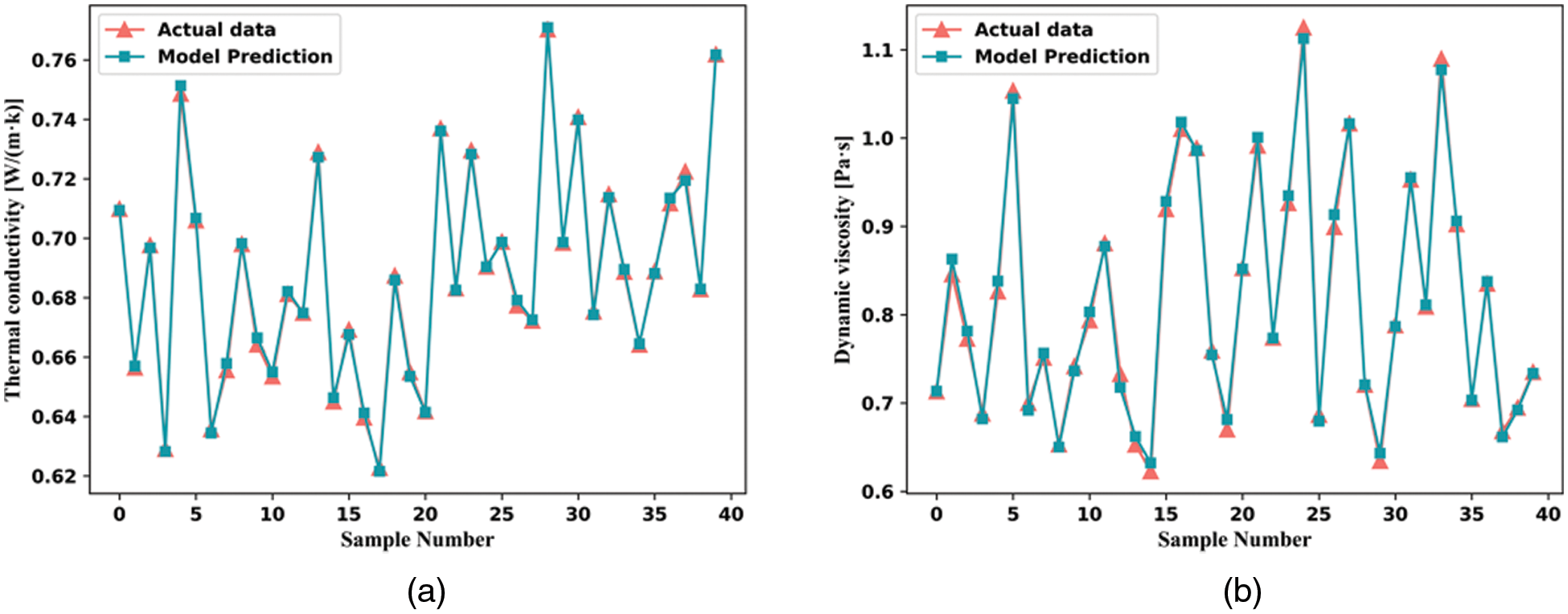
Figure 6: Comparison of actual and predicted data from TiO2/water nanofluid thermal conductivity (a) and viscosity (b) RBF-BP models
The RB-SVM model selects the radial basis as the kernel function and the regularization parameter (c) according to the kernel function. Fig. 7 shows how the appropriate parameters are selected based on the MSE for each grid of
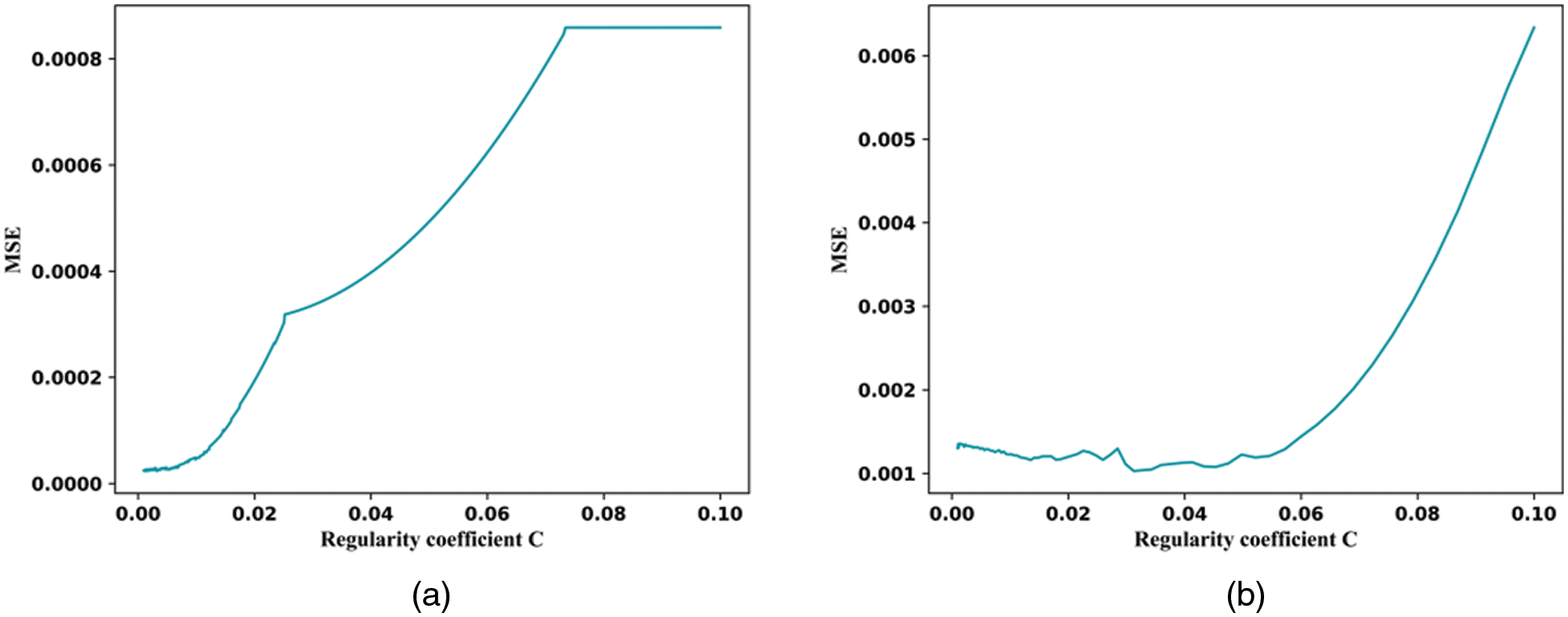
Figure 7: MSE of RB-SVM model for thermal conductivity (a) and viscosity (b) of TiO2/water nanofluid vs. regularized parameters
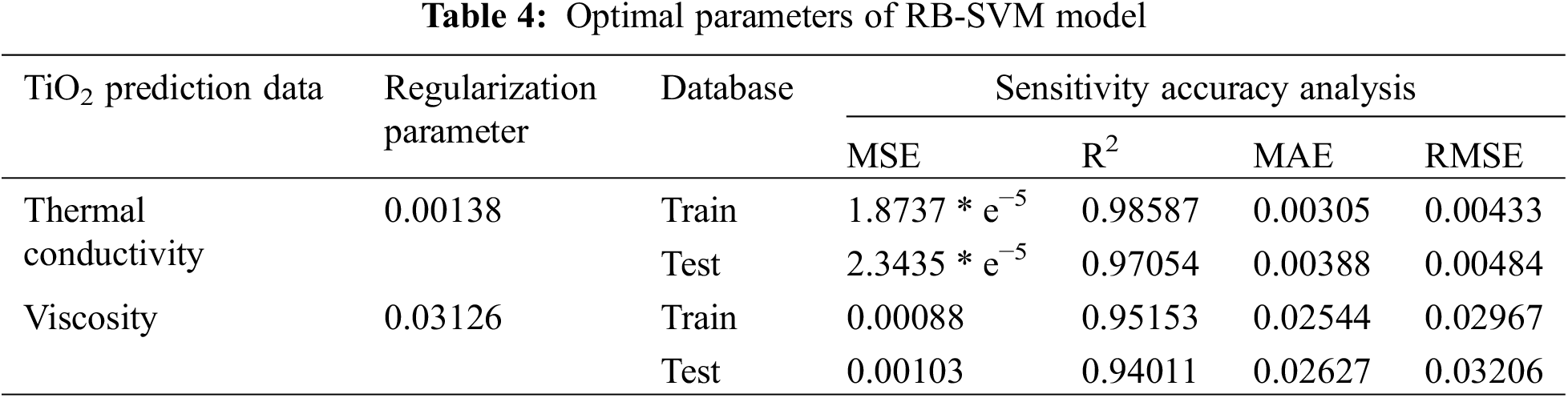
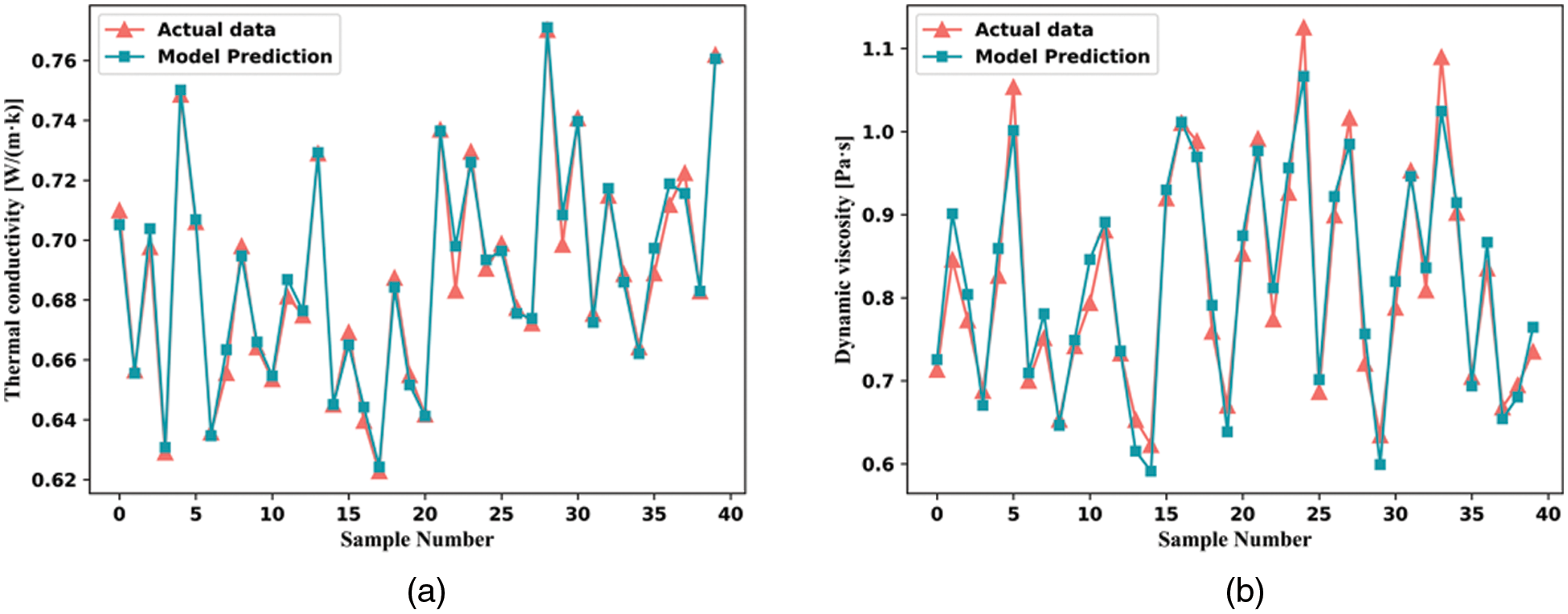
Figure 8: TiO2/water nanofluid thermal conductivity (a) and viscosity (b) RB-SVM model actual data vs. predicted data
According to the model parameters
Fig. 9 shows the results of the selection of different regularization parameters, as well as judging the MSE values for the results obtained. Table 5 indicates that the LS-SVM model with c = 94.7322 and c = 4155.4553 has the best structural model parameters. Fig. 10 compares the selected LS-SVM best model prediction data with the actual data.
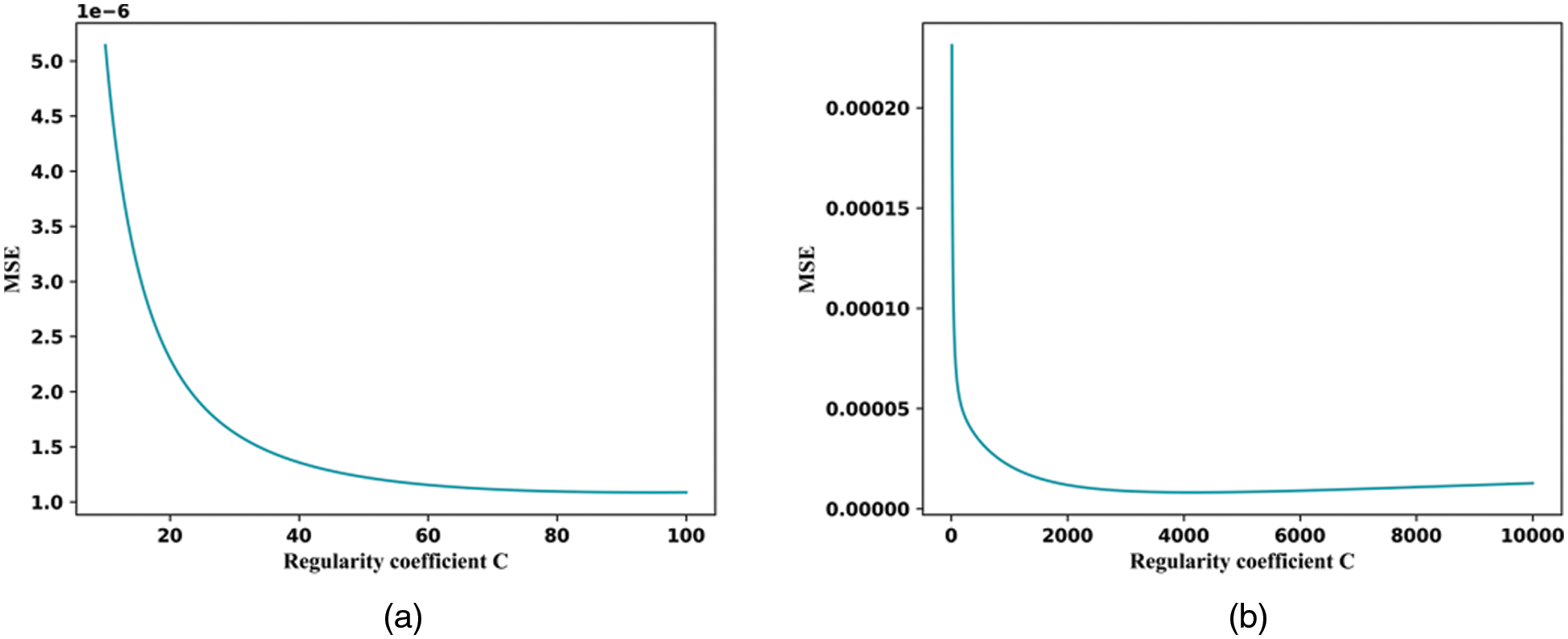
Figure 9: LS-SVM model MSE vs. regularized parameters for thermal conductivity (a) and viscosity (b) of TiO2/water nanofluid
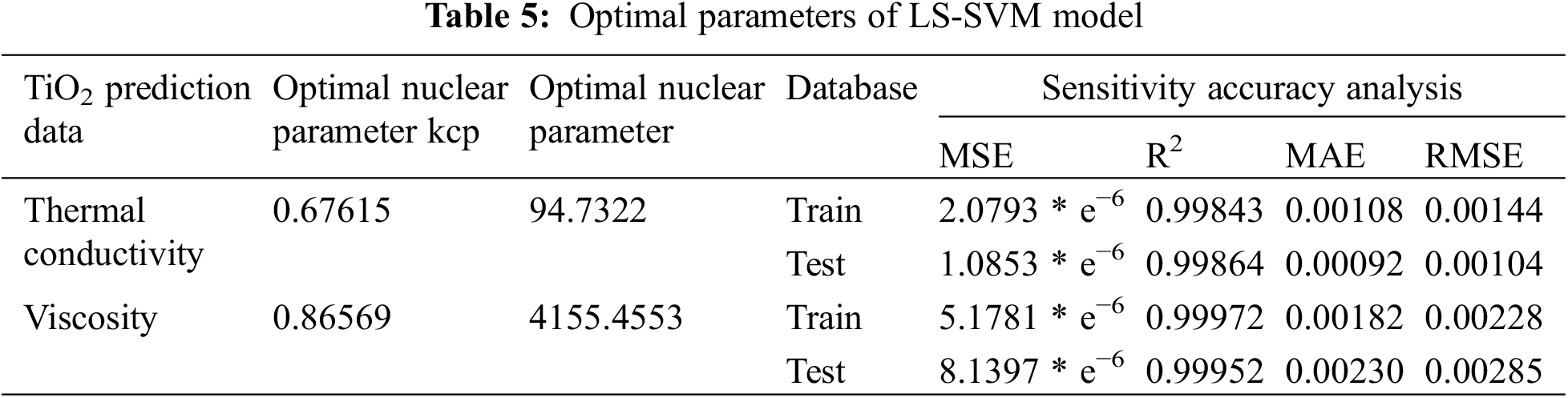
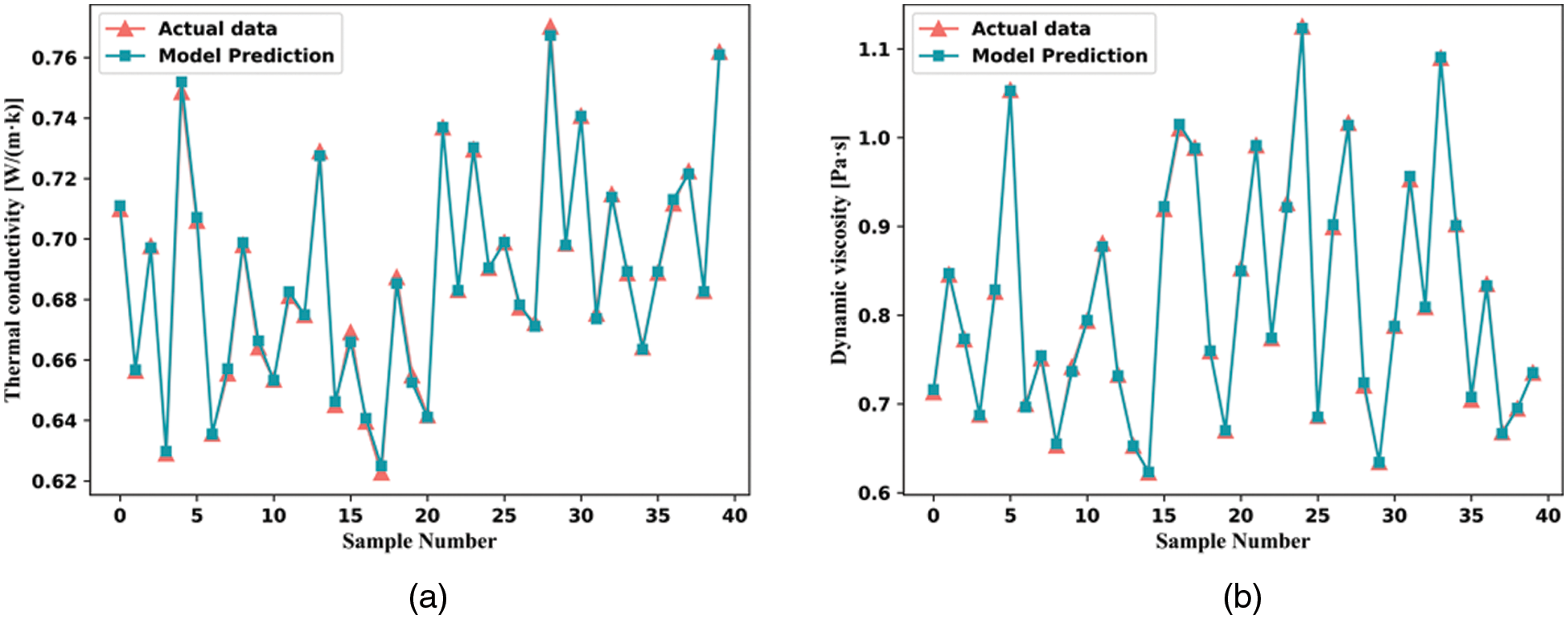
Figure 10: TiO2/water nanofluid thermal conductivity (a) and viscosity (b) LS-SVM model actual data vs. predicted data
This study aims to determine the most accurate model to predict the thermal conductivity of TiO2 nanofluid using small data volumes and therefore compares the prediction accuracy of multiple models. The optimal parameter results for BP, RBF-BP, RB-SVM, and LS-SVM applied in this paper are reported in Table 6, along with their data results for MSE, R2, MAE, and RMSE.
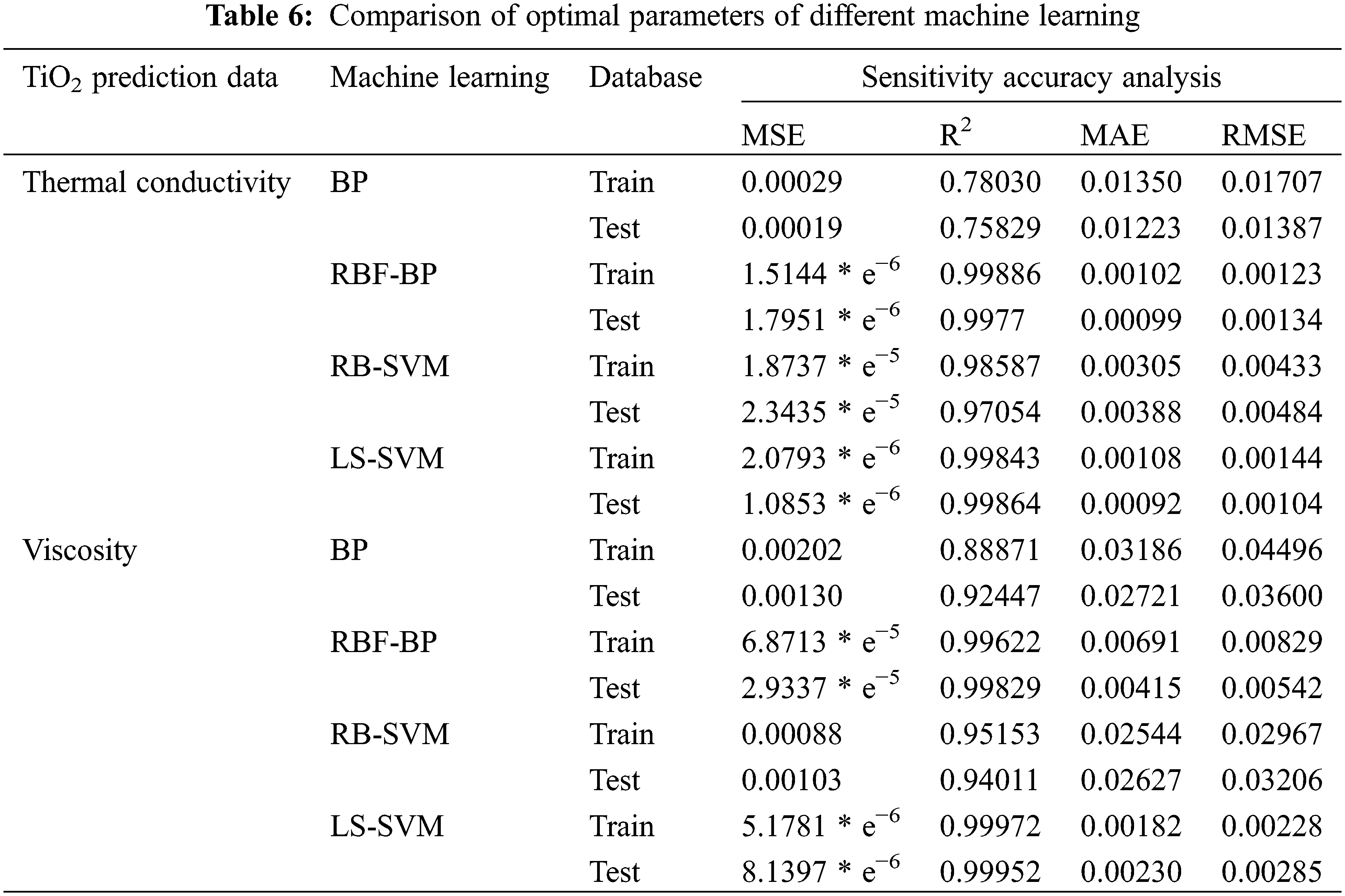
It can be concluded from this that the BP artificial neural network is unsuitable for small data volume TiO2/water nanofluid compared to the support vector machine. When predicting two sets of data with the RB-SVM model, the parameters fluctuate wildly, which indicates that its predictive classification of two sets of data will be biased due to fuzzy classifications of some data, resulting in poor accuracy as a result. The LS-SVM model shows better prediction accuracy when predicting both data sets, but the LS-SVM model has higher accuracy in comparison. Therefore, LS-SVM is the most accurate neural network model for predicting the thermal conductivity of TiO2 nanofluid with a small amount of data. In contrast, the other models are less accurate in comparison.
4.3 Accuracy Analysis of the Optimal Model
Figs. 11 and 12 compare the laboratory and machine learning predictions to understand better whether the predicted values are similar to the experimental values. The model accuracy is high when the prediction points are on or near the contour. The LS-SVM model has most of its points near the contour, as shown in the figure. The proposed machine learning algorithm has the highest accuracy among the selected models.
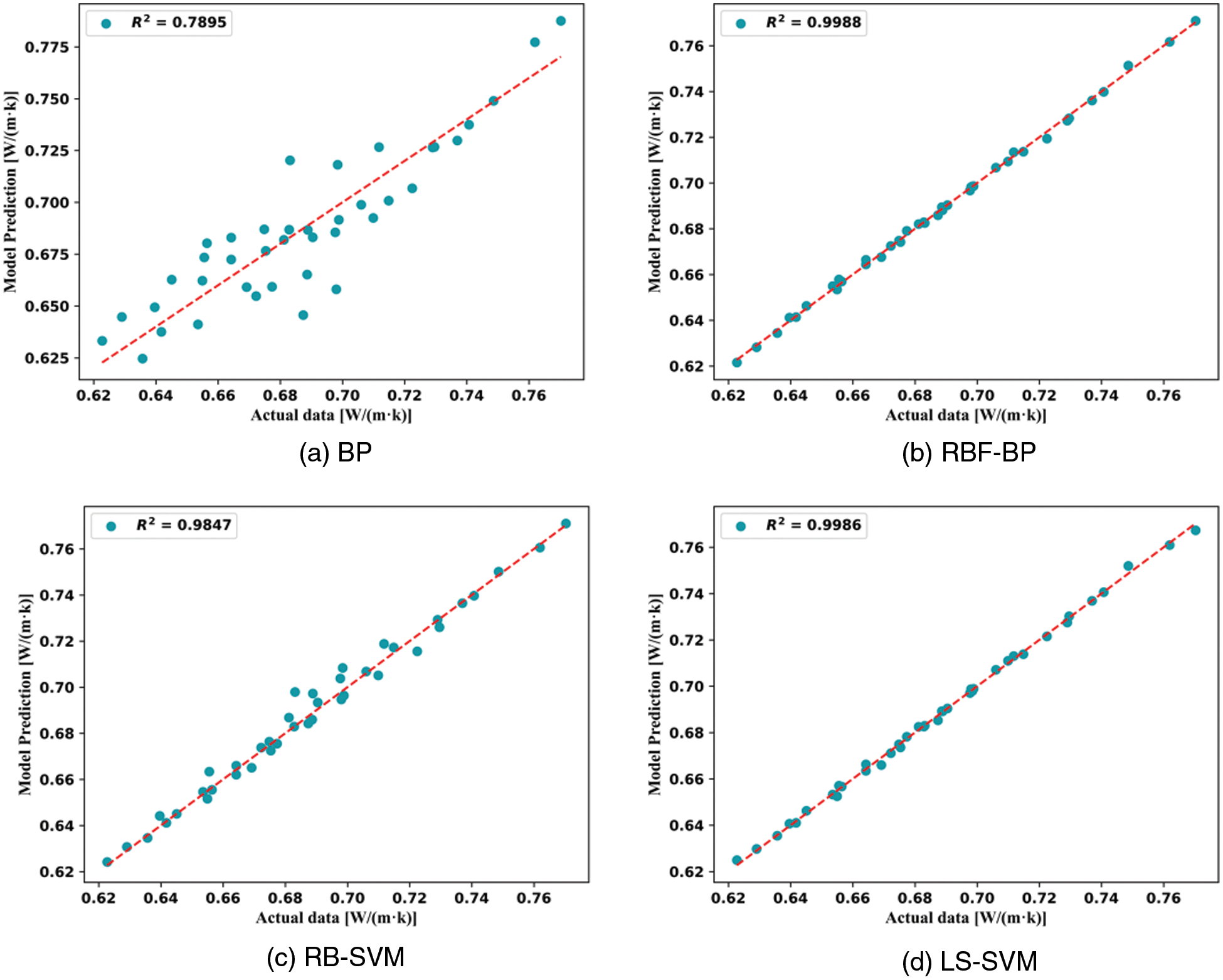
Figure 11: Comparison of actual data on thermal conductivity of TiO2/water nanofluid with machine learning
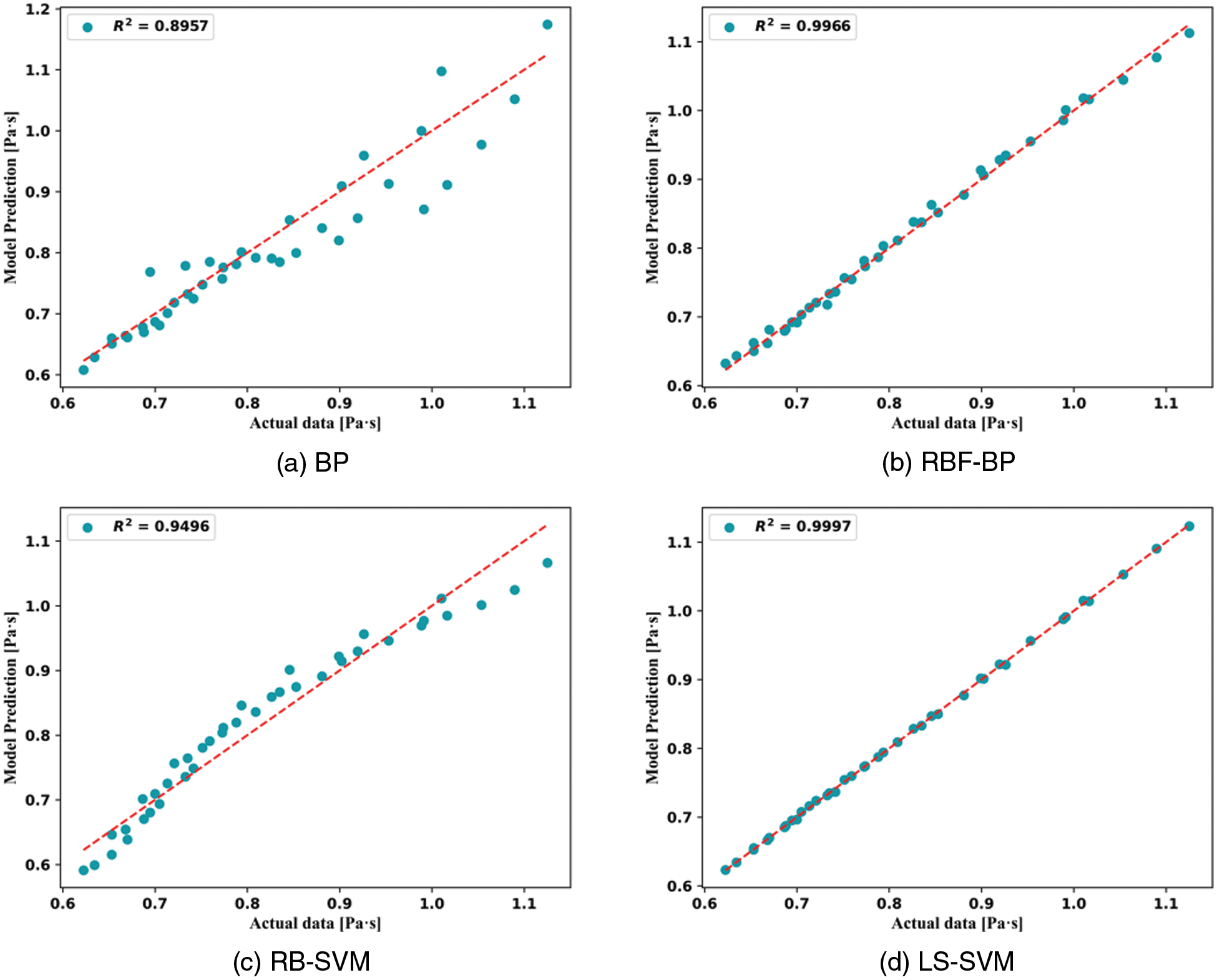
Figure 12: Comparison of actual TiO2/water nanofluid viscosity data with machine learning
Nanofluids are famous heat and mass transfer materials in various fields at this stage. Thermal conductivity and viscosity are the most important thermophysical properties, and nanofluids operating temperature, volume fraction, particle morphology, and particle size directly affect their thermal conductivity and viscosity. In this study, focusing on experimental data, the effects of TiO2 concentration and temperature on nanofluids’ thermal conductivity and viscosity were investigated by curve fitting, artificial neural network, and support vector machine methods. We propose a simple bivariate correlation using curve fitting to show the relationship between the parameters. Then, four machine learning models are selected to predict thermal conductivity and viscosity, with temperature and concentration as input variables. Based on the MSE = 1.82 * e−6 and MSE = 0.4942 [64,65] models in the literature, it can show that the four models have reasonable predictions after normalization and grid search CV. In addition, the LS-SVM model shows high accuracy through four evaluation indexes without over-fitting or under-fitting. Curve fitting and neural networks are both good prediction tools. However, the LS-SVM model is more accurate and can better predict nanofluids’ thermal conductivity and viscosity.
The results show that a better and more accurate model can better predict the model. For future research, it is necessary to examine the universal application of the model. This includes the influence of different input conditions on the model as well as the possibility that the model can still be applied after replacing the nanofluid. It is also necessary to develop a database of the model with high accuracy and strong applicability. As a result, this area requires further research.
Funding Statement: This research is financially supported by the National Natural Science Foundation of China (Nos. 51966005, 51866003) and Yunnan Basic Research Program Project (2019FB071).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Cao, Y., Doustgani, A., Salehi, A., Nemati, M., Ghasemi, A. et al. (2020). The economic evaluation of establishing a plant for producing biodiesel from edible oil wastes in oil-rich countries: Case study Iran. Energy, 213, 118760. https://doi.org/10.1016/j.energy.2020.118760 [Google Scholar] [CrossRef]
2. Toghraie, D., Sina, N., Jolfaei, N. A., Hajian, M., Afrand, M. (2019). Designing an artificial neural network (ANN) to predict the viscosity of silver/ethylene glycol nanofluid at different temperatures and volume fraction of nanoparticles. Physica A: Statistical Mechanics and its Applications, 534, 122142. https://doi.org/10.1016/j.physa.2019.122142 [Google Scholar] [CrossRef]
3. Toghraie, D., Aghahadi, M. H., Sina, N., Soltani, F. (2020). Application of artificial neural networks (ANNs) for predicting the viscosity of tungsten oxide (WO3)-MWCNTs/engine oil hybrid nanofluid. International Journal of Thermophysics, 41(12), 1–17. https://doi.org/10.1007/s10765-020-02749-x [Google Scholar] [CrossRef]
4. Karim, S. H. T., Tofiq, T. A., Shariati, M., Rad, H. N., Ghasemi, A. (2021). 4E analyses and multi-objective optimization of a solar-based combined cooling, heating, and power system for residential applications. Energy Reports, 7, 1780–1797. https://doi.org/10.1016/j.egyr.2021.03.020 [Google Scholar] [CrossRef]
5. Ali, M. K. A., Xianjun, H., Abdelkareem, M. A., Gulzar, M., Elsheikh, A. H. (2018). Novel approach of the graphene nanolubricant for energy saving via anti-friction/wear in automobile engines. Tribology International, 124, 209–229. https://doi.org/10.1016/j.triboint.2018.04.004 [Google Scholar] [CrossRef]
6. Ali, M. K. A., Hou, X. J., Abdelkareem, M. A., Elsheikh, A. H. (2019). Role of nanolubricants formulated in improving vehicle engines performance. IOP Conference Series: Materials Science and Engineering, 563(2), 022015. https://doi.org/10.1088/1757-899X/563/2/022015 [Google Scholar] [CrossRef]
7. Essa, F. A., Yu, J., Elsheikh, A. H., Tawfik, M. M. (2019). A new M50 matrix composite sintered with a hybrid Sns/Zno nanoscale solid lubricants: An experimental investigation. Materials Research Express, 6(11), 116523. https://doi.org/10.1088/2053-1591/ab4675 [Google Scholar] [CrossRef]
8. Reddy, P. S., Chamkha, A. J. (2016). Influence of size, shape, type of nanoparticles, type and temperature of the base fluid on natural convection MHD of nanofluids. Alexandria Engineering Journal, 55(1), 331–341. https://doi.org/10.1016/j.aej.2016.01.027 [Google Scholar] [CrossRef]
9. Zayed, M. E., Sharshir, S. W., Shaibo, J., Hammad, F. A., Ali, M. K. A. et al. (2019). Applications of nanofluids in direct absorption solar collectors. In: Nanofluids and their engineering applications, pp. 405–429. CRC Press. [Google Scholar]
10. Elsheikh, A. H., Sharshir, S. W., Mostafa, M. E., Essa, F. A., Ali, M. K. A. (2018). Applications of nanofluids in solar energy: A review of recent advances. Renewable and Sustainable Energy Reviews, 82, 3483–3502. https://doi.org/10.1016/j.rser.2017.10.108 [Google Scholar] [CrossRef]
11. Huminic, A., Huminic, G., Fleaca, C., Dumitrache, F., Morjan, I. (2015). Thermal conductivity, viscosity and surface tension of nanofluids based on FeC nanoparticles. Powder Technology, 284, 78–84. https://doi.org/10.1016/j.powtec.2015.06.040 [Google Scholar] [CrossRef]
12. Sharshir, S. W., Peng, G., Elsheikh, A. H., Edreis, E. M., Eltawil, M. A. et al. (2018). Energy and exergy analysis of solar stills with micro/nano particles: A comparative study. Energy Conversion and Management, 177, 363–375. https://doi.org/10.1016/j.enconman.2018.09.074 [Google Scholar] [CrossRef]
13. Sharshir, S. W., Kandeal, A. W., Ismail, M., Abdelaziz, G. B., Kabeel, A. E. et al. (2019). Augmentation of a pyramid solar still performance using evacuated tubes and nanofluid: Experimental approach. Applied Thermal Engineering, 160, 113997. https://doi.org/10.1016/j.applthermaleng.2019.113997 [Google Scholar] [CrossRef]
14. Sharshir, S. W., Peng, G., Wu, L., Yang, N., Essa, F. A. et al. (2017). Enhancing the solar still performance using nanofluids and glass cover cooling: Experimental study. Applied Thermal Engineering, 113, 684–693. https://doi.org/10.1016/j.applthermaleng.2016.11.085 [Google Scholar] [CrossRef]
15. Sundar, L. S., Ramana, E. V., Graça, M. P. F., Singh, M. K., Sousa, A. C. (2016). Nanodiamond-Fe3O4 nanofluids: Preparation and measurement of viscosity, electrical and thermal conductivities. International Communications in Heat and Mass Transfer, 73, 62–74. https://doi.org/10.1016/j.icheatmasstransfer.2016.02.013 [Google Scholar] [CrossRef]
16. Agarwal, R., Verma, K., Agrawal, N. K., Singh, R. (2017). Sensitivity of thermal conductivity for Al2O3 nanofluids. Experimental Thermal and Fluid Science, 80, 19–26. https://doi.org/10.1016/j.expthermflusci.2016.08.007 [Google Scholar] [CrossRef]
17. Kim, H. J., Lee, S. H., Lee, J. H., Jang, S. P. (2015). Effect of particle shape on suspension stability and thermal conductivities of water-based bohemite alumina nanofluids. Energy, 90, 1290–1297. https://doi.org/10.1016/j.energy.2015.06.084 [Google Scholar] [CrossRef]
18. Sarafraz, M. M., Nikkhah, V., Madani, S. A., Jafarian, M., Hormozi, F. (2017). Low-frequency vibration for fouling mitigation and intensification of thermal performance of a plate heat exchanger working with CuO/water nanofluid. Applied Thermal Engineering, 121, 388–399. https://doi.org/10.1016/j.applthermaleng.2017.04.083 [Google Scholar] [CrossRef]
19. Sheikhbahai, M., Esfahany, M. N., Etesami, N. (2012). Experimental investigation of pool boiling of Fe3O4/ethylene glycol–water nanofluid in electric field. International Journal of Thermal Sciences, 62, 149–153. https://doi.org/10.1016/j.ijthermalsci.2011.10.004 [Google Scholar] [CrossRef]
20. Salari, E., Peyghambarzadeh, M., Sarafraz, M., Hormozi, F. (2016). Boiling heat transfer of alumina nano-fluids: Role of nanoparticle deposition on the boiling heat transfer coefficient. Periodica Polytechnica Chemical Engineering, 60(4), 252–258. [Google Scholar]
21. Nakhjavani, M., Nikkhah, V., Sarafraz, M. M., Shoja, S., Sarafraz, M. (2017). Green synthesis of silver nanoparticles using green tea leaves: Experimental study on the morphological, rheological and antibacterial behaviour. Heat and Mass Transfer, 53(10), 3201–3209. https://doi.org/10.1007/s00231-017-2065-9 [Google Scholar] [CrossRef]
22. Nikkhah, V., Sarafraz, M. M., Hormozi, F. (2015). Application of spherical copper oxide (II) water nano-fluid as a potential coolant in a boiling annular heat exchanger. Chemical and Biochemical Engineering Quarterly, 29(3), 405–415. https://doi.org/10.15255/CABEQ.2014.2069 [Google Scholar] [CrossRef]
23. Kamalgharibi, M., Hormozi, F., Zamzamian, S. A. H., Sarafraz, M. M. (2016). Experimental studies on the stability of CuO nanoparticles dispersed in different base fluids: Influence of stirring, sonication and surface-active agents. Heat and Mass Transfer, 52(1), 55–62. https://doi.org/10.1007/s00231-015-1618-z [Google Scholar] [CrossRef]
24. Said, Z., Sharma, P., Sundar, L. S., Afzal, A., Li, C. (2021). Synthesis, stability, thermophysical properties and AI approach for predictive modelling of Fe3O4 coated MWCNT hybrid nanofluids. Journal of Molecular Liquids, 340, 117291. https://doi.org/10.1016/j.molliq.2021.117291 [Google Scholar] [CrossRef]
25. Sharma, P., Sharma, A. K. (2021). Application of response surface methodology for optimization of fuel injection parameters of a dual fuel engine fuelled with producer gas-biodiesel blends. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 1–18. https://doi.org/10.1080/15567036.2021.1892883 [Google Scholar] [CrossRef]
26. Sharma, P. (2022). Prediction-optimization of the effects of di-tert butyl peroxide-biodiesel blends on engine performance and emissions using multi-objective response surface methodology. Journal of Energy Resources Technology, 144(7). https://doi.org/10.1115/1.4052237 [Google Scholar] [CrossRef]
27. Sharma, P. (2020). Gene expression programming-based model prediction of performance and emission characteristics of a diesel engine fueled with linseed oil biodiesel/diesel blends: An artificial intelligence approach. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 1–15. https://doi.org/10.1080/15567036.2020.1829204 [Google Scholar] [CrossRef]
28. Sharma, P. (2021). Artificial intelligence-based model prediction of biodiesel-fueled engine performance and emission characteristics: A comparative evaluation of gene expression programming and artificial neural network. Heat Transfer, 50(6), 5563–5587. https://doi.org/10.1002/htj.22138 [Google Scholar] [CrossRef]
29. Wang, J., Zhai, Y., Yao, P., Ma, M., Wang, H. (2020). Established prediction models of thermal conductivity of hybrid nanofluids based on artificial neural network (ANN) models in waste heat system. International Communications in Heat and Mass Transfer, 110, 104444. https://doi.org/10.1016/j.icheatmasstransfer.2019.104444 [Google Scholar] [CrossRef]
30. Said, Z., Sundar, L. S., Rezk, H., Nassef, A. M., Ali, H. M. et al. (2021). Optimizing density, dynamic viscosity, thermal conductivity and specific heat of a hybrid nanofluid obtained experimentally via ANFIS-based model and modern optimization. Journal of Molecular Liquids, 321, 114287. https://doi.org/10.1016/j.molliq.2020.114287 [Google Scholar] [CrossRef]
31. Jamei, M., Ahmadianfar, I., Olumegbon, I. A., Asadi, A., Karbasi, M. et al. (2021). On the specific heat capacity estimation of metal oxide-based nanofluid for energy perspective–A comprehensive assessment of data analysis techniques. International Communications in Heat and Mass Transfer, 123, 105217. https://doi.org/10.1016/j.icheatmasstransfer.2021.105217 [Google Scholar] [CrossRef]
32. Alnaqi, A. A., Alsarraf, J., Al-Rashed, A. A. (2021). Using response surface methodology and artificial neural network to examine the rheological behavior of tungsten trioxide/ethylene glycol nanofluid under various sonication times. Journal of Molecular Liquids, 337, 116022. https://doi.org/10.1016/j.molliq.2021.116022 [Google Scholar] [CrossRef]
33. Ilyas, S. U., Ridha, S., Sardar, S., Estellé, P., Kumar, A. et al. (2021). Rheological behavior of stabilized diamond-graphene nanoplatelets hybrid nanosuspensions in mineral oil. Journal of Molecular Liquids, 328, 115509. https://doi.org/10.1016/j.molliq.2021.115509 [Google Scholar] [CrossRef]
34. Li, X., Wang, H., Luo, B. (2021). The thermophysical properties and enhanced heat transfer performance of SiC-MWCNTs hybrid nanofluids for car radiator system. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 612, 125968. https://doi.org/10.1016/j.colsurfa.2020.125968 [Google Scholar] [CrossRef]
35. Akhgar, A., Toghraie, D., Sina, N., Afrand, M. (2019). Developing dissimilar artificial neural networks (ANNs) to prediction the thermal conductivity of MWCNT-TiO2/Water-ethylene glycol hybrid nanofluid. Powder Technology, 355, 602–610. https://doi.org/10.1016/j.powtec.2019.07.086 [Google Scholar] [CrossRef]
36. Rostami, S., Toghraie, D., Shabani, B., Sina, N., Barnoon, P. (2021). Measurement of the thermal conductivity of MWCNT-CuO/water hybrid nanofluid using artificial neural networks (ANNs). Journal of Thermal Analysis and Calorimetry, 143(2), 1097–1105. https://doi.org/10.1007/s10973-020-09458-5 [Google Scholar] [CrossRef]
37. Li, X., Zeng, G., Lei, X. (2020). The stability, optical properties and solar-thermal conversion performance of SiC-MWCNTs hybrid nanofluids for the direct absorption solar collector (DASC) application. Solar Energy Materials and Solar Cells, 206, 110323. https://doi.org/10.1016/j.solmat.2019.110323 [Google Scholar] [CrossRef]
38. Ahammed, N., Asirvatham, L. G., Wongwises, S. (2016). Effect of volume concentration and temperature on viscosity and surface tension of graphene–water nanofluid for heat transfer applications. Journal of Thermal Analysis and Calorimetry, 123(2), 1399–1409. https://doi.org/10.1007/s10973-015-5034-x [Google Scholar] [CrossRef]
39. Harandi, S. S., Karimipour, A., Afrand, M., Akbari, M., D’Orazio, A. (2016). An experimental study on thermal conductivity of F-MWCNTs–Fe3O4/EG hybrid nanofluid: Effects of temperature and concentration. International Communications in Heat and Mass Transfer, 76, 171–177. https://doi.org/10.1016/j.icheatmasstransfer.2016.05.029 [Google Scholar] [CrossRef]
40. Toghraie, D., Chaharsoghi, V. A., Afrand, M. (2016). Measurement of thermal conductivity of ZnO–TiO2/EG hybrid nanofluid. Journal of Thermal Analysis and Calorimetry, 125(1), 527–535. https://doi.org/10.1007/s10973-016-5436-4 [Google Scholar] [CrossRef]
41. Soylu, S. K., Acar, Z. Y., Asiltürk, M., Atmaca, İ. (2022). Effects of doping on the thermophysical properties of Ag and Cu doped TiO2 nanoparticles and their nanofluids. Journal of Molecular Liquids, 368, 120615. [Google Scholar]
42. Alirezaie, A., Saedodin, S., Esfe, M. H., Rostamian, S. H. (2017). Investigation of rheological behavior of MWCNT (COOH-functionalized)/MgO-engine oil hybrid nanofluids and modelling the results with artificial neural networks. Journal of Molecular Liquids, 241, 173–181. [Google Scholar]
43. Sharma, P., Said, Z., Kumar, A., Nizetic, S., Pandey, A. et al. (2022). Recent advances in machine learning research for nanofluid-based heat transfer in renewable energy system. Energy & Fuels, 36(13), 6626–6658. [Google Scholar]
44. Esfahani, N. N., Toghraie, D., Afrand, M. (2018). A new correlation for predicting the thermal conductivity of ZnO–Ag (50%–50%)/water hybrid nanofluid: An experimental study. Powder Technology, 323, 367–373. [Google Scholar]
45. Said, Z., Cakmak, N. K., Sharma, P., Sundar, L. S., Inayat, A. et al. (2022). Synthesis, stability, density, viscosity of ethylene glycol-based ternary hybrid nanofluids: Experimental investigations and model-prediction using modern machine learning techniques. Powder Technology, 400, 117190. [Google Scholar]
46. Sharma, P., Said, Z., Memon, S., Elavarasan, R. M., Khalid, M. et al. (2022). Comparative evaluation of AI-based intelligent GEP and ANFIS models in prediction of thermophysical properties of Fe3O4-coated MWCNT hybrid nanofluids for potential application in energy systems. International Journal of Energy Research, 46(13), 19242–19257. [Google Scholar]
47. Ariana, M. A., Vaferi, B., Karimi, G. (2015). Prediction of thermal conductivity of alumina water-based nanofluids by artificial neural networks. Powder Technology, 278, 1–10. [Google Scholar]
48. Masoumi, N., Sohrabi, N., Behzadmehr, A. (2009). A new model for calculating the effective viscosity of nanofluids. Journal of Physics D: Applied Physics, 42(5), 055501. [Google Scholar]
49. Kanti, P. K., Sharma, K. V., HN, A. R., Karbasi, M., Said, Z. (2022). Experimental investigation of synthesized Al2O3 ionanofluid’s energy storage properties: Model-prediction using gene expression programming. Journal of Energy Storage, 55, 105718. [Google Scholar]
50. Kanti, P., Sharma, K. V., Yashawantha, K. M., Dmk, S. (2021). Experimental determination for viscosity of fly ash nanofluid and fly ash-Cu hybrid nanofluid: Prediction and optimization using artificial intelligent techniques. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 1–20. [Google Scholar]
51. Kanti, P. K., Sharma, K. V., Said, Z., Jamei, M., Yashawantha, K. M. (2022). Experimental investigation on thermal conductivity of fly ash nanofluid and fly ash-Cu hybrid nanofluid: Prediction and optimization via ANN and MGGP model. Particulate Science and Technology, 40(2), 182–195. [Google Scholar]
52. Kanti, P., Sharma, K. V., Jamei, M., Kumar, H. P. (2021). Thermal performance of hybrid fly ash and copper nanofluid in various mixture ratios: Experimental investigation and application of a modern ensemble machine learning approach. International Communications in Heat and Mass Transfer, 129, 105731. [Google Scholar]
53. Kanti, P., Sharma, K. V., Yashawantha, K. M., Jamei, M., Said, Z. (2022). Properties of water-based fly ash-copper hybrid nanofluid for solar energy applications: Application of RBF model. Solar Energy Materials and Solar Cells, 234, 111423. [Google Scholar]
54. Hemmat Esfe, M., Rostamian, H., Toghraie, D., Yan, W. M. (2016). Using artificial neural network to predict thermal conductivity of ethylene glycol with alumina nanoparticle. Journal of Thermal Analysis and Calorimetry, 126(2), 643–648. [Google Scholar]
55. He, W., Ruhani, B., Toghraie, D., Izadpanahi, N., Esfahani, N. N. et al. (2020). Using of artificial neural networks (ANNs) to predict the thermal conductivity of zinc oxide–silver (50%–50%)/water hybrid newtonian nanofluid. International Communications in Heat and Mass Transfer, 116, 104645. [Google Scholar]
56. Rostami, S., Toghraie, D., Esfahani, M. A., Hekmatifar, M., Sina, N. (2021). Predict the thermal conductivity of SiO2/water–ethylene glycol (50:50) hybrid nanofluid using artificial neural network. Journal of Thermal Analysis and Calorimetry, 143(2), 1119–1128. [Google Scholar]
57. Tian, S., Arshad, N. I., Toghraie, D., Eftekhari, S. A., Hekmatifar, M. (2021). Using perceptron feed-forward artificial neural network (ANN) for predicting the thermal conductivity of graphene oxide-Al2O3/water-ethylene glycol hybrid nanofluid. Case Studies in Thermal Engineering, 26, 101055. [Google Scholar]
58. Zhang, H., Qing, S., Xu, J., Zhang, X., Zhang, A. (2022). Stability and thermal conductivity of TiO2/water nanofluids: A comparison of the effects of surfactants and surface modification. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 641, 128492. [Google Scholar]
59. Sonawane, S. S., Khedkar, R. S., Wasewar, K. L. (2015). Effect of sonication time on enhancement of effective thermal conductivity of nano TiO2–water, ethylene glycol, and paraffin oil nanofluids and models comparisons. Journal of Experimental Nanoscience, 10(4), 310–322. [Google Scholar]
60. LeCun, Y., Touresky, D., Hinton, G., Sejnowski, T. (1988). A theoretical framework for back-propagation. Proceedings of the 1988 Connectionist Models Summer School, 1, 21–28. [Google Scholar]
61. Hearst, M. A., Dumais, S. T., Osuna, E., Platt, J., Scholkopf, B. (1998). Support vector machines. IEEE Intelligent Systems and their Applications, 13(4), 18–28. https://doi.org/10.1109/5254.708428 [Google Scholar] [CrossRef]
62. Ahmadi, M. A., Ebadi, M., Marghmaleki, P. S., Fouladi, M. M. (2014). Evolving predictive model to determine condensate-to-gas ratio in retrograded condensate gas reservoirs. Fuel, 124, 241–257. https://doi.org/10.1016/j.fuel.2014.01.073 [Google Scholar] [CrossRef]
63. Fazeli, H., Soleimani, R., Ahmadi, M. A., Badrnezhad, R., Mohammadi, A. H. (2013). Experimental study and modeling of ultrafiltration of refinery effluents using a hybrid intelligent approach. Energy & Fuels, 27(6), 3523–3537. https://doi.org/10.1021/ef400179b [Google Scholar] [CrossRef]
64. Maleki, A., Haghighi, A., Mahariq, I. (2021). Machine learning-based approaches for modeling thermophysical properties of hybrid nanofluids: A comprehensive review. Journal of Molecular Liquids, 322, 114843. https://doi.org/10.1016/j.molliq.2020.114843 [Google Scholar] [CrossRef]
65. Gholami, E., Vaferi, B., Ariana, M. A. (2018). Prediction of viscosity of several alumina-based nanofluids using various artificial intelligence paradigms-comparison with experimental data and empirical correlations. Powder Technology, 323, 495–506. https://doi.org/10.1016/j.powtec.2017.10.038 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools