 Open Access
Open Access
ARTICLE
A Comparative Study of Different Drying Processes for a Deformable Saturated Porous Medium
1 Laboratory of Wind Energy Management and Waste Energy Recovery, Research and Technology Center of Energy, Hammam-Lif, Tunisia
2 Laboratory of Studies and Research on Wood Material (LERMAB), University of Lorraine, Longwy, France
3 National Engineering School of Monastir, University of Monastir, Monastir, Tunisia
* Corresponding Author: Nour El Houda Ben Mustaphaa. Email:
(This article belongs to the Special Issue: Materials and Energy an Updated Image for 2021)
Fluid Dynamics & Materials Processing 2023, 19(6), 1339-1348. https://doi.org/10.32604/fdmp.2023.022888
Received 30 March 2022; Accepted 01 September 2022; Issue published 30 January 2023
Abstract
Drying of a deformable saturated porous medium based on convective tempering is a novel method that can enhance energy efficiency and the quality of the dried product itself. In this experimental investigation, the performances of this specific technique are compared with those of a standard stationary drying process in terms of deformation, drying kinetics, moisture redistribution, and energy consumption. In particular, the response of a deformable saturated porous medium (Kaolin) is considered. The results are critically discussed pointing out advantages and drawbacks.Graphic Abstract

Keywords
Nomenclature
| Α | Tempering ratio |
| m0 | Dry weight |
| mt | Sample weight at time t |
| W | Moisture content |
| w0 | Initial moisture content |
| MR | Moisture ratio |
Drying, an essential operation in many industrial sectors plays an important role in many industries and walks of life. According to the nature of the treated products, the drying process can happen under multiple techniques and ways. The drying operation is often done by convection. Stationary convective drying is considered a simple and easy method with good performance. However, it remains an energy-intensive operation, and the process can damage the dried material due to high shrinkage and the generation of excessive stresses [1,2]. In fact, during convective drying, the application of heat is permanently throughout the drying process and the surface moisture content of the dried material becomes too low; therefore, the continuation of drying under the same conditions results in poor product quality, wastage of energy, and hence low efficiency of the drying process [3]. Likewise, the non-uniform moisture content distribution induces stress formation that can cause a material fracture [4]. Therefore, this latter method is considered limited.
It is essential to highlight that one percent of energy savings from drying processes can save more than 10% of total production costs in the industry [4]. Accordingly, several researchers are looking to optimize drying processes and/or strategies to improve the final product’s quality without extending the drying time and increasing energy consumption [5–7]. Developing an efficient and time-saving drying system is a crucial concern for many manufacturers [5,8]. Hence, several new techniques are in development. Tempering drying, a non-stationary process, is one of these novel methods. It is a promising alternative in connection with energy efficiency and product quality without increasing the capital cost of the drier. It is based on periodical changes in drying conditions such as temperature and airflow rate, relative humidity, pressure, and the mode of energy application (convection, conduction, radiation, and microwave) [9,10]. Tempering or intermittent drying involves rest periods to apply heat discontinuously during processes. It allows internal moisture to diffuse to the surface of the material when there is no heating or the heat level is reduced, resulting in a higher drying rate thanks to the redistribution of the moisture content during the cooling period [10]. Likewise, tempering drying is an adaptable and reliable process for drying heat-sensitive products. Many researchers have shown that this process has a prominent effect on drying characteristics, energy consumption, and product quality by reducing drying time and energy consumption [10,11]. During a comparative study of convective drying in stationary and non-stationary conditions, Hammouda et al. [6] showed that non-stationary convective drying (90–60°C) of a porcelain slab is a good alternative that provides a real possibility to optimize costs and quality by reducing the drying time and maintaining Von Mises stress values under the admissible stress. Moreover, a recent study performed by Ben Mustapha et al. [7] showed that tempering drying is more effective than continuous drying based on energy consumption qualifications. A reduction of energy consumption varying from 13% to 67% was achieved. Besides, when using temporary drying, an improvement in the drying time, energy consumption, and product quality is recorded [7]. Moreover, several researchers have adopted different techniques to improve the drying process, such as stationary convective drying enhanced with microwave and infrared drying [3]. Still, these alternatives often involve high investment and operating costs.
The main aim of this work is to achieve an experimental study to monitor the evolution of moisture content, drying rate, and power consumption during different drying modes of a cylindrical kaolin-clay sample. A comparative study was performed to assess the optimized drying process regarding energy consumption. Overall, the drying processes are commonly adopted based on simulation studies considering the high economic and time costs. Nevertheless, few studies were based on experimental data, hence the novelty of this research study.
For all experiments, the samples are prepared at room temperature by mixing the kaolin with different amounts of water. Each sample was cut into a cylindrical piece with a height of 5 mm. The cylindrical kaolin samples, already prepared, had an average weight of 8.9 g and an average initial moisture content (w0) of 0.45 kg/kg d.b.
The experimental setup, used for studying the drying process of kaolin samples by controlling the variation of their weights, temperature, and power at irregular time intervals, is composed of the following instruments:
• A closed-loop convective tunnel drier (Fig. 1) operating totally with electrical energy. It was composed of a tunnel with a horizontal flow, whose dimensions were 1.5 × 0.27 × 0.27 m, a centrifugal fan with a variable velocity ranging from 0.3 to 5 m.s−1, an electrical resistance for air heating, a duct for hot air recirculation, and a command board to adjust air temperature and velocity.
• An electronic balance RADWAG WLC 0.6/B1 (Max: 600 g, Min: 0.5 g, d = 0.01 g) for weighing kaolin samples.
• Power and energy logger PEL 103 provides all the power and energy measurements simultaneously, remotes reading of all the quantities on serval network instruments, and ensures energy cost evaluation.
• Acquisition chain (AGILENT 34970A) connected to a computer through “Agilent technologies” software permitting the measurement of the sample and drying air temperatures from K-type thermocouples.

Figure 1: Schematic view of the drying system (1: Control of electrical power; 2: Pump; 3: Heather; 4, 5: Thermocouple of type K; 6: Energy meter; 7: Sample; 8: Acquisition chain; 9: Digital scale; 10: Computer)
Two cylindrical kaolin samples were put on supports and placed in the dryer that was maintained at the desired temperature (from 45°C to 70°C). Drying of Kaolin samples was carried out under stationary and intermittent conditions until reaching a constant weight. At the end of the experiment, samples were placed in an oven at 105°C for about 24 h to obtain their dry weights ( m0 ). By using an electronic balance (9 in Fig. 1) connected to a computer through “Pomiar Win” software, it was possible to measure the sample weight at fixed times (2 s). Moisture content (Mc) values (Eq. (1)) were determined based on the dry weight of the sample ( m0 ) and its weight at a given time t ( mt ). Accordingly, the evolution of water content in the sample is monitored through moisture content evolution. On the other hand, measuring sample and drying air temperatures was performed using four K-type thermocouples related to an acquisition chain (AGILENT 34970A) connected to a computer through “Agilent technologies” software.
The moisture content (w) values were determined as follows (Eq. (1)):
w=mt−m0m0 (1)
where m0 and mt are the dry weight of the sample and its weight at a given time t, respectively.
The moisture ratio (MR) was given by Eq. (2):
MR=ww0 (2)
where w0 and w are the moisture content of the sample initially and at a given time t, respectively.
2.3 Characterization of the Dried Product Quality
Microscopic image observation of dried products was performed using a digital processing unit composed of a conventional optical microscope (of type Zeiss Stemi 2000-C Stereo: Zoom Range: 6.5x− 50x), a camera, and a PC/Notebook.
3.1 Drying in Constant Conditions
In this part of the study, the stationary convective drying of the kaolin samples is performed. The effect of temperature on moisture ratio and power consumption was evaluated. The tested drying air temperatures ranged from 45 to 70°C. The evolution of the drying curve and moisture ratio is presented in Figs. 2 and 3, respectively.
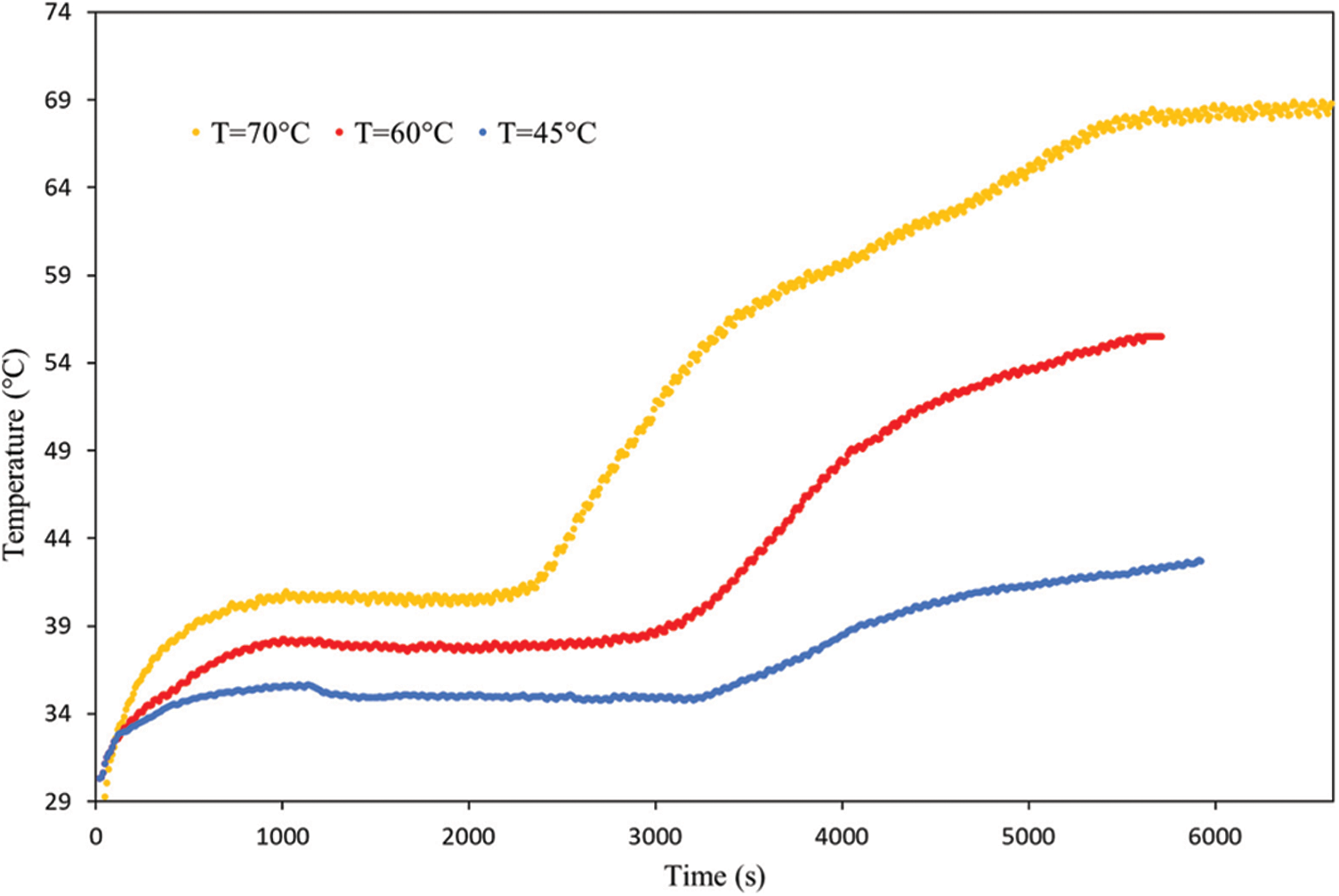
Figure 2: Evolution of the sample temperature vs. drying time at different drying air temperatures
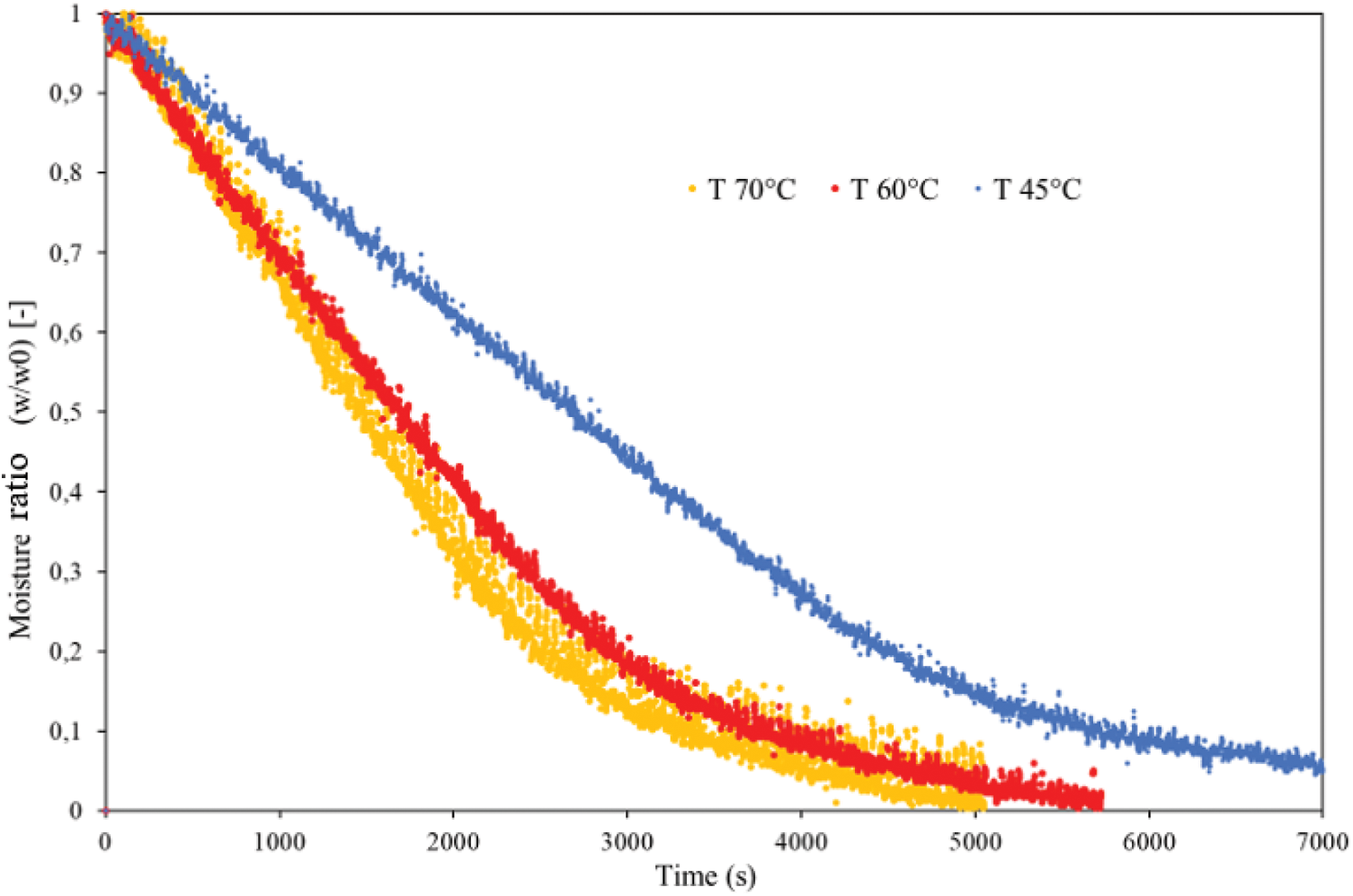
Figure 3: Effect of drying air temperature on the moisture ratio of Kaolin samples
As shown in Fig. 2, there are three classical phases during the convective drying process, whatever the drying air temperatures. At the beginning of the drying operation, the Kaolin sample temperature regularly rises until it reaches the wet bulb temperature of 35°C, 37°C, and 39°C, for the drying air temperatures of 45°C, 60°C, and 70°C, respectively. This corresponds to the preheating stage, where the kaolin sample is completely saturated. Accordingly, the moisture ratio, as shown in Fig. 3, is slowly decreasing. In the second phase, the drying rate is constant, and the water molecules move towards the surface of the kaolin sample by capillary forces to gradually evaporate. The heat exchange is mainly performed by water vaporizing on the material surface, which corresponds to an isenthalpic phase. Hence, the moisture ratio evolution follows a linear decrease (Fig. 3). When the material reaches equilibrium, it immediately enters a hygroscopic range, and the internal water vapor diffusion controls the drying process. As a result, the temperature rises quickly to attend to the drying air temperature. The same observations have been reported by Ben Abdelhamid et al. [11] during their numerical study of the effect of different drying conditions on the induced stresses within a deformable media (bentonite) during stationary and intermittent drying.
Moreover, it is clear from Fig. 3 that the temperature of the drying air has a significant influence on the drying time. Indeed, the comparison of curves shows that the drying time decreases by increasing the drying air temperature. In fact, at 70°C, the drying time is assessed as 5000 s, whereas it is equal to 7000 s at 45°C.
The variation of energy consumption during stationary convective drying at different drying air temperatures is presented in Fig. 4. According to this Figure, it is clear that the evolution of the power consumption depends strongly on the applied temperature and the drying time. In fact, after 40 min, the drier consumes at 45°C, 60°C, and 70°C 1100, 1600, and 2000 W, respectively, which confirms that the increase in temperature causes an increase in energy consumption. This result confirms that it is necessary to act on drying air temperature to reduce energy consumption.
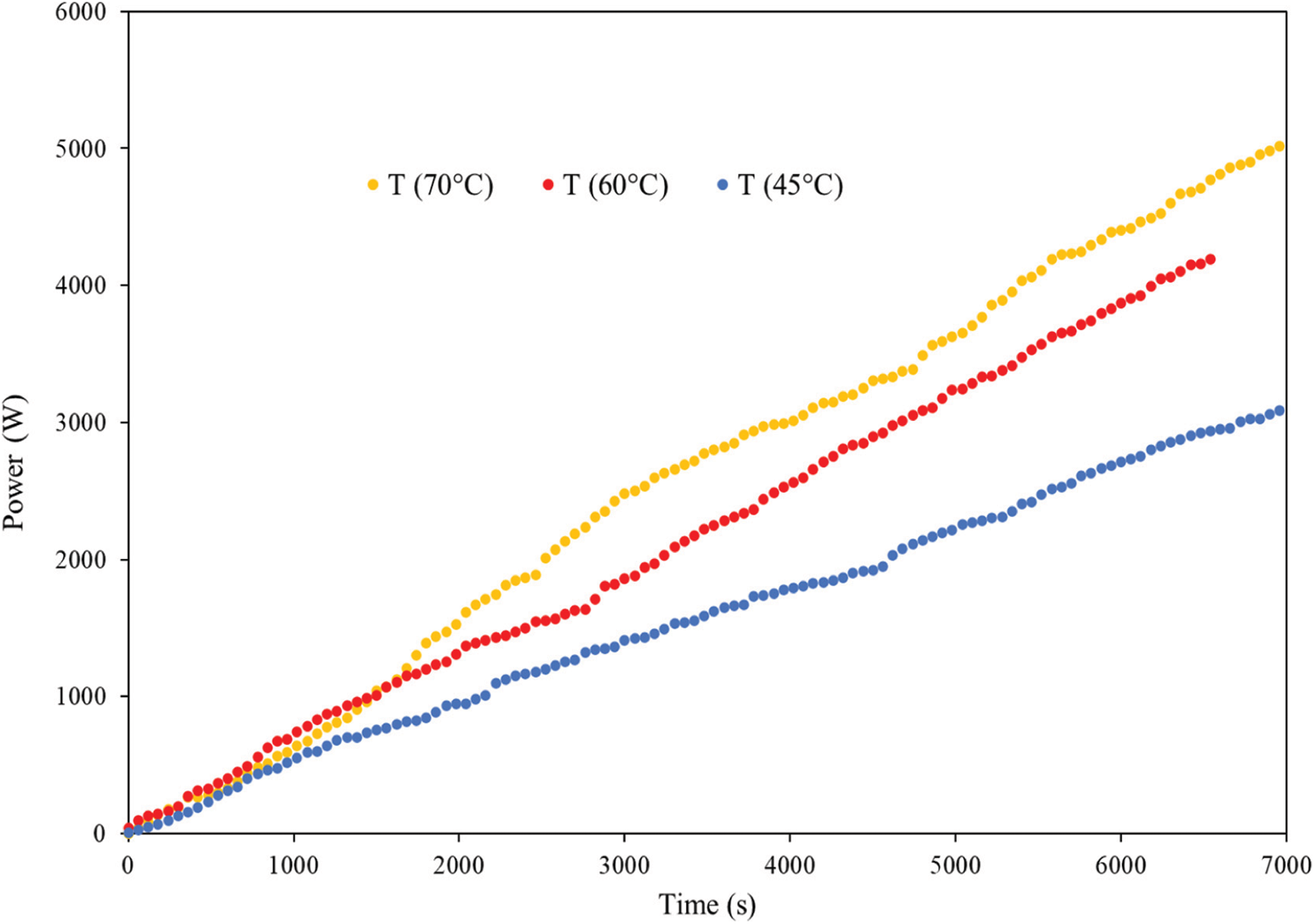
Figure 4: Effect of drying air temperature on power consumption
3.2 Drying in Tempering Conditions
In the second part of this study, tempering convective drying at periodically changed drying air temperatures between 65°C and 20°C was performed. The purpose of tempering is to control the moisture distribution in the dried products at three different tempering ratios to improve the drying efficiency and product quality. Since tempering drying is associated with modifying drying conditions, it was decided to apply an alternating cooling cycle. Accordingly, a progressive change in the air temperature period (heating and cooling periods) was performed. The tempering ratio, referred to as α, is expressed by Eq. (3).
α= Time of heating Total drying time (3)
Different tempering ratios were adopted namely 5 min heating and 25 min cooling (α = 0.16), 10 min heating and 20 min cooling (α = 0.33), and 15 min heating and 15 min cooling (α = 0.5). During all the experiments, the total drying period was fixed at 30 min, and the drying air temperature was between 20°C and 65°C.
The variation of the moisture ratio and the product temperature vs. time at different tempering ratios is illustrated in Fig. 5. According to Fig. 5a, the moisture content of the product during 5 min (α = 0.16), 10min (α = 0.33), and 15 min (α = 0.5) of heating are 0.41, 0.35, and 0.36, respectively. Consequently, the tempering drying at different moisture content will affect the total drying time and the product quality. The alternated increase in tempering ratio causes a significant variation in the temperature and the drying rate. When the tempering ratio increases, the heating time rises, leading to a faster drying rate and a great variation in the temperature of the kaolin samples to attend to the drying air temperature. The drying curve presents a session of stationary drying for the different drying periods. The maximum drying rate is achieved during the heating period but decreases with drying time. The drying rate is improved after the tempering period, demonstrating the benefits of allowing moisture redistribution. The drying curves showed that when the tempering ratio is equal to 0.5, the drying process is more profitable than for α = 0.16 and α = 0.33. This phenomenon can probably be explained by the cooling time effect and the moisture profile distribution in the sample. For the tempering ratio of 0.5, the moisture profile seems to be more uniform due to the high heating period. Afterward, moisture redistribution during the resting of material (15 min of cooling time) leads to a faster drying rate. In fact, during the cooling time, the internal moisture is allowed to be diffused from the inner to the surface of the material resulting in a higher drying rate thanks to the redistribution of the moisture content. Furthermore, it is clearly seen in Fig. 5a that increasing the tempering ratio from 0.16 to 0.5 leads to the reduction of the drying time [12]. Likewise, when the tempering ratio is increased, the frequency and amplitude of swings are also increased (Fig. 5b). Compared to the stationary convective drying process, the kinetics using the intermittent mode has been reduced. Accordingly, the drying rate during the intermittent mode is minimized to develop moisture homogeneity, and, therefore, avoid material damage. The same findings have been reported by Kowalski et al. [13]. They have proved experimentally that the quality of the dried kaolin samples depends significantly on the frequency and amplitude of the air temperature and relative humidity variation during the drying process.
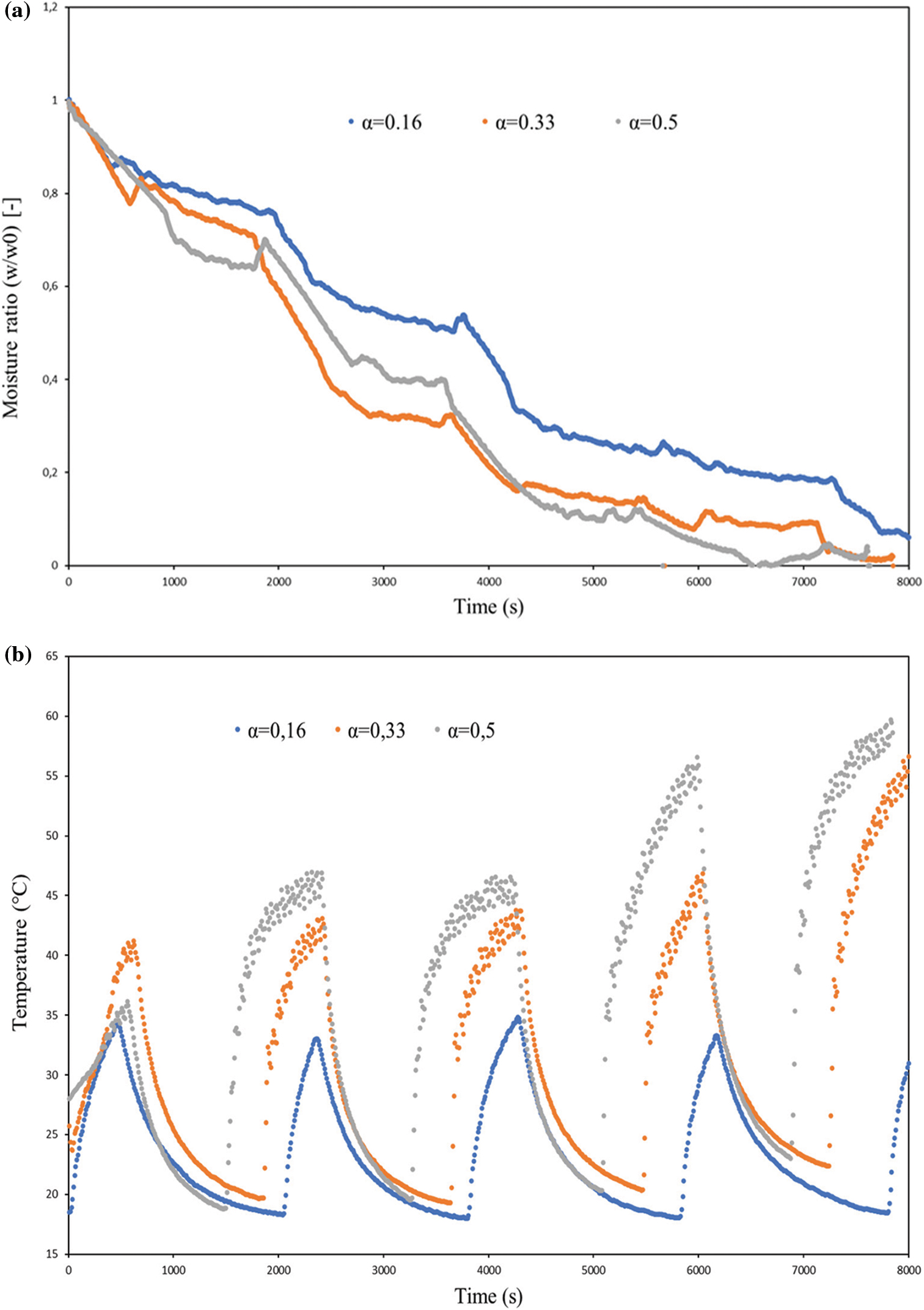
Figure 5: Effect of tempering ratio on the evolution of (a) moisture ratio and (b) product temperature
Fig. 6 shows that power consumption is very low whatever the applied tempering ratio. As regarded with the energy consumption attributed to the stationary convective drying process, the tempering mode is more efficient. During the intermittent drying process, results point out that the best tempering ratio for energy savings is 0.16. After 45 min of intermittent drying, the percent energy consumption saved over stationary drying is assessed as 62%.
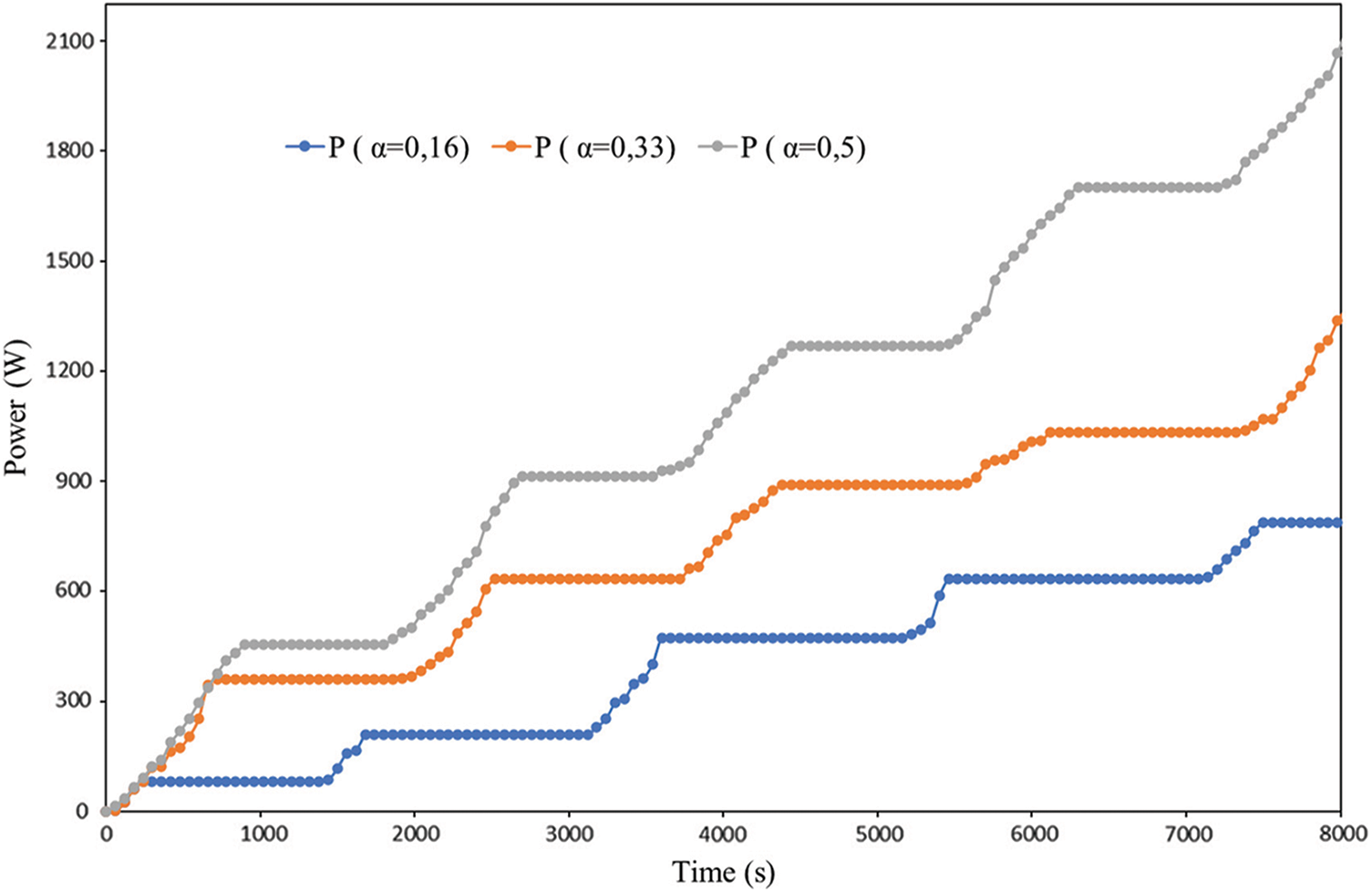
Figure 6: Effect of tempering ratio on power consumption during the tempering drying process
3.3 Comparative Study between Stationary and Tempering Convective Drying Processes
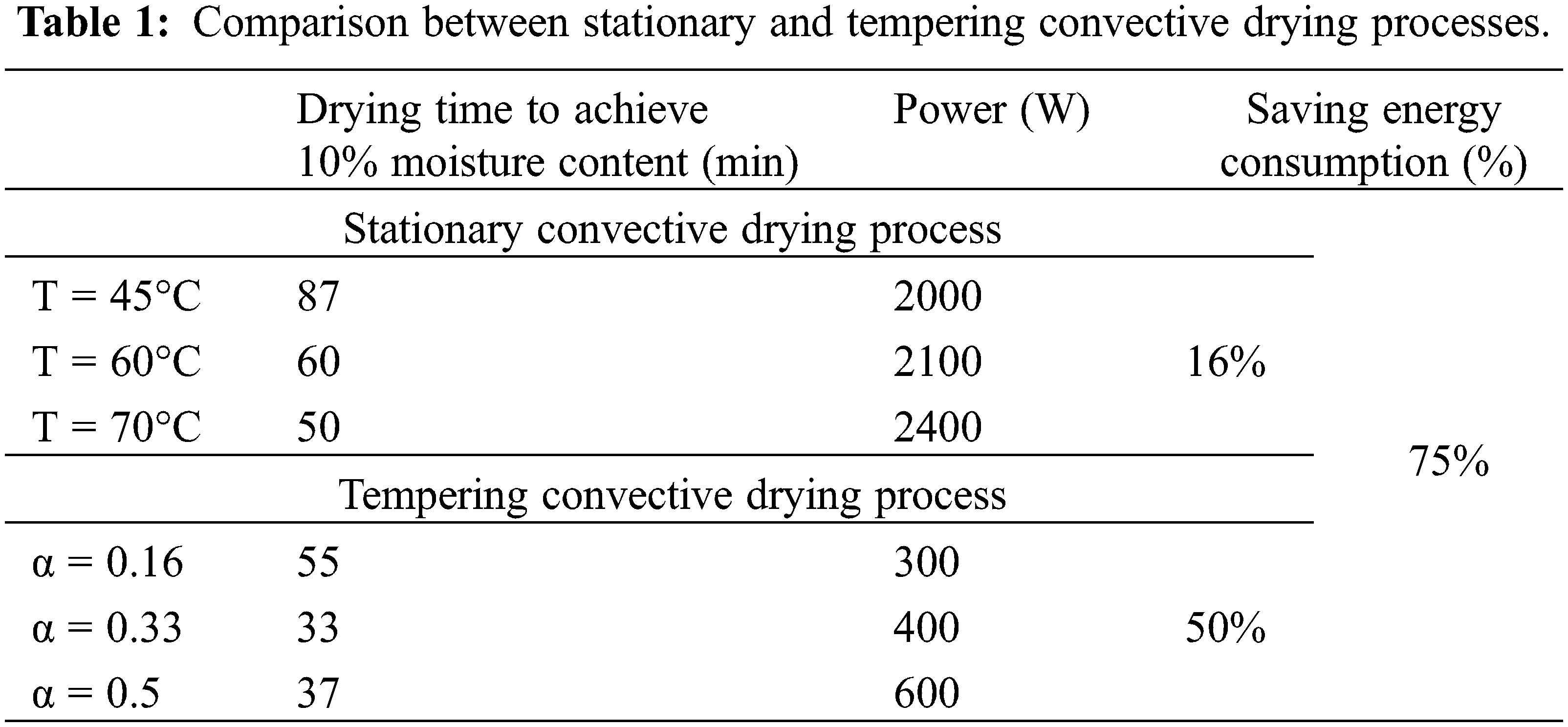
Table 1 shows the effect of drying mode (stationary or intermittent) on power consumption. This table reveals that the power consumption is reduced from 2400 W for stationary drying mode at 70°C up to 600 W for tempering drying process at a tempering ratio of 0.5 [14].
Using the optical microscope, selected images of the final products dried according to the stationary and intermittent process (α = 0.5) at a drying air temperature of 80°C were used to confirm the final product quality (Fig. 7). As shown in this Figure, the stationary drying mode involves lateral and surfaced material cracking. On the other hand, intermittent drying at a tempering ratio of 0.5 provides a smooth and compact product without any crack formation. Moreover, it is worth noting that whatever the applied drying mode, the color of the final product was not modified. These latter observations show that the tempering convective drying appears to contribute to improving the dried product quality.

Figure 7: Microscopic images of (a) sample before drying (b) stationary drying product and (c) tempering convective drying product
In this paper, an experimental study has been carried out to monitor the evolution of water content and energy consumption during stationary and tempering convective drying modes. A logical evolution of drying kinetics was obtained at the tested temperatures. Drying air temperature has a significant influence on the drying time. Moreover, it has been shown that the power consumption during stationary convective drying depends strongly on the applied temperature. In fact, after 40 min, the drier consumption at 45°C, 60°C, and 70°C was at 1100, 1600, and 2000 W, respectively. On the other hand, the alternated increase in tempering ratio causes a significant variation in the drying rate. The drying curves showed that when the tempering ratio is equal to 0.5, the drying process is more profitable than for α = 0.16 and α = 0.33. This finding can be explained probably by the cooling time effect and water distribution in the sample. The drying in tempering conditions reduces the energy consumption from 2400 W during the stationary drying mode at 70°C up to 600 W in the tempering drying process at a tempering ratio of 0.5.
Acknowledgement: The authors acknowledge the financial support of the Ministry of Higher Education (TUNISIA) and Professor Hassen Abdallah from the Energy Research and Technology Center (CRTEn, Hammam-Lif, Tunisia) for providing the digital processing units used to perform the microscopic image observation.
Funding Statement: The authors have received financial support from the Ministry of Higher Education (TUNISIA).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Mujumdar, A. S. (2006). Handbook of industrial drying. Third Edition. Boca Raton, USA: Taylor & Francis Group, LLC, CRC. [Google Scholar]
2. Putranto, A., Chen, X. D., Devahastin, S., Xiao, Z., Web, P. A. (2011). Application of the reaction engineering approach (REA) for modeling intermittent drying under time-varying humidity and temperature. Chemical Engineering Science, 66(10), 2149–2156. DOI 10.1016/j.ces.2011.02.025. [Google Scholar] [CrossRef]
3. Kumar, C., Karim, M. A., Joaddar, M. U. H. (2014). Intermittent drying of food products: A critical review. Journal of Food Engineering, 121(7–8), 48–57. DOI 10.1016/j.jfoodeng.2013.08.014. [Google Scholar] [CrossRef]
4. Salin, J. G. (2003). A theoretical analysis of timber drying in oscillating climates. Holzforschung, 57(4), 427–432. DOI 10.1515/HF.2003.063. [Google Scholar] [CrossRef]
5. Beedie, M. (1995). Energy saving a question of quality. Dairy Industries International, 60(12), 27. [Google Scholar]
6. Hammouda, I., Mihoubi, D. (2017). Influence of stationary and non-stationary conditions on drying time and mechanical properties of a porcelain slab. Heat and Mass Transfer, 53(12), 3571–3580. DOI 10.1007/s00231-017-2084-6. [Google Scholar] [CrossRef]
7. Ben Mustapha, N., Boumnijel, I., Mihoubi, D. (2022). Tempering drying and energy consumption. Journal of Heat Transfer, 144(10), 102103. DOI 10.1115/1.4055045. [Google Scholar] [CrossRef]
8. Glouannec, P., Lecharpentier, D., Noel, H. (2002). Experimental survey on the combination of radiating infrared and microwave sources for the drying of porous material. Applied Thermal Engineering, 22(15), 1689–1703. DOI 10.1016/S1359-4311(02)00071-6. [Google Scholar] [CrossRef]
9. Berk, Z. (2009). Dehydration. In: Food process engineering and technology, pp. 459–510. DOI 10.1016/b978-0-12-373660-4.00022-3. [Google Scholar] [CrossRef]
10. Kowalski, S. J., Pawłowski, A. (2011). Energy consumption and quality aspect by intermittent drying. Chemical Engineering and Processing: Process Intensification, 50(4), 384–390. DOI 10.1016/j.cep.2011.02.012. [Google Scholar] [CrossRef]
11. Manel, B. A., Mihoubi, D., Jalila, S., Ahmed, B. (2014). Strain-stress formation during stationary and intermittent drying of deformable media. Drying Technology, 32(10), 1245–1255. DOI 10.1080/07373937.2014.899246. [Google Scholar] [CrossRef]
12. Chin, S. K., Law, C. L. (2010). Product quality and drying characteristics of intermittent heat pump drying of Ganoderma tsugae murrill. Drying Technology, 28(12), 1457–1465. DOI 10.1080/07373937.2010.482707. [Google Scholar] [CrossRef]
13. Kowalski, S. J., Szadzińska, J. (2012). Non-stationary drying of ceramic-like materials controlled through acoustic emission method. Heat and Mass Transfer, 48(12), 2023–2032. DOI 10.1007/s00231-012-1042-6. [Google Scholar] [CrossRef]
14. Putranto, A., Chen, X. D., Devahastin, S., Xiao, Z., Webley, P. A. (2011). Application of the reaction engineering approach (REA) for modeling intermittent drying under time-varying humidity and temperature. Chemical Engineering Science, 66(10), 2149–2156. DOI 10.1016/j.ces.2011.02.025. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
