A Study on the Physical Properties of Banana Straw Based on the Discrete Element Method

1  Introduction

Secondary utilisation of banana straw substrate is of great significance to green development across the world. Crushing it as feed is a primary utilization means [1]. Establishing a physical model of banana straw plays a significant guiding role in the design process of the banana straw crusher itself. The discrete element method (DEM) is the primary method to establish the physical model of agricultural plants with [2], and the calibration process of a large number of unknown parameters in DEM significantly influences the accuracy of simulation experiments under crushing conditions.

Because there will be some errors between the intrinsic parameters of the actual material and the granular material in the DEM, the intrinsic parameters of the actual material can be approximated by parameter calibration [3]. Shen et al. [4] measured the inherent parameters of sweet potatoes by a compression experiment and studied the axial and radial mechanical properties of sweet potatoes at different compression rates. Luo et al. [5] carried out bending, axial, and radial compression experiments on straw and obtained the relationship between wheat straw compression characteristics and moisture content. Zhang et al. [6] reduced the millet stalk’s cutting force and power consumption by single factor and response surface experiments. There will be a lot of collisions between different materials in the crushing condition, which requires high basic contact parameters of the discrete element model. Cui et al. [7] measured the rolling friction coefficient between corn seeds and other materials by high-speed camera technology and verified the feasibility of the parameters by comparing the repose angle experiment with the simulation results. Hao et al. [8] determined the optimal combination of the static friction coefficient and dynamic friction coefficient among oil sunflower seeds through a response surface optimisation experiment and proved the reliability of the parameters through experiments. The contact model in EDEM can characterise the special contact characteristics between materials. Because the required parameters are modelled and abstract, it is difficult to calculate with the actual material parameters. A complicated calibration process is required actual to determine the contact model parameters. Kovács et al. [9,10] used a variety of particle types to establish discrete element models for different parts of the outer epidermis of corn straw and set other bond parameters to characterise the mechanical relationship between straw fibres, thus realising the natural stress of the fibre structure when cutting materials by cutter. Zhang et al. [11] checked the bonding parameters of the discrete element model of corn straw through compression and shear experiments and compared the crushing results with the experiments, verifying the accuracy of the DEM used in the simulation of the crushing process of straw shredding. The contact model is often used to consider only a single mechanical relationship between particles, and it is difficult to reproduce the actual physical characteristics. Previous studies show that the accuracy of the discrete element model is mainly affected by the reduction degree of the actual structure of crops; and the rationality of the calibration process of a large number of unknown parameters in the discrete element model.

The current research on the DEM of crops focuses on seeds and solid or hollow straws. Still, there is little research on the complex discrete element model of banana straws, including fibre structure, porous structure, and leaf sheath coating structure. Most of the current studies tend to ignore the structure of the material and oversimplify the actual structural characteristics by simple particle stacking, so much so, that the bonding model cannot express the mechanical relationship between the actual structure of the material, and the simplified discrete element model is difficult to be useful in the mechanical design. Based on previous studies of other crops, aiming at the complex mechanical characteristics caused by the actual structure of banana straw, this paper implemented a discrete element model to reduce the complex physical features of banana straw by using the API interface of EDEM software. It characterized the mechanical relationship among different structures of banana straw and viscosity characteristics by using the particle aggregating bonding model and the particle surface energy contact model.

2  Establishment of Discrete Element Model

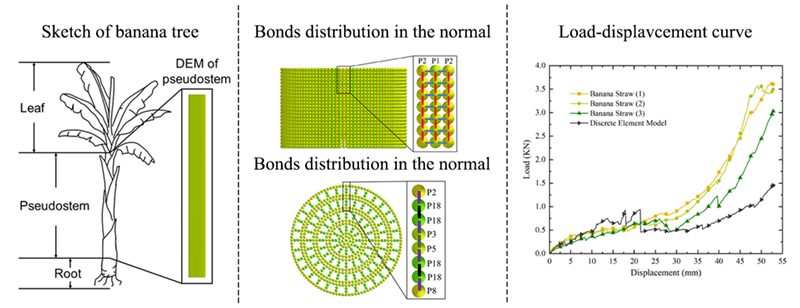
Banana straws from Honghe Prefecture, Yunnan Province, in harvest season were selected as the experimental object. Banana trees can be divided into leaves, pseudostems, and roots, as shown in Fig. 1. Pseudostems are used as the main object of consideration in this paper. The appearance of the banana straw was approximately cylindrical. Considering its necessary structural characteristics, therefore, the thickness change of the leaf sheath coating was ignored.

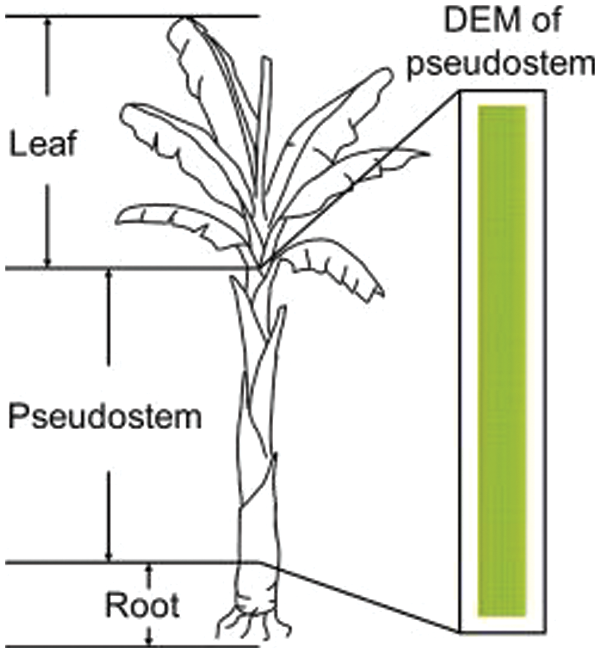
Figure 1: Sketch of banana tree

Considering the complex structure characteristics of banana straw, EDEM software was used to establish a banana straw discrete element model with particles having a size of 0.95 mm [12]. The internal porous structure of banana straw was characterised by combining one layer closely arranged particles and four layers of particles with voids. In the radial direction, it was composed of 18 layers of particles with a cross-sectional radius of 36 mm. Every four radial layers of particles represented a layer of leaf sheath coating structure of banana straw. The complete banana straw discrete element model consists of 400 layers of particles in the axial direction, with a length of 760 mm. The structural characteristics of the banana straw discrete element model are shown in Fig. 2.

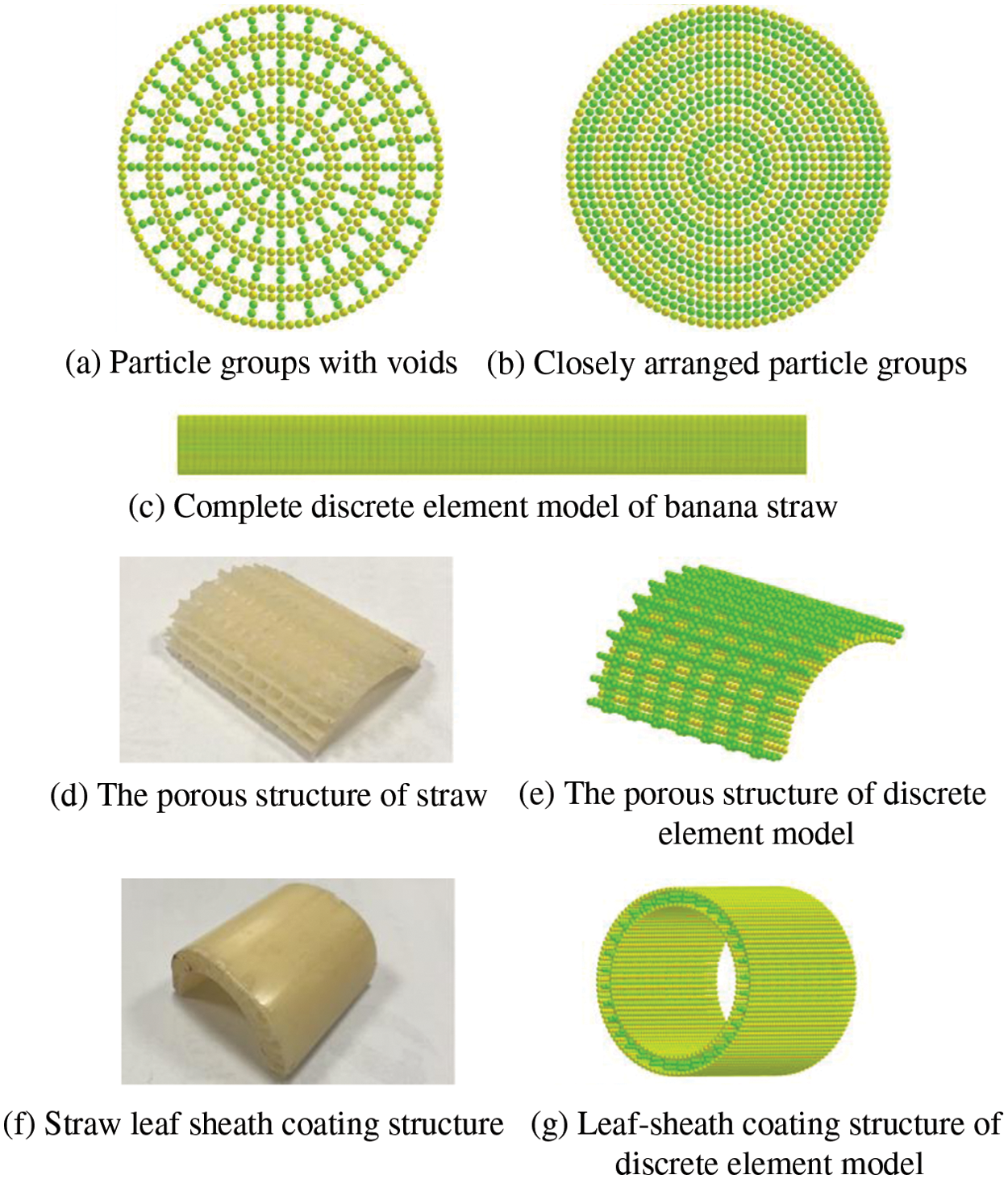
Figure 2: Banana straw discrete element model

To meet the mechanical characteristics among different structures of banana straw, the particles were divided into 18 types. The results of particle division are shown in Fig. 3, where P1-P17 represents the particles that make up the inner and outer epidermis of each layer of leaf sheath coating structure, and P18 represents the particles that make up the porous structure inside the banana straw.

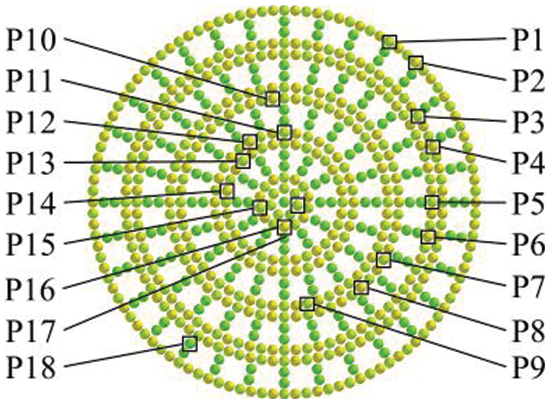
Figure 3: Particle type division

The particles representing different structures were differentiated according to the actual physical properties of banana straw. To properly represent the leaf sheath coating structure of banana straw, a distinction was made between the particles adjacent to the inner and outer skin of the cladding layer. In order to reflect the differences between the leaf sheath coating structure, the particles that make up each leaf sheath coating structure were divided. P18 represents the porous structure to distinguish the internal structure from the external structure.

3  Particle Parameter Experiment

3.1 Experiment of Intrinsic Parameters and Basic Contact Parameters of Particles

There are a lot of unknown material parameters in the particles that make up the physical model of banana straw.

The elastic modulus of banana straw was 3.447 Mpa [13], measured by a compression experiment. The Poisson’s ratio of banana straws was 0.4 [14]; the density of three groups of banana straws was measured by the buoyancy method [15], and the average result was 552.158 Kg·m−3. The particle density was 1647.259 Kg·m−3, calculated by the relationship between the total volume and the total mass of the particles in the discrete element model, and the densities of the different structures of banana straw were measured separately, and the results are shown in Table 1.

The inclined plane sliding experiment measured the dynamic friction coefficient, and the dynamic friction coefficient between banana straw and a Q235 steel plate was 0.00192 and 0.00321, respectively. An inclined plane slip experiment measured the static friction coefficient. The static friction coefficient between banana straw and a Q235 steel plate was 0.579 and 0.768, respectively. The inclined plate collision experiment measured the recovery coefficient, and the recovery coefficient between banana straws and a Q235 steel plate was 0.437 and 0.487, respectively. The experiment process of basic contact parameters of actual materials is shown in Fig. 4.

Figure 4: Experiment on basic contact parameters of materials

3.2 Parameter Experiment of Particle Contact Model

Particles were bonded by particle aggregating bonding model. The model endows certain mechanical relationships between particles [16–19]. According to the real mechanical characteristics of banana straw, the bonds were classified into five types: representing axial interparticles of fiber structure, representing radial interparticles of fiber structure, representing interparticles of porous structure particles, and inner and outer epidermis particles, representing interparticles of porous structure particles, and representing interparticles of contact particles of each leaf sheath coating layer.

The particle bonding model imparts certain mechanical properties to the particles to resist the tangential and normal relative motion between them. After the bond of the particle is generated, with the initial values of force (Fn,t) = 0 and torque (Tn,t) = 0. Iterate in each period according to Eq. (1) until the maximum normal, and tangential shear stresses set in the model are reached.

δFn=−vnSnAδtδFt=−vtStAδtδMn=−ωnStJδtδMt=−ωnSnJ2δtJ=12πRB4 (1)

A——Cross-sectional area of the bond

RB——Radius of the bond

Sn,t——Normal stiffness and shear stiffness

δ t——Timestep

νn,t——Velocity in the normal and tangential directions of the particles

ωn,t——Angular velocity in the normal and tangential directions of the particle

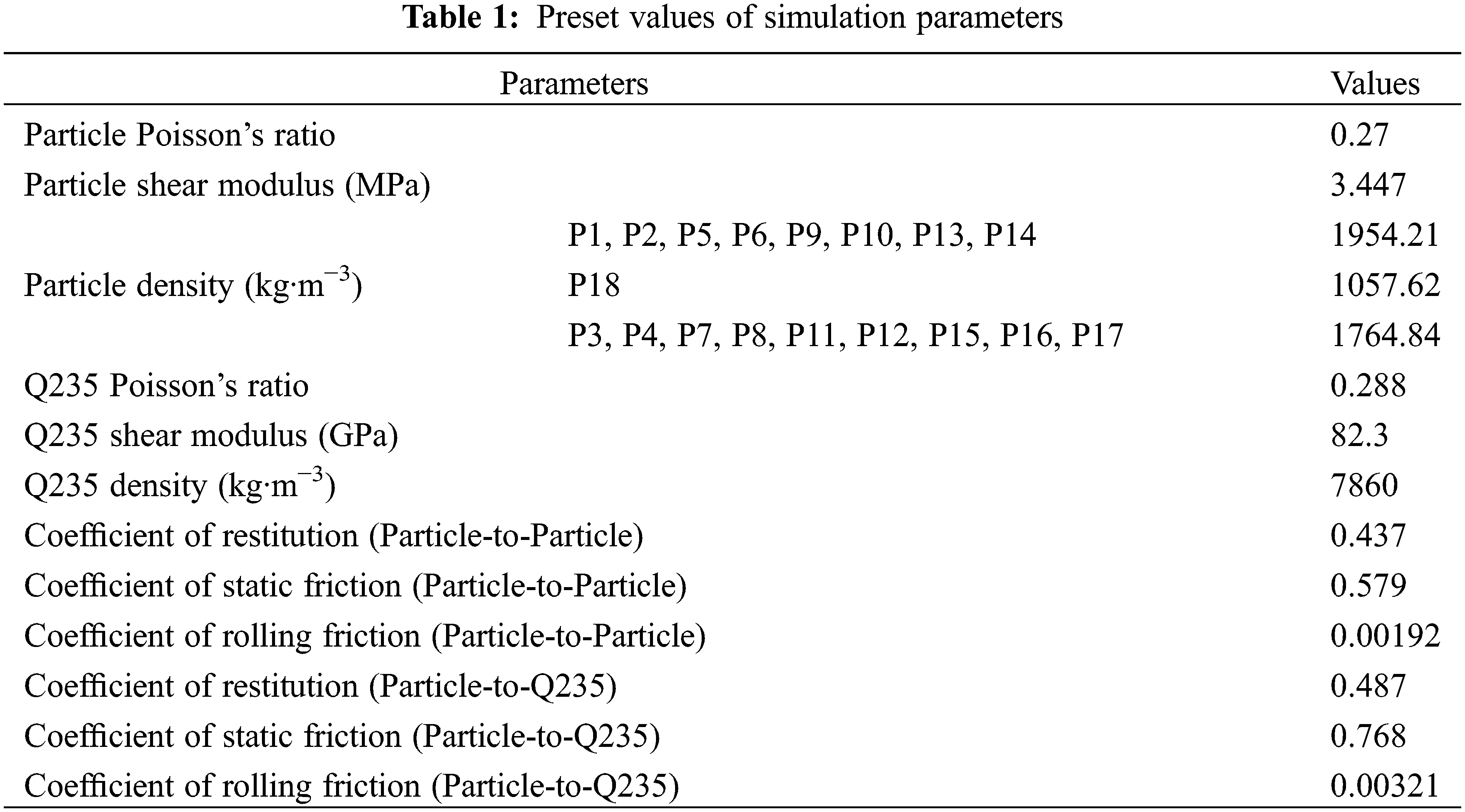
Fig. 5 shows the distribution of axial particles and particle bonds of banana straw, in which the inner and outer epidermis particles of each leaf sheath coating layer are divided into two types. The red bond is the axial bonding force of fibers, and the blue bond is the bonding force between adjacent fibers. The bonding force represented by the red bond is larger than that represented by the blue bond to characterize the fiber structure of banana straw. The closer the coating particles are to the radial center, the water content gradually increases, and the bonding force gradually decreases.

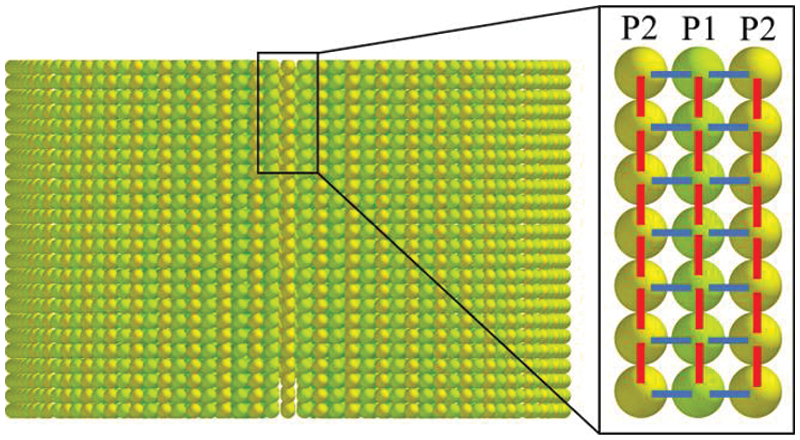
Figure 5: Particle bonds in the axial direction

Fig. 6 shows the distribution of radial particles and bonds of banana straw. Light green and yellow particles represent the inner and outer epidermis parts of each coating layer of banana straw. Green particles represent the inner porous structure of banana straw; grey bond represents the bonding force between the sheaths, and black bond represents the bonding force between the porous structures of banana straw. The purple bond represents the bonding force between the inner and outer epidermis of banana straw and the inner porous structures. According to the actual mechanical relationship, the bonding force of the purple bond is greater than that of the black bond, and the bonding force of the black bond is greater than that of the gray bond.

Figure 6: Particle bonds in the radial direction

According to the results of the bench experiments and the calibration of the simulation experiments, the preset values of the simulation parameters are shown in Table 1.

Bond parameters were calibrated by crush experiment. The experiment results are shown in Fig. 7. The physical and simulation experiments were compared and analyzed at three points. At 10 s, the coating layers began to separate. In the 20 s, the coating layers broke axially, and in the 30 s, the whole structure collapsed. According to Fig. 7c, the force situation of bonds is close to the actual one; the closer the bonds in the middle are, the greater the force is, and they fracture gradually at the location where the force is concentrated, the bonds between the cladding layers are the first to fracture, followed by the axial fracture of the cladding layers on both sides. Comparing the EDEM simulation results with the physical experiment, the particle status, and bond fracture at each time point were in good agreement with the physical experiment, proving the feasibility of the discrete element model. The load-displacement curve obtained by physical experiment and EDEM simulation is shown in Fig. 8.

Figure 7: Comparison of crush experiments and simulation results

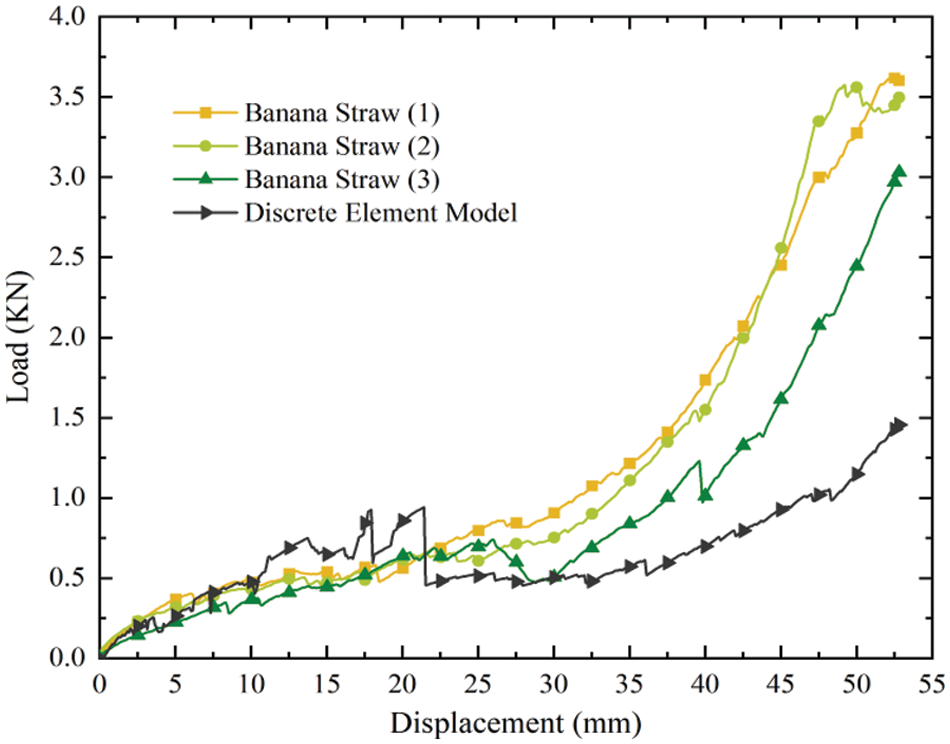
Figure 8: Load-displacement curve

In Fig. 7c, the stress relation of bonds is: blue < green < red. For bonds of the same color, the larger the diameter of the bond, the greater the stress.

The parameters of bonds are calibrated according to the correspondence between the parameters of the bonding model and the banana straw. Where the normal and shear stiffnesses represent the ability of two particles connected by a bond to resist elastic deformation in the normal and shear directions, respectively when subjected to force. The critical normal stress and critical shear stress indicate the maximum normal stress and shear stress that the bond between two particles can withstand, respectively. Bond radius is related to the extension between the two particles. The parameters of the bonding model were calibrated by adjusting the parameters of the bonding model and comparing the change in the appearance of the particle groups and the Load-displacement curve between the crush experiment and the simulation experiment.

By comparing the physical experiment results and simulation results, the mechanical performance and load-displacement curve of the discrete element model under the action of particle bonds were close to the actual situation, the four curves show an overall upward trend, and all show a sharp drop in load at some locations, corresponding to the fracture of the enveloping structure along the weak fibers. Proving the feasibility of bond parameters and the discrete element model itself. At the same time, a large number of bonds also realized the complex mechanical relationship in the actual structure. The bond parameters calibrated by parameters are shown in Table 2.

Group A in Table 1 denotes the reactive bonds sets that make up the particle axes of each fibrous structure, group B denotes the reactive bonds sets that connect each fibrous structure, group C denotes the reactive bonds sets that connect the inner and outer epidermis of the leaf sheath cladding structure to the inner porous structure of the discrete metamodel, and group D denotes the reactive bonds sets that connect each layer of the leaf sheath cladding structure.

Agricultural materials tend to be anisotropic. The characterization of special structures and the stresses between different structures during the crushing of banana straw can be achieved through the division of particles and bonds. Accurate numerical simulations allow for better application of discrete element models in the mechanical design process.

In the actual situation, banana straw has certain viscosity characteristics after being crushed. Thus, certain surface energy was applied to the particles through the particle surface energy contact model to simulate the viscosity characteristics of crushed materials in the actual situation [20–23].

Ball screw structure and Arduino control panel were used to make a cylinder lifting device, as shown in Fig. 9. The crushed materials of banana straws were subjected to a cylinder lifting experiment to get the crushed materials piles under natural accumulation. Three photos of the materials piles were taken at an included angle of 120°, respectively. Photoshop was used to extract the boundary and grayscale of the photos, and then the data points were manually selected by Origin’s image digitization tool. The data points were linearly fitted to obtain six groups of linear fitting equations of contour lines and corresponding stacking angles, as shown in Fig. 10. The calculated average stacking angle of the physical experiment was 29.156° (all the experiment results in this paper retain three significant figures).

Figure 9: Cylinder lifting device. 1. Motor 2. Rack 3. Ball screws 4. Tube 5. Placement table for materials 6. Control panel

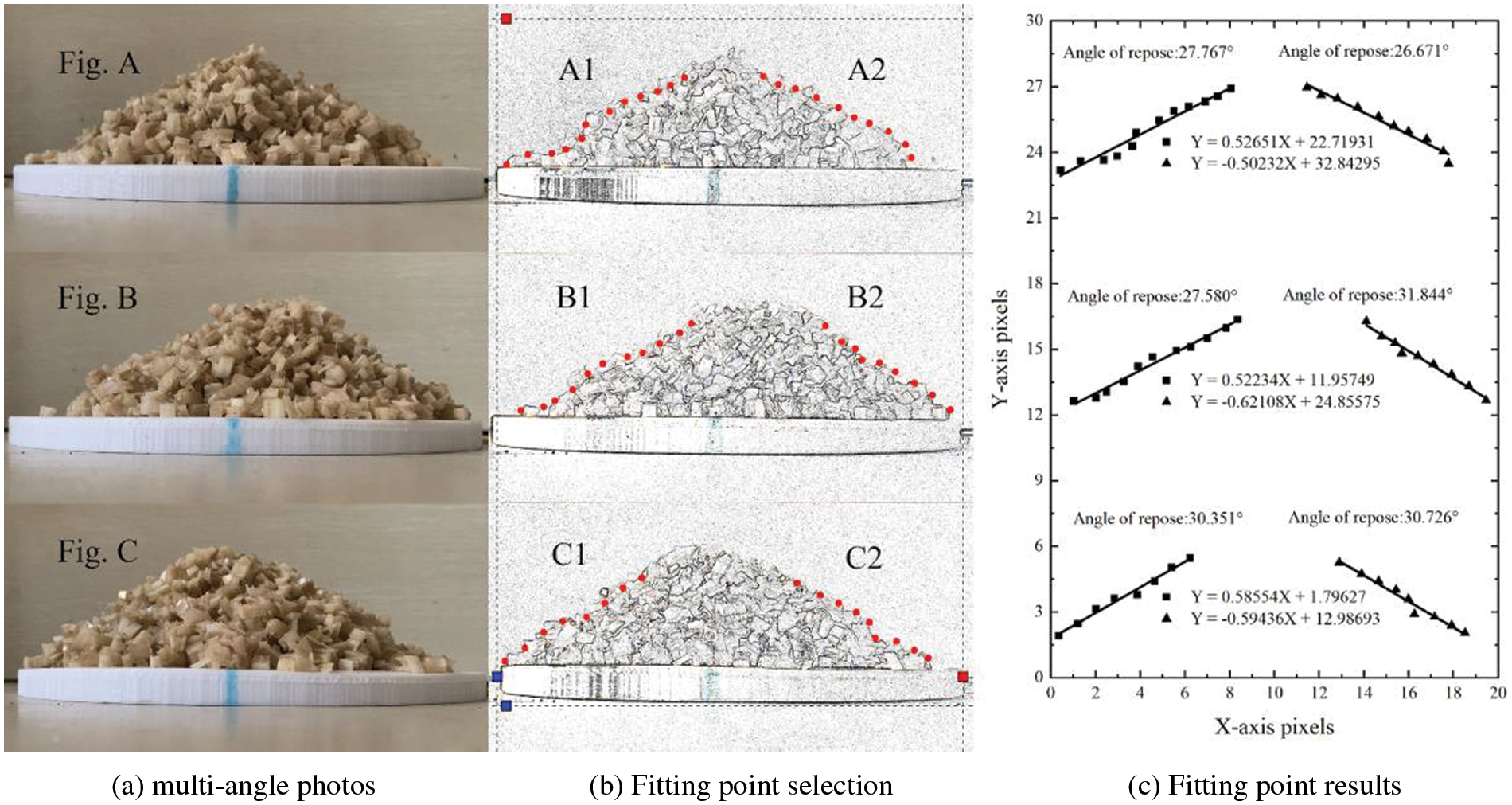
Figure 10: Experimental results of material accumulation angle

4  Single Factor Experiment Design

In EDEM, the same simulation environment as the cylinder lifting experiment was established. The JKR surface energy experimented with a single factor with the initial value of 0 J·m−2 and the step size of 0.1 J·m−2. The rest particle parameters were measured by physical experiment.

In the Python development environment, the third-party library EDEMPy was called to identify the simulation file information, and the material pile’s particle configuration information and coordinate parameters were obtained. Numpy was called to process the particle data, and the radial measurement slices of the particle material pile were made at an interval of 60°. The average of each slice angle was used as the stacking angle result of the cylinder lifting simulation experiment. The results of the JKR surface energy single factor experiment are shown in Table 3. Matplotlib was used to draw three-dimensional images of particles, sampling points, and linear fitting results, as shown in Fig. 11.

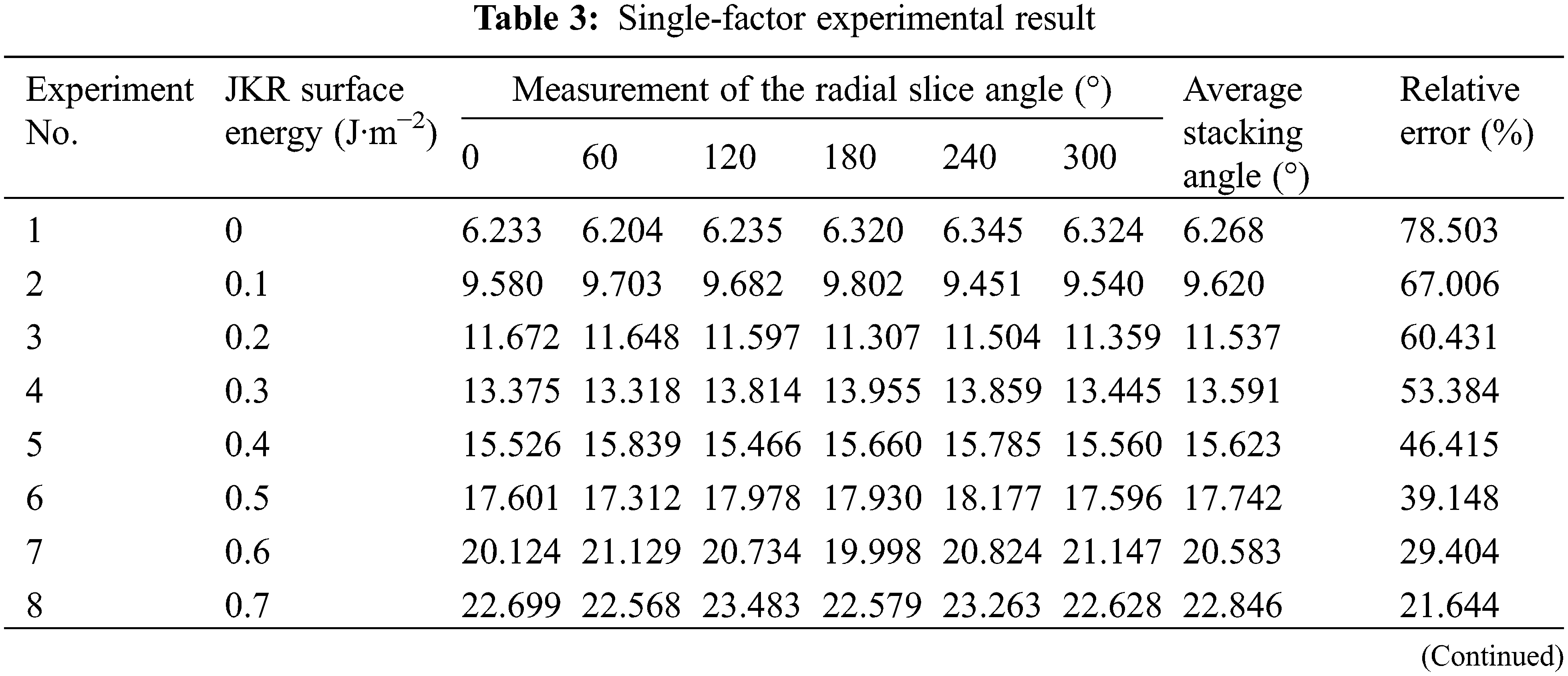
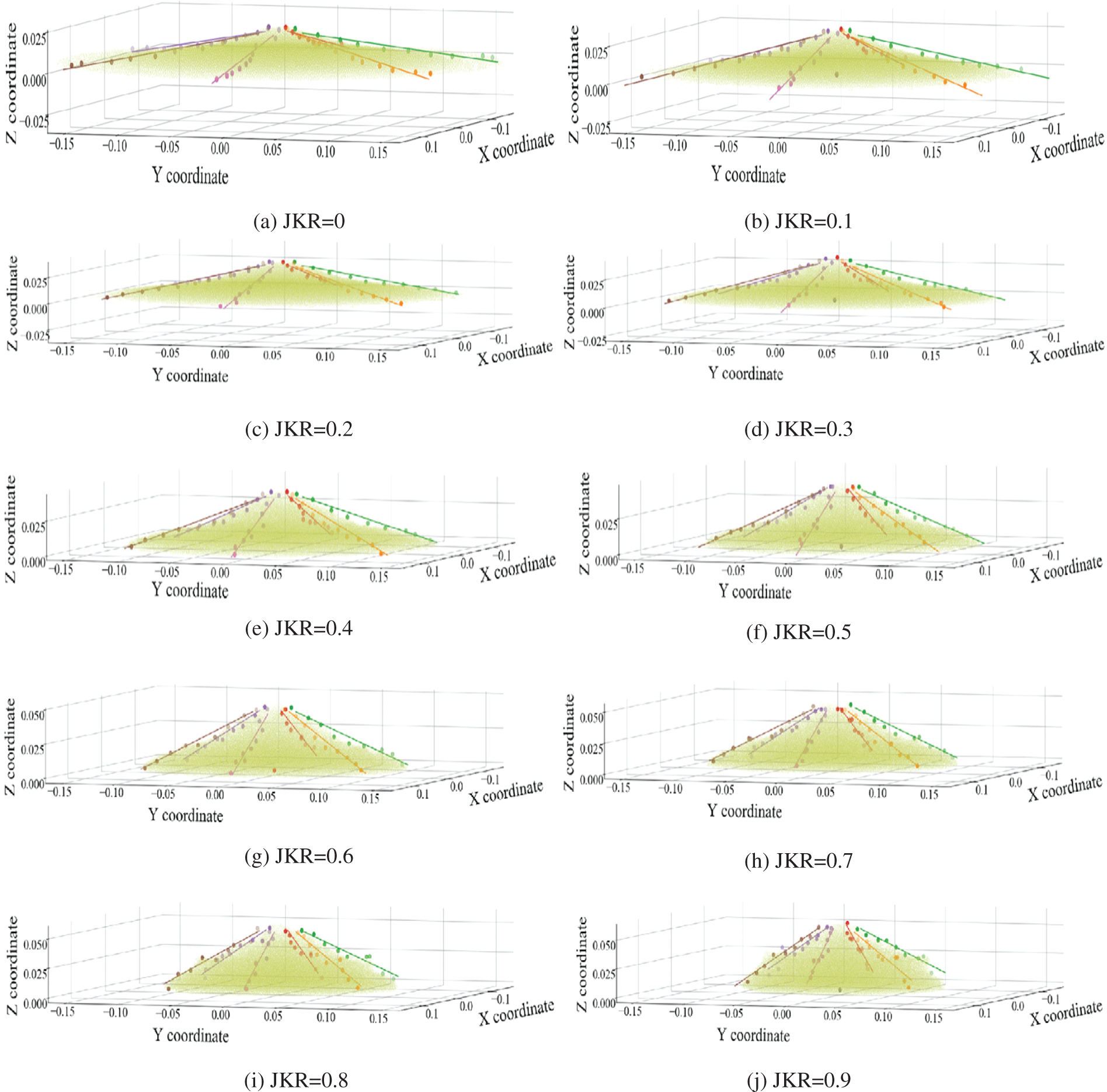
Figure 11: EDEM cylinder lifting simulation results

According to Table 2, the effect of JKR surface energy on stacking angle is positive. When JKR surface energy is 0.9 J·m−2, the results of the simulation experiment and physical experiment are the closest, with a relative error of 5.288%.

5  Conclusions

In this study, a high-accuracy physical model using banana straw was implemented based on the discrete element method. The intrinsic and basic contact parameters of the particles were measured by compression and bench experiments, and the contact model parameters of the particles were calibrated. Finally, the relationship between the parameters and the stacking angle of crushed materials was analyzed by JKR surface energy single factor experiment, proving the feasibility of the parameters of the banana straw discrete element model.

(1) The secondary development interface of EDEM software and particles with a size of 0.95 mm were used to establish the banana straw, discrete element model. In the discrete element model, the fiber structure, leaf sheath coating structure, and porous structure of banana straw were characterized, and the actual complex structure characteristics of banana straw were reproduced.

(2) The intrinsic parameters and basic contact parameters of banana straw were measured by physical experiments. According to the position distribution of different particles, the bonds between particles were divided into five groups with 57 types by the particle bonding model, representing the mechanical relationship between different structures of actual banana straw. The bonding parameters between particles were calibrated by crush experiment, and the feasibility of bond parameters was proved by comparing the load-displacement curves of the physical experiment and simulation experiment. When the JKR surface energy parameter was calibrated as 0.9 J·m−2 by a single factor experiment, the relative error between simulation and physical experiment results of stacking angle was 5.288%. It proves that the model can well restore the complex mechanical relationship between different tissues of actual banana straw and has great significance for the subsequent application of the discrete element model in the design of agricultural crushers.

(3) The high precision discrete element modeling method proposed in this paper can be applied to different agricultural materials, and the same method as this paper can be used for similar fiber structures, covering structures, etc. The calibration of bonding model parameters can guide other similar materials. The bonding contact model is used in constructing the discrete element model of banana straw in this paper, which is difficult to calculate quickly on a computer with weak performance and can be changed to the bonding V2 model subsequently to improve the calculation efficiency.

Acknowledgement: The authors wish to acknowledge Yunnan University Research Center of Mechatronics Technology and Applied Engineering of Plateau Agricultural Machinery and Honghe Agricultural Machinery Research Institute for providing the experimental equipment.

Contribution of All Authors: Jiang Jie: Funding acquisition, Supervision, Writing-review & Editing. Zhang Sen: Formal analysis, Writing-original draft, Visualization. Wang Yuedong: Project administration.

Funding Statement: Youth Fund of National Natural Science Foundation of China, 61801175, JJ, https://www.nsfc.gov.cn/.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Liu, G. H., Kuang, J. Y., Li, C., Wang, X., Liang, Q. D. et al. (2012). Research progress of banana straw resource utilization. Renewable Energy Resources, 30(5), 64–68+74. [Google Scholar]

 2.  Zeng, Z. W., Ma, X., Cao, X. L., Li, Z. H., Wang, X. C. (2021). Application status and prospect of discrete element method in agricultural engineering research. Transactions of the Chinese Society for Agricultural Machinery, 52(4), 1–20. [Google Scholar]

 3.  Liu, W. Z., He, J., Li, H. W., Li, X. Q., Zheng, K. et al. (2018). Micro-potato simulation parameter calibration based on discrete element. Transactions of the Chinese Society for Agricultural Machinery, 49(5), 125–135+142. [Google Scholar]

 4.  Shen, H. Y., Ji, L. L., Hu, L. L., Wang, B. Wan, G. P. et al. (2020). Study on the mechanical and physical parameters of sweet potato tuber during harvest. Journal of Chinese Agricultural Mechanization, 41(12), 55–61. [Google Scholar]

 5.  Luo, Q. J., Chen, Y. S., Xie, H., Han, B. H., Chen, M. J. et al. (2021). Experimental study on compression and bending characteristics of wheat straw. Journal of Agricultural Mechanization Research, 43(2), 132–138. [Google Scholar]

 6.  Zhang, Y. Q., Cui, Q. L., Guo, Y. M., Li, H. B. (2019). Experiment and analysis of mechanical characteristics of millet stalk cutting. Transactions of the Chinese Society for Agricultural Machinery, 50(4), 146–155+162. [Google Scholar]

 7.  Cui, T., Liu, J., Yang, L., Zhang, D. X., Zhang, R. et al. (2013). Experiment and simulation of rolling friction characteristics of corn seeds based on high-speed camera. Transactions of the Chinese Society of Agricultural Engineering, 29(15), 34–41. [Google Scholar]

 8.  Hao, J. J., Wei, W. B., Huang, P. C., Qin, J. H., Zhao, J. G. (2021). Calibration and experimental verification of discrete element parameters of oil sunflower seeds. Transactions of the Chinese Society of Agricultural Engineering, 37(12), 36–44. [Google Scholar]

 9.  Kovács, Á., Kerényi, G. (2019). Physical characteristics and mechanical behaviour of maize stalks for machine development. International Agrophysics, 33(4), 427–436. DOI 10.31545/intagr/113335. [Google Scholar] [CrossRef]

10. Kovács, Á., Kerényi, G. (2016). Stochastic variatio in discrete element method (DEM) for agricultural simulations. Hungarian Agricultural Engineering, 30, 31–38. [Google Scholar]

11. Zhang, F. W., Song, X. F., Zhang, X. K., Zhang, F. Y., Wei, W. C. et al. (2019). Simulation and experiment of mechanical properties of corn stalk during shredding. Transactions of the Chinese Society of Agricultural Engineering, 35(9), 58–65. [Google Scholar]

12. Tavares, L. M., Rodriguez, V. A., Sousani, M., Padros, C. B., Ooi, J. Y. (2021). An effective sphere-based model for breakage simulation in DEM. Powder Technology, 392, 473–488. DOI 10.1016/j.powtec.2021.07.031. [Google Scholar] [CrossRef]

13. Burmeister, C. F., Hofer, M., Molaiyan, P., Michalowski, P., Kwade, A. (2022). Characterization of stressing conditions in a high energy ball mill by discrete element simulations. Processes, 10(4), 692. [Google Scholar]

14. Lu, W. (2018). Study on the density of high density polyethylene (HDPE) by density buoyancy method. China Petroleum and Chemical Standard and Quality, 38(24), 40–43+45. [Google Scholar]

15. Friedrich, T., Kuhn, M., Nasato, D. S., Briesen, H. (2022). Material properties in cake filtration–discrete element simulation of compression-permeability cells. Chemical Engineering & Technology, 45(5), 898–906. DOI 10.1002/ceat.202100476. [Google Scholar] [CrossRef]

16. Teixeira, M. H. P., Skorych, V., Janssen, R., González, S. Y. G., de Noni Jr, A. et al. (2021). High heating rate sintering and microstructural evolution assessment using the discrete element method. Open Ceramics, 8, 100182. DOI 10.1016/j.oceram.2021.100182. [Google Scholar] [CrossRef]

17. Lai, Q. H., Yu, Q. X., Dong, J. Y. (2018). Dynamic analysis of rotary tiller gearbox based on EDEM, ADAMS and ANSYS. Journal of Intelligent & Fuzzy Systems, 36(2), 1153–1160. [Google Scholar]

18. Kishida, N., Nakamura, H., Takimoto, H., Ohsaki, S., Watano, S. (2021). Coarse-grained discrete element simulation of particle flow and mixing in a vertical high-shear mixer. Powder Technology, 390, 1–10. DOI 10.1016/j.powtec.2021.05.028. [Google Scholar] [CrossRef]

19. Pol, A., Gabrieli, F. (2021). Discrete element simulation of wire-mesh retaining systems: An insight into the mechanical behaviour. Computers and Geotechnics, 134, 104076. DOI 10.1016/j.compgeo.2021.104076. [Google Scholar] [CrossRef]

20. Bor, A., Jargalsaikhan, B., Lee, J., Choi, H. (2020). Effect of different milling media for surface coating on the copper powder using two kinds of ball mills with discrete element method simulation. Coatings, 10(9), 898. DOI 10.3390/coatings10090898. [Google Scholar] [CrossRef]

21. Ilia, I. B., Aleksei, V. B., Pavel, A. P. (2020). Discrete element simulation of powder sintering for spherical particles. Key Engineering Materials, 854, 164–171. [Google Scholar]

22. Kawabata, D., Yoshida, M., Shimosaka, A., Shirakawa, Y. (2020). Discrete element method simulation analysis of the generation mechanism of cooperative behavior of disks falling in a low-density particle bed. Advanced Powder Technology, 31(4), 1381–1390. [Google Scholar]

23. Perepelkin, N. V., Borodich, F. M. (2021). Explicit transformation between non-adhesive and adhesive contact problems by means of the classical Johnson Kendall Roberts formalism. Philosophical Transactions of the Royal Society A, 379(2203), 20200374. DOI 10.1098/rsta.2020.0374. [Google Scholar] [CrossRef]