Simulation of Gas-Water Two-Phase Flow in Tight Gas Reservoirs Considering the Gas Slip Effect

1  Introduction

The recoverable reserves of conventional oil and natural gas continue to decrease. Unconventional oil and gas resources, especially shale gas, have gradually become a hot topic for researchers [1]. Shale gas reservoirs have extremely low flow capacity, complex fluid fugacity, and interacting gas-water two-phase flow. It has brought many challenges to shale gas production and analytical calculations [2–4].

Fractured horizontal wells can make up for the deficiencies of vertical wells in some aspects. Especially in developing tight gas reservoirs, fractured horizontal wells have shown their unique advantages [5–7]. To effectively develop fractured tight gas reservoirs and optimize oil recovery. It is necessary to predict the production dynamics of multi-stage fractured horizontal wells [8]. Soliman et al. [9] conducted a simulation study of the production capacity of fractured horizontal wells under constant bottom flow pressure conditions. To verify the optimal number of transverse fractures in a finite or infinite reservoir, the production distribution of a set of lateral fractures was studied. To optimize the selection of vertical fracture parameters, the production model is studied by comparing fractured vertical and horizontal wells. The results show that the model is more applicable to tight gas reservoirs. the concept of trilinear flow in hydraulically fractured horizontal wells was proposed by Ozkan et al. [10,11]. They noted that the fluid contribution from the non-reservoir modified zone is negligible. And the flow is mainly linear perpendicular to hydraulic fracturing. The model proposes three linear flow zones. These include the hydraulically fractured zone, the inner zone between fractures, and the zone beyond the fracture tip. Guo et al. [12] considered the complex flow mechanisms in shale gas reservoirs. And a dual-porosity model was proposed to evaluate the effect of each parameter on shale gas production. The model considered three transport mechanisms. Gas diffusion in nanoscale pores, Darcy flow in microscopic pores, and non-Darcy flow in near-wellbore hydraulic fractures. The simulation results can better guide the optimal hydraulic fracturing design in unconventional tight reservoirs. An apparent permeability model was introduced by Zhan et al. [13]. It is used to describe gas flow (slip, Knudsen diffusion, etc.) in shale gas reservoirs. The model was also used to develop a numerical model to predict the production of multistage fractured horizontal wells. The results show that the model can quantify the effect of transient gas flow on gas well production in shale gas reservoirs.

As mentioned above, analytical and numerical models are the two most widely used models for fractured horizontal well capacity prediction [14,15]. In addition, semi-analytical models are also used for capacity prediction [16]. Analytical models require more assumptions. Its advantage is that it is computationally simple and more suitable for steady-state or proposed steady-state flow. However, it is difficult to solve the problems of real complex reservoirs [17,18]. In contrast, numerical models that can more detail characterize reservoir and fluid characteristics are suitable for nonlinear flows. It is the preferred technical tool and development direction for the future study of production dynamics of fractured horizontal wells.

A great deal of previous work has been done to improve mathematical models for multistage fractured horizontal wells in unconventional gas reservoirs (e.g., tight gas reservoirs). They have been developed mainly for the single-phase flow of natural gas [19,20]. Although pristine shale reservoirs generally develop ultra-low water saturation. Due to the retention of fracturing fluids, the water saturation of the pore space is higher than the bound water saturation of the reformed zone. This leads to a significant gas-water two-phase flow in shale production. Its transport pattern is also more complex. Furthermore, few papers have comprehensively considered the special flow phenomena such as slip, stress-sensitive, and high-rate non-Darcy that exist in tight gas reservoirs during the development process [21,22].

Based on the flow characteristics of different media systems in low permeability tight reservoirs modified by fractured horizontal wells [23]. Luo et al. [24] developed a discrete numerical model based on a triple media model considering capillary forces, gravity, high velocity undamped, and oil-water two-phase flow difference. The model was solved using the implicit pressure explicit saturation method (IMPES). The effects of parameters such as high-velocity non-damping coefficients are simulated and investigated. Based on the flow characteristics of fractured horizontal wells in tight gas reservoirs. He et al. [25] developed a mathematical model of flow considering stress sensitivity, slip-off effect, and high-velocity non-damping effect of gas in the fracture by solving the proposed pressure steady-state method. The effects of the production water to gas ratio and fracture parameters on the production capacity of fractured horizontal wells were analyzed. It is concluded that the effect of gas slip effect on gas production is small and negligible.

In addition, many literatures have performed parametric sensitivity analyses. The influencing factors have not been comprehensively considered [26,27]. Therefore, this paper will develop a set of mathematical models of flow that are integrated with multiple flow mechanisms in tight gas reservoirs. The model considers more comprehensive and systematic characteristics of tight gas reservoirs.

Next, this paper is based on the characteristics of dense sandstone gas reservoirs. Based on the discrete fracture model. A mathematical model of gas-water two-phase nonlinear seepage is established. The model integrates the matrix system slip effect, stress sensitivity, and high-speed non-Darcy flow in the artificial fracture system. The model was solved using the finite element method. In Section 3, a conceptual arithmetic example is established. A comparison with the commercial numerical simulation software CMG is also made. In Section 4, considers the effects of different initial water saturation, matrix permeability, and fracture conductivity on this paper’s model.

2  Gas-Water Two-Phase Flow Model for Horizontal Wells in Tight Gas Reservoirs

2.1 Physical Model

In this paper, we assume that the original tight gas reservoir has no microfracture development. It is a homogeneous reservoir. A multi-stage fractured horizontal well modifies the reservoir. The fluid seeps from the reservoir matrix into the artificial fractures. Finally, it flows to the wellbore through the hydraulic fractures. The model sets the external boundary of the tight gas reservoir as a closed boundary. The well type is set as a multi-stage fractured horizontal well, as shown in Fig. 1.

Figure 1: Physical model of a multi-stage fractured horizontal well in a tight gas reservoir

Multi-scale flow mechanisms are considered. Slip effects are considered for gas-phase flows in matrix systems. Stress-sensitive and high-velocity non-Darcy effects are considered for the artificial fracture system. The following assumptions are also given for the above model for calculation purposes:

(1)   There are only two types of fluids in the gas reservoir. There is a gas phase and a water phase. And the gas phase is insoluble in the water phase.

(2)   The rock and water are slightly compressible. And the compression coefficient is constant. Gas-phase is compressible.

(3)   The effect of the capillary force of gas and water phases is neglected.

(4)   The effect of gravity is neglected.

(5)   The flow process is isothermal percolation.

2.2 Mathematical Model

The source-sink term is considered. Based on the principle of conservation of matter, the continuity equation of the gas-water two-phase is obtained by using the infinitesimal unit analysis from reference [14].

Gas-phase

∇[kkrgμgBg∇pg]+qgBg=∂∂t(ϕSgBg) (1)

where k is the permeability, mD; krg is the relative permeability of the gas phase, mD; μg is the viscosity of the gas, mPa⋅s; pg is the gas pressure, MPa; Bg is gas compressible coefficient; ϕ is the porosity; Sg is the gas saturation.

Water phase

∇[kkrwμwBw∇pw]+qwBw=∂∂t(ϕSwBw) (2)

where krw is the relative permeability of the gas phase, mD; μw is the viscosity of the gas, mPa⋅s; pw is the gas pressure, MPa; Bw is the gas compressible coefficient; Sw is the gas saturation.

The gas and water saturation satisfy the following equation:

Sw+Sg=1 (3)

The capillary pressure satisfies the following equation:

Pc(Sw)=Pg−Pw (4)

where Pc is a capillary force between the gas and water phase.

2.3 Model Discretization

Here, the subscript m represents the bedrock system, f represents the fracture system, w represents the water phase, and g represents the gas phase.

For the two-dimensional matrix system, the gas slip effect [28] is considered, and the apparent permeability is introduced as

ke=k(1+bp¯) (5)

where b parameters are determined mainly by experiments; km is the reservoir permeability without correction

To simplify the model, we assume that the capillary force profile of the matrix system is a function depending on the saturation [29], which is neglected in the fractured system.

pc=−Bcln⁡(Se)Se=Sw−Srw1−Srg−Srw (6)

where Bc is capillary force parameters; Srw is residual water saturation; Srg is residual gas saturation.

For the fracture system, the description is proposed to use the Forchheimer formula considering the high-speed non-Darcy phenomenon generated by the high-speed motion of the fluid. Neglecting the non-Darcy percolation of the water phase then, the non-Darcy correction factor of the gas phase under multiphase flow conditions is assumed to be ξn [30].

vn=ξnkkrgμg∇p(n=x,y,z) (7)

where vn the gas flow velocity.

In addition, the effective stress on the fracture increases as the formation pressure decreases, and the flow conductivity of the fracture decreases a lot, so it is necessary to consider the presence of stress sensitivity in the fracture system. The apparent permeability of the fracture system considering the stress-sensitive effect is given by

Ke=Ki(1+bp¯)e−αf(pi−p) (8)

where Ki is absolute reservoir permeability, mD; α is sensitivity index, MPa−1; Pi is original formation pressure, MPa.

The water saturation in the fracture can be expressed by the water saturation in the matrix, then the differential equation for gas-water two-phase flow in a discrete fracture model for a multi-stage fractured horizontal well in a tight gas reservoir can be abbreviated as

The gas-phase pressure equation for the matrix is

M∇(kmekrgμgBg∇Pgm)+∇[kkrwμwBw∇pgm]−∇[kkrwμwBw∇pcm]−δqmfT∗=Mp∂pgm∂t (9)

The equation for the water phase saturation of the matrix system is

∇[kmekrgμgBg∇pgm]−δqmfg∗=−Cg1∂Swm∂t+Cg2∂pwm∂t (10)

The pressure equation in the fracture system is

M∂∂l(kkrgfμgf∂pgf∂l)+∂∂l(kkrwfμwf∂pgf∂l)+Qwf+Qgf+δqmfT∗=Mp∂pgf∂t (11)

In the above equation M=(Cw1−Cw2dpcdSw)Cg1 , Cg1=ϕBg , Cg2=ϕSgBg(Cg+Cϕ) , Cw1=ϕBg , Cw2=ϕSwBw(Cw+Cϕ) , qmfT∗=qmfw∗+qmfg∗ are total tamper flow. δ={10Source and sinkNo

The three flow equations above are solved by the finite volume method, and the specific steps to derive the equivalent ∭ integral weak form are as follows, taking Eq. (9) as an example.

∫∫∫Vi⁡M∇(KmeKrgμgBg∇Pgm)dVi+∫∫∫Vi⁡∇[KKrwμwBw∇pgm]dVi−∫∫∫Vi⁡∇[KKrwμwBw∇pcm]dVi=∫∫∫Vi⁡(Mp∂pgm∂t+δqmfT∗)dVi (12)

Applying Gauss’s theorem to the Darcy formula term on the left side of Eq. (12).

∫∫∫Vi⁡M∇(KμB∇P)dVi=∫∫◯s⁡KμB∇P⋅nds (13)

By approximating the pressure gradient as the quotient of the pressure difference ∇P between grids i and j and the node distance, Eq. (13) can be rewritten as

∫∫∫Vi⁡M∇(KμB∇P)dVi=∑jTij(Pj−Pi) (14)

In the above equation, Tij is the flow coefficient, defined as Tij=(KμB)Aijlij .

The cumulative term on the right-hand side of Eq. (12) can be rewritten as

∫∫∫Vi⁡(Mp∂pgm∂t+δqmfT∗)dVi=ViΔt[(Mppgm)n+1−(δqmfT∗)n+1+(δqmfT∗)n] (15)

where the superscript n represents the current time step, and n + 1 represents the next time step.

Solving them sequentially yields pgm , Swm and pgf .

3  Model Validation

To verify the correctness of the model proposed in this paper and the reliability of the calculation results. In this paper, the daily production data of a fractured gas well in a tight gas reservoir are fitted to the history. And the calculation results of this simulator are compared with those of the commercial software CMG. The burial depth of the model is about 3280 m∼3740 m. Other essential parameters are shown in Table 1. The relative permeability curves of gas and water phases are shown in Fig. 2. The 3D grid profile of the model is shown in Fig. 3. The model size is 1300 m * 1000 m * 420 m.

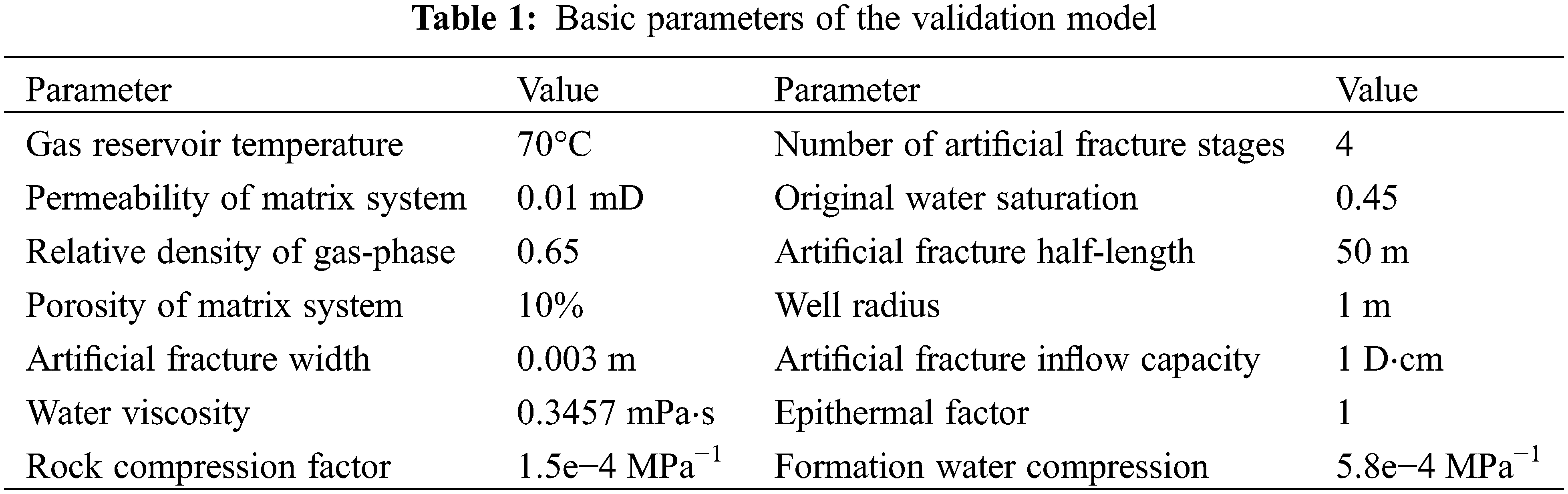
Figure 2: Gas-water two-phase phase percolation diagram

Figure 3: Model mesh 3D profile

Figs. 4 and 5 show the comparison curves of the historical fitted and simulated calculated results for the daily gas and water production of the well, respectively. The figures show that the results obtained by the method and CMG calculation in this paper basically match the actual measured data in the field. This indicates that this paper’s relevant theories and methods have some practical value. In addition, the overall trend of the yield obtained by the method in this paper and the CMG numerical simulation software is consistent. There are only minor differences. The main reason is that the method in this paper considers more nonlinear flow characteristics than the CMG model. Such as slip, fracture stress sensitivity, and high-speed non-Darcy.

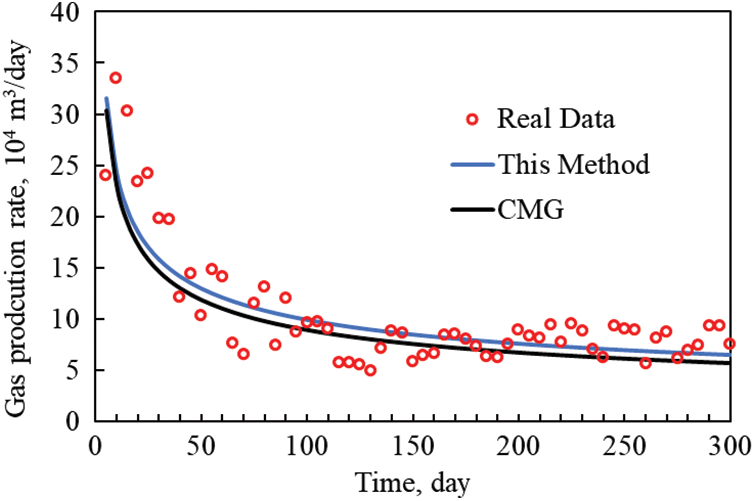
Figure 4: Comparison of daily oil production rate history fitting and simulation results

Figure 5: Comparison of historical fitting and simulation results of daily water production rate

4  Sensitivity Analysis

4.1 Effect of Initial Water Saturation

The original water saturation (Sw) of a reservoir is an important parameter in the development of oil and gas fields. During the development process, the value of water saturation is constantly changing. For tight gas reservoirs containing lateral and bottom water. It is particularly important to consider the effect of water saturation on production. To investigate the effect of raw water saturation on the production of tight gas reservoirs. In this paper, the basic parameters of the conceptual model are kept constant. Only the pristine water of the reservoir is changed. The production dynamics of a multi-stage fractured horizontal well in a tight gas reservoir are simulated for 300 days under different pristine water saturation conditions. The specific scenarios are initial water saturation of 0.55, 0.65, and 0.75.

As shown in Figs. 6 and 7, the decreasing rates of daily gas production and daily water production still exhibit a fast and slowly decreasing rate. In addition, a single well’s daily gas production decreases as the basal raw water saturation increases. In contrast, the daily water production of single well increases. When Sw is 0.55, the daily gas production at the beginning of production is 280,000 m3/day, respectively. When Sw is 0.65, the value is 50,000 m3/day. When Sw is 0.75, the value is 205,200 m3/day. This indicates that increasing reservoir pristine water saturation increases the resistance to gas flow. This resulted in a decrease in gas production from the wells. Specifically from the daily water production curve, when Sw is 0.75, the daily water production after 100 days of production is about 3 m3/day.

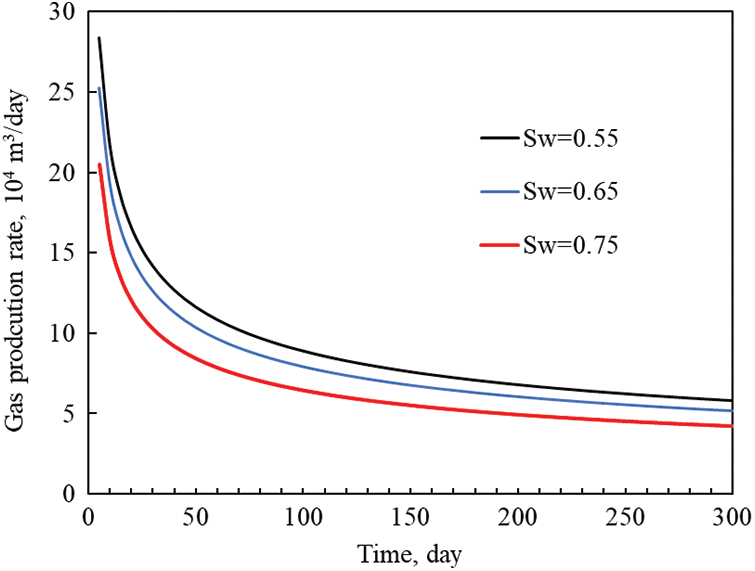
Figure 6: Original water saturation on gas production curve

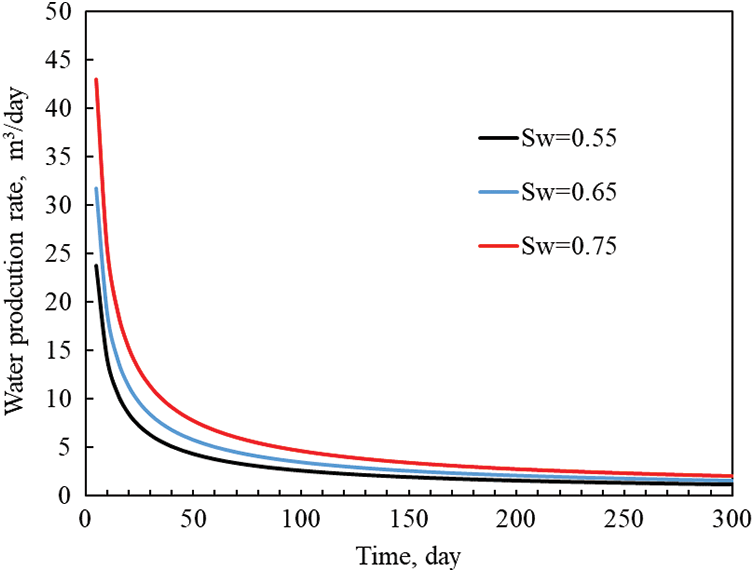
Figure 7: Original water saturation influence curve on gas production

4.2 Effect of Matrix Permeability

The effect of matrix permeability on the production of fractured horizontal wells in tight gas reservoirs is investigated. In this paper, while keeping the basic parameters of the conceptual model unchanged, only the matrix permeability parameters were changed. The matrix permeability was set to 0.0001, 0.001, 0.01 and 0.1 mD to simulate the production dynamics of multi-stage fractured horizontal wells in tight gas reservoirs for 300 days.

Figs. 8 and 9 show the production dynamics of fractured horizontal wells in tight gas reservoirs under different matrix permeability conditions. Figs. 8 and 9 show the effect of reservoir matrix permeability on production. With the increase of reservoir matrix permeability, daily gas and water production will increase significantly. The daily gas and water production curves corresponding to different matrix permeabilities are compared. It can also be found that the smaller the matrix permeability is, the less significant its effect size on the fractured horizontal wells in the matrix pore space of tight gas reservoirs. This is mainly because when the reservoir matrix permeability is too small, the flow of tight gas in the matrix pore space is complicated. This makes the matrix contribution to production smaller.

Figure 8: Influence curve of reservoir matrix permeability on gas production

Figure 9: Influence curve of reservoir matrix permeability on water production

4.3 Effect of Fracture Conductivity

Fracture conductivity (Fcd) is an important parameter in fracturing construction. It is defined as the product of artificial fracture closure and artificial fracture permeability. It is mainly influenced by proppant type, fracture closure pressure, and fluid properties. To investigate the effect of artificial fracture inflow on the production of fractured horizontal wells in tight gas reservoirs. In this paper, while keeping the basic parameters of the conceptual model unchanged, only the parameter of artificial fracture inflow is changed. In this paper, the production dynamics of a multi-stage fractured horizontal well in a tight gas reservoir are simulated for 300 days under different artificial fracture inflow capacities. The specific scenario is to set the inflow capacity to 1, 5, 20, and 30 D⋅cm.

From Figs. 10 and 11, the daily gas production and daily water production of fractured horizontal wells in tight gas reservoirs increase with the increase of artificial fracture inflow. Specifically, observe the cumulative production curve. It can be found that: the cumulative production increases less and less with the increase of fracturing inflow. When Fcd is 10 D⋅cm and Fcd is 30 D⋅cm, the cumulative production curves overlap. In addition, the decreasing rate of daily gas and water production still shows the characteristics of fast and then slow.

Figure 10: Influence curve of fracture inflow capacity on daily gas production

Figure 11: Influence curve of fracture inflow capacity on daily water production

5  Conclusion

Through the above research, the paper mainly draws the following conclusions:

(1)   The mathematical model established in this paper considers the gas-slip effect of the matrix system, the stress sensitivity of the artificial fracture system, and the high-speed non-Darcy phenomenon. It can more accurately describe the dense gas flow characteristics in the production process. Compared with the commercial numerical simulation software CMG, the proposed method is more reliable and effective.

(2)   In this paper, the gas-water flow law is analyzed under different initial water saturation. The initial water saturation was set to 0.55, 0.65 and 0.75. The initial daily production rate decreased by 10.7% and 29%, respectively. It was found that the decrease in matrix permeability led to a reduction in both daily gas and daily water production. This paper also simulates the effect of different fracture permeability on its production. The production was found to decrease gradually with the increase of fracture permeability.

(3)   Although the seepage law of tight gas reservoirs is systematically considered in this paper. However, capillary force and gravity are not considered. It still has some limitations.

Data Availability Statements: The datasets generated during and analyzed during the current study are available from the corresponding author on reasonable request.

Funding Statement: This work was supported by the China Postdoctoral Science Foundation (2021M702304) and Natural Science Foundation of Shandong Province (ZR2021QE260).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Wang, W., Fan, D., Sheng, G., Chen, Z., Su, Y. (2019). A review of analytical and semi-analytical fluid flow models for ultra-tight hydrocarbon reservoirs. Fuel, 256, 115737. DOI 10.1016/j.fuel.2019.115737. [Google Scholar] [CrossRef]

 2.  Ross, D. J., Bustin, R. M. (2009). The importance of shale composition and pore structure upon gas storage potential of shale gas reservoirs. Marine and Petroleum Geology, 26(6), 916–927. DOI 10.1016/j.marpetgeo.2008.06.004. [Google Scholar] [CrossRef]

 3.  Kolawole, O., Wigwe, M., Ispas, I., Watson, M. (2020). How will treatment parameters impact the optimization of hydraulic fracturing process in unconventional reservoirs? SN Applied Sciences, 2(11), 1–21. DOI 10.1007/s42452-020-03707-w. [Google Scholar] [CrossRef]

 4.  Xu, Y., Hu, Y., Rao, X., Zhao, H., Zhong, X. et al. (2022). A fractal physics-based data-driven model for water-flooding reservoir (FlowNet-fractal). Journal of Petroleum Science Engineering, 210, 109960. DOI 10.1016/j.petrol.2021.109960. [Google Scholar] [CrossRef]

 5.  Cipolla, C. L., Lolon, E. P., Erdle, J. C., Rubin, B. (2010). Reservoir modeling in shale-gas reservoirs. SPE Reservoir Evaluation & Engineering, 13(4), 638–653. DOI 10.2118/125530-PA. [Google Scholar] [CrossRef]

 6.  Hajamalala, A. M., Noarijaona, R., Belkacem, Z. (2022). Modeling the unsteady flow of a Newtonian fluid originating from the hole of an open cylindrical reservoir. Fluid Dynamics & Materials Processing, 18(6), 1737–1748. DOI 10.32604/fdmp.2022.022047. [Google Scholar] [CrossRef]

 7.  Sheng, G., Su, Y., Wang, W. (2019). A new fractal approach for describing induced-fracture porosity/permeability/compressibility in stimulated unconventional reservoirs. Journal of Petroleum Science Engineering, 179, 855–866. DOI 10.1016/j.petrol.2019.04.104. [Google Scholar] [CrossRef]

 8.  Karcher, B., Giger, F., Combe, J. (1986). Some practical formulas to predict horizontal well behavior. SPE Annual Technical Conference and Exhibition, New Orleans, Louisiana, OnePetro. [Google Scholar]

 9.  Soliman, M., Hunt, J., Azari, M. (1996). Fracturing horizontal wells in gas reservoirs. SPE Mid-Continent Gas Symposium, Amarillo, Texas, OnePetro. [Google Scholar]

10. Ozkan, E., Brown, M. L., Raghavan, R. S., Kazemi, H. (2009). Comparison of fractured horizontal-well performance in conventional and unconventional reservoirs. SPE Western Regional Meeting, San Jose, California, OnePetro. [Google Scholar]

11. Brown, M., Ozkan, E., Raghavan, R., Kazemi, H. (2011). Practical solutions for pressure-transient responses of fractured horizontal wells in unconventional shale reservoirs. SPE Reservoir Evaluation & Engineering, 14(6), 663–676. DOI 10.2118/125043-PA. [Google Scholar] [CrossRef]

12. Guo, C., Wang, J., Wei, M., He, X., Bai, B. (2015). Multi-stage fractured horizontal well numerical simulation and its application in tight shale reservoirs. SPE Russian Petroleum Technology Conference, Moscow, Russia, OnePetro. [Google Scholar]

13. Zhan, J., Lu, J., Fogwill, A., Ulovich, I., Cao, J. P. et al. (2017). An integrated numerical simulation scheme to predict shale gas production of a multi-fractured horizontal well. Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, OnePetro. [Google Scholar]

14. Xu, Y., Sheng, G., Zhao, H., Hui, Y., Zhou, Y. et al. (2021). A new approach for gas-water flow simulation in multi-fractured horizontal wells of shale gas reservoirs. Journal of Petroleum Science Engineering, 199, 108292. DOI 10.1016/j.petrol.2020.108292. [Google Scholar] [CrossRef]

15. Sheng, G., Zhao, H., Su, Y., Javadpour, F., Wang, C. et al. (2020). An analytical model to couple gas storage and transport capacity in organic matter with noncircular pores. Fuel, 268, 117288. DOI 10.1016/j.fuel.2020.117288. [Google Scholar] [CrossRef]

16. Suri, Y., Islam, S. Z., Stephen, K., Donald, C., Thompson, M. et al. (2020). Numerical fluid flow modelling in multiple fractured porous reservoirs. Fluid Dynamics & Materials Processing, 16(2), 245–266. DOI 10.32604/fdmp.2020.06505. [Google Scholar] [CrossRef]

17. Sheng, G., Su, Y., Wang, W., Liu, J., Lu, M. et al. (2015). A multiple porosity media model for multi-fractured horizontal wells in shale gas reservoirs. Journal of Natural Gas Science Engineering, 27, 1562–1573. DOI 10.1016/j.jngse.2015.10.026. [Google Scholar] [CrossRef]

18. Wang, W., Su, Y., Sheng, G., Cossio, M., Shang, Y. (2015). A mathematical model considering complex fractures and fractal flow for pressure transient analysis of fractured horizontal wells in unconventional reservoirs. Journal of Natural Gas Science and Engineering, 23, 139–147. DOI 10.1016/j.jngse.2014.12.011. [Google Scholar] [CrossRef]

19. Sheng, G., Su, Y., Wang, W. (2019). A new fractal approach for describing induced-fracture porosity/permeability/compressibility in stimulated unconventional reservoirs. Journal of Petroleum Science and Engineering, 179, 855–866. DOI 10.1016/j.petrol.2019.04.104. [Google Scholar] [CrossRef]

20. Sheng, G., Su, Y., Zhao, H., Liu, J. (2020). A unified apparent porosity/permeability model of organic porous media: Coupling complex pore structure and multi-migration mechanism. Advances in Geo-Energy Research, 4(2), 115–125. DOI 10.26804/ager.2020.02.01. [Google Scholar] [CrossRef]

21. Mahdaviara, M., Sharifi, M., Ahmadi, M. (2022). Toward evaluation and screening of the enhanced oil recovery scenarios for low permeability reservoirs using statistical and machine learning techniques. Fuel, 325, 124795. DOI 10.1016/j.fuel.2022.124795. [Google Scholar] [CrossRef]

22. Andrianov, N., Bech, N. M., Nielsen, C. M., Al-Masri, W., Shapiro, A. (2022). Impact of Gas liberation effects on the performance of low permeability reservoirs. Energies, 15(10), 3707. DOI 10.3390/en15103707. [Google Scholar] [CrossRef]

23. Zhang, H., Sheng, J. J. (2020). Numerical simulation and optimization study of the complex fracture network in naturally fractured reservoirs. Journal of Petroleum Science and Engineering, 195, 107726. DOI 10.1016/j.petrol.2020.107726. [Google Scholar] [CrossRef]

24. Luo, Z., Zhang, N., Zhao, L., Ran, L., Zhang, Y. (2019). Numerical evaluation of shear and tensile stimulation volumes based on natural fracture failure mechanism in tight and shale reservoirs. Environmental Earth Sciences, 78(5), 1–15. DOI 10.1007/s12665-019-8157-8. [Google Scholar] [CrossRef]

25. He, J., Teng, W., Xu, J., Jiang, R., Sun, J., (2016). A Quadruple-porosity model for shale gas reservoirs with multiple migration mechanisms. Journal of Natural Gas Science Engineering, 33, 918–933. DOI 10.1016/j.jngse.2016.03.059. [Google Scholar] [CrossRef]

26. Zhang, Q., Su, Y., Wang, W., Lu, M., Sheng, G. (2017). Apparent permeability for liquid transport in nanopores of shale reservoirs: Coupling flow enhancement and near wall flow. International Journal of Heat Mass Transfer, 115, 224–234. DOI 10.1016/j.ijheatmasstransfer.2017.08.024. [Google Scholar] [CrossRef]

27. Sheng, G., Wang, W., Zhao, H., Lun, Z., Xu, Y. et al. (2020). Study of fracturing fluid imbibition impact on gas-water two phase flow in shale fracture-matrix system. SPE/AAPG/SEG Unconventional Resources Technology Conference, Virtual, OnePetro. [Google Scholar]

28. Klinkenberg, L. (1941). The permeability of porous media to liquids and gases. Drilling Production Practice, 2, 200–213. [Google Scholar]

29. Monteagudo, J., Firoozabadi, A. (2004). Control-volume method for numerical simulation of two-phase immiscible flow in two-and three-dimensional discrete-fractured media. Water Resources Research, 40(7), DOI 10.1029/2003WR002996. [Google Scholar] [CrossRef]

30. Moridis, G. J., Blasingame, T. A., Freeman, C. M. (2010). Analysis of mechanisms of flow in fractured tight-gas and shale-gas reservoirs. SPE Latin American and Caribbean Petroleum Engineering Conference, Lima, Peru, OnePetro. [Google Scholar]