Numerical Investigation of the Thermal Behavior of a System with a Partition Wall Incorporating a Phase Change Material

Nomenclature

1  Introduction

High energy consumption leads to the necessity of reducing the energy demand of the building. This could be realized by using efficient insulators [1,2] and new construction materials [3]. The use of passive storage such as PCM is recommended not only in buildings [4–6], but also in other contexts, such as transportation [7], industrial applications [8], electronics and electric systems [9,10], storage devices for solar heating or cooling [10,11]. Thus, thermal energy storage can be accomplished either using sensible heat storage and/or using latent heat storage. In building thermal applications, the partition wall is considered an essential element for thermal comfort to reduce the employment of air-conditioners. The outdoor thermal conditions and the activity in the neighboring room through the partition wall influence the thermal comfort inside buildings. So, PCM embedding inside the partition wall improves the characteristics involved and reduces the energy transmitted to the building premises. The PCM insertion effect plays out according to thermal melting temperature [12], latent heat of melting [13], phase change material emplacement and thickness [14]. The criteria of these studies are the flux density transmitted to the room or the daily and the annual energy per unit area consumed. In this current study, the principal aim is to study the impact of PCM emplacement regarding melting thermal level, and melting range temperature on the dimensionless amount of the energy charged in the composite wall comparatively to that involved for the basic wall. This study is carried out for the same thermal conditions in a periodically established regime.

2  Equations and Mathematical Expressions

The study concerns the comparison of a referential partition wall with that integrating PCM (Fig. 1), without changing the basic structure L=30cm . The partition walls consisted of concrete and are subjected to the following boundary conditions: the indoor temperature Tint is assumed constant and the outdoor temperature To is varied between Tint as the minimum temperature value and Tmax as the maximum value.

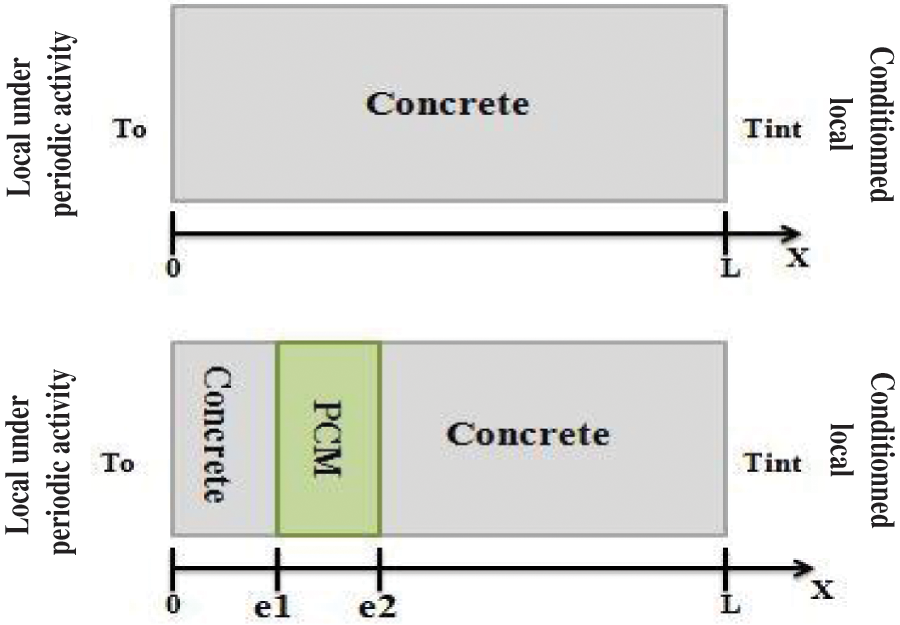
Figure 1: Scheme of the referential partition wall and that with PCM

In this work, we are interested in studying the effect of location, melting temperature Tf and melting range factor ε on the PCM’s thermal state. PCM is localized at the position e1 and displaced from the left to the right of the partition wall. Furthermore, the thickness of the PCM is taken as e2 − e1 = 3 cm. The maximum temperature of the adjacent local placed on the left of the partition wall is taken equal to 35°C. In contrast, for the comfort temperature, we have taken two values Tint = 18°C and 20°C to study their effect.

The energy equation for the multilayer partition wall system is as follows [15]:

∂T∂t+Lfc∂f∂t=α∂2T∂x2 (1)

Lfc is only present in the case when the PCM is on fusion at T=Tf .

The above equation is associated to:

-Interfaces conditions:

(Ti)=(Ti+1) (2)

−ki∂Ti∂x=−ki+1∂Ti+1∂x (3)

-Boundary conditions:

kc∂Tc∂x|x=0=ho(To−Tc|x=0) (4)

kc∂Tc∂x|x=L=hint(Tc|x=L−Tint) (5)

With:

To=[(Tmax+Tint)2+(Tmax−Tint)2]sin⁡(ωt) (6)

The numerical code has been successfully validated [16] by comparison with analytical results corresponding to the Newman problem [17].

3  Results and Discussion

The study concerns comparing the amount of thermal energy charged into the composite partition wall (with PCM) to the referential wall (without PCM). The energy in the wall taken as a reference; is purely in sensible form. However, for the composite partition wall, it is either in a sensible form, or in sensible and latent form depending on the PCM’s fusion temperature, its melting range, its location, and also reposing on the thermal level of the neighboring local. Thus, we have calculated the dimensionless latent heat charged in PCM qPCMLatent and the dimensionless global heat charged in the composite wall qCompositewall in an established periodic regime [15].

These parameters are defined as:

qPCMLatent=∫e1e2ρpcpLffdx∫0Lρccc[Tc(x)−Tint]dx (7)

qCompositewall=(∫0e1ρccc(Tc(x)−Tint)dx+∫e1e2ρP(cP(TP(x)−Tint)+Lff)dx+∫e2Lρccc(Tc(x)−Tint)dx))/(∫0Lρccc(Tc(x)−Tint)dx) (8)

With:

{f=0ifTf≻Tp0<f<1ifTf=Tpf=1ifTf≺Tp (9)

As the PCM takes place over a range temperature, the melting factor ε , which varies between 1% and 3%, is introduced to evaluate the melting range effect. The melting factor ε is defined as:

{Tf1=Tf−(ε∗Tf)Tf2=Tf+(ε∗Tf) (10)

Three PCMs are selected for this study, with melting temperatures equal to Tf=19∘C , Tf=21∘CandTf=23∘C .

The physical properties for the concrete and the PCMs are indicated in Table 1:

The results of the study are summarized in the Tables 2–7 associated to the Figs. 2–7. They show the effect of the melting factor ε , the PCM location, the maximum temperature of the adjacent local Tmax=35∘C as well as comfort temperatures Tint=18∘C and Tint=20∘C of the conditioned local on the variation of latent and global heat inside the partition wall. The parameter qPCMLatent indicates if the melting takes place and for which emplacement of the PCM. However, the parameter qcompositewall indicates where the composite partition wall is more efficient than the referential one. PCM’s thickness is e2−e1 . The displacement step in the partition wall is taken equal to 5 cm from the left to the right of the partition wall. As the total thickness of the partition wall is L=30cm . Thus, five PCM emplacements have been chosen: 5 cm, 10 cm, 15 cm, 20 cm and 25 cm.

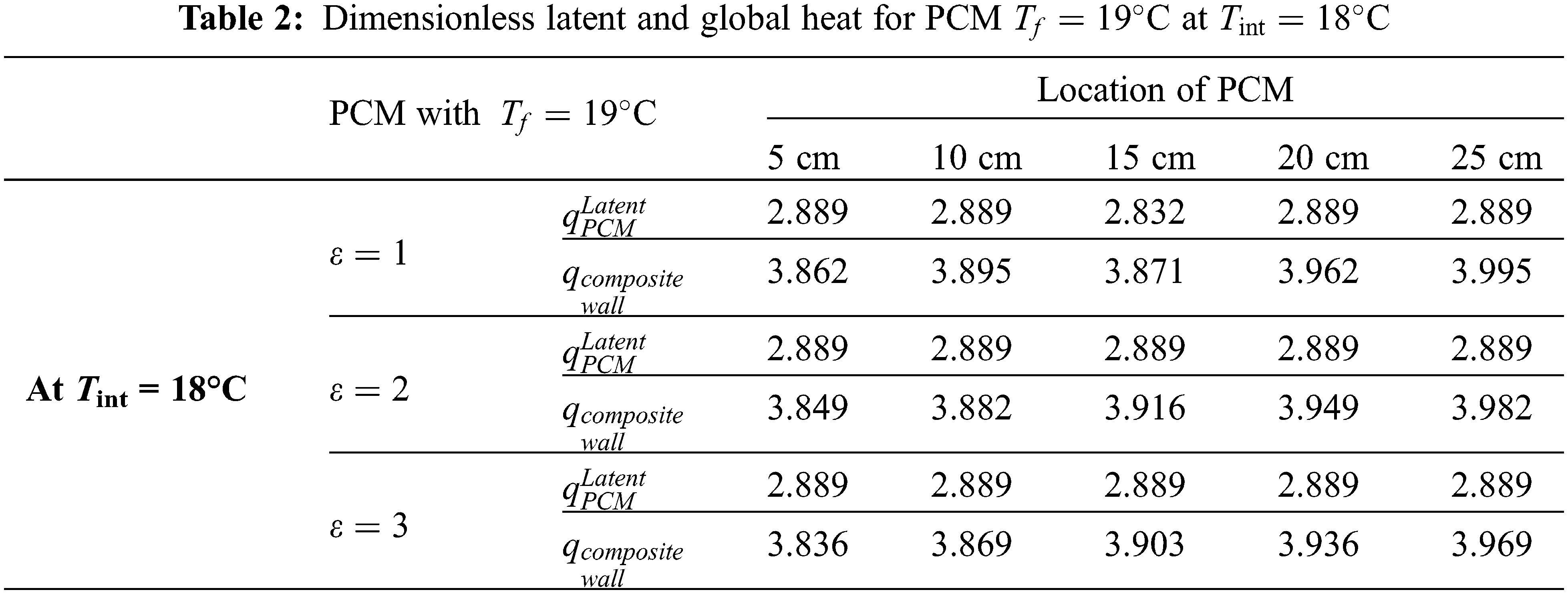
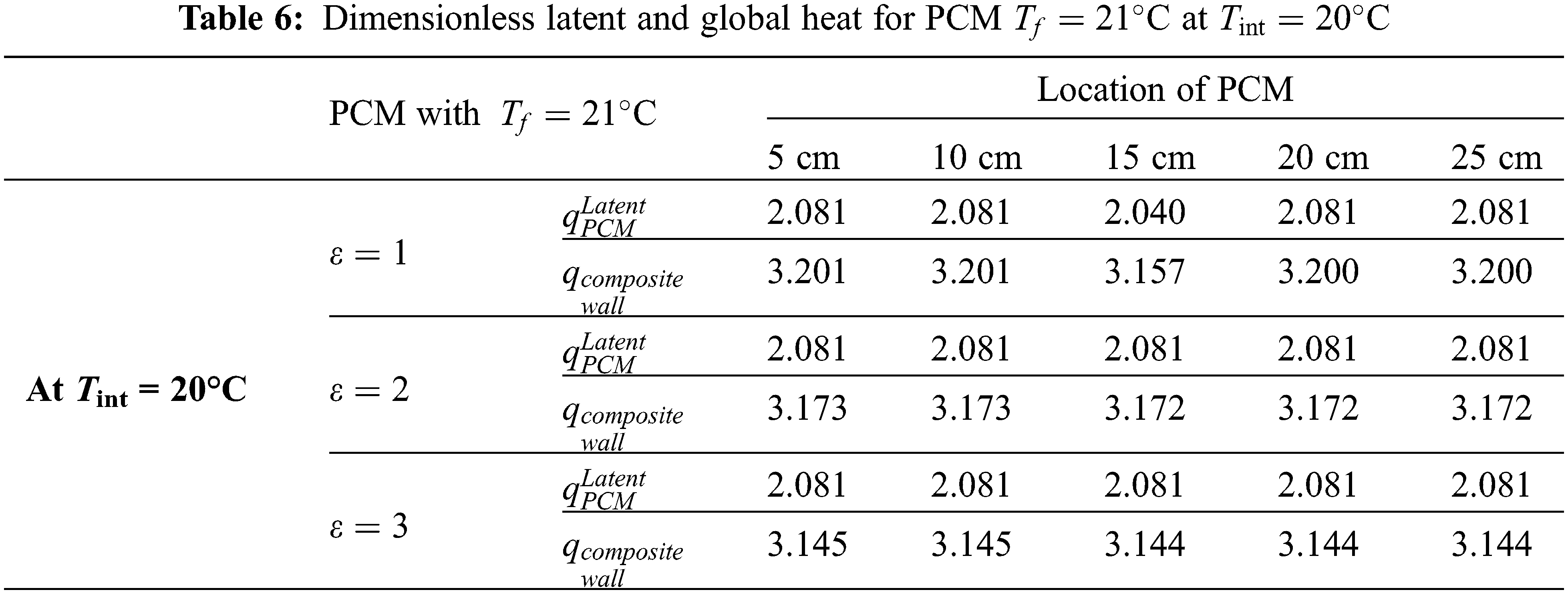
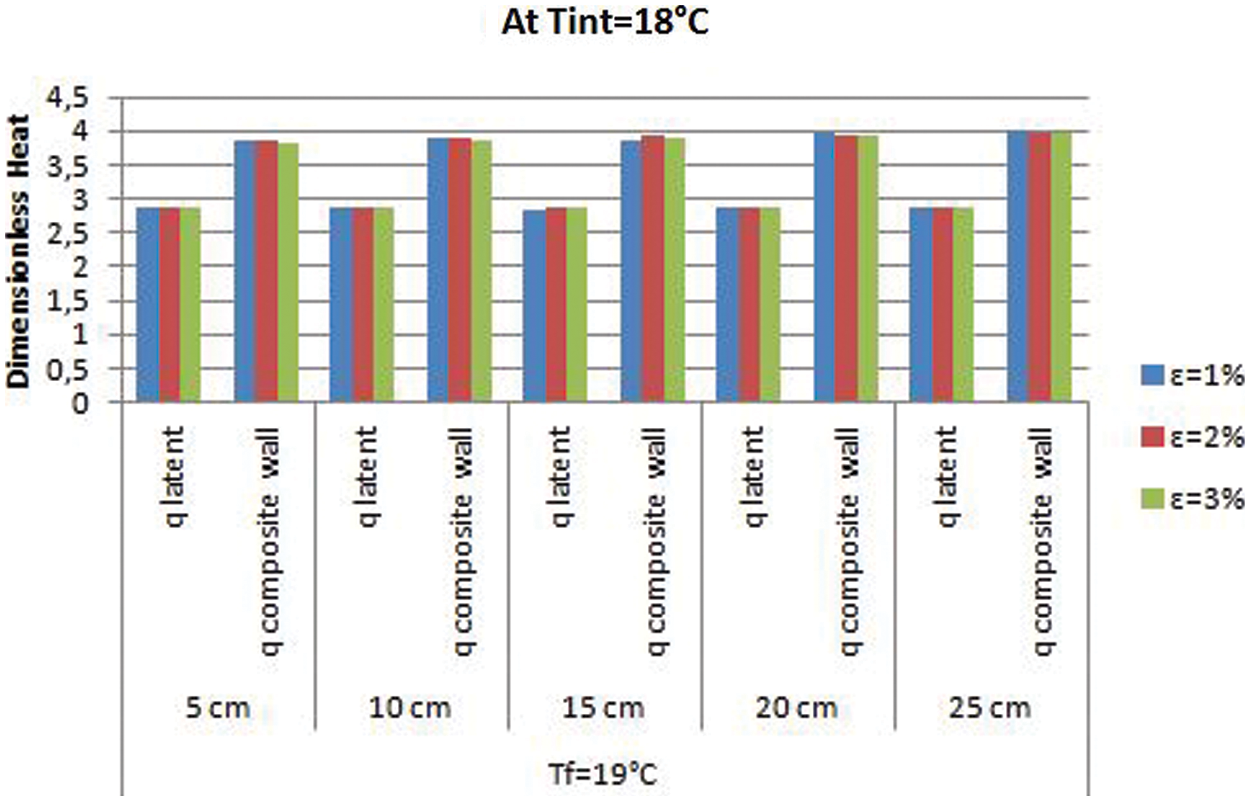
Figure 2: Dimensionless latent and global heat histograms at Tint=18∘C and for Tf=19∘C

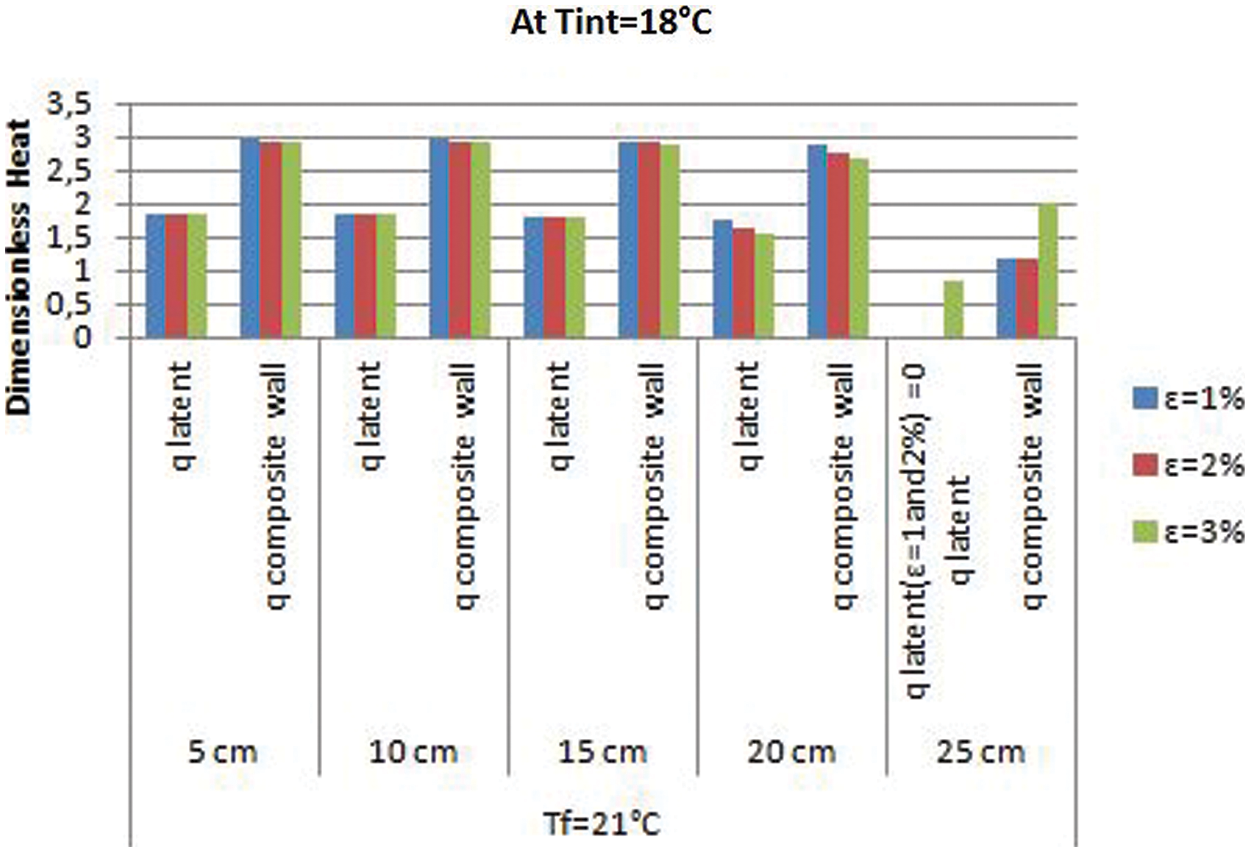
Figure 3: Dimensionless latent and global heat histograms at Tint=18∘C and for Tf=21∘C

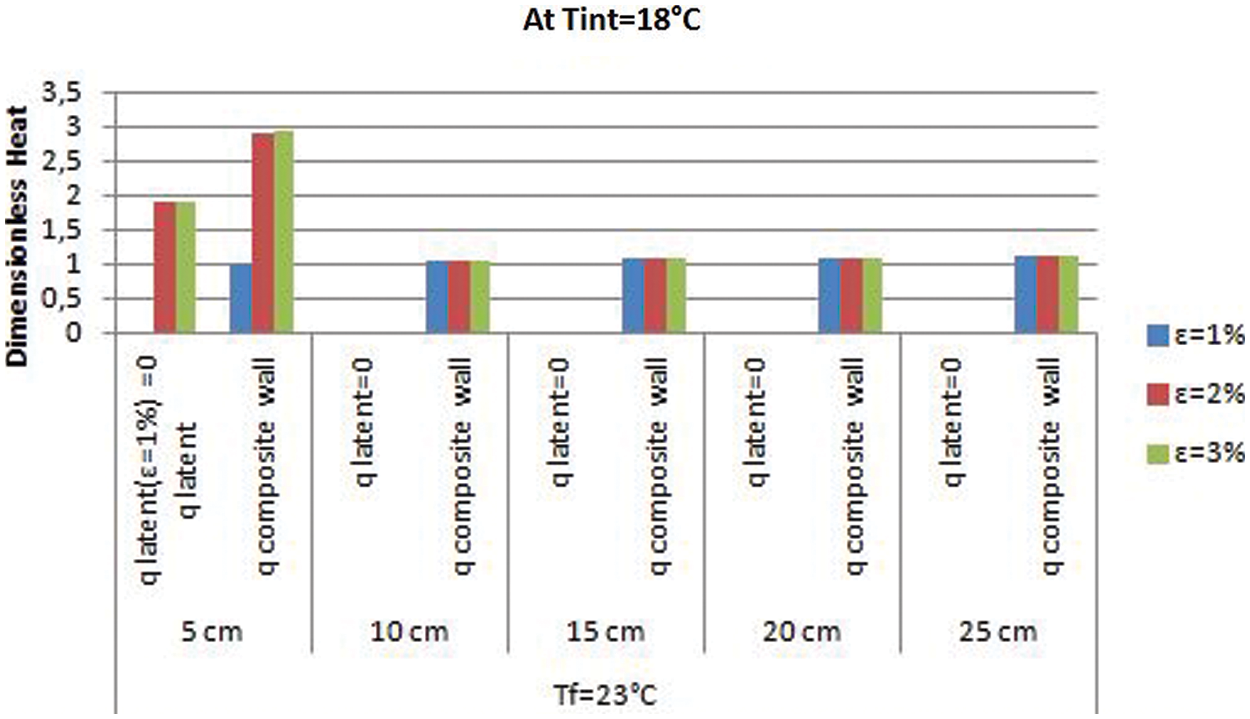
Figure 4: Dimensionless latent and global heat histograms at Tint=18∘C and for Tf=23∘C

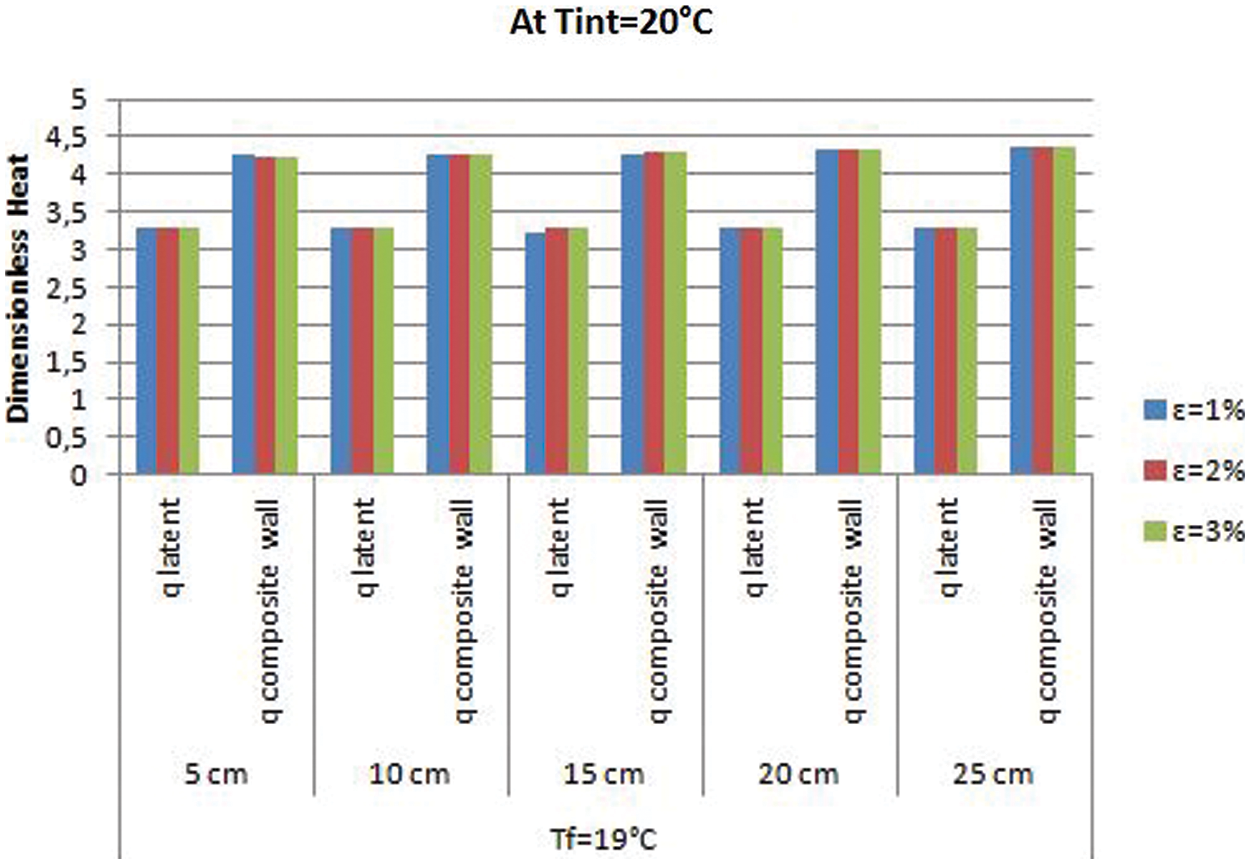
Figure 5: Dimensionless latent and global heat histogram at Tint=20∘C and for Tf=19∘C

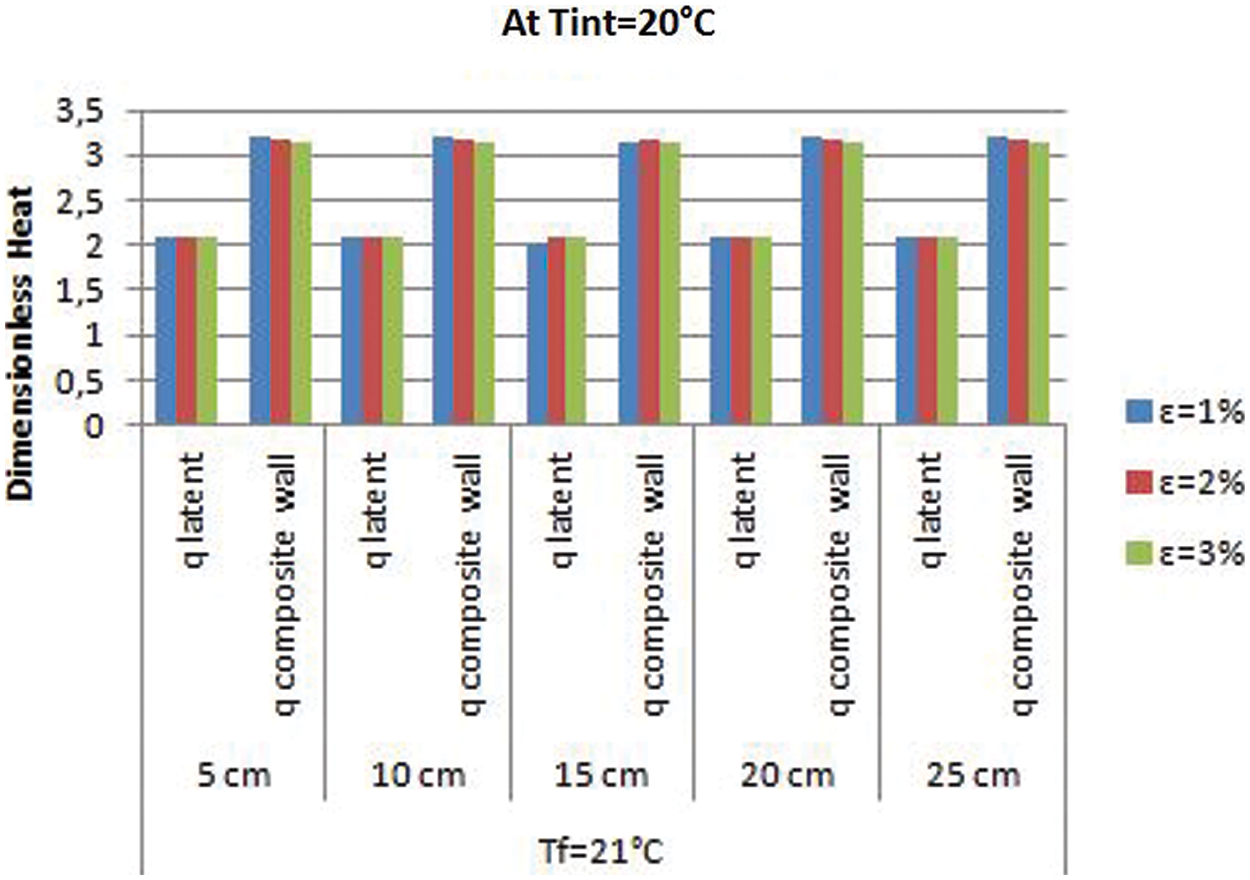
Figure 6: Dimensionless latent and global heat histograms at Tint=20∘C and for Tf=21∘C

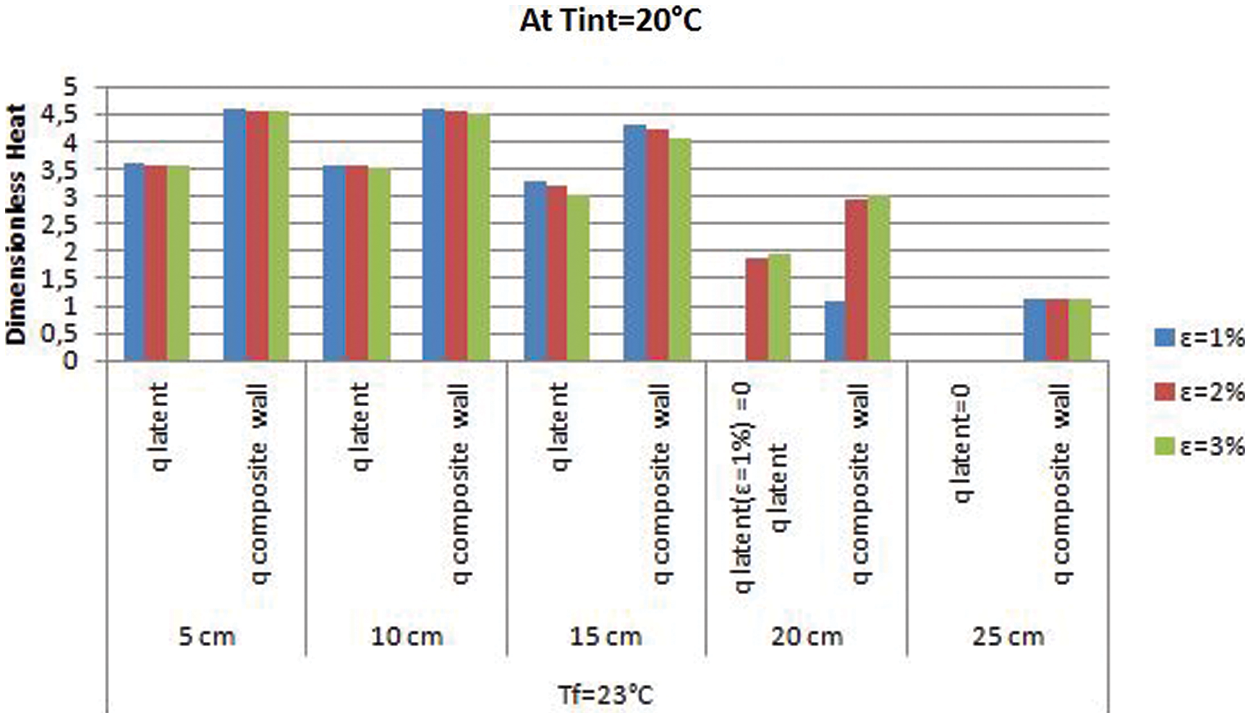
Figure 7: Dimensionless latent and global heat histograms at Tint=20∘C and for Tf=23∘C

We noted that the PCM with the melting temperature (19°C) is associated with a thermal state characterized by a continuous melting in which all the amounts of qPCMLatent are different from zero and qcompositewall takes high values for all locations. Moreover, the amounts of the dimensionless latent and global heat for PCM Tf=19∘C are more efficient at Tint=20∘C than at Tint=18∘C .

However, for the melting temperatures 21°C and 23°C, there is melting or an absence of melting depending on the melting interval, the thermal level, the comfort temperature of the conditioned room and the PCM location within the wall. For the PCM of melting temperature (21°C), the best results are shown at Tint=20∘C . At Tint=18∘C , we notice the absence of melting only in the PCM location equal to 25 cm and for the melting factor ε = 1% and 2%. Thus, the continuous melting is noted for the other locations according to the variation of ε . For the PCM of melting temperature (23°C), the results are the best at Tint=20∘C . Each PCM location and each melting factor ε involve different results. Thus, this has a direct influence on the melting or the absence of melting of the PCM inside the partition wall.

Results of the study show that the PCM embedding is beneficial in terms of charged energy, for all the cases when qcompositewall≻1 . PCM enhances the amount of charged energy when the melting temperature range and level, and the PCM emplacement are suitable. Increasing melting factor and judicious location are characterized by qPCMLATENT≠0 , which gives the best results. Furthermore, the results show that PCM must have a thermal level of melting close to the comfort temperature, localized in the vicinity of local under activity.

4  Conclusion

In this paper, we have studied the effect of the location, the melting temperature, and the melting range factor ε on the PCM’s fusion. We have been interested in latent heat charged in the PCM and the global heat charged in the composite partition wall separating two locals with different thermal environments. PCM embedding enhances the amount of the charged energy when the thermal level of melting is close to the comfort temperature of the conditioned room, as well as when the PCM location is not so far from the adjacent local. The best results are noticed when the dimensionless global heat charged in the composite wall is, qcompositewall≻1 and the dimensionless latent heat charged in PCM is qPCMLATENT≠0 . This shows that the wall with PCM is more efficient than the referential one and indicates that the melting takes place for judicious emplacements of the PCM and the appropriate melting level. PCM increases the energy involved in the composite partition wall and reduces the energy transmitted to the conditioned room. In addition, results indicate that the increase of the melting factor ε and the variation of the external maximum temperature could give the best storage performance.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Jain, M., Pathak, K. K. (2018). Thermal modelling of insulator for energy saving in existing residential building. Journal of Building Engineering, 19(4), 62–68. DOI 10.1016/j.jobe.2018.04.012. [Google Scholar] [CrossRef]

 2.  Barrios, G., Huels, G., Rojas, J. (2012). Thermal performance of envelope wall/roofs of intermittent air conditioned rooms. Applied Thermal Engineering, 40, 1–7. DOI 10.1016/j.applthermaleng.2012.01.051. [Google Scholar] [CrossRef]

 3.  Kanchidurai, S., Krishanan, P. A., Baskar, K., Mohan, K. S. R. (2019). Strength characteristic of novel mesh embedment technique for new brick construction with least expensive material. Engineering Structures, 178(2), 484–492. DOI 10.1016/j.engstruct.2018.10.062. [Google Scholar] [CrossRef]

 4.  Stritih, U., Tyagi, V. V., Stropnik, R., Paksoy, H., Haghighat, F. et al. (2018). Integration of passive PCM technologies for net-zero energy buildings. Sustainable Cities and Society, 41(6), 286–295. DOI 10.1016/j.scs.2018.04.036. [Google Scholar] [CrossRef]

 5.  Tatsidjodoung, P., Le Pierrès, N., Luo, L. (2013). A review of potential materials for thermal energy storage in building applications. Renewable and Sustainable Energy Reviews, 18, 327–349. DOI 10.1016/j.rser.2012.10.025. [Google Scholar] [CrossRef]

 6.  Saffari, M., Gracia, A., Fernández, C., Cabeza, L. F. (2017). Simulation-based optimization of PCM melting temperature to improve the energy performance in buildings. Applied Energy, 202, 420–434. DOI 10.1016/j.apenergy.2017.05.107. [Google Scholar] [CrossRef]

 7.  Liu, M., Saman, W., Bruno, F. (2012). Development of a novel refrigeration system for refrigerated trucks incorporating phase change material. Applied Energy, 92, 336–342. DOI 10.1016/j.apenergy.2011.10.015. [Google Scholar] [CrossRef]

 8.  Nomura, T., Okinaka, N., Akiyama, T. (2010). Waste heat transportation system, using phase change material (PCM) from steelworks to chemical plant. Resources, Conservation and Recycling, 54(11), 1000–1006. DOI 10.1016/j.resconrec.2010.02.007. [Google Scholar] [CrossRef]

 9.  Wen, S., Fleming, E., Shi, L., da Silva, A. K. (2014). Numerical optimization and power output control of a hot thermal battery with phase change material. Numerical Heat Transfer, Part A: Applications, 65(9), 825–843. DOI 10.1080/10407782.2013.846621. [Google Scholar] [CrossRef]

10. Hammou, Z. A., Lacroix, M. (2005). A new PCM storage system for managing simultaneously solar and electric Power. Energy and Building, 38(3), 258–265. [Google Scholar]

11. Koś.ny, J., Biswas, K., Miller, W., Kriner, S. (2012). Field thermal performance of naturally ventilated solar roof with PCM heat sink. Solar Energy, 86(9), 2504–2514. [Google Scholar]

12. Zhou, G., Yang, Y., Wang, X., Cheng, J. (2010). Thermal characteristics of shape-stabilized phase change material wallboard with periodical outside temperature waves. Applied Energy, 87(8), 2666–2672. DOI 10.1016/j.apenergy.2010.02.001. [Google Scholar] [CrossRef]

13. Li, D., Zheng, Y., Liu, C., Wu, G. (2015). Numerical analysis on thermal performance of roof contained PCM of a single residential building. Energy Conversion and Management, 100(1), 147–156. DOI 10.1016/j.enconman.2015.05.014. [Google Scholar] [CrossRef]

14. Hamza, H., Hanchi, N., Abouelkhayrat, B., Lahjomri, J., Oubarra, A. (2016). Location and thickness effect of two phase change materials between layers of roof on energy consumption for air-conditioned room. Journal of Thermal Science and Engineering Applications, 8(2), 1–7. DOI 10.1115/1.4031924. [Google Scholar] [CrossRef]

15. Hanchi, N., Hamza, H., Zniber, K., Lahjomri, J., Oubarra, A. (2021). Effect of phase change material insertion on thermal energy stored inside a partition wall separating a conditioned room and a room of periodic temperature. Computational Thermal Sciences, 13(4), 77–92. DOI 10.1615/ComputThermalScien.v13.i4.50. [Google Scholar] [CrossRef]

16. Hanchi, N., Hamza, H., Idmoussa, R., Lahjomri, J., Oubarra, A. (2020). Influence of thermal insulation’s and phase change material’s insertion within a partition wall on the energy consumption of a conditioned room under adjacent local periodical temperature effect. MATEC Web of Conferences, 307, 01024. DOI 10.1051/matecconf/202030701024. [Google Scholar] [CrossRef]

17. Alexiades, V., Solomon, A. D. (1993). Mathematical modeling of melting and freezing processes. Washington DC: Hemisphere Publishing Corporation. [Google Scholar]

18. Socaciu, L., Pleşa, A., Ungureşan, P., Giurgiu, O. (2014). Review on phase change materials for building applications. Leonardo Electronic Journal of Practices and Technologies, 25, 179–194. [Google Scholar]