Bending and Free Vibration Analysis of Porous-Functionally-Graded (PFG) Beams Resting on Elastic Foundations

Nomenclature

1  Introduction

Nowadays functionally graded materials (FGMs) are an alternative materials widely used in aerospace, nuclear, automotive civil, biomechanical, mechanical, electronic, chemical, and shipbuilding industries. FGMs have been proposed, developed and successfully used in industrial applications since 1980’s [1]. FGMs are microscopically inhomogeneous and spatial composite materials which are usually composed of two different materials such as a pair of ceramic-metal.

Several studies have been performed to analyze the mechanical responses of FG structures. Simsek et al. [2] have investigated the free and forced vibration characteristics of an FG Euler–Bernoulli beam under a moving harmonic load. Hu et al. [3] presented a parametric study on vibration and stability behavior of the functionally graded ceramic-metal plate subjected to in-plane excitation. Akbaş [4] studied the wave propagation of a functionally graded beam in thermal environments.

In FGM fabrication, micro voids or porosities can occur within the materials during the process of sintering. This is because of the large difference in solidification temperatures between material constituents [5]. Recently, Wattanasakulpong et al. [6] studied linear and nonlinear vibration problems of elastically end restrained FG beams having porosities. Beg et al. [7] investigated exact third-order static and free vibration analyses of functionally graded porous curved beam.

Structures resting on an elastic foundation are used in a variety of fields, including missile and rocket launchers in the military and aerospace industries, various applications in technology, civil and mechanical engineering, industry. Therefore, it is critical to include the superstructure-foundation-soil interaction in modern structural design and analysis for the applications to be adequately served.

In the years that followed, scientists experimented with different soil continuity factors to make the Winkler foundation model more realistic One of these models is the Winkler-Pasternak type foundation model with two parameters which includes shearing layer and Winkler layer has been the most widely utilized of these models [8]. The examination of bending and vibration of perfect/imperfect FG beams resting the elastic foundation is still an attractive topic for scientists.

According to the preceding literature review, while numerous researchers have been performed for mechanical behaviors of FG structures with or without elastic foundations, the number of studies on the bending and free vibration of FG beams including the effects of two-parameter elastic foundations and porosity simultaneously is still limited. Hence, the current study attempts to address the banding and free vibration of imperfect FG beams resting on two-parameter elastic foundations. The impacts of the two-parameter elastic foundation, porosity volume fraction, type of porosity models, and and span-to-depth ratio, on the bending and fundamental natural frequency of the beams, are investigated in detail.

2  Refined Beam Theory for Functionally Graded Beams

2.1 Preliminary Concepts and Definitions

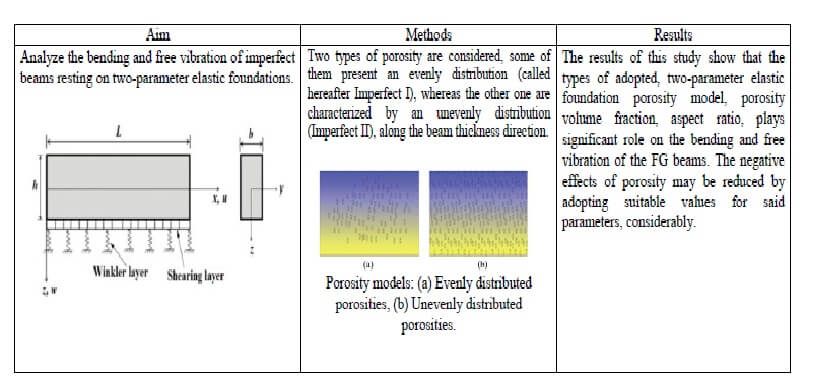
Consider a functionally graded beam with length L and rectangular cross section b × h, with b being the width and h being the height as shown in Fig. 1. The beam is made of isotropic material with material properties varying smoothly in the thickness direction.

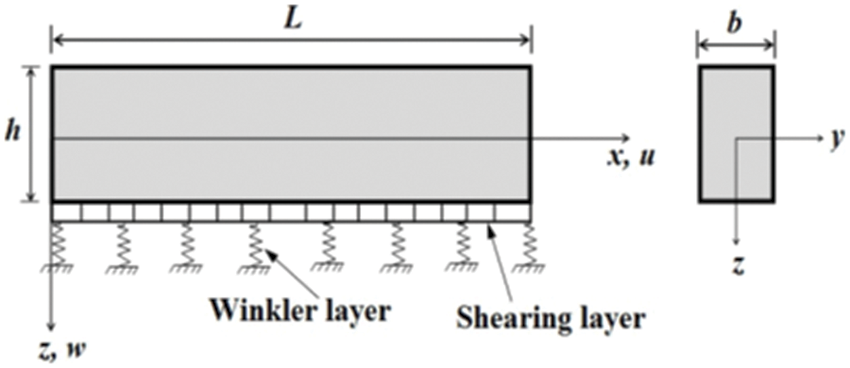
Figure 1: FGM Beam resting on a two parameters elastic foundation

2.2 Material Properties

Beam’s material is made from metal with a volume fraction Vm(z) and from ceramic with a volume fraction Vc(z). The volume fraction of ingredient materials is distributed as the equations below:

Vc(z)=(zh+12)k,Vm(z)=1−Vc(z), (1)

where k is volume fraction index 0 ≤ k ≤ ∞. In case k = 0, the beam is made entirely from ceramic. When k = ∞ the beam made completely from metal. Coefficient k defines the material distribution of the structure.

The characteristic of material made beams are written

P(z)=(Pc−Pm)(zh+12)k+Pm−Ppor (2)

In this study, two types of porosity are considered, some of them present an evenly distribution (called hereafter Imperfect I), whereas the other one are characterized by an unevenly distribution (Imperfect II), along the beam thickness direction (Fig. 2).

Figure 2: Porosity models: (a) Evenly distributed porosities, (b) Unevenly distributed porosities

The various expressions of the porosity distribution are presented in the following equations:

Imperfect-I:

Ppor=α2(Pc+Pm) (3)

Imperfect-II:

Ppor=α2(1−2|z|h)(Pc+Pm) (4)

The material properties of FGM porous beam such as the elastic modulus E, the thermal expansion coefficient β, and mass density ρ can be written, for the various porosity distribution models, as follows:

Imperfect-I:

[E(z)β(z)ρ(z)]=[Ecmβcmρcm](zh+12)k+[Emβmρm]−α2[Ec+Emβc+βmρc+ρm] (5a)

Imperfect-II:

[E(z)β(z)ρ(z)]=[Ecmβcmρcm](zh+12)k+[Emβmρm]−α2(1−2|z|h)[Ec+Emβc+βmρc+ρm] (5b)

where

Ecm = Ec − Em, βcm = βc − βm, ρcm = ρc − ρm and the Poisson ratio ν(z) is assumed to be constant ν(z) = ν.

2.3 Kinematics and Constitutive Equations

The assumed displacement field is as follows:

u(x,z,t)=u0(x,t)−z∂wb∂x−f(z)∂ws∂x (6a)

w(x,z,t)=wb(x,t)+ws(x,t) (6b)

The strains associated with the displacements in Eqs. (6a) and (6b) are

εx=εx0+zkxb+f(z) kxs (7a)

γxz=g(z) γxzs (7b)

where

εx0=∂u0∂x,kxb=−∂2wb∂x2,kxs=−∂2ws∂x2,γxzs=∂ws∂x (7c)

f(z)=hsinh⁡(zh)−z(cosh⁡(12)−1),g(z)=1−df(z)dz (7d)

By assuming that the material of FG beam obeys Hooke’s law, the stresses in the beam become

σx=Q11(z)εxandτxz=Q55(z)γxz (8a)

where

Q11(z)=E(z)andQ55(z)=E(z)2(1+ν) (8b)

2.4 Equations of Motion

Hamilton’s principle is used herein to derive the equations of motion. The principle can be stated in analytical form as [9]

∫t1t2(δU+δUef+δV−δK)dt=0 (9)

where t is the time; t1 and t2 are the initial and end time, respectively; δU is the virtual variation of the strain energy; δUef the potential energy of elastic foundation; δV is the variation of work done by external forces; and δK is the virtual variation of the kinetic energy. The variation of the strain energy of the beam can be stated as

δU=∫0L∫−h2h2(σxδεx+τxzδγxz)dzdx=∫0L(Nxdδu0dx−Mxbd2δwbdx2−Mxsd2δwsdx2+Qxzdδwsdx)dx (10)

where Nx, Mxb , Mxs and Qxz are the stress resultants defined as

(Nx,Mxb,Mxs)=∫−h2h2(1,z,f(z))σxdzandQxz=∫−h2h2g(z)τxzdz (11)

The variation of the potential energy of elastic foundation given by

δUef=∫0L[KW(wb+ws)δ(wb+ws)−KP∂2(wb+ws)∂x2δ(wb+ws)]dx (12)

where KW and KP are the transverse and shear stiffness coefficients of the foundation, respectively.

The variation of work done by externally transverse load q can be expressed as

δV=−∫0Lqδ(wb+ws)dx (13)

The variation of the kinetic energy can be expressed as

δK=∫0L∫−h2h2ρ(z)[u˙δu˙+w˙δw˙]dznsdx=∫0L{I0[u˙0δu˙0+(w˙b+w˙s)(δw˙b+δw˙s)]−I1(u˙0dδw˙bdx+dw˙bdxδu˙0)+I2(dw˙bdxdδw˙bdx)−J1(u˙0dδw˙sdx+dw˙sdxδu˙0)+K2(dw˙sdxdδw˙sdx)+J2(dw˙bdxdδw˙sdx+dw˙sdxdδw˙bdx)}dx (14)

where dot-superscript convention indicates the differentiation with respect to the time variable t; ρ(z) is the mass density; and (I0, I1, J1, I2, J2, K2) are the mass inertias defined as

(I0,I1,J1,I2,J2,K2)=∫−h2h2(1,z,f,z2,zf,f2)ρ(z)dz (15)

Substituting the expressions for δU, δUef, δV and δT from Eqs. (10), (12)−(14) into Eq. (9) and integrating the displacement gradients by parts and setting the coefficients of δu0, δwb and δws to zero separately, the following equations of motion are obtained:

δu0:dNxdx=I0u¨0−I1dw¨bdx−J1dw¨sdx (16a)

δwb:d2Mbdx2+q+KP(d2(wb+ws)dx2)−KW(wb+ws)=I0(w¨b+w¨s)+I1du¨0dx−I2d2w¨bdx2−J2d2w¨sdx2 (16b)

δws:d2Msdx2+dQxzdx+q+KP(d2(wb+ws)dx2)−KW(wb+ws)=I0(w¨b+w¨s)+J1du¨0dx−J2d2w¨bdx2−K2d2w¨sdx2 (16c)

Introducing Eq. (11) into Eqs. (16a)–(16c), the equations of motion can be expressed in terms of displacements (u0, wb,ws) and the appropriate equations take the form

A11∂2u0∂x2−B11∂3wb∂x3−B11s∂3ws∂x3=I0u¨0−I1dw¨bdx−J1dw¨sdx (17a)

B11∂3u0∂x3−D11∂4wb∂x4−D11s∂4ws∂x4+q+KP(d2(wb+ws)dx2)−KW(wb+ws)=I0(w¨b+w¨s)+I1du¨0dx−I2d2w¨bdx2−J2d2w¨sdx2 (17b)

B11s∂3u0∂x3−D11s∂4wb∂x4−H11s∂4ws∂x4+A55s∂2ws∂x2+q+KP(d2(wb+ws)dx2)−KW(wb+ws)=I0(w¨b+w¨s)+J1du¨0dx−J2d2w¨bdx2−K2d2w¨sdx2 (17c)

where A11, D11, etc., are the beam stiffness, defined by

(Aij,Aijs,Bij,Dij,Bijs,Dijs,Hijs)=∫−h2h2Qij(1,g2(z),z,z2,f(z),zf(z),f2(z))dz (18)

3  Analytical Solution

Navier-type analytical solutions are obtained for the bending and free vibration analysis of functionally graded beams resting on two parameter elastic foundation. According to the Navier-type solution technique, the unknown displacement variables are expanded in a Fourier series as given below:

{u0wbws}=∑m=1∞{Umcos⁡(λx)eiωtWbmsin⁡(λx)eiωtWsmsin⁡(λx)eiωt} (19)

where Um, Wbm, and Wsm are arbitrary parameters to be determined, ω is the eigenfrequency associated with mth eigenmode, and λ = mπ/L.

The transverse load q is also expanded in Fourier series as

q(x)=∑m=1,3,5∞Qmsin⁡λx (20)

where Qm is the load amplitude calculated from

Qm=2L∫0Lq(x)sin⁡(λx)dx (21)

The coefficients Qm are given below for some typical loads. For the case of a sinusoidally distributed load, we have

m=1andQ1=q0 (22)

Substituting Eqs. (19) and (20) into Eq. (17), the analytical solutions can be obtained by the eigenvalue equations below, for any fixed value of m.

For free vibration problem:

([K]−ω2[M]){Δ}={0} (23a)

For static problems, we obtain the following operator equation:

[K]{Δ}={F} (23b)

where

[K]=[a11a12a13a12a22a23a13a23a33], (24a)

[M]=[m11m12m13m12m22m23m13m23m33], (24b)

and

{Δ}={UmWbmWsm},{F}={0QmQm} (24c)

with

a11=A11α2,a12=−B11α3,

a13=−B11sα3,a22=D11α4+Kw+Kpα2,

a23=D11sα4+Kw+Kpα2, (25a)

a23=H11sα4+A55sα2+Kw+Kpα2

m11=I0,m12=−I1α,

m13=−J1α,m22=I0+I2α2, (25b)

m23=I0+J2α2,

m33=I0+K2α2

4  Results and Discussion

This section looks at the current situation using numerical examples. The imperfect/perfect FG beams on elastic foundations supposed to be composed of Al (metal) and Al2O3 (ceramic). (ceramic The material properties are taken to be Em = 70 GPa; ν = 0.3; ρm = 2702 kg/m3; Ec = 380 GPa; ν = 0.3; ρc = 3960 kg/m3 and the subsequent non-dimensional forms are used

w¯=100Emh3q0L4w(L2),σ¯x=hq0Lσx(L2,h2),τ¯xz=hq0Lτxz(0,0),ω¯=ωL2hρmEm

Finally, the non-dimensional elastic foundation parameters are: ξw=Kwl2Emh,ξp=KpEmh .

Note that ξw = ξp = 0, ξw = 0.1, ξp = 0 and ξw = ξp = 0.1 represents the foundationless case, Winkler foundation case and Winkler-Pasternak foundation case, α = 0 indicates perfect FG beams and α = 0.1 and 0.2 indicate imperfect FG beams, respectively.

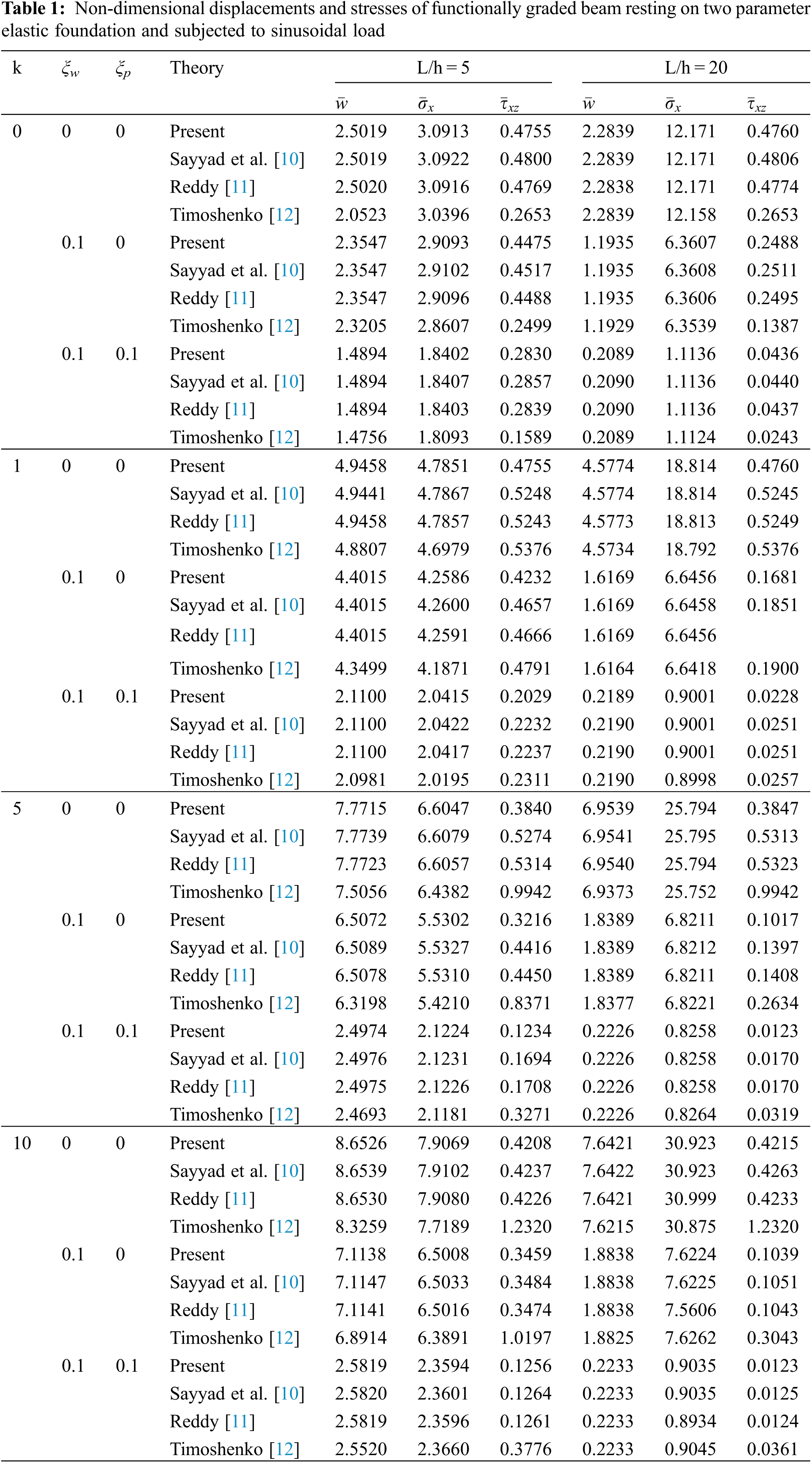
Example 1: To begin, comparison is done to establish the existing formulations’ validity. For this aim, the results for perfect FG beam with and without elastic foundation are compared those of references [10–12]. Table 1 reveals that present findings are consistent with those previously reported. Here aspect ratios is taken to be L/h = 5 and 20.

Example 2: In order to explicitly understand the porosity effect on the bending behavior of FG beams, Fig. 3 shows variations of the nondimensional axial normal stress σ¯x of FG perfect and imperfect beams across the depth under sinusoidal load at a constant value of span-to-depth ratio (L/h = 5). From this figure, it can be concluded that the influence of the porosity on the bending of imperfect beams with even porosities distribution (Imperfect-I) and uneven porosities distribution (Imperfect-II) is very clear. The stresses are tensile at the top surface and compressive at the bottom surface and take the maximum and the minimum values for the even porosities distribution (Imperfect-I), respectively.

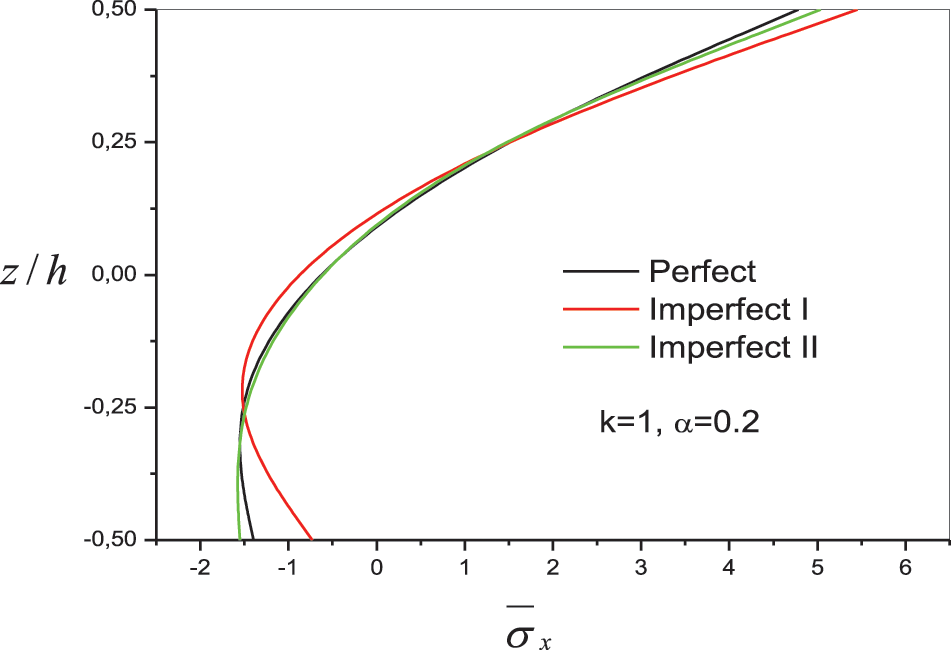
Figure 3: Variation of nondimensional axial normal stress σ¯x(l/2,z) of embedded perfect and imperfect FG beams across the depth

Fig. 4 shows the distribution of the shear stresses of embedded perfect and imperfect FG beams across the depth under sinusoidal load. The volume fraction exponent of the FG beam in taken as k = 1. It is clear that the distributions are not parabolic and the stresses increase for the imperfect FG beam. The even porosities distribution (Imperfect-I) gives the highest value of shear stress compared to other distributions of porosity.

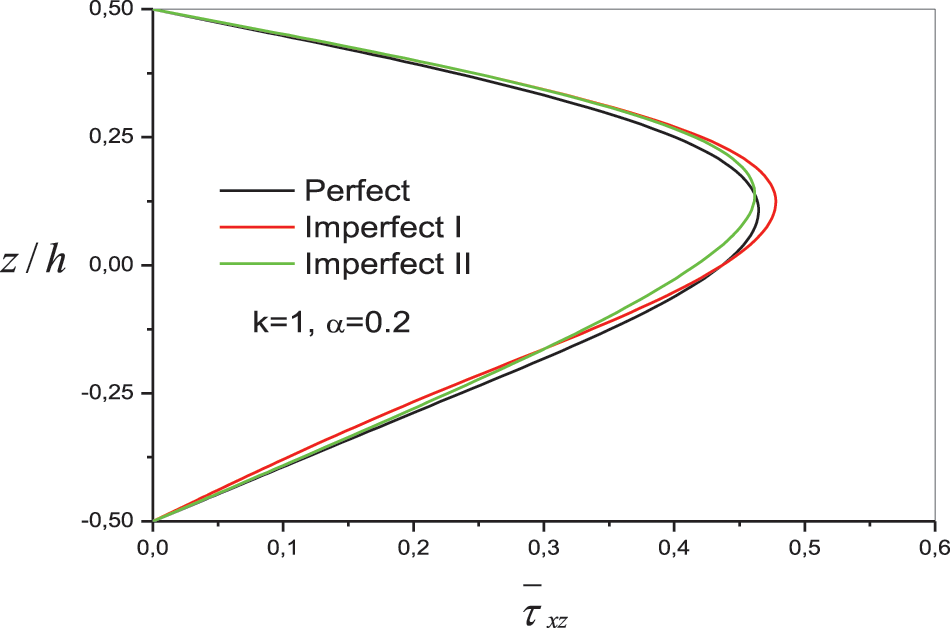
Figure 4: Variation of nondimensional transverse shear stress τ¯xz(0,z) of embedded perfect and imperfect FG beams across the depth of FG beams

Example 3: Table 2 shows the variations of the fundamental frequencies of perfect and imperfect FG beams with and without elastic foundations vs. varying volume fraction index, k. Here aspect ratios is taken to be L/h = 5 and 20. The present results are compared with those presented by Sayyad et al. [10]. The examination of Table 2 reveals that the frequencies obtained using the present theory are in excellent agreement with the previously published results. It is observed that an increase in the value of the k index leads to a reduction of fundamental frequencies and a decrease in the value of elasticity modulud. Also, it is observed that the natural frequencies are increased when beam is resting on two parameters elastic foundation.

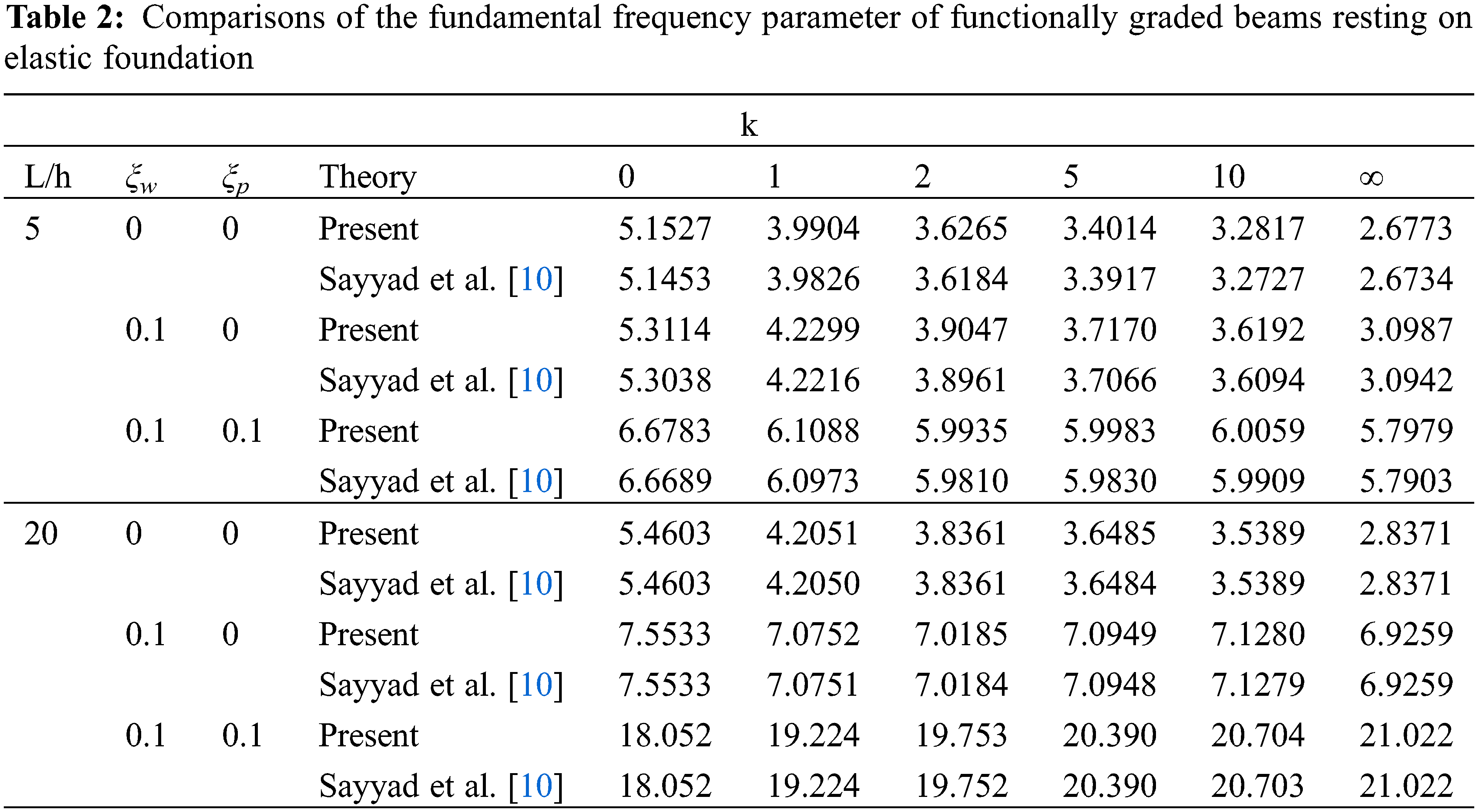
Fig. 5 illustrates the variation of the fundamental frequency ω¯ of embedded perfect and imperfect FG beams vs. L/h ratio with α = 0.2. It can be also seen that the span-to-depth ratio L/h has a considerable effect on the non-dimensional fundamental natural frequency ω¯ where this latter is reduced with decreasing L/h. This dependence is related to the effect of shear deformation.

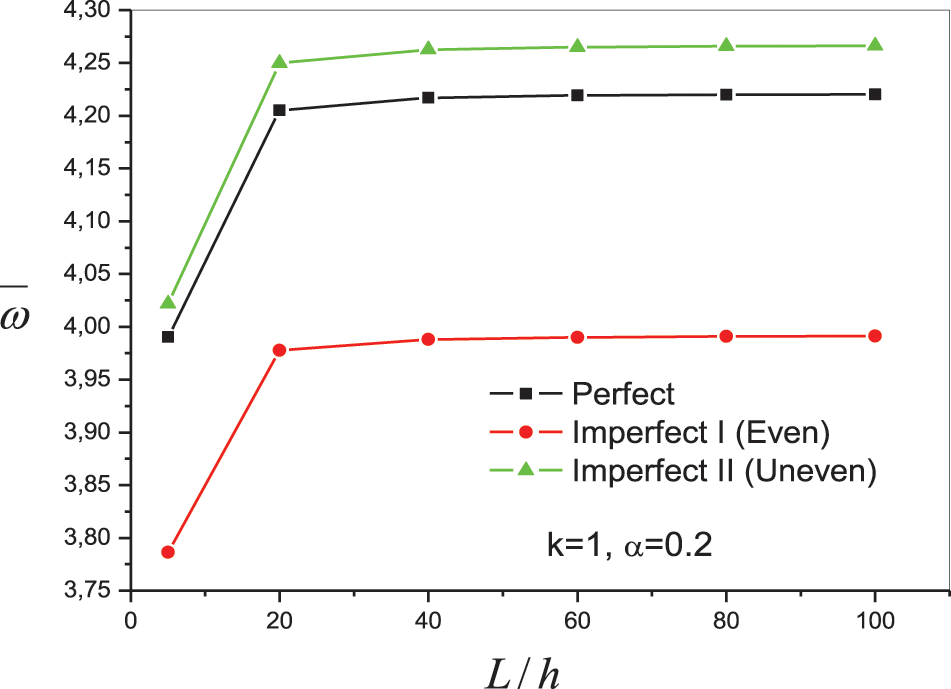
Figure 5: Variation of the fundamental frequency ω¯ of embedded perfect and imperfect FG beams vs. L/h ratio

5  Conclusions

In the present work, bending and free vibration of imperfect FG beams resting on two-parameter elastic foundations was investigated. To accomplish this, the material properties of the beam are assumed to change continuously along the thickness direction based on the volume fraction of constituents defined by the modified rule of the mixture. In addition, to describe the elastic foundation’s response on the imperfect FG beam, the foundation medium is assumed to be linear, homogenous, and isotropic, and it has been modeled using the Winkler-Pasternak model with two parameters. Moreover, in the kinematic relationship of the imperfect FG beam resting on a two-parameter elastic foundation, hyperbolic shear deformation theory is used, and the equations of motion are derived using Hamilton’s principle. For the bending and free vibration analysis of imperfect FG beams resting on a two-parameter elastic foundation with simply supported edges, an analytical solution is obtained. The impacts of the two-parameter elastic foundation, porosity volume fraction, type of porosity models, and aspect ratio, on the bending and fundamental natural frequency of the beams, are investigated in detail. Finally, it is concluded that the types of adopted, two-parameter elastic foundation porosity model, porosity volume fraction, aspect ratio, plays significant role on the bending and free vibration of the FG beams. The negative effects of porosity may be reduced by adopting suitable values for said parameters, considerably.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Koizumi, M. (1993). The concept of FGM. Ceramic transactions. Advanced Functional Materials, 34, 3–10. [Google Scholar]

 2.  Simsek, M., Kocaturk, T. (2009). Free and forced vibration of a functionally graded beam subjected to a concentrated moving harmonic load. Composite Structures, 90(4), 465–473. DOI 10.1016/j.compstruct.2009.04.024. [Google Scholar] [CrossRef]

 3.  Hu, Y. D., Zhang, X. G. (2011). Parametric vibrations and stability of a functionally graded plate. Mechanics Based Design of Structures and Machines, 39(3), 367–377. DOI 10.1080/15397734.2011.557970. [Google Scholar] [CrossRef]

 4.  Akbaş, S. D. (2015). Wave propagation of a functionally graded beam in thermal environments. Steel and Composite Structures, 19(6), 1421–1447. DOI 10.12989/scs.2015.19.6.1421. [Google Scholar] [CrossRef]

 5.  Zhu, J., Lai, Z., Yin, Z., Jeon, J., Lee, S. (2001). Fabrication of ZrO2–NiCr functionally graded material by powder metallurgy. Materials Chemistry and Physics, 68, 130–135. DOI 10.1016/S0254-0584(00)00355-2. [Google Scholar] [CrossRef]

 6.  Wattanasakulpong, N., Ungbhakorn, V. (2014). Linear and nonlinear vibration analysis of elastically restrained ends FGM beams with porosities. Aerospace Science and Technology, 32(1), 111–120. DOI 10.1016/j.ast.2013.12.002. [Google Scholar] [CrossRef]

 7.  Beg, M. S., Khalid, H. M., Yasin, M. Y., Hadji, L. (2021). Exact third-order static and free vibration analyses of functionally graded porous curved beam. Steel and Composite Structures, 39(1), 1–20. DOI 10.12989/scs.2021.39.1.001. [Google Scholar] [CrossRef]

 8.  Kerr, A. D. (1964). Elastic and viscoelastic foundation models. Journal of Applied Mechanics, 31, 491–498. DOI 10.1115/1.3629667. [Google Scholar] [CrossRef]

 9.  Thai, H. T., Choi, D. H. (2012). A refined shear deformation theory for free vibration of functionally graded plates on elastic foundation. Composites Part B: Engineering, 43(5), 2335–2347. DOI 10.1016/j.compositesb.2011.11.062. [Google Scholar] [CrossRef]

10. Sayyad, A. S., Ghugal, Y. M. (2018). Analytical solutions for bending, buckling, and vibration analyses of exponential functionally graded higher order beams. Asian Journal of Civil Engineering, 19, 607–623. DOI 10.1007/s42107-018-0046-z. [Google Scholar] [CrossRef]

11. Reddy, J. N. (1984). A simple higher order theory for laminated composite plates. ASME Journal of Applied Mechanics, 51, 745–75 2. DOI 10.1115/1.3167719. [Google Scholar] [CrossRef]

12. Timoshenko, S. P. (1921). On the correction for shear of the differential equation for transverse vibrations of prismatic bars. Philosophical Magazine, 41, 742–746. DOI 10.1080/14786442108636264. [Google Scholar] [CrossRef]