 Open Access
Open Access
ARTICLE
Influence of Thermophoresis and Brownian Motion of Nanoparticles on Radiative Chemically-Reacting MHD Hiemenz Flow over a Nonlinear Stretching Sheet with Heat Generation
1 Department of Engineering Mathematics, College of Engineering, Koneru Lakshmaiah Education Foundation, Vaddeswaram, Andhra Pradesh, 522302, India
2 Department of Mathematics, GITAM (Deemed to be University), Visakhapatnam, Andhra Pradesh, 530045, India
3 Department of Industrial Engineering, University of Parma-Parco Area Delle Scienze , Parma, 43124, Italy
* Corresponding Author: G. Lorenzini. Email:
Fluid Dynamics & Materials Processing 2023, 19(4), 855-868. https://doi.org/10.32604/fdmp.2022.019796
Received 15 October 2021; Accepted 22 February 2022; Issue published 02 November 2022
Abstract
In this study, a radiative MHD stagnation point flow over a nonlinear stretching sheet incorporating thermophoresis and Brownian motion is considered. Using a similarity method to reshape the underlying Partial differential equations into a set of ordinary differential equations (ODEs), the implications of heat generation, and chemical reaction on the flow field are described in detail. Moreover a Homotopy analysis method (HAM) is used to interpret the related mechanisms. It is found that an increase in the magnetic and velocity exponent parameters can damp the fluid velocity, while thermophoresis and Brownian motion promote specific thermal effects. The results also demonstrate that as the Brownian motion parameter is increased, the concentration values become smaller.Keywords
Nanofluids are nanometer-sized particles less than 100 nanometres in size that are introduced into base fluids such as oil, water, bio fluids, ethylene, and lubricants. Despite their essential worth in industry, medicine, and a variety of other efficacious domains of science and technology, countless researchers have gained an interest in nanofluids as opposed to other fluids. However, nanofluids still occupy an indispensable key position in medical sectors, such as the use of gold nanoparticles in the screening of cancerous tumours and the processing of minuscule bombs that are exploited to eradicate cancerous tumours. Choi [1] was the one who came up with the idea of nano materials. He inferred from his observations that infusing these particles strengthens the thermal conductivity of the fluid. Hayat et al. [2] produced analytical solutions for MHD nanofluid squeezing flow between two parallel plates. Hussain et al. [3] studied the dynamics of Jeffery nano-fluid across an exponentially stretched sheet, but also radiation consequences. In a magnetised nanofluid flow, Abbas et al. [4] investigated the role of thermal radiation and chemical reaction response. Hayat et al. [5] studied the characteristics of heat and mass transfer by imposing the convective conditions. Ganesh Kumar et al. [6] have investigated the boundary layer flows and melting heat transfer of a Prandtl fluid over a stretching surface in the presence of fluid particle suspensions. Jalali et al. [7] conducted a numerical investigation of the competition between viscosity and thermal conductivity about their effects on heat transfer by Al2O3-water nanofluid. Much insight on this theme can be found in [8–12].
Modern metallurgical and metal-working technologies rely heavily on understanding MHD flow of an electrically-conducting fluid. Mabood et al. [13] acknowledged the Laplace transform outcomes for the unsteady natural convective motion of revolving magnetohydrodynamics motion in a permeable medium over an oscillating sheet. Mahantesh et al. [14] inspected the effect of the chemical reaction of a magnetohydrodynamic free convective motion of a moving liquid over a vertical sheet. The problem of Marangoni mixed convection in the presence of an inclined magnetic field with uniform strength in a nanofluid is addressed numerically by Sastry et al. [15].
The Hiemenz flow pattern, including its applications in the monitoring of flows over submarine tips, ship tips, and aeroplanes, occupies a crucial role in the exploration of many industrial and natural phenomena. It’s also essential in various of fields, including hydrodynamic processes, electronic fan cooling, and nuclear device freezing, to name a few. The optimum values to the aforementioned phenomenon were provided by Ariel [16]. Motsa et al. [17] ascertained numerically the Maxwell fluid outcomes for two-dimensional Hiemenz flow on the way to a diminishing sheet. Parand et al. [18] assessed Hiemenz flow with heat transfer through a porous medium of an incompressible non-Newtonian Rivlin-Ericksen fluid.
In many industries, the significance of thermal radiation on MHD flow and heat transfer is rapidly getting crucial. Heat transfer by thermal radiation has substantial applications in space technology and projects that grasps high temperatures. Aamir Hamid et al. [19] looked at the implications of variable thermal conductivity on MHD Williamson nanofluid flow. A porous mechanism is a material that has a solid matrix and has an interconnected void that allows fluid to flow through it. Pandey et al. [20] reported the collective impact of thermal radiation and porous medium nanofluid flow. Bandari [21] examined the steady state of the two-dimensional incompressible magnetohydrodynamics (MHD) flow of a micropolar nanofluid over a stretching sheet in the presence of chemical reactions, radiation and viscous dissipation. Inayat et al. [22] examined the two-dimensional nanomaterials based mixed flow. The consequences of thermal radiation on convective phenomena in MHD nanofluid over a non-linear stretching surface under heat generation and chemical reaction were studied by considering thermophoresis and Brownian motion using HAM [23–27].
In evident references to modern works, our investigation “The effects of thermal radiation and chemical reaction on MHD Hiemenz flow over a non-linear stretching sheet in presence of thermophoresis and Brownian motion” will certainly appear more viable now. The investigation is approved out for the 2D steady MHD Hiemenz flow. Using a similarity method to reshape the underlying Partial differential equations into a set of ordinary differential equations (ODEs), the implications of heat generation, and chemical reaction on the flow field are described in detail. Moreover a Homotopy analysis method (HAM) is used to interpret the related mechanisms. The influence of numerous parameters is graphically studied and numerically investigated.
We review a non-linear continuously stretched horizontal plate impinging on a steady, two-dimensional, incompressible stagnation-point flow. The plate and free stream velocities are analogous to
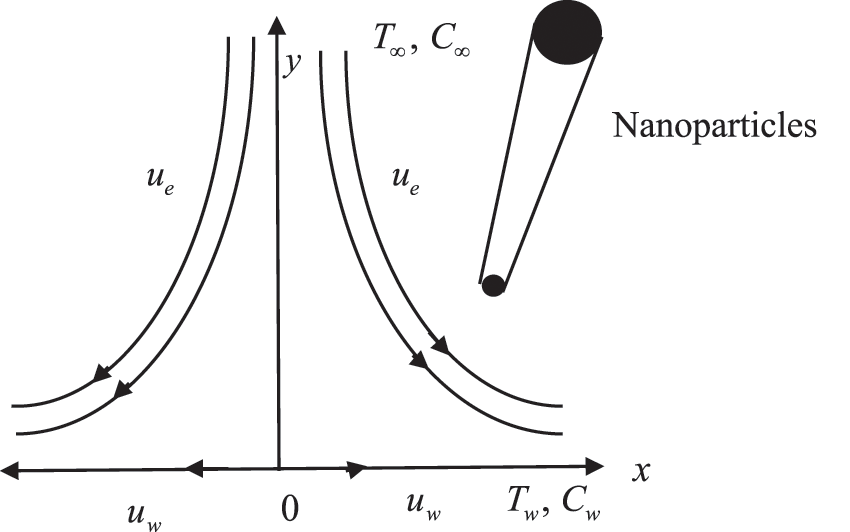
Figure 1: Physical model of the flow
•
• The nonlinear stretching velocity of the flat plate is assumed as
• The ambient fluid’s moving velocity has the form
• A variable magnetic field
Under above assumptions, the governing equations are
where ū, ⊽ are respectively the velocity constituents on the way to the
The appropriate boundary conditions are
where
The radiative heat flux is determined by using Rosseland approximation
where
Now, we introduce the following similarity transformations:
Substituting Eq. (6) in Eqs. (2)–(5), we obtain
where
The boundary conditions are
where prime denotes differentiation with respect to
Non-dimensional skin friction coefficient
where
Substituting
where
We now adopt aforementioned initial guesses and linear operators to encapsulate the homotopic solutions of Eqs. (7)–(10):
with
where
We construct the zeroth-order deformation equations
subject to the boundary conditions
where
where
The nth-order deformation equations are follows:
with the following boundary conditions:
where
Here we choose
3.2 Convergence of HAM Solution
The auxiliary parameters
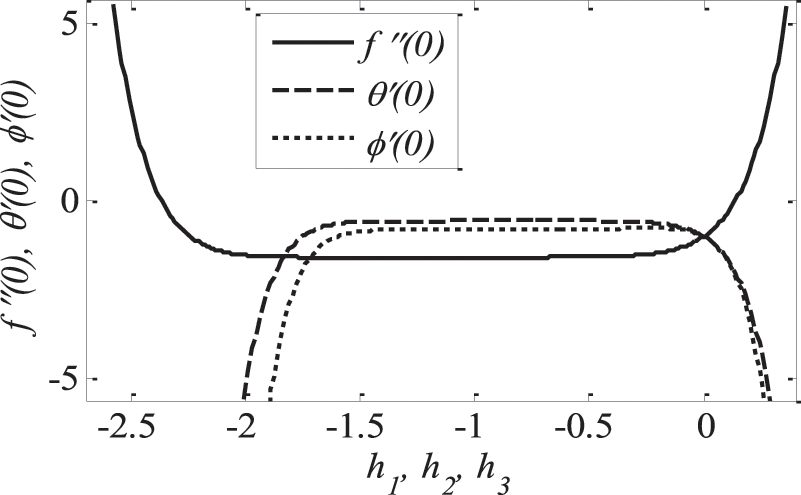
Figure 2:
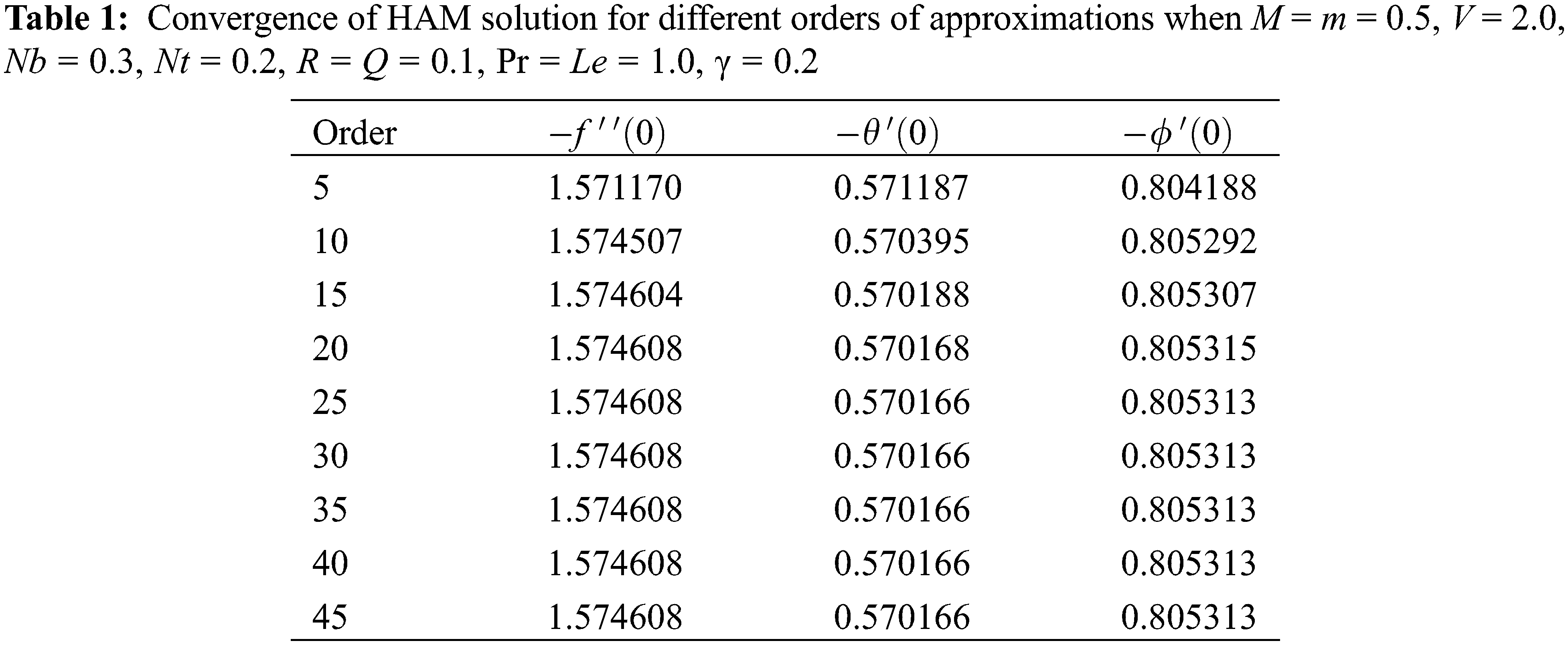
For a wide range of physical characteristics, tables and charts are often performed to ascertain and describe the nature of flow, temperature, concentration, skin friction coefficient, and local Nusselt and Sherwood numbers. We check out the following values all across the exploration, apart from renovated quantities as revealed in the tables and charts.
Figs. 3–5 illustrate the impression of magnetic parameter M on distributions. It is insinuated that as M strengthens the velocity distribution of the fluid degrades. Whenever a magnetic field is imparted to an electrically conducting fluid, the Lorentz force generates, and this energy contradicts the flow pattern, forcing velocity drawings to deteriorate, while the thermal and solutal boundary layer thickness improves. As the space variable turns away from the boundary surface, modifications in the velocity exponent parameter m restrain the growth of the momentum boundary layer, which reaches zero. The plots of temperature and concentration find similar results. This is shown in Figs. 6–8.
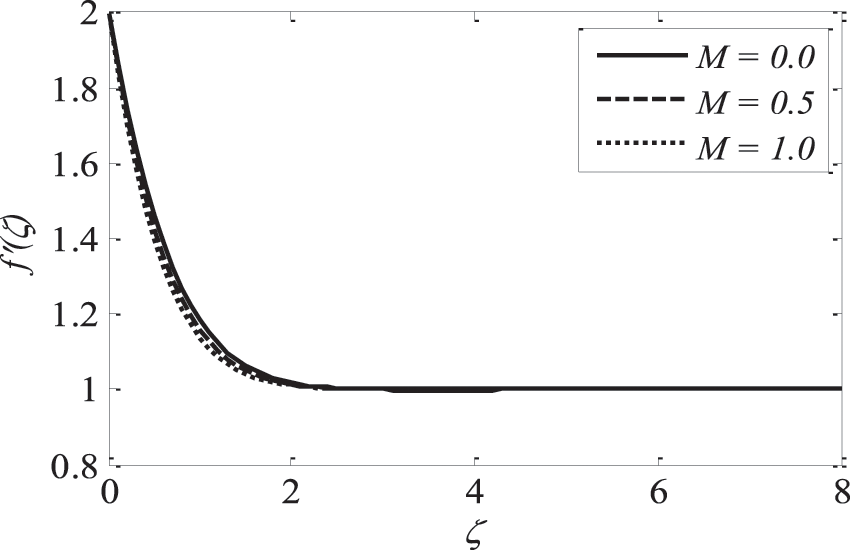
Figure 3: Effect of M on
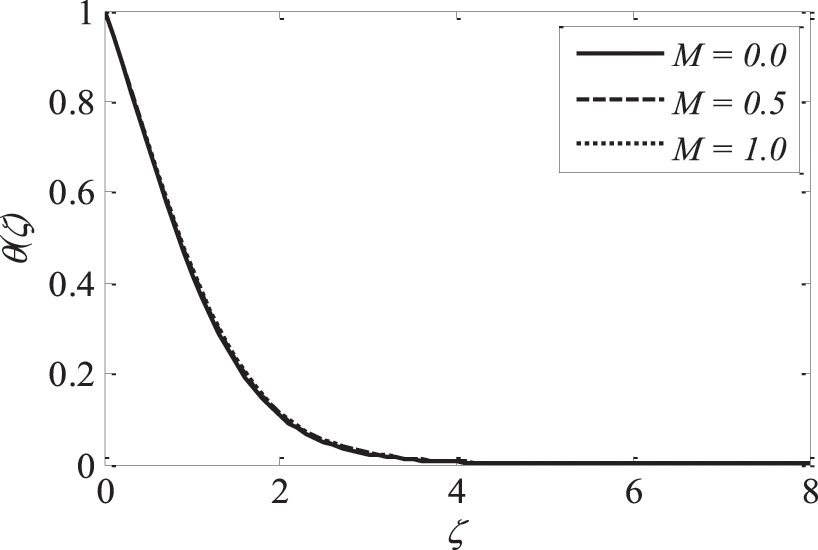
Figure 4: Effect of M on
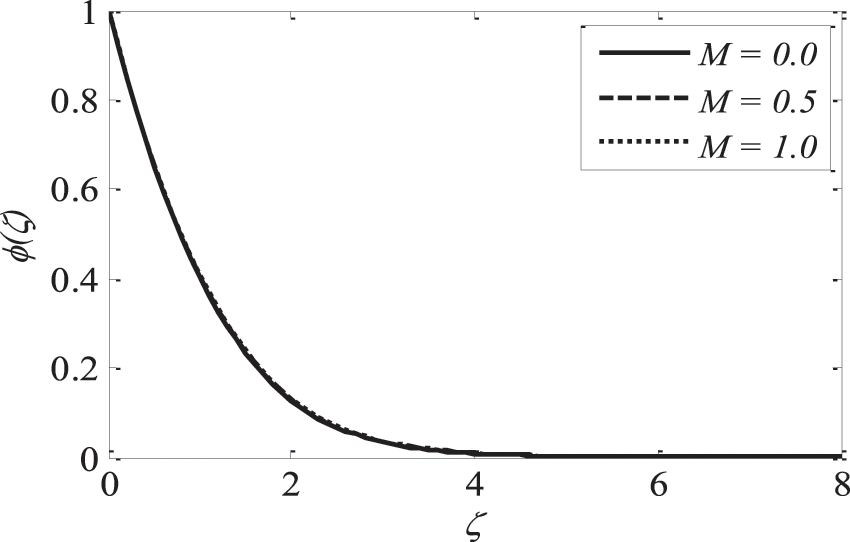
Figure 5: Effect of M on
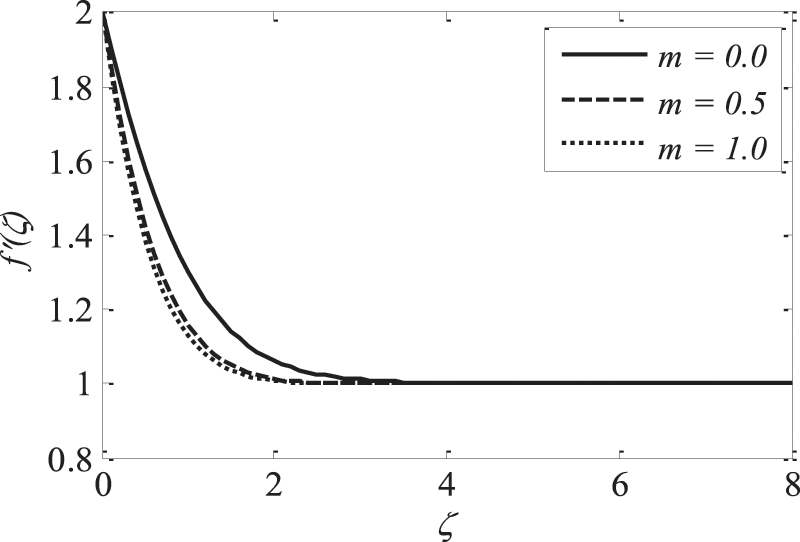
Figure 6: Effect of m on
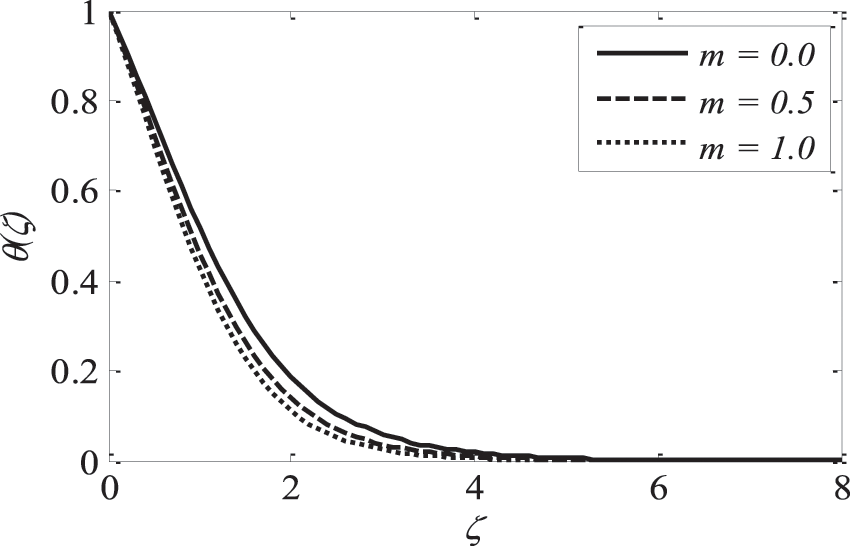
Figure 7: Effect of m on
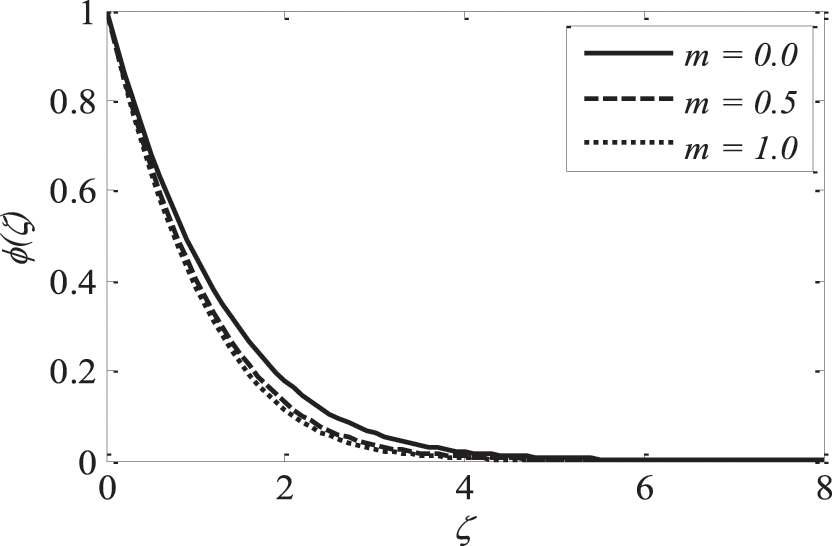
Figure 8: Effect of m on
Fluid velocity amplifies as the velocity ratio parameter V accelerates, whereas the fluid temperature and concentration drop. This is observed from Figs. 9–11. Figs. 12 and 13 reveal the implications of the Brownian motion parameter
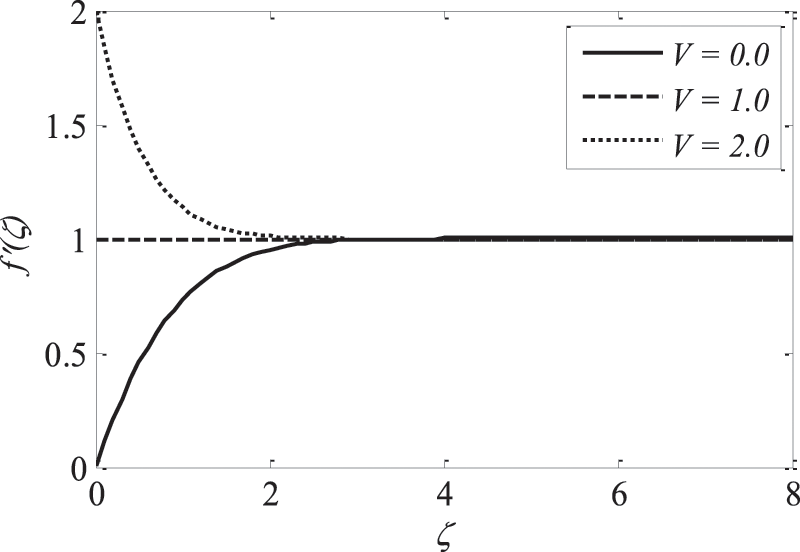
Figure 9: Effect of V on
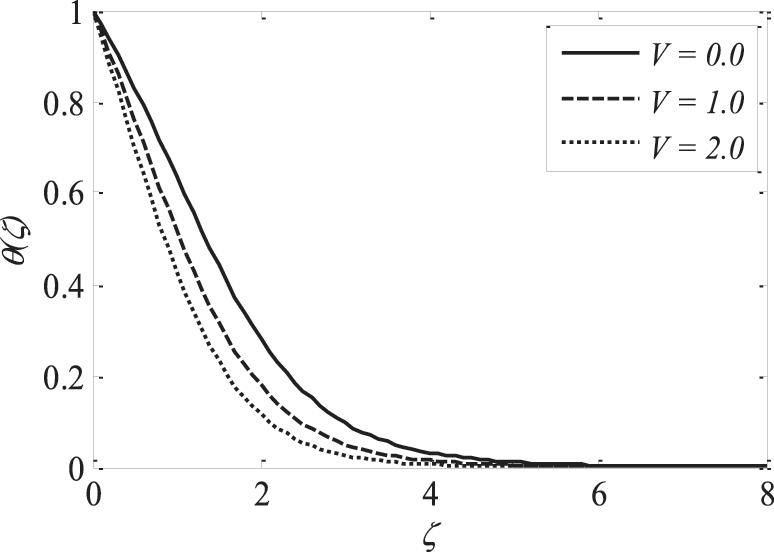
Figure 10: Effect of V on
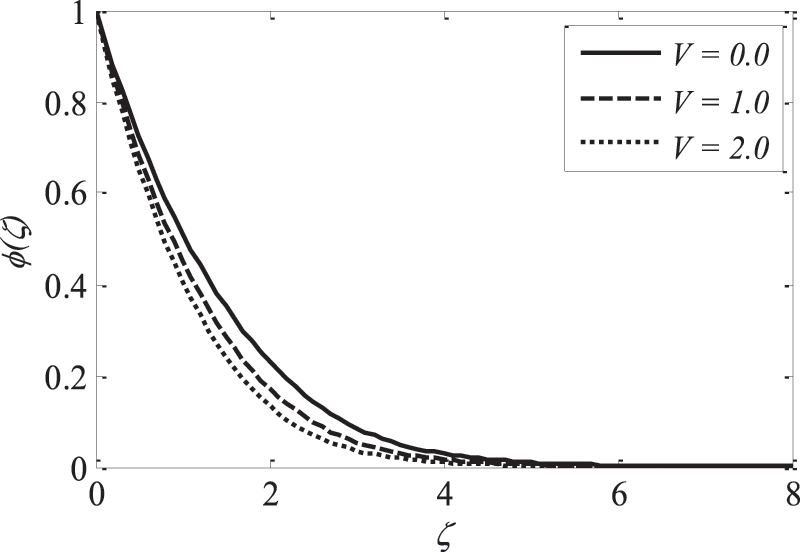
Figure 11: Effect of V on
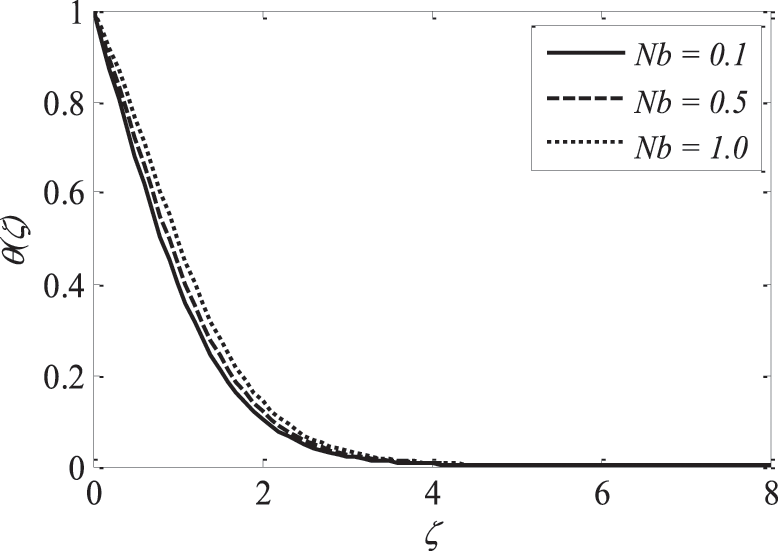
Figure 12: Effect of
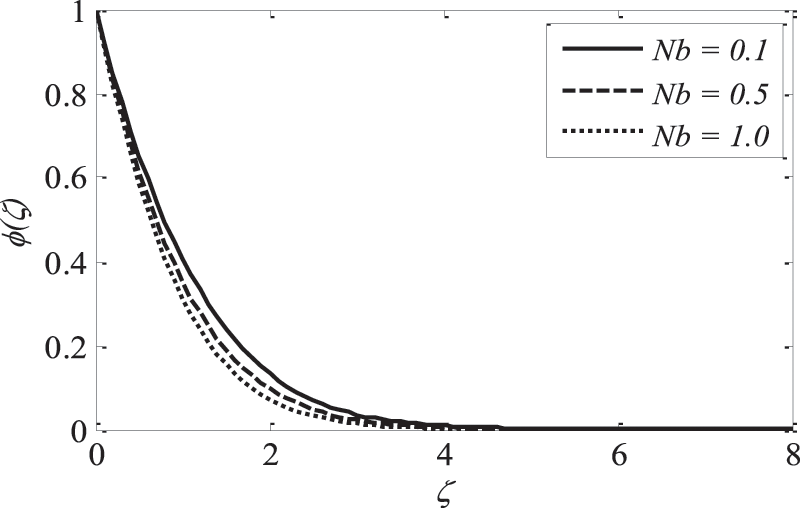
Figure 13: Effect of
The inclusion of nanoparticles externally allowed the thermophoresis parameters
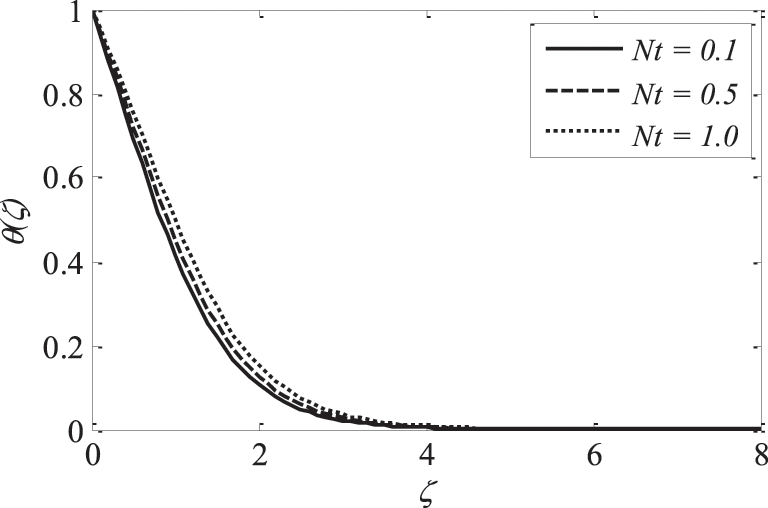
Figure 14: Effect of
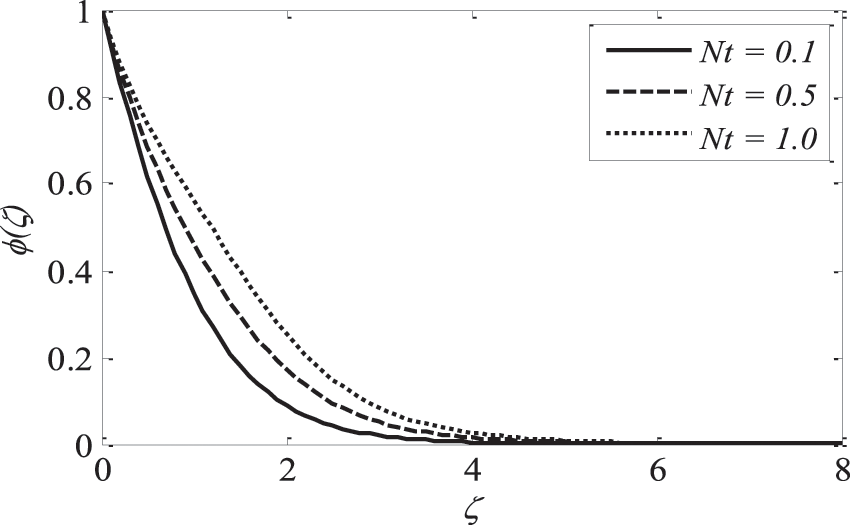
Figure 15: Effect of
Fig. 16 highlights temperature recuperation for diverse levels of the radiation parameter R. With altered measurements of R, temperature sketches accelerate as well. This is owing to the belief that heightened radiative heat transmission makes the establishment of thermal boundary layers simpler. The deviation of Prandtl number
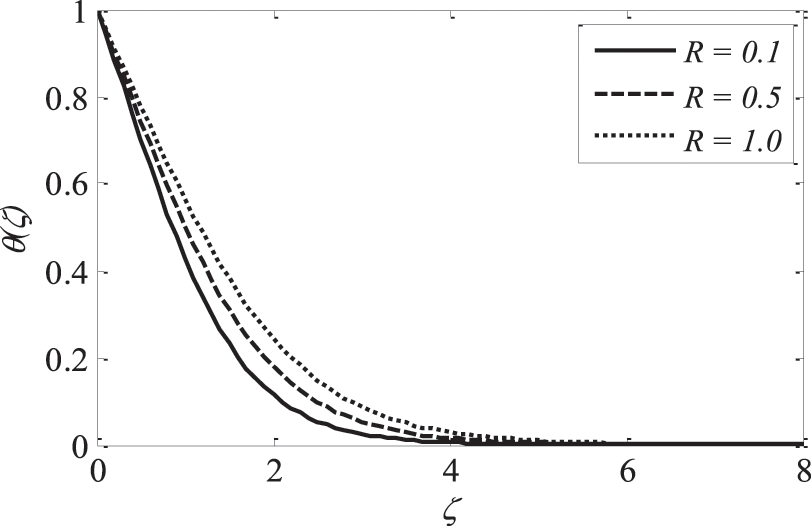
Figure 16: Effect of R on
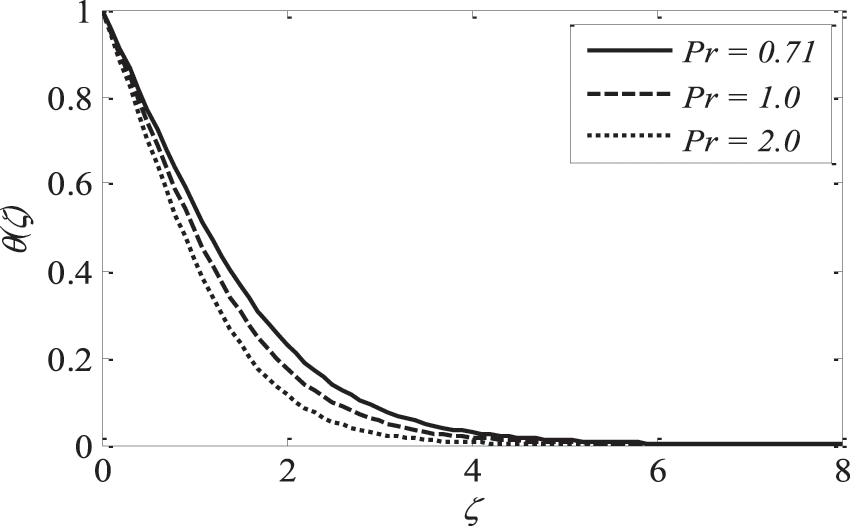
Figure 17: Effect of
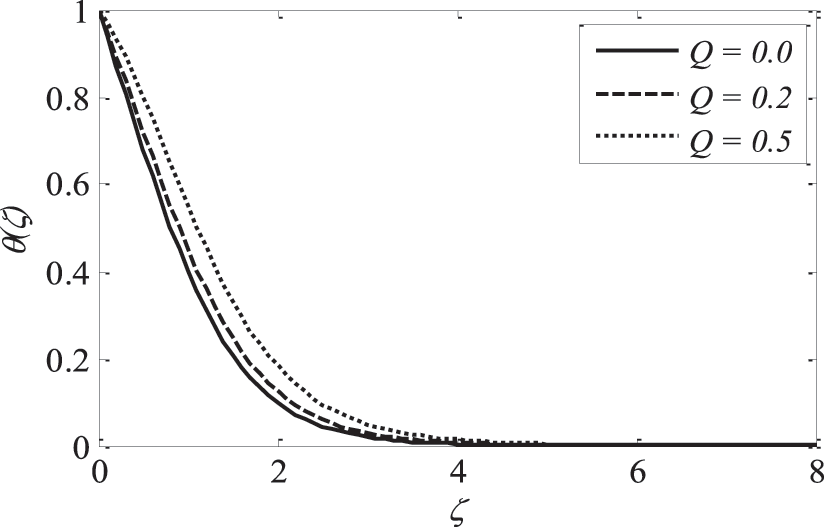
Figure 18: Effect of Q on
Fig. 19 illustrates that as the Lewis number
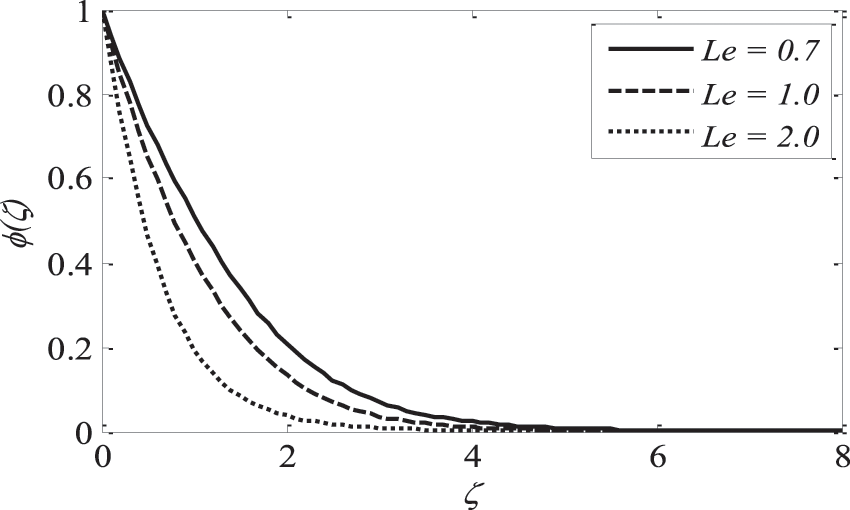
Figure 19: Effect of
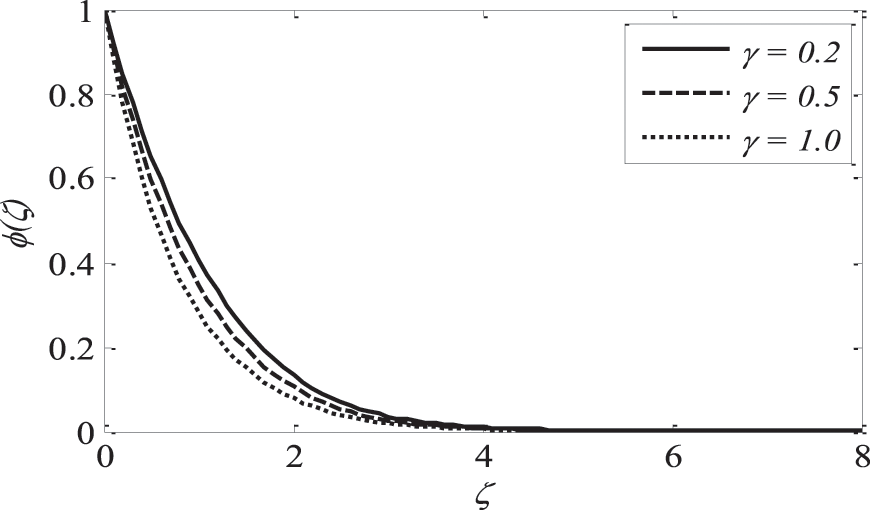
Figure 20: Effect of
When the plate and fluid advance at the similar tempo
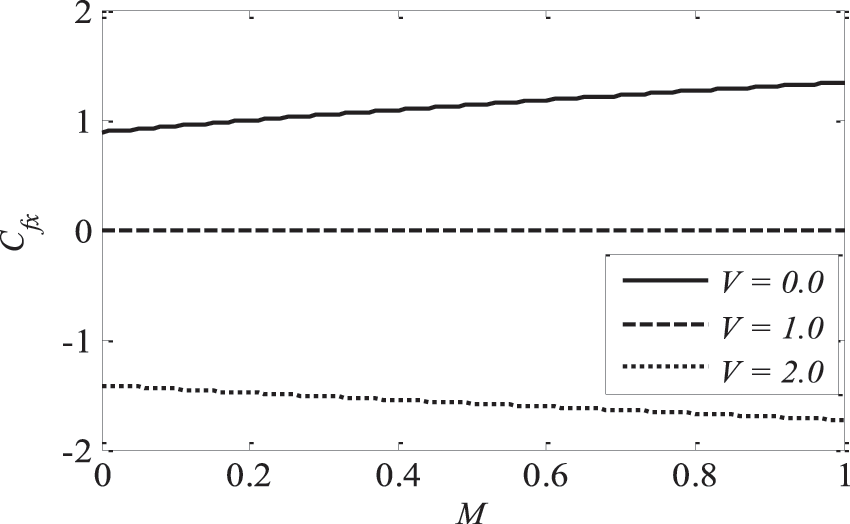
Figure 21: Effect of M and V on
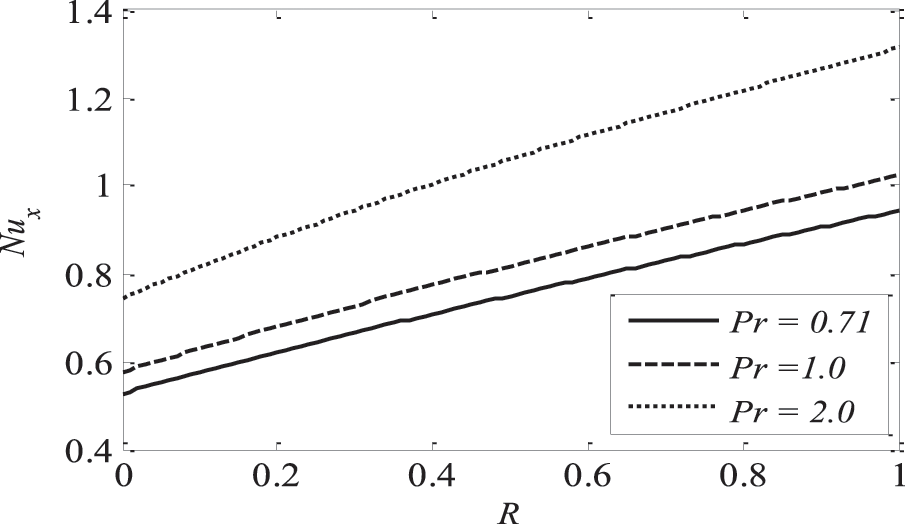
Figure 22: Effect of R and
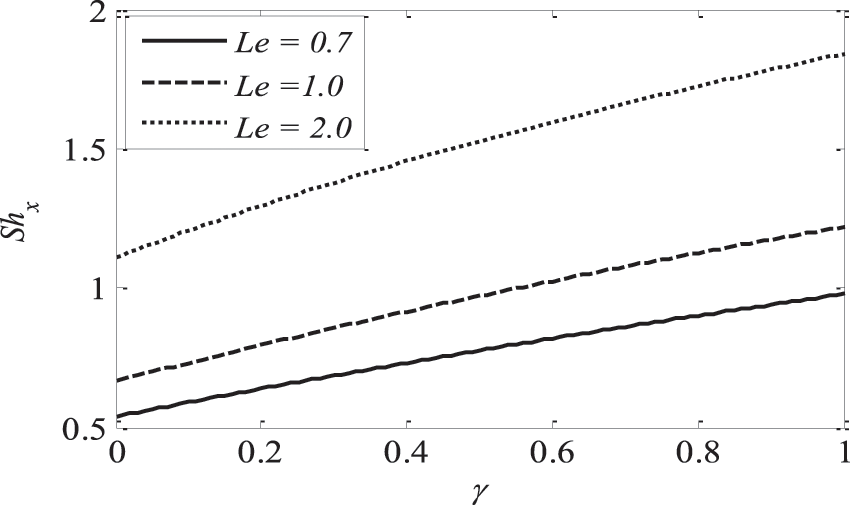
Figure 23: Effect of
Assessments of


The analytical exploration of two-dimensional steady forced convective flow of a Newtonian fluid past a convectively heated vertically moving plate towards the face of a variable magnetic field and the radiation factor is reviewed in this report using HAM. The foregoing are the crucial insights reached from the graphical and numerical solutions to the problem:
• The temperature profile is significantly amplified by the heat source parameter.
• Thermal radiation and thermophoresis parameters lead enhance temperature.
• The concentration profile lowers as both the Lewis number and the chemical reaction parameters expand.
• The rate of heat transfer elevates with R and
• The rate of mass transfer elevates with
Acknowledgement: We are very much thankful to learned reviewers for their useful suggestions for the improvement in the quality of our manuscript.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Choi, S. U. S. (1995). Enhancing thermal conductivity of fluids with nanoparticles. Proceedings of the ASME International Mechanical Engineering Congress and Exposition, 66, 99–105. [Google Scholar]
2. Hayat, T., Sajjad, R., Alsaedi, A., Muhammad, T., Ellahi, R. (2017). On squeezed flow of couple stress nanofluid between two parallel plates. Results in Physics, 7, 553–561. DOI 10.1016/j.rinp.2016.12.038. [Google Scholar] [CrossRef]
3. Hussain, T., Shehzad, S. A., Hayat, T., Alsaedi, A., Al-Solamy, F. et al. (2014). Radiative hydromagnetic flow of jeffrey nanofluid by an exponentially stretching sheet. PLoS One, 9(8), e103719. DOI 10.1371/journal.pone.0103719. [Google Scholar] [CrossRef]
4. Abbas, M. A., Bhatti, M. M., Sheikholeslami, M. (2019). Peristaltic propulsion of jeffrey nnanofluid with thermal radiation and chemical reaction effects. Inventions, 4(4), 68–83. DOI 10.3390/inventions4040068. [Google Scholar] [CrossRef]
5. Hayat, T., Qayyum, S., Alsaedi, A. (2017). Mechanisms of nonlinear convective flow of jeffrey nanofluid due to nonlinear radially stretching sheet with convective conditions and magnetic field. Results in Physics, 7, 2341–2351. DOI 10.1016/j.rinp.2017.06.052. [Google Scholar] [CrossRef]
6. Ganesh Kumar, K., Manjunatha, S., Rudraswamy, N. G. (2020). MHD flow and nonlinear thermal radiative heat transfer of dusty prandtl fluid over a stretching sheet. Fluid Dynamics & Material Processing, 16(2), 131–146. DOI 10.32604/fdmp.2020.0152. [Google Scholar] [CrossRef]
7. Jalali, H., Abbassi, H. (2020). Analysis of the influence of viscosity and thermal conductivity on heat transfer by Al2O3-water nanofluid. Fluid Dynamics & Materials Processing, 15(3), 253–270. DOI 10.32604/fdmp.2019.03896. [Google Scholar] [CrossRef]
8. Shamshuddin, M., Krishna, C. B. (2019). Heat absorption and joule heating effects on transient free convective reactive micropolar fluid flow past a vertical porous plate. Fluid Dynamics & Materials Processing, 15(3), 207–231. DOI 10.32604/fdmp.2019.00449. [Google Scholar] [CrossRef]
9. Ibrahim, S. M., Lorenzini, G., Kumar, P. V., Raju, C. S. K. (2017). Influence of chemical reaction and heat source on dissipative MHD mixed convection flow of a casson nanofluid over a nonlinear permeable stretching sheet. International Journal of Heat and Mass Transfer, 111, 346–355. DOI 10.1016/j.ijheatmasstransfer.2017.03.097. [Google Scholar] [CrossRef]
10. Reddy, T. S., Roja, P., Ibrahim, S. M., Lorenzini, G. (2022). Thermal radiation and viscous dissipation effects on (MHD) bioconvection stream of Maxwell nanoliquid over a permeable vertical plate Due to gyrotactic microorganisms. Mathematical Modelling of Engineering Problems, 9(2), 325–335. DOI 10.18280/mmep.090205. [Google Scholar] [CrossRef]
11. Kumar, P. V., Sunitha, Ch., Lorenzini, G., Ibrahim, S. M. (2022). A study of thermally radiant williamson nanofluid over an exponentially elongating sheet with chemical reaction via homotopy analysis method. CFD Letter, 14(5), 68–86. DOI 10.37934/cfdl.14.5.6886. [Google Scholar] [CrossRef]
12. Mabood, F., Ibrahim, S. M., Kumar, P. V., Lorenzini, G. (2020). Effects of slip and radiation on convective MHD casson nanofluid flow over a stretching sheet influenced by variable viscosity. Journal of Engineering Thermophysics, 29, 303–315. DOI 10.1134/S1810232820020125. [Google Scholar] [CrossRef]
13. Mabood, F., Khan, W. A., Ismail, A. I. M. (2015). MHD boundary layer flow and heat transfer of nanofluids over a nonlinear stretching sheet: A numerical study. Journal of Magnetism and Magnetic Materials, 374, 569–576. DOI 10.1016/j.jmmm.2014.09.013. [Google Scholar] [CrossRef]
14. Mahantesh, N., Vajravelu, K., Subhas Abel, M. (2011). Heat transfer in MHD viscoelastic boundary layer flow over a stretching sheet with thermal radiation and non-uniform heat source/sink. Communications in Nonlinear Science and Numerical Simulation, 16(9), 3578–3590. DOI 10.1016/j.cnsns.2010.12.033. [Google Scholar] [CrossRef]
15. Sastry, D. R. V. S. R. K., Kameswaran, P. K., Hatami, M. (2021). MHD and viscous dissipation effects in marangoni mixed flow of a nanofluid over an inclined plate in the presence of ohmic heating. Fluid Dynamics & Materials Processing, 17(2), 285–300. DOI 10.32604/fdmp.2021.014429. [Google Scholar] [CrossRef]
16. Ariel, P. D. (1994). Hiemenz flow in hydromagnetics. Acta Mechanica, 103, 31–43. DOI 10.1007/BF01180216. [Google Scholar] [CrossRef]
17. Motsa, S. S., Khan, Y., Shateyi, S. (2012). A new numerical solution of Maxwell fluid over a shrinking sheet in the region of a stagnation point. Mathematical Problems in Engineering, 2012, 290615. DOI 10.1155/2012/290615. [Google Scholar] [CrossRef]
18. Parand, K., Lotfi, Y., Amani Rad, J. (2018). An efficient analytic approach for solving hiemenz flow through a porous medium of a non-newtonian rivlin-ericksen fluid with heat transfer. Nonlinear Engineering, 7(4), 287–301. DOI 10.1515/nleng-2017-0160. [Google Scholar] [CrossRef]
19. Aamir Hamid, H., Khan, M. (2018). Unsteady mixed convective flow of williamson nanofluid with heat transfer in the presence of variable thermal conductivity and magnetic field. Journal of Molecular Liquids, 260, 436–446. DOI 10.1016/j.molliq.2018.03.079. [Google Scholar] [CrossRef]
20. Pandey, A. K., Kumar, M. (2017). Natural convection and thermal radiation influence on nanofluid flow over a stretching cylinder in a porous medium with viscous dissipation. Alexandria Engineering Journal, 56(1), 55–62. DOI 10.1016/j.aej.2016.08.035. [Google Scholar] [CrossRef]
21. Bhandari, A. (2019). Radiation and chemical reaction effects on nanofluid flow over a stretching sheet. Fluid Dynamics & Materials Processing, 15(5), 557–582. DOI 10.32604/fdmp.2019.04108. [Google Scholar] [CrossRef]
22. Inayat, U., Iqbal, S., Manzoor, T. (2022). Theoretical investigation of two-dimensional nonlinear radiative thermionics in nano-MHD for solar insolation: A semi-empirical approach. Computer Modeling in Engineering & Sciences, 130(2), 751–776. DOI 10.32604/cmes.2022.018665. [Google Scholar] [CrossRef]
23. Liao, S. J. (2011). Beyond perturbation: Introduction to Homotopy analysis method. Boca Raton: Chapman and Hall, CRC Press. [Google Scholar]
24. Kumar, P. V., Ibrahim, S. M., Jyothsna, K. (2019). Numerical modelling on radiative MHD flow of a chemically casson fluid over an exponentially inclined stretching sheet. Mathematical Modeling of Engineering Problems, 6(4), 491–501. DOI 10.18280/mmep.060403. [Google Scholar] [CrossRef]
25. Ibrahim, S. M., Kumar, P. V., Makinde, O. D. (2018). Chemical reaction and radiation effects on non-newtonian fluid flow over a stretching sheet with non-uniform thickness and heat source. Defect and Diffusion Forum, 387, 319–331. DOI 10.4028/www.scientific.net/DDF.387.319. [Google Scholar] [CrossRef]
26. Hayat, T., Shehzad, S. A., Alsaedi, A. (2012). Soret and dufour effects on magnetohydrodynamic (MHD) flow of casson fluid. Applied Mathematics and Mechanics, 33, 1301–1312. DOI 10.1007/s10483-012-1623-6. [Google Scholar] [CrossRef]
27. Kumar, P. V., Ibrahim, S. M., Lorenzini, G. (2021). Investigation of the heat transfer and flow characteristics on hiemenz flow under the influence of heat source and thermal radiation with hydrodynamic–thermal slips effects. Journal of Mechanical Engineering Research and Developments, 44(9), 369–383. [Google Scholar]
28. Uddin, M. J., Khan, W. A., Ismail, A. I. (2013). MHD forced convective laminar boundary layer flow of convectively heated moving vertical plate with radiation and transpiration effect. PLoS One, 8(5), e62664. DOI 10.1371/journal.pone.0062664. [Google Scholar] [CrossRef]
29. Kechil, S. A., Hashim, I. (2009). Approximate analytical solution for MHD stagnation-point flow in porous media. Communications in Nonlinear Science and Numerical Simulation, 14(4), 1346–1354. DOI 10.1016/j.cnsns.2008.02.007. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools