Numerical Analysis of the Mixed Flow of a Non-Newtonian Fluid over a Stretching Sheet with Thermal Radiation

List of symbols

1  Introduction

Many neoteric engineering applications require control of both the cooling mechanism and the high-speed transfer of fluid flow, particularly the flow produced by stretching the sheet. Abundant examples can be cited in chemical engineering and particularly in the manufacturing of plastic and rubber sheets, crystal growing, food processing, solidification of liquid crystals, glass blowing, hot rolling, continuous cooling, fiber spinning, exotic lubricants, and several other areas of technology. Many assumptions regarding the nature of fluid flow over a stretching sheet, along with properly chosen boundary conditions, result in accurate and numerical solutions to the conservation equations that describe flow velocity, heat transfer mechanisms, and mass transfer processes [1–6]. While the prediction of cooling phenomena is extremely useful, certain other information such as suction or injection, thermal radiation and heat flux is also valuable [7–10]. A reasonably straightforward correlation between proper physical circumstances and some physical assumptions, in particular, becomes useful in predicting model performance or setting cooling parameters [11–13]. Because of its biological, geological, and engineering applications in purification processes, liquid film evaporation, filtration processes, petroleum industries, and subsurface water resources, the topic of fluid flow within a porous medium has recently gotten a lot of interest. As shown in the diagram, the porous medium can be classified into two types based on its porosity: porous medium with high porosity and porous medium with low porosity (Fig. 1).

Figure 1: (a) Porous medium with low porosity (b) Porous medium with high porosity

The flow and temperature fields are considered over linear and non-linear stretching sheets in all of the preceding investigations. Theoreticians have been less enthusiastic to study the non-Newtonian Powell-Eyring fluid because they believe that this sort of boundary-layer fluid is unsuitable for industrial use. However, they observed that non-Newtonian fluids caused by stretching sheets provide a significant engineering and technological problem because of their widespread engineering and technological applications in a variety of industrial and engineering processes [14–19]. In references [20–38], you can find some additional interesting contributions on Newtonian and non-Newtonian nanofluid flow and its applications in manufacturing.

The fundamental purpose of this research is to look at the heat transfer properties of an Eyring-Powell fluid flow caused by a stretching sheet immersed in a porous media and influenced by thermal radiation. Our focus here is on two fundamental physical phenomena: mixed convection and thermal stratification, both of which have significant effects on cooling rates. The results of the current analysis were obtained after employing the efficient Chebyshev spectral method.

2  Formulation of the Problem

A layer of finite thickness is constrained on one side by a stretched wall in the physical model. This surface is assumed to has a temperature Tw and it is stretching with a velocity Uw=ax in the vertical direction toward the x-axis (Fig. 2).

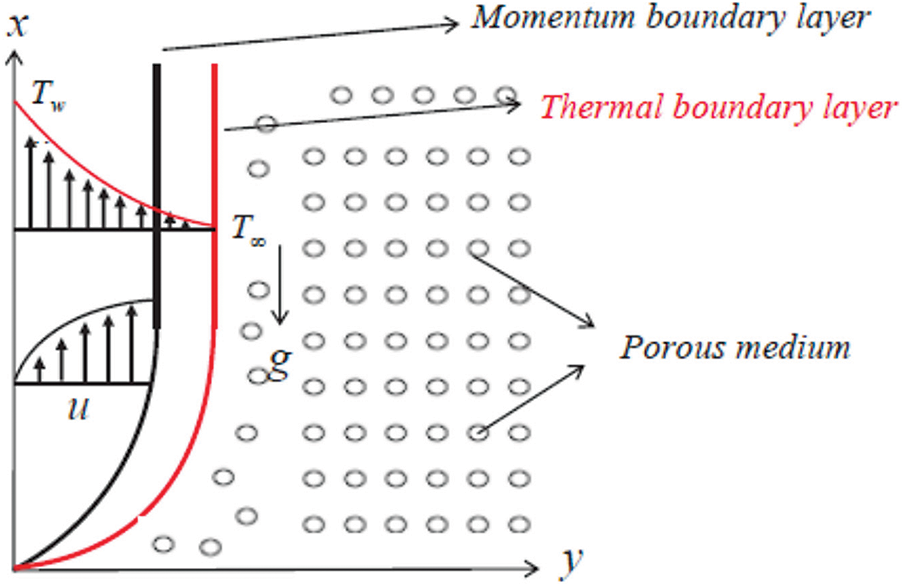
Figure 2: A schematic representation of the model

In order to be as precise as possible, the number of governing parameters for this physical model is introduced by assuming that there are heat sources with a coefficient Q and thermal radiation phenomenon with radiative heat flux qr and that the steady-state exists. Steady mixed convection flow for the Powell-Eyring fluid with density ρ is assumed to move over a stratified sheet and some of fluid properties are taken to be dependent of temperature such as viscosity μ and thermal conductivity κ .

The temperature distribution and energy transfer across the thermal layer can be predicted using the thermal characteristics and boundary conditions. The shear stress relation, which describes the Powell-Eyring model, is [39]:

τij=μ∂ui∂xj+1βsinh−1(1C∂ui∂xj) (1)

where β,C are the characteristics of Powell-Eyring Model.

Considering sinh−1(1C∂ui∂xj)≅1C∂ui∂xj−16(1C∂ui∂xj)3 , |1C∂ui∂xj|≤1 .

For the above physical situation, basic equations for mass, momentum and energy after using the appropriate boundary layer approximations are thus:

∂u∂x+∂v∂y=0 (2)

u∂u∂x+v∂u∂y=1ρ∞∂∂y(μ∂u∂y+1βC∂u∂y−16βC3(∂u∂y)3)+gβ∗(T−T∞)−μρ∞ku, (3)

ρ∞cp(u∂T∂x+v∂T∂y)=∂∂y(κ∂T∂y)−∂qr∂y+Q(T−T∞), (4)

where u and v are the velocity components along x and y directions, respectively. g denotes the gravitational acceleration, ρ∞ is the fluid density away from the sheet, k is the permeability of the porous medium, T is the temperature of the fluid, β∗ is the coefficient of thermal expansion and cp is the specific heat at constant pressure. Likewise, qr is then given by [40]:

qr=−4σ∗3k∗∂T4∂y, (5)

with the band of physical model and application of simplification for T4 about T0 , the expression for T4 becomes [41]:

T4≅4T03T−3T04, (6)

where T0 is the reference temperature. It is required to supply the relevant boundary conditions in order to complete the formulation of the suggested problem. As a result, the current problem’s boundary conditions are as follows:

u=Uw=ax,v=0,T=Tw=T0+b1x,y=0, (7)

u→0,T→T∞=T0+b2x,y→∞, (8)

in which T1 and b2 are positive dimensional constants and T∞ is the ambient temperature. The following non-dimensional variables are now used to simplify the governing equations for the suggested physical problem:

ψ=aν∞xf(η),η=aν∞y (9)

θ=T−T∞Tw−T0 (10)

For mathematical convenience, viscosity of the fluid μ can be represented as μ=μ∞e−γθ [42] which is a nonlinear function of dimensionless temperature θ alone, whereas the fluid thermal conductivity κ can be taken as κ=κ∞(1+εθ) [42] which is a linear function of θ alone, where μ∞ is the dynamic viscosity away from the sheet, γ is the non-dimensional viscosity parameter, κ∞ is the fluid conductivity at the free surface and ε is the fluid thermal conductivity parameter.

The following rigorous transformation for both the flow and heat transfer fields (3) and (4) could be obtained by using Eqs. (9) and (10) along with the boundary conditions (7) and (8) as follows:

f′′′(e−γθ+α(1−δf′′2))−γf′′θ′e−γθ−f′2+ff′′+λθ−Δf′e−γθ=0 (11)

1Pr((1+R+εθ)θ″+εθ′2)+fθ′−f′θ−e1f′+Γθ=0 (12)

f(0)=0,f′(0)=1,θ(0)=1−e1, (13)

f′→0,θ→0,η→∞ (14)

where α=1μ∞βC and δ=aρ∞Uw22μ∞C2 are the dimensionless Powell-Eyring fluid parameters, Δ=ν∞ak is the porous parameter, λ=gβ∗b1a2 is the mixed convection parameter, R=16σ∗T033κ∞k∗ is the radiation parameter, e1=b2b1 is the thermal stratification parameter, Γ=Qρ∞cpa is the heat generation/absorption parameter and Pr=μ∞cpκ∞ is the Prandtl number. Here, it is very necessary to mention that our physical model is furnished previously by Bilal et al. [43]. In other words, when Δ=γ=R=ε=0 , our present model can be reduced to the previously base model of Bilal et al. [43].

Apart from the preceding system that governs our physical problem and allows us to quickly recognize flow features and heat transfer mechanisms, it is very serious to study the following significant physical quantities, the local skin-friction coefficient ( Cfx ) and the local Nusselt number ( Nux ) which take the following form:

CfxRe12=−[(e−γ+α)f′′(0)−αδ3f′′3(0)],NuxRe−121+R=−θ′(0) (15)

where Re=Uwxν∞ is the local Reynolds number.

3  Results and Discussion

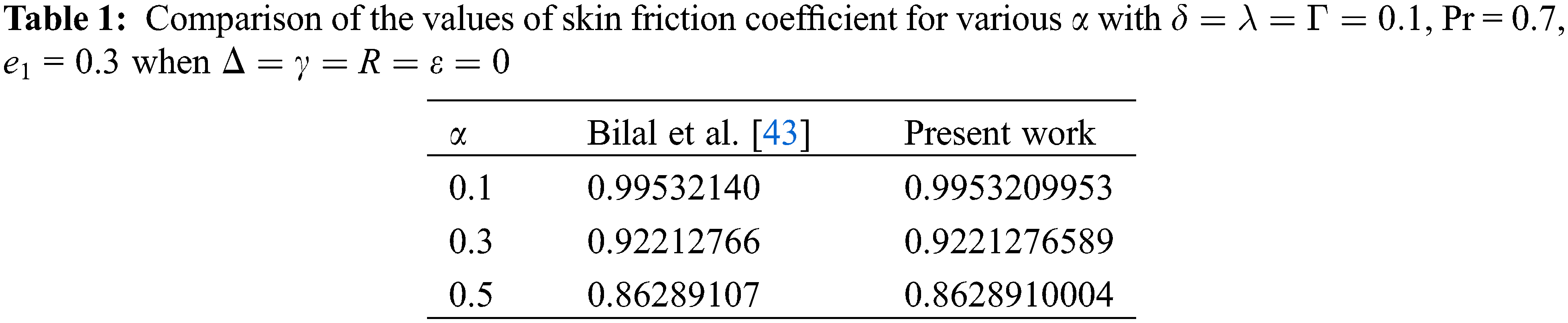
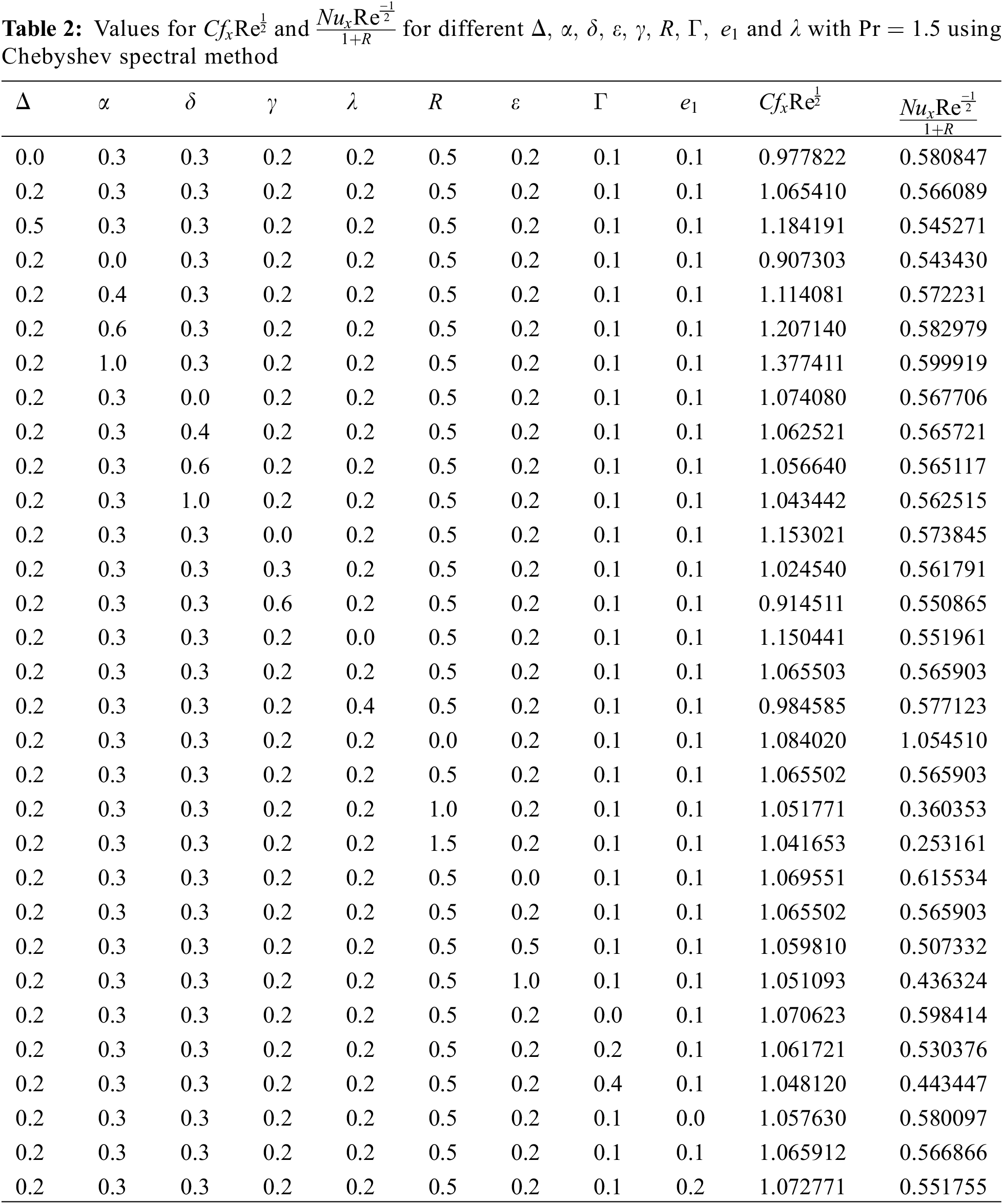
To validate the reliability and precision of the numerical process utilized here via the Chebyshev spectral method, calculations for the values of the skin-friction coefficient are done below. The data obtained is compared to Bilal and Ashbar’s previously published findings [43]. From our observations of the tabular data in Table 1, we have found that our results are in good accord.

The preceding considerations and assumptions lead to the current results and discussion section. As a result, while describing the physical problem of hydrodynamics, a system of ordinary differential equations with novel governing parameters emerges, giving us the opportunity to choose which of them is required to develop the suggested model. The Chebyshev spectral approach [44] is appealing because it achieves more precision than other numerical methods for solving the system that regulates our situation. It is also worth noting that all of the results produced utilizing the Chebyshev spectral approach, as well as other associated published results, are mutually supportive. The results of the fully developed velocity and temperature profiles for governing parameter runs in the laminar flow region are plotted in Figs. 3–11. Fig. 3 depicts the numerical result of the present analysis, which offers a close examination of the impact of the porous parameter Δ on the non-Newtonian fluid flow and heat transfer characteristics. A startling result shown in Fig. 3a is that the presence of a porous media in a fluid flow causes a significant resistance force that slows the fluid velocity. As a result, the induced warming heat inside the fluid layers is caused by this resistive force. As shown in Fig. 3b, the porosity parameter can be used as a warming factor for the fluid within the thermal boundary layer.

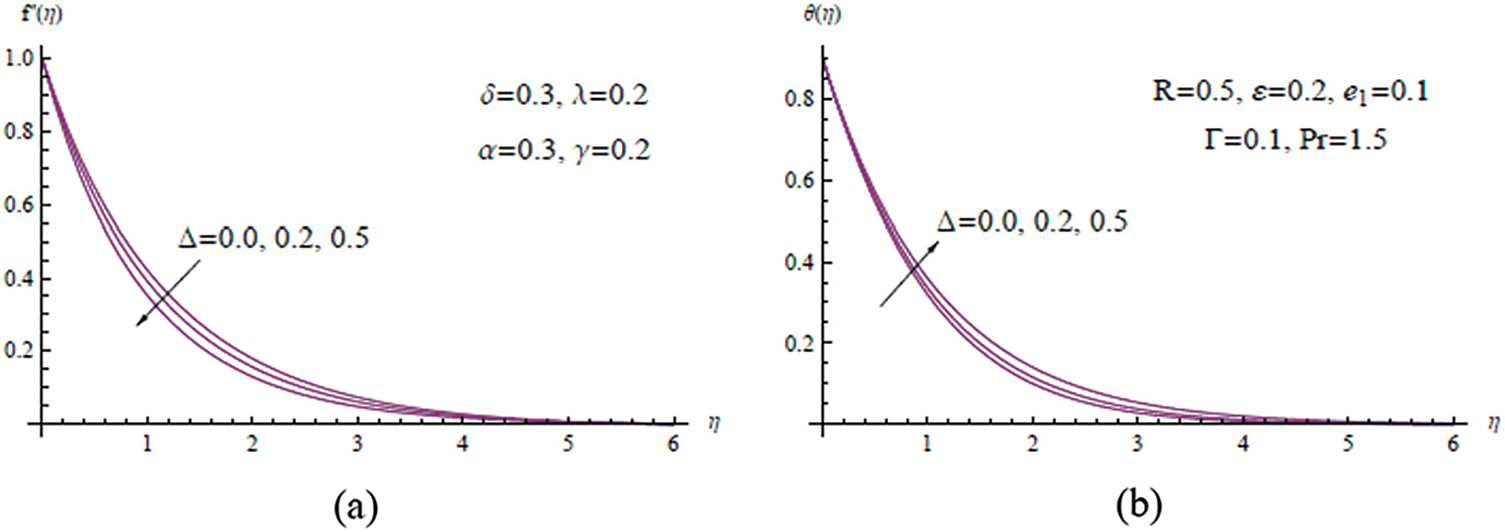
Figure 3: (a) f′(η) for assorted values of Δ (b) θ(η) for assorted values of Δ

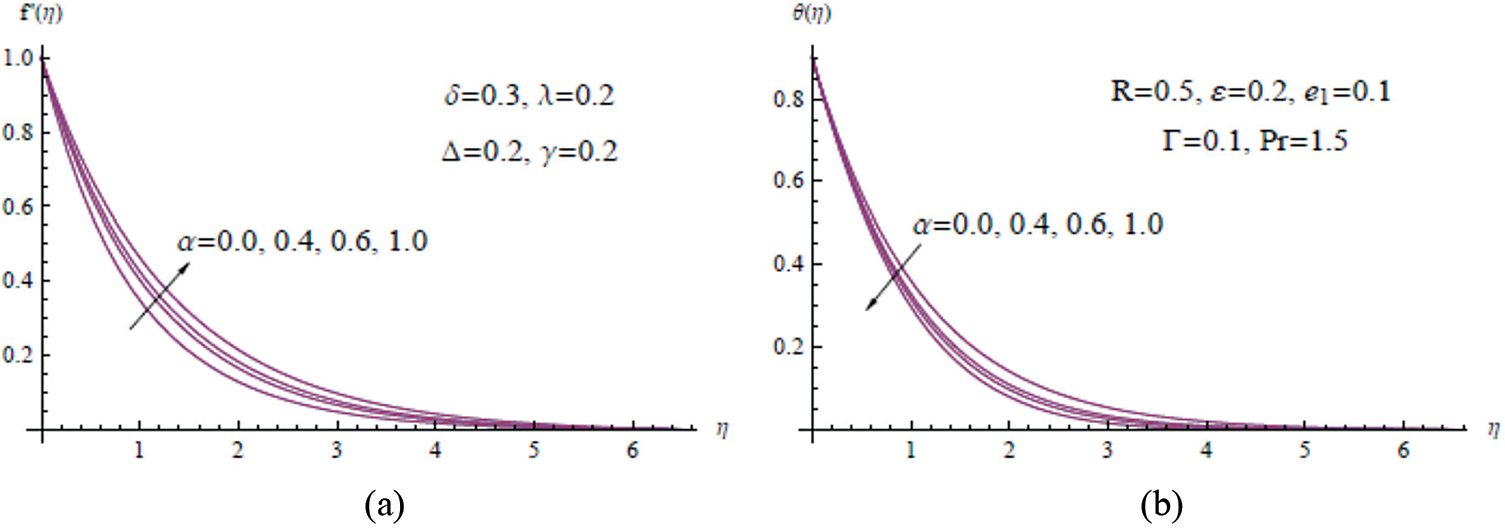
Figure 4: (a) f′(η) for assorted values of α (b) θ(η) for assorted values of α

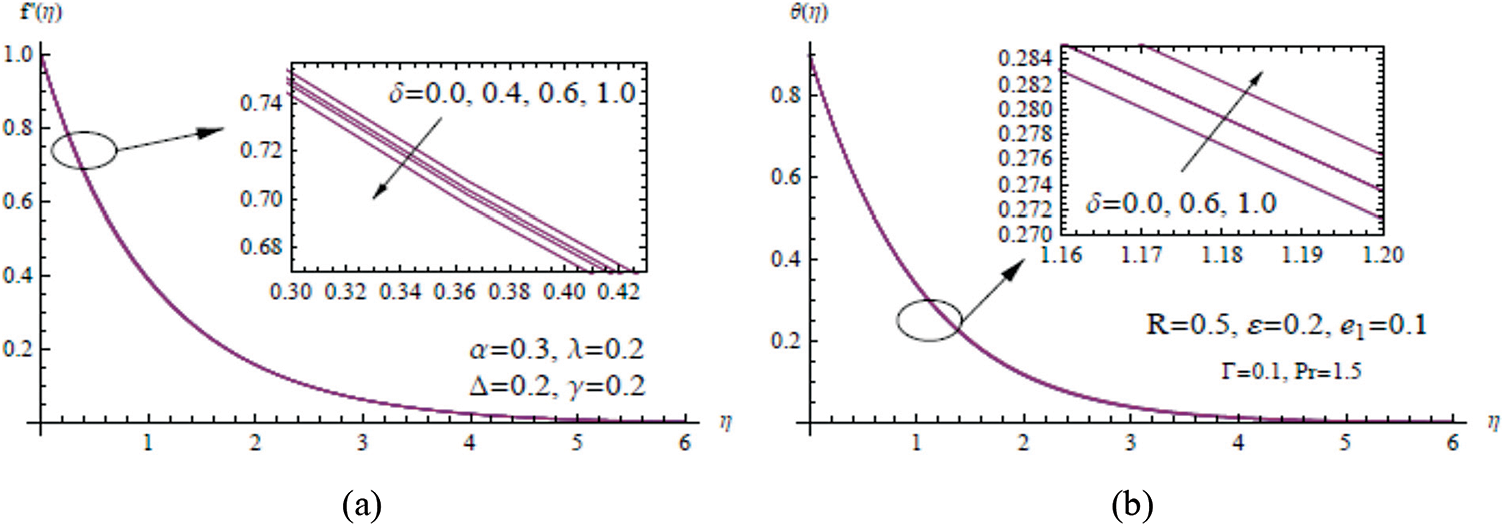
Figure 5: (a) f′(η) for assorted values of δ (b) θ(η) for assorted values of δ

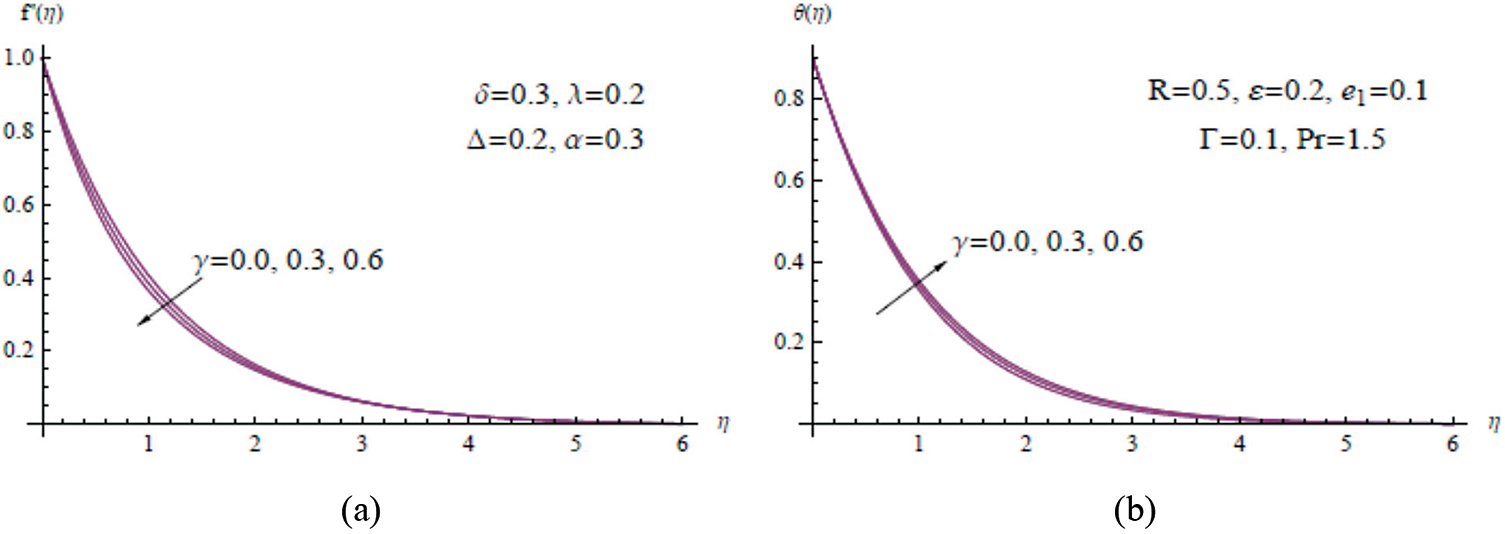
Figure 6: (a) f′(η) for assorted values of γ (b) θ(η) for assorted values of γ

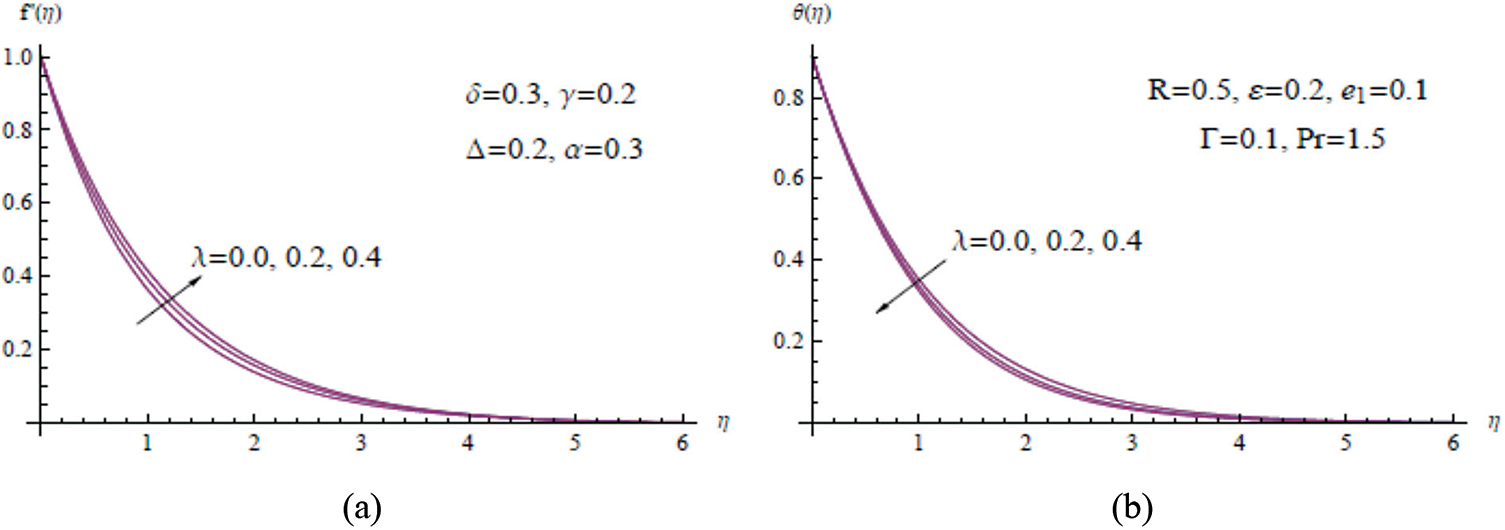
Figure 7: (a) f′(η) for assorted values of λ (b) θ(η) for assorted values of λ

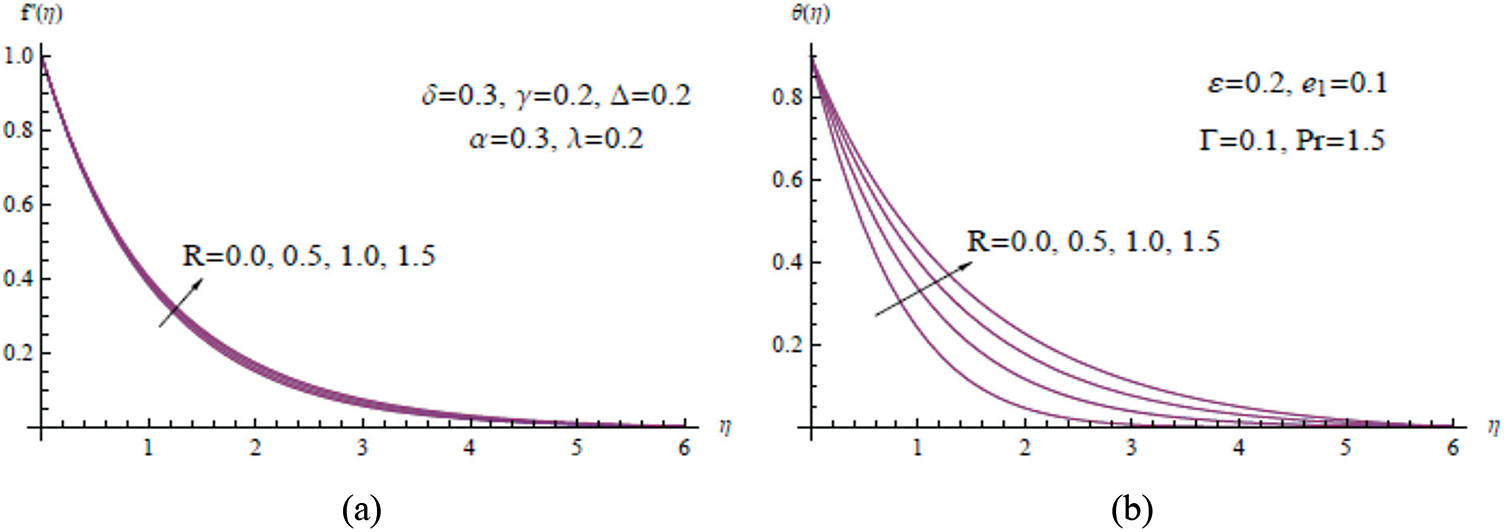
Figure 8: (a) f′(η) for assorted values of R (b) θ(η) for assorted values of R

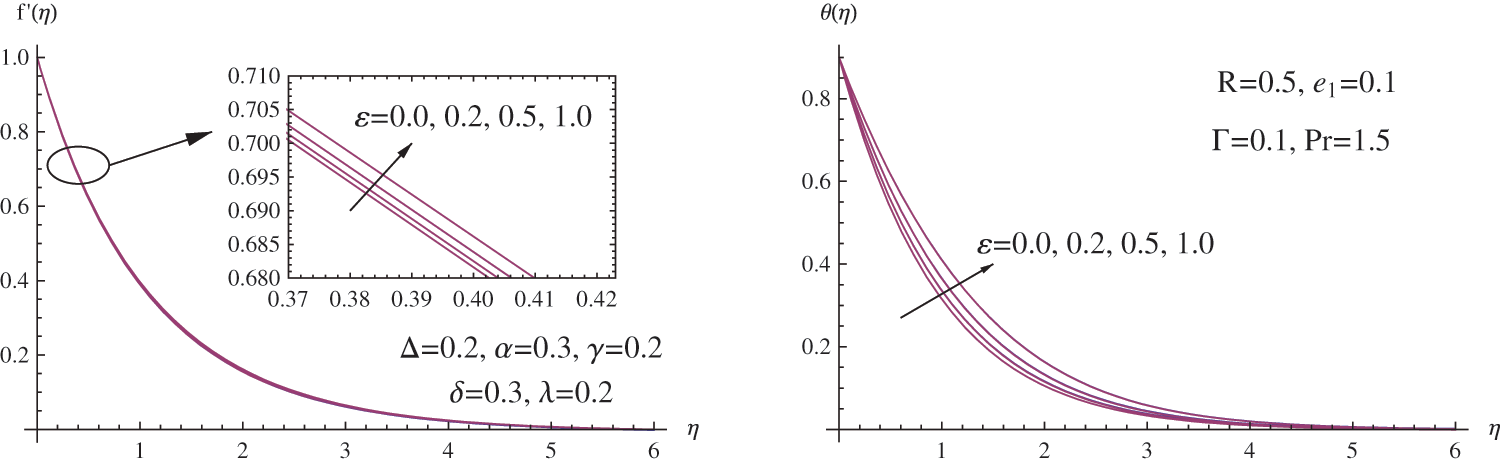
Figure 9: (a) f′(η) for assorted values of ε (b) θ(η) for assorted values of ε

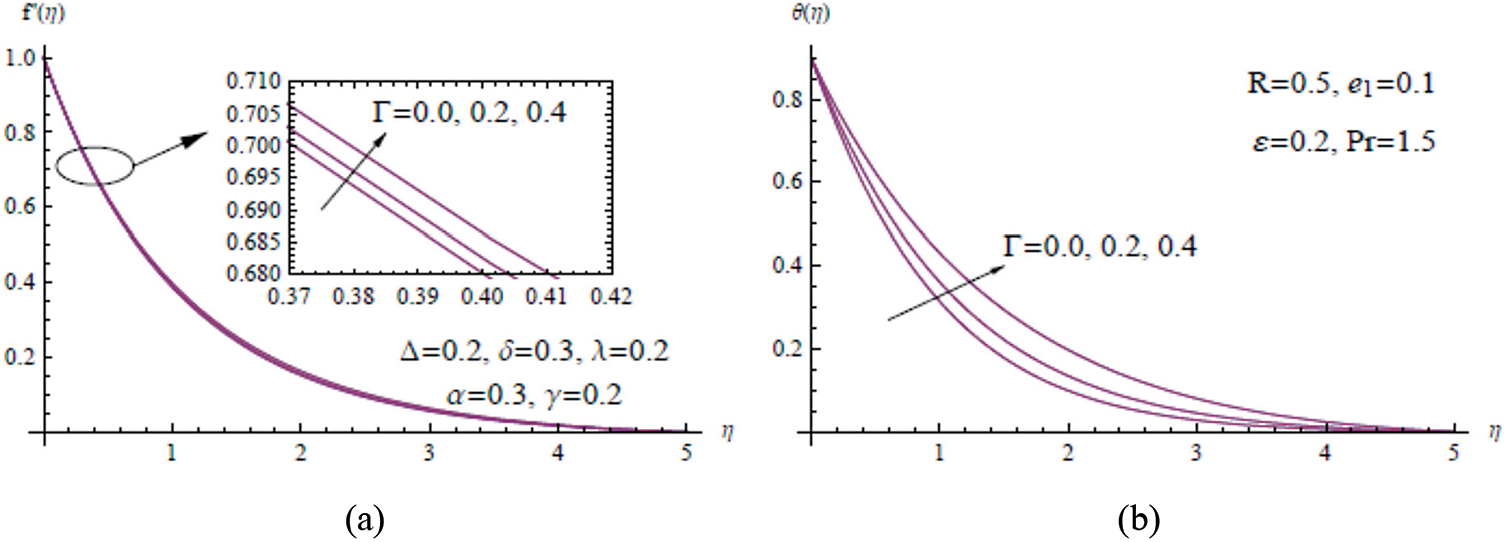
Figure 10: (a) f′(η) for assorted values of Γ (b) θ(η) for assorted values of Γ

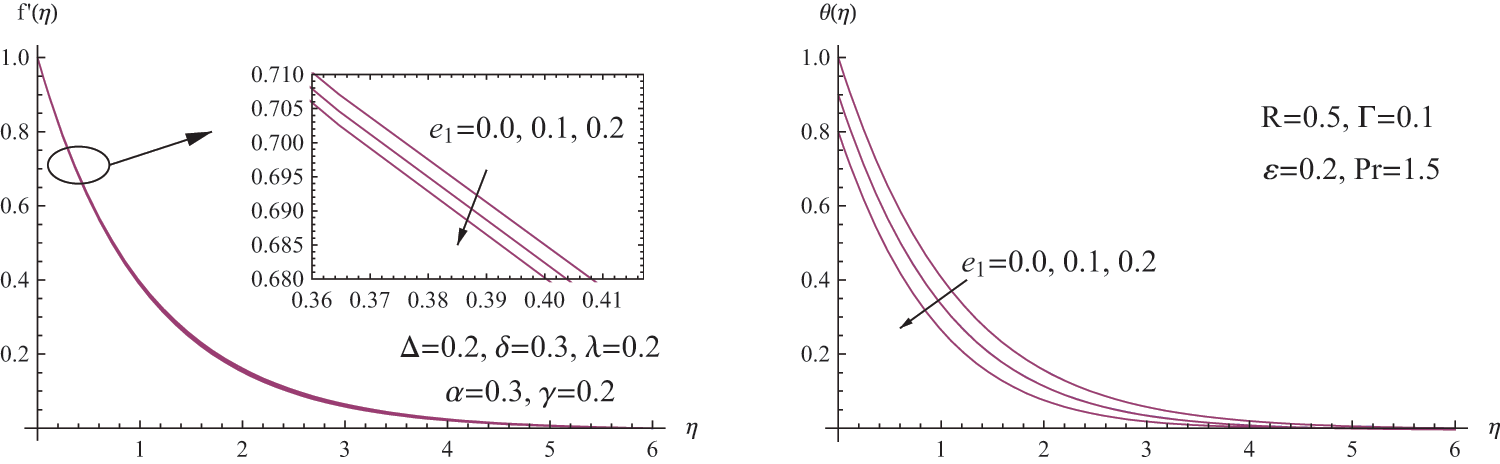
Figure 11: (a) f′(η) for assorted values of e1 (b) θ(η) for assorted values of e1

Figs. 4a and 4b show how the velocity and temperature fields vary as the α value increases. The velocity field and the thickness of the boundary layer are increased as the α value increases in these pictures, whereas the temperature field decreases.

The velocity and temperature profiles in Figs. 5a and 5b indicate the impact of the dimensionless Powell-Eyring parameter δ on the flow and heat transfer mechanism. The existence of the δ parameter imposes an additional viscous force on the fluid layers, resulting in a decrease in velocity distribution across the boundary layer and a modest improvement in the temperature field mechanism.

The curves in Figs. 6a and 6b show that for low viscosity parameter γ the velocity distribution was slightly increased only near the sheet surface, whereas near the ambient, there was no effect of altering in viscosity on the velocity distribution. Similarly, changing the viscosity parameter causes a backflow for heat distribution, which was clearly established as shown in Fig. 6b.

Regarding the mixed convection parameter λ and its influence on both the velocity and temperature distribution, there are curves on Figs. 7a and 7b. It can be seen from these figures that the high distribution of the velocity can be achieved with great mixed convection parameters, while we reach the reverse for the distribution of the temperature.

Figs. 8a and 8b show the effect of the radiation parameter R as defined previously on both the velocity and the temperature fields. It is clear that the temperature field is strikingly affected by the radiation mechanism due to the increased importance of the thermal radiation mechanism in faster heat flow. The same trend is observed for the velocity field but with slightly different behavior.

Further, a typical steady flow and heat transfer pattern for different values of the thermal conductivity parameter ε are shown in Figs. 9a and 9b. Thus, the influence of the thermal conductivity parameter ε might be strong enough to cause more velocity fluid flow and more heat distribution, resulting in a thicker thermal boundary layer.

Figs. 10a and 10b show the variations in velocity f′(η) and temperature θ(η) as a function of the space coordinate η for various values of the heat generation parameter Γ . For relatively high temperature distribution, the primary mechanism for this mission was the great heat generation parameter Γ . In general, the heat generation parameter Γ has a small effect on the velocity field in comparison with the results given for the heating field.

In order to illustrate the effect of the thermal stratification parameter e1 on the velocity field clearly, the curves in Fig. 11a are drawn on an expanded scale. During the fluid flow, the flow process was discovered to be essentially laminar, with a slight retarding effect on the velocity distribution as the thermal stratification parameter e1 increased. One qualitative observation of some importance is the influence of the same parameter, e1 on the temperature field as obtained from Fig. 11b. A very interesting feature of the stratification parameter e1 is that it can achieve and govern the cooling process for the sheet surface.

Now, both the physical quantities Cfx and Nux according to Eq. (15), which describes the drag force and the heat transfer at the sheet surface; respectively, are shown in Table 2 for different values of governing parameters α,δ,ε,γ,R,Δ,e1 and λ with Pr=1.5 . The increase in local Nusselt number due to large dimensionless Powell-Eyring parameter α and the mixed convection parameter λ can be attributed to the increase in heat capacity or decrease in resistance to heat flow. It is seen from this table that an increase in the parameters δ,γ,λ,R,ε and Δ decreases the local skin-friction coefficient while the reverse trend is observed for parameters δ , α and e1 . On the other hand, the porous parameter δ , the variable viscosity parameter γ and the radiation parameter R can have a significant influence on the rate of heat transfer as clearly noticed from Table 2.

4  Conclusions

The current investigation’s overall goal is to determine the velocity distribution, temperature distribution, heat transfer rate, and drag properties of Powell-Eyring fluid flow in the boundary layer region. The material presented in this research is limited to the measurement of the flow and heat transfer of the Powell-Eyring fluid with mixed convection and heat generation and the determination of their effect on the cooling mechanism through a porous medium. This data would contribute considerably to the understanding of the mixed-convection heat transfer phenomena. Numerically, a solution to the present physical problem using the Chebyshev spectral method was introduced. The main findings of our study are summarized as follows:

1.    It is even possible that with large values of the first Powell-Eyring parameter and smaller values of the porous parameter, the boundary layer thickness will be totally increased.

2.    Another interesting situation is that in which both the porous parameter and the thermal conductivity parameter increase significantly, the temperature distribution may be regarded as being enhanced uniformly.

3.    Thermal radiation and heat generation have another important effect insofar as they can establish a thicker thermal layer with the thermal stratification phenomenon.

4.    It is interesting to note that the thickness of the fluid layer depends very little on the second Powell-Eyring parameter, the thermal conductivity parameter, and the thermal stratification parameter.

5.    A strong relationship between the cooling mechanism and both of the thermal stratification parameters and the radiation parameter is found.

Acknowledgement: The authors wish to express their sincere thanks to the editor and referees for their valuable time spent reading this paper and for their valuable comments and suggestions, which improved the quality of this paper.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Ali, M. E. (1995). On thermal boundary layer on a power-law stretched surface with suction or injection. International Journal of Heat and Mass Transfer, 16, 280–290. DOI 10.1016/0142-727x(95)00001-7. [Google Scholar] [CrossRef]

 2.  Andersson, H. T., Aarseth, J. B., Dandapat, B. S. (2000). Heat transfer in a liquid film on an unsteady stretching surface. International Journal of Heat and Mass Transfer, 43(1), 69–74. DOI 10.1016/S0017-9310(99)00123-4. [Google Scholar] [CrossRef]

 3.  Afzal, N. (1993). Heat transfer from a stretching surface. International Journal of Heat and Mass Transfer, 36, 1128–1131. DOI 10.1016/s0017-9310(05)80296-0. [Google Scholar] [CrossRef]

 4.  Chen, C. K., Char, M. (1988). Heat transfer on a continuous stretching surface with suction or blowing. Journal of Mathematical Analysis and Applications, 35(2), 568–580. DOI 10.1016/0022-247X(88)90172-2. [Google Scholar] [CrossRef]

 5.  Grubka, L. J., Bobba, K. M. (1985). Heat transfer characteristics of a continuous stretching surface with variable temperature. ASME Journal of Heat Transfer, 107(1), 248–260. DOI 10.1115/1.3247387. [Google Scholar] [CrossRef]

 6.  Magyari, E., Keller, B. (1999). Heat transfer characteristics of the separation boundary flow induced by a continuous stretching surface. Journal of Physics D: Applied Physics, 32(22), 2876–2881. DOI 10.1088/0022-3727/32/22/308. [Google Scholar] [CrossRef]

 7.  Carragher, P., Crane, L. J. (1982). Heat transfer on a continuous stretching sheet. Journal of Applied Mathematics and Mechanics, 62, 564–573. DOI 10.1002/(ISSN)1521-4001. [Google Scholar] [CrossRef]

 8.  Elbashbeshy, E. M. A. (2001). Heat transfer over an exponentially stretching continuous surface with suction. Archives of Mechanics, 53, 643–651. [Google Scholar]

 9.  Ishak, A., Nazar, R., Pop, I. (2008). Heat transfer over an unsteady stretching surface with prescribed heat flux. Canadian Journal of Physics, 86(6), 853–855. DOI 10.1139/p08-005. [Google Scholar] [CrossRef]

10. Mahapatra, T. R., Gupta, A. S. (2003). Stagnation-point flow towards a stretching surface. The Canadian Journal of Chemical Engineering, 81(2), 258–263. DOI 10.1002/cjce.5450810210. [Google Scholar] [CrossRef]

11. Liu, I. C., Megahed, A. M. (2012). Numerical study for the flow and heat transfer in a thin liquid film over an unsteady stretching sheet with variable fluid properties in the presence of thermal radiation. Journal of Mechanics, 28(2), 291–297. DOI 10.1017/jmech.2012.32. [Google Scholar] [CrossRef]

12. Megahed, A. M. (2012). Variable viscosity and slip velocity effects on the flow and heat transfer of a power-law fluid over a non-linearly stretching surface with heat flux and thermal radiation. Rheologica Acta, 51(9), 841–874. DOI 10.1007/s00397-012-0644-8. [Google Scholar] [CrossRef]

13. Megahed, A. M. (2014). Variable heat flux effect on MHD flow and heat transfer over an unsteady stretching sheet in the presence of thermal radiation. Canadian Journal of Physics, 92(1), 86–91. DOI 10.1139/cjp-2012-0543. [Google Scholar] [CrossRef]

14. Eldabe, N. T. M., Hassan, A. A., Mohamed, M. A. A. (2003). Effect of couple stresses on the MHD of a non-Newtonian unsteady: Flow between two parallel porous plates. Zeitschrift für Naturforschung, 58(4), 204–210. DOI 10.1515/zna-2003-0405. [Google Scholar] [CrossRef]

15. Hayat, T., Iqbal, Z., Qasim, M., Obaidat, S. (2012). Steady flow of an Eyring Powell fluid over a moving surface with convective boundary conditions. International Journal of Heat and Mass Transfer, 55(7–8), 1817–1822. DOI 10.1016/j.ijheatmasstransfer.2011.10.046. [Google Scholar] [CrossRef]

16. Khader, M. M., Megahed, A. M. (2016). Numerical treatment for flow and heat transfer of Powell-Eyring fluid over an exponential stretching sheet with variable thermal conductivity. Meccanica, 51(8), 1763–1770. DOI 10.1007/s11012-015-0336-4. [Google Scholar] [CrossRef]

17. Mahmoud, M. A. A., Megahed, A. M. (2016). Slip flow of Powell-Eyring liquid film due to an unsteady stretching sheet with heat generation. Brazilian Journal of Physics, 46(3), 299–307. DOI 10.1007/s13538-016-0412-9. [Google Scholar] [CrossRef]

18. Mushtaq, A., Mustafa, M., Hayat, T., Rahi, M., Alsaedi, A. (2013). Exponentially stretching sheet in a Powell-Eyring fluid. Zeitschrift für Naturforschung A, 68, 791–798. DOI 10.5560/ZNA.2013-0063. [Google Scholar] [CrossRef]

19. Patel, M., Timol, M. G. (2009). Numerical treatment of Powell-Eyring fluid flow using method of satisfaction of asymptotic boundary conditions (MSABC). Applied Numerical Mathematics, 59(10), 2584–2592. DOI 10.1016/j.apnum.2009.04.010. [Google Scholar] [CrossRef]

20. Ramzan, M., Gul, N., Chung, J. D., Kadry, S., Chu, Y. M. (2020). Numerical treatment of radiative Nickel-Zinc ferrite-Ethylene glycol nanofluid flow past a curved surface with thermal stratification and slip conditions. Scientific Reports, 10(1), 16832. DOI 10.1038/s41598-020-73720-x. [Google Scholar] [CrossRef]

21. Ramesh, K., Khan, S. U., Jameel, M., Khan, M. I., Chu, Y. M. et al. (2020). Bioconvection assessment in Maxwell nanofluid configured by a Riga surface with nonlinear thermal radiation and activation energy. Surfaces and Interfaces, 21(18), 100749. DOI 10.1016/j.surfin.2020.100749. [Google Scholar] [CrossRef]

22. Ramzan, M., Rafiq, A., Chung, J. D., Kadry, S., Chu, Y. M. (2020). Nanofluid flow with autocatalytic chemical reaction over a curved surface with nonlinear thermal radiation and slip condition. Scientific Reports, 10(1), 18339. DOI 10.1038/s41598-020-73142-9. [Google Scholar] [CrossRef]

23. Qayyum, S., Khan, M. I., Masood, F., Chu, Y. M., Kadry, S. et al. (2020). Interpretation of entropy generation in Williamson fluid flow with nonlinear thermal radiation and first-order velocity slip. Mathematical Methods in the Applied Sciences, 44, 1–10. DOI 10.1002/mma.6735. [Google Scholar] [CrossRef]

24. Zhao, T. H., Khan, M. I., Chu, Y. M. (2021). Artificial neural networking (ANN) analysis for heat and entropy generation in flow of non-Newtonian fluid between two rotating disks. Mathematical Methods in the Applied Sciences, 44, 1–19. DOI 10.1002/mma.7310. [Google Scholar] [CrossRef]

25. Akram, S., Razia, A., Afzal, F. (2020). Effects of velocity second slip model and induced magnetic field on peristaltic transport of non-Newtonian fluid in the presence of double-diffusivity convection in nanofluids. Archive of Applied Mechanics, 90(7), 1583–1603. DOI 10.1007/s00419-020-01685-4. [Google Scholar] [CrossRef]

26. Akram, S., Afzal, Q., Aly, E. (2020). Half-breed effects of thermal and concentration convection of peristaltic pseudoplastic nanofluid in a tapered channel with induced magnetic field. Case Studies in Thermal Engineering, 22(2), 100775. DOI 10.1016/j.csite.2020.100775. [Google Scholar] [CrossRef]

27. Song, Y. K., Khan, S. A., Imran, M., Waqas, H., Khan, S. U. et al. (2021). Applications of modified Darcy law and nonlinear thermal radiation in bioconvection flow of micropolar nanofluid over an off centered rotating disk. Alexandria Engineering Journal, 60(5), 4607–4618. DOI 10.1016/j.aej.2021.03.053. [Google Scholar] [CrossRef]

28. Khan, M. I., Waqas, H., Khan, S. U., Imran, M., Chu, Y. M. et al. (2021). Slip flow of micropolar nanofluid over a porous rotating disk with motile microorganisms, nonlinear thermal radiation and activation energy. International Communications in Heat and Mass Transfer, 22(10), 105161. DOI 10.1016/j.icheatmasstransfer.2021.105161. [Google Scholar] [CrossRef]

29. Waqas, H., Khan, M. I., Khan, S. U., Khan, M. I., Kadry, S. et al. (2021). Falkner-Skan time-dependent bioconvrction flow of cross nanofluid with nonlinear thermal radiation, activation energy and melting process. International Communications in Heat and Mass Transfer, 120(2), 105028. DOI 10.1016/j.icheatmasstransfer.2020.105028. [Google Scholar] [CrossRef]

30. Ramzan, M., Riasat, S., Kadry, S., Chu, Y. M., Ghazwani, H. A. S. et al. (2021). Influence of autocatalytic chemical reaction with heterogeneous catalysis in the flow of Ostwald-de-Waele nanofluid past a rotating disk with variable thickness in porous media. International Communications in Heat and Mass Transfer, 128(6), 105653. DOI 10.1016/j.icheatmasstransfer.2021.105653. [Google Scholar] [CrossRef]

31. Chu, Y. M., Ahmad, F., Khan, M. I., Nazeer, M., Hussain, F. et al. (2021). Numerical and scale analysis of non-Newtonian fluid (Eyring-Powell) through pseudo-spectral collocation method (PSCM) towards a magnetized stretchable Riga surface. Alexandria Engineering Journal, 60(2), 2127–2137. DOI 10.1016/j.aej.2020.12.017. [Google Scholar] [CrossRef]

32. Afzal, Q., Akram, S. (2021). Impact of double-diffusivity convection in nanofluids and induced magnetic field on peristaltic pumping of a Carreau fluid in a tapered channel with different waveforms. Journal of Thermal Analysis and Calorimetry, 143(3), 2291–2312. DOI 10.1007/s10973-020-09776-8. [Google Scholar] [CrossRef]

33. Akram, S., Athar, M., Saeed, K., Umair, M. Y. (2021). Double-diffusivity convection on Powell-Eyring nanofluids in non-uniform inclined channel under the impact of peristaltic propulsion and induced magnetic field. The European Physical Journal Plus, 136(5), 1–14. DOI 10.1140/epjp/s13360-021-01506-9. [Google Scholar] [CrossRef]

34. Akram, S., Saleem, N., Umair, M. Y., Munawar, S. (2021). Impact of partial slip and lateral walls on peristaltic transport of a couple stress fluid in a rectangular duct. Science Progress, 104(2), 1–17. DOI 10.1177/00368504211013632. [Google Scholar] [CrossRef]

35. Afzal, Q., Akram, S., Ellahi, R., Sait, S. M., Chaudhry, F. (2021). Thermal and concentration convection in nanofluids for peristaltic flow of magneto couple stress fluid in a nonuniform channel. Journal of Thermal Analysis and Calorimetry, 144(6), 2203–2218. DOI 10.1007/s10973-020-10340-7. [Google Scholar] [CrossRef]

36. Akram, S., Athar, M., Saeed, K. (2021). Hybrid impact of thermal and concentration convection on peristaltic pumping of Prandtl nanofluids in non-uniform inclined channel and magnetic field. Case Studies in Thermal Engineering, 25(2), 100965. DOI 10.1016/j.csite.2021.100965. [Google Scholar] [CrossRef]

37. Akram, S., Razia, A. (2021). Hybrid effects of thermal and concentration convection on peristaltic flow of fourth grade nanofluids in an inclined tapered channel: applications of double-diffusivity. Computer Modeling in Engineering & Sciences, 127(3), 901–922. DOI 10.32604/cmes.2021.014469. [Google Scholar] [CrossRef]

38. Akram, S., Athar, M., Saeed, K., Razia, A. (2021). Crossbreed impact of double-diffusivity convection on peristaltic pumping of magneto Sisko nanofluids in non-uniform inclined channel: A bio-nanoengineering model. Science Progress, 104(3), 1–23. DOI 10.1177/00368504211033677. [Google Scholar] [CrossRef]

39. Powell, R. E., Eyring, H. (1944). Mechanism for relaxation theory of viscosity. Nature, 154(3909), 427–428. DOI 10.1038/154427a0. [Google Scholar] [CrossRef]

40. Prasad, K. V., Vajravelu, K., Datti, P. S., Raju, B. T. (2013). MHD flow and heat transfer in a power-law liquid film at a porous surface in the presence of thermal radiation. Journal of Applied Fluid Mechanics, 6, 385–395. DOI 10.36884/jafm.6.03.19563. [Google Scholar] [CrossRef]

41. Raptis, A. (1998). Flow of a micropolar fluid past a continuously moving plate by the presence of radiation. International Journal of Heat and Mass Transfer, 41(18), 2865–2866. DOI 10.1016/S0017-9310(98)00006-4. [Google Scholar] [CrossRef]

42. Mahmoud, M. A. A., Megahed, A. M. (2009). MHD flow and heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet with variable fluid properties. Canadian Journal of Physics, 87(10), 1065–1071. DOI 10.1139/P09-066. [Google Scholar] [CrossRef]

43. Bilal, M., Ashbar, S. (2020). Flow and heat transfer analysis of Eyring-Powell fluid over stratified sheet with mixed convection. Journal of the Egyptian Mathematical Society, 28(1), 40. DOI 10.1186/s42787-020-00103-6. [Google Scholar] [CrossRef]

44. El-Gendi, S. E. (1969). Chebyshev solution of differential, integral and integro-differential equations. The Computer Journal, 12(3), 282–287. DOI 10.1093/comjnl/12.3.282. [Google Scholar] [CrossRef]