Fluid Dynamics & Materials Processing

---

DOI: 10.32604/fdmp.2023.020049

ARTICLE

Uncertainty Analysis of the Residual Strength of Non-Uniformly Loaded Casings in Deep Wells

Jingpeng Wang1, Wei Zhang1, Zhiwei Lin1, Lin Song1, Shiyuan Xie1, Qi Liu2, Wei Wang2, Tao Yang2, Kai Xu2, Meng Li2 and Yuqiang Xu3,*

1PetroChina Xinjiang Oilfield Company, Karamay, 834000, China
2School of Petroleum and Natural Gas Engineering, Chongqing University of Science and Technology, Chongqing, 401331, China
3School of Petroleum Engineering, China University of Petroleum (East China), Qingdao, 266580, China
*Corresponding Author: Yuqiang Xu. Email: auyuqiang@163.com
Received: 31 October 2021; Accepted: 20 December 2021

1  Introduction

With the increase of deep well drilling and ultra-deep well drilling, the wear of the drill string to the inner wall of the technical casing has always being a problem that cannot be ignored. According to estimates, there exist casing wear issues and fracture or collapse accidents in more than 20 deep wells, including Yingke 1, Kecan 1, Dongqiu 5, Chegu 204, Yacheng 13-1-3, Bohai Caofeidian 18-2-1, Bozhong 13-1-12, Haoke 1, Quele 1, Yangxia 1 and Wushen 1 [1].

Studies have explored the residual strength of worn casing by using finite element method and theoretical analysis method. For instance, Jin et al. [2] calculated the collapse strength of casing under composite wear by analytical method, which was verified by finite element simulation. Since the field measured casing wear shape is very complex and there are many uncertain factors, Saiprakash et al. [3] pointed out that it is necessary to establish a more accurate casing wear prediction model. According to the crescent wear model, White et al. [4] analyzed the collapse failure behavior and collapse strength variation law of three kinds of high collapse strength casings widely used in deep and ultra-deep wells under different wear rates of 0% to 70% using finite element simulation analysis method. The collapse failure type and collapse strength data of casing under different wear rates were obtained. Pattilo et al. [5] achieved the residual collapse strength and residual internal pressure strength of the worn casing, regarding that the circumferential stress of the thinnest inner wall of the worn casing reached the yield limit of the casing as the judgment condition.

In deep wells, the movement of drill pipe is complex. As the lateral force acting on the casing wall increases, the friction and wear between the drill string and the casing during drilling are intensified. Therefore, this directly affects casing design strength and safety and reliability of well completion and production. El-Sayed et al. [6–8] studied the effects of drilling conditions, BHA, hole dogleg degree and drilling fluid performance on casing wear. Based on energy transfer, a casing wear efficiency model is established to predict and analyze the casing wear. Using the stress distribution theory of worn casings. Guan et al. [9] analyzed the influence of non-uniform in-situ stress on the residual strength of casings with different sizes, steel grades and wear depths. On this basis, considering the strength calculation error that may be caused by wellbore shape, Li et al. [10] carried out a three-dimensional curved wellbore casing wear degree and residual strength analysis.

In fact, due to the randomness of process and formation parameters, the parameters affecting the casing strength of deep walls are also difficult to achieve accurately. Considering the uncertainty of casing load in deep wells and the randomness of casing geometric size and performance parameters [11,12], Yin et al. [13] gave a probability distribution calculation method of casing strength by means of stochastic theoretical analysis. Mitkin et al. [14] analyzed the influence law of the randomness of various influencing factors on the reliability of the casing, and calculated the reliability of casing in the practical project. It was concluded that the randomness of various factors can reduce the reliability of the casing. Vislovich et al. [15,16] proposed a non-probabilistic reliability index based on interval theory, and suggested a reliability evaluation model for three-dimensional casing strength and the upper and lower limits of confidence intervals for relevant parameters.

The above investigations have gradually analyzed the effects of geometric parameters, performance parameters and process parameters on the residual strength of casing after wear. However, the above parameters have the characteristics of randomness, and there are few studies on the influence of parameter randomness on the residual strength of casing after wear under non-uniform load. Therefore, the influence of the randomness of multi-source parameters such as wear depth, residual stress and formation non-uniform load on the uncertainty of residual strength after casing wear is analyzed in this paper, and the residual strength after casing wear is quantitatively evaluated, so as to provide guidance on on-site casing safety selection and design.

2  Residual Strength Model of Casing after Wear

Considering the effects of casing residual stress, out-of-roundness, unevenness and formation non-uniform load on casing strength, the residual collapse strength model and residual internal pressure strength model after casing wear can be obtained based on the casing wear efficiency model proposed by White et al. [4].

The residual anti-collapse model under non-uniform load after casing wear is:

Punweff=12Pc[s1+21−mc2|m2s3−(1+m2)s2|]⋅[Pe+Py−(Pe−Py)2+gPePy] (1)

The parameter description in Eq. (1) can be found in the Appendix.

The residual internal pressure strength of casing after wear is:

Piw=2σy(t−kae)[(12)n+1+(13)n+1][D−(t−kae)] (2)

where, n=0.1693−1.1774×10−4σy ; Piw is the residual internal pressure strength of casing after wear, MPa; is the internal pressure strength coefficient, and the quenched and tempered 13Cr material casing is taken as 1.0.

3  Uncertainty Analysis of Residual Strength of Casing

3.1 Randomness of Residual Strength Parameters of Casing

Casing residual collapse strength model and residual internal pressure strength model are functions of multi-source parameters such as wear parameters, casing performance parameters, casing geometric parameters and formation parameters. However, the multi-source parameters of deep well casings have the characteristics of randomness. According to a large number of on-site process parameters and data provided by the manufacturer, nonlinear fitting is performed according to the literature [6], and the results are shown in Fig. 1.

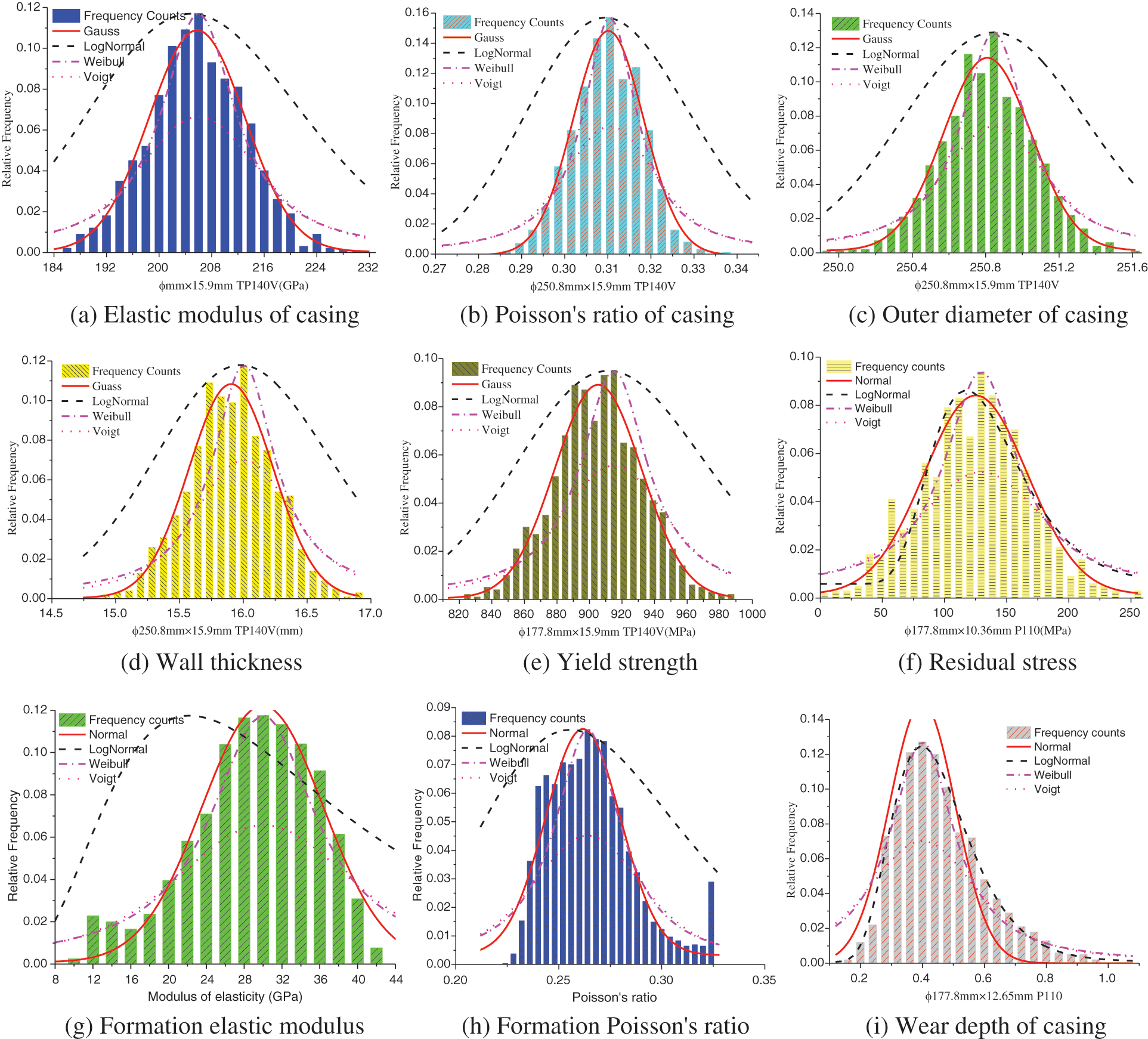
Figure 1: Distribution statistics and fitting of multi-source parameters

Through the correlation test of distribution type between the statistical results and the fitting curve [6], the average correlation coefficients of wear depth, outer diameter, wall thickness, elastic modulus and other parameters of various distribution forms in the statistics can be calculated (Table 1).

The fitting results show that the statistical laws of the above parameters are in good agreement with the normal distribution, and the correlation coefficients with the normal distribution are greater than 0.92, which is a significant strong correlation. The correlation coefficient of the normal distribution is greater than the average correlation coefficient of the lognormal distribution, Weibull distribution and Voigt distribution, so the statistical results of the above parameters fitted with the normal distribution.

3.2 Comparison of Variation Coefficients of Casing Strength Parameters

The variation coefficient is an index to measure the degree of randomness of a parameter. The selection of the main randomness parameter can reduce the dimensionality and also lower the computational workload. The variation coefficient can be defined as [7]:

COV=σμ (3)

The statistical results show that the variation coefficients of wear depth, formation elastic modulus and formation Poisson’s ratio (strip width as shown in Fig. 2) are 0.54, 0.40 and 0.37, respectively, which are much larger than the variation coefficients of other parameters. Briefly, the randomness of these three parameters can be used as the main factors affecting the uncertainty of casing residual strength after wear and tear. Therefore, in terms of the influence of the randomness of parameters on the uncertainty of casing strength after abrasion, the wear depth, formation elastic modulus and formation Poisson’s ratio can be regarded as variables, and the other parameters can be regarded as constants [8]. Then Eq. (1) can be changed to:

Punweff=s(Es,υs)[a−b+cg(ζ)] (4)

where, s(Es,υs)=12Pc[s1+21−mc2|mc2s3−(1+mc2)s2|] , a=Pe+Py , b=(Pe−Py)2 , c=PePy .

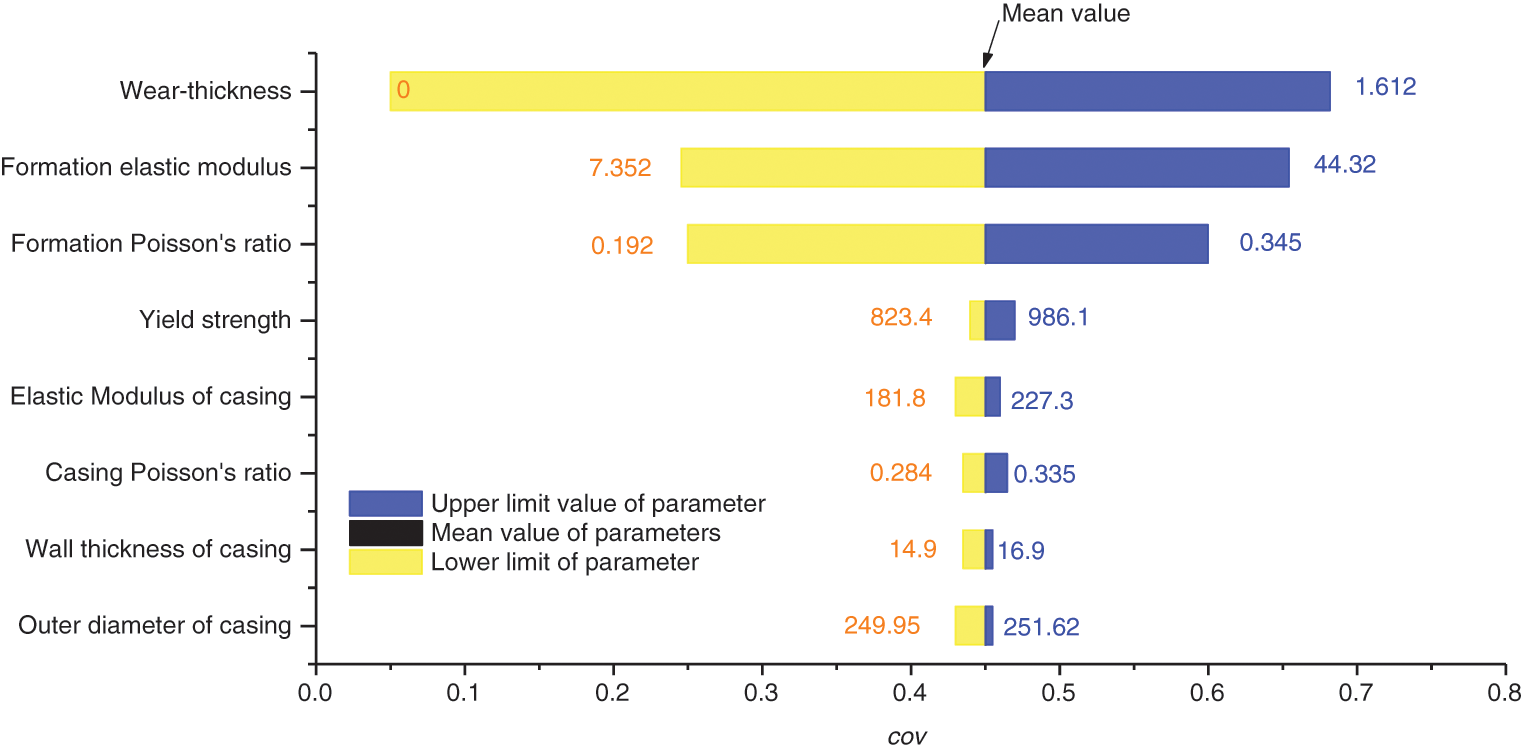
Figure 2: Variation coefficient

Since the randomness of elastic modulus, Poisson’s ratio and wear thickness are the main factors impacting the uncertainty of residual collapse strength of casing after wear, they can be regarded as three-dimensional random variables that affect the uncertainty of residual collapse strength of casing. Let Φ represent the residual crush strength P after abrasion, and its corresponding random value is φ . Also, Ξ characterizes the formation elastic modulus Es , and its corresponding random value is ξ . Similarly, Γ denotes Poisson’s ratio υs , and its corresponding random value is η . In addition, Z gives the wear depth e, and its corresponding random number is ζ .

Therefore, Eq. (4) can be expressed as:

φ=hI(ξ,η,ζ)=s(ξ,η)[a−b+cg(ζ)] (5)

Then,

g(ζ)=hI−1(ξ,η,φ)=uI(ξ,η,φ)=1c[a−φs(ξ,η)]−bc (6)

The partial derivative of φ in uI(ξ,η,φ) is:

∂uI∂φ=1cs(ξ,η) (7)

Let the probability density function of ( Ξ , Γ , Z) be f(Ξ,Γ,Z)I(ξ,η,ζ) , since Ξ , Γ and Z are independent of each other, it can be attained that [8]:

f(Ξ,Γ,Z)I(ξ,η,ζ)=f(Ξ)1(ξ)⋅f(Γ)1(η)⋅f(Z)1(ζ) (8)

where, f(Ξ)1(ξ) , f(Γ)1(η) and f(Z)1(ζ) are the probability density functions of random variables Ξ , Γ and Z, respectively.

According to the probability theory, the probability density function of φ can be expressed as:

f(Φ)I(φ)=∫−∞+∞∫−∞+∞f(Ξ,Γ,Z)1(ξ,η,h1−1)∂h1−1∂φdξdη=∫−∞+∞∫−∞+∞f(Ξ)1(ξ)f(Γ)1(η)f(Z)1[u1(ξ,η,φ)]×∂u1∂φdξdη (9)

Since the wear depth, the formation elastic modulus and the formation Poisson’s ratio are normally distributed, the normal distribution function can be substituted into Eq. (9), and the probability density function of residual collapse strength after casing abrasion can be obtained as follows:

f(Φ)I(φ)=1c(2π)32σξσησζ∫−∞+∞∫−∞+∞1s(ξ,η)exp⁡[−(ξ−μξ)22σξ2−(η−μη)22ση2−(1c[a−b−φs(ξ,η)]−μξ)22σζ2]dξdη (10)

Integrating Eq. (10), the cumulative probability function of residual collapse strength after casing wear under non-uniform external extrusion load is:

F(Φ)I(φ)=1c(2π)32σξσησζ∫−∞+∞∫−∞+∞∫−∞1c[ a−φs(ξ,η) ]−bc                 1s(φ,η)exp[ −(ξ−μξ)22σξ2−(η−μη)22ση2−(1c[ a−φs(ξ,η) ]−bc−μξ)2σξ2 ]dξdηdφ (11)

Similarly, the residual internal pressure strength after casing wear can be expressed as:

φ=h(ζ)=k0+k1ζk2+k3ζ (12)

where, k0=2σyt[(12)n+1+(13)n+1] , k1=−2σyka[(12)n+1+(13)n+1] , k2=D−t , k3=ka , ζ replaces e.

Then:

ζ=h−1(φ)=u(φ)=k0−k2φk3φ−k1 (13)

The partial derivative of φ in u(φ) is:

∂u∂φ=(k1−k0)k3k3φ−k1 (14)

Therefore, the probability density function of residual collapse strength after casing abrasion can be written as:

f(Φ)II(φ)=(k1−k0)k3k3φ−k1exp⁡[−(k0−k2φk3φ−k1−μζ)22σζ2] (15)

The corresponding cumulative probability function is:

F(Φ)II(φ)=1σζ2π∫−∞k0+k1ζk2+k3ζ(k1−k0)k3k3φ−k1exp⁡[−(k0−k2φk3φ−k1−μζ)22σζ2]dφ (16)

According to Eqs. (10) and (11) and Eqs. (15) and (16), the probability density curve and cumulative probability curve of residual collapse strength and residual internal pressure strength after casing abrasion can be depicted, as shown in Fig. 3.

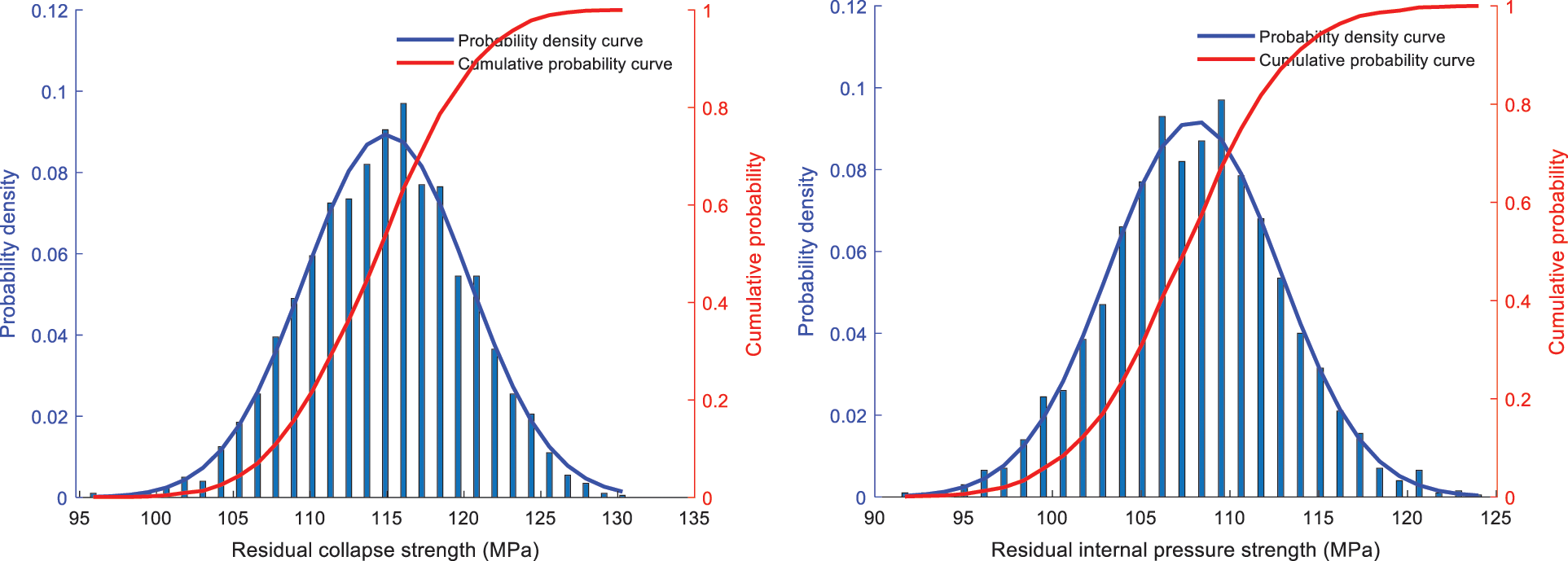
Figure 3: Probability curve of casing residual strength confidence interval analysis of residual strength of casing after wear

According to Eqs. (11) and (16), the cumulative probability distribution function of casing residual strength at different well depths can be obtained:

FΦ,H(φ)={FΦ,h1(φ),FΦ,h2(φ),FΦ,h3(φ),⋯,FΦ,hn(φ)} (17)

When the cumulative probabilities of casing residual strength are u and v (V > U), the set elements, and the corresponding residual strength are:

[p]u={[p]h1,u,[p]h2,u,[p]h3,u,⋯,[p]hn,u}[p]v={[p]h1,v,[p]h2,v,[p]h3,v,⋯,[p]hn,v} (18)

where, [p]hi,u and [p]hi,v are the residual strength of the casing when the cumulative probability at well depth hi is u and v, respectively.

Consequently, the distribution interval of casing residual strength with the confidence level (v − u) is: [[p]hi,u,[p]hi,v] .

4  Case Study

Based on the above calculation method of residual strength after wear, the residual strength of casing after wear of more than 10 wells in the southern edge of Xinjiang Oilfield was calculated and analyzed. Taking the technical casing of well X101 as an example, the structure of well X101 is shown in Fig. 4. Located in the Gaoquandong Anticline of Sikeshu sag of the thrust belt in the southern margin of Junggar basin, it is a key exploration well in the southern margin of the Junggar basin. At 800∼1500 m and 5200∼5400 m, the in-situ stress of the well is highly uneven (as shown in Fig. 4), and drilling is difficult. According to the judgment of the drilling engineer, the technical casing of the well is seriously worn, and the corresponding wear depth, the formation elastic modulus and the formation Poisson are indicated in Fig. 4. Therefore, from the logging data and drilling parameters of X101 well, the residual strength (Φ244.5 mm × 11.99 mm) was analyzed by the residual strength analysis method after casing wear.

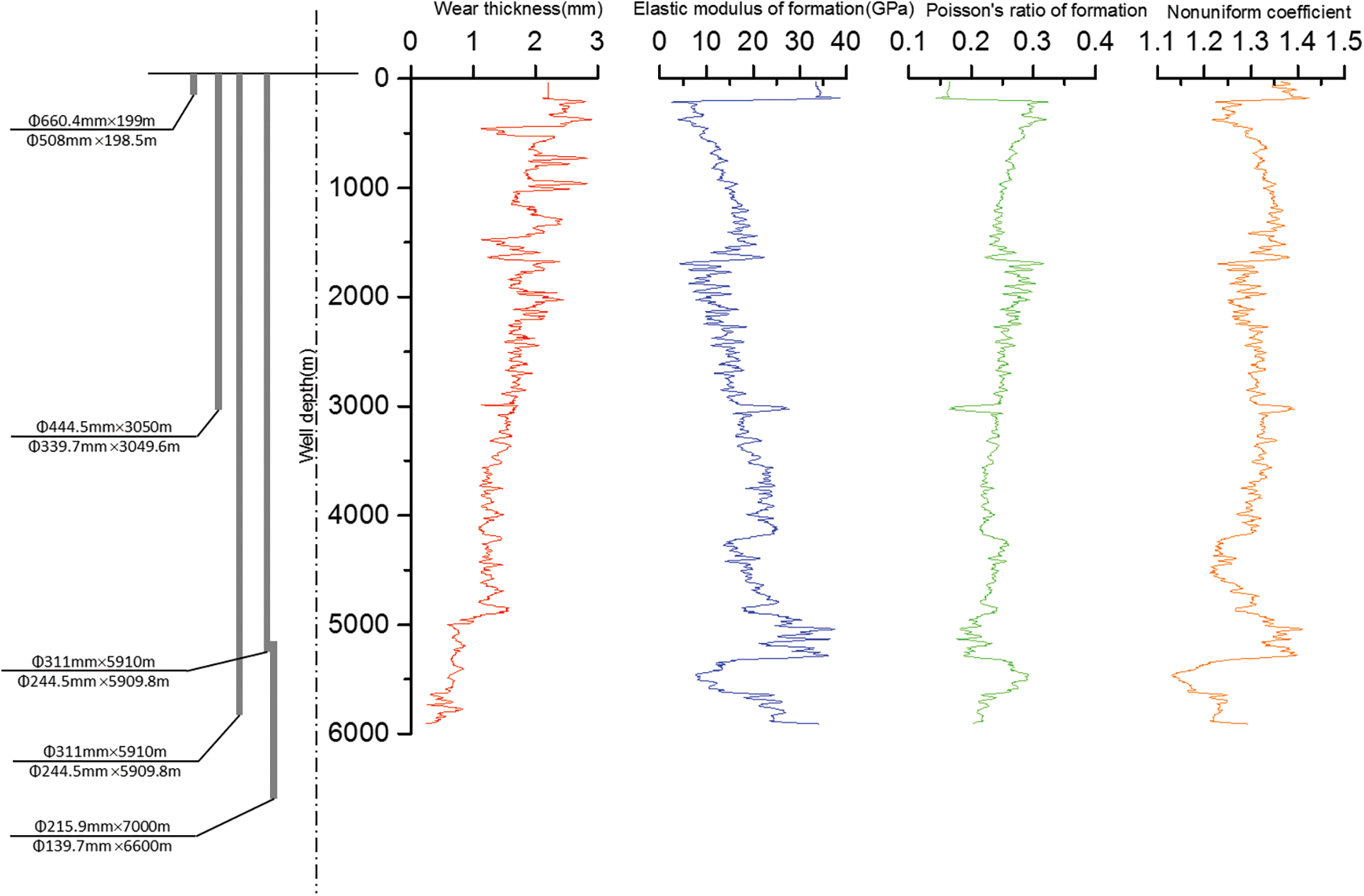
Figure 4: Basic data of well X101

The residual internal pressure strength after casing wear and tear is mainly affected by the wear depth. Therefore, the residual internal pressure strength of the casing is roughly negatively correlated with the wear depth (compared with Figs. 4 and 5). The severely worn parts appear in the upper well section, and the internal pressure resistance of casing can be reduced by about 15%∼20%. The residual collapse strength after casing wear is mainly affected by the wear depth, the formation elastic modulus and the Poisson’s ratio. In particular, when the well depth is between 800∼1500 m and between 5200∼5400 m, the non-uniformity of in-situ stress is becoming large (as shown in Fig. 4). In these well sections, the residual collapse strength after casing wear is significantly reduced, and the collapse strength can be lowered by 20%∼23%. The casing wear depth at the well depth of 4900∼5300 m is small, but under the influence of non-uniform load, the collapse strength of the casing decreases suggestively after wear, and the degree of reduction reaches 21% at the well depth of 4980 m. The casing collapse accidents frequently occurred in this place. In addition, at the well depth of 5260 m, the average reduction of casing collapse strength is only 11%, but the collapse accident can still happen. The analysis shows that the residual strength of casing here is close to the lower limit of residual strength of casing, which is caused by the uncertainty of residual strength after casing wear due to the randomness of parameters.

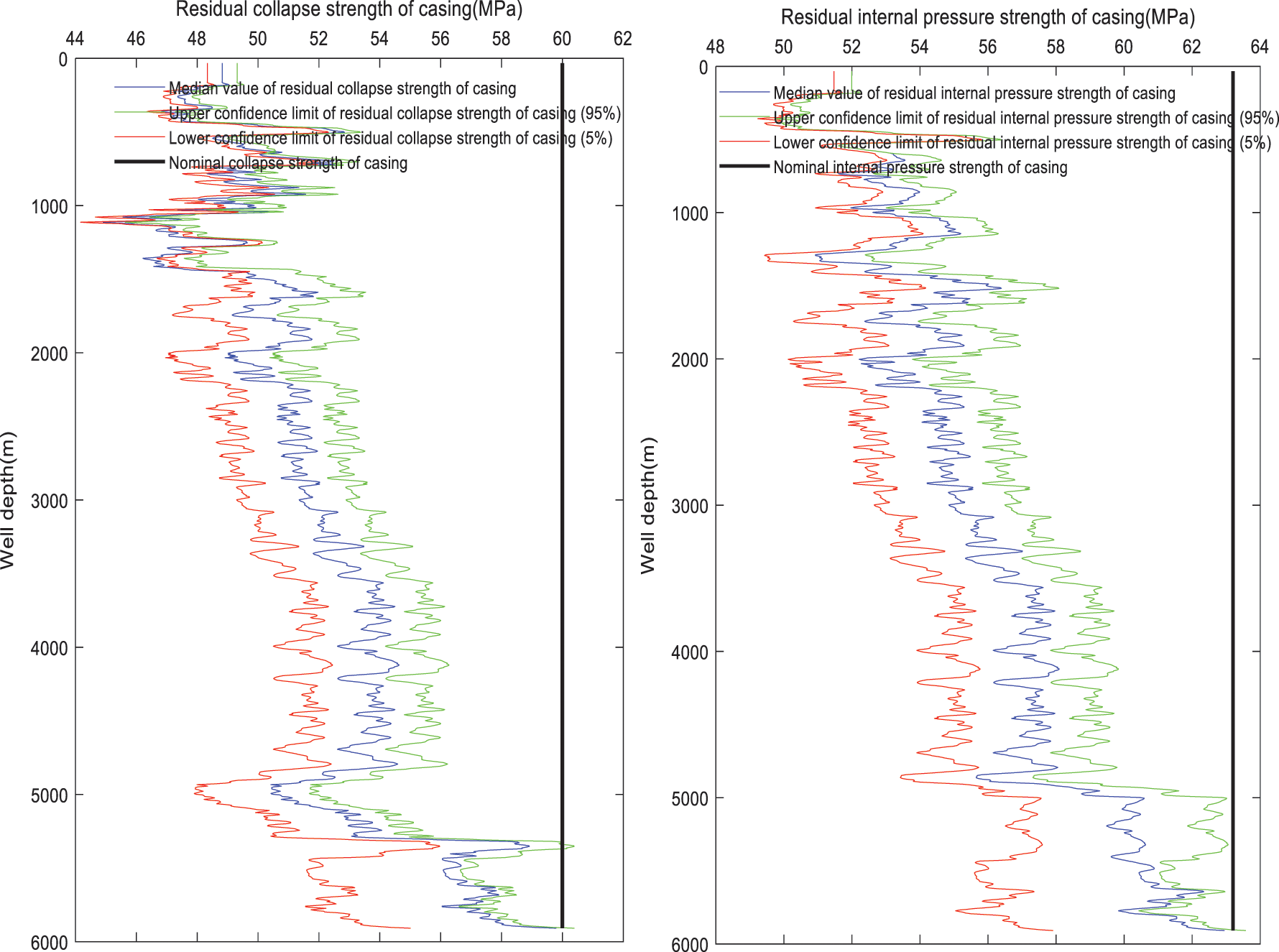
Figure 5: Residual strength of casing after wear

As shown in Fig. 5, the residual strength of the casing after wear obtained by the traditional calculation method is a single curve or a single value. In fact, affected by uncertain factors such as downhole technology and formation, the residual strength after casing wear is usually much higher or lower than the residual strength obtained by the traditional single value calculation method. If the casing strength is calculated according to the traditional casing residual strength prediction method, the illusion of excessive casing residual strength may appear. The fact is that the residual strength of the casing may not be that large, leading to a casing crushing or collapse accident. From the traditional residual strength calculation method, we may also get the result that the predicted residual strength of casing is too small. In fact, the residual strength of casing may be so large that the casing level selected based on the predicted residual strength would be too high, resulting in more economic costs.

It can also be seen from Fig. 5 that under the same confidence level in the whole well section, the upper confidence interval is narrower and the lower confidence interval is wider. Briefly, it indicates the wider the confidence interval, the lower the credibility. This is due to the different degrees of randomness of the multi-source parameters obtained at different well depths. The deeper the well, the harder it is to obtain accurate data, and therefore the wider the confidence interval. In this case, the evaluation can be based on the actual situation of adjacent wells. The confidence interval can be effectively reduced by eliminating the process parameters and formation parameters with large errors. In this way, the distribution range of residual strength after casing wear will be reduced.

Therefore, compared with a single curve, the residual strength interval with certain reliability information is more concerned with the residual strength value that may exist at any well depth. For engineering designers, it is more practical and effective to grasp the possible range of residual strength than to understand a single value. Designers can formulate corresponding emergency standby scheme according to the interval results. Thus, the impact of accidents on the drilling process can be reduced.

5  Conclusion

In this paper, an uncertainty analysis approach is proposed for evaluating the residual strength of a casing subjected to wear and non-uniform loads in deep wells. The three aspects can be summarized as follows:

1.    Considering the influence of casing geometric, casing performance, drilling process and formation parameters on the residual strength after casing wear, the variation coefficients of multi-source parameters are analyzed. It is established that the randomness of wear depth, formation elastic modulus and formation Poisson’s ratio are the main factors affecting the uncertainty of collapse strength after casing wear. The multi-source parameter sensitivity parameter analysis can reduce the dimension of the residual strength model after casing wear. The statistical results indicate that the sensitivity random parameters primarily obey the normal distribution.

2.    The probability density function and cumulative probability function of residual collapse strength and residual internal pressure strength after casing wear are derived by the probability theory. The confidence interval expression method of residual strength after casing wear in deep wells with a specific probability can be achieved.

3.    The analysis and calculation of several wells in the southern edge of Xinjiang oilfield demonstrate that compared with the traditional single value calculation method, the uncertainty calculation method of residual strength can determine a more reasonable safety threshold of casing strength. This can provide a more powerful basis for the selection of ultra-deep well casing.

Acknowledgement: Thanks are due to Qi Liu for assistance with the experiments and to Meng Li for valuable discussion.

Funding Statement: This work was supported by the National Natural Science Foundation of China [51804061, 51974052, 51774063], the Academician Led Special Project of Chongqing Science and Technology Commission [cstc2017zdcy-yszxX0009], the Chongqing Research Program of Basic Research and Frontier Technology [cstc2019jcyj-msxmX0199, cstc2018jcyjAX0417], and the Chongqing Education Committee foundation [KJQN201901544, KJZD-K201801501].

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Wan, L. V., Li, G., Guan, Z. (2012). A Numerical analysis of the actual external collapse load on deep-well casing in its strength design. Petroleum Machinery,40(4), 1–4. DOI 10.16082/j.cnki.issn.1001-4578.2012.04.009. [Google Scholar] [CrossRef]

 2.  Jin, C., Qian, F. (2020). Influence of compound wear on the collapse strength of bending casing. Petroleum Machinery, 48(8), 123–130. DOI 10.16082/j.cnki.issn.1001-4578.2020.08.019. [Google Scholar] [CrossRef]

 3.  Saiprakash, M., Senthilkumar, C., Kadam, S. G. (2019). Effects of Angle of attack and bluntness on heating rate distribution of blunt models at hypersonic speeds. Fluid Dynamics, 54(6), 850–862. DOI 10.1134/S0015462819060090. [Google Scholar] [CrossRef]

 4.  White, J. P., Rapier, D. (1987). Casing wear: Laboratory measurements and field predictions. SPE Drilling Engineering, 2(1), 56–62. DOI 10.2118/14325-PA. [Google Scholar] [CrossRef]

 5.  Pattilo, P. D., Last, N. C., Asbill, W. T. (2003). Effect of nonuniform loading on conventional casing collapse resistance. SPE Drilling & Completion,19(3), 156–163. [Google Scholar]

 6.  El-Sayed, A. H., Khalaf, F. (1992). Resistance of cemented concentric casing strings under non-uniform loading. SPE Drilling Engineering, 7(1), 59–64. DOI 10.2118/17927-PA. [Google Scholar] [CrossRef]

 7.  Adams, A. J., Hodgson, T. (2020). Calibration of casing/tubing design criteria by use of structural reliability techniques. SPE Drilling & Completion, 14(1), 21–27. DOI 10.2118/55041-PA. [Google Scholar] [CrossRef]

 8.  Beck, D., Andre, T. (2009). Empirical random kick model and casing reliability. SPE Drilling & Completion, 35(4), 644–654. DOI 10.2118/201200-PA. [Google Scholar] [CrossRef]

 9.  Guan, Y. (2020). Analysis of casing wear degree and residual strength in three-dimensional curved well. Xi’an, Shaanxi: Xi’an Petroleum University. [Google Scholar]

10. Li, M., Su, K. H., Li, Z. J. (2017). Uncertainty analysis method of casing extrusion load for ultra-deep wells. Computer Modeling in Engineering & Sciences, 113(4), 475–495. DOI 10.3970/cmes.2017.113.475. [Google Scholar] [CrossRef]

11. Klever, F. J., Tallin, A. G. (2005). The role of idealization uncertainty in understanding design margins. SPE High Pressure/High Temperature Sour Well Design Applied Technology Workshop, The Woodlands, Texas. [Google Scholar]

12. Fan, C., Wu, Y., Yu, Y. (2020). Dynamic thin-airfoil stall and leading-edge stall of oscillating wings at low Reynolds number. Fluid Dynamics, 54(5), 691–704. DOI 10.1134/S0015462819040128. [Google Scholar] [CrossRef]

13. Yin, J., Jia, T., Gao, D. (2021). Numerical investigation of the characteristics and interference effect of flow past multi-cylinder at low Reynolds numbers. Fluid Dynamics, 56(2), 242–254. DOI 10.1134/S0015462821020130. [Google Scholar] [CrossRef]

14. Mitkin, V. V., Prokhorov, V. E., Chashechkin, Y. D. (1998). Investigation of the variability of the structure of a stratified wake behind a horizontal cylinder using optical and acoustic methods. Fluid Dynamics, 33(3), 303–312. DOI 10.1007/BF02698177. [Google Scholar] [CrossRef]

15. Vislovich, A. N., Sukhotskii, A. B. (2001). Forces exerted on a plate in a magnetic fluid located in a magnetic field with exponential inhomogeneity. Fluid Dynamics, 36(6), 855–865. DOI 10.1023/A:1017933806616. [Google Scholar] [CrossRef]

16. Silva, T. B., Lima, J., Gouveia, L. P. (2019). Structural reliability applied to analytical modeling of the tensile strength of standard API casing connections. Brazilian Journal of Petroleum and Gas, 13(4), 33–35. DOI 10.5419/bjpg2019-0025. [Google Scholar] [CrossRef]

Appendix

s1=−2[(1−2υs)σ+1−υc21+υsEsEcm21−m2p0][1+11−m21+υc1+υsEsEc(1−2υc+m2)]−1

s2=C22+C12C11C22−C12C21R,

s3=−C21+C11C11C22−C12C21R

C11=(1−23υc)+(5−6υc)m2+(3−2υc)m4+(53−2υc)m6+1+υs1+υcEcEs(53−υs)(1−m2)3

C12=C21=−23υc+2υcm2−2(2−υc)m4−(43−2υc)m6−1+υs1+υcEcEs(43−2υs)(1−m2)3

C22=(1−23υc)−(3−2υc)m2+(3−2υc)m4+(53−2υc)m6+1+υs1+υcEcEs(53−2υs)(1−m2)3

R=−4(1+υs2)1+υcEcEs(1−m2)3s,

σ=σH+σh2, s=σH−σh2

Pe=2Ec(1−υc)1(D/t)[(D/t)−1]2,

Py=2σy[(D/t)−1](D/t)2[1+1.47(D/t)−1]

g=0.3232δ0(%)+0.00228ε(%)−0.5648σRσy,

δ0=2e2D−4t+e, ε=2e2D−e

where, Punweff is the remaining collapse strength of the casing after wear, MPa; υs is the formation Poisson’s ratio, dimensionless; υc is the Poisson’s ratio of the casing, dimensionless; σH is the maximum horizontal in-situ stress, MPa; σh is the minimum horizontal in-situ stress, MPa; Ec is the elastic modulus of formation, MPa; m is the ratio of internal and external diameters of the casing; D is the outer diameter of the casing, mm; t is the wall thickness of the casing, mm; σR is residual stress of casing, MPa; σy is the casing yield strength, MPa; e is the wear depth of casing, mm.

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.