Fluid Dynamics & Materials Processing

---

DOI: 10.32604/fdmp.2023.019763

ARTICLE

Assessment of Different Optimization Algorithms for a Thermal Conduction Problem

Mohammad Reza Hajmohammadi1, Javad Najafiyan1 and Giulio Lorenzini2,*

1Department of Mechanical Engineering, Amirkabir University of Technology, Tehran, Iran
2Dipartimento di Ingegneria e Architettura, Università Degli Studi di Parma, Parma, Italy
*Corresponding Author: Giulio Lorenzini. Email: giulio.lorenzini@unipr.it
Received: 13 October 2021; Accepted: 07 February 2022

Nomenclature

A	Area (m2)
H	Height (m)
k	Thermal conductivity (W.m−1.K−1)
L	Length (m)
c	Coordinate normal to the surfaces (m)
N	Number
q′′′	Volumetric uniform heat generation in the piece (W.m−3)
V	Volume (m3)
W	Width (m)
x, y, z	Cartesian coordinates (m)
Greek Symbols
β	Thermal conductivity ratio, kh/kl
θ	Temperature (K)
ω	Volume fraction occupied by the inserts
Subscripts
0	Hot medium
B	Branches
H	High conductivity material (inserts)
L	Low conductivity material (hot medium)
Max	Maximum
Min	Minimum
N	Each branch
S	Segments
T	Total (hot medium and conductive pathway)
Superscripts
−	Dimensionless variables

1  Introduction

The failure of electronic chips manifested as increased device temperature is a significant concern today. Accordingly, many researchers seek new cooling solutions. Convection cooling methods famously suffer many disadvantages that render them impractical: high-volume occupancy and impairing electronic chips’ efficiency. However, there is an alternating manner using inserts (highly conductive materials) with a unique advantage: low volume occupancy.

Because of the complexity of suggested structures and consequently multiplicity of optimization parameters, recently, some researchers have employed optimization algorithms to introduce valuable solutions to heat transfer problems [1–3]. Bejan et al. proposed cooling hot mediums by inserts for the first time [4] and introduced the constructal law (CL) [5], attracting many authors to this law, including [6–11].

As the suggested configuration of inserts gets complicated, the significance of choosing the most efficient method for optimizing the geometrical shape of high conductivity inserts with lower time cost is more than ever. With the growth and development of computers in engineering applications, optimization algorithms have become an inseparable part of solving various problems [12]. With the many optimization methods used in engineering, identifying the perfect method specific to problems is a serious challenge. Optimization algorithms are commonly selected to solve optimization problems since they have numerous optimization variables.

Optimization algorithms are generally divided into derivative-free (direct) and gradient-based methods. Gradient-based optimization algorithms are essentially simple methods that direct the search process using derivative information. However, with the difficulty of obtaining derivatives, derivative-free methods are a more popular alternative. Derivative-free methods employ no derivative information derived from objective functions to find optimal solutions. In cases when derivative information of the objective function is inaccessible or untrustworthy to obtain, these methods are very applicable. Thus, derivative-free methods can be used when the objective function is not continuous or differentiable. The key advantage of derivative-free optimization strategies is their potential to solve problems complicated for gradient-based methods [13–15]. Therefore, to tackle this problem in this study, two popular derivative-free optimization algorithms, the genetic algorithm (GA) and the pattern search (PS) algorithm, were employed. Their efficiency was compared with the direct method (DM).

Firstly, Estrada et al. [16] presented an optimization for the geometry of asymmetric V-shaped inserts for minimizing the peak temperature of a hot square body through the CL and GA. Their work resulted in some optimal shapes concerning the DOF.

Avendaño et al. [17] employed the GA, CL, and the evolutionary theory and proposed two approaches to cool a hot medium. They found insert configurations that were superior to the I-shaped insert case [18].

Then, the innovative fast algorithm was introduced based on recursive localization of high conductivity materials rectangular pieces [19]. The main optimization objective in that study was to minimize the thermal resistance of a hot piece. They showed the higher efficiency and faster performance of the mentioned algorithm than a time-consuming algorithm, such as the GA.

Recently, two distinguished types for tree-shaped inserts with non-uniform unequal branches, intruding a hot square body, have been presented in [20], where the PS optimization algorithm was employed to minimize the body’s hotspot temperature. The results indicated that the minimized peak temperature of the designed configurations was up to 61% less than the minimized hotspots presented in relevant previous research. Also, the unequal branches were superior to those with equal branch length.

Furthermore, some researchers have used an optimization algorithm to solve thermal optimization problems: covariance matrix adaptation evolution strategy (CMA-ES), which is an evolution strategy to solve heat transfer problems [21,22].

In the current research work, the principal goal is to compare and choose the most efficient and fastest numerical optimization method for the particular problem of cooling electronics using highly conductive inserts in the form of multiple tree-shaped of unequal branches with the constraint of a finite extent of high conductivity materials. Since optimization algorithms are very diverse, the results of this study can help thermal optimization studies select the most efficient optimization method. As mentioned, mathematical modeling was not the main purpose of the problem in this work, but it has been given in the following to better dissect the problem. To that end, the study examined three methods, including DM, GA, and PS optimization algorithms, to find the most cost-effective method with an optimal design corresponding to the minimum thermal resistance of the hot body.

2  Problem Definition and Mathematical Formulation

Suppose a square body with uniform heat generation (Fig. 1). The thickness of the body W is sufficiently long compared to length L0 and height H0 of total volume. The low conductivity body (thermal conductivity kl) is squared (L0 = H0) and intruded by unequal multiple conductive branches (thermal conductivity kh). Heat is generated uniformly in the medium with the volumetric rate q’’’ (W/m3), and a heat sink with the minimum temperature T0 situated in the rim removes the generated heat. The outward body surfaces are perfectly adiabatic (Fig. 1).

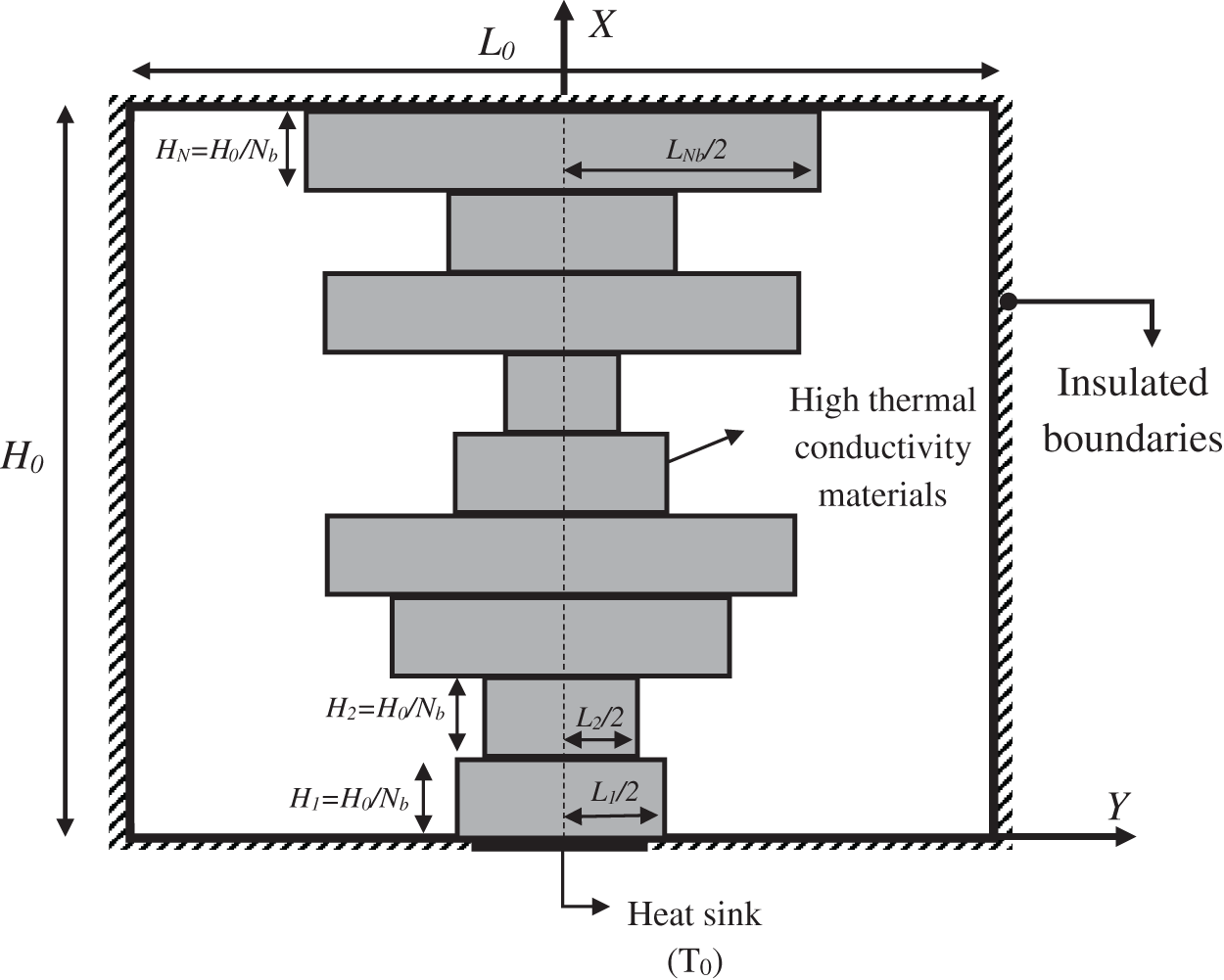
Figure 1: Hot medium with highly conductive unequal branches

Sake of selecting unequal branches returns to Bejan’s CL [5], which states that raising DOF increases system efficiency. Hence, the Nb number of branches with the various length of Ln and the equal height of Hn = H0/Nb, embedded into the body (Fig. 1). In this problem, the initial length of every branch begins from the symmetry line. Moreover, one-half of the geometry is assumed due to the symmetry condition (Fig. 2). The total volume of the entire system (hot piece and conductive inserts) is fixed.

Vt=Vl+Vh=WL02(constant) (1)

where l and h return to the low conductivity material (body) and the high conductivity material (inserts), respectively. For the sake of simplifying the problem, the variation of all parameters perpendicular to the plane of Fig. 1 is assumed negligible. So, the total area of the entire system is fixed:

At=Al+Ah=L02(constant) (2)

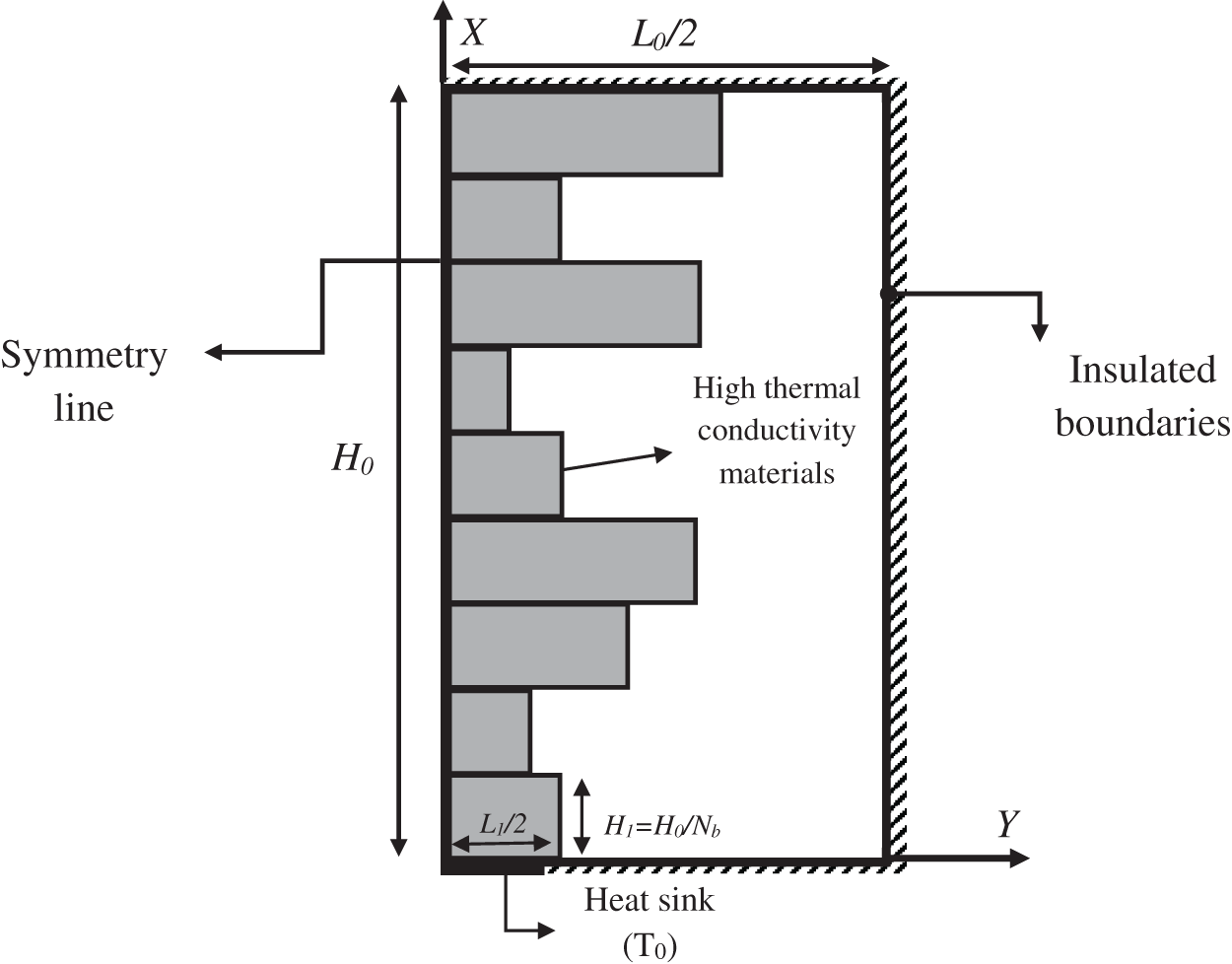
Figure 2: Computational domain of the cooling problem of a hot medium with highly conductive unequal branches (half of the geometry)

The area allocated to highly thermal conductive branches is fixed:

Ah=∑n=1NbHnLn=L0Nb∑n=1NbLn (3)

The fraction ω for the area allocated to the inserts is described as the high conductivity inserts embedded in the whole body:

ω=VhVt=AhAt (4)

Rising the body’s temperature through the thermal resistance of the piece higher than the minimal system temperature (heat sink temperature T0) is the point that might damage the electronic chip or affect its performance. Therefore, the main aim is to find the optimal configuration of inserts that facilitate the heat flow access through the inserts by finding an optimal (efficient and fast) numerical optimization method.

The steady-state two-dimensional conduction equation for the area of lowly conductive materials (piece) is:

∂2θ¯l∂x¯2+∂2θ¯l∂y¯2+1=0 (5)

The steady-state equation of thermal conduction for the domain of high conductivity inserts with no heat-generating can be given as:

∂2θ¯h∂x¯2+∂2θ¯h∂y¯2=0 (6)

where:

θ¯=θ−θ0q′′′At/kl (7)

(x¯,y¯,c¯)=(x,y,c)At1/2 (8)

The boundary conditions for the outer adiabatic surfaces give:

∂θ¯∂c¯=0 (9)

The boundary condition of the heat sink is:

θ¯=0 (10)

Continuity in temperature and heat flux at the interface gives:

∂θ¯l∂n¯=β∂θ¯h∂n¯ (11)

θ¯l=θ¯h (12)

where the fraction β described as:

β=kh/kl (13)

The purpose of optimization is to determine the length (end) of each branch for two specified branches’ number Nb = 5, 10 and several cases of β = 100, ω = 0.1, β = 200, ω = 0.2 and β = 300, ω = 0.05 with respect to the constraint of constant volume fraction for minimizing the maximum dimensionless temperature:

θ¯max=θmax−θ0q′′′At/kl (14)

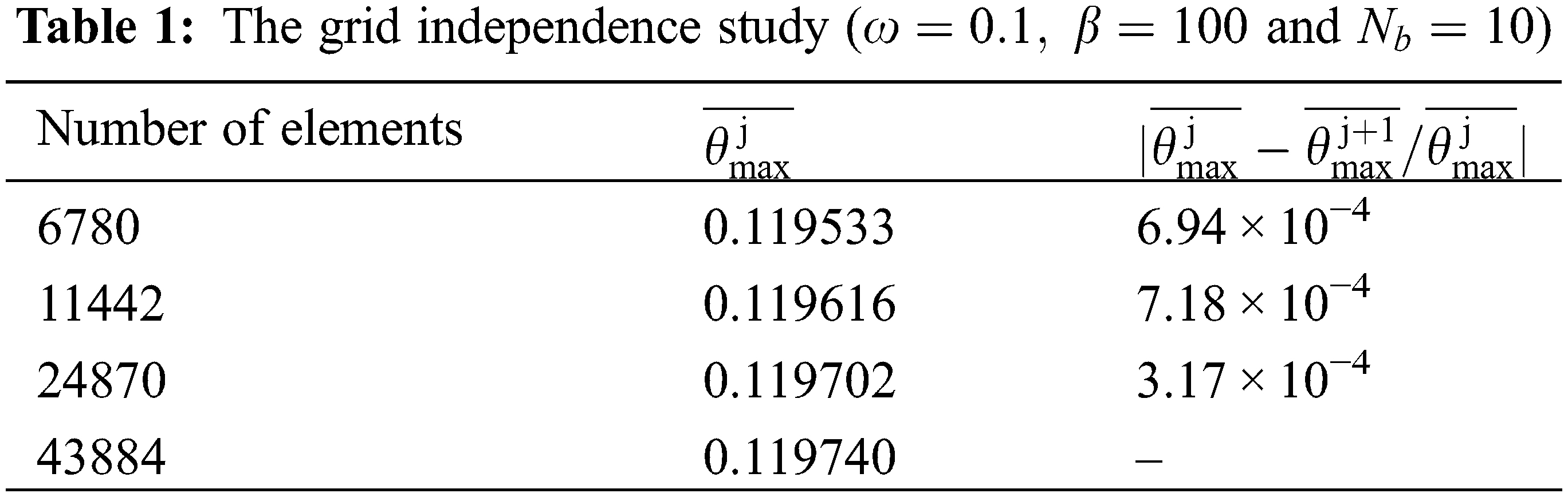
The numerical simulation performed was based on the finite element method (FEM) developed in the MATLAB PDE toolbox environment. The governing equations of heat conduction for the body and conductive pathways (Eqs. (5) and (6)) are solved numerically considering the set of boundary conditions (Eqs. (9)–(12)). The objective function of the problem is the maximum dimensionless temperature of the body (Eq. (14)), and the constraints of the problem are the total area of the entire system and the area of highly conductive materials (Eqs. (2) and (3)). The grid contains non-uniform triangular elements, and the appropriate mesh size was determined by incrementing the elements’ number until the successive refinements criterion was met.

|θ¯maxj+1−θ¯maxjθ¯maxj|<5×10−4 (15)

where “j” refers to the current element size and “j+1” refers to the latter element size. As shown in Table 1, in the mesh-size independence study, independence from meshing is well met.

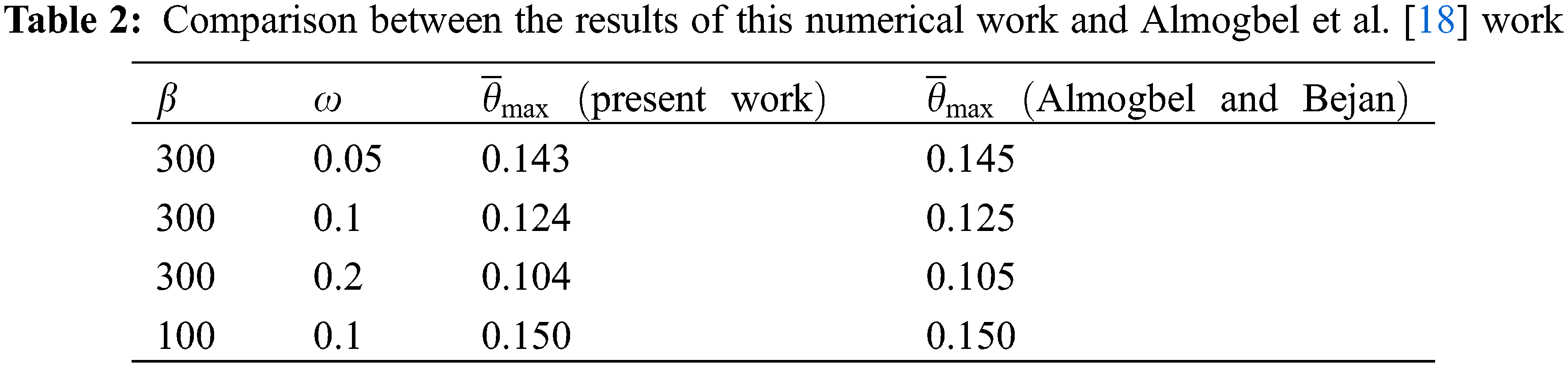
Besides, the results were compared with the numerical results in [18] (Table 2) to test the accuracy of the current work for multiple cases of β and ω.

3  Proposed Optimization Methodologies

The proper selection of an optimization algorithm is crucial to solving an optimization problem. As previously mentioned, the optimization aims to minimize Eq. (14) (peak dimensionless temperature). The design variables include the number of branches (Nb), the volume fraction (ω), the thermal conductivity ratio (β), and the length of each branch (Ln). Three popular and practical optimization methods were considered:

•   Direct Method (DM): This method is statically guaranteed to find the optimal hotspot dimensionless temperature. However, this approach is not efficient in its search strategy. It determines all possible modes for the geometrical arrangement of conductive branches concerning the constraint of a constant extent of high conductivity materials. In this method, highly conductive branches are composed of several segments that increment in the number of segments cause an increase in the DOF, and consequently, the minimized hot spot temperature is expected to decline. It determines all possible modes in three numbers of segments. In the first possible number of segments, all possible modes are determined. However, in the subsequent numbers of segments, the previous results of the determined length of each branch are used as a primary point for the latter case, indicating that the obtained length in the number of segments Ns is used for the case with the number of segments 2Ns. In this method, Ns is the additional design variable.

•   Pattern Search (PS): Patterns search is a systematic direct search type that dynamically generates and maintains multi-dimensional search directions. The PS algorithm does not explore the global structure of the objective function and can get attracted by any minimum, whether global or local [23,24]. The PS algorithm is employed in the MATLAB environment.

The PS algorithm needs a primary guess as a starting point for each branch. Accordingly, at the beginning of the optimization with Nb = 5, the primary guess for all branches considered equal lengths ( L¯1=L¯2=,…,=L¯Nb ). After that, the optimal lengths obtained from Nb = 5 are utilized as the initial optimization point in Nb = 10. Therefore, we can nominate this procedure as an evolutionary method.

•   Genetic Algorithm (GA): The GA is an exploratory search approach based on the theory of natural evolution. GA is a random algorithm that frequently adjusts a population of individual solutions. It means at each step, the GA randomly chooses individuals from the current population as parents and utilizes them as the next generation children [25]. In other words, the GAs are population-based search strategies that maintain the locations and values of a set of points in a function space. The comparison standard for which old points are discarded or new points are generated depends on the current population [26].

Unlike the PS algorithm, the GA does not need any initial guess. GA is also employed in MATLAB software.

4  Results and Discussion

Here, this section presents the minimal peak temperature corresponding to the optimal structures of branches obtained from three different numerical methods and their execution times for each case presented. Afterward, the results obtained from each optimization method were compared together. The computer specification on which these three methods were run was Intel Corei5-3320M CPU and 4 GB RAM.

The optimization results were obtained from DM, GA, and PS numerical processes. In the DM, three levels for the number of segments Ns are supposed. With the increment in the number of segments Ns, the maximum temperature max is predicted to decrease at a lower degree due to the increase in the DOF. However, an increment in the number of segments causes more accuracy in the DM, despite increasing the runtime.

Tables 3–5 show the minimal dimensionless maximum temperature respectively for three cases of β = 200, ω = 0.2, β = 100, ω = 0.1, and β = 300, ω = 0.05 while Nb = 5, 10 and for three numerical methods of DM (in the number of segments Ns = 10, 20, 40), GA and PS.

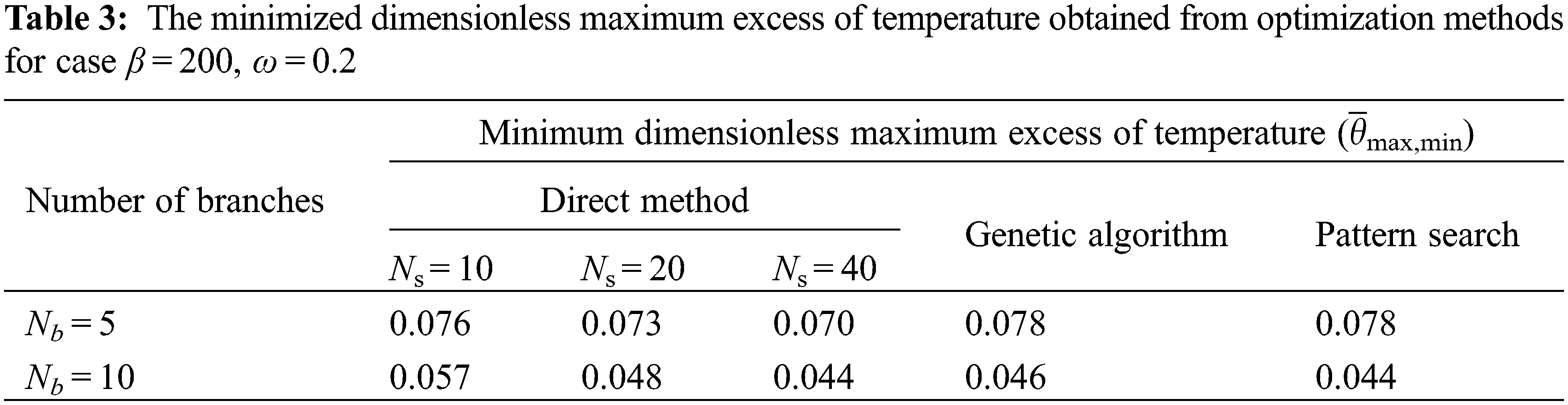
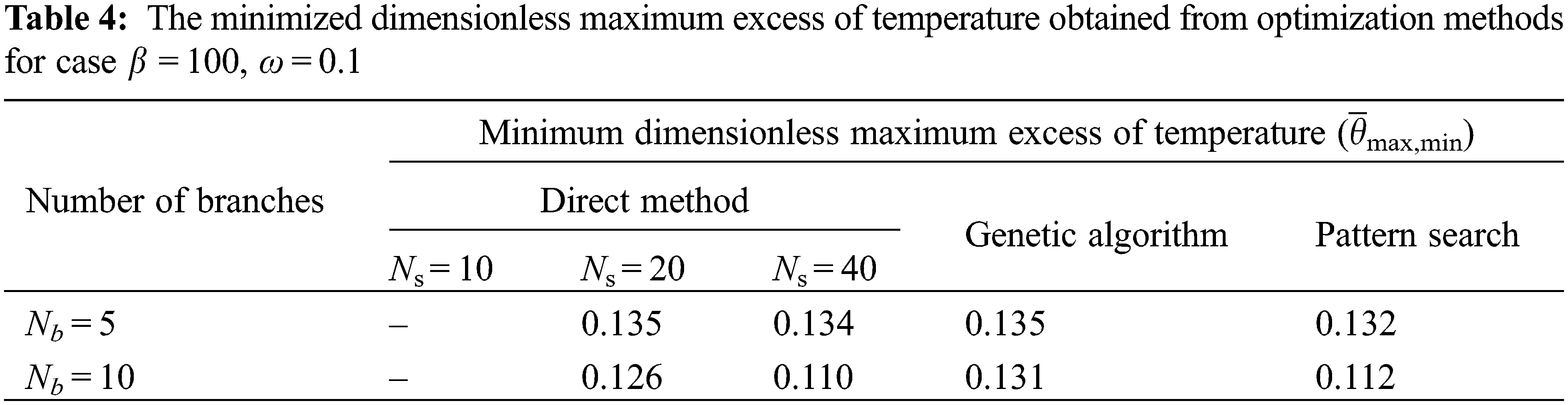
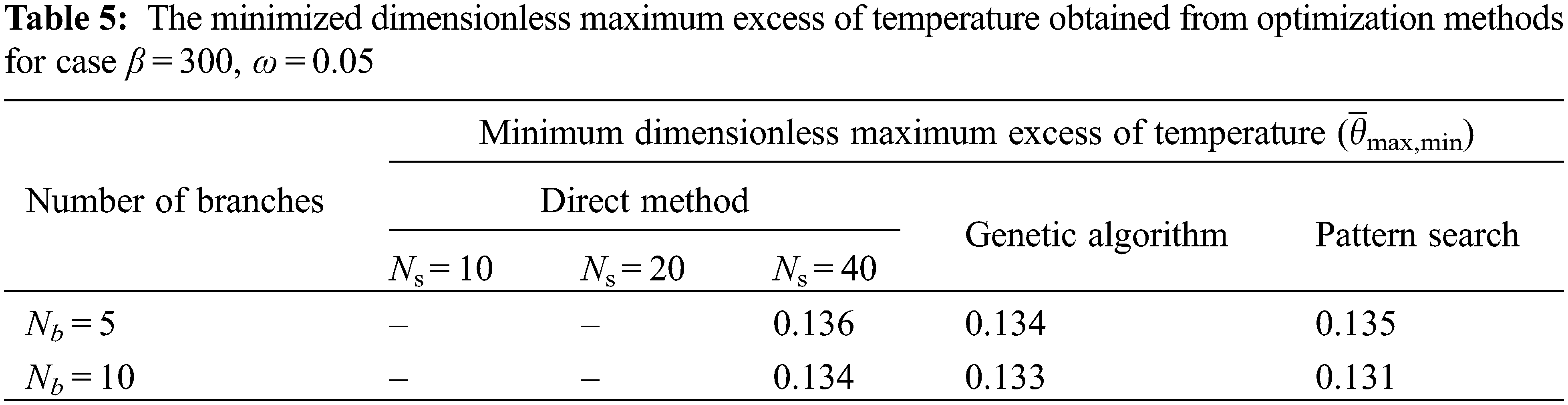
For the case β = 200, ω = 0.2 in Table 3, it can be found that the first possible number of segments is Ns = 10. For the cases, β = 100, ω = 0.1 (Table 4), and β = 300, ω = 0.05 (Table 5), the first possible number of segments are Ns = 20 and Ns = 40, respectively.

As expected, the minimized hotspot dimensionless temperature θ¯max,min declined by an increment in the number of segments for all three cases. Also, the increase in the Nb decreased the body’s minimized peak temperature.

In Tables 3–5, discovered that the minimal peak dimensionless temperature of DM and PS are very close together and they are less than the magnitude of minimum peak temperature obtained from the GA method that it can be assumed that the minimized hotspot obtained from the DM and PS methods are approximately equal. Thus, the execution time (runtime) is the important parameter to select the most efficient method for optimizing this problem.

The execution time is a critical factor in selecting the most efficient numerical optimization method. The runtime of cases of β = 200, ω = 0.2, β = 100, ω = 0.1 and β = 300, ω = 0.05 presented in Tables 6–8, respectively, when Nb = 5, 10 and three methods of DM, in three number of segments Ns = 10, 20, 40, GA and PS.

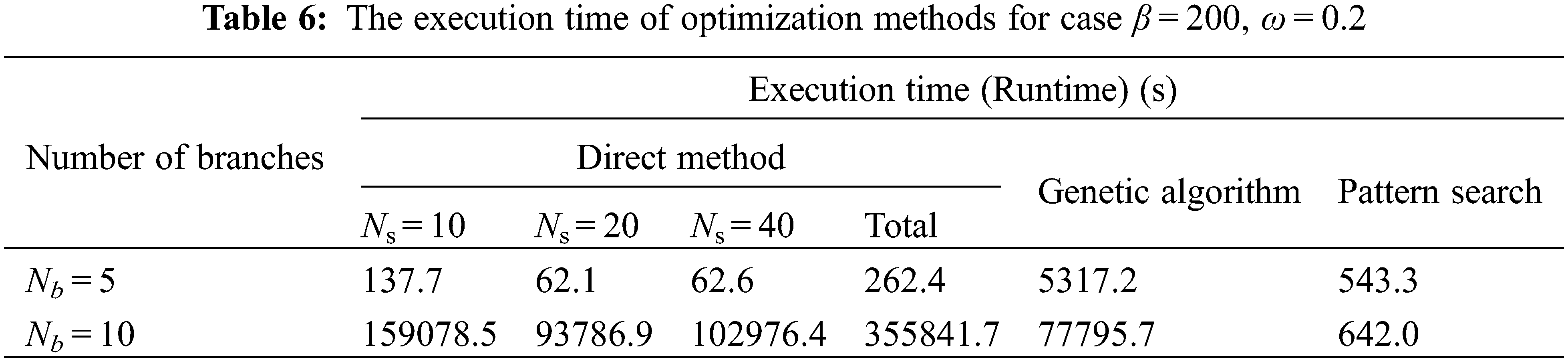
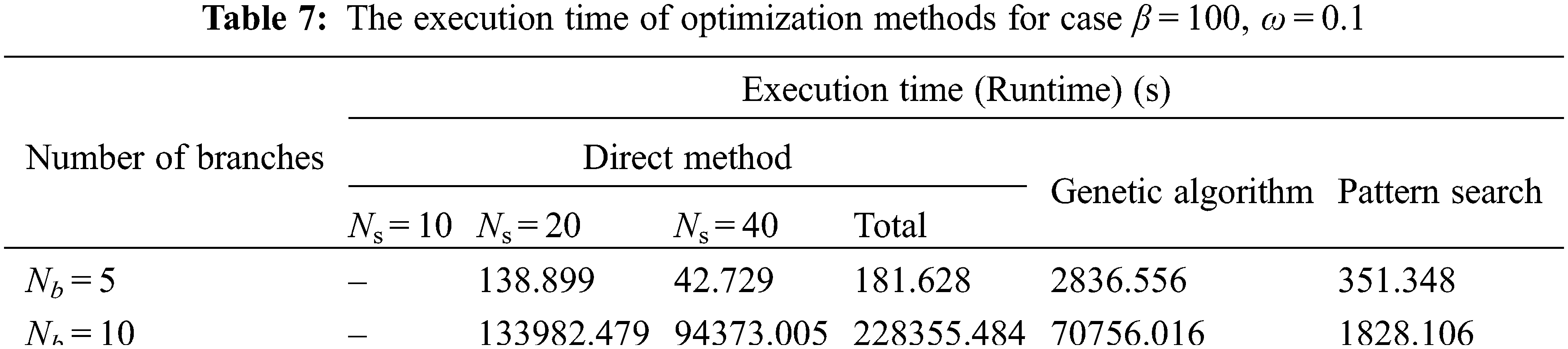
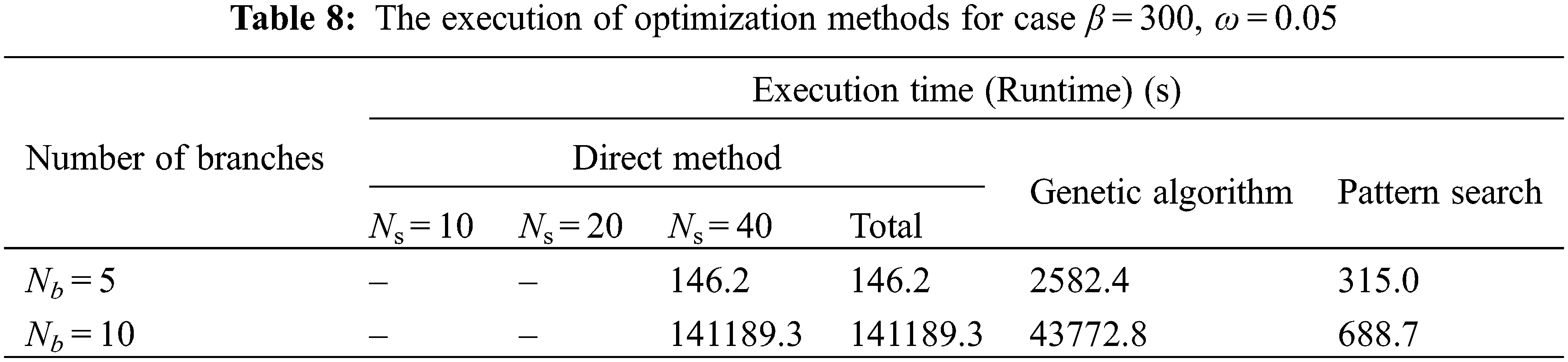
Since the results obtained from DM in the first possible number of segments Ns, used in the latter number of segments 2Ns, and so on, the runtime of DM is the sum of runtimes of all number of segments. Thus, for the DM, the total time is considered.

As shown in Tables 6–8 and Figs. 3–5, the total execution time for optimizing the maximum dimensionless temperature by DM is fewer than the two other optimization algorithms (GA & PS). In Nb = 5, the runtime for the optimization with GA is much more than the two other algorithms. For example, for case β = 200, ω = 0.2 in Nb = 5, the DM and about ten times greater than the PS algorithm. Nevertheless, the difference between the PS algorithm and the DM is much smaller and about two times. It means for Nb = 5, because of the approximate equality between minimal hot spot dimensionless temperature obtained from three optimization algorithms, the DM is the fastest method. But in Nb = 10, the proposition is quite different from the state Nb = 5. As presented in Tables 6–8, it can be detected that the total execution time for the DM is a huge amount, especially compared to the PS algorithm. For example, for the case β = 200, ω = 0.2, the execution time for the DM in Nb = 10 is more than 554 times greater than the PS algorithm that is a huge difference. Also, the difference between the PS and the GA is fewer and about 121 times: as the Nb increases, the runtime of each three methods will increase in a very different amount, indicating that optimization algorithms such as PS and GA are more efficient and applicable in cases of the multiplicity of optimization parameters. Thus, the increase in execution time of the PS algorithm, as the Nb increases, is less than the two other methods (Figs. 3–5).

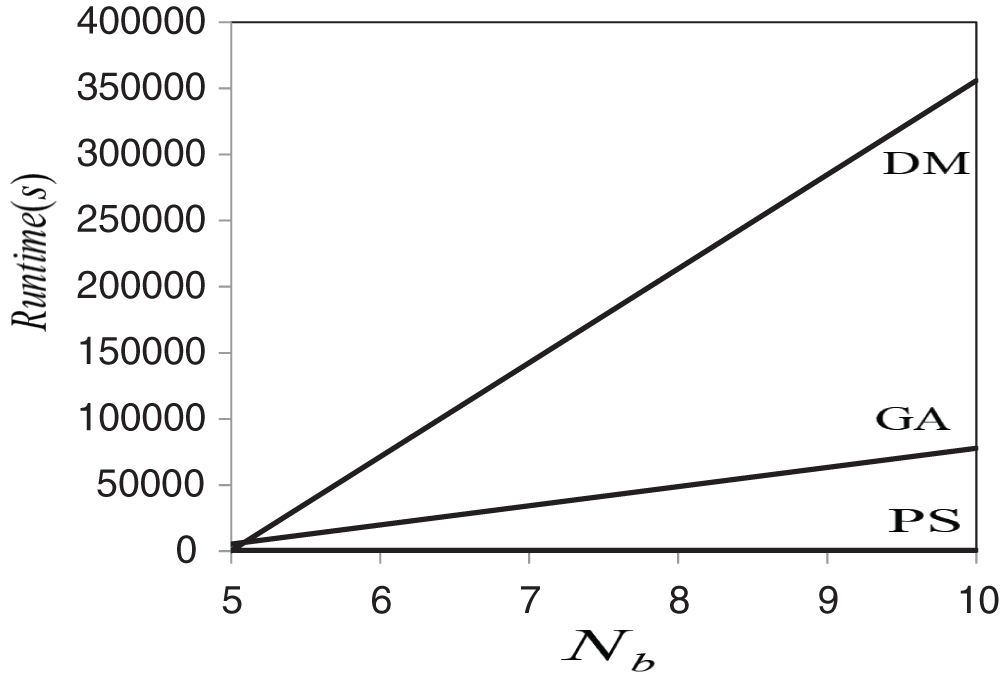
Figure 3: The execution time of optimization methods for case β = 200, ω = 0.2

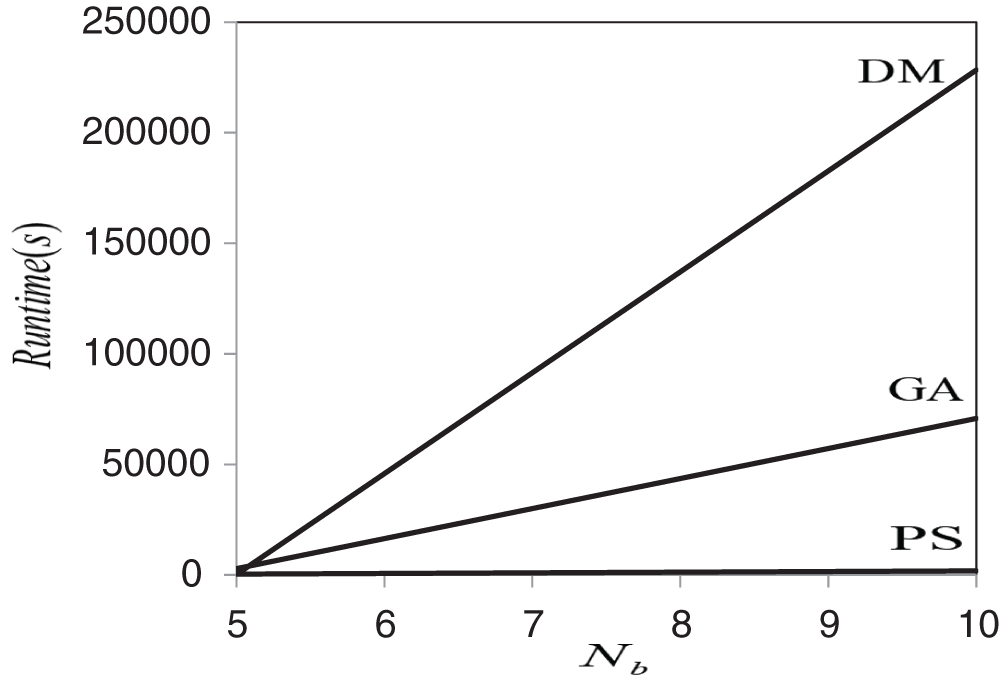
Figure 4: The execution time of optimization methods for case β = 100, ω = 0.1

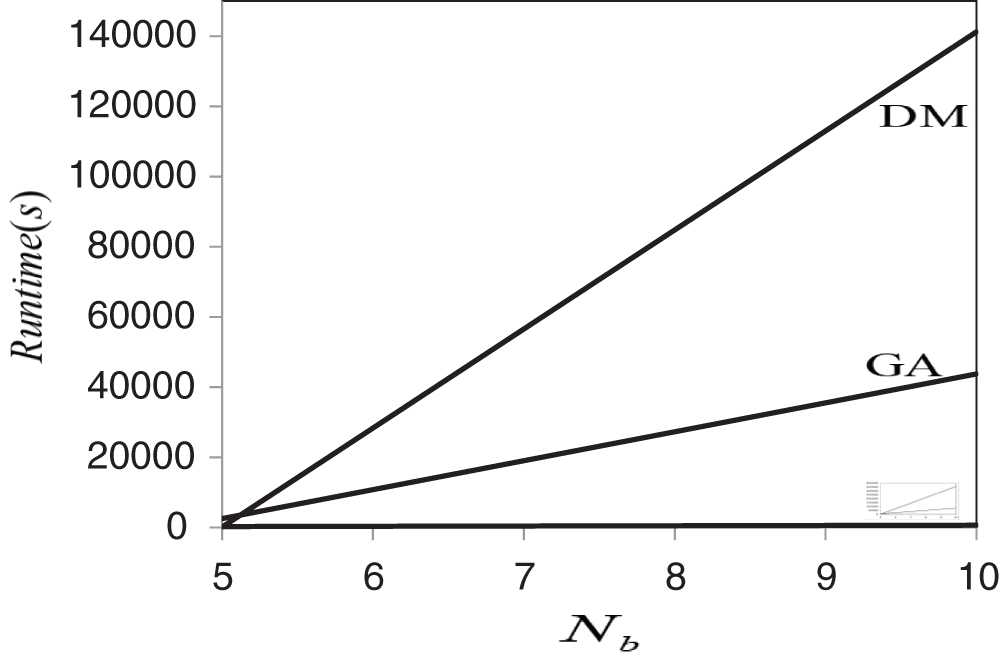
Figure 5: The execution time of optimization methods for case β = 300, ω = 0.05

5  Conclusions

In this research, the CL and three numerical optimization methods, including DM, GA, and PS, were employed to optimize the configuration of highly conductive branches intruding a hot medium. Then the minimized hot spot temperature corresponding to the optimal arrangement was obtained. The suggested insert design was tree-shaped with multiple non-uniform branches, all of which began from the middle plane of the body. The main goal was to compare and find the most efficient and fastest numerical optimization approach.

The study results indicated that DM and PS methods could reach an acceptable and roughly equal result and outperform the GA method. Even though the DM was faster in the lower number of branches, raising the Nb increased this method’s execution time. The study findings show that the optimization algorithms, especially PS, are more efficient than DM by an increment in the complexity of structures. When the optimization parameters increased, the DM was computationally expensive. The results indicate that when β = 200, ω = 0.2, and Nb = 10, the runtime of DM is more than 554 times greater than PS, and the runtime of GA is about 121 times greater than PS. It can be concluded that raising the DOF causes a considerable difference between the PS method and the two other methods, especially DM.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Song, J. (2022). Analysis of the heat transfer efficiency of an automobile engine under different grille opening and closing conditions. Fluid Dynamics & Materials Processing, 18, 345–354. DOI 10.32604/fdmp.2022.017382. [Google Scholar] [CrossRef]

 2.  Du, X., Liu, M., Sun, Y. (2022). Optimization of the internal circulating fluidized bed using computational fluid dynamics technology. Fluid Dynamics & Materials Processing, 18, 303–312. DOI 10.32604/fdmp.2022.016242. [Google Scholar] [CrossRef]

 3.  Jia, Y., Wang, J., Shang, L. (2020). Optimization of a heat exchanger using an ARM core intelligent algorithm. Fluid Dynamics & Materials Processing, 16, 871–882. DOI 10.32604/fdmp.2020.09957. [Google Scholar] [CrossRef]

 4.  Bejan, A. (1997). Constructal-theory network of conducting paths for cooling a heat generating volume. International Journal of Heat & Mass Transfer, 40(4), 799–811. DOI 10.1016/0017-9310(96)00175-5. [Google Scholar] [CrossRef]

 5.  Bejan, A., Lorente, S. (2005). The constructal Law (La Loi Constructale). International Journal of Heat & Mass Transfer, 49, 445. DOI 10.1016/j.ijheatmasstransfer.2005.07.031. [Google Scholar] [CrossRef]

 6.  Hazarika, S. A., Deshamukhya, T., Bhanja, D., Nath, S. (2017). Thermal analysis of a constructal T-shaped porous fin with simultaneous heat and mass transfer. Chinese Journal of Chemical Engineering, 25, 1121–1136. DOI 10.1016/j.cjche.2017.03.034. [Google Scholar] [CrossRef]

 7.  Fagundes, T. M., Lorenzini, G., Estrada, E., Isoldi, L. A., Santos, E. D. et al. (2019). Constructal design of conductive asymmetric tri-forked pathways. Journal of Engineering Thermophysics, 28(1), 26–42. DOI 10.1134/S181023281901003X. [Google Scholar] [CrossRef]

 8.  Teixeira, F. B., Lorenzini, G., Errera, M. R., Rocha, L. A. O., Isoldi, L. A. et al. (2018). Constructal design of triangular arrangments of square bluff bodies under forced convective turbulent flow. International Journal of Heat & Mass Transfer, 126, 521–535. DOI 10.1016/j.ijheatmasstransfer.2018.04.134. [Google Scholar] [CrossRef]

 9.  Ribeiro, P., Queiros-Condé, D. (2019). On the entropy production of the elemental construct of the constructal designed plate generating heat. International Journal of Thermal Sciences, 145, 106043. DOI 10.1016/j.ijthermalsci.2019.106043. [Google Scholar] [CrossRef]

10. Pedroti, V. A., de Escobar, C. C., Dos Santos, E. D., Souza, J. A. (2020). Thermal analysis of tubular arrangements submitted to external flow using constructal theory. International Communications in Heat and Mass, 111, 104458. DOI 10.1016/j.icheatmasstransfer.2019.104458. [Google Scholar] [CrossRef]

11. Dadsetani, R., Salimpour, M. R., Tavakoli, M. R., Goodarzi, M. et al. (2019). Thermal and mechanical design of reverting microchannels for cooling disk-shaped electronic parts using constructal theory. International Journal of Numerical Methods for Heat & Fluid Flow, 30, 245–265. DOI 10.1108/HFF-06-2019-0453. [Google Scholar] [CrossRef]

12. Chen, H., Wang, M., Zhao, X. (2020). Multi-strategy enhanced sine cosine algorithm for global optimization and constrained practical engineering problems. Applied Mathematics and Computation, 369, 124872. DOI 10.1016/j.amc.2019.124872. [Google Scholar] [CrossRef]

13. Hassan, B. A., Rashid, T. A. (2020). Operational framework for recent advances in backtracking search optimisation algorithm: A systematic review and performance evaluation. Applied Mathematics and Computation, 370, 124919. DOI 10.1016/j.amc.2019.124919. [Google Scholar] [CrossRef]

14. Larson, J., Menickelly, M., Wild, S. (2019). Derivative-free optimization methods. Acta Numerica, 28, 287–404. DOI 10.1017/S0962492919000060. [Google Scholar] [CrossRef]

15. Li, Q., Zheng, B., Zheng, Y. (2019). An efficient nonmonotone adaptive cubic regularization method with line search for unconstrained optimization problem. Applied Mathematics Letters, 98, 74–80. DOI 10.1016/j.aml.2019.05.040. [Google Scholar] [CrossRef]

16. Estrada, E., Fagundes, T. M., Isoldi, L. A., Santos, E., Xie, G. et al. (2015). Constructal design associated to genetic algorithm of asymmetric v-shaped pathways. Journal of Heat Transfer, 137(6), 061010.1–061010.7. DOI 10.1115/1.4029868. [Google Scholar] [CrossRef]

17. Avendaño, P. A., Souza, J. A., Adamatti, D. F. (2018). Construction of conductive pathways using genetic algorithms and constructal theory. International Journal of Thermal Sciences, 134, 200–207. DOI 10.1016/j.ijthermalsci.2018.08.013. [Google Scholar] [CrossRef]

18. Almogbel, M., Bejan, A. (1999). Conduction trees with spacings at the tips. International Journal of Heat & Mass Transfer, 42, 3739–3756. DOI 10.1016/S0017-9310(99)00051-4. [Google Scholar] [CrossRef]

19. Hajmohammadi, M. R., Rezaei, E. (2019). Proposing a new algorithm for the optimization of conduction pathways based on a recursive localization. Applied Thermal Engineering, 151, 146–153. DOI 10.1016/j.applthermaleng.2019.01.109. [Google Scholar] [CrossRef]

20. Hajmohammadi, M. R., Parsa, H., Najafian, J. (2019). Proposing an optimal tree-like design of highly conductive material configuration with unequal branches for maximum cooling a heat-generating piece. International Journal of Heat and Mass Transfer, 142, 118422. DOI 10.1016/j.ijheatmasstransfer.2019.07.072. [Google Scholar] [CrossRef]

21. Fujii, G., Akimoto, Y., Takahashi, M. (2018). Exploring optimal topology of thermal cloaks by CMA-ES. Applied Physics Letters, 112(6), 061108. DOI 10.1063/1.5016090. [Google Scholar] [CrossRef]

22. Fujii, G., Akimoto, Y. (2019). Topology-optimized thermal carpet cloak expressed by an immersed-boundary level-set method via a covariance matrix adaptation evolution strategy. International Journal of Heat and Mass Transfer, 137, 1312–1322. DOI 10.1016/j.ijheatmasstransfer.2019.03.162. [Google Scholar] [CrossRef]

23. Findler, N. V., Lo, C., Lo, R. (1987). Pattern search for optimization. Mathematics and Computers in Simulation, 29, 41–50. DOI 10.1016/0378-4754(87)90065-6. [Google Scholar] [CrossRef]

24. Gardeux, V., Omran, H., Mahamed, G., Chelouah, R., Siarry, P. et al. (2017). Adaptive pattern search for large-scale optimization. Applied Intelligence, 47, 319–330. DOI 10.1007/s10489-017-0901-8. [Google Scholar] [CrossRef]

25. Ingber, L., Rosen, B. (1992). Genetic algorithms and very fast simulated reannealing: A comparison. Mathematical & Computer Modeling, 16(11), 87–100. DOI 10.1016/0895-7177(92)90108-W. [Google Scholar] [CrossRef]

26. Silva, F. T., Silva, M. X., Belchior, J. C. (2019). A new genetic algorithm approach applied to atomic and molecular cluster studies. Frontiers in Chemistry, 7, DOI 10.3389/fchem.2019.00707. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.