Fluid Dynamics & Materials Processing

DOI: 10.32604/fdmp.2022.021759

ARTICLE

Numerical Study of Temperature and Electric Field Effects on the Total Optical Absorption Coefficient in the Presence of Optical Inter-Conduction-Subband Transitions in InGaN/GaN Single Parabolic Quantum Wells

Redouane En-nadir1,*, Haddou El-ghazi2, Anouar Jorio1, Izeddine Zorkani1, Hassan Abboudi1 and Fath Allah Jabouti1

1LPS, Sidi Mohamed Ben Abdullah University, Fez, 30000, Morocco
2ENSAM, Hassan-II University, Casablanca, 20470, Morocco
*Corresponding Author: Redouane En-nadir. Email: redouane.en-nadir@usmba.ac.ma
Received: 02 February 2022; Accepted: 25 February 2022

Nomenclature

1  Introduction

Due to their particular thermodynamic and chemical proprieties, III-nitride semiconductor materials alloys such as InN, GaN, AlN, InGaN have gained much interest and have emerged as a very attracted and promising materials for optoelectronic applications. Their direct band gap make them a great candidate for solar cells, Laser, Photo-detectors and so on [1–4]. A variety of nanostructure forms such us quantum well (QW), quantum well wire (QWW), quantum dot (QD) and quantum ring (QR) are experimentally manufactured. Since the revolutionary work of Bastard [5] related to QWs, intense studies have been reported that take into account of different structure forms, with and without the impurity, the well and barrier concentration and the exciton. Among different types of QWs, we can indicate rectangular [6] as a perfect profile, semi-triangular [4], triangular [7], semi-parabolic [8], infinite parabolic corresponding to one type of material extending in infinite space and finite parabolic profile with finite potential confining determined by the band offset between the well and barrier considering two types of materials.

The linear and third order nonlinear optical absorptions in different shapes and different confinement potential profiles (infinite and/or finite) are one of the most important proprieties of nano-structured semiconductor materials. For instance, Ungan et al. [9–13] have investigated the effects of hydrostatic pressure and intense laser field on the linear and nonlinear optical properties for typical square GaAs/AlxGa1−xAs single quantum well system. They have studied the linear and nonlinear optical properties in GaAs/AlxGa1−xAs double inverse parabolic quantum wells under applied electric and magnetic fields. Moreover, the linear and third order nonlinear optical absorptions in typical asymmetric double triangular QWs are investigated theoretically under the applied electric field influences [7]. In addition, Yesilgul et al. have examined theoretically the changes in the refractive index and inter-subband optical absorption coefficients in symmetric double semi-V-shaped QWs under the effects of the incident optical intensity and structure parameters for a finite confinement potential profile [14].

Recently, Aydinoglu et al. have studied the nonlinear optical properties of asymmetric double-graded quantum wells under the effects of the structure parameters such as the central barrier’s thickness and the aluminum concentrations [13]. Additionally, hydrostatic pressure and temperature effects on the nonlinear optical properties in semi-parabolic and semi-inverse squared QW have been investigated by Xu et al. [15]. In our recently published paper [16], we investigated the influence of several types of confinement potential on the photovoltaic conversion properties of a single-intermediate band solar cell based on (In,Ga)N quantum well emerged in the intrinsic area of the typical p-i-n structure in which it is revealed that the performance of solar cells decreases with increasing temperature. Additionally, Ungana et al. [17] have showed that the linear and nonlinear optical properties in a GaAs/Ga0.7Al0.3As parabolic quantum well under the intense laser field can be tuned by changing the hydrostatic pressure and temperature. Xu et al. [15] have examined the hydrostatic pressure and temperature effects on the nonlinear optical properties in semi-parabolic plus semi-inverse squared quantum well. They showed that hydrostatic pressure and temperature have significant impact on the optical properties of semi-parabolic plus semi-inverse squared QWs, and that the energy levels and magnitudes of the resonant peaks of the total OACs vary according to the shape of the limiting potential, the hydrostatic pressure, and the temperature. This promise a new degree of freedom in the tunability of various electro-optical devices.

However, all authors cited above have reported their works without considering the presence of the impurity, which generally alters the electronic and optical properties leading to the degradation of the performance of devices based-on. In the present paper, on the one hand, our aim is to investigate the combined effects of temperature and electrical field on the total optical absorption related to 1S-2P and 2S-2P transitions in In.2Ga.8N/GaN typical single parabolic QW considering a finite confinement barrier and on-center hydrogen-like impurity based on the finite difference method. Therefore, this work aims to complete our recently published work for a double-coupled parabolic QWs [18] in which the electric field effect and the presence of an impurity have been ignored, which could be considered as an outstanding work to better understand the optical process in the next generation solar cells, and also leads to improve their efficiency.

2  Theory and Mathematical Expressions

Within the framework of the effective-mass approximation, the time-independent Schrödinger equation in the effective units describing an electron in the presence of the impurity and electric field is given by the following expression:

[−Δ+V(z)Rb∗−2ε∗|r→−r→0|+μz]ψ(z)=Eψ(z) (1)

where, ℏ is the Planck’s constant, e is the electron charge, m∗ is the electron effective mass which is position dependent, r→−r→0 is the electron-impurity distance and ε∗ is the dielectric constant. V(z) is the finite parabolic confinement potential along z-axis given as following:

V(z)={4Q[EgGaN(T)−EgInGaN(T)]l2(z−L−l2)2,WellQ[EgGaN(T)−EgInGaN(T)]Elsewhere (2)

where, L, l are respectively the barrier and the well widths, respectively. Q(=0.7) and ΔEg(T) are respectively the conduction band off-set parameter and the difference between the band gap energies of GaN and InGaN materials.

To obtain the ground (1S-state), second-excited state (2P-state) and their associated energy levels of the Hamiltonian (1), the finite element method (FEM) was used taking into account the continuty of electron effective-mass as well as the dielectric constant at the interfaces between the barriers (GaN) and the well (InGaN). The boundary conditions are given by the following equation:

[→n.→∇⁡(ψme,b∗)]Barriers=[→n.→∇⁡(ψme,w∗)]QW (3)

The mesh-grid of 3N + 1 point is considered for both layers (Barriers/wells). We provided A specific discretization step for each layer was provided. For the well, the step is hw (= l /N) whereas for the barrier regions it is given as hb (= L/N). Moreover, for 0<i<N(=50pts) , the mesh’s nodes of the investigated structures are given respectively as fellows, left barrier zi (= i * hb), in the well region zi (= L + i * hb) and in the right barrier region is given as zi(= L + l + i * hb).

The derivatives electron wave functions are given by the following expressions:

∂2ψ(z)∂z2)zi=ψi+1−2ψi+ψi−1(zi+1−zi)2 (4.a)

∂ψ(z)∂z)zi=ψi+1−ψizi+1−zi (4.b)

3  Optical Absorption Coefficients

Based on the compact density matrix approach and the iterative procedure, the linear, third-order nonlinear and total optical absorption coefficients are given as the same that was described in our previous works [18–20] as follows:

α1(ω) = ℏωμεr∗ε0Γif|Mfi|2ρ(Efi−ℏω)2+(ℏΓif)2 (5)

α3(ω,I)=−μεr∗(I2nr∗ε0c)4Γif|Mfi|4ρℏω[(Efi−ℏω)2+(ℏΓif)2]2[1−|Mff−Mii|24|Mff|23Efi2−4ℏωEfi+(ℏω)2−(ℏΓif)2Efi2−(ℏΓif)2] (6)

where, the total optical absorption coefficient is defined as the sum of both linear and third order nonlinear contributions. It is given as following:

αT(ω,I)=α1(ω)+α3(ω,I) (7)

where, c is the speed of light in vacuum, ω and nr∗ are respectively the resonance frequency and the refractive index of the considered material. The difference of the energy between the implied states given as ΔEfi=Ef−Ei , while Γfi=1τfi(=5×1012s−1) is the relaxation time between the implied states. For an incident electromagnetic radiation polarized along z-axis, the electric dipole matrix element between the implied states is given as |Mfi|=⟨ψi|e.cos(θ)|ψf⟩ . Notice that the transitions between different energy levels are allowed only when the selection rule (Δℓ=±1) is satisfied. For simplicity, our numerical calculations are given in the effective unit, i.e., the effective Bohr radius ( a∗ ) is considered as the size unit while μ(=eFa∗Rb∗) is a non-dimensional parameter taking into account of the applied electric field.

4  Results and Discussion

To ensure the validity of this approach, we have discussed along this paper the electric field and temperature effects on the implied subband transitions for finite parabolic confinement profile.

All parameters related to the ternary InxGa1−xN are obtained by the linear interpolation of those of InN and GaN except the band gap energy. The geometrical sizes are chosen in order to have three states located in the well. Also, for z=0 and z=∞ , the potential barrier is assumed to be infinite to take in consideration the real situation in which the SPQW is emerged in dielectric environment or vacuum. Primarily, Fig. 1 shows the parabolic potential profile and three lowest electron probability densities in symmetric In.2Ga.8N/GaN SPQW for l=3L=3a∗,T=300 K , and θ=π/3 for two different values of the electric field strengths: μ=0 (Solid-line) and μ=6 (Dashed-line). For more visibility, we have translated each probability density to be located on its corresponding eigen value. It is obvious that, without applied electric field ( μ=0 ), the electron states are symmetrically localized in the well’s centre. However, for applied electric field ( μ=6 ), the electron states are collapsed and slightly shifted toward the opposite sense of the growth direction as expected. Additionally, it is clear that the electronic energy levels augment with increasing the electric field strength. Also, it is apparent that the tunnel phenomenon related to the ground state is more pronounced that that related to the first and second excited states.

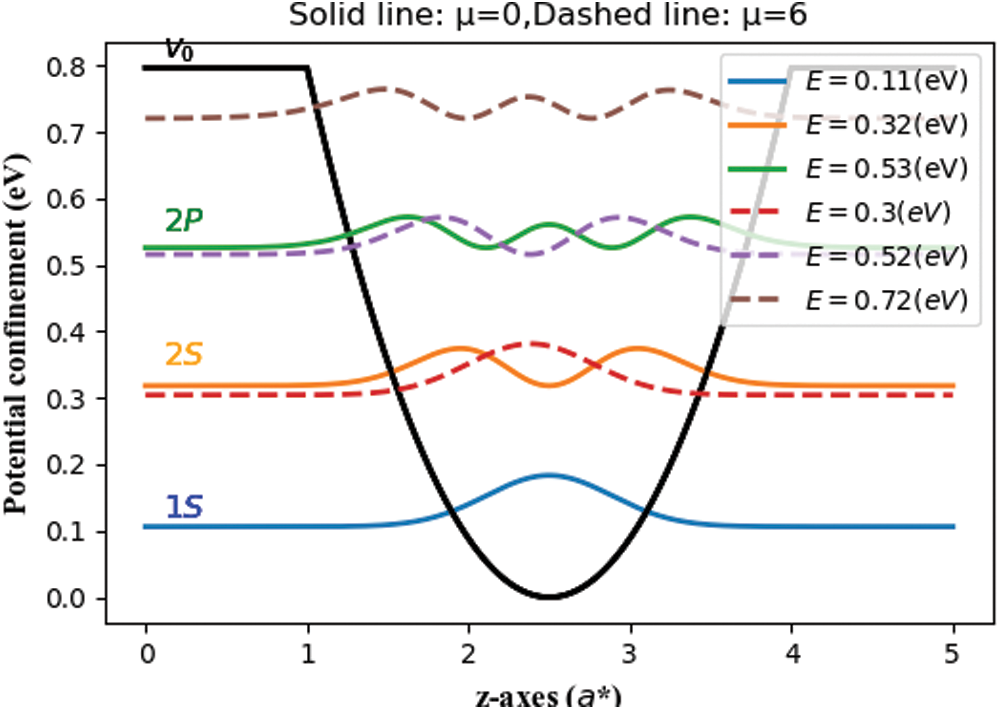
Figure 1: The three first electron wave functions in symmetric InGaN/GaN SPQW showing the changes of the confinement potential vs. the growth direction (z-axes) with l=3L=3a∗,T=300K , x=0.2 , and θ=π3 for two values of the electric field: μ=0 (Solid-line) and μ=6 (Dashed-line)

Fig. 2 depicts the variation of the dipole matrix element related to 1S-2P and 2S-2P transitions in In.2Ga.8N/GaN SPQW according to the electric field strength for l=2L=2a∗ and θ=π/3 and for two different values of the temperature. The main characteristic of its changes vs. the applied electric field intensity is its linear behaviour, i.e., regardless the temperature value, |Mfi|2 increases (decreases) linearly for 1S-2P and 2S-2P, respectively. In certain way, the electric dipole matrix element measuring the wave function overlapping, can be explained and interpreted based on the results reported in Fig. 1. The second principle feature is the decreasing behaviour of |Mfi|2 as a function of the temperature for all values of applied electric field. Compared to high strength electric field, the SPQW structure is less sensitive to the temperature impact.

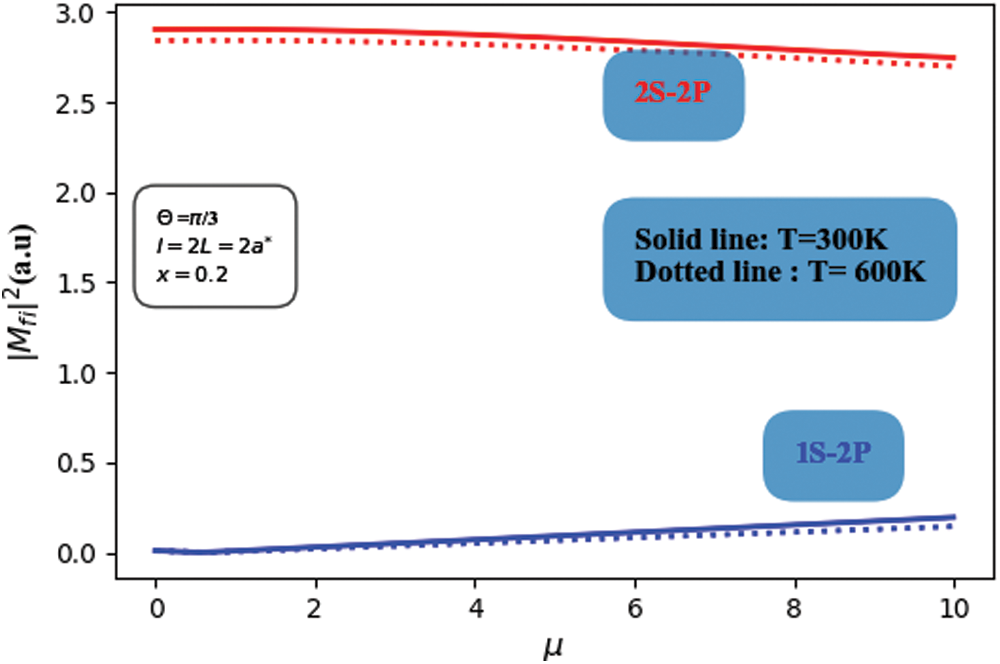
Figure 2: The square of the dipole matrix element of 1S-2P and 2S-2P subband transitions in symmetric In.2Ga.8N/GaN SPQW vs. the electric field parameter (µ) for l=2L=2a∗ and θ=π3 and for two different values of temperature ( 100 K and 600 K )

From Eqs. (5) and (6), it is clear that the total absorption coefficient mastering passes through the exact knowledge of the energy difference of all implied transitions. In this sense, Fig. 3 displays the changes of the energy difference related to 1S-2P and 2S-2P transitions vs. the electric field and temperature effects in In.2Ga.8N/GaN SPQW. One can see via panels (a) and (b) that regardless the electric field, E1S−2P(E2S−2P) shrinks with the increase of the temperature. Furthermore, the temperature impact is less marked for high electric field strength. In addition, for a fixed value of the temperature, E1S−2P(E2S−2P) drops slightly as the electric field strength augments. This can be explained by the fact that the enhancement of the 1S- and 2S-states energies with increasing the electric field is greater than that of 2P-state, and then the both difference energies can only decrease. It is also observed that the electric field impact is less felt for lower temperatures. Moreover, both energy differences are observed to be great for lower values of temperature and electric field strength. Taking into account of the above results concerning the two main parameters, electric dipole matrix element and energy difference which are required to interpret the optical properties, let us to discuss the total optical absorption of interest vs. the photon energy. For this reason, unperturbed schematic diagram of l=2L=2a∗ and on-center impurity is chosen. Fig. 4 illustrates the 1S-2P and 2S-2P conduction subband transitions related to TOAC in symmetric In.2Ga.8N/GaN SPQW vs. the incident photon energy (ℏω) for θ=π/3 considering the electric field impacts at room temperature. It is clearly seen that with increasing the applied electric field, the TOAC spectra move to lower energies showing a significant redshift for both transitions. Such behaviour can be explained by the results of the energy difference as reported in Fig. 3.

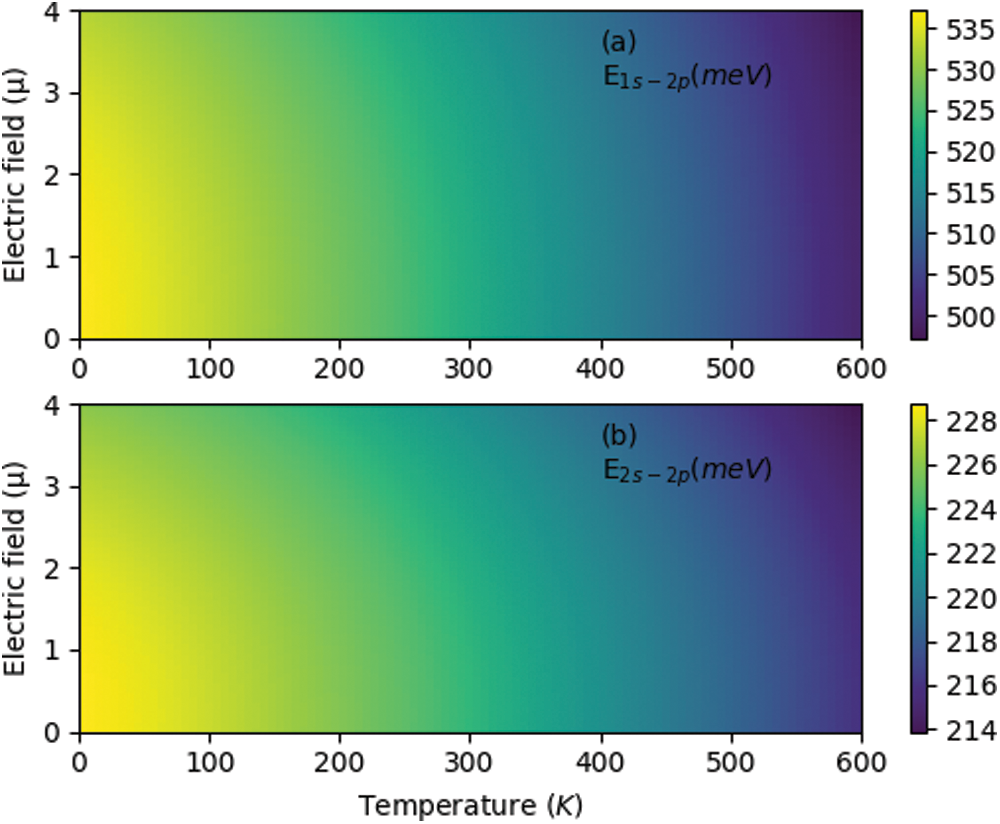
Figure 3: The variation of the energy difference of 1S-2P transition (a) and 2S-2P transition (b) in symmetric In.2Ga.8N/GaN SPQW vs. the temperature and electric field strength for L=2l=2a∗,T=300 K, and θ=π3

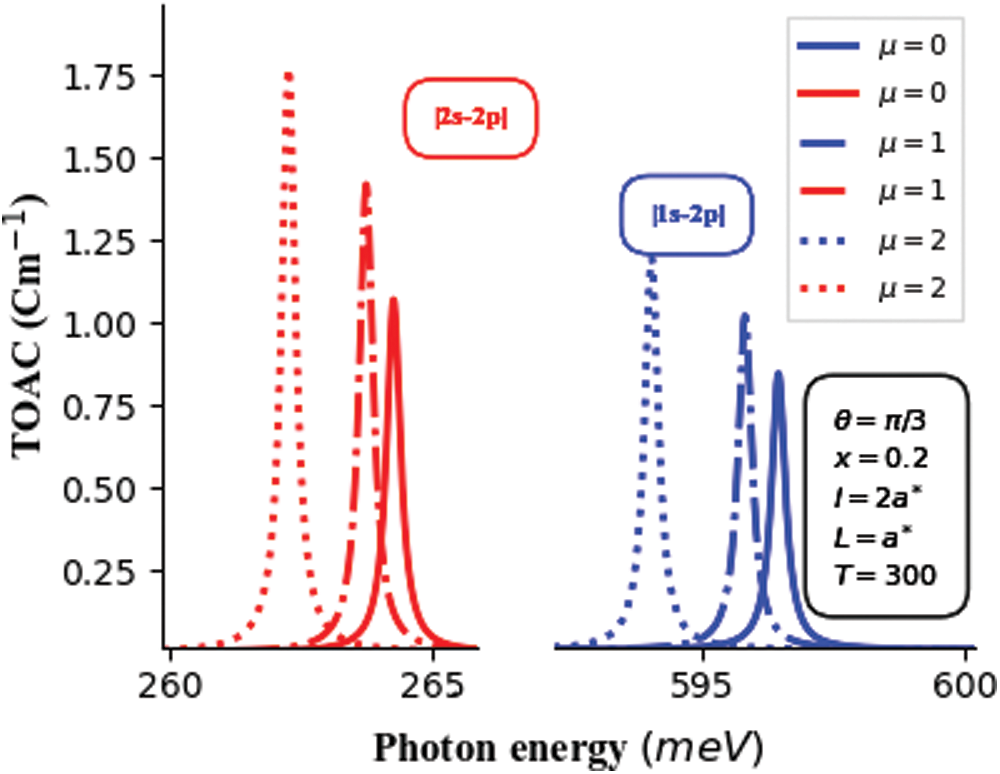
Figure 4: The total optical absorption coefficient (TOAC × 104) of 1S-2P and 2S-2P subband transitions in symmetric In.2Ga.8N/GaN SPQW vs. the incident photon energy with l=2L=2a∗ and θ=π3 for three different values of the electric field strength

It is interesting to notice that the amplitudes of both transitions induced spectra appear to be enhanced as μ increase. This result can be assigned to the fact that the augment of the nonlinear absorption coefficient is dominated by that of linear one. For 1S-2P transition, it is obtained that with increasing μ , |Mfi|2 increases while ΔEfi decreases which act in the same sense to augment more the linear counterpart compared to nonlinear one. On the other hand, 2S-2P amplitude increasing can be explained by the fact that the diminishing ΔEfi dominates that of |Mfi|2 .

Finally, TOAC related to 1S-2P and 2S-2P subband transitions in symmetric In.2Ga.8N/GaN SPQW according to the incident photon energy (ℏω) for three different values of temperature (300 K, 350 K, and 400 K) are displayed in Fig. 5. As can be seen from this figure, as the temperature increases the 1S-2P and 2S-2P related optical-absorption spectra are found to be red-shifted. Such behaviour is due to ΔEfi dependence where an optical transition occurs as a function of the temperature, i.e., this is in accordance with the presented result in Fig. 3. In addition, we noticed that the maximum of the optical spectra show a slightly change as the temperature varies from 300 K to 400 K. This can be due to the fact that, the magnitude of the linear contribution change is compensated with the nonlinear one.

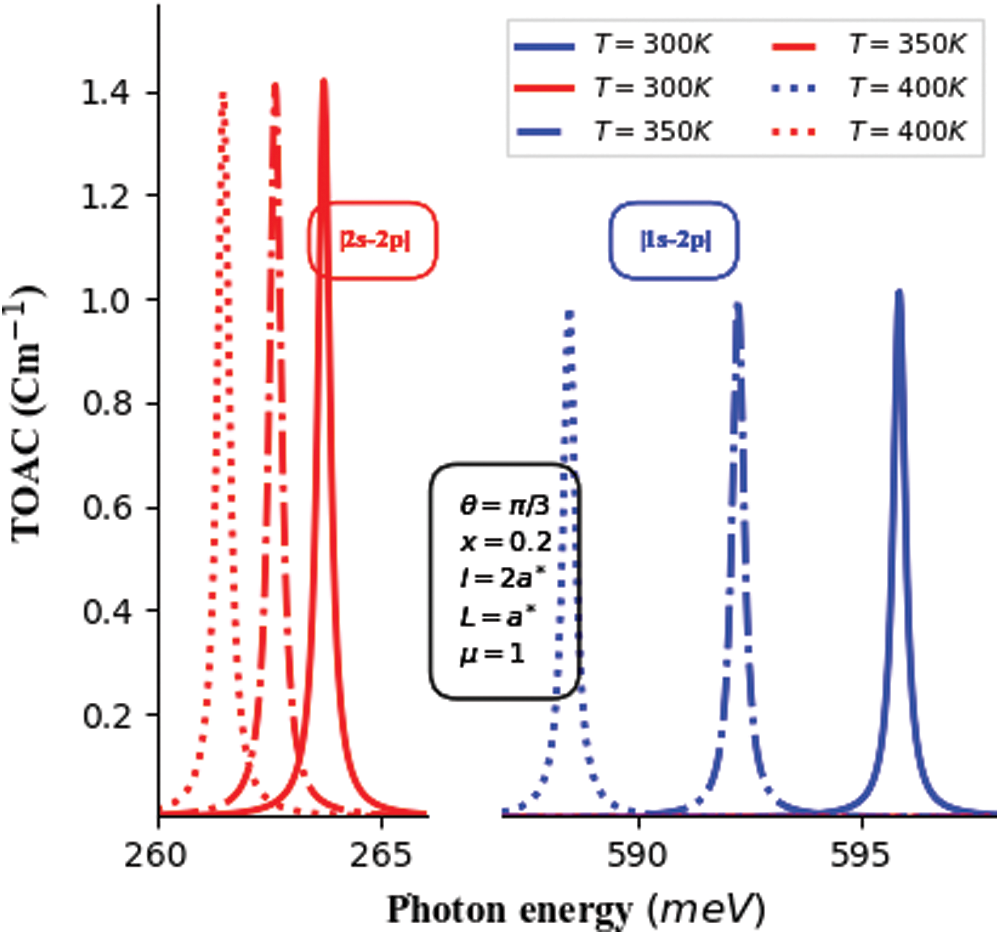
Figure 5: The total optical absorption coefficient (TOAC × 104) of 1S-2P and 2S-2P subband transitions in symmetric In.2Ga.8N/GaN SPQW vs. the incident photon energy with l=2L=2a∗ , μ=1 , and θ=π3 for three values of temperature

Generally, our obtained results related to 1S-2P and 2S-2P transitions induced TOAC in SPQW based on In.2Ga.8N/GaN under the temperature and electric field effects are in good agreement with the findings in the literature corresponding. However, some discrepancies remain due probably different materials, shapes and mathematical methods used in each work. For instance, Baskoutas et al. have investigated, the linear and nonlinear OAC in GaAs/Ga1−xAlxAs subjected to an external electric field for inverse single and double parabolic QWs [21]. Moreover, Yesilgul et al. have theoretically reported the effects of the intense laser field on the optical absorption coefficients and the refractive index changes in a GaAs/(Ga,Al)As parabolic-quantum well under the external applied electric field. He also, investigated the effects of magnetic field, hydrostatic pressure and temperature on the linear and nonlinear optical properties in GaAs/AlxGa1−xAs symmetric double semi-triangular quantum well [14,22]. Furthermore, similar behaviors have been reported for the effects of electric and magnetic fields on the linear and nonlinear OAC of (Al,Ga)As/GaAs PQW [23].

5  Conclusion

To sum up, this work is devoted to the theoretical study of the effects of external applied electric field and temperature on total optical absorption coefficients (OACs) of a single parabolic quantum well (QW). The results show that the applied electric field and temperature have significant influences on the optical properties of single parabolic QW. It is obtained that the wave functions, the energy levels and magnitudes of the resonant spectra of the total OACs vary according to the electric field and the temperature. A significant red-shift of the optical spectra is obtained with increasing both the electric field and the temperature. Therefore, it is revealed that the optical characteristics can be adjusted by changing the intensity of electric field and temperature which promise a new degree of freedom in the next generation of eventual GaN/(In,Ga)N based solar cells.

Owing to the importance of the III-nitrides semiconductors, particularly in optoelectronics, we assume that the present work provides a modest contribution to optimizing optical absorption for solar cell applications. In addition, it would induce further theoretical and experimental research works on Gan/InGaN based Multi-QWs for LEDs, lasers, and photo-detector applications.

Acknowledgement: I thank all authors with whom I have had the pleasure to work during this paper and other related project.

Funding Statement: This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Chiou, Y. Z., Su, Y. K., Chang, S. J., Lin, Y. C., Chang, C. S. et al. (2002). InGaN/GaN MQW p/n junction photodetectors. Solid State Electronics, 46(12), 2227–2229. DOI 10.1016/S0038-1101(02)00230-7. [Google Scholar] [CrossRef]

 2.  Itakura, H., Nomura, T., Arita, N., Okada, N., Wetzel, C. M. et al. (2020). Effect of InGaN/GaN superlattice as underlayer on characteristics of AlGaN/GaN HEMT. AIP Advances, 10(2), 025133. DOI 10.1063/1.5139591. [Google Scholar] [CrossRef]

 3.  Kang, H. C., Liu, G., Lee, C., Alkhazragi, O., Jonathan, M. W. et al. (2019). Semipolar InGaN/GaN micro-photodetector for gigabit-per-second visible light communication. Applied Physics Express, 13(1), 014001. DOI 10.7567/1882-0786/ab58eb. [Google Scholar] [CrossRef]

 4.  Yesilgul, U., Ungan, F., Al, E. B., Kasapoglu, E., Sari, H. et al. (2016). Effects of magnetic field, hydrostatic pressure and temperature on the nonlinear optical properties in symmetric double semi-V-shaped quantum well. Optical Quantum Electronics, 48(12), 560. DOI 10.1007/s11082-016-0838-x. [Google Scholar] [CrossRef]

 5.  Bastard, G. (1984). Quantum-size effects in the continuum states of semiconductor quantum wells. Physical Review B, 30(6), 3547–3549. DOI 10.1103/PhysRevB.30.3547. [Google Scholar] [CrossRef]

 6.  Belov, P. A. (2019). Energy spectrum of excitons in square quantum wells. Physica E: Low-Dimensional Systems & Nanostructures, 112, 96–108. DOI 10.1016/j.physe.2019.04.008. [Google Scholar] [CrossRef]

 7.  Chen, B., Guo, K. X., Wang, R. Z., Zhang, Z. H., Liu, Z. L. (2009). Linear and nonlinear intersubband optical absorption in double triangular quantum wells. Solid State Communications, 149(7), 310–314. DOI 10.1016/j.ssc.2008.11.032. [Google Scholar] [CrossRef]

 8.  Keshavarz, A., Karimi, M. J. (2010). Linear and nonlinear intersubband optical absorption in symmetric double semi-parabolic quantum wells. Physics Letter A, 374(26), 2675–2680. DOI 10.1016/j.physleta.2010.04.049. [Google Scholar] [CrossRef]

 9.  Ungan, F., Mora-Ramos, M. E., Duque, C. A., Kasapoglu, E., Sari, H. et al. (2014). Linear and nonlinear optical properties in a double inverse parabolic quantum well under applied electric and magnetic fields. Superlattices & Microstructures, 66, 129–135. DOI 10.1016/j.spmi.2013.12.006. [Google Scholar] [CrossRef]

10. Sabaeian, M., Shahzadeh, M., Farbod, M. (2014). Electric field-induced nonlinearity enhancement in strained semi-spheroid-shaped quantum dots coupled to wetting layer. AIP Advances, 4(12), 127105. DOI 10.1063/1.4903368. [Google Scholar] [CrossRef]

11. El-Ghazi, H., Jorio, A., Zorkani, I. (2014). Linear and nonlinear intra-conduction band optical absorption in (In,Ga)N/GaN spherical QD under hydrostatic pressure. Optics Communications, 331, 71–73. DOI 10.1016/j.optcom.2014.05.055. [Google Scholar] [CrossRef]

12. Dakhlaoui, H., Ungan, F., Martínez-Orozco, J. C., Mora-Ramos, M. E. (2021). Theoretical investigation of linear and nonlinear optical properties in anheterostructure based on triple parabolic barriers: Effects of external fields. Physica B: Condensed Matter, 607, 412782. DOI 10.1016/j.physb.2020.412782. [Google Scholar] [CrossRef]

13. Aydinoglu, H. S., Sakiroglu, S., Sari, H., Ungan, F., Sökmen, I. (2018). Nonlinear optical properties of asymmetric double-graded quantum wells. Philosophical Magazine, 98(23), 2151–2163. DOI 10.1080/14786435.2018.1476785. [Google Scholar] [CrossRef]

14. Yesilgul, U., Ungan, F., Sakiroglu, S., Mora-Ramos, M. E., Duque, C. A. et al. (2014). Effect of intense high-frequency laser field on the linear and nonlinear intersubband optical absorption coefficients and refractive index changes in a parabolic quantum well under the applied electric field. Journal of Luminiscence, 145, 379–386. DOI 10.1016/j.jlumin.2013.07.062. [Google Scholar] [CrossRef]

15. Xu, G. L., Zhen, Z., Shi, Y. S., Guo, K. X., Feddi, F. et al. (2021). Hydrostatic pressure and temperature effect on the nonlinear optical properties in semi-parabolic plus semi-inverse squared quantum well. Communication Theoretical Physics, 73(8085502. [Google Scholar]

16. Abboudi, H., El-Ghazi, H., Benhaddou, F., En-nadir, R., Jorio, A. et al. (2021). Temperature-related photovoltaic characteristics of (In,Ga)N single-intermediate band quantum well solar cells for different shapes. Physica B: Condensed Matter, 626, 413495. [Google Scholar]

17. Ungana, F., Yesilgula, U., Sakiroglub, S., Mora-Ramosc, M. E., Duque, C. A. et al. (2013). Simultaneous effects of hydrostatic pressure and temperature on the nonlinear optical properties in a parabolic quantum well under the intense laser field. Optical Communications, 309, 158–162. DOI 10.1016/j.optcom.2013.07.006. [Google Scholar] [CrossRef]

18. En-nadir, R., El-Ghazi, H., Belaid, W., Jorio, A., Zorkani, I. (2021). Intraconduction band-related optical absorption in coupled (In,Ga)N/GaN double parabolic quantum wells under temperature, coupling and composition effects. Results in Optics, 5(5), 100154. DOI 10.1016/j.rio.2021.100154. [Google Scholar] [CrossRef]

19. En-nadir, R., El-Ghazi, H., Jorio, A., Zorkani, I. (2020). Inter and intra band impurity-related absorption in (In,Ga) N/GaN QW under composition, size and impurity effects. MATEC Web of Conferences, 330, 01017. DOI 10.1051/matecconf/202033001017. [Google Scholar] [CrossRef]

20. En-nadir, R., El-Ghazi, H., Belaid, W., Jorio, A., Zorkani, I. et al. (2021). Ground and first five low-lying excited states related optical absorption in In.1Ga.9N/GaN double quantum wells: Temperature and coupling impacts. Solid State Communications, 338(765), 114464. DOI 10.1016/j.ssc.2021.114464. [Google Scholar] [CrossRef]

21. Baskoutas, S., Garoufalis, C., Terzis, A. F. (2011). Linear and nonlinear optical absorption coefficients in inverse parabolic quantum wells under static external electric field. European Physical Journal B, 84(2), 241–247. DOI 10.1140/epjb/e2011-20470-9. [Google Scholar] [CrossRef]

22. Yesilgul, U., Ungan, F., Sakiroglu, S., Mora-Ramos, M. E., Duque, C. A. et al. (2014). Effect of intense high-frequency laser field on the linear and nonlinear intersubband optical absorption coefficients and refractive index changes in a parabolic quantum well under the applied electric field. Journal of Luminiscence, 145, 379–386. DOI 10.1016/j.jlumin.2013.07.062. [Google Scholar] [CrossRef]

23. Almansour, S. (2019). Numerical simulation of the effects of electric and magnetic fields on the optical absorption in a parabolic quantum well. Journal of the Korean Physical Society, 75(10), 806–810. DOI 10.3938/jkps.75.806. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.