

 | Fluid Dynamics & Materials Processing |  |
DOI: 10.32604/fdmp.2022.021564
ARTICLE
Effect of Hole Configuration on Heat Transfer through a Hollow Block Subjected to Solar Flux
1Polydiscilinary Faculty of Ouarzazate, Ibn Zohr University, Ouarzazate, 638, Morocco
2Faculty of Sciences Semlalia, Cadi Ayyad University, Marrakesh, 2390, Morocco
*Corresponding Author: Mourad Najjaoui. Email: mourad.najjaoui@edu.uiz.ac.ma
Received: 21 January 2022; Accepted: 20 February 2022
Abstract: In this paper, some effort is provided to optimize the geometry of a concrete hollow brick (used in the construction of building roofs) in order to increase the related thermal resistance, thereby reducing energy consumption. The analysis is conducted for three different configurations of the hollow concrete bricks. Coupling of conduction, natural convection and thermal radiation phenomena is considered. Moreover, the flows are assumed to be laminar and two-dimensional for the whole range of parameters examined. The conservation equations are solved by a finite difference method based on the control volumes approach and the SIMPLE algorithm for velocity-pressure coupling. The results show that the aspect ratio affects neither the nature of the fluid flow nor the number of convective cells. However, the extension of the circulation cells increases with this parameter. Moreover, the cavities with a large aspect ratio lead to significant reductions in the heat transfer through the hollow block, these reductions reaching approximately 14%.
Keywords: Heat transfers coupled; hollow block; solar flux; aspect ratio; control volumes
Nomenclature
| Ac: | aspect ratio of the inner cavity, h/l |
| dF: | view factor between finite surfaces |
| dS: | finite area (m2) |
| E: | incident radiative heat flux (W.m–2) |
| ex: | horizontal partition thickness (m) |
| ey: | vertical partition thickness (m) |
| S: | incident solar flux (W.m–2) |
| H: | structure height (m) |
| he: | heat transfer coefficient at the outdoor surface of wall (W/m2°C) |
| hi: | heat transfer coefficient at the indoor surface of wall (W/m2°C) |
| J: | radiosity(W.m–2) |
| k: | thermal conductivity (W.m–1.K–1) |
| L: | structure depth (m) |
| l: | cavity width (m) |
| Nk: | thermal conductivity ratio |
| Nr: | radiation to conduction number |
| P: | dimensionless pressure |
| p: | pressure (Pa) |
| Pr: | Prandtl number |
| Qa: | dimensionless average heat flux |
| Q: | average heat flux, (W.m–2) |
| qr,k: | net radiative heat flux at surface k (W.m–2) |
| Qr,k: | dimensionless net radiative heat flux at surface k |
| r: | position on the cavity surface |
| Ra: | Rayleigh number |
| T: | temperature (K) |
| U,V: | dimensionless velocity components in x and y directions |
| X,Y: | dimensionless Cartesian coordinates in x and y directions |
| Greek symbols | |
| α: | thermal diffusivity (m2.s–1) |
| β: | thermal expansion coefficient (K–1) |
| ε: | cavity surface emissivity |
| η: | dimensionless coordinate normal to a cavity surface |
| ρ: | fluid density, (kg.m–3) |
| σ: | Stephan-Boltzman constant (W.m–2.K–4) |
| θ: | dimensionless temperature, (T-Tin)/ΔT |
| Ψ: | dimensionless streamline function |
| Subscripts | |
| f: | fluid |
| i: | inside |
| e: | outside |
| s: | solid |
The growth of the population and harsh weather conditions in Marrakech city (Morocco) increase the demand for electricity due to the overwhelming usage of air-conditioning system for cooling during the excessively hot weather summer conditions. Therefore, it is immensely important to find solutions that guarantee the reduction of thermal loads tariffs. The building roofs are the facades that are more exposed to the outside temperature and solar radiation, hence the importance of the study of energy efficiency. The use of composite building elements with air cavities is among the areas where there is a lot of research, thanks to the advantages of the materials used for construction (lightweight structure and high thermal resistance).
Hollow structures are used, in the conception of the building envelopes (walls and roofs). In general, the heat transfer in such structures is complex and done simultaneously by conduction, natural convection and radiation. Therefore, clear non-linear attributes exist inside the heat transfer of these holes. So, the problems of coupling between the three modes of heat transfer are of great importance in recent years.
In this context we can cite the works presented by Ragui et al. [1–3], in which the authors studied, by means of the finite volume method, the natural convection within a differentially heated square cavity with centrally located partitions and off-set partitions, filled with a Bingham fluid. Their results show that the average Nusselt number is a decreasing function of the Bingham number. In addition, they noticed that the location of the partitions has an important effect on both fluid flow and heat transfer and that their thickness enhanced heat transfers. The same authors are extended their studies to thermo-solutal convection in a rectangular porous enclosure whose side walls are maintained at uniform temperature and concentration by using finite volume method. Also Bouarnouna et al. [4] studied numerically the flow field and heat transfer of a Newtonian fluid flowing this time within an horizontal channel, partially filled with a porous medium. The results obtained show the important effect of control parameters, which cannot be neglected, on both flow and the heat transfer structure, within this kind of channels. Other detailed numerical studies that take in to account the simultaneous existence of the three modes of heat transfer in vertical or horizontal cellular hollow structures differentially heated were presented respectively by Abdelbaki et al. [5], we note that these systems are specific to the construction of walls. The results of this work have shown that the flow structures and the thermal behaviors of the different types of slabs are similar. After this idea of the coupling between conduction, convection and surface radiation in the horizontal hollow structures heated this time from below or from above have the subject of a series of a numerical studies investigated by Ait-Taleb et al. [6,7]. In these investigations, the overall thermal conductance’s are determined for the hollow concrete blocks for the two cases of heating and Transfer Function Coefficients (TFC) are generated for three different types of hollow concrete bricks mostly used in practice. It is shown that the empirical transfer function coefficients permit fast and accurate prediction of heat transfer for thermal excitations that differ markedly from those used to generate these coefficients without solving the complex system of equations governing the coupled heat transfer mechanisms.
In the same sense, the previous study is extended by Boukendil et al. [8] to the case of a double wall formed by a vertical cavity separating two honeycomb walls, outer and inner, with two rows of cells each. The interaction between the mechanisms of heat transfer developing by natural convection, conduction and radiation within the alveolar structures composing the investigated system are studied in detail. The effects of the dimensions (height and thickness) of the vertical cavity on the horizontal heat transfer through the considered system are also discussed. In the literature, several studies partitioned the cavities in the block to reduce the heat transfer rate [9,10].
From this literature scientific review, it is revealed that most of the studies concerning the coupling between the three modes of heat transfer (conduction, convection and/or radiation) are devoted to simple configurations consisting in rectangular cavities with or without conducting walls, differentially heated. In addition, we note that there are only a few studies relating to simple configurations heated from below or from above via imposed temperatures.
In very practical situations we find the buildings roofs constructed by cellular structures and which are submitted to an incident solar flux. This situation has been the subject of work carried out, very recently, by Najjaoui et al. [11] in which the authors have treated numerically the effects of thermal conductivity of hollow blok on heat flows through the hollow tile submitted to the incident solar flux. The results in term of streamlines, isotherms and overall heat flux show that the global heat transfer through this system is strongly depends on the thermal conductivity. In the present work we try to extend numerically this study to the cases of cavities subjected to a constant incident solar flux and exchange heat with the ambient air with surface exchange coefficients. It is particularly important to examine the effect of the geometric the aspect ratio on the overall heat transfer in a hollow block with three horizontal cavities. We attempt to give a detailed analysis of the nature flow and temperature field for different types of the block and to quantify the overall heat flux crossing the hollow structure which constitutes the building roofs.
A schematic of the hollow block is shown in Fig. 1, This hollow block is formed by three rectangular cavities of width l and height h surrounded by vertical solid partitions of thicknesses ex and horizontal partitions of thicknesses ey. The top horizontal surface is exposed to an incident solar flux (S) and outdoor environment temperature Te with a surface exchange coefficient he. The inside surface is submitted to indoor environment temperature, Ti and with a surface exchange coefficient hi, while the vertical faces are considered adiabatic.
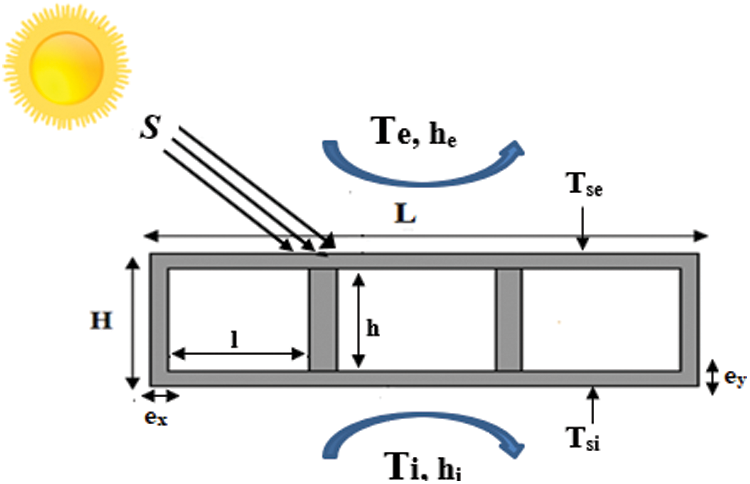
Figure 1: Schematic representation of the studied structure
By using the Boussinesq approximation, the obtained dimensionless governing equations are:
∂U∂X+∂V∂Y=0 (1)
∂U∂τ+U∂U∂X+V∂U∂Y=−∂P∂X+Pr(∂2U∂X2+∂2U∂Y2) (2)
∂V∂τ+U∂V∂X+V∂V∂Y=−∂P∂Y+Pr(∂2V∂X2+∂2V∂Y2)+Ra.Pr.θf (3)
∂θf∂τ+U∂θf∂X+V∂θf∂Y=∂2θf∂X2+∂2θf∂Y2 (4)
where U and V are the dimensionless velocity components in X and Y directions, respectively, P is the pressure, θf is the dimensionless fluid temperature, Pr is the Prandtl number and Ra is the Rayleigh number given respectively by:
Pr=υαfandRa=gβH3ΔTυ2Pr
The dimensionless equation for heat conduction in solid walls is:
αfαs∂θs∂τ=∂2θs∂X2+∂2θs∂Y2 (5)
where θs is the dimensionless solid temperature and αf and αs are the fluid and the solid thermal diffusivities, respectively.
The adopted thermal boundary conditions are:
Adiabaticity condition on the vertical sides:
(∂θs∂X)X=0=(∂θs∂X)X=1=0,0≤Y≤1 (6)
For the outside horizontal face:
HksΔTαS+heHks(θe−θse)=−dθsdY (7)
For the inner horizontal face:
hiHks(θsi−θi)=−dθSdY (8)
The continuity of the temperature and the heat flux at the fluid–solid interfaces gives:
θs(X,Y)=θf(X,Y) and−∂θs∂η=−Nk∂θf∂η+NrQr (9)
where η represents the dimensionless coordinate normal to the interface. The dimensionless net radiative heat flux is given by [12]:
Qr,k(r′k)=εk(|1−TinTout|θk(r′k)+TinTout)4−εk4∑j=1∫SjJ′j(r′j)dFdSk−dSj (10)
The dimensionless average heat flux across the structure is given by:
Qa=−HLLH∫0dθSdY)Y=0dX=−HLLH∫0dθSdY)Y=1dX (11)
The dimensionless stream function Ψ is defined as:
U=−∂Ψ∂YandV=∂Ψ∂X (12)
3 Numerical Procedure and Validation
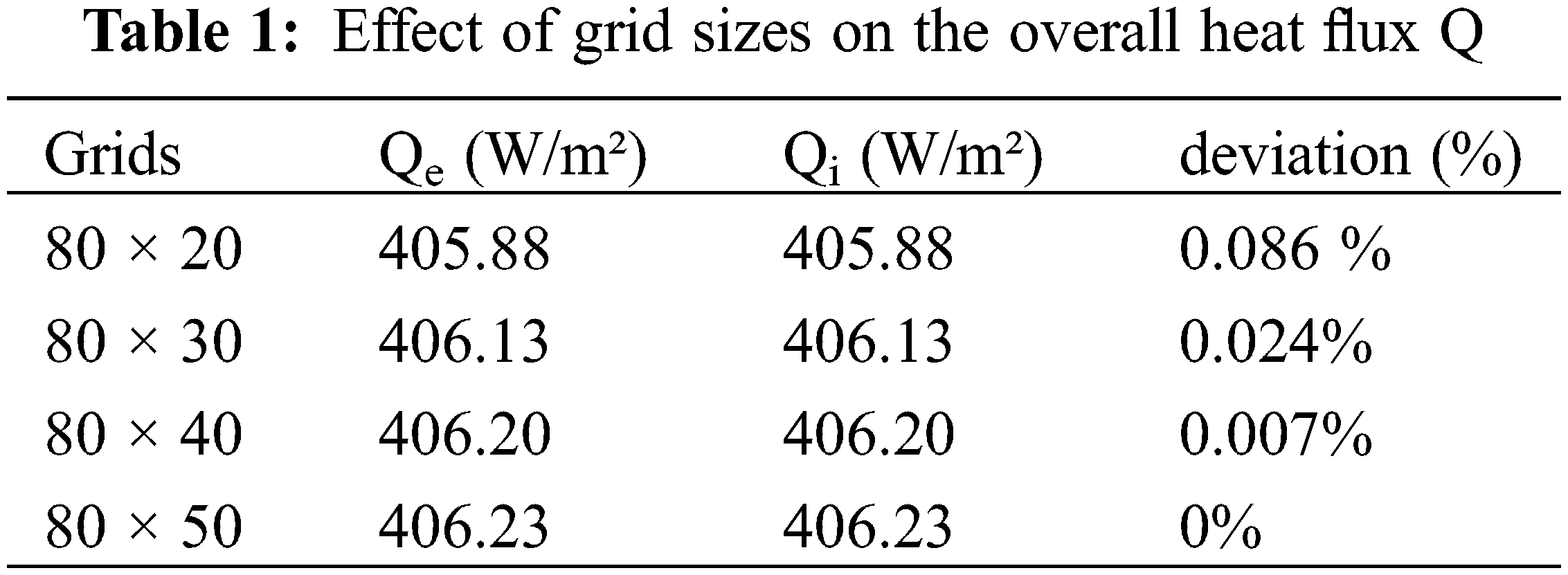
The governing equations were solved using a code based on the finite volume method [13] with a power law scheme, to realize a compromise between accuracy and computation time, a study on the effects of both grid spacing and time step on the simulation results has been conducted. Table 1 indicates that the non-uniform grid of 80 × 40 is sufficient to modeling accurately the heat transfer and fluid flow inside the hollow structure since the difference between the results does not exceed 0.007%. The dimensionless time used is 10–6. The convergence criterion is 10–4.
In order to check the validity of the numerical code, the obtained results were compared with those of Akiyama et al. [14], who studied the effect of radiation on natural convection in a differentially heated square cavity. The convective Nusselt numbers calculated at the hot wall are compared in Table 2 for a range of Rayleigh number 103 ≤ Ra ≤ 106 and for different values of the emissivity. The comparative results show an excellent agreement, with a maximum deviation of 0.9%.

The results presented in this study are obtained for hollow blocks constructed of light concrete of thermal conductivity ks = 0.5 W/mK. The geometric dimensions of the various hollow blocks studied are grouped together in Table 3 where 1 and h designate respectively the width and the height of the cavity. Ac is the aspect ratio of these which plays the role of the control parameter of this study. ex and ey are respectively the thicknesses of vertical and horizontal solid partitions. The thermal conductivity of air is ka = 0.0262 W/mK and the Prandtl number is Pr = 0.71. The emissivity of the internal surfaces is 0.9. and the incident solar flux S is fixed at the value 1000 W/m2, In accordance to real conditions. The average surface exchange coefficients (or the external and the internal heat transfer coefficients) were set respectively at the values, ho = 17 W/m2°C and hi = 8.3 W/m2°C [15]. The indoor air temperature is fixed to Ti = 20°C, while the outdoor environment temperature is set to Te = 40°C.

In order to have a precise idea about the structure of the air flow and the heat transfer, Figs. 2(a)–2(c) present the streamlines and the isotherms obtained respectively for Ac = h/l ≈ 1/4, Ac ≈ 1/2 and Ac ≈ 1. From this figure, we notice that the flow structures is characterized by the presence of four small cells circulating in opposite directions testifying the two-dimensional flow. This is due to low intensity flows. Indeed, the maximum values of the stream function Ψmax are equal to 0.70; 0.745 and 0.933 respectively for Ac ≈ 1/4, 1/2 and 1. These low intensities due from the temperature gradients created by conduction and by radiation at the corners of the different cavities. Concerning the effect of the aspect ratio, examination of the current lines shows that for an aspect ratio Ac ≈ 1/4 and Ac ≈ 1/2 it does not affect the nature of the flow in terms of number of fluid recirculation cells. Indeed, the nature of flow is similar in the different cavities, but in terms of volume of these cells, it increases as Ac increases. Concerning the temperature fields, it can be seen that the isotherms are almost parallel lines in the cavities with small deformations at the level of the vertical solid walls, above all for Ac ≈ 1/4. This is due to the difference between the solid and air thermal conductivities. It can be noted that as the aspect ratio increases, the isotherms become more and more spaced and almost parallel.
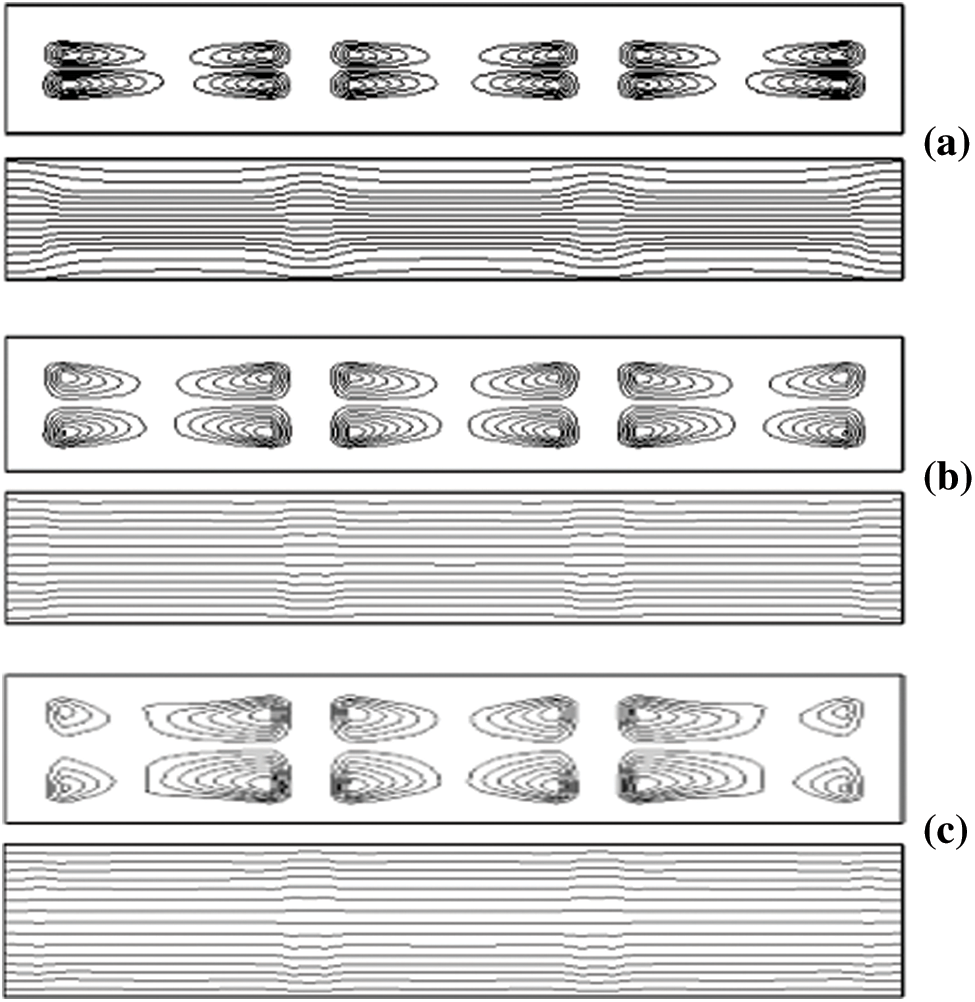
Figure 2: Streamlines (top) isotherms (bottom) for (a) Ac ≈ 1/4 ; (b) Ac ≈ 1/2 and (c) Ac ≈ 1
The Temperature profiles on both the top and the bottom horizontal surfaces of the studied hollow block is given in Fig. 3, for an incident solar flux S = 1000 W/m2. According to this figure, we first note that the temperature profiles have the same aspect of variation for the three geometric configurations treated. Also, we observe that the temperature of the top wall increases when the aspect ratio Ac increases. Moreover, we observe that for the hot surfaces and for the two aspect ratios Ac ≈ 1/2 and Ac ≈ 1, the temperature profile is practically constant as a function of X. On the other hand, in a hollow block of aspect ratio Ac ≈ 1/4, we observe that in the upper horizontal surface the temperature is low in the lower corner and increases as function of the dimensionless Cartesian coordinates X. It reaches its maximum inside every cavity as we decrease and move the higher corner. This situation is reversed for the lower horizontal face where the temperature decreases gradually as the aspect ratio increases. Indeed, the temperature decreases by 3°C when the aspect ratio varies from Ac ≈ 1/2 to Ac ≈ 1. This effect can be explained by that when we increase the aspect ratio of the hollow block hole, the radiative heat exchange attenuating the natural convection which decreases the overall heat transfer through the walls.
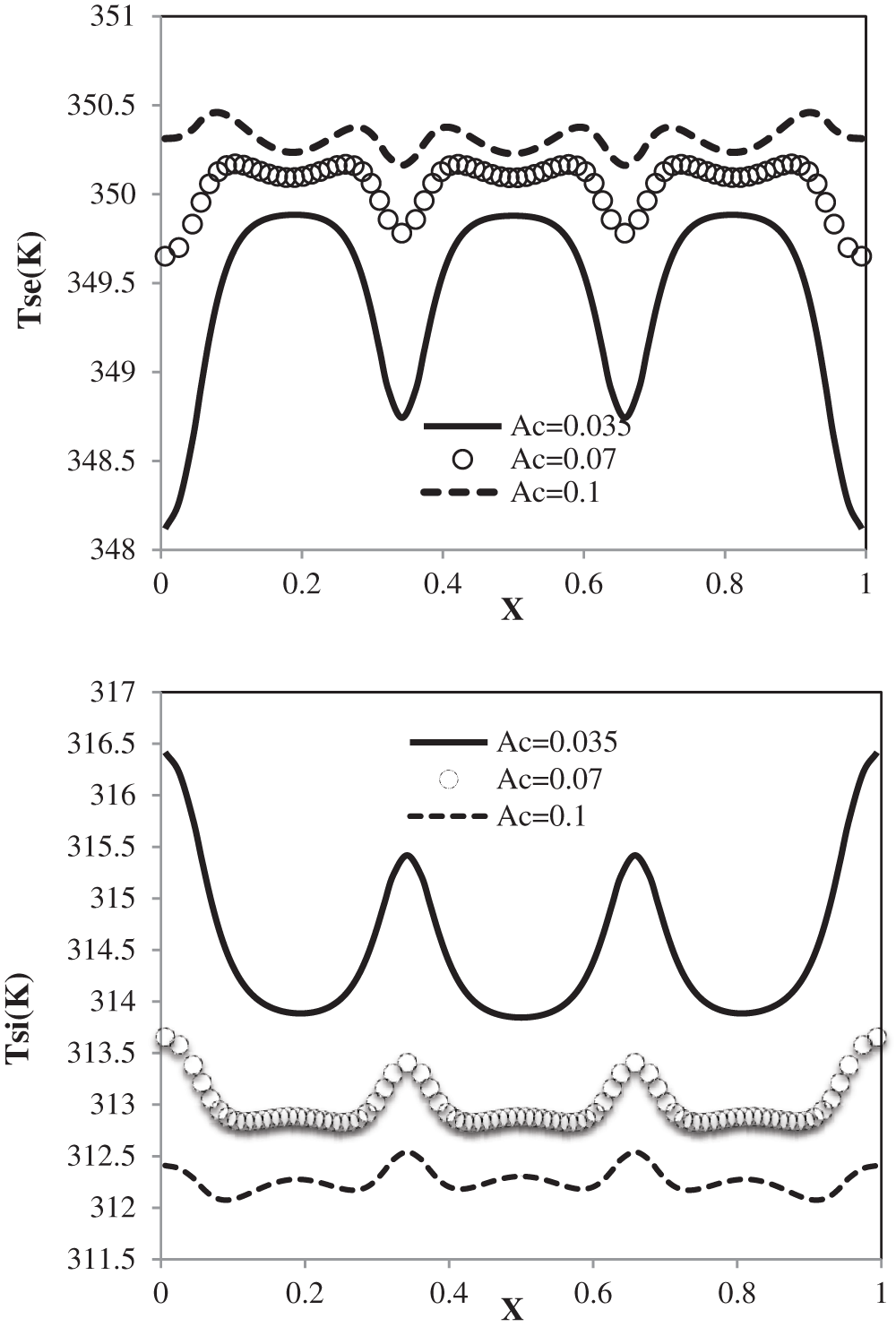
Figure 3: Temperature distributions (top) upper horizontal face, (down) lower horizontal face
The variation of the overall heat flux Qs as a function of the width X crossing through the active faces cold and the hot of the hollow block are given in Fig. 4, and this for the different types of hollow block studied. the results of this figure, it can be seen as expected that when the aspect ratio increases there is a decrease in heat flux. This is because the thermal conductivity of the air much lower than the thermal conductivity of the solid. Indeed, the average value of the total flux increases from value 349.52 W/m² for Ac ≈ 1/4 to 307.47 W/m² for Ac ≈ 1. This corresponds to an increase of about 14%. The analysis of these results shows that a roof built with hollow block of an aspect ratio Ac ≈ 1 reduces the heat transfer and then improves the thermal resistance compared to a roof built with hollow block of an aspect ratio Ac ≈ 1/2 or Ac ≈ 1/4.
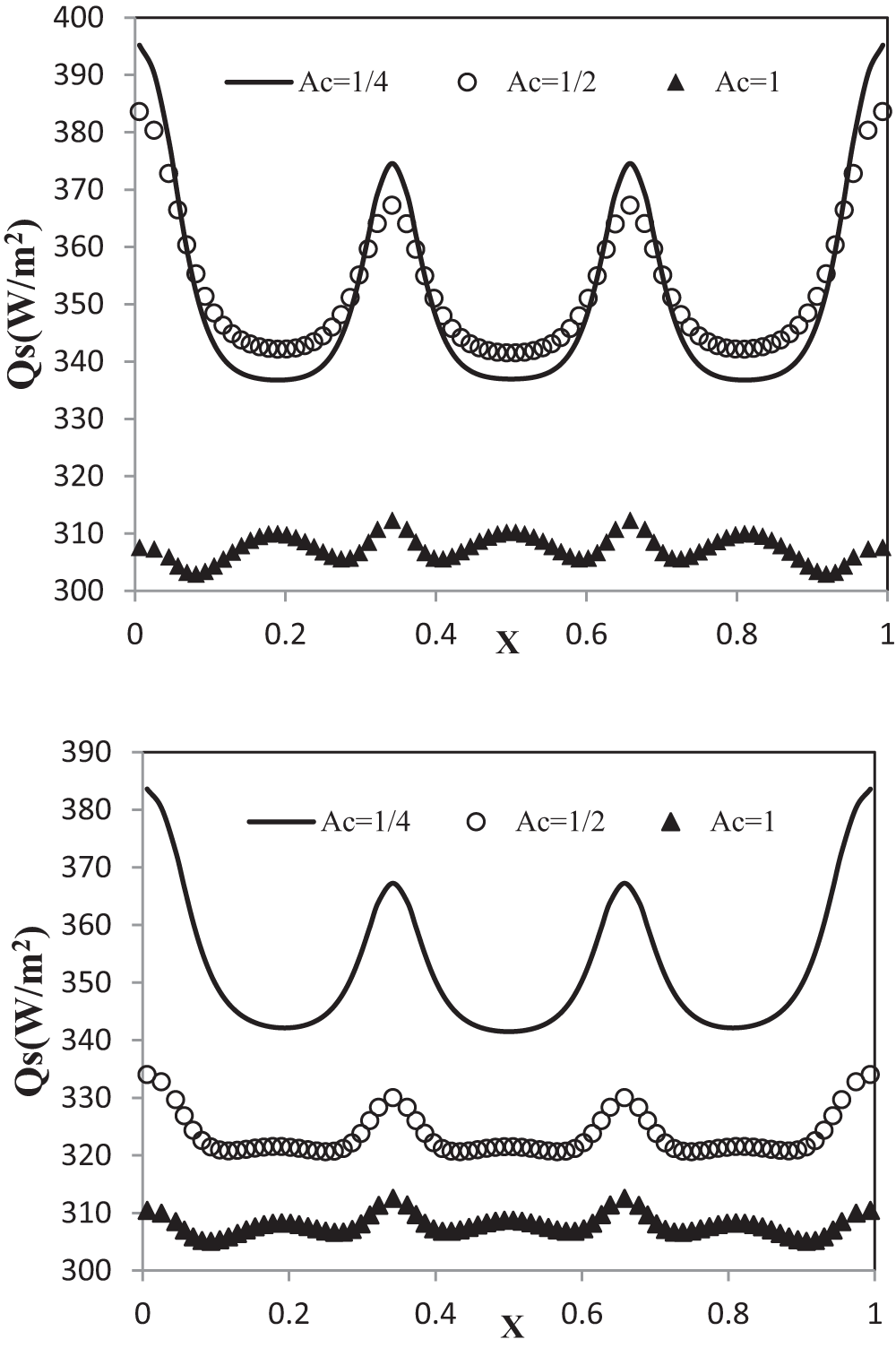
Figure 4: Variation of the heat flux Qs: upper (top) and lower (bottom) horizontal surface for Ac ≈ 1/4; Ac ≈ 1/2 and Ac ≈ 1
This work presented a two-dimensional numerical investigation of coupled heat transfer in a three-cavity hollow block subjected to incident solar flux. We examined the effect of the geometric aspect ratio on the dynamic fluid flow, on the temperature field and on overall heat transfer; the following conclusions could be drawn:
The aspect ratio does not affect the nature of the flow in circulating cell numbers however the cell volume increases with this parameter. The cavities with a high aspect ratio Ac (Ac ≈ 1), lead to reductions in heat transfer through the hollow block, could reduce heat flux by 42 W/m2 (14%), the use of the geometric aspect ratio Ac = 1 is a good combination to improve the building roof thermal performance. These results can contribute to the future building envelope design in terms of insulation capacity and fill the gaps for research in the area of insulation systems. In addition, it can also be encouraging for architects to use the optimal construction with regard to details such as flow distribution, arrangement and dimension of air cavities for this hollow system so as to achieve optimal insulation. Further investigations are recommended to perform experiment to study the influence of thickness or size of air cavities on wall insulation performance.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Ragui, K., Benkahla, Y. K., Labsi, N., Boutra, A. (2015). Natural convection heat transfer in a differentially heated encloseure with adiabatic partitions and filled with a Bingham fluid. Journal Heat Transfer Research, 46(8), 765–783. DOI 10.1615/HeatTransRes.2015007477. [Google Scholar] [CrossRef]
2. Ragui, K., Boutra, A., Benkahla, Y. K. (2016). On the validity of a numerical model predicting heat and mass transfer in porous squares with a bottom thermal and solute source: Case of pollutants spreading and fuel leaks. Mechanics & Industry, 17, 311. DOI 10.1051/meca/2015109. [Google Scholar] [CrossRef]
3. Ragui, K., Boutra, A., Benkahla, Y. K., Labsi, N., Feddaou, M. (2016). TiO2-water nanofluid within a tilted triangular enclosure including a square heater: Optimum heat transfer. Mechanics & Industry, 17(6), 612. DOI 10.1051/meca/2016009. [Google Scholar] [CrossRef]
4. Bouarnouna, K., Boutra, A., Ragui, K., Labsi, N., Benkahla, Y. K. (2019). Multiple-relaxation-time lattice Boltzmann model for flow and convective heat transfer in channel with porous media. Journal of Statistical Physics, 174(5), 972–991. DOI 10.1007/s10955-018-02219-7. [Google Scholar] [CrossRef]
5. Abdelbaki, A., Zrikem, Z. (1999). Simulation numérique des transferts thermiques couplés à travers les parois alvéolaires des bâtiments. International Journal of Thermal Sciences, 38(8), 719–730. DOI 10.1016/S1290-0729(99)80065-9. [Google Scholar] [CrossRef]
6. Ait-Taleb, T., Abdelbaki, A., Zrikem, Z. (2008). Numerical simulation of coupled heat transfers by conduction, natural convection and radiation in hollow structures heated from below or above. International Journal of Thermal Sciences, 47(4), 378–387. DOI 10.1016/j.ijthermalsci.2007.01.035. [Google Scholar] [CrossRef]
7. Ait-Taleb, T., Abdelbaki, A., Zrikem, Z. (2014). Simulation of coupled heat transfers in a hollow tile with two vertical and three horizontal uniform rectangular cavities heated from below or above. Energy and Buildings, 84(4), 628–632. DOI 10.1016/j.enbuild.2014.09.010. [Google Scholar] [CrossRef]
8. Boukendil, M., Abdelbaki, A., Zrikem, Z. (2012). Detailed numerical simulation of coupled heat transfer by conduction, natural convection and radiation through double honeycomb walls. Building Simulation, 5(4), 337–344. DOI 10.1007/s12273-012-0064-9. [Google Scholar] [CrossRef]
9. Al-Hazmy, M. M. (2006). Analysis of coupled natural convection conduction effects on the heat transport through hollow building blocks. Energy and Buildings, 38(5), 515–521. DOI 10.1016/j.enbuild.2005.08.010. [Google Scholar] [CrossRef]
10. Baig, H., Antar, M. (2008). Conduction/natural convection analysis of heat transfer across multi-layer building blocks. 5th European Thermal Science Conference, Netherlands. [Google Scholar]
11. Najjaoui, M., Ait-Taleb, T., Abdelbaki, A., Zrikem, Z., Chaib, H. (2018). Coupled heat transfers in a three cavity hollow block subjected to an incident solar flux: Effect of heat conductivity. IOP Conference Series: Earth and Environmental Science, 161(1), 012002. DOI 10.1088/1755-1315/161/1/012002. [Google Scholar] [CrossRef]
12. Siegel, R., Howell, J. R. (1981). Thermal radiation heat transfer. 2nd ed. New York: McGraw-Hill. [Google Scholar]
13. Patankar, S. V. (1980). Numerical heat transfer and fluid flow. New York: Hemisphere. [Google Scholar]
14. Akiyama, M., Chong, O. (1997). Numerical analysis of natural convection with surface radiation in a square enclosure. Numerical Heat Transfer, Part A: Applications, 31(4), 419–433C. DOI 10.1080/10407789708913899. [Google Scholar] [CrossRef]
15. Document Technique Unifié DTU, Cahiers du Centre Scientifique et Technique du Bâtiment, CSTB, Paris 16, livraison 378, cahier 2946, “Règles de calcul des caractéristiques thermiques utiles des parois de construction”. Reference AFNOR DTU P 50-702, Février 1997. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |