

 | Fluid Dynamics & Materials Processing |  |
DOI: 10.32604/fdmp.2022.021200
REVIEW
A Review of Methods Based on Nanofluids and Biomimetic Structures for the Optimization of Heat Transfer in Electronic Devices
School of Low-Carbon Energy and Power Engineering, China University of Mining and Technology, Xuzhou, 221116, China
*Corresponding Author: Cong Qi. Email: qicong@cumt.edu.cn
Received: 31 December 2021; Accepted: 21 April 2022
Abstract: Nowadays, the utilization rate of electronic products is increasing while showing no obvious sign of reaching a limit. To solve the associated “internal heat generation problem”, scientists have proposed two methods or strategies. The first approach consists of replacing the heat exchange medium with a nanofluid. However, the high surface energy of the nanoparticles makes them prone to accumulate along the heat transfer surface. The second method follows a different approach. It tries to modify the surface structure of the electronic components in order to reduce the fluid-dynamic drag and improve the rate of heat exchange. This article reviews these effects considering different types of nanofluid and different shapes, sizes, and arrangements of “biomimetic grooves”. The idea to use these two methods in a combined fashion (to improve heat transfer and reduce flow resistance at the same time) is also developed and discussed critically to a certain extent.
Keywords: Nanofluids; biomimetic structure; drag reduction characteristic; thermal management
As society develops, the human demand for energy is increasing daily, although energy resources are in short supply. Since the available energy resources are limited, the energy shortage has become the biggest global restriction to scientific/technological developments and economic growth. To achieve the goal of sustainable development for all humanity, society must not only apply cleaner and more effective technologies but also reduce its consumption of energy as much as possible. In the present study, energy loss is concentrated in a variety of industrial fields in which the resistance generated during the fluid flow process consumes a significant amount of energy [1].
With the development of the semiconductor industry and the application of high-power electronic components, the power consumption of electronic chips per unit size is gradually increasing, the core working frequency of central processing units (CPUs) is becoming ever higher, the number of transistors on a chip has reached one billion, and the heat load of high-power electronic components in electronic equipment is as high as 106 W/m2 [2]. However, as radiators must be controlled at an area of about 4 cm2, the realization of high integration also increases the calorific value. Therefore, investigating lightweight heat-exchange equipment with a small volume and high heat-transfer efficiency is essential.
The application of the traditional enhanced heat-exchange method to such a unique heat-transfer field is difficult. Since the low thermal conductivity of traditional heat-exchange media, e.g., water, oil, and alcohol, makes obtaining a high heat-transfer capacity difficult, many researchers focused on the field of nanofluids. In 1995, Choi [3] (of the Argonne National Laboratory of the United States) proposed a new concept: nanofluids. These fluids are formed after stabilization following the addition of a certain amount of a dispersive suspension medium to a base liquid (generally, liquid, or liquid–metal) [4]. Nanofluids exhibit a large heat-transfer capacity and high thermal conductivity, and they can significantly change interfacial wettability after adsorption at an interface [5–7]. Consequently, they are widely applied in heat exchangers [8–11], electronic component cooling [12–14], fuel cells [15,16], and nuclear reactors [17]. In the future, nanofluids are likely to become efficient heat-transfer working fluids.
However, despite the advantages of the superior heat-transfer characteristics of nanofluids, the increase in the flow resistance of the system cannot be ignored. When nanoparticles are added to a fluid, the fluid’s viscosity will inevitably increase, resulting in a pressure drop in the circulatory system [18]. For electronic components, such as CPUs, the greater the flow resistance, the greater the power consumption. This also restricts the application of nanofluids in industrial production. Therefore, finding a solution to reduce the flow resistance of nanofluids in industrial systems has become a critical issue [19,20].
To determine how to reduce the flow resistance and maintain enhanced heat-transfer capacity, most research institutions conducted in-depth studies from two perspectives. The first involves designing a new type of drag-reducing nanofluid by altering the flow medium; this must demonstrate not only a better heat-transfer effect in terms of production and lifetime but also a lower flow resistance. The second involves the application of special drag-reduction treatments to the flow surface, e.g., superhydrophobic coatings and non-smooth surface microstructures in bionics. However, combining the two approaches to realize enhanced resistance reduction is a novel concept.
This review is divided into three parts. Parts one and two present the latest research on the flow and heat-transfer properties of nanofluids and drag-reducing nanofluids, and part three presents the current research status in terms of the drag-reduction of bionic structures. Achieving sustainable development goals requires both the reduction of energy consumption and the development of energy-saving technologies. Flow-reduction technology can reduce the loss of electricity, and it presents a new concept for future research into energy-saving technology. The structure of this review is shown in Fig. 1.
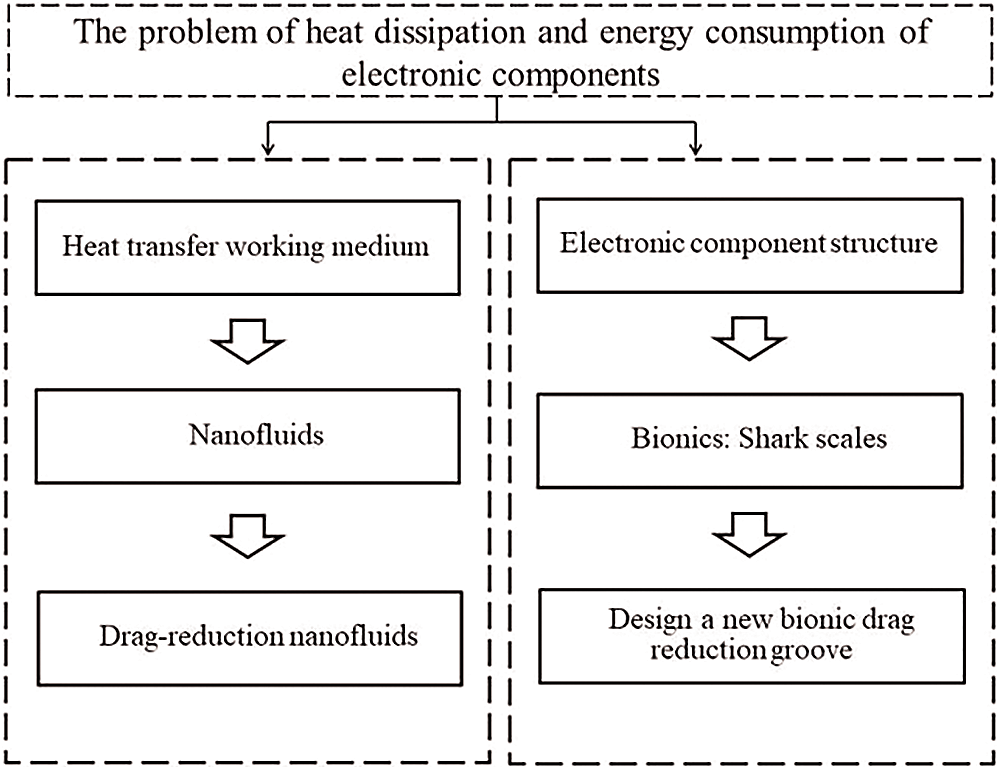
Figure 1: Solutions to the heat dissipation problem of electronic components
To enable the characteristics of nanofluids to be studied effectively, first, they must be prepared. At present, two commonly used preparation methods exist: the one-step method [21] and the two-step method [22].
(1) One-step method. In the one-step method, the base solution and nanoparticles do not require separate preparation as shown in Fig. 2. Two kinds of single-step synthesis exist, namely, gas-phase synthesis and liquid-phase synthesis.
Figure 2: Schematic diagram of single-step device for preparation of nanofluids [1]
The advantage of the one-step method is that it can prepare stable mixed suspensions that are difficult to precipitate. However, its disadvantage is that the amount of single preparation is less, and the cost is higher.
(2) Two-step method. In the two-step method, first, the required nanoparticles are prepared before being added to the base solution to prepare the mixed suspension as shown in Fig. 3. It differs from the one-step method in that it involves two separate stages.
Figure 3: Schematic diagram of the two-step method for preparing nanofluids [1]
The advantage of the two-step method is that it is simple, it can meet the needs of mass production, and it is more suitable for large-scale applications. The two-step method is often used in production experiments.
2.2 Physical Properties of Nanofluids
The addition of nanoparticles is one of the main reasons why nanofluids can enhance heat-transfer compared with ordinary heat-transfer masses. When nanoparticles are added to pure fluids, the thermal conductivity of the obtained mixture increases. Furthermore, due to the Brownian motion of nanoparticles, the laminar boundary layer flow is broken, and the disturbance is strengthened, which further improves thermal conductivity. However, if the nanoparticles’ mass fraction in the nanofluids is continuously raised, the nanofluids’ visibility will also increase, which will enhance the heat-transfer resistance and cause a certain degree of heat-transfer deterioration.
2.2.1 Heat Conductivity of Nanofluids
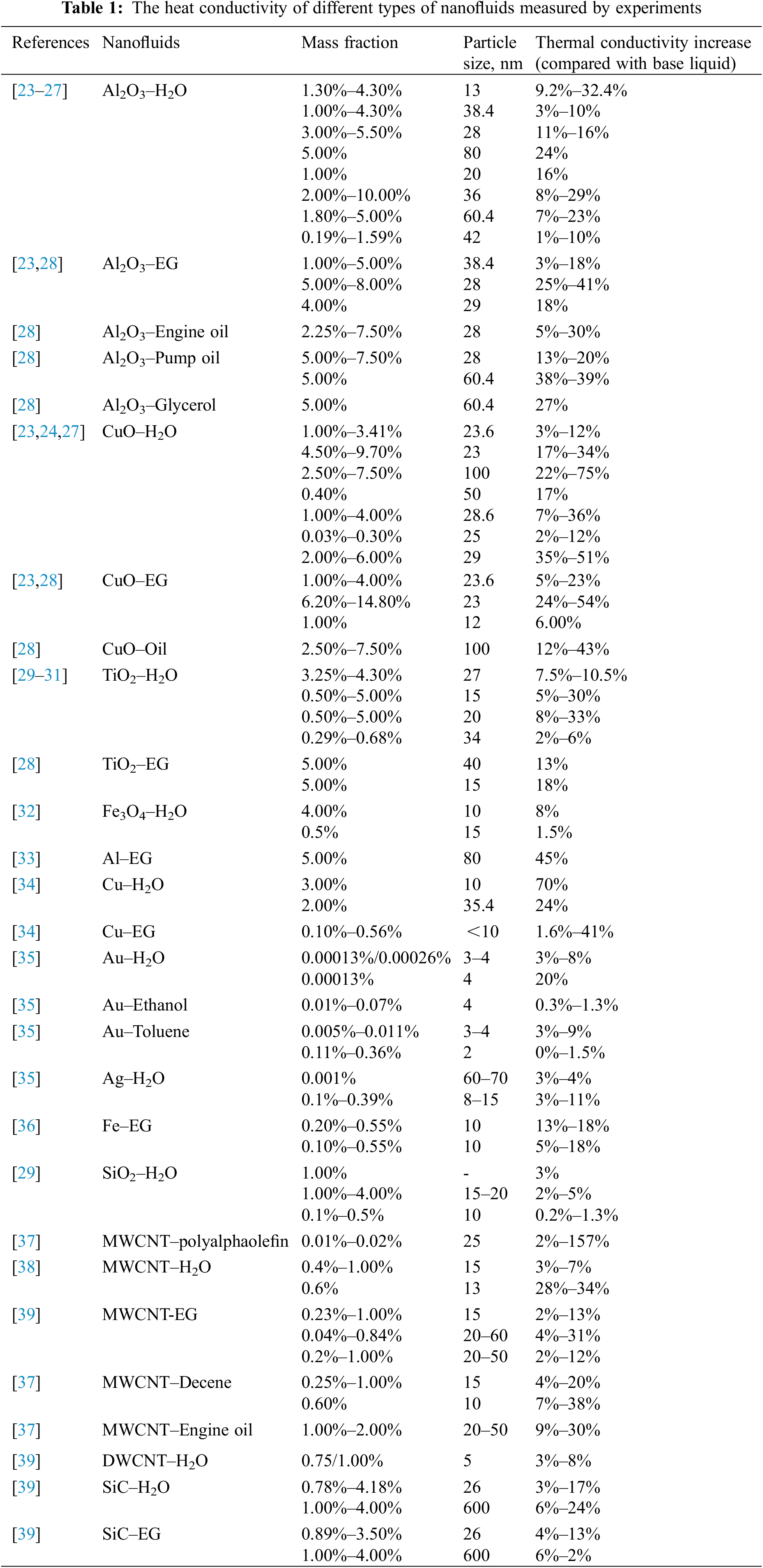
In nanofluids, heat conductivity is one of their most important physical properties, which have been studied and tested by numerous researchers. Researchers found that the mass fraction, size, shape, and pH value of nanofluids can significantly affect their heat-transfer coefficients. Common nanofluid systems use nanoparticles comprising metal oxides (Al2O3, CuO, TiO2, Fe3O4), metals (Al, Cu, Au, Ag, Fe), non-metallic oxides (SiO2), carbon nanotubes (CNTs) (MWCNT, DWCNT), and carbides (SiC). Deionized water, glycol, glycerol, toluene, and engine oil are commonly used in the configuration of the base liquid. Over the past decade, much research has been conducted on the effects of different types, concentrations, and sizes of nanoparticles on the heat conductivity of nanofluids. Table 1 summarizes the heat conductivity of different nanofluids over the past 10 years [23–39] and shows that the addition of nanoparticles enhanced the thermal conductivity of the nanofluids compared with the original base fluid.
Hu et al. [40] explored the influence of the dimension and concentration of silica nanofluids mixed with glycol and water on the heat conductivity of nanofluids. Their results revealed that when the diameter of the nanoparticles decreased from 120 to 84 nm, the heat conductivity of the nanofluids increased. Additionally, as the concentration of nanoparticles increased, the heat conductivity of the nanofluids first increased rapidly before rising slowly in the concentration range of 0.25%–1.00%.
Research by Timofeva et al. [41] and Al-Waeli et al. [42] revealed that the heat conductivity of nanofluids comprising cylindrical nanoparticles was greater than that of nanofluids comprising ball-shaped nanoparticles, to a certain extent.
Qi et al. [43] investigated the effect of pH value on heat conductivity when preparing titanium dioxide–water nanofluids. Their results showed that the optimal heat conductivity of nanofluids was realized at a pH of 8.
Although the addition of nanoparticles to a base solution increases the thermal conductivity of the fluid, if the viscosity of the prepared nanofluids increases too much compared with the base solution, it will result in the deterioration of heat-transfer. Three main factors affect the viscosity of nanofluids:
(1) Nanoparticle size: The smaller the nanoparticle, the greater the influence of molecular thermal motion; the internal disturbance of nanofluids increases, leading to an increase in friction resistance. A study by Lu et al. [44] used a simulation to explore the effect of the dimension of alumina nanoparticles on the viscosity of nanofluids. Alumina water and alumina glycol nanofluids were used in the experiment, and the results revealed that when the size was greater than 30 nm, the smaller the dimension, the larger the increase in the nanofluids’ viscosity. However, at sizes less than 30 nm, the viscosity change was not obvious.
(2) Nanoparticle concentration: Mir-Shahabeddin et al. [45] studied the viscosity change of EG–water nanofluids and Al–water nanofluids using a molecular dynamics simulation. The simulation results, which were in good agreement with the experimental values, showed that a decrease in the volume fraction of Al nanofluids led to a decrease in their viscosity. Heris et al. [46] experimentally measured the viscosity of Al–water nanofluids and Cu–water nanofluids at different volume fractions and revealed that the viscosity of the water-based nanofluids increased as the volume fraction of the nanosized particles increased. Zhong et al. [47] determined the viscosity of Cu–glycol nanofluids at mass fractions of 0.5%–4.0%. Their experimental results highlighted that the greater the concentration of nanoparticles, the more significant the shear effect, which increased the flow resistance of the nanofluids and, consequently, the viscosity. Fig. 4 reveals that the viscosity of Cu–glycol nanofluids increased with a rise in nanoparticle concentration.
(3) Temperature: Anish et al. [48] studied the viscosity of nanofluids comprising zinc oxide and heat-transfer oil 55. The results, which are presented in Fig. 5, reveal that the viscosity of the fluid decreased as the temperature of the medium. The increase in temperature caused the Brownian motion of the particles to intensify, the mutual attraction between the particles to reduce, and the viscosity of the nanofluids to decrease. Li et al. [49] investigated the viscosity change of CuO–water nanofluids under temperature changes. They revealed that when the temperature increased, the viscosity gradually decreased, and they reported the influence of temperature on viscosity to be more significant than the volume fraction.
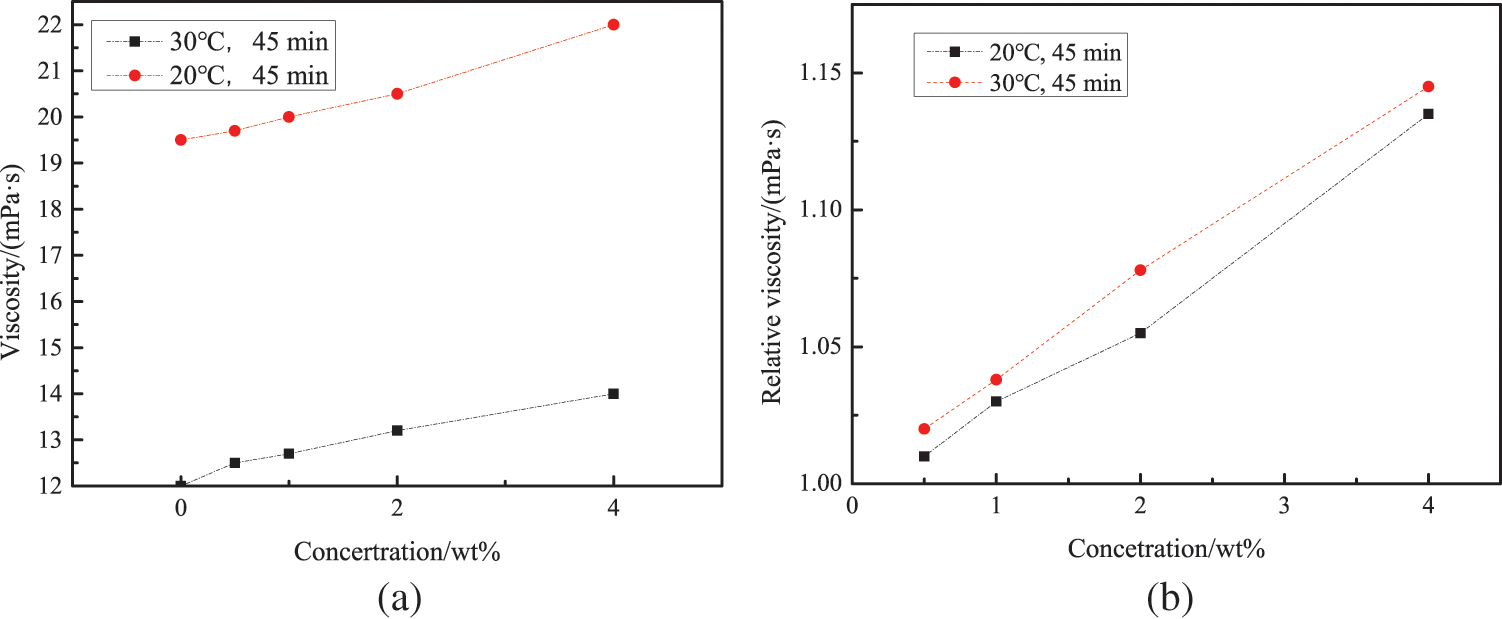
Figure 4: Viscosity and relative viscosity of Cu-ethylene glycol nanofluids, (a) viscosity, (b) relative viscosity [47]
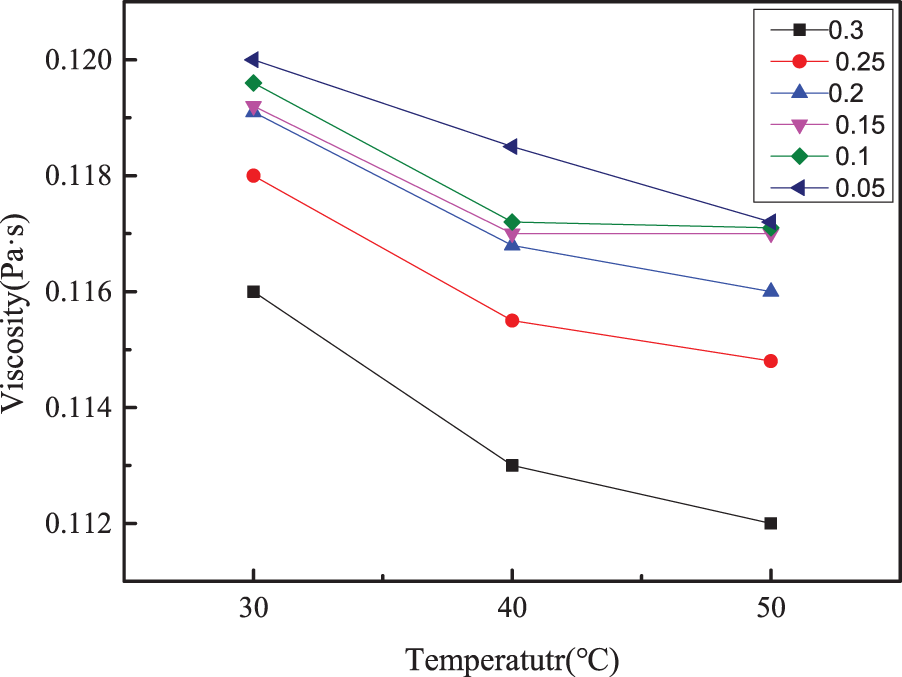
Figure 5: Variation curve of viscosity of zinc oxide nanofluids with different concentrations with temperature [48]
Finally, to investigate the influence of temperature on the viscosity of alumina water nanofluids, Zhao et al. [50] used rheometer experiments. The viscosity of the nanofluids increased with rising temperature. As can be seen in Fig. 6, the increase in viscosity is more obvious.
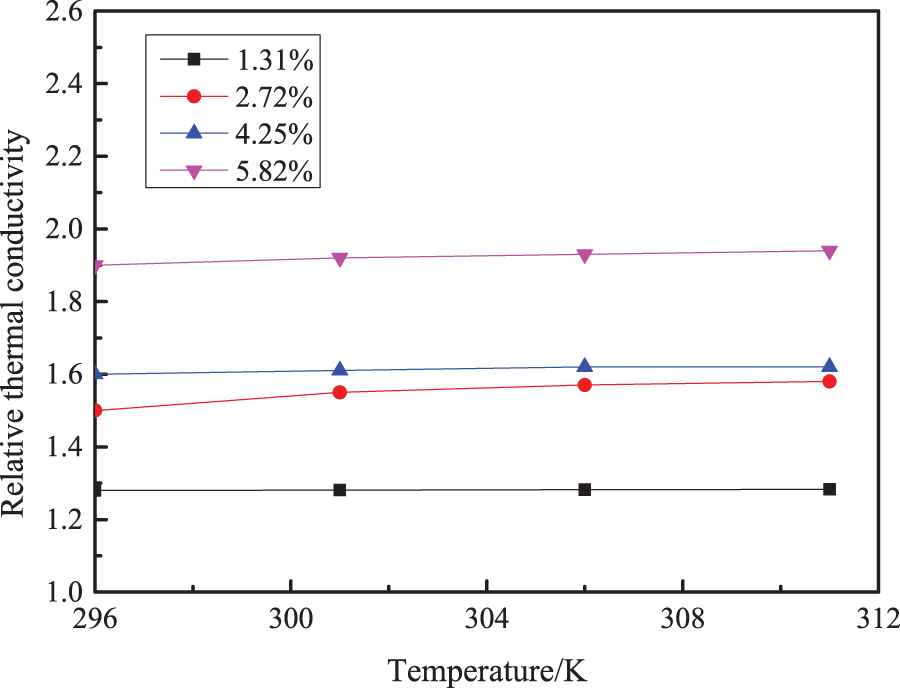
Figure 6: The effect of temperature on the thermal conductivity and viscosity of nanofluids [50]
2.3 Flow Characteristics of Nanofluids
(1) Experiment
To investigate the flow characteristics of Cu/CuO–H2O nanofluids, Sun et al. [51–53] experimentally explored the flow and convective thermal characteristics of multi-walled CNTs in Cu, Al, A12O3, Fe2O, and graphite nanofluids with mass fractions of 0.1%, 0.2%, 0.3%, 0.4%, 0.5%, and 0.6% in threaded tubes with built-in twisted tape. The results revealed an optimal concentration ratio of 0.5% for different nanofluids at the same Reynolds number. The heat-transfer performance of Cu–H2O nanofluids was the best, although their flow resistance was larger. The comprehensive performance of these nanofluids in terms of thermal performance and the drag-reduction of graphite were superior to other nanofluids.
Based on an experimental study of Al2O3–H2O nanofluids, Zhong et al. [54] used an engine cooler test to measure the heat-exchange coefficient and flow resistance of 1%–5% Al2O3–H2O nanofluids. The results revealed that the nanofluids significantly improved the heat-exchange coefficient of the base fluid in the engine oil cooler, and the contribution of the increase in the particle volume fraction to the heat-transfer coefficient was greater than the deterioration in flow resistance. On the premise of ensuring the suspension stability of nanofluids, increasing the volume fraction of particles is beneficial to enhancing heat-transfer. In another study, Doshmanziari et al. [55] investigated the flow and heat-exchange of different concentrations of Al2O3–H2O nanofluids in a turbulent state. The results demonstrated that the nanofluids significantly improved the heat-transfer coefficient of the base fluid by up to 14%.
In their experimental study of TiO2–H2O nanofluids, Yang [56] and Zhai [57] prepared TiO2–H2O nanofluids with different mass fractions and tested their flow characteristics. The experimental results showed that under a constant temperature, the viscosity of the working fluid increased along with the resistance of the nanofluids. When the comprehensive performance index [58] is used to evaluate TiO2–H2O nanofluids, the index will first increase and then decrease according to the Reynolds number, and the critical Reynolds number can provide the optimal performance. Ding et al. [59] studied the flow characteristics of TiO2–H2O nanofluids in bellows and revealed that the Nusselt number of TiO2–H2O nanofluids increased by 62% compared with pure water.
However, due to high experimental costs, many researchers attempted to use the numerical simulation method to explore the flow characteristics of nanofluids.
(2) Numerical simulation
As stated above, to save costs, many scholars explored the flow properties of nanofluids from the perspective of numerical simulations using methods such as the single-phase model, the two-phase model, and the lattice Boltzmann method (LBM).
Wang et al. [60] used the MATLAB programming language to simulate the enhanced heat-exchange and flow properties of Al2O3–H2O nanofluids in a horizontal circular tube. The simulation results indicated that in the horizontal direction, the heat-transfer in the inlet section is active, and the mean Nusselt number is large; this number decreases rapidly and tends to stabilize at a certain point. At this time, the heat-transfer gradually stabilizes.
Barnoon et al. [61] simulated the flow and heat-transfer of nanofluids under the action of a magnetic field using both single- and two-phase models (i.e., a hybrid model). The results revealed the Nusselt number in the two-phase model to be higher than in the single-phase model.
Sheikholeslami et al. [62,63] used the control volume finite-element method to investigate the natural convection heat-transfer of magnetic nanofluids in porous media by considering the influence of the external magnetic field. They concluded that the Lorentz force weakened the movement of the nanofluids and thickened the thermal boundary layer. Additionally, the temperature gradient increased with rising temperature.
Qi et al. [64–68] used the LBM method to simulate the boiling enhancement of molten-metal-based nanofluids in cavities with different shapes. The results confirmed that nanofluids can significantly improve the heat-transfer effect of natural convection.
The above experimental and simulation results revealed that the heat-transfer effect of nanofluids is generally better than that of conventional fluids, and this effect is affected by many factors, such as the mass fraction of nanofluids, the size of nanoparticles, and pH values. However, the findings indicated that nanofluids cause increased flow resistance. Accordingly, many researchers started to study drag-reducing nanofluids, whose contribution to thermal conductivity is greater than the deterioration of flow resistance.
3 Characteristics of Drag-Reducing Nanofluids
3.1 Preparation of Drag-Reducing Nanofluids
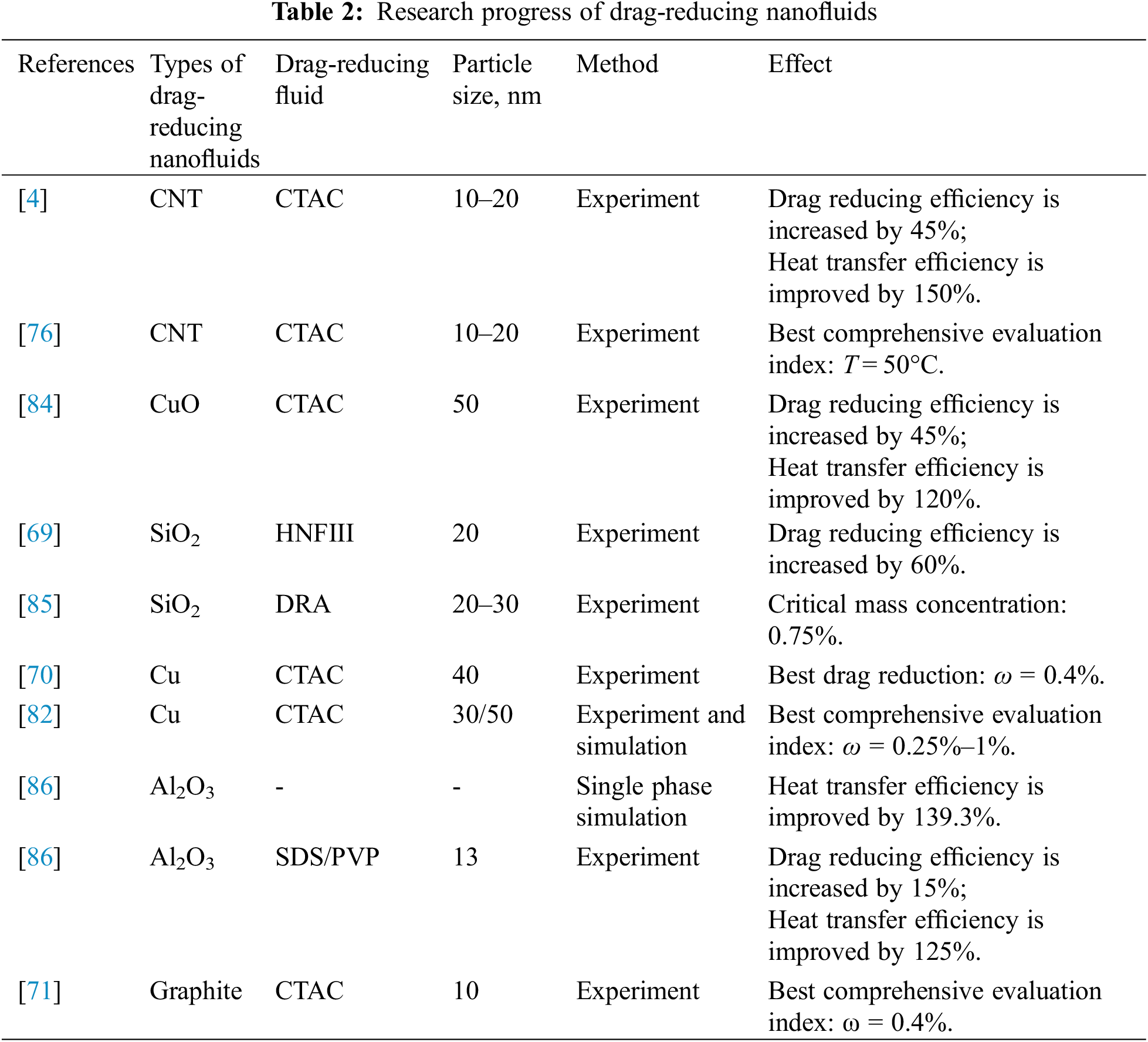
The original drag-reducing nanofluids used diesel as a base fluid; however, due to the high cost and poor safety of diesel, researchers since developed low-cost, safe, and effective water-based drag-reducing nanofluids [69]. The preparation method for water-based drag-reducing nanofluids is similar to that of nanofluids. The difference is the addition of a drag-reducing agent to the base fluid when preparing drag-reducing nanofluids. However, a few types of currently studied drag-reducing nanofluids exist that cannot be analyzed systematically. The configuration methods of various researchers are as follows [70,71]: first, Yang et al. [72] prepared water-based nanofluids before adding CTAC and sodium salicylate (nasal) (mass ratio of 1:1) to the mixed solution before stirring. Next, Wei et al. [73] found that the microstructure of a prepared viscoelastic fluid was stable when the mass ratio of CTAC–sodium salicylate was 1:1.
Pang et al. [69] prepared drag-reducing nanofluids using the dilution method. First, water, diesel oil, and sodium hexadecyl sulfonate were mixed to prepare a dispersant. Then, white nano-SiO2 with a particle size of 20 nm and good hydrophobicity was dispersed uniformly into the prepared dispersant to obtain a nano-SiO2 slurry. Then, the slurry was stirred by an emulsifier at 7,000 r/min for 15 min. The mass ratio of nano-SiO2 to water was 1:9. The drag-reducing nanofluids were obtained by combining the mixtures of the two components.
Sun et al. [71] prepared drag-reducing nanofluids using a two-step [74] technique. The drag-reducing fluid was obtained by stirring in an electromagnetic stirrer for 30 min. A certain mass of nanoparticles (multi-walled CNTs, graphite, Al2O3, Cu, Al, Fe2O3, and Zn) was added to the obtained drag-reducing fluid, which was vibrated for 60 min with an ultrasonic oscillator to form stable and dispersed drag-reducing nanofluids. As can be seen in Fig. 7, the drag-reducing graphite and Cu nanofluids obtained using this method were well dispersed and stable without particle deposition.
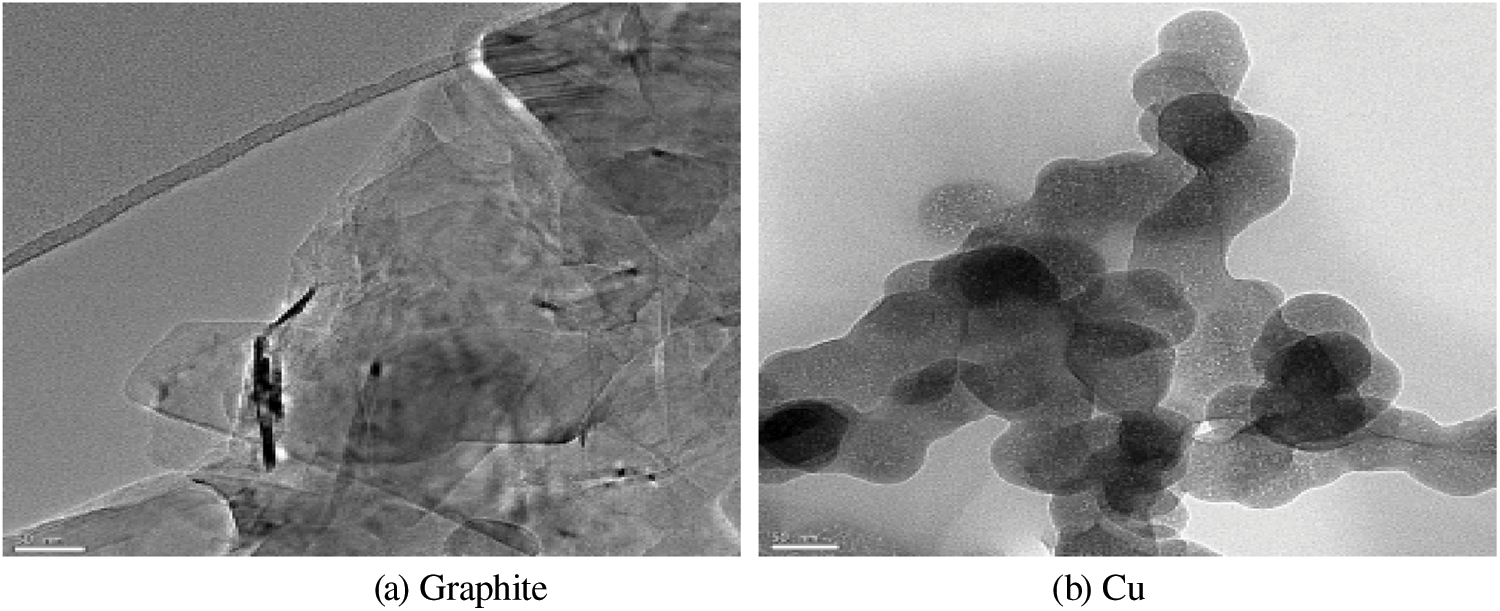
Figure 7: Transmission electron microscope (TEM) photo of drag-reducing nanofluids [57]
3.2 Heat Transfer and Flow Characteristics of Drag-Reducing Nanofluids
(1) Experiment
Micha et al. [75] combined a drag-reducing solution with nanofluids and discussed the influence of non-ionic surface-active agents on the drag-reduction effect of metallic oxide–water nanofluids. The results of their experimental research revealed that the addition of a non-ionic surfactant reduced the friction coefficient of the water and nanofluids, and the addition of a surfactant demonstrated no significant effect on the resistance reduction effect of the system.
Song et al. [76] developed water-based CNT nanofluids (suspension) with drag-reduction characteristics and measured their thermophysical and rheological properties. The results showed that the liquid temperature strongly influenced both resistance reduction and heat-exchange characteristics. Although the drag-reduction performance of the fluid was unchanged, its heat-transfer performance was significantly improved after the addition of CNTs. Nanofluids with drag-reduction characteristics can improve the comprehensive heat-exchange characteristics of forced convection or further enhance the heat-exchange enhancement characteristics of nanofluids.
Zhang et al. [70] experimentally investigated the optimal mass fraction of drag-reducing graphite nanofluids and Cu nanofluids. The results revealed the optimal quality fraction of drag-reducing graphite nanofluids and Cu nanofluids to be 0.4%, which demonstrates the optimal comprehensive effect of convective heat-exchange and drag-reduction.
Adam et al. [77] experimentally demonstrated the drag-reduction effect of CNTs and additives in a tube. Their results showed that CNTs could enhance the drag-reduction performance of polymer additives; however, CNTs could not provide drag-reduction under turbulent flow conditions, and their additional benefits were lost once the polymer was degraded.
(2) Numerical simulation
Experimental restrictions mean that research into drag-reducing nanofluids cannot accurately determine the instantaneous physical quantities near the wall; therefore, many researchers use the numerical simulation method. For example, Li et al. [78,79] used a straightforward digital simulation to investigate the flow and heat-exchange characteristics of viscoelastic alumina nanofluids in a channel with a uniformly heated wall. Next, their experimental results revealed that compared with the based fluid of the viscoelastic fluid, the increase in the fractional volume of the nanoparticles provided a superior heat-transfer effect, with the highest heat-transfer enhancement efficiency of 39.3%. Viscoelastic alumina nanofluids exhibit better drag-reduction characteristics compared with ordinary nanofluids.
Zou et al. [80] used FLUENT software’s user-defined function to write the constitutive equation of viscoelastic fluid. It proposed the numerical method of “unsteady computation of steady problems”. This method can improve the stability and convergence of viscoelastic flow field numerical calculations.
Yang et al. [81–83] used numerical simulations and experiments to confirm the turbulence drag-reduction of viscoelastic nanofluids and reported an enhanced heat-transfer effect compared with the viscoelastic base fluid. Different concentrations of viscoelastic fluid-based Cu nanofluids were prepared experimentally. As the Cu nanoparticles increased, the flow resistance coefficient increased slightly. Also, the heat-transfer properties were enhanced relative to the base fluid. The results of the numerical simulations were consistent with those obtained from experimental measurements.
Ma et al. [84] experimentally investigated the influence of different surfactants on the rheological and thermophysical properties of mixed nanofluids. Their experimental results revealed that among PVP, SDS, and CTAB, the drag-reducing nanofluids prepared by PVP surface-active agents demonstrated the greatest stability. Next, for the Al2O3–CuO/water and Al2O3–TiO2/water mixed nanofluids, the optimal ratios of the PVP surfactant were 0.005% and 0.01%, respectively. At 60°C, the highest thermal conductivity reached 0.73 and 0.75 w/(m⋅K), and the drag-reduction effect was relatively good. Table 2 summarizes the drag-reducing nanofluids [4,69–71,76,82,84–86] and shows that in comparison with the original fluid, the thermal conductivity and drag-reduction of the new fluid (obtained by the addition of nanoparticles to the drag-reducing fluid) were improved in specific cases.
4 Drag Reduction Characteristics of Bionic Structure
4.1 Drag Reduction Mechanism of Bionic Microstructure
From the perspectives of bionics and environmental adaption during the millions of years of evolution on Earth, organisms are constantly changing their surface microstructures to obtain a better drag-reduction effect. As can be seen in Fig. 8, sailfish can reach top swimming speeds of 190 km/h. This speed is needed to enable sailfish to prey on small fast-moving fish. Research revealed that the scales on the skin of sailfish produce tiny eddies, wrapping the whole body in a layer of bubbles instead of higher-density seawater, thereby reducing resistance and facilitating fast swimming. Next, the fastest speed of airborne swifts is 352.5 km/h, although their skin surface is not smooth [87]. Earthworms and dung beetles living in moist soil demonstrate non-clay characteristics, and they also exhibit the microstructure of a non-smooth surface [88]. Figs. 9 and 10 show the microstructure of its uneven surface.

Figure 8: Animals used as references for bionics

Figure 9: Dung beetle with a dimpled surface [89]

Figure 10: Yellow-margin true dragon louse with convex hull surface [90]
After studying these organisms, many scholars found that non-smooth micro-surfaces can produce unexpected reductions in drag performance. Currently, three types of surface microstructures exist: the groove type [91], the concave type, and the convex hull type [92]. Sharks are a typical example of a creature with a grooved surface. The surface of the shark is covered with “cortical scales convex” in which the scales overlap. Viewed from the length direction, its surface is covered with V-shaped ribs, which is a typical ridge structure. Each ridge tissue is covered with between three and four radial grooves [93]. At present, many scholars are investigating how the microgrooves on the surface of sharks’ skin reduce resistance, and it is accepted that the V-rib structure on the skin’s surface is a three-dimensional interlocking arrangement formed by the insertion of a small rib into two ribs [94] in Fig. 11. This structure reduces fluid sloshing, inhibits and delays the occurrence of turbulence, and achieves the purpose of drag-reduction; therefore, shark skin is the perfect template for human learning.

Figure 11: Shark with grooved surface [94]
Much research has been conducted into drag-reduction with grooves. Three main views on the principle of drag-reduction exist: The second vortex group theory, the protruding height theory, and the micro-air-bearing theory. Table 3 provides details of research into the drag-reduction mechanism of the trench [3,95–98].
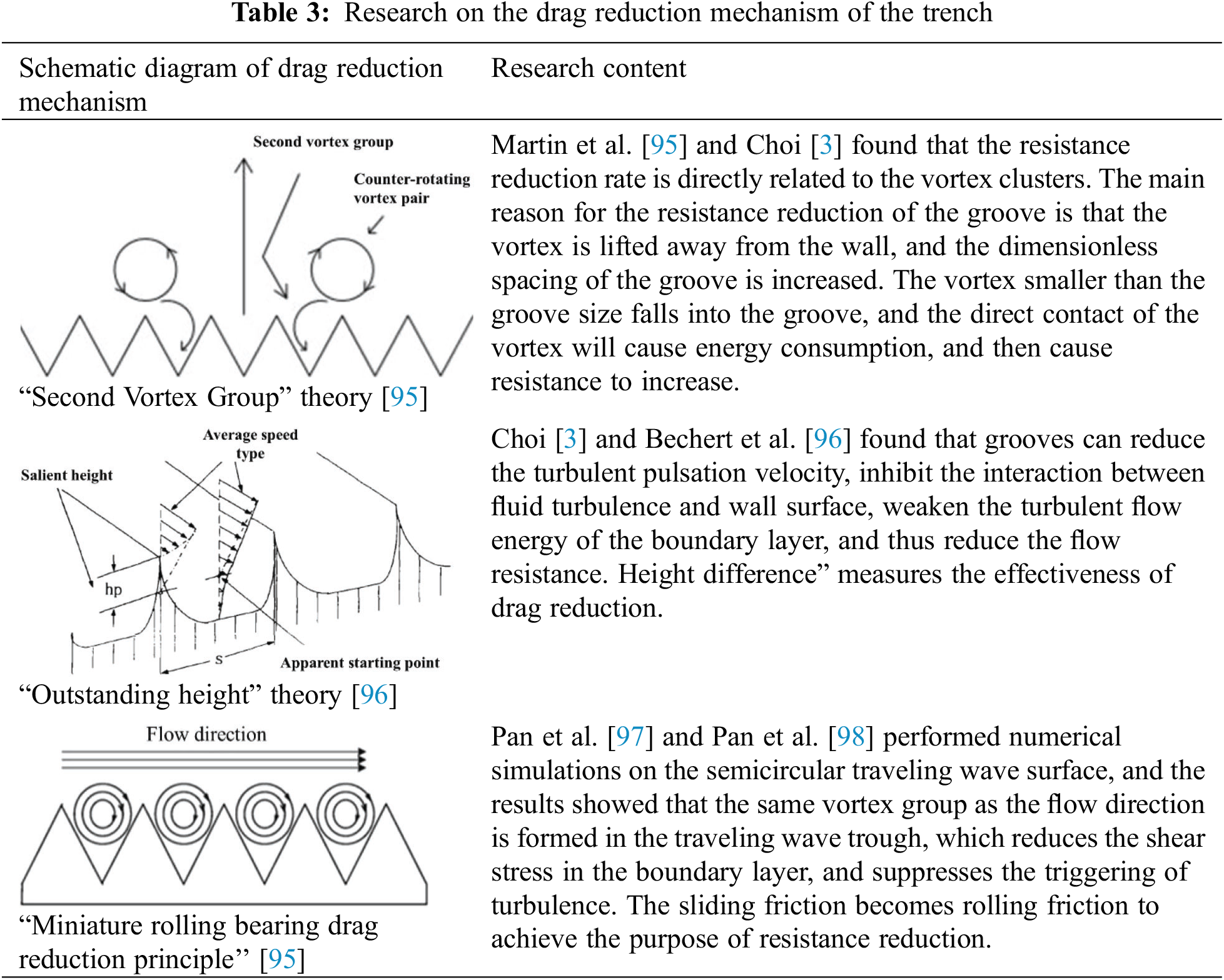
The second vortex group theory was proposed by Bacher et al. [99–101]. A groove is fixed at the bottom of a water tunnel, and pigment is added at the entrance. The turbulent flow states of the groove surface and plane are determined by observing the state of the pigment band passing through the groove surface and plane. The visualization experiment results showed the secondary vortex to be formed at the roof of the trench; this secondary vortex delays the development of the boundary layer of the turbulent flow and reduces surface drag.
The protrusion height theory was proposed by Bechert et al. [102] of the DRL center in Germany. In this theory, the protrusion of the groove inhibits the occurrence of cross flow caused by the instantaneous turbulent motion near the wall, thereby weakening the turbulent kinetic energy of the boundary layer and reducing flow resistance.
The theory of micro-air bearing was proposed by Pan [98], whose research found that the air vortex formed in the groove is equivalent to the air bearing; the latter transforms the sliding friction between air and moving objects into rolling friction, thereby reducing flow resistance.
The drag-reduction mechanism of a shark’s surface groove is not determined by a single theory but by the above three mechanisms.
4.2 Simulation and Experimental Study of Bionic Microstructure
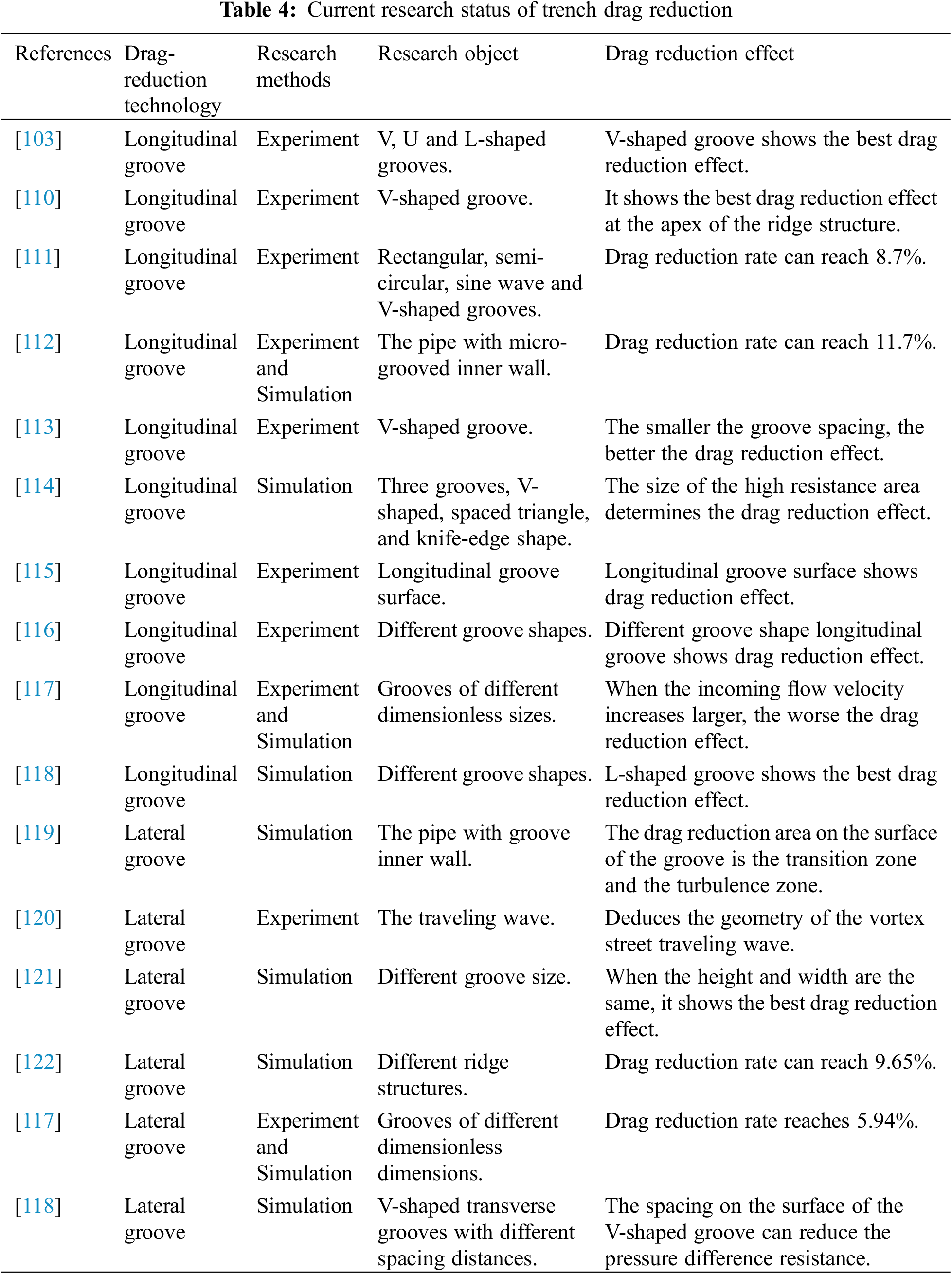
The first researchers to explore the drag-reduction principle of the two-dimensional grooved plate were Walsh et al. [103]. Their results showed that the symmetrical V-rib groove demonstrates the greatest drag-reduction performance among V-, U-, and L-shaped microgrooves. The drag-reduction effect of the grooved plate is better than that of the sleek plate when the dimensionless height of the groove is less than 25 and the dimensionless spacing is less than 30.
With the gradual progression of science and technology, Shi et al. [104] conducted similar research. They found that V-grooves with dimensionless height and dimensionless spacing of 15–18 achieved a good resistance reduction of up to 10%. Next, Gong et al. [105] used a hot-wire anemometer to compare the drag-reduction effect of a grooved surface under different Reynolds numbers. The results showed that when the dimensionless parameters were 11.91, 17.67, and 23.22 and the Reynolds numbers were 118,000, 263,000, and 368,000, the drag-reduction rates of the groove were 7.43%, 6.2%, and 0%, respectively.
As computer technology gradually advanced, many researchers conducted simulations into groove drag-reduction from the perspective of numerical simulations to compensate for the limitations of theoretical research and the harsh requirements of experimental conditions. For instance, Yang et al. [106] investigated the resistance reduction effect of grooves with various structures and dimensions in different flow fields using FLUENT software. The results revealed that the smaller the groove size, the smaller the depth–width ratio, while the higher the flow rate, the more effective the resistance reduction.
Tong et al. [107] used the CFD technique (using a Reynolds averaged N-S equation and RNG K- ε) to simulate the flow field characteristics of turbulent fluid at different Reynolds numbers on the surface of a two-dimensional triangular groove. The results revealed that the higher the Reynolds number, the better the drag-reduction effect of shark skin film, and its numerical value could reach 15.5%. The simulation results agreed well with the experimental results.
He et al. [108] established a numerical simulation model for a marine riser based on the large eddy simulation method. The results showed that the larger the Reynolds number, the more obvious the drag-reduction effect of the riser.
Finally, Li et al. [109] used the finite-difference method to simulate the turbulent flow in a channel with a symmetrical V-shaped grooved surface. Their simulation outcomes showed a range of heights in the fluid field above the groove; within this height range, the flow field was influenced by different parts of the groove to varying degrees. Outside of this height range, the flow field was influenced by different parts of the grooves, while the fluid field was little affected.
Based on these drag-reduction theories, many researchers investigated non-smooth groove surfaces. Table 4 presents the current status of domestic and overseas research into trench drag-reduction [103,110–122].
This paper summarized the methods and principles of drag-reduction from the two perspectives of changing the flow medium and modifying the flow surface, specifically for viscoelastic nanofluids and non-smooth grooved surfaces. Previous studies showed that viscoelastic nanofluids and non-smooth grooved surfaces can produce a good drag-reduction effect. The stability and production costs of drag-reducing nanofluids were also identified as the main factors hindering the industrialization of nanofluids.
However, the discussion on the drag-reduction mechanism of non-smooth surfaces is incomplete, and the published results of some studies are inconsistent. Therefore, future research must focus on identifying the main parameters affecting the thermal conductivity of nanofluids and the drag-reduction rate of non-smooth surfaces and establishing a reliable mathematical model. The combination of the two means that, in the future, they can be widely applied in the fields of fire protection, transportation, and heat dissipation of electronic components. The heat-transfer effect and drag-reduction mechanism require further discussion to focus more research attention and enable better application.
Funding Statement: This work is financially supported by “National Natural Science Foundation of China” (Grant No. 51606214).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1. Qi, C. (2013). Investigation into natural convection and boiling heat transfer of nanofluids based on LBMb (Ph.D. Thesis). Harbin Institute of Technology, China. [Google Scholar]
2. He, F. Y., Liu, X., Lu, J. S. (2011). Research on heat dissipation of power components. Mechanical Engineering and Automation, 1(1), 205–206+209. [Google Scholar]
3. Choi, S. U. S. (1995). Enhancing thermal conductivity of fluids with nanoparticles, in developments and applications of non-newtonian flows. ASME FED Applied Physics A, 231(66), 99–105. [Google Scholar]
4. Liao, L. (2009). The flow and heat transfer characteristics of drag reduction nanoparticle suspension (Ph.D. Thesis). Shanghai Jiaotong University, China. [Google Scholar]
5. Zhao, M. W., Song, X. G., Li, Y. (2021). Design of comprehensive experiment for changing interface wettability of nanofluid. Research and Exploration in Laboratory, 40(3), 164–166. [Google Scholar]
6. Hosseini, M. S., Khazaei, M., Misaghi, M., Koosheshi, M. H. (2022). Improving the stability of nanofluids via surface-modified titanium dioxide nanoparticles for wettability alteration of oil-wet carbonate reservoirs. Materials Research Express, 9, 035005. DOI 10.1088/2053-1591/ac4fdf. [Google Scholar] [CrossRef]
7. Zhang, T., Zou, Q., Jia, X., Liu, T., Jiang, Z. et al. (2022). Effect of cyclic water injection on the wettability of coal with different SiO2 nanofluid treatment time. Fuel, 312, 122922. DOI 10.1016/j.fuel.2021.122922. [Google Scholar] [CrossRef]
8. Moraveji, A., Toghraie, D. (2017). Computational fluid dynamics simulation of heat transfer and fluid flow characteristics in a vortex tube by considering the various parameters. International Journal of Heat and Mass Transfer, 113, 432–443. DOI 10.1016/j.ijheatmasstransfer.2017.05.095. [Google Scholar] [CrossRef]
9. Samadifar, M., Toghraie, D. (2018). Numerical simulation of heat transfer enhancement in a plate-fin heat exchanger using a new type of vortex generators. Applied Thermal Engineering, 133, 671–681. DOI 10.1016/j.applthermaleng.2018.01.062. [Google Scholar] [CrossRef]
10. He, W., Toghraie, D., Lotfipour, A., Pourfattah, F., Karimipour, A. et al. (2020). Effect of twisted-tape inserts and nanofluid on flow field and heat transfer characteristics in a tube. International Communications in Heat and Mass Transfer, 110, 104440. DOI 10.1016/j.icheatmasstransfer.2019.104440. [Google Scholar] [CrossRef]
11. Rahmati, A. R., Akbari, O. A., Marzban, A., Toghraie, D., Karimi, R. et al. (2018). Simultaneous investigations the effects of non-newtonian nanofluid flow in different volume fractions of solid nanoparticles with slip and no-slip boundary conditions. Thermal Science and Engineering Progress, 5, 263–277. DOI 10.1016/j.tsep.2017.12.006. [Google Scholar] [CrossRef]
12. Saidina, D. S., Abdullah, M. Z., Hussin, M. (2020). Metal oxide nanofluids in electronic cooling: A review. Journal of Materials Science: Materials in Electronics, 31(6), 4381–4398. [Google Scholar]
13. Aglawe, K. R., Yadav, R. K., Thool, S. B. (2021). Preparation, applications and challenges of nanofluids in electronic cooling: A systematic review. Materials Today: Proceedings, 43, 366–372. [Google Scholar]
14. Bahiraei, M., Heshmatian, S. (2018). Electronics cooling with nanofluids: A critical review. Energy Conversion and Management, 172, 438–456. DOI 10.1016/j.enconman.2018.07.047. [Google Scholar] [CrossRef]
15. Islam, R., Shabani, B. (2019). Prediction of electrical conductivity of TiO2 water and ethylene glycol-based nanofluids for cooling application in low temperature PEM fuel cells. Energy Procedia, 160, 550–557. DOI 10.1016/j.egypro.2019.02.205. [Google Scholar] [CrossRef]
16. Sayed, E. T., Abdelkareem, M. A., Mahmoud, M. S., Baroutaji, A., Elsaid, K. et al. (2021). Augmenting performance of fuel cells using nanofluids. Thermal Science and Engineering Progress, 25, 101012. DOI 10.1016/j.tsep.2021.101012. [Google Scholar] [CrossRef]
17. Mukherjee, S., Ebrahim, S., Mishra, P. C., Ali, N., Chaudhuri, P. (2022). A review on pool and flow boiling enhancement using nanofluids: Nuclear reactor application. Processes, 10(1), 177. DOI 10.3390/pr10010177. [Google Scholar] [CrossRef]
18. Waqas, H., Farooq, U., Shah, Z., Kumam, P., Shutaywi, M. (2021). Second-order slip effect on bio-convectional viscoelastic nanofluid flow through a stretching cylinder with swimming microorganisms and melting phenomenon. Scientific Reports, 11(1), 11208. DOI 10.1038/s41598-021-90671-z. [Google Scholar] [CrossRef]
19. Wang, C. Q., Wang, D., Zhan, N. Y. (2016). Summarize about the research on energy saving of small electronic device heat dissipation. Journal of Jilin Institute of Civil Engineering and Architecture, 33(1), 51–54. [Google Scholar]
20. Guye, K., Dong, D., Kim, Y., Lee, H., Dogruoz, B. et al. (2021). Guidelines for designing micropillar structures for enhanced evaporative heat transfer. Journal of Electronic Packaging, 143(4), 041106. DOI 10.1115/1.4052465. [Google Scholar] [CrossRef]
21. Khirid, A. V., Ugle, V., Kengale, D. B., Khatke, N. L., Chavan, N. G. (2021). Performance of double pipe heat exchanger using nanofluids. International Journal of Contemporary Architecture, 8(2), 1570–1575. [Google Scholar]
22. Wan, Y. L. (2017). Study on natural convection and forced convection heat transfer characteristics of TiO2-water nanofluids (Master Thesis). China University of Mining and Technology, China. [Google Scholar]
23. Gulzar, O., Qayoum, A., Gupta, R. (2021). Experimental study on thermal conductivity of mono and hybrid Al2O3-TiO2 nanofluids for concentrating solar collectors. International Journal of Energy Research, 45(3), 4370–4384. DOI 10.1002/er.6105. [Google Scholar] [CrossRef]
24. Das, S. K., Putra, N., Thiesen, P., Roetzel, W. (2003). Temperature dependence of thermal conductivity enhancement of nanofluid. ASME Journal of Heat Transfer, 125(4), 567–574. DOI 10.1115/1.1571080. [Google Scholar] [CrossRef]
25. Kamel, M. S., Al-Oran, O., Lezsovits, F. (2021). Thermal conductivity of Al2O3 and CeO2 nanoparticles and their hybrid based water nanofluids: An experimental study. Periodica Polytechnica Chemical Engineering, 65(1), 50–60. DOI 10.3311/PPch.15382. [Google Scholar] [CrossRef]
26. Kim, G., Baek, S., Choi, W., Lee, A., Lee, S. (2021). Stability, surface tension, and thermal conductivity of Al2O3/water nanofluids according to different types of alcohol and their proportion. Case Studies in Thermal Engineering, 28, 101385. DOI 10.1016/j.csite.2021.101385. [Google Scholar] [CrossRef]
27. Li, C. H., Peterson, G. P. (2006). Experimental investigation of temperature and volume fraction on the effective thermal conductivity of nanoparticle suspensions (nanofluid). Journal of Applied Physics, 99(8), 084314. DOI 10.1063/1.2191571. [Google Scholar] [CrossRef]
28. Goudarzi, K., Jamali, H. (2017). Heat transfer enhancement of Al2O3-EG nanofluid in a car radiator with wire coil inserts. Applied Thermal Engineering, 118, 510–517. DOI 10.1016/j.applthermaleng.2017.03.016. [Google Scholar] [CrossRef]
29. Masuda, E., Terama, E. K. (1993). Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fineparticles (dispersion of A12O3, SiO2, and TiO2 ultra-fine particles). Netsu Bussei, 7, 227–233. DOI 10.2963/jjtp.7.227. [Google Scholar] [CrossRef]
30. Yang, L., Du, K. (2017). A comprehensive review on heat transfer characteristics of TiO2 nanofluids. International Journal of Heat and Mass Transfer, 108, 11–31. DOI 10.1016/j.ijheatmasstransfer.2016.11.086. [Google Scholar] [CrossRef]
31. Ali, H. M., Babar, H., Shah, T. R., Sajid, M. U., Qasim, M. A. et al. (2018). Preparation techniques of TiO2 nanofluids and challenges: A review. Applied Sciences, 8(4), 587. DOI 10.3390/app8040587. [Google Scholar] [CrossRef]
32. Mei, S. Y. (2019). Study on heat transfer enhancement mechanisms of Fe3O4-water nanofluids in tube under magnetic field (Master Thesis). China University of Mining and Technology, China. [Google Scholar]
33. Li, D. D., Yang, Z. Z., Zhang, W. (2017). Study on the influence of alumina-ethylene glycol-water nanofluid on the cooling of HICE. Automobile Applied Technology, 2017(1), 50–52. [Google Scholar]
34. Xuan, Y., Li, Q. (2000). Heat transfer enhancement of nanofluids. International Journal of Heat and Fluid Flow, 21(1), 58–64. DOI 10.1016/S0142-727X(99)00067-3. [Google Scholar] [CrossRef]
35. Kang, H. U., Kim, S. H. (2006). Estimation of thermal conductivity of nanofluid using experimental effective particle volume. Experimental Heat Transfer, 19(3), 181–191. DOI 10.1080/08916150600619281. [Google Scholar] [CrossRef]
36. Arjmandfard, A., Toghraie, D., Mehmandoust, B., Hashemian, M., Karimipour, A. (2020). The study of atomic porosity effect on water/Fe nanofluid flow in a microchannel with a molecular dynamics method. Journal of Molecular Liquids, 317, 114291. DOI 10.1016/j.molliq.2020.114291. [Google Scholar] [CrossRef]
37. Nasrin, R., Rahim, N. A., Fayaz, H., Hasanuzzaman, M. (2018). Water/MWCNT nanofluid based cooling system of PVT: Experimental and numerical research. Renewable Energy, 121, 286–300. DOI 10.1016/j.renene.2018.01.014. [Google Scholar] [CrossRef]
38. Afzal, A., Samee, A. M., Razak, R. A., Ramis, M. K. (2018). Heat transfer characteristics of MWCNT nanofluid in rectangular mini channels. International Journal of Heat and Technology, 36(1), 222–228. DOI 10.18280/ijht. [Google Scholar] [CrossRef]
39. Esfe, M. H., Esfandeh, S., Afrand, M., Rejvani, M., Rostamian, S. H. (2018). Experimental evaluation, new correlation proposing and ANN modeling of thermal properties of EG based hybrid nanofluid containing ZnO-DWCNT nanoparticles for internal combustion engines applications. Applied Thermal Engineering, 133, 452–463. DOI 10.1016/j.applthermaleng.2017.11.131. [Google Scholar] [CrossRef]
40. Hu, Y. W., Li, H., He, Y. R., Liu, Z. Y., Zhao, Y. H. (2017). Effect of nanoparticle size and concentration on boiling performance of SiO2 nanofluid. International Journal of Heat and Mass Transfer, 107, 820–828. DOI 10.1016/j.ijheatmasstransfer.2016.11.090. [Google Scholar] [CrossRef]
41. Timofeeva, E. V., Routbort, J. L., Singh, D. (2009). Particle shape effects on thermophysical properties of alumina nanofluids. Journal of Applied Physics, 106(1), 014304. DOI 10.1063/1.3155999. [Google Scholar] [CrossRef]
42. Al-Waeli, A. H., Sopian, K., Chaichan, M. T., Kazem, H. A., Hasan, H. A. et al. (2017). An experimental investigation of SiC nanofluid as a base-fluid for a photovoltaic thermal PV/T system. Energy Conversion and Management, 142, 547–558. DOI 10.1016/j.enconman.2017.03.076. [Google Scholar] [CrossRef]
43. Qi, C., Wang, G. Q., Ma, Y. F. (2017). Experimental research on stability and natural convection of TiO2-water nanofluid in enclosures with different inclination angles. Nanoscale Research Letters, 12(1), 396. DOI 10.1186/s11671-017-2170-1. [Google Scholar] [CrossRef]
44. Lu, W. Q., Fan, Q. M. (2006). Study for the particle’s scale effect on some thermophysical properties of nanofluids by a simplified molecular dynamics method. Engineering Analysis with Boundary Elements, 32(4), 282–289. DOI 10.1016/j.enganabound.2007.10.006. [Google Scholar] [CrossRef]
45. Mir-Shahabeddin, I., Saeed, Z. H. (2019). Influence of Al2O3 nanoparticles on the stability and viscosity of nanofluids. Journal of Thermal Analysis and Calorimetry, 138(1), 623–631. DOI 10.1007/s10973-019-08228-2. [Google Scholar] [CrossRef]
46. Heris, S. Z., Etemad, S. G., Esfahany, M. N. (2006). Experimental investigation of oxide nanofluids laminar flow convective heat transfer. International Communications in Heat and Mass Transfer, 33(4), 529–535. DOI 10.1016/j.icheatmasstransfer.2006.01.005. [Google Scholar] [CrossRef]
47. Zhong, G. J., Zhai, Y. L., Bao, G. R. (2020). Analysis of factors influencing stability and viscosity of nanofluid. Journal of Materials Science and Engineering, 38(1), 74–80+87. [Google Scholar]
48. Anish, M., Jayaprabakar, J., Nivin, J., Prabhu, A., Krishna, K. R. B. et al. (2020). Measurement of temperature-dependent thermal conductivity, viscosity and density of ZnO-Theminol 55 nanofluids. Materials Today: Proceedings, 21, 148–151. [Google Scholar]
49. Li, J., Li, Z., Wang, B. (2002). Experimental viscosity measurements for copper oxide nanoparticle suspensions. Tsinghua Science and Technology, 7(2), 198–201. [Google Scholar]
50. Zhao, N. B., Zheng, H. T., Li, S. Y. (2018). Experimental study on thermal conductivity and viscosity of Al2O3-H2O nanofluids. Journal of Harbin Engineering University, 39(1), 60–66. [Google Scholar]
51. Sun, B., Chen, C., Yang, D. (2016). Heat transfer and flow characteristics of nanofluids flowing through semicircular microchannels. Journal of Engineering for Thermal Energy and Power, 31(6), 27–34. [Google Scholar]
52. Sun, B., Yan, D. F., Yang, D. (2016). Heat transfer and flow characteristics of Cu-water nanofluids in twisted-tape inserts in tubes. Journal of Northeast Dianli University, 36(1), 74–81. [Google Scholar]
53. Sun, B., Zuo, R. L., Yang, D. (2016). Experimental study on heat transfer characteristics of nanofluids in plate heat exchangers. Chemical Engineering & Machinery, 43(2), 148–153. [Google Scholar]
54. Zhong, X., Yu, X. L., Wu, J. (2009). Fluid flow and heat transfer characteristics of alumina organic nanofluid. CIESC Journal, 60(1), 35–41. [Google Scholar]
55. Mansoury, D., Doshmanziari, F. I., Kiani, A., Chamkha, A. J., Sharifpur, M. (2019). Heat transfer and flow characteristics of Al2O3/water nanofluid in various heat exchangers: Experiments on counter flow. Heat Transfer Engineering, 41(3), 220–234. DOI 10.1080/01457632.2018.1528051. [Google Scholar] [CrossRef]
56. Yang, L. Y. (2019). Study on heat transfer and flow characteristics of TiO2-H2O nanofluids in elliptical tubes (Master Thesis). China University of Mining and Technology, China. [Google Scholar]
57. Zhai, X. F. (2019). Study on heat transfer and flow characteristics of TiO2-H2O nanofluids flowing through spiral tubes (Master Thesis). China University of Mining and Technology, China. [Google Scholar]
58. Xu, G. X., Deng, X. H., Xu, X. Y., Wang, Z. J. (2005). Analysis on heat transfer enhancement performance evaluation. Journal of Huaihai Institute of Technology (Natural Science Edition), 2005(2), 42–44. [Google Scholar]
59. Ding, M., Liu, C., Rao, Z. (2019). Experimental investigation on heat transfer characteristic of TiO2-H2O nanofluid in microchannel for thermal energy storage. Applied Thermal Engineering, 160, 114024. DOI 10.1016/j.applthermaleng.2019.114024. [Google Scholar] [CrossRef]
60. Wang, S. X., Lin, Z. N. (2019). Numerical simulation of flow and heat transfer of water-based nanofluids. Energy Engineering, 2019(6), 79–84. [Google Scholar]
61. Barnoon, P., Toghraie, D., Eslami, F., Mehmandoust, B. (2019). Entropy generation analysis of different nanofluid flows in the space between two concentric horizontal pipes in the presence of magnetic field: Single-phase and two-phase approaches. Computers & Mathematics with Applications, 77(3), 662–692. DOI 10.1016/j.camwa.2018.10.005. [Google Scholar] [CrossRef]
62. Sheikholeslami, M., Seyednezhad, M. (2018). Simulation of nanofluid flow and natural convection in a porous media under the influence of electric field using CVFEM. International Journal of Heat and Mass Transfer, 120, 772–781. DOI 10.1016/j.ijheatmasstransfer.2017.12.087. [Google Scholar] [CrossRef]
63. Sheikholeslami, M., Shehzad, S. (2017). Magnetohydrodynamic nanofluid convection in a porous enclosure considering heat flux boundary condition. International Journal of Heat and Mass Transfer, 106, 1261–1269. DOI 10.1016/j.ijheatmasstransfer.2016.10.107. [Google Scholar] [CrossRef]
64. Qi, C., He, Y. R., Yan, S., Tian, F. L., Hu, Y. W. (2013). Numerical simulation of natural convection in a square enclosure filled with nanofluid using the two-phase lattice boltzmann method. Nanoscale Research Letters, 8(1), 56. DOI 10.1186/1556-276X-8-56. [Google Scholar] [CrossRef]
65. Qi, C., He, Y. R., Hu, Y. W., Yang, J. C., Li, F. C. et al. (2011). Natural convection of Cu-gallium nanofluid in enclosures. ASME Journal of Heat Transfer, 133(12), 973–979. DOI 10.1115/1.4004431. [Google Scholar] [CrossRef]
66. Qi, C., Wang, G., Yang, L. Y., Wan, Y. L., Rao, Z. H. (2017). Two-phase lattice boltzmann simulation of the effects of base fluid and nanoparticle size on natural convection heat transfer of nanofluid. International Journal of Heat and Mass Transfer, 105, 664–672. DOI 10.1016/j.ijheatmasstransfer.2016.10.043. [Google Scholar] [CrossRef]
67. Qi, C., Cui, X., Liu, Y. B., Yang, Z. B., Huang, C. (2015). Natural convection heat transfer of liquid metal gallium nanofluids in a rectangular enclosure. Heat Transfer-Asian Research, 46(1), 1–17. DOI 10.1002/htj.21190. [Google Scholar] [CrossRef]
68. Qi, C., Hu, Y. W., Yan, S. N. (2014). Two phase lattice boltzmann simulation of natural convection in a rectangular enclosure filled with nanofluid. Journal of Engineering Thermophysics, 2014(2), 282–286. [Google Scholar]
69. Pang, D. S., Gu, C. Y., Di, Q. F. (2016). Research of rheology of friction-reducing nano silicon dioxide fluid. Journal of Xi’an Shiyou University (Natural Science Edition), 31(5), 78–83. [Google Scholar]
70. Zhang, Z. M. (2016). Research on heat transfer and flow resistance characteristics of drag reduction nanofluids in tubes (Master Thesis). Northeast Electric Power University, China. [Google Scholar]
71. Sun, B., Zhang, Z. M., Yang, D. (2015). Heat transfer and flow resistance characteristics with drag reducing nanofluids in circular tube. CIESC Journal, 66(11), 4401–4411. [Google Scholar]
72. Yang, J. C. (2013). Study on the turbulent flow and heat transfer characteristics of viscoelastic fluid based nanofluid (Ph.D. Thesis). Harbin Institute of Technology, China. [Google Scholar]
73. Wei, J. J., Kawaguchi, Y., Li, F. C., Yu, B., Zakin, J. L. et al. (2009). Drag-reducing and heat transfer characteristics of a novel zwitterionic surfactant solution. International Journal of Heat and Mass Transfer, 52(15), 3547–3554. DOI 10.1016/j.ijheatmasstransfer.2009.03.008. [Google Scholar] [CrossRef]
74. Eid, M. R., Mabood, F. (2021). Thermal analysis of higher-order chemical reactive viscoelastic nanofluids flow in porous media via stretching surface. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 235(22), 6099–6110. [Google Scholar]
75. Micha, D., Andrzej, G., Grzegorz, D., Marcin, L. (2013). Influence of nonionic surfactant addition on drag reduction of water based nanofluid in a small diameter pipe. Chinese Journal of Chemical Engineering, 21(1), 104–108. DOI 10.1016/S1004-9541(13)60447-4. [Google Scholar] [CrossRef]
76. Song, B., Liao, L., Liu, Z. H. (2010). Flow drag and heat transfer performances of drag-reducing fluid with carbon nanotubes added. Journal of Shanghai Jiaotong University, 44(10), 1332–1336+1341. [Google Scholar]
77. Adam, S., Ilker, S., Bayer, E. L. (2014). Pipe flow drag reduction effects from carbon nanotube additives. Carbon, 7, 1183–1186. [Google Scholar]
78. Li, D. Y., Li, F. C., Yang, J. C. (2013). Direct numerical simulation of turbulent convective heat transfer in viscoelastic nanofluids. Journal of Engineering Thermophysics, 34(5), 961–964. [Google Scholar]
79. Li, D. Y. (2012). Direct numerical simulation on turbulent convective heat transfer of viscoelastic-fluid-based nanofluids (M.S. Thesis). Harbin Institute of Technology. [Google Scholar]
80. Zou, H., Wang, Q. K., Xue, Z. Z. (2021). Numerical research on secondary development of viscoelastic fluid based on UDF. Light Industry Machinery, 39(4), 14–19. [Google Scholar]
81. Yang, J. C., Li, F. C., Cai, W. H. (2015). Direct numerical simulation of viscoelastic-fluid-based nanofluid turbulent channel flow with heat transfer. Chinese Physics B, 24(8), 404–420. DOI 10.1088/1674-1056/24/8/084401. [Google Scholar] [CrossRef]
82. Yang, J. C., Li, F. C., Zhou, W. W., Xu, H. P. (2014). Experimental investigation on flow and heat transfer of viscoelastic fluid based Cu nanofluids. Journal of Engineering Thermophysics, 35(2), 366–370. [Google Scholar]
83. Yang, J. C., Li, F. C., He, Y. R., Huang, Y. M., Jiang, B. C. (2013). Experimental study on the characteristics of heat transfer and flow resistance in turbulent pipe flows of viscoelastic-fluid-based Cu nanofluid. International Journal of Heat and Mass Transfer, 62, 303–313. DOI 10.1016/j.ijheatmasstransfer.2013.02.074. [Google Scholar] [CrossRef]
84. Ma, M. Y. (2021). Effect of surfactant on the rheological behavior and thermophysical properties of hybrid nanofluids. Powder Technology, 379, 373–383. DOI 10.1016/j.powtec.2020.10.089. [Google Scholar] [CrossRef]
85. Pouranfard, A. R., Mowla, D., Esmaeilzadeh, F. (2015). An experimental study of drag reduction by nanofluids in slug two-phase flow of air and water through horizontal pipes. Chinese Journal of Chemical Engineering, 23, 471–475. DOI 10.1016/j.cjche.2014.11.023. [Google Scholar] [CrossRef]
86. Xia, G. D., Jiang, H. M., Liu, R. (2014). Effects of surfactant on the stability and thermal conductivity of Al2O3/de-ionized water nanofluids. International Journal of Thermal Sciences, 84, 118–124. DOI 10.1016/j.ijthermalsci.2014.05.004. [Google Scholar] [CrossRef]
87. Wang, Z., Li, T., Li, M. (2017). Review of mechanical research and aerodynamic drag reduction of bionic surface micro-structures. Journal of Hebei University of Science and Technology, 38(4), 325–334. [Google Scholar]
88. Liu, Z. Y., Hu, H. B., Song, B. W. (2009). Numerical simulation research about riblet surface with different spacing. Journal of System Simulation, 21(19), 6025–6028. [Google Scholar]
89. Wu, Z. R., He, X. F., Rong, R. (2014). Study on drag-reduction mechanism of riblet surface on aerofoil blade of centrifugal fan. Journal of System Simulation, 26(6), 1355–1361. [Google Scholar]
90. Li, G. J., Pu, X., Lei, C. Y., Su, R. H. (2008). Brief introduction to the research on biomimetic drag-reduction materials with non-smooth surface. Materials Research and Application, 2(4), 455–459. [Google Scholar]
91. Zhang, K., Ma, C., Zhang, J., Zhang, B., Zhao, B. (2022). Drag reduction characteristics of bionic structure composed of grooves and mucous membrane acting on turbulent boundary layer. Journal of Applied Fluid Mechanics, 15(1), 283–292. [Google Scholar]
92. Wu, H. W., Chen, T. H., Kelana, N. P., Huang, D. A. (2020). Influence of dimple height on turbulent heat transfer of fin array with alternate convex/concave dimples. Inventions, 5(3), 33. DOI 10.3390/inventions5030033. [Google Scholar] [CrossRef]
93. Wang, C. J., Cheng, L. D., Xue, S. X. (2019). Manufacturing technologies of bionic micro-structures for drag reduction: A review. Journal of Netshape Forming Engineering, 11(3), 88–98. [Google Scholar]
94. Zhu, Y. D., Meng, Q. W. (1983). A study on patterns of placoid scales of sharks. Journal of Fisheries of China, 7(3), 251–265. [Google Scholar]
95. Martin, S., Bhushan, B. (2014). Fluid flow analysis of a shark-inspired microstructure. Journal of Fluid Mechanics, 756, 5–29. DOI 10.1017/jfm.2014.447. [Google Scholar] [CrossRef]
96. Bechert, D. W., Bruse, M., Hage, W. (2000). Experiments with three-dimensional riblets as an idealized model of shark skin. Experiments in Fluids, 28(5), 403–412. DOI 10.1007/s003480050400. [Google Scholar] [CrossRef]
97. Pan, G., Guo, X. J., Hu, H. B. (2006). Numerical simulation of semicircular traveling wave surface and study on its drag-reduction mechanism. Journal of System Simulation, 18(11), 3073–3074 + 3094. [Google Scholar]
98. Pan, J. Z. (1996). The experimental approach to drag reduction of the transverse ribbons on turbulent flow. Acta Aerodynamica Sinica, 14(3), 304–310. [Google Scholar]
99. Bacher, E. V., Smith, C. R. (1985). A combined visualization-anemometry study of the turbulent drag reducing mechanisms of triangular micro-groove surface modifications. AIAA Shear Flow Control Conference, 2, 53–86. DOI 10.2514/MSFC85. [Google Scholar] [CrossRef]
100. Bacher, E. V., Smith, C. R. (1986). Turbulent boundary-layer modification by surface ribs. AIAA Journal, 24(8), 1382–1385. DOI 10.2514/3.48695. [Google Scholar] [CrossRef]
101. Bacher, E. V. (1984). An experimental study of the modifying effects of a streamwise grooved surface of triangular cross-section on the flow structure and statistical characteristics of turbulent boundary layers (M.S. Thesis). Lehigh University, USA. [Google Scholar]
102. Bechert, D. W., Bartenwerfer, M. (1989). The viscous flow on surfaces with longitudinal ribs. Journal of Fluid Mechanics, 206, 105–129. DOI 10.1017/S0022112089002247. [Google Scholar] [CrossRef]
103. Walsh, M. J. (1983). Riblets as a viscous drag reduction technique. AIAA Journal, 21(4), 485–486. DOI 10.2514/3.60126. [Google Scholar] [CrossRef]
104. Shi, X. H., Song, B. W., Bao, Y. P. (1996). The experimental research on turbulent drag reduction with riblets. Journal of Hydrodynamics, 11(5), 546–553. [Google Scholar]
105. Gong, W. Q., Li, X. H., Huang, S. J. (2002). Experiment study on the mechanism of riblets drag reduction. Journal of Engineering Thermophysics, 23(5), 579–582. [Google Scholar]
106. Yang, X. F. (2018). Study on large area molding technology and drag reduction performance of bionic shark skin (Master Thesis). Dalian University of Technology, China. [Google Scholar]
107. Tong, G. (2012). Numerical simulation and experimental study on the mechanism of drag reduction of the shark scales structure. Proceeding of the 11th National Congress on Hydrodynamics & 24th National Conference on Hydrodynamics and Commemoration of the 110th Anniversary of Zhou Pei-Yuan’s Birth, vol. 8, pp. 258–265. Wuxi, China. [Google Scholar]
108. He, X. (2020). Flow around analysis of riser based on large eddy numerical simulation. Chinese Journal of Hydrodynamics, 35(1), 106–112. [Google Scholar]
109. Li, C. Q., Li, Y., Zhang, C. X., Tang, S. (2020). Direct numerical simulation of flow field over streamwise micro riblets. Acta Aeronautica et Astronautica Sinica, 41(11), 152–163. [Google Scholar]
110. Choi, H., Moin, P., Kim, J. (1991). On the effect of riblets in fully developed laminar channel flows. Physics of Fluids A: Fluid Dynamics, 3(8), 1892–1896. DOI 10.1063/1.857918. [Google Scholar] [CrossRef]
111. Bechert, D. W., Bruse, M., Hage, W. (1997). Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. Journal of Fluid Mechanics, 338, 59–87. DOI 10.1017/S0022112096004673. [Google Scholar] [CrossRef]
112. Sasamori, M., Mamori, H., Iwamoto, K. A. (2014). Experimental study on drag-reduction effect due to sinusoidal riblets in turbulent channel flow. Experiments in Fluids, 55(10), 1828. DOI 10.1007/s00348-014-1828-z. [Google Scholar] [CrossRef]
113. Djenidi, L., Antonia, R. A. (1996). Laser Doppler anemometer measurements of turbulent boundary layer over a riblet surface. AIAA Journal, 34(5), 1007–1012. DOI 10.2514/3.13180. [Google Scholar] [CrossRef]
114. Liu, D. J., Yu, Y., Wang, G. F. (2016). The characteristic and mechanism of three different shaped of riblets on drag reduction. Journal of Engineering Thermophysics, 37(7), 1411–1415. [Google Scholar]
115. Wang, J. J., Chen, G. (2001). Experimental studies on the near wall turbulent coherent structures over riblets surface. Acta Aeronautica Et Astronautica Sinica, 22(5), 400–405. [Google Scholar]
116. Cong, Q., Feng, Y., Ren, L. Q. (2006). Affecting of riblets shape of nonsmooth surface on drag reduction. Journal of Hydrodynamics (A), 21(2), 232–238. [Google Scholar]
117. You, L. Q. (2016). Study on the relationship between structure characteristics and drag reduction performance of V shaped groove surface (Master Thesis). Dalian University of Technology, China. [Google Scholar]
118. Dou, R. H. (2020). Numerical study of bionic non-smooth surface for drag reduction (Master Thesis). Qingdao University of Science and Technology, China. [Google Scholar]
119. Mark, W. Douglas, J. G. (2009). Molecular mechanisms of insulin resistance in chronic hepatitis C. World Journal of Gastroenterology, 15(35), 4356–4364. DOI 10.3748/wjg.15.4356. [Google Scholar] [CrossRef]
120. Zhang, X. C. (2001). Traveling wave pasted layer of high-speed underwater vehicles for reducing noise and drag. Journal of Ship Mechanics, 5(2), 1–4. [Google Scholar]
121. Wan, J., Ma, L. (2017). Numerical investigation and experimental test on aerodynamic noises of the bionic rear view mirror in vehicles. Journal of Vibroengineering, 19(6), 4799–4815. DOI 10.21595/jve.2017.18750. [Google Scholar] [CrossRef]
122. Zhou, J., Ren, L. Q. (2006). The relationship between the body surface structure of cybister bengalensis and its unction of reducing resistance. Journal of Northeast Normal University (Natural Science Edition), 38(2), 109–113. [Google Scholar]
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |