Fluid Dynamics & Materials Processing

DOI: 10.32604/fdmp.2022.020509

REVIEW

Hydromagnetic Nanofluid Film Flow over a Stretching Sheet with Prescribed Heat Flux and Viscous Dissipation

Nourhan I. Ghoneim1,* and Ahmed M. Megahed2

1International Maritime College Oman (IMCO), Suhar, 322, Sultanate of Oman
2Department of Mathematics, Faculty of Science, Benha University, Benha, 13518, Egypt
*Corresponding Author: Nourhan I. Ghoneim. Email: norhan@imco.edu.om
Received: 27 November 2021; Accepted: 07 February 2022

1  Introduction

Nanofluids are novel fluids that have distinct thermal properties due to the presence of suspensions of nanoparticles that spread throughout the whole base fluid. The fundamental cause of increasing fluid thermophysical properties such as heat conduction, heat convection, fluid thermal conductivity, and fluid viscosity is the permanent presence of nanoparticles (Fig. 1) in the base fluid. Nanofluid is more efficient in a wide range of key industrial and engineering problems, including heat exchangers, solar panels, electronic equipment cooling, microchannels, and chemical processes, thanks to this artificial enhancement in fluid properties [1–3]. Fluid flow and heat transfer together with magneto-hydrodynamic and thermal radiation phenomena are encountered widely in several studies due to their important applications [4–13].

Figure 1: Spreading nanoparticles in base fluid

A body of important theoretical research regarding nanofluid flow, which is very beneficial, especially in the processes of heat transfer enhancement, has been obtainable in the literature [14–19] since the work of Vasu et al. [20] which discussed analytically the mechanism of convective heat transfer for the nanofluid that is saturated with nanostructured particles.

Many major engineering and technological fields tackle fluid flow and heat mass transfer mechanisms, particularly those that occur through a region of thin liquid layer over an unstable stretched sheet [21]. Wire and fibre coating, heat exchanger design, extrusion procedures, chemical processing equipment, and food processing are all examples of key applications [22,23]. The degree of quality of the finished product, on the other hand, is mostly determined by the flow and heat transmission mechanisms. Therefore, the precise analysis of thermal energy transitions within a liquid thin film is very important for gaining some essential understanding of such significant processes [24–26]. Recently, Noor et al. [27] have extended the problem of Noor et al. [28] by studying the thermocapillarity and magnetic field effects on the flow and heat transfer in a thin liquid film due to an unsteady stretching sheet. Further contributions have been made since that time by many researchers [29–31]. They have discussed the various physical and thermal phenomena to obtain the accurate solutions valid for different physical assumptions. They also pointed out that the ability of the fluid on the drag based both on the physical parameters and the geometry of the proposed system. Several important researches regarding the topic of nanoliquids flow and heat mass transfer have been reported [32–38].

The major goal of this work is to use the shooting approach on Newtonian fluids to examine thin liquid film flow and heat mass transfer processes that are exposed to the magnetic field, viscous dissipation phenomenon, thermal radiation, and variable heat flux.

2  Formulation of the Problem

The effect of thermal radiation, variable heat flux, and the phenomenon of viscous dissipation on the liquid thin film flow of MHD nanofluid due to an unsteady stretching sheet is investigated in this study. As previously stated by Liu et al. [30], we assume that the thermal conductivity of nanofluids varies linearly with temperature. In this work, we assume an unsteady flow of an incompressible Newtonian fluid within a thin liquid film having a uniform thickness h(t) on a resilient sheet that emerges from a very narrow slit at the origin, as shown below in Fig. 2.

Figure 2: Schematic configuration of the physical problem

Firstly, we must refer that an exhaustive understanding and explanation about the variable heat flux qs(x, t) is introduced previously by Liu et al. [39] according to the following relation:

qs(x,t)=−κ(∂T∂y)=dx2Tr(1−at)−52, (1)

where κ is the fluid thermal conductivity, d is a constant, a is a dimension constant which reciprocal time and Tr is the reference temperature. The nature of the nanofluid which characterized by the presence of the suspended particles results in the Brownian motion for these hanging particles with a coefficient called Brownian diffusion DB and a thermophoretic diffusion coefficient DT. Further, the nanofluid flow characteristics are affected by the impacts of the magnetic field in the absence of the Hall current effect, which is supposed to act only in the positive y direction as follows [40] :

B→(t)=B0(1−at)−12j→, (2)

where B0 is the constant magnetic field strength. Additionally, the nanofluid is assumed to be controlled by the continuously sheet velocity which takes the form [40]:

us(x,t)=bx1−at, (3)

where b is a constant representing the rate of stretching for the elastic sheet. With the usual Rosseland diffusion approximations and Boussinesq assumptions and following Liu et al. [40], the fundamental equations for this physical problem are:

∂u∂x+∂v∂y=0, (4)

∂u∂t+u∂u∂x+v∂u∂y=ν∂2u∂y2−σ|B→|2ρfu, (5)

∂T∂t+u∂T∂x+v∂T∂y=1ρfcp∂∂y(κ∂T∂y)+νcp(∂u∂y)2+τ(DB(∂C∂y∂T∂y)+(DTT0)(∂T∂y)2)−1ρfcp∂qr∂y, (6)

∂C∂t+u∂C∂x+v∂C∂y=DB∂2C∂y2+(DTT0)∂2T∂y2. (7)

In these previous equations, u and v are the components of the velocity of the nanofluid. Also, ρf, T, κ, ν, τ and T0 are the nanofluid density, the nanofluid temperature, the nanofluid thermal conductivity, the kinematic viscosity, the ratio of the micro-particles heat capacity to the fundamental fluid heat capacity and a slot constant temperature, respectively. Further, C is the nanoparticle volume fraction, cp is the specific heat at constant pressure and σ is the electric conductivity of the nanofluid. In order to avoid making extensive calculations especially with the presence of the thermal radiation phenomenon, it is affirmed here to focus attention on the previously simplifications for the radiative heat flux qr which presented by Raptis [41,42] in which he presented a linear simplification for qr. Referring to the physical problem of the proposed nanofluid flow, the assumptions are fulfilled with the following conditions:

u=us(x,t), v=0, −κ∂T∂y=qs(x,t), Cw=C0−Cr(bx22ν)(1−at)−32,  at  y=0, (8)

∂u∂y=0, ∂T∂y=0, ∂C∂y=0, v=dhdt  at  y=h, (9)

where Tr is the constant reference temperature, Cw is the sheet nanoparticle volume fraction, C0 is the constant concentration at the slot and Cr is the constant reference nanoparticle volume fraction.

Substituting the following non-dimensional transformations [40]:

η=bν(1−at)−12y, ψ=νb(1−at)−12xf(η), (10)

θ(η)=T−T0Trdx2(1−at)2vbκ0, C=C0−Cr(bx2(1−at)−32ν)ϕ(η), (11)

into the mathematical governing Eqs. (4)–(7) and the pertinent boundary conditions (8) and (9), we have

f′′′+ff′′−f′2−S(η2f′′+f′)−Mf′=0, (12)

1Pr((1+R+εθ)θ′′+εθ′2)+fθ′−2f′θ−S(2θ+η2θ′)+Ecf′′2+Ntθ′2−Nbθ′ϕ′=0, (13)

ϕ′′+Sc(fϕ′−2f′ϕ−S2(3ϕ+ηϕ′))+NtNbθ′′=0, (14)

f(0)=0, f′(0)=1, θ′(0)=−11+R+εθ(0), ϕ(0)=1, (15)

f(γ)=γ2S, f′′(γ)=0, θ′(γ)=0, ϕ′(γ)=0, (16)

where the governing parameters appeared above can be defined as S=ab,M=σB02ρfb,R=16σ∗T033k∗κ0 , Pr=να,Nt=dx2τDTTrκ0νb(1−at)2T0,Nb=τDB(Cw−C0)ν,Ec=κ0b52dcpTrν and Sc=νDB , which named respectively, the unsteadiness parameter, the magnetic number, the radiation parameter, the Prandtl number, the thermophoresis parameter, the Brownian motion parameter, the Eckert number and the Schmidt number. Furthermore, the parameter γ which represents the dimensionless film thickness can be calculated with the aid of Eq. (10) as follows:

γ=(bν(1−at))12h(t).  (17)

Clearly that γ is an unknown constant which must be obtained for the group of governing Eqs. (12)–(16) as a whole.

Three important physical quantities in engineering and practical applications which they must be mentioned, respectively, the local skin-friction coefficient Cfx, the local Nusselt number Nux and the wall concentration gradient Shx, and they are given as follows:

CfxRe12=−f′′(0), NuxRe−12=1θ(0), ShxRe−12=−ϕ′(0), (18)

where Re=usxν is the local Reynolds number.

3  Results and Discussion

The following tabular data (Table 1) comprises a comparison between our results and those previously published by Liu et al. [40], in order to assess the accuracy of our numerical results. This comparison is made between both the film thickness γ and the skin friction coefficient values − f′′(0) for different values of the magnetic parameter M with S = 0.8. The present findings, then, are clearly in great accord with those previously obtained by Liu et al. [40] which confirm the thoroughness of the numerical method used.

Variations in velocity, temperature, and concentration are depicted in figures for a variety of governing parameter values. It can be noted from Fig. 3, that, for an instant shown, a decrease in unsteadiness parameter S results in thickening of the thin film length, whereas the opposite trend is observed for both the free surface velocity f′(γ) and the velocity distribution f′(η) through the film region.

Figure 3: f′(η) for assorted values of S

In Fig. 4, the effect of the same parameter S on temperature profiles is illustrated. The diminution of the sheet temperature θ(0) as well as the temperature profiles beside the sheet for rising S is manifest. While the analysis refers to a opposite trend for the free surface temperature θ(γ).

Figure 4: θ(η) for assorted values of S

Fig. 5 shows the wall concentration variation along the thin film region with the S as an unsteadiness parameter. It is easily clear that S enhances both the concentration distribution ϕ(η) and the free surface concentration ϕ(γ) through the thin film layer.

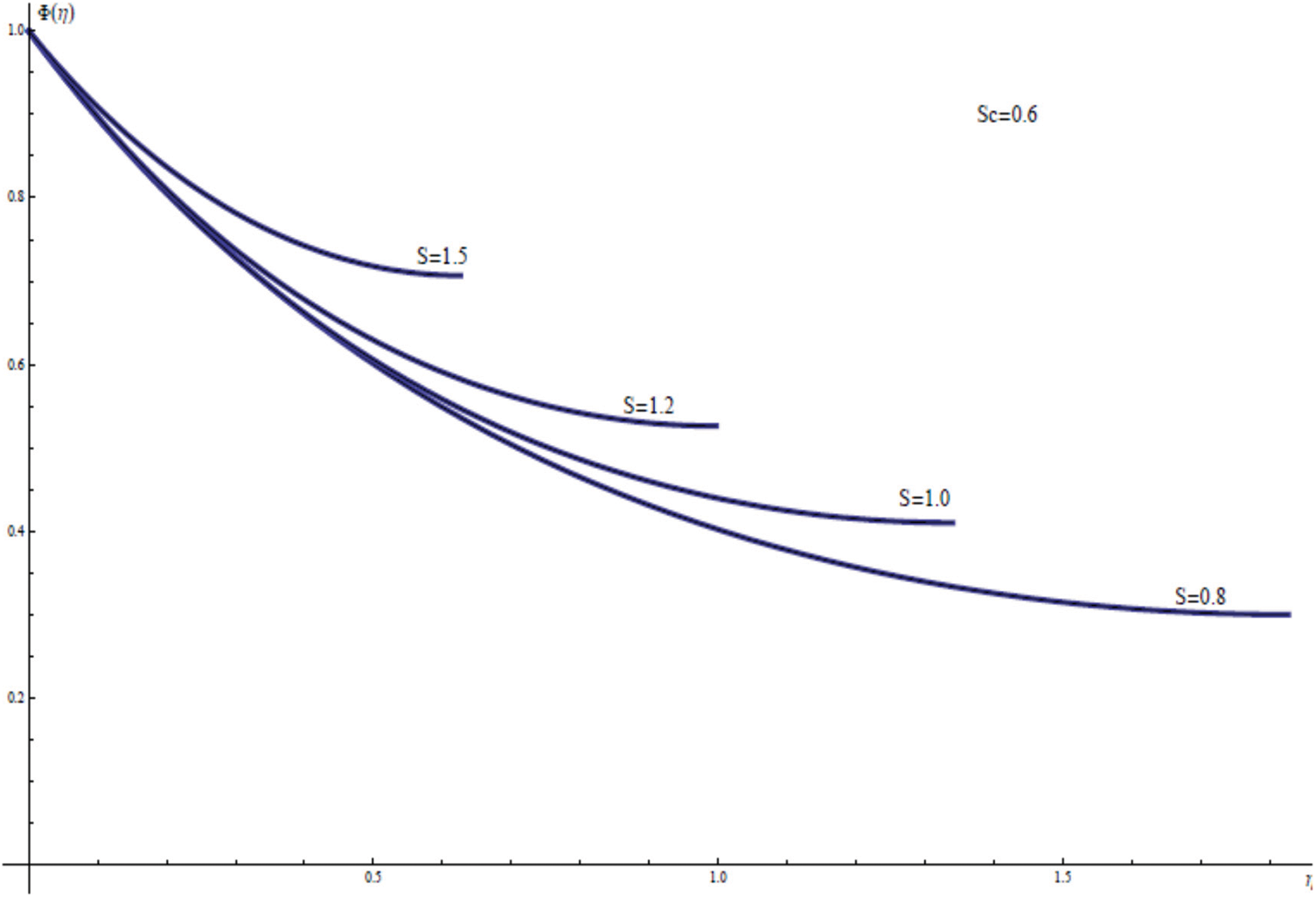
Figure 5: ϕ(η) for assorted values of S

Fig. 6 shows the effect of the magnetic field on the flow characteristics, obtained by keeping all parameters constant and allowing M varying. It would appear, therefore, that the maximum free surface velocity f′(γ), maximum film thickness, and the highly velocity distributions f′(η) within the film region occurs for the absence of magnetic field M = 0.

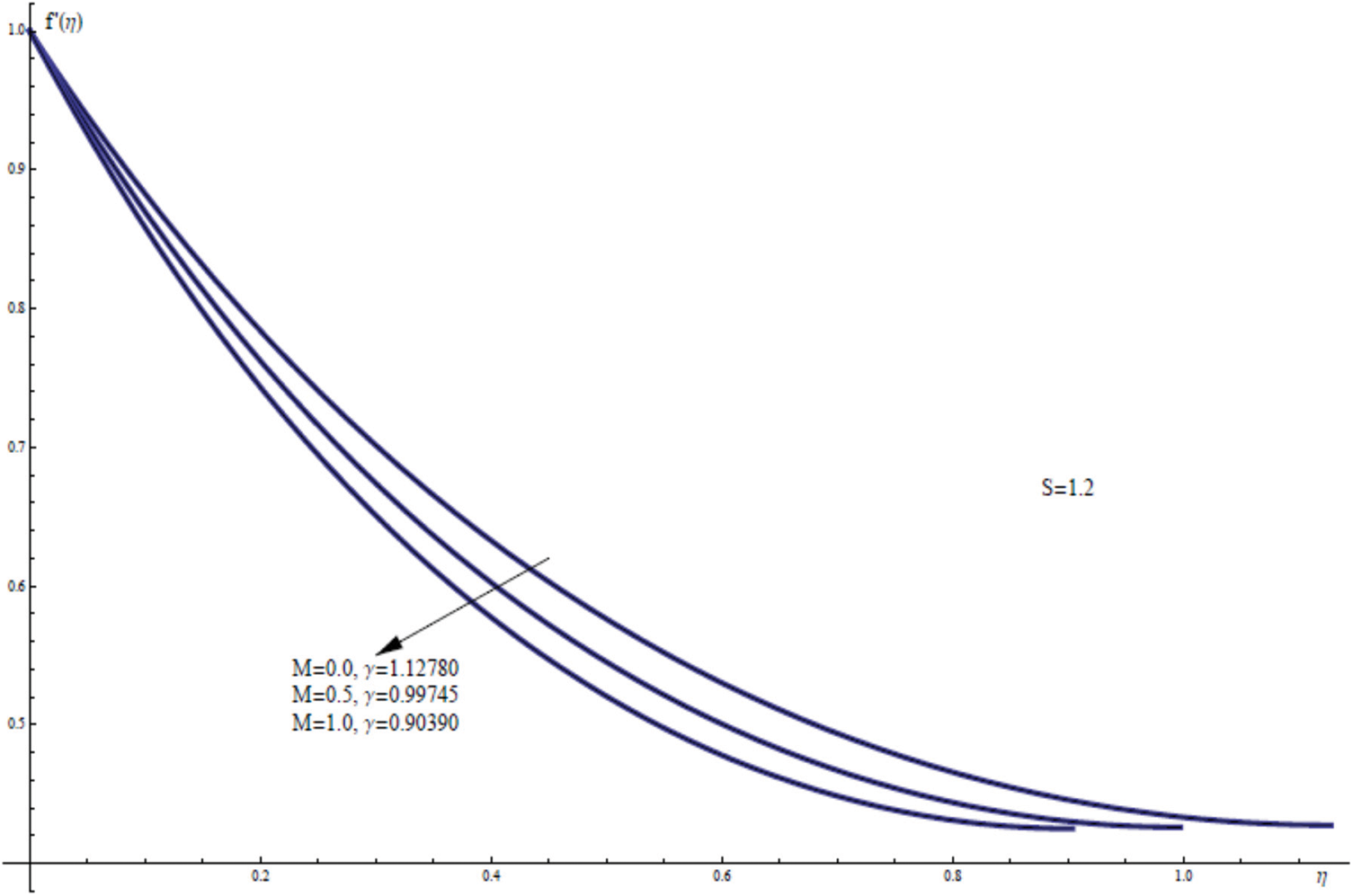
Figure 6: f′(η) for assorted values of M

Fig. 7 elucidates the temperature profiles for varying values of the magnetic parameter M, keeping the other physical parameters fixed. For the impact of M on the thermal film layer it can be shown that the temperature profile clearly varies with M, indicating strongly the heating character for the stretching sheet as well as increasing the free surface temperature θ(γ) as M increases. On the other hand, a similar behavior for the free surface concentration ϕ(γ) and the concentration distribution ϕ(η) is observed from Fig. 8 as this for thin film flow within the thermal film layer. Physically, the presence of magnetic field in this study acts as an internal heat factor within the thermal thin film layer.

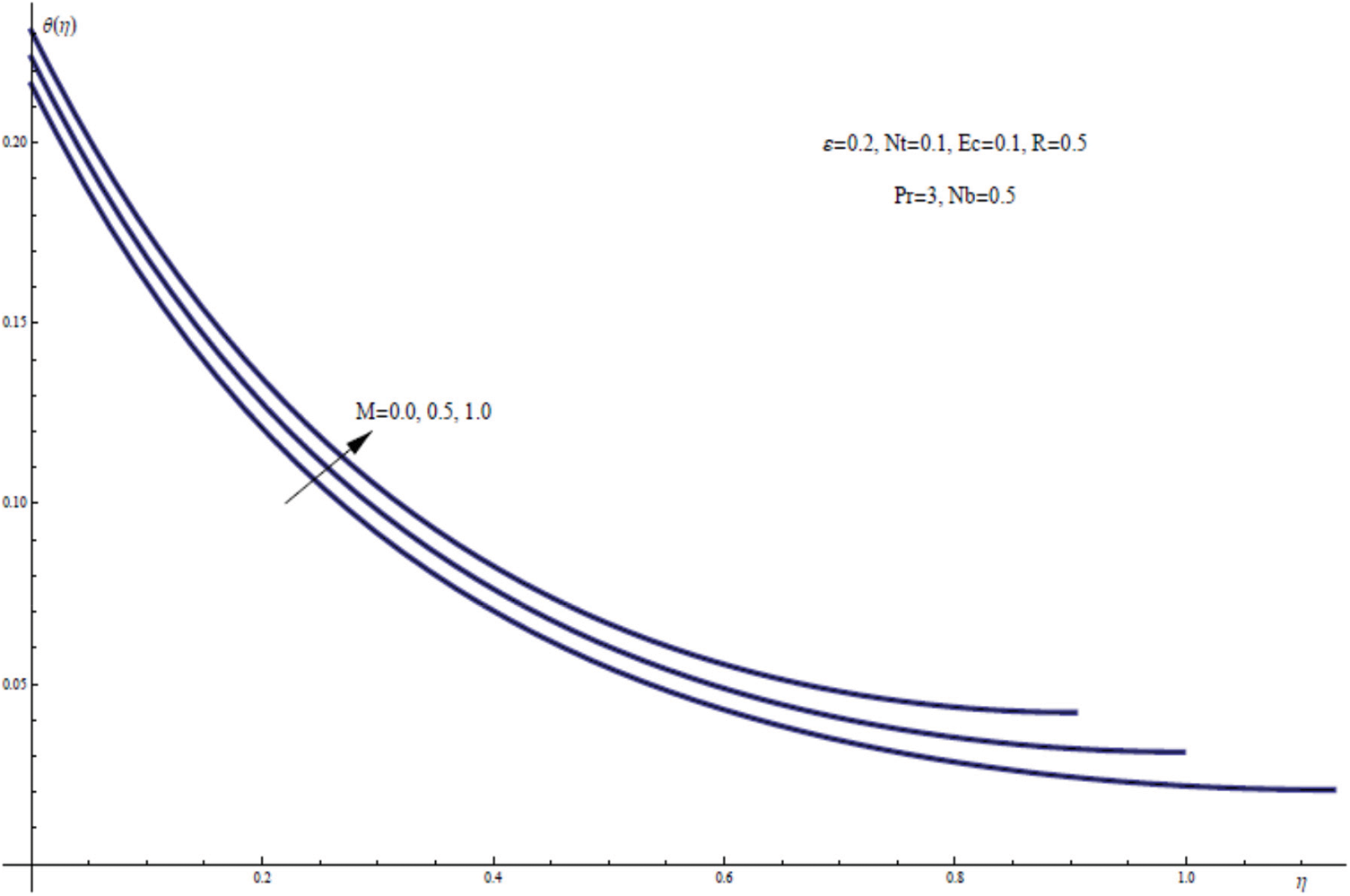
Figure 7: θ(η) for assorted values of M

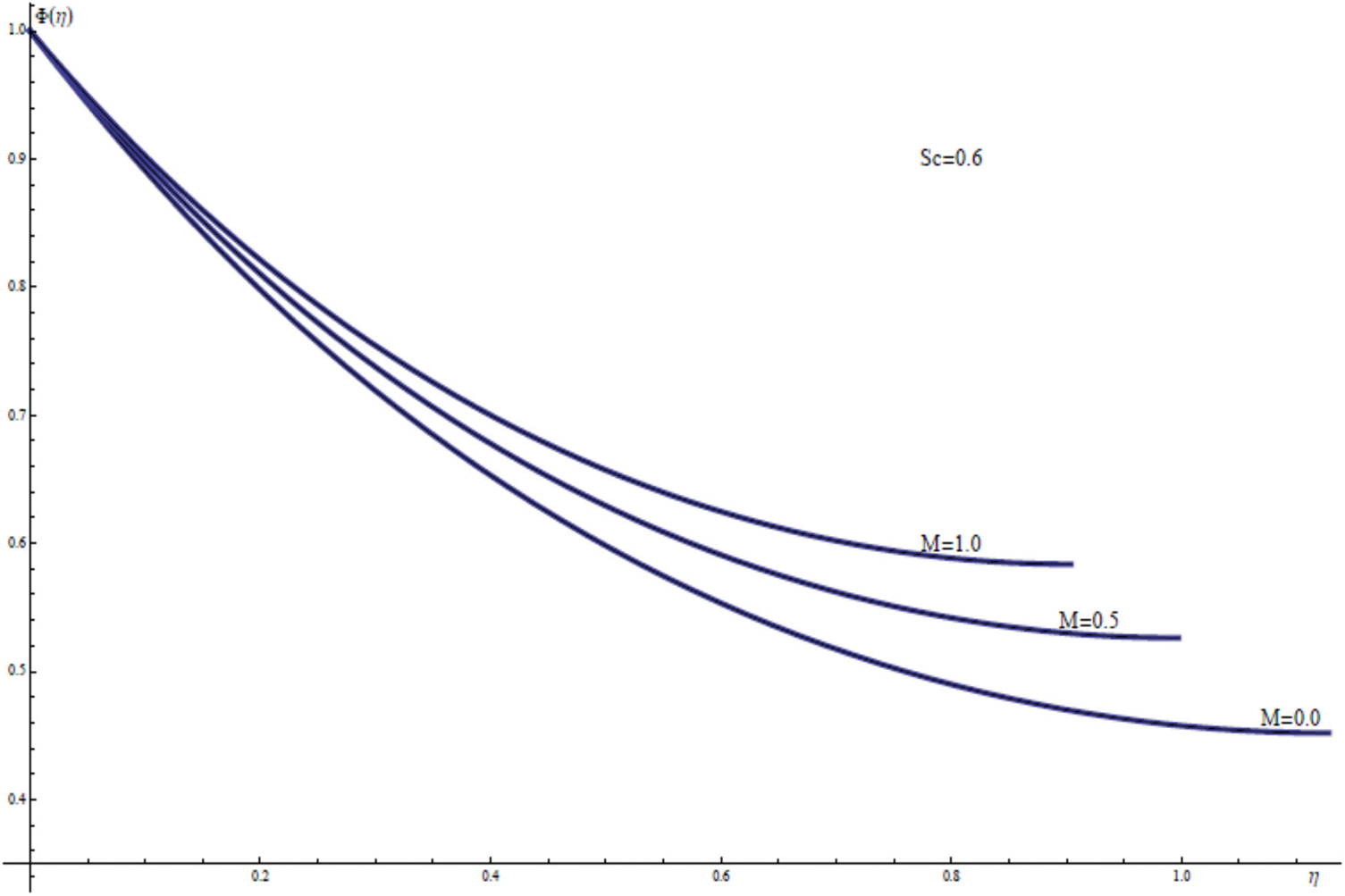
Figure 8: ϕ(η) for assorted values of M

Variation of the temperature field θ(η) as a function of η is shown in the following Fig. 9 for three various values of thermal radiation parameter R. It is observed that enhancing the radiation parameter can result in diminishing the temperature distribution along the sheet as well as the sheet temperature θ(0). As a result, the thermal radiation phenomena can be used as a coolant for the sheet in this physical model in the presence of a changing heat flux.

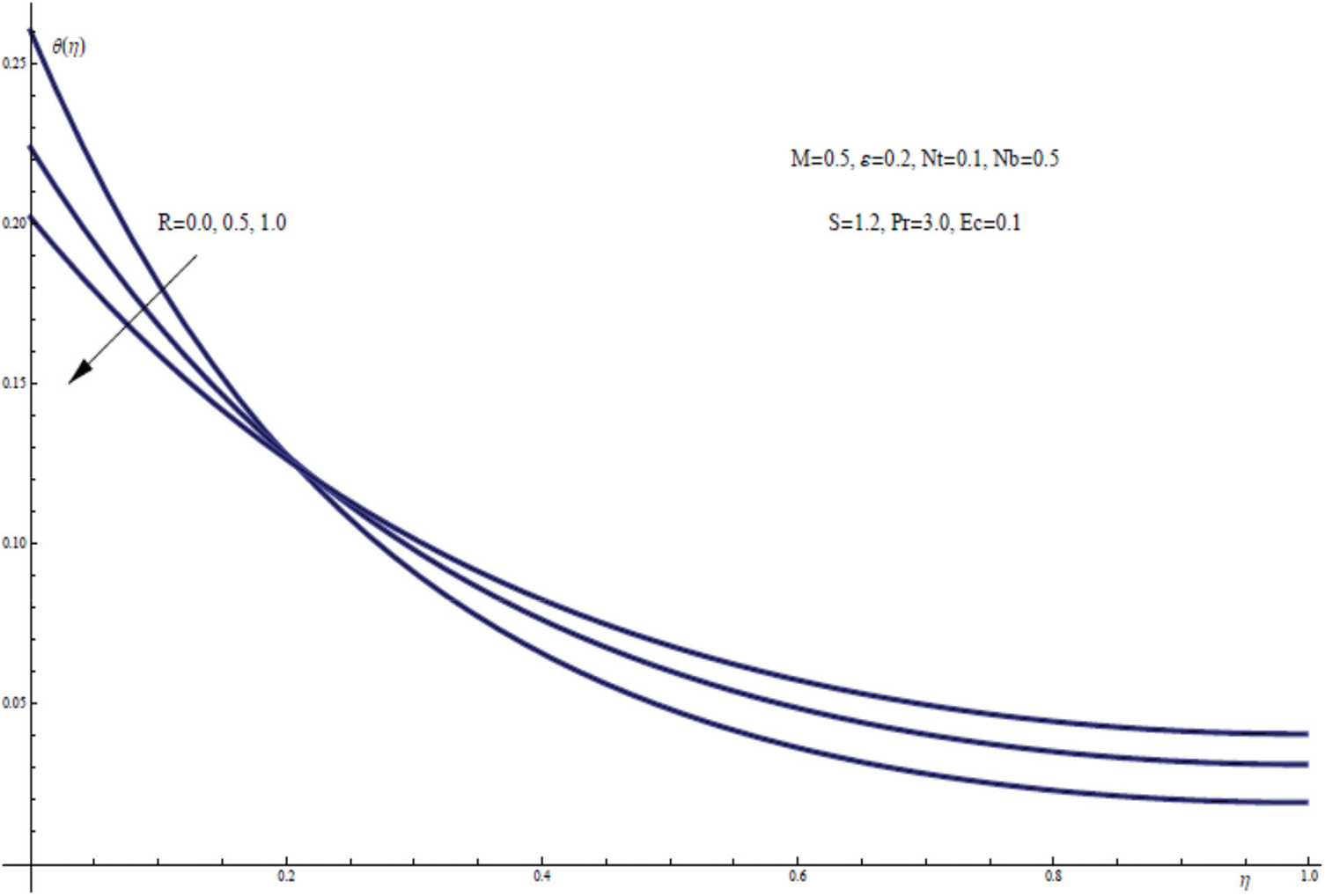
Figure 9: θ(η) for assorted values of R

Fig. 10 depicts the influence of R on the concentration field ϕ(η) when the other parameters are taken as fixed values. The increase in the radiation parameter R has resulted in a somewhat lower nanofluid concentration.

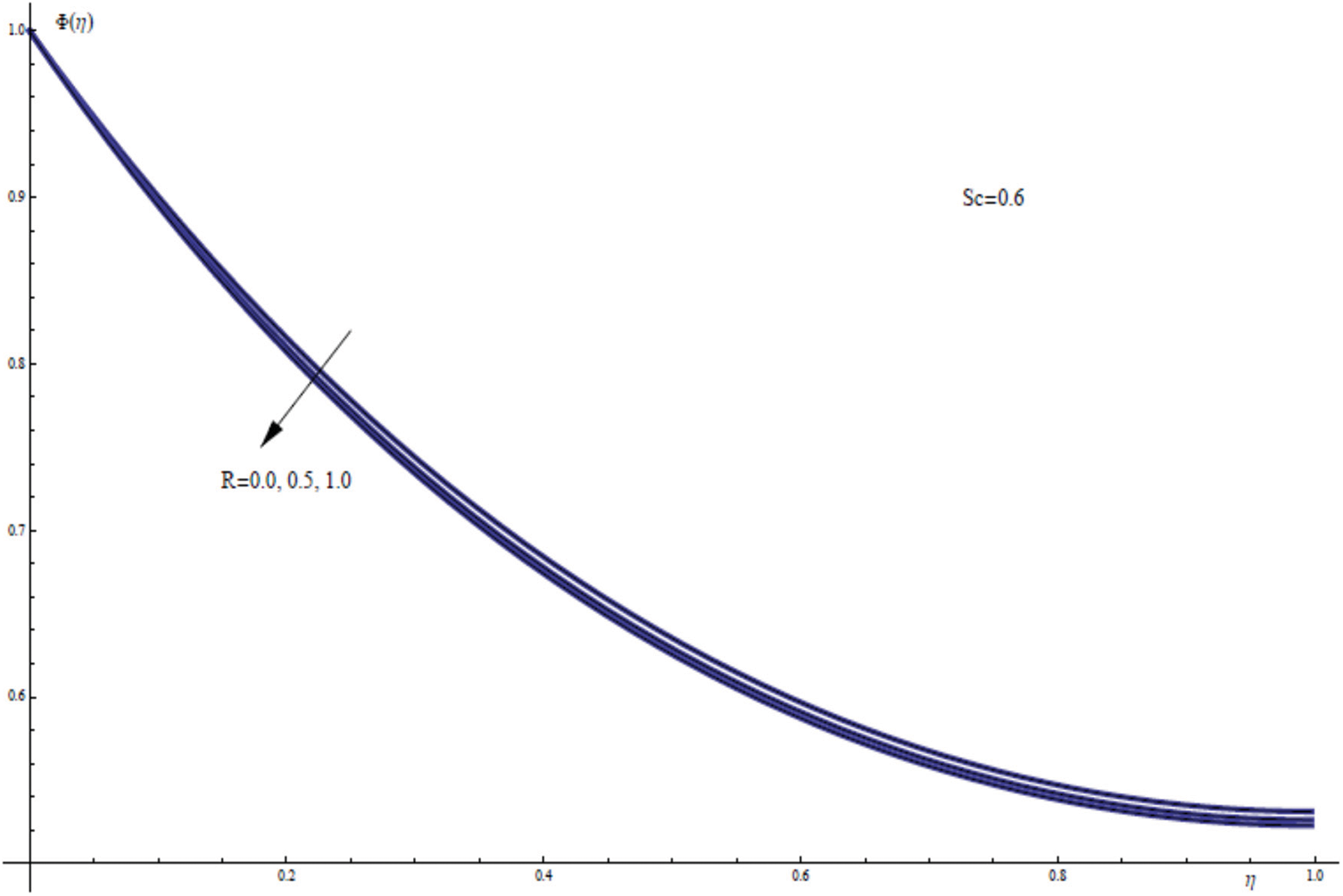
Figure 10: ϕ(η) for assorted values of R

Fig. 11 depicts the effect of the Eckert number Ec on the wall temperature using three curves. This graph clearly shows that Ec has a major influence on the temperature field. The temperature distribution within the thermal film layer clearly increases as the viscous dissipation parameter is increased. The temperature of the stretched sheet is then raised as a result of this.

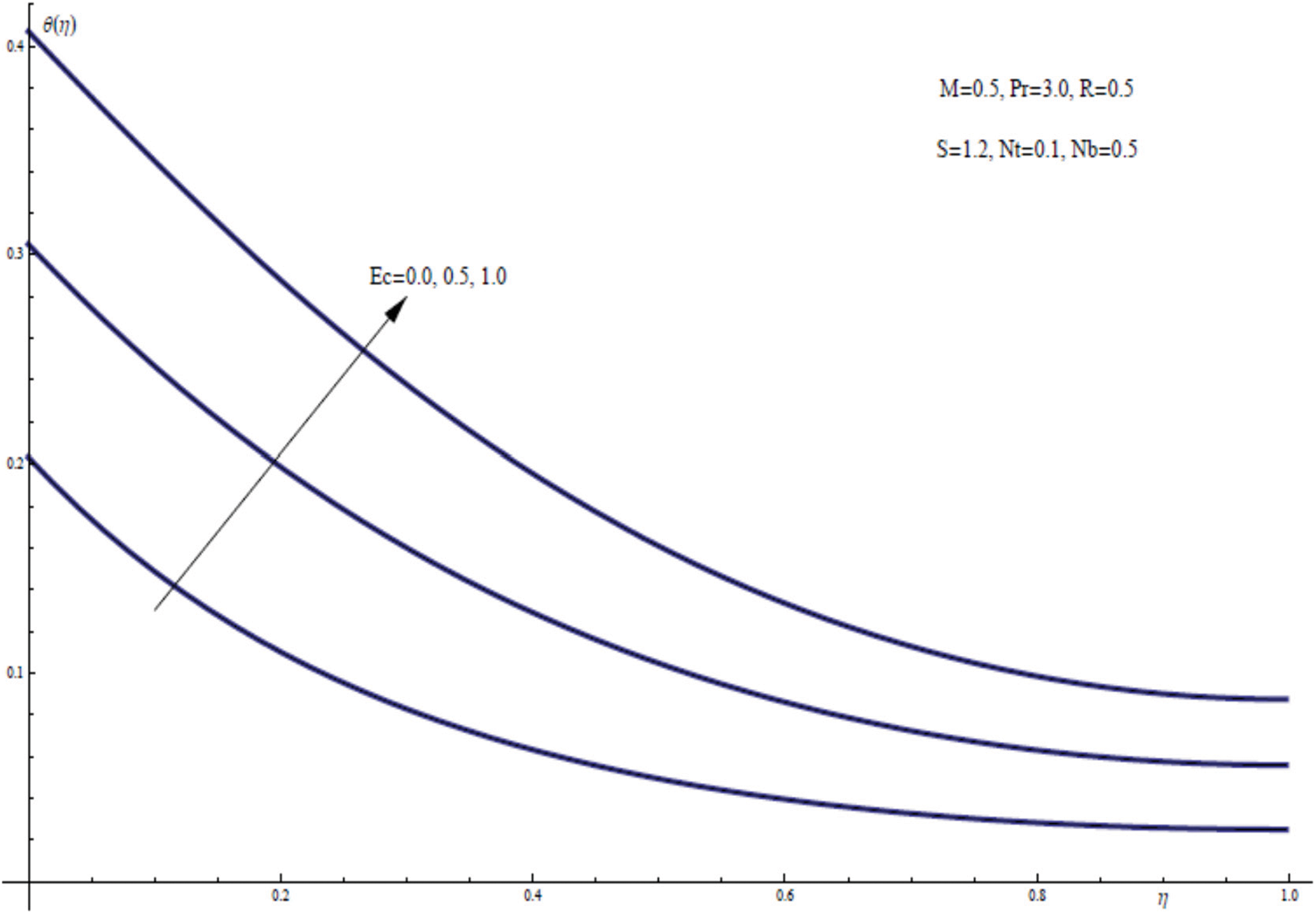
Figure 11: θ(η) for assorted values of Ec

Fig. 12 shows a plot of the nanofluid concentration ϕ(η) against the similarity variable η for various values of the Eckert number Ec. Clearly that the major feature of the curve, the slightly variation in the value of the nanofluid concentration as Ec increases. Because the viscous dissipation phenomena impacts the thermal field directly, but not the nanofluid concentration, this behavior happens.

Figure 12: ϕ(η) for assorted values of Ec

In Fig. 13 we have given a graph of the temperature distribution θ(η) against the similarity variable η for assorted values of the thermophoresis parameter Nt in the inner region of the thin liquid film. It is seen that, for great values of Nt, higher temperature distribution exists within the liquid thin film region than for the smallest value of Nt. The cooling mechanism for the sheet can be performed physically for the least value of Nt.

Figure 13: θ(η) for assorted values of Nt

Fig. 14 shows the effect of the variation of the thermophoresis parameter Nt on the nanofluid concentration field ϕ(η). Thermophoresis force is a phenomenon which can be observed in a nanofluid where the suspended particles present several responses to the temperature gradient force. When Nt increases through values from zero to 0.2, the concentration of the nanofluid increases throughout the thin film region. In terms of physics, this figure shows that larger thermophoresis parameter estimation enhances the concentration distribution through the thin film layer.

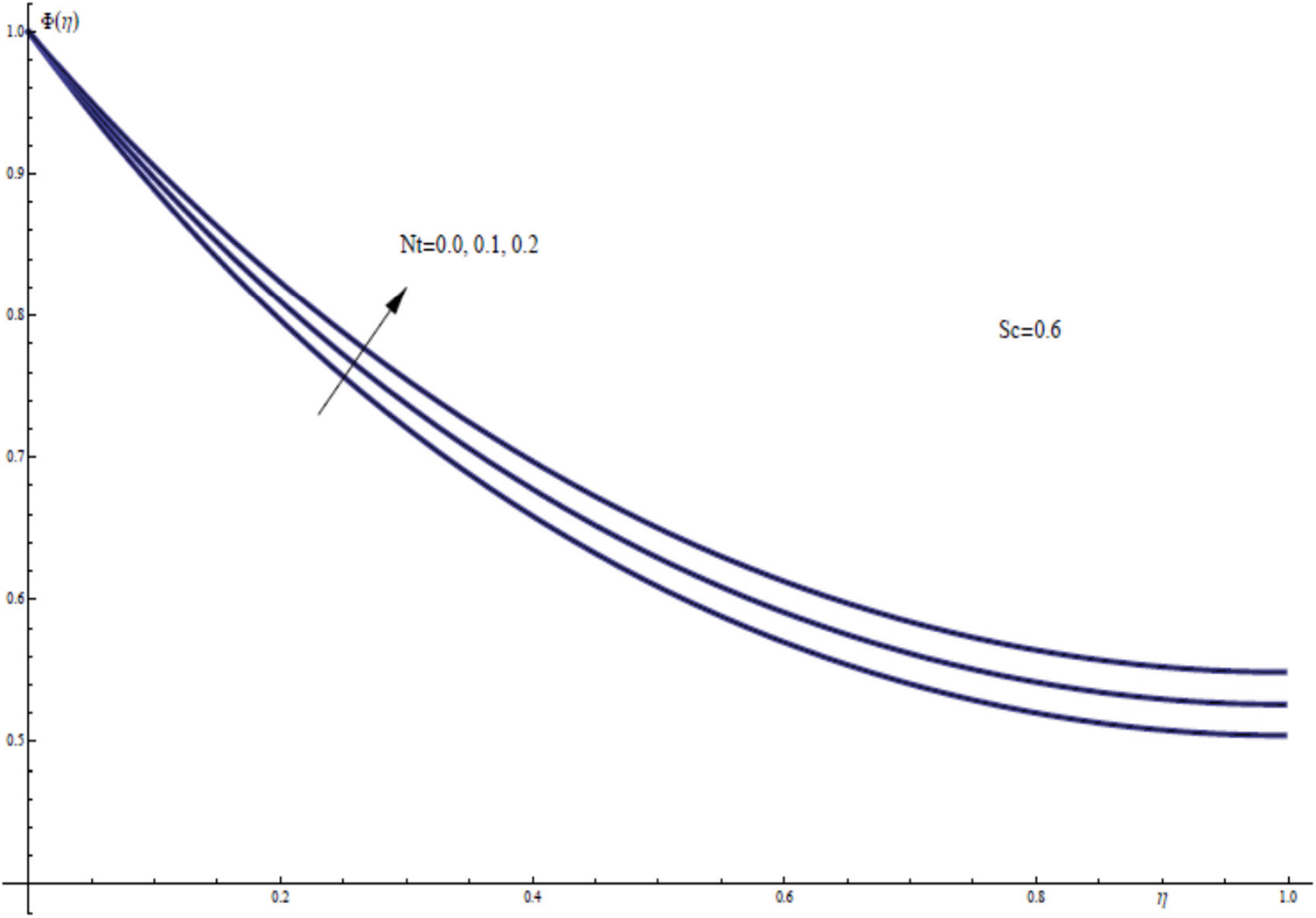
Figure 14: ϕ(η) for assorted values of Nt

In Fig. 15, the function of temperature θ(η) is plotted vs. η for for different values of the Brownian motion parameter Nb. The particles Brownian motion are the random motion of suspended particles in a nanofluid medium. Fig. 15 clearly shows that when the Brownian motion parameter Nb assumes a large value, the temperature drops and reaches a minimum near the sheet, resulting in a very important conclusion that the Brownian motion parameter can be used as a cooling factor for the nanofluid.

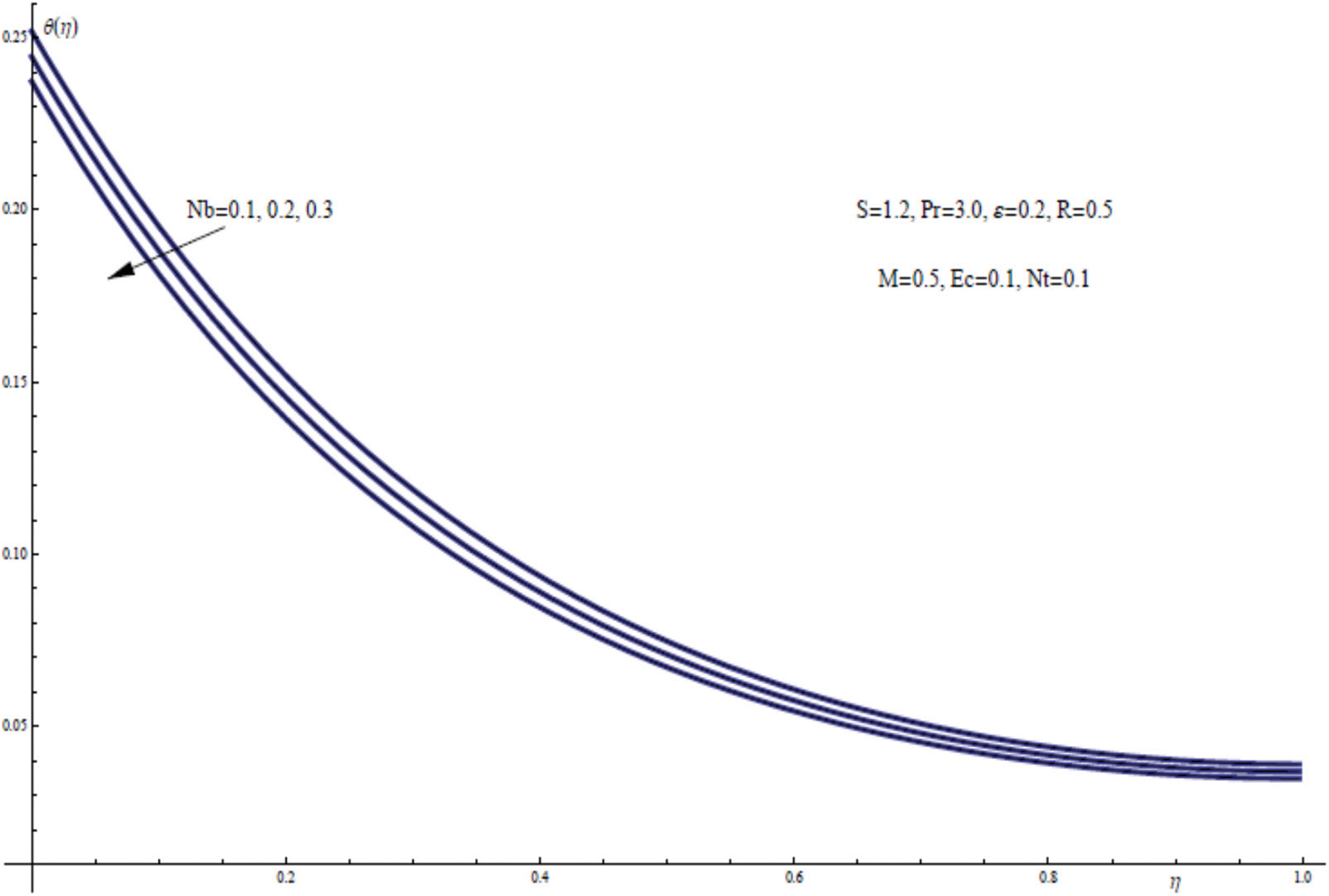
Figure 15: θ(η) for assorted values of Nb

Fig. 16 showes the theoretical data obtained for the nanofluid concentration field ϕ(η) which plotted against the similarity variable η. From Fig. 16 we see that enlargement of the Brownian motion parameter Nb results in diminishing for both the nanofluid concentration field ϕ(η) and the free surface concentration ϕ(γ). Physically, the mass diffusivity of nanofluids decreases as the Brownian motion parameter is increased. As a result, the concentration of nanofluid and all connected nanoparticles in the film layer degrades.

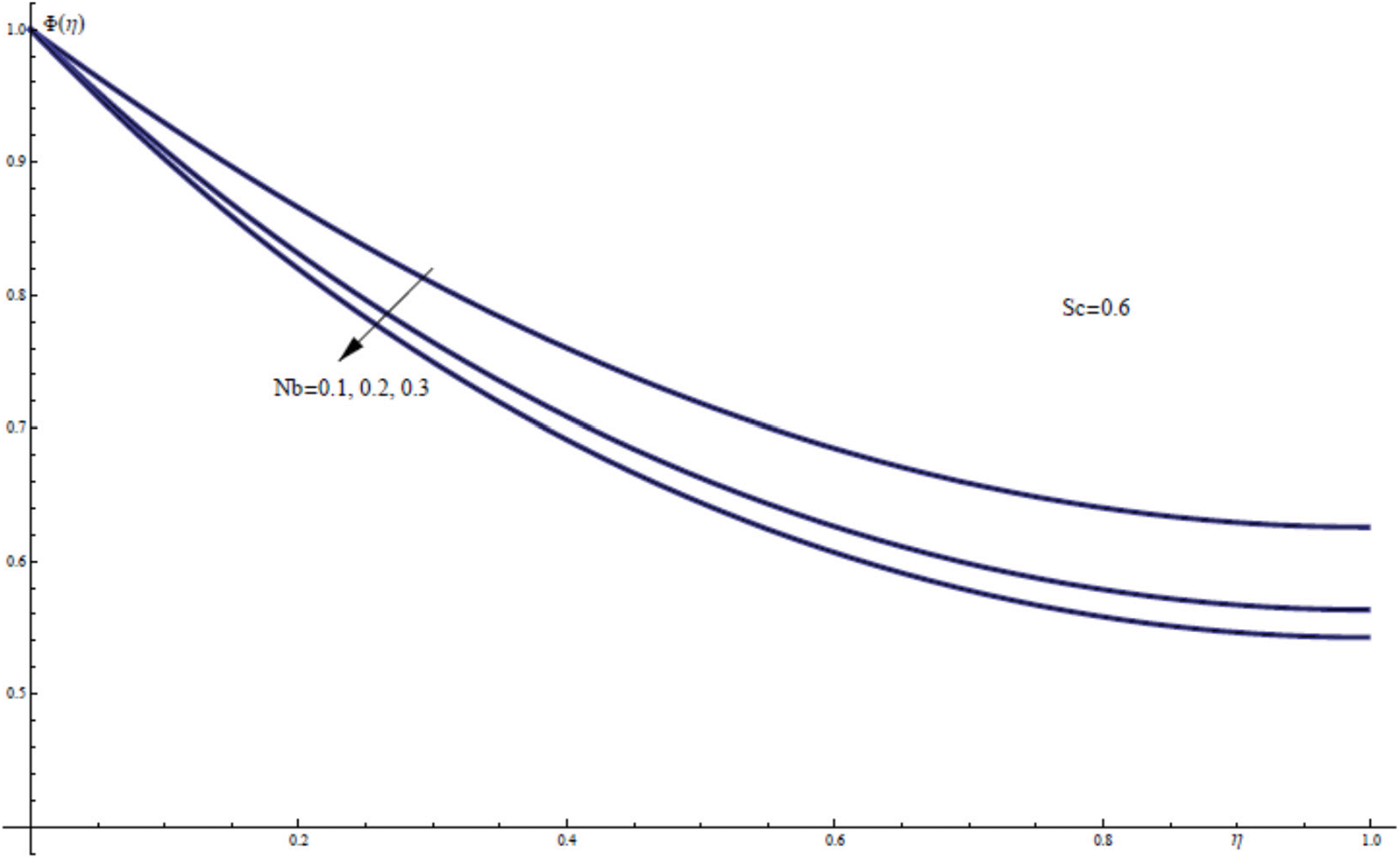
Figure 16: ϕ(η) for assorted values of Nb

Fig. 17 demonstrates the effect of the dimensionless thermal conductivity parameter ε on the thermal field of the nanofluid flow within a liquid thin film together with the heat flux phenomenon. The graphic indicates that the higher the thermal conductivity parameter ε, the better the sheet cooling.

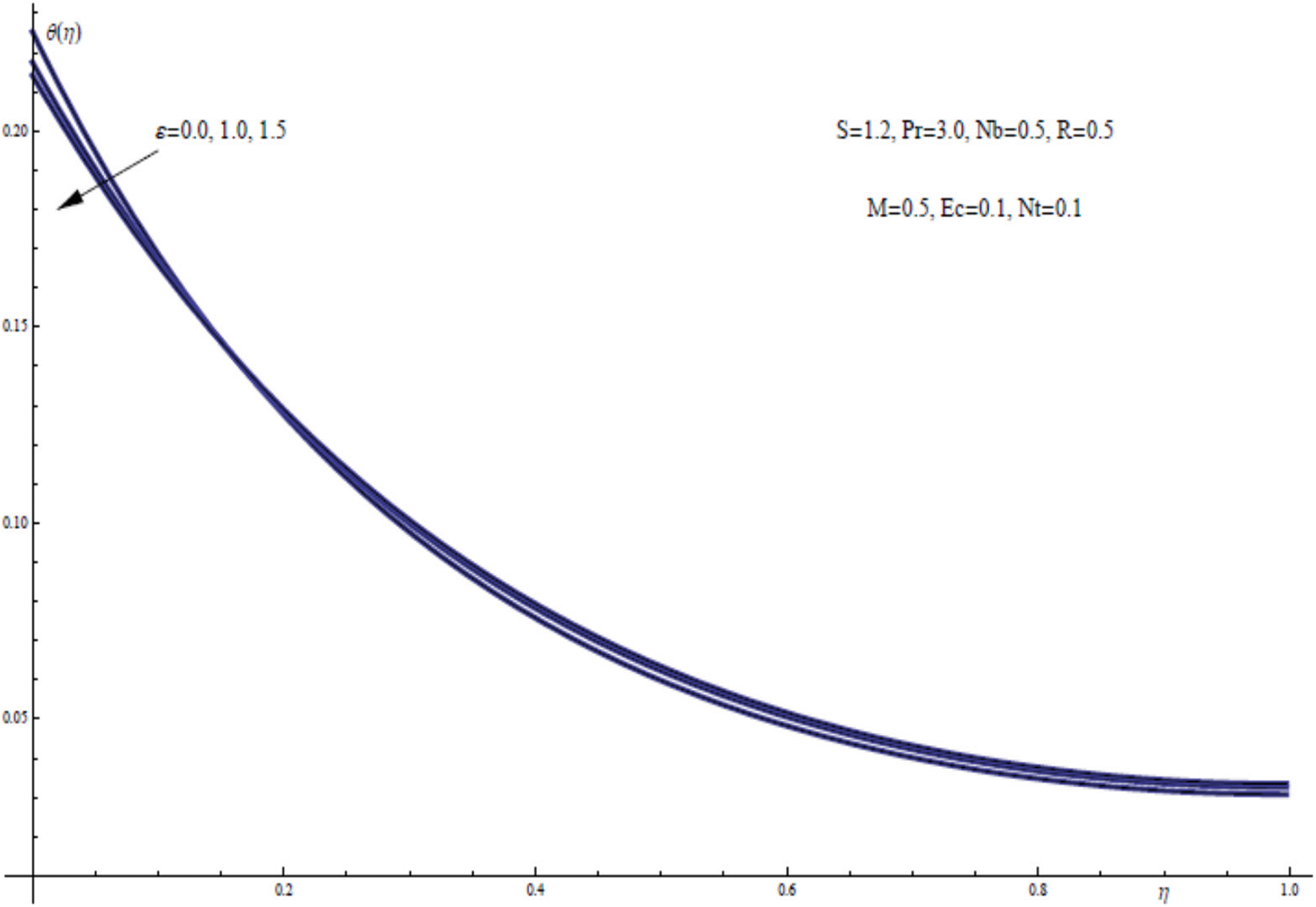
Figure 17: θ(η) for assorted values of ε

4  Conclusions

We investigated the influence of thermal radiation and variable thermal conductivity on the nanofluid flow of a liquid film in the presence of a magnetic field and a prescribed heat flux in the current study. Due to the effect of the viscous dissipation phenomena, we also evaluated the flow and heat mass properties of nanofluid thin films. The results are drawn after the resulting system of ordinary differential equations is numerically assessed using the shooting technique for various values of the physical governing factors. We may draw some useful conclusions regarding the process of heat and mass transmission through the flow of nanofluid film from the current study. The major reasons for controlling the sheet cooling process are the rise in thermal radiation parameter, thermal conductivity parameter, and Brownian motion of nanoparticles suspended in the base fluid. This clearly indicates that the thermal radiation phenomena, as well as temperature-dependent conductivity and Brownian motion, must be included in heat conduction mechanisms throughout the nanofluids research. Furthermore, for both large values of the magnetic parameter and the unsteadiness parameter, compactness of thin film thickness is clearly visible. Furthermore, the presence of the magnetic field force enhances both the nanofluid concentration and temperature distributions, while also assisting in the reduction of both the film thickness and velocity distribution. Similarly, increasing the unsteadiness parameter leads the nanofluid film thickness to decrease, while increasing the same value causes the free surface velocity to increase.

Acknowledgement: We would like to thank International Maritime College Oman (IMCO), for Supporting Project No. (CRG14), Oman. Also, the authors wish to express their sincere thanks to the editor and referees for their valuable time spent reading this paper and for their valuable comments and suggestions, which improved the quality of this paper.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Khanafer, K., Vafai, K., Lightstone, M. (2003). Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. International Journal of Heat and Mass Transfer, 46, 3639–3653. DOI 10.1016/S0017-9310(03)00156-X. [Google Scholar] [CrossRef]

 2.  Liu, M. S., Lin, M. C. C., Huang, I. T., Wang, C. C. (2005). Enhancement of thermal conductivity with carbon nanotube for nanofluids. International Communications in Heat and Mass Transfer, 32, 1202–1210. DOI 10.1016/j.icheatmasstransfer.2005.05.005. [Google Scholar] [CrossRef]

 3.  Choi, S. U. S. (2009). Nanofluids: From vision to reality through research. Journal of Heat Transfer, 131, 1–9. DOI 10.1115/1.3056479. [Google Scholar] [CrossRef]

 4.  Aslani, K. E., Mahabaleshwar, U. S., Singh, J., Sarris, E. I. (2021). Combined effect of radiation and inclined MHD flow of a Micropolar fluid over a porous stretching/shrinking sheet with mass transpiration. International Journal of Applied and Computational Mathematics, 7, 60. DOI 10.1007/s40819-021-00987-7. [Google Scholar] [CrossRef]

 5.  Mahabaleshwar, U. S., Nagaraju, K. R., Vinay Kumar, P. N., Azese, M. N. (2020). Effect of radiation on thermosolutal Marangoni convection in a porous medium with chemical reaction and heat source/sink. Physics of Fluids, 32, 113602. DOI 10.1063/5.0023084. [Google Scholar] [CrossRef]

 6.  Xenos, M. A., Petropoulou, E. N., Siokis, A., Mahabaleshwar, U. S. (2020). Solving the nonlinear boundary layer flow equations with pressure gradient and radiation. Symmetry, 12, 710. DOI 10.3390/sym12050710. [Google Scholar] [CrossRef]

 7.  Mahabaleshwar, U. S., Nagaraju, K. R., Sheremet, M. A., Vinay Kumar, P. N., Lorenzini, G. (2019). Effect of mass transfer and MHD induced Navier’s slip flow due to a non linear stretching sheet. Journal of Engineering Thermophysics, 28, 578–590. DOI 10.1134/S1810232819040131. [Google Scholar] [CrossRef]

 8.  Kumar, P. N. V., Mahabaleshwar, U. S., Sakanaka, P. H., Lorenzini, G. (2018). An MHD effect on a Newtonian fluid flow due to a superlinear stretching sheet. Journal of Engineering Thermophysics, 27, 501–506. DOI 10.1134/S1810232818040112. [Google Scholar] [CrossRef]

 9.  Siddheshwar, P. G., Chan, A., Mahabaleswar, U. S. (2014). Suction-induced magnetohydrodynamics of a viscoelastic fluid over a stretching surface within a porous medium. IMA Journal of Applied Mathematics, 79, 445–458. DOI 10.1093/imamat/hxs074. [Google Scholar] [CrossRef]

10. Siddheshwar, P. G., Mahabaleswar, U. S., Andersson, H. I. (2013). A new analytical procedure for solving the non-linear differential equation arising in the stretching sheet problem. International Journal of Applied Mechanics and Engineering, 18, 955–964. DOI 10.2478/ijame-2013-0059. [Google Scholar] [CrossRef]

11. Mahabaleshwar, U. S., Sneha, K. N., Huang, H. N. (2021). An effect of MHD and radiation on CNTS-water based nanofluids due to a stretching sheet in a Newtonian fluid. Case Studies in Thermal Engineering, 28, 101462. DOI 10.1016/j.csite.2021.101462. [Google Scholar] [CrossRef]

12. Mahabaleshwar, U. S., Anusha, T., Sakanaka, P. H., Bhattacharyya, S. (2021). Impact of inclined Lorentz force and Schmidt number on chemically reactive Newtonian fluid flow on a stretchable surface when stefan blowing and thermal radiation are significant. Arabian Journal for Science and Engineering, 46, 12427–12443. DOI 10.1007/s13369-021-05976-y. [Google Scholar] [CrossRef]

13. Mahabaleshwar, U. S., Anusha, T., Hatami, M. (2021). The MHD Newtonian hybrid nanofluid flow and mass transfer analysis due to super-linear stretching sheet embedded in porous medium. Scientific Reports, 11, 22518. DOI 10.1038/s41598-021-01902-2. [Google Scholar] [CrossRef]

14. Kakac, S., Pramuanjaroenkij, A. (2009). Review of convective heat transfer enhancement with nanofluids. International Journal of Heat and Mass Transfer, 52, 3187–3196. DOI 10.1016/j.ijheatmasstransfer.2009.02.006. [Google Scholar] [CrossRef]

15. Khan, W. A., Pop, I. (2010). Boundary-layer flow of a nanofluid past a stretching sheet. International Journal of Heat and Mass Transfer, 53, 2477–2483. DOI 10.1016/j.ijheatmasstransfer.2010.01.032. [Google Scholar] [CrossRef]

16. Hamad, M. A., Pop, I. (2011). Scaling transformations for boundary layer flow near the stagnation-point on a heated permeable stretching surface in a porous medium saturated with a nanofluid and heat generation/absorption effects. Transport in Porous Media, 87, 25–39. DOI 10.1007/s11242-010-9683-8. [Google Scholar] [CrossRef]

17. Hamad, M. A. A., Ferdows, M. (2012). Similarity solution of boundary layer stagnation-point flow towards a heated porous stretching sheet saturated with a nanofluid with heat absorption/generation and suction/blowing: A Lie group analysis. Communications in Nonlinear Science and Numerical Simulation, 17, 132–140. DOI 10.1016/j.cnsns.2011.02.024. [Google Scholar] [CrossRef]

18. Makinde, O. D., Khan, W. A., Khan, Z. H. (2013). Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet. International Journal of Heat and Mass Transfer, 62, 526–533. DOI 10.1016/j.ijheatmasstransfer.2013.03.049. [Google Scholar] [CrossRef]

19. Alali, E., Megahed, A. M. (2022). MHD dissipative casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon. Nanotechnology Reviews, 11, 463–472. DOI 10.1515/ntrev-2022-0031. [Google Scholar] [CrossRef]

20. Vasu, V., Rama Krishna, K., Kumar, A. C. S. (2007). Analytical prediction of forced convective heat transfer of fluids embedded with nanostructured materials (nanofluids). Pramana Journal of Physics, 69, 411–421. DOI 10.1007/s12043-007-0142-1. [Google Scholar] [CrossRef]

21. Wang, C. Y. (1990). Liquid film on an unsteady stretching surface. Quarterly of Applied Mathematics, 48, 601–610. DOI 10.1090/qam/1079908. [Google Scholar] [CrossRef]

22. Andersson, H. I., Aarseth, J. B., Dandapat, B. S. (2000). Heat transfer in a liquid film on an unsteady stretching surface. International Journal of Heat and Mass Transfer, 43, 69–74. DOI 10.1016/S0017-9310(99)00123-4. [Google Scholar] [CrossRef]

23. Chen, C. H. (2003). Heat transfer in a power-law Fluid film over a unsteady stretching sheet. Heat Mass Transfer, 39, 791–796. DOI 10.1007/s00231-002-0363-2. [Google Scholar] [CrossRef]

24. Liu, I. C., Andersson, H. I. (2008). Heat transfer in a liquid film on an unsteady stretching sheet. International Journal of Thermal Sciences, 47, 766–772. DOI 10.1016/j.ijthermalsci.2007.06.001. [Google Scholar] [CrossRef]

25. Mahmoud, M. A. A., Megahed, A. M. (2009). MHD flow and heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet with variable fluid properties. Canadian Journal of Physics, 87, 1065–1071. DOI 10.1139/P09-066. [Google Scholar] [CrossRef]

26. Abel, M. S., Mahesha, N., Tawade, J. (2009). Heat transfer in a liquid film over an unsteady stretching surface with viscous dissipation in presence of external magnetic field. Applied Mathematical Modelling, 33, 3430–3441. DOI 10.1016/j.apm.2008.11.021. [Google Scholar] [CrossRef]

27. Noor, N. F. M., Hashim, I. (2010). Thermocapillarity and magnetic field effects in a thin liquid film on an unsteady stretching surface. International Journal of Heat and Mass Transfer, 53, 2044–2051. DOI 10.1016/j.ijheatmasstransfer.2009.12.052. [Google Scholar] [CrossRef]

28. Noor, N. F. M., Abdulaziz, O., Hashim, I. (2010). MHD flow and heat transfer in a thin liquid film on an unsteady stretching sheet by the homotopy analysis method. International Journal for Numerical Methods in Fluids, 63, 357–373. DOI 10.1002/fld.2078. [Google Scholar] [CrossRef]

29. Nandeppanavar, M. M., Vajravelu, K., Abel, M. S., Ravi, S., Jyoti, H. (2012). Heat transfer in a liquid film over an unsteady stretching sheet. International Journal of Heat and Mass Transfer, 55, 1316–1324. DOI 10.1016/j.ijheatmasstransfer.2011.09.007. [Google Scholar] [CrossRef]

30. Liu, I. C., Megahed, A. M. (2012). Numerical study for the flow and heat transfer in a thin liquid film over an unsteady stretching sheet with variable fluid properties in the presence of thermal radiation. Journal of Mechanics, 28, 291–297. DOI 10.1017/jmech.2012.32. [Google Scholar] [CrossRef]

31. Khader, M. M., Megahed, A. M. (2013). Numerical studies for flow and heat transfer of the Powell-Eyring fluid thin film over an unsteady stretching sheet with internal heat generation using the Chebyshev finite difference method. Journal of Applied Mechanics and Technical Physics, 54, 440–450. DOI 10.1134/S0021894413030139. [Google Scholar] [CrossRef]

32. Shahzad, F., Sagheer, M., Hussain, S. (2019). Numerical solution of rotating flow of a nanofluid over a stretching surface in the presence of magnetic field. Journal of Nanofluids, 8, 359–370. DOI 10.1166/jon.2019.1578. [Google Scholar] [CrossRef]

33. Shahzad, F., Ul Haq, R., Al-Mdallal, Q. (2016). Water driven Cu nanoparticles between two concentric ducts with oscillatory pressure gradient. Journal of Molecular Liquids, 224, 322–332. DOI 10.1016/j.molliq.2016.09.097. [Google Scholar] [CrossRef]

34. Shahzad, F., Jamshed, W., Sathyanarayanan, S. U. D., Aissa, A., Madheshwaran, P. et al. (2021). Thermal analysis on Darcy-Forchheimer swirling Casson hybrid nanofluid flow inside parallel plates in parabolic trough solar collector: An application to solar aircraft. International Journal of Energy Research, 45, 20812–20834. DOI 10.1002/er.7140. [Google Scholar] [CrossRef]

35. Shahzad, F., Jamshed, W., Ibrahim, R. W., Nisar, K. S., Qureshi, M. A. et al. (2021). Comparative numerical study of thermal features analysis between Oldroyd-B Copper and molybdenum disulfide nanoparticles in engine-oil-based nanofluids flow. Coatings, 11, 1196. DOI 10.3390/coatings11101196. [Google Scholar] [CrossRef]

36. Shahzad, F., Sagheer, M., Hussain, S. (2021). Transport of MHD nanofluid in a stratified medium containing gyrotactic microorganisms due to a stretching sheet. Scientia Iranica, 28, 3786–3805. DOI 10.24200/sci.2021.56459.4734. [Google Scholar] [CrossRef]

37. Shahzad, F., Jamshed, W., Sajid, T., Nisar, K. S., Eid, M. R. (2021). Heat transfer analysis of MHD rotating flow of Fe3O4 nanoparticles through a stretchable surface. Communications in Theoretical Physics, 73, 075004. DOI 10.1088/1572-9494/abf8a1. [Google Scholar] [CrossRef]

38. Shahzad, F., Sagheer, M., Hussain, S. (2019). MHD tangent hyperbolic nanofluid with chemical reaction, viscous dissipation and Joule heating effects. AIP Advances, 9, 025007. DOI 10.1063/1.5054798. [Google Scholar] [CrossRef]

39. Liu, I. C., Megahed, A. M., Hung-Hsun, W. (2013). Heat transfer in a liquid film due to an unsteady stretching surface with variable heat flux. ASME Journal of Applied Mechanics, 80, 041003. DOI 10.1115/1.4007966. [Google Scholar] [CrossRef]

40. Liu, I. C., Hung-Hsun, W., Umavathi, J. C. (2013). Effect of viscous dissipation, internai heat source/sini, and thermai radiation on a hydromagnetic liquid fiim over an unsteady stretching sheet. Journal of Heat Transfer, 135, 031701. DOI 10.1115/1.4007818. [Google Scholar] [CrossRef]

41. Raptis, A. (1998). Flow of a micropolar fluid past a continuously moving plate by the presence of radiation. International Journal of Heat and Mass Transfer, 41, 2865–2866. DOI 10.1016/S0017-9310(98)00006-4. [Google Scholar] [CrossRef]

42. Raptis, A. (1999). Radiation and viscoelastic flow. International Communications in Heat and Mass Transfer, 26, 889–895. DOI 10.1016/S0735-1933(99)00077-9. [Google Scholar] [CrossRef]

This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.