Experimental Study on Seepage Characteristics of a Soil-Rock Mixture in a Fault Zone

Pengfei Wang; Xiangyang Zhang

doi:10.32604/fdmp.2022.017882

1Key Laboratory of Safety and High-Efficiency Coal Mining, Ministry of Education, Anhui University of Science and Technology, Huainan, 232001, China
2School of Architecture and Civil Engineering, Huangshan University, Huangshan, 245041, China
*Corresponding Author: Xiangyang Zhang. Email: pfwang@hsu.edu.cn
Received: 14 June 2021; Accepted: 12 August 2021

Abstract: A mixture of fault gouge and rubble taken out from a fault zone is used to prepare a S-RM (Soil-Rock Mixture) sample with rock block proportions of 20%, 30%, 40%, 50%, 60% and 70%, respectively. A GDS triaxial test system is used accordingly to measure the seepage characteristics of such samples under different loading and unloading confining pressures in order to determine the variation law of the permeability coefficient. The test results show that: (1) The permeability coefficient of the S-RM samples decreases as the pressure increases, and the decrease rate of this coefficient in the initial stage of confining pressure loading is obviously higher than in the semi-late period; (2) The permeability coefficient at different confining pressure levels presents a common trend as the rock block proportion is increased, i.e., it decreases first then it increases (the permeability coefficient of the sample with rock block proportion 40% being the smallest, 70% the largest); (3) In the stage of confining pressure unloading, the recovery degree of the permeability coefficient grows with the increase of rock block proportion (the recovery rate of S-RM sample with rock block proportion 70% reaches 50.2%); (4) In the stage of confining pressure loading and unloading, the sensitivity of the permeability coefficient to the rock block proportion displays the inverse “Z” variation rule (when rock block proportion reaches 60%, the sensitivity is highest); (5) In the stage of confining pressure loading, the relationship between the permeability coefficient and confining pressure can be described by an exponential relationship.

Keywords: Fault zone; rock block proportion; soil-rock mixture; confining pressure loading and unloading; seepage characteristic

Among the water inrush accidents in mine roadway and stope, the water inrush accidents caused by faults account for 41% and 45%, respectively [1–3], it can be seen that the water inrush in fault fracture zone has a very serious impact on mine safety mining [4–6]. Through field investigation and research, it is found that continuous mixture of fault breccia and fault gouge with different thickness is developed in most fault fracture zones, which makes the seepage characteristics of faults basically depend on the seepage characteristics of soil-rock mixture in fault fracture zones [7–10].

Soil-rock mixture is a special geological body between soil and rock mass [11–15], due to the interaction between soil particles and gravel, soil-rock mixture has unique structure, naturalness, heterogeneity and discontinuity [16–19]. At present, experimental methods and numerical simulation methods are mostly used to study its seepage characteristics. Mokwa et al. [20] carried out permeability tests on 14 kinds of coarse-grained soils with different gradation, and the results show that porosity and pore structure characteristics are the main factors affecting the permeability of coarse-grained soils. Zhou et al. [21] proposed a simple and effective calculation model for permeability and relative content of soil-rock mixture, which was verified by experiments. Xu et al. [22] developed the random generation system R-SRM of meso structure of soil-rock mixture, and studied the characteristics of meso seepage field, seepage failure mechanism and the quantitative relationship between macro permeability coefficient and meso structure of soil-rock mixture by using numerical test method. Xu et al. [23] analyzed and studied the permeability of gravelly soil by means of mathematical statistics. Zhou et al. [24] carried out permeability test with self-made constant head permeameter to study the effects of gravel content, pore ratio and particle shape on the permeability coefficient of soil-rock mixture at different levels. The above research is mainly carried out for the permeability and influencing factors of earth rock mixture in earth rock dam, soil slope and other projects, which needs to be further studied [25–27]. The soil-rock mixture in the fault fracture zone is a mixture of clay like fine mineral particles (fault gouge) and rock breccia filled in the fault fracture zone or between the two walls of the fault [28] formed by crushing, repeated grinding and underground circulating diffusion solution during fault dislocation, it has high compactness and permeability and is the main place for seepage and disaster of mine water, however, there are few reports on its seepage characteristics.

During the permeability test, the soil samples taken from the fault fracture zone are made into soil-rock mixture plastic samples with different rock block proportion, and then the permeability coefficient under different confining pressure levels is measured by GDS triaxial test system to study the stress seepage coupling characteristics of soil-rock mixture in the fault fracture zone.

The natural moisture content of the test soil sample is about 9.5%, and the fault gouge matrix is gray white with strong cementation. The results of X-ray diffraction pattern and mineral relative content analysis showed that, the content of muscovite is 65.7%, quartz is 32.1%, and there is a small amount of kaolinite. The gravel in the fault zone is granite with clear edges and corners and regular shape.

The permeability test adopts the soil-rock mixture remolded sample with the diameter of 50 mm and the height of 100 mm. According to the calculation formula d = 0.05Lc (d is the soil/stone threshold, Lc is the sample diameter) proposed by Xu et al. [29] and Shen et al. [30], it is determined that the soil/stone threshold in this test is 2.5 mm, that is, the larger than 2.5 mm is block stone, the smaller than 2.5 mm is soil. According to the ASTM Standard [31], the maximum diameter of the block stone in the soil-rock mixture is 1/6 of the diameter of the sample, it is determined that the maximum particle size of the soil-rock mixture in this test is 8.3 mm. The ratio of the mass of block stone to the total mass of the sample is defined as the rock block proportion of the soil-rock mixture sample. In this paper, six kinds of soil-rock mixture samples with rock block proportion of 20%, 30%, 40%, 50%, 60% and 70% are prepared to be prepared, and their seepage characteristics are studied. Fig. 1 shows the grading curve of six rock block proportion soil-rock mixtures, and the particle size distribution characteristic indexes of each soil-rock mixture are shown in Table 1. According to the data in the table, only the soil-rock mixture with stone content of 20% has good uniformity and continuous grading, and the other soil-rock mixtures with stone content belong to uneven soil, lack of middle particle size and poor grading.

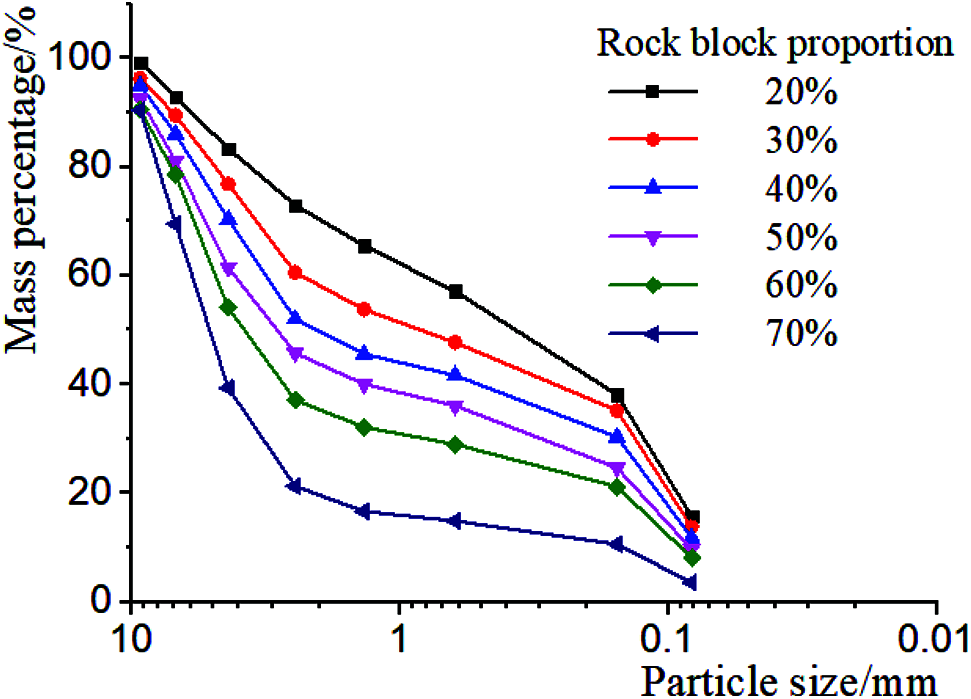
Figure 1: Grading curves of Soil-Rock Mixture (S-RM) with different rock block proportion

This paper mainly studies the influence of the rock block proportion on the seepage characteristics of the soil-rock mixture in the fault fracture zone, in order to make the density of the soil in the samples with different rock block proportion the same, before making samples, first carry out compaction test on soil samples with different rock block proportion, so as to obtain the compaction curve of the soil in the soil-rock mixture with different rock block proportion, as shown in Fig. 2. As shown in Fig. 2, when the soil density in the soil-rock mixture is 1.82 g/cm3, the required compaction times for the rock block proportion of 20%, 30%, 40%, 50%, 60% and 70% of the soil-rock mixture are respectively 3, 4, 6, 8, 11 and 13 times, which are used as standard samples.

Figure 2: Relationship curve of the density of soil in S-RM and hammer count with different rock block proportion

During sample preparation, the soil and block stone shall be mixed according to the determined soil rock mix proportion, and the initial mixing shall be uniform, and then the water shall be added to make the soil sample further uniform, the optimal water content is determined as 9% by the relationship curve of dry density and water content of the soil. Finally, the soil samples are loaded into the sample cylinder in three layers and compacted to the predetermined height. The soil-rock mixture at the real-time interface shall be roughened and a total of 6 samples shall be prepared according to the above steps. After the sample is prepared, it is cured in a protective box for 28 days to improve the probability of free water transforming into combined water in the sample and make the strength of the remolded sample close to the strength of the original soil-rock mixture. See Fig. 3 for the prepared sample of soil-rock mixture.

The permeability test of the soil-rock mixture is completed with the saturated unsaturated triaxial test system produced by GDS company, as shown in Fig. 4. In the figure, the test instrument is composed of three parts: controller (three hydraulic controllers control the axial pressure, confining pressure and back pressure respectively, one pneumatic controller controls the pore pressure), pressure chamber and data acquisition system (including sensor, data acquisition board and computer), four controllers are connected with data acquisition board and pressure chamber to transmit pressure through water and gas.

Under natural conditions, the soil-rock mixture in the fault fracture zone is in a state of compaction due to the effect of different sizes of hydrostatic pressure, dynamic hydraulic pressure and structural stress, which has certain self stabilizing ability and storage of deformation energy. Under the influence of natural geological tectonic movement or disturbance of tunnel excavation, the equilibrium state of soil-rock mixture in fault fracture zone is destroyed and energy is released, which is in the state of stress relaxation. In this test, two loading methods, confining pressure loading and confining pressure unloading are used to characterize the two engineering states of the soil-rock mixture in the fault fracture zone. In order to simplify the test conditions and reduce the influence of other factors, it is set that the soil-rock mixture sample is only affected by confining pressure and seepage pressure, and no load is applied axially, the inlet water pressure is set as 0.08 MPa, the outlet is open to the atmosphere, and only the confining pressure changes. According to the purpose of this test, and to ensure that there is no water leakage between the outer wall of the soil-rock mixture sample and the latex sleeve during the test, the confining pressure is selected as 0.10, 0.12, 0.14, 0.16, 0.18 and 0.20 MPa six stress points respectively, and the seepage characteristics of the soil-rock mixture with different rock block proportion during the process of confining pressure loading and unloading are analyzed, respectively.

The permeability test of soil-rock mixture adopts the steady-state method [32], in order to improve the test accuracy, distilled water seepage is adopted. Before the test, after loading the prepared sample, first apply a low water pressure of 0.02 MPa to the sample until the sample is saturated. During the test, keep the seepage pressure of 0.08 MPa unchanged, record the stable seepage flow of the sample under each level of confining pressure, and calculate the permeability coefficient. According to Darcy’s law, the calculation formula of permeability coefficient of soil-rock mixture sample is deduced as follows:

where, γw is the weight of water (KN/m3); Q is the water volume passing through the sample in unit time (m3/s); L is the height of the sample (m); A is the cross-sectional area of the sample (m2); Δh is the water pressure difference at both ends of the sample (MPa).

3.1 Variation Law of Permeability Coefficient of Soil-Rock Mixture Sample with Confining Pressure

According to the test results, the change curve of the permeability coefficient of the soil-rock mixture samples with different rock block proportion in the process of confining pressure loading and unloading is drawn, as shown in Fig. 5. It can be seen from the figure that the permeability coefficients of the soil-rock mixture samples with different rock block proportion under the same horizontal confining pressure are different, but there is no difference in order of magnitude. When the confining pressure is loaded to 0.16 MPa, the permeability coefficients of 20%, 30%, 40%, 50%, 60% and 70% soil-rock mixture samples are (3.61, 3.16, 2.79, 3.15, 3.96, 4.53) × 10–6 cm/s, respectively; when the confining pressure is unloaded to 0.16 MPa, the permeability coefficients of 20%, 30%, 40%, 50%, 60% and 70% soil-rock mixture samples are (3.11, 2.73, 2.53, 2.78, 3.53, 3.96, respectively) × 10–6 cm/s, it can be seen that the permeability coefficient of soil-rock mixture is closely related to the rock block proportion and confining pressure level.

Figure 5: Variation curve of permeability coefficient of S-RM with different rock block proportion with confining pressure (a) Rock block proportion 20% (b) Rock block proportion 30% (c) Rock block proportion 40% (d) Rock block proportion 50% (e) Rock block proportion 60% (f) Rock block proportion 70%

The permeability coefficient of soil-rock mixture samples with different rock block proportion changes with the change of confining pressure level. In the confining pressure loading stage, the permeability coefficient decreases with the increase of confining pressure; In the confining pressure unloading stage, the permeability coefficient of the sample recovers to a certain extent with the decrease of confining pressure, and the change slope of the permeability coefficient in the confining pressure loading stage is significantly greater than that in the confining pressure unloading stage; Under the same confining pressure level, the permeability coefficient in confining pressure loading stage is greater than that in confining pressure unloading stage. The permeability coefficient of the soil-rock mixture sample is closely related to its porosity, under the action of confining pressure, the pores in the soil and between the soil and the block stone are gradually compressed, and the porosity decreases, therefore, in the confining pressure loading stage, the permeability coefficient of the sample decreases with the increase of confining pressure; In the unloading stage of confining pressure, with the release of confining pressure, the internal pores of the sample recover slightly, the connectivity becomes better and the porosity increases, so the permeability coefficient of the sample increases with the decrease of confining pressure; At the same time, in the confining pressure loading stage, plastic deformation occurs at weak positions such as soil and soil rock interface in the sample, and some closed seepage channels still cannot be reopened after the confining pressure is released, so the permeability coefficient of the sample in the unloading stage is small.

At the initial stage of confining pressure loading (0.10–0.14 MPa), the permeability coefficient of soil-rock mixture samples with different rock block proportion decreased rapidly, while at the middle and late stage of confining pressure loading (0.14–0.20 MPa), the permeability coefficient of samples decreased relatively slowly. Now, the reduction degree of permeability coefficient of soil-rock mixture samples with different rock block proportion at the initial stage of loading is described by the ratio of the difference of permeability coefficient of the sample when the confining pressure is loaded to 0.14 MPa (the difference between the permeability coefficient of the sample at any loading time and the permeability coefficient of the sample when the initial confining pressure is 0.10 MPa) to the difference of permeability coefficient of the sample when the confining pressure is loaded to 0.20 MPa, it also shows the influence of confining pressure on the permeability coefficient of soil-rock mixture. Through calculation, the reduction degree of permeability coefficient of soil-rock mixture samples with rock block proportion of 20%, 30%, 40%, 50%, 60% and 70% at the initial stage of confining pressure loading is 57%, 45%, 58%, 61%, 55% and 50%, respectively, therefore, the influence of confining pressure on the permeability coefficient of soil-rock mixture sample is very obvious. This is because at the initial stage of confining pressure loading, the soil-rock mixture sample is compressed and deformed, the soil compactness increases and the porosity decreases obviously, at the same time, the main seepage channel formed between block stones is blocked, resulting in the rapid decline of the permeability coefficient of the sample. In the middle and late stage of confining pressure loading, because the soil-rock mixture sample has been compacted in the early stage, under the continuous action of confining pressure, the internal spatial structure of the sample changes and the porosity further decreases, resulting in the closure of the remaining seepage channels, however, at this time, the increase of confining pressure has relatively little impact on the internal seepage channels of the sample, resulting in the slow reduction of the permeability coefficient of the sample. From the above analysis, it can be seen that the permeability coefficient of soil-rock mixture samples is strongly affected by confining pressure, and there are differences in permeability coefficients between samples with different rock block proportion.

3.2 Influence of Rock Block Proportion on Permeability Coefficient of Soil-Rock Mixture

Considering the influence of the rock block proportion on the permeability coefficient of the soil-rock mixture sample, the relationship curve between the permeability coefficient and the rock block proportion of the sample under different confining pressure levels at the loading and unloading stages is drawn in the same coordinate system for further analysis, as shown in Fig. 6.

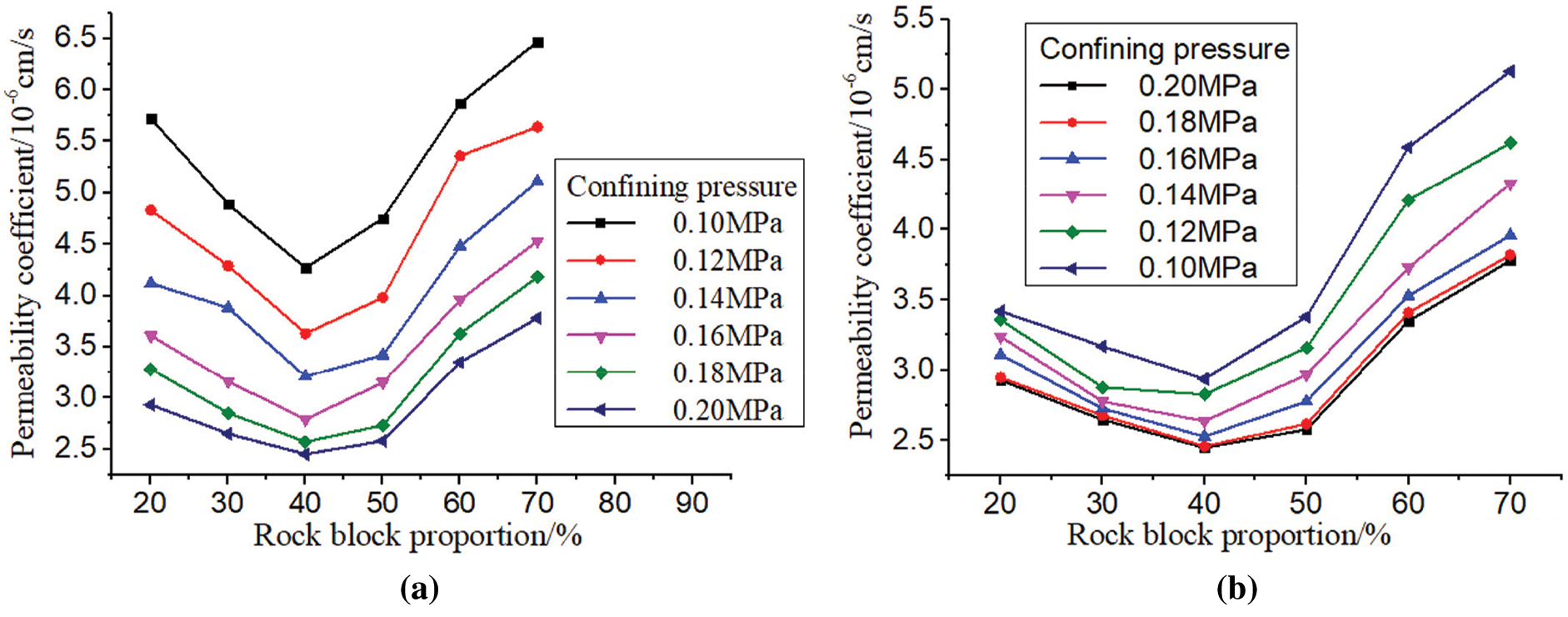
Figure 6: Variation curve of permeability coefficient of S-RM with different rock block proportion with confining pressure (a) loading stage (b) unloading stage

It can be seen from Fig. 6 that in the confining pressure loading stage and unloading stage, with the increase of the rock block proportion, the permeability coefficient of the soil-rock mixture sample decreases first and then increases, reaching the lowest when the rock block proportion is 40%, and then increases rapidly. This is because when the rock block proportion is low (20%–40%), the soil is dominant in the soil-rock mixture sample, the block stone is in the suspension state in the sample of soil-rock mixture, the pores between the block stones are completely filled by the soil, the porosity of the sample is small, and the permeability coefficient is low; At this time, adding the block stone to the soil matrix to improve the rock block proportion is equivalent to blocking the flow channel of soil with the block stone, resulting in the decrease of the permeability coefficient of the soil-rock mixture sample. When the rock block proportion continues to increase from 40% (40%–70%), the block stone in the soil-rock mixture sample gradually transits to the dominant position, the main seepage channel of the sample is surrounded by the block stone, with large porosity, and forms a large permeability drop at the soil-rock interface, resulting in the permeability coefficient of soil-rock mixture rose rapidly.

As shown in Fig. 6b, in the confining pressure unloading stage, with the decrease of confining pressure level (0.20∼0.10 MPa), the permeability coefficient of soil-rock mixture samples with different rock block proportion is restored, and the higher the rock content is, the stronger the recovery ability is, this phenomenon is characterized by calculating the ratio of the recovery of permeability coefficient (the difference between the maximum and minimum permeability coefficient in the unloading stage) and the reduction of permeability coefficient (the difference between the maximum and minimum permeability coefficient in the loading stage) in the confining pressure loading stage. It is calculated that the recovery rates of permeability coefficients of soil-rock mixture samples with rock block proportion of 20%, 30%, 40%, 50%, 60% and 70% in the confining pressure unloading stage are 17.6%, 23.3%, 26.9%, 36.9%, 48.4% and 50.2%, respectively. Under the action of confining pressure, the soil mass in the soil-rock mixture with low rock block proportion has a large degree of plastic deformation, but its permeability coefficient is difficult to recover after the release of confining pressure; For the soil-rock mixture sample with high rock block proportion, the confining pressure has relatively little effect on its internal structure, when the confining pressure is released, the internal pores of the sample are restored and the permeability coefficient rises greatly.

3.3 Sensitivity Analysis of the Permeability Coefficient of Soil-Rock Mixture to the Change of the Rock Block Proportion

This paper mainly studies the influence of the rock block proportion on the seepage characteristics of soil-rock mixture, and now defines the sensitivity coefficient of the permeability coefficient of soil-rock mixture to the change of the rock block proportion, ck:

where, k20 is the permeability coefficient of the soil-rock mixture sample with rock block proportion of 20% (cm/s); ∂k is the absolute value of the difference of the permeability coefficient (cm/s), and ∂(rbp) is the difference of the rock block proportion (%).

The sensitivity coefficient ck can reflect the sensitivity of the permeability coefficient of the soil-rock mixture to the change of the rock block proportion. If its value is large, it indicates that the permeability coefficient of the sample is more sensitive to the change of the rock block proportion, otherwise, it indicates that the permeability coefficient of the sample is not sensitive to the change of the rock block proportion. Now, the sensitive coefficient of permeability coefficient to the change of rock block proportion under different confining pressure levels in the loading stage and unloading stage is plotted in the same coordinate system, as shown in Fig. 7.

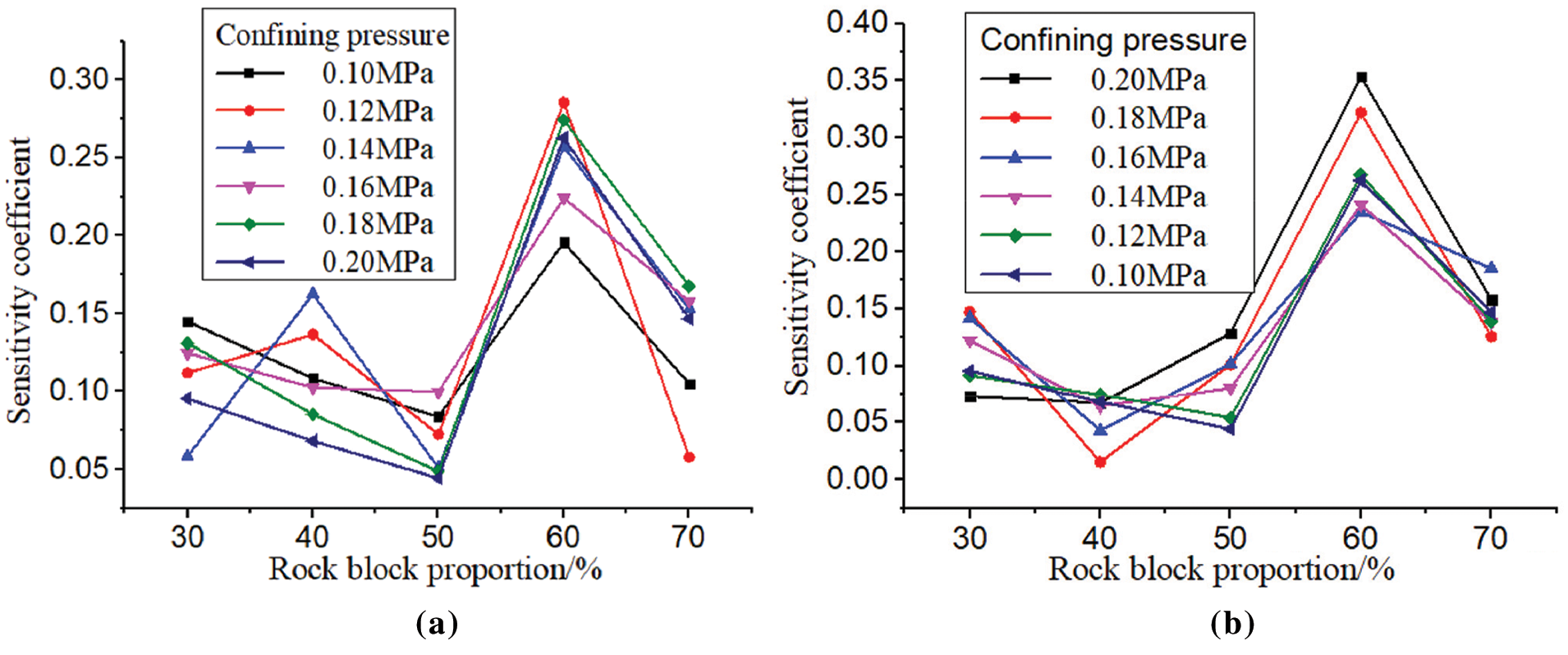
Figure 7: Variation curves between sensitive coefficient of S-RM sample and rock block proportion with different confining pressure (a) loading stage (b) unloading stage

It can be seen from the Fig. 7 that in the confining pressure loading and unloading stage, with the increase of rock block proportion, the sensitivity coefficient of the permeability coefficient of soil-rock mixture to the change of the rock block proportion shows the trend of first decreasing, then increasing and then decreasing. In the stage of confining pressure loading (see Fig. 7a), the sensitivity coefficient of the soil-rock mixture sample is basically the same under other confining pressure conditions except for some fluctuations under confining pressure of 0.12 MPa and 0.14 MPa. When the rock block proportion increases from 20% to 50%, the sensitivity coefficient of the sample decreases gradually and the sensitivity becomes worse; when the rock block proportion increases from 50% to 60%, the sensitivity of the sample reaches the strongest; when the rock block proportion continues to increase to 70%, the sensitivity of the sample begins to decline again. In the unloading stage of confining pressure (see Fig. 7b), the rock block proportion increases from 20% to 40%, and the sensitivity coefficient of soil-rock mixture sample decreases gradually; when the rock block proportion continues to increase from 40%, the sensitivity of the sample starts to increase under other confining pressure conditions except for the slightly decreased sensitivity under the confining pressure of 0.10 MPa and 0.12 MPa; when the rock block proportion reaches 60%, the sensitivity of the sample is the highest, and then began to decline.

The reason for the above phenomenon is that when the rock block proportion is low (20%∼50%), the soil is dominant in the soil-rock mixture, the sample is dense and the porosity is low, at this time, the increase of the rock block proportion is conducive to the influence of the soil on the permeability coefficient of the sample, resulting in the decrease of the sensitivity of the permeability coefficient of the sample to the change of rock block proportion. The rock block proportion continues to increase (50%∼60%), and the soil-rock mixture sample is in the transition stage from soil dominated to block stone dominated, at this time, the small change of rock block proportion may cause a great change in the porosity of the sample, so the permeability coefficient of the sample is highly sensitive to the change of rock block proportion; When the rock block proportion increases to 70%, the block stone is in the dominant position in the soil-rock mixture sample, and the influence of its content change on the sample porosity is very limited, resulting in the gradual decline of the sensitivity of the sample permeability coefficient to the change of rock block proportion.

3.4 Function Relationship between Permeability Coefficient and Confining Pressure of Soil-Rock Mixture

For the test results of the confining pressure and permeability coefficient of the soil-rock mixture samples with different rock block proportion in the process of confining pressure loading and unloading, all can be described by the function (3) through nonlinear fitting.

In the formula, k is the permeability coefficient of the soil-rock mixture sample (cm/s); k0 is the permeability coefficient when the confining pressure is equal to 0 (cm/s); b is the fitting parameter; pc is confining pressure (MPa).

In the process of confining pressure loading and unloading, the fitting curve and results of the relationship between the permeability coefficient and confining pressure of the earth rock mixture samples with different rock block proportion are shown in Fig. 8 and Table 2, respectively.

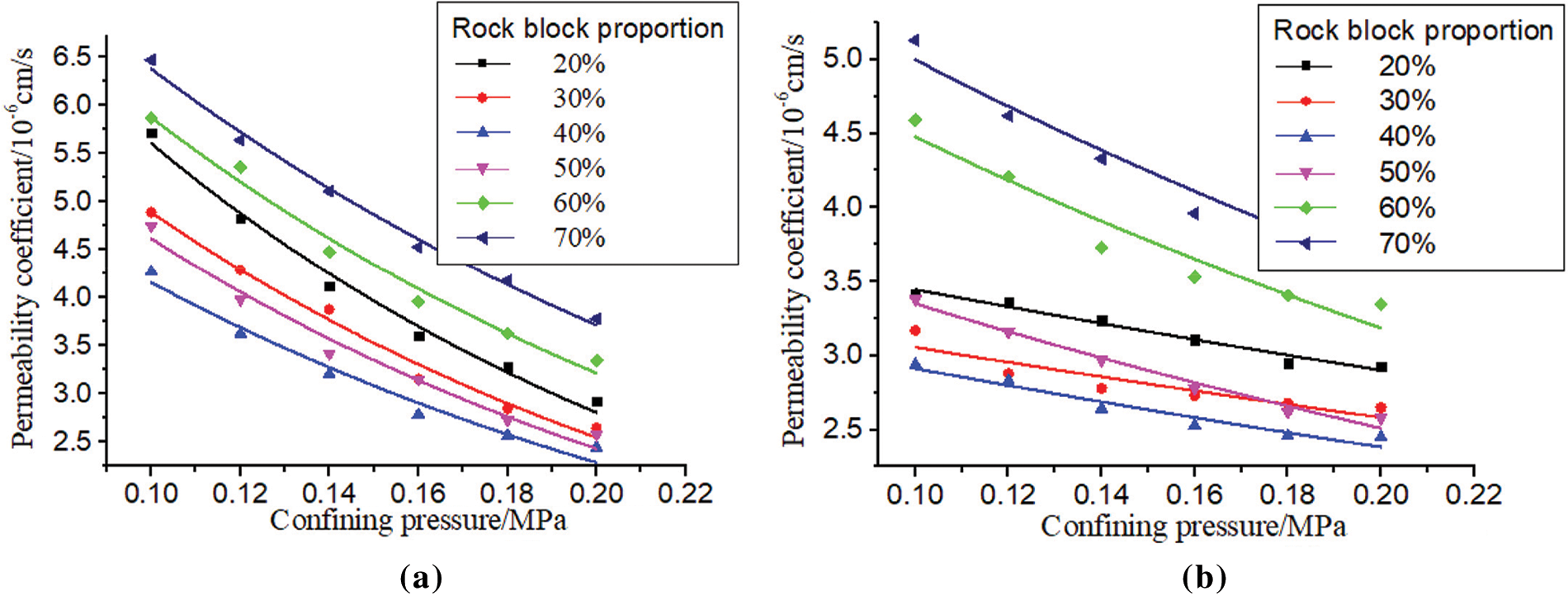
Figure 8: Fitting curves between permeability coefficient of S-RM sample and confining pressure (a) loading stage (b) unloading stage

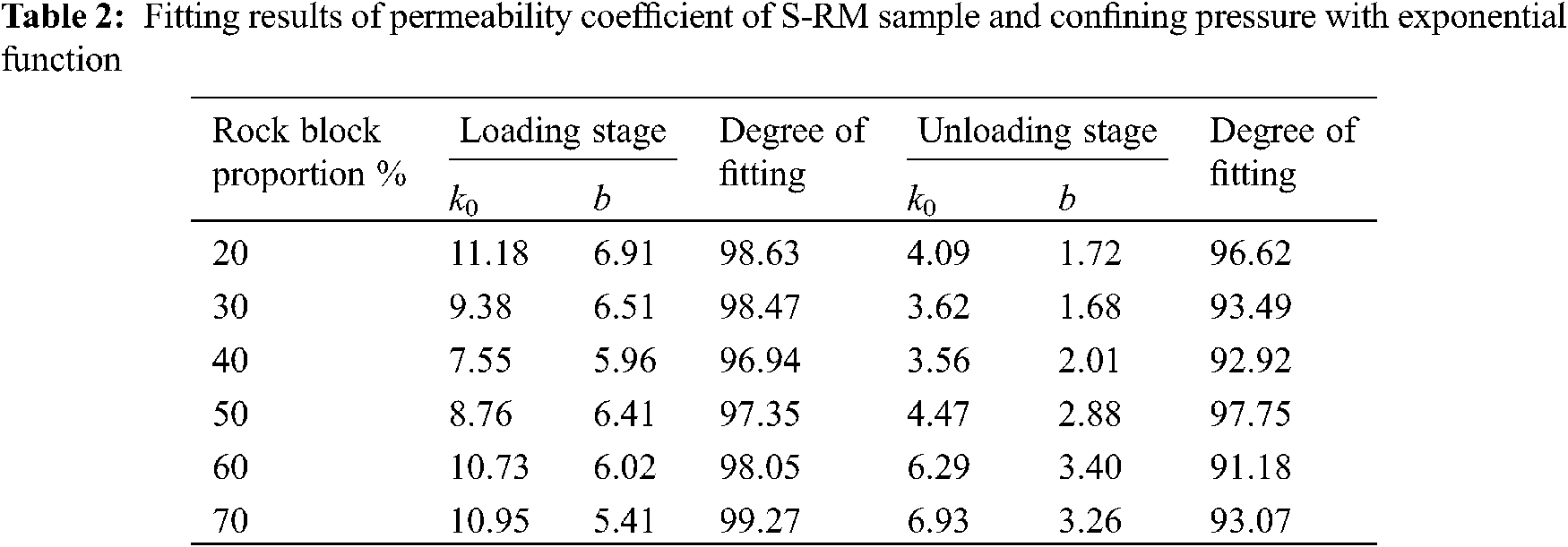
It can be seen from Fig. 8 and Table 2 that the curve fitting degree is higher than 91%, and the fitting effect is good. When the confining pressure is equal to 0.20 Mpa, the difference of the permeability coefficient of the six rock block proportion soil-rock mixture samples under the loading and unloading state is less than 0.1, which shows that the fitting curve of the two stages of loading and unloading has good closure, so this function can be used to describe the relationship between the permeability coefficient and confining pressure of the different rock block proportion soil-rock mixture samples.

(1) The permeability coefficient of soil-rock mixture samples with different rock block proportion decreases with the increase of confining pressure, and the decrease rate of permeability coefficient of samples is faster in the early stage of confining pressure loading, while the decrease rate of permeability coefficient of samples is relatively slow in the middle and late stage of confining pressure loading.

(2) In the stage of confining pressure loading and unloading, the permeability coefficient of soil-rock mixture samples under different confining pressure levels decreases first and then increases with the increase of rock block proportion, the permeability coefficient of samples with rock block proportion of 40% is the smallest and that of samples with rock block proportion of 70% is the largest.

(3) In the confining pressure unloading stage, the recovery degree of permeability coefficient of soil-rock mixture samples increases with the increase of rock block proportion, the recovery rate of permeability coefficient of samples with rock block proportion of 70% reaches 50.2%.

(4) In the stage of confining pressure loading and unloading, with the increase of rock block proportion, the sensitivity coefficient of permeability coefficient of soil-rock mixture to the change of rock block proportion shows a trend of first decreasing, then increasing and then decreasing, when the rock block proportion is 60%, the permeability coefficient of sample is the most sensitive to the change of rock block proportion.

(5) In the stage of confining pressure loading and unloading, the relationship between permeability coefficient and confining pressure can be described by exponential function.

Acknowledgement: The authors would like to thank the editors and the anonymous reviewers for their helpful and constructive comments.

Funding Statement: This work was supported by the Key Laboratory of Safety and High-Efficiency Coal Mining, Ministry of Education, Anhui University of Science and Technology (JYBSYS2020209), the Natural Science Research Project of Anhui Provincial Department of Education (KJHS2020B13) and the Huangshan University School Level Talent Launch Project (No. 2020XKJQ001).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

Zhang, Y. H. (2021). Study on technology of mine water disater prevention and control in underground mine under complex hydrogeological conditions. Coal Science and Technology, 49(3), 167-174. [Google Scholar]
Alimoradi, A., Moradzadeh, A., & Naderi, R. (2008). Prediction of geological hazardous zones in front of a tunnel face using TSP-203 and artificial neural networks. Tunnelling and Underground Space Technology, 23(6), 711-726. [Google Scholar] [CrossRef]
Raeesi, M., Moradzadeh, A., & Ardejani, F. D. (2012). Classification and identification of hydrocarbon reservoir lithofacies and their heterogeneity using seismic attributes, logs data and artificial neural networks. Journal of Petroleum Science and Engineering, 82, 151-165. [Google Scholar] [CrossRef]
Chen, Z. H., & Hu, Z. P. (2011). Fracture mechanical model and criteria of insidious fault water inrush in coal mines. Journal of China University of Mining & Technology, 40(5), 673-677. [Google Scholar]
Li, L. P. (2011). Water inrush mechanism study of fault activation induced by coupling effect of stress-seepage-damage. Chinese Journal of Rock Mechanics and Engineering, 30(1), 3295-3304. [Google Scholar]
Li, H. Y., & Zhang, H. J. (2017). The seepage-flowing conversion mechanism of the fault lagging water inrush and its numerical simulation. Journal of Mining & Safety Engineering, 34(2), 323-329. [Google Scholar]
Afifipour, M., & Moarefvand, P. (2014). Failure patterns of geomaterials with block-in-matrix texture: Experimental and numerical evaluation. Arabian Journal of Geosciences, 7(7), 2781-2792. [Google Scholar] [CrossRef]
Alshibli, K. A., Sture, S., & Costes, N. C. (2000). Assessment of localized deformations in sand using X-ray computed tomography. Geotechnical Testing Journal, 23(3), 274-299. [Google Scholar] [CrossRef]
Coli, N., Berry, P., & Boldini, D. (2011). non-conventional shear tests for the mechanical characterization of a bimrock. International Journal of Rock Mechanics and Mining Sciences, 48(1), 95-102. [Google Scholar] [CrossRef]
Kim, F. H., Penumadu, D., & Gregor, J. (2013). High-resolution neutron and X-ray imaging of granular materials. Journal of Geotechnical and Geoenvironmental Engineering, 139(5), 715-723. [Google Scholar] [CrossRef]
Medley, E. W. (2001). Orderly characterization of chaotic franciscan melanges. Engineering Geology, 4, 20-33. [Google Scholar]
Michalowski, R. L., & Shi, L. (2003). Deformation patterns of reinforced foundation sand at failure. Journal of Geotechnical and Geoenvironmental Engineering, 29(6), 439-449. [Google Scholar] [CrossRef]
Muirwood, D. (2002). Some observations of volumetric instabilities in soils. International Journal of Solids and Structures, 39(13), 3429-3449. [Google Scholar] [CrossRef]
Rahardjo, H., Indrawan, I., & Leong, E. C. (2008). Effects of coarse-grained material on hydraulic properties and shear strength of top soil. Engineering Geology, 101(3), 165-173. [Google Scholar] [CrossRef]
Springman, S. M., Jomm, C., & Teysseire, P. (2003). Instabilities on moraine slopes induced by loss of suction: A case history. Geotechnique Letters, 53(1), 3-10. [Google Scholar] [CrossRef]
Iannacchione, A. T. (1997). Shear strength of saturated clays with floating rock particles (Ph.D. Thesis). University of Pittsburgh, Pennsylvania, Pittsburgh.
Otani, J., Mukunoki, T., & Obara, Y. (2000). Characterization of failure in sand under triaxial compression using an industrial X-ray CT scanner. Soil and Foundations, 40(2), 111-118. [Google Scholar] [CrossRef]
Sun, H. F. (2014). Review of the study on deformation failure and the mesomechanisms of rock-soil mixture (RSM). SCIENTIA SINICA Technologica, 44(2), 172-181. [Google Scholar] [CrossRef]
Yang, Z. P. (2021). Influence of stone content on shear mechanical properties of soil-rock mixture-bedrock interface. Chinese Journal of Geotechnical Engineering, 12(5), 323-329. [Google Scholar]
Mokwa, R. L., & Robert, N. R. (2008). Permeability of coarse-grain soil from void space and pore distribution. Geotechnical Special Publication, 179, 428-435. [Google Scholar] [CrossRef]
Zhou, Z., & Yang, H. (2017). Model development and experimental verification for permeability coefficient of soil-rock mixture. International Journal of Geomechanics, 17(4), [Google Scholar]
Xu, W. J., & Wang, Y. G. (2010). Meso-structural permeability of S-RM based on numerical tests. Chinese Journal of Geotechnical Engineering, 32(4), 542-550. [Google Scholar]
Xu, J. C., & Shang, Y. Q. (2016). Influence of permeability of gravel soil on debris landslide stability. Chinese Journal of Rock Mechanics and Engineering, 25(11), 2264-2271. [Google Scholar] [CrossRef]
Zhou, Z., & Fu, H. L. (2016). Orthogonal tests on permeability of soil-rock-mixture. Chinese Journal of Geotechnical Engineering, 28(9), 1134-1138. [Google Scholar] [CrossRef]
Zabler, S., Rack, A., & Manke, I. (2008). High-resolution tomography of cracks, voids and micro-structure in greywacke and limestone. Journal of Structural Geology, 30(7), 876-887. [Google Scholar] [CrossRef]
Vallejo, L. E., & Mawby, R. (2000). Porosity influence on the shear strength of granular material-clay mixtures. Engineering Geology, 58(2), 125-136. [Google Scholar] [CrossRef]
Vardoulakis, I., Sulem, J. (1995). Bifurcation analysis in geomechanics. Glasgow: Blackie Academic & Professional.
Gu, J. L. (2009). Development of servo-control rock and soil aggregate permeability test apparatus. Journal of Engineering Geology, 17(5), 711-716. [Google Scholar] [CrossRef]
Xu, W. J., Hu, R. L., & Yue, Z. Q. (2018). Meso-structure character of soil-rock mixtures based on digital image. Journal of Liaoning Technical University, 27(1), 51-53. [Google Scholar]
Shen, H. (2017). Numerical simulation of internal erosion characteristics of block in matrix soil aggregate. Rock and Soil Mechanics, 38(5), 1497-1509. [Google Scholar] [CrossRef]
Tang, J. Y., Xu, D. S., & Liu, H. B. (2018). Effect of gravel control on shear behavior of sand-gravel mixture. Rock and Soil Mechanics, 39(1), 93-102. [Google Scholar] [CrossRef]
Huang, Z. Q., Wu, C., Bi, L. Y., Zhang, R., & Zhang, Z. H. (2017). Experimental study on influencing factors of dynamic shear module and damping ratio of fault gouge. Journal of Engineering Geology, 25(1), 50-57. [Google Scholar] [CrossRef]