 Open Access
Open Access
ARTICLE
Phase Transition in a Dense Swarm of Self-Propelled Bots
Applied Physics Department, Perm National Research Polytechnic University, Perm, 614990, Russia
* Corresponding Author: Dmitry Bratsun. Email:
(This article belongs to the Special Issue: Advanced Problems in Fluid Mechanics)
Fluid Dynamics & Materials Processing 2024, 20(8), 1785-1798. https://doi.org/10.32604/fdmp.2024.048206
Received 30 November 2023; Accepted 01 March 2024; Issue published 06 August 2024
Abstract
Swarms of self-organizing bots are becoming important elements in various technical systems, which include the control of bacterial cyborgs in biomedical applications, technologies for creating new metamaterials with internal structure, self-assembly processes of complex supramolecular structures in disordered media, etc. In this work, we theoretically study the effect of sudden fluidization of a dense group of bots, each of which is a source of heat and follows a simple algorithm to move in the direction of the gradient of the global temperature field. We show that, under certain conditions, an aggregate of self-propelled bots can fluidize, which leads to a second-order phase transition. The bots’ program, which forces them to search for the temperature field maximum, acts as an effective buoyancy force. As a consequence, one can observe a sudden macroscopic circulation of bots from the edge of the group to its center and back again, which resembles classical Rayleigh-Benard thermal convection. In the continuum approximation, we have developed a mathematical model of the phenomenon, which reduces to the equation of a self-gravitating porous disk saturated with an incompressible fluid that generates heat. We derive governing equations in the Darcy-Boussinesq approximation and formulate a nonlinear boundary value problem. An exact solution to the linearized problem for infinitesimal perturbations of the base state is obtained, and the critical values of the control parameter for the onset of the bot circulation are calculated. Then we apply weakly nonlinear analysis using the method of multiple time scales. We found that as the number of bots increases, the swarm exhibits increasingly complex patterns of circulation.Graphic Abstract
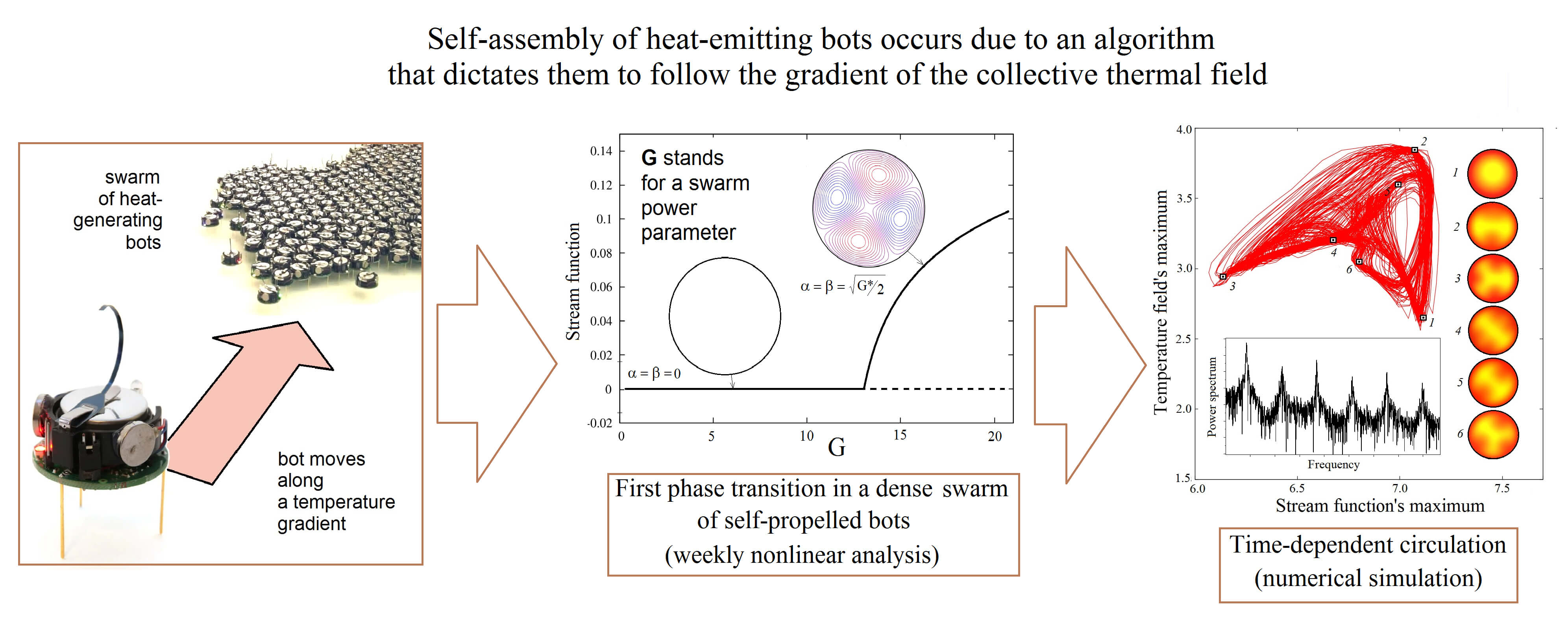
Keywords
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools