Monthly Reduced Time-Period Scheduling of Thermal Generators and Energy Storage Considering Daily Minimum Chargeable Energy of Energy Storage

1  Introduction

i) Motivation

The development of renewable energy is a crucial approach to mitigating the energy and environmental crises [1]. However, the continuous increase in renewable energy penetration has reduced the flexibility of power generation sources, resulting in mismatches between power supply and demand within the system [2]. This issue becomes particularly pronounced during extreme cold weather, when renewable energy output is severely constrained, leading to prolonged power shortages lasting several hours or even multiple days [3−5]. Under such circumstances, effective scheduling on a longer monthly time scale and the reasonable formulation of operation plans for flexible resources, such as thermal generators and energy storage systems, are essential to bridging the power supply-demand gap and maintaining system balance.

ii) Literature review

For monthly scheduling, Reference [6] developed a multi-objective monthly power generation planning model that accounts for energy supply constraints. Reference [7] proposed a long-term power generation planning approach that considers extreme scenarios within the month to enhance the feasibility and reliability of the scheduling process. Reference [8] introduced a stochastic decision-making model for monthly unit commitment and maintenance planning, achieving the joint optimization of power generation scheduling and maintenance tasks. Reference [9] presented a monthly joint maintenance and power generation scheduling model using fuzzy chance-constrained programming. References [10,11] constructed a mixed-integer linear programming (MILP) model for monthly optimization scheduling that incorporates fuel supply uncertainty, thereby improving the efficiency and reliability of fuel supply scheduling. Reference [12] proposed a short-term multi-objective economic and emissions optimization method for combined heat and power (CHP) systems based on an enhanced epsilon-constraint technique and fuzzy decision-making. This method optimizes both total costs and pollutant emissions while considering non-linear fuel cost characteristics, valve-point effects, and power transmission losses. Reference [13] introduced a decentralized monthly scheduling method for cascade hydropower systems under multiple time scales. Reference [14] developed a robust preventive-corrective security-constrained optimal power flow model, systematically addressing both short-term emergency limits and long-term operational constraints following incidents, to optimize the reliability of generation scheduling strategies. The aforementioned studies primarily focus on monthly scheduling based on hourly time granularity, resulting in more refined scheduling outcomes. However, such models also increase the complexity of monthly scheduling, limiting their applicability in real-world scenarios.

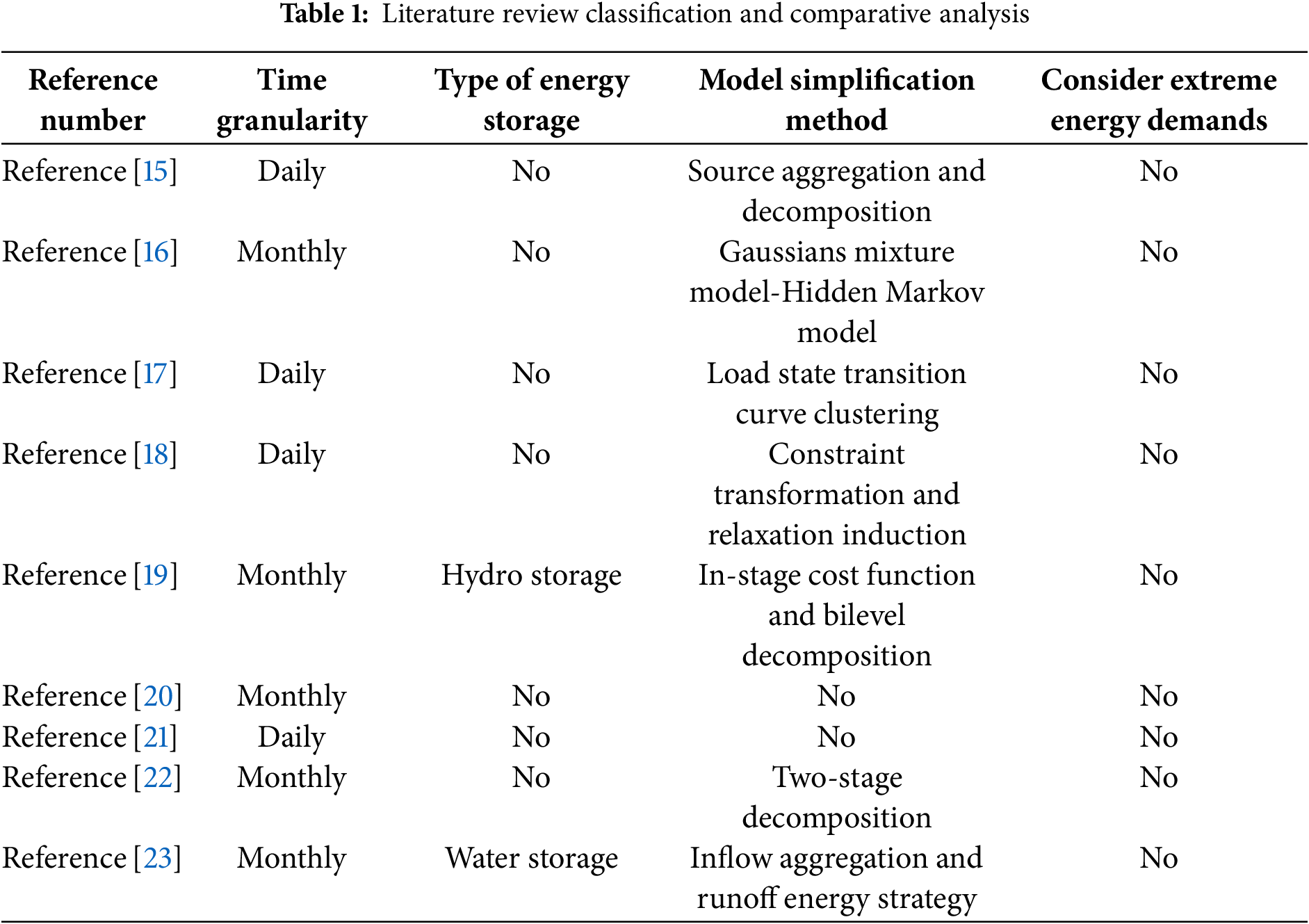
To address the issue of the excessive scale of monthly power generation decision-making, Reference [15] proposed a monthly power generation optimization method based on a power aggregation-decomposition model. Reference [16] introduced a Gaussian Mixture Model-Hidden Markov Model (GMM-HMM) approach to construct generation models for long-term correlated output time series across multiple wind farms, improving the modeling accuracy of wind power output sequences. Reference [17] developed an efficient unit commitment model using load state transition analysis, which reduced computational time while maintaining high accuracy. Reference [18] constructed a multi-scenario monthly scheduling model for coordinated short-term scheduling and proposed an improved branch-and-bound algorithm for solving it. Reference [19] presented a two-stage Benders decomposition and dual dynamic programming method to build a phased cost function model for medium-term planning, enhancing the reliability of scheduling strategies. Reference [20] introduced a monthly unit commitment model incorporating wind power interval prediction information and wind curtailment costs, with a solution strategy based on the Memetic algorithm. Reference [21] proposed a monthly thermal unit commitment model that considers multi-level transmission constraints and includes a heuristic method for transmission section over-limit verification and unit start-up and shut-down corrections. Reference [22] developed a two-stage renewable energy system unit commitment model, achieving optimal coordination between unit commitment and economic scheduling. Reference [23] proposed a long-term generation scheduling optimization method based on inflow aggregation and runoff energy flow, improving both scheduling efficiency and economics. While these studies primarily focus on the development of monthly scheduling models and efficient solution algorithms to accelerate model computation, they often fail to adequately simplify monthly scheduling models. Moreover, they do not fully account for the energy storage charging and discharging processes under various net load conditions. This limitation may lead to insufficient chargeable energy during operation, making it challenging to effectively meet discharge demands during periods of power shortages. The classification and comparative analysis of the literature review are shown in Table 1.

iii) Research gaps

Although existing literature has made notable contributions to monthly scheduling optimization, several gaps remain:

(1) High computational complexity: Scheduling studies utilizing hourly time granularity often involve numerous variables and constraints. The complexity escalates further when robust optimization methods are applied, thereby limiting the feasibility of these approaches in large-scale power systems.

(2) Impact of simplification strategies on accuracy: To mitigate computational complexity, some studies employ daily time granularity to simplify scheduling models. However, this approach overlooks the dynamic characteristics at shorter time scales, resulting in an inadequate representation of load fluctuations and inter-period coupling effects, which ultimately diminishes the accuracy of the model.

(3) Insufficient modeling of energy storage: Current research tends to simplify the modeling of energy storage charge and discharge processes, failing to incorporate dynamic constraints under extreme operating conditions. In particular, during high-load scenarios, energy storage scheduling may not meet supply demands, thereby undermining the system’s reliability and adaptability in extreme conditions.

iv) Contributions

To address the large model size due to the long monthly scheduling period, this study consolidates unit startup/shutdown periods based on the varying degrees of net load fluctuations in renewable energy systems, reducing the number of variables and model complexity. A thermal-storage operational constraint is developed, considering the daily net load fluctuations and ensuring energy storage charging limits are met under maximum net load conditions. The objective is to minimize thermal power operation and load shedding costs while incorporating coupling constraints between thermal power and energy storage across multiple time periods. A variable-period fire-storage monthly scheduling model with daily minimum rechargeable capacity constraints is constructed. Case analysis demonstrates that the proposed model provides an economically efficient monthly operation plan, significantly reducing solution time while meeting energy storage charging requirements under extreme net load conditions.

This paper presents several main contributions and innovation points:

(1) A variable-time-period collaborative scheduling strategy for thermal power and energy storage is proposed, considering load fluctuation characteristics. Through a time-period clustering simplification method, the number of decision variables for unit startup and shutdown is reduced, significantly decreasing the computational scale of the model and improving solution efficiency.

(2) The daily minimum charging capacity constraint for the energy storage system is introduced, and a monthly scheduling model that integrates both the minimum charging demand and maximum discharge capacity is constructed. This model enhances the energy storage system’s ability to regulate under extreme load and climatic conditions.

(3) A case study for extreme cold weather conditions was constructed. Simulation results demonstrate that this method effectively addresses power supply and demand imbalances under extreme weather conditions, improving the system’s reliability and flexibility under extreme load conditions.

v) Organization

The paper is structured as follows: Section 2 outlines the fire-storage scheduling framework. Section 3 discusses reducing unit startup/shutdown periods and its impact on scalability. Section 4 addresses the daily minimum charging constraint and storage charging demand. Section 5 presents the fire-storage model and analysis. Section 6 validates the method through case studies. Section 7 concludes with key findings and future directions.

2  Framework of the Monthly Reduced Time-Period Scheduling

Considering the operating constraints of conventional thermal generators and new regulating resources such as hydrogen energy storage and electrochemical energy storage, a monthly scheduling plan for thermal generators and energy storage with the best operating economy is formulated, and energy storage discharge energy is reasonably reserved to make up for the shortfall in power supply and demand.

The monthly scheduling time-period is long, and the number of decision time-periods for unit start-up and shut-down is large, which may lead to a long solution time for the monthly scheduling problem and make it difficult to meet the calculation time requirements, at the same time, the net load (the difference between load power and renewable energy generation power) of the high-proportion renewable energy power system has strong uncertainty. To formulate a monthly scheduling plan, it is necessary to ensure that energy storage has sufficient chargeable space under various net load scenarios to meet future discharge needs.

In this regard, the framework of the monthly reduced time-period scheduling of thermal generators and energy storage is designed as shown in Fig. 1. Based on the net load fluctuation characteristics, the number of decision periods for unit start-up and shut-down variables is reduced to effectively decrease the number of start-up and shut-down decision variables and reduce the scale of the monthly scheduling problem, a minimum chargeable amount constraint for energy storage that meets the charging and discharging needs under extreme net load scenarios is constructed, so that the energy storage can be charged with enough electricity every day to cope with future discharge needs, considering power balance constraints, operating constraints of thermal generators and energy storage, with the goal of minimizing the thermal generators and energy storage operating cost and load loss cost, a monthly scheduling model is constructed, based on this, a monthly unit commitment and energy storage charging and discharging plan are obtained.

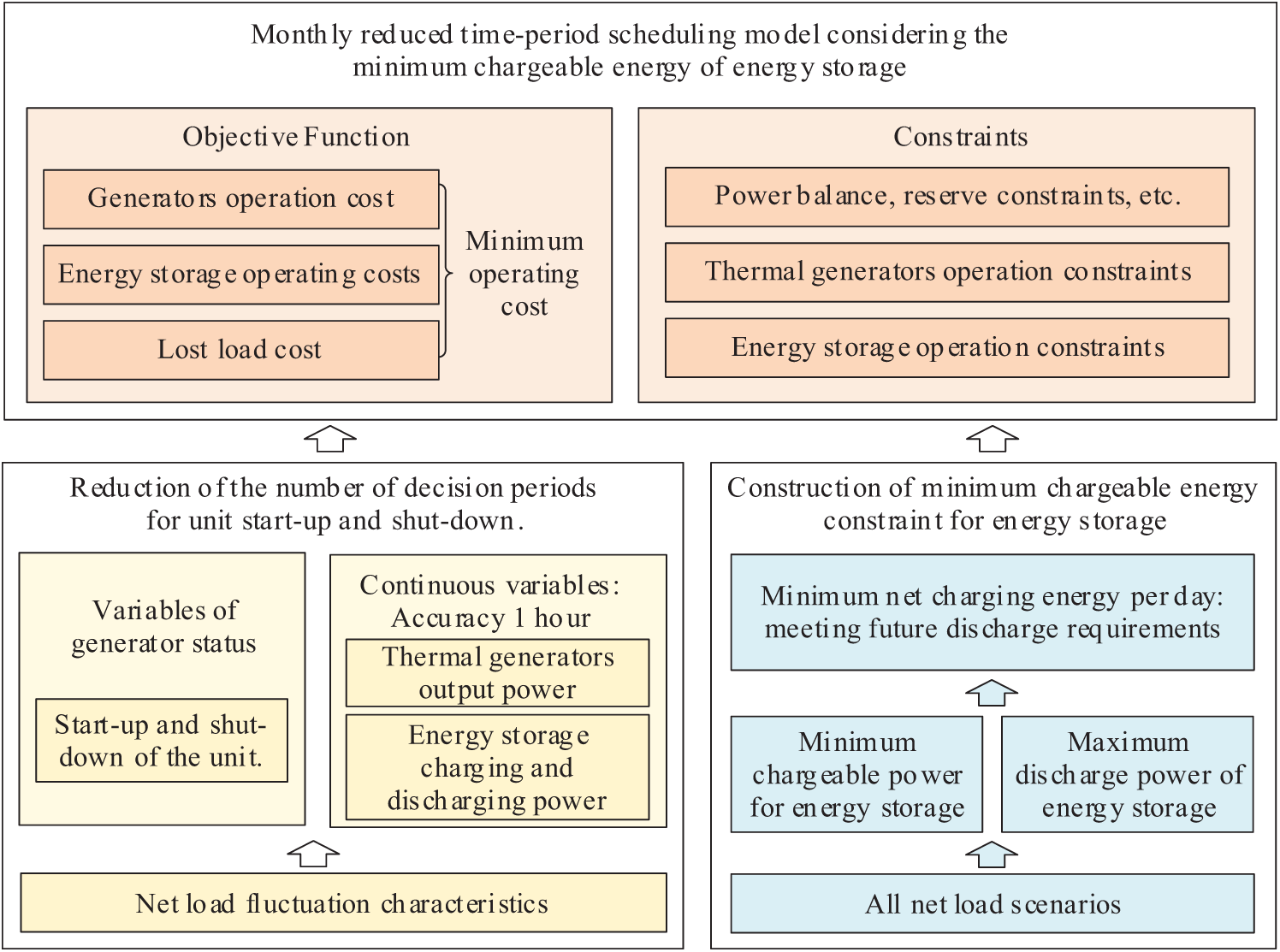
Figure 1: Sketch of the monthly reduced time-period scheduling framework

3  Reduction of the Number of Decision Periods for Start-Up and Shut-Down Variables Based on Net Load Fluctuation Characteristics

Considering that unit start-up and shut-down occur less frequently when net load fluctuations are small, it is approximated that the unit’s status remains unchanged during periods of minor load changes. Therefore, several adjacent time intervals with small load variations can be merged into a single time-period for start-up and shut-down, reducing the number of decisions for unit status. The specific implementation method is as follows.

3.1 Clustering of Net Load Power

The net load power is:

(1)

where is the set of all time-periods, each time-period is 1 h, and T is the number of time-periods, , and are the predicted mean values of load power, renewable energy output, and net load power at time t, respectively.

Normalize the net load, and assume the normalized load is , then:

(2)

where is the set of all time-periods, is the set of time-periods on the d-th day, Th is the number of time-periods per day, is the set of all days, and D is the number of days.

The net load is clustered based on the k-means algorithm. The idea is to divide a large number of net load data points into several clusters according to their power size. The basic calculation steps are as follows [24,25]:

(a) The net load sample set for cluster analysis is defined as .

(b) Determine the number of clusters as N, select N sample points as the initial cluster centers, and represent the i-th cluster center.

(c) For each sample point , calculate its distance from all cluster centers :

(3)

where represents the t-th sample point, and represents the i-th cluster center corresponding to the t-th sample point.

(d) Assign sample to the cluster center with the shortest distance to form clusters corresponding to N cluster centers. The net load data set of the i-th cluster is .

(e) Update the cluster center and calculate the average value of all sample points in each cluster as the new cluster center :

(4)

where Mi is the number of samples in the i-th cluster , and is the new cluster center of the cluster.

(f) Determine whether the cluster center of each cluster after the update is different from the cluster center before the update. If yes, repeat steps (d) and (e). Otherwise, the classification ends.

3.2 Reduction of Decision Time-Periods for Unit Start-Up and Shut-Down

Combined with the method described in 3.1, the net loads are clustered into several categories, where the power of adjacent net loads in the same category is relatively similar. It is approximated that the unit’s status remains unchanged during these time-periods, allowing the corresponding time-periods to be merged into a single decision time-period for start-up and shut-down.

The process of reducing decision time-periods for unit start-up and shut-down is illustrated in Fig. 2. By continuously rolling forward the calculations, adjacent time periods with similar net load power are merged into a single decision time-period for unit start-up and shut-down.

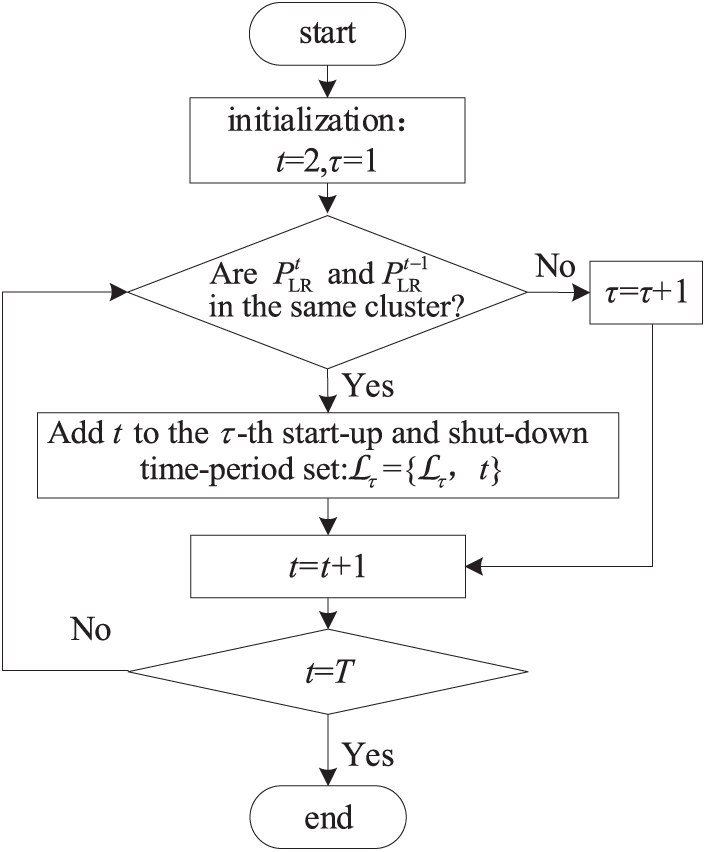
Figure 2: Flowchart for reducing decision time-periods for unit start-up and shut-down

The effect of reducing decision time-periods for unit start-up and shut-down is shown in Fig. 3. In the figure, is the set of hours in the τ-th decision period for start-up and shut-down, tst.τ, Tτ are the starting hour and number of hours of the τ-th time-period for start-up and shut-down, respectively. is the set of decision time-periods for unit start-up and shut-down, , is the number of decision time-periods for unit start-up and shut-down. , .

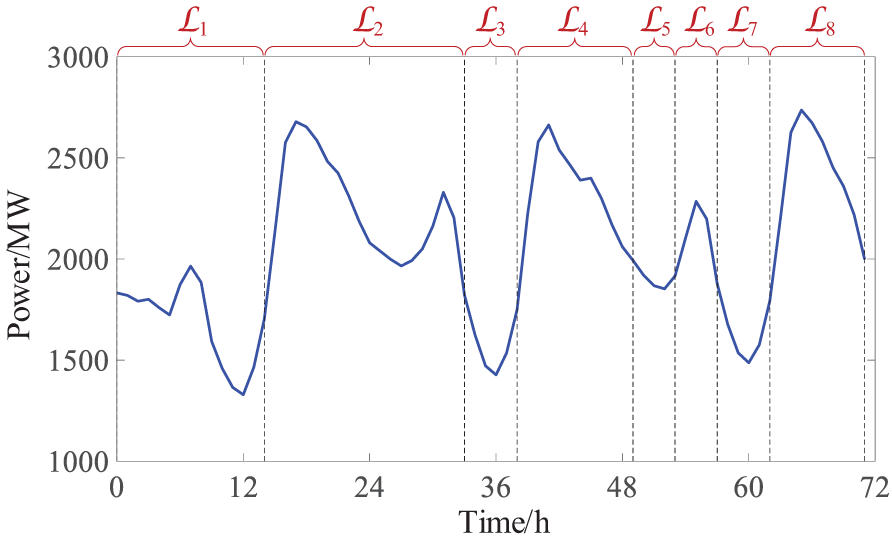
Figure 3: Schematic diagram showing the reduction effects on decision time-periods for unit start-up and shut-down

The number of decision time-periods for unit start-up and shut-down after reduction is significantly fewer than the number of hours, which can greatly reduce the scale of the generator status (0: ‘off’, 1: ‘on’) variables and shorten the solution time of the monthly scheduling model.

4  The Minimum Daily Chargeable Energy Constraint for Energy Storage

Under the maximum net load, the discharge power of the energy storage is the largest and the chargeable power is the smallest. If the charge and discharge power integral meets the energy constraint at this time, the charging demand of the energy storage under various net loads can be met. Therefore, the chargeable capacity constraint of the energy storage under the maximum net load can be constructed. The specific method is as follows.

4.1 Calculation of Maximum Discharge Power and Minimum Chargeable Power of Energy Storage

According to the net load fluctuation characteristics, the maximum discharge power and minimum chargeable power of energy storage are analyzed, as shown in Fig. 4. When the maximum net load is greater than the maximum output of thermal generators, energy storage needs to be discharged, and the gray shaded part is the energy storage that needs to be discharged, when the maximum net load is less than the maximum output of thermal generators, the energy storage can be charged, and the green shaded part is the energy storage that can be charged.

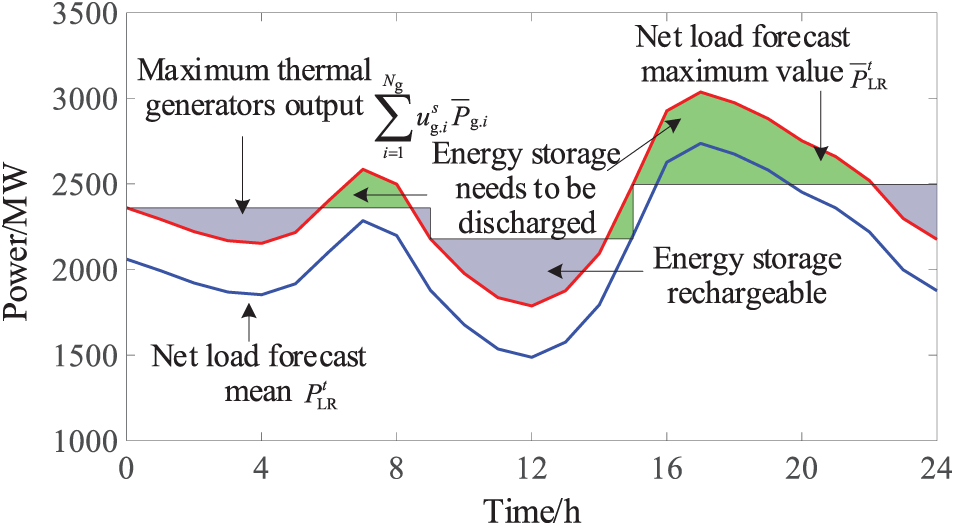
Figure 4: Schematic diagram of calculation of minimum chargeable capacity and maximum discharge capacity of energy storage day

Assume and are the maximum discharge power and minimum chargeable power of energy storage at time t, respectively. According to the meaning shown in Fig. 1, considering load loss and thermal generators output adjustment, the calculation formula can be summarized as follows:

(5)

where is the set of all units, Ng is the number of units, is the set of all energy storage systems, is the number of energy storage systems, , and are the maximum load forecast at time t, the maximum renewable energy output forecast and the corresponding load loss power, respectively, and represent the maximum output of unit i and the generator status (0: ‘off’, 1: ‘on’) in the τ-th decision time-period for unit start-up and shut-down, respectively. represents the unit status is on and represents the unit status is off, represents the reduction value of thermal generators output compared to its total maximum output.

4.2 Energy Storage Charging and Discharging Energy Constraints under the Most Extreme Net Load

It is required that under the maximum net load, the difference between the minimum chargeable amount and the maximum discharge amount of the energy storage every day meets the energy constraint and is greater than the energy storage energy at the end time of each day in the monthly decision:

(6)

(7)

(8)

where and are the discharge power and charging power of the energy storage at time t, respectively, and are the discharge efficiency and charging efficiency of the energy storage, respectively, is the energy storage charge and discharge energy coefficient, , is the upper limit of the energy storage capacity. The left-hand side of Eq. (6) represents the minimum charge power of the energy storage system on a given day under the maximum net load, while the right-hand side represents the charging power of the energy storage system on that day according to the monthly scheduling plan. Eq. (6) ensures that the minimum charge energy of the energy storage system under the maximum net load can still meet the charging requirements of the scheduling plan, meaning the monthly scheduling plan remains feasible even under the maximum net load.

5  Monthly Scheduling Model

Combined with the reduction of the time-periods for unit start-up and shut-down and the construction of the daily minimum chargeable capacity constraint of energy storage, a monthly thermal generators and energy storage scheduling model is constructed by considering constraints such as thermal generators and energy storage operation cost, load loss cost and thermal generators and energy storage operation.

5.1 Objective Function

The goal is to minimize the total operating costs and load loss costs of thermal generators and energy storage.

(9)

where , , and are the thermal generators output, energy storage charging and discharging power, and load loss power at time t, respectively, , , and are the thermal generators cost, energy storage operation cost, and load loss cost, respectively:

(10)

(11)

(12)

(13)

5.2 Constrained Conditions

(1) Power balance constraints

(14)

where and are the load power and renewable energy output at time t, respectively.

(2) Reserve constraints

(15)

(16)

where and are the upper and lower reserve requirements at time t, respectively.

(3) Thermal generators operation constraints

① Output upper and lower limit constraints

(17)

where and are the upper and lower limits of thermal generators output, respectively.

② Climbing constraint

(18)

where and are the maximum power increase rate and decrease rate of thermal generators, respectively, and are the maximum start-up power change rate and shut-down power change rate of thermal generators power, respectively.

③ Minimum start-up and shut-down time constraints

(19)

(20)

where and are the number of the decision time-periods for unit start-up and shut-down that thermal generators i needs to maintain starting up and shutting down from the τ start-stop periods. Since the time window length of each time-period for unit start-up and shut-down is different, and are related to the unit start-up and shut-down time-period. The calculation formula is as follows:

(21)

(22)

where and are the minimum start-up time and shut-down time of thermal generators, respectively.

(4) Energy storage operation constraints

Considering electrochemical energy storage and hydrogen energy storage, for the convenience of modeling and analysis, the unified operating constraints for both types of energy storage are established by referring to the method in [26], as follows:

① Charge and discharge power constraints [27]

(23)

(24)

(25)

(26)

where and are the maximum discharge power and maximum charging power of energy storage, respectively. and are binary decision variables indicating whether discharging and charging operations occur at time t, respectively. Specifically, denotes discharging, while denotes charging. These variables take values of 0 or 1, determining the execution of corresponding operations.

② Energy-power integration constraint

(27)

where is the energy storage at time t.

③ Energy constraint

(28)

(29)

For different types of energy storage, , , and correspond to different physical meanings. For example, for hydrogen energy storage, they represent the equivalent electrical quantity of the fuel cell power, the hydrogen electrolyzer power, and the hydrogen storage capacity of the hydrogen storage tank, respectively.

(5) Load loss constraint

(30)

where is the maximum allowable load loss at time t.

The current model assumes fixed parameters for thermal power plants and energy storage systems, but these can fluctuate due to environmental conditions. For example, thermal plant efficiency and load regulation are affected by temperature, while hydrogen storage efficiency and energy losses depend on temperature and pressure. Such variations may reduce optimization accuracy and model adaptability. Future research should incorporate environmental dynamics through parameter prediction models and use robust optimization or Monte Carlo simulations to address uncertainties, improving robustness and predictive accuracy for coordinated operations under complex conditions.

6  Case Study

6.1 Case Setup

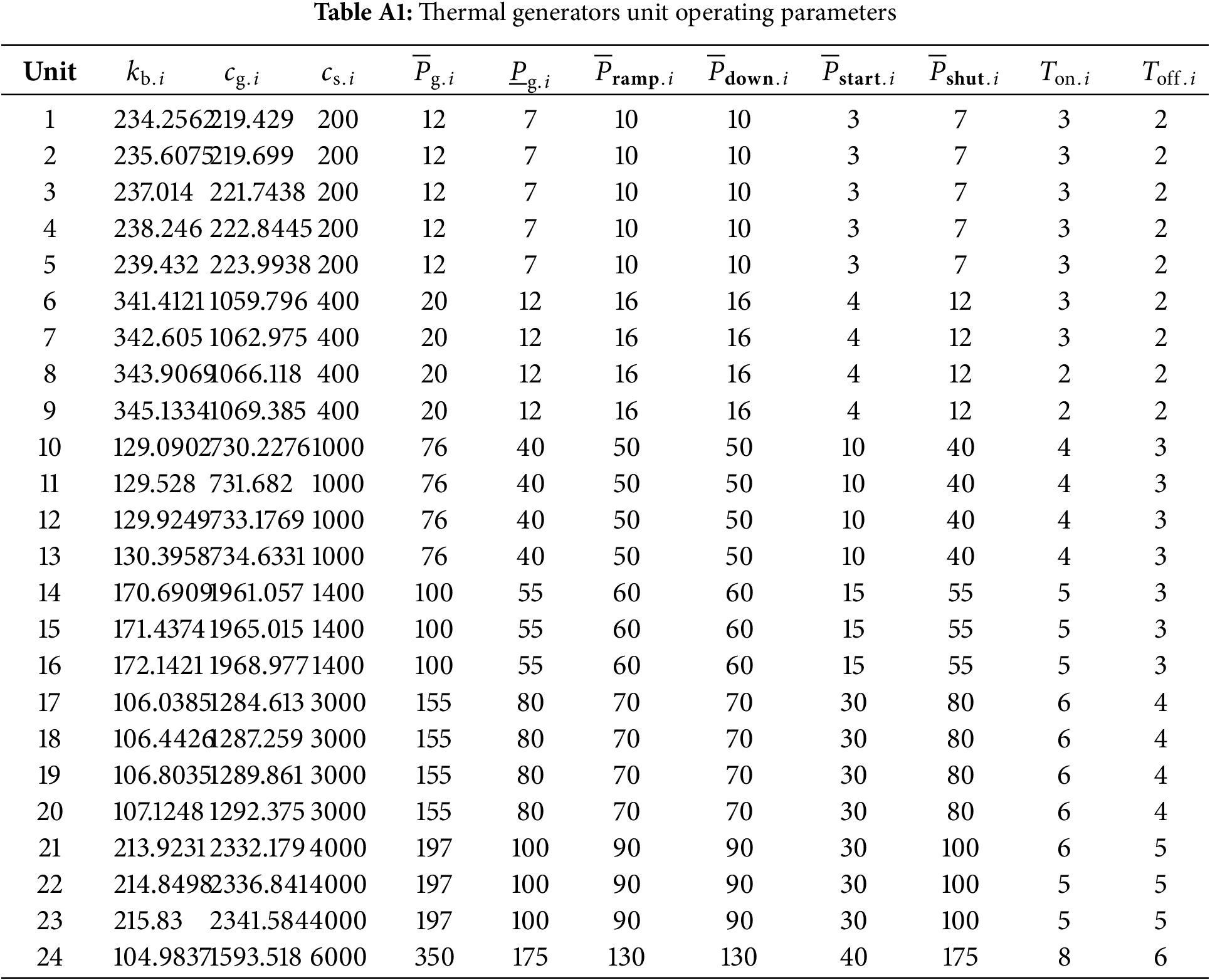
Consider a high-ratio wind-solar system, with thermal generators installed capacity of 2305 MW, wind power and photovoltaic installed capacities of 1100 and 935 MW, respectively, and battery energy storage and hydrogen energy storage configurations of 200 MW × 2 h and 200 MW × 10 h, respectively. The parameters of the thermal power plant are detailed in Table A1, while the storage parameters are outlined in Table 2 [28]. The parameter setting of energy storage systems is based on their technical characteristics. Electrochemical energy storage typically uses lithium batteries, which have high charge/discharge efficiency and low energy density. Therefore, when selecting, the focus is on efficiency and smaller rated capacity. In contrast, hydrogen storage generates hydrogen through an electrolyzer and utilizes fuel cells for charge and discharge. Due to the large capacity of hydrogen storage tanks, the selection focuses more on lower efficiency but larger rated energy capacity.

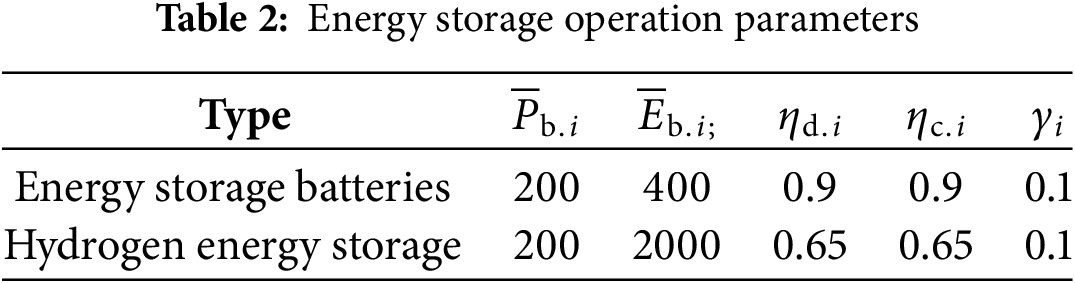
The load, wind, and solar output curves are shown in Figs. 5 to 7, respectively. On the 22nd and 23rd days, there was extreme cold weather. The load increased, while the wind and solar output decreased significantly. The maximum allowable load loss power is 5% of the load in the corresponding period on the 22nd and 23rd days, and 0 on the other days.

Figure 5: Monthly load power

Figure 6: Monthly wind power

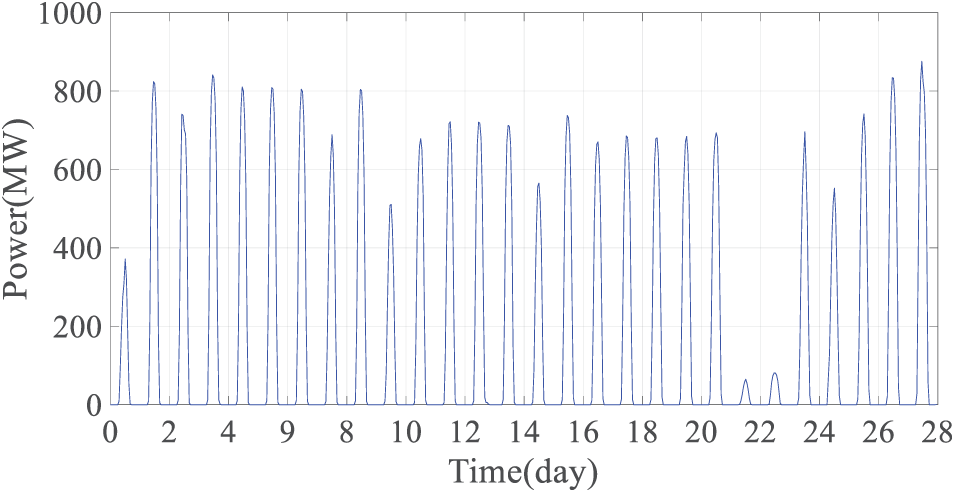
Figure 7: Monthly photovoltaic power generation

6.2 Case Results

6.2.1 Evaluation of Monthly Scheduling Outcomes

The reduced time-periods for unit start-up and shut-down for the units are shown in Fig. 8. During periods of significant net load fluctuations, the number of the decision time-periods for unit start-up and shut-down obtained through reduction is larger. This enables thermal generators to respond effectively to substantial net load fluctuations, adapting to the more frequent start-up and shut-down occurrences during these periods. Conversely, during periods of smaller net load fluctuations, the number of the decision time-periods for unit start-up and shut-down is reduced, minimizing the number of decision variables while still meeting the operational requirements of the thermal generators. According to statistics, the number of reduced decision time-periods for unit start-up and shut-down is 149. At this stage, the number of 0–1 integer decision variables (generator status (0:‘off’, 1:‘on’), variables of generator status) is reduced from 2106 (24 × 28 × 3) to 447 (149 × 3), significantly decreasing the scale of the monthly decision model.

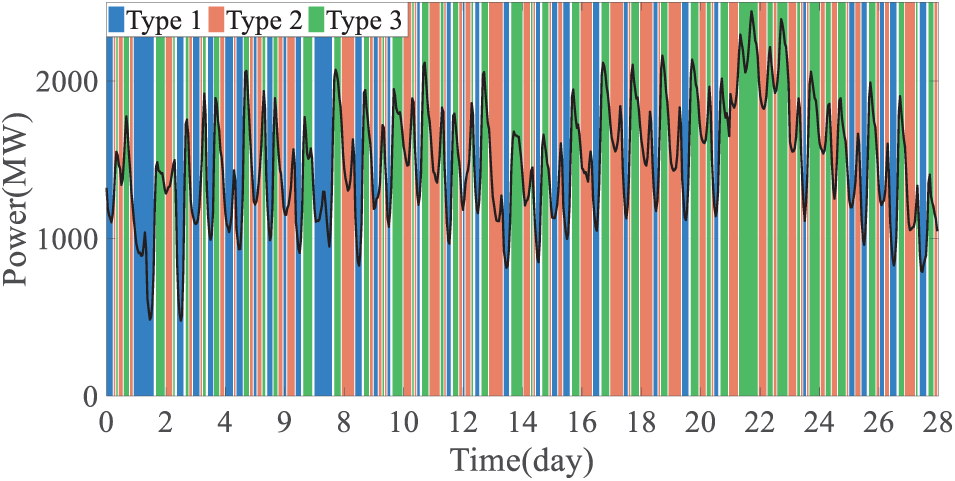
Figure 8: Results of reducing the unit start-up and shut-down time-periods

The output power of thermal generators and energy storage and the results of wind curtailment and load loss are shown in Fig. 9. The output of each thermal generators, the charging and discharging power and energy of battery energy storage and hydrogen energy storage are shown in Figs. 10–12, respectively.

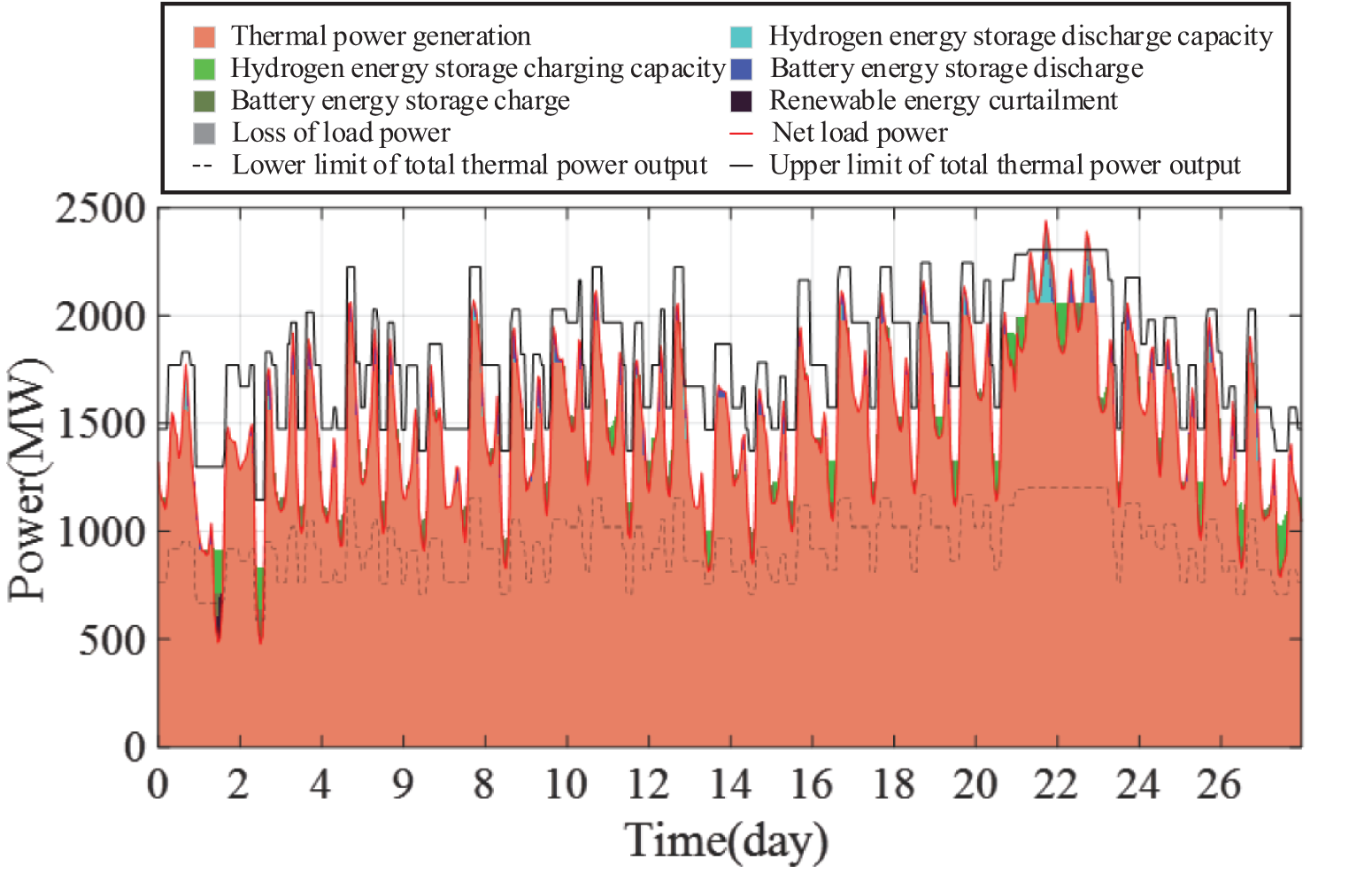
Figure 9: Monthly scheduling results of thermal generators and energy storage, wind curtailment and load loss

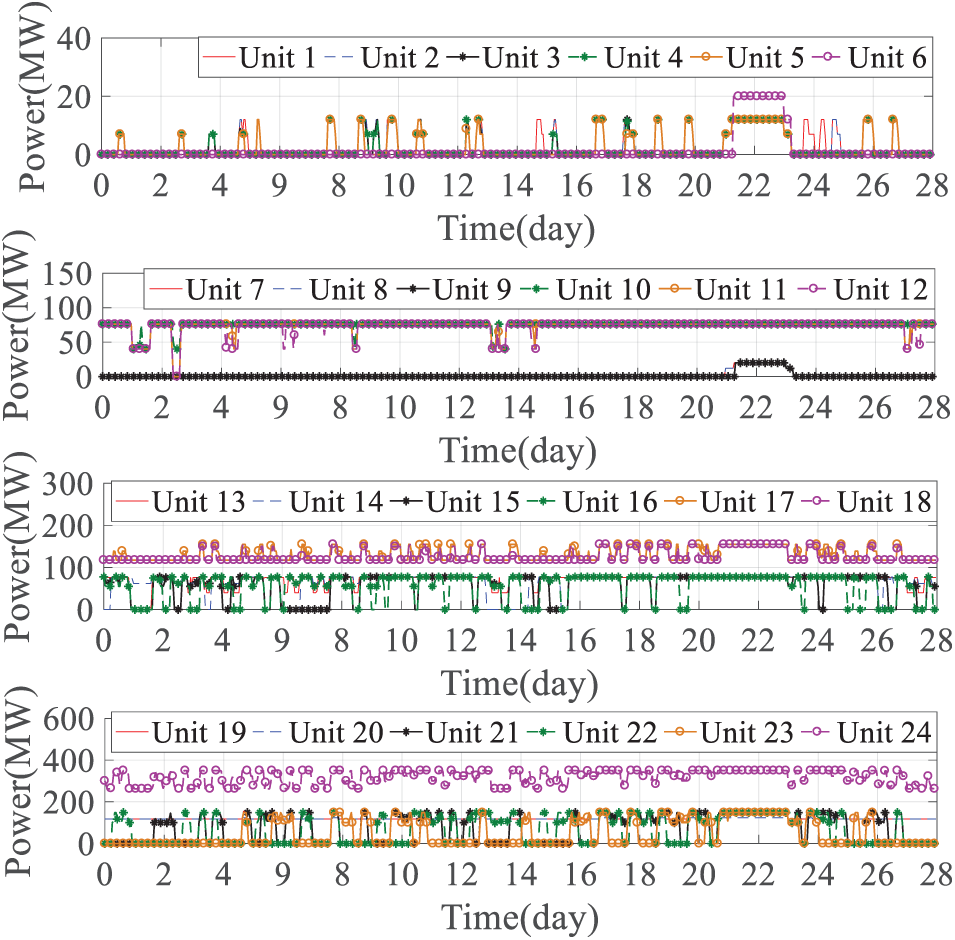
Figure 10: Output of each unit

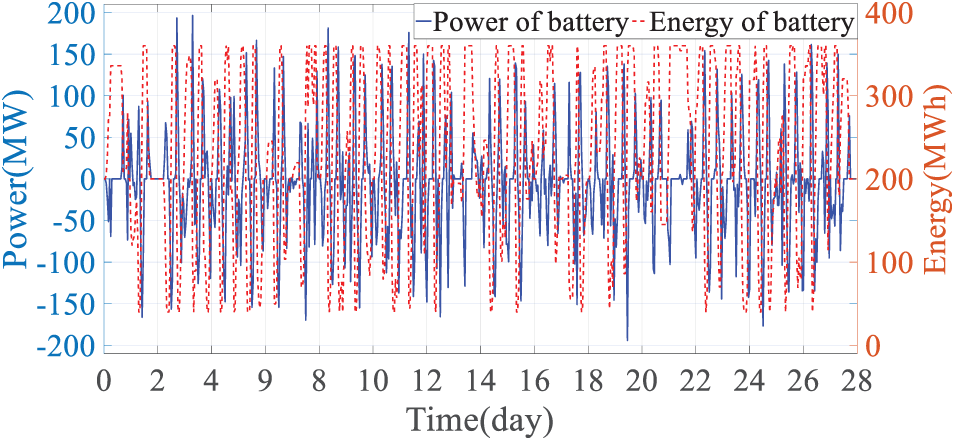
Figure 11: Battery energy storage charging and discharging power and energy changes

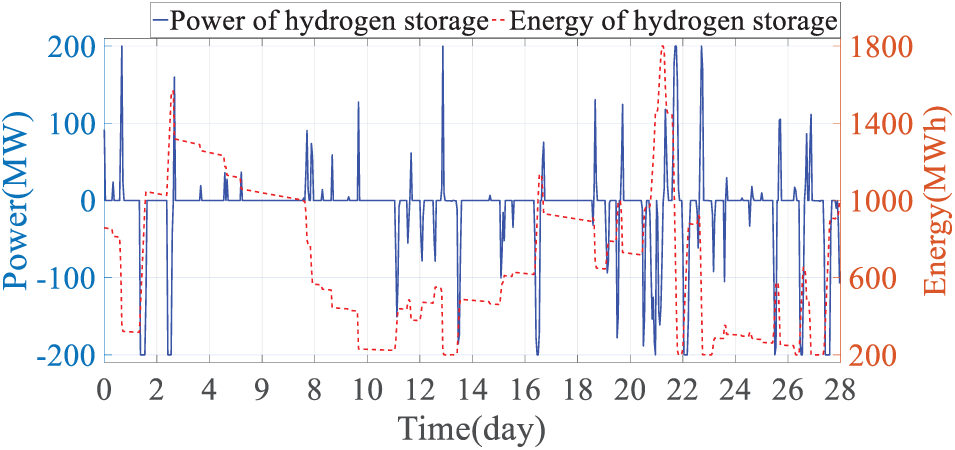
Figure 12: Hydrogen energy storage charging and discharging power and energy changes

As shown in Fig. 9, it can be observed that the total maximum output of thermal generators varies with net load fluctuations, indicating that start-up and shut-down operations are conducted to improve the economic efficiency of thermal generator operation while satisfying power balance and reserve constraints. During the extremely cold weather period (the 22nd and 23rd days), the total output of thermal generators is maintained at the maximum value, and the energy storage discharge should increase the net load and reduce the load loss, as a result, the load loss is minimized due to the increased net load and energy storage discharge during extremely cold weather. Combined with Fig. 10, it can be seen that without considering maintenance, the coal consumption cost of units 10–12, 16–20, and 24 is relatively small, and they are kept in the start-up state most of the time, the coal consumption cost of units 1, 2, 6, and 9 is relatively large, and they are kept in the off state for a long time, the economy of the remaining units is in the middle, starting when the net load is large and shutting down when the net load is small, reducing the cost of power generation.

Combining Figs. 9, 11, and 12, it can be seen that battery energy storage has a daily charge and discharge cycle, charging during the daily net load valley and discharging during the net load peak, which can reduce the number of start-up and shut-down of thermal generators, and transfer the output of thermal generators during the period of low marginal cost of net load valley to the period of high marginal cost of net load peak, thereby reducing the system operation cost. Compared with battery energy storage, hydrogen energy storage has a longer energy change cycle, charging before the occurrence of extreme cold weather, discharging during the extreme cold weather period to make up for the power shortage caused by the increase in net load as much as possible, and charging to restore energy after the extreme cold weather, in addition, the charging and discharging efficiency of hydrogen energy storage is low, so there are fewer charging and discharging actions in each period except the extreme cold weather, which can minimize its charging and discharging energy loss.

6.2.2 Assessment of the Effectiveness in Reducing Decision Time-Periods for Unit Start-Up and Shut-Down

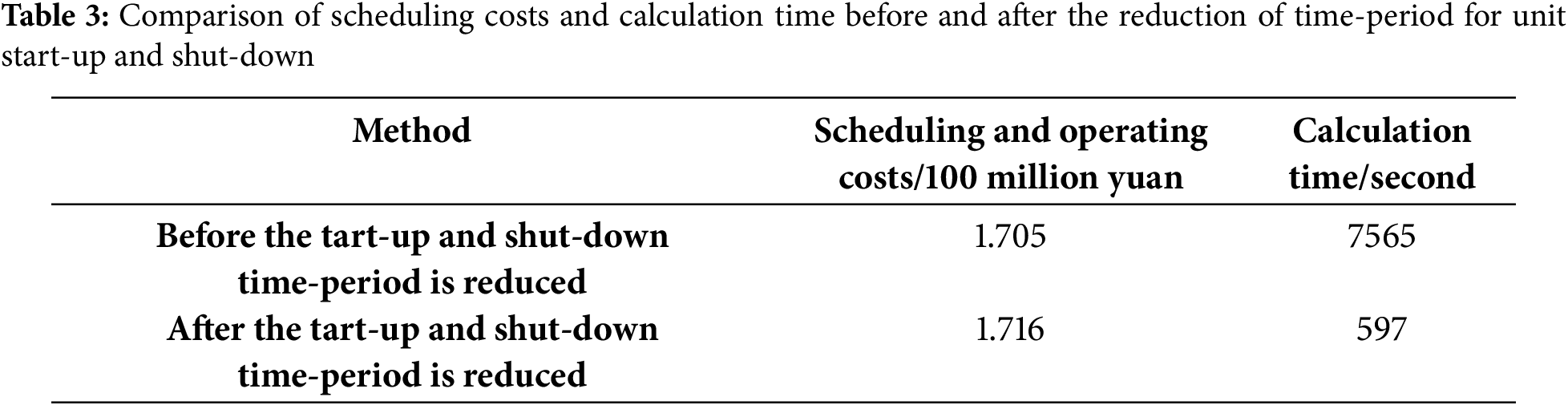
The total maximum output, monthly scheduling cost and calculation time of the unit before/after the unit start-stop period is reduced are shown in Fig. 13 and Table 3, respectively. It can be seen from Fig. 13 that the total maximum output of the unit after the time-period for unit start-up and shut-down is reduced has the same change trend as before the reduction, indicating that the reduction of the time-period for unit start-up and shut-down has a small impact on the unit’s start-up and shut-down decision-making. It can be seen from Table 1 that the monthly scheduling model solution time before and after the time-period for unit start-up and shut-down is reduced is 7565 and 597 s, respectively. The cost is 170.5 and 171.6 million yuan, respectively. Compared with before the time-period for unit start-up and shut-down is reduced, the monthly scheduling model after the reduction is the calculation time for solving the scheduling model was reduced by 92.1%, while the scheduling cost only increased by 0.006%. It can be seen that the reduction of time-period for unit start-up and shut-down can significantly shorten the monthly scheduling model solution time without significantly increasing the scheduling cost, and effectively improve the formulation of scheduling plans efficiency.

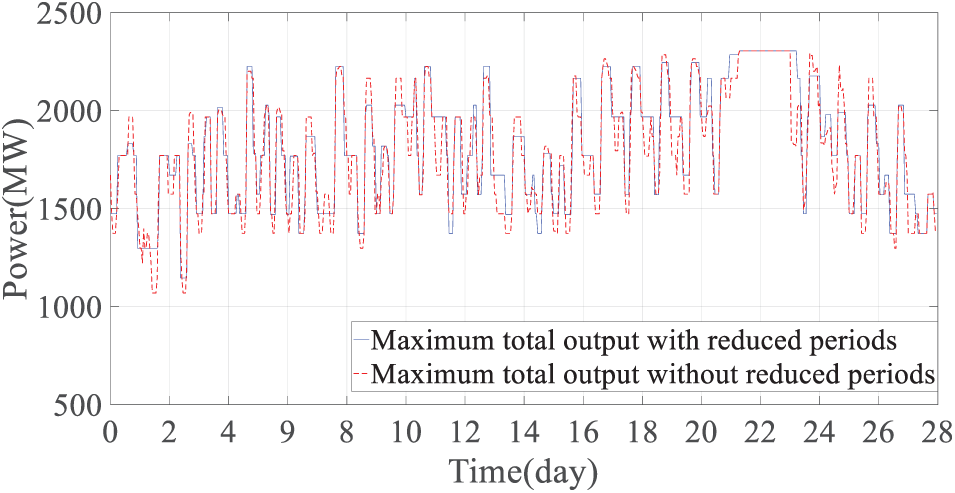
Figure 13: Comparison of the total maximum output of the units before and after the reduction of the time-period for unit start-up and shut-down

6.2.3 Evaluation of the Effectiveness in Constructing the Minimum Chargeable Energy Constraint for Energy Storage

The total maximum output of thermal generators with or without the minimum chargeable capacity constraint of energy storage is shown in Fig. 14. Hydrogen energy storage with a longer charge and discharge cycle is selected for analysis, and the charge and discharge power, energy, and load loss of hydrogen energy storage under maximum net load are shown in Figs. 15–17, respectively.

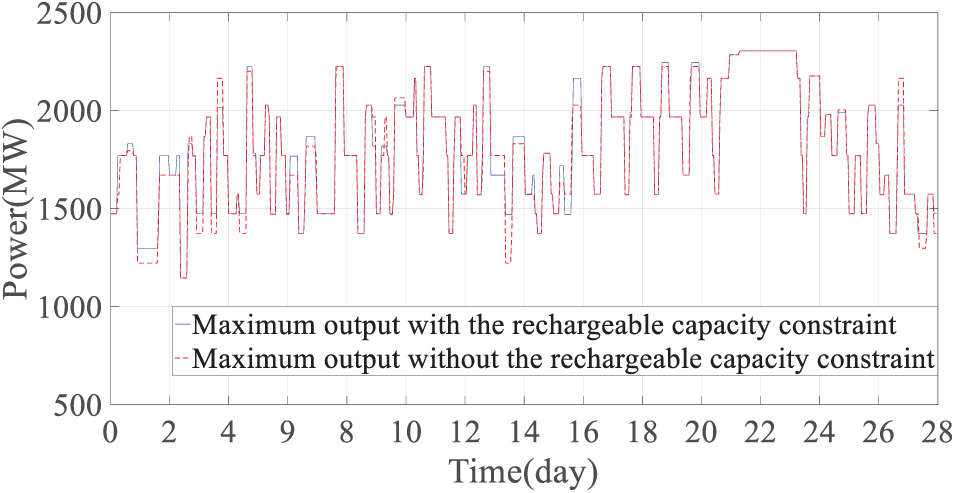
Figure 14: Comparison of maximum output of thermal generators with and without considering the minimum chargeable capacity constraint of energy storage

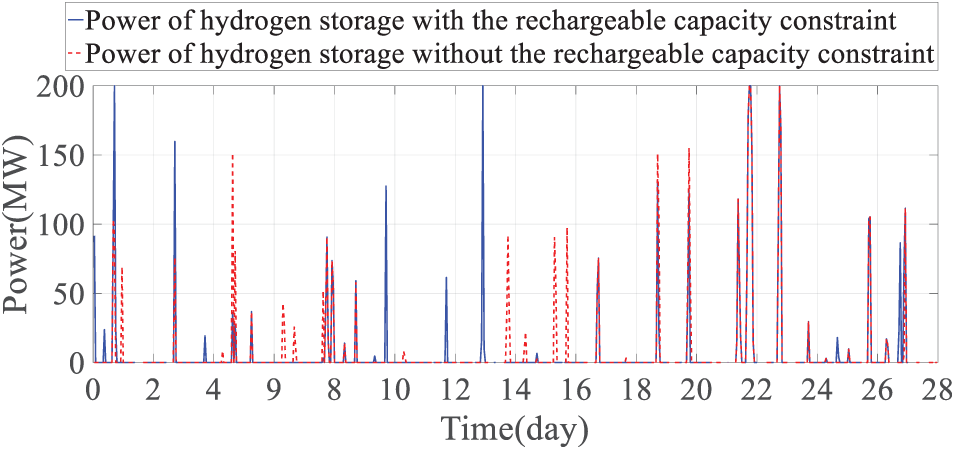
Figure 15: Comparison of hydrogen energy storage charging and discharging power with and without considering the minimum chargeable capacity constraint at maximum load power

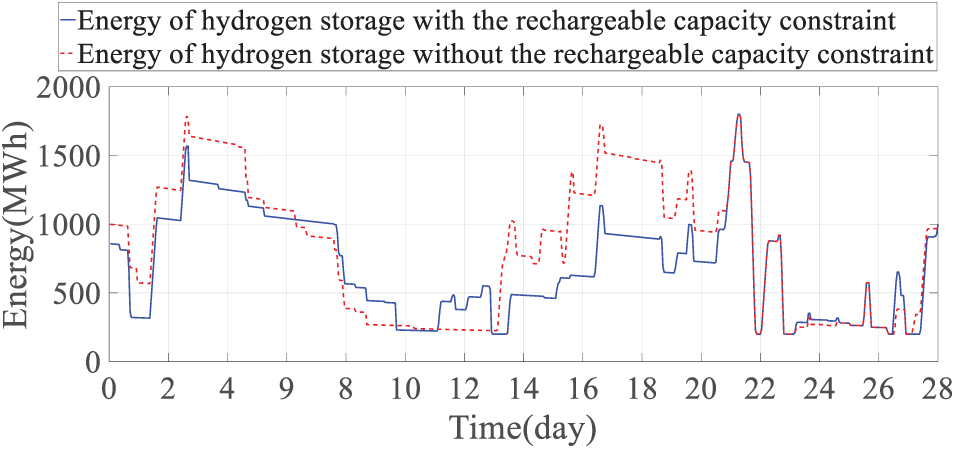
Figure 16: Comparison of hydrogen energy storage energy with and without considering the minimum charge capacity constraint at maximum load power

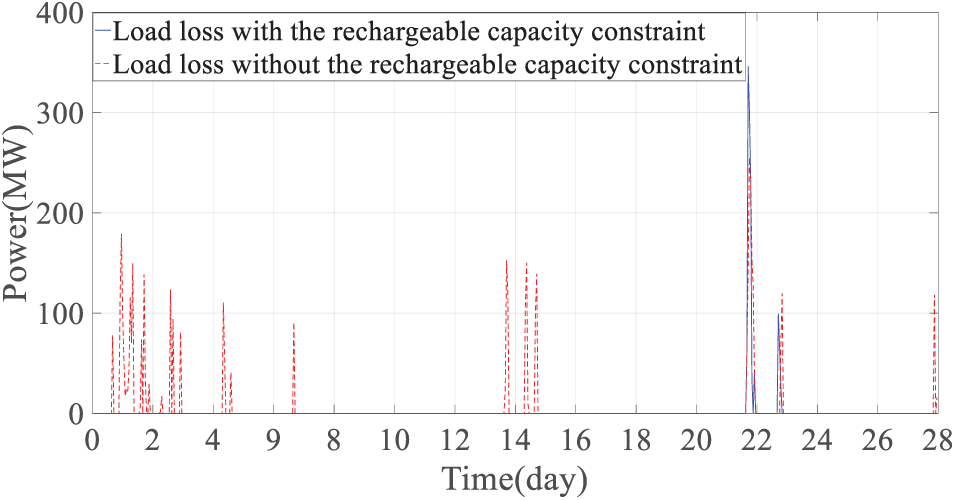
Figure 17: Comparison of load loss power with and without considering the minimum chargeable energy storage capacity constraint at maximum load power

As shown in Fig. 14, compared with not considering the minimum chargeable capacity constraint, the maximum output of thermal generators obtained by considering the minimum chargeable capacity constraint is slightly higher during the daily net load valley period, and the number of thermal generators in operation is more, which can reserve sufficient chargeable space for energy storage.

Combined with Figs. 15–17, it can be seen that when the net load is large, the energy storage can charge more electricity to meet future discharge needs, and load loss only occurs during extremely cold weather periods, when the minimum chargeable capacity constraint is not considered, the chargeable space of energy storage is insufficient under the maximum net load, and the power shortage matching effect when thermal generators and wind and solar power generation are insufficient is poor. Load loss occurs during extremely cold weather and other periods, and the load loss power is relatively large. When the system load is high and the energy storage system’s state of charge (SOC) is near its lower limit, the system’s discharge capacity is constrained, leading to a loss of load, particularly in high-load conditions like extreme cold weather. For instance, during high-load periods on the 22nd day (18:00–21:00) and the 23rd day (08:00–10:00), the SOC approaches its lower limit, limiting discharge and failing to meet demand. Conversely, during low-load periods (e.g., 02:00–04:00 on the 21st day and 02:00–05:00 on the 24th day), when the SOC is near the upper limit, charging is restricted, resulting in curtailment of excess renewable energy. These findings highlight that SOC limits significantly affect the energy storage system’s charge-discharge capacity, supply-demand balance, and system flexibility, especially under extreme conditions. Therefore, based on the proposed monthly strategy that considers the minimum chargeable capacity constraint, the decision result can still reserve enough charging space for energy storage, better match the energy storage discharge demand caused by the larger actual value of net load, reduce possible load loss, and improve system power supply reliability.

7  Conclusions and Future Perspectives

Considering the differences in unit startup and shutdown times and the rechargeable capacity of energy storage under maximum net load, a time-varying scheduling strategy for coal-fired and energy storage systems with a daily minimum chargeable capacity constraint is proposed. Case study results show:

(1) The proposed method yields an economically efficient operation plan for thermal power and energy storage, where long-term storage (e.g., hydrogen) operates in a “low storage, high output” mode to balance power supply and demand during peak net load periods.

(2) The start-stop decision time reduction method reduces decision variables and shrinks the fire-storage monthly scheduling model without significantly impacting economic performance. Optimization reduces decision periods from 672 to 149, decision variables from 2106 to 447, solving time by 92.1%, with a 0.006% increase in scheduling cost, demonstrating efficiency gains while maintaining economic viability.

(3) The minimum rechargeable energy constraint strategy reserves sufficient charging space for long-term storage under extreme net loads, ensuring cross-day discharge capability and improving system reliability. During extreme cold weather, it reduces load shedding by approximately 30%, significantly enhancing power supply stability and adaptability.

(4) Future research will enhance the method’s applicability and practical value. The current model ignores transmission line capacity limits, which may affect accuracy in high renewable scenarios. Future work will incorporate transmission constraints and regional capacity to refine the optimization model and account for the transmission network’s impact on system operation.

Acknowledgement: None.

Funding Statement: This study was supported by State Grid Corporation headquarters technology project (4000-202399368A-2-2-ZB).

Author Contributions: Xingxu Zhu: Conceptualization, Methodology, Formulated the conclusions of this study, Writing—original draft. Shiye Wang: Conceptualization, Methodology, Formal analysis, Data collection and curation, Application, Visualization, Revision, Writing—original draft. Gangui Yan: Methodology, Visualization, Writing—review & editing. Junhui Li: Formal analysis, Visualization, Writing—review & editing. Hongda Dong: Validation, Writing—review & editing. Chenggang Li: Validation, Writing—review & editing.

Availability of Data and Materials: All data generated or analyzed during this study are included in the published article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Appendix A Thermal Generation Units and Energy Storage Parameters

References

1. Yang B, Guo Z, Wang J, Duan C, Ren Y, Chen Y. Key optimization issues for renewable energy systems under carbon-peaking and carbon neutrality targets: current states and perspectives. Energy Eng. 2022;119(5):1789–95. doi:10.32604/ee.2022.022217. [Google Scholar] [CrossRef]

2. Basu M, Jena C, Khan B, Ali A. Optimal bidding strategies of microgrid with demand side management for economic emission dispatch incorporating uncertainty and outage of renewable energy sources. Energy Eng. 2024;121(4):849–67. doi:10.32604/ee.2024.043294. [Google Scholar] [CrossRef]

3. Gonçalves ACR, Costoya X, Nieto R, Liberato MLR. Extreme weather events on energy systems: a comprehensive review on impacts, mitigation, and adaptation measures. Sustain Energy Res. 2024;11(1):4. doi:10.1186/s40807-023-00097-6. [Google Scholar] [CrossRef]

4. Mi X, Liu Z, Wang T, Yu Z, Feng J. Adaptive random forests algorithm for disaster loss prediction of distribution network in extreme weather. Distrib Utiliz. 2023;40(7):57–62,81. doi:10.19421/j.cnki.1006-6357.2023.07.008. [Google Scholar] [CrossRef]

5. Zhong J, Chen C, Zhang H, Shen W, Bian Y, Li G, et al. Rapid restoration strategy for cyber-physical integrated failures in distribution systems under extreme weather conditions. Automat Elect Power Syst. 2024. doi:10.7500/AEPS20240428002. [Google Scholar] [CrossRef]

6. Owaid SAH. Multi-objective monthly generation scheduling considering the supply constraints of adjustable energy. In: 2022 Asian Conference on Frontiers of Power and Energy (ACFPE); 2022 Oct 21–23; Chengdu, China: IEEE; 2022. p. 313–7. doi:10.1109/ACFPE56003.2022.9952245 [Google Scholar] [CrossRef]

7. Lin Y, Qiao Y, Lu Z. Long-term generation scheduling for renewable-dominant systems concerning limited energy supporting capability of hydrogeneration. IET Generation Trans Dist. 2022;16(1):57–70. doi:10.1049/gtd2.12276. [Google Scholar] [CrossRef]

8. Zhou M, Xia S, Li Y, Li G. A joint optimization approach on monthly unit commitment and maintenance scheduling for wind power integrated power systems. Proc CSEE. 2015;35(7):1586–95. doi:10.13334/j.0258-8013.pcsee.2015.07.005. [Google Scholar] [CrossRef]

9. Zhang H, Liu D, Yin S, Wang W, Bai C, Zhang H. A joint optimization approach on monthly balancing mechanism and unit maintenance scheduling. IEEE Access. 2024;12(4):49535–47. doi:10.1109/ACCESS.2024.3384479. [Google Scholar] [CrossRef]

10. Truong HQ, Jeenanunta C. Fuzzy mixed integer linear programming model for national level monthly unit commitment under price-based uncertainty: a case study in Thailand. Electr Power Syst Res. 2022;209(3):107963. doi:10.1016/j.epsr.2022.107963. [Google Scholar] [CrossRef]

11. Truong HQ, Jeenanunta C. Mixed integer linear programming model for monthly unit commitment in the national level power system. In: 11th International Conference on Information Technology and Electrical Engineering (ICITEE); 2019 Oct 10–11; Pattaya, Thailand: IEEE; 2019. p. 1–6. doi:10.1109/iciteed.2019.8930000 [Google Scholar] [CrossRef]

12. Ahmadi A, Ahmadi MR, Nezhad AE. A lexicographic optimization and augmented ε-constraint technique for short-term environmental/economic combined heat and power scheduling. Electr Power Compon Syst. 2014;42(9):945–58. doi:10.1080/15325008.2014.903542. [Google Scholar] [CrossRef]

13. Ma Y, Huang Y, Wu G, Liu J, Liu Y, Xiang Y, et al. Decentralized monthly generation scheduling of cascade hydropower plants in multiple time scale markets. Int J Electr Power Energy Syst. 2022;135(1):107420. doi:10.1016/j.ijepes.2021.107420. [Google Scholar] [CrossRef]

14. Huang L, Lai CS, Zhao Z, Yang G, Zhong B, Lai LL. Robust security-constrained optimal power flow incorporating preventive and corrective generation dispatch to improve power system reliability. CSEE J Power Energy Syst. 2023;9(1):351–64. doi:10.17775/CSEEJPES.2021.06560. [Google Scholar] [CrossRef]

15. Li P, Fan Y, Huang Y, Sun Y, Wang W, Liu C, et al. Monthly generation scheduling method of renewable energy power system based on power plant aggregation & decomposition models. Power System Technol. 2020;44(9):3281–93. [Google Scholar]

16. Li Y, Hu B, Niu T, Gao S, Yan J, Xie K, et al. GMM-HMM-based medium- and long-term multi-wind farm correlated power output time series generation method. IEEE Access. 2021;9:90255–67. doi:10.1109/ACCESS.2021.3091460. [Google Scholar] [CrossRef]

17. Shao C, Feng C, Wang X, Wang X. Mid-long term fast unit commitment based on load state transfer curve. Proc CSEE. 2019;39(S1):141–7. (In Chinese). doi:10.13334/j.0258-8013.pcsee.190998. [Google Scholar] [CrossRef]

18. Yuan YP, Wang JX, Zhou K, Wang XL, Wang XB, Zhang SJ. Monthly unit commitment model coordinated short-term scheduling and efficient solving method for renewable energy power system. Proc CSEE. 2019;39(18):5336–45,5580. (In Chinese). doi:10.13334/j.0258-8013.pcsee.182075.. [Google Scholar] [CrossRef]

19. Júnior CA, Dias B, Diniz A. Integrated two-stage benders decomposition and dual dynamic programming for hydrothermal-wind planning with intra-stage cost functions. IEEE Trans Sustain Energy. 2024;15(4):2263–75. doi:10.1109/TSTE.2024.3411577. [Google Scholar] [CrossRef]

20. Zhu Y, Liu X, Deng R, Zhai Y. Memetic algorithm for solving monthly unit commitment problem considering uncertain wind power. J Contr Autom Electr Syst. 2020;31(2):511–20. doi:10.1007/s40313-019-00541-3. [Google Scholar] [CrossRef]

21. Su C, Zhang J, Shen J, Zhou H. Method for monthly thermal unit commitment with multi-level transmission constraints. Electr Power Construct. 2019;40(12):30–7. [Google Scholar]

22. Sun S, Zhao P, Qi J, Xu F, Zhou Y, Li W. Optimization of monthly power generation plan for thermal power units considering access of large-scale new energy. In: 2019 IEEE Sustainable Power and Energy Conference (iSPEC); 2019 Nov 21–23; Beijing, China: IEEE; 2019. p. 1812–16. doi:10.1109/ispec48194.2019.8975164 [Google Scholar] [CrossRef]

23. Fredo GLM, Finardi EC, Larroyd PV, Picarelli LB. Inflow aggregation and Run-of-the-river inflow energy for reducing dimensionality in the long-term generation scheduling problem. IEEE Access. 2021;9:98542–60. doi:10.1109/ACCESS.2021.3096143. [Google Scholar] [CrossRef]

24. Zhou X, Wang FH, Fu J, Lin JY, Jin ZJ. Mechanical condition monitoring of on-load tap changers based on chaos theory and K-means clustering method. Proc CSEE. 2015;35(6):1541–8. (In Chinese). doi:10.13334/j.0258-8013.pcsee.2015.06.031. [Google Scholar] [CrossRef]

25. Zhu J, Han X. Big data clustering algorithm of power system user load characteristics based on K-means and SOM neural network. Multimed Tools Appl. 2024;11(3):100208. doi:10.1007/s11042-024-19156-1. [Google Scholar] [CrossRef]

26. Liu N, Zhang K, Zhang K. Coordinated configuration of hybrid energy storage for electricity-hydrogen integrated energy system. J Energy Storage. 2024;95(1):112590. doi:10.1016/j.est.2024.112590. [Google Scholar] [CrossRef]

27. Esmaeel Nezhad A, Rahimnejad A, Nardelli PHJ, Gadsden SA, Sahoo S, Ghanavati F. A shrinking horizon model predictive controller for daily scheduling of home energy management systems. IEEE Access. 2022;10:29716–30. doi:10.1109/ACCESS.2022.3158346. [Google Scholar] [CrossRef]

28. Dai W. Research on the optimal operation of electricity-hydrogen integrated energy system [dissertation]. Jinan, China: Shandong University; 2023. [Google Scholar]