Recent Advancements in the Optimization Capacity Configuration and Coordination Operation Strategy of Wind-Solar Hybrid Storage System

Nomenclature

1  Introduction

Renewable energy from wind and photovoltaic power generation are intermittency and unpredictable energy sources, that seriously affect the normal function of the power system [1–3]. The fluctuations in energy sources bring serious challenges to the power quality and stability of the grid network [4–7]. Coupling electrical grid systems with different aspects of power production can increase power production flexibility and plant operation [8–11]. The use of an energy storage system of charging and discharging can smoothly encounter the output power fluctuations and flexibly adjust the power imbalance situation, which not only affects the supply, demand, and balance of the power system but also solves the intermittency and volatility of wind power and photovoltaic power generation [12,13]. This results in the enhancement of country revenue through constant power supply in the industry and production sectors [14–17]. Based on this, it is vital to introduce a hybrid wind-solar energy storage system to reduce the power fluctuation impact on the power grid and to improve the stability of the power grid.

Recently, the use of renewable energy has drawn much attention around the world [18–21]. Solar energy technology, as a crucial origin of renewable energy, has long-term merits, improves sustainability, and encounters pollution [22–25]. Despite, providing flexible power, it faces challenges due to the occasional energy source [26–29] On the other hand, Concentrated Solar Power (CSP) has drawn much attention in recent years, due to its flexibility and capability to be incorporated with other sources of energy like thermal energy [30–33]. Wen et al. [26] aimed at the problems of large loss and low efficiency of wind power generation system, multi-field coupling method was adopted to conduct multidimensional analysis of electromagnetic field and temperature field in wind power generation system, and the system loss region was accurately obtained, and the wind power generation efficiency was improved by optimizing the composition structure of wind power generation system. Wen et al. [27] proposed a wind power + energy storage model to explore the influence of different energy storage modes on various power quality indicators in wind power generation, and Ansys software was used to simulate and explore the inside of the wind power generation system. Liu et al. [28] proposed a solar power plant with multiple combinations, including photovoltaic power station, thermal storage system, Concentrated Solar Power (CSP) and other equipments, and takes standardized energy cost and power failure probability as evaluation criteria to obtain the best component coordination and capacity configuration through multi-objective optimization. The results show that the proposed system can effectively reduce power generation costs and improve power generation reliability. Kandi et al. [29] proposed a new type of solar power generation and energy storage power station, which is mainly composed of Thermal Electric Generator (TEG) and Phase Change Material (PCM), which can effectively improve energy storage efficiency. At present, there are few studies on PCM integrating TEG, and this field has great research prospects.

Moreover, wind energy commonly contains the most negligible effect on climate change compared to other sources of energy like fossil fuels [34–37] A wind turbine is used to produce electricity [38]. On the contrary, it faces challenges such as weather variation and high load requirements in some areas [39–42]. The main challenge of using wind and solar energy is their constant weather dependence [43,44] Consequently, a hybrid renewable energy system is necessary to ensure a constant supply of energy.

Hybrid wind and solar energy can be converged to encounter the fluctuation of high energy demand through different forms of energy storage, so as to ensure the stability of the power grid. Moreover, References [45–47] proposed an Intelligent Adaptive Control (IAC) architecture to address the impact of renewable energy on microgrids due to various meteorological factors. The architecture was designed by combining Artificial Neural Network-Proportional Integral (ANN-PI) and regulated voltage by adjusting the inverter secondary network. The experimental findings proved that IAC architecture could effectively reduce microgrid fluctuations. Likewise, Mahesh et al. [48] proposed a genetic algorithms approach to optimize hybrid solar photovoltaic-wind-battery systems and found that genetic algorithms minimized cost while maintaining power stability. Multi-objective genetic algorithm has a strong global search ability and high processing complexity, which is suitable for complex constraints and targets in the allocation of scenery capacity. Moreover, the population nature of genetic algorithm enables it to process multiple solutions in parallel and has high efficiency. Therefore, this paper chooses to use multi-objective genetic algorithm to solve the objective function. Based on this, it is vital to enhance the power grid through a hybrid energy system.

This paper presents a wind-solar hybrid energy storage system combining electricity and heat through the optimization of efficiency system of electric-thermal combined energy storage. Secondly, it investigates the primary allocation of wind and solar power through empirical modal decomposition to obtain the grid-connected power to avoid the phenomenon of insufficient or excessive grid-connected power suppression through HESS capacity configuration [49,50]. This work will help the global energy sector to mitigate the effect of intermittent energy challenges and enhance operation strategy through power volatility, economy, and power quality control.

2  Model of Wind-Photovoltaic and Storage System

In this work, a wind-solar hybrid model was developed to analyze the energy potential of a coupled energy system. The structure of the wind-solar hybrid energy storage system is shown in Fig. 1. It mainly consists of a power generation system, a hybrid energy storage system, a load, and a process switching system utilized for monitoring wind and solar power production systems and different energy storage scenarios.

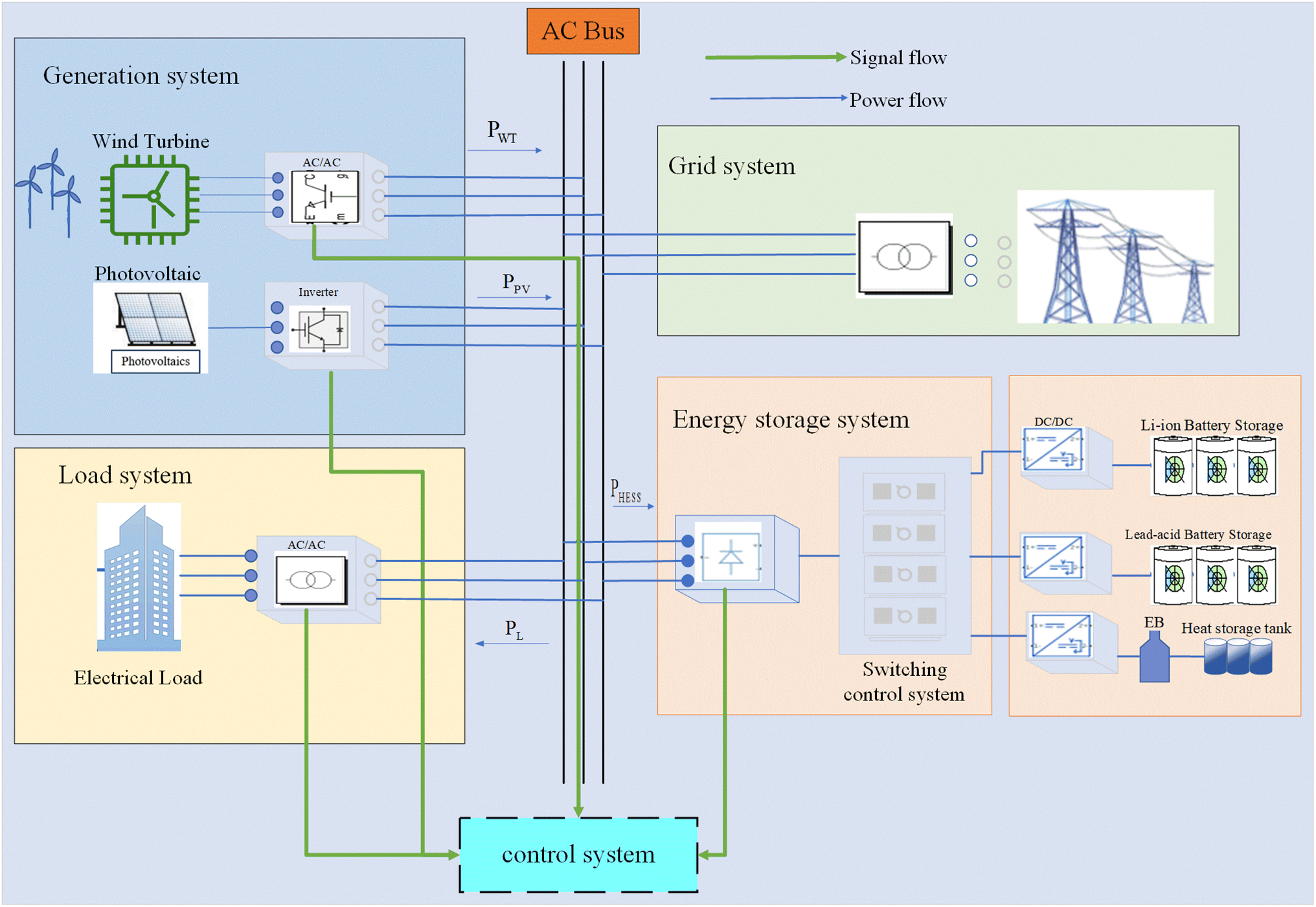
Figure 1: Diagram of hybrid energy storage systems for wind power generation

Wind farms and photovoltaic power plants were used to generate power for the grid and energy storage and consumption depending on the power utility. If the power volatility is large it will affect the power quality and reliable operation. In utilizing the wind and solar complementary system, the first part is the power generation system, load system, control system, grid system, and energy storage system are all smoothed out. Hybrid energy storage implemented in this work consists of battery and thermal storage. The complementary power of wind and solar output meets the power merger and acquisition of grid-connected fluctuations through power decomposition and carries out energy storage if it does not meet the requirements and further rational distribution of electric heating energy storage in the process of energy storage and release.

2.1 Fluctuating Characteristics of Wind and Photovoltaic Generation

Considering the actual output energy of the system and the degree of operational fluctuation, the power fluctuation rate is defined as the evaluation index, indicated in Eq. (1) below:

δ=PMAX(t)−PMIN(t)Pave(t)×100%(1)

where δ is the power fluctuation rate and t is time interval, PMAX(t) represents maximum, PMIN(t) represent minimum and Pave(t) represents the average power in time interval, respectively.

2.2 Power Allocation Strategy

In power power distribution, the basic idea is to divide the power by high and low frequency. The normalized power signal is obtained by the ratio of the original power signal to the grid-connected power, and the normalized power signal is decomposed into several fixed mode functions (IMFs), which are combined with the fluctuation limit of wind power grid-connected. Each order IMF is reconstructed into a high-frequency component and a low-frequency component by Eqs. (2) and (3), and each IMF represents a frequency component in the original signal. The constraint of wind power fluctuation limit is shown in Eq. (4).

Plow=c2f(i)=∑i=m+1kIMFi+res(2)

Phigh=f2c(i)=∑i=1mIMFi(3)

maxPc2f(p)−minPc2f(p)≤Plimit(4)

where Pc2f(p) is the power value within the pth-order component of the low-frequency reconstruction in the specified time; Plimit is the fluctuation volume limit. K-means clustering is carried out for the wind-solar power output, modal decomposition is carried out for grid-connection power, and energy storage according to grid-connected limits. The specific power allocation process is shown in Fig. 2.

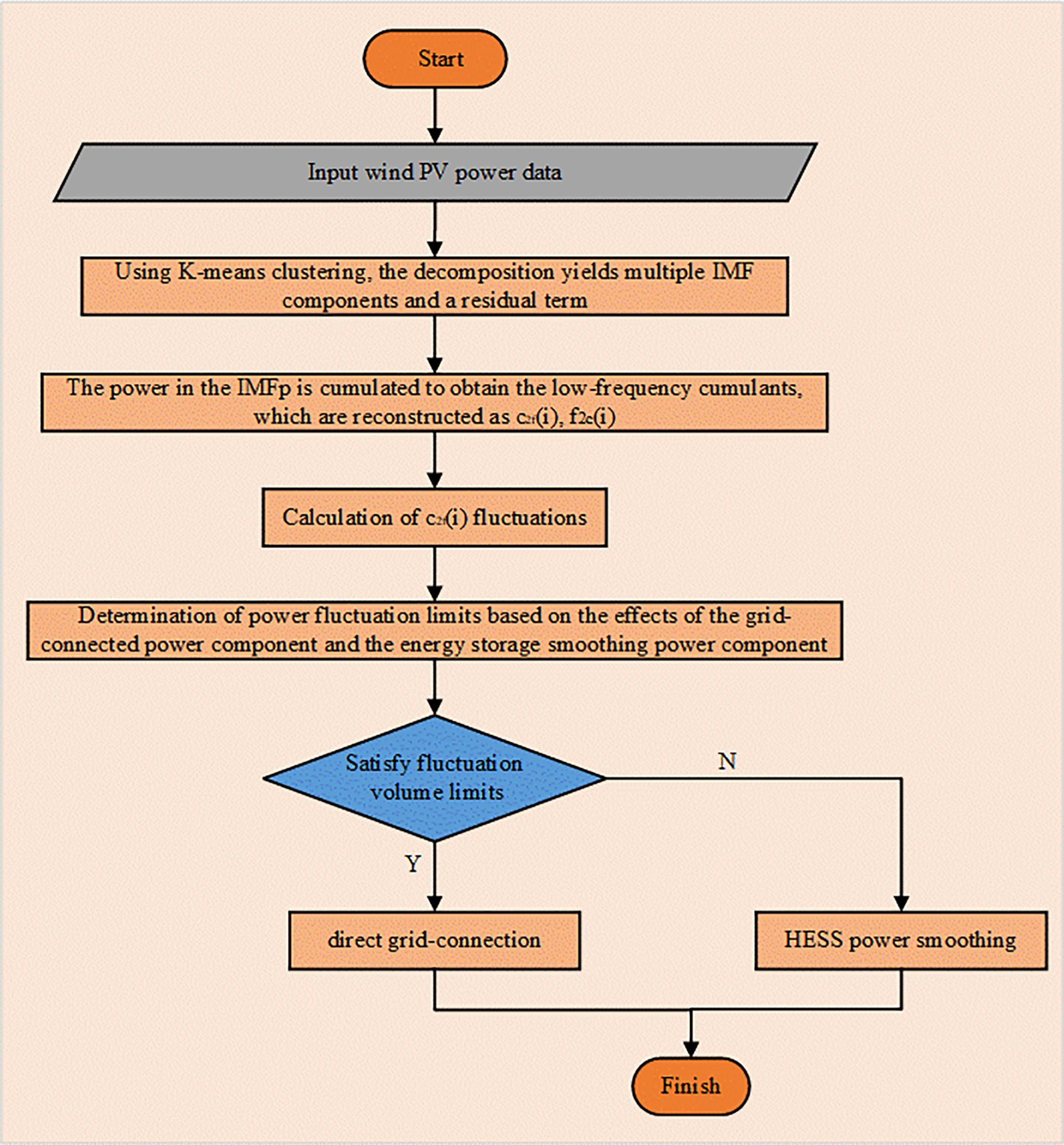
Figure 2: Flow chart of wind PV power allocation strategy

2.3 Electric-Thermal Hybrid Energy Storage Operation Strategy

In the process of an electric-thermal hybrid energy storage operation, the mode in each area is formulated by delineating different working areas of the energy storage system, as shown in Table 1. Where SOCsecmax and SOCsecmin represent the upper and lower limits of the normal working area of the energy storage, and also the opening threshold of the heat storage. Likewise, SOCmaxstop and SOCminstop represent the upper and lower alarm limits of the SOC power storage, and SOCmax, SOCmin represent the upper and lower limits of the emergency area of the power storage.

Through the SOC seven-region design, the SOC with electrochemical energy storage provides enough power and capacity space, better shallow charging and discharging, to avoid excessive use of electric energy storage, and smooth fluctuations. The energy operation strategy is shown in Table 1. During charging, when SOCsecmax is reached and the heat storage is within a reasonable range, the heat storage is turned on. When SOC reaches SOCmaxstop, the charging is stopped to avoid current sudden change and overcharging of the battery. SOCmaxstop~SOCmax is reserved as the overcharge buffer area. When the heat storage reaches the maximum, the heat storage is closed. On the contrary, the discharge process is similar. The specific process is shown in Fig. 3 below.

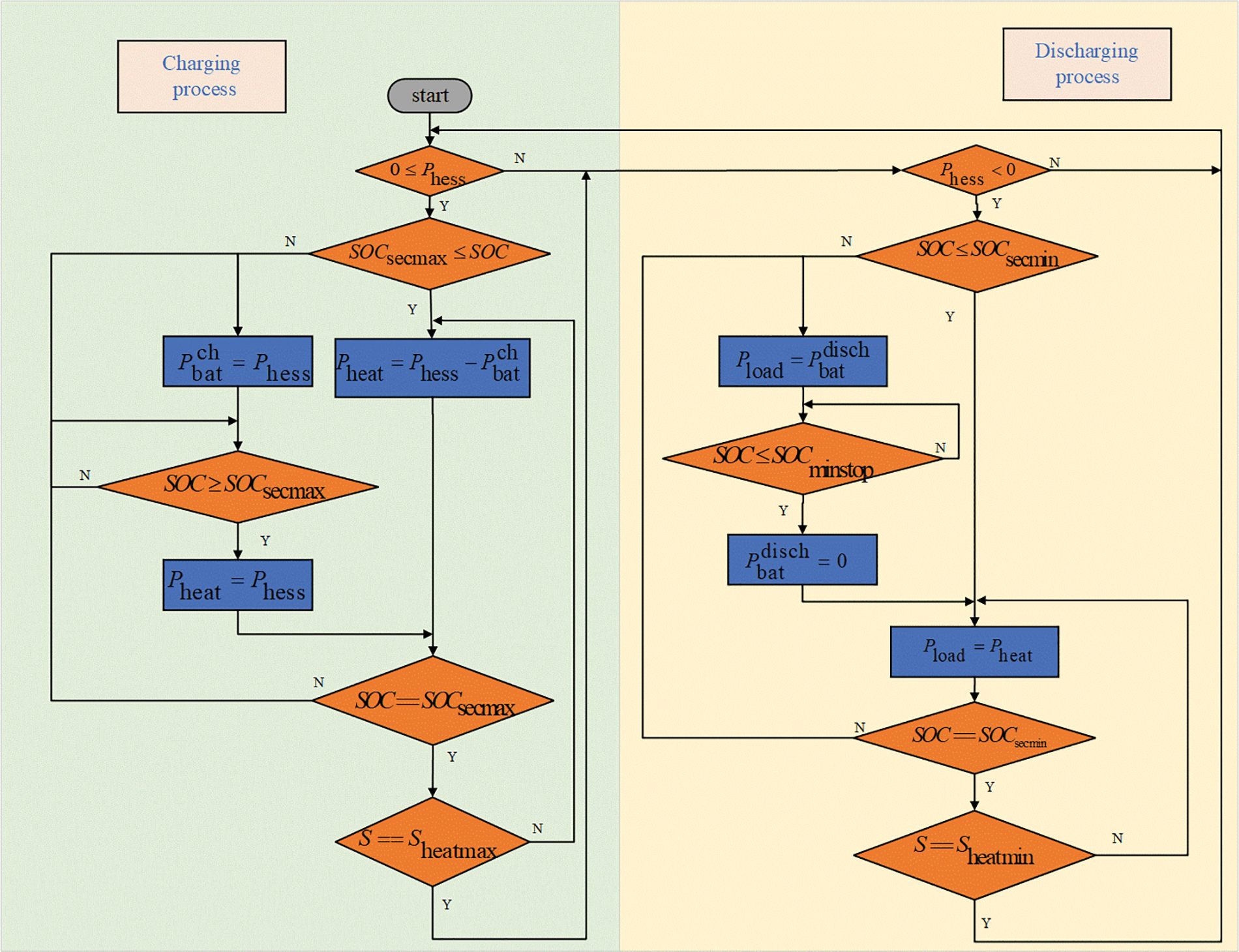
Figure 3: Flow chart of energy management strategy for electric and thermal energy storage

3  Hybrid Energy Storage Capacity Optimization Model

3.1 Objective Function

For several combined objective optimization allocation problem for a wind-source hybrid energy storage system, the lowest comprehensive cost and the longest cycle life are set as the optimization objectives function under the premises to ensure a stable and reliable operation system. For hybrid energy storage capacity, with the lowest comprehensive cost and the longest cycle life as optimization objectives, the multi-objective genetic algorithm is used to optimize the electric heating energy storage configuration. The objective function is expressed as indicated in Eq. (5), as previously explained by

minC=CBatLi+CBatLA+CHeat+Ccomp(5)

where C is the comprehensive energy storage cost, CBatLi is the lithium-ion battery energy storage cost, CBatLA is the lead-acid battery energy storage cost, CHeat is the thermal energy storage investment operating cost, and Ccomp base power compensation cost, where CBatLi, and CHeat are expressed as Eq. (6).

{CBatLi=CBat,Liinv+CBat,LioperCBatLA=CBat,LAinv+CBat,LAoperCHeat=CHeatinv+CHeatoper(6)

where CBat,Liinv and CBat,LAinv are the investment costs of lithium and lead-acid battery storage, CBat,Lioper and CBat,LAoper are the operation and maintenance costs of lithium and lead-acid battery storage, CHeatinv and CHeatoper are the investment costs and operation and maintenance costs of thermal storage respectively Eqs. (7) and (8).

(1) Investment costs

The investment cost expression is as follows:

{CBat,Liinv=n1CBLi1inv(1−r1)CBat,LAinv=n2CBLA1inv(1−r2)CHeatinv=(n3×C tank1inv+Cboilerinv)(1−r3)(7)

{CBLi1inv=CBLi,rateinv−(cBLi,Nd×n1)+c1CBLA1inv=CBLA,rateinv−(cBLA,Nd×n2)+c2Ctank1inv=Ctank,rateinv−(ctank,Nd×n3)+c3Cboilerinv=Cboiler1inv×η(8)

The investment cost is calculated by the product of the unit capacity investment cost, capacity, and depreciation rate, where the unit capacity investment cost takes into account the actual market preference and adjusts the unit capacity investment cost. Where CBLi1inv and CBLA1inv are the unit capacity investment costs of lithium-ion and lead-acid batteries respectively, n1 and n2 denote the number of lithium-ion batteries and lead-acid batteries, respectively, and Ctan⁡k1inv is the unit capacity investment cost of the heat storage tank, Cboilerinv is the investment cost of the electric boiler heater, and n3 is the number of heat storage tanks. r1, r2 and r3 are the depreciation rates for lithium-ion, lead-acid batteries, thermal storage tanks, and electric boiler heaters, respectively. CBli,rateinv, CBLA,rateinv and Ctan⁡k,rateinv are the nominal investment costs per unit capacity of lithium-ion batteries, lead-acid batteries, and thermal storage tanks, respectively. cBli,Nd, cBLA,Nd and ctan⁡k,Nd are the preferential costs per unit capacity of lithium-ion, lead-acid batteries, and heat storage tanks, respectively. c1, c2 and c3 are the cost preference factors. η is the power cost factor of the electric boiler heater.

(2) Operation and maintenance costs

Operation and maintenance can be simplified by estimating it as a percentage of the investment cost expressed in Eq. (9).

{CBat,Lioper=αCBat,LiinvCBat,LAoper=εCBat,LAinvCHeatoper=μCHeatinv(9)

where α, ε and μ are the coefficients of the ratio of the operation and maintenance cost of the electrochemical energy storage system and heat storage system to the investment cost, which are positively correlated with the investment.

(3) Compensation costs for wind energy output fluctuations

When the power of wind fluctuates greatly, the high-frequency fluctuation component of wind power output that exceeds the upper limit of the power of the energy storage system needs is supplemented by dispatching other resources, which increases the compensation cost, as measured in Eq. (10).

Ccomp=∑t=1Nccomp(Pcomp+,n(t)−Pcomp−,n(t))(10)

where ccomp is the base power compensation cost coefficient, Pcomp+,n(t) and Pcomp-,n(t) are the positive under-compensated power and negative under-compensated power at moment n, respectively.

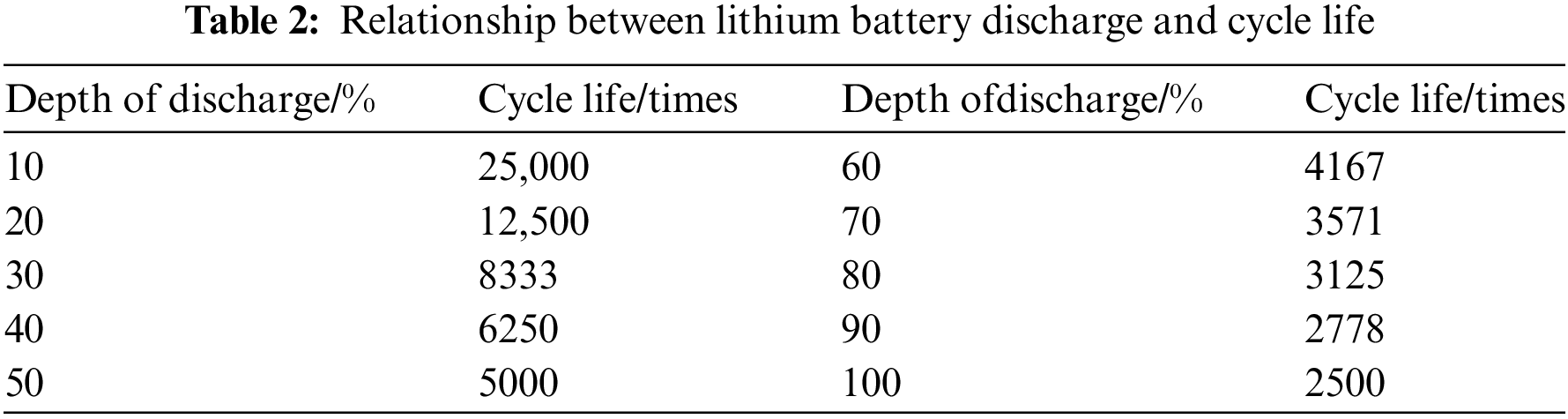
(4) Cycle life model

The life cycle for a device of energy storage mainly consider the effect of battery discharge depth (Dod) on battery life. The relationship between the depth of discharge and cycle life of Li-ion batteries according to [48] is shown in Table 2.

The relationship between depth of discharge and cycle life was fitted using the multiplicative power function approximation Eq. (11).

Nc=249992/Dod(11)

where Nc is the equivalent cycle life of the battery; Dod is the depth of discharge. The equivalent charge/discharge cycle factor of the battery is defined as

β(Dod,i)=Nc(Dod,1)/Nc(Dod,i)(12)

where Dod,i is the depth of the battery when the number of discharges is I, Nc(DOd,i) is the cycle of life when the depth of discharge is Dod,i where the value β is usually set as the cycle life when the depth of discharge is 100%. It is usually set as the cycle life at 100% discharge depth, and β range of 0–1. Battery discharge depth and cycle life are shown in Fig. 4.

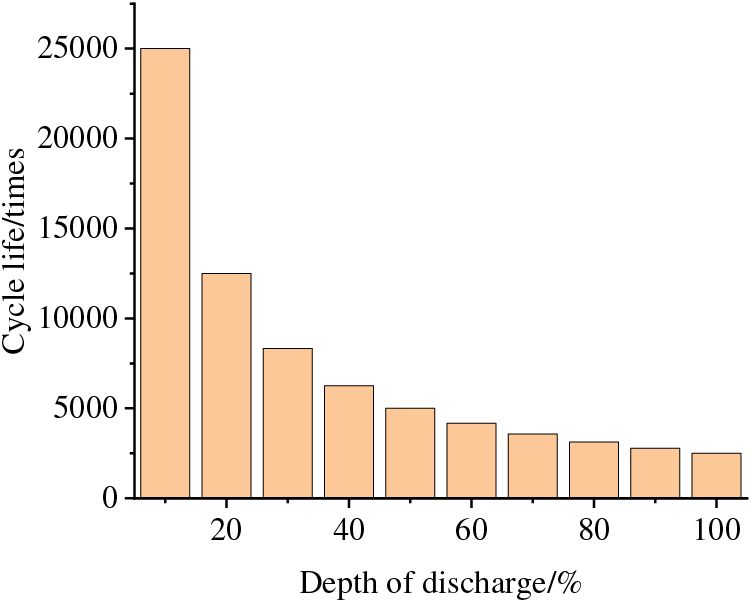
Figure 4: Diagram of the relationship between battery discharge depth and cycle life

3.2 Model Constraints

The charge and discharge power constraints for energy storage devices in this work are stipulated below, where the energy storage device charging and discharging power constraint can be expressed as in Eq. (13).

Px=Pgrid+PWT+PPV−Pload(13)

where at Px>0 denotes charging of the energy storage system and denotes Px<0 discharging of the energy storage system. The constraints are shown in Eq. (14) below:

{0<Pxch≤PmaxPmin≤Pxdisch(14)

Electrothermal hybrid energy storage system, both electrochemical and thermal energy storage systems should be charged and discharged within the appropriate range of SOC constraints as in Eq. (15).

{SBLi,minstop≤SBLi(t)≤SBLi,maxstopSBLA,minstop≤SBLA(t)≤SBLA,maxstopSHeat,minstop≤SHeat(t)≤SHeat,maxstop(15)

where in the formula above, SBLi,maxstop and SBLi,minstop are the upper and lower limits of SOC for lithium batteries, SBLA,maxstop and SBLA,minstop are the upper and lower limits of SOC for lead-acid batteries, and SHeat,max, and SHeat,min are the upper and lower limits of SOC for heat storage tanks. The specific optimization flow chart is shown in Fig. 5.

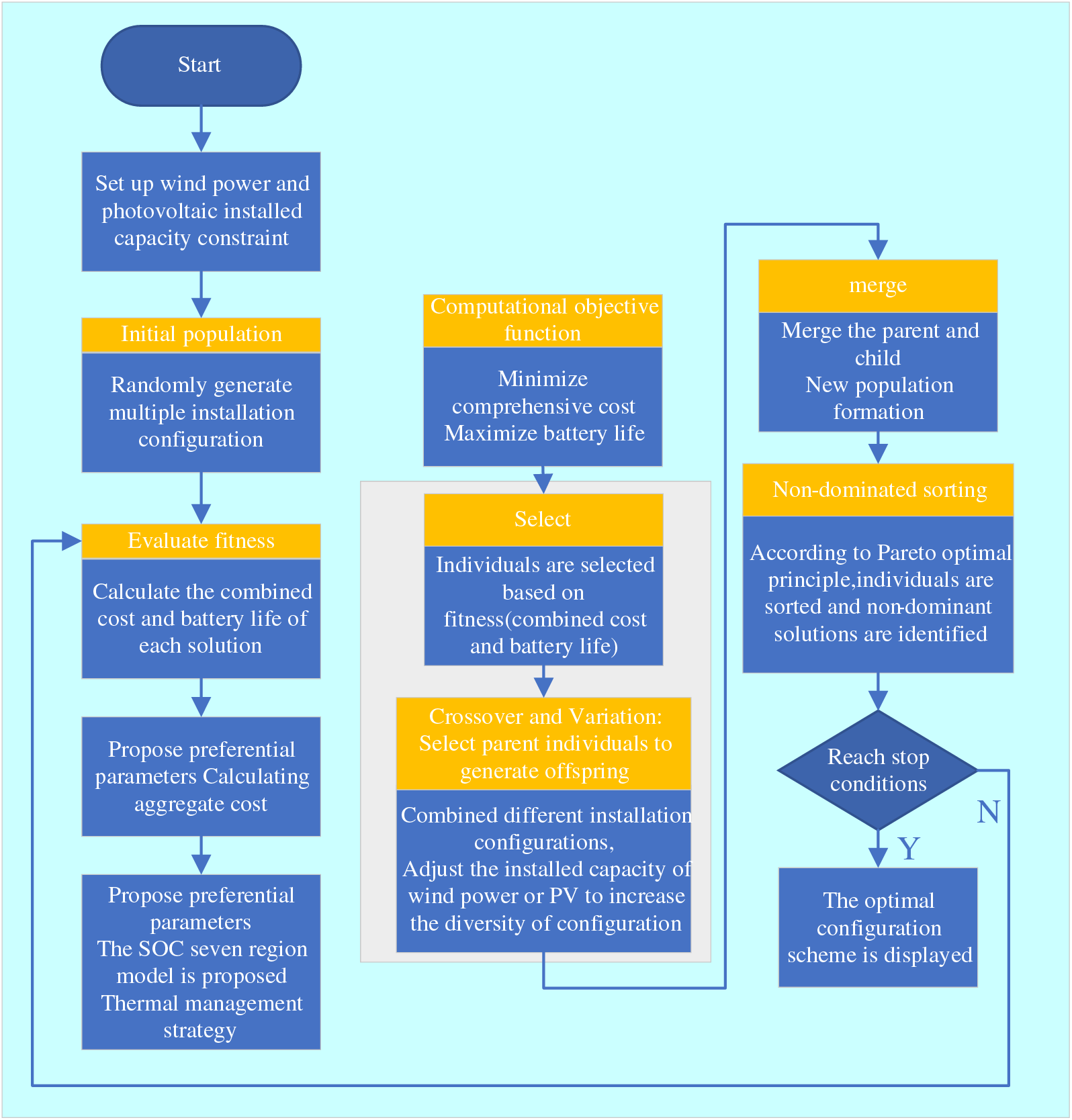
Figure 5: Flow chart of wind-wind capacity configuration optimization algorithm

4  Simulation Analysis

4.1 Analysis of System Operation

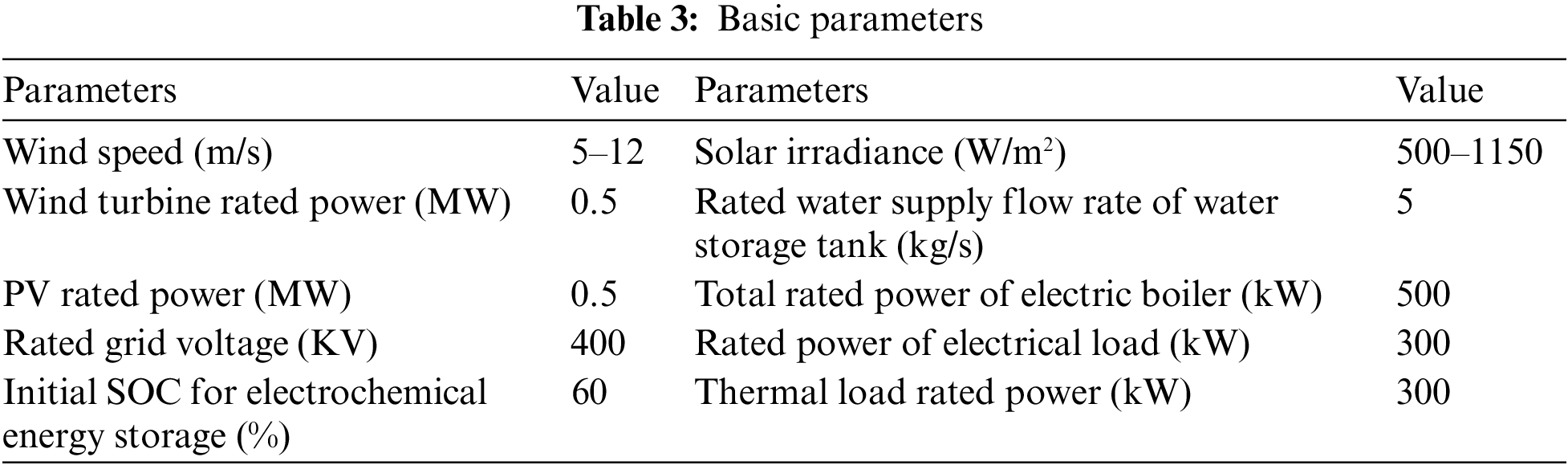
Based on MATLAB/Simulink and Real Time Labratory (RT-LAB) semi-physical simulation platform, a wind-source hybrid energy storage system was constructed. Both the wind speed and solar irradiance models are fitted with real-world wind speed and solar irradiance data and are used as inputs to the wind turbine model and the PV model. The rated capacity of the electrochemical energy storage system in the system depends on the installed capacity configuration of the wind power generation system, and the electrochemical energy storage model did not consider the effects of temperature and cycle life. The electric boiler in the thermal storage system model adopts a multi-stage heating mode, and the water supply tank is regarded as an infinite water source. The basic parameters of the system are shown in Table 3.

The results of wind and PV power volatility curves are shown in Fig. 6. It can be seen that from a time perspective, the two changes are complementary, thus, the PV power fluctuations with time at the point of wind power volatility are smaller, likewise the wind power fluctuations in the node of the PV fluctuation are also smaller. Moreover, the volatility of wind power and PV after complementary is demonstrated in Fig. 7.

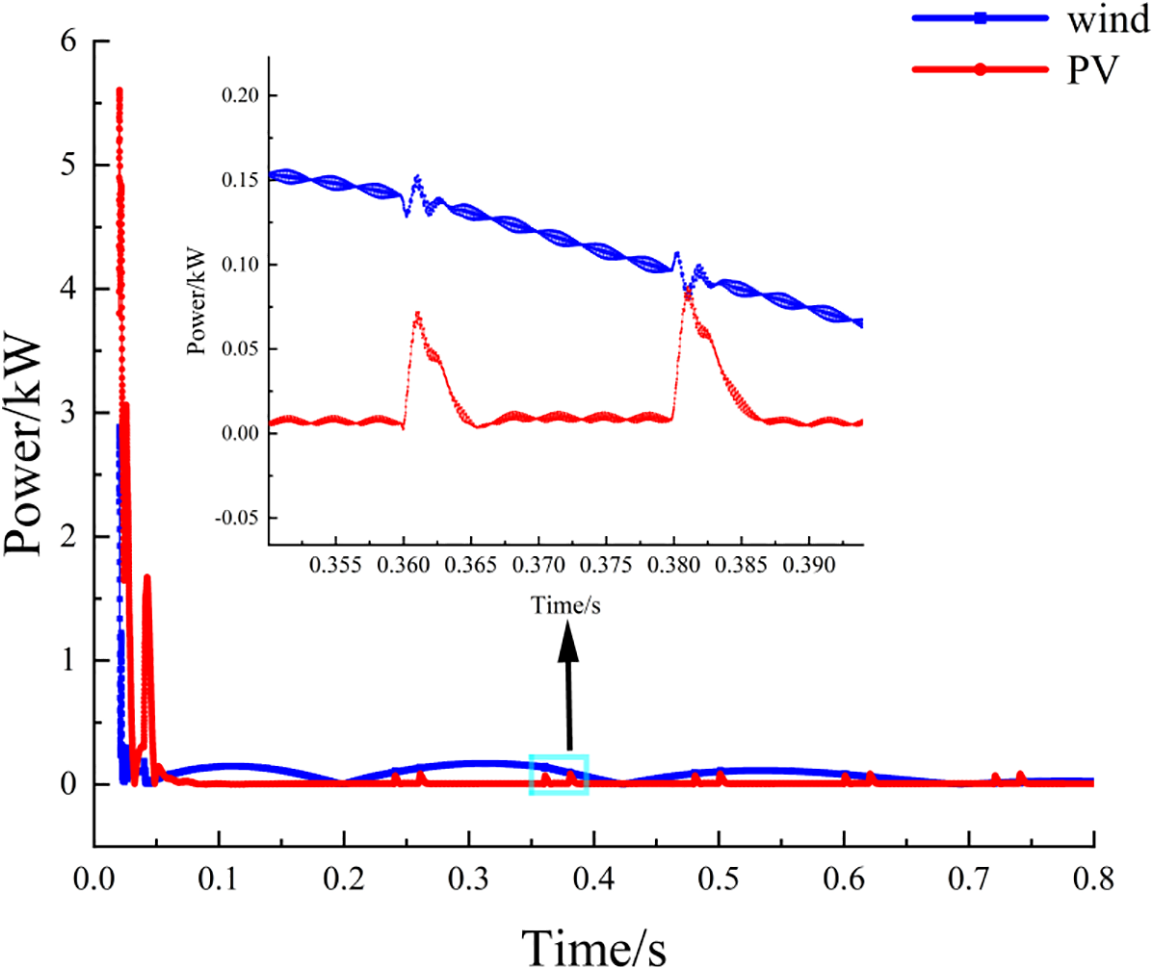
Figure 6: Graph of power fluctuations in wind and photovoltaic power generation

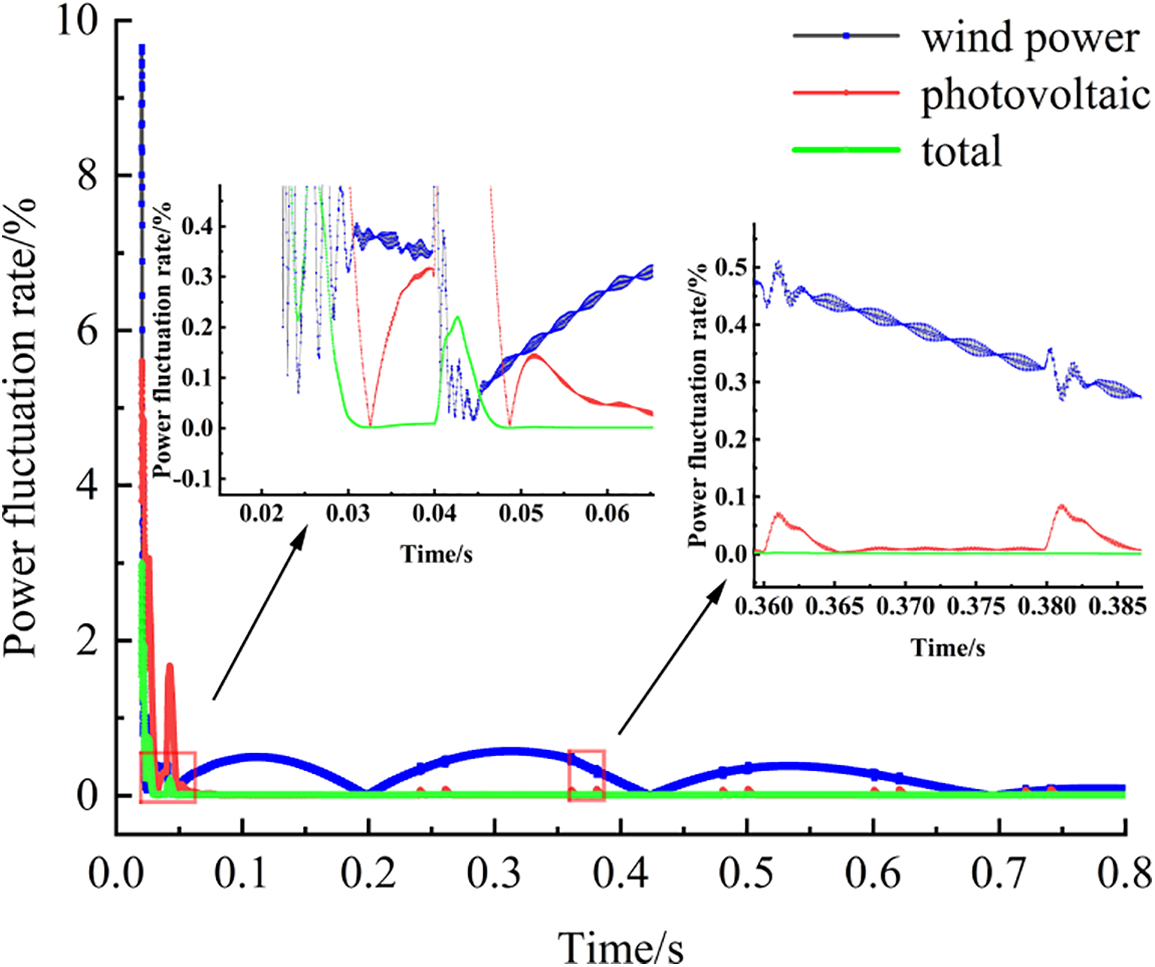
Figure 7: Wind, PV, and total power volatility graphs

It is indicated that the power fluctuation in the wind and photovoltaic hybrid power generation begins at 0.047 and 0.31 s, respectively. This produces the weak wave peak within the fluctuation rate of 0.59, The fluctuation of PV at 0.27 s is 0.09. The variation characteristics of wind energy and PV are not completely lifetime capable of achieving the volatility of the mutual offset.

4.2 Power Distribution

Before power allocation, to avoid the effect of extreme data, the data were clustered. The K-means algorithm was used to cluster the 5 s scenery data to obtain four scenery power-out scenarios. The time and probability corresponding to each scenario are listed below in Table 4. The median cumulative fluctuation is used as an indicator for each scenario, and the selected clustering scenarios are shown in Table 4.

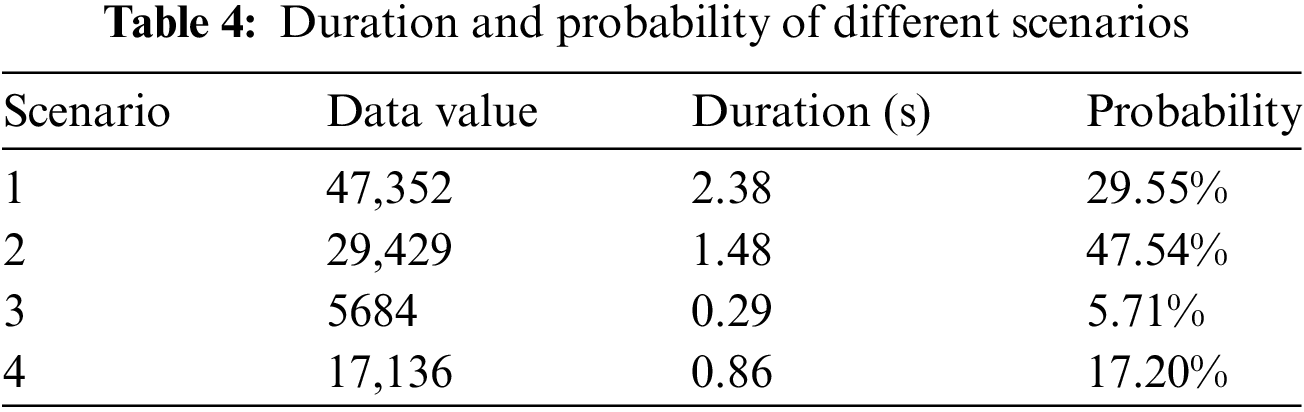
The results of wind energy clustering are indicated in Figs. 8 and 9, where the cluster findings of four scenarios were 514.58, 347.10, −10.78, and 210.28 at each point, respectively.

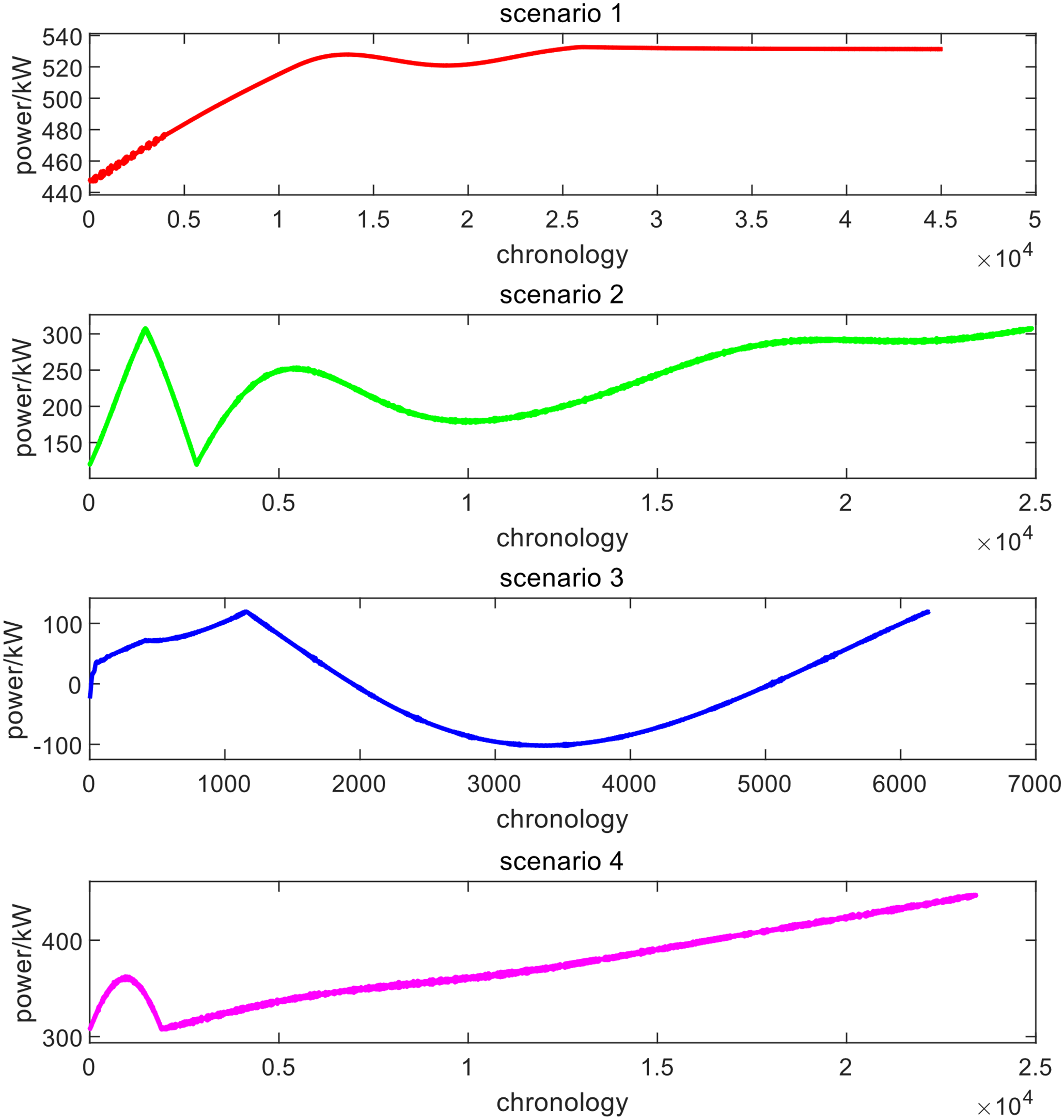
Figure 8: Clustering effect diagram for different scenarios

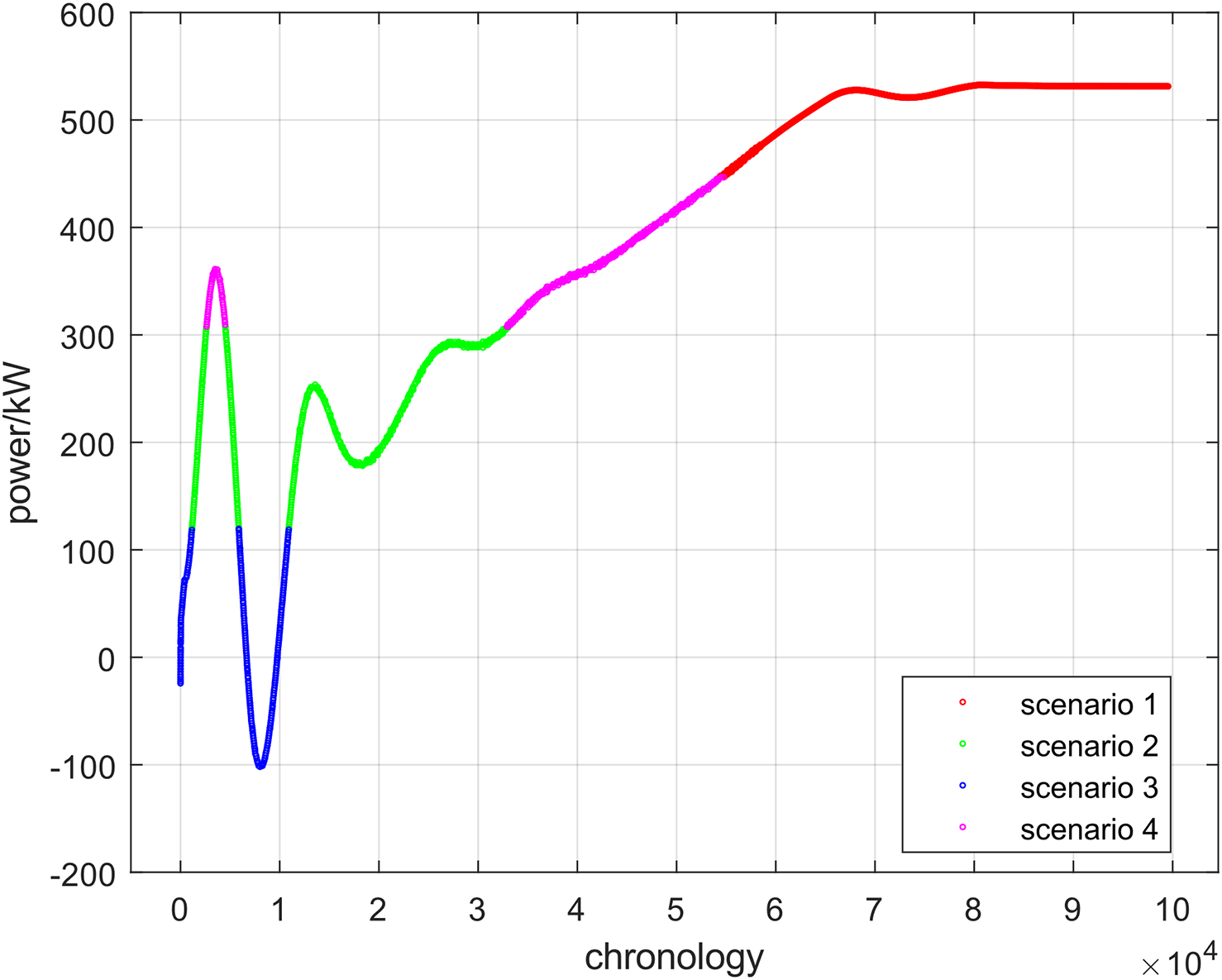
Figure 9: Curves of power output clustering results

Moreover, the grid-connection fluctuation volume limit was determined to obtain the grid-connection component and the hybrid energy storage power component. It was discovered that the lower the fluctuation limit occurred, the smoother the direct grid connection of the component. Likewise, the higher the fluctuation of the energy storage, the better the grid performance. For the case where there is too small, a limit value leads to frequent charging as well as discharging of the power storage system, which increases the loss. Fig. 10 indicates the direct grid-connected component at a fluctuation limit of 30, 20, and 10. It is observed that when the fluctuation occurs, it is reduced to 10 and the waveform is being distorted. Likewise, Fig. 11 indicates the multiple fluctuation volume constraints, where the low-frequency reconfiguration component is greater than the grid-connected fluctuation limit, specifically at 20 indicating the fluctuation in grid-connection.

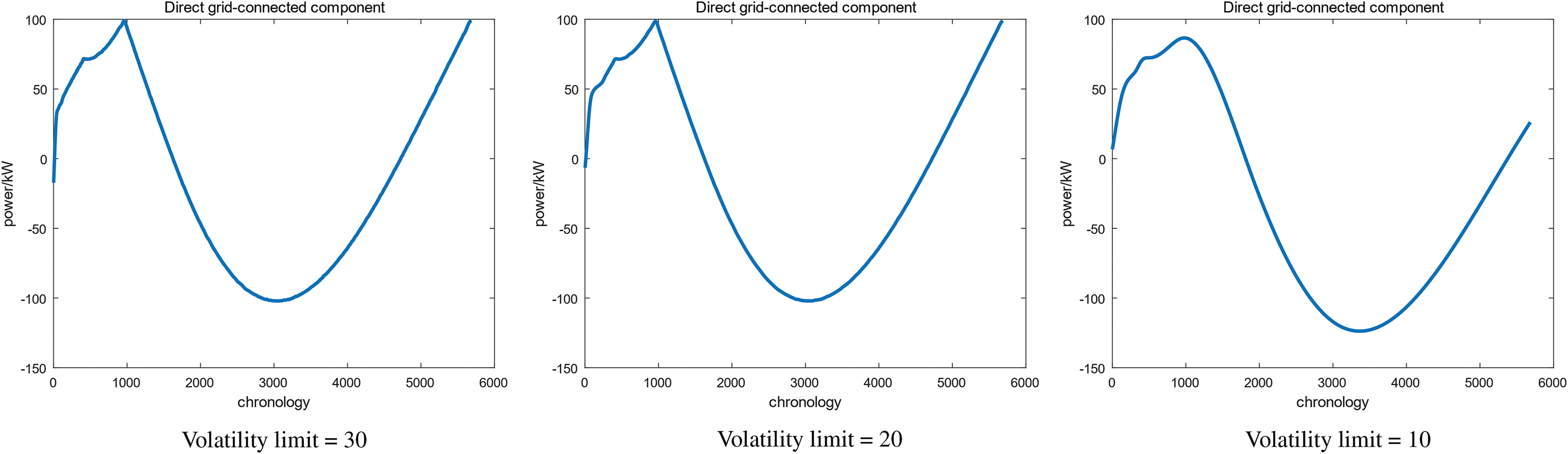
Figure 10: Grid-connected component diagrams for multiple fluctuation-limited quantities

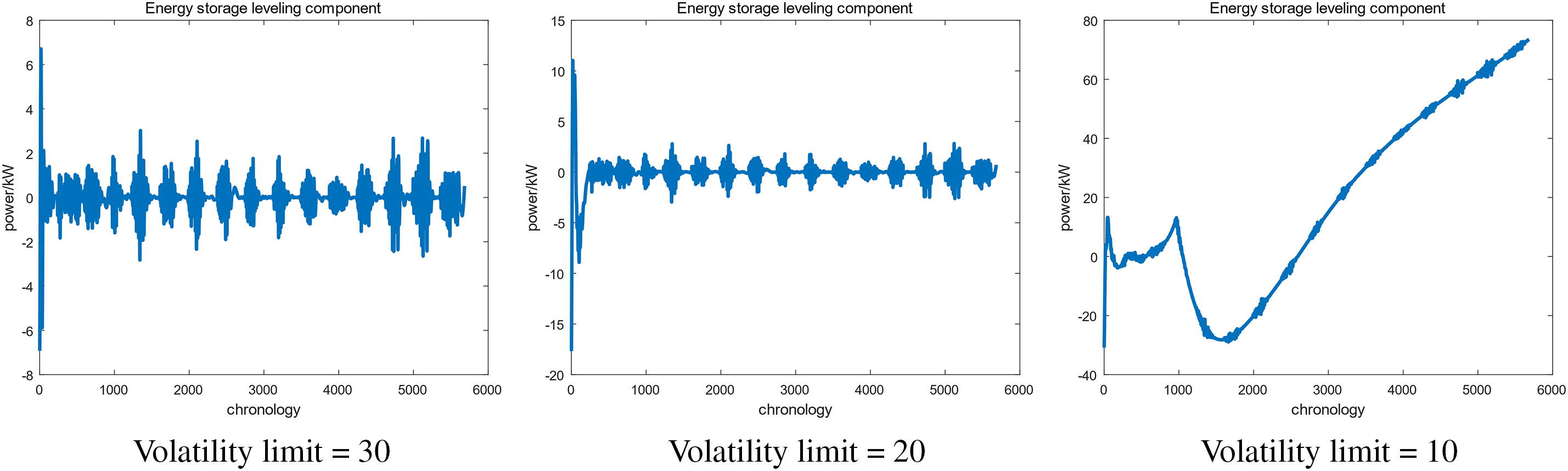
Figure 11: Graph of storage smoothing components under multiple fluctuation volume constraints

The maximum fluctuation of the low-frequency reconfiguration component c2f(4) is close to and not greater than the grid-connected fluctuation limit of 20, as shown in Fig. 12, with the DC grid-connected component of c2f(4) and the hybrid energy storage smoothing component of c2f(5).

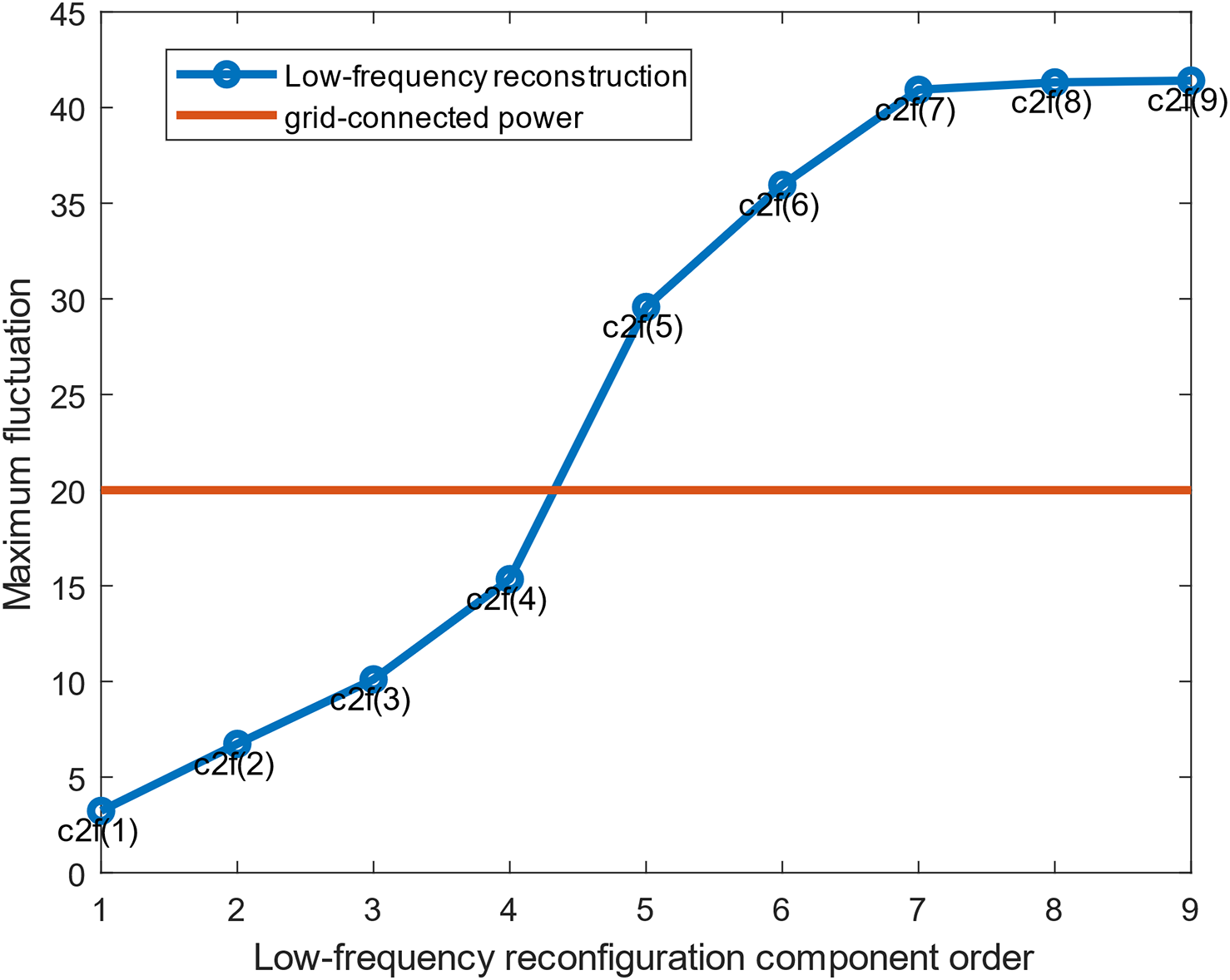
Figure 12: Curves of low-frequency reconstructed component orders

4.3 Configuration Results Analysis

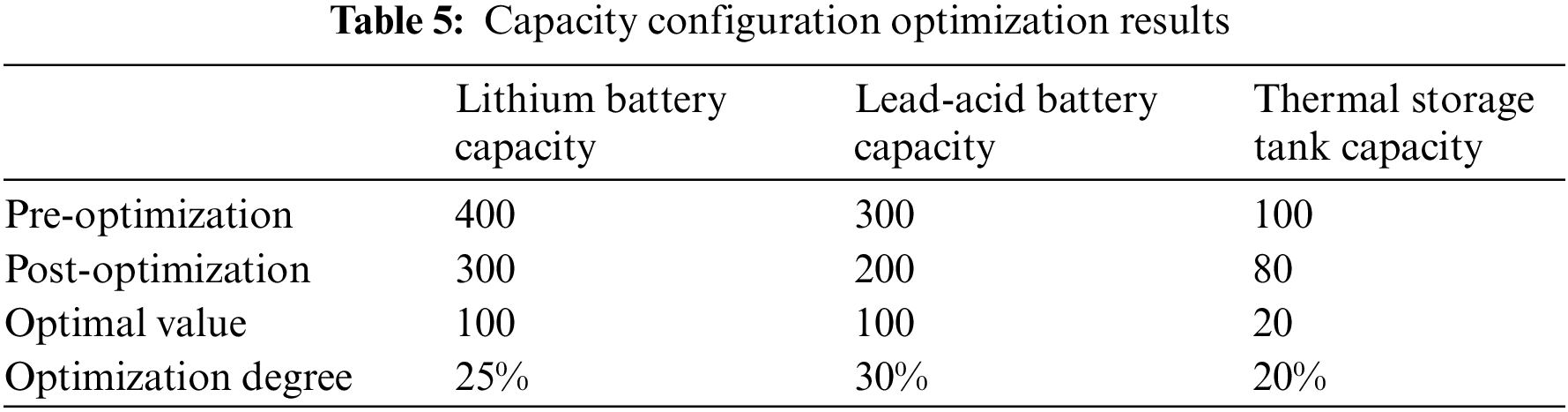
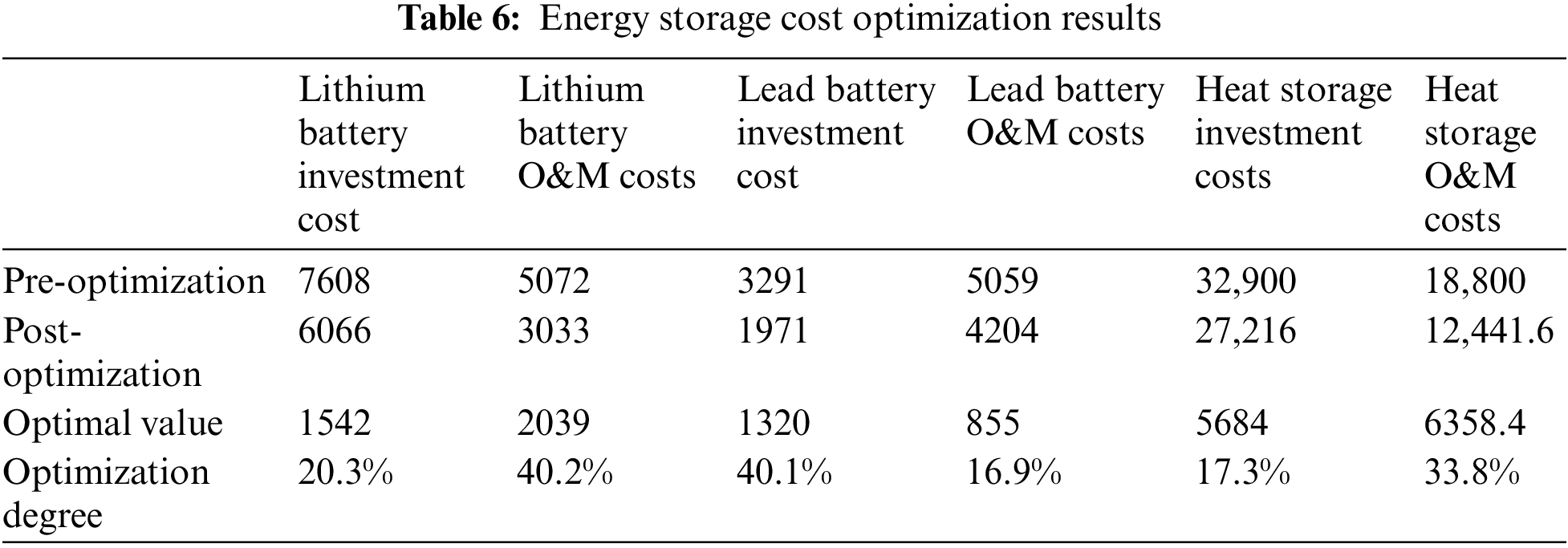
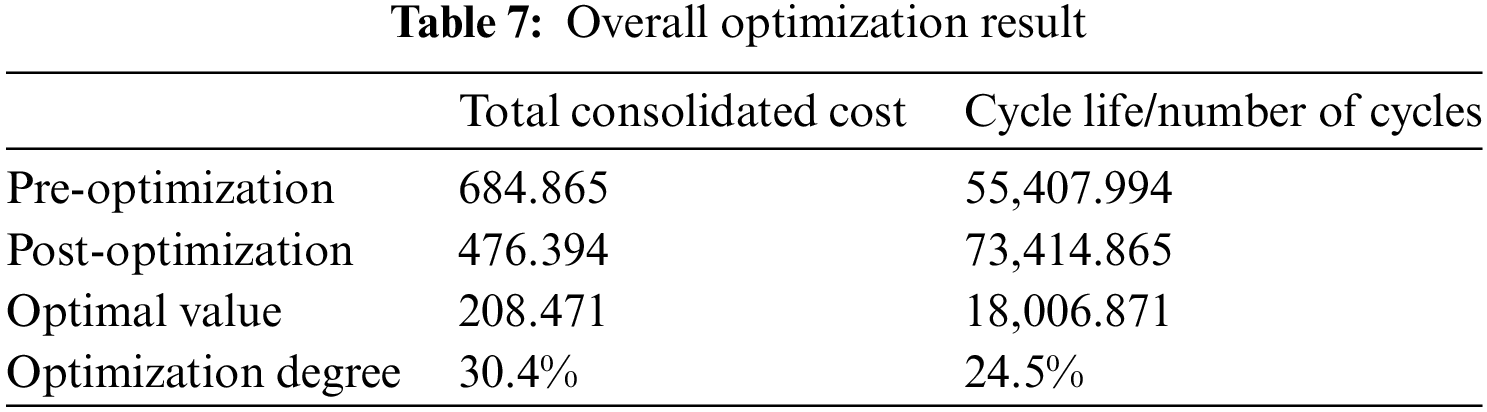
Using the multi-objective optimization genetic algorithm, the hybrid energy storage potential is optimized by the number of lithium batteries, lead-acid batteries, heat storage tanks, storage cost, and the number of electrochemical energy storage cycles as the objective function. The optimized capacity configuration results are shown in Tables 5–7. The comprehensive total cost decreased by 18,006.87 yuan at the total consolidated cost of 24.5%. Lithium battery capacity decreased from the original 400 to 300 Ah, lead-acid battery capacity from the original 300 to 200 Ah. Lithium battery and lead-acid battery capacity decline directly affect the system construction costs, operation, and maintenance costs, while improving the economy of the system. Before optimization, the energy storage cost accounted was 16.7% of the total system cost, and after optimization, it dropped to 12.5%, and the optimization degree was 4.2%. The economic feasibility of the energy storage system configuration was improved through algorithm optimization. The number of electrochemical energy storage in a cycle increased from 4515 to 4660, and the depth of discharge decreased from 55.37% to 53.65%. The main reason for the reduction of all costs is the cost of the battery is higher than the heat storage, and the strategy is utilized to effectively dispatch the heat storage and reduce the cost. Moreover, the depth of discharge was reduced to obtain shallow charging and shallow discharging to improve the battery life.

4.4 Analysis of the Effect of Strategy Optimization

(1) Trend analysis of electrochemical energy storage SOC

Using time charging and discharging cycle data analysis, lithium batteries had a faster decrease in power than lead-acid batteries. Likewise, the rate of charging and discharging was found to be small as shown in Fig. 13.

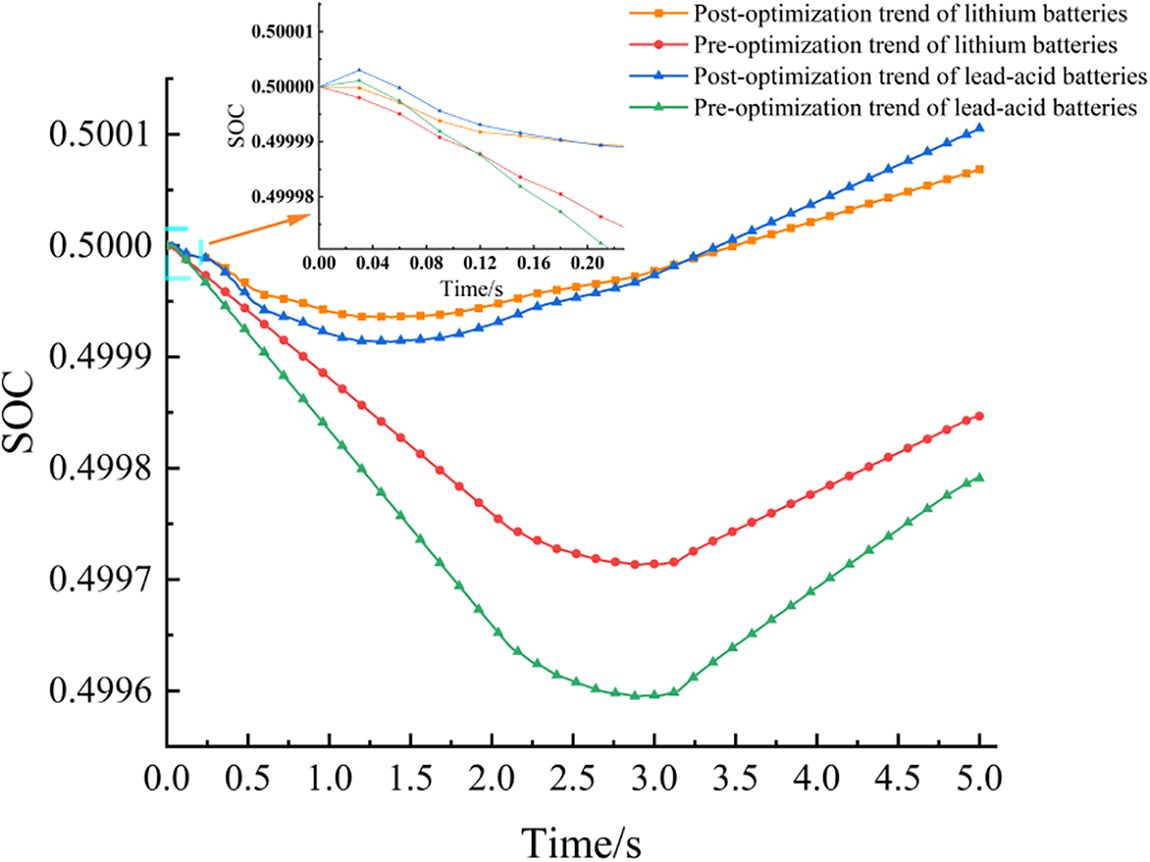
Figure 13: Curves of the trend of SOC for electrochemical energy storage

Moreover, the chemical characteristics of lead-acid batteries are more easily affected by temperature, charging, and discharging rate during the charging and discharging process, resulting in relatively fast SOC changes. The SOC change rate of Li-ion batteries is lower than that of lead-acid batteries, and Li-ion batteries are more stable and have greater energy density during the charging and discharging process. After optimization, the discharge depth of both batteries is reduced, which helps to extend the service life of the battery and reduce the damage to the battery structure caused by deep discharge. The results show that the proposed strategy achieves shallow charging and shallow discharge, which provides a research direction for considering the service life of electrochemical energy storage.

(2) Analysis of the impact of different strategies on voltage fluctuations

Rapid changes in loads in the system faults, and shock at the load end can lead to voltage fluctuations. The larger the value of ∆U, the higher the RMS value of the 10 cycles of the voltage. The operating process is analyzed with 4–4.2 s at 10 cycles.

Result in Fig. 14 indicate that voltage variation changes periodically, and the peak voltage fluctuation of the proposed strategy was observed to decrease from 2.92 to 2.86. compared to Harmonics as one of the important factors for voltage fluctuation, and it was noted that improving the harmonic distortion rate improved the voltage fluctuation challenges with respect to time. To reduce the voltage fluctuation better peak and valley regulation was conducted, to balance supply and demand. The results show that the optimization strategy has a good effect on improving power quality such as harmonics and voltage fluctuations.

Figure 14: Curves comparing the effect of voltage fluctuation

5  Conclusion

This paper proposes a new operation strategy for wind and solar hybrid energy storage systems. The strategy is optimized by power allocation and a multi-objective genetic algorithm, and the conclusions are drawn following:

(1) It was observed that the proposed strategy performed power decomposition and determined the minimum fluctuation volume limit for initial allocation. The optimized objectives function of dynamic cost with the lowest integrated cost and longer life cycle was depicted and verified to be effective in enhancing wind power fluctuation, economy, and battery cycle life. The power decomposition obtained by the proposed strategy can be widely used in frequency division energy storage technology, which provides a reference for smoothing the fluctuation of wind and wind output while improving the economy.

(2) The results show that the proposed electro-thermal hybrid energy management strategy based on the SOC reduces the depth of discharge and increases the cycle life by 145 times. Likewise, it reduces battery overuse, maintains sufficient capacity to smooth fluctuations, reduces cost, and improves battery cycle life. This management strategy provides a new way to solve the problem of over-charge and over-discharge extremes by providing a feasible stabilizing power system volatility.

(3) In general, the proposed strategy adds an electro-thermal HESS complementary mechanism, which improves thermal energy utilization and reduces the cost of hybrid energy storage, while the complementary mechanism improves the service period of the electrochemical energy system. However, the role of the battery for high-frequency compensation is not enough, and the system combined with power storage such as supercapacitors needs further research to better utilize the advantages of HESS.

Acknowledgement: The authors would like to thank the new energy storage Department of Ordos Energy Research Institute of Peking University for its important support in providing RT-LAB and other simulation tools, and the Key Laboratory of Wind Energy and Solar Energy of Inner Mongolia University of Technology for providing the necessary test site for this paper. Finally, the authors thank the editors and anonymous reviewers for their critical and constructive comments.

Funding Statement: This work was supported by a Horizontal Project on the Development of a Hybrid Energy Storage Simulation Model for Wind Power Based on an RT-LAB Simulation System (PH2023000190); the Inner Mongolia Natural Science Foundation Project and the Optimization of Exergy Efficiency of a Hybrid Energy Storage System with Crossover Control for Wind Power (2023JQ04).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Caifeng Wen, Hongliang Hao; fund preparation: Hongliang Hao, Yuwen Zhang; data collection and sorting: Hao Qiu, Chaoyu Wang; draft manuscript writing: Feifei Xue, Ning Yang; paper translation: Edwin E. Nyakilla. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors ensure the authenticity and validity of the materials and data in the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. D. Suchet, A. Jeantet, T. Elghozi, and Z. Jehl, “Defining and quantifying intermittency in the power sector,” Energies, vol. 13, no. 13, 2020, Art. no. 3366. doi: 10.3390/en13133366. [Google Scholar] [CrossRef]

2. N. M. Kumar, A. Ghosh, and S. S. Chopra, “Power resilience enhancement of a residential electricity user using photovoltaics and a battery energy storage system under uncertainty conditions,” Energies, vol. 13, no. 16, 2020, Art. no. 4193. doi: 10.3390/en13164193. [Google Scholar] [CrossRef]

3. M. Lucu, I. Gandiaga, and H. Camblong, “A critical review on self-adaptive Li-ion batteryageing models,” J. Power Sources, vol. 401, pp. 85–101, 2018. doi: 10.1016/j.jpowsour.2018.08.064. [Google Scholar] [CrossRef]

4. A. Ali, G. Abbas, M. Keerio, E. Touti, Z. Ahmed and O. Alsalman, “A bi-level techno-economic optimal reactive power dispatch considering wind and solar power integration,” IEEE Access, vol. 11, pp. 62700–62819, 2023. doi: 10.1109/ACCESS.2023.3286930. [Google Scholar] [CrossRef]

5. J. Kabouris and F. D. Kanellos, “Impacts of large-scale wind penetration on designing and operation of electric power systems,” IEEE Trans. Sustain. Energy., vol. 1, no. 2, pp. 107–114, 2010. doi: 10.1109/TSTE.2010.2050348. [Google Scholar] [CrossRef]

6. G. Ren, W. Wang, J. Wan, F. Hong, and K. Yang, “A novel metric for assessing wind and solar power complementarity based on three different fluctuation states and corresponding fluctuation amplitudes,” Energy Convers. Manag., vol. 278, no. 7830, 2023, Art. no. 116721. doi: 10.1016/j.enconman.2023.116721. [Google Scholar] [CrossRef]

7. Q. Hassan, S. Algburi, A. Z. Sameen, H. M. Salman, and M. Jaszczur, “A review of hybrid renewable energy systems: Solar and wind-powered solutions: Challenges, opportunities, and policy implications,” Results Eng., vol. 20, no. 18, 2023, Art. no. 101621. doi: 10.1016/j.rineng.2023.101621. [Google Scholar] [CrossRef]

8. A. Kumar, Y. R. Sood, and R. N. Mahia, “Hybrid energy system simulation and modelling incorporating wind and solar power,” in IEEE Int. Stud. Conf. Elect., Elect. Comput. Sci. (SCEECS), Bhopal, India, 2024, pp. 1–5. doi: 10.1109/SCEECS61402.2024. [Google Scholar] [CrossRef]

9. I. Rahimi, M. R. Nikoo, and A. H. Gandomi, “Techno-economic analysis for using hybrid wind and solar energies in Australia,” Energy Strategy Rev., vol. 47, no. 7, 2023, Art. no. 101092. doi: 10.1016/j.esr.2023.101092. [Google Scholar] [CrossRef]

10. I. J. Fernández, C. F. Calvillo, and J. Boal, “Capacity fade and aging models for electric batteries and optimal charging strategy for electric vehicles,” Energy, vol. 60, no. 12, pp. 35–43, 2023. doi: 10.1016/j.energy.2013.07.068. [Google Scholar] [CrossRef]

11. Y. Guo, B. Ming, Q. Huang, Z. Yang, Y. Kong and X. Wang, “Variation-based complementarity assessment between wind and solar resources in China,” Energy Convers. Manag., vol. 278, 2023, Art. no. 116726. doi: 10.1016/j.enconman.2023.116726. [Google Scholar] [CrossRef]

12. M. A. Adesanya et al., “Dynamic modeling and techno-economic assessment of hybrid renewable energy and thermal storage systems for a net-zero energy greenhouse in South Korea,” Clean Technol. Environ. Policy, vol. 26, no. 13, pp. 551–576, 2024. doi: 10.1007/s10098-023-02656-3. [Google Scholar] [CrossRef]

13. Y. Gong, Q. Jiang, and R. Baldick, “Ramp event forecast based wind power ramp control with ESS,” IEEE Trans. Power Syst., vol. 31, no. 3, pp. 1831–1844, 2016. doi: 10.1109/TPWRS.2015.2445382. [Google Scholar] [CrossRef]

14. R. Pedruzzi et al., “Review of mapping analysis and complementarity between solar and wind energy sources,” Energy, vol. 283, no. 15, 2023, Art. no. 129045. doi: 10.1016/j.energy.2023.129045. [Google Scholar] [CrossRef]

15. T. Okazaki, Y. Shirai, and T. Nakamura, “Concept study of wind power utilizing direct thermal energy conversion and thermal energy storage,” Renew. Energy, vol. 83, no. 10, pp. 332–338, 2015. doi: 10.1016/j.renene.2015.04.027. [Google Scholar] [CrossRef]

16. Y. Xiao, C. Zou, M. Dong, H. Chi, Y. Yan and S. Jiang, “Feasibility study: Economic and technical analysis of optimal configuration and operation of a hybrid CSP/PV/wind power cogeneration system with energy storage,” Renew. Energy, vol. 225, no. 8, 2024, Art. no. 120273. doi: 10.1016/j.renene.2024.120273. [Google Scholar] [CrossRef]

17. J. Graça Gomes et al., “Hybrid solar PV-wind-battery system bidding optimisation: A case study for the Iberian and Italian liberalised electricity markets,” Energy, vol. 263, no. 15, 2023, Art. no. 126043. doi: 10.1016/j.energy.2022.126043. [Google Scholar] [CrossRef]

18. L. Qing, M. Usman, M. Radulescu, and M. Haseeb, “Towards the vision of going green in South Asian region: The role of technological innovations, renewable energy and natural resources in ecological footprint during globalization mode,” Resour. Policy, vol. 88, no. 11, 2024, Art. no. 104506. doi: 10.1016/j.resourpol.2023.104506. [Google Scholar] [CrossRef]

19. U. Kahraman and I. Dincer, “Development and assessment of an integrated underground gasification system for cleaner outputs,” Energy, vol. 285, no. 15, 2023, Art. no. 128676. doi: 10.1016/j.energy.2023.128676. [Google Scholar] [CrossRef]

20. J. Tian, S. Zhou, and Y. Wang, “Assessing the technical and economic potential of wind and solar energy in China—A provincial-scale analysis,” Environ. Impact Assess. Rev., vol. 102, 2023, Art. no. 107161. doi: 10.1016/j.eiar.2023.107161. [Google Scholar] [CrossRef]

21. A. S. Alghamdi, “Optimal power flow of hybrid wind/solar/thermal energy integrated power systems considering costs and emissions via a novel and efficient search optimization algorithm,” Appl. Sci., vol. 13, no. 8, 2023, Art. no. 4670. doi: 10.3390/app13084760. [Google Scholar] [CrossRef]

22. P. Pérez-López et al., “ENVI-PV: An interactive Web Client for multi-criteria life cycle assessment of photovoltaic systems worldwide,” Photovolt: Res. Appl., vol. 25, no. 10, pp. 484–498, 2016. doi: 10.1002/pip.2841. [Google Scholar] [CrossRef]

23. M. Parhizi, M. Pathak, J. K. Ostanek, and A. Jain, “An iterative analytical model for aging analysis of Liion cells,” J. Power Sources, vol. 517, no. 1, 2022, Art. no. 230667. doi: 10.1016/j.jpowsour.2021.230667. [Google Scholar] [CrossRef]

24. J. Yang, H. Chi, M. Cheng, M. Dong, S. Li and H. Yao, “Performance analysis of hydrogen supply using curtailed power from a solar-wind-storage power system,” Renew. Energy, vol. 212, no. 2, pp. 1005–1019, 2023. doi: 10.1016/j.renene.2023.05.094. [Google Scholar] [CrossRef]

25. M. S. Alam et al., “Solar and wind energy integrated system frequency control: A critical review on recent developments,” Energies, vol. 16, no. 2, 2023, Art. no. 812. doi: 10.3390/en16020812. [Google Scholar] [CrossRef]

26. C. Wen, Q. Wang, Y. Cao, L. Zhang, and W. Wang, “Correlation analysis of wind turbine temperature rise and exergy efficiency based on field-path coupling,” Energy Eng., vol. 120, no. 7, pp. 1603–1619, 2023. doi: 10.32604/ee.2023.027074. [Google Scholar] [CrossRef]

27. C. Wen, B. Zhang, Y. Dai, W. Wang, and W. Xie, “The correlation between the power quality indicators and entropy production characteristics of wind power + energy storage systems,” Energy Eng., vol. 121, no. 10, pp. 2961–2979, 2024. doi: 10.32604/ee.2024.041677. [Google Scholar] [CrossRef]

28. T. Liu, J. Yang, Z. Yang, and Y. Duan, “Techno-economic feasibility of solar power plants considering PV/CSP with electrical/thermal energy storage system,” Energ. Convers. Manag., vol. 255, no. 2, 2022, Art. no. 115308. doi: 10.1016/j.enconman.2022.115308. [Google Scholar] [CrossRef]

29. R. P. Kandi, M. M. Sudharmini, A. Suryan, and S. Nižetić, “State of the art and future prospects for TEG-PCM Systems: A review,” Energy Sustain. Dev., vol. 74, no. 6, pp. 328–348, 2023. doi: 10.1016/j.esd.2023.04.012. [Google Scholar] [CrossRef]

30. M. Emamjome Kashan, A. S. Fung, and A. Hossein Eisapour, “Insulated concrete form foundation wall as solar thermal energy storage for cold-climate building heating system,” Energy Convers. Manag. X, vol. 19, no. 9, 2023, Art. no. 100391. doi: 10.1016/j.ecmx.2023.100391. [Google Scholar] [CrossRef]

31. B. Koçak, A. I. Fernandez, and H. Paksoy, “Review on sensible thermal energy storage for industrial solar applications and sustainability aspects,” Solar Energ., vol. 209, no. 8, pp. 135–169, 2020. doi: 10.1016/j.solener.2020.08.081. [Google Scholar] [CrossRef]

32. S. Guo, Q. Liu, J. Sun, and H. Jin, “A review on the utilization of hybrid renewable energy,” Renew. Sustain. Energ. Rev., vol. 91, pp. 1121–1147, 2018. doi: 10.1016/j.rser.2018.04.105. [Google Scholar] [CrossRef]

33. L. Liu and Z. Wang, “The development and application practice of wind-solar energy hybrid generation systems in China,” Renew. Sustain. Energ. Rev., vol. 13, no. 6–7, pp. 1504–1512, 2009. doi: 10.1016/j.rser.2008.09.021. [Google Scholar] [CrossRef]

34. M. K. Deshmukh and S. S. Deshmukh, “Modeling of hybrid renewable energy systems,” Renew. Sustain. Energ. Rev., vol. 12, no. 1, pp. 235–249, 2008. doi: 10.1016/j.rser.2006.07.011. [Google Scholar] [CrossRef]

35. S. Rekik and S. El Alimi, “Optimal wind-solar site selection using a GIS-AHP based approach: A case of Tunisia,” Energy Convers. Manag. X, vol. 18, no. 2, 2023, Art. no. 100355. doi: 10.1016/j.ecmx.2023.100355. [Google Scholar] [CrossRef]

36. B. Ghobadian, G. Najafi, H. Rahimi, and T. F. Yusaf, “Future of renewable energies in Iran,” Renew. Sustain. Energ. Rev., vol. 13, no. 3, pp. 689–695, 2009. doi: 10.1016/j.rser.2007.11.010. [Google Scholar] [CrossRef]

37. H. X. Yang, L. Lu, and J. Burnett, “Weather data and probability analysis of hybrid photovoltaic-wind power generation systems in Hong Kong,” Renew. Energ., vol. 28, no. 11, pp. 1813–1824, 2003. doi: 10.1016/S0960-1481(03)00015-6. [Google Scholar] [CrossRef]

38. H. J. Wagner, “Introduction to wind energy systems,” in EPJ Web of Conf., Bochum, Germany, 2020, vol. 246. doi: 10.1051/epjconf/202024600004. [Google Scholar] [CrossRef]

39. H. J. Wagner, “Introduction to wind energy systems,” in EPJ Web of Conf., Bochum, Germany, 2018, vol. 189. doi: 10.1051/epjconf/201818900005. [Google Scholar] [CrossRef]

40. J. Fan, X. Huang, J. Shi, K. Li, J. Cai and X. Zhang, “Complementary potential of wind-solar-hydro power in Chinese provinces: Based on a high temporal resolution multi-objective optimization model,” Renew. Sustain. Energ. Rev., vol. 184, 2023, Art. no. 113566. doi: 10.1016/j.rser.2023.113566. [Google Scholar] [CrossRef]

41. L. Yao, Y. Wang, and X. Xiao, “Concentrated solar power plant modeling for power system studies,” IEEE Trans. Power Syst., vol. 12, no. 2, pp. 1–12, 2023. doi: 10.1109/TPWRS.2023.3301996. [Google Scholar] [CrossRef]

42. L. Liu et al., “Climate change impacts on planned supply-demand match in global wind and solar energy systems,” Nat. Energy, vol. 8, no. 8, pp. 870–880, 2023. doi: 10.1038/s41560-023-01304-w. [Google Scholar] [CrossRef]

43. M. L. Sørensen, P. Nystrup, M. B. Bjerregård, J. K. Møller, P. Bacher and H. Madsen, “Recent developments in multivariate wind and solar power forecasting,” Wires Energ. Environ., vol. 12, no. 2, 2022, Art. no. 465. doi: 10.1002/wene.465. [Google Scholar] [CrossRef]

44. J. Nematian and I. Rahimi, “Feasibility study of using renewable energies in Iranian Seas: A comparative study,” Renew. Energy, vol. 189, no. 7, pp. 383–391, 2022. doi: 10.1016/j.renene.2022.02.109. [Google Scholar] [CrossRef]

45. R. Hemmati, S. M. S. Ghiasi, and A. Entezariharsini, “Power fluctuation smoothing and loss reduction in grid integrated with thermal-wind-solar-storage units,” Energy, vol. 152, no. 2, pp. 759–769, 2018. doi: 10.1016/j.energy.2018.04.004. [Google Scholar] [CrossRef]

46. H. Su, S. Song, and X. Wang, “Probabilistic calculation of tidal currents for wind powered systems using PSO improved LHS,” Energy Eng., vol. 121, no. 11, pp. 3289–3303, 2024. doi: 10.32604/ee.2024.054643. [Google Scholar] [CrossRef]

47. S. K. Sarker, S. R. Fahim, N. Sarker, K. Z. Tayef, A. B. Siddique and D. Datta, “Ancillary voltage control design for adaptive tracking performance of microgrid coupled with industrial loads,” IEEE Access, vol. 9, pp. 143690–143706, 2021. doi: 10.1109/ACCESS.2021.3121548. [Google Scholar] [CrossRef]

48. A. Mahesh and K. S. Sandhu, “A genetic algorithm based improved optimal sizing strategy for solar-wind-battery hybrid system using energy filter algorithm,” Front. Energy, vol. 14, no. 1, pp. 139–151, 2017. doi: 10.1007/s11708-017-0484-4. [Google Scholar] [CrossRef]

49. X. Ma, M. Deveci, J. Yan, and Y. Liu, “Optimal capacity configuration of wind-photovoltaic-storage hybrid system: A study based on multi-objective optimization and sparrow search algorithm,” J. Energy Storage, vol. 85, 2024, Art. no. 110983. doi: 10.1016/j.est.2024.110983. [Google Scholar] [CrossRef]

50. M. Gao, Z. Han, C. Zhang, P. Li, D. Wu and P. Li, “Optimal configuration for regional integrated energy systems with multi-element hybrid energy storage,” Energy, vol. 277, 2023, Art. no. 127672. doi: 10.1016/j.energy.2023.127672. [Google Scholar] [CrossRef]