Grid-Connected/Islanded Switching Control Strategy for Photovoltaic Storage Hybrid Inverters Based on Modified Chimpanzee Optimization Algorithm

Nomenclature

1  Introduction

As global energy demand escalates and environmental protection awareness intensifies, the study and application of renewable energy sources, particularly solar photovoltaic systems, have garnered significant interest. Photovoltaic storage hybrid inverters, a crucial component of these systems, not only facilitate efficient and stable energy conversion but also permit seamless transitioning between grid-connected and island modes [1–3]. Hoseinzadeh et al. [4,5] have discovered, through optimized analysis of regional hydropower stations and photovoltaic panels, that the adoption of renewable energy and eco-friendly systems can significantly reduce the cost of electricity generation. In addition, they have proposed an improved technology for solar distillation power generation, which significantly increases economic benefits.

Currently, photovoltaic storage hybrid inverters predominantly employ droop control strategies, with power distribution achieved via predefined droop coefficients. Recently, researchers worldwide have investigated methods to decouple the droop control strategy. Kallamadi et al. [6] introduced a decoupling approach integrating virtual inductance compensation with voltage control, aiming to realize power decoupling and enhance microgrid control performance. Voltage controllers can compensate for voltage, yet determining the precise value of line impedance remains challenging. Han et al. [7] suggestd enhanced droop control characteristics and an adaptive approach to reduce reliance on line impedance in complex networks, thereby improving power sharing. Nonetheless, adjusting the droop slope can lead to significant output voltage deviations, impacting system stability. Hirase et al. [8] adopted a minimalist algebraic virtual synchronous generator (VSG) model with the fewest parameters, effectively mitigating system frequency and voltage deviations to overcome these challenges. Awal et al. [9] proposed a hierarchical controller based on a virtual oscillator, which facilitates voltage and frequency regulation and grid synchronization in islanded microgrids. Chowdhury et al. [10] introduced a VSG control scheme with a fuzzy secondary controller (FSC) for inverters connected to distributed generation (DG), enhancing microgrid frequency and voltage stability. Wang et al. [11] presented an enhanced droop control strategy to offset voltage drops due to line impedance mismatches. While this method reduces reactive power sharing errors to a minimum, complete elimination is not achieved. Moslemi et al. [12] introduced a dynamic virtual inductance to offset line impedance mismatches, aiming to enhance reactive power balance. These methods, however, overlook the influence of line resistance, leading to unpredictable performance and generally suboptimal voltage quality. Zhang et al. [13] proposed a unified scheme that allows conventional current controllers to provide a specified voltage to the local load when islanded, while conventional sag controllers directly regulate the grid current when connected to the grid. As a result, the scheme allows seamless switching between modes in very short transient cycles.

Furthermore, Sellamna et al. [14,15] suggested alternative adaptive virtual impedance methods to improve power sharing in low-voltage networks and to enhance reactive power sharing among distributed generators. Despite virtual adjustments to the inverter’s output impedance for precise power balance, voltage drops between distributed generators remain unavoidable with these methods. Liang et al. [16,17] incorporated virtual resistance into inverter control, using adaptive control to track and adjust for active power output deviations, without addressing its compatibility issues with parallel operation in microgrids. Yang et al. [18] employed an adaptive control strategy that integrates segmented regulation and frequency modulation to refine droop control, utilizing automatic adjustment of the droop curve to optimize power distribution. This method, however, does not account for the potential adverse effects of an excessively large droop coefficient on the system. Bai et al. [19] employed a self-adjusting enhanced droop control strategy. This strategy is integrated into traditional inverter droop control, incorporating a proportional-integral module to optimize the reactive voltage droop control relationship for improved output balancing. Nonetheless, this approach has its drawbacks, including diminished stability and feasibility during the system’s operation.

However, the scope of application of the above strategies is limited by their complex structure, neglect of the dynamic properties of the system, and the need for complex communication networks. Furthermore, neglecting the influence of the output impedance of photovoltaic storage hybrid inverters and line impedance alters the bus voltage’s operating condition. This affects power quality adversely and causes imbalanced power distribution, necessitating the exploration of new control strategies.

In traditional droop control, active power regulation depends exclusively on angular frequency, whereas reactive power is controlled solely through voltage. This indicates a two-dimensional process for power regulation. Overlooking the effects of power coupling may render the strategy unable to control power coupling effectively. This study introduces a control strategy based on the improved Chimpanzee Optimization Algorithm (MChOA) for grid-connected/island switching in photovoltaic storage hybrid inverters. Simultaneous adjustment of angular frequency and voltage enhances the distribution of active and reactive power, particularly in multi-inverter parallel systems. Differential action allows the system to rapidly detect load changes and adjust power distribution promptly, thereby improving voltage stability and power distribution efficiency. The MChOA algorithm optimizes the droop control parameters of photovoltaic-storage hybrid inverters by incorporating learning behavior and emotional behavior operators, enhancing local exploitation and optimization accuracy. These improvements markedly enhance the algorithm’s robustness and adaptability, effectively addressing frequency deviations during changes in inverter operating conditions. A Simulink model was constructed to validate the effectiveness of the enhanced control strategy, ensuring efficient and seamless transitions between grid-connected and island modes for the photovoltaic storage hybrid inverter.

The structure of this paper is as follows: Section 2 provides a detailed introduction to the structure and principles of the photovoltaic storage hybrid power generation system. Section 3 describes the control strategies employed by the photovoltaic storage hybrid inverter during the grid-connected/islanded switching process, and elaborates on the improvement process and its integration with MCHOA. Section 4 presents a comparison of experimental results between the proposed control strategy and the traditional droop control strategy in response to load changes and during transitions between the two modes. Section 5 concludes the paper.

2  Structure and Principle of Photovoltaic Storage Hybrid Power Generation System

The structure and principle of the photovoltaic storage hybrid power generation system is shown in Fig. 1. The photovoltaic storage hybrid inverter is mainly composed of a DC power source PV module, a three-phase full-bridge converter, a filter inductor Lf and capacitor Cf, a local load RLoad, a static transfer switch (STS), a grid-side inductor Lg, a grid-side resistor Rg, and a Grid. When STS is closed, the optical storage microgrid is connected to the main grid and the inverter system works in grid-connected mode; when STS is disconnected, the system operates in islanding mode.

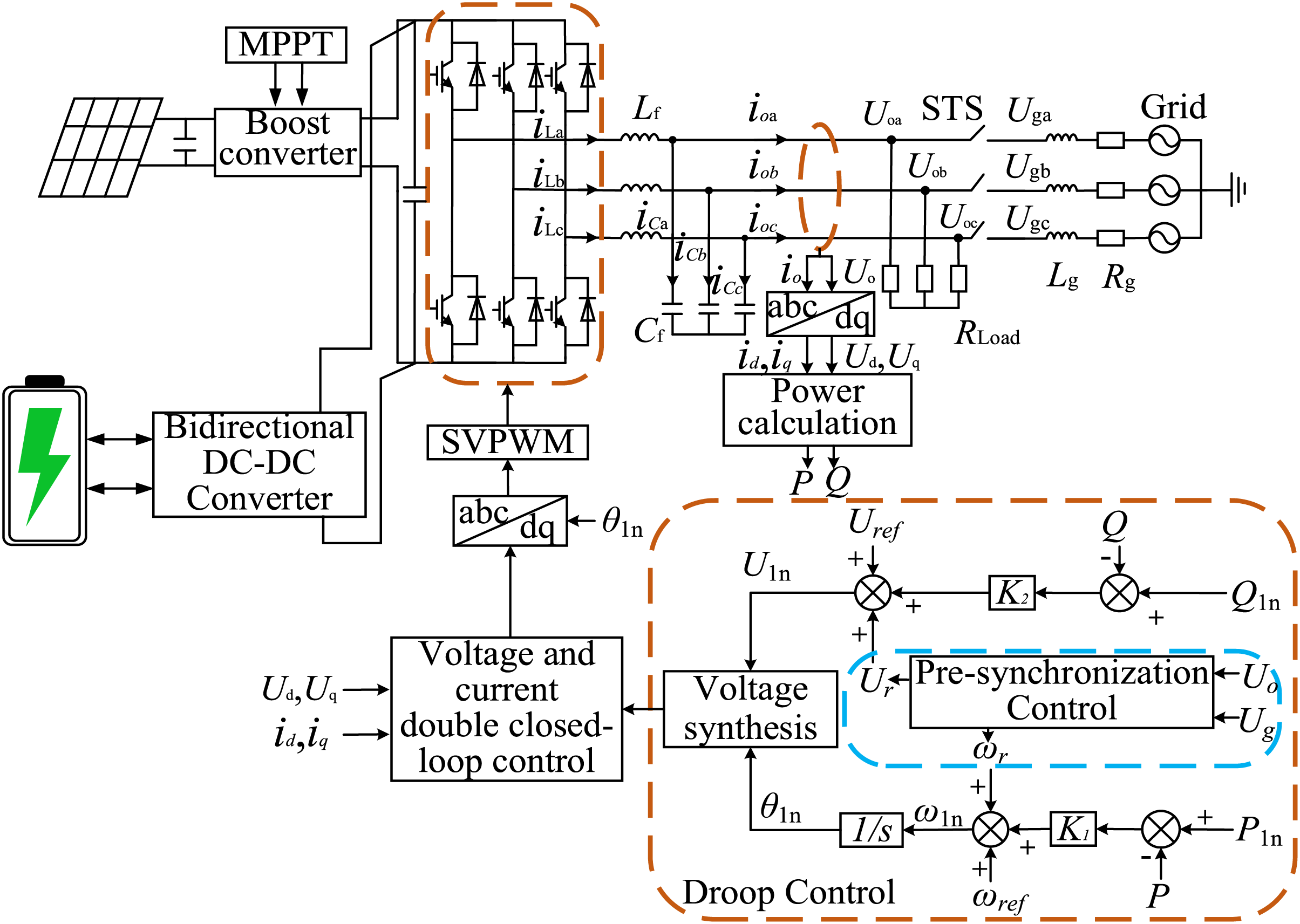
Figure 1: Diagram of the structure and principles for the photovoltaic storage hybrid power generation system

In Fig. 1, Uo is the output voltage of the hybrid inverter (Uoa, Uob and Uoc are its three-phase voltages), which also refers to the AC bus voltage of the photovoltaic storage microgrid.

io is the output current of the inverter (ioa, iob, ioc are its three-phase currents); Ug is the voltage at the point of common coupling (PCC) (Uga, Ugb, Ugc are its three-phase voltages), and the grid voltage mentioned in this paper refers to the voltage at the PCC point; id, iq are the dq-axis components of the output currents; Ud, Uq are the dq-axis components of the output voltages; Usin⁡θ is the three-phase voltage synthesis link, θ is the phase; θ1n is the reference phase; Uref is the rated voltage magnitude; U1n is the reference voltage magnitude; ωref is the rated angular frequency; ω1n is the reference angular frequency; P1n and Q1n are the reference values of active and reactive power; Ur and ωr are the voltage and angular frequency adjustments; P and Q are the actual active and reactive power; K1 and K2 are the sag coefficients of active and reactive power; s is Laplace operator.

3  Grid-Connected/Islanded Switching Control Strategy for Photovoltaic Storage Hybrid Inverters

3.1 Pre-Synchronization Control Strategy

The conventional phase pre-synchronization technique employs a Phase Locked Loop (PLL) to capture the phase angles of the photovoltaic storage microgrid and the main grid voltages. Synchronization is achieved by aligning their phase difference to zero. This approach necessitates three PI controllers, resulting in a multitude of tuning parameters and a complex control architecture. Moreover, the PLL is highly sensitive to abrupt variations in voltage phase. During voltage anomalies, its dynamic response is sluggish, compromising the stability of the photovoltaic storage microgrid system.

The proposed strategy employs a phase-locked loop-free pre-synchronization control for photovoltaic storage hybrid inverters. Initially, the virtual current is calculated using the voltage deviation phasor between the photovoltaic storage microgrid and the main grid, combined with virtual impedance. Subsequently, voltage pre-synchronization is attained by setting the virtual current to zero. The proposed strategy obviates the need for a phase-locked loop or PI regulators, featuring a simple structure and ease of parameter tuning. It is also immune to phase-locked loop delays and inaccuracies, enabling swift phase tracking. The control strategy is depicted in Fig. 2.

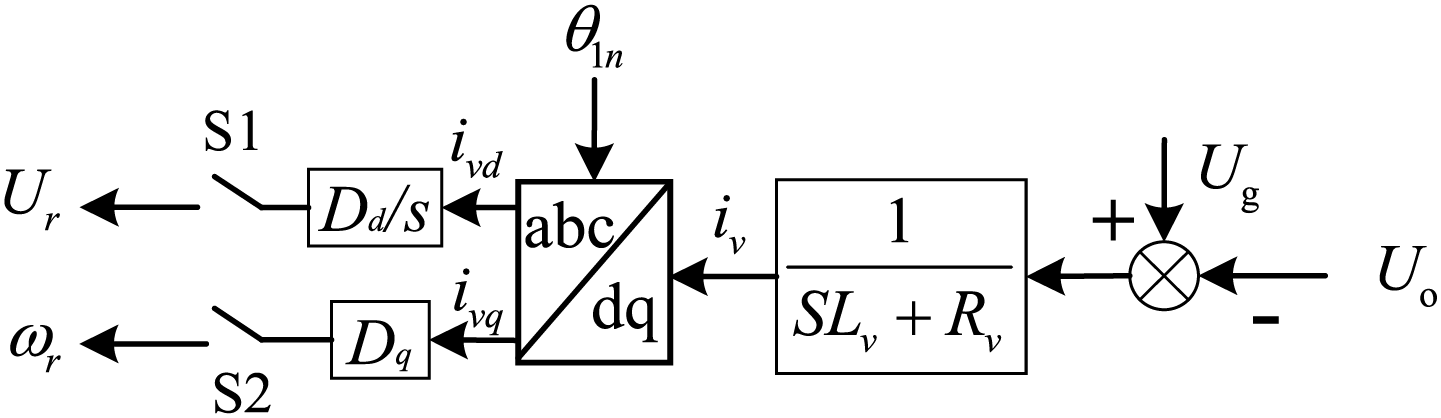
Figure 2: Pre-synchronization control strategy without phase-locked loop

In order to achieve voltage synchronization between the optical storage microgrid and the main grid, a virtual impedance Zv=sLv+Rv, where Lv is the virtual inductance and Rv is the virtual resistance, is introduced between the two.

The virtual current is obtained by dividing the voltage deviation by the virtual impedance:

I•v=U•g−U•oZv(1)

That is:

I•v=Ug(cos⁡θg+jsin⁡θg)−Uo(cos⁡θo+jsin⁡θo)Zv(2)

In the equation, θg and θo represent the phases of the photovoltaic storage microgrid voltage and the main grid voltage, respectively. Synchronization is achieved when the amplitude and phase of the photovoltaic storage microgrid voltage equal those of the main grid voltage, indicated by Ug=Uo and θg=θo. Regardless of whether the virtual impedance is inductive or resistive, the virtual current will be zero. Thus, synchronization between the photovoltaic storage microgrid and the grid voltage can be attained by designing a control strategy that sets the virtual current to zero.

Iv•=UerrRv∠θerr(3)

where Uerr is the amplitude of the voltage deviation and θerr is its phase.

The virtual three-phase currents are:

{iva=Ivcos⁡θerrivb=Ivcos⁡(θerr−2π3)ivc=Ivcos⁡(θerr+2π3)(4)

The PARK transformation matrix is:

TPark=23[cos⁡θrefcos⁡(θref−2π3)cos⁡(θref+2π3)−sin⁡θref−sin⁡(θref−2π3)−sin⁡(θref+2π3)](5)

From Eqs. (4) and (5):

[ivdivq]=TPark[ivaivbivc]=Iv[cos⁡(θerr−θref)sin⁡(θerr−θref)](6)

At this time, the pre-synchronization control strategy consists of two links, the angular frequency compensation link ωr is used to realize the phase synchronization of the voltage of the optical storage microgrid, which is controlled by the switch S2. And the amplitude compensation link Ur is used to realize the amplitude synchronization, which is controlled by the switch S1. The reference phase signal θ1n generated by the sag control is used as the reference for PARK transformation. And the virtual current iv is transformed to obtain the d-axis component ivd and the q-axis component ivq. ivq outputs the angular frequency regulation quantity ωr after the phase adjustment, and similarly, ivd outputs the voltage regulation quantity Ur after the integration link.

3.2 Improved Droop Control Strategy

The traditional droop control has been optimized to address the issues of voltage frequency fluctuation and voltage instability resulting from mismatched line impedance during load switching in the photovoltaic storage hybrid power generation system. Additionally, notable power distribution errors arising from uncontrollable power coupling are mitigated. The optimized strategy involves the integration of coupling compensation and power differentiation components, leading to the development of an enhanced droop control equation, presented as follows:

ω1n=ωref+K1(P1n−P)−τ(U1n−Uref)+MdPdt(7)

U1n=Uref+K2(Q1n−Q)−σ(ω1n−ωref)+NdQdt(8)

where τ, σ are voltage deviation coupling coefficients and angular frequency deviation coupling coefficients; M, N are active differential coefficients and reactive differential coefficients, respectively.

The traditional droop control strategy has been augmented with coupling compensation, with the regulation of active and reactive power governed by angular frequency and voltage. This integration significantly diminishes the impact of uncontrollable power coupling and augments the flexibility in power regulation. Furthermore, the incorporation of the power differentiation element enhances the system’s ability to mitigate voltage fluctuations and optimize power allocation. These measures facilitate a more rapid and precise response of the system to changes in voltage and power, thereby enhancing its dynamic stability and operational efficiency.

At this point, the output regulation ωr of the pre-synchronization control strategy without phase-locked loop is added with the angular frequency obtained from the improved droop control to generate a new reference angular frequency ω1n. The output regulation Ur is added with the improved voltage magnitude to generate a new reference voltage magnitude U1n.

Therefore, the droop control equation is updated at this point:

ω1n=ωref+ωr+K1(P1n−P)−τ(U1n−Uref)+MdPdt(9)

U1n=Uref+Ur+K2(Q1n−Q)−σ(ω1n−ωref)+NdQdt(10)

The schematic diagram of the improved droop control strategy is shown in Fig. 3. The voltage deviation is obtained from reactive power regulation and angular frequency deviation compensation. The angular frequency deviation is obtained from active power regulation and voltage deviation compensation.

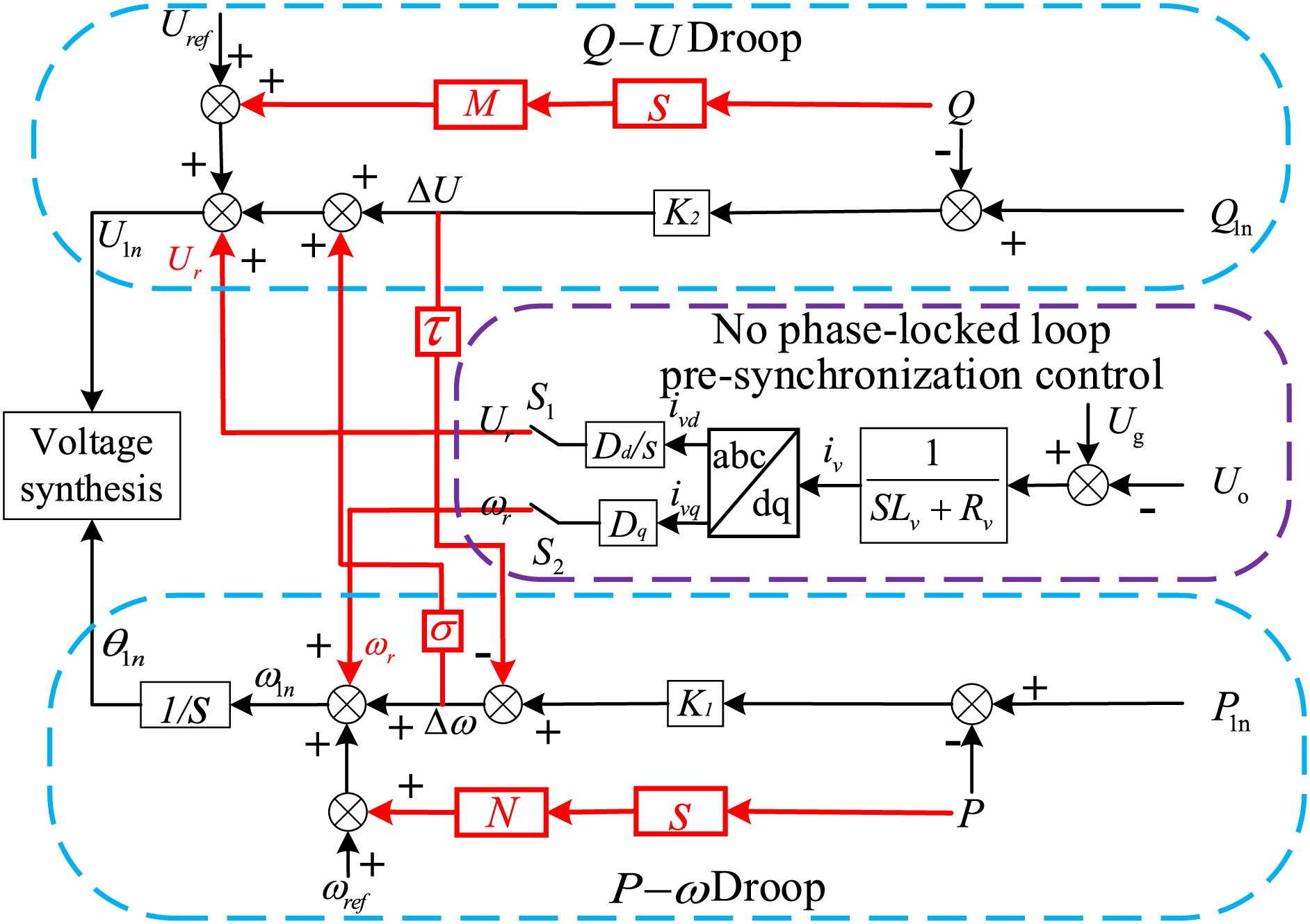
Figure 3: Schematic diagram of the improved droop control strategy

The adjustment process involves randomness and requires time. These parameters are interdependent, and system stability might necessitate some overshoot sacrifice to meet dynamic performance standards. Hence, the paper employs algorithms to dynamically optimize these parameters for system stability. During optimization, focus is on control efficiency, endurance, and other performance metrics. The main challenge in control parameter optimization is the high dimensionality and complexity due to nonlinearity in the microgrid. The optimized droop control aims to ensure system stability and meet power quality standards.

3.3 Improved Droop Control Strategy Based on MChOA

Given that there are mutual constraints between these parameters, an increase in the amount of overshooting of the system needs to be accommodated to some extent in order to satisfy the system’s dynamic performance metrics. Consequently, this study employs an algorithm as a means to ensure system stability, dynamically adjusting parameters like K1 and K2 to maintain system performance and optimize inverter parameter settings.

This paper introduces an enhanced chimpanzee optimization algorithm, incorporating intelligent brain behavior strategies. Initially, a brain behavior strategy tailored for chimpanzees is developed, incorporating a quasi-opposite learning approach to mitigate the risk of local optima entrapment. This strategy reinforces the algorithm’s global search and balances its exploration capabilities. Subsequently, the algorithm is augmented with dynamic nonlinear decreasing convergence factors and adaptive weight factors to enhance optimization efficacy and facilitate escape from local optima. Thereafter, “learning behavior” and “emotional behavior” operators are derived based on the chimpanzee’s cognitive level, and their incorporation into individual chimpanzees aims to augment the algorithm’s local exploitation capabilities.

Active power deviation ΔP from the photovoltaic storage hybrid inverter, system reactive power deviation ΔQ, voltage deviation ΔU, and angular frequency deviation Δω are inputs for the chimpanzee population’s position vectors. The outputs are the corresponding active sag coefficient K1, active differential coefficient M, reactive sag coefficient K2, reactive differential coefficient N, voltage deviation compensation coefficient τ, and angular frequency deviation compensation coefficient σ in order. The voltage frequency of the photovoltaic-storage microgrid is included in the algorithm’s fitness function. The system utilizes MChOA to find the optimal coefficients at the equilibrium point, guaranteeing stability and rapid response.

Fig. 4 is the control structure diagram of a photovoltaic storage hybrid inverter based on MChOA. The pre-synchronization control, which operates without a phase-locked loop, feeds the output regulation parameters ωr and Ur into the enhanced droop control. Optimization within the MChOA module yields a global optimal solution, thereby updating the droop coefficients and related parameters. Consequently, the voltage components on the dq-axes, derived from the synthesization dq coordinate system, are fed into a voltage-current dual closed-loop control system, culminating in space vector pulse width modulation.

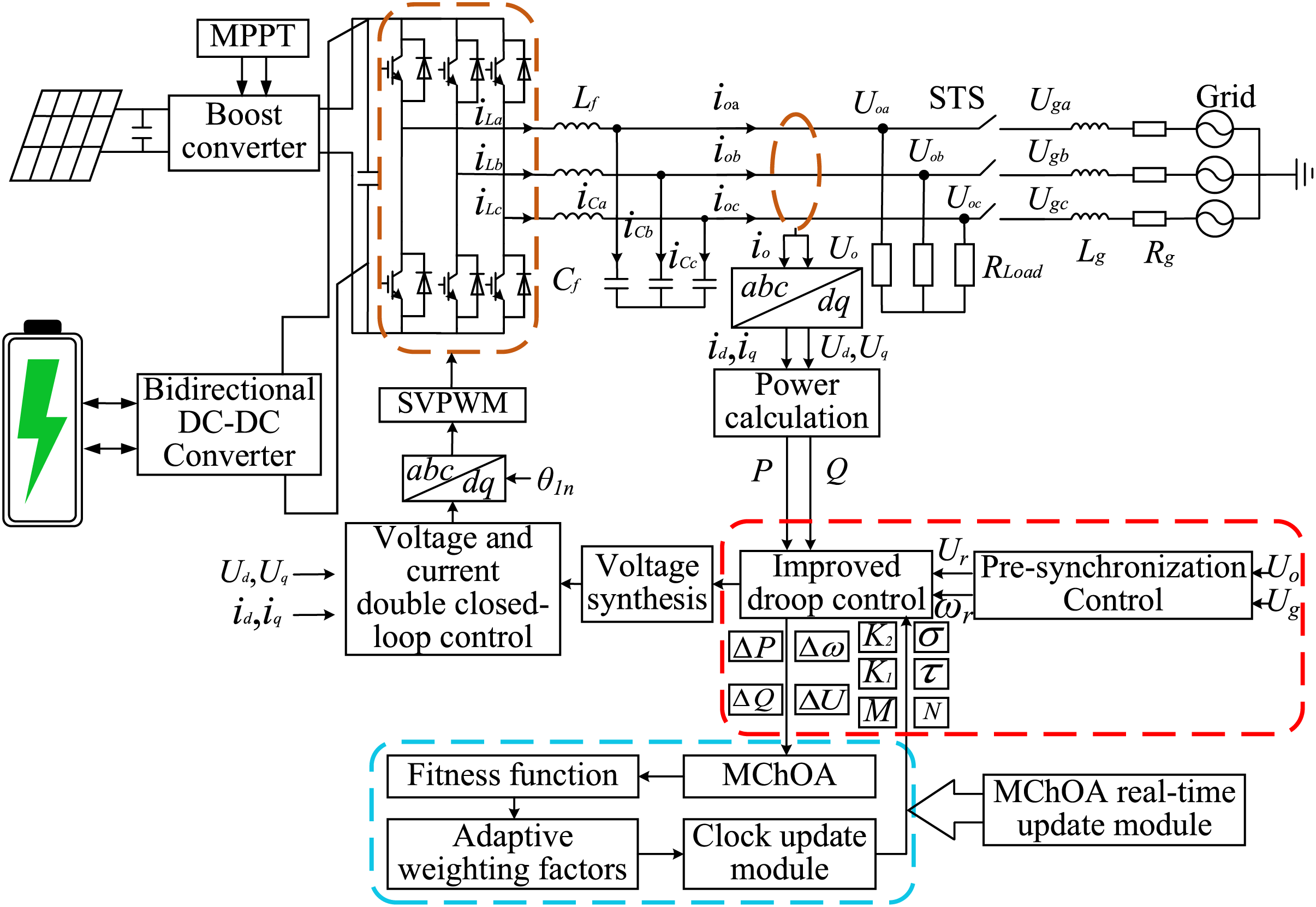
Figure 4: Control structure diagram of the photovoltaic storage hybrid inverter based on MCHOA

The specific process of MChOA is as follows:

(1) Initializing the population through the improved Circle chaotic mapping and the quasi-opposite learning strategy:

The chimpanzee population size is set to 100, ensuring it is sufficiently large. The maximum number of iterations is set as an odd multiple of the simulation’s sampling time. The average of ΔP, ΔQ, ΔU, and Δω is denoted as X1, which is then incorporated into the improved Circle chaotic mapping formula, as depicted below:

Xt+1={2arcsin⁡(5mod(Xt+0.2−0.52πsin⁡(2π×Xt),1)),0≤Xt<0.9πmod(Xt+0.2−0.52πsin⁡(2π×Xt),1),0.9≤Xt≤1(11)

The expression mod (a, b) denotes the modulo operation of a by b. Xt and Xt+1 denote the position vectors of the chimpanzee individual at the t-th and (t + 1)-th iterations, respectively. Following chaotic mapping, the positions of the chimpanzee individuals undergo quasi-opposite learning. The formula for this process is presented below:

Xi={CS+rand×(MP−CS),MP>CSMP+rand×(CS−MP),MP<CS(12)

MP=LB+UB−Xt(13)

CS=LB+UB2(14)

where CS is the midpoint of the upper and lower boundaries of the search space, MP is the standard inverse solution, LB and UB represent the upper and lower boundaries of the search space taken as 0 and 1, respectively. Xi is the quasi-inverse solution of the chimpanzee’s individual location, and randdenotes a random number between [0, 1].

(2) Calculate the fitness value J for each chimpanzee and the expression for the fitness value function:

J=∑t=1NXtN+X1Uoη+(f−f0)Ug(15)

where N takes the value of 100; η is the number of inverters. Comparing the fitness value of each individual chimpanzee, the optimal four categories of chimpanzee leader individuals were derived, which were noted as attacker Xa, encloser Xb, driver Xc, and pursuer Xd, respectively. f is the voltage frequency of the optical storage microgrid, and f0 is the rated frequency of the grid, typically 50 Hz.

(3) Fine search for individual chimpanzees for local optimization:

I: Adopting a dynamic nonlinear decreasing convergence factor gn, which improves the optimization search:

Utilizing the convergence factor speeds up convergence in later iterations and boosts the algorithm’s local development. Meanwhile, the beta distribution can prevent the convergence factor from converging to 0 too early, enhance the ability of optimality seeking, and better jump out of the local optimum, the dynamic nonlinear decreasing convergence factor is shown as follows:

gn=gin(1−e5ln⁡(t−tmaxtmax))+l×beta(h,g)(16)

where tmax is the maximum number of iterations 500, gin is the initial value of the convergence factor, which takes the value of 2.5, and λ takes the value of 0.05; beta is the beta distribution function, and η,γ are the beta distribution parameters, which take the values of 4 and 1, respectively.

II: Adaptive weighting factor T is used to further improve the convergence accuracy:

During the middle and late stages of the algorithm’s operation, the algorithm is tailored to better search for an optimal individual, thereby improving its optimization accuracy in local development. At this time, the algorithm is given a smaller weight, which is conducive to the algorithm to accurately search for the optimal individual position with a small step size, as shown in the following formula:

T=Ts−(Ts−Te)(1+e10(t−tmaxtmax))(17)

where Ts is the initial value of the weighting factor taken as 0.9 and Te is the termination value of the weighting factor taken as 0.4. Now the location of the optimal four categories of chimpanzee individuals is obtained and the update equation is:

X1=T1×|Xa−A1×Da|(18)

X2=T2×|Xb−A2×Db|(19)

X3=T3×|Xc−A3×Dc|(20)

X4=T4×|Xd−A4×Dd|(21)

where T1, T2, T3, T4 are the adaptive weight factors of the attacker, encloser, driver and pursuer, A1, A2, A3, A4 are the coefficient vectors of the four, respectively, the formula is shown in Eq. (22), and Da, Db, Dc, Dd are the distances between the four and the prey, respectively, and the formula is shown below:

A=2gn×r1−gn(22)

{Da=|C1×Xa−M1×Xiit|Db=|C2×Xb−M2×Xiit|Dc=|C3×Xc−M3×Xiit|Dd=|C4×Xd−M4×Xiit|(23)

C=2×r2(24)

M=Chaotic_value(25)

In the equation, r1 and r2 denote random variables within the interval [0, 1]. gn represents a dynamic, non-linearly decreasing convergence factor, which linearly decays from 2.5 to 0 with the iteration count. A is a random vector defining the distance between the chimpanzee and the prey, with values ranging from −gn to gn. M stands for the chaotic mapping vector, indicating the impact of neutral motivation on the hunting behavior of chimpanzees. C is the control coefficient reflecting the influence of the prey’s position on the chimpanzee’s location, with values randomly selected from [0, 2]. Xiit specifies the position of the i-th chimpanzee at the t-th iteration.

(4) Position update for the remaining other chimpanzee individuals:

Updating the positions of the optimal four leaders followed by the other chimpanzee individuals fosters greater communication among the population, thereby enhancing the algorithm’s ability to seek local optimality. And allow the algorithm to better search for the global optimal position, as shown in the following formula:

Xiit+1=r3×Y2+X1+X2+X3+X44×Y1(26)

where r3 is a random number taking values between [0, 1]; Y1 and Y2 are differential scaling factors, both taking values of 0.5.

(5) Updating the global optimal position with the intelligent brain behavior strategy:

Having acquired the most recent positions of all chimpanzee individuals, we employ a strategy that integrates Gaussian and Cauchy mutations. Gaussian mutation, with its narrower perturbation range, excels in local exploitation. In contrast, Cauchy mutation, with its broader range, enhances global search capabilities. The formulation is given by:

Xnewa={Xa×tanh⁡(ttmax+deedemo×G(0,1)),t≤tmax2Xa×tanh⁡(C(0,1)×deedlean×(1−ttmax)),t>tmax2(27)

where S is a random number subject to Gaussian distribution; D is a random number subject to Cauchy distribution; F is the new solution obtained.

The formulas for the “learning behavior” and “emotional behavior” operators are as follows:

deedemo=(Xt1−Xt2)×Agn(28)

deedlearn=XtXr×(tmax−t)×τ(29)

wherein, Xt1 and Xt2 represent two chimpanzee individuals at the t-th iteration; Xr is the position vector of the learning object; τ is the “learning coefficient” with a value of 0.8.

The “learning behavior” operator mimics the learning process of chimpanzees, enabling the algorithm to more effectively locate potential high-quality solutions in the search space. This operator utilizes mathematical models to leverage historical experience, thus accelerating convergence during the optimization process. The “emotional behavior” operator simulates the emotional state changes of chimpanzees, influencing the balance between exploration and exploitation in the algorithm. Mathematically, this operator dynamically adjusts the search strategy based on the current search state of the algorithm to avoid premature convergence to local optima.

The fitness value is compared after the position is updated using the brain-wise behavioral strategy. Then, select the better one among the original optimal solution and the solution of the brain-wise behavioral strategy to get the updated position of the optimal chimpanzee individual.

(6) Determine whether the maximum number of iterations is reached at this point, if not jump to Step (3), otherwise end the algorithm and output the location vector X∗ of the optimal chimpanzee individual. Fig. 5 is a flowchart of MChOA.

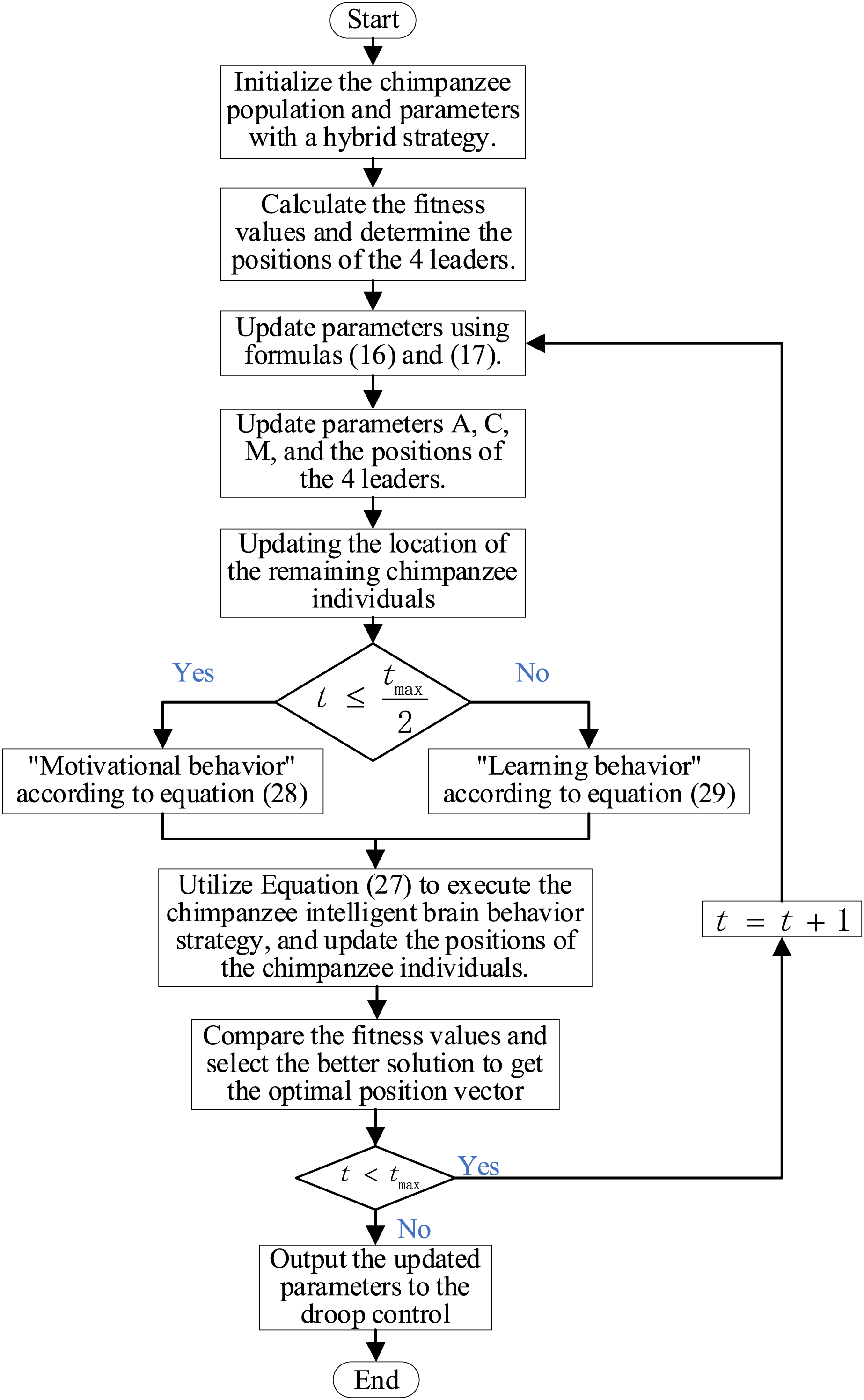
Figure 5: Flowchart of MChOA

4  Simulation Verification and Analysis

The effectiveness of the improved droop control strategy for seamless transitioning between islanding and grid-connected modes in photovoltaic storage hybrid inverters is tested using Simulink. The simulation model of the light-storage microgrid with DG1 and DG2 connected in parallel is built, and the capacity ratio of DG1 and DG2 is 1:1, and the parameters used in the experiment are shown in Table 1.

4.1 Islanded Operation Load Mutation Experiment

In the islanded mode, the photovoltaic storage hybrid inverter disconnects from the common point switch, with each distributed generator independently powering its respective load. Jointly, the two inverters supply the load on the common busbar. Initially, the load1 is 10kW+j5kVar, and the load2 is 10kW+j5kVar; the common load3 is 20kW+j10kVar. After 1 s of system operation, the load 40kW+j20kVar on the common busbar is incremented. This additional load is then disconnected at the 2-s mark. Waveforms for the traditional droop control experiment are presented in Fig. 6, while those for the improved droop control are in Fig. 7.

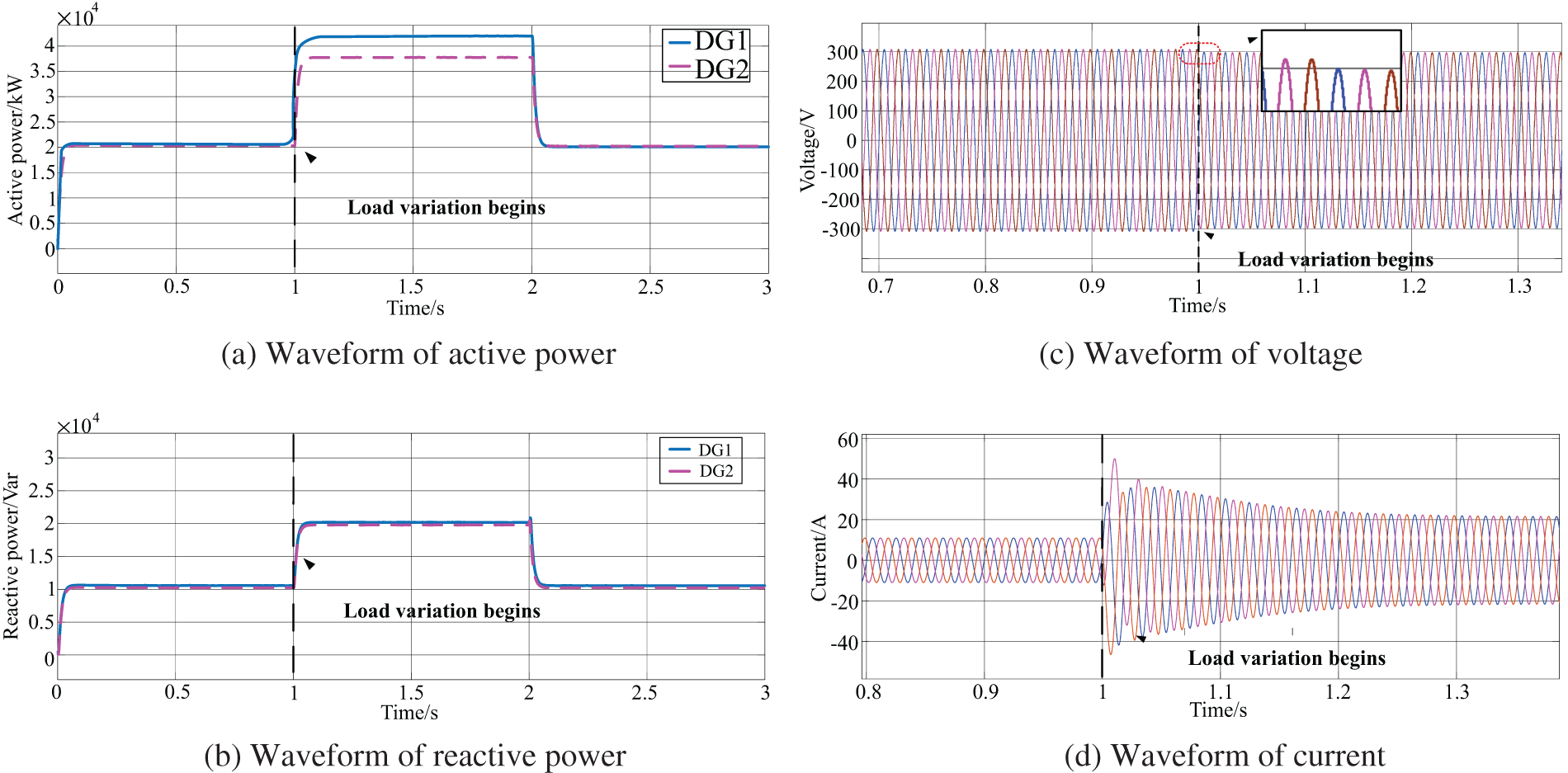
Figure 6: Experimental waveforms of load mutations in islanded operation with traditional droop control

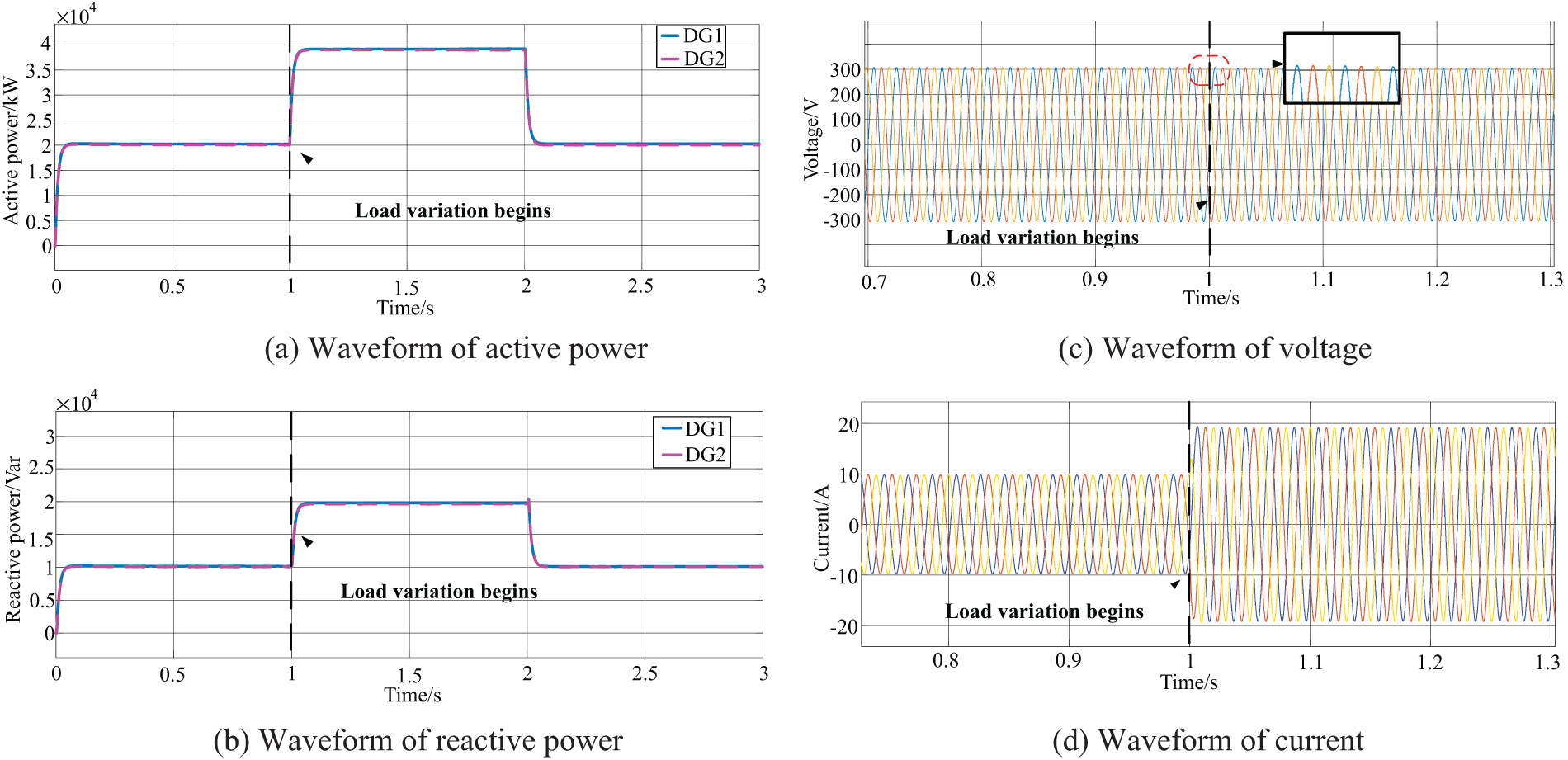
Figure 7: Experimental waveforms of load mutations in islanded operation with improved droop control

Fig. 6 presents the waveforms of active power, reactive power, inverter output voltage, and current under conventional control settings. The reactive power output by the two inverters can be evenly shared. However, there are obvious power deviations in the active power. When the load is increased at 1 s, the difference in active power becomes larger, and the distribution of active power is even more unbalanced. Upon a sudden load increase, the inverter output voltage amplitude falls from 308.5 to 300.3 V, exhibiting substantial fluctuations. Concurrently, the output current surges, increasing from 10.75 to 20.25 A to cater to the heightened power demand. The waveform, however, exhibits pronounced distortion and lacks a smooth transition.

Fig. 7 displays the waveforms of active and reactive power, as well as inverter output voltage and current, under improved droop control. Both inverters evenly distribute reactive power, and active power is also evenly shared. Load increments at 1 s do not disrupt this equal distribution of active power. Upon a sudden load increase, the inverter output voltage decreases from 308.5 to 305.7 V, showing minimal fluctuation. The output current increases from 10.75 to 19.35 A to meet the elevated load demand without significant waveform distortion, ensuring a smooth transition. The proposed improved droop control strategy demonstrates robust performance, maintaining load power sharing through droop characteristics even during sudden load changes.

4.2 Transition From Islanded Mode to Grid-Connected Mode

In order to mitigate voltage discrepancies between the photovoltaic storage hybrid inverter and the main grid, pre-synchronization control is applied prior to the transition to grid connection, thereby preventing current surges during this process. This process is illustrated in Fig. 8. Initially, load1 is set to 5kW+j5kVar, and switches S4 and S5 are opened. The photovoltaic storage hybrid inverter operates in islanded mode until 0.2 s prior, when the virtual current is computed using the three-phase voltages of both the grid and the inverter. At 0.2 s, S2 is closed, initiating angular frequency compensation. The q-axis component ivq of the virtual current decreases gradually. Upon ivq nearing zero, S1 is closed to start amplitude compensation. Pre-synchronization concludes as the d-axis component ivd approaches zero. At 0.3 s, STS is closed, and switches S1 and S2 are opened, achieving a seamless transition from islanded to grid-connected mode for the photovoltaic storage hybrid inverter.

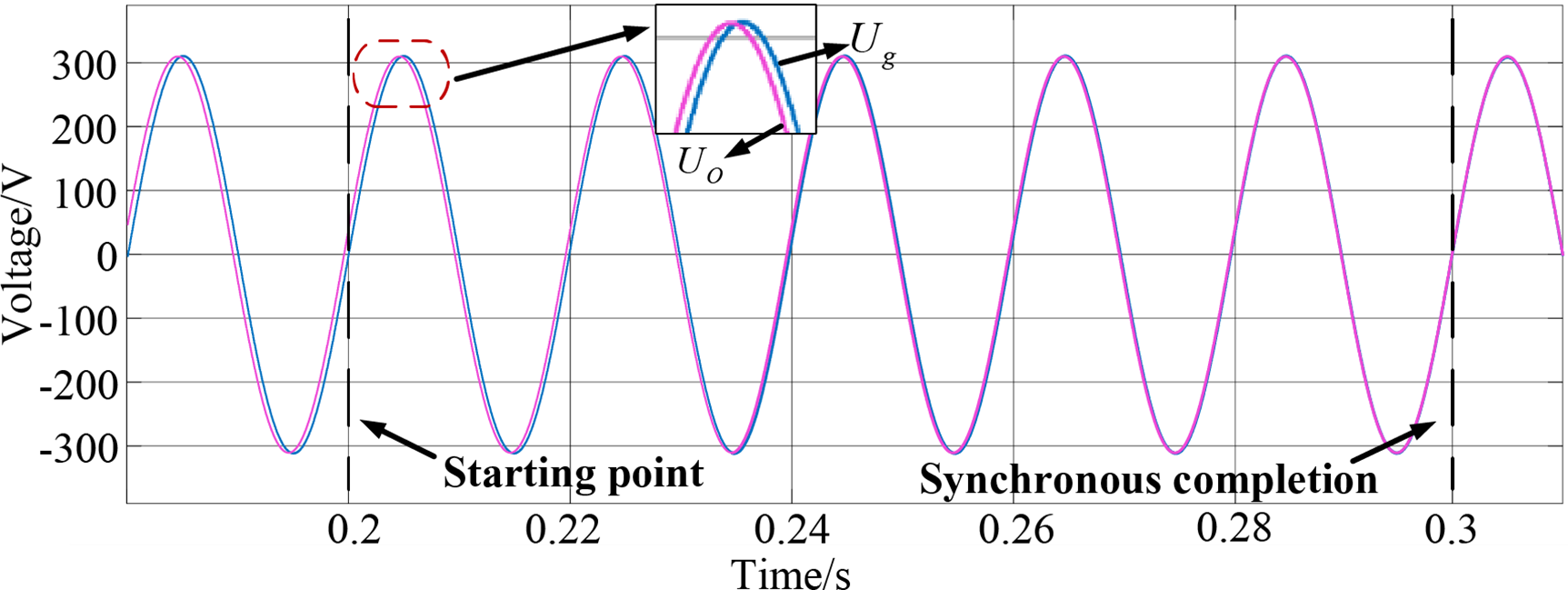
Figure 8: Simulation waveforms of the pre-synchronization process

Simulation results for traditional droop control are depicted in Fig. 9, while those for the improved droop control method are presented in Fig. 10.

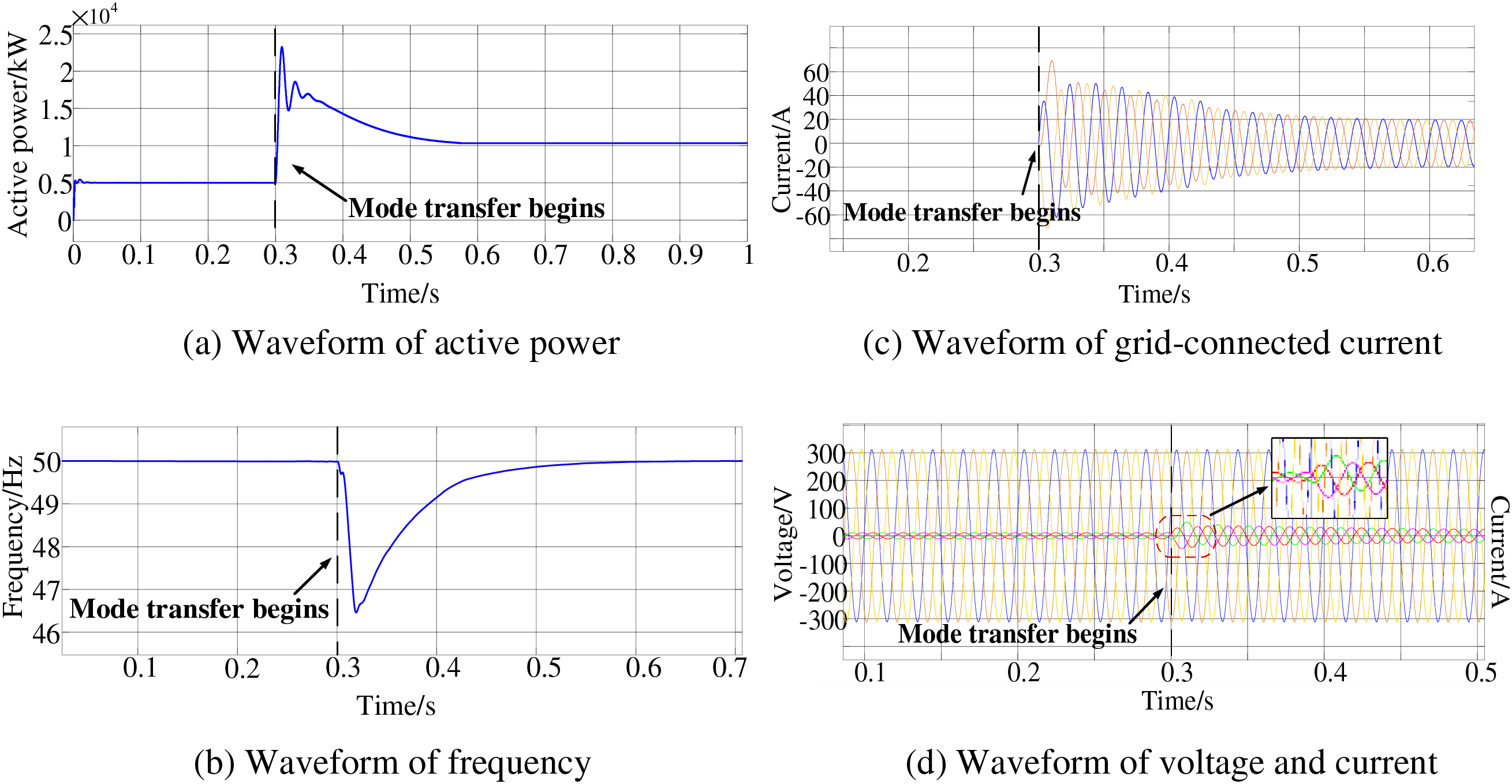
Figure 9: Experimental waveforms of the traditional droop control system during the transition from islanded to grid-connected mode

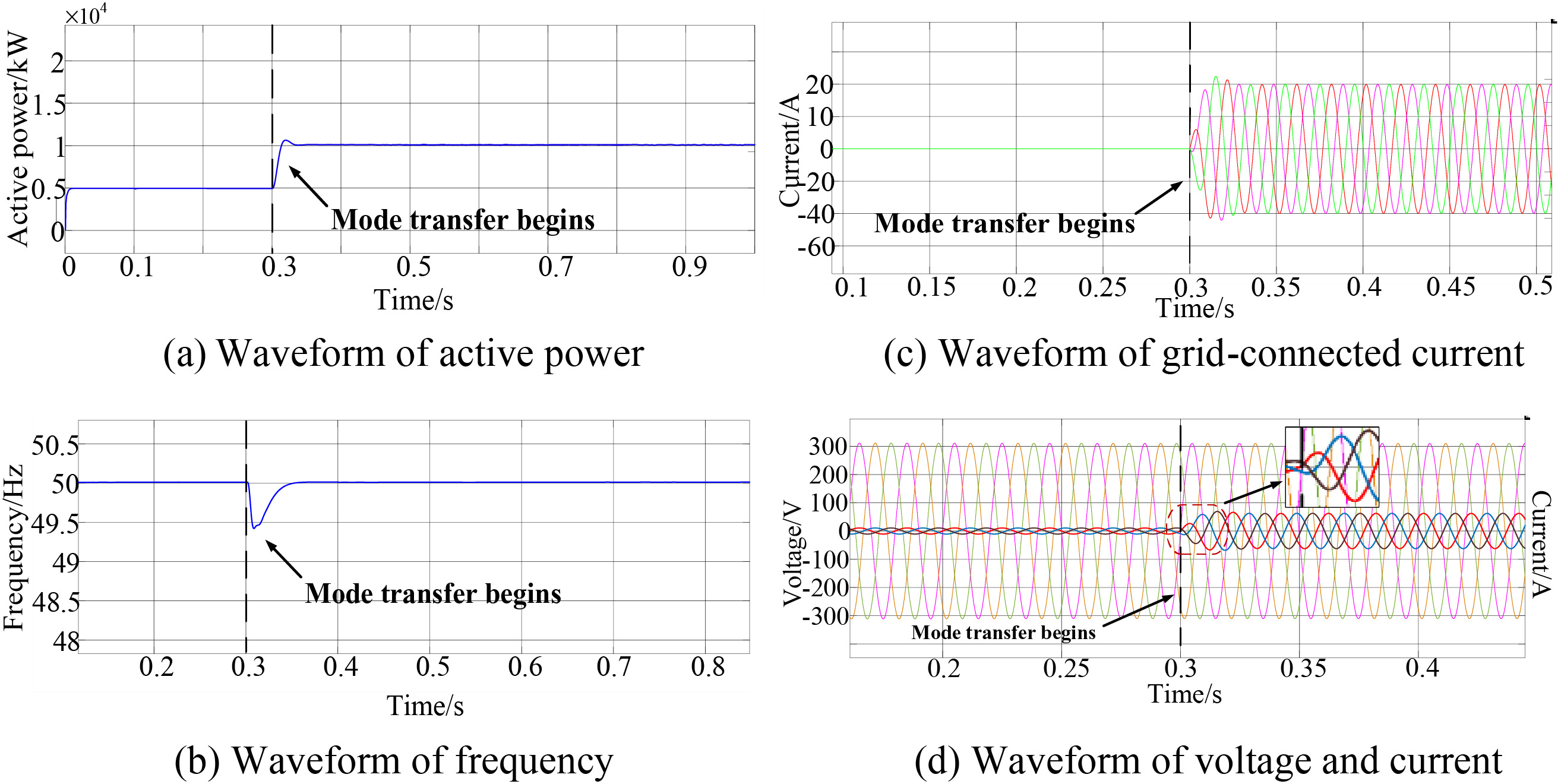
Figure 10: Experimental waveforms of the improved droop control system during the transition from islanded to grid-connected mode

It can be found from Fig. 10 that the voltage of the optical storage microgrid system will be supported by the distribution network and the bus voltage increases at the moment when the switch STS is closed. Consequently, the active power output from the distributed generators under traditional control methods rises abruptly, exhibiting significant distortion. Concurrently, the inverter’s output voltage experiences significant fluctuations, with a voltage deviation of 6.8 V. The output current and frequency oscillate excessively, reaching a maximum frequency deviation of 7%. The curve clearly indicates an overshoot condition. Fig. 9c illustrates that the grid current takes an extended period to achieve a sinusoidal state, and the transition is not sufficiently smooth.

As observed in Fig. 10, the improved droop control strategy proposed herein results in a rapid and smooth transition of the output active power and frequency. The response is swift, and the inverter output voltage remains largely stable, minimizing voltage spikes. The grid-connected current, injected at the PCC point, transitions rapidly and smoothly, preserving a high degree of sinusoidality. The maximum frequency deviation is reduced to 1.25%, and the stabilization time is shortened by 0.13 s compared to traditional control methods. Additionally, the inverter’s output current increases uniformly, unaffected by the control mode transition, ensuring a smooth switching process.

4.3 Transition From Grid-Connected Mode to Islanded Mode

Initially, the photovoltaic storage hybrid inverter system operates in grid-connected mode, connected to the main grid. At 0.7 s, the switch at the PCC point is disconnected, transitioning the system to islanded mode. Droop control exhibits voltage-source output characteristics, offering voltage and frequency support for the photovoltaic storage hybrid inverter in islanded mode. As it generates internal phase, phase considerations are unnecessary during the transition to islanded mode. Simulation results for traditional droop control are depicted in Fig. 11, while those for the improved droop control method are presented in Fig. 12.

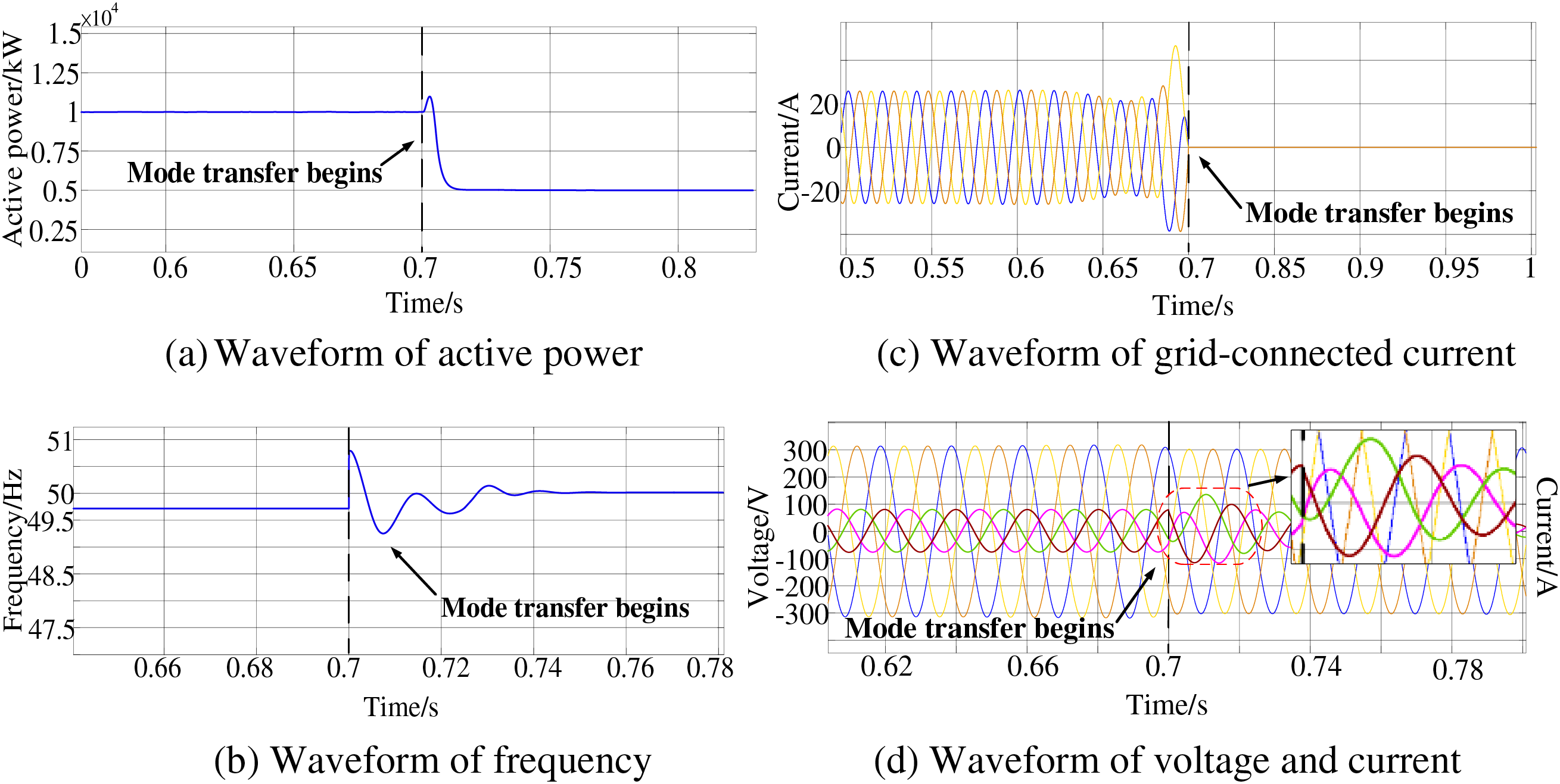
Figure 11: Experimental waveforms of the traditional droop control system during the transition from grid-connected to islanded mode

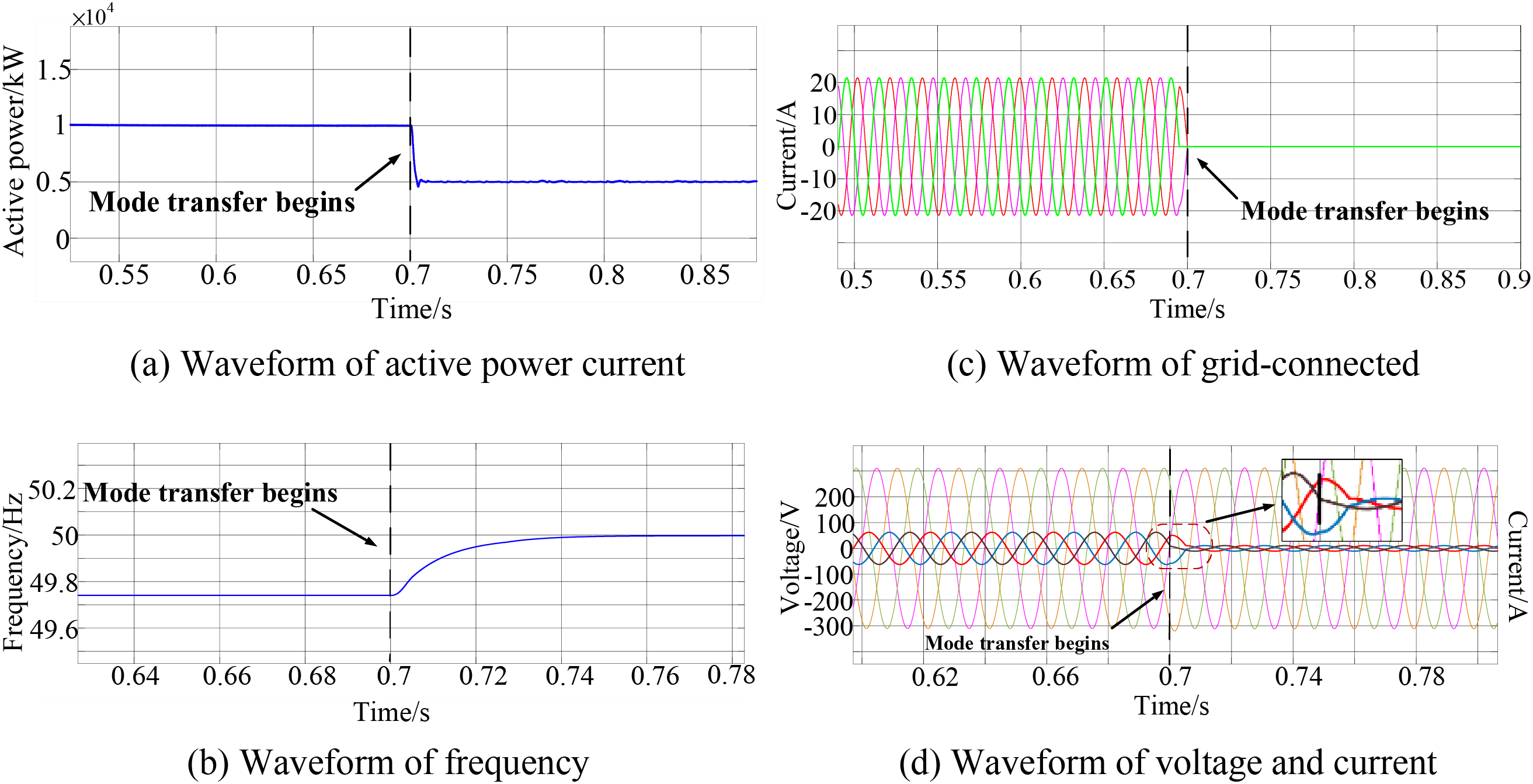
Figure 12: Experimental waveforms of the improved droop control system during the transition from grid-connected to islanded mode

At 0.7 s, as depicted in Figs. 11 and 12, the photovoltaic storage hybrid inverter transitions from grid-connected to islanded mode. Traditional droop control makes the output active power and output frequency curves of the inverter oscillate widely. In contrast, the improved droop control stabilizes these outputs, nearing the rated values. The maximum frequency deviation decreases from 1.54% to 0.55%, and the stabilization time is shortened by 0.1 s. The curve exhibits no significant overshoot and remains smooth, thereby reducing power oscillation. Upon tripping, the improved droop control strategy promptly reduces the grid current to zero, without distortion, and maintains stable inverter output voltage, ensuring a seamless transition from grid-connected to islanded mode. Following the transition to islanded mode from grid-connected mode, the photovoltaic storage hybrid inverter, no longer supported by the main grid, maintains voltage-source characteristics due to droop control, ensuring continuous inverter operation. The experimental results confirm that the improved droop control strategy proposed herein achieves both load power sharing and seamless transitioning between grid-connected and islanded modes, addressing the dual control objectives.

5  Conclusion

A novel grid-connected/islanded switching control strategy for photovoltaic storage hybrid inverters based on MChOA, is introduced. The approach enhances traditional droop control by incorporating coupling compensation and power differentiation mechanisms. Additionally, it utilizes phase-locked loop-free pre-synchronization control for angular frequency and voltage amplitude adjustments. An enhanced Circle chaotic mapping and a quasi-inverse learning strategy for population initialization are proposed to rectify the optimization accuracy deficit in the chimpanzee algorithm. A dynamic, nonlinearly decreasing convergence factor has been formulated to avoid convergence to local optima due to the progressive erosion of diversity. The integration of intelligent brain behavior strategies is aimed at improving global search and local exploitation capabilities. This ensures high-precision and high-reliability optimization of the droop control parameters for photovoltaic storage hybrid inverters during transitions between grid-connected and island modes.

Simulation results indicate that the improved control strategy based on MChOA, as compared to conventional droop control, exhibits substantial enhancements in control stability and reliability. It mitigates the effects of uncontrollable power coupling, facilitating smooth and stable transitions for the photovoltaic storage hybrid inverter between grid-connected and island modes.

6  Future Scope and Limitation

Future research will not only delve into the comparative analysis of MChOA with a suite of optimization algorithms to refine control during grid-connected/islanded mode switches but will also encompass a holistic enhancement of droop control mechanisms. This includes investigating the integration of advanced control parameters and algorithms to bolster system stability and responsiveness. Moreover, the application of these strategies to larger and more complex microgrid systems will be explored, with a focus on scalability and adaptability. By synthesizing these avenues of inquiry, we aim to drive the field towards more sophisticated and resilient control solutions that can meet the evolving demands of modern energy systems. When considering the integration of MChOA into more complex systems, the following technical adjustments would be necessary:

1. Scalability: Ensuring that the algorithm can handle a larger number of variables and constraints typical of complex microgrid or smart grid systems.

2. Robustness: Implementing mechanisms to maintain the algorithm’s performance in the face of system disturbances and uncertainties.

3. Real-Time Adaptability: Adjusting the algorithm to make real-time decisions in response to rapid changes in system conditions.

Acknowledgement: The authors would like to thank and acknowledge the Jiangsu Key Laboratory of Power Transmission & Distribution Equipment Technology.

Funding Statement: The authors received funding from the Postgraduate Research & Practice Innovation Program of Jiangsu Province (SJCX23_1633), and 2023 University Student Innovation and Entrepreneurship Training Program (202311463009Z), and Changzhou Science and Technology Support Project (CE20235045), and Open Project of Jiangsu Key Laboratory of Power Transmission & Distribution Equipment Technology (2021JSSPD12).

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Chao Zhou; data collection: Narisu Wang; analysis and interpretation of results: Fuyin Ni; draft manuscript preparation: Chao Zhou, Narisu Wang, Fuyin Ni and Wenchao Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data used in this study are available on request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. F. Sun, X. L. Liu, and J. X. Teng, “Power balance strategy of cascaded H-bridge photovoltaic inverter based on hybrid configuration of photovoltaic and energy storage,” (in Chinese), Proc. CSEE, vol. 44, no. 5, pp. 1948–1962, 2024. doi: 10.13334/j.0258-8013.pcsee.223461. [Google Scholar] [CrossRef]

2. D. Li and T. Zhang, “Modeling and coupling analysis of DC and grid side of solar-storage inverter based on impedance method,” (in Chinese), Trans. China Electrotech. Soc., vol. 39, no. 10, pp. 3038–3048, 2024. doi: 10.19595/j.cnki.1000-6753.tces.230286. [Google Scholar] [CrossRef]

3. W. Q. Chen, X. N. Xin, and Z. P. Cheng, “Control of grid-connected of photovoltaic system with storage based on virtual synchronous generator,” (in Chinese), Trans. China Electrotech. Soc., vol. 33, no. S2, pp. 538–545, 2018. doi: 10.19595/j.cnki.1000-6753.tces.L80095. [Google Scholar] [CrossRef]

4. S. Hoseinzadeh, D. A. Garcia, and L. Z. Huang, “Grid-connected renewable energy systems flexibility in Norway islands’ Decarbonization,” Renew. Sustain. Energy Rev., vol. 185, no. 3, Sep. 2023. doi: 10.1016/j.rser.2023.113658. [Google Scholar] [CrossRef]

5. S. Hoseinzadeh, M. Soltanian, M. Makabadi, B. Nastasi, D. Groppi and D. A. Garcia, “Innovative continuous heating-enhance solar still farm—A case study for irrigation in a pistachio orchard,” Sustain. Energy Techn., vol. 64, no. 19, 2024. doi: 10.1016/j.seta.2024.103735. [Google Scholar] [CrossRef]

6. M. Kallamadi and V. Sarkar, “Enhanced real-time power balancing of an ac microgrid through transiently coupled droop control,” IET Gener. Transmiss. Distrib., vol. 11, no. 8, pp. 1933–1942, 2017. doi: 10.1049/iet-gtd.2016.1250. [Google Scholar] [CrossRef]

7. H. Han, Y. Liu, Y. Sun, M. Su, and J. M. Guerrero, “An improved droop control strategy for reactive power sharing in islanded microgrid,” IEEE Trans. Power Electron, vol. 32, no. 3, pp. 2427–2451, Mar. 2017. doi: 10.1109/TPEL.2016.2569597. [Google Scholar] [CrossRef]

8. Y. Hirase, K. Abe, K. Sugimoto, K. Sakimoto, H. Bevrani and T. Ise, “A novel control approach for virtual synchronous generators to suppress frequency and voltage fluctuations in microgrids,” Appl. Energy, vol. 210, pp. 699–710, Jan. 2018. doi: 10.1016/j.apenergy.2017.06.058. [Google Scholar] [CrossRef]

9. M. A. Awal, H. Yu, H. Tu, and S. M. Lukic, “Hierarchical control for virtual oscillator based grid-connected and islanded microgrids,” IEEE Trans. Power Electron, vol. 35, no. 1, pp. 988–1001, Jan. 2020. doi: 10.1109/TPEL.2019.2912152. [Google Scholar] [CrossRef]

10. A. -B. -K. Chowdhury, X. Liang, and H. Zhang, “Fuzzy-secondary controller-based virtual synchronous generator control scheme for interfacing inverters of renewable distributed generation in microgrids,” IEEE Trans. Ind. Appl., vol. 54, no. 2, pp. 1047–1061, Mar./Apr. 2018. doi: 10.1109/TIA.2017.2773432. [Google Scholar] [CrossRef]

11. B. Wang, S. Liu, and Y. Zhang, “Reactive power sharing control based on voltage compensation strategy in microgrid,” in Proc. 36th Chin. Control Conf., Jul. 2017, pp. 10745–10750. doi: 10.23919/ChiCC.2017.8029069. [Google Scholar] [CrossRef]

12. R. Moslemi and J. Mohammadpour, “Accurate reactive power control of autonomous microgrids using an adaptive virtual inductance loop,” Elec. Power Syst. Rsch., vol. 129, no. 1, pp. 142–149, 2015. doi: 10.1016/j.epsr.2015.08.001. [Google Scholar] [CrossRef]

13. W. Zhang, H. Liu, W. Wang, and P. C. Loh, “Seamless transfer scheme for parallel PV inverter system,” IET Power Electron., vol. 13, no. 5, pp. 1051–1058, 2020. doi: 10.1049/iet-pel.2019.0735. [Google Scholar] [CrossRef]

14. H. Sellamna, A. Massi Pavan, A. Mellit, and J. M. Guerrero, “An iterative adaptive virtual impedance loop for reactive power sharing in islanded meshed microgrids,” Sust. Energy Grids Netw., vol. 24, no. 7, 2020. doi: 10.1016/j.segan.2020.100395. [Google Scholar] [CrossRef]

15. R. An, Z. Liu, and J. Liu, “Successive-approximation-based virtual impedance tuning method for accurate reactive power sharing in islanded microgrids,” IEEE Trans. Power Electron., vol. 36, no. 1, pp. 87–102, Jan. 2021. doi: 10.1109/TPEL.2020.3001037. [Google Scholar] [CrossRef]

16. X. Liang, C. Andalib-Bin-Karim, W. Li, M. Mitolo, and M. N. S. K. Shabbir, “Adaptive virtual impedance-based reactive power sharing in virtual synchronous generator controlled microgrids,” IEEE Trans. Ind. Appl., vol. 57, no. 1, pp. 46–60, Jan./Feb. 2021. doi: 10.1109/TIA.2020.3039223. [Google Scholar] [CrossRef]

17. E. Y. Wang and S. Wang, “Low voltage microgrid droop control strategy based on adaptive virtual resistance,” (in Chinese), Power Syst. Prot. Control, vol. 48, no. 2, pp. 144–149, 2020. doi: 10.19783/j.cnki.pspc.190282. [Google Scholar] [CrossRef]

18. H. Z. Yang, G. W. Yue, and L. Kang, “Research on piecewise dynamic adaptive droop control strategy for microgrid,” (in Chinese), Power Syst. Prot. Control, vol. 47, no. 8, pp. 80–87, 2019. doi: 10.7667/PSPC180543. [Google Scholar] [CrossRef]

19. G. Bai, Z. Chen, and F. Liu, “Parallel operation technology of distributed generation based on self-regulation droop control,” (in Chinese), Power Syst. Prot. Control, vol. 47, no. 8, pp. 120–126, 2019. doi: 10.7667/PSPC180466. [Google Scholar] [CrossRef]