Optimal Scheduling of an Independent Electro-Hydrogen System with Hybrid Energy Storage Using a Multi-Objective Standardization Fusion Method

Nomenclature

1  Introduction

Currently, new energy sources including wind and solar energy are widely used around the world to alleviate the depletion of fossil fuels and carbon emissions [1,2]. Meanwhile, improving the utilization rate of new energy sources by electrolyzing water to produce hydrogen gas and using fuel cell to support electrical load have become popular topics in modern power system research [3]. Then, the economic viability and energy consumption of green hydrogen production are the difficult issues that constrain the development of the combination of new energy sources and hydrogen energy [4]. Therefore, to apply the electro-hydrogen system more inexpensively and efficiently, the optimization scheduling of the system has become a crucial research topic deserving further investigation [5].

Currently, there are studies on the economy, energy consumption, planning schemes, and control strategies of green hydrogen systems and the feasibility has been verified [6–8]. References [9] and [10] have discussed typical cases of household energy systems in South Africa and Nigeria. The independent wind-solar-hydrogen-storage system has been evaluated to demonstrate that this system is robust in providing energy to users. As the cost of hydrogen energy subsystems decreases, the deep application of hydrogen energy systems will be accelerated [11]. The economy of this system has been analyzed, but further exploration on optimal control strategies is lacking. In Reference [12], a simulation model of wind-hydrogen coupled energy storage and power generation system (WHPG) has been developed. Then, it is presented that the effects of operating temperatures on hydrogen production and power consumption in alkaline electrolyzer. The factors affecting hydrogen production and power consumption should be considered more comprehensively. References [13] and [14] have utilized fuzzy theory to implement intelligent management strategies for photovoltaic-battery-hydrogen system. In the power control process of the EL and the FC, more factors have been considered, such as net power variation, battery energy, and hydrogen level, etc. To minimize the total life cost of greenhouse farms in Saudi Arabia, a renewable energy system model for photovoltaic hydrogen production based on mixed-integer linear programming has been studied [15]. Although this study comprehensively considers the economic viability of the system, there is a lack of discussion on issues such as energy loss and resource idleness.

Moreover, researchers have found that a single metric can’t show the pros and cons of green hydrogen systems. A comprehensive numerical simulation is established to evaluate the feasibility of hydrogen production from onshore wind farms in for the arid costal community south of Aqaba Gulf, Saudi Arabia [16]. This study has provided the economic, technological, and environmental elements for a comprehensive analysis of an onshore wind-hydrogen system (OWHS). In a constrained multi-objective optimization problem, the diversity of multi-objective functions is being reduced based on multi-service attribute utility evaluation [17]. In this study, the weight calculation method for multiple optimization objectives has been provided, but the theoretical basis is incomplete. In Reference [18], based on the electricity demand of three small communities on Manoka Island in Douala District, Cameroon, the total cost of a hybrid renewable energy system and the loss of power probability (LPSP) are considered in optimizing scheduling. But LPSP has been added to the constraints, not as an objective function. In fact, only the economics of the system is optimized, which is a limitation. In References [19–21], the Non-dominated Sorting Genetic Algorithm (NSGA-II) has been applied to solve the control instructions of an independent electric hydrogen system, and the non-dominated solution set and Pareto frontier have been obtained. Then, in a new hybrid PV-FC system for green hydrogen and electricity production, a robust techno-enviro-economic (3E) analysis is conducted by MATLAB/Simulink, and the NSGA-II coupled with the technique for order preference by similarity to an ideal (TOPSIS) decision-making approach is also utilized to optimize 3E performances of this system [22]. The optimal results are finite in the solution set. In the heating and cooling of 100 conex in Riyadh, Saudi Arabia, which used hydrogen storage as the central storage system [23], the dependency of the system on the urban power grid and the cost of the electrolyzer and fuel cell are minimized by deep learning artificial intelligence and genetic algorithm (GA). In the above multiple objective optimization problem, NSGA-II or GA is a common and effective method. However, based on this method, a workable solution set is obtained instead of a definite solution.

To address the diversity of solutions in a multi-objective optimization problem, an effective solution is to transform this multi-objective problem into a single objective function by weighted linear summation [24]. Such as, many multiple optimization objectives including battery operation power, charging/discharging depth, and hydrogen production capacity are transformed into a single optimization objective with the same physical dimension using a cost function. Then, an optimal energy management of an independent renewable energy system is achieved [25]. Similarly, five different optimization objectives, namely those related to electricity and natural gas procurement, battery operation status, and hydrogen production costs, are integrated into a single objective function representing the cost [26]. In Reference [27], the net present cost (NPC) and cost of energy (COE) of a hybrid renewable system are calculated, and three swarm intelligent optimization algorithms are used to identify the optimal configuration of the system. A series of optimization objective functions such as power interaction between park buildings and the power grid, equipment operation and maintenance, power interaction between buildings, and carbon benefits are unified via the cost function. Then, the low-carbon optimal scheduling of the park is completed on the alternating direction method of multipliers (ADMM) [28]. Based on the above optimization approach, an unique optimal solution can be obtained. However, this optimal solution is greatly influenced by the weights of multiple optimization objective functions. But there is a lack of research on weight allocation principles. References [29] and [30] respectively use analytic hierarchy process (AHP) and intuitive fuzzy number (IFN) to determine the relative importance of multiple optimization objective functions. Then, the weight of each optimization objective function is assigned. But the theoretical validity of the method is not demonstrated.

Currently, some literature on green hydrogen systems focuses on their economics. It pays insufficient attention to energy loss. In a multi-objective optimization problem, the weight coefficients of each objective lack a basis for selection. This can cause the optimal solution to favor a specific objective. Thus, a standardization fusion method (SF) by standardizing multi-optimization objective functions is proposed to address the above issues. Compared with the previous similar studies, the advantages of the proposed study are as follows. From the perspectives of economy and energy loss, the impact factors are analyzed and the optimization scheduling plan of IEHS is developed. Then, the concept and method of standardizing optimization objective functions are first proposed and discussed. The contribution of this manuscript is summarized as follows:

1) A method of standardize multiple objective functions is firstly proposed. It aims to change a multi-objective optimization problem into a single one. Introducing the concept of data standardization, the proposed method effectively achieves the standardizing fusion of optimization objective functions. It provides a more reasonable way to solve multi-objective optimization problems.

2) The energy loss and economy of the independent electro-hydrogen system (IEHS) with hybrid energy storage system (HESS) exhibit a complex coupling relationship by the efficiency and cost per kilowatt hour of new energy sources, battery energy storage system (BESS), electrolyzer (EL) and fuel cell (FC). The proposed method will unify multiple optimization objective functions. It will avoid analyzing the coupling between energy loss and economy. This will help optimally schedule the IEHS with the HESS.

The organization of this manuscript is as follows. Section 2 shows a mathematical model for optimizing the scheduling of an IEHS with HESS. Section 3 analyzes the standardization fusion process in a multi-objective optimization problem. In Section 4, the performance of the proposed method is compared, and the parameter is discussed. Finally, the research conclusions and future research are summarized in Section 5.

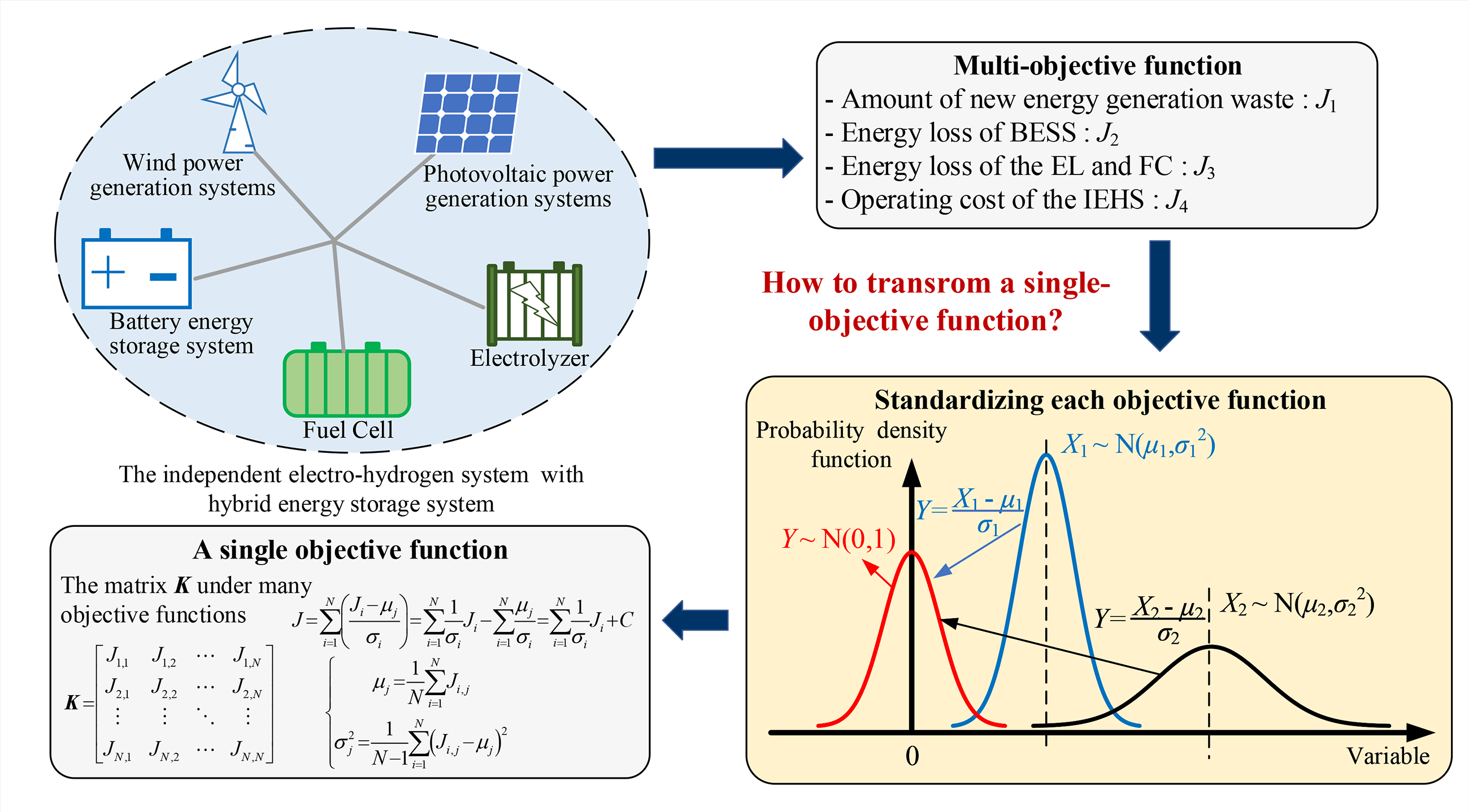
2  The Mathematical Model of the IEHS with HESS

2.1 Structure of the IEHS

Fig. 1 shows the structure of the IEHS with new energy generation system and HESS, including a power network and a hydrogen network. In the power network, there are some photovoltaic power generation systems (PVGs), wind power generation systems (WPGs), BESS, EL, FC, and power loads. And there are EL, FC, hydrogen storage tank, hydrogen sales unit, and purchase unit in the hydrogen energy network. Obviously, the core equipment is EL and FC for the interaction between electrical energy and hydrogen energy in the system. In addition, the HESS is composed of BESS and hydrogen energy storage (HES) that includes EL, FC and hydrogen storage tanks. This study will discuss optimizing the scheduling of this IEHS. It will focus on three things: 1) the consumption of the new energy generation system, 2) the operational losses of the HESS, and 3) the system’s overall operational costs. Then, the IEHS scheduling scheme’s multi-objective optimization problem needs standardizing its different objective functions. A novel solution has been proposed. Therefore, this section first established the IEHS’s mathematical model. It includes the operational constraints and multiple optimization objectives.

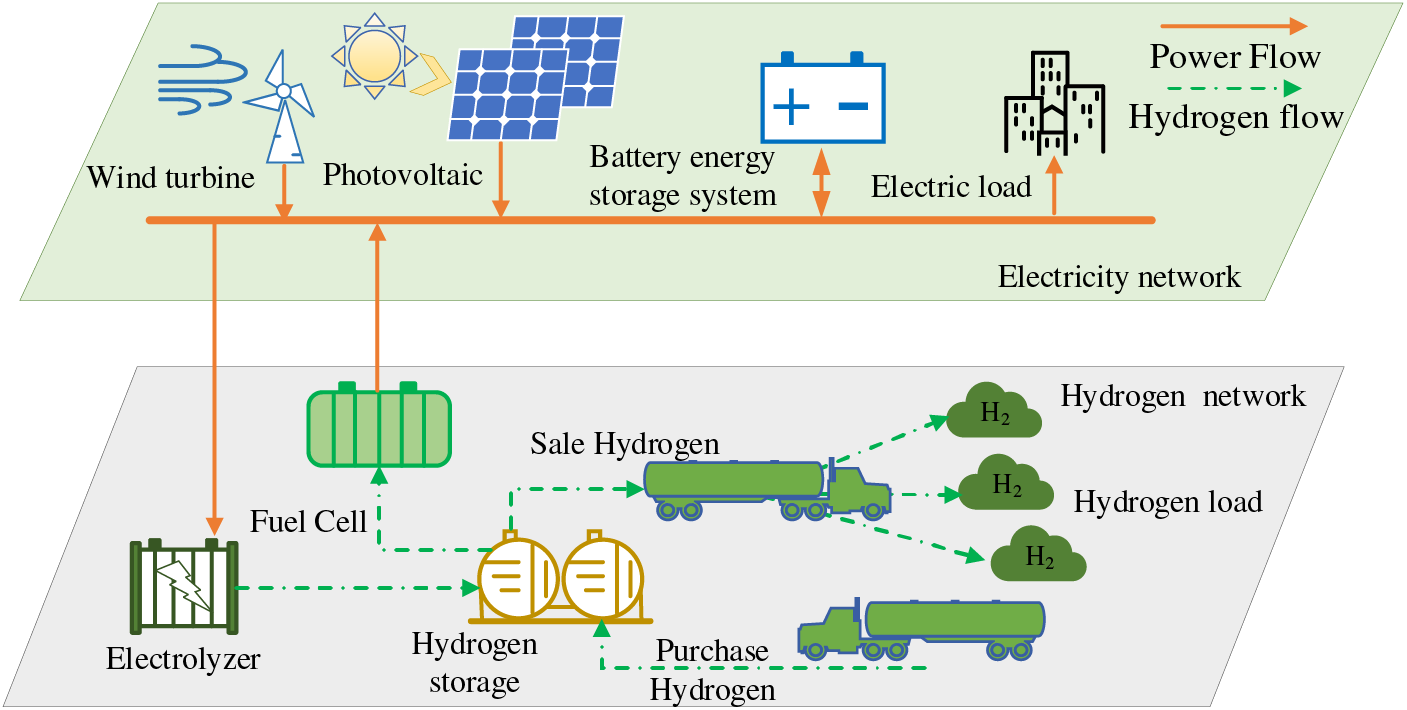
Figure 1: An independent electro-hydrogen system with hybrid energy storage

2.2 Operational Constraints of the IEHS with HESS

Base on the structure of the IEHS with HESS as shown in Section 2.1, it has been established that the operation constraints derived from the overall system, new energy generation system, BESS, and HES. The operation constraints include: 1. The real-time power and energy balance of the IEHS [31]. 2. The actual output power of PVGs and WPGs. 3. The actual output power and state of energy (SOE) of BESS [32]. 4. The restrictions on the production, storage, sale, and purchase of hydrogen gas [33,34]. Firstly, the real-time power balance constraint of the IEHS is presented as Eq. (1). Where PPV(t), PWIND(t), PBESS,d(t), PBESS,c(t), PFC(t), PEL(t), and PL,ref(t) respectively represent the output power of the PVGs and WPGs, discharge and charge power of BESS, the hydrogen production power of EL, the output power of FC, and the power of electric loads.

Ppv(t)+Pwind(t)+PBESS,d(t)+PBESS,c(t)+PFC(t)+PEL(t)−PL,ref(t)=0(1)

Then, Eq. (2) shows the operational constraints of PVGs and WGs [31]. Where PPV(t) and PPV,max(t) represent the actual output power and maximum power of the PVGs at time t, respectively. Similarly, at time t, the actual output power and maximum power of the WGs are defined as PWIND(t) and PWIND,max(t).

{0≤Ppv(t)≤Ppv,max(t)0≤Pwind(t)≤Pwind,max(t)(2)

During the operation of the BESS, the energy balance equation, the range of SOE and the output power limits are shown in Eqs. (3) and (4), respectively [32]. In these expressions, SSOE(t) is the SOE of BESS at time t; EBESSN, PBESSN, ηd, and ηc represent the rated capacity, rated power, discharge and charging efficiency of BESS, respectively; the initial, lower, and upper SOE for BESS are described as SSOEinit, SSOEL and SSOEU, respectively; the sampling time and ending time are Δt and T; ud(t) and uc(t) care indicator variables that represents the discharge and charging state of BESS, respectively. They are some binary optimization variables. If ud(t) = 1, it indicates that the BESS is in a discharged state. If the battery energy storage is in a charging state, uc(t) = 1.

{SSOE(t+Δt)=SSOE(t)−(PBESS,d(t)/ηd+PBESS,c(t)×ηc)×Δt×100/EBESSNSSOE(0)=SSOE(T)=SSOEinit(3)

{SSOEL≤SSOE(t)≤SSOEU0≤PBESS,d(t)≤ud(t)×PBESSN−uc(t)×PBESSN≤PBESS,c(t)≤0uc(t)+ud(t)≤1uc(t)=0or1ud(t)=0or1(4)

For hydrogen energy, there are constraints in production, use, storage, and sales. See Eqs. (5) to (8). Further, Eq. (5) lists the equation relationship between the volume and power of hydrogen produced by EL and hydrogen used by FC [31]. Eq. (6) characterizes the hydrogen balance relationship in the hydrogen energy network [33]. Eq. (7) limits the state of hydrogen (SOH) in the hydrogen storage tank, the actual output power and climbing rate of EL and FC [34]. In addition, the restrictions on the sale and purchase of hydrogen are shown in Eq. (8).

{VEL(t)=1000PEL(t)ηELρH2λH2ELPFC(t)=VFC(t)ρH2λH2FC1000PFC(t)ηFC(5)

where VEL(t) and PEL(t) represent the hydrogen production volume and power of the EL at time t, respectively. Then, ηEL and λH2EL are the hydrogen production efficiency and electro-hydrogen ratio of the EL. In FC, VFC(t) and PFC(t) are the hydrogen consumption volume and power generation of the FC at time t. Then, ηFC and λH2FC represent the hydrogen consumption efficiency and electro-hydrogen ratio of the FC, respectively. And ρH2 is the hydrogen density of 0.9 kg/m3.

{SSOH(t+Δt)=SSOH(t)+(−VEL(t)−VFC(t)−VSale(t)+VPurchase(t))×Δt×100/VHESSNSSOH(0)=SSOH(T)=SSOHinit(6)

{SSOHL≤SSOH(t)≤SSOHUuFC(t)×PFCmin≤PFC(t)≤uFC(t)×PFCN−uEL(t)×PELN≤PEL(t)≤−uEL(t)×PELminuEL(t)+uFC(t)≤1uEL(t)=0or1uFC(t)=0or1|PFC(t+Δt)−PFC(t)|≤αFC×PFCN|PEL(t+Δt)−PEL(t)|≤αEL×PELN(7)

In the above equations, SSOH(t), VEL(t), VFC(t), VSale(t), and VPurchase(t) represent the SOH, the hydrogen production, consumption, sales, and purchase volume at time t, respectively; the initial, lower, and upper SOH for the hydrogen storage tank are described as SSOHinit, SSOHL and SSOHU, respectively; then, the rated power of the EL, FC and the rated capacity of the hydrogen storage tank are defined as PELN, PFCN and VHESSN. Then, uEL(t) and uFC(t) are indicator variables that represent the state of the EL and FC, respectively. They are some binary optimization variables. If uEL(t) = 1, it means that the EL is working. If the FC is operating, uFC(t) = 1. And it is not allowed that the EL and FC runs simultaneously. αEL and αFC represent the ramping rates of EL and FC, respectively.

{0≤VSale(t)≤uSale(t)×VSale,max(t)0≤VPurchase(t)≤uPurchase(t)×VPurchase,max(t)uPurchase(t)+uSale(t)≤1uPurchase(t)=0or1uSale(t)=0or1(8)

where VSale(t) and VPurchase(t) represent the hydrogen volume sold and purchased by the IEHS at time t, respectively; VSale,max(t) and VPurchase,max(t) are the maximum hydrogen volumes sold and purchased by the IEHS at time t. Then, uSale(t) and uPurchase(t) are indicator variables of selling or purchasing hydrogen for the IEHS at time t. Certainly, they are some binary optimization variables. If uSale(t) = 1, it means that the IEHS is in the state of selling hydrogen gas. If the IEHS is purchasing hydrogen gas, uPurchase(t) = 1. Equally, it is prohibited for the operational status to simultaneously sell and purchase hydrogen externally.

2.3 Objective Functions of the IEHS with HESS

To fully leverage the advantages of the new energy generation system and HESS in IEHS, the multiple optimization objective functions are designed as follows. Firstly, in terms of new energy generation, an optimization objective function J1 is defined to characterize the amount of new energy generation waste, as shown in Eq. (9). Where Pi,max(t) and Pi(t) are the maximum and actual power generation of PVGs and WGs at time t, respectively. And i represents the photovoltaic power generation system or wind power generation system, respectively.

minJ1=∑i{pv,wind}∑t=0T(Pi,max(t)−Pi(t))(9)

Then, during the charging and discharging process of BESS, the energy loss of BESS is considered as an optimization objective function J2 shown in Eq. (10). Where at time t, PBESS,d(t) and PBESS,c(t) represent the output power of the discharge and charge power of BESS, respectively. ηd and ηc are the discharge and charging efficiency of BESS.

minJ2=∑t=0T(PBESS,d(t)(1ηd−1)−PBESS,c(t)(1−ηc))(10)

In the same way, Eq. (11) describes the third optimization objective function J3 that indicates the energy loss of the EL and FC. Where at time t, PEL(t) and PFC(t) represent the output power of EL and FC, respectively. ηEL and ηFC are the efficiencies of EL and FC.

minJ3=∑t=0T(PFC(t)(1ηFC−1)−PEL(t)(1−ηEL))(11)

Finally, the operating cost of the IEHS should be considered as an independent optimization objective J4, shown as Eq. (12). Where cPV, cWIND, cBESS, cEL, and cFC represent the cost per kilowatt hour of PVGs, WGs, BESS, EL, and FC, respectively. Then, cSale and cPurchase mean that the sales revenue and purchase cost per unit volume of hydrogen gas.

J4=cPV∑t=0TPPV(t)+cWIND∑t=0TPWIND(t)+cBESS∑t=0T(PBESS,d(t)−PBESS,c(t))−∑t=0T(cEL1000PEL(t)ηELλH2EL)…+∑t=0T(cFC1000FC(t)ηFCλH2FC)−∑t=1T(VSale(t)ρH2cSale)+∑t=1T(VPurchase(t)ρH2cPurchase)(12)

The above model shows that 1) the optimization scheduling problem of an IEHS with HESS is a typical multi-constraint and multi-objective optimization problem; 2) the physical dimensions among multiple optimization objective functions differ in scale, such as the physical quantities of optimization objective functions J1~J3 are the quantity of electricity, measured by kWh. But the optimization objective J4 is the cost and its unit is ¥. In this study, it will be the focus to avoid the adverse effects of physical dimensions among the different optimization objective functions on the optimization results.

3  Standardizing the Multi-Objective Functions

3.1 The Necessity and Methods of Data Standardization

In data analysis and machine learning, especially clustering, the differences in data magnitude between different data will have an undeniable impact on the analysis results. And this reason is generally caused by differences in physical dimensions. For example, the impacts of datasets magnitude are displayed on Euclidean space ranging and probability distribution in Fig. 2.

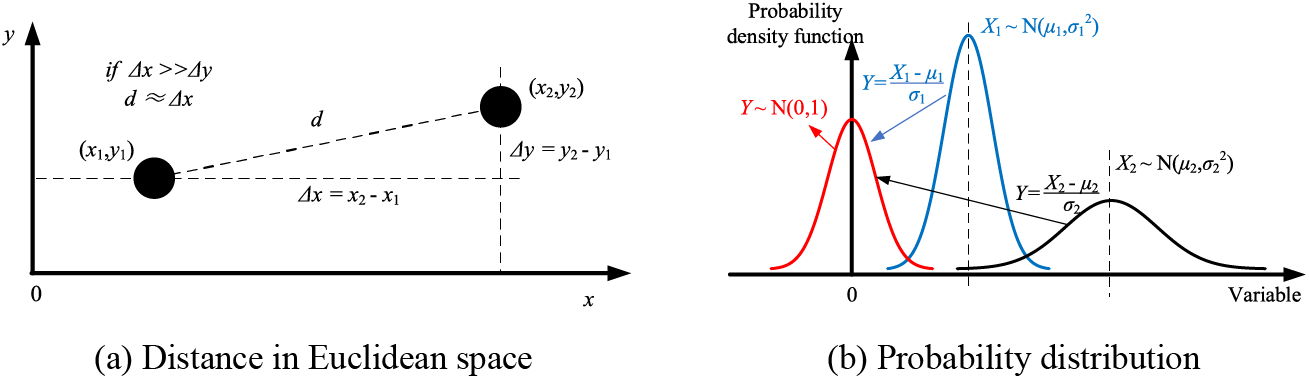
Figure 2: Schematic diagram of the impact of differential data magnitude

In Fig. 2a, if the magnitude of variable x is much greater than that of variable y, it means that the distance between two points in Euclidean space is almost equal to their deviation in the x-direction. Then, it results in the failure of variable y in distance calculation applications and the role of variable y can be ignored. If the reason for the magnitude deviation between variables x and y is the differences in their physical dimensions, it is obvious that the above results are unreasonable. Therefore, it is necessary to normalize the two variables. Otherwise, it is assumed that an independent random variable X1 follows a normal distribution of (μ1,σ12), and another independent random variable X2 follows a normal distribution of (μ2,σ22). In Fig. 2b, it can be seen that the difference in mean and standard deviation between these two variables is significant. If a new random variable Z is defined as X1 + X2, then the random variable Z will satisfy a normal distribution of (μ1+μ2,σ12+σ22). Obviously, the mean and variance of the random variable Z are more affected by μ2 and σ22, respectively. And Z is a new random variable. It is the equal weighted sum of two independent random variables, the impact of the two independent random variables X1 and X2 on the new random variable Z is different.

The above results indicate that standardization data is an important and necessary step in data analysis. Currently, Eq. (13) is a common approach to solve the problem presented in Fig. 2a. This method limits the range of each coordinate in space to within 0~1. Then, in the problem shown in Fig. 2b, Eq. (14) can be used to transform the probability distribution of each random variable to a standard normal distribution.

β=α−αminαmax−αmin,α∈{x,y}(13)

Y=Xi−μiσi,i∈{1,2}(14)

where α, αmin and αmax are the original data value, minimum value, and maximum value, respectively; β is the standardization data value; Xi, μi, σ2i and Y represent the original random variable, mean, variance, and the standardized random variable.

3.2 A Standardization Fusion Method for Multi-Objective Functions

As stated in Section 3.1, it is necessary to standardize data with different physical dimensions. Similarly, in a multi-objective optimization scheduling of the IEHS with HESS described in Section 2, significant differences exist in the physical dimensions of multiple optimization objective functions. It is clearly unreasonable to transform a multi-objective optimization problem into a single objective optimization problem through a commonly used direct summation method. Thus, in this manuscript, a standardization fusion method has been proposed for multi-objective functions. The framework procedure of the presented study is illustrated in Fig. 3.

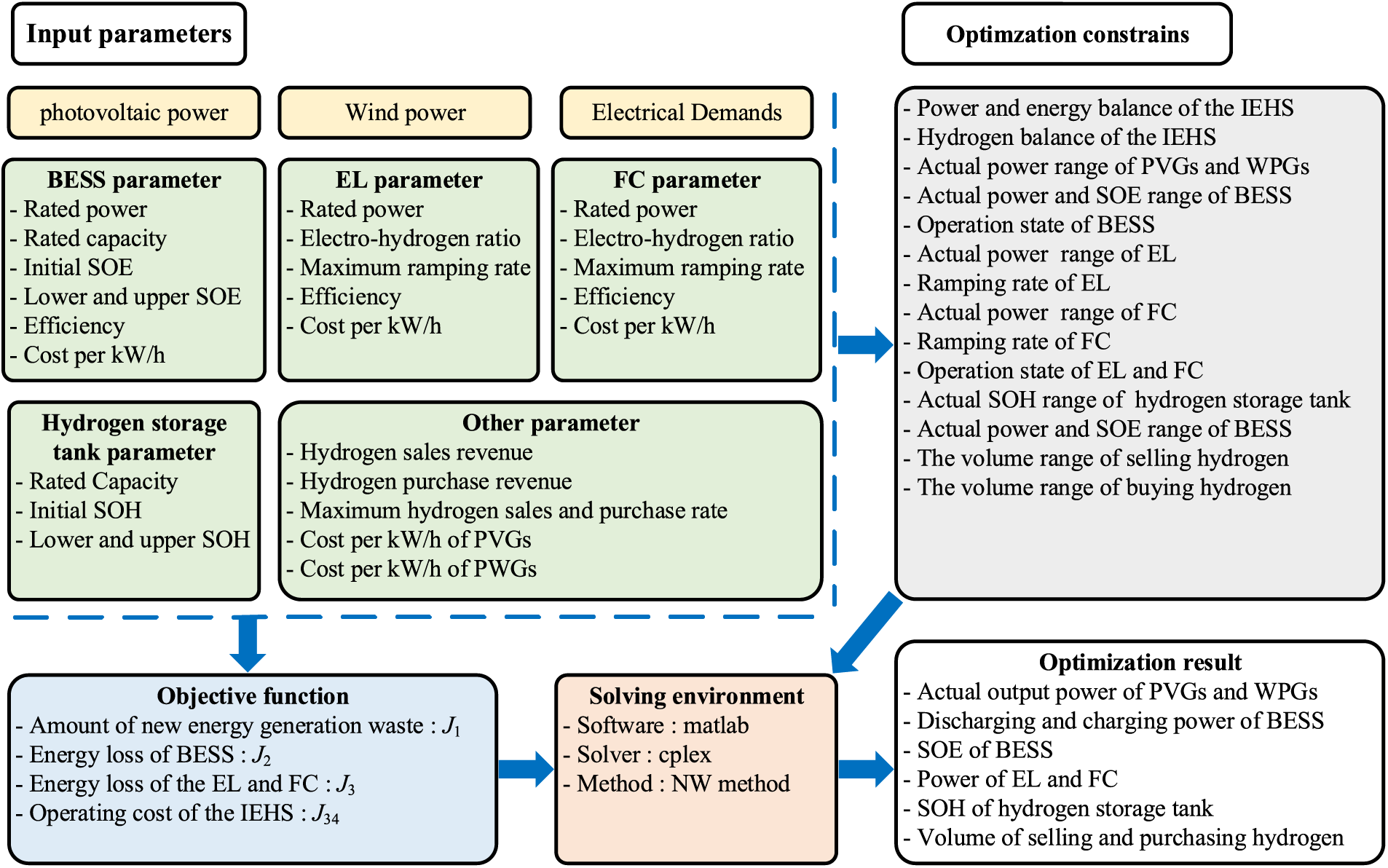
Figure 3: Framework procedure of the presented study

The standardization data method shown in Eq. (13) is a way of mapping the maximum and minimum values of data to the range of 0 to 1. Therefore, the maximum and minimum values of data are necessary in the standardization process. If this approach is used in the standardization process of the objective function, the maximum and minimum values of each optimization objective function will also be required. By independently optimizing each optimization objective function, the minimum value of each optimization objective can be obtained. Unfortunately, the maximum value of each optimization objective function is difficult to solve. Therefore, this method is hard to apply to the standardization of multiple optimization objective functions.

Another standardization approach, shown in Eq. (14), requires the mean and standard deviation in each direction of the optimization objective function to standardize it. Therefore, a calculation method should be designed to obtain the mean and standard deviation in the direction of each optimization objective function. Then, the specific implementation process is as follows. Fig. 4 represents the process of the standardization fusion method for multiple optimization objective functions.

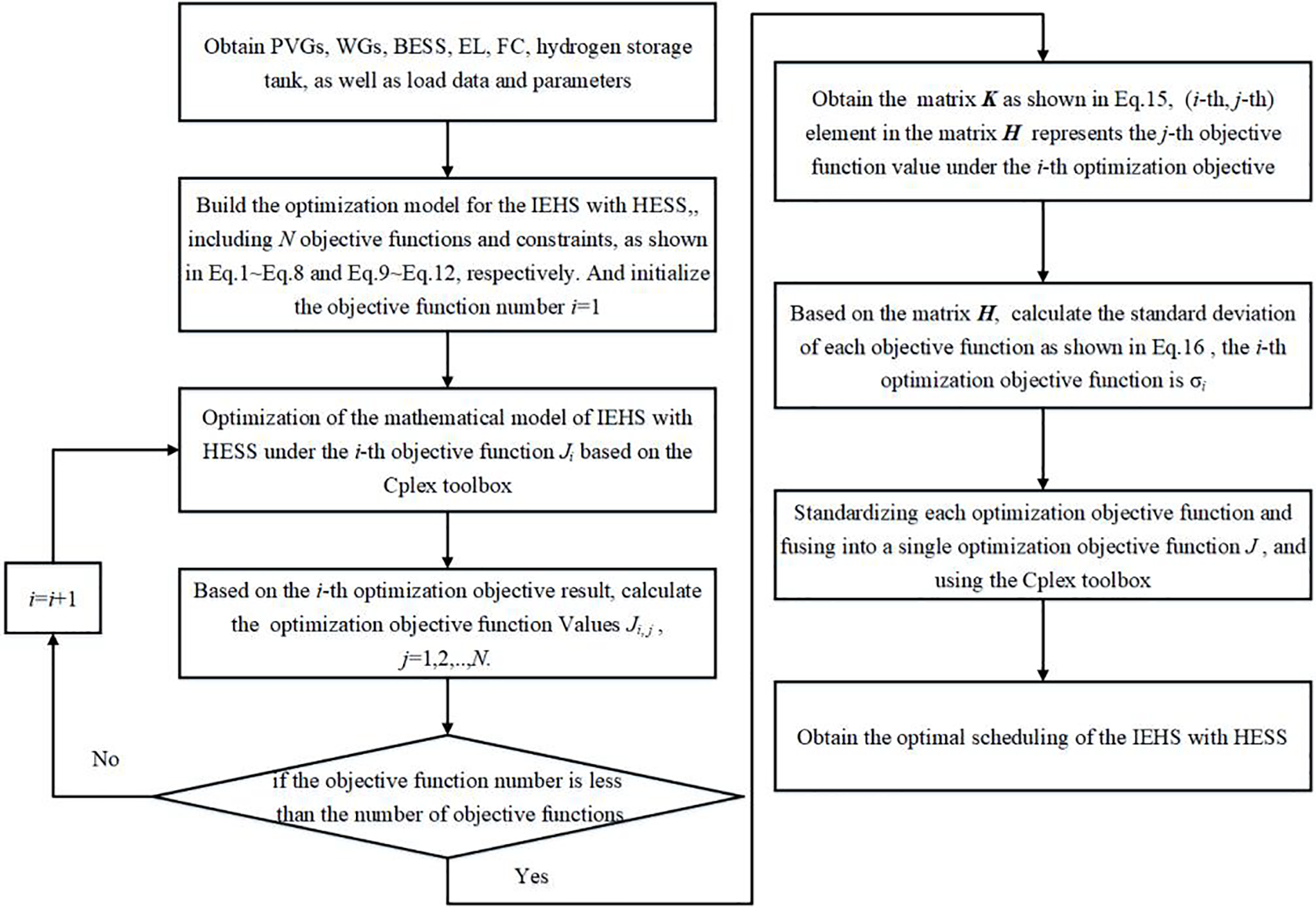
Figure 4: The flow chart of the proposed method

Step 1 The CPLEX tool is used to optimize the IHES with HESS in Section 1. It optimizes each objective function as a single goal. This gives the optimal scheduling results for the IHES. Then, the values of other optimization objective functions can be calculated to form a matrix as shown in Eq. (15). The element Ji,j from the (i-th, j-th) position in the matrix K represents the value of the j-th optimization objective function when the i-th optimization objective is taken as the single optimization objective function, i = 1, 2, …, N, j = 1, 2, …, N. And in this study, N is 4. Obviously, the elements on the diagonal of the matrix K are the minimum values of each individual optimization objective function, ∀s∈[1, N], Ji,i ≤ Js,i.

K=[J1,1J1,2⋯J1,NJ2,1J2,2⋯J2,N⋮⋮⋱⋮JN,1JN,2⋯JN,N](15)

Step 2 The matrix K from Eq. (15) is analyzed by column. The element in the j-th column of the matrix K can be viewed as the numerical variation of the optimization objective function Jj under the different optimization objective functions. Then, the mean and standard deviation of the j-th optimization objective function can be calculated as described in Eq. (16).

{μj=1N∑i=1NJi,jσj2=1N−1∑i=1N(Ji,j−μj)2(16)

Step 3 Referring to the data standardization process described in Eq. (15), the mean and standard deviation of each optimization objective function are used to standardize each optimization objective function. Then, the standardized multiple optimization objective functions are fused into a single optimization objective function J as shown in Eq. (17). The fused single optimization objective function is the sum of the quotient of each optimization objective and its standard deviation, plus a constant C. Apparently, minimizing the fused single objective function is, it seems, equivalent to minimizing the sum of the quotient values of each optimization objective function and its standard deviation, as shown in Eq. (18).

J=∑i=1N(Ji−μjσi)=∑i=1N1σiJi−∑i=1Nμjσi=∑i=1N1σiJi+C(17)

minJ⇔min∑i=1N1σiJi(18)

Thus, when transforming a multi-optimization objective problem into a single optimization objective problem by weighted summation, the weights of each optimization objective are equal to the reciprocal of their standard deviation. It is worth noting that, in calculating the quotient of each optimization objective function with its standard deviation, the physical dimension of the optimization objective function is eliminated. And this quotient value represents the physical dimension of 1. Obviously, it is beneficial for the reasonable integration of different optimization objective functions.

4  Case Analysis and Discussion

4.1 Parameter Description

Based on the IEHS with HESS shown in Fig. 1, a simulation case has been established to verify the effectiveness of the proposed method. In this simulation case, there are PVGs, GWs, and HESS that include BESS, EL and FC. The parameters of this system are shown in Table 1 [31,32,35,36]. Then, Fig. 5 shows the power curves of the load, PVGs, and GWs in a typical day.

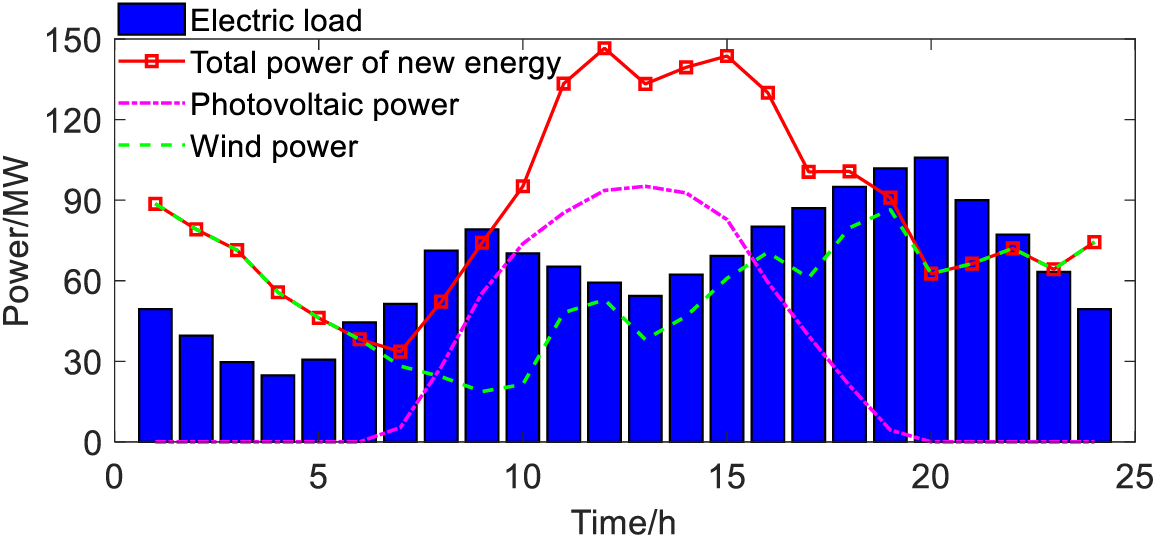
Figure 5: The power curve from new energy stations and load under typical day

In Table 1, it can be seen that the cost per kilowatt hour of PVGs and WGs is lower than that of HESS. This means that when IEHS operates with economic goals, HESS will fail to improve the utilization rate of PVGs and WGs. In the HESS, the charging and discharging efficiency of BESS is much higher than that of EL and FC. Its cost per kilowatt hour is lower than theirs. It indicates that regardless of whether the system operates with energy losses or economic goals, the BESS is superior to the HES composed of EL and FC. Under the condition that the BESS does not work, the HES supports the continuous operation of the IEHS.

As shown in Fig. 5, within the range of 0–5 h, 10–18 h, and 23–24 h, the power of PVGs and WGs is greater than the electric load. If an energy storage system does not exist, a large amount of photovoltaic and wind power will be abandoned during the above time periods. In the range of 6–9 h and 19–22 h, if the power consumption of the load is greater than the PVGs and WGs, there will be a situation causing electricity problems for users’ production and daily life. Therefore, to avoid the above situation, the energy storage system is necessary in IEHS. Besides, at 20 h, the power deviation between the electric load and the new energy generation power has exceeded the rated power of the BESS. FC is an important component of assisting BESS and supporting the electric load.

4.2 Result Analysis

Based on the above simulation parameters and data, the optimization scheduling of the IEHS with HESS is analyzed, and the effectiveness of the proposed method is verified. Table 2 compares the results of SF, equal weight method (EW) [27], and single objective optimization method on four optimization objectives. Then, Fig. 6 shows the standard deviation calculation results of the proposed method for different optimization objectives, i.e., the reciprocal of the weights assigned to each objective function. The operational results of IEHS with HESS under different methods are shown in Fig. 7.

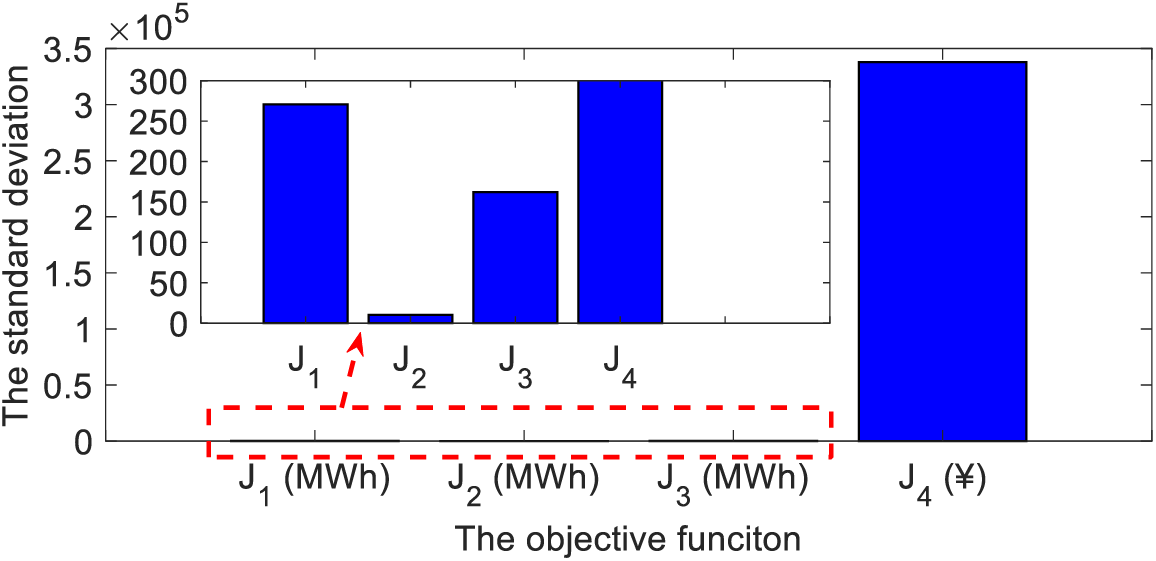
Figure 6: Standard deviation of J1~J4 indicator values

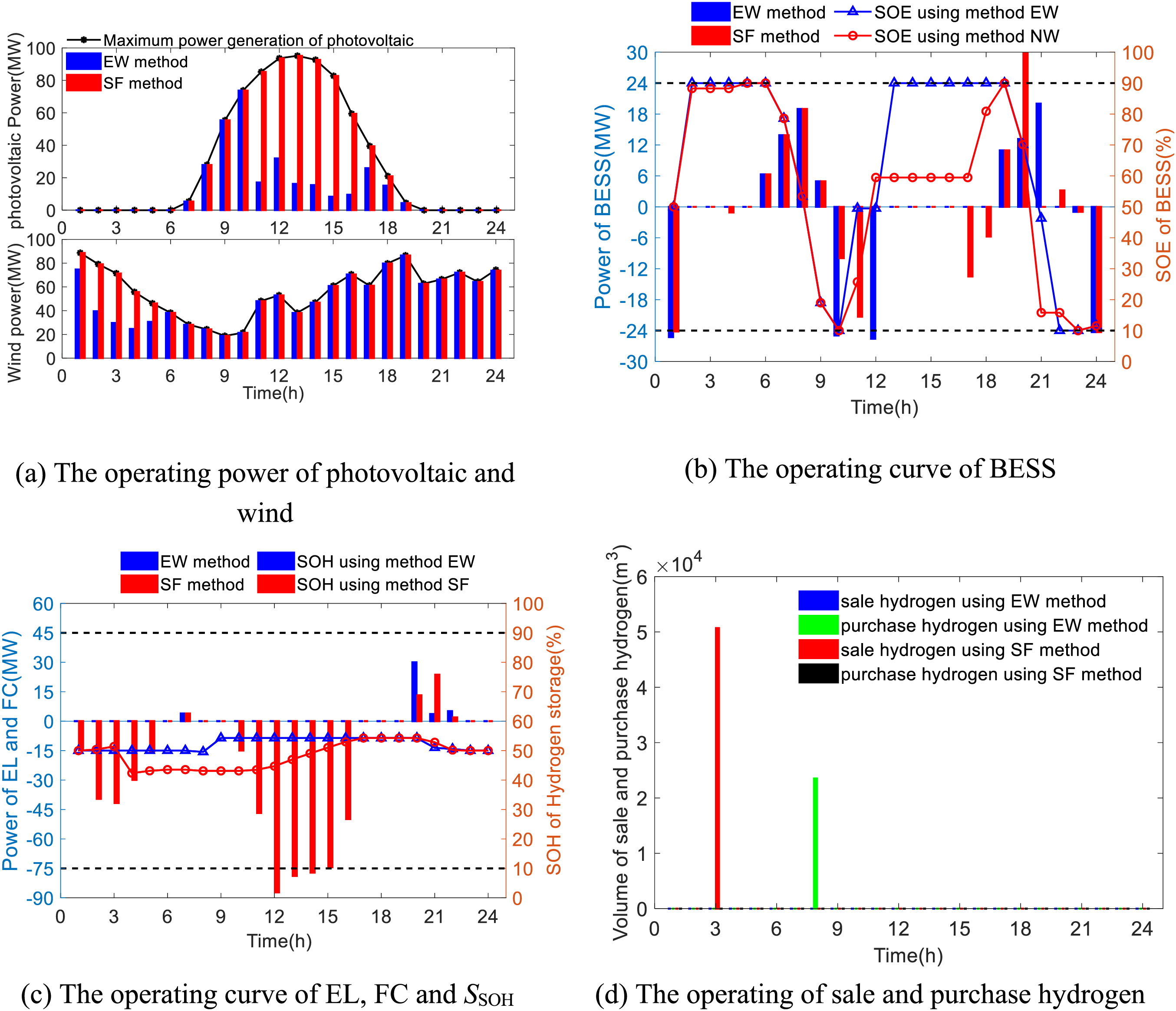
Figure 7: Comparison results of operational performance of electric and hydrogen network with different methods

In Table 2, the conclusions are as follows:

1) Under different optimization methods, the numerical differences of the optimization objective functions J1, J2, J3, and J4 reached 571.68, 23.905, 292.315, and 685,541.894, respectively. Comparing the whole energy loss and economy of IEHS with HESS under different optimization methods, their optimization results can reach 2–3 times.

2) The optimization results based on the equal weight method are consistent with the single objective optimization results using the objective function J4. The reason is that the value of the optimization objective function J4 is much larger than that of other optimization objective functions. It means that when assigning the same weight to each optimization objective function, reducing the optimization objective function J4 is more appropriate. Further, the fundamental reason for this problem lies in the difference in physical dimensions among different optimization objective functions. Then, the optimization results are influenced by these significant differences.

3) Compared with other optimization methods, the proposed method exhibits suboptimal solutions in all optimization objective directions of J1~J4. It reflects that the proposed method can better consider the needs of different optimization objective functions and can balance them.

4) Compared to minimizing the objective function J1, the proposed method wastes 0.621 MWh of energy from PVGs and WGs, but reduces the energy loss of BESS J2, the energy loss of HES J3, and operating cost J4 by 13.07, 92.445 MWh, and 40.93%, respectively. From the perspective of energy utilization, to fully absorb the power of PVGs and WGs, more energy loss will be caused in BESS, EL, and FC. Obviously, minimizing the objective function J1 is inappropriate.

5) Compared to minimizing the objective function J2, the proposed method increases the energy loss of BESS J2 by 10.84 MWh. But in the direction of new energy power abandonment J1, the energy loss of HES J3, and operating costs J4, they have decreased by 455.42, 68.494 MWh, and 42.96%, respectively. Apparently, the results of the proposed method are more reasonable.

6) Compared to minimizing the objective function J3, the proposed method increases the energy loss of HES J3 by 199.87 MWh, but reduces new energy power abandonment J1, the energy loss of BESS J2, and operating costs J4 by 564.186, 6.872 MWh, and 5.59%, respectively. The proposed method performs better in terms of energy utilization and economy.

7) Compared to minimizing the objective function J4, the proposed method increased operating costs J4 and the energy loss of HES J3 by 16.1% and 199.87 MWh, respectively, but recovered 571.059 MWh of new energy power abandonment J1. After calculations, the cost per kilowatt hour of recovering new energy generation is 0.314 ¥/kWh, slightly higher than the cost per kilowatt hour of PVGs and WGs. In terms of operating costs, the reasons for the disadvantage of the proposed method should be further analyzed.

In Fig. 6, it can be seen that the standard deviation of the optimization objective function J4 is much larger than the other three optimization objective functions. The reason is the different physical dimensions among different optimization objective functions. Furthermore, combining Eq. (15), the proposed method can effectively eliminate physical dimensions. It will ensure that all optimization objective functions are represented as dimensionless values.

In Fig. 7, the conclusions are summarized as follows:

1) Using the EW method, there is a situation of abandonment of wind power generation from 1 to 5 h and photovoltaic power generation from 11 to18 h as shown in Fig. 7a. But, the SF method did not. The reason for this phenomenon is that the value of the optimization objective function J4 is too large. The more fundamental reason lies in the physical dimensional differences among all optimization objective functions. If the weights of all optimization objective functions are equal, such as EW method, the optimization results will tend towards J4. Under the condition of high hydrogen production cost and the limited rated power and capacity of BESS, it is normal for photovoltaic power generation and wind power generation to be abandoned. Obviously, this is not conducive to improving the effective utilization of new energy.

2) Affected by the limited power and capacity of BESS, the demand of the electric load in 20–22 h cannot be satisfied in Fig. 7b,c. Therefore, to support the electric load, FC has to be used. At the same time, to maintain the hydrogen balance within the IEHS, it is necessary to purchase cheaper hydrogen from external sources as shown in Fig. 7d. It leads to the IEHS’s dependence on external air sources.

3) The proposed method removes the dimension of each optimization objective function. It avoids over-focusing on optimization objective functions with excessively large values, and takes into account the energy utilization and operating costs of the IEHS. Further, it can be seen that the new energy generation has been effectively enhanced to product hydrogen for FC, and the dependence on external gas sources has been reduced. On the other hand, from the SOE of the BESS, it can be seen that the EL absorbs the power generated by new energy generation. It leads to a reduction in the full charge and discharge time of BESS, avoiding the situation of overcharging and discharging. Combined with Table 2, it can be concluded that the proposed method is superior.

4.3 Discussion

To further analyze the impact of energy and economic parameters on four optimization objectives, shown as Fig. 8. It shows their variations under different efficiencies of EL and FC. Then, Fig. 9 represents the impact of the cost per kilowatt hour of BESS and the new energy generation system on four optimization objective functions. In addition, the effects of hydrogen production and hydrogen consumption costs of EL and FC on the four optimization objective functions are described in Fig. 10.

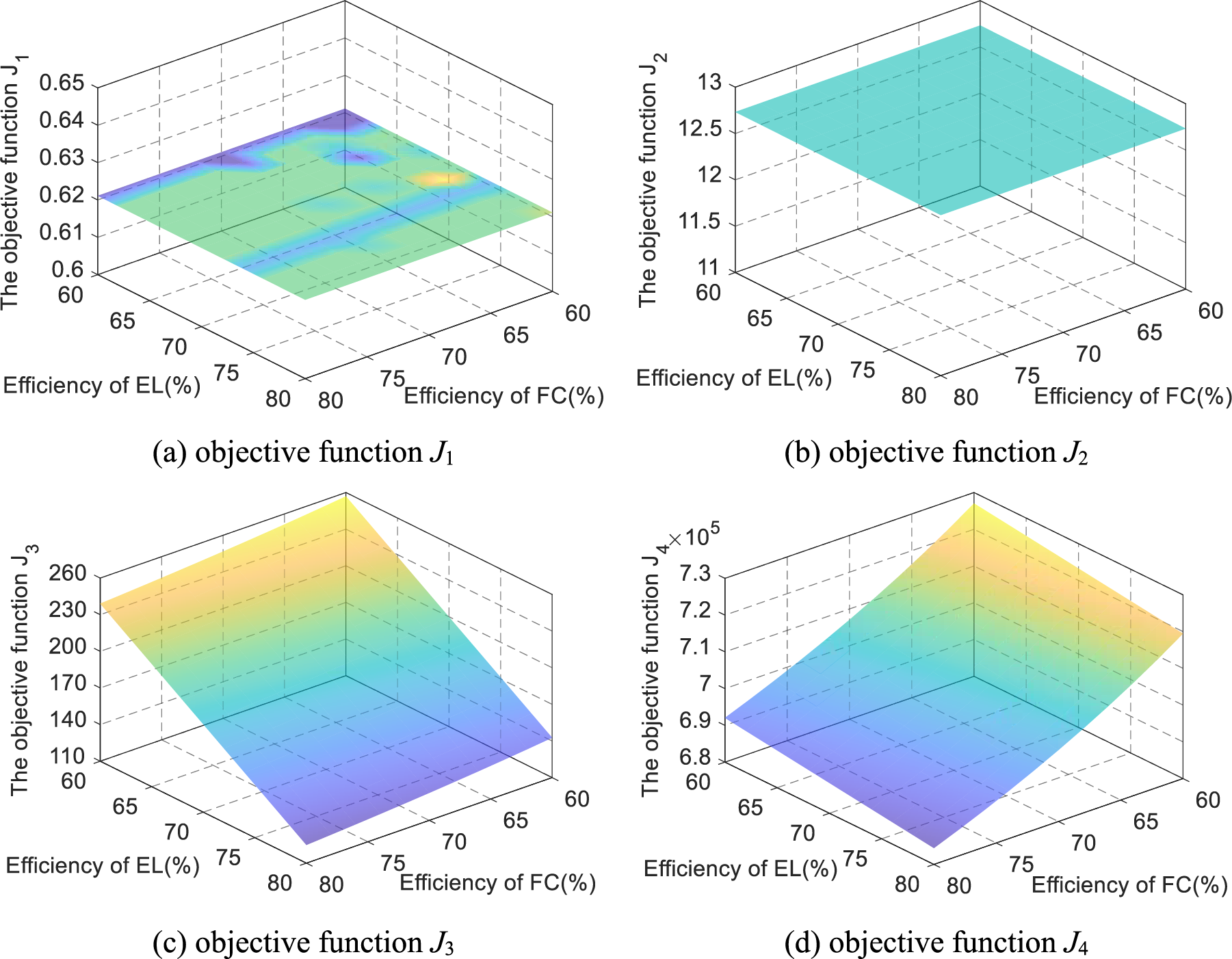
Figure 8: The optimization results with changes in efficiency of EL and FC

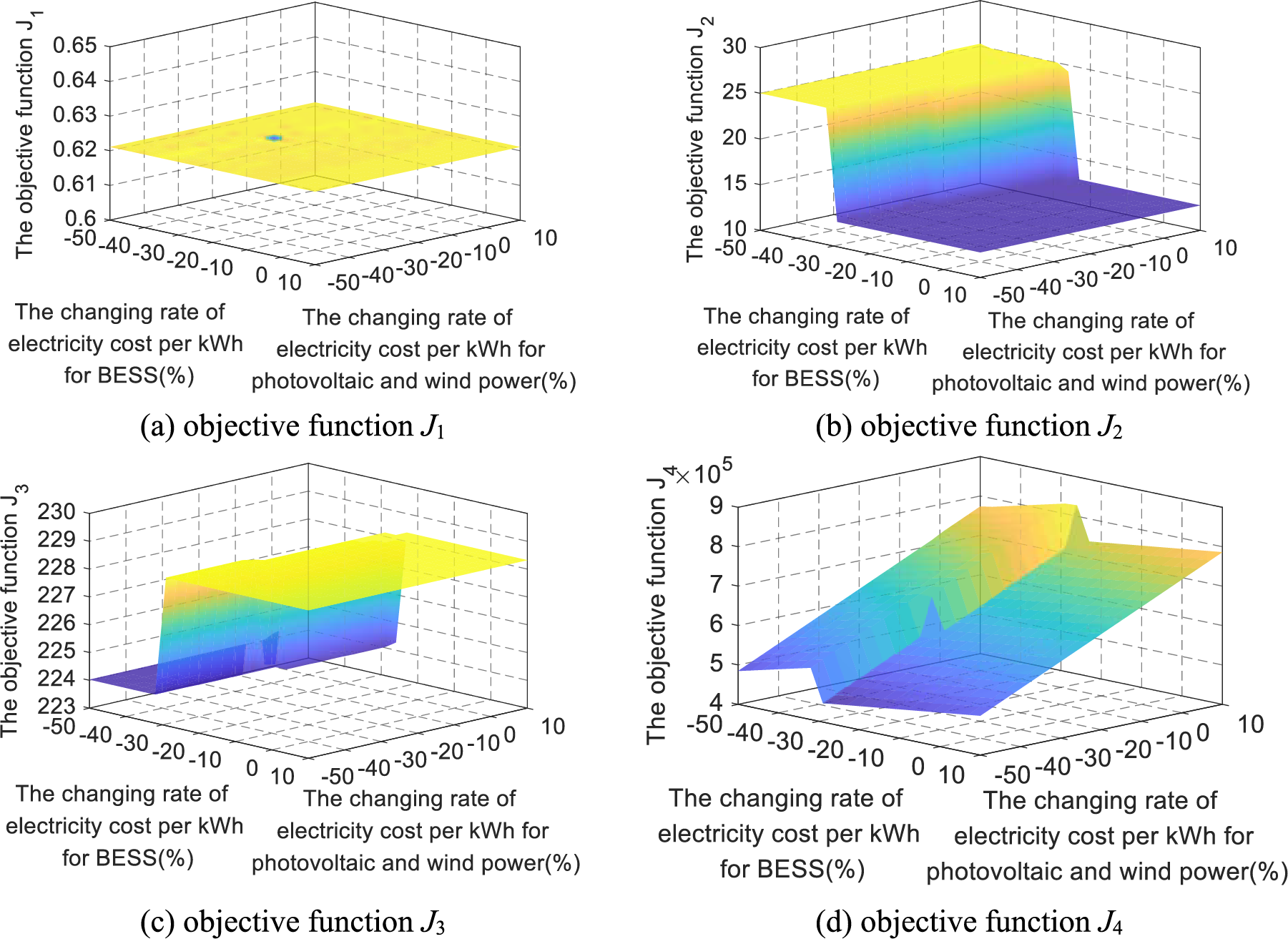
Figure 9: The optimization results with changes in electricity cost per kWh of photovoltaic, wind and BESS

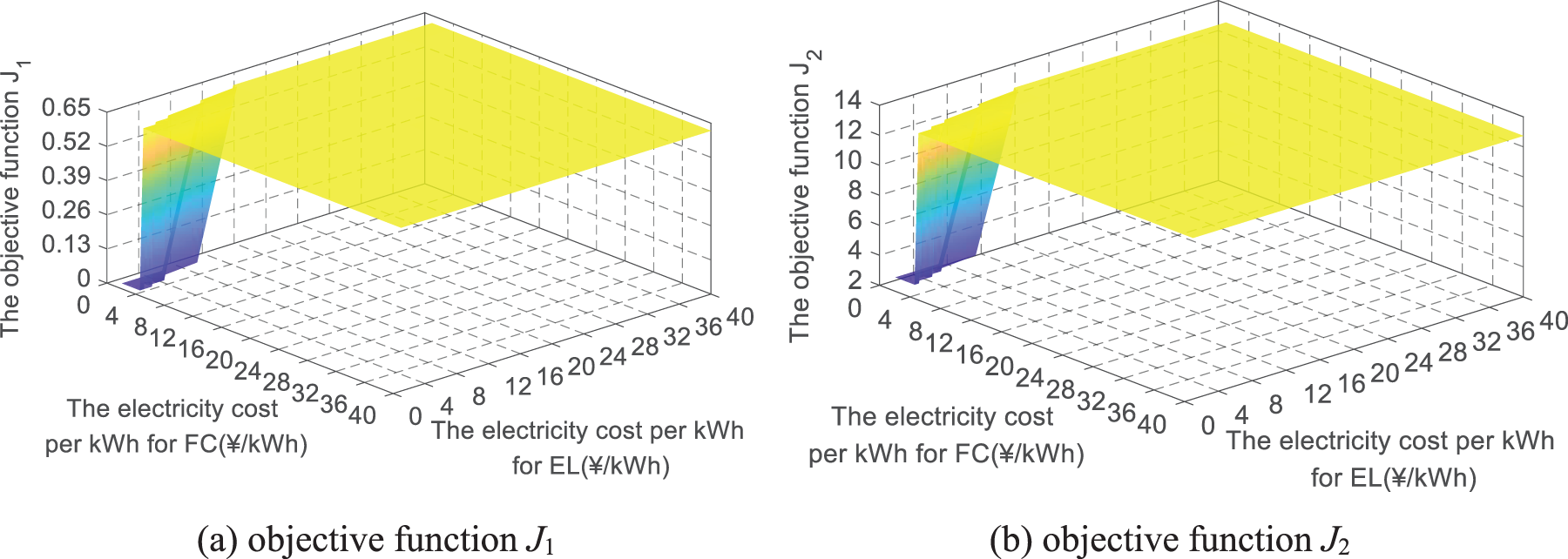
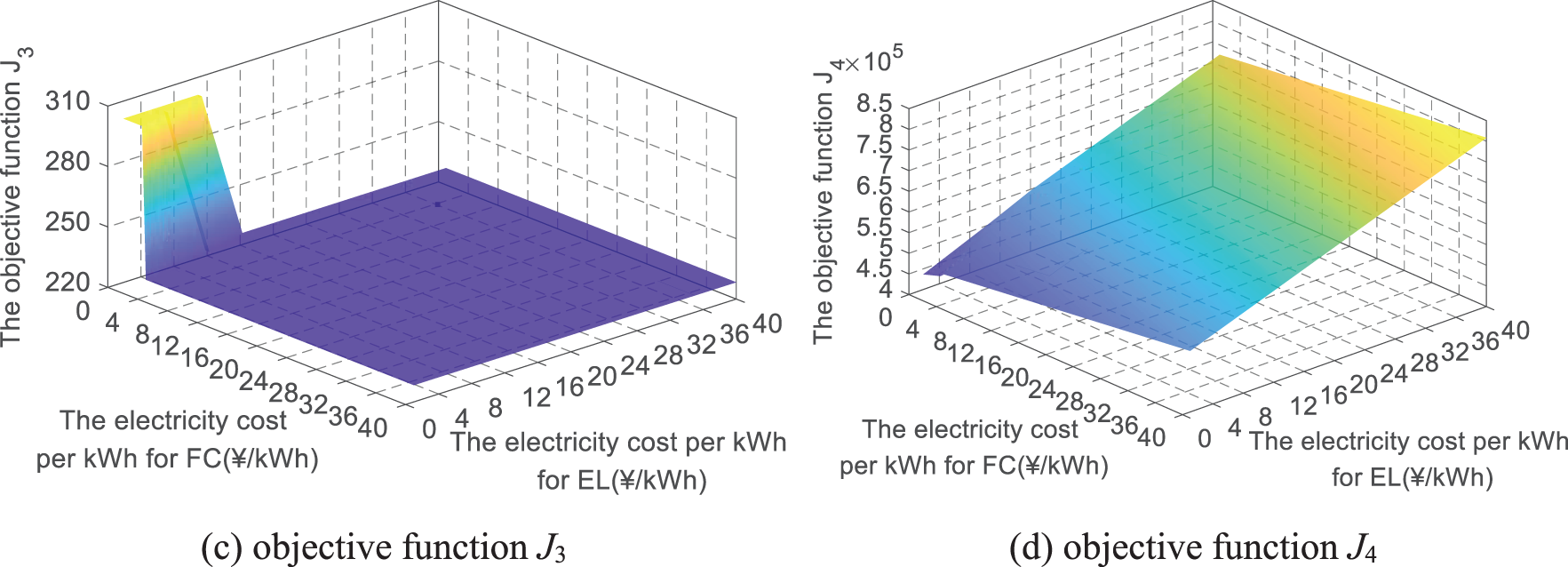
Figure 10: The optimization results with changes in producing cost of hydrogen by EL and FC

In Fig. 8, as the EL’s hydrogen production and the FC’s power generation efficiencies improve, hydrogen energy loss drops significantly. The reason why the impact of the EL efficiency is greater than that of the FC efficiency is that the power generation of PVGs and WGs is much greater than that of the electric load. The EL is more involved in the operation process. Then, when hydrogen production increases, more hydrogen can be sold to maintain hydrogen balance and the operating cost of IEHS will decrease. On the other hand, in terms of operating cost J4, the impact of FC efficiency is greater than that of EL efficiency is that the cost of FC is higher than the cost of EL.

Remarkably, the efficiency of EL and FC has not affected the amount of new energy power abandonment J1, the energy loss of BESS J3. The reason is that the hydrogen production and generation power is the result of the supply-demand relationship between PVGs, WGs, BESS, and the electric load. The efficiency of EL and FC just determines the conversion process of electricity and hydrogen. They directly affect hydrogen production and consumption and indirectly work the operating cost of IEHS. Therefore, the efficiency of EL and FC is a key indicator that affects the energy losses, hydrogen utilization, and operating cost of the IEHS. But it is not the core factor that involves the operational process of PVGs, WGs, and BESS in the IEHS.

Fig. 9 represents the impact of changes in the cost of new energy generation and BESS on various optimization objective functions. At present, the cost per kilowatt hour of new energy generation is far lower than that of HESS, and the proposed method has significantly reduced the amount of new energy waste. It has resulted in insufficient impact of the above changes on the amount of new energy abandonment J1. While the cost per kilowatt hour of BESS is reducing, the charging and discharging behavior of BESS will intensify. Under the condition of the fixed efficiency of BESS, the energy loss of BESS will increase.

In Fig. 9b, if the cost per kilowatt hour of the BESS decreases by about 30% (0.5 ¥/kWh), the energy loss of the BESS shows a step increase. The electricity consumption of the EL and the power generation of the FC will decrease. Then, the energy loss of the HES J3 will fall. In addition, when the hydrogen production power of the EL decreases, the revenue generated from selling hydrogen in the IEHS reduces. The operating cost J4 of the IEHS suddenly increases and then slowly decreases. Therefore, the cost of new energy generation and the BESS directly affects the economy of the IEHS. Then, changes in the allocation of output power in the HESS affect the energy consumption and hydrogen production. However, it has little effect on improving the consumption of new energy generation with lower electricity costs.

In Fig. 10, while the electricity cost of the EL and FC decreases, the operating cost J4 continues to decrease. But the amount of new energy power abandonment, the energy loss of BESS and HES remains unchanged. When the cost per kilowatt hour of the EL is less than 15 ¥/kWh or the FC is less than 4 ¥/kWh, the consumption of new energy power is improved. Meanwhile, the charging and discharging losses of BESS reduce and the energy loss of HES increases. It indicates that the participation of BESS falls, HES including EL and FC rises in the power supply. Therefore, the electricity cost of EL and FC directly affects the economy of the IEHS. Then, the impact on the energy utilization of the IEHS is reflected in the power allocation results of BESS and HES.

5  Conclusion

The scheduling of IEHS and HESS involves complex multi-objective optimization problems with numerous constraints. A common approach is to convert multiple objective functions into a single one by summing them. However, this often overlooks the differences in the physical dimensions of the objectives, leading to a disproportionate focus on certain functions. To address this issue, we propose a standardization fusion method. The main conclusions are as follows:

1) In IEHS with HESS, using different optimization methods, the value of the economy and the whole energy loss can reach 2 to 3 times. The reason is the difference in their physical dimensions. This phenomenon should be regarded seriously in multi-objective optimization problems.

2) A standardization fusion method has been established. It analyzes the changes in the same optimization objective function value under different optimization objective functions. This method improves the balance among all objectives and reduces the effects of their complexity.

3) The efficiency of the EL and FC is crucial. It affects hydrogen use and the IEHS’s operating cost. However, it can be ignored that their impact on the operational process of PVGs, WGs, and BESS.

4) In IEHS with HESS, when the cost of BESS decreases to about 30%, the participation of BESS will deepen by about 1 time and the HES gradually exits. Then, if the cost per kilowatt hour of the EL is less than 15 ¥/kWh or the FC is less than 4 ¥/kWh, the participation of HES will improve markedly.

Future research should improve the proposed method. It should explore the probability distributions of each optimization objective function and their couplings. They will be key to using the proposed method to solve multi-objective optimization problems.

Acknowledgement: This paper was completed with the hard help of every author.

Funding Statement: This study was sponsored by R&D Program of Beijing Municipal Education Commission (KM202410009013).

Author Contributions: Suliang Ma proposed the concept, method, principle and first draft of the manuscript. Zeqing Meng was responsible for data analysis, drawing, and formulating the conclusions of this study. Mingxuan Chen contributed through review, modification, and final approval of the manuscript. Yuan Jiang provided supervision and approval of the work. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. L. P. Van, L. H. Hoang, and T. N. Duc, “A comprehensive review of direct coupled photovoltaic-electrolyser system: Sizing techniques, operating strategies, research progress, current challenges, and future recommendations,” Int. J. Hydrogen Energy, vol. 48, no. 65, pp. 25231–25249, Jul. 2023. doi: 10.1016/j.ijhydene.2023.03.257. [Google Scholar] [CrossRef]

2. M. Nasser, T. F. Megahed, S. Ookawara, and H. Hassan, “A review of water electrolysis-based systems for hydrogen production using hybrid/solar/wind energy systems,” Environ. Sci. Pollut. Res., vol. 29, no. 58, pp. 86994–87018, Dec. 2022. doi: 10.1007/s11356-022-23323-y. [Google Scholar] [PubMed] [CrossRef]

3. R. Niepelt et al., “The influence of falling costs for electrolyzers on the location factors for green hydrogen production,” Sol. RRL, vol. 7, no. 17, Sep. 2023. doi: 10.1002/solr.202300317. [Google Scholar] [CrossRef]

4. M. Awad et al., “A review of water electrolysis for green hydrogen generation considering PV/wind/hybrid/hydropower/geothermal/tidal and wave/biogas energy systems, economic analysis, and its application,” Alex Eng. J., vol. 87, pp. 213–239, Jan. 2024. doi: 10.1016/j.aej.2023.12.032. [Google Scholar] [CrossRef]

5. M. A. Hossain, M. R. Islam, M. A. Hossain, and M. J. Hossain, “Control strategy review for hydrogen-renewable energy power system,” J. Energy Storage, vol. 72, Nov. 2023, Art. no. 108170. doi: 10.1016/j.est.2023.108170. [Google Scholar] [CrossRef]

6. N. Ibagon, P. Muñoz, V. Díaz, E. Teliz, and G. Correa, “Techno-economic analysis for off-grid green hydrogen production in Uruguay,” J. Energy Storage, vol. 67, Sep. 2023, Art. no. 107604. doi: 10.1016/j.est.2023.107604. [Google Scholar] [CrossRef]

7. C. M. de León, C. Ríos, and J. J. Brey, “Cost of green hydrogen: Limitations of production from a stand-alone photovoltaic system,” Int. J. Hydrogen Energy, vol. 48, no. 32, pp. 11885–11898, Apr. 2023. doi: 10.1016/j.ijhydene.2022.05.090. [Google Scholar] [CrossRef]

8. S. Toghyani, E. Baniasadi, and E. Afshari, “Performance assessment of an electrochemical hydrogen production and storage system for solar hydrogen refueling station,” Int. J. Hydrogen Energy, vol. 46, no. 47, pp. 24271–24285, Jul. 2021. doi: 10.1016/j.ijhydene.2021.05.026. [Google Scholar] [CrossRef]

9. M. Zoladek, R. Figaj, A. Kafetzis, and K. Panopoulos, “Energy-economic assessment of self-sufficient microgrid based on wind turbine, photovoltaic field, wood gasifier, battery, and hydrogen energy storage,” Int. J. Hydrogen Energy, vol. 52, pp. 728–744, Jan. 2024. doi: 10.1016/j.ijhydene.2023.04.327. [Google Scholar] [CrossRef]

10. M. Zoladek, A. Kafetzis, R. Figaj, and K. Panopoulos, “Energy-economic assessment of islanded microgrid with wind turbine, photovoltaic field, wood gasifier, battery, and hydrogen energy storage,” Sustainability, vol. 14, no. 19, Oct. 2022, Art. no. 12470. doi: 10.3390/su141912470. [Google Scholar] [CrossRef]

11. O. M. Babatunde, J. L. Munda, and Y. Hamam, “Off-grid hybrid photovoltaic-micro wind turbine renewable energy system with hydrogen and battery storage: Effects of sun tracking technologies,” Energ. Convers. Manage., vol. 255, Mar. 2022, Art. no. 115335. doi: 10.1016/j.enconman.2022.115335. [Google Scholar] [CrossRef]

12. Z. X. Meng, Q. He, X. P. Shi, D. H. Cao, and D. M. Du, “Research on energy utilization of wind-hydrogen coupled energy storage power generation system,” Sep. Purif. Technol., vol. 313, May 2023, Art. no. 123439. doi: 10.1016/j.seppur.2023.123439. [Google Scholar] [CrossRef]

13. N. Zidane and S. L. Belaid, “A new fuzzy logic solution for energy management of hybrid photovoltaic/battery/hydrogen system,” Rev. Roum. Sci. Techn.-Électrotechn. Énerg., vol. 67, no. 1, pp. 21–26, Jan.–Mar. 2022. [Google Scholar]

14. I. Abadlia, L. Hassaine, A. Beddar, F. Abdoune, and M. R. Bengourina, “Adaptive fuzzy control with an optimization by using genetic algorithms for grid connected a hybrid photovoltaic-hydrogen generation system,” Int. J. Hydrogen Energy, vol. 45, no. 43, pp. 22589–22599, Sep. 2020. doi: 10.1016/j.ijhydene.2020.06.168. [Google Scholar] [CrossRef]

15. H. Bahri, A. Harrag, and H. Rezk, “Optimal configuration and techno-economic analysis of hybrid photovoltaic/PEM fuel cell power system,” J. New Mat. Electr. Sys., vol. 25, no. 2, pp. 116–125, Apr. 2022. doi: 10.14447/jnmes.v25i2.a05. [Google Scholar] [CrossRef]

16. S. Rehman et al., “Techno-economic evaluation and improved sizing optimization of green hydrogen production and storage under higher wind penetration in Aqaba Gulf,” J. Energy Storage, vol. 99, 2024, Art. no. 113368. doi: 10.1016/j.est.2024.113368. [Google Scholar] [CrossRef]

17. S. L. Ma, Y. W. Wu, Y. Jiang, Y. X. Li, and G. L. Sha, “Research on two-stage optimization control method for energy storage systems based on multi service attribute utility evaluation,” Energy Sources Part A: Recov. Util. Environ. Eff., vol. 46, no. 1, pp. 3041–3060, Dec. 2024. doi: 10.1080/15567036.2024.2308647. [Google Scholar] [CrossRef]

18. A. Mohammed, “An optimization-based model for a hybrid photovoltaic-hydrogen storage system for agricultural operations in Saudi Arabia,” Processes, vol. 11, no. 5, Apr. 2023, Art. no. 1371. doi: 10.3390/pr11051371. [Google Scholar] [CrossRef]

19. H. Alili and J. Mahmoudimehr, “Techno-economic assessment of integrating hydrogen energy storage technology with hybrid photovoltaic/pumped storage hydropower energy system,” Energ. Convers. Manage., vol. 294, Oct. 2023, Art. no. 117437. doi: 10.1016/j.enconman.2023.117437. [Google Scholar] [CrossRef]

20. N. S. Attemene, K. S. Agbli, S. Fofana, and D. Hissel, “Optimal sizing of a wind, fuel cell, electrolyzer, battery and supercapacitor system for off-grid applications,” Int. J. Hydrogen Energy, vol. 45, no. 8, pp. 5512–5525, Feb. 2020. doi: 10.1016/j.ijhydene.2019.05.212. [Google Scholar] [CrossRef]

21. Z. Li, Y. H. Liu, M. P. Du, Y. H. Cheng, and L. Shi, “Modeling and multi-objective optimization of a stand-alone photovoltaic-wind turbine-hydrogen-battery hybrid energy system based on hysteresis band,” Int. J. Hydrogen Energy, vol. 48, no. 22, pp. 7959–7974, Mar. 2023. doi: 10.1016/j.ijhydene.2022.11.196. [Google Scholar] [CrossRef]

22. B. Shboul et al., “New hybrid photovoltaic-fuel cell system for green hydrogen and power production: Performance optimization assisted with Gaussian process regression method,” Int. J. Hydrogen Energy, vol. 59, pp. 1214–1229, Mar. 2024. doi: 10.1016/j.ijhydene.2024.02.087. [Google Scholar] [CrossRef]

23. I. B. Mansir, F. Musharavati, and A. A. Abubakar, “Using deep learning artificial intelligence and multiobjective optimization in obtaining the optimum ratio of a fuel cell to electrolyzer power in a hydrogen storage system,” Int. J. Energy Res., vol. 46, no. 15, pp. 21281–21292, 2022. doi: 10.1002/er.8281. [Google Scholar] [CrossRef]

24. R. Moltames, E. Assareh, F. Mohammadi Bouri, and B. Azizimehr, “Simulation and optimization of a solar based trigeneration system incorporating PEM electrolyzer and fuel cell,” J. Solar Energy Res., vol. 6, no. 1, pp. 664–677, 2021. doi: 10.22059/jser.2021.296369.1139. [Google Scholar] [CrossRef]

25. A. Cecilia, J. Carroquino, V. Roda, R. Costa-Castelló, and F. Barreras, “Optimal energy management in a standalone microgrid, with photovoltaic generation, short-term storage, and hydrogen production,” Energies, vol. 13, no. 6, 2020, Art. no. 1454. doi: 10.3390/en13061454. [Google Scholar] [CrossRef]

26. G. Wu et al., “Chance-constrained energy-reserve co-optimization scheduling of wind-photovoltaic-hydrogen integrated energy systems,” Int. J. Hydrogen Energy, vol. 48, no. 19, pp. 6892–6905, Mar. 2023. doi: 10.1016/j.ijhydene.2022.03.084. [Google Scholar] [CrossRef]

27. A. S. Menesy et al., “Techno-economic optimization framework of renewable hybrid photovoltaic/wind turbine/fuel cell energy system using artificial rabbits algorithm,” IET Renew. Power Gen., vol. 11, pp. 1–18, Jan. 2024. doi: 10.1049/rpg2.12938. [Google Scholar] [CrossRef]

28. L. Kong, L. Shi, Z. Shi, S. Wang, and G. Cai, “Low-carbon optimal dispatch of electric-hydrogen-heat system in park based on alternating direction method of multipliers,” (in Chinese), Trans. China Electrotech. Soc., vol. 38, no. 11, pp. 2932–2944, 2023. doi: 10.19595/j.cnki.1000-6753.tces.220773. [Google Scholar] [CrossRef]

29. Y. Ren et al., “Modelling and capacity allocation optimization of a combined pumped storage/wind/photovoltaic/hydrogen production system based on the consumption of surplus wind and photovoltaics and reduction of hydrogen production cost,” Energ. Convers. Manage., vol. 296, Nov. 2023, Art. no. 117662. doi: 10.1016/j.enconman.2023.117662. [Google Scholar] [CrossRef]

30. Y. M. Ke, H. Y. Tang, M. Liu, Q. X. Meng, and Y. Xiao, “Optimal sizing for wind-photovoltaic-hydrogen storage integrated energy system under intuitionistic fuzzy environment,” Int. J. Hydrogen Energy, vol. 48, no. 88, pp. 34193–34209, Oct. 2023. doi: 10.1016/j.ijhydene.2023.05.245. [Google Scholar] [CrossRef]

31. F. M. Guo et al., “A planning method for off-grid wind-solar hydrogen storage system based on 8760 hours production simulation,” Power Syst. Technol., vol. 48, no. 5, pp. 2227–2235, May 2024. doi: 10.13335/j.1000-3673.pst.2023.1728. [Google Scholar] [CrossRef]

32. S. L. Ma, Y. X. Li, Y. Jiang, Y. W. Wu, and G. L. Sha, “The multiobjective control based on tolerance optimization in a multienergy system,” Int. Trans. Electr. Energy Syst., vol. 2024, Apr. 2024, Art. no. 9991046. doi: 10.1155/2024/9991046. [Google Scholar] [CrossRef]

33. C. J. Huang, Y. Zong, S. You, and C. Traeholt, “Economic model predictive control for multi-energy system considering hydrogen-thermal-electric dynamics and waste heat recovery of MW-level alkaline electrolyzer,” Energ. Convers. Manage., vol. 265, Aug. 2022, Art. no. 115697. doi: 10.1016/j.enconman.2022.115697. [Google Scholar] [CrossRef]

34. F. Kbidi, C. Damour, D. Grondin, M. Hilairet, and M. Benne, “Multistage power and energy management strategy for hybrid microgrid with photovoltaic production and hydrogen storage,” Appl. Energy, vol. 323, Oct. 2022, Art. no. 119549. doi: 10.1016/j.apenergy.2022.119549. [Google Scholar] [CrossRef]

35. Q. Lin, H. Qi, J. Huang, B. Zhang, Z. Chen and Z. Xiao, “Levelized cost of combined hydrogen production by water electrolysis with alkaline-proton exchange membrane,” Energy Stor. Sci. Technol., vol. 12, no. 11, pp. 3572–3580, 2023. doi: 10.19799/j.cnki.2095-4239.2023.0527. [Google Scholar] [CrossRef]

36. X. Zhang, X. Fan, Z. Wu, and L. Zheng, “Hydrogen energy supply chain cost analysis and suggestions,” Chem. Ind. Eng. Progress., vol. 41, no. 5, pp. 2364–2371, 2022. doi: 10.16085/j.issn.1000-6613.2021-1062. [Google Scholar] [CrossRef]