Multi-Stage Voltage Control Optimization Strategy for Distribution Networks Considering Active-Reactive Co-Regulation of Electric Vehicles

1  Introduction

Distributed renewable energy presents strong uncertainty, and electric vehicle (EV) charging is affected by traveling behavior with randomness. With a high proportion of distributed power and large-scale EV integration to the distribution network, the voltage fluctuation problem in the distribution network is becoming increasingly prominent. When the uncertainties of EV charging and distributed photovoltaic (PV) output are superimposed, the distribution network has to simultaneously address the rapid changes in distributed power output and EV charging power. This problem further exacerbates the voltage fluctuation in the distribution network, and poses a serious challenge to the operational safety and voltage stability of the distribution network [1]. Therefore, the distribution network must fully explore the available voltage control means and propose effective voltage control strategies to reduce the impact of random uncertainty of distributed power sources and EVs, and improve the voltage stability and operational efficiency of the grid [2,3].

With the integration of distributed power sources and EVs, multi voltage control means have been applied in the distribution network [4], including capacitor bank adjusting, distributed power sources, EVs, network reconfiguration, etc. However, their regulation characteristics are different, and the response times and regulation mechanisms are significantly different. How to achieve coordinated control of these heterogeneous voltage controls on the long time scale is challenging and also of great research significance. It is necessary to fully consider the dynamic characteristics and complementary characteristics of various types of voltage regulators, and design an efficient coordinated control strategy to improve the overall operational efficiency of the distribution network while ensuring voltage stability.

The distribution network optimization model covers a large number of structural variables and nonlinear constraints and involves discrete devices such as on-load tap changer (OLTC) and shunt capacitor bank (CB), which have coupled characteristics over multiple periods. Therefore, the voltage optimization problem is essentially a complex spatio-temporally coupled mixed integer nonlinear programming problem. Existing studies have mostly concentrated on traditional optimization algorithms such as particle swarm algorithms [5] and differential evolutionary algorithms [6] in dealing with such challenges, which often face limitations such as high computational complexity and the tendency to fall into locally optimal solutions when dealing with complex distribution network optimization problems. To further improve the efficiency and effectiveness of distribution network voltage control optimization, a series of modern optimization algorithms, such as the flow direction algorithm (FDA) [7], equilibrium optimizer, golden jackal optimizer, stochastic search algorithm, arithmetic optimizer, and African vulture optimization algorithm have received wide attention in recent years for their excellent performance in solving nonlinear and multi-objective optimization problems. These algorithms can efficiently search for the global optimal solution in a complex optimization space by simulating group behavior or physical phenomena in nature, thus providing new ideas and methods for distribution network voltage control optimization.

For the distribution network voltage problem, Reference [8] established a reactive power optimization model for the distribution network and solves the model by particle swarm algorithm. Reference [9] proposed an active-reactive power coordination optimization method for a high proportion of new energy grid-connected scenarios starting from energy storage regulation. Reference [10] designed a novel multi-segment reactive voltage profile for PV inverters in a multi-timescale voltage control framework for distribution network reactive power compensation. Reference [11] performed a hybrid time-scale cooperative reactive power/voltage control of the distribution network taking into account the PV output uncertainty. Reference [12] considered distributed PV, reactive power compensators, and network reconfiguration voltage control methods and used an improved ant colony algorithm for solving to achieve reactive power optimization. Reference [13] proposed the use of conventional reactive power compensation devices in combination with inverters, resulting in a significant increase in the adjustable reactive capacity compared to the remaining capacity of the inverter. Reference [14] used a multi-objective framework to provide a feasible scope for coupling power and transport networks. However, the further increase in the proportion of distributed power sources, a short period may be a large power drop, only through the reactive resources in the distribution network is difficult to meet the demand for grid regulation, and the existing reactive resources cannot satisfy the requirements of the case without increasing new investment, and how reactive resources and active voltage control resources co-control lack of in-depth exploration. Meanwhile, the multi-objective optimization framework of the above studies focuses more on the complementarity of multiple regulators on the time scale and lacks spatial synergy.

Regarding the use of EV regulation capability to regulate distribution network voltage, Reference [15] and others used the Monte Carlo method to simulate EV charging demand, transform the distribution network voltage control problem into a Markov game, and achieve distribution network reactive voltage coordinated optimization based on a two-stage voltage control method. Reference [16] designed a day-ahead and real-time coordinated optimization model for EV charging stations connected to the distribution network and established a layered power optimization model for the distribution network to achieve coordinated optimization of reactive voltage in the distribution network. Reference [17] proposed a coordinated active-reactive power optimization method under dual time scales for the power and voltage fluctuation problem of EV stations accessing the distribution network and constructed a Markov decision model based on the switchable capacitor blocking position to achieve long-timescale optimization. Reference [18] achieved network loss reduction by optimizing the active power of EVs in each period. Reference [19] proposed an intelligent approach with a parameter-sharing framework to effectively solve the problem of coordinated power control of EVs in distribution networks. Reference [20] used the deep deterministic policy gradient (DDPG) algorithm and exploited the training capabilities of deep neural network (DNN), i.e., Actor neural network and Critic neural network, to evaluate the effectiveness of the proposed deep learning scheme from a systematic point of view and its performance. However, the above research focuses on the active power regulation of EVs, lacks refined analysis of reactive power regulation characteristics during EV charging, fails to achieve voltage control support for distribution networks from the perspective of EV active-reactive synergistic control, and fails to deeply analyze the synergistic control of EV active-reactive regulation characteristics and other voltage control resources. And does not adequately consider the charging needs and uncertainties of electric vehicles, ignoring user characteristics. At the same time, the optimization solution algorithms of the existing methods have high computational complexity and easily fall into local optimal solutions when dealing with complex multi-level and multi-decision variable optimization problems, which can easily lead to poor control effects in different time scales.

To solve the problems in the above methods, a multilevel linkage voltage control optimization strategy for distribution networks considering the active-reactive regulation characteristics of electric vehicles is proposed. Firstly, a capacitor bank reactive power compensation regulation model, a distributed photovoltaic active-reactive power regulation model, and a network reconfiguration voltage control model are established. Secondly, the four-quadrant operating characteristics of EV chargers are considered to establish a model of the external characteristics of EV voltage control, and then a multi-objective optimization model of the distribution network is constructed by considering the constraints of EVs and distributed photovoltaic active-reactive power regulation. The multi-objective optimization model is constructed to consider the active-reactive co-regulation of EVs. The model takes into account the minimization of voltage deviation and the reduction of network loss and realizes the double regulation of active and reactive power in the charging process of EVs, to improve the stability of the grid voltage and the operation efficiency. Then, by combining the multi-timescale characteristics of the different regulating means and the impact on the user’s demand for energy and new energy consumption, the optimization strategy of regulating the voltage at the four levels of the distribution network is proposed. Finally, for the complex multi-level and multi-decision variable optimization problem, this paper adopts an improved fruit fly algorithm for solving the problem to achieve multi-level linkage collaborative voltage control optimization under power fluctuation in the distribution network.

Section 2 specifically introduces four types of voltage regulators, namely capacitor bank, distributed photovoltaic, electric vehicle, and network reconfiguration, and analyses in detail their operational characteristics and roles in voltage control. Section 3 proposes a multi-objective optimization model and a four-level linkage coordinated optimization strategy of the distribution network oriented to the complementarity of various types of regulators with multiple time scales. Section 4 introduces the use of the improved Drosophila algorithm to solve the multi-objective optimization function. Finally, Sections 5 and 6 discuss the experimental results and conclusions, respectively.

2  Operational Characteristics of Voltage Control Resources in Distribution Networks

The voltage fluctuation is caused by the active and reactive power variations caused by distributed power fluctuations, EV access, and load variations in the distribution network [21]. This voltage fluctuation can be given by Eq. (1).

ΔU=QcjSd+12(PcjSd)2(1)

where Pcj and Qcj represent the active power and reactive power provided by the load during load fluctuations in the distribution network; and Sd is the short-circuit capacity of the busbar.

An increase in power variations results in an increase in voltage fluctuations ΔU. Therefore, in this case, the voltage-adjustable resources in the distribution network are particularly important. In order to cope with the challenges posed by load variations, it is necessary to make full use of distribution network voltage control resources such as reactive power compensation equipment, distributed PVs, and EVs.

2.1 Reactive Power Compensation Equipment

A shunt capacitor bank (super-capacitor, SC) can compensate for the reactive power of inductive loads of a power system, improve the power factor, and reduce the losses. The reactive power model of SC can be given by Eq. (2).

Qi,SCt=Ni,SCtQi,SC(2)

where Ni,SCt represents the number of switched capacitor (SC) groups connected to node i at time t; Qi,SC represents the reactive power compensation per single SC group connected to node i; and Qi,SCt represents the reactive power compensation of SCs connected to node i at time t.

2.2 Voltage Control Characteristics of Distributed PVs

Distributed PV voltage reactive power regulation is usually controlled by reactive power regulation, and then active power is regulated to satisfy voltage control requirements when voltage control requirements cannot be met. The operating region of distributed PV power is shown in Fig. 1 [22].

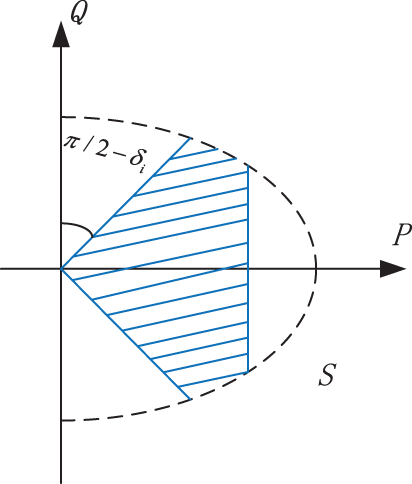
Figure 1: PV operating power range

The PV system is constrained by the maximum apparent power and power factor during operation, which can be given by Eq. (3).

{PPV,i2(t)+QPV,i2(t)≤(SPV,i)2−PPV,i(t)tan⁡δPV,i≤QPV,i(t)≤PPV,i(t)tan⁡δPV,i(3)

where PPV,i(t) and QPV,i(t) respectively represent the active and reactive power output of the PV at node i at time t; SPV,i represents the distributed PV capacity at node i, and δPV,i δPV,i is the allowable power factor angle at node i.

2.3 Voltage Control Characteristics of EVs

The EV is connected to a bi-directional charger for active and reactive power interaction with the grid. The capacity curve of the charger is shown in Fig. 2. Reference [23] is the active power consumed by the EV for charging, and is the reactive power absorbed or emitted by the charger to the grid. The figure shows the different operating states of the charger through four quadrants: the first quadrant is the charging state, where both active and reactive power are positive. The second quadrant is the charger absorbing active power but still providing reactive power. The third quadrant is the discharging state, where both are negative, and the fourth quadrant is the braking energy recovery, where the active power is positive but the reactive power is negative.

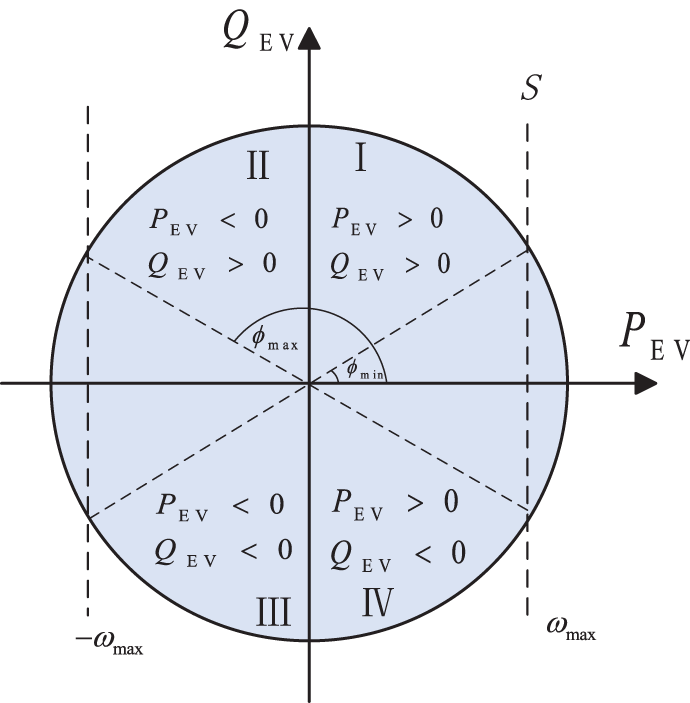
Figure 2: Charger operating characteristics

During charging, the rated power of the charger depends on the state of the EV and the charging port, so the actual charging power may be lower than the rated value. Among them, ωmax represents the maximum power factor of the charger, ϕmin and ϕmax represent the minimum and maximum power factor angles of the charger.

The active and reactive power for charging is as defined as PEV and QEV.

{PEV=Scos⁡ϕQEV=Ssin⁡ϕ(4)

where S represents the capacity of the charger; and ϕ is the power factor angle.

The rated capacity of the charger is certain, and when it interacts with the grid’s active and reactive power in both directions, the increase or decrease of active and reactive power is complementary. Therefore, it is necessary for the charger to reduce part of the active power to compensate for the reactive power.

PEV=S2−QEV2(5)

Ve=Vs−(S2−QEV2+Pe)×R+(QEV+Qe)×XVs(6)

where s is the starting node; Vs is the starting voltage; R and X are the equivalent resistance and equivalent inductance in the distribution network line, respectively; Ve is the terminal voltage, and Pe and Qe are respectively the active and reactive power of the terminal conventional load.

Ve=Z−S2−QEV2×R+QEV×XVs(7)

where Z=Vs−(Pe×R+Qe×X)/Vs.

When the charger operates in quadrant I, the derivation of Eq. (7) yields.

dVedQEV=−−QEV×RS2−QEV2+XVs(8)

When the charger is in inductive mode and maintains Vs constant, the relationship between the terminal voltage Ve and the reactive power QEV1 is shown in Fig. 3, and it is not monotonic. In the figure, Ve0 represents the terminal voltage when the charger is not performing reactive compensation. When QEV is below QEV1, its derivative is negative, and increasing inductive reactive power will further reduce the voltage. When QEV exceeds QEV1, its derivative is positive, and the direction of voltage change is opposite to that when QEV is below QEV1. At point QEV1, the voltage control effect is optimal, referred to as the optimal operating point, and the terminal voltage at this time is Ve1.

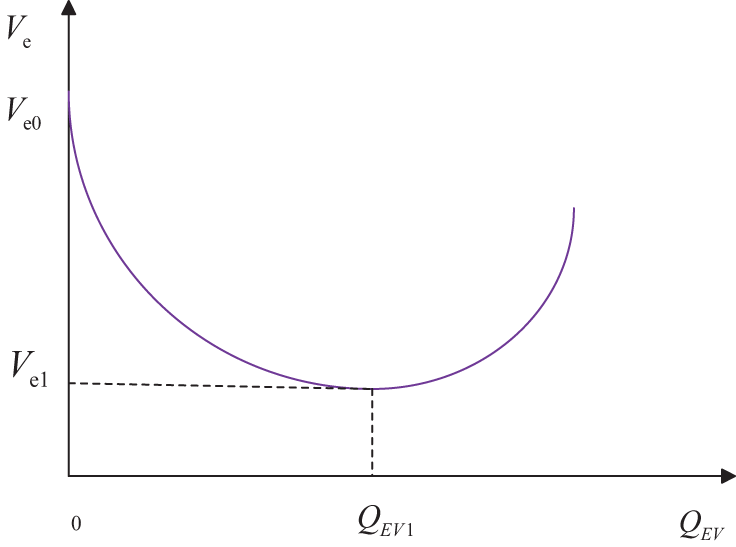
Figure 3: Inductive mode of EV charge

When the charger operates in quadrant IV, it charges the EV in capacitive mode. According to Eq. (8), its derivative is less than zero, so the terminal voltage Ve and reactive power QEV have a monotonically decreasing relationship, as shown in Fig. 4. When QEV=−QEV max , the regulation effect is optimal, with the terminal voltage being Ve2. When the node voltage is low and needs to be increased, reactive power should be injected into the system. At this time, the charger should be adjusted to capacitive mode to send reactive power to the grid.

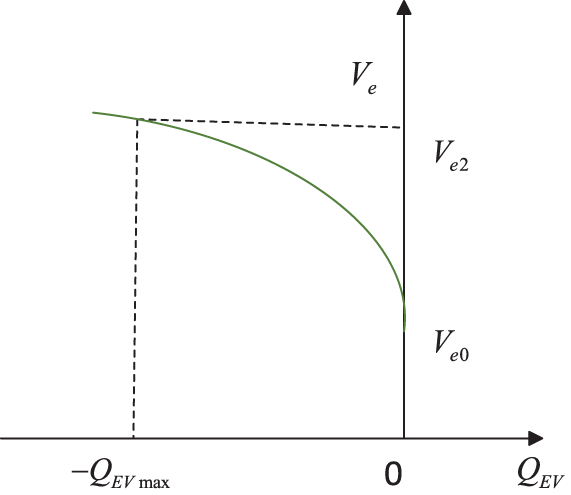
Figure 4: Capacitive mode of EV charger

EV charging is constrained by both the owner’s charging goals and the operational limits of the charger.

2.3.1 Charging Objectives for Vehicle Owners

It is difficult to satisfy the target state of charge (SOC) requirements of each EV user during user participation in the regulation process. Therefore, the minimum SOC value Sd after user participation is given by Eq. (9).

Sd=Sh+MdMf(9)

where Sh is the charge margin, valued at 0.3 [24]; and Md and Mf are the driving range and cruising range that need to be met with a single charge, respectively.

After charging is completed, the user’s SOC value Sdep must satisfy the following constraints as given by Eq. (10).

Sd≤Sdep≤SH(10)

where SH is the upper limit of the electric quantity.

The charging time of EVs to meet user needs must satisfy the following constraints as given by Eq. (11).

Tstart ⩽Tp⩽Tdep (11)

where Tp represents the current time of the p-th controllable EV; and Tstart  and Tdep  represent the start charging time and the departure time.

2.3.2 Constraints on the Operational Characteristics of the Charger

The power factor angle must meet the operational characteristic constraints of the charger, which is given by Eq. (12).

{ϕmin<ϕ<ϕmax−ϕmax<ϕ<−ϕmin(12)

where ϕmin and ϕmax represent the minimum and maximum power factor angles of the charger.

2.4 Network Reconstruction

Network reconfiguration can effectively balance loads, eliminate overload conditions, improve the quality of power supply, and increase the security of power supply. In addition, by optimizing switching combinations, the operation of the power system can be optimized, the distribution of active and reactive power can be adjusted and voltage control can be achieved, which can reduce operating losses. When performing network reconfiguration, it is necessary to ensure the connectivity and radiality requirements of the distribution network to maintain the stability and reliability of the system [25].

The network reconfiguration schematic is shown in Fig. 5.

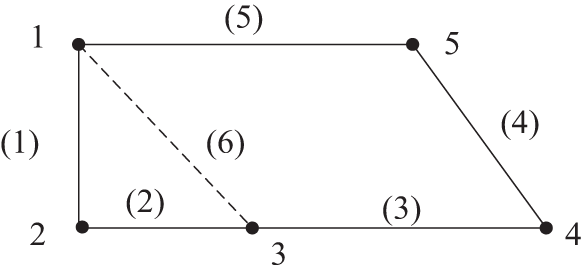
Figure 5: Network reconfiguration schematic

3  Multi-Level Linkage Model

Load variations cause voltage fluctuations, which become more significant as the uncertainty of EV loads and distributed light sources increases. To cope with this challenge, four voltage control tools, namely distributed PV power generation, reactive power compensation equipment, EV chargers, and network reconfiguration, need to be utilized in an integrated manner and their coupling characteristics on long time scales need to be fully exploited by working in conjunction with each other. The combined objective of minimizing voltage deviation and network loss at distribution network nodes is thus transformed into a multi-objective long-timescale combinatorial optimization problem.

3.1 Optimization Objectives

The fluctuation of distribution network node voltage affects the charging of EVs and the penetration rate of access to the distribution network, and reasonable control of the distribution network node voltage can improve the operating economy of the distribution network and reduce the operating deviation [26,27].

The objective function Gdb(x) for minimizing the voltage deviation at distribution network nodes is given by Eq. (13).

Gdb(x)=min∑i=1N|Vio−VirVimax−Vimin|(13)

where N represents the number of nodes in the distribution network; and Vimax, Vimin, Vir, Vio respectively represent the maximum, minimum, rated, and actual operating voltage values of node i.

Construct the objective function Gloss(x) for minimizing active power loss in the distribution network, given by Eq. (14).

Gloss(x)=min∑d=1Ndhd(i,j)(Vi2+Vj2−2ViVjcos⁡ϑij)(14)

where Nd represents the number of distribution network lines; hd(i,j) represents the conductance value between i and j; Vi and Vi represent the voltage values at nodes i and j; d represents the number of lines between nodes i and j; and ϑij represents the voltage phase difference between the two nodes.

In this paper, in the multi-level linkage co-optimization of the distribution network, network loss and voltage deviation are used as the comprehensive objective function of each level. The multi-objective optimization function G is given by Eq. (15).

G=min{Gloss(x),Gdb(x)}(15)

where Gdb(x) and Gloss(x) are the objective function for minimizing voltage deviation at distribution network nodes and the objective function for minimizing active losses in the distribution network, respectively.

3.2 Optimal Strategy for Coordinated Control of Four-Level Power Distribution Network

In the actual operation of the distribution network, the reactive power resources in the distribution network can be used to regulate the voltage deviation, and when the reactive regulating resources cannot satisfy the requirements of voltage stability, it is further necessary to use the way of changing the current distribution and active power regulation for voltage control [28–30].

The current distribution network is affected by distributed new energy and charging loads, and the voltage fluctuation caused by strong power volatility is frequent, it is difficult to fully satisfy the demand for voltage control only by relying on a single means of voltage control, and this paper considers four means of voltage control, such as capacitor bank switching, reactive power regulation of electric vehicles and photovoltaic inverters, network reconfiguration, and active power regulation of EVs and PV inverters.

The four-level linkage control strategy aims to ensure the effective synergy of voltage control resources over long time scales. The strategy performs a comprehensive four-level optimization based on the qualification of voltage levels by implementing a tidal current calculation covering the first, second, and third levels of control. The specific coordination process is shown in Fig. 6. In Fig. 6, the importance of the capacitor bank as a first level of regulation is first highlighted, which is prioritized for voltage control due to its low cost, despite its limited number of cuts. However, in the case of large voltage fluctuations due to the superposition of new energy sources and charging behavior uncertainties, the capacitor bank may not be able to meet the voltage control requirements. In this case, other means of voltage control in the distribution network need to be invoked. Considering that PV inverters and EVs have reactive power response capability, they can provide reactive power support to the distribution network through inverters and chargers without affecting PV active output and user charging. If the above two means still cannot meet the voltage control requirements, it is necessary to consider changing the active and reactive power distribution of the distribution network utilizing network reconfiguration to reduce the voltage deviation at the nodes with more serious voltage problems. Finally, if the above three means still cannot satisfy the voltage control requirements, it is necessary to regulate the active power, using the active regulation of PV inverters and EVs as the final means of voltage control. This is also to minimize the impact of the regulation control on the PV active output and user charging.

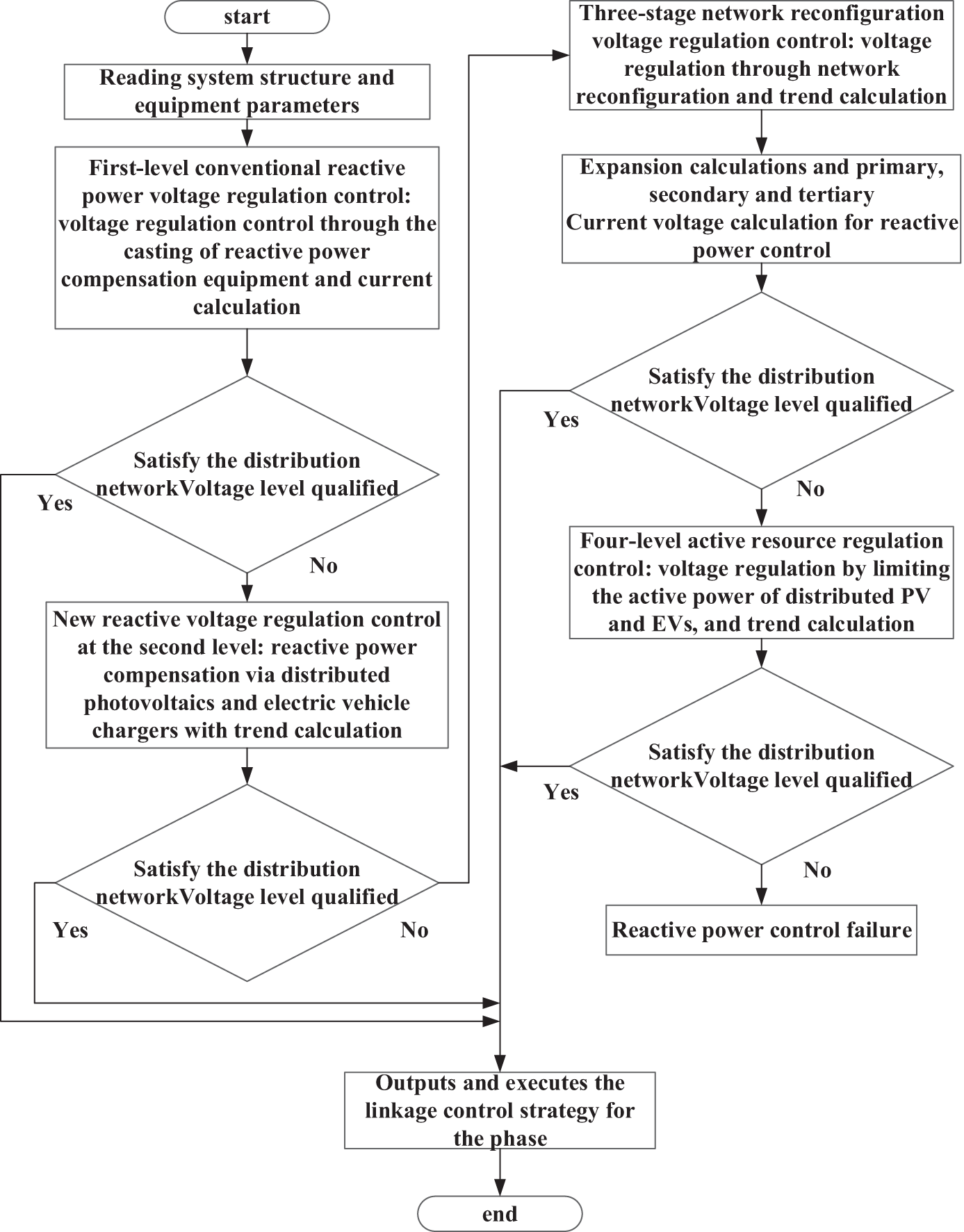
Figure 6: Four-level linkage control process of the distribution network

Therefore, considering the regulation characteristics of the four voltage control means, the specifics of the four-level linkage coordination and optimization strategy for distribution networks proposed in this paper are as follows:

First-level conventional reactive power voltage control control: Capacitors for reactive power compensation. Capacitor banks are fast-responding and low-cost, and can quickly regulate the voltage to maintain system stability. To reduce network losses and voltage deviations, reactive power is regulated by connecting capacitors in parallel, so that the voltage can meet the system demand.

Second-level new reactive power voltage control control: Reactive power compensation using distributed PVs and EVs. When shunt capacitors cannot satisfy the requirements of reactive voltage control for large load fluctuations, the generation power and users’ charging demand are not affected by reactive power regulation. By regulating the reactive power output of PV inverters and EV chargers, reactive power regulation of the entire grid is realized, thus reducing network losses and voltage deviations.

Third-level network reconfiguration voltage control control: Network reconfiguration. When the required voltage control cannot be achieved through the first two strategies in the distribution network system, network reconfiguration is carried out. Network reconfiguration can adjust the topology of the distribution network to achieve voltage control, satisfying the system’s voltage stability and reliability requirements.

Fourth-level active resource voltage control: Limiting active power of PVs and EVs. When the first three types of control strategies cannot satisfy system requirements, limiting the active power of PVs and EVs is used as a last resort. This strategy aims to ensure system voltage stability and reliability by limiting the active power of PVs and EVs.

In summary, the four-level linkage control strategy ensures that voltage control resources coordinate over long time scales. It conducts power flow calculations that account for primary, secondary, and tertiary control, and performs comprehensive optimization based on the voltage level qualifications. The specific coordination process is shown in Fig. 6.

3.3 Constraints

3.3.1 Operational Constraints of EVs

−PEV,i,krel⩽PEV,i,k⩽PEV,i,krel(16)

QEV,i,kdown⩽QEV,i,k⩽QEV,i,kup(17)

(PEV,i,k)2+(QEV,i,k)2⩽S(18)

SOCst≤SOCi,k≤SOCdep(19)

where PEV,i,k represents the active power of the k-th EV participating at control node i; PEV,i,krel is the rated charging power the k-th EV participating at control node i; QEV,i,k, QEV,i,kdown, QEV,i,kup are the reactive power and its limits of the k-th EV participating at control node i; S is the rated capacity; SOCi,k represents the SOC of the k-th EV participating in the regulation at node i; SOCst represents the initial SOC value of the EV at the start of charging; and SOCdep represents the target SOC value at the end of charging.

3.3.2 Power Flow Constraints in the Distribution Network

{Pi=Vi∑j∈vVj(Hijcos⁡θij+Bijsin⁡θij)Qi=Vi∑j∈vVj(Hijcos⁡θij−Bijsin⁡θij)(20)

where Qi and Pi represent the reactive and active power values at node i of the distribution network, respectively; Hij represents the conductance value between nodes i and j of the distribution network; and Bij represents the susceptance value between nodes i and j of the distribution network.

The node voltage Vo is an important constraint in the distribution network optimization problem, which is given by Eq. (21).

Vomin≤Vo≤Vomax,o∈[0,N](21)

where Vomin and Vomax represent the upper and lower limits of the node voltage.

Taking the transmission capacity of the distribution network branch as a constraint condition, which is given by Eq. (22).

Ii≤Iimax,i∈[0,N](22)

where Ii represents the current flowing through the branch; and i represents the maximum current value allowed by the branch of the circuit i.

3.3.3 Constraints of Distributed PVs

{0≤PPVi≤PPVi,maxPPVi2+QPVi2≤SPVi2−QPVi,min≤QPVi≤QPVi,max(23)

where PPVi and QPVi represent the actual active and reactive power outputs of the distributed PV system connected to node i, respectively; PPVi,max represents the maximum active power output of the distributed PV system at node i; and QPVi,max represents the maximum reactive power output of the distributed PV system at node i.

3.3.4 Network Reconstruction Constraints

The number of lines connected to the distribution network is equal to the total number of nodes minus the number of root nodes.

∑ij∈ΩLλij,t=Nj−∑j∈ΩJγj,t(24)

where λij,t is a binary variable representing the state of power line ij at time t, and if λij,t=1, the line is undamaged and closed, otherwise, the line is damaged or open; Nj is the total number of nodes in the distribution network; ΩL and ΩJ are the sets of lines in the distribution network; γj,t indicates whether node j is a root node, and if γj,t=1, the node is a root node, otherwise, it is not a root node.

The reconfigured network topology g0 of the distribution network is taken as a constraint, which is given by Eq. (25).

g0∈G0(25)

where G0 represents the set of distribution network topologies.

3.3.5 Constraints of Reactive Power Compensation Equipment

{∑t=1T(Ni,SCt,++Ni,SCt,−)≤Di,SCmax0≤Ni,SCt≤Ni,SCmax,Ni,SCt∈ int(26)

where Ni,SCt,+ and Ni,SCt,− represent the numbers of compensation groups for the increase and decrease of SC at node i at time t, respectively, both being non-negative; Di,SCmax is the upper limit of SC operations within a scheduling period T; and Ni,SCmax is the maximum number of SC groups connected to node i.

In this article, the comprehensive objective function at each level is to minimize network losses and voltage deviations, the optimization constraints for the first level of conventional reactive voltage control are defined by Eq. (26), the optimization constraints for the second level of new reactive voltage control are defined by Eqs. (16)–(19) and Eq. (23), the optimization constraints for the third level of network reconfiguration voltage control are defined by Eqs. (24) and (25), the optimization constraints for the fourth level of active resource voltage control are defined by Eqs. (16)–(19) and Eq. (23).

4  Improved Fruit Fly Algorithm

Fruit fly optimization algorithm is a population-intelligent global optimization technique, which simulates the behavior of fruit flies during foraging, searching, and optimizing through olfaction and vision. The main steps include: initializing the position of the fruit fly population, randomly searching for food sources through olfaction, searching for the global optimal position using vision, evaluating and updating the fitness values of individuals, and iterating repeatedly until the termination conditions are met. Although the basic fruit fly optimization algorithm is simple and easy to use, it may converge prematurely or fall into a local optimal solution when facing complex optimization problems.

In this paper, we propose an improved fruit fly algorithm, which takes the classical fruit fly optimization algorithm as the main framework and carries out various optimizations based on it. By transforming the two-dimensional coordinate representation of the individual into one-dimensional coordinates, and obtaining the fitness function for evaluating the strengths of the individual fruit flies based on the distance f from the fruit fly’s position, the complexity of the operation can be reduced. At the same time, we introduce a decreasing factor of the search radius in the iterative search for the optimal. The specific steps are as follows:

Initialize the parameters required by the algorithm.

The search operation is carried out for an initial fruit fly population of size psize1. The position equation for fruit fly individual f is given by Eq. (27).

f=fa+R×rand(⋅)(27)

where rand(⋅) represents the random number between [−1,1]; R represents the search radius; and fa represents the initial position of the fruit fly.

The equation for calculating the concentration fbest of the fruit fly’s position odor is given by Eq. (28).

So=K(f)(28)

where K represents the fitness function.

Identify the individual with the highest concentration of the scent and record its position coordinates fbest. Subsequently, set this optimal position as the starting point for the search of the fruit fly group in the next iteration, guiding the group to explore more promising areas.

Based on the fruit fly positions obtained in the previous step, continue the iterative optimization process using the fruit fly population with a scale of psize2.

Introducing the search radius decay factor ϕ, the equation for the individual fruit fly’s position fo is given by Eq. (29).

fo=fbest+R×rand(⋅)×ϕ(29)

The equation for calculating the position and odor concentration of individual fruit flies So is given by Eq. (30).

So=K(fo)(30)

Search for and record the precise location of fruit flies where the concentration of flavor reaches its peak fbest′, and then use this information to guide other fruit flies towards that location.

Repeat Eqs. (29) and (30) until the maximum iteration requirement is satisfied and the optimal Drosophila individual is obtained, i.e., the optimal solution is found.

5  Case Study Analysis

A modified IEEE 33-node distribution system is used for simulation and analysis. As shown in Fig. 7, the system consists of 33 network nodes and 32 branch circuits with five operable contact lines (switches numbered 6–21(34), 8–15(35), 13–23(36), and 18–33(37)). Distributed PV generation equipment with a capacity of 1200 kW is provided at nodes 12 and 29, setting a total maximum active output of 960 kW with an adjustable power factor range of −0.9 to 0.9. All branch circuits are equipped with sectional switches. The total load of the system is set to 5920 kW and 2320 kvar, and the EV charging station is connected to node 11 and node 19, equipped with 10 sets of chargers with a power of 120 kW, a maximum power factor of 0.95, and a battery capacity of 100 kWh for EVs. In addition, shunt capacitor compensation devices are equipped at node 6, node 13, and node 25, with 10 sets of capacitors for each device. The device has 10 sets of capacitors with a compensation capacity of 500 kvar. The fluctuation curve of the load and the output curve of distributed PV in this network are analysed as shown in Fig. 8. As shown in Fig. 8, the PV output gradually increases from early morning to late afternoon and then weakens after peaking in the late afternoon. The load curve, on the other hand, shows a trend of increasing during the day and decreasing at night, with the peak hours concentrated in the daytime, especially in the late afternoon. The two highly overlap in the 10:00 to 15:00 time period, indicating that power supply and demand are tight during this time.

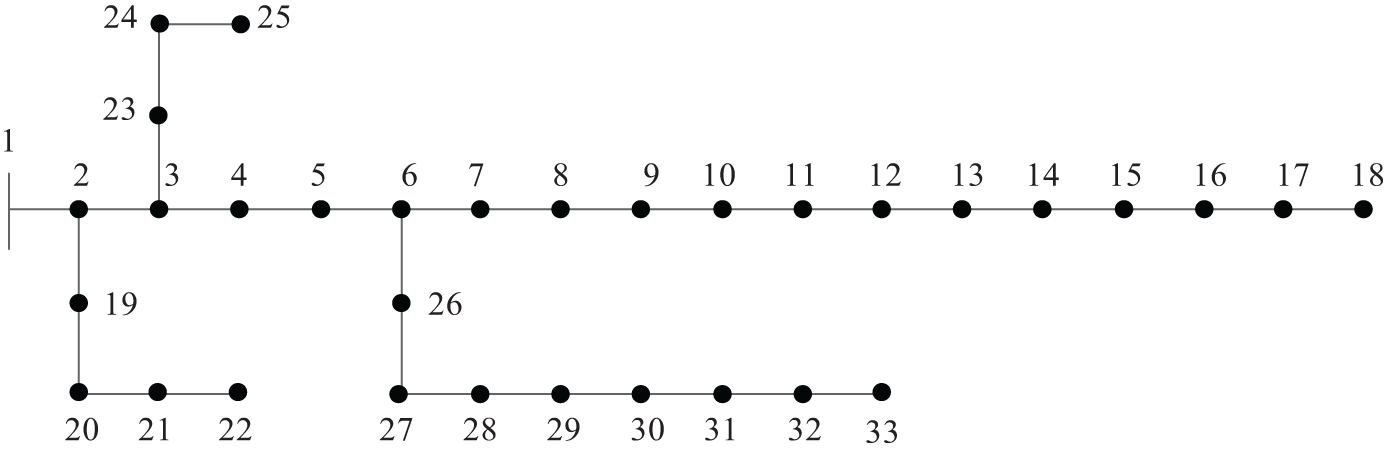
Figure 7: IEEE 33 power distribution system

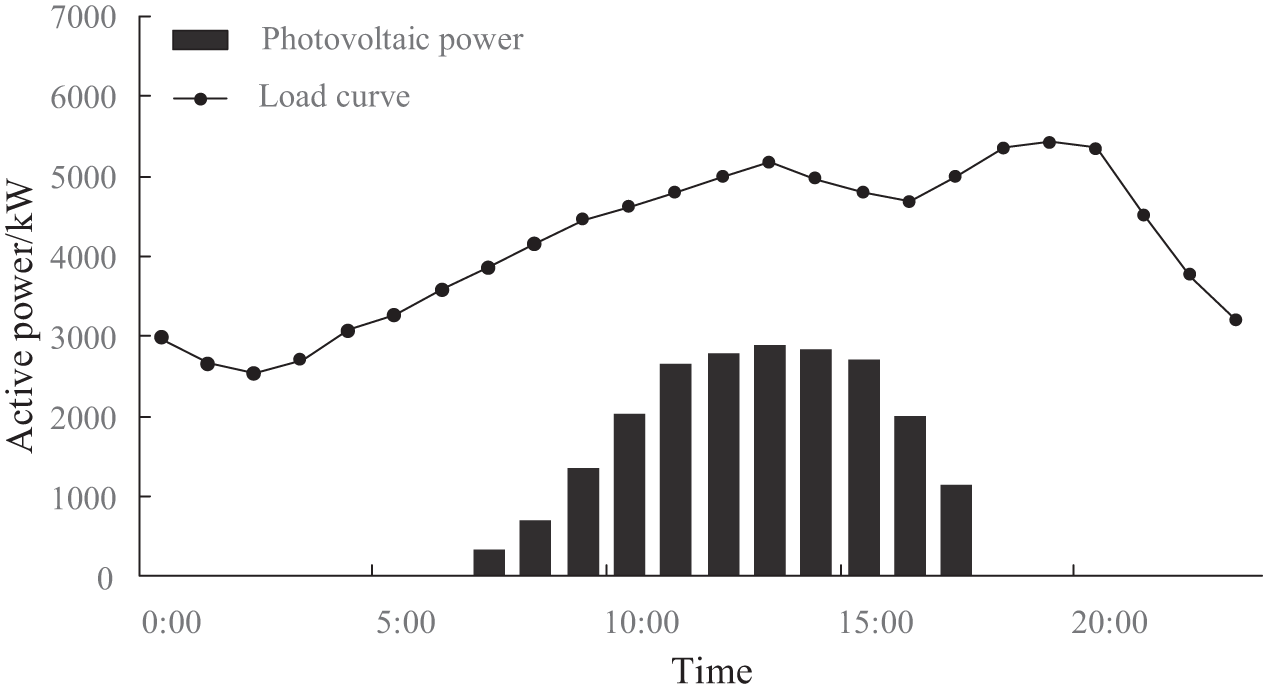
Figure 8: Daily PV power and load

A total of three simulation scenarios are set up for evaluation and analysis.

Scenario 1: Switching of shunt capacitors alone;

Scenario 2: Optimization by integrated linkage coordination of the first, second, and third levels;

Scenario 3: Optimization strategy by four-level linkage coordination.

Firstly, 14:00 is selected for linkage coordination optimization analysis, and the simulation results are shown in Table 1 and Fig. 9.

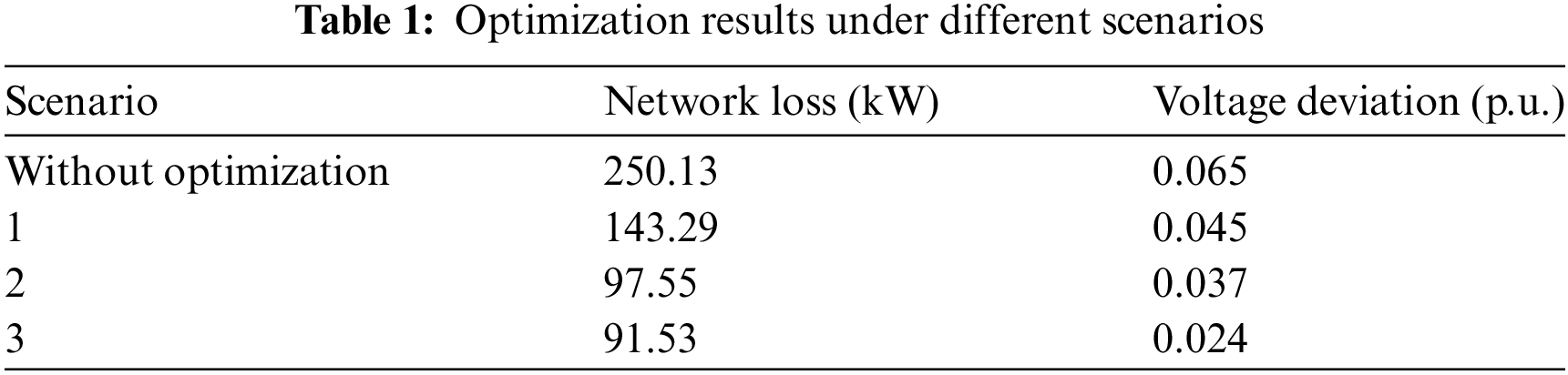
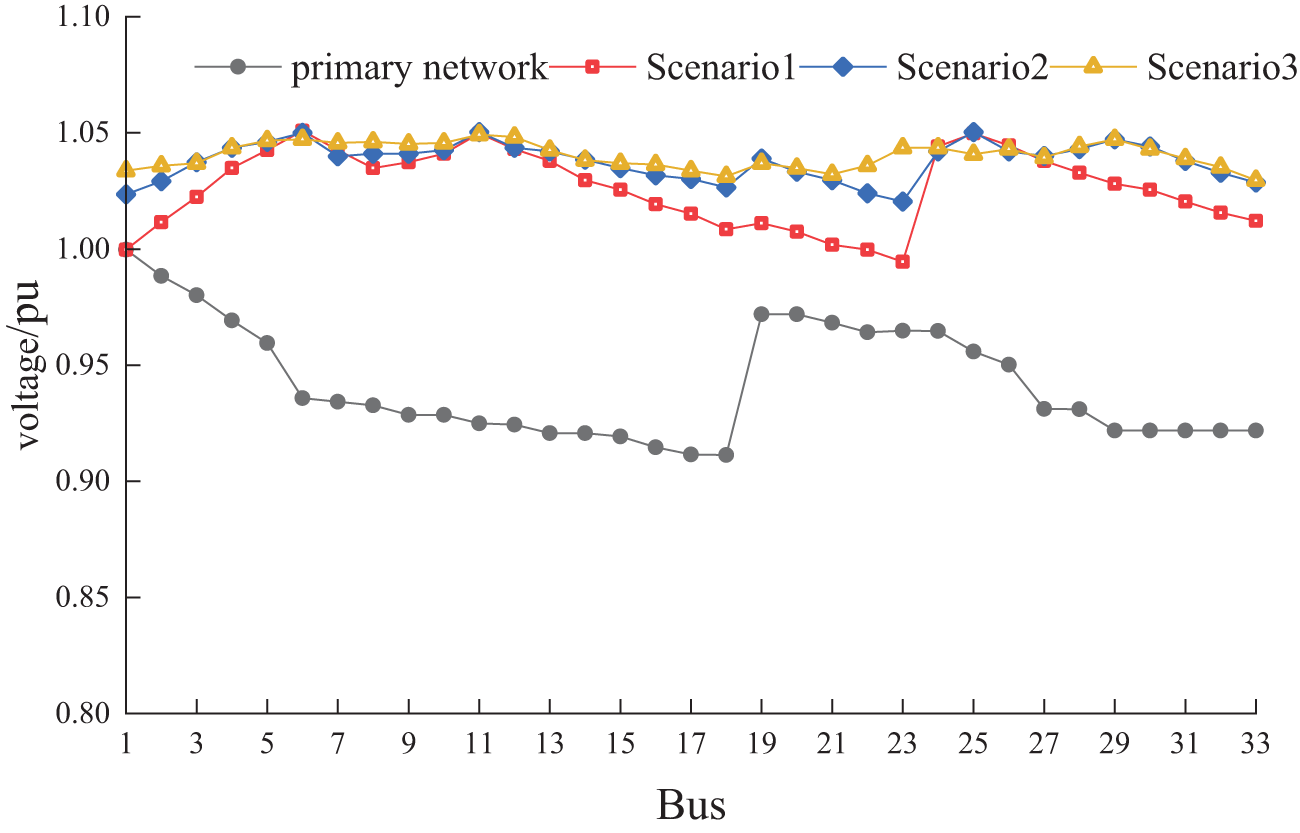
Figure 9: The distribution of system voltage at 14:00 across three scenarios

The data in Table 1 shows the significant optimization effect of different optimization strategies on the grid performance. In the no-optimization condition, the system net loss is as high as 250.13 kW and the voltage deviation reaches 0.065 p.u., showing a large operational burden and voltage instability. In Scenario 1, a 42.7% reduction in network loss to 143.29 kW and an improvement in voltage deviation to 0.045 p.u. are achieved by regulating the voltage with shunt capacitors only, when the first three levels of the optimization strategy introduced in Scenario 2 further cuts the network loss to 97.55 kW, a reduction of 61%, and the voltage deviation is scaled down to 0.037 p.u., which significantly improves the network economy and stability. However, in Scenario 3, using the four-level linkage coordinated optimization proposed in this paper, the fourth-level system reduces the network loss value from the initial 250.13 to 91.53 kW by limiting the active power of EVs and distributed PVs, which is reduced by 63.4% comparing with the no-optimization scenario, meanwhile, the voltage deviation is reduced to 0.024 p.u., which strengthens the reliability of the system, and meets the requirements of the grid’s stable operation. Operation requirements. The results show that the four-level linkage regulation strategy proposed in this paper effectively improves the voltage control effect of the grid and reduces the operating losses of the distribution network.

The voltage distribution of the system in three scenarios is recorded as shown in Fig. 9.

As shown in Fig. 9, it is demonstrated that in Scenario 3, the voltage fluctuation of the distribution network is significantly improved and reduced to a smooth state by implementing the four-level linkage coordination optimization strategy. The voltage fluctuation control performance in Scenario 3 is much better compared to the use of shunt capacitor casting and switching alone in Scenario 1, as well as the integrated one-, two-, and three-level linkage coordinated optimization in Scenario 2. Specifically, the fluctuation range of voltage values is significantly reduced under Scenario 3, and at node 15, the voltage fluctuation is reduced from ±5% in Scenario 1 to within ±1% in Scenario 3, showing the superiority of the four-stage linkage strategy in voltage stability control. This shows that through the four-level linkage control, the distribution network can better cope with various load variations and maintain voltage stability, thus improving the overall operation efficiency and power supply quality of the power system.

To further validate the advancement and advantages of the strategy proposed in this paper, a full-day optimization simulation is carried out. The network reconfiguration results for Scenario 3 are shown in Table 2. The voltage variation at the end of the line (node 18) is shown in Fig. 10.

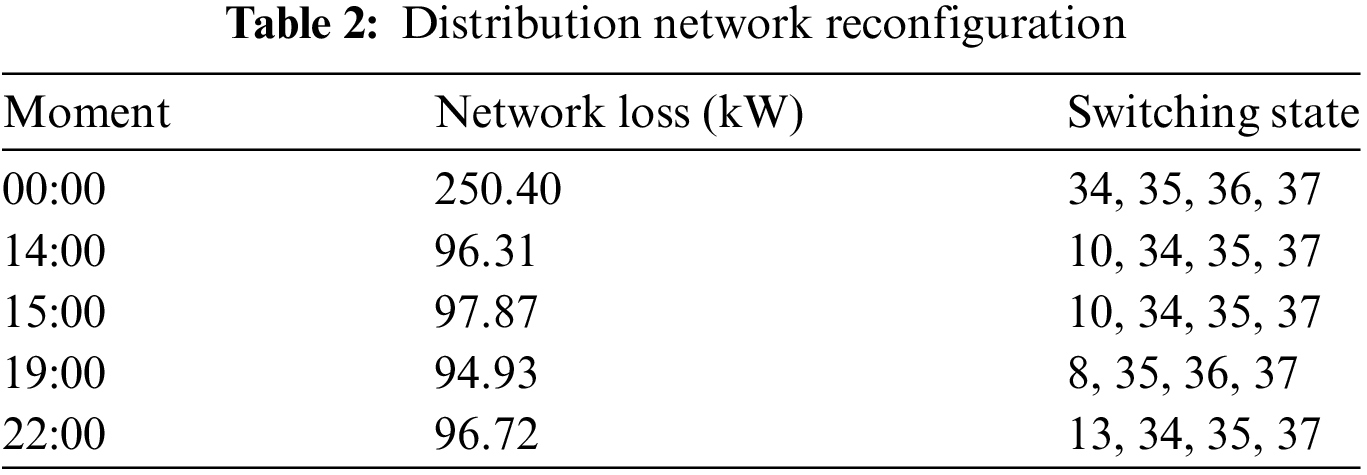
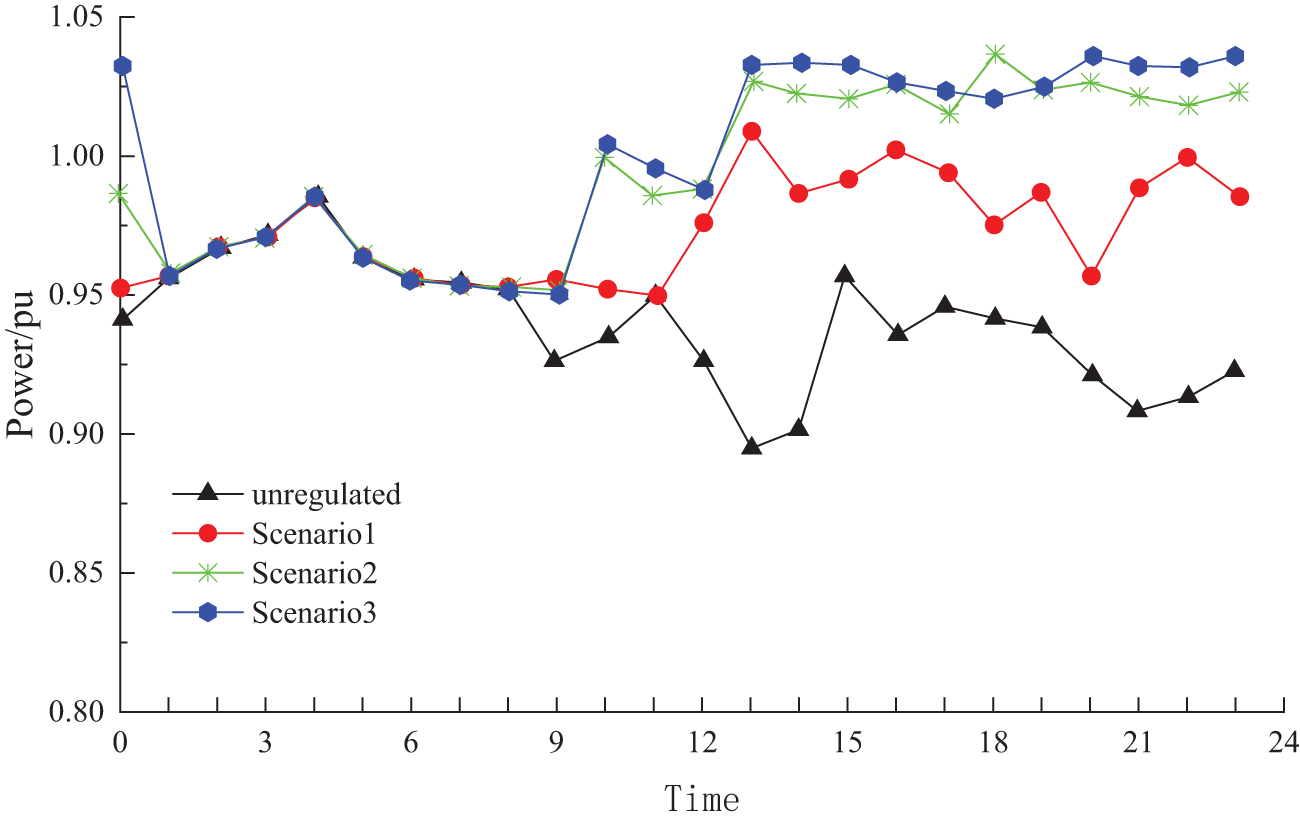
Figure 10: Voltage distribution at node 18

As shown in Table 2, network reconfiguration was performed at 14:00, 15:00, 19:00, and 22:00. Meanwhile, the data in the table indicate that the strategy proposed in this paper can significantly reduce system network losses and improve the economic efficiency of the power grid.

As shown in Fig. 10, the significant effects of different voltage control schemes on the voltage at the end of the line are shown. In Scenario 1, relying on the capacitor bank alone to regulate the voltage achieves an initial improvement, but the voltage slips below 0.95 p.u. several times, indicating that its regulation capability is limited and it is difficult to meet the stability criteria. In contrast, both Scenario 2 and Scenario 3 show more positive voltage improvement, with Scenario 3 being particularly outstanding. The voltage in Scenario 3 is not only stable above 0.98 p.u., but also has a very small range of fluctuation, which is significantly better compared to Scenario 2, where the voltage level is similar but the fluctuation is larger. This low-fluctuation and high-stability voltage characteristic is crucial for enhancing the overall stability and reliability of the distribution network and is a preferred solution for improving the quality of grid operation.

Fig. 11 shows the active power and reactive power situation of the charging station connected to node 11 over 96 time periods within a day.

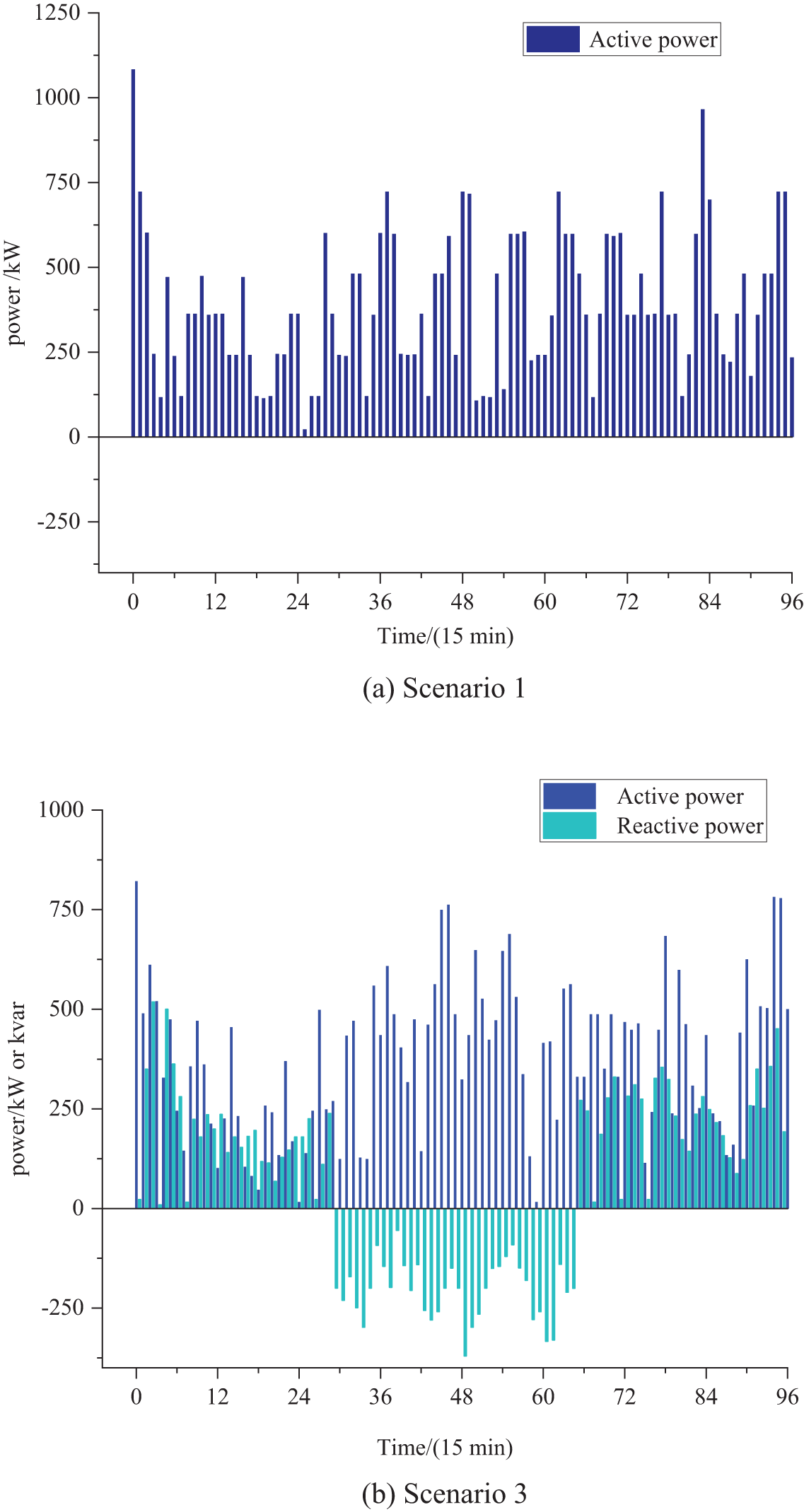
Figure 11: Active and reactive power of the charging station at node 11 across different scenarios

In Scenario 1, the charging station acts as a load consuming active power from the grid. In Scenario 3, the voltage is regulated by utilizing the adjustability of the active and reactive power of the EVs while interoperating with the voltage control means of PV active-reactive power regulation, capacitor bank casting, and network reconfiguration in the distribution network. The two time periods, before 1:00 and after 17:30, alleviate the power peak pressure on the grid and reduce the voltage deviation at the nodes.

Fig. 12 compares the charging power of EVs at node 19 before and after participating in voltage control at the charging station.

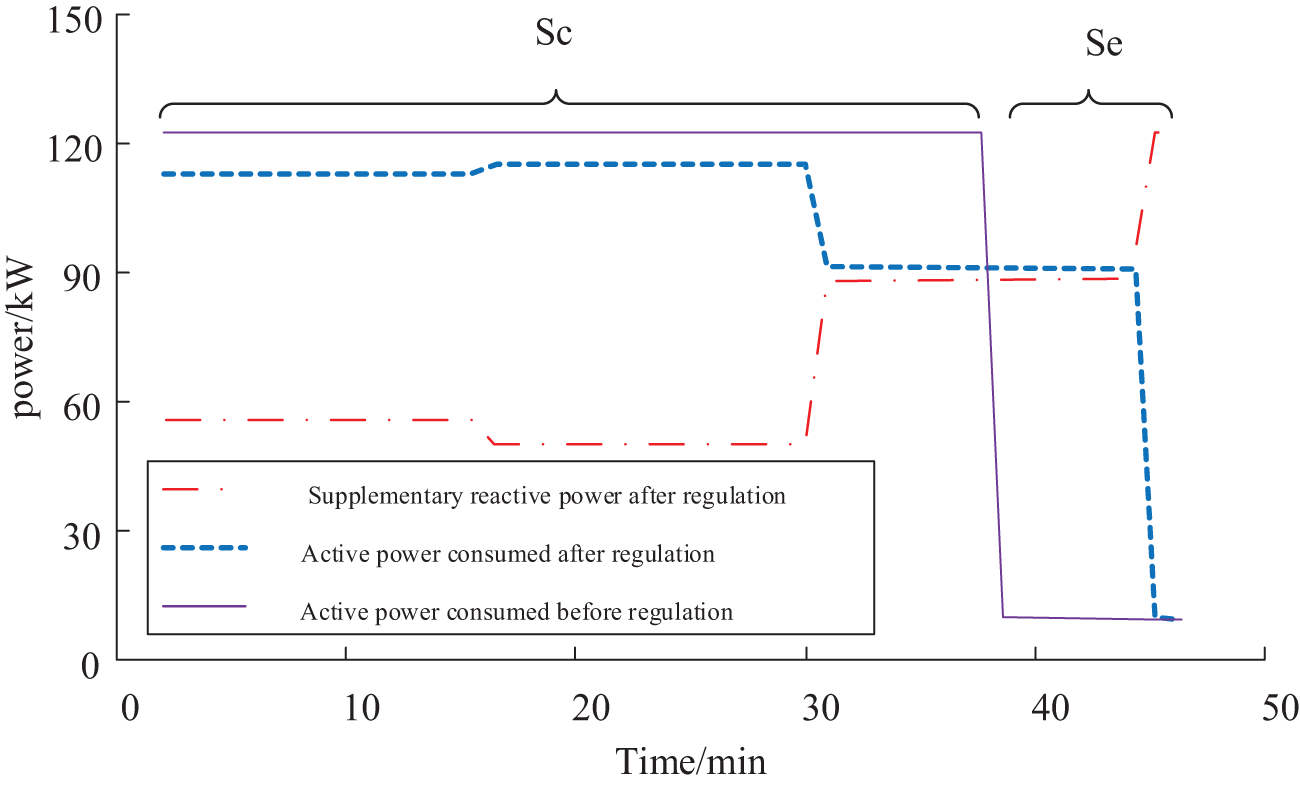
Figure 12: Power before and after regulation of EVs

As shown in Fig. 12, the effect of power regulation of EVs during the charging period (Sc) and idle period (Se) and the potential for grid optimization it brings are demonstrated. During the charging period Sc, the EVs are stably charged at the rated power, which ensures charging efficiency. However, after entering the idle period Se, by implementing the regulation strategy proposed in this paper, the active power of EVs can be flexibly adjusted according to the actual demand of the grid. This strategy not only allows EVs to rapidly charge most of the power in a relatively short period to fully cope with the situation where the owner may drive away early, thus not affecting the owner’s charging demand, but also realizes the effective optimization of the voltage stability of the distribution network by intelligently regulating the power output of the charging machine, which not only meets the charging demand of the EV, but also improves the operational efficiency of the grid, and thus optimizes the distribution network’s voltage stability.

Comparing the improved fruit fly optimization algorithm with the particle swarm optimization algorithm, the convergence characteristics of the two algorithms are shown in Fig. 13, from which it can be seen that the improved fruit fly optimization algorithm achieves better results than the particle swarm optimization algorithm, both in terms of speed of convergence and convergence accuracy.

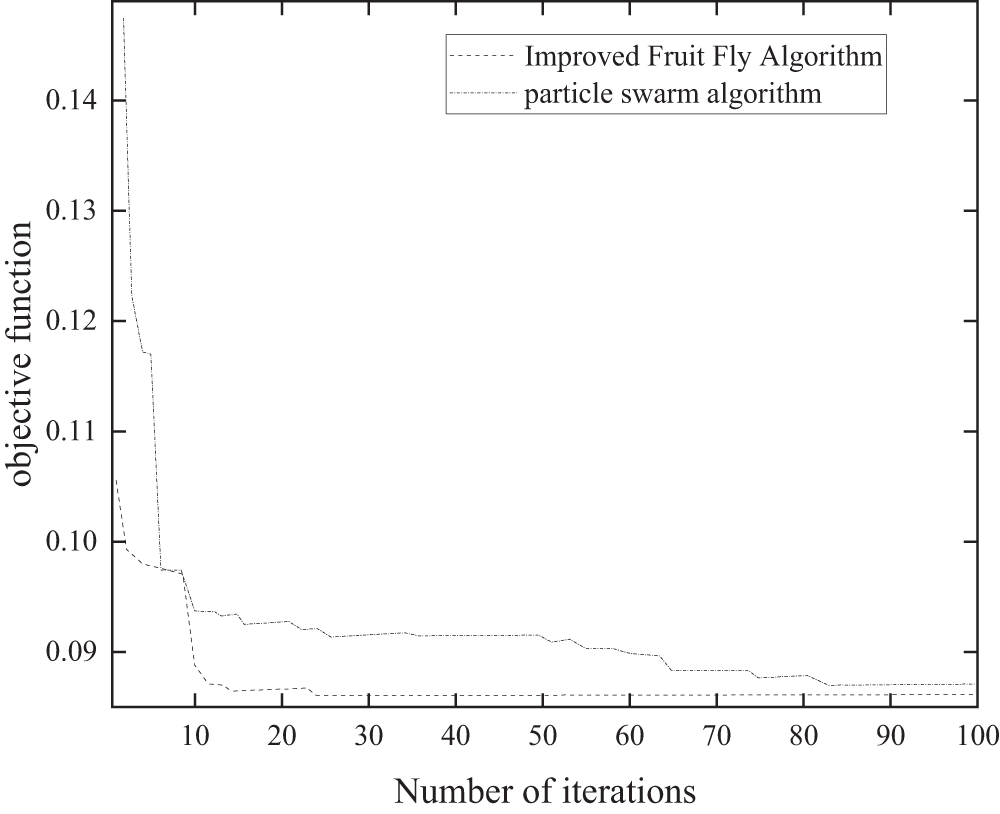
Figure 13: Comparison of convergence characteristics

6  Conclusion

The proposed multi-stage voltage control optimization strategy for distribution network demonstrates a significant quantitative performance improvement in the arithmetic score. Specifically, by implementing the strategy, the network losses are significantly reduced from 250.13 kWh in the no-optimization state to a minimum of 91.53 kWh, causing a reduction of 63.4%. Meanwhile, voltage deviation also improved significantly from 0.065 to 0.024 p.u. In addition, the four-level coordinated optimization also significantly reduces the voltage fluctuation range and further optimizes the grid voltage stability through active and reactive power regulation of EV charging stations. The specific research conclusions are as follows:

•   The proposed four-level coordinated voltage control optimization strategy improves the voltage control effect of the distribution network. The strategy effectively reduces the operating loss of the distribution network and significantly reduces the voltage deviation, thus improving the overall operating efficiency and stability of the grid.

•   The adjustable capabilities of EVs in terms of active and reactive power are fully used, and they are coordinately controlled with other voltage control means in the distribution network (photovoltaic active-reactive power regulation, capacitor bank adjusting, and network reconfiguration) on multiple time scales. This integrated regulation and control approach maximizes the potential of multiple types of voltage control resources in the distribution network, achieving efficient use of resources and complementary advantages.

•   In solving the optimization problem with multi stages and multi-decision variables, the improved Drosophila optimization algorithm is adopted in this study. By comparing with the traditional particle swarm algorithm, the results show that the improved fruit fly optimization algorithm has a stronger ability to find the optimum in solving the multi-level voltage coordination optimization problem. This advantage makes the algorithm better able to cope with complex grid voltage control optimization problems and provides a powerful tool to support the formulation of voltage control strategies for distribution networks.

In summary, by proposing a four-level coordinated voltage control optimization strategy and making full use of multiple types of voltage control resources such as electric vehicles, combined with the improved fruit fly optimization algorithm, this paper effectively enhances the voltage control effect of the distribution network, reduces the operation loss and voltage deviation, and provides strong theoretical support and practical guidance for the optimal operation of the distribution network.

In the future, how to tap the user’s psychological affordability, how to optimize incentive value for users to participate in the flexible regulation of the power grid needs to be further studied. We can develop an incentive mechanism considering the various types of user uncertainty. This could involve offering different types of incentives such as the financial reward, the discounts on electricity bills, and the access to premium services.

Acknowledgement: We would like to thank all collaborators who have made outstanding contributions to this article, as well as the support of the relevant staff of the Energy Engineering journal.

Funding Statement: This research was funded by the State Grid Corporation Science and Technology Project (5108-202218280A-2-391-XG).

Author Contributions: The authors confirm their contribution to the paper as follows: Study conception and design: Shukang Lyu and Fei Zeng; data collection: Xiaodong Yuan; analysis and interpretation of results: Huachun Han; draft manuscript preparation: Huiyu Miao, Yi Pan and Shukang Lyu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All relevant data are included within the paper. The data used to support the findings of this study are available from the corresponding author upon request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. A. Tavakoli, S. Saha, M. T. Arif, M. E. Haque, N. Mendis and A. M. T. Oo, “Impacts of grid integration of solar PV and electric vehicle on grid stability, power quality and energy economics: A review,” IET Energy Syst. Integrat., vol. 2, no. 3, pp. 243–260, Sep. 2020. doi: 10.1049/iet-esi.2019.0047. [Google Scholar] [CrossRef]

2. A. Ciocia, V. A. Boicea, G. Chicco, P. D. Leo, A. Mazza and E. Pons, “Voltage control in low-voltage grids using distributed photovoltaic converters and centralized devices,” IEEE Trans. Ind. Appl., vol. 55, no. 1, pp. 225–237, Sep. 2018. doi: 10.1109/TIA.2018.2869104. [Google Scholar] [CrossRef]

3. Y. Zhao, G. Zhang, W. Hu, Q. Huang, Z. Chen and F. Blaabjerg, “Meta-learning based voltage control for renewable energy integrated active distribution network against topology change,” IEEE Trans. Power Syst., vol. 38, no. 6, pp. 5937–5940, Nov., Sep. 2023. doi: 10.1109/TPWRS.2023.3309536. [Google Scholar] [CrossRef]

4. Y. Wang, D. Qiu, G. Strbac, and Z. Gao, “Coordinated electric vehicle active and reactive power control for active distribution networks,” IEEE Trans. Ind. Inform., vol. 19, no. 2, pp. 1611–1622, Apr. 2023. doi: 10.1109/TII.2022.3169975. [Google Scholar] [CrossRef]

5. G. Shuai, “Active distribution network reactive power optimization based on an improved genetic particle swarm optimization algorithm,” J. Phys.: Conf. Series, vol. 2655, no. 1, Nov. 2023, Art. no. 012035. doi: 10.1088/1742-6596/2655/1/012035. [Google Scholar] [CrossRef]

6. A. A. Abou El Ela, M. A. Abido, and S. R. Spea, “Optimal power flow using differential evolution algorithm,” Elect. Power Syst. Res., vol. 80, no. 7, pp. 878–885, Jul. 2010. doi: 10.1016/j.epsr.2009.12.018. [Google Scholar] [CrossRef]

7. Z. A. Ansari, and G. L. Raja, “Raja enhanced cascaded frequency controller optimized by flow direction algorithm for seaport hybrid microgrid powered by renewable energies,” Appl. Energy, vol. 374, 2024, Art. no. 123996. doi: 10.1016/j.apenergy.2024.123996. [Google Scholar] [CrossRef]

8. K. Z. Oo, K. M. Lin, and T. N. Aung, “Particle swarm optimization based optimal reactive power dispatch for power distribution network with distributed generation,” Int. J. Energy Power Eng., vol. 6, no. 4, pp. 53–60, Aug. 2017. doi: 10.11648/j.ijepe.20170604.12. [Google Scholar] [CrossRef]

9. A. Sleptchenko and S. Sgouridis, “Joint optimization of energy production & storage,” in 2019 IEEE 6th Int. Conf. Ind. Eng. Appl. (ICIEA), Tokyo, Japan, May 2019, pp. 913–917. doi: 10.1109/IEA.2019.8714874. [Google Scholar] [CrossRef]

10. D. Lee, C. Han, and G. Jang, “Stochastic analysis-based Volt-Var curve of smart inverters for combined voltage regulation in distribution networks,” Energies, vol. 14, no. 10, Mar. 2021, Art. no. 2785. doi: 10.3390/en14102785. [Google Scholar] [CrossRef]

11. Z. Zhang, T. Shuai, and S. Yiliang, “Multi-time scale adaptive reactive power and voltage control of distribution network based on random forest algorithm,” in Proc. 3rd Asia-Pacific Conf. Image Process., Electron. Comput., China, Jul. 2022, pp. 1060–1065. doi: 10.1145/3544109.3544998. [Google Scholar] [CrossRef]

12. B. Tolabi, H. Ali, and M. H. Rizwan, “Simultaneous reconfiguration, optimal placement of DSTATCOM, and photovoltaic array in a distribution system based on Fuzzy-ACO approach,” IEEE Trans. Sustain. Energy, vol. 1, no. 6, pp. 210–218, Jan. 2015. doi: 10.1109/TSTE.2014.2364230. [Google Scholar] [CrossRef]

13. R. G. Wandhare and V. Agarwal, “Reactive power capacity enhancement of a PV grid system to increase PV penetration level in smart grid scenario,” IEEE Trans. Smart Grid, vol. 5, no. 4, pp. 1845–1854, Jul. 2014. doi: 10.1109/TSG.2014.2298532. [Google Scholar] [CrossRef]

14. F. Arman, Y. D. Sayed, G. Ali, and H. K. Mohammad, “Utilization of dynamic wireless power transfer technology in multi-depot, multi-product delivery supply chain,” Sustain. Energy, Grids Netw., vol. 32, Dec. 2022, Art. no. 100836. doi: 10.1016/j.segan.2022.100836. [Google Scholar] [CrossRef]

15. X. Sun and J. Qiu, “A customized voltage control strategy for electric vehicles in distribution networks with reinforcement learning method,” IEEE Trans. Ind. Inform., vol. 17, no. 10, pp. 6852–6863, Oct. 2021. doi: 10.1109/TII.2021.3050039. [Google Scholar] [CrossRef]

16. A. Amin et al., “An integrated approach to optimal charging scheduling of electric vehicles integrated with improved medium-voltage network reconfiguration for power loss minimization,” Sustainability, vol. 12, no. 21, Sep. 2020, Art. no. 9211. doi: 10.3390/su12219211. [Google Scholar] [CrossRef]

17. J. Zhang, M. Cui, and Y. He, “Dual timescales voltages regulation in distribution systems using data-driven and physics-based optimization,” Power Syst. Autom., vol. 47, no. 20, pp. 64–71, May 2023. doi: 10.1109/TII.2023.3274216. [Google Scholar] [CrossRef]

18. H. Nafisi, S. M. M. Agah, H. A. Abyaneh, and M. Abedi, “Two-stage optimization method for energy loss minimization in microgrid based on smart power management scheme of PHEVs,” IEEE Trans. Smart Grid, vol. 7, no. 3, pp. 1268–1276, May 2016. doi: 10.1109/TSG.2015.2480999. [Google Scholar] [CrossRef]

19. L. Tan, H. Xie, Z. Wu, R. Wang, and X. Huang, “An optimized power-efficiency coordinated control method for EVs charging and discharging applications,” IEEE Trans. Ind. Electron., vol. 70, no. 7, pp. 7257–7267, Aug. 2022. doi: 10.1109/TIE.2022.3201326. [Google Scholar] [CrossRef]

20. A. Fathollahi, M. Gheisarnejad, J. Boudjadar, M. Homayounzadeh, and M. -H. Khooban, “Optimal design of wireless charging electric buses-based machine learning: A case study of Nguyen-Dupuis network,” IEEE Trans. Vehicular Technol., vol. 72, no. 7, pp. 8449–8458, Jul. 2023. doi: 10.1109/TVT.2023.3247838. [Google Scholar] [CrossRef]

21. X. Wu, L. Zhu, H. Wang, H. Zhang, R. Xu and Q. Duan, “Coordinated control for multi-level reactive power and voltage,” in 2022 IEEE 6th Conf. Energy Internet Energy Syst. Integrat. (EI2), China, May 2022, pp. 420–427. doi: 10.1109/EI256261.2022.10117027. [Google Scholar] [CrossRef]

22. H. Gao, J. Liu, and L. Wang, “Robust coordinated optimization of active and reactive power in active distribution systems,” IEEE Trans. Smart Grid, vol. 9, no. 5, pp. 4436–4447, Jan. 2017. doi: 10.1109/TSG.2017.2657782. [Google Scholar] [CrossRef]

23. C. K. Mithat, O. Burak, and M. T. Leon, “EV/PHEV bidirectional charger assessment for V2G reactive power operation,” IEEE Trans. Power Electron., vol. 28, no. 12, pp. 5717–5727, Mar. 2013. doi: 10.1109/TPEL.2013.2251007. [Google Scholar] [CrossRef]

24. J. R. Pillai and B. Bak-Jensen, “Integration of vehicle-to-grid in the western Danish power system,” IEEE Trans. Sustain. Energy, vol. 2, no. 1, pp. 12–19, Sep. 2011. doi: 10.1109/VPPC.2012.6422588. [Google Scholar] [CrossRef]

25. W. Zheng, W. Huang, D. J. Hill, and Y. Hou, “An adaptive distributionally robust model for three-phase distribution network reconfiguration,” IEEE Trans. Smart Grid, vol. 12, no. 2, pp. 1224–1237, Oct. 2021. doi: 10.1109/TSG.2020.3030299. [Google Scholar] [CrossRef]

26. T. Ding, Q. Yang, Y. Yang, C. Li, Z. Bie and F. Blaabjerg, “A data-driven stochastic reactive power optimization considering uncertainties in active distribution networks and decomposition method,” IEEE Trans. Smart Grid, vol. 9, no. 5, pp. 4994–5004, Mar. 2017. doi: 10.1109/TSG.2017.2677481. [Google Scholar] [CrossRef]

27. M. A. Azzouz, H. E. Farag, and E. F. El-Saadany, “Real-time fuzzy voltage regulation for distribution networks incorporating high penetration of renewable sources,” IEEE Syst. J., vol. 11, no. 3, pp. 1702–1711, Jul. 2014. doi: 10.1109/JSYST.2014.2330606. [Google Scholar] [CrossRef]

28. J. Wong, Y. Seng Lim, and E. Morris, “Distributed energy storage systems with an improved fuzzy controller for mitigating voltage unbalance on low-voltage networks,” J. Energy Eng., vol. 142, no. 1, Dec. 2016. doi: 10.1061/(ASCE)EY.1943-7897.0000260. [Google Scholar] [CrossRef]

29. K. Y. Lim, Y. S. Lim, J. Wong, and K. H. Chua, “Distributed energy storage with real and reactive power controller for power quality issues caused by renewable energy and electric vehicles,” J. Energy Eng., vol. 142, no. 4, Dec. 2016. doi: 10.1061/(ASCE)EY.1943-7897.0000334. [Google Scholar] [CrossRef]

30. J. Yin, L. Liu, Z. Peng, and R. Chen, “Multi-objective genetic algorithm-based wind turbines control,” J. Comput. Methods Sci. Eng., vol. 23, no. 2, pp. 1053–1068, 2023. doi: 10.3233/JCM226582. [Google Scholar] [CrossRef]