 Open Access
Open Access
ARTICLE
Enhancing Solar Photovoltaic Efficiency: A Computational Fluid Dynamics Analysis
1 Faculty of Mechanical and Automotive Engineering, Universiti Malaysia Pahang Al-Sultan Abdullah, Pekan, 26600, Pahang, Malaysia
2 Faculty of Engineering Science & Technology, Hamdard University, Karachi, 74600, Pakistan
3 Electrical Engineering Department, SUKKUR IBA University, Sukkur, 65200, Pakistan
4 Berlin School of Business and Innovation BSBI, Faculty of Computer Science and Informatics, Berlin, 12043, Germany
5 Automotive Engineering Centre, University Malaysia Pahang Al Sultan Abdullah, Pekan, 26600, Pahang, Malaysia
6 Centre for Research in Advanced Fluid & Processes (Fluid Centre), Universiti Malaysia Pahang Al-Sultan Abdullah (UMPSA), Paya Besar, Kuantan, 26300, Pahang, Malaysia
* Corresponding Authors: Rahool Rai. Email: ,
; Sudhakar Kumaramsay. Email:
Energy Engineering 2025, 122(1), 153-166. https://doi.org/10.32604/ee.2024.051789
Received 15 March 2024; Accepted 01 July 2024; Issue published 27 December 2024
Abstract
The growing need for sustainable energy solutions, driven by rising energy shortages, environmental concerns, and the depletion of conventional energy sources, has led to a significant focus on renewable energy. Solar energy, among the various renewable sources, is particularly appealing due to its abundant availability. However, the efficiency of commercial solar photovoltaic (PV) modules is hindered by several factors, notably their conversion efficiency, which averages around 19%. This efficiency can further decline to 10%–16% due to temperature increases during peak sunlight hours. This study investigates the cooling of PV modules by applying water to their front surface through Computational fluid dynamics (CFD). The study aimed to determine the optimal conditions for cooling the PV module by analyzing the interplay between water film thickness, Reynolds number, and their effects on temperature reduction and heat transfer. The CFD analysis revealed that the most effective cooling condition occurred with a 5 mm thick water film and a Reynolds number of 10. These specific parameters were found to maximize the heat transfer and temperature reduction efficiency. This finding is crucial for the development of practical and efficient cooling systems for PV modules, potentially leading to improved performance and longevity of solar panels. Alternative cooling fluids or advanced cooling techniques that might offer even better efficiency or practical benefits.Keywords
Highlight
• Solar panel efficiency decreases due to high temperatures at midday.
• Water cooling the front surface of the panel improves efficiency.
• CFD tool is employed to analyze the water film thickness and Reynold number on temperature reduction.
• A water film thickness of 5 mm with a Reynolds number of 35 achieves optimal cooling.
• Water flow rate, Reynolds number, and diameter of the water channel affect heat transfer.
Nomenclature
| PV | Photovoltaic |
| a | Thickness of Water Film |
| b | Width of the Water Film/ PV Module |
| IV | Current Voltage |
| Dh | Hydraulic Diameter |
| Q | Heat Transfer per Unit Time |
| K | Thermal Conductivity of Material |
| dT | Temperature difference between hot and cold body |
| dx | Thickness of the body |
| hc | Coefficient of convective heat transfer |
| A | Area of heat transfer |
| ΔT | Temperature difference |
Pakistan suffers from acute power shortages, with blackouts lasting up to eighteen hours a day in rural areas and twelve to thirteen hours in urban areas [1–3]. Economic limitations, the depletion of energy resources, and rising electrical consumption are the main causes of this dilemma [4,5]. The government has responded by enacting modest reforms to the power sector. Considering worries about global climate change, the nation also needs to guarantee energy security [6,7]. To tackle these issues, scientists are looking to renewable energy sources like solar energy. On the other hand, PV panel efficiency drops as temperature rises; for every degree Celsius above 25°C, efficiency drops by 5% [8]. Numerous investigations have investigated cooling techniques to help with this problem. For example, efficiency has increased in experimental setups using water cooling and ventilation systems [9–11].
The understanding and optimization of photovoltaic (PV) systems, with a focus on different cooling strategies and environmental interactions, have been greatly improved by contemporary advances in computational fluid dynamics (CFD) [12]. Research using ANSYS Fluent has shown that ground source and active air cooling can significantly lower PV operating temperatures, increasing efficiency [13]. An increasing number of reviews of CFD applications show that PV-environment interactions are being modeled, underscoring the need for improved parameterization techniques and more straightforward models for urban-scale simulations [14]. The use of phase change materials (PCM) and nanofluids in cooling systems has shown great potential in improving thermal efficiency [15]. Research on wind effects shows that strategic array topologies, especially those with inter-row spacing, can enhance PV performance under different wind situations. These findings emphasize the necessity of CFD in designing efficient cooling mechanisms and PV system designs for sustainability.
Attia et al. [16] conducted comparative analysis of two photovoltaic thermal (PVT) systems—one with a standard straight zigzag-gilded tube cooling conduit (Case A) and another with a novel three-section zigzag-plated tube cooling channel (Case B)—showed that Case B improved thermal efficiency by 7.23% (water) and 15.75% (air), and electrical efficiency by 4.0% (water) and 4.6% (air). This indicates that the innovative design significantly enhances PVT performance and ensures a more uniform coolant flow. However, Khelifa et al. [17] in his study analyzed the heat-based performance of photovoltaic thermal (PVT) collectors cooled with absorbent flax strings in water, finding the optimal configuration to be a 50 mm thick flax fiber layer with a 0.907 m/s water flow rate, which increased the Nusselt number by 173.46% compared to pure water. The PVT system’s thermal efficiencies were 69.58% with water/flax fibers, 50.02% with pure water, and 34.60% with air.
Prior research has mostly concentrated on experimental configurations and particular cooling techniques as illustrated in Table 1, with a dearth of thorough simulation-based assessments that can be applied to various scenarios. Despite these developments, there is still a clear research deficit in using computational fluid dynamics (CFD) simulations to improve PV panel cooling. By using ANSYS Fluent for CFD simulations, this study seeks to lower the surface temperature of PV modules and increase their efficiency. The objective of this study is as follows:
• To offer a scalable method for utilizing sophisticated simulations to enhance cooling parameters.
• To determine the ideal parameters for maintaining surface temperatures of PV between 20 and 25°C using CFD analysis.
• To optimize heat transfer by adjusting Reynolds numbers and water film thickness.
2.1 Computational Fluid Dynamics (CFD)
With the rise of computational fluid dynamics, it is widely used techniques to solve challenging issues in the current age of Engineering, Technology, and Innovation. CFD was originally motivated by a scientific understanding of the mechanics of fluids and heat transfer. It has cut costs and improved the performance of the equipment which has culminated in greater quality discoveries through computational simulation [23,24]. It is a multidisciplinary tool that led to the evolution of computer science, mathematics, and fluid mechanics. The dedication of CFD is only for the fluids that are in movement. Mathematical simulations of any fluid flow fall under the umbrella of the computational part [25,26].
ANSYS Fluent has a built-in design tool for creating 3D sketches, which can be used to draw different geometric specifications which is known as Space-Claim. A 3.4 mm-thick sketch of a photovoltaic PV panel’s glass was drawn. Nevertheless, as shown in Fig. 1, a rectangle that resembled a duct was also constructed above the glass [15,27].
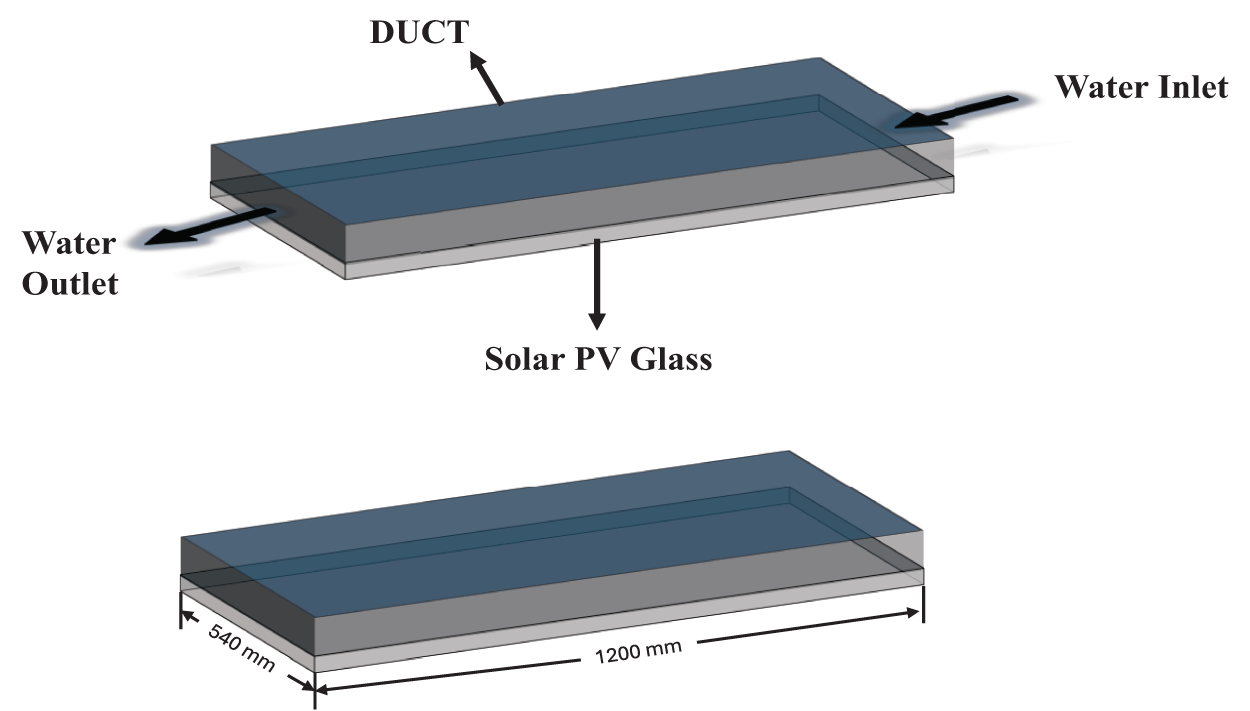
Figure 1: Solid model of glass with duct
It is the important phase in CFD which arises after geometry. In this step simply, cells are built on which the flow variables are computed in a computational globe. There are distinct forms of cells, such as (Triangles, Quadrilateral, tetrahedrons, hexahedrons, etc.) out of which a fine mesh has been created of 5 mm.
Following the geometry phase, mesh generation represents a pivotal step in Computational Fluid Dynamics (CFD) as depicted in Fig. 2. During this stage, cells are intricately designed to facilitate the calculation of flow variables within a computational domain. Various cell shapes, including triangles, quadrilaterals, tetrahedral, and hexahedrals, are available for this purpose. The selection of an appropriate cell shape is contingent upon the specific characteristics of the flow under consideration. In this context, a fine mesh with a nominal size of 5 mm was employed to ensure a detailed representation of the computational domain. This meticulous mesh refinement is crucial for accurately capturing the intricacies of fluid flow and enhancing the reliability of the CFD simulations [28].
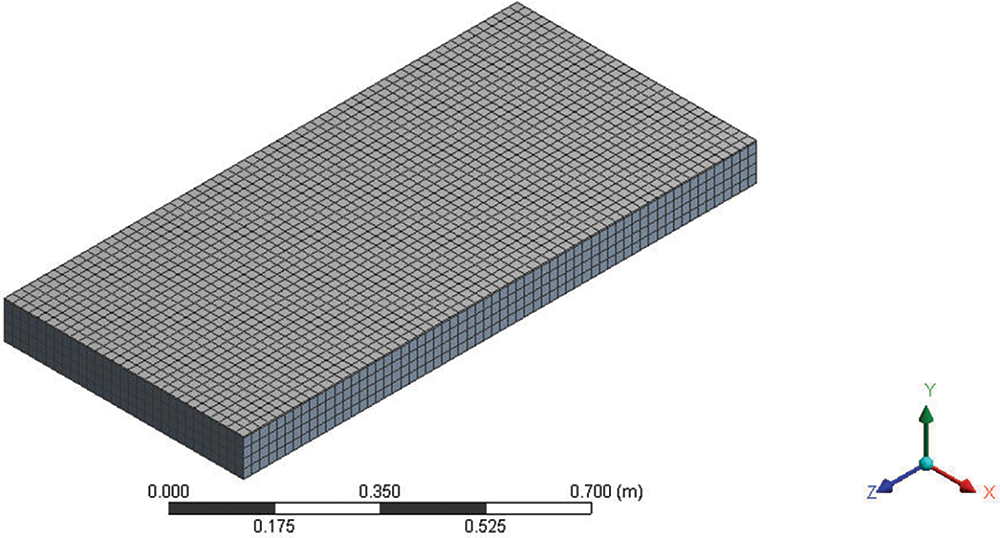
Figure 2: Structure mesh of the 3-D model
Eqs. (1) and (2) were the basic equations to be considered for the heat transfer from PV module glass to water (Coolant). However, the following parameters for the glass were considered as a standard to calculate heat transfer. Table 2 shows data for the glass. Whereas properties of glass and water are the standard values for calculating the effect [29–31].

Boundary conditions are applied without any reluctance. Velocity in any application of equipment can be varied by the variation in Boundary conditions. Besides, in real-time applications, it gets changed by the change of equipment of higher power as in the pump for variation flow rate and velocity. Altogether the same procedure is recalled for temperature and pressure whereas for many other conditions. Above mentioned technique reduces the cost of the system. CFD helps to simulate multiple conditions at different rates and variations in different parameters [32]. However, boundary conditions are also illustrated in tabular form in Table 3.

The most useful and dynamic input variable that immediately gets affected by the flow includes velocity. Remember that a temperature of 323 K is fixed at the glass’s surface. Even variations in Reynolds number have an impact on velocity. Therefore, velocity was computed at various Reynolds numbers between 5 and 50 as an input parameter [33].
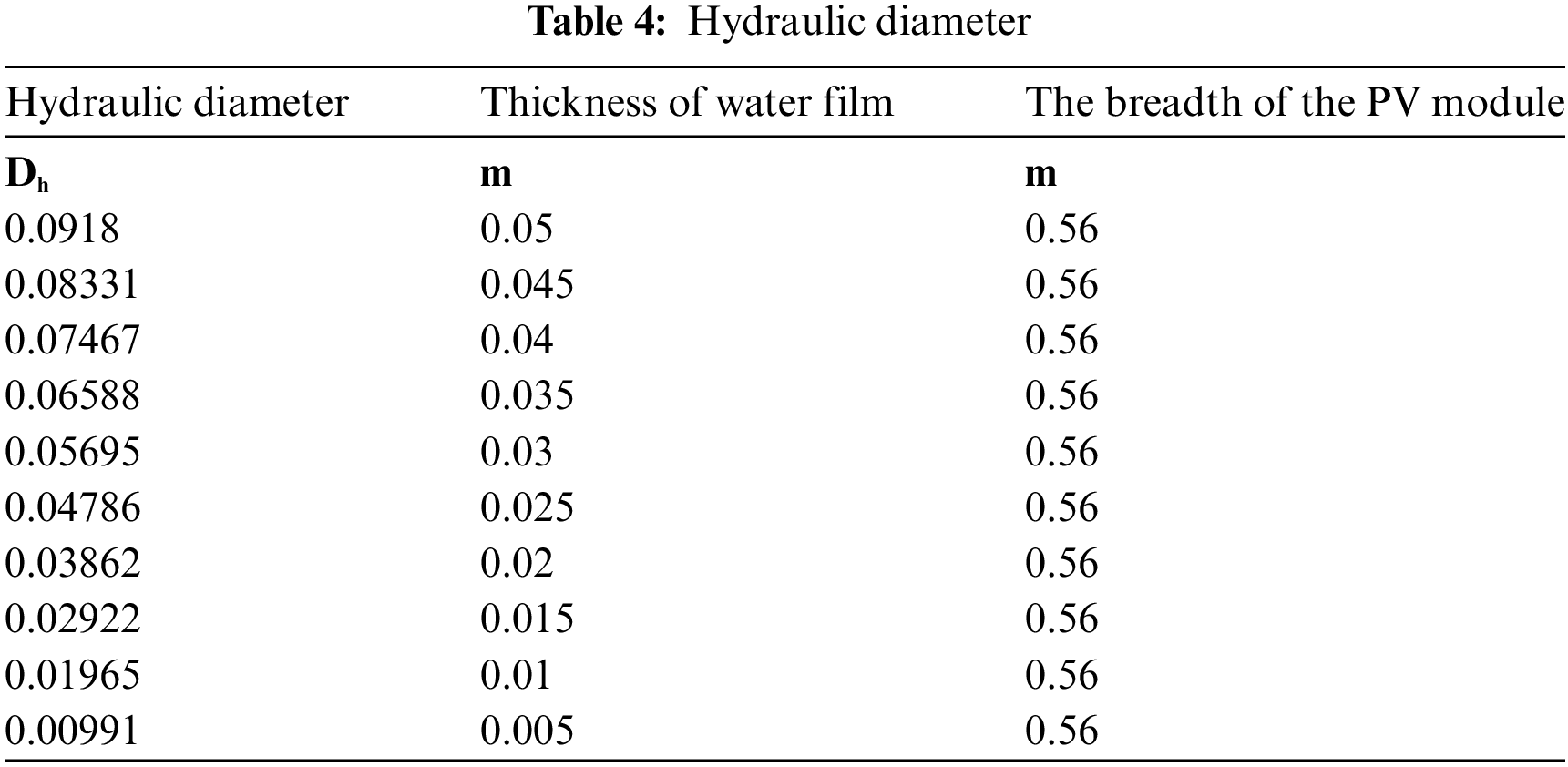
Considering the duct as a rectangular shape over the surface of the PV Glass it was considered that velocity will be the primary input variable. So, the hydraulic diameter was taken in the Reynolds number formula and calculations were done as given in following Table 4 and these calculations were carried out by Eq. (3).
The supposed geometry was meshed, allowing for simulations in ANSYS Fluent Academic Version V18R2. The laminar flow pattern was picked for the current shape due to its transparency throughout the PV module surface, enabling maximum irradiance absorption for electricity generation. So, the framework was solved using Energy Eq. (4) under steady-state circumstances [1–3].
The calculations were performed On ANSYS FLUENT software at different Reynolds numbers ranging from 5 to 45 as shown in Table 5. Geometry and meshing were done with the help of ANSYS workbench. Water was used as a fluid and the solid was modeled as Glass of photovoltaic. The flow was modeled as laminar and incompressible. Because of incompressible flow, the solver was used as pressure-based in ANSYS fluent. Then calculations were run on various Reynolds numbers. It was observed that with the increase of Reynolds number, the temperature change also increases. However, From Re = 35 the change in temperature becomes constant as clearly visible in Fig. 3.
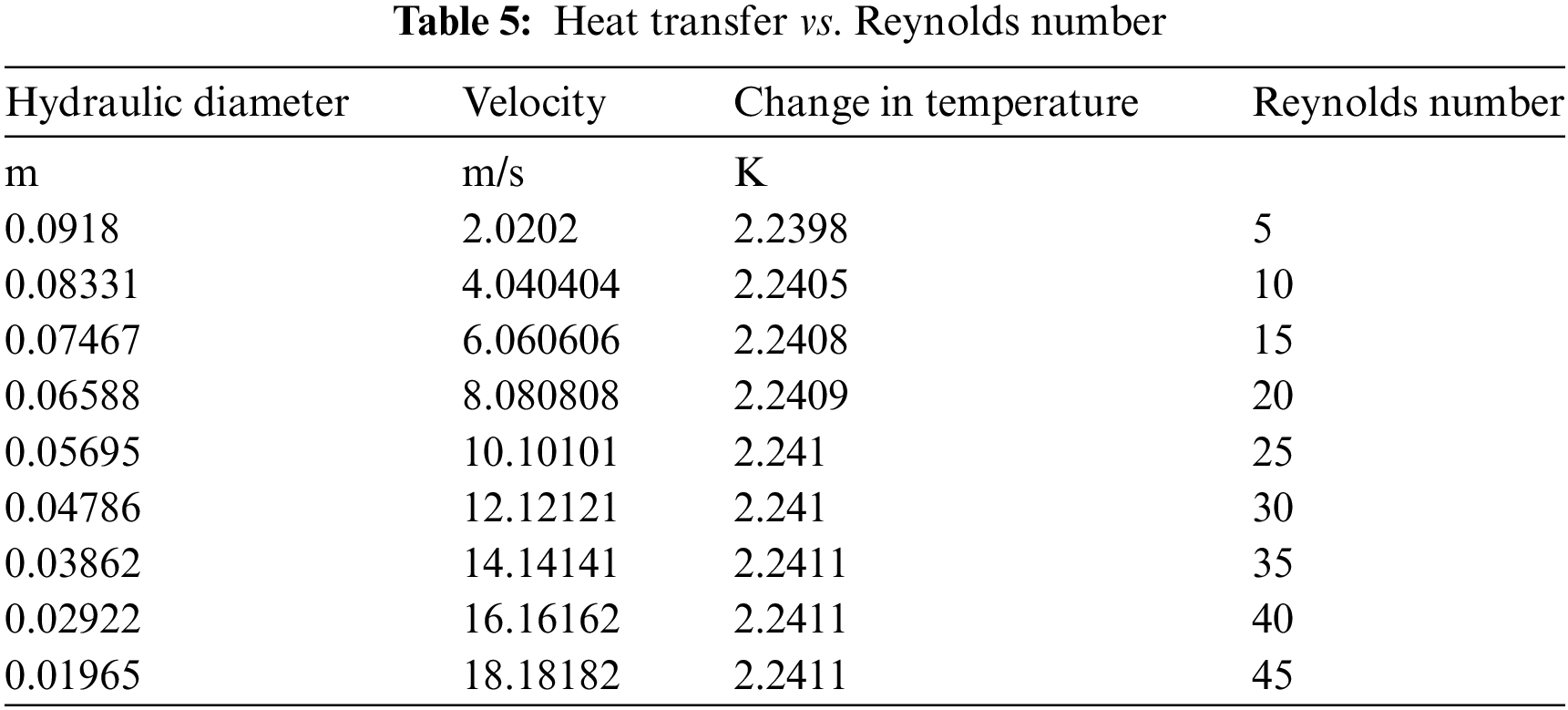
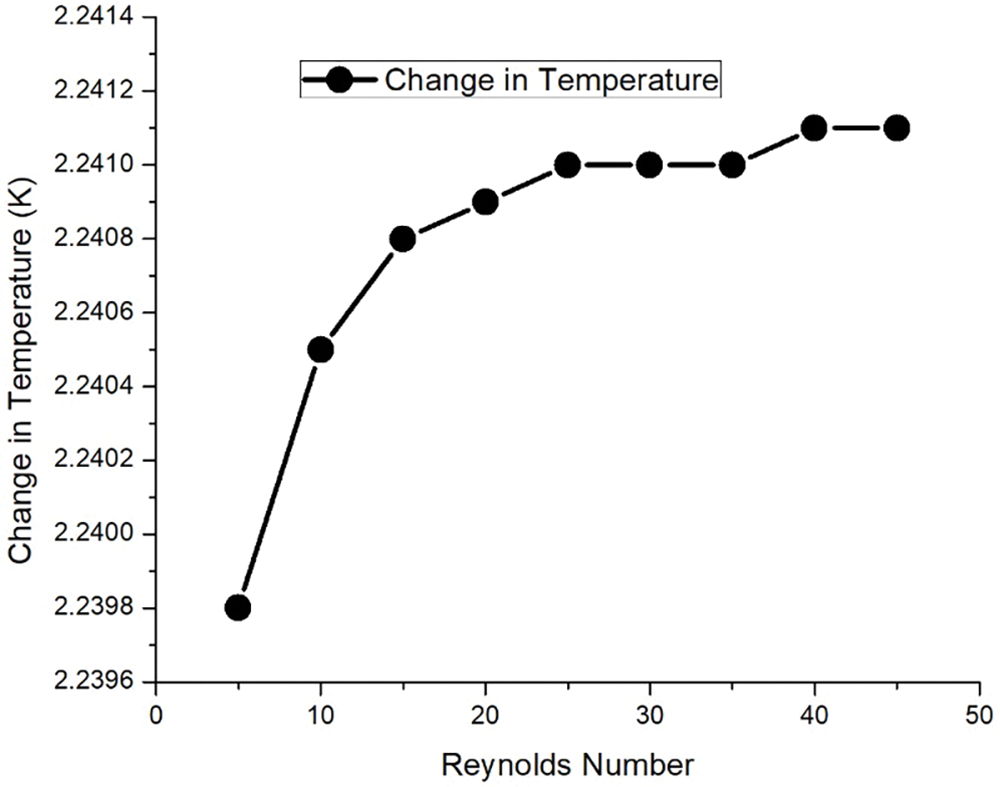
Figure 3: Reynolds number vs. Change in temperature
Therefore, the value of Reynolds is suggested as 35 at hydraulic diameter 0.04786 for maximum heat transfer.
After calculating optimum Reynolds number 35, for maximum heat transfer. Secondly, the optimum thickness was calculated. For the calculation of optimum thickness, different values of thickness were taken ranging from 5 to 50 mm. Based on thickness, the hydraulic diameter was calculated. Wherein the Change in temperature between the inlet and outlet was calculated on different thickness values as shown in Table 6. It can be observed from Fig. 4 and Table 6 that the maximum change in temperature occurs at 5 mm thickness of water. Moreover, as the value of thickness is increased the change of temperature is decreased. The maximum heat transfer occurs at Re = 35 and thickness = 5 mm in comparison to Re = 30, thickness = 30 mm. Therefore, it has been selected as the optimum value of Reynolds and the optimum value of thickness.
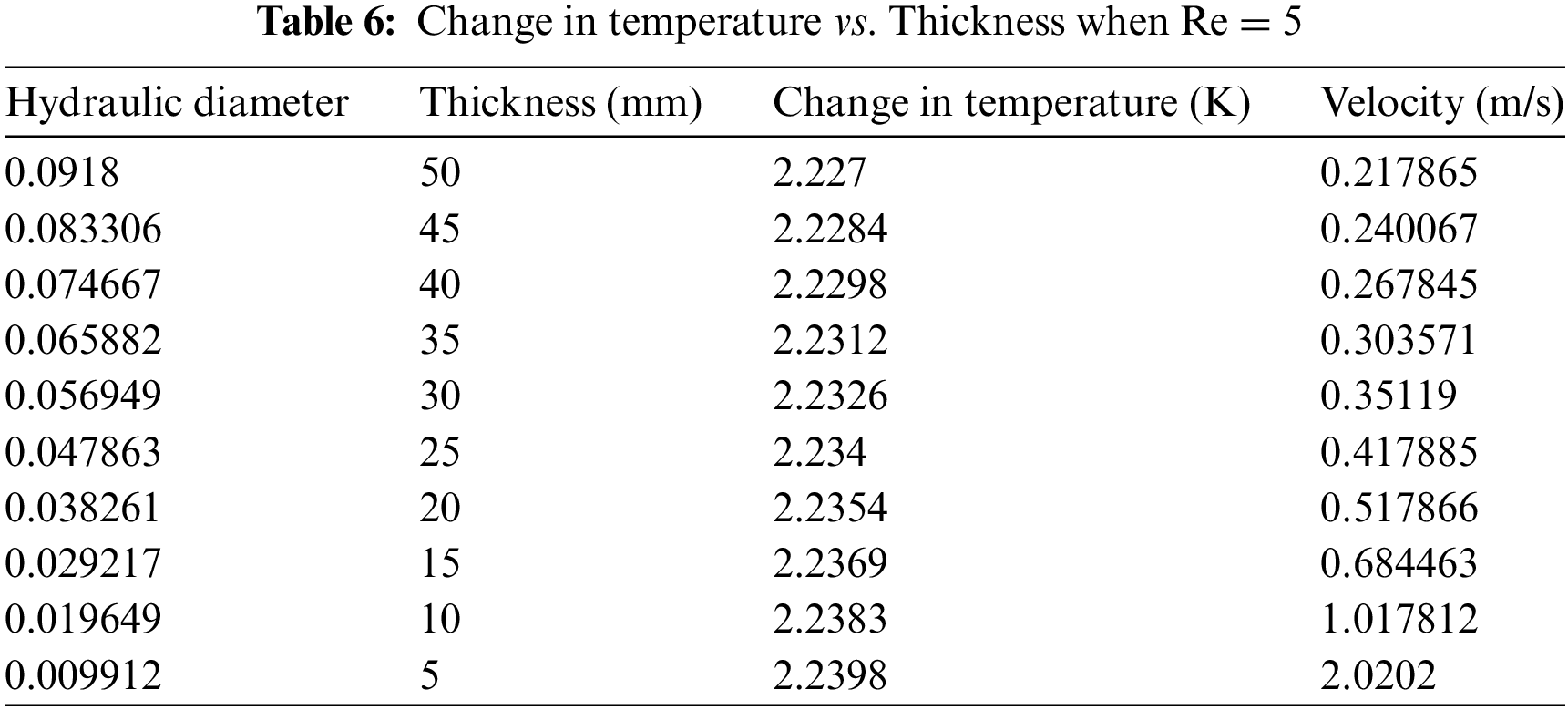
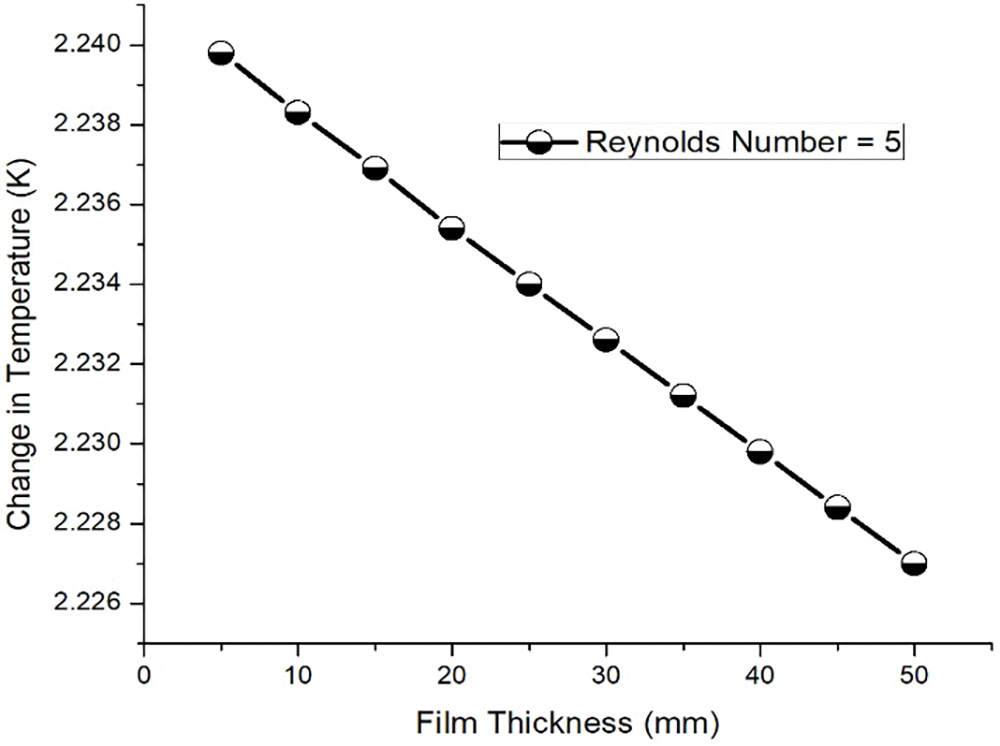
Figure 4: Thickness vs. Change in temperature
The rapid cooling of photovoltaic (PV) modules is essential for enhancing overall performance as shown in Fig. 5a–d, particularly electrical output during midday operations at peak temperatures. Various methods are employed to reduce working temperature, including the use of water as a cooling medium above the module’s front transparent glass to extract surface temperature generated by irradiance. Water flow is regulated using the fundamental principles of the Reynolds number and hydraulic diameter as drawn in Table 6. Importantly, empirical observations reveal that the most significant temperature reduction occurs at a Reynolds number of 35 and a film thickness (T) of 5 mm demonstrated in Fig. 5c. The analysis in Fig. 5a–d implies a marked advancement in electrical efficiency by reducing the surface temperature of the PV Glass. Fig. 5b,d is the contours of the Glass surface and Fig. 5a,c is the contours of the Duct. when these optimal cooling parameters are applied, confirming the efficacy of this cooling strategy. Additionally, Table 6 focuses on the correlation between hydraulic parameters and cooling performance, providing a comprehensive framework for optimizing PV module cooling under varying operational conditions.
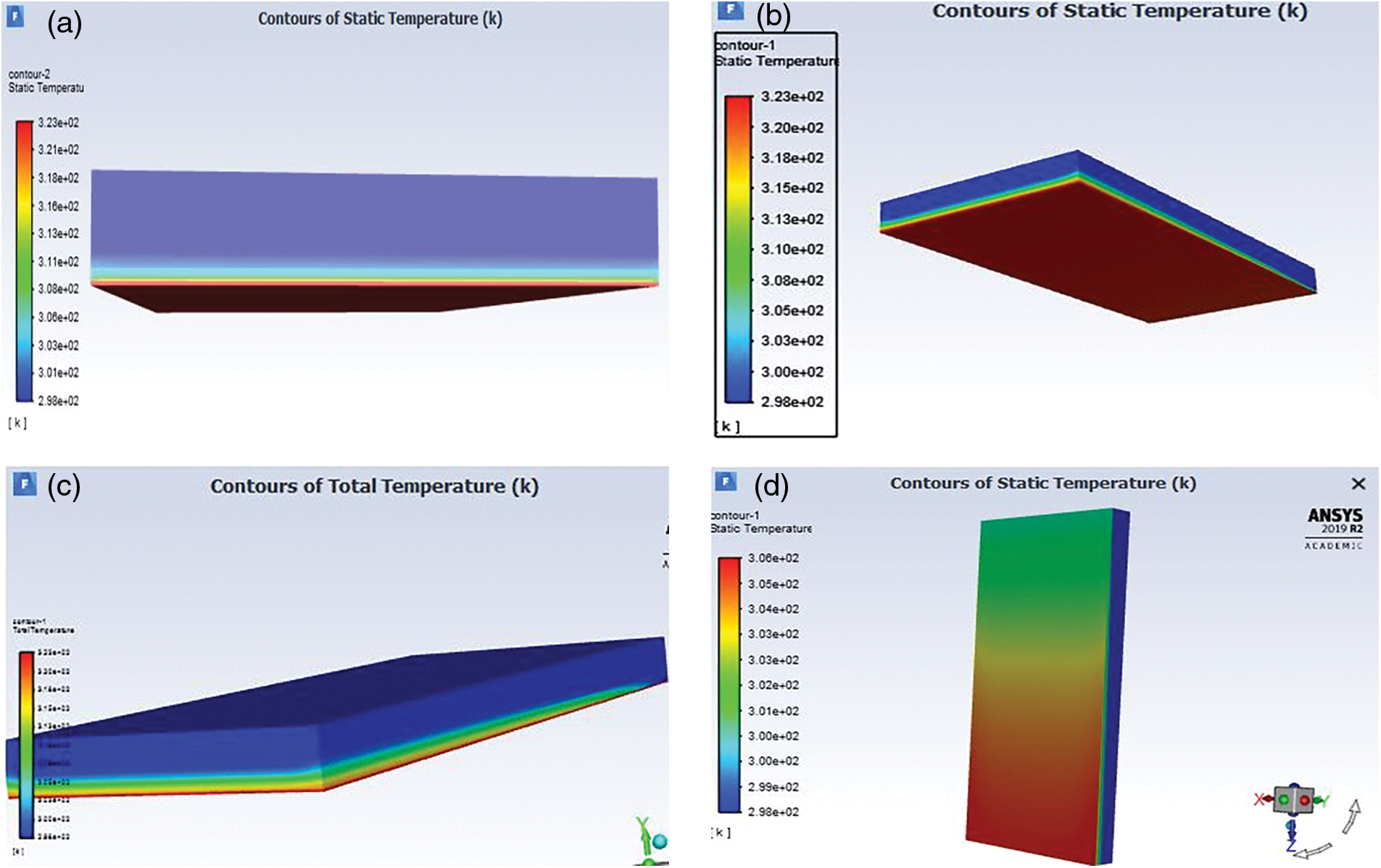
Figure 5: Contours of simulated model
Fig. 6a,b displays the CFD study of the system including duct and PV glass. It is observed that the flow of water extracts the heat from the solar PV glass. From Fig. 6b, the contours of PV glass and interaction surface are illustrated. At Point 1, PV glass has the highest temperature, but water is very cold as compared to glass. However, with the optimal parameters the same contour shifts and takes place in opposite directions. At Point 2, the water is very hot, and the PV glass becomes very cold by achieving the standard temperature and pressure (STP) condition and maintaining room temperature at 25°C or 298 K.
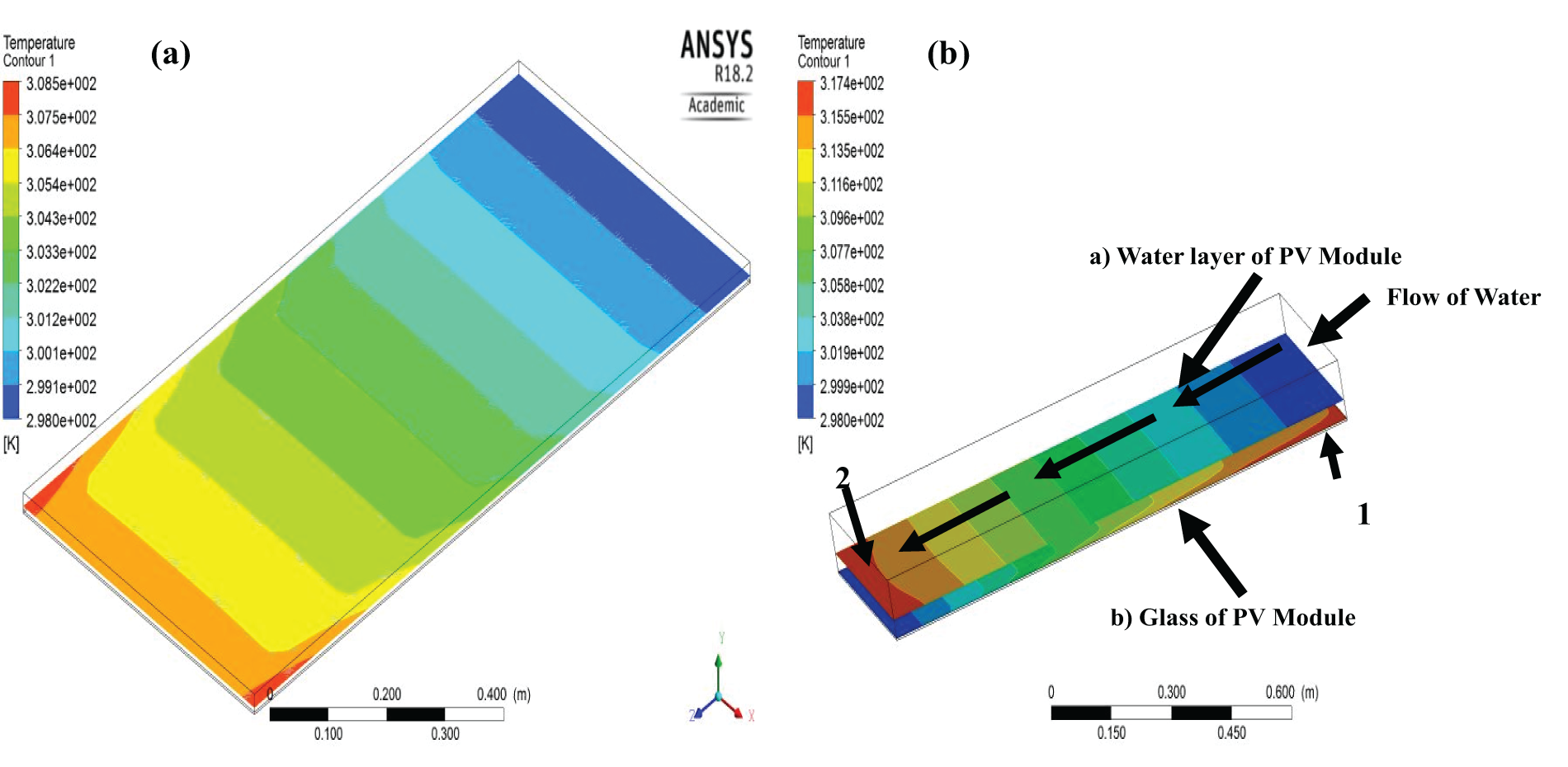
Figure 6: Interacting layer of water and PV glass
Our study molded the optimal cooling conditions for photovoltaic (PV) modules, with a Reynolds number of 35 and a water film thickness of 5 mm. Which ultimately increases the electrical power of the PV module [34]. This discovery aligns with previous research by Hosseini et al. [35] which also identified water cooling as an effective method for temperature control in PV modules. However, our study extends this research by pinpointing specific optimal parameters, whereas Smith et al. provided a broader range of effective Reynolds numbers (500–1500) without specifying the exact optimal point, and his study concluded the turbulent flow. Whereas, our study focused on laminar flow.
In contrast, Raju et al. [36] suggested a three-dimensional computational model for water spray cooling of photovoltaic panels, which reduced operating temperatures and enhanced performance, validated by an average deviation of 1.4 K from experimental data. The optimal flow rate of 170 L/h achieved an electrical efficiency of 15.73%, a panel power output of 40.25 W, and a pump power requirement of 0.77 W, with a maximum system power output of 39.48 W.
However, Patil et al. [12] disclosed the operating temperature of the PV panel significantly impacts its conversion efficiency, with high temperatures reducing output power under identical solar radiation conditions. His CFD Analysis with ANSYS Fluent software presents a solar PV/T system with a bottom active air-cooling system, finding that at an airflow rate of 0.1 kg/s and 800 W/m² irradiance, the maximum temperatures of the PV/T system’s top surface, cell, bottom surface, and air inlet/outlet were 48.8°C, 48.4°C, 47.3°C, and 24.5°C, respectively. So, the discrepancies between our findings and those of Martin Raju and Malagouda Patil may be attributed to differences in experimental setups, such as the Martin Raju sprayed water with sprinklers, and we used free flow. Malagouda Patil tested the system with air as a fluid, but we used water as the fluid. Our study’s improvements in cooling efficiency underscore the importance of fine-tuning cooling parameters, which had not been as precisely addressed in previous research.
The rapid advancement of cooling techniques for photovoltaic (PV) panels is crucial for enhancing their performance and electricity output, particularly during peak daytime temperatures. This research focuses on enhancing the performance of photovoltaic (PV) modules by effectively cooling them using a water film applied to the front transparent glass, thereby reducing surface temperature. The following are the main findings from the study:
• This study demonstrates a significant breakthrough in cooling photovoltaic (PV) panels. By strategically applying water film cooling to the front surface, we successfully mitigated the detrimental effects of irradiance-induced heat, particularly during peak daytime temperatures. This translates to a notable enhancement in PV performance and electricity output.
• Simulations reveal that the best cooling conditions occur at a Reynolds number of 35 and a film thickness of 5 mm for this particular geometry.
• This study demonstrates that optimal cooling can be achieved by adhering to fundamental engineering principles, specifically the Reynolds number and hydraulic diameter.
Implementing effective cooling methods, such as applying water over the front glass of the PV module, helps mitigate heat generated by irradiance. This research provides a practical and scalable approach to improving PV technology, establishing a foundation for further innovation and exploration in the field. Implementing these parameters in the design of cooling systems can lead to maximized temperature reduction and superior cooling efficiency. This research paves the way for substantial advancements in PV technology, offering a robust foundation for further exploration and innovation.
Future Scope
Future research could explore additional parameters and their impact on the cooling process, offering comprehensive insights for refining cooling techniques in PV technology. Investigating variables such as different cooling mediums, flow rates, ambient temperature conditions, and the potential of advanced materials holds immense promise for significantly improving PV module efficiency. Integrating computational modeling with real-world testing will be essential to optimize these parameters, driving the development of more effective and sustainable cooling strategies. By synergistically integrating computational modeling with real-world testing, we can optimize these parameters, paving the way for the development of even more effective and sustainable cooling strategies. This continuous exploration will ensure that PV technology evolves to meet the growing demands for renewable energy solutions.
Acknowledgement: The authors acknowledge the resources provided by Sukkur IBA University and technical support from Universiti Malaysia Pahang Al Sultan Abdullah (www.umpsa.edu.my) (accessed on 30 June 2024).
Funding Statement: The authors received no specific funding for this project.
Author Contributions: Rahool Rai: Writing—original draft preparation, Methodology, Software, Conceptualization, Formal analysis. Fareed Hussain Mangi: Conceptualization, Supervision, Resources, Data curation. Kashif Ahmed: Software, Visualization, Investigation. Sudhakar Kumarasamy: Supervision, Validation, Writing—reviewing and editing. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data supporting the findings of this study is available within the article.
Conflicts of Interest: The authors disclose conflicts of interest about authorship, Dr. Sudhakar Kumarsamy is the member of the Editorial Board of Energy Engineering Journal. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
1. S. Hussain, W. Wang, and R. Maqbool, “Understanding the power disruption and its impact on community development: An empirical case of Pakistan,” Sustain. Energy Technol. Assess., vol. 55, no. 14, 2023, Art. no. 102922. doi: 10.1016/j.seta.2022.102922. [Google Scholar] [CrossRef]
2. R. Rai, S. Jamali, A. A. Zaıdı, M. Ali, and A. H. Memon, “Development of a small scale photovoltaic thermal hybrid (PV/T) system for domestic applications in Pakistan,” Clean Ener. Technol. J., vol. 1, no. 2, pp. 60–70, 2023. doi: 10.14744/cetj.2023.0006. [Google Scholar] [CrossRef]
3. S. Kanwal, M. T. Mehran, M. Hassan, M. Anwar, S. R. Naqvi and A. H. Khoja, “An integrated future approach for the energy security of Pakistan: Replacement of fossil fuels with syngas for better environment and socio-economic development,” Renew. Sustain. Energ. Rev., vol. 156, no. 80, 2022, Art. no. 111978. doi: 10.1016/j.rser.2021.111978. [Google Scholar] [CrossRef]
4. S. Sreenath, A. M. Azmi, N. Y. Dahlan, and K. Sudhakar, “A decade of solar PV deployment in ASEAN: Policy landscape and recommendations,” Energy Rep., vol. 8, pp. 460–469, 2022. doi: 10.1016/j.egyr.2022.05.219. [Google Scholar] [CrossRef]
5. P. Dwivedi, S. A. Ganesh, K. Sudhakar, A. Soni, and S. S. Priya, “Thermal and electrical performance of uncooled, nature-cooled, and photovoltaic thermal module,” Int. J. Photoenergy, vol. 2023, 2023, Art. no. 4720545. doi: 10.1155/2023/4720545. [Google Scholar] [CrossRef]
6. E. G. Merritt, N. Bowers, and S. E. Rimm-Kaufman, “Making connections: Elementary students’ ideas about electricity and energy resources,” Renew. Energy, vol. 138, no. 9, pp. 1078–1086, 2019. doi: 10.1016/j.renene.2019.02.047. [Google Scholar] [CrossRef]
7. R. Rai, A. R. Larik, K. Ahmed, S. Kumaramasy, and A. A. Zaidi, “Comparative analysis of finned absorber plate with and without black paint in Solar Air Heater,” in 4th Int. Conf. Comput., Math. Eng. Technol. (iCoMET), Sukkur, Pakistan, Mar. 16-17, 2023, pp. 1–4. doi: 10.1109/iCoMET57998.2023.10099171. [Google Scholar] [CrossRef]
8. A. Allouhi, S. Rehman, M. S. Buker, and Z. Said, “Recent technical approaches for improving energy efficiency and sustainability of PV and PV-T systems: A comprehensive review,” Sustain. Energy Technol. Assess., vol. 56, 2023, Art. no. 103026. doi: 10.1016/j.seta.2023.103026. [Google Scholar] [CrossRef]
9. Y. Hiben, M. B. Kahsay, and J. Lauwaert, “A review on solar thermal system design, integration, and techno-economic modeling for industrial heating and cooling processes,” in Proc. SOLAR, 2021 Conf., Online, International Solar Energy Society, Aug. 03–06, 2021, pp. 1–12. doi: 10.18086/solar.2021.01.02. [Google Scholar] [CrossRef]
10. A. Saxena, S. Deshmukh, S. Nirali, and S. Wani, “Laboratory based experimental investigation of photovoltaic (PV) thermo-control with water and its proposed real-time implementation,” Renew. Energy, vol. 115, no. 1, pp. 128–138, 2018. doi: 10.1016/j.renene.2017.08.029. [Google Scholar] [CrossRef]
11. S. M. Shalaby, M. K. Elfakharany, B. M. Moharram, and H. F. Abosheiasha, “Experimental study on the performance of PV with water cooling,” Energy Rep., vol. 8, no. 3, pp. 957–961, 2022. doi: 10.1016/j.egyr.2021.11.155. [Google Scholar] [CrossRef]
12. M. Patil, A. Sidramappa, A. M. Hebbale, and J. S. Vishwanatha, “Computational fluid dynamics (CFD) analysis of air-cooled solar photovoltaic (PV/T) panels,” in Mat. Today: Proc., May 2023, Art. no. S2214785323028249. doi: 10.1016/j.matpr.2023.05.198. [Google Scholar] [CrossRef]
13. Q. Zhou, P. Dong, M. Li, and Z. Wang, “Analyzing the interactions between photovoltaic system and its ambient environment using CFD techniques: A review,” Energy Build., vol. 296, no. 1, 2023, Art. no. 113394. doi: 10.1016/j.enbuild.2023.113394. [Google Scholar] [CrossRef]
14. E. J. Mahdi, S. Algburi, N. Al-Abadi, O. K. Ahmed, and A. K. Ahmed, “Photovoltaic panel cooling using ground source energy: CFD simulation,” Results in Eng., vol. 22, 2024, Art. no. 102144. doi: 10.1016/j.rineng.2024.102144. [Google Scholar] [CrossRef]
15. A. S. Abdelrazik et al., “ANSYS-Fluent numerical modeling of the solar thermal and hybrid photovoltaic-based solar harvesting systems,” J. Therm. Anal. Calorim., vol. 148, no. 21, pp. 11373–11424, 2023. doi: 10.1007/s10973-023-12509-2. [Google Scholar] [CrossRef]
16. M. E. H. Attia, M. E. Zayed, A. E. Kabeel, A. Khelifa, M. Arıcı and M. Abdelgaied, “Design and performance optimization of a novel zigzag channeled solar photovoltaic thermal system: Numerical investigation and parametric analysis,” J. Clean. Prod., vol. 434, no. 9, 2024, Art. no. 140220. doi: 10.1016/j.jclepro.2023.140220. [Google Scholar] [CrossRef]
17. A. Khelifa, A. E. Kabeel, M. E. H. Attia, M. E. Zayed, and M. Abdelgaied, “Numerical analysis of the heat transfer and fluid flow of a novel water-based hybrid photovoltaic-thermal solar collector integrated with flax fibers as natural porous materials,” Renew. Energy, vol. 217, no. 15, 2023, Art. no. 119245. doi: 10.1016/j.renene.2023.119245. [Google Scholar] [CrossRef]
18. P. Nahani, M. Eslami, and R. Hamzehzarghani, “Effects of wind on cooling and performance of photovoltaic arrays: A case study CFD modeling,” Energy, vol. 293, no. 12, 2024, Art. no. 130596. doi: 10.1016/j.energy.2024.130596. [Google Scholar] [CrossRef]
19. C. J. Ramanan, K. H. Lim, J. C. Kurnia, S. Roy, B. J. Bora and B. J. Medhi, “Floating solar PV study on the effect of water velocity and temperature,” in 2024 Int. Conf. Green Energy, Comput. Sustain. Technol. (GECOST), Miri Sarawak, Malaysia, IEEE, Jan. 2024, pp. 370–374. doi: 10.1109/GECOST60902.2024.10475107. [Google Scholar] [CrossRef]
20. A. Hussien, A. Eltayesh, and H. M. El-Batsh, “Experimental and numerical investigation for PV cooling by forced convection,” Alex. Eng. J., vol. 64, no. 11–12, pp. 427–440, 2023. doi: 10.1016/j.aej.2022.09.006. [Google Scholar] [CrossRef]
21. J. Sun, Y. He, X. Li, Z. Lu, and X. Yang, “CFD simulations for layout optimal design for ground-mounted photovoltaic panel arrays,” J. Wind Eng. Ind. Aerodynamics, vol. 242, no. 17, 2023, Art. no. 105558. doi: 10.1016/j.jweia.2023.105558. [Google Scholar] [CrossRef]
22. C. Kalkan, J. Duquette, and M. Akif Ezan, “Development of a novel computational fluid dynamics-based model for a solar photovoltaic/thermal collector-assisted domestic hot water system with sensible heat storage,” Appl. Therm. Eng., vol. 228, 2023, Art. no. 120424. doi: 10.1016/j.applthermaleng.2023.120424. [Google Scholar] [CrossRef]
23. D. G. Roychowdhury, “Overview of CFD,” in Computational Fluid Dynamics for Incompressible Flows, 1st ed. Boca Raton, USA: CRC Press, vol. 1, pp. 1–7, 2020. doi: 10.1201/9780367809171 [Google Scholar]
24. J. H. Ferziger, M. Perić, and R. L. Street, “Introduction to numerical methods,” in Computational Methods for Fluid Dynamics, 4th ed. Cham: Springer International Publishing, pp. 23–40, 2020. doi: 10.1007/978-3-319-99693-6 [Google Scholar]
25. J. Tu, G. H. Yeoh, C. Liu, and Y. Tao, “Governing equations for CFD—fundamentals,” in Computational Fluid Dynamics. Elsevier, pp. 63–122, 2024. doi: 10.1016/B978-0-323-93938-6.00019-1 [Google Scholar]
26. D. Anderson, J. C. Tannehill, R. H. Pletcher, R. Munipalli, and V. Shankar, “Numerical methods for boundary-layer-type equations,” in Computational Fluid Mechanics and Heat Transfer, 4th ed. Boca Raton, USA: CRC Press, pp. 534–620, 2020. doi: 10.1201/9781351124027 [Google Scholar] [CrossRef]
27. J. E. Matsson, An Introduction to Ansys Fluent. SDC Publications, 2023. [Google Scholar]
28. F. Schiro, A. Benato, A. Stoppato, and N. Destro, “Improving photovoltaics efficiency by water cooling: Modelling and experimental approach,” Energy, vol. 137, no. 7, pp. 798–810, 2017. doi: 10.1016/j.energy.2017.04.164. [Google Scholar] [CrossRef]
29. Y. A. Cengel and A. Ghajar, Heat and Mass Transfer: A Practical Approach, SI version, McGraw-670 HillEducation, 2011, vol. 671, no. 52. [Google Scholar]
30. J. H. Lienhard IV and J. H. Lienhard V, A Heat Transfer Textbook. Mineola, NY: Dover Publications, 2019. [Google Scholar]
31. S. Patankar, “Convection and diffusion,” in Numerical Heat Transfer and Fluid Flow, 1st ed. Boca Raton: CRC Press, pp. 76–109, 1980. 2018. doi: 10.1201/9781482234213. [Google Scholar] [CrossRef]
32. Y. A. Çengel and J. M. Cimbala, “Bernoulli and energy equations,” in Fluid Mechanics Fundamentals and Applications, Fourth ed. McGraw-Hill Education, 2019. [Google Scholar]
33. W. Al-Aloosi, Y. Alaiwi, and H. Hamzah, “Thermal performance analysis in a parabolic trough solar collector with a novel design of inserted fins,” Case Stud. Therm. Eng., vol. 49, no. 1, 2023, Art. no. 103378. doi: 10.1016/j.csite.2023.103378. [Google Scholar] [CrossRef]
34. M. Sheikholeslami and Z. Khalili, “Investigation of solar Photovoltaic cell utilizing hybrid nanofluid confined jet and helical fins for improving electrical efficiency in existence of thermoelectric module,” Appl. Therm. Eng., vol. 234, no. 15, 2023, Art. no. 121329. doi: 10.1016/j.applthermaleng.2023.121329. [Google Scholar] [CrossRef]
35. F. Hosseini and M. Sheikholeslami, “Effects of self-cleaning technique and nanofluid cooling on performance of photovoltaic solar unit employing sinusoidal surfaces,” Appl. Therm. Eng., vol. 240, no. 15, 2024, Art. no. 122223. doi: 10.1016/j.applthermaleng.2023.122223. [Google Scholar] [CrossRef]
36. M. Raju, R. N. Sarma, A. Suryan, P. P. Nair, and S. Nižetić, “Investigation of optimal water utilization for water spray cooled photovoltaic panel: A three-dimensional computational study,” Sustain. Energy Technol. Assess., vol. 51, no. 3, 2022, Art. no. 101975. doi: 10.1016/j.seta.2022.101975. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools