Characteristics of Rock Mechanics Response and Energy Evolution Regime of Deep Reservoirs in the Bozhong Sag, Bohai Bay Basin

1  Introduction

Conventional fossil energy (i.g., coal and gas) have always held a dominant position in Chinese national economy [1,2]. With the increase of energy demand and improvement of development technology, the exploitation depth of resources is increasing [3]. However, deep reservoirs face significant challenges due to increased reservoir depth, including high ground stress, high osmotic pressure and in-situ temperatures. These factors posed considerable difficulties for drilling engineering and reservoir development [4,5]. Among various methods for oil/gas extraction, hydraulic fracturing has emerged as a mature and effective technology for developing oil/gas in deep reservoirs [6,7]. Understanding the mechanical properties of deep reservoirs is crucial for oil/gas reservoir evaluation [1,6]. Accurate knowledge of the mechanical properties for reservoir rocks will provide essential theoretical references for implementation of deep oil/gas drilling engineering, hydraulic fracturing, and other development technologies.

Usually, the mechanical response law of rocks can be obtained by deformation and failure tests. The deformation tests include triaxial compression, uniaxial compression, three-point bending experiments and tensile shear tests [1]. For instance, Zhang et al. used deformation tests to derive the evolution law of strength parameters and strain softening model for Three Gorges Granite [8]. Combining triaxial compression tests with fracture mechanics theory, Zhu et al. revealed that tension cracks in rock are predominant, and the initiation angle obtained from elliptical crack model closely matched experimental results [9]. Qiao et al. conducted triaxial compression tests and investigated the acoustic emission features of deep granitic amphibolite [10]. Under the context of studying mechanics response for deep rocks, Zhang et al. carried out mechanical experiments for coal at different depths (ranging from 300 to 1050 m) [11]. After that, Jia et al. studied the uniaxial mechanical characteristics for coal with different depths in Pingmei mining area, and revealed the nonlinear variation law of elastic modulus with depth [12]. In addition, they also expounded the evolution law of mining dynamic behavior of coal in the depth range of 300 to 1050 m. Their findings indicated that the unloading strength and residual stress of coal increased continuously with depth. Li et al. conducted three-point bending experiments on shales of different sizes to investigate the influence of size effect on the anisotropy [13]. Xie et al. studied the anisotropic creep characteristics for shale and its correlation with stress [14].

The deformation test can effectively obtain the rocks strain under different stress, allowing for the exploration of evolution law in rock mechanical parameters. However, the deformation process involves the emergence, expansion, and extension of fractures until penetration. That process accompanied by energy input, accumulation, and dissipation. Through theory of rock energy dissipation and deformation test, the understanding of rock failure mechanism can be deepened. For instance, Miao et al. investigated the evolution mechanism of dissipative energy, frictional energy, and fracture energy for rock by triaxial cyclic mechanical tests [15]. Then the mechanical characteristics of rocks are explored. Zhang et al. conducted cyclic triaxial loading and unloading tests with acoustic emission monitoring on coal rocks at different depths, and studying the characteristic laws of energy evolution in coal [16]. By analyzing the test results of uniaxial cyclic loading and unloading on red sandstone, Meng et al. revealed the law of energy accumulation, dissipation, and distribution for damaged rocks [17]. Ao et al. proposed an effective method to construct a numerical model by three-dimensional agglomerates of pre-cracked granite [18]. Furthermore, mechanism for rock energy dissipation can not only describe deformationprocess, but also determine the destabilization process and intensity of damage more comprehensively [19,20]. Meng et al. proposed an area calculation method based on the loading, and used energy consumption ratio “ku” to judge the damage destabilization process in rock [21]. Ma et al. evaluated the change in strength and damage degree of rocks during the energy dissipation process [22,23].

In this work, we focus on outcrop cores with metamorphic granite as the research object to analyze characteristics of rock mechanical response in the deep reservoir of Bozhong Sag. By conducting rock mechanics tests under high stress conditions with rock mechanics equipment, then the deformation characteristics of deep rock under various stress are examined. Moreover, combining energy dissipation mechanism, the impact of stress on the energy evolution characteristics for rock specimens are also revealed. A comprehensive discussion on the intensity of rock damage in deep reservoir of Bozhong Sag is provided, which aims to provide theoretical guidance for oil/gas production in this area.

2  Experimental Work

2.1 Regional Geological Overview

As depicted in Fig. 1, the Bohai Central Depression serves as a secondary tectonic unit within the Bohai Bay Basin, positioned in the middle of the basin with a NE trend. It covers an area of approximately 8660 km2, making it the largest depression in the Bohai Sea. Moreover, it serves as sedimentation center and oil/gas production center of entire Bohai Bay Basin. The lithology of Bozhong Sag is complex due to influence of multiple tectonic movements. It comprises Archaean Taishan Group, Lower Paleozoic Cambrian and Ordovician, Upper Paleozoic Carboniferous and Permian, and Mesozoic Jurassic and Cretaceous rocks, with Archaean metamorphic rocks, Paleozoic carbonate rocks, and Mesozoic volcanic rocks being particularly well-developed [24]. These formations are considered crucial subduction reservoirs. The Archaean metamorphic subduction suture reservoirs, in particular, serve as main gas-producing formations [25].

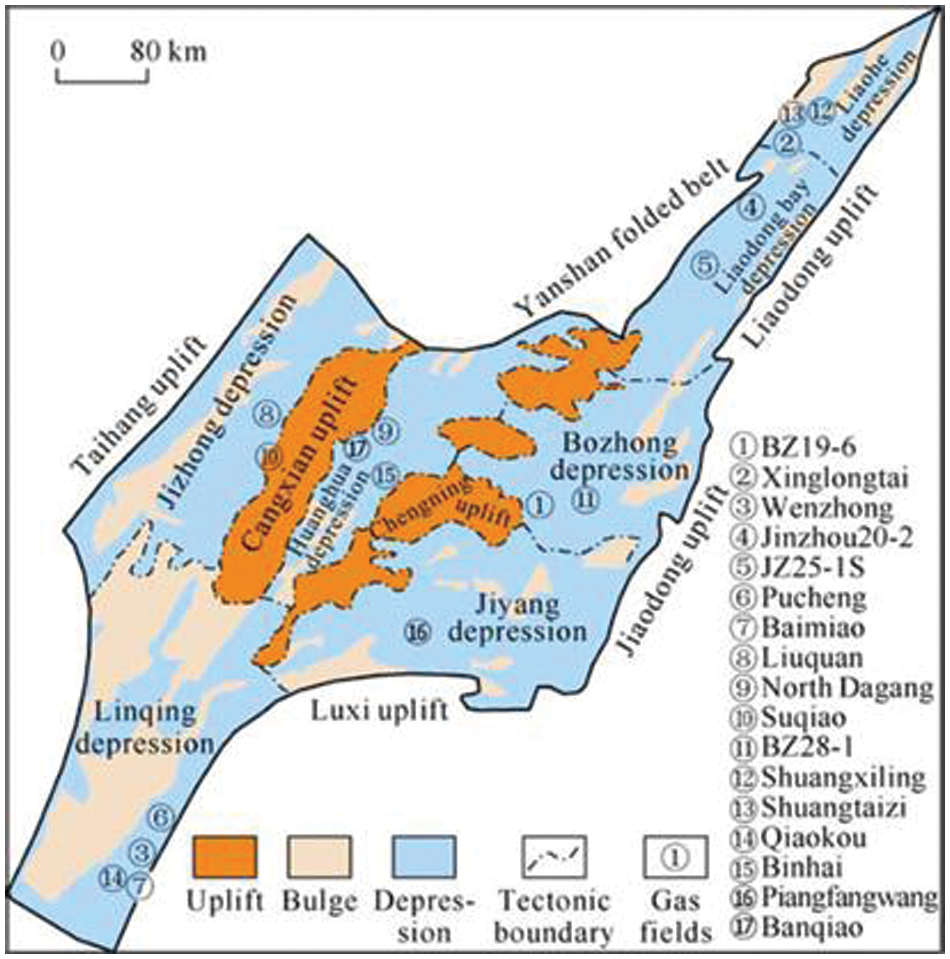
Figure 1: Regional overview of Bohai Bay Basin (from Xue et al. [25])

2.2 Specimens Preparation

Drilling data reveals that the Bozhong 19–6 submerged mountain is primarily composed of diabase, diabase gneiss, and mixed gneiss, all of which belong to Archaean reservoirs. The internal reservoir exhibits a combination of pores and fractures, classifying it as a dual pore medium. To further explore rock mechanics response characteristics for reservoirs in the Bozhong Sag, outcrops of metamorphic rocks from the Swire boundary are selected for relevant experiments. The deep strata outcrops in the Bozhong area, extending to the western part of Shandong Province, share some lithological resemblance with the Bozhong 19–6 submerged mountain reservoir [21]. Therefore, the tests conducted in this paper are determined to be based on the outcrop cores from this specific region. Careful selection of large cores is carried out on-site, and the cores are processed into cylindrical specimens with a diameter of 50 mm and a height of 100 mm using rock mechanics internationally recommended methods of cutting and grinding. First of all, the X-Ray Diffraction (XRD) test was carried out on sample by using the DMAX-3C X-ray diffractometer produced by Nippon Shinrikyo Corporation (Tokyo, Japan). That test is employed to determine the basic mineral fractions of the specimens. And the results show that sample was consisted of mica, quartz, potassium feldspar, and plagioclase, as illustrated in Fig. 2.

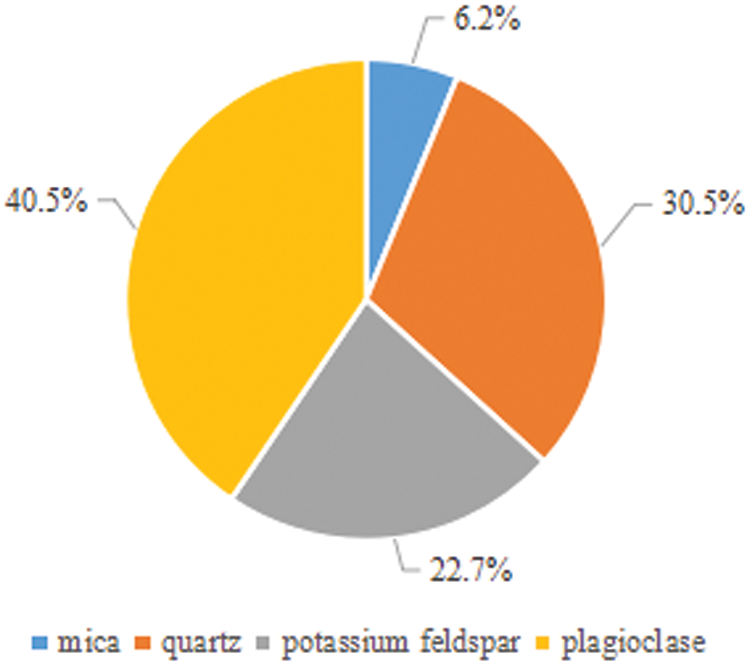
Figure 2: Percentage of mineral composition of specimens

Subsequently, the surface morphology characteristics of samples were obtained by JSM-7500F cold field emission scanning electron microscope (SEM) of Shenzhen University, as shown in Fig. 3. The SEM images demonstrate the presence of both micro-fractures and pores within the specimens. Therefore, that rock can be determined as a dual porous medium.

Figure 3: Microscopic morphology of rock specimens at different magnifications

2.3 Testing Method

The test equipment used in this paper is primarily the MTS815Flex Test GT electro-hydraulic servo rock mechanics test system, which depicted in Fig. 4. That test system contains a pressurization system, control system, acquisition system, and acoustic emission system, among others.

Figure 4: Rock mechanics test system

Firstly, the confining stress was set to 0, and uniaxial compression tests are conducted on specimens to obtain the basic physical parameters. Subsequently, triaxial compression tests are performed by incrementally setting the confining stress to 15, 30, 45, 60, 75, and 90 MPa, respectively. Specific test procedures is that: (1) Processed specimen is carefully placed at the center between two rigid gaskets, and the upper and bottom portions of specimen are sealed. The entire specimen is then enclosed with a heat-shrinkable tube to prevent hydraulic oil from contacting rock, thus avoiding any interference with the test results; (2) The specimen and rigid gaskets are accurately positioned at the center of the bearing table, ensuring that the pressure head is in contact with the specimen. The circumferential extensometer and axial extensometer are then installed; (3) The pressure chamber is slowly lowered, and the sealing bolts around are tightened. Afterward, the pressure chamber is filled with oil; (4) Upon completion of oil filling, the confining stress is gradually increased at a rate of 3 MPa/min until reaching the desired hydrostatic pressure. Subsequently, the axial pressure is applied at a rate of 30 kN/min. Once rock sample enters the yielding stage, circumferential displacement control is initiated, maintaining a set rate of 0.04 mm/min. To quickly obtain residual strength after the peak, the control method is switched to displacement control, continuing until the specimen failure occurs.

3  Characteristics of Rock Mechanics Response of Deep Reservoir

3.1 The Mechanism of Rock Mechanics Response

The mechanical parameters of rock are intricately linked to its deformation behavior. Typically, the fundamental physical and mechanical properties can be determined through uniaxial compression tests. During these tests, as axial pressure increases, primary fractures in rock gradually shift from static to continuous secondary extension fractures, developing along structural weak surfaces and within the metamorphic rock matrix. Stress-strain curves obtained from uniaxial compression tests, which illustrated in Fig. 5.

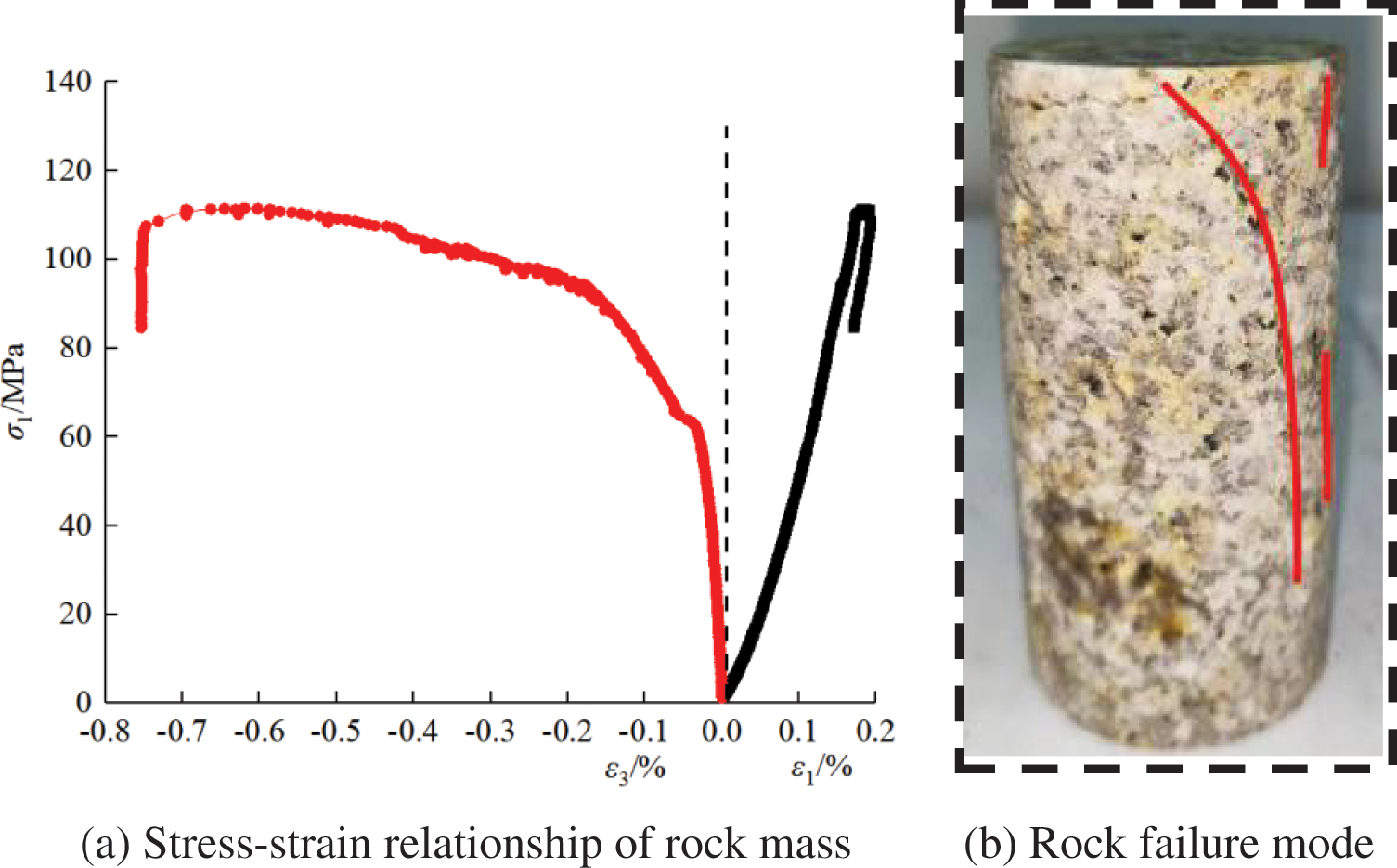
Figure 5: Uniaxial compression stress-strain curve of the rock specimen

As depicted in Fig. 5, the stress-strain curve exhibits distinctive stages during uniaxial compression test. Initially, the specimen undergoes an initial compression-density stage, characterized by limited nonlinearity in the stress-strain relationship. As load increases, the curve demonstrates pronounced linear elasticity, reflecting the rock ability to deform elastically in response to stress. Following an extended elastic stage, a slight reduction in the curve slope indicates a transition to a strain-hardening stage, where the elastic limit approaches the yield limit. At this point, failure becomes imminent. Once peak strength is reached, failure occurs rapidly, leading to a steep drop in stress-strain curve. The testing machine ceases to exert force, but energy released by specimen itself sustains the failure process, rendering it uncontrollable [19]. Nevertheless, it is noteworthy that deformation remains predominantly linearly elastic until the peak stress is attained. Subsequently, the stress diminishes rapidly, signifying evident brittle characteristics of rock. In summary, the stress-strain behavior during uniaxial compression exhibits distinct stages, including initial compression-density, linear elasticity, strain-hardening, and eventual failure. The rock’s behavior remains predominantly elastic until it reaches its peak strength, after which it undergoes brittle failure.

In order to delve deeper into the mechanical behavior of the deep reservoir in Bozhong Sag, triaxial compression tests are conducted on rocks under various stress. The results provided insights into the response of deformation for rock under different stress, as depicted in Fig. 6.

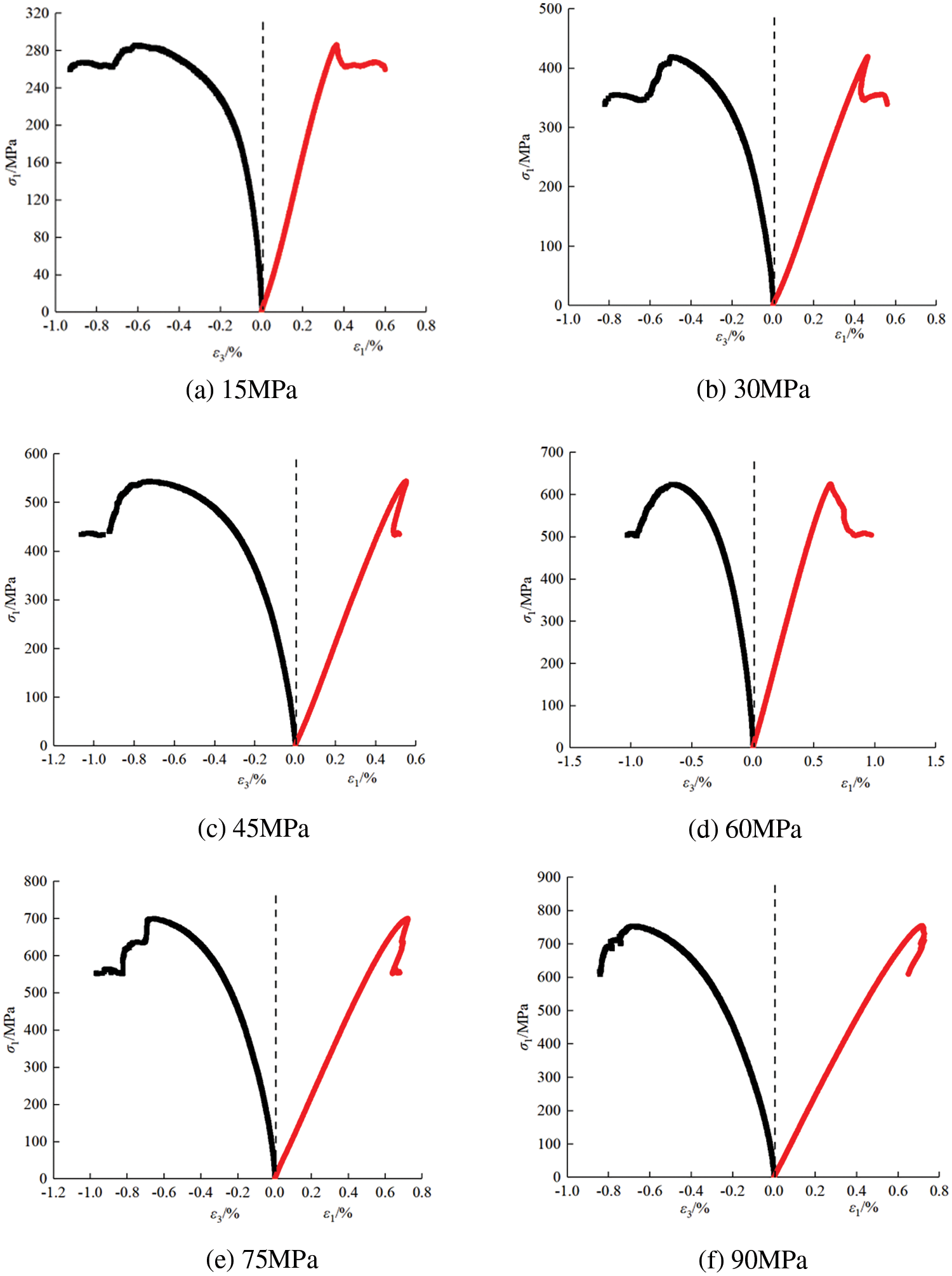
Figure 6: Stress-strain relationship curves of rock specimens under different confining stress

As depicted in Figs. 6 and 7, the deformation processes of six specimen groups under varying stress exhibit similarities, with axial and circumferential strains displaying an initial increase followed by a decrease. The fracture compression stage experienced by each specimen group is relatively short, indicating higher density of deep reservoir in Bozhong Sag, limiting the available space for compressional density. This observation aligns with previous research findings [13,15]. Comparing the deformation and damage processes in rock under each confining stress, it becomes evident that rock strength and other characteristics are significantly enhanced with increasing confining stress. The response mechanism between confining stress and rock deformation can be summarized as: (1) The full stress-strain curves of outcrop metamorphic granite cores from Bozhong Sag, under triaxial compression, exhibit typical “5 stage” characteristics, i.e., encompassing fracture compression, new fracture formation, stable fracture expansion, fracture unstable expansion, and post-peak residual. Due to the dense and robust nature in core, the fracture compression stage and non-stable fracture extension stage are relatively short. The deformation processes of rock specimens mainly concentrate on three stages, i.g., new fracture formation, stable fracture expansion, and post-peak residual deformation. (2) Under different confining stress, the stress-strain curves of rock specimens display a rapid drop after reaching peak stress, accompanied by sudden damage and a crisp sound. Subsequently, the specimens enter post-peak residual deformation stage, where rock bearing capacity rapidly declines with increased deformation. However, the bearing capacity does not fall to zero, indicating that the granite retains a trace of compressive capacity even after failure. (3) All specimens exhibit significant radial strains after the peak, signifying the gradual release of strain energy within rock under the influence of circumferential strain. Furthermore, the axial stress rapidly declines after reaching peak strength, and only a few specimens enter residual stage with certain residual strength, exhibiting strong characteristics of brittle damage.

Figure 7: Typical stages of rock failure under triaxial stress (15 MPa)

3.2 Analysis of the Evolution of Rock Mechanical Characteristics Parameters of Deep Reservoir

Both elastic modulus and Poisson’s ratio are crucial mechanical parameters that reflect deformation characteristics of rock. Therefore, it is essential to investigate variations in these parameters with different depths. The elastic modulus and Poisson’s ratio of rock under triaxial stress can be obtained using the following equation [11,12]:

E=σ1−2μσ3ε1(1)

μ=Bσ1−σ3σ3(2B−1)−σ1(2)

B=ε3ε1(3)

where E is elastic modulus, MPa; μ is the Poisson’s ratio; σ1 is axial stress, MPa; σ3 is lateral stress, MPa; ε1 is the measured axial strain; ε3 is the measured lateral strain.

The elastic modulus and Poisson’s ratio of core in different depth can be obtained according to the above equations and stress-strain curves, as depicted in Fig. 8.

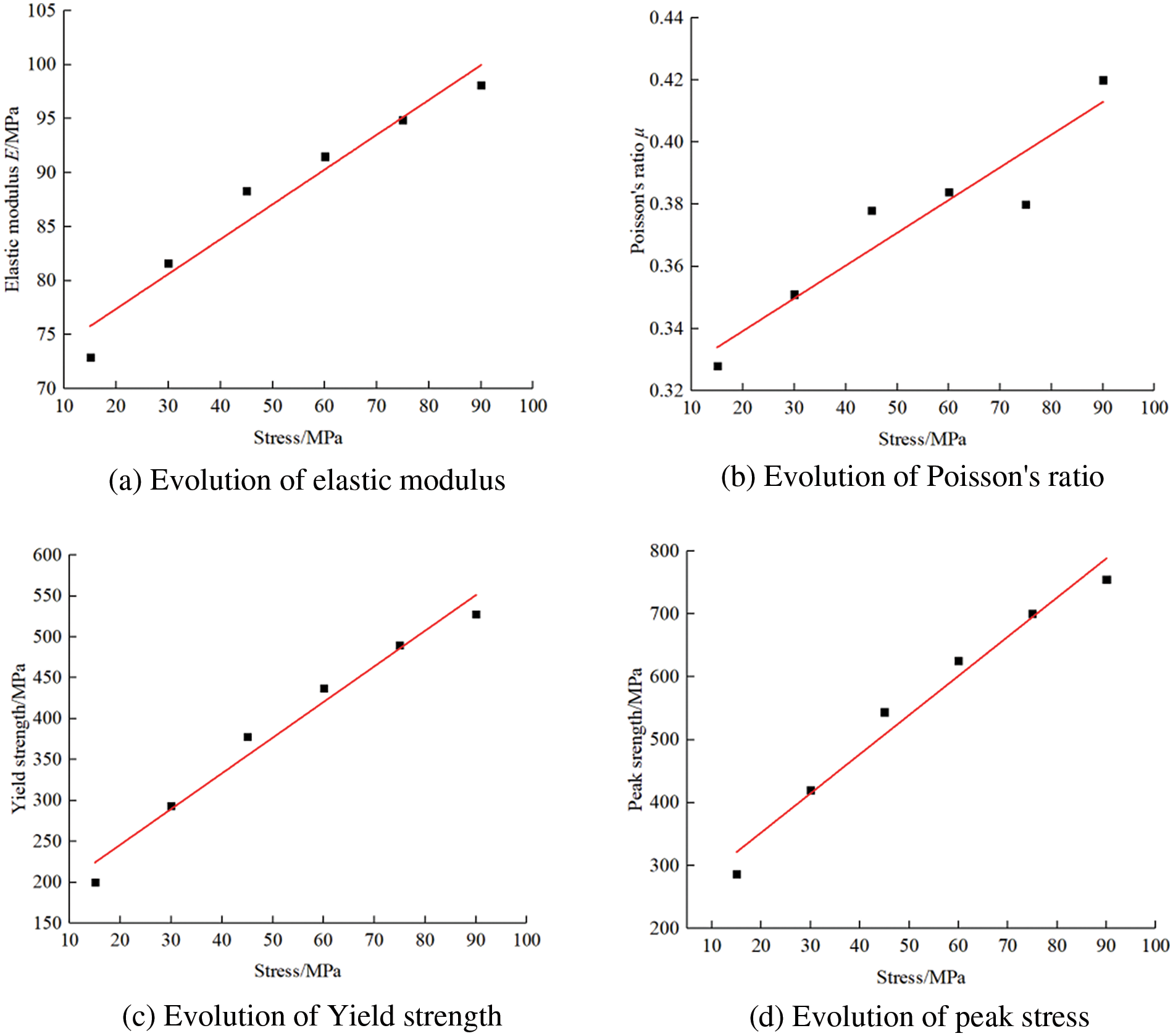
Figure 8: Evolution of rock mechanical parameters under different confining stress

As depicted in Fig. 8, the characteristic parameters (such as E, v, and peak strength) demonstrate varying degrees of increase with the rise of confining stress. These observations can be attributed to several factors. Firstly, the variability of reservoir geological environment, particularly the fluctuations in crustal stress environment, result in a denser arrangement of material particles and reduced porosity in the deep rock. Additionally, the high crustal stress environment within reservoir necessitates rock damage driven by larger external loads [26]. The elastic modulus, as a fundamental mechanical parameter measuring the material’s elastic deformation capacity. Which indicates that with increasing depth, the stress generated in deeper rocks for the same deformation becomes larger. In other words, the stiffness of rocks increases with depth. Poisson’s ratio reflects the rock’s ability to rupture under stress, and the elastic modulus reflects the rock’s ability to maintain fracture after rupture. Moreover, the strain corresponding to yield strength signifies the end of the primary elastic deformation stage, and gradually increasing strength value represents accumulating total energy stored in reservoir prior to failure. The higher confining stress leads to greater hardness of reservoir rock and enhances its resistance to failure. Moreover, the increase in peak strength indicates a significantly heightened difficulty in both stable and unstable rupture of deep reservoir specimens due to elevated confining stress. It is evident that confining stress restricts sprouting and expansion of rock fractures, leading to an increase in the rock bearing capacity. As depth increases, the formation of various fractures in reservoir after fracturing becomes more challenging [11,26].

3.3 Analysis of Rock Damage Patterns in Deep Reservoirs

According to experimental results of triaxial compression test of rocks with different stress, the failure pattern of specimens are obtained, as shown in Fig. 9.

Figure 9: Damage pattern of rocks after triaxial test under different confining stress

As depicted in Fig. 8, the failure behavior of rock specimens under triaxial compression tests generally conforms to compression-shear failure criterion [15,21]. For all rocks under different stress, a typical single shear damage surface is observed, which transforms into shear slip damage along weak surface after the circumferential deformation of specimens is controlled by the confining stress. At an confining stress of 60 MPa, a significant amount of powdered fragments is generated around core, and the quantity of powdered fragments at shear surface increases with higher stress. This indicates that the rock damage in form of fractures intensifies with increasing depth and confining stress. Furthermore, scanning electron microscopy (SEM) tests are conducted on specimens after triaxial compression under different stress using a JSM-7500F electron microscope, with a scale of 150 μm selected for examination to observe internal morphology and characteristics of the specimens, as shown in Fig. 10.

Figure 10: Microscopic fracture characteristics of rocks under different confining stress

From Fig. 10, it is evident that microscopic cracks exhibit varying degrees of change after undergoing triaxial compression tests with different stress. Apart from differences in initial defects, the main reason is attributed to distinct stress, which results in different levels of deformation in deep rock during triaxial compression. A comparison of the microscopic morphology of specimens tested under different stress which reveals that rock damage is accompanied by more crack generation when confining stress is low (Figs. 10a–10c). Conversely, macroscopic cracks are significantly reduced under high confining stress conditions (Figs. 10e and 10f), indicating that confining stress effectively inhibits the development of micro-cracks, consistent with previous research findings [27,28]. Therefore, this also indicates that it is less likely to produce complex micro-cracks in deep reservoir, which may not be conducive to the implementation of hydraulic fracturing.

4  Discussion

4.1 Energy Dissipation Mechanism of Deep Reservoir in Bozhong Sag

The energy input, accumulation, dissipation, and release, along with continuous transformation of loaded rock during the process of deformation, represent the essence of the physical behavior of rock. Rock failure is characterized as a destabilization phenomenon driven by energy [15,21]. In this paper, the focus is on the irreversibility of dissipation energy and the reversibility of elastic energy, along with their respective effects on rock bulk crushing intensity. As such, only releasable elastic energy and dissipation energy are considered. The latter encompasses fracture surface energy and plastic energy, contributing to damage formation and resulting in strength loss. The release of accumulated elastic energy in rocks serves as the intrinsic cause of sudden rock failure. By applying the law of conservation of energy [11,12], it can be deduced that:

U=Uid+Ue(4)

where U is external input energy; Ue is the elastic energy accumulated in the rock; Uid is energy dissipated during the deformation and damage of the rock, and the relationship is shown in Fig. 11.

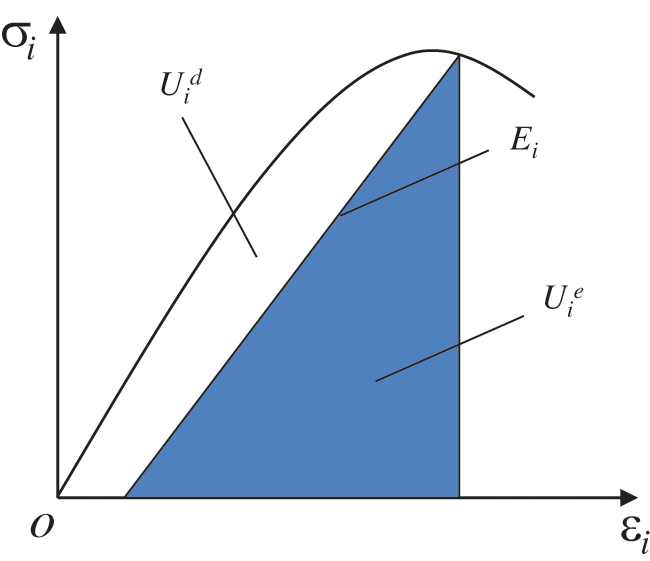
Figure 11: Quantitative relationship between energy dissipation Uid and releasable strain energy Uie of rock unit [12]

In general, elastic energy is determined by analyzing rock loading and unloading stress-strain curve. Specifically, the energy released during unloading is considered to be elastic energy accumulated at the corresponding stress level during unloading. The difference between total energy during loading, and reduced value after unloading represents dissipated energy under that specific stress level [12]. For sake of calculation convenience, the elastic energy Uie is appropriately simplified, and the unloading elastic modulus is taken as the initial elastic modulus. The energy of each part of the rock unit in the main stress space can be expressed as follows:

U=∫0ε1σ1dε1+∫0ε2σ2dε2+∫0ε3σ3dε3(5)

U e=12E0[σ12+σ22+σ32−2μ(σ1σ2+σ2σ3+σ1σ3)](6)

4.2 Energy Evolution Law of Deep Rock Reservoir

Based on rock stress-strain curves obtained under various stress, the accumulated input energy, elastic energy, and dissipated energy during deformation of rocks in reservoirs with different stress are calculated using energy calculation method described above. The results are presented in Fig. 12.

Figure 12: Relationship between dissipation energy and axial strain in rocks under different stress

From Fig. 12, it can be observed that the energy changes of each specimen under different stress exhibit similar trends, with an initial increase followed by a decrease as strain progresses. The process of energy dissipation in the rock under different stress corresponds to characteristic stages observed in deformation-damage curve, which aligns with previous findings [15,21]. The specific evolution process can be described as follows: (1) Fracture compaction and elastic deformation stage: During this stage, the input energy curve approximately coincides with the elastic strain energy curve, while the dissipation energy curve remains near the zero point. As the strain increases, the growth rate of elastic strain energy gradually rises, primarily due to the compacting of fracture specimens and the increase in strain energy stored per unit strain. (2) Stable fracture extension stage: In this stage, fractures start to sprout and expand, leading to a decrease in the specimen’s strength. The growth rate of elastic strain energy gradually slows down, and the dissipation energy increases gradually, albeit at a relatively low rate. (3) Unstable fracture extension stage: The growth rate of the elastic strain energy curve decreases significantly and moves away from the input energy curve. Meanwhile, the growth rate of dissipation energy curve increases significantly. This is mainly attributed to accelerated the dissipation rate of strain energy resulting from rapid new growth, expansion, and intersection of fractures. (4) Post-peak stage: When peak stress is reached, the elastic strain energy curve experiences a sharp decline, while the dissipation energy curve increases significantly in a stepwise manner. This is mainly due to the release of a large amount of strain energy at the moment of primary fracture penetration. Additionally, even in post-peak stage, the specimens still retain some load-bearing capacity. As fractures expand and energy is dissipated, the elastic strain energy curve gradually decreases, and the dissipation energy curve continues to increase.

4.3 Effect of Confining Stress on Energy Transformation during the Evolution of Rock Fracture

The process of rock deformation and damage essentially involves the occurrence, expansion, and extension of fractures. The mechanical energy provided by testing machine continuously transforms into internal energy of rocks. This continuous energy dissipation promotes deterioration of mechanical properties of rocks. The release of energy directly leads to expansion of rock fractures and eventually results in instability [21,29]. Examining mechanical properties of deep rocks from an energy perspective allows for a closer understanding of their deformation and damage characteristics. In line with studies by Du et al. [29,30], this paper analyzes the energy at points of fracture initiation, damage, and peak during the rock damage process to further investigate mechanisms of deformation damage and fracture extension. The relationship between energy at different characteristic points and the confining stress is illustrated in Fig. 13.

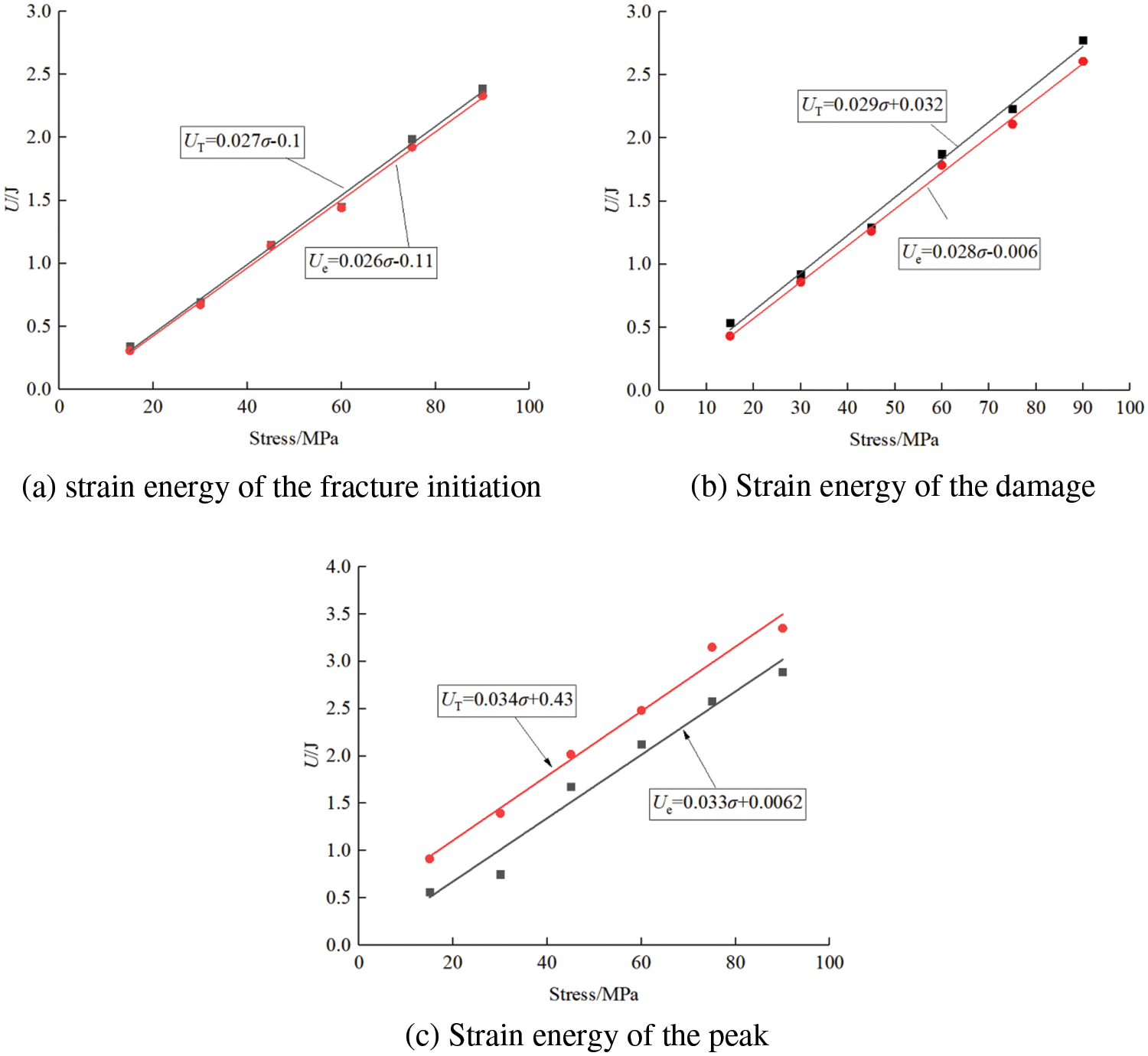
Figure 13: The evolution of the characteristic energy with the confining stress where UT is the total energy of the rock

During the drilling and hydraulic fracturing process, rock undergoes engineering disturbances, leading to continuous energy accumulation. When a sufficient amount of energy accumulates, the stored elastic energy is rapidly released, resulting in expansion and extension of rock fractures until complete penetration occurs. With increasing confining stress, the elastic strain and total input energy at fracturing stress tend to increase. Higher confining stress requires more energy to initiate expansion of original fractures in rock specimens and absorb higher elastic strain energy to promote unstable fracture expansion. However, high confining stress also restricts fracture formation and slip [21,29]. The damage stress point corresponds to unstable extension stage of fractures, thus damage strain energy follows a similar pattern as fracture initiation strain energy. Moreover, energy at peak stress represents the ultimate energy of rock damage, and both elastic energy and total energy at peak point tend to increase with higher confining stress.

4.4 Damage Evolution Mechanism of Deep Reservoir in Bozhong Sag

With increasing depth, geological structure becomes more complex, and the influence of high crustal stress on the reservoir environment becomes more significant, resulting in different mechanical deformation and damage characteristics compared to the shallow part [1]. Among these, the deformation of rock mainly involves sprouting, expansion, and extension of fractures, accompanied by energy dissipation. The dissipation energy indirectly reflects internal deformation and damage process of loaded rock specimens, transitioning from an intact structure to a fractured structure, and eventually reaching a relatively stable state after internal structural reorganization of the rock specimens [15]. The process of loaded rock specimens transitioning from a steady state to an unstable state represents the accumulation of internal damage leading to unstable failure, and it also involves a sudden change in energy transformation within rock specimens [19]. Therefore, energy dissipation can be used to define damage variables that characterize accumulation of internal damage in loaded rock specimens [15].

D=UdUpd(7)

where Upd is the dissipated energy corresponding to the peak point.

By analyzing rock damage process, the fracture initiation point, damage point, and peak point of the rock are determined, and the curve depicting the change of damage variable in the rock is obtained, as illustrated in Fig. 14.

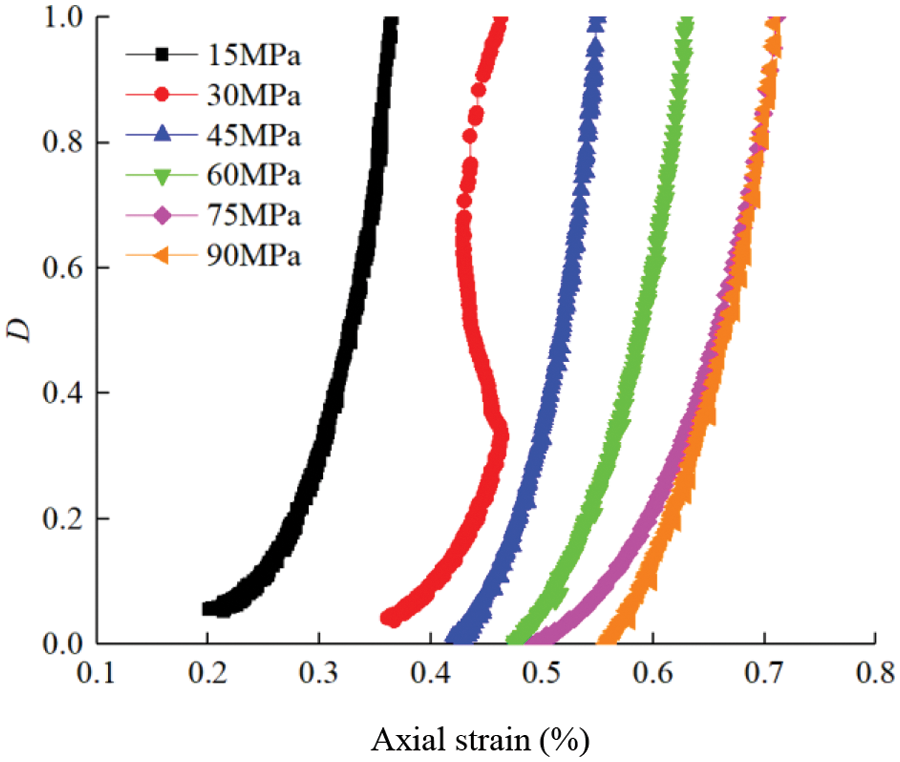
Figure 14: Evolution of energy consumption ratio index of rocks under different confining stress

From Fig. 14, it is evident that during the process of strain increase, the internal damage within the rock exhibits nonlinear growth with the increase in stress, while in the initial loading stage, the internal damage within the rock shows approximately linear growth with the increase in strain. As the strain further increases, the growth rate of internal damage gradually accelerates after the rock enters the plastic stage, and the growth rate of damage reaches its maximum as the rock approaches failure. When comparing different stress, it can be observed that the inflection point of damage variables in the loaded rock specimens is more pronounced at lower stress. This is because under low confining stress, brittle damage still occurs in the loaded rock sample, and when the rock sample is damaged within a short time, the accumulated elastic energy is rapidly released, leading to a sharp increase in dissipation energy. As a result, the damage variable instantaneously increases, and a distinct peak inflection point appears [15,21]. On the other hand, as the confining stress increases, the inflection point of energy consumption ratio gradually shifts backward and becomes less pronounced. The reason for this is that the confining stress can restrain the formation and intensity of fractures in loaded rock specimens, thereby to some extent inhibiting rate of energy dissipation and release when the rock specimens undergo fracturing or failure [26].

5  Conclusion

In this paper, we conducted simulations and analyses of the rock mechanics response of the deep reservoir in Bozhong Sag, focusing on the outcrop cores from the Archean Group. We performed rock mechanical tests under high-stress conditions using the rock mechanics equipment and investigated deformation and damage characteristics of the deep reservoir rocks under different stresses. With the energy dissipation mechanism, the influence of confining stress on the energy evolution and distribution characteristics of rocks is revealed. By combining experimental and theoretical analyses, the following conclusions can be drawn:

1.    Regardless of confining stress conditions, the deformation process of the deep reservoir in Bozhong Sag goes through five stages (i.g., fracture compacting stage, new fracture formation stage, fracture stable expansion stage, fracture unstable expansion stage, and post-peak residual deformation stage). Wherein, the failure of rock is mainly tensile shear failure. The microscopic scanning results of the damaged samples show that the greater the confining stress, the less likely it is for the rocks to form complex cracks. This also shows that the deeper you go, the worse it is for fracturing technology.

2.    The elastic stage of the rock grows with the increase of the initial confining stress, and the peak strength and yield strength are significantly enhanced with the increase of the initial confining stress, which shows the obvious confining stress effect during the test. Additionally, the stress-strain curves of rock specimens under different confining stress conditions all exhibit a rapid decline after reaching peak stress, displaying distinct characteristics of brittle fracture.

3.    The energy change pattern of each specimen is similar under different stress, and the energy dissipation process of the rock aligns with the trend of the deformation damage curve, displaying stage characteristics. The characteristic energy of the rock specimens increases with the rise in confining stress. In the pre-peak stage, the energy of the loaded rock specimens rises with the increase in confining stress, with a major portion of the work done by the testing machine on the rock specimen being converted into elastic energy stored within it. In the post-peak stage, the proportion of dissipation energy gradually increases.

4.    The damage variable D is introduced to quantify the degree of deformation and damage of the loaded rock. During the process of strain increase, the internal damage of the rock exhibits nonlinear growth with the increase in stress, and the rate of internal damage growth gradually intensifies as the rock enters the plastic stage, reaching its peak when close to failure. Lower stress shows a more pronounced inflection point in the change of the damage variable for the loaded rock specimens. As the confining stress increases, the inflection point of the damage variable curve gradually shifts backwards and become less apparent. This phenomenon is primarily attributed to the ability of confining stress to restrict the rate of energy dissipation and release during the fracture or failure of rock specimens to some extent.

Acknowledgement: All authors acknowledge the support and cooperation of their respective institutions.

Funding Statement: This research is funded by the Scientific and Technological Service Project of CNOOC Tianjin Branch “Research on Rock Mechanical Response Characteristics and Fracture Extension Mechanism of Metamorphic Reservoirs in the Southwest Ring of the Archaean Group in the Bozhong Sag, Bohai Bay Basin”. CCL2022TJX0NST1189.

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Suogui Shang; data collection: Kechao Gao; analysis and interpretation of results: Qingbin Wang, Xinghua Zhang; draft manuscript preparation: Pengli Zhou, Jianhua Li, and Peng Chu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data are presented in the paper.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. H. Xie et al., “Experimental study on rock mechanical behavior retaining the in situ geological conditions at different depths,” Int. J. Rock Mech. Min., vol. 138, pp. 104548, Feb. 2021. doi: 10.1016/j.ijrmms.2020.104548. [Google Scholar] [CrossRef]

2. J. Lu et al., “Effect of microwave radiation on mechanical behaviors of tight fine sandstone subjected to true triaxial stress,” Int. J. Rock Mech. Min., vol. 152, pp. 105063, Feb. 2022. doi: 10.1016/j.ijrmms.2022.105063. [Google Scholar] [CrossRef]

3. J. H. Li, B. B. Li, Q. Y. Cheng, and Z. Gao, “Characterization of the fracture compressibility and its permeability for shale under the effects of proppant embedment and compaction: A preliminary study,” Pet Sci., vol. 19, no. 3, pp. 1125–1138, Jun. 2022. doi: 10.1016/j.petsci.2021.12.021. [Google Scholar] [CrossRef]

4. P. Chu et al., “Influence of desorption hysteresis effects on coalbed methane migration and production based on dual-porosity medium model incorporating hysteresis pressure,” Comput. Geotech., vol. 165, pp. 105893, Jan. 2024. doi: 10.1016/j.compgeo.2023.105893. [Google Scholar] [CrossRef]

5. J. Li, H. Xie, J. Lu, M. Gao, B. Li and Y. Wu, “New permeability model of deep coal rock considering the structure and 3D stress compression-induced anisotropy,” Geomech. Geophys. Geo., vol. 8, pp. 204, Nov. 2022. doi: 10.1007/s40948-022-00505-z. [Google Scholar] [CrossRef]

6. P. Ibemesi and P. Benson, “Effect of pressure and stress cycles on fluid flow in hydraulically fractured, low-porosity, anisotropic sandstone,” Rock Mech. Rock Eng., vol. 56, no. 1, pp. 19–34, Sep. 2023. doi: 10.1007/s00603-022-03043-y. [Google Scholar] [CrossRef]

7. M. Fazio, P. Ibemesi, P. Benson, D. Bedoya-González, and M. Sauter, “The role of rock matrix permeability in controlling hydraulic fracturing in sandstones,” Rock Mech. Rock Eng., vol. 54, no. 10, pp. 5269–5294, Jul. 2021. doi: 10.1007/s00603-021-02580-2. [Google Scholar] [CrossRef]

8. F. Zhang, Q. Sheng, Z. Zhu, and Y. Zhang, “Study on post-perk mechanical behaviour and strain-softening Model of Three Gorges Granite,” (in ChineseChinese J. Rock Mech. Eng., vol. 27, no. s1, pp. 2651–2655, Dec. 2008. [Google Scholar]

9. Z. Zhu, Q. Sheng, X. Leng, and Z. Zhang, “Study on crack initiation mechanism of Three Gorges Granite,” (in ChineseChinese J. Rock Mech. Eng., vol. 26, no. 12, pp. 2570–2575, Dec. 2007. [Google Scholar]

10. L. Qiao, X. Wang, and Y. Li, “Study of acoustic emission and characteristic stress in deep granodiorite failure process,” (in ChineseChinese J. Rock Mech. Eng., vol. 33, no. S1, pp. 2773–2778, Dec. 2014. [Google Scholar]

11. Z. Zhang et al., “Deformation damage and energy evolution characteristics of coal at different depths,” Rock Mech. Rock Eng., vol. 52, no. 52, pp. 1491–1503, Jul. 2018. doi: 10.1007/s00603-018-1555-5. [Google Scholar] [CrossRef]

12. Z. Jia et al., “Energy evolution of coal at different depths under unloading conditions,” Rock Mech. Rock Eng., vol. 52, no. 52, pp. 4637–4649, May 2019. doi: 10.1007/s00603-019-01856-y. [Google Scholar] [CrossRef]

13. C. Li, D. Yang, H. Xie, L. Ren, and J. Wang, “Size effect of fracture characteristics for anisotropic quasi-brittle geomaterials,” Int. J. Min. Sci. Tech., vol. 33, no. 2, pp. 201–213, Feb. 2023. doi: 10.1016/j.ijmst.2022.11.004. [Google Scholar] [CrossRef]

14. Y. Xie, M. Z. Hou, H. Liu, and C. Li, “Anisotropic time-dependent behaviors of shale under direct shearing and associated empirical creep models,” J. Rock Mech. Geotech., vol. 16, no. 4, pp. 1262–1279, 2024. doi: 10.1016/j.jrmge.2023.05.001. [Google Scholar] [CrossRef]

15. S. Miao, J. Liu, X. Zhao, and Z. Huang, “Energy dissipation and damage characteristics of Beishan granite under cyclic loading and unloading,” (in ChineseChinese J. Rock Mech. Eng., vol. 40, no. 5, pp. 928–938, May 2021. [Google Scholar]

16. A. Zhang et al., “Mechanical properties and energy characteristics of coal at different depths under cyclic triaxial loading and unloading,” Int. J. Rock Mech. Min., vol. 161, pp. 105271, Jan. 2023. doi: 10.1016/j.ijrmms.2022.105271. [Google Scholar] [CrossRef]

17. Q. B. Meng, J. F. Liu, H. Pu, B. X. Huang, Z. Z. Zhang and J. Y. Wu, “Effects of cyclic loading and unloading rates on the energy evolution of rocks with different lithology,” Geomech. Energy Envir., vol. 34, pp. 100455, Jun. 2023. doi: 10.1016/j.gete.2023.100455. [Google Scholar] [CrossRef]

18. Y. Ao, B. Jia, C. Sun, and F. Liu, “Fracture characteristics and energy evolution analysis of pre-cracked granite under uniaxial compression based on a 3D-Clump model,” Theor. Appl. Fract. Mec., vol. 124, pp. 103756, Apr. 2023. doi: 10.1016/j.tafmec.2023.103756. [Google Scholar] [CrossRef]

19. T. Wen, H. Tang, and Y. Wang, “Brittleness evaluation based on the energy evolution throughout the failure process of rocks,” J. Petrol Sci. Eng., vol. 194, pp. 107361, Nov. 2020. doi: 10.1016/j.petrol.2020.107361. [Google Scholar] [CrossRef]

20. Z. Li, G. Wu, T. Huang, and Y. Liu, “Variation of energy and criteria for strength failure of shale under traixial cyclic loading,” (in ChineseChinese J. Rock Mech. Eng., vol. 37, no. 3, pp. 662–670, Mar. 2018. [Google Scholar]

21. Q. Meng, C. Wang, B. Huang, H. Pu, and Z. Zhang, “Rock energy evolution and distribution law under triaxial cyclic loading and unloading conditions,” (in ChineseChinese J. Rock Mech. Eng., vol. 39, no. 10, pp. 2047–2059, Oct. 2020. [Google Scholar]

22. Q. Ma, Z. Liu, Y. Qin, J. Tian, and S. Wang, “Rock plastic-damage constitutive model based on energy dissipation,” (in ChineseRock Soil Mech., vol. 42, no. 5, pp. 1210–1219, May 2020. [Google Scholar]

23. L. Kong, H. Xie, and C. Li, “Coupled microplane and micromechanics model for describing the damage and plasticity evolution of quasi-brittle material,” Int. J. Plastic, vol. 162, pp. 103549, Mar. 2023. doi: 10.1016/j.ijplas.2023.103549. [Google Scholar] [CrossRef]

24. W. Tao et al., “Experiment study on microfracturing of deep reservoirs in the Bozhong Sag, Bohai Bay Basin,” (in ChineseGeotectonica et Metallogenia, vol. 45, no. 1, pp. 229–241, Jan. 2021. [Google Scholar]

25. Y. Xue and D. Wang, “Formation conditions and exploration direction of large natural gas reservoirs in the oil-prone Bohai Bay Basin, East China,” Petrol Explor. Develop., vol. 47, no. 2, pp. 280–291, Feb. 2020. doi: 10.1016/S1876-3804(20)60046-5. [Google Scholar] [CrossRef]

26. Q. Li and S. Li, “Experimental study on ultra-deep sandstone rock mechanical properties,” (in ChineseChinese J. Rock Mech. Eng., vol. 40, no. 5, pp. 948–957, May 2021. [Google Scholar]

27. B. Liu, M. Yu, J. Sun, R. Huang, and T. Deng, “Study on mechanical properties and damage constitutive model of shale under hydro-mechanical coupling,” (in ChineseChinese J. Rock Mech. Eng., vol. 42, no. 5, pp. 1042–1054, May 2023. [Google Scholar]

28. T. Qin, H. R. Sun, H. Liu, and G. Liu, “Mechanical and acoustic emission characteristics of sandstone samples under different stress,” (in ChineseJ. Heilongjiang Uni. Sci. Tech., vol. 28, no. 2, pp. 131–135, Feb. 2018. [Google Scholar]

29. X. Du et al., “Triaxial mechanical behaviour and energy conversion characteristics of deep coal bodies under confining stress,” Energy, vol. 266, pp. 126443, Mar. 2023. doi: 10.1016/j.energy.2022.126443. [Google Scholar] [CrossRef]

30. P. Li, M. F. Cai, P. T. Wang, Q. F. Guo, S. J. Miao and F. H. Ren, “Mechanical properties and energy evolution of jointed rock specimens containing an opening under uniaxial loading,” Int. J. Min. Met. Mater., vol. 28, no. 12, pp. 1875–1886, Nov. 2021. doi: 10.1007/s12613-020-2237-3. [Google Scholar] [CrossRef]