 Open Access
Open Access
ARTICLE
Maximizing Solar Potential Using the Differential Grey Wolf Algorithm for PV System Optimization
1 Department of Electrical and Electronics Engineering, Pandian Saraswathiyadav Engineering College, Sivagangai, Tamil Nadu, 630561, India
2 Department of Electrical and Electronics Engineering, Sri Balaji Chockalingam Engineering College, Arni, Tamil Nadu, 632317, India
3 Department of Information Science and Engineering, New Horizon College of Engineering, Bangalore, 560103, India
4 Department of Electrical and Electronics Engineering, Rajalakshmi Engineering College, Chennai, Tamil Nadu, 602105, India
5 Department of Electrical and Electronics Engineering, Sona College of Technology, Salem, Tamil Nadu, 636005, India
6 School of Electronics Engineering, Vellore Institute of Technology, Chennai, Tamil Nadu, 600127, India
7 Department of Electrical and Electronics Engineering, Sri Krishna College of Engineering and Technology, Coimbatore, Tamil Nadu, 641008, India
* Corresponding Author: Karthikeyan Balakrishnan. Email:
Energy Engineering 2024, 121(8), 2129-2142. https://doi.org/10.32604/ee.2024.052280
Received 28 March 2024; Accepted 31 May 2024; Issue published 19 July 2024
Abstract
Maximum Power Point Tracking (MPPT) is crucial for maximizing the energy output of photovoltaic (PV) systems by continuously adjusting the operating point of the panels to track the point of maximum power production under changing environmental conditions. This work proposes the design of an MPPT system for solar PV installations using the Differential Grey Wolf Optimizer (DGWO). It dynamically adjusts the parameters of the MPPT controller, specifically the duty cycle of the SEPIC converter, to efficiently track the Maximum Power Point (MPP). The proposed system aims to enhance the energy harvesting capability of solar PV systems by optimizing their performance under varying solar irradiance, temperature and shading conditions. Simulation results demonstrate the effectiveness of the DGWO-based MPPT system in maximizing the power output of solar PV installations compared to conventional MPPT methods. This research contributes to the development of advanced MPPT techniques for improving the efficiency and reliability of solar energy systems.Keywords
Abbreviations
| MPPT | Maximum Power Point Tracking |
| PV | Photovoltaic |
| DGWO | Differential Grey Wolf Optimizer |
| P&O | Perturbation and observation |
| STD | Standard Irradiation Condition |
| PSC | Partial Shading Condition |
| DE | Differential Evolution |
Solar panels are indeed popular renewable energy systems (RES) due to several advantages such as low maintenance, modularity and scalability, etc. [1]. Many research studies indeed focus on maximizing the benefits of electrical energy produced by PV systems. These research efforts are crucial for advancing PV technology, making it more efficient, cost-effective, and accessible. This, in turn, enhances its role in the global transition to RES [2–4].
These research investigations can be broadly categorized into two main groups: one dedicated to improving the efficiency of PV cells and modules and the other aimed at enhancing the utilization of PV energy [5].
Therefore, to optimize the performance of PV systems irrespective of environmental changes and to draw the maximum power from the solar panels, an MPPT algorithm is implemented. The MPPT algorithm prevents voltage collapse by keeping the system operating close to its MPP. The primary advantages of the MPPT algorithm are its robustness and ease of application [6]. In the MPPT topology, the reference voltage and current are continually adjusted (increased or decreased) based on the previous power values until the MPP is reached.
The power output of a solar module fluctuates due to various factors, leading to a shift in the working point of the PV array towards MPP. To track the MPP effectively, the PV voltage is continuously perturbed, and as the perturbation’s power increases, the working point moves closer to the MPP. Once the maximum power is achieved, the perturbation is reversed to maintain the power variation at its smallest possible size.
To achieve precise perturbation control, an additional proportional-integral (PI) controller was incorporated to adjust the duty cycle ratio of the MPPT based converter. This adjustment establishes the reference perturbation voltage. However, it was observed that this perturbation technique resulted in some power loss and occasionally hindered the system from rapidly tracking power changes during dynamic atmospheric conditions.
Evolutionary Computation (EC) techniques have been suggested as a means to address the MPPT topology. However, EC techniques may suffer from poor convergence rates and slow convergence times. In contrast, metaheuristic techniques have shown better convergence rates and faster convergence compared to EC techniques [7–9]. Metaheuristic algorithms have become popular in the MPPT field because they can handle complex functions without needing extra information like derivatives. They’re good at searching and optimizing real-world problems with multiple possible solutions, which makes them a good fit for MPPT tasks [10,11].
Several metheuristic methodologies with notable topologies, including PSO, GWO, ACO, ABC and WOA have been incorporated for MPPT [12,13]. Similarly, a modified version of the Seagull Optimization (MSOA) has been proposed for MPPT. This approach integrates the Levy Flight (LFM) and the heat exchange formula from TEO into SOA [14]. However, these algorithms may require a large number of iterations to converge [15–17] and can be time-consuming [18,19].
To address the complexities present in the above said methods, researchers introduced the DGWO, which is a comprehensive approach designed to tackle computationally expensive problems. It can efficiently explore the search space, making it suitable for optimizing complex problems with multiple variables. It offers a promising and effective approach to optimizing the performance of PV systems, leading to increased energy harvesting efficiency, reduced power loss, and improved system stability under varying environmental conditions.
Thus, this study proposed a novel PV system architecture that effectively integrates SEPIC converter. The integration of this converter allows for enhanced power conversion efficiency and better management of power fluctuations in the PV system. To achieve optimal performance, the researchers utilized the DGWO based MPPT algorithm. The findings of this research are expected to have significant implications for the development of advanced PV systems, contributing to the wider adoption of PV as a sustainable and environmentally friendly power source in grid-tied applications.
The block diagram of the proposed topology is depicted in Fig. 1.
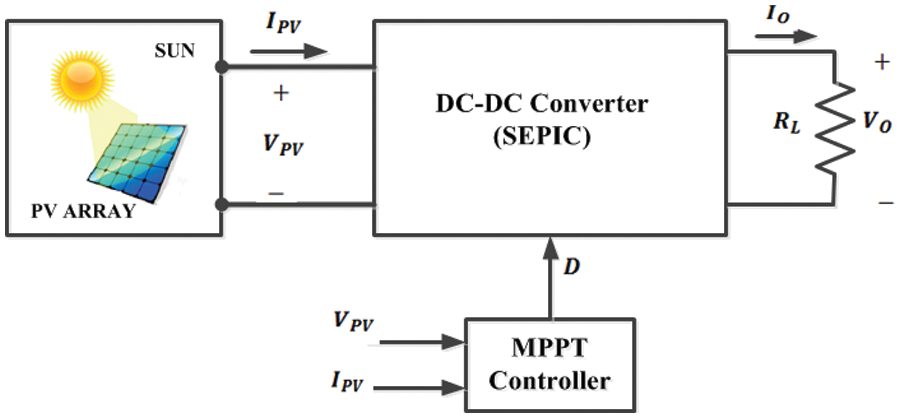
Figure 1: Block diagram-proposed system
Therefore, the suggested configuration includes a PV array coupled with an innovative DGWO based MPPT topology. The PV output is elevated utilizing a SEPIC boost converter, with its functionality regulated by the MPPT topology.
PV cells, also known as solar cells, are the fundamental building blocks of solar panels. When sunlight interacts with the semiconductor material within the PV cell, it excites electrons, creating an internal electrical field. The Equivalent circuit of PV Cell is depicted in Fig. 2.
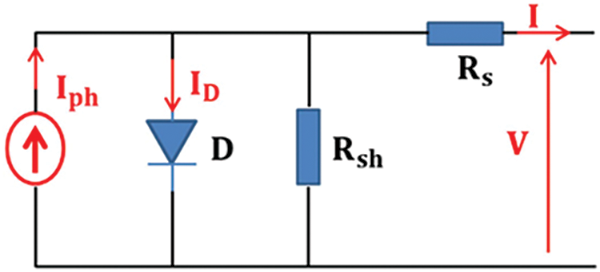
Figure 2: Equivalent circuit (PV cell) [20]
A basic representation of a PV cell depicted in Fig. 2 comprises a diode connected in parallel with an ideal current source. The current source generates a current that mirrors the intensity of incident solar radiation.
Thus, the current and voltage obtained from the output is depicted in Eqs. (1) and (2).
SEPIC converter is a versatile and efficient DC-DC converter that plays a significant role in modern power electronics systems, providing stable and regulated voltage conversion for a wide range of applications. This converter has the ability to maintain continuous input and output currents, which reduces output voltage ripple and makes it suitable for sensitive electronic devices.
Thus, it consists of an inductor, a capacitor and a switch. It has two separate capacitors, one on the input side and one on the output side, allowing for the unique ability to handle both step-up and step-down voltage conversion. The circuit diagram of the SEPIC converter is given in Fig. 3.
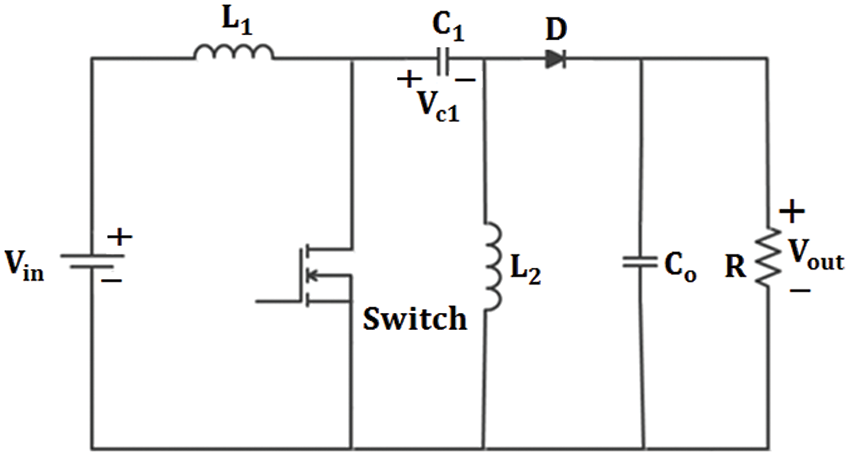
Figure 3: Circuit diagram of SEPIC converter
The operation of the SEPIC converter is as follows:
1. During the first phase, when the switches are closed, the inductor stores energy from the input voltage (Vin) in its magnetic field.
2. In the second phase, when the switches are open, the stored energy in the inductor is transferred to the output capacitor (Co) and the load. At this point, the output voltage (Vout) is higher or lower than the input voltage, depending on the duty cycle of the switches.
3. The unique feature of the SEPIC converter is that during the second phase, the inductor also transfers energy to the input capacitor (Cin). This allows it to handle step-up and step-down voltage conversion without requiring a transformer.
Fig. 4 depicts the circuit during on and off cycles of the power button (respectively in Fig. 4a,b).
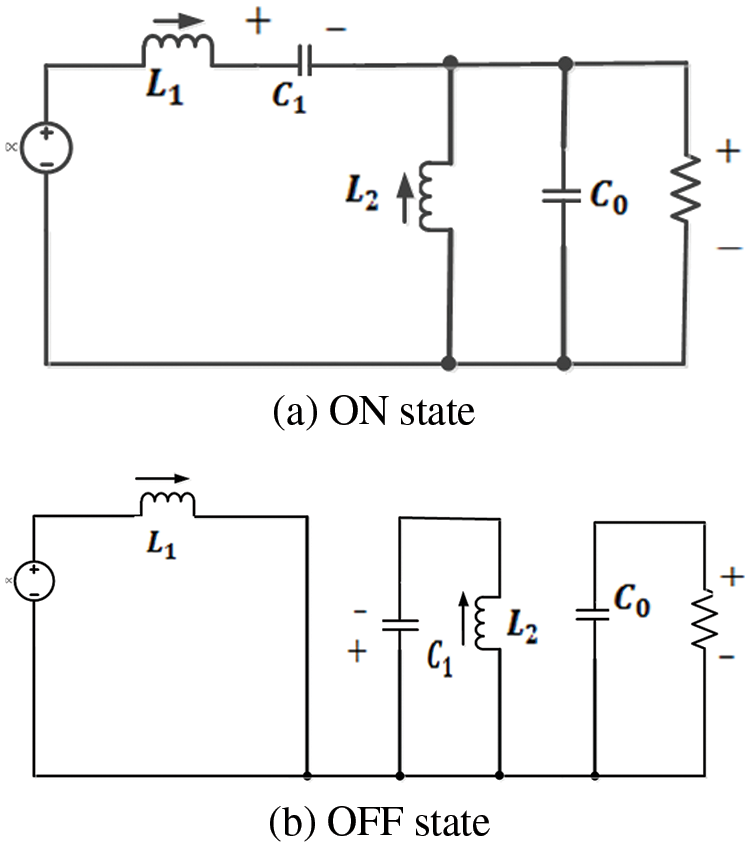
Figure 4: Equivalent circuit diagram
Thus, the voltage gain of the circuit is depicted in Eq. (3).
When designing an inductor, it is essential to account for the inductor ripple current (IL). Therefore, it becomes necessary to calculate this ripple current using Eq. (4).
Using this ripple current, values of
where
Similarly, the capacitor at the output can be derived using Eq. (6).
where
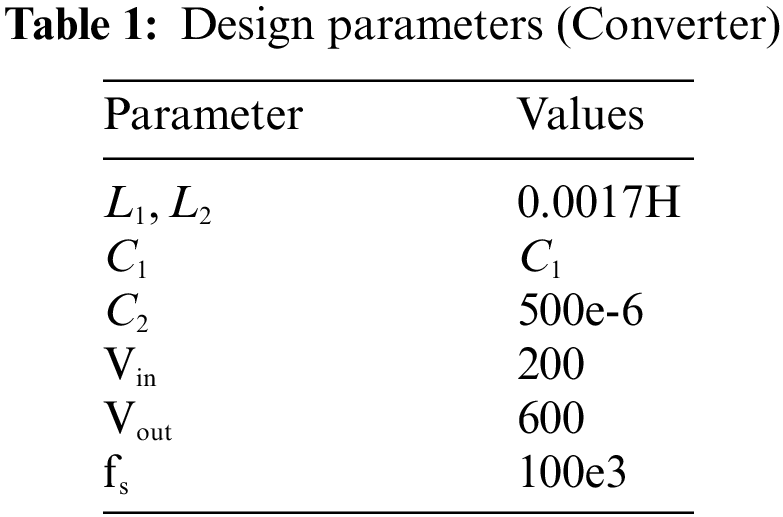
Consequently, the design constraints of the components utilized during simulation are presented in Table 1.
2.3 Differential Grey Wolf Optimizer (DGWO)
Thus, the proposed DGWO integrates the GWO and DE algorithms to enhance optimization performance. Initially, the GWO algorithm is employed for global exploration due to its effective domain detection abilities. The DE algorithm is then utilized to refine solutions and prevent convergence to local optima.
The working of the algorithm is depicted below:
1. Initialization: Generate an initial population of candidate solutions. For GWO, this could involve randomly positioning a pack of grey wolves within the search space. For DE, it typically involves randomly initializing a population of vectors representing potential solutions.
2. Fitness Evaluation: Evaluate the fitness of each candidate solution using the objective function. In the context of optimization problems, this function quantifies the quality of a solution.
3. GWO Global Search: Employ the GWO algorithm to perform global exploration. Grey wolves iteratively adjust their positions in the search space based on fitness values, aiming to converge toward optimal solutions. This phase focuses on exploring diverse regions of the search space.
4. DE Local Refinement: Apply the DE algorithm to refine solutions and prevent premature convergence. DE iteratively generates new candidate solutions by combining and mutating existing ones, thereby facilitating local exploration and refinement.
5. Termination Criterion: Determine whether a termination criterion is met.
6. Output: Return the best solution found during the optimization process.
Thus, the suggested DGWO-based MPPT algorithm’s flowchart is depicted in Fig. 5.
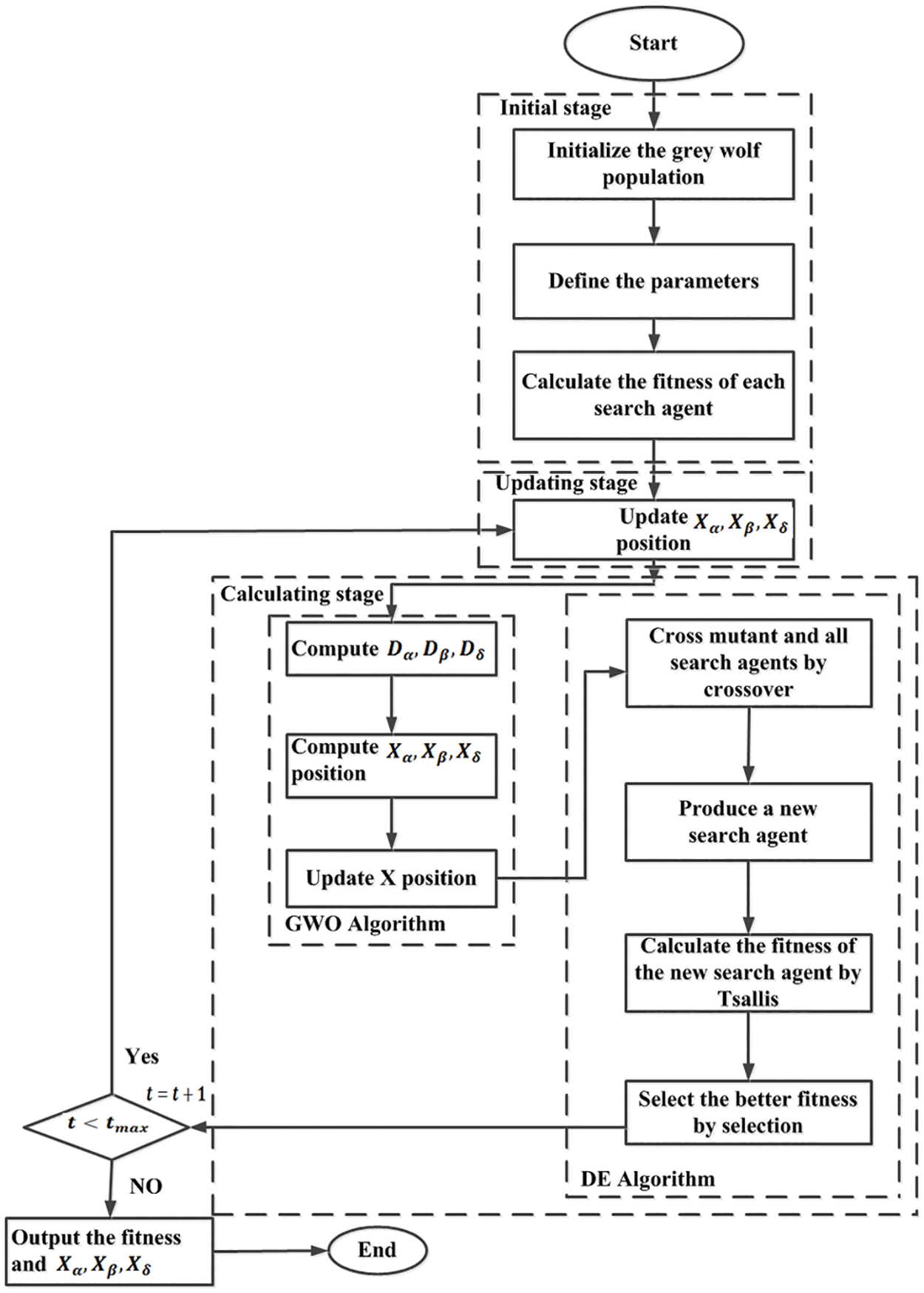
Figure 5: Flowchart of GWO
The fitness function of the DGWO algorithm is given as
where
p–Power,
d–Duty Cycle,
k–No. of iterations.
The MPPT implementation involves the utilization of a SEPIC converter. The essential waveforms of the devised system under this operational scenario are illustrated in the figures below. Remarkably, the incorporated DGWO-MPPT has effectively mitigated the oscillations typically observed around the MPP, thereby enhancing the overall stability and consistency of the system’s performance.
To comprehensively evaluate the efficacy of the proposed topology, a series of distinct cases with different PSC has been considered for the investigation of its performance. The results of these cases are summarized in Table 2, highlighting the system’s response and behavior under varying conditions.
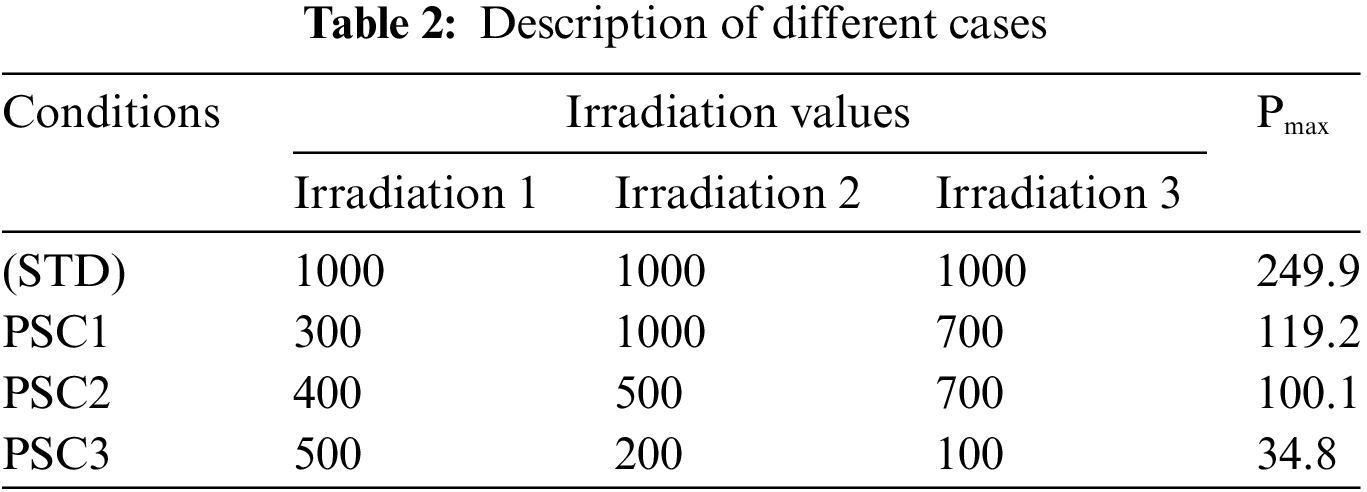
Thus, to prove the efficiency of the proposed DGWO topology, it is compared with the traditional P&O algorithm and cuckoo search optimization algorithm. P&O is a widely used algorithm for MPPT. It continuously perturbs the operating point of the PV system and observes the resulting change in power output. Based on this observation, it adjusts the operating point in the direction that maximizes power output. Cuckoo Search Algorithm (CSA) depending on Levy flight concepts, provides a versatile and efficient approach in solving optimization problems.
Standard Irradiation Condition
A comprehensive assessment of PV module performance under consistent irradiance conditions (250 Watts) through power-vs.-time analysis, as depicted in Fig. 6. It is important to note that all PV modules receive equivalent irradiance levels in this setup.
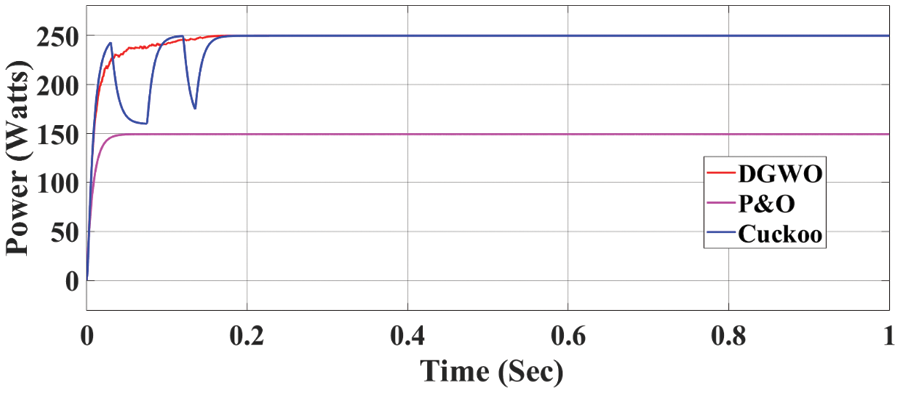
Figure 6: Standard shading condition for DGWO
Through rigorous simulation testing, the DGWO-MPPT has demonstrated significant performance outcomes. Specifically, it has yielded an MPP of 249.9 Watts with a notably reduced time duration. This achievement surpasses the results obtained using the cuckoo algorithm (249.6 Watts) and the P&O algorithm (149.29 Watts). These findings are visually presented in Fig. 6, where the simulation outcomes of the DGWO, cuckoo and P&O algorithms are displayed for comparison. Furthermore, its efficiency has been quantified at an impressive 99.9%, which notably exceeds the efficiencies of the cuckoo algorithm (99.8%) and the P&O algorithm (59.6%).
The performance evaluation extends to the analysis of duty cycles, as illustrated in Fig. 7. The outcomes clearly establish the superior performance of the DGWO MPPT in comparison to alternative approaches.
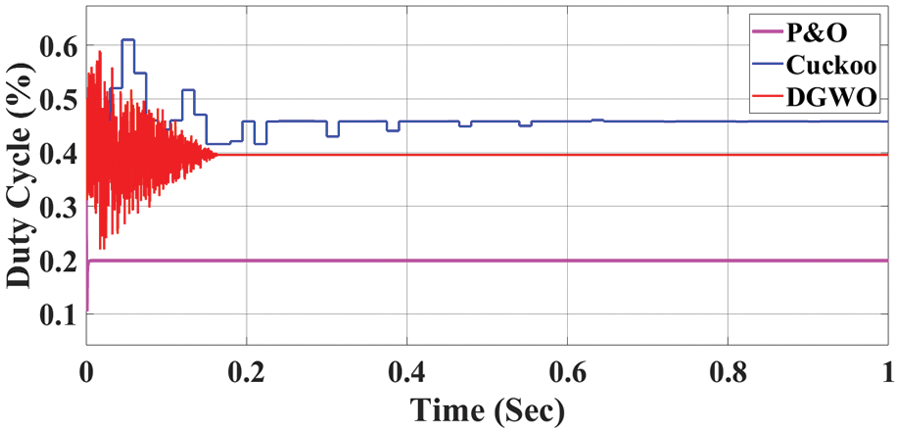
Figure 7: Duty cycle for standard shading condition
Partial Shading Condition 1
Under the specified irradiance conditions (300, 1000, and 700 units), a thorough analysis has been conducted. Notably, the DGWO algorithm emerges as the frontrunner, achieving the highest power output at an impressive 119.2 W. Close behind, the Cuckoo algorithm achieves 119.1 W, while the P&O algorithm attains 84.3 W. These achievements are depicted in Fig. 8.
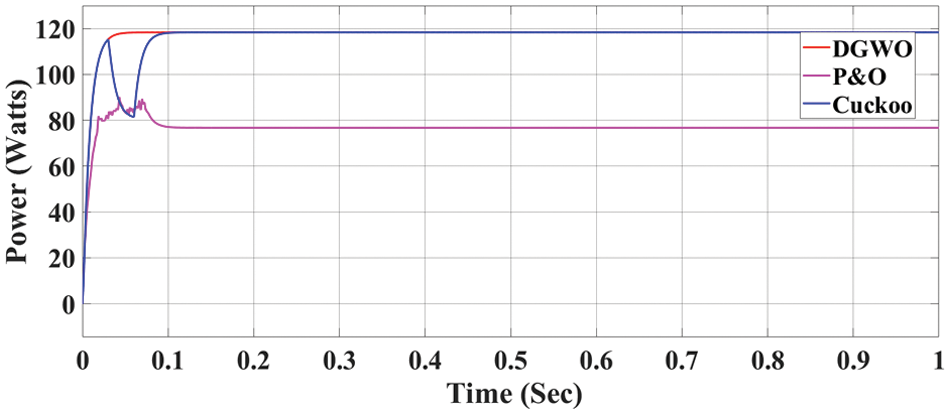
Figure 8: Power output
An important facet of this comparison is efficiency. In this regard, the DGWO algorithm excels with a remarkable efficiency of 99.7% whereas the Cuckoo algorithm follows with an efficiency of 99.5%, and the P&O algorithm lags behind with an efficiency of 70%.
Fig. 9 distinctly illustrates the changes in the duty cycle graph. Notably, the red line represents the DGWO algorithm’s duty cycle, which demonstrates a remarkable degree of stability after attaining its maximum power output during steady-state time. This observation underscores the DGWO algorithm’s proficiency in achieving and maintaining optimal operating conditions.
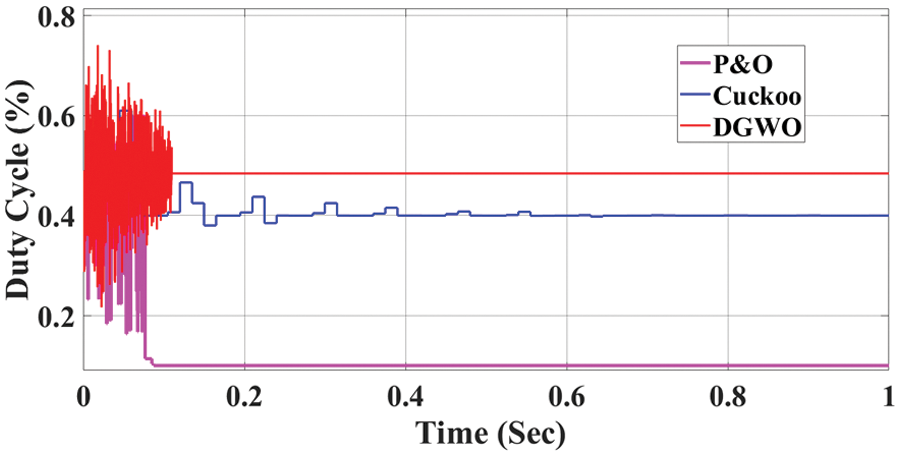
Figure 9: Duty cycle
Partial Shading Condition 2
In the context of a partial shading condition (400, 500, 700 units), the DGWO algorithm emerges as the optimal performer, achieving the highest power output of 100.1 W. This is followed by the Cuckoo algorithm, which attains 99.4 W, and the P&O algorithm, reaching 87.3 W. These results are evaluated against the backdrop of a total available power of 119.5 W, as illustrated in Fig. 10.
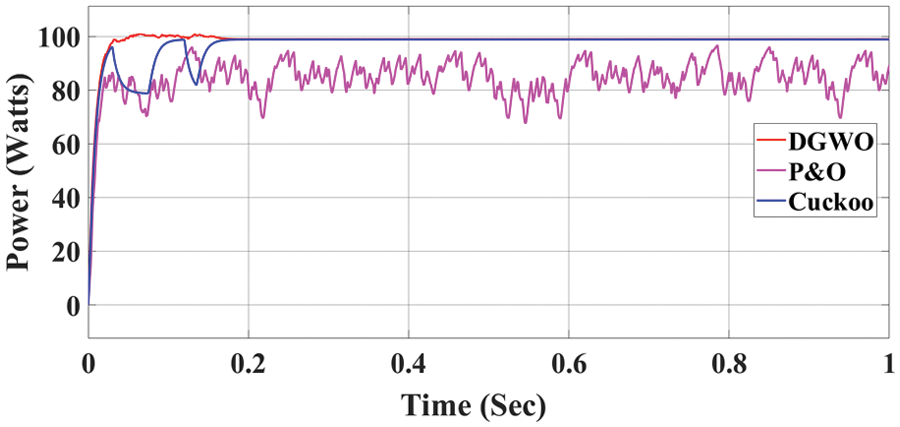
Figure 10: Output power
The DGWO achieves an impressive efficiency of 99.7%, outperforming the Cuckoo algorithm at 99.5% and the P&O algorithm at 70%.
Fig. 11 portrays the alterations in the duty cycle. The red line signifies the DGWO algorithm’s duty cycle, which showcases remarkable stability subsequent to achieving its maximum power output during the steady-state time. This distinctive behavior highlights the DGWO algorithm’s effectiveness in promptly attaining and sustaining optimal operational conditions.
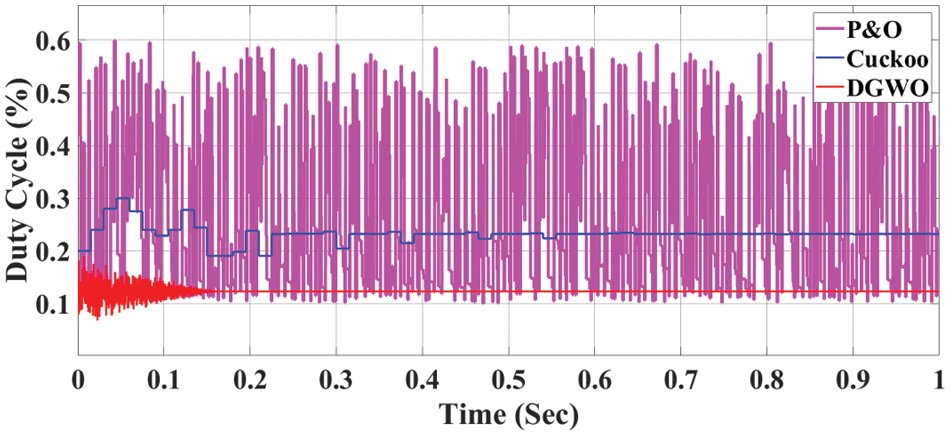
Figure 11: Duty cycle
Partial Shading Condition 3
Under the conditions of partial shading (500, 200, 100 units), the DGWO algorithm achieves power output of 34.8 W which is higher than both the Cuckoo algorithm (34.2 W) and the P&O algorithm (32.5 W). These outcomes are evaluated in relation to a total available power of 34.9 W, visually depicted in Fig. 12. Similarly, the duty cycle of the proposed topologies have been explored in Fig. 13.
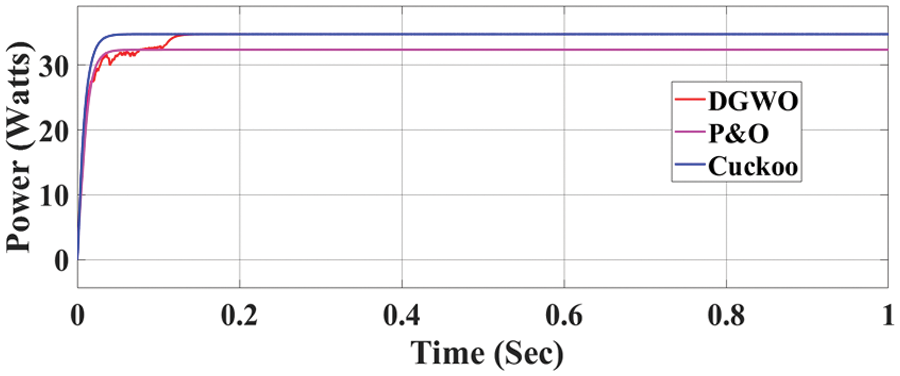
Figure 12: Partial shading condition 3 for DGWO
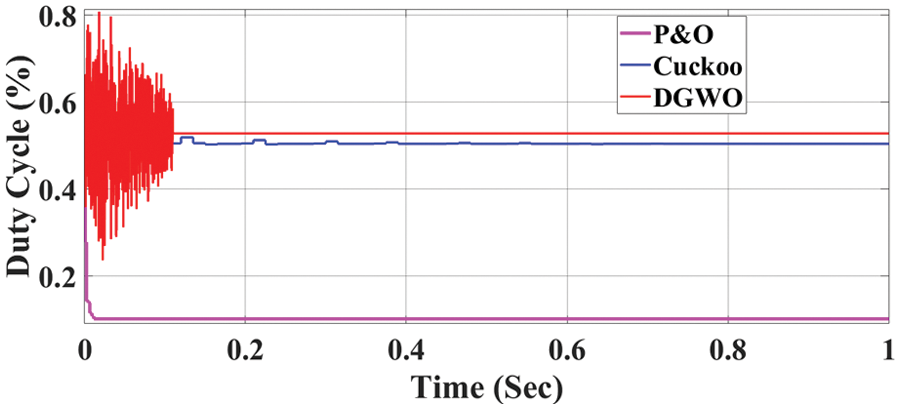
Figure 13: Duty cycle for partial shading condition 3
Table 3 and Fig. 14 display the proposed DGWO algorithm is compared with the other two algorithms in terms of tracking time, maximum power and efficiency.
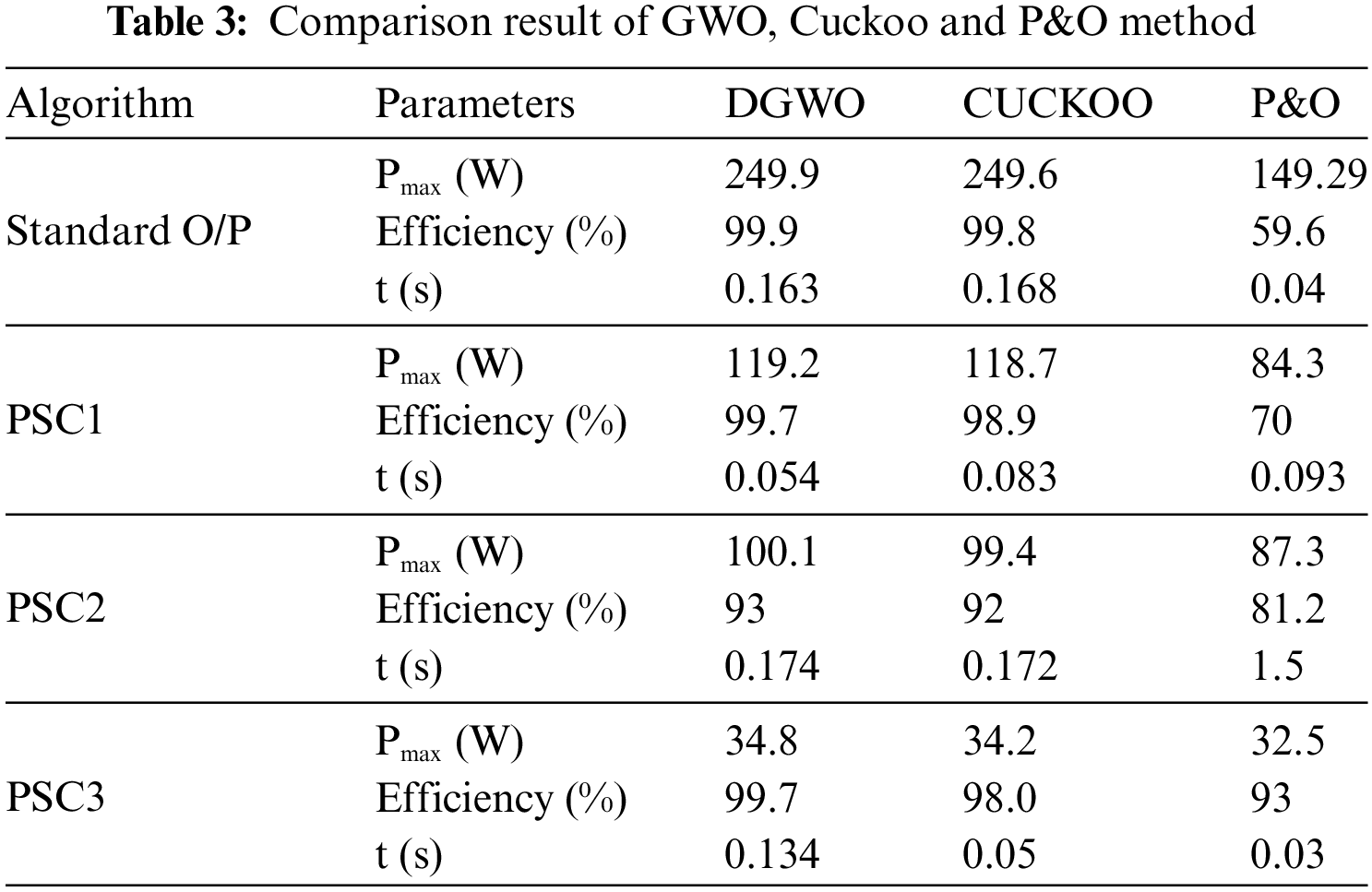
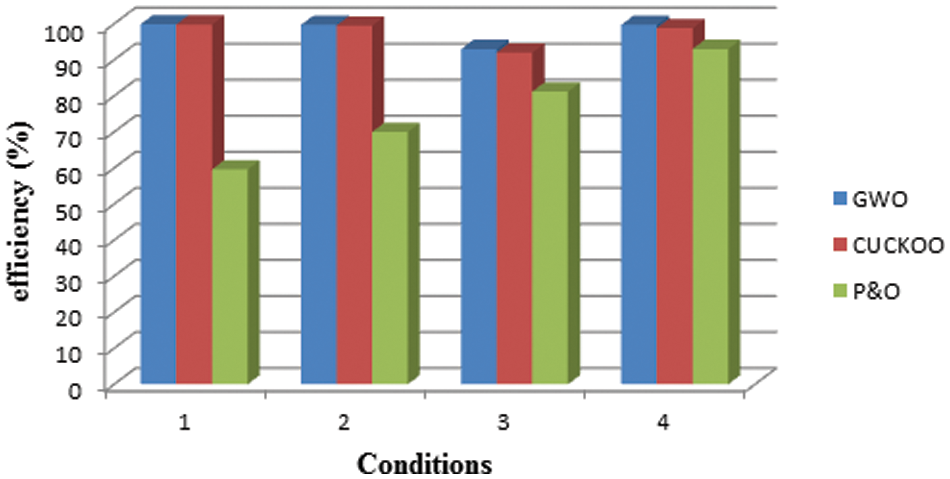
Figure 14: Comparative analysis
The hardware implementation confirms the effectiveness of the DGWO-MPPT approach. In this PV system setup, three series-connected PV modules form the PV array. A microcontroller, specifically the dsPIC30F4011, receives current and voltage data from sensors connected to the PV array. It then generates a Pulse Width Modulation (PWM) signal for the boost converter’s switch. The DGWO MPPT algorithm determines this signal, ensuring the boost converter’s duty cycle is optimized to match the Global Maximum Power Point (GMPP).
The results of the hardware implementation under uniform irradiation conditions are depicted in Fig. 15.
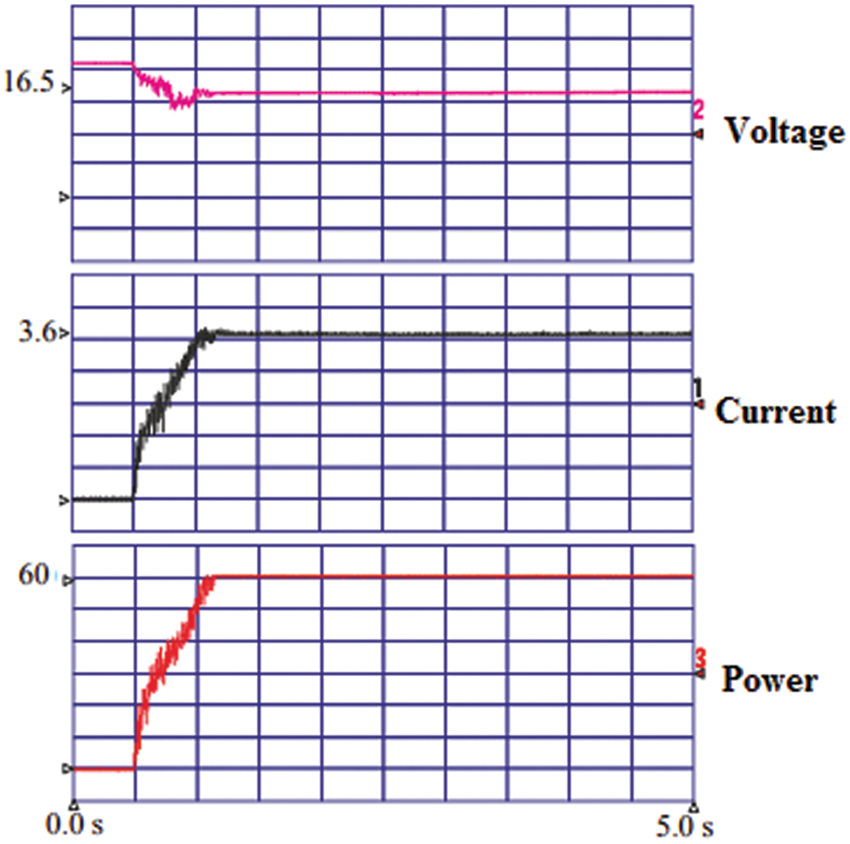
Figure 15: Hardware results (Standard condition)
In this work, a SEPIC converter along with a DGWO-based MPPT algorithm is tailored for PV systems. The MPPT algorithm, based on the DGWO method, adjusts the converter’s duty cycle. Simulation results show that this combined approach can effectively track the MPP of a PV system, even when there are sudden changes in sunlight. It responds quickly to these changes and reduces fluctuations around the MPP, leading to more stable performance. Thus, the results obtained during the different irradiance conditions are listed below.
Under STD, the efficiency reaches approximately 99.9%, surpassing that of traditional methods. Conversely, the Cuckoo algorithm achieves about 99.8%, closely aligning with the proposed topology. However, when subjected to PSC, the DGWO demonstrates remarkable efficiency at around 99%, whereas the CSA is about 98% across all PSC. Consequently, the superiority of the DGWO algorithm has been proved.
Additionally, the use of the SEPIC converter eliminates non-operational zones and allows monitoring of the PV module’s MPP at various input voltage levels. The adoption of advanced optimization techniques such as DGWO fosters innovation in the renewable energy sector. It encourages the development of more efficient and reliable solar energy solutions, making renewable energy technologies more accessible and economically viable.
Acknowledgement: None.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Ezhilmathi Nagarathinam, Karthikeyan Balakrishnan; Data collection: Buvana Devaraju, Santhana Lakshmi ChandraMohan; Analysis and interpretation of results: Karthiyayini Jayamoorthy, Padmavathi Radhakrishnan; Draft manuscript preparation: Karthikeyan Balakrishnan, Vijayakumar Perumal. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. L. B. Bosman, W. D. Leon-Salas, W. Hutzel, and E. A. Soto, “PV system predictive maintenance: Challenges, current approaches, and opportunities,” Energies, vol. 13, no. 6, pp. 1398, 2020. [Google Scholar]
2. O. A. Al-Shahri, “Solar photovoltaic energy optimization methods, challenges and issues: A comprehensive review,” J. Clean. Prod., vol. 284, pp. 125465, 2021. [Google Scholar]
3. S. Hoseinzadeh, D. A. Garcia, and L. Huang, “Grid-connected renewable energy systems flexibility in Norway islands decarbonization,” Renew. Sustain. Energ. Rev., vol. 185, pp. 113658, 2023. [Google Scholar]
4. S. Hoseinzadeh, D. Groppi, B. Nastasi, D. Bruschi, and D. A. Garcia, “Designing high-share 50% and 100% renewable energy scenarios for Ragusa by sustainable energy toolkit application,” Sustain. Energy Technol. Assess., vol. 63, pp. 103645, 2024. [Google Scholar]
5. D. Pilakkat and S. Kanthalakshmi, “Single phase PV system operating under partially shaded conditions with ABC-PO as MPPT algorithm for grid connected applications,” Energy Rep., vol. 6, pp. 1910–1921, 2020. [Google Scholar]
6. M. Kermadi, “Recent developments of MPPT techniques for PV systems under partial shading conditions: A critical review and performance evaluation,” IET Renew. Power Gener., vol. 14, no. 17, pp. 3401–3417, 2020. doi: 10.1049/iet-rpg.2020.0454. [Google Scholar] [CrossRef]
7. S. Chtita et al., “A novel hybrid GWO-PSO-based maximum power point tracking for photovoltaic systems operating under partial shading conditions,” Sci. Rep., vol. 12, no. 1, pp. 1–15, 2022. doi: 10.1038/s41598-022-14733-6. [Google Scholar] [PubMed] [CrossRef]
8. M. Dehghani, M. Taghipour, G. B. Gharehpetian, and M. Abedi, “Optimized fuzzy controller for MPPT of grid-connected PV systems in rapidly changing atmospheric conditions,” J. Mod. Power Syst. Clean Energy, vol. 9, no. 2, pp. 376–383, 2020. doi: 10.35833/MPCE.2019.000086. [Google Scholar] [CrossRef]
9. A. Jendoubi, F. Tlili, and F. Bacha, “Sliding mode control for a grid connected PV-system using interpolation polynomial MPPT approach,” Math. Comput. Simul., vol. 167, pp. 202–218, 2020. doi: 10.1016/j.matcom.2019.09.007. [Google Scholar] [CrossRef]
10. M. N. Ali, K. Mahmoud, M. Lehtonen, and M. M. Darwish, “Promising MPPT methods combining metaheuristic, fuzzy-logic and ANN techniques for grid-connected photovoltaic,” Sensors, vol. 21, no. 4, pp. 1244, 2021. doi: 10.3390/s21041244. [Google Scholar] [PubMed] [CrossRef]
11. Y. Alharbi, A. Darwish, and X. Ma, “A comprehensive review of distributed MPPT for grid-tied PV systems at the sub-module level,” Energies, vol. 16, no. 14, pp. 5468, 2023. doi: 10.3390/en16145468. [Google Scholar] [CrossRef]
12. C. Kumar, G. Subramaniam, and J. Jasper, “A novel ROA optimized Bi-LSTM based MPPT controller for grid connected hybrid solar-wind system,” COMPEL Int. J. Comput. Math. Electr. Electron Eng., vol. 42, no. 2, pp. 378–401, 2022. doi: 10.1108/COMPEL-11-2021-0453. [Google Scholar] [CrossRef]
13. B. Babypriya, A. J. Renoald, M. Shyamalagowri, and R. Kannan, “An experimental simulation testing of single-diode PV integrated MPPT grid-tied optimized control using grey wolf algorithm,” J. Intell. Fuzzy Syst., vol. 43, no. 5, pp. 5877–5896, 2022. doi: 10.3233/JIFS-213259. [Google Scholar] [CrossRef]
14. A. Subramaniana and J. Raman, “Modified seagull optimization algorithm based MPPT for augmented performance of photovoltaic solar energy systems,” Automatika, vol. 63, no. 1, pp. 1–15, 2022. doi: 10.1080/00051144.2021.1997253. [Google Scholar] [CrossRef]
15. M. N. Ali, K. Mahmoud, M. Lehtonen, and M. M. Darwish, “An efficient fuzzy-logic based variable-step incremental conductance MPPT method for grid-connected PV systems,” IEEE Access, vol. 9, pp. 26420–26430, 2021. doi: 10.1109/ACCESS.2021.3058052. [Google Scholar] [CrossRef]
16. X. Ge, F. W. Ahmed, A. Rezvani, N. Aljojo, S. Samad and L. K. Foong, “Implementation of a novel hybrid BAT-Fuzzy controller based MPPT for grid-connected PV-battery system,” Control Eng. Pract., vol. 98, no. 3, pp. 104380, 2020. doi: 10.1016/j.conengprac.2020.104380. [Google Scholar] [CrossRef]
17. A. S. Saidi, C. B. Salah, A. Errachdi, M. F. Azeem, J. K. Bhutto and V. T. Ijyas, “A novel approach in stand-alone photovoltaic system using MPPT controllers & NNE,” Ain Shams Eng. J., vol. 12, no. 2, pp. 1973–1984, 2021. doi: 10.1016/j.asej.2021.01.006. [Google Scholar] [CrossRef]
18. S. Vijayakumar and C. Govindaraju, “Generation of maximum power in grid connected PV system based MPPT control using hybrid elephant herding optimization algorithm,” Elect. Power Compon. Syst., vol. 50, no. 6–7, pp. 301–317, 2022. doi: 10.1080/15325008.2022.2136293. [Google Scholar] [CrossRef]
19. D. Kumar et al., “A novel hybrid MPPT approach for solar PV systems using particle-swarm-optimization-trained machine learning and flying squirrel search optimization,” Sustainability, vol. 15, no. 6, pp. 5575, 2023. doi: 10.3390/su15065575. [Google Scholar] [CrossRef]
20. M. Rosa-Clot and G. M. Tina, “Introduction to PV plants,” in Submerged and Floating Photovoltaic Systems. Elsevier, 2018, pp. 33–64. doi: 10.1016/B978-0-12-812149-8.00003-X. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools