 Open Access
Open Access
ARTICLE
Adaptive Predefined-Time Backstepping Control for Grid Connected Photovoltaic Inverter
1 Key Laboratory of Smart Grid of Ministry of Education, Tianjin University, Tianjin, 300072, China
2 State Grid Hubei Electric Power Research Institute, Wuhan, 430077, China
3 State Grid Hubei Electric Power Co., Ltd., Wuhan, 430077, China
* Corresponding Author: Dan Liu. Email:
Energy Engineering 2024, 121(8), 2065-2083. https://doi.org/10.32604/ee.2024.050342
Received 03 February 2024; Accepted 10 April 2024; Issue published 19 July 2024
Abstract
The system performance of grid-connected photovoltaic (PV) has a serious impact on the grid stability. To improve the control performance and shorten the convergence time, a predefined-time controller based on backstepping technology and dynamic surface control is formulated for the inverter in the grid-connected photovoltaic. The time-varying tuning functions are introduced into state-tracking errors to realize the predefined-time control effect. To address the “computational explosion problem” in the design process of backstepping control, dynamic surface control is adopted to avoid the analytical calculations of virtual control. The disturbances of the PV system are estimated and compensated by adaptive laws. The control parameters are chosen and the global stability of the closed-loop is ensured by Lyapunov conditions. Simulation results confirm the effectiveness of the proposed controller and ensure the predefined time control in the photovoltaic inverter.Keywords
As economic development accelerates, the demand for energy transformation continues to rise due to the increasing consumptions of fossil fuels [1]. In comparison to traditional fossil fuels, renewable energy offers the benefits of widespread distribution, diverse sources and reduced environmental pollution [2]. Consequently, the grid-connection rate for renewable energy is on the rise within the energy sector [3]. Furthermore, the rapid development of power electronics technology has significantly enhanced access to the deployment of renewable energy [4]. Recently, as a sustainable and clean energy source, photovoltaics has attracted more attention and investments in many countries [5–7]. Grid-connected inverters receive important research value in photovoltaic powers and renewable energy fields [8–10].
Large-scale grid-connection of photovoltaic strives for new requirements in system stability and convergence [11]. Currently, kinds of control methods have been explored in engineering practices [12–14]. In the field of microgrid control, finite-time control algorithms have been developed to track reference commands within a finite time [15–17]. In the islanded systems, the smooth power control for PV inverters has been designed using an adaptive finite-time sliding mode technique, ensuring finite-time stability and convergence of the tracking errors [18]. Reference [19] proposes a continuous sliding mode control within finite time for grid-connected photovoltaic arrays, addressing modeling uncertainties arising from variations in converter parameters, system frequency and exogenous factors. To mitigate power chattering in the photovoltaic inverter of the master-slave island microgrid system, the adaptive sliding mode backstepping control has been studied, which can ensure the finite-time stability, favorable robustness performance and shortened convergence time of system states [20]. Finite-time control can ensure the finite time tracking of the system’s solution, while the upper bound of the convergence time is influenced by the system’s initial state.
Subsequently, a fixed-time control algorithm is investigated, which can ensure the convergence of tracking errors in a fixed time range. The convergence speed of fixed-time control is further enhanced and the convergence time is independent of the system’s initial conditions [21]. However, the upper bound of the convergence time cannot be explicitly determined by the control parameters [21–23]. Regarding the issue of the system level frequency deviation by the power output randomness and PV generation, the control of bus overvoltage and power output is accomplished, ensuring the fixed time response in the battery energy storage systems [24]. Considering the intermittent power from renewable energy sources and frequent load fluctuations affecting the microgrid cluster, a two-layer two-level control is developed to enhance the dynamic performance of the microgrids within a fixed time [25]. Recently, deep researches on predefined time control algorithms have appeared [26,27].
Predefined time control is proposed while the upper limit of the stable time function can be determined by selecting system parameters appropriately. In [28], the secondary controller with a predefined time is formulated for the direct current (DC) microgrid, facilitating voltage regulation and current sharing among different distributed generators within a specified time. The predefined time control algorithm can provide a preset convergence time, which can be determined explicitly by the controller gains in advance [29]. The harmonics in photovoltaics have serious effects on the grid, therefore the rapid convergence of the voltage/current in photovoltaic inverters is important. Table 1 shows the comparison results of different control methods. Compared with finite time control and fixed-time control, the maximum limit of the convergence time in a predefined time control can make the theoretical value of the convergence time a simple and adjustable parameter.
Based on the aforementioned research, a predefined-time backstepping control is studied for the grid-connected photovoltaic inverters. The main contributions of the paper lie in:
1. A predefined time backstepping control based on initial states is proposed for the three-phase grid-connected photovoltaic inverter. The proposed control scheme ensures that the output states can convergent into a small region around the origins in a predefined time.
2. Compared to semi-global stability in [12–14], the control algorithm adopts the Lyapunov condition to ensure global closed-loop stability, realizes DC voltage tracking and unit power factor grid-connection within the predefined time.
3. In comparison with the finite-time control and fixed-time control, the proposed predefined-time control can effectively improve the convergence speed of the PV system and achieve an accurate estimation of the upper limit of convergence time.
The remainder of the paper is outlined as follows. Section 2 describes the topology architecture of the PV system, the mathematical model of the inverter and time-varying functions. Section 3 devises a predefined-time control based on backstepping and adaptive control. In Section 4, the global closed-loop stability analysis and the choices of the controller gains are present. Section 5 carries on the simulation experiments and analyses. Section 6 summarizes the paper.
The control objective of grid-connected inverters is to maintain the stability of the DC side voltage and achieve unit power factor grid-connection. Inverters are susceptible to device aging, thermal effects, grid voltage uncertainty and external disturbances. Therefore, the control of grid-connected inverter should meet grid-connection requirements and exhibit robustness, while providing the improved system stability and convergence speed. A three-phase voltage source inverter (VSI) is modeled in a single-stage non-isolated grid-connected topology and a predefined-time control is formulated.
As shown in Fig. 1, the topology structure diagram of a three-phase photovoltaic grid-connected inverter is stated, where Cdc is the DC side capacitor of the inverter, upv is the output voltage of the PV array and idc is the output current. By applying Kirchhoff’s voltage law, the three-phase voltage and three-phase current satisfy [31]
{Ldiadt=−Ria−ea+udc3(2ka−kb−kc)Ldibdt=−Rib−eb+udc3(−ka+2kb−kc)Ldicdt=−Ric−ec+udc3(−ka−kb+2kc)(1)
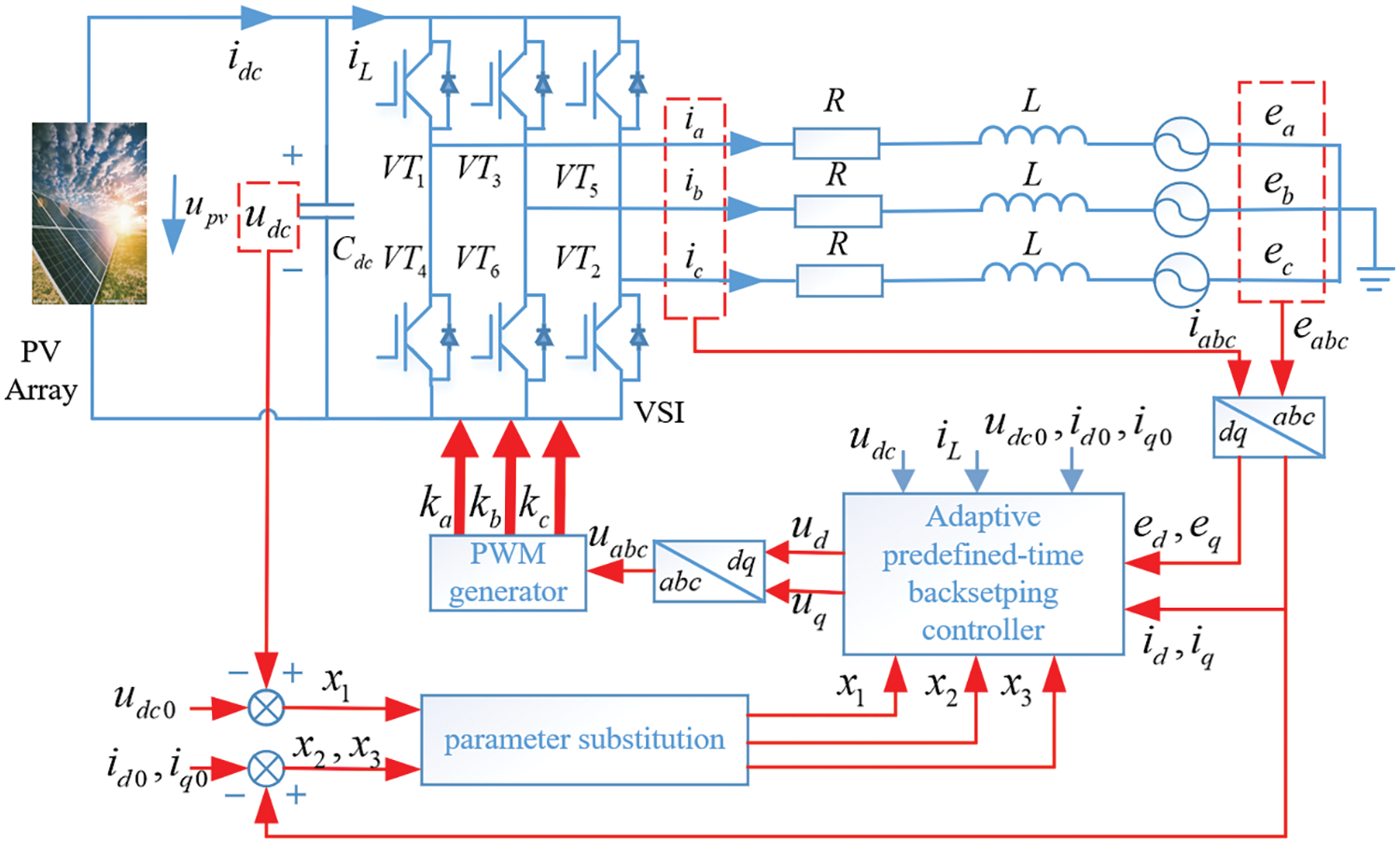
Figure 1: Topological structure diagram of three-phase PV grid-connected inverter
Eq. (1) provides the relationship of current and voltage in the three-phase grid-connected system, where ea,eb,ec are the alternating current (AC) voltages of the PV system, ia,ib,ic are the AC currents of the PV system, ka,kb,kc are the input switch signals, L is the inductance, R is the resistance and udc is the DC voltage of the inverter. Transforming the system (1) from the ABC coordinate into the DQ coordinate, yields
{diddt=−RLid−edL+ωiq+udLdiqdt=−RLiq−eqL−ωid+uqL(2)
with ud=udckd and uq=udckq, kd and kq are the switch signals, id and iq are the grid side currents in the DQ-axis, ed,eq are the grid side voltages in the DQ-axis and ω is the angular frequency of the PV system.
Basen on the Kirchhoff’s current law, the voltage udc of the capacitor Cdc is obtained as
Cdcdudcdt=idc−iL(3)
where iL represents the input current of VSI, idc represents the output current of the PV array, p is the active power and q is the reactive power. p and q are oriented using the vector of the grid voltage in the DQ coordinate system, ed=|E|, eq=0. Here |E| is the amplitude of the grid phase voltage and
{p=32(edid+eqiq)q=32(ediq−eqid)(4)
After ignoring the fluctuation of |E|, ed is maintained as a constant, the active power p and reactive power q are proportional to the output current id and iq, respectively. Therefore, ignoring the losses of VSI, the DC side voltage udc of VSI can be controlled by id, one has
idcudc=p=3edid2(5)
By invoking Eqs. (3) and (5), we can obtain
dudcdt=1Cdc(3edid2udc−iL)(6)
Define the reference signal of voltage udc as udc0, and the reference signal of currents id,iq as id0,iq0. The resulting system model for VSI is
{dx1dt=3ed(x2+id0)2Cdc(x1+udc0)−iLCdc+d1dx2dt=udL−RL(x2+id0)+ω(x3+iq0)−edL+d2dx3dt=uqL−RL(x3+iq0)−ω(x2+id0)−eqL+d3(7)
where the system state variables are chosen as x1=udc−udc0, x2=id−id0 and x3=iq−iq0, the control inputs are ud and uq. Note that d1, d2 and d3 represent the unknown external disturbances of the PV system.
For all headings, please capitalize the first character of each word except prepositions, and conjunctions.
The control object is to formulate the predefined time control laws ud and uq, then the DC voltage udc can be regulated to track the reference signal udc0 at the D-axis, while the AC current iq of the Q-axis can track the reference signal iq0. Especially, the tracking errors are stable and can be ensured to remain bounded in a predefined time T1.
Lemma 1 [32]. For an n-order system ˙x=f(x,t,T) and a constant δ∈R+, the solution of x is globally predefined-time stable if ∀x0∈Rn and x(x0,t,T)=0n hold in t≥T. The solution of x satisfies globally predefined-time boundedness if ∀x0∈Rn and ‖x(x0,t,T)‖≤δ hold when t≥T. The constant parameter T represents the upper boundedness of the system stability time.
Lemma 2 [33]. For ∀γ>0 and e∈R, the inequality γ>|e|−e⋅sg(e,γ)≥0 holds, where sg(e,γ)=e/√e2+γ2.
The following assumptions hold for the VSI system (7).
Assumption 1 [34]. The unknown external disturbances d1, d2 and d3 are bounded and continuous. That is, there exist positive constants D1∈R+,D2∈R+,D3∈R+, such that the inequalities |d1(t)|≤D1, |d2(t)|≤D2 and |d3(t)|≤D3 hold when t≥0.
Assumption 2. The gain functions in inverter dynamics (7) are uniformly continuous satisfying 3ed/(2Cdc(x1+udc0))≥G1≥0 and 1/L≥G2≥0, with G1,G2∈R+ are known constants.
Assumption 3. Other functions in inverter dynamics (7) and their first time-derivatives are uniformly continuous.
Remark 1. Due to the randomness of photovoltaic power generation, the uncertainty of bus voltage, the aging problems and thermal effects in the inverter, disturbances terms should be considered. In practical systems, disturbances are usually subjected to various physical limitations, such as power supply stability, circuit design and the effects of filters. These factors result in the limited magnitude of disturbances within a certain range, making the disturbances bounded. Therefore, Assumption 1 holds. Assumptions 2 and 3 are reasonable as active power p and reactive power q are controlled and distributed, while the grid voltage can be stabilized and considered as a constant value.
For all headings, please capitalize the first character of each word except prepositions, and conjunctions.
The predefined time constant is introduced directly in the predefined-time control, allowing for the adjustment of different predefined times by choosing the value of the time constant in advance. The time-varying function ρ(t) is adopted to achieve the predefined-time tracking of the D-axis, which satisfies the following conditions.
Condition 1. Time-varying function ρ(t), the first derivative ˙ρ(t) and the second derivative ¨ρ(t) are bounded on t≥0.
Condition 2. Time-varying function ρ(t), the first derivative ˙ρ(t) and the second derivative ¨ρ(t) are continuous on t≥0.
Condition 3.ρ(t)=0 always holds when t≥T1.
Condition 4. The initial values ρ(0) and ˙ρ(0) fulfill
ρ(0)=m=x1(0)˙ρ(0)=h=3ed(x2(0)+id0)2Cdc(x1(0)+udc0)−iLCdc+d1(0)(8)
where m and h are parameters related to the initial conditions, d1(0)=0 is the initial disturbance. Apparently, there are different candidates for the time-varying function ρ(t). A viable option ρ(t) is the quadruple polynomial form [35]
ρ(t)={−(3mT41+hT31)t4+(8mT31+3hT21)t3−(6mT21+3hT1)t2+ht+m,t<T10,t≥T1(9)
For the 1-order system of the Q-axis, the time-varying function υ(t) fulfills the following conditions.
Condition 5. υ(t) and ˙υ(t) are bounded on t≥0.
Condition 6. υ(t) and ˙υ(t) are continuous on t≥0.
Condition 7. υ(t)=0 always holds when t≥T1.
Condition 8. The initial value υ(0) satisfies
υ(0)=l=x3(0)(10)
and l is a parameter determined by the initial conditions.
υ(t) is chosen as
υ(t)=−{3lT41t4+8lT31t3−6lT21t2+l,t<T10,t≥T1(11)
Remark 2. Time-varying functions are used to achieve the desired tracking performance with a stable time-upper limit. The controller design ensures that the output tracking errors of the system can track the desired trajectory. The upper limit of the system’s convergence time can be adjusted by determining the time constant T1 in the time-varying function.
3 Adaptive Predefined-Time Backstepping Control
The adaptive control is formulated to estimate and compensate for the disturbances in inverter model (7). The time-varying function ρ(t) of the D-axis and the time-varying function υ(t) of the Q-axis are introduced in the definitions of the tracking errors. Based on the framework of backstepping control, the controllers ud and uq for the PV grid-connected inverter are designed. By presetting the upper limit of the convergence time, the closed-loop system achieves the global stability within the predefined time. For the D-axis system, a control law ud is designed to satisfy condition |x1|≤ε at t≥T1, where ε represents a small neighborhood of the origin. For the Q-axis, a control law uq is designed to satisfy condition |x3|≤ε at t≥T1.
Fig. 2 states the signal diagram of the closed-loop system. Adaptive control laws are introduced to estimate and compensate for the upper limit Di of the external disturbances di(i=1,2,3), while the estimated values are denoted as ⌢Di. Defining the parameter estimation errors as ˜Di=Di−⌢Di. The adaptive control law is designed as
˙⌢Di=rieisg(ei,γi)−σi⌢Di(12)
where ri>0,γi>0,σi>0 are adaptive constants.
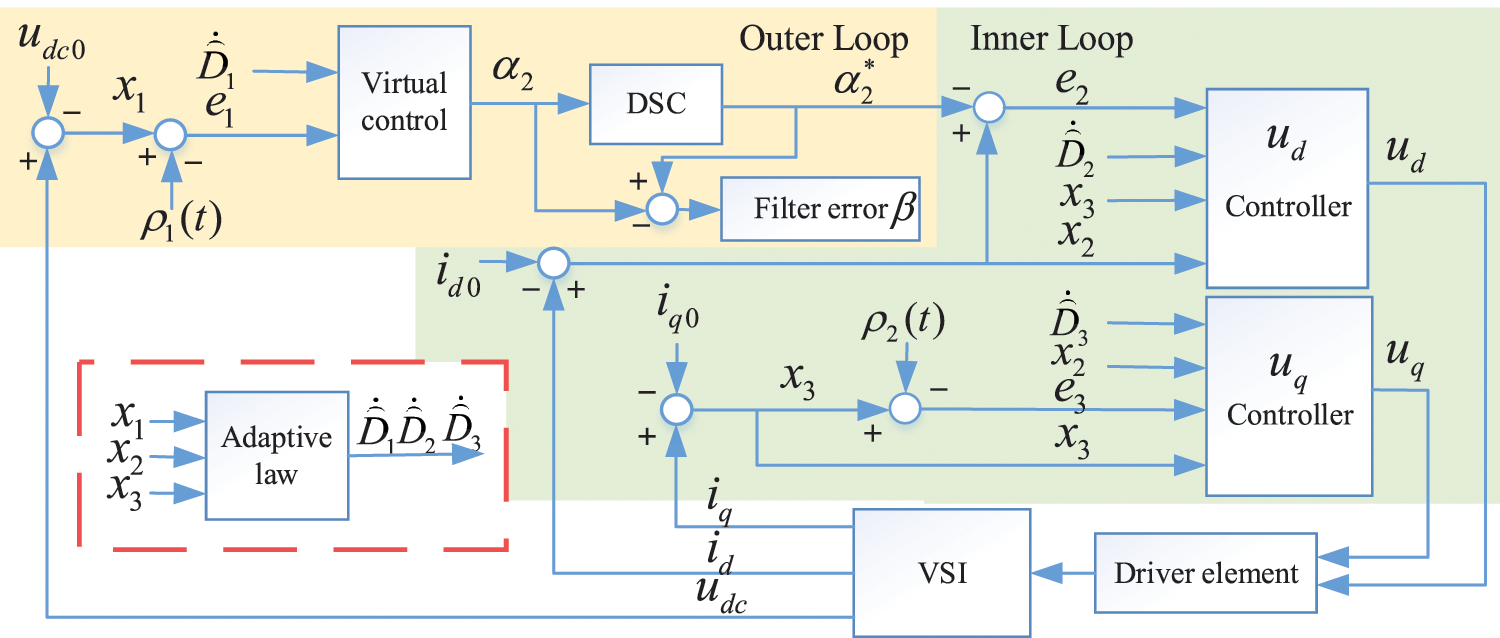
Figure 2: Signal diagram of the closed-loop system
The state tracking error is designed
e1=x1−ρ(t)(13)
where ρ(t) is the time-varying function of the D-axis.
The first-time derivative of e1 is
˙e1=3ed(x2+id0)2Cdc(x1+udc0)−iLCdc+d1−˙ρ(t)(14)
The virtual control law α2 is defined as
α2=−id0+2Cdc(e1+udc0)3ed[−k1e1+iLCdc−⌢D1sg(e1,γ1)+˙ρ(t)](15)
where k1, γ1 are positive parameters and sg(e1,γ1)=e1/√e21+γ21.
Substituting the virtual controller (15) into Eq. (14) yields
˙e1=−k1e1+3ed2Cdc(x1+udc0)(e2+β)+d1−⌢D1sg(e1,γ1)(16)
Choose a Lyapunov function candidate V1 as
V1=12e21+12r1˜D21(17)
Along the trajectories (12), (15) and (16), the first-time derivative of V1 is
˙V1=−k1e21+3ede1(e2+β)2Cdc(x1+udc0)+e1d1−e1⌢D1sg(e1,γ1)−e1˜D1sg(e1,γ1)+σ1r1˜D1⌢D1≤−[k1−3ed4Cdc(x1+udc0)](e21+β2)+3ede1e22Cdc(x1+udc0)+γ1D1−σ12r1(˜D21−D21)(18)
The following inequalities hold by Young’s inequality
{3ede1β2Cdc(x1+udc0)≤3ed4Cdc(x1+udc0)(e21+β2)e1d1−e1D1sg(e1,γ1)≤γ1D1σ1r1˜D1⌢D1=σ1r1˜D1(D1−˜D1)≤σ12r1(D21−˜D21)(19)
To avoid the “computational explosion problem” in backstepping control, the dynamic surface control (DSC) is introduced. That is, the signal α∗2 acts as the filtered signal of the virtual controller α∗2
˙α∗2=(α2−α∗2)/μ(20)
where μ is the filter gain and α∗2(0)=α2(0). Then the filtering error β is characterized as
β=α∗2−α2(21)
Define the state tracking errors e2 as
e2=x2−α∗2(22)
The first-time derivative of e2 is
˙e2=udL−RL(x2+id0)+ω(x3+iq0)−edL+d2−˙α∗2(23)
The control laws ud is constructed as
ud=L[−k2e2+RL(x2+id0)−ω(x3+iq0)+edL+˙α∗2−⌢D2sg(e2,γ2)−3ede12Cdc(x1+udc0)](24)
where k2 and γ2 are the controller parameters and sg(e2,γ2)=e2/√e22+γ22. Substituting Eqs. (12), (20) and (24) into Eq. (23), gives
˙e2=−k2e2−3ede12Cdc(x1+udc0)+d2−⌢D2sg(e2,γ2)(25)
Consider the following Lyapunov function V2 as
V2=12e22+12β2+12r2˜D22(26)
Substituting Eq. (25) into the differential dynamic of V2, one has
˙V2=−k2e22−3ede1e22Cdc(x1+udc0)−β2μ−β˙α2+e2d2−e2D2sg(e2,γ2)+σ2r2˜D2⌢D2≤−k2e22−3ede1e22Cdc(x1+udc0)+γ2D2−(1μ−˙α22)β2+14−σ22r2(˜D22−D22)(27)
with inequalities −β˙α2≤β2˙α22+1/4, e2d2−e2D2sg(e2,γ2)≤γ2D2 and ˜D2⌢D2≤(D22−˜D22)/2 hold.
The state tracking errors e3 of Q-axis is defined as
e3=x3−υ(t)(28)
where υ(t) is the time-varying function of the Q-axis.
The first-time derivative of e3 is
˙e3=uqL−RL(x3+iq0)−ω(x2+id0)−eqL+d3−˙υ(t)(29)
The control laws uq is designed as
uq=L[−k3e3+RL(x3+iq0)+ω(x2+id0)+˙υ(t)−⌢D3sg(e3,γ3)+eqL](30)
where k3 and γ3 are controller gains to be determined later, sg(e3,γ3)=e3/√e23+γ23. Recalling the adaptive law (12) and the VSI controller (30), one can get
˙e3=−k3e3+d3−⌢D3sg(e3,γ3)(31)
Define a Lyapunov function candidate V3 as
V3=12e23+12r3˜D23(32)
The time derivative of V3 can be expressed as
˙V3=−k3e23+e3d3−e3D3sg(e3,γ3)+σ3r3˜D3˙⌢D3≤−k3e23+γ3D3−σ32r3(˜D23−D23)(33)
where the inequalities e3d3−e3D3sg(e3,γ3)≤γ3D3 and ˜D3⌢D3≤(D23−˜D23)/2 hold.
Choosing the total Lyapunov function V as
V=V1+V2+V3(34)
From Eqs. (18), (27) and (33), ˙V can be represented as
˙V≤−(k1−3ed4Cdc(x1+udc0))e21−k2e22−k3e23−σ12r1˜D21−σ22r2˜D22−σ32r3˜D23−(1μ−3ed4Cdc(x1+udc0)−˙α22)β2+Γ(35)
where Γ≜γ1D1+γ2D2+γ3D3+14+σ12r1D21+σ22r2D22+σ32r3D23.
By the Lyapunov theory, the predefined time stability of the closed-loop system is achieved, which is summarized in Theorem 1.
Theorem 1. For the inverter (7) in the PV system, the control laws ud and uq are proposed in (24) and (30), and the first-order filter is given by Eq. (20). For any constant ε∈R+, all signals in the closed-loop system can be bounded at t≥0 under the proper control gains ki,i=1,2,3. After the selection of control parameter T1, |x1(t)|≤ε and |x3(t)|≤ε holds when t≥T1. The predefined-time stability of photovoltaic inverter is realized.
Poof. Define a vector ζ=[e1,e2,e3,β,˜D1,˜D2,˜D3]T∈R7 and a compact set Ω
Ω={ζ∈R7:e21+e22+e23+β2+˜D21r1+˜D22r2+˜D23r3≤ε2}(36)
The controller gains are selected as
{k1−3ed4(x1+udc0)Cdc>Γε2,k2>Γε2,k3>Γε21μ−3ed4(x1+udc0)Cdc−˙α22>Γε2σ12>Γε2,σ22>Γε2,σ32>Γε2(37)
From Eqs. (35)–(37), we can deduce that
˙V<−2Γε2V+Γ(38)
Next, the discussion focuses on the boundedness of signals in the closed-loop system in the compact set Ω. Based on Condition 1 and Condition 2, it can be inferred that ρ(t), ˙ρ(t), and ¨ρ(t) are consistently bounded on t≥0. From Condition 5 and Condition 6, υ(t) and ˙υ(t) are always bounded on t≥0. While ei and β are bounded on the set Ω.
Invoking the definition x1=e1+ρ(t), as x1 is bounded on Ω, then α2 is bounded on the compact set Ω by virtual controller (15) and Assumption 2. The boundedness of x2 can be ensured by the definition of x2=e2+α2+β. Similarly, the boundedness of x3 is given by x3=e3+υ(t). Considering the virtual controller (15), first-order filter (20) and filter error (21), the boundedness of ud and uq on the set Ω can be obtained from Assumption 2 and Assumption 3.
The first derivation of the virtual controller α2 can be expressed as
˙α2=(3ed2Cdc(x1+udc0))−1[−k1˙e1−(⌢D1sg(e1,γ1))′+¨ρ(t)](39)
Apparently ˙α2 is bounded on Ω from Assumption 2. Then, the second formula in Eq. (37) holds. An analysis is conducted on the initial states of the tracking errors. For the D-axis signal, substituting Condition 3, virtual controller Eq. (15) and the controller Eq. (24) into tracking errors Eqs. (13) and (22), one has e1(0)=e2(0)=0 on the compact set Ω. Based on α∗2(0)=α2(0), β(0)=0 holds. The Q-axis signal e3(0)=0 on the compact set Ω can be obtained. According to the controller Eqs. (24) and (39) implies that ˙V<0 on V=ε2/2. Thus, from V(0)=0<ε2/2, V(t)≤ε2/2 always holds for t≥0.
In addition, according to Eq. (36), |e1(t)|≤ε and |e3(t)|≤ε holds when t≥0. Considering Conditions 3 and Conditions 7, ρ(t)=0 and υ(t)=0 hold when t≥T1. Eqs. (13) and (28) implied that |x1(t)|≤ε and |x3(t)|≤ε holds when t≥T1. Therefore, the solution of the PV system (7) is global predefined-time bounded according to Lemma 1. □
Remark 3. For i=1,2,3, the detailed design process of the proposed control scheme is
1. Based on the initial states (8) and (10), select the suitable time-varying functions (9) and (11) to fulfill the predefined time stability conditions.
2. Choose the appropriate parameters μ and determine the first-order filter (20).
3. Choose appropriate parameters ki, ri, σi, γi to determine the adaptive laws (12), virtual control law (15), controllers (24) and (30).
The simulation is carried on the photovoltaic system to demonstrate the effectiveness of the proposed control method. The physical parameters are as follows: Cdc=4.4mF, R=0.5Ω, L=2.5mH, iL=50A, ed=270V, eq=0V, f=50Hz, ω=314rad/s, udc0=500V, iq0=0A. Choose the controller gains as k1=120, k2=150 and k3=200; The filter gain for DSC is selected as μ=0.001. Set the adaptive gains to r1=2, r2=r3=5, σ1=0.8, σ2=σ3=0.6, γ1=γ2=γ3=0.1.
Case1. Simulations under different predefined times T1=0.1s,T1=0.08s,T1=0.15s
The initial condition is set to x1(0)=−8V, x2=−2A, x3(0)=2A. The disturbances d1=4.4,d2=5,d3=5 are added between 0.2 and 0.4 s.
Fig. 3 shows the trajectories of state x1, x2 and x3 when the predefined time is set to T1=0.1s. From Fig. 3, the system state variables can convergent to the small neighborhood of the origin within T1=0.1s. That is, the proposed predefined time backstepping control method has completed DC voltage tracking and unit power factor grid connection within the specified time, while the predefined time control goal is achieved.
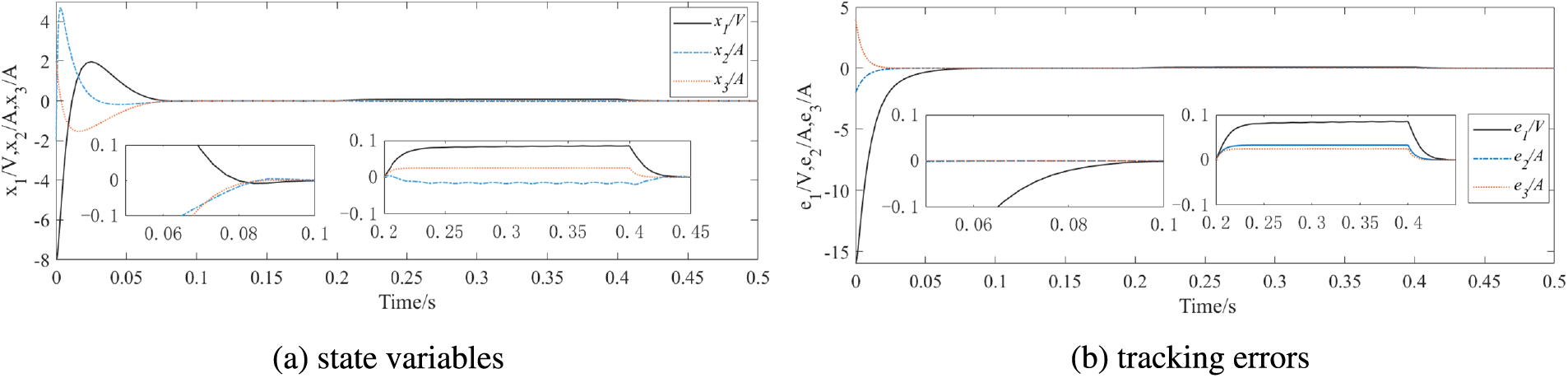
Figure 3: State variables and tracking errors at T1=0.1s
Figs. 4a and 5a show the trajectories of state variables x1, x2 and x3 at different predefined times of T1=0.08s and T1=0.15s, respectively. Figs. 4b and 5b show the trajectories of tracking errors e1, e2 and e3. When the preset convergence times changes, the proposed predefined time backstepping control method still completes DC voltage tracking and unit power factor grid connection within the preset time.
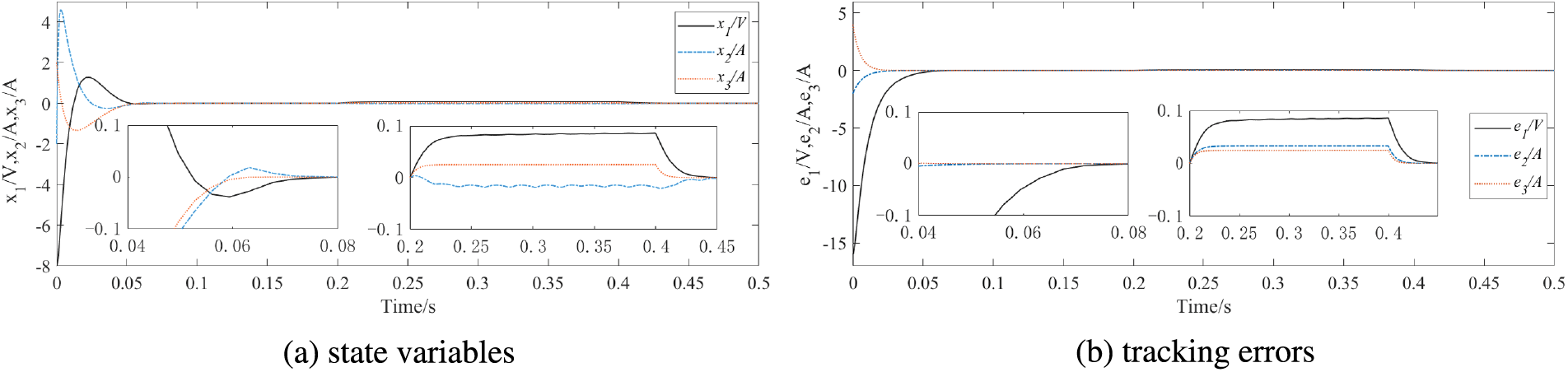
Figure 4: State variables and tracking errors at T1=0.08s
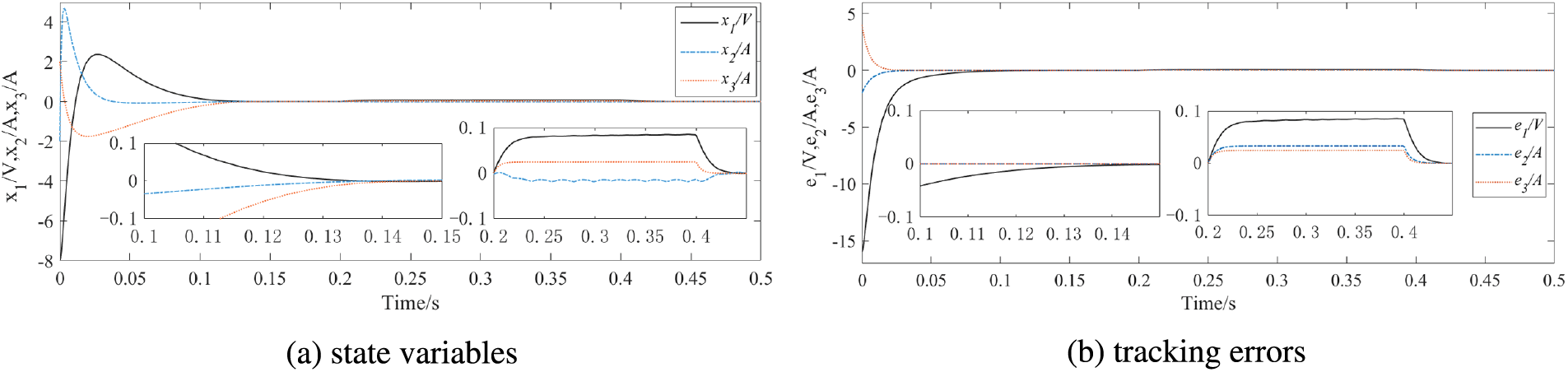
Figure 5: State variables and tracking errors at T1=0.15s
A comparison simulation of finite-time backstepping control and fixed-time backstepping control are performed. Fig. 6a shows the trajectories of state variables x1, x2, x3 and tracking error e2 in finite-time control, while Fig. 6b shows the trajectories of state variables x1, x2, x3 and tracking error z2 in the fixed-time control. The finite-time control can achieve the tracking in 0.35 s, while the convergence time in fixed-time control is 0.2 s. Compared with finite-time and fixed-time, the predefined time control can customize the upper limit of convergence time within the range supported by physical parameters. The proposed predefined time backstepping control can improve the convergence speed of PV systems, achieve predefined time control objectives and provide a satisfactory control performance. After disturbances are triggered, the robust performance is effectively improved.
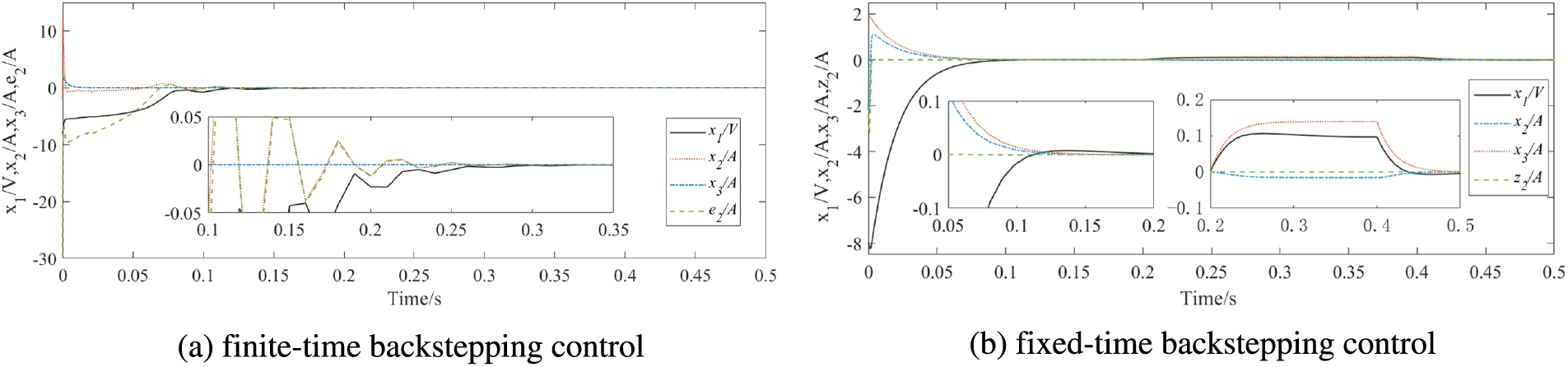
Figure 6: State variables and tracking errors in traditional backstepping controller
Fig. 7 shows the estimation value of the virtual control at T1=0.1s. Fig. 8 shows the curves of controllers ud and uq under different predefined times. Although the preset time value changes, the controller achieves stable control within the different predefined time.
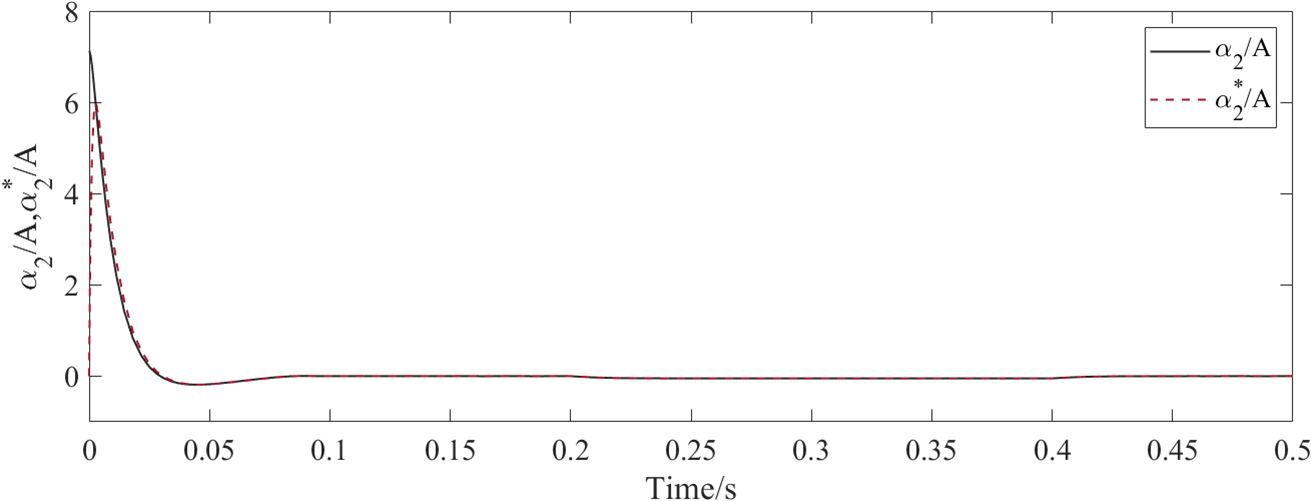
Figure 7: Estimation value of virtual controller at T1=0.1s
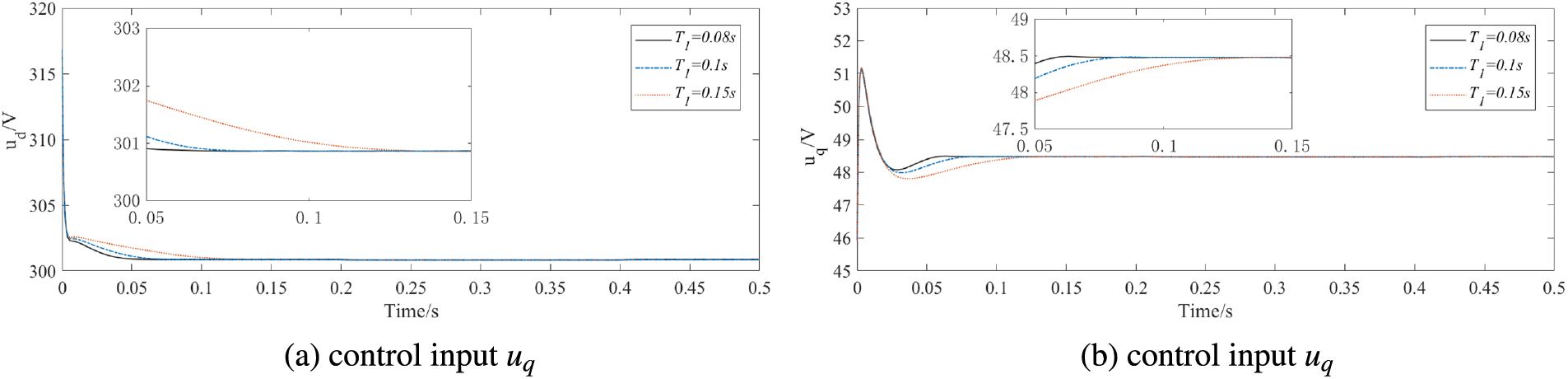
Figure 8: Controllers under different predefined times
Case2. Simulation under different initial states
To address the tracking performance of the controller, different initial states (4V,3A,−1A), (−5V,−3A,6A) and (10V,6A,−5A) are considered.
Fig. 9 displays the state responses x1, x2 and x3 under different initial states, while Fig. 10 illustrates the tracking errors e1, e2 and e3 under different initial states, set the predefined time to 0.1 s. The control can achieve effective tracking within the predefined time under the different initial values.
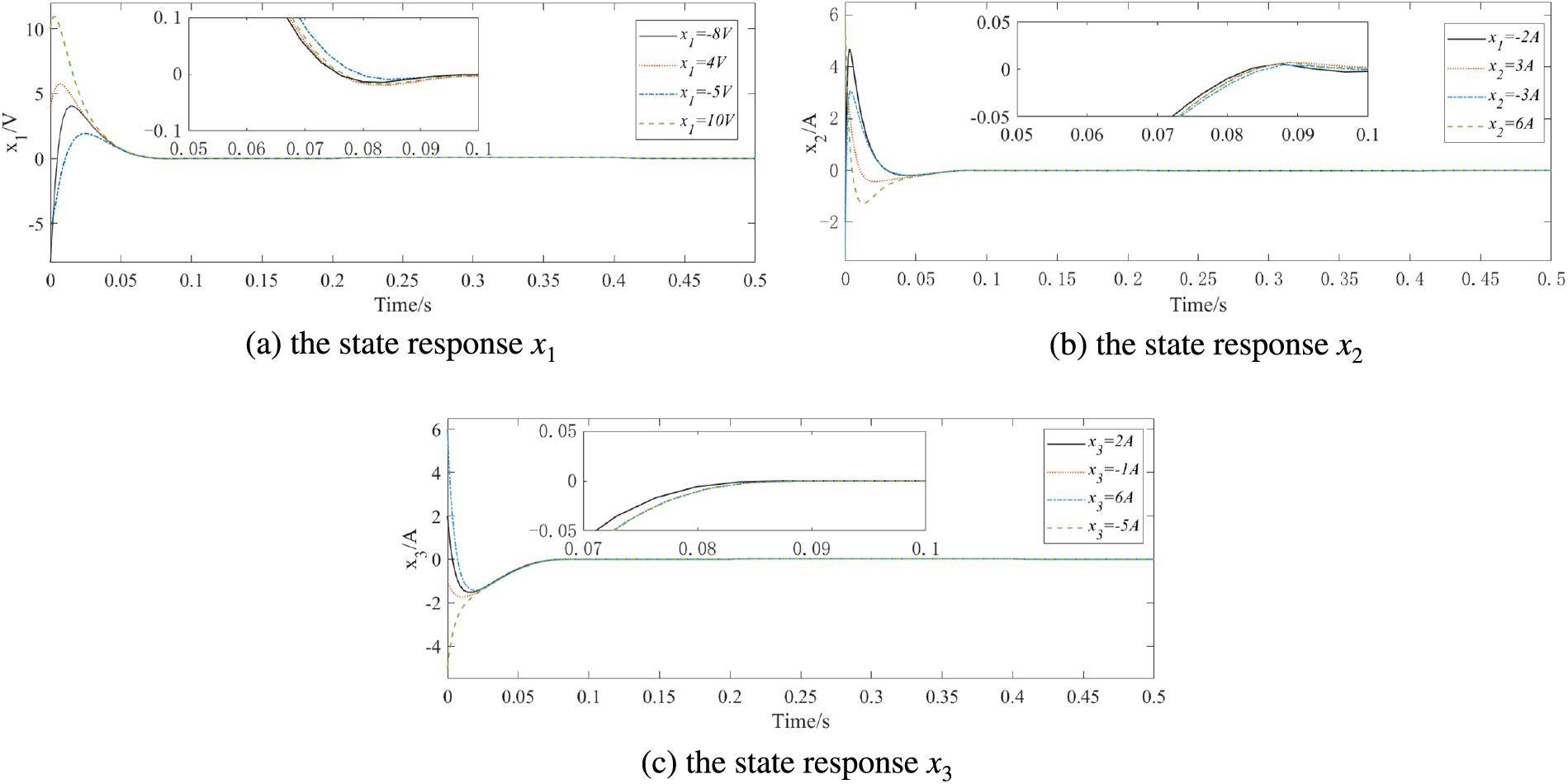
Figure 9: State response under different initial states at T1=0.1s
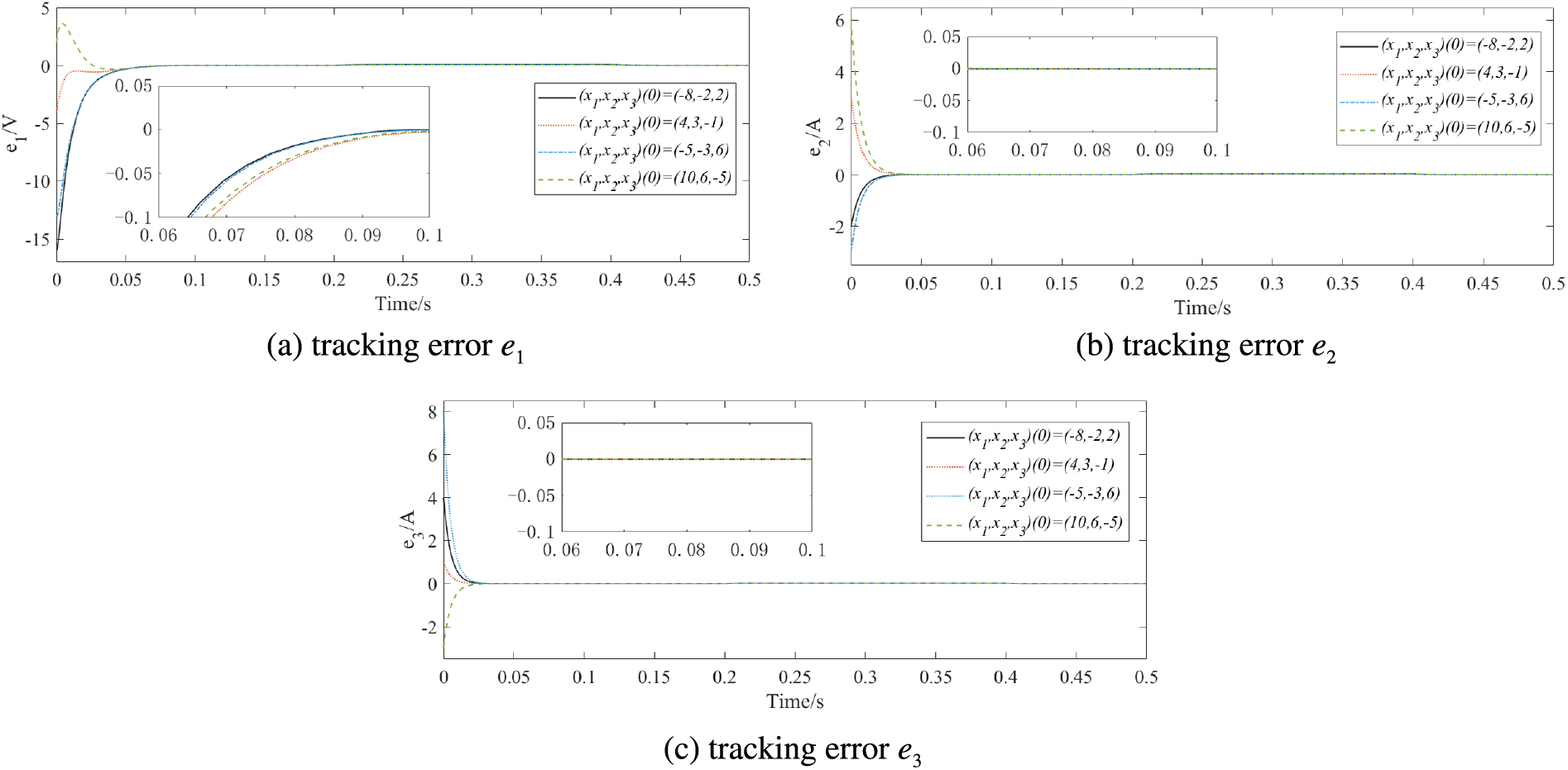
Figure 10: Tracking errors under different initial states at T1=0.1s
Fig. 11 illustrates the curves of state variables in finite time backstepping control under different initial states. Apparently, the tracking process of state variables is slow and the trajectory changes are small under different initial states, achieving tracking about 0.35 s. Fig. 12 depicts the state responses variables in a fixed-time controller under different initial states. The convergence time of fixed time control has been improved and effective tracking can be achieved in different initial states, while the tracking goal is reached within 0.2 s. Compared with finite-time control and fixed-time control, predefined time control can approach the upper limit of convergence time more accurately, while provide the improved convergence speed and control performance effectively.
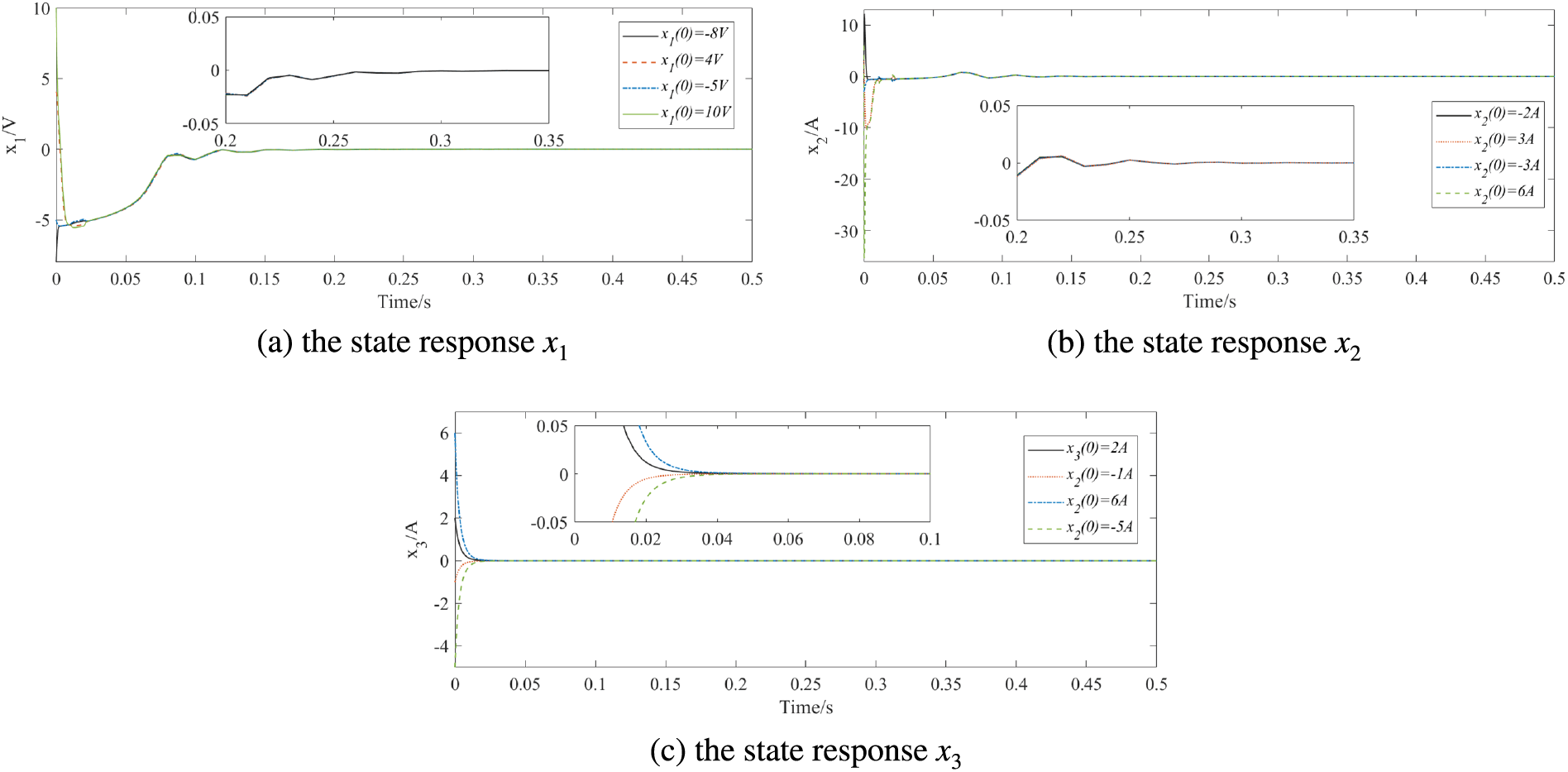
Figure 11: State responses under different initial states in finite-time backstepping controller

Figure 12: State responses under different initial states in fixed-time backstepping controller
Figs. 13–15 show the controllers’ trajectories in finite-time control, fixed-time control, and predefined-time control, respectively. Based on the simulation results, the predefined-time backstepping controllers and can achieve grid-connection objectives within the predefined time, effectively reduce the convergence time and improve the quality of grid-connected electrical energy.
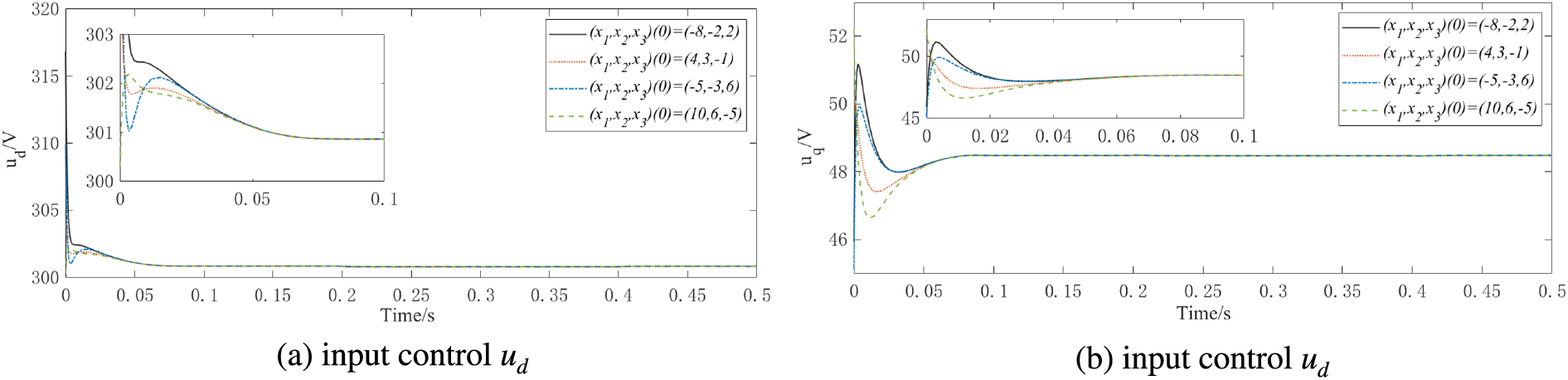
Figure 13: Controllers under different initial states at T1=0.1s
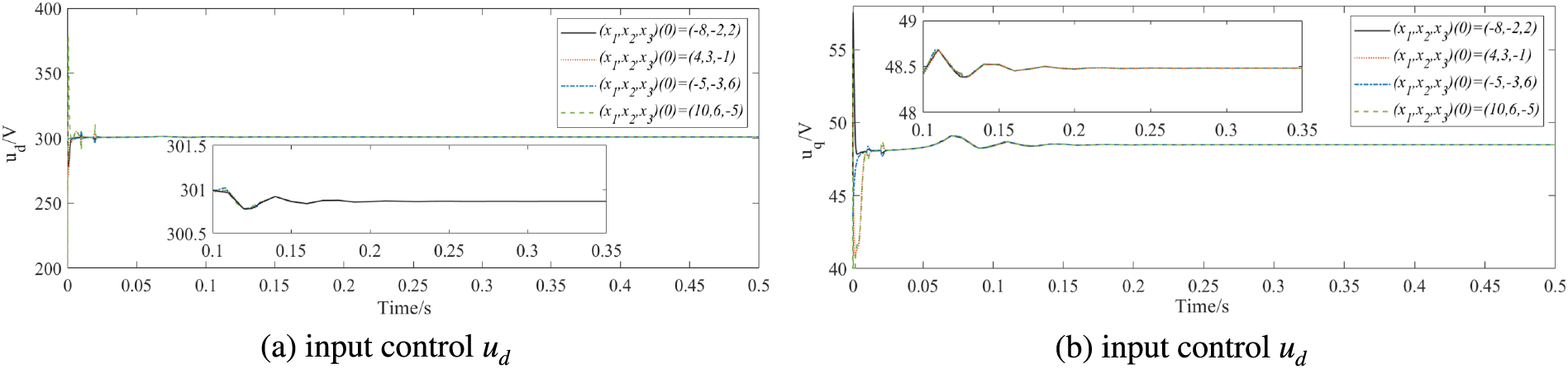
Figure 14: Controllers under different initial states in finite-time backstepping controller
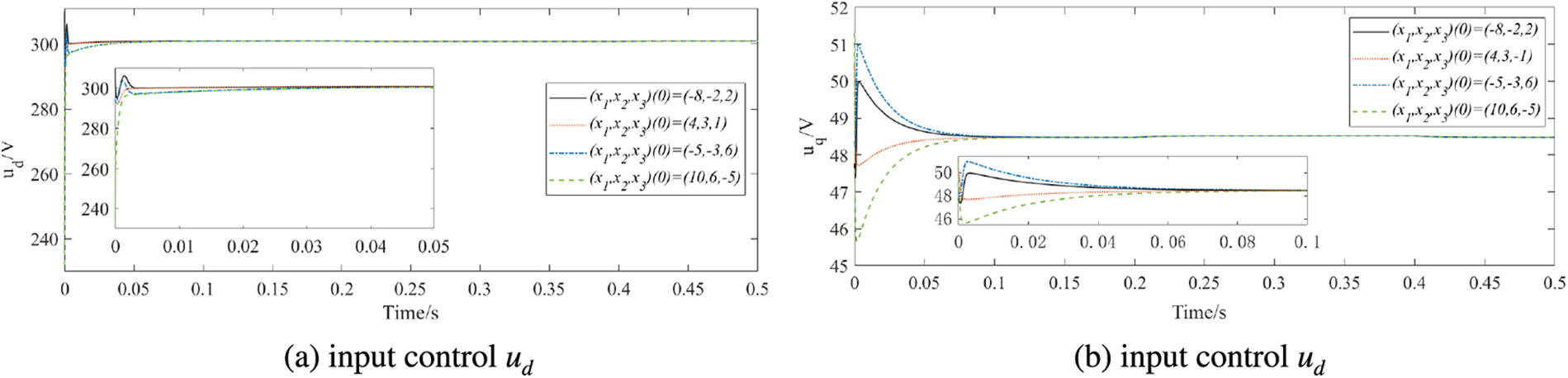
Figure 15: Controllers under different initial states in fixed-time backstepping controller
To realize the effective control of VSI in a grid-connected PV system, a predefined-time controller is formulated. The time-varying functions are introduced in state tracking errors during the backstepping recursive design. Analytical differential calculation of the virtual control in backstepping control is avoided by the DSC strategy, and the disturbance compensation is realized by adaptive control. Furthermore, the global stability of the proposed predefined time control is verified by the Lyapunov theory. The simulation results demonstrate that the proposed predefined-time controller can implement predefined-time control and has excellent control performance for the inverter. The predefined time control method proposed in this paper can track the DC voltage and connect the unit power factor to the grid in the predefined time, but it depends on the initial states of the system, which should be solved in the future research.
Acknowledgement: Thanks to the editors and the anonymous reviewers for the helpful comments and suggestions that improve the presentation of the manuscript.
Funding Statement: This work was supported by the State Grid Corporation of China Headquarters Science and Technology Project under Grant No. 5400-202122573A-0-5-SF.
Author Contributions: The authors confirm contribution to the paper as follows: Dan Liu and Yanze Xu contributed to controller formulation. Kan Cao and Ping Xiong contributed to system stability analysis. Jiarui Zhang and Yunfei Mu wrote the manuscript and performed the simulations experiment. Xiaotong Ji contributed to the conception of the paper significantly. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article. Additional data that support the findings of this study are available upon request from the corresponding author, subject to reasonable request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. J. Chen, Y. Lv, and T. Fan, “Research on the evolution and driving factors of digitalization of energy in China–A new perspective based on coupling coordination,” Heliyon, vol. 9, no. 3, May 2023. doi: 10.1016/j.heliyon.2023.e14138. [Google Scholar] [PubMed] [CrossRef]
2. D. Pullaguram, S. Mishra, and N. Senroy, “Event-triggered communication based distributed control scheme for DC microgrid,” IEEE Trans. Power Syst., vol. 33, no. 5, pp. 5583–5593, Sep. 2018. doi: 10.1109/TPWRS.2018.2799618. [Google Scholar] [CrossRef]
3. R. H. Lasseter, Z. Chen, and D. Pattabiraman, “Grid-forming inverters: A critical asset for the power grid,” IEEE J. Emerg. Sel. Top. Power Electron., vol. 8, no. 2, pp. 925–935, Dec. 2019. doi: 10.1109/JESTPE.2019.2959271. [Google Scholar] [CrossRef]
4. Y. X. Ji, W. He, S. J. Cheng, K. Jürgen, and M. Zhan, “Dynamic network characteristics of power-electronics-based power systems,” Sci. Rep., vol. 10, no. 1, pp. 9946, Jun. 2020. doi: 10.1038/s41598-020-66635-0. [Google Scholar] [PubMed] [CrossRef]
5. L. Zhang, Z. Chen, H. Zhang, Z. H. Ma, B. W. Cao and L. H. Song, “Accurate study and evaluation of small PV power generation system based on specific geographical location,” Energy Eng., vol. 117, no. 6, pp. 453–470, Aug. 2020. doi: 10.32604/EE.2020.013276. [Google Scholar] [CrossRef]
6. H. Abubakr, J. C. Vasquez, K. Mahmoud, M. M. F. Darwish, and J. M. Guerrero, “Comprehensive review on renewable energy sources in Egypt-current status, grid codes and future vision,” IEEE Access, vol. 10, pp. 4081–4101, Mar. 2022. doi: 10.1109/ACCESS.2022.3140385. [Google Scholar] [CrossRef]
7. F. Hasan, J. H. Ahmed, and N. K. Abdul Hadi, “Performance analysis of a rooftop hybrid connected solar PV system,” Energy Eng., vol. 119, no. 4, pp. 1729–1744, 2022. doi: 10.32604/ee.2022.021190. [Google Scholar] [CrossRef]
8. M. Inci, “Technoeconomic analysis of fuel cell vehicle-to-grid (FCV2G) system supported by photovoltaic energy,” Energy Technol., vol. 11, no. 4, pp. 2201162, Apr. 2023. doi: 10.1002/ente.202201162. [Google Scholar] [CrossRef]
9. M. İnci and K. Ç. Bayındır, “Single-stage vehicular fuel cell system with harmonic elimination capability to suppress distortion effects of electric vehicle parking lots,” J. Power Sources, vol. 597, pp. 234175, Mar. 2024. doi: 10.1016/j.jpowsour.2024.234175. [Google Scholar] [CrossRef]
10. M. İnci, “Connecting multiple vehicular PEM fuel cells to electrical power grid as alternative energy sources: A case study,” Int. J. Hydrogen Energy, vol. 52, pp. 1035–1051, Jan. 2024. doi: 10.1016/j.ijhydene.2023.08.228. [Google Scholar] [CrossRef]
11. X. Deng, F. P. Da, H. J. Shao, and X. Wang, “A survey of the researches on grid-connected solar power generation systems and power forecasting methods based on ground-based cloud atlas,” Energy Eng., vol. 120, no. 2, pp. 385–408, Jul. 2023. doi: 10.32604/ee.2023.023480. [Google Scholar] [CrossRef]
12. D. Z. Xu, Y. C. Dai, C. S. Yang, and X. G. Yan, “Adaptive fuzzy sliding mode command-filtered backstepping control for islanded PV microgrid with energy storage system,” J. Frank. Inst. Eng. Appl. Math., vol. 356, no. 4, pp. 1880–1898, Mar. 2019. doi: 10.1016/j.jfranklin.2019.01.012. [Google Scholar] [CrossRef]
13. X. Shi, Y. Cheng, C. Yin, X. Huang, and S. M. Zhong, “Design of adaptive backstepping dynamic surface control method with RBF neural network for uncertain nonlinear system,” Neurocomputing, vol. 330, pp. 490–503, Feb. 2019. doi: 10.1016/j.neucom.2018.11.029. [Google Scholar] [CrossRef]
14. S. Dhar and P. K. Dash, “Adaptive backstepping sliding mode control of a grid interactive PV-VSC system with LCL filter,” Sustain. Energy, Grids Netw., vol. 6, pp. 109–124, Jun. 2016. doi: 10.1016/j.segan.2016.03.001. [Google Scholar] [CrossRef]
15. Z. X. Zhong, X. Y. Wang, and H. K. Lam, “Finite-time fuzzy sliding mode control for nonlinear descriptor systems,” IEEE/CAA J. Autom. Sin., vol. 8, no. 6, pp. 1141–1152, Jun. 2021. doi: 10.1109/JAS.2021.1004024. [Google Scholar] [CrossRef]
16. El. J. Khazane and E. H. Tissir, “Achievement of MPPT by finite time convergence sliding mode control for photovoltaic pumping system,” Sol. Energy, vol. 166, pp. 13–20, May 2018. doi: 10.1016/j.solener.2018.03.026. [Google Scholar] [CrossRef]
17. M. Y. Xie, M. M. Gulzar, H. Tehreem, M. Y. Javed, and S. T. H. Rizvi, “Automatic voltage regulation of grid connected photovoltaic system using Lyapunov based sliding mode controller: A finite-time approach,” Int. J. Control Autom. Syst., vol. 18, pp. 1550–1560, Jun. 2020. doi: 10.1007/s12555-019-0563-x. [Google Scholar] [CrossRef]
18. P. Zhang, G. R. Zhang, and H. B. Du, “Finite-time consensus for power regulation of parallel PV Grid-connected inverters,” IEEE Trans. Circuits Syst. II-Express Briefs, vol. 67, no. 11, pp. 2632–2636, Nov. 2020. doi: 10.1109/TCSII.2020.2964956. [Google Scholar] [CrossRef]
19. S. Dhar and P. K. Dash, “A new backstepping finite time sliding mode control of grid connected PV system using multivariable dynamic VSC model,” Int. J. Electr. Power& Energy Syst., vol. 82, pp. 314–330, Nov. 2016. doi: 10.1016/j.ijepes.2016.03.034. [Google Scholar] [CrossRef]
20. C. S. Yang, S. F. Ni, Y. C. Dai, X. N. Huang, and D. D. Zhang, “Anti-disturbance finite-time adaptive sliding mode backstepping control for PV inverter in master-slave-organized islanded microgrid,” Energies, vol. 13, no. 17, pp. 4490, Sep. 2020. doi: 10.3390/en13174490. [Google Scholar] [CrossRef]
21. W. Y. Jiang, S. S. Ge, and D. Y. Li, “Fixed-time-synchronized control: A system-dimension-categorized approach,” Sci. China Inf. Sci., vol. 66, no. 7, pp. 1–18, Jul. 2023. doi: 10.1007/s11432-022-3649-1. [Google Scholar] [CrossRef]
22. L. N. Liu and G. H. Yang, “Distributed fixed-time optimal resource management for microgrids,” IEEE Trans. Autom. Sci. Eng., vol. 20, no. 1, pp. 404–412, Jan. 2022. doi: 10.1109/TASE.2022.3155163. [Google Scholar] [CrossRef]
23. S. Shi, G. S. Zhang, H. F. Min, Y. L. Hu, and Y. H. Sun, “Exact uncertainty compensation of linear systems by continuous fixed-time output-feedback controller,” J. Syst. Eng. Electron., vol. 33, no. 3, pp. 706–715, Jun. 2022. doi: 10.23919/JSEE.2022.000065. [Google Scholar] [CrossRef]
24. L. Y. Xiong et al., “Voltage and frequency regulation with WT-PV-BESS in remote weak grids via fixed-time containment control,” IEEE Trans. Power Syst., vol. 38, pp. 2719–2735, May 2023. doi: 10.1109/TPWRS.2022.3190847. [Google Scholar] [CrossRef]
25. S. Sahoo, S. Mishra, S. Fazeli, F. R. Li, and T. Dragicevic, “A distributed fixed-time secondary controller for DC microgrid clusters,” IEEE Trans. Energy Convers., vol. 34, no. 4, pp. 1997–2007, Dec. 2019. doi: 10.1109/TEC.2019.2934905. [Google Scholar] [CrossRef]
26. Y. N. Pan, W. Y. Ji, and H. J. Liang, “Adaptive predefined-time control for Lü chaotic systems via backstepping approach,” IEEE Trans. Circuits Syst. II: Express Briefs, vol. 69, no. 12, pp. 5064–5068, Dec. 2022. doi: 10.1109/TCSII.2022.3204050. [Google Scholar] [CrossRef]
27. R. E. Jiménez, T. J. D. Sánchez, G. D. Gómez, and A. G. Loukinanov, “Variable structure predefined-time stabilization of second-order systems,” Asian J. Control, vol. 21, no. 3, pp. 1179–1188, May 2019. doi: 10.1002/asjc.1785. [Google Scholar] [CrossRef]
28. Y. Zhang, Y. W. Wang, J. W. Xiao, and X. K. Liu, “Predefined-time secondary control for DC microgrid,” IEEE Trans. Ind. Electron., vol. 69, no. 12, pp. 13504–13513, Dec. 2021. doi: 10.1109/TIE.2021.3128899. [Google Scholar] [CrossRef]
29. F. L. Jia, J. Huang, and X. He, “Adaptive predefined-time tracking control for high-order strict-feedback nonlinear systems with unknown mismatched disturbances,” Int. J. Adapt Control Signal Process, vol. 36, no. 11, pp. 2903–2919, Sep. 2022. doi: 10.1002/acs.3502. [Google Scholar] [CrossRef]
30. J. A. Moreno, “Arbitrary-order fixed-time differentiator,” IEEE Trans. Automat. Contr., vol. 67, no. 3, pp. 1543–1549, May 2022. doi: 10.1109/TAC.2021.3071027. [Google Scholar] [CrossRef]
31. D. Xu, G. Wang, W. Yan, and C. Shen, “Nonlinear adaptive command-filtered backstepping controller design for three-phase grid-connected solar photovoltaic with unknown parameters,” presented at the 2017 Chinese Autom. Congr., Jinan, China, Oct. 20–22, 2017, pp. 7823–7827. [Google Scholar]
32. R. E. Jiménez, V. A. Muñoz, T. J. D. Sánchez, M. Defoort, and A. G. Loukianov, “A Lyapunov-like characterization of predefined-time stability,” IEEE Trans. Automat. Contr., vol. 65, no. 11, pp. 4922–4927, Nov. 2020. doi: 10.1109/TAC.2020.2967555. [Google Scholar] [CrossRef]
33. C. Song, H. B. Sun, and L. L. Hou, “A predefined time decentralized adaptive tracking control method for interconnected nonlinear systems,” Int. J. Robust Nonlinear Control, vol. 33, no. 13, pp. 7986–8014, Sep. 2023. doi: 10.1002/rnc.6806. [Google Scholar] [CrossRef]
34. H. Bécerra, C. Vázquez, G. Arechavaleta, and J. Delfin, “Predefined-time convergence control for high-order integrator systems using time base generators,” IEEE Trans. Control Syst. Technol., vol. 26, no. 5, pp. 1866–1873, Sep. 2018. doi: 10.1109/TCST.2017.2734050. [Google Scholar] [CrossRef]
35. B. J. Liu, M. S. Hou, C. H. Wu, W. C. Wang, Z. H. Wu and B. Huang, “Predefined-time backstepping control for a nonlinear strict-feedback system,” Int. J. Robust Nonlinear Control, vol. 31, no. 8, pp. 3354–3372, Feb. 2021. doi: 10.1002/rnc.5425. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF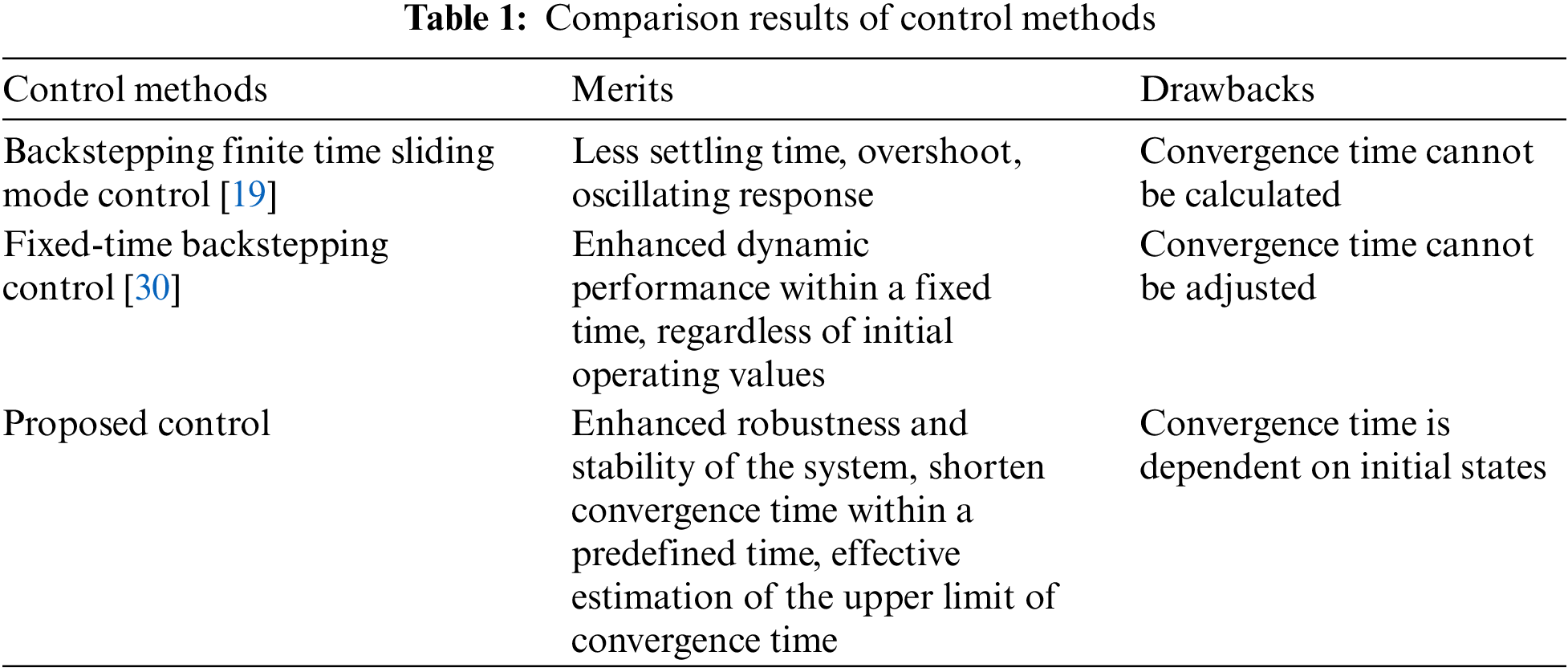
 Downloads
Downloads
 Citation Tools
Citation Tools
