 Open Access
Open Access
ARTICLE
Applying an Ordinal Priority Approach Based Neutrosophic Fuzzy Axiomatic Design Approach to Develop Sustainable Geothermal Energy Source
Department of Industrial Engineering and Management, National Kaohsiung University of Science and Technology, Kaohsiung, 807618, Taiwan
* Corresponding Author: Thuy-Duong Thi Pham. Email:
Energy Engineering 2024, 121(8), 2039-2064. https://doi.org/10.32604/ee.2024.050224
Received 31 January 2024; Accepted 18 March 2024; Issue published 19 July 2024
Abstract
Geothermal energy is considered a renewable, environmentally friendly, especially carbon-free, sustainable energy source that can solve the problem of climate change. In general, countries with geothermal energy resources are the ones going through the ring of fire. Therefore, not every country is lucky enough to own this resource. As a country with 117 active volcanoes and within the world’s ring of fire, it is a country whose geothermal resources are estimated to be about 40% of the world’s geothermal energy potential. However, the percentage used compared to the geothermal potential is too small. Therefore, this is the main energy source that Indonesia is aiming to exploit and use. However, the deployment and development of this energy source are still facing many obstacles due to many aspects from budget sources due to high capital costs, factory construction location, quality of resources, and conflicts of the local community. In this context, determining the optimal locations for geothermal energy sites (GES) is one of the most important and necessary issues. To strengthen the selection methods, this study applies a two-layer fuzzy multi-criteria decision-making method. Through the layers, the Ordinal Priority Approach (OPA) is proposed to weight the sub-criteria, the main criterion, and the sustainability factors. In layer 2, the Neutrosophic Fuzzy Axiomatic Design (NFAD) is applied to rank and evaluate potential locations for geothermal plant construction. Choosing the right geothermal energy site can bring low-cost efficiency, no greenhouse gas emissions, and quickly become the main energy source providing electricity for Indonesia. The final ranking shows Papua, Kawah Cibuni, and Moluccas as the three most suitable cities to build geothermal energy systems. Kawah Cibuni was identified as the most potential GES in Indonesia, with a score of 0.46. Papua is the second most promising GES with a score of 0.45. Next is the Moluccas, with a score of 0.39. However, the three least potential sites among the 15 studied sites are Lumut Balai, Moluccas and Patuha, with scores of 0.08, 0.11 and 0.17, respectively. The conclusion of this study also classifies positions into groups to aid in decision-making.Keywords
Renewable energy not only brings a lot of positive impacts to individuals but also makes great contributions to each country and territory, such as economic growth and poverty alleviation by creating jobs, people having higher incomes, reducing the risk of social decentralization, and protecting the environment at all levels. Providing people with reliable energy at low prices is a step forward that can improve access to energy services in urban and rural areas [1]. Which Geothermal is a source of energy available in the soil, unaltered by fluctuations in the price of fossilized oil or resource scarcity. When compared to fossil fuel energy sources, it is a reliable source of energy [2]. Therefore, the development of this energy source is a means to achieve the above goals. With the benefits that geothermal energy brings, we should maintain and develop it. Choosing the right location to build a power plant has a great consequence on the viability of geothermal energy sites (GES) in Indonesia. Therefore, this article aims to identify the preferred locations for the placement of geothermal plants, while taking into account the most influential and conflicting criteria. These criteria include qualitative and quantitative, random, and deterministic categories. In many recent studies, in order to determine the location for renewable energy with comprehensive development potential, in addition to economic aspects, environmental, technical, and geological factors are also important to the evaluation and selection process [3]. To address the selection of facility sites, multi-criteria decision-making (MCDM) approaches have been successfully used for this purpose. In the first layer, the Ordinal Priority Approach (OPA) method was used to determine the sub-criteria, main criteria as well as their weights. Then, the qualitative efficiency of the geothermal plant sites was deliberated using the Neutrosophic Fuzzy Axiomatic Design (NFAD) process. Finally, GES is classified into different groups to support selection decisions. The main contributions of this paper are as follows: Applying the proposed method will increase value in site selection decision-making and reduce unnecessary expenses. Although there have been several implementations of MCDM methods in the field of geothermal energy, there have been no studies that have applied OPA-NFAD to select suitable geothermal energy sites observed in the fields previous research and this motivated us to present this study. Furthermore, this study applies a valuable reference to the problem of geothermal site selection in Indonesia in plant construction. Besides the contributions and novelties of the current research, there are still potential challenges. First, the decision maker’s subjective assessment is an important input to the decision-making process. Therefore, the decision-making results may not be applicable to geothermal site selection elsewhere. Second, many other researchers have applied quantitative and qualitative criteria with different mathematical methods to select geothermal energy locations. Finally, there have been no studies applying Axiomatic Design (AD) in neutrophil fuzzy environments for geothermal energy site selection, so introducing a new decision-making framework based on NFAD is important. The remaining part of this paper is analyzed: An abstract of the related studies carried out in Section 2, a detailed profile of the paper is presented in Section 3, and a discussion, as well as a description of the results, is the epilogue of the paper.
2.1 The Criteria and the Sub-Criteria
In this chapter, the criteria used for selecting GES will be developed in detail. Over the past decade, many studies have recognized the sub-criteria and criteria for this as presented in Table 1. The criteria are Economic, Social, Geological, Temperature, Technological, Cultural, Volcanic dome density, Environmental, and Political GES are the main selection criteria. The sub-criteria relate to air pollution, water pollution, noise pollution, social acceptance, plant design, construction costs, or operation. There are many studies using a variety of primary and secondary criteria. Research by Bilić et al. [4] analyzed potential geothermal sites in Northeastern Croatia. In the process of hydrocarbon exploration, this place has been discovered to have a high geothermal potential. Besides technical assessment, because of indirect effects, influence on the environment and social deliberations are also examined so that the plan can be fortunately developed and accepted by the local community. At the same time in 2020, Chen et al. [5] used a multi-criteria approach based on economic, energy and environmental factors. This article exploits local energy sources to save energy, save fossil fuels and reduce greenhouse gas emissions. Or the study by Mostafaeipour et al. [6], said that the density of volcanic domes is classified as the most significant criterion for the selection of potential geothermal plant construction sites in Afghanistan. In the study by Raos et al. [7], advanced geothermal projects and long-term use plans are considered using related criteria. The criteria include: Technology details, geothermal characteristics, energy prices, spatial data, social impact and environmental impact. To evaluate the enhanced geothermal system. Raos et al. [8] used an MCDM tool based on a set of criteria such as geological characteristics, technical specifications, heat and energy prices as well as environmental and social impacts.
From the different criteria used in prior papers, it can be seen that the criteria such as Environmental, Geological, Economic, and Technological are the four most prominent and used in different fields of research due to the urgency of their application for the construction of a geothermal plant.
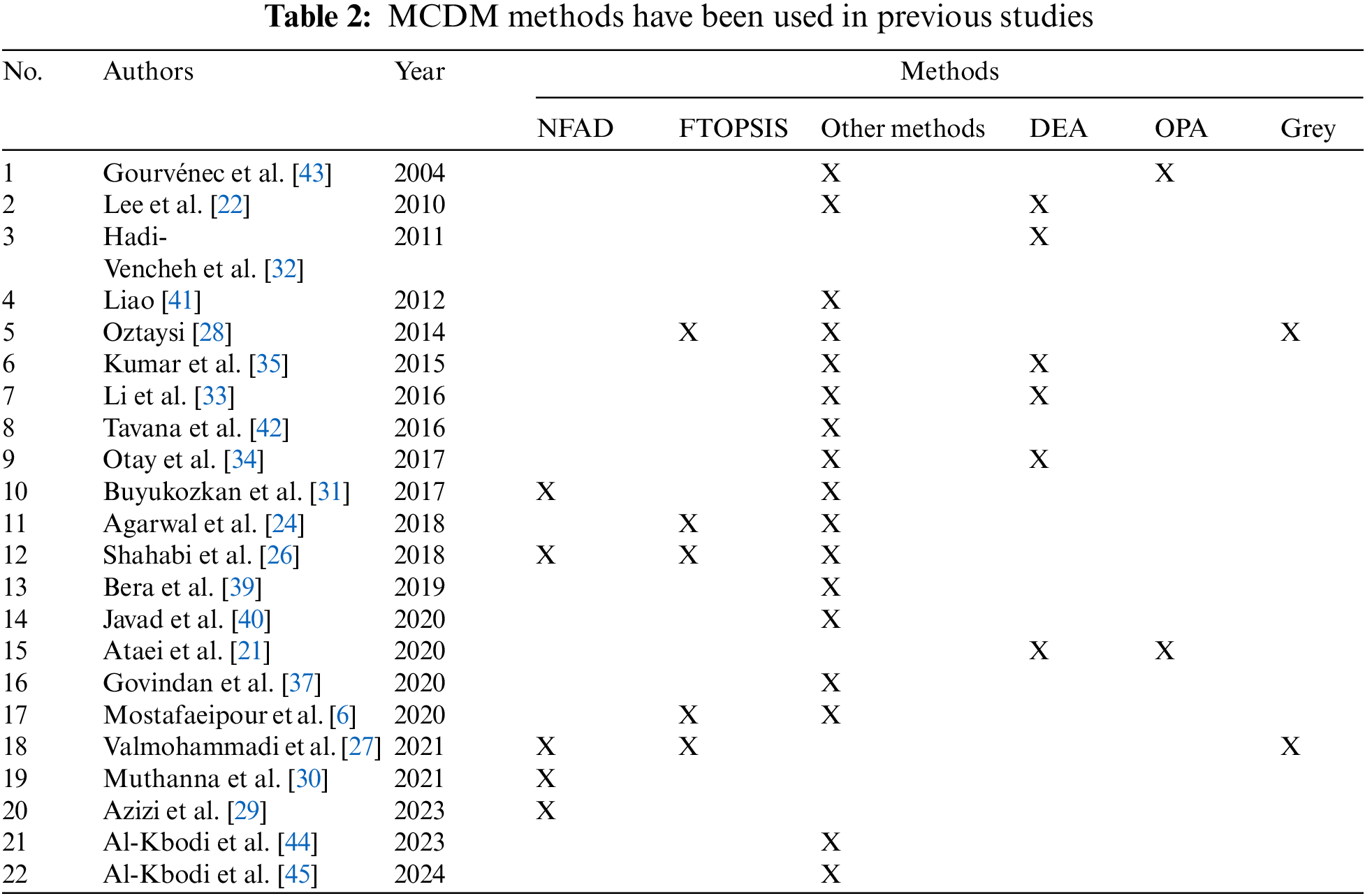
As recapitulated in Table 2, a handful of methods for alternatives problems have been described in the document, most of the techniques in the document are from the field of MCDM, such as OPA [20–23], fuzzy Technique for Order Performance by Similarity to Ideal Solution (FTOPSIS) [6,24–26], Gray model [27–29], NFAD [30,31]. This issue may have been partially solved by previous papers using Data Envelopment Analysis (DEA) models [22,30,32–36], and other MCDM [6,24,26,28,37–42]. The authors apply or combine these methods to compare results. Ataei et al. [21] selected the best supplier based on the sustainability framework in the super project. Modeling is done using Goods and Services Tax (GST) to consider multiple ranks for criteria and alternatives using the OPA approach. Mahmoudi et al. [23] combined the FTOPSIS and OPA methods to analyze criteria and rank alternatives in information management and data storage. The strengths of the two MCDM methods proposed in this study are integrated to handle the problem. The FTOPSIS method is distance-based, so it effectively considers ideal positive and negative distances. Besides, the OPA method is easy to use and can handle MCDM problems with incomplete data well. There are now many MCDM approaches that can be used for classification inventory. Hadi-Vencheh et al. [32] integrated the Analytic Hierarchy Process-Data Envelopment Analysis method for A (very important), B (moderately) and C (least important) inventory classification. It turns out that the new integrated FAHP-DEA method is simple enough, easy to apply, suitable for any decision alternative, and particularly effective and useful for heterogeneous MCDM problems. A study that greatly benefits the Department of Road Transport and Highways in creating safer roads in the future, Ganesh et al. [25] used a combination of FAHP-FTOPSIS method to analyze road transport network. Especially about the renewable energy industry in the world, in previous studies the authors also used a combination of multi-criteria decision-making methods. Mostafaeipour et al. [6] suggested that volcanic dome density ranks as the most important criterion when analyzing potential geothermal project sites in Afghanistan using a variety of MCDM. When analyzing the criteria, the Step Weight Assessment Ratio Analysis (SWARA) method was the optimal choice, while A new additive ratio assessment (ARAS) method was applied for the hierarchical ranking of geothermal locates potential and utilizes preferred engineering as an efficient solution. All procedures identified Ghazni district as the most potential site for the construction of geothermal sites in Afghanistan. This paper aims to promote the development of sustainable energy sources with priority methods similar to the FTOPSIS method.
Through the use of the previous methods, it can be seen that the MCDM methods are considered to be the most suitable alternative implementations compared to the existing types. Aim to measure the uncertainty carefully during the selection process. This study focuses on extending MCDM, with a combination of OPA and NFAD methods. OPA method is considered one of the most widely used MCDM methods by researchers. NFAD is one of the mathematical weighting methods that have the function of determining the rank of different properties with respect to the target. With the main goal of finding an optimal solution from several alternatives, and testing the certainty of the solutions, this study proposes OPA and NFAD methods for selecting the best locality to build a geothermal plant in Indonesia.
This study selected GES and evaluated 15 sites with geothermal potential in Indonesia, as shown in Fig. 1, in addition to the quantitative and qualitative criteria. As shown in Fig. 2, the research adopted a layered decision-making approach to performance evaluation GES. In layer 1, OPA is used to address heterogeneity in the initial decision-making process. There are twelve sub-criteria and four main criteria to be investigated in GES as follows: Economic (costs of field development, plant design, construction), geological (temperature, depth of resources, degree of mineralization of water resources), technical (power of the source, installed power, load factor), environmental criteria (air pollution, water pollution, noise pollution). NFAD was used to rate all alternatives in layer 2. Through the first and second layers, an overall score of GES was determined. However, these scores also include subjective opinions and judgments of experts in linguistics. The results of this method are applied to rank potential geothermal sites.
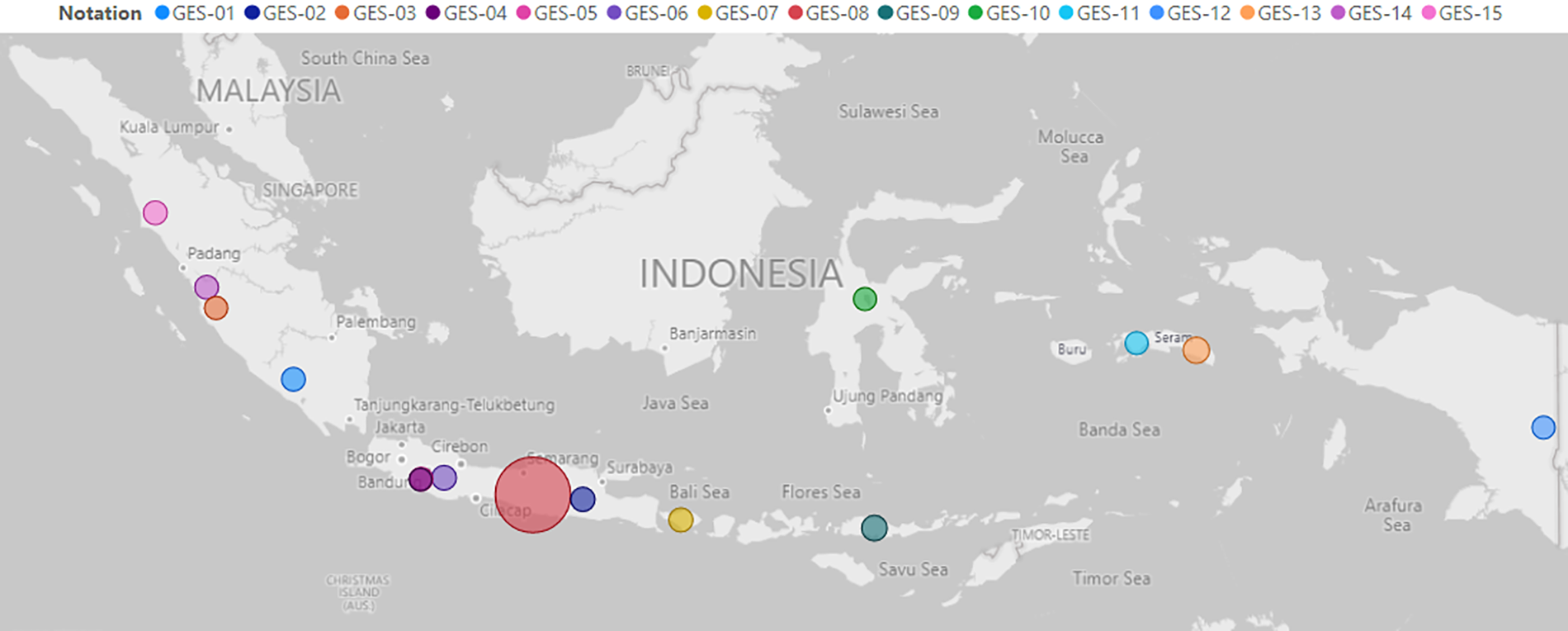
Figure 1: Locations with geothermal potential in Indonesia
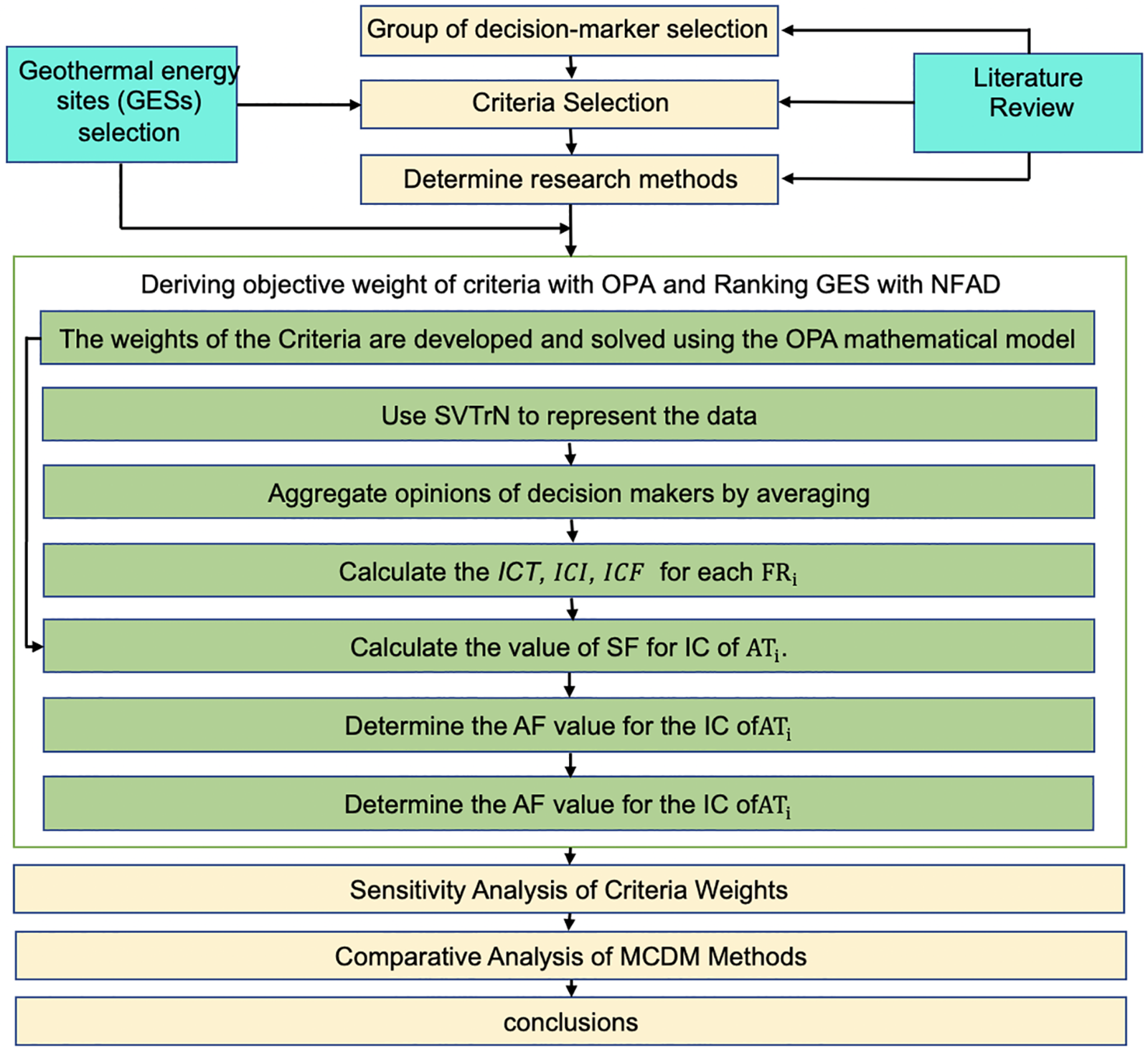
Figure 2: Methodology flow chart
Neutrosophic set (NS) [46]. Let ξ be the universe, and NS is D in ξ presented by a T function
There is no cap on the amount of
Score function (SF) and accuracy function (AF) are suitable functions for comparing SVN. Assume
(SVTrN-number)
Figure 3: A triangular neutrophil count with standard single value
Operations of SVTrN-number. If
SC and AF of SVTrN-number. The SF s (
Ranking of SVTrN-number.
AF(
AF(
AF(
Axiom design principles. The most important of the AD principles are the axiom of independence and the axiom of information. The independence axiom is used to determine the independence of functional requirements (FR). The FR indicates the smallest set of independent requirements that represent the design goals. The most important benefits of these techniques is that the model prevents the best choice from being selected if an alternative does not satisfy the FRs. The information axiom states that among designs that satisfy the independence axiom, the design with the lowest information content (IC) is the best design [47].
The information axiom is determined by the IC which is related to the ability to maintain planned objectives. The
The completion probability specified by the designer to be achieved is relative to the design scope (DR) and the system’s demand capabilities relative to the system scope (SR). The region of intersection of DR and SR is a common area for which a satisfactory solution exists, as shown in Fig. 4.
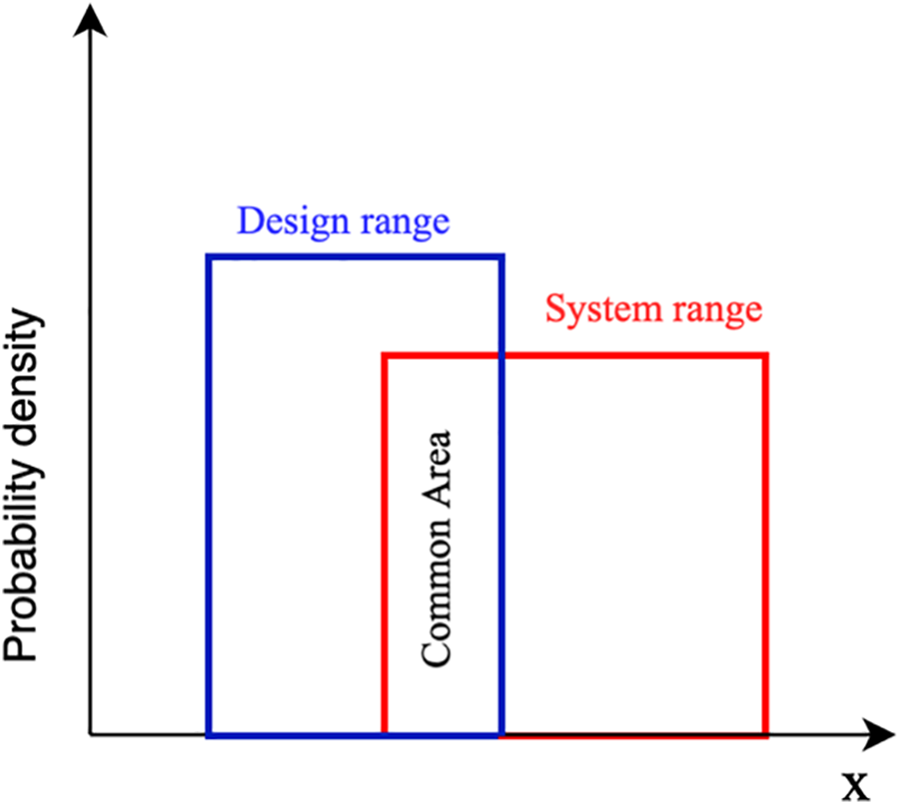
Figure 4: The common area of SR and DR
The key ideas of AD in a neutrosophic setting are introduced in the current section. Additionally, a fresh MCDM method for choosing suitable medical picture modalities is described.
Criterion values are presented using LV in the neutrophil domain, as shown in Table 3. The junction region of the TM, IM and FM functions of the neutrophil count can be achieved as illustrated in Fig. 5.
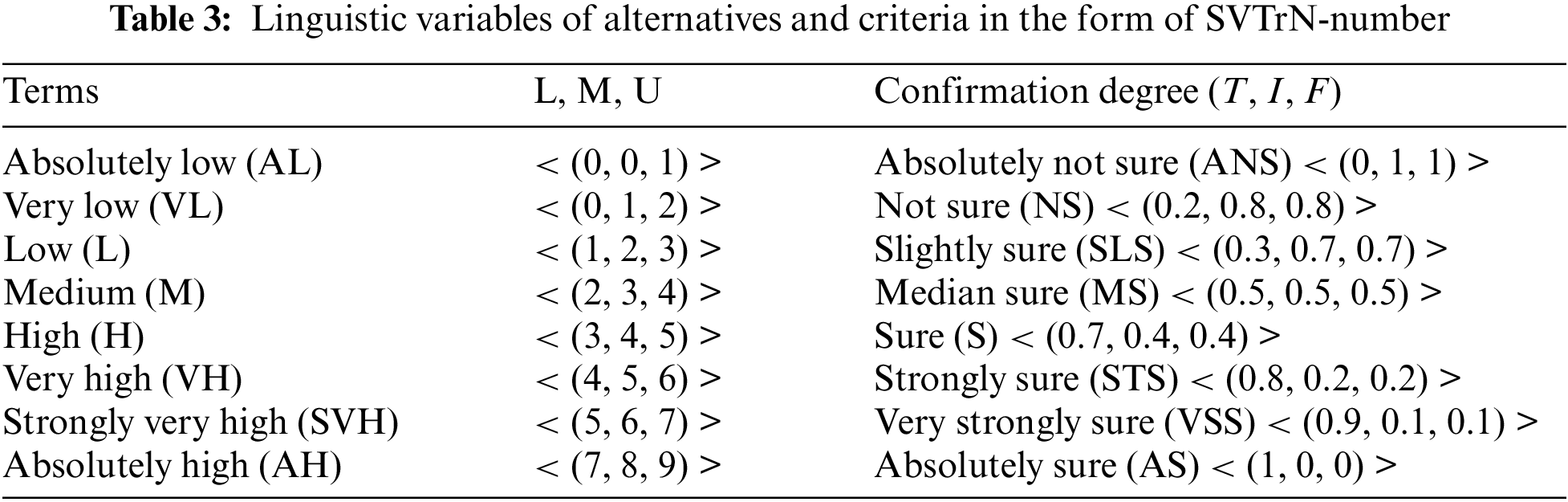
Figure 5: SR and DR intersection of neutrophil counts
The (ICT), (ICI), and (ICF) symbols, which stand for the TM, IM, and FM of information content, respectively, can be shown as follows:
The SF and the AF are employed in the NS-domain to compare neutrosophic values that may be represented as s and a, respectively. With the IC in the AD environment, we extend s and a in this method. We represent
3.2 Ordinal Priority Approach (OPA) Based on Neutrosophic Fuzzy Axiomatic Design (NFAD)
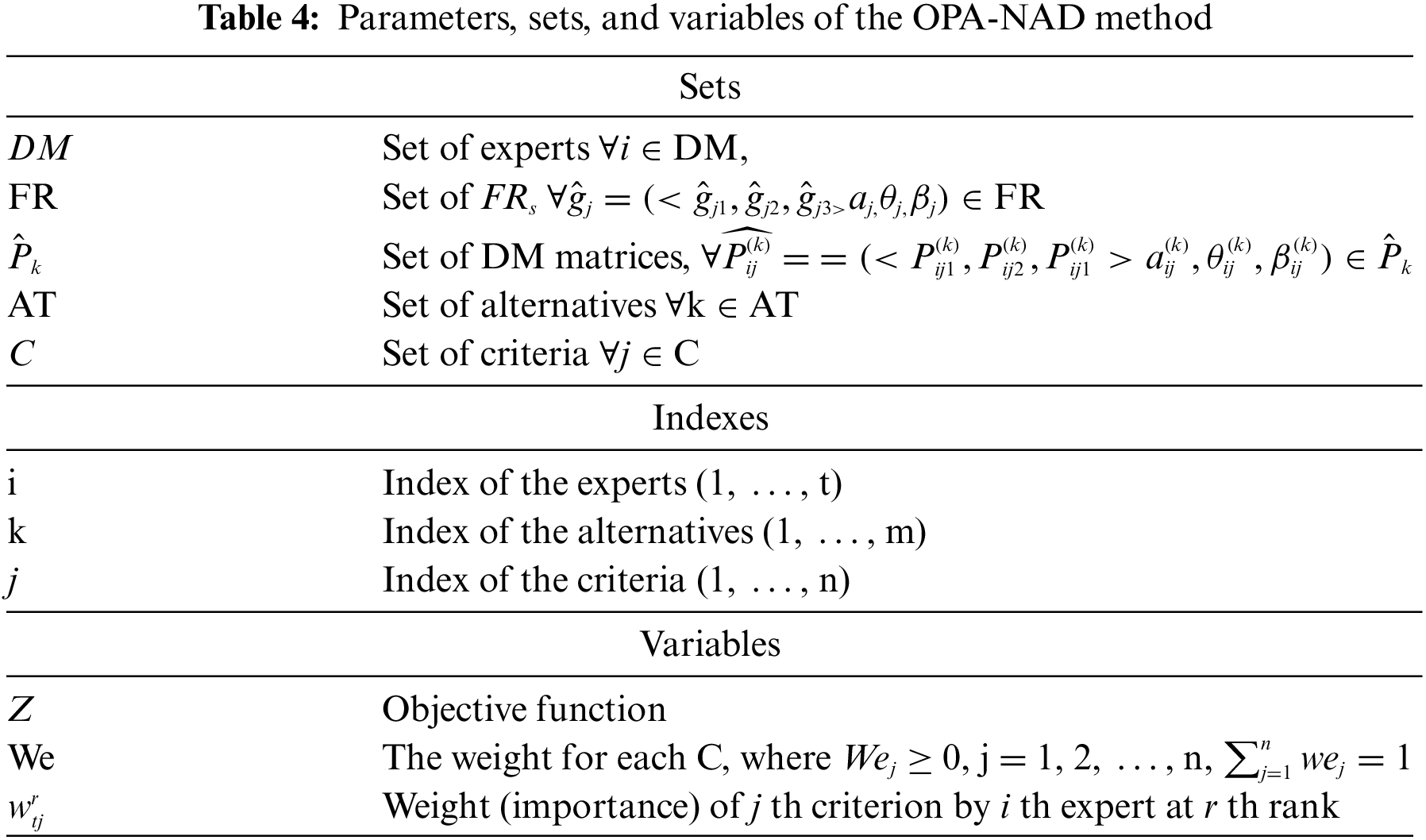
The Ordinal Priority Approach (OPA) based on Neutrosophic Fuzzy Axiomatic Design (NFAD) is an emerging MCDM method. This method is recognized by researchers as an effective, objective, and flexible method. This approach has the particular advantages of not requiring the normalization process, pairwise comparisons, or data completeness. Table 4 presents the set, parameters and decision variables of the OPA-NAD mathematical model.
The following procedures are used in this study’s OPA-NAD approach for weighting and rating the criteria:
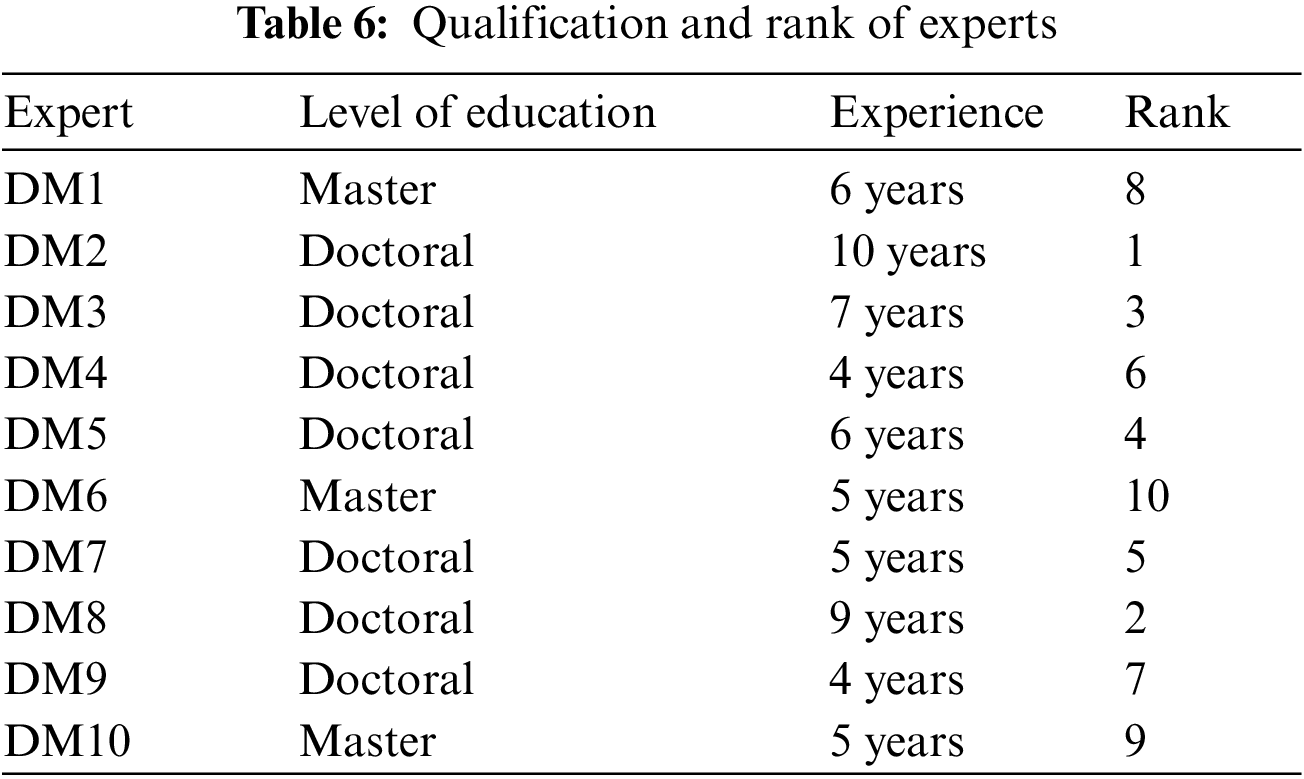
Step 1: Choose a team of decision-makers or experts. Experts are rated by ordinal numbers depending on amount of education and years of experience since their competence vary.
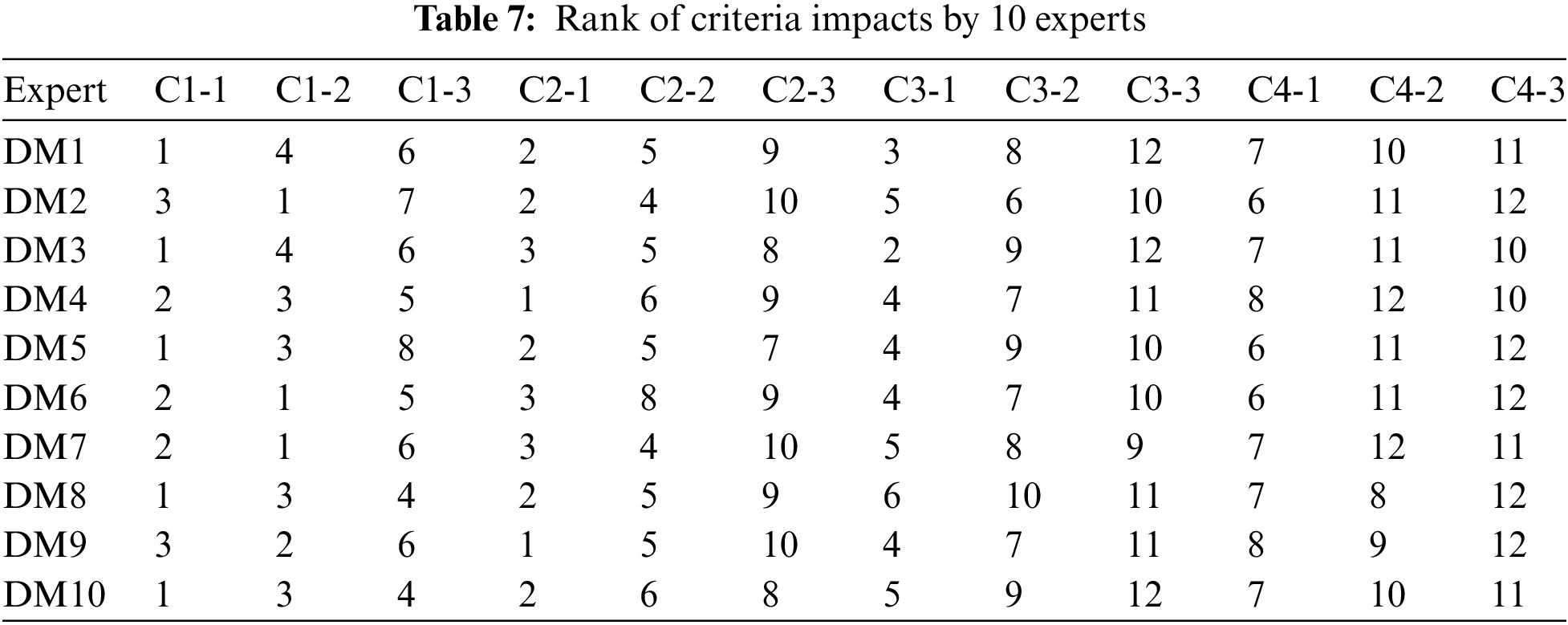
Step 2: Each expert assigns a priority to the criterion.
Step 3: Based on the ordinal judgments in steps 1 and 2, the mathematical model (20) is developed and solved.
where
The criteria and expert weights are determined using Eqs. (21) and (22):
Step 4: Use SVTrN, which has the form of <Low value (L), Mean value (M), Upper value (U); confirmation degree (CD)>, to represent the data. The data representation method is shown in Table 4.
Step 5: Aggregate opinions of decision makers by averaging using Eq. (7).
Step 6: Calculate the ICT,
where
Step 7: Calculate the value of SF for IC of
After calculating the
Step 8: Determine the AF value for the IC of
After computing the
Step 9: Rank alternatives.
Select the best alternative based on the ranking of the SVTrN using Eqs. (12) and (13). Then ranking them based on
4.1 Description of the Case Study
In this paper, a fuzzy MCDM model is proposed to support the efficiency analysis of GES. In this stage, the purpose of refining the list of sites is to select DMUs with perfect efficiency scores from previous studies. In general, all geothermal areas of Indonesia are associated with volcanic arcs. Found in about 276 locations are geothermal areas located along volcanic arcs. Areas such as Karaha, Bedugul, Sallura, Hulu Lais, Lumut Balai, Sungai Penuh, Iyang Argopuro, Kawah Cibuni, Ulubelu, Patuha, and Kotamobagu are potential sources that are yet to be developed for power generation. Other potential geothermal resources are also located in remote areas and small islands in eastern Indonesia, such as Halmahera, Ambon, Lomblen, and Flores [48]. The study by Asokawaty et al. [49]. showed geothermal potential in the western part of the islands of Sumatera, Bali, Kalimantan, and Java and the eastern part of Indonesia, where the so-called ‘ring of fire islands includes Nusa Tenggara, Sulawesi, Moluccas, Papua, and Maluku. The pipeline of the 1,257 MW Geothermal Power Plant Project includes 15 extremely high potentials in Indonesia, as shown in Table 5. The hierarchical position of sub-criteria and main criteria depicted in Fig. 6 is based on expert survey results and literature reviews. Which the determining factors of technical, environmental, economic, and geological characteristics are the four criteria to evaluate the performance of GES. Firstly, economies of scale include costs, plant design, and construction. The construction of geothermal plants is suitable for places that are not really developed because geothermal plants provide a source of electricity as well as long-term, stable jobs and bring millions of dollars to the local community local economy. Secondly, geological includes temperature, depth of resources, and water resources mineralization. Depending on the plant’s geothermal use to select different construction sites, the Earth’s temperature increases with the depth of resources. The next criteria are related to the technical aspects, including the power of the source, installed power, and load factor. Installed capacity is the most important parameter that determines both cost and revenue. The last criteria are related to the environment, including air pollution, water pollution, and noise pollution. The construction of geothermal plants should be ensured with issues such as minimizing impacts on the environment, not causing noise to residential areas, and not building in protected areas (lakes, streams, lagoons, etc.). Based on the experience of 10 experts in the field of renewable energy assess the impact of the selected primary and secondary criteria.
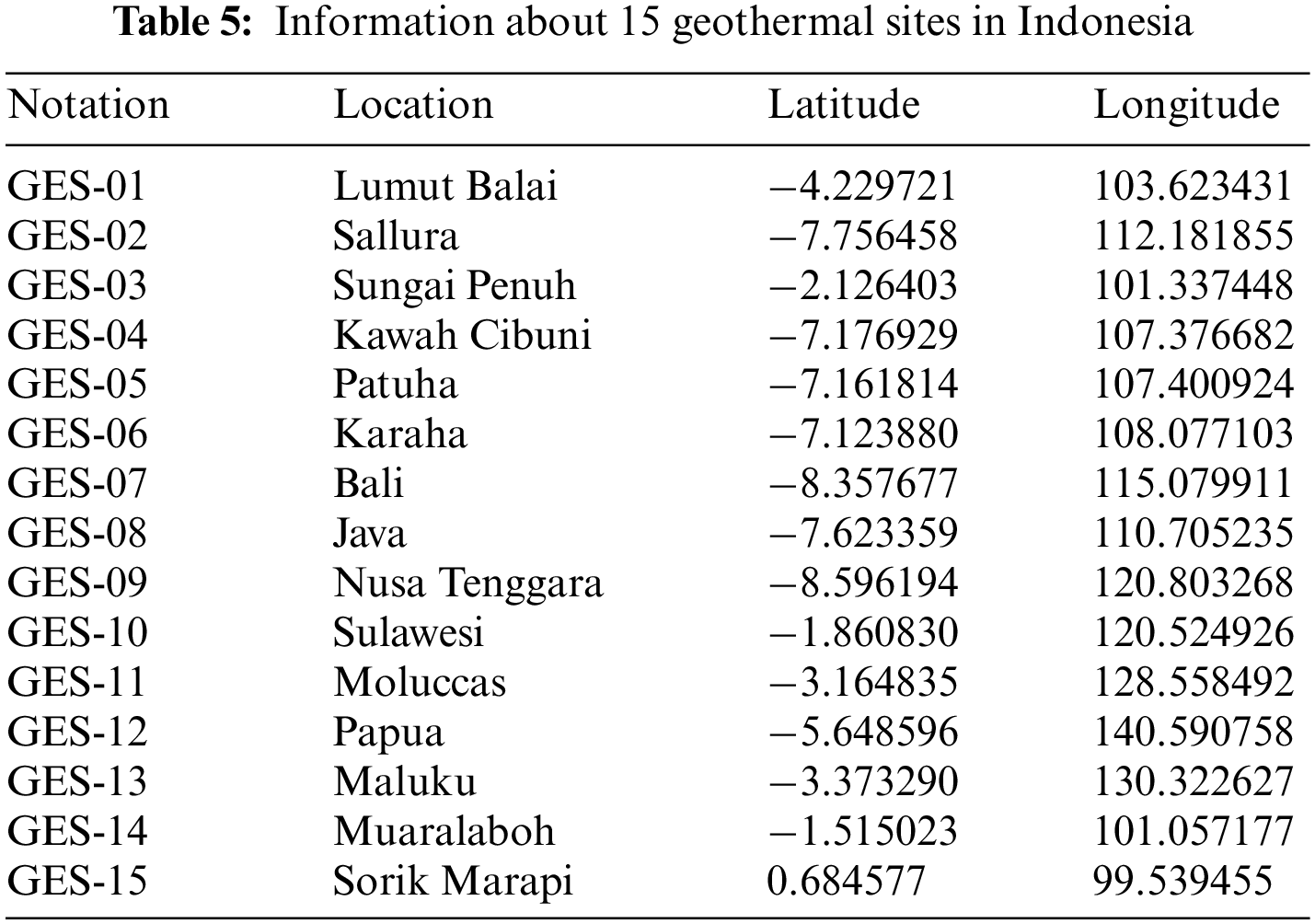
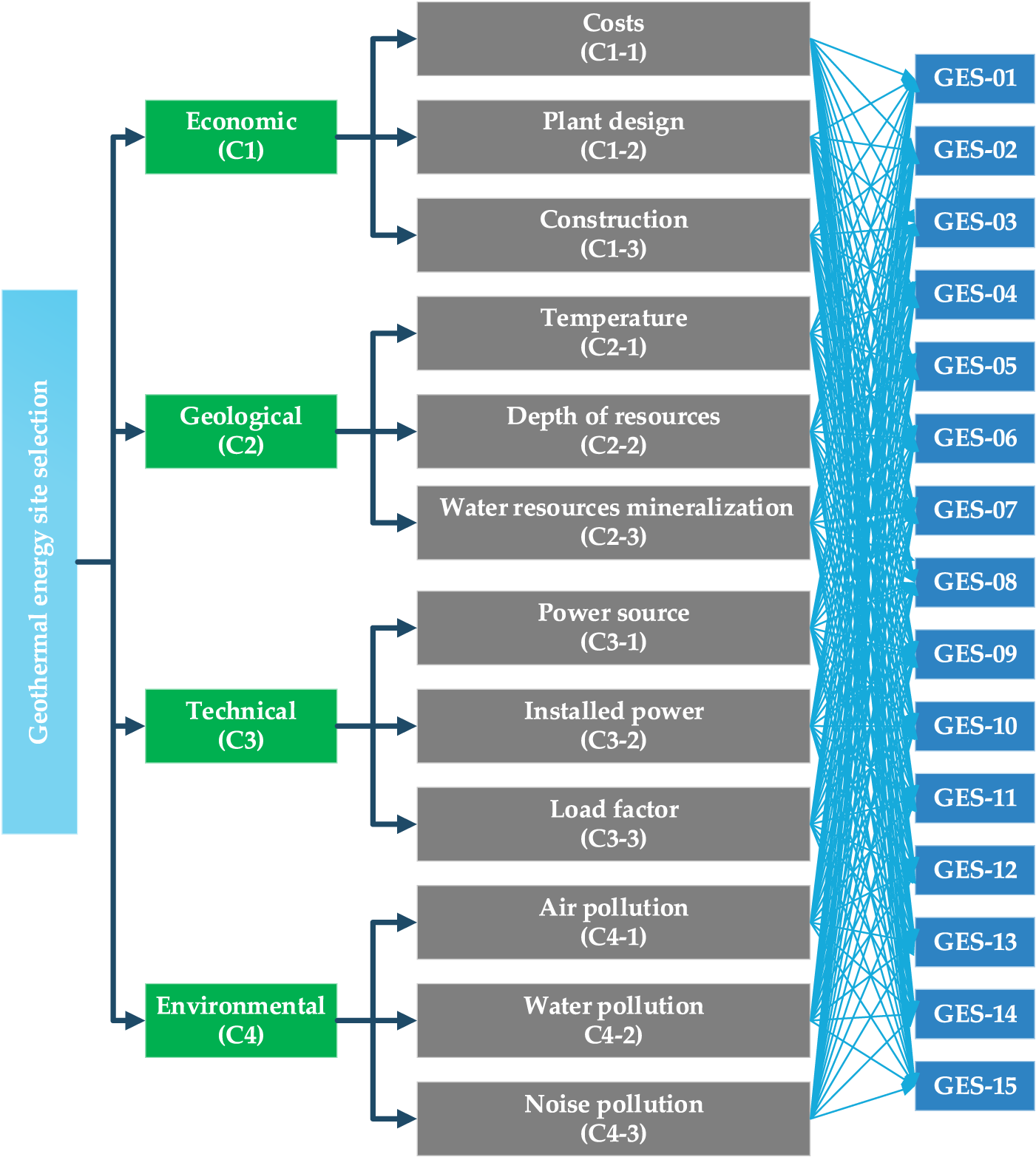
Figure 6: Criteria hierarchy
4.2 Ordinal Priority Approach (OPA) Based on Neutrosophic Fuzzy Axiomatic Design (NFAD)
Initially, a group of ten experts was established and investigated the influence of evaluation criteria on the selection of GES in Indonesia. Experts are scored in Table 6 to increase the accuracy of their judgments because the expertise of the experts is different. Based on references as well as experts’ opinions, 12 criteria that impact the GES selection problem has been identified, as shown in Fig. 6.
Then, each expert rated the importance of the criteria on the order of 1 to 10. Criteria with higher priority are considered more important. These ordinal assessments are presented in Table 7. According to the top-level expert, criterion C1-2 is the most important and deserves the most attention.
Based on the ranking order of 10 experts in Table 7. CPLEX Solver is used to program and solve the OPA model. The optimization results determine the weights of the criteria as shown in Fig. 7.
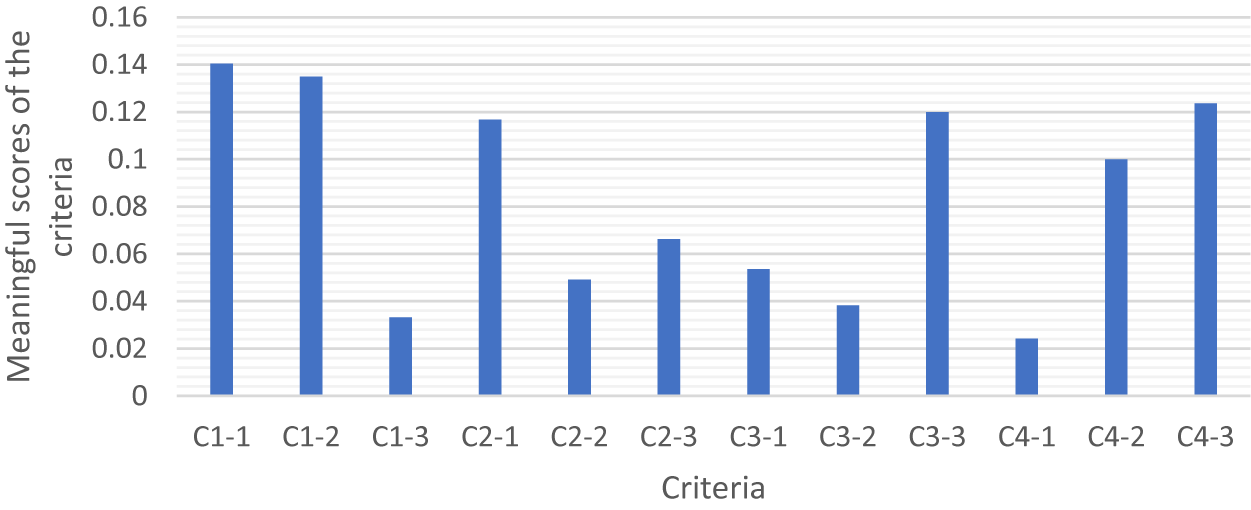
Figure 7: Criteria weight according to OPA results
In the next step, after calculating the weights of those decision-makers. Then, summarize the opinions of decision-makers as in Table 8. In this section, the average method is synthesized according to Eq. (7).
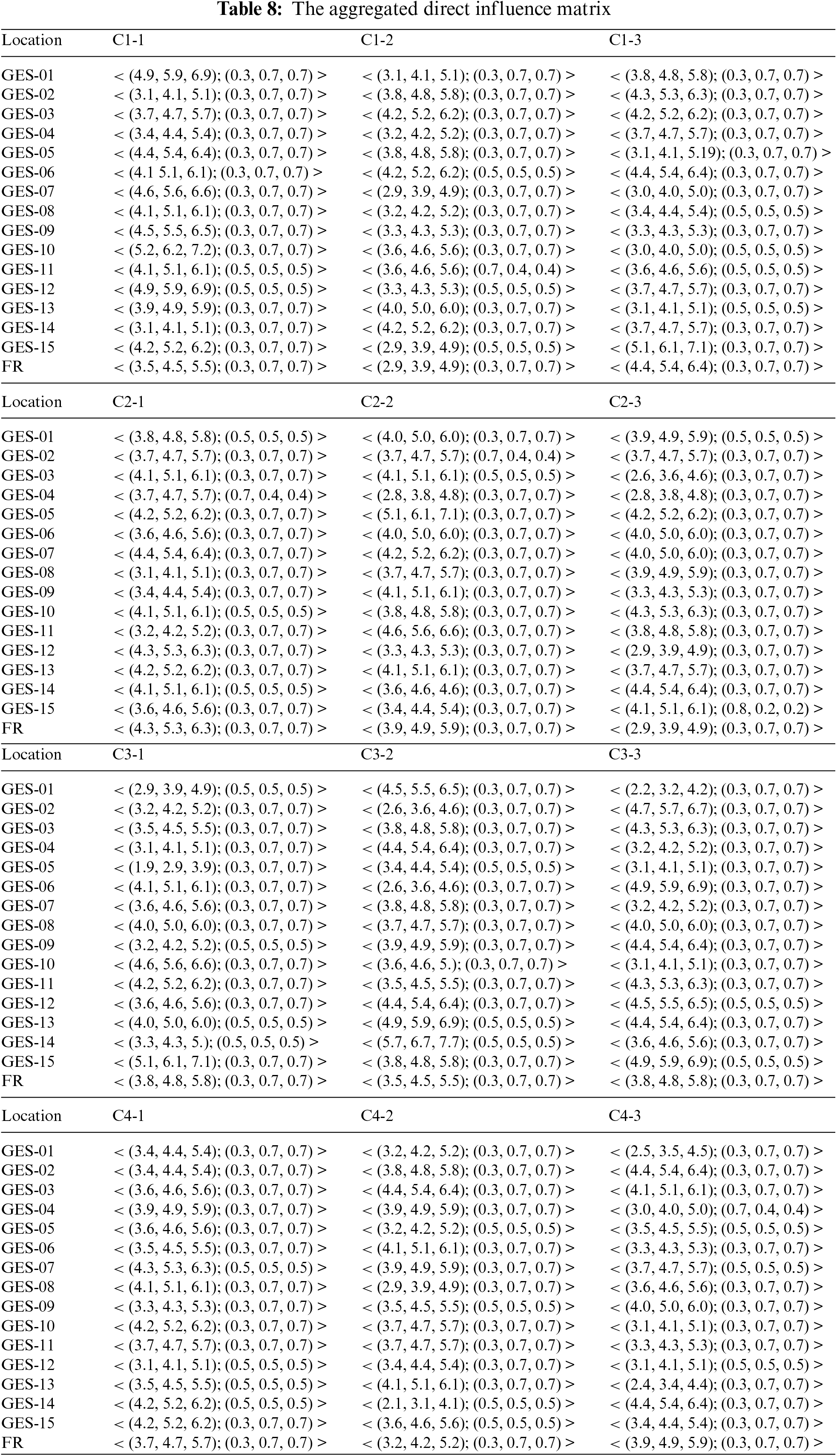
Table 9 shows the results of Truth-membership, Indeterminacy-membership, and False-membership for each function requirement. Compute the Truth-membership, Indeterminacy-membership, and False-membership according to the Eqs. (23)–(25), respectively.
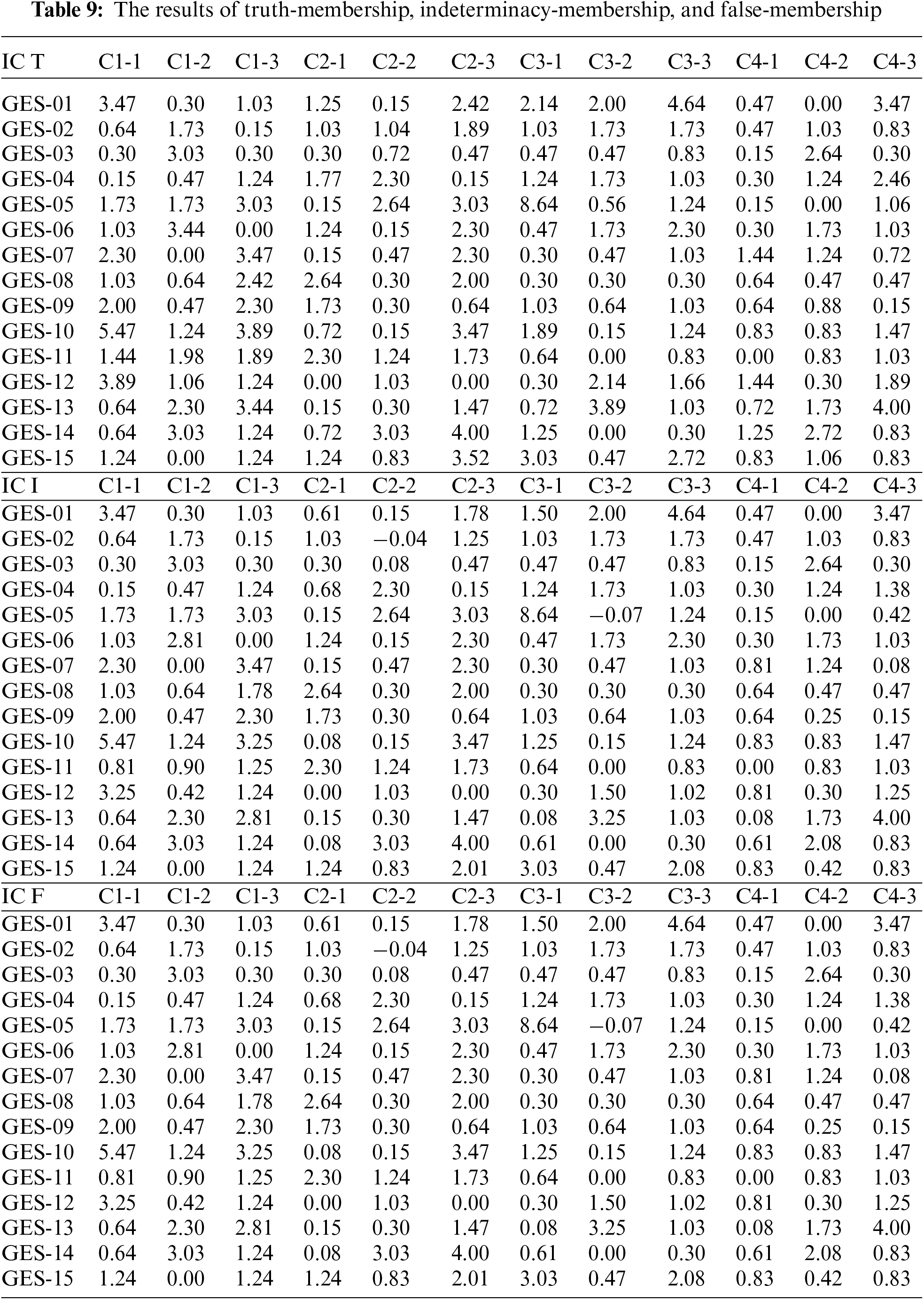
In Table 10. the results of computing the SF value are shown. SF is calculated using Eq. (2).
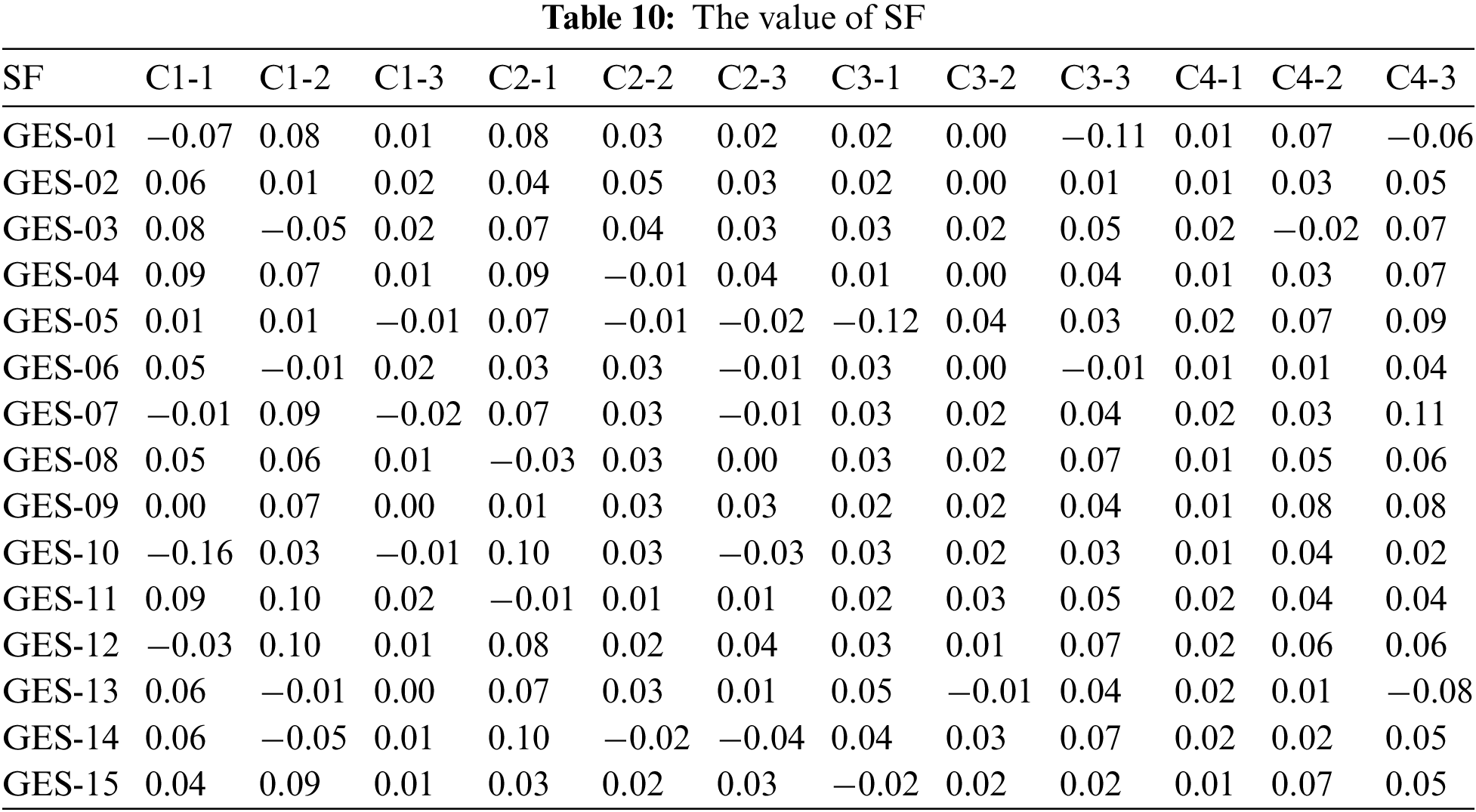
Calculate the AF value for IC of each alternative. The AF is calculated using Eq. (3). Finally, the final rating of the places is calculated according to Eqs. (12) and (13). The best alternative is chosen according to
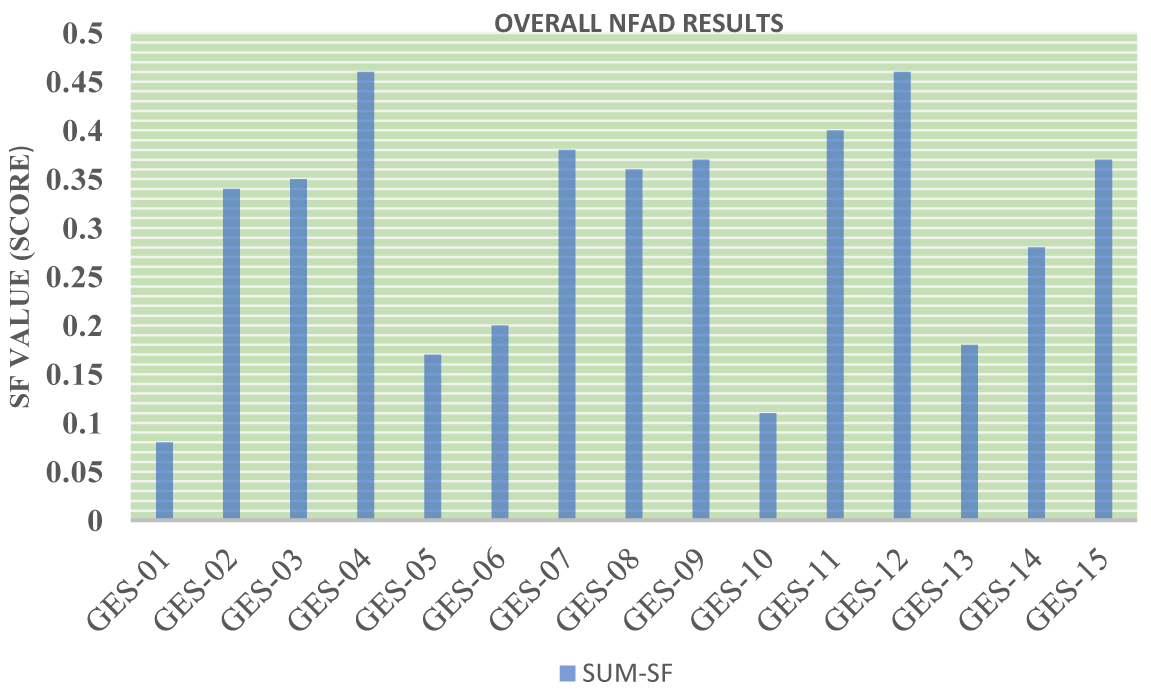
Figure 8: Overall NFAD results
In MCDM related problems, the majority of input data is dynamic data instead of stable or continuous data. Therefore, sensitivity analysis can help you make better decisions. The sensitivity analysis method of MCDM problems was used in this study. This method allows us to determine that the solution to the problem changes if the weight of a criterion changes. Changes include changes related to the weighting of other criteria, as well as changes to the final ranking of alternatives. For this reason, each criterion is eliminated and the final ranking is influenced by them [50]. Therefore, the sensitivity analysis of the criteria weights includes twelve scenarios. The weights of the criteria for each scenario are shown in Table 11. Table 12 shows the potential values of the alternatives in every scenario, and Fig. 9 depicts their ranking. The final ranking remained unchanged, with Kawah Cibuni considered the most potential GES in Indonesia in any case. Regardless of the change in the weights of the attributes, the alternative rankings remained robust in this study, according to the results of the sensitivity stages. Therefore, the proposed OPA and NFAD models show high applicability and stability.
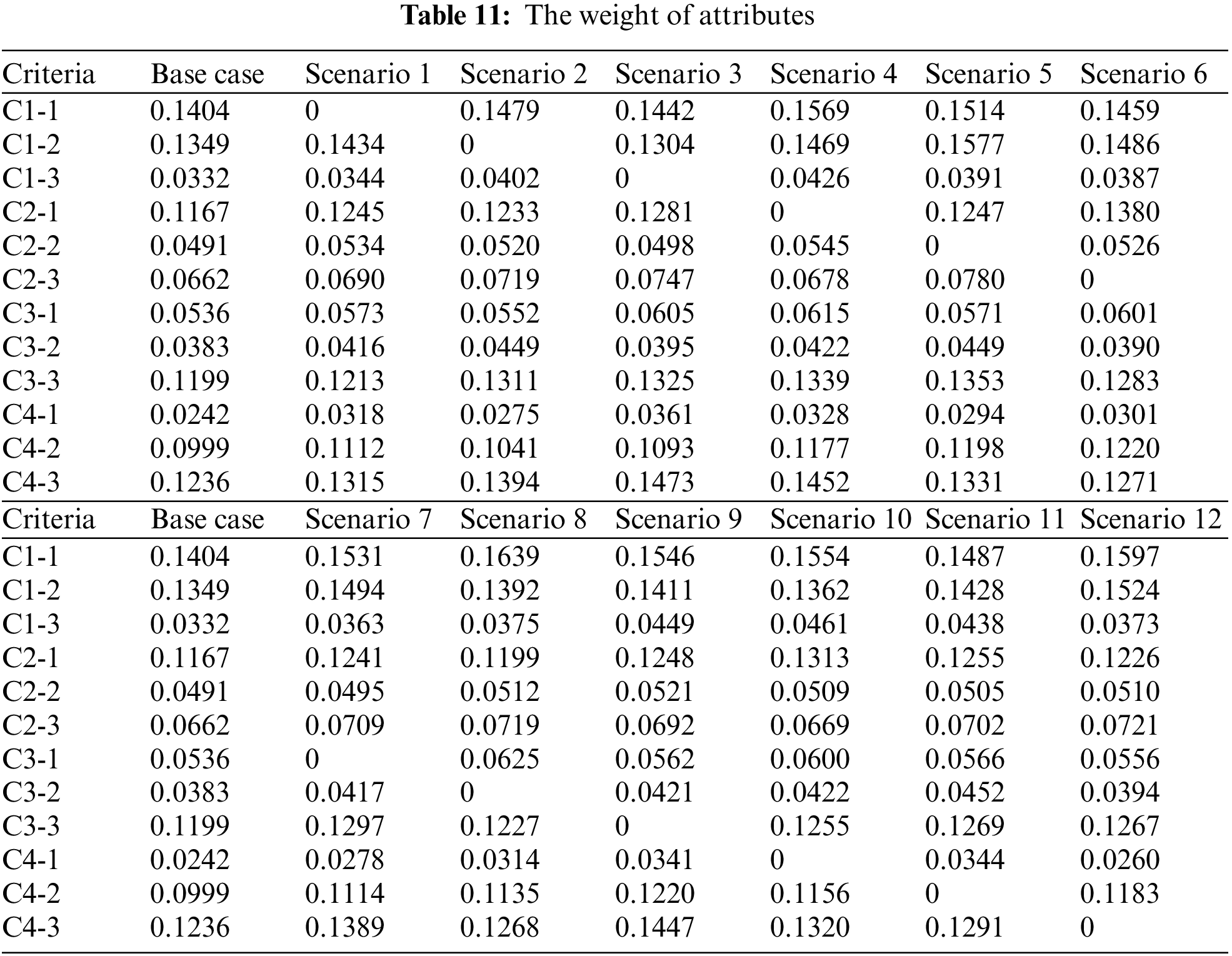
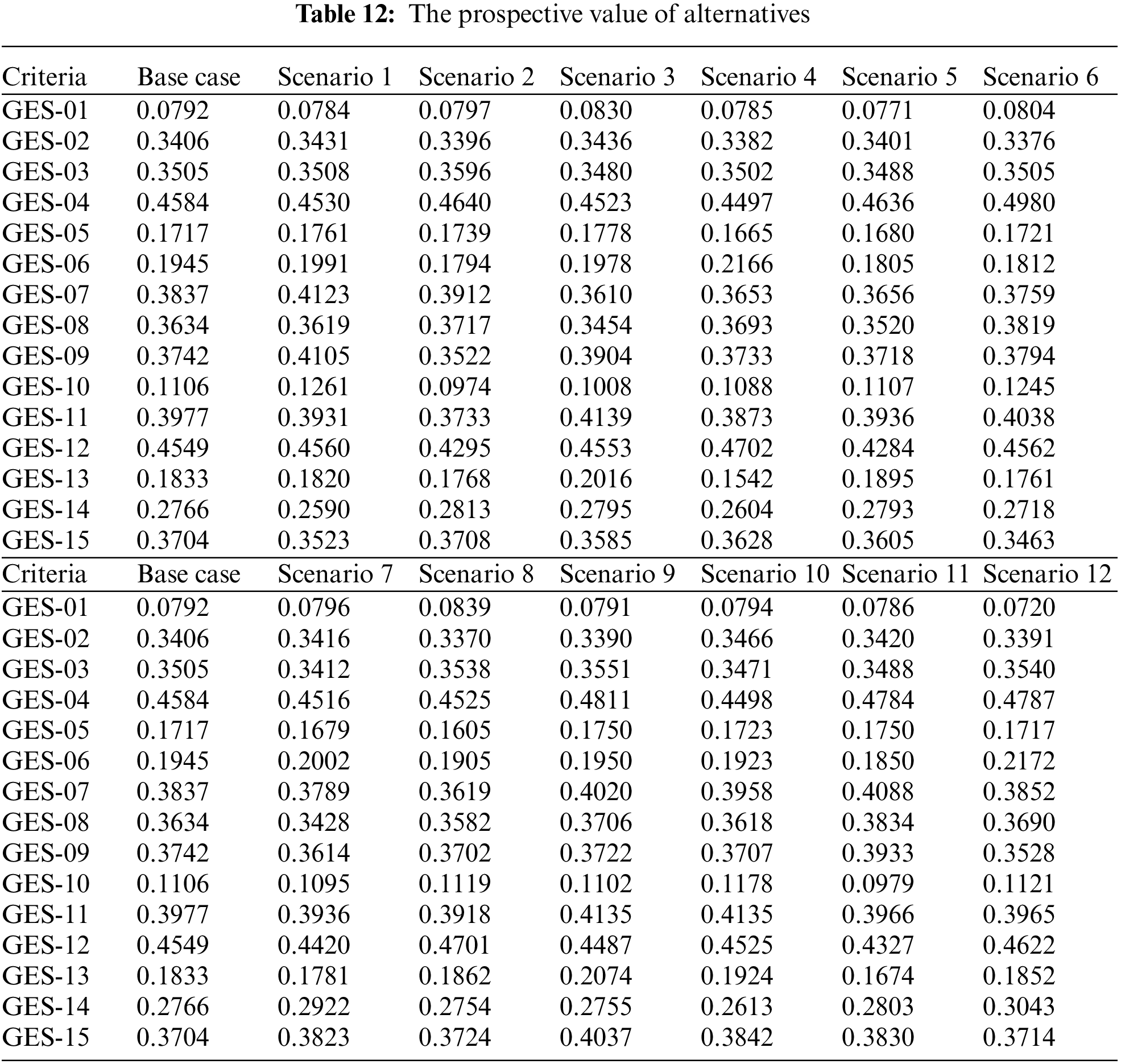
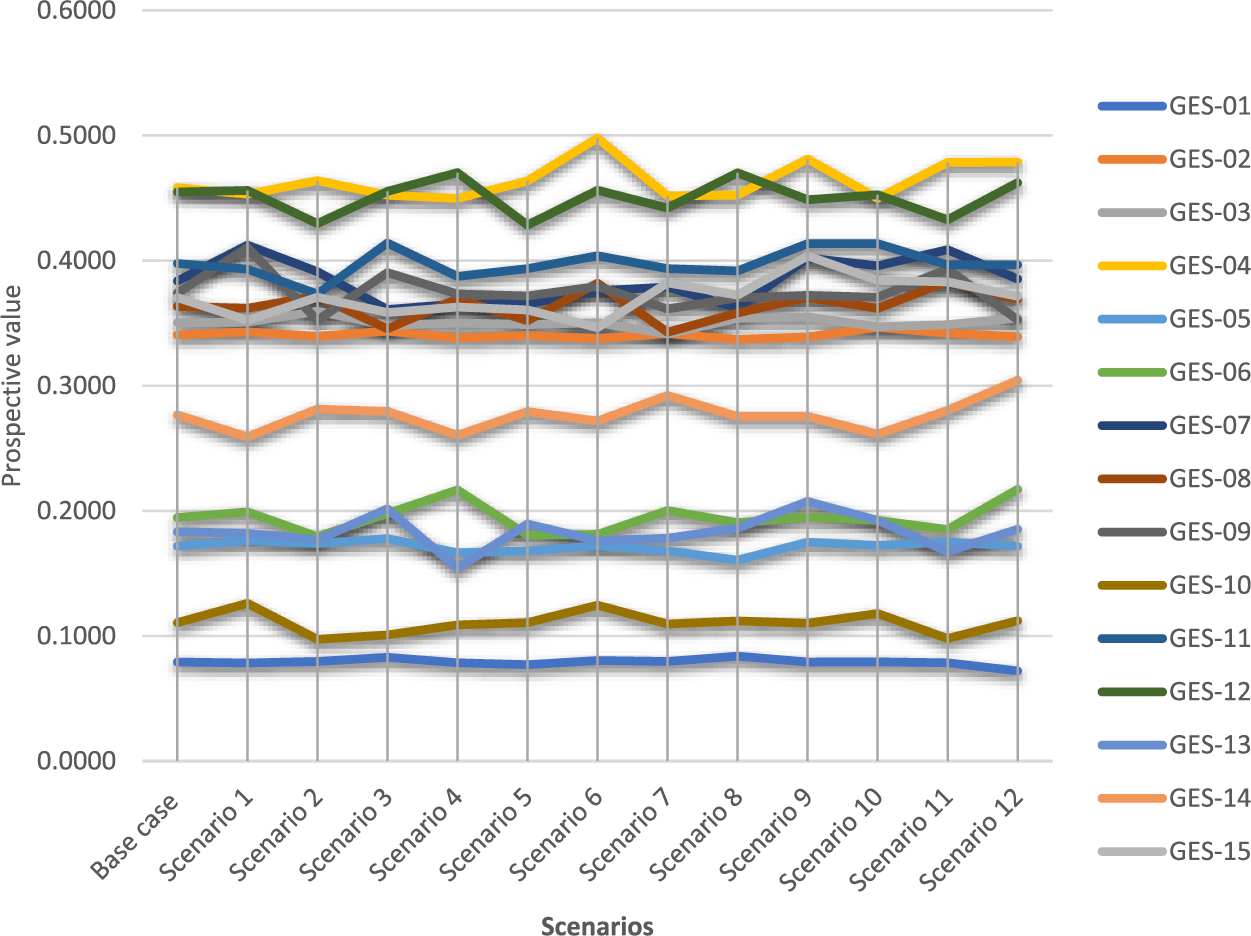
Figure 9: Rank the alternatives for all scenarios
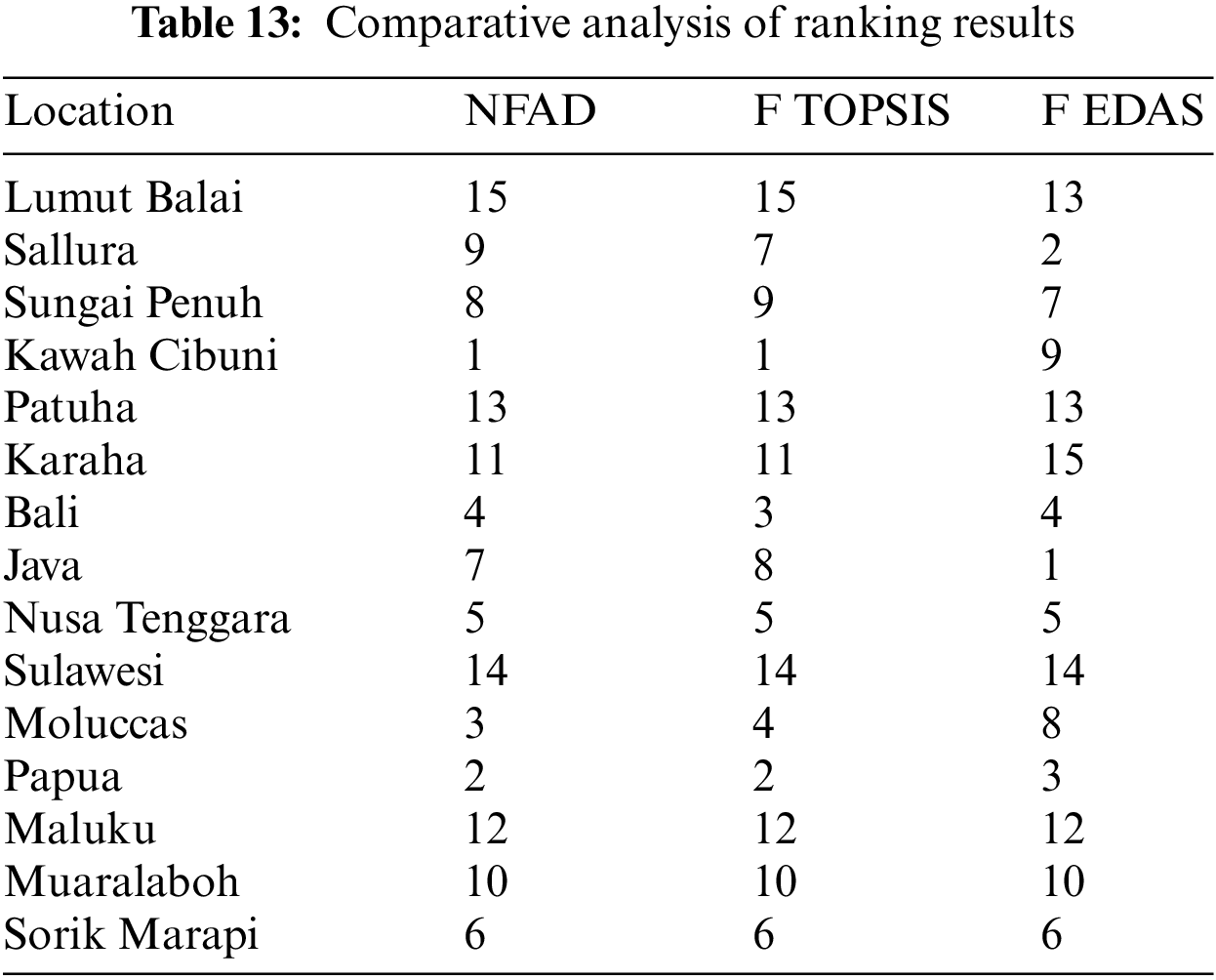
In this section, the values of the flexibility and stability coefficients of the three methods NFAD, F TOPSIS, and Fuzzy Evaluation based on Distance from Average Solution (F EDAS), are given for comparison. The results of this comparison are summarized in Table 13. As shown in Table 13, Patuha, Nusa Tenggara, Sulawesi, Maluku, Muaralaboh, and Sorik Marapi are the locations with similar rankings for all three methods. Next, Lumut Balai, Sungai Penuh, Karaha, Bali, and Papua are locations with similar ranking results. In contrast to the above two groups, Sallura, Kawah Cibuni, Java, and Moluccas are four locations with almost opposite ranking results. In general, through the table comparing the ranking results between the three methods, it can be seen that the application of the NFAD method in terms of ranking results is quite similar to the F TOPSIS method. However, the NFAD method applied in the case of this article is more outstanding in its novelty.
Recently, occurring events like the COVID-19 epidemic as well as global warming are posing great challenges to countries around the world. However, there are also chances for both government and private investors. Renewable energy is a chance, it promotes economic growth, reduces dependence on fossil fuels and promotes the development of each country. Geothermal is an environmentally friendly, sustainable, and available form of energy compared to other forms of renewable energy such as solar, hydro or wind power, and geothermal. And especially not being dependent on weather and climate factors. Therefore, geothermal also has a very large power factor, the geothermal source is always active. In the near future, with outstanding advantages such as low-cost efficiency and no greenhouse gas emissions, it is expected that geothermal energy will quickly become the dominant energy source to supply electricity for the world. To make efficient use of geothermal energy, choosing the right mining site is very important. This study combines MCDM methods introduced and applied by related studies with the aim of analyzing large areas to filter out some highly efficient sites. Large areas can be analyzed according to different criteria to rank points with the help of relevant experts and research. The findings show that cost ranks first among all the indicators, followed by plant design, load factor and noise pollution. Notably, these 4 indicators account for more than half of the total ratio of 12 indicators; therefore, the energy industry should focus most of its attention on these indicators. Construction and air pollution are the two indices ranked at the bottom. From the rankings, Kawah Cibuni was identified as the most potential GES in Indonesia, with a score of 0.46. Papua is the second most promising GES, with a score of 0.45. The place that needs to be considered and prioritized when choosing the next GES is Moluccas, with a score of 0.39. However, the three least potential sites out of the 15 studied were Lumut Balai, Moluccas, and Patuha, with scores of 0.08, 0.11, and 0.17, respectively. Below is a summary of the contributions of this paper. In terms of methodology, this paper proposes a combined OPA and NFAD approach to assess geothermal resources under different factors. Regarding legal implications, firstly, the contribution of this study could be an important document for renewable energy stakeholders in Indonesia and other countries. Secondly, promoting the development of renewable energy in the context of renewable energy with rapid technological progress with the goals of environmental protection and sustainable development. MCDM models are used to make informed decisions during the planning phase of geothermal plants or any other renewable energy project. In this way, it saves costs and resources for the country. In future studies, managers can apply this proposed method to determine the most suitable energy site based on their criteria and psychological characteristics.
Acknowledgement: The authors acknowledge the reviewers for providing valuable comments and helpful suggestions to improve the manuscript.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contributions to this paper as follows: Study conception and design: Chia-Nan Wang, Thuy-Duong Thi Pham, and Nhat-Luong Nhieu; data collection: Thuy-Duong Thi Pham; analysis and interpretation of results: Thuy-Duong Thi Pham, Chia-Nan Wang and Nhat-Luong Nhieu; draft manuscript preparation: Thuy-Duong Thi Pham. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Y. Noorollahi, M. S. Shabbir, A. F. Siddiqi, L. K. Ilyashenko, and E. Ahmadi, “Review of two decade geothermal energy development in Iran, benefits, challenges, and future policy,” Geothermics, vol. 77, pp. 257–266, Jan. 01, 2019. doi: 10.1016/j.geothermics.2018.10.004. [Google Scholar] [CrossRef]
2. A. Kagel and K. Gawell, “Promoting geothermal energy: Air emissions comparison and externality analysis,” Electr. J., vol. 18, no. 7, pp. 90–99, Aug. 2005. doi: 10.1016/j.tej.2005.07.004. [Google Scholar] [CrossRef]
3. G. Gamboa and G. Munda, “The problem of windfarm location: A social multi-criteria evaluation framework,” Energy Policy, vol. 35, no. 3, pp. 1564–1583, Mar. 2007. doi: 10.1016/j.enpol.2006.04.021. [Google Scholar] [CrossRef]
4. T. Bilić, S. Raos, P. Ilak, I. Rajšl, and R. Pašičko, “Assessment of geothermal fields in the South Pannonian basin system using a multi-criteria decision-making tool,” Energies, vol. 13, no. 5, pp. 1026, 2020. doi: 10.3390/en13051026. [Google Scholar] [CrossRef]
5. Y. Chen, J. Wang, and P. D. Lund, “Thermodynamic performance analysis and multi-criteria optimization of a hybrid combined heat and power system coupled with geothermal energy,” Energy Convers. Manag., vol. 210, pp. 112741, Apr. 2020. doi: 10.1016/j.enconman.2020.112741. [Google Scholar] [CrossRef]
6. A. Mostafaeipour, S. J. H. Dehshiri, S. S. H. Dehshiri, M. Jahangiri, and K. Techato, “A thorough analysis of potential geothermal project locations in afghanistan,” Sustainability, vol. 12, no. 20, pp. 8397, Oct. 2020. doi: 10.3390/su12208397. [Google Scholar] [CrossRef]
7. S. Raos, P. Ilak, I. Rajšl, T. Bilić, and G. Trullenque, “Assessment of enhanced geothermal projects and their optimal long-term usage plans by using the DMS-TOUGE decision-making support tool,” in Eur. Geotherm. Congr. 2019, Den Haag, Jun. 2019. [Google Scholar]
8. S. Raos, P. Ilak, I. Rajšl, T. Bilić, and G. Trullenque, “Multiple-criteria decision-making for assessing the enhanced geothermal systems,” Energies, vol. 12, no. 9, pp. 1597, 2019. doi: 10.3390/en12091597. [Google Scholar] [CrossRef]
9. R. Dipippo, “Geothermal energy electricity generation and environmental impact,” Energy Policy, vol. 19, no. 8, pp. 798–807, Oct. 1991. doi: 10.1016/0301-4215(91)90050-X. [Google Scholar] [CrossRef]
10. D. Milenić, P. Vasiljević, and A. Vranješ, “Criteria for use of groundwater as renewable energy source in geothermal heat pump systems for building heating/cooling purposes,” Energy Build, vol. 42, no. 5, pp. 649–657, May 2010. doi: 10.1016/j.enbuild.2009.11.002. [Google Scholar] [CrossRef]
11. M. K. Moghaddam, F. Samadzadegan, Y. Noorollahi, M. A. Sharifi, and R. Itoi, “Spatial analysis and multi-criteria decision making for regional-scale geothermal favorability map,” Geothermics, vol. 50, pp. 189–201, Apr. 2014. doi: 10.1016/j.geothermics.2013.09.004. [Google Scholar] [CrossRef]
12. M. Borzoni, F. Rizzi, and M. Frey, “Geothermal power in Italy: A social multi-criteria evaluation,” Renew. Energy, vol. 69, pp. 60–73, 2014. doi: 10.1016/j.renene.2014.03.026. [Google Scholar] [CrossRef]
13. K. Chawla, Use of Multi-Criteria Decision Analysis for Energy Planning. Ann Arbor, MI, USA: University of Michigan, 2015. [Google Scholar]
14. G. Ravier, C. Baujard, E. Dalmais, V. Maurer, and N. Cuenot, “Towards a comprehensive environmental monitoring of a geothermal power plant in the Rhine graben,” 2016. Accessed: Dec. 15, 2023. [Online]. Available: http://www.iksr.org [Google Scholar]
15. F. A. Boyaghchi and M. Chavoshi, “Multi-criteria optimization of a micro solar-geothermal CCHP system applying water/CuO nanofluid based on exergy, exergoeconomic and exergoenvironmental concepts,” Appl. Therm. Eng., vol. 112, pp. 660–675, Feb. 2017. doi: 10.1016/j.applthermaleng.2016.10.139. [Google Scholar] [CrossRef]
16. S. Rusek and R. Goňo, “The criteria for suitable location of geothermal power plant,” in Proc. 2017 18th Int. Sci. Conf. Electric Power Eng. (EPE), Hotel Dlouhé Stráně, Kouty nad Desnou, Czech Republic, May 17–19, 2017. [Google Scholar]
17. M. Yalcin and F. K. Gul, “A GIS-based multi criteria decision analysis approach for exploring geothermal resources: Akarcay basin (Afyonkarahisar),” Geothermics, vol. 67, pp. 18–28, May 2017. doi: 10.1016/j.geothermics.2017.01.002. [Google Scholar] [CrossRef]
18. F. Tinti, S. Kasmaee, M. Elkarmoty, S. Bonduà, and V. Bortolotti, “Suitability evaluation of specific shallow geothermal technologies using a GIS-based multi criteria decision analysis implementing the analytic hierarchic process,” Energies, vol. 11, no. 2, pp. 457, Feb. 2018. doi: 10.3390/en11020457. [Google Scholar] [CrossRef]
19. P. Chavot, C. Heimlich, A. Masseran, Y. Serrano, J. Zoungrana and C. Bodin, “Social shaping of deep geothermal projects in Alsace: Politics, stakeholder attitudes and local democracy,” Geotherm. Energy, vol. 6, no. 1, pp. 26, Dec. 2018. doi: 10.1186/s40517-018-0111-6. [Google Scholar] [CrossRef]
20. A. Mahmoudi, M. Abbasi, and X. Deng, “Evaluating the performance of the suppliers using hybrid DEA-OPA model: A sustainable development perspective,” Group Decis. Negot., vol. 31, no. 2, pp. 335–362, 2022. doi: 10.1007/s10726-021-09770-x. [Google Scholar] [CrossRef]
21. Y. Ataei, A. Mahmoudi, M. R. Feylizadeh, and D. F. Li, “Ordinal priority approach (OPA) in multiple attribute decision-making,” Appl. Soft Comput. J., vol. 86, Jan. 2020. doi: 10.1016/j.asoc.2019.105893. [Google Scholar] [CrossRef]
22. S. K. Lee, G. Mogi, S. K. Lee, K. S. Hui, and J. W. Kim, “Econometric analysis of the R&D performance in the national hydrogen energy technology development for measuring relative efficiency: The fuzzy AHP/DEA integrated model approach,” Int. J. Hydrog. Energy, vol. 35, no. 6, pp. 2236–2246, Mar. 2010. doi: 10.1016/j.ijhydene.2010.01.009. [Google Scholar] [CrossRef]
23. A. Mahmoudi, X. Deng, S. A. Javed, and J. Yuan, “Large-scale multiple criteria decision-making with missing values: Project selection through TOPSIS-OPA,” J. Ambient Intell. Humaniz. Comput., vol. 12, no. 10, pp. 9341–9362, Nov. 2020. doi: 10.1007/s12652-020-02649-w. [Google Scholar] [CrossRef]
24. D. Agarwal, A. K. S. Singholi, and I. Gandhi, “Performance analysis of a FLP problem using AHP-TOPSIS and FAHP-FTOPSIS,” Int. J. Ind. Syst. Eng., vol. 30, no. 4, pp. 401–424, Nov. 2018. doi: 10.1504/IJISE.2018.096159. [Google Scholar] [CrossRef]
25. A. H. Ganesh, A. H. Shobana, and R. Ramesh, “Identification of critical path for the analysis of bituminous road transport network using integrated FAHP-FTOPSIS method,” in Mater Today: Proc., Elsevier Ltd., 2020, pp. 193–206. doi: 10.1016/j.matpr.2020.05.015. [Google Scholar] [CrossRef]
26. R. S. Shahabi, M. H. Basiri, and M. R. Kahag, “Ranking of productivity improvement strategies in Iran mineral sector based on integrated SWOT-FAHP-FTOPSIS analysis,” Arab J. Geosci., vol. 11, no. 3, pp. 65, Feb. 2018. doi: 10.1007/s12517-018-3402-0. [Google Scholar] [CrossRef]
27. C. Valmohammadi, F. F. Razi, and F. Einy, “Six sigma project selection using the hybrid approach FAHP-FTOPSIS and grey relational analysis model,” IEEE Eng. Manage. Rev., vol. 49, no. 2, pp. 134–146, Apr. 2021. doi: 10.1109/EMR.2021.3071368. [Google Scholar] [CrossRef]
28. B. Oztaysi, “A decision model for information technology selection using AHP integrated TOPSIS-Grey: The case of content management systems,” Knowl.-Based Syst., vol. 70, pp. 44–54, Nov. 2014. doi: 10.1016/j.knosys.2014.02.010. [Google Scholar] [CrossRef]
29. A. Azizi, D. O. Aikhuele, and F. S. Souleman, “A fuzzy TOPSIS model to rank automotive suppliers,” Procedia Manuf., vol. 2, pp. 159–164, 2015. doi: 10.1016/j.promfg.2015.07.028. [Google Scholar] [CrossRef]
30. B. G. Muthanna, O. Bouledroua, M. Meriem-Benziane, M. R. Setvati, and M. B. Djukic, “Assessment of corroded API 5L X52 pipe elbow using a modified failure assessment diagram,” Int. J. Press. Vessel. Pipe., vol. 190, pp. 4291, Apr. 2021. doi: 10.1016/j.ijpvp.2020.104291. [Google Scholar] [CrossRef]
31. G. Büyüközkan and F. Göçer, “Application of a new combined intuitionistic fuzzy MCDM approach based on axiomatic design methodology for the supplier selection problem,” Appl. Soft Comput. J., vol. 52, pp. 1222–1238, Mar. 2017. doi: 10.1016/j.asoc.2016.08.051. [Google Scholar] [CrossRef]
32. A. Hadi-Vencheh and A. Mohamadghasemi, “A fuzzy AHP-DEA approach for multiple criteria ABC inventory classification,” Expert. Syst. Appl., vol. 38, no. 4, pp. 3346–3352, Apr. 2011. doi: 10.1016/j.eswa.2010.08.119. [Google Scholar] [CrossRef]
33. X. Li, Y. Liu, Y. Wang, and Z. Gao, “Evaluating transit operator efficiency: An enhanced DEA model with constrained fuzzy-AHP cones,” J. Traffic Transp. Eng., vol. 3, no. 3, pp. 215–225, Jun. 2016. doi: 10.1016/j.jtte.2016.05.004. [Google Scholar] [CrossRef]
34. İ. Otay, B. Oztaysi, S. C. Onar, and C. Kahraman, “Multi-expert performance evaluation of healthcare institutions using an integrated intuitionistic fuzzy AHP&DEA methodology,” Knowl.-Based Syst., vol. 133, pp. 90–106, Oct. 2017. doi: 10.1016/j.knosys.2017.06.028. [Google Scholar] [CrossRef]
35. A. Kumar, R. Shankar, and R. M. Debnath, “Analyzing customer preference and measuring relative efficiency in telecom sector: A hybrid fuzzy AHP/DEA study,” Telemat. Inform., vol. 32, no. 3, pp. 447–462, Aug. 2015. doi: 10.1016/j.tele.2014.10.003. [Google Scholar] [CrossRef]
36. C. N. Wang, V. T. Nguyen, D. H. Duong, and H. T. Do, “A hybrid fuzzy analytic network process (FANP) and data envelopment analysis (DEA) approach for supplier evaluation and selection in the rice supply chain,” Symmetry, vol. 10, no. 6, pp. 221, Jun. 2018. doi: 10.3390/sym10060221. [Google Scholar] [CrossRef]
37. K. Govindan, H. Mina, A. Esmaeili, and S. M. Gholami-Zanjani, “An integrated hybrid approach for circular supplier selection and closed loop supply chain network design under uncertainty,” J. Clean Prod., vol. 242, pp. 118317, Jan. 2020. doi: 10.1016/j.jclepro.2019.118317. [Google Scholar] [CrossRef]
38. C. N. Wang, N. A. T. Nguyen, T. T. Dang, and C. M. Lu, “A compromised decision-making approach to third-party logistics selection in sustainable supply chain using fuzzy ahp and fuzzy vikor methods,” Math., vol. 9, no. 8, pp. 886, Apr. 2021. doi: 10.3390/math9080886. [Google Scholar] [CrossRef]
39. A. K. Bera, D. K. Jana, D. Banerjee, and T. Nandy, “Supplier selection using extended IT2 fuzzy TOPSIS and IT2 fuzzy MOORA considering subjective and objective factors,” Soft Comput., vol. 24, no. 12, pp. 8899–8915, Jun. 2020. doi: 10.1007/s00500-019-04419-z. [Google Scholar] [CrossRef]
40. M. O. M. Javad, M. Darvishi, and A. O. M. Javad, “Green supplier selection for the steel industry using BWM and fuzzy TOPSIS: A case study of Khouzestan steel company,” Sustain. Futures, vol. 2, pp. 100012, Jan. 2020. doi: 10.1016/j.sftr.2020.100012. [Google Scholar] [CrossRef]
41. C. N. Liao, “Applying fuzzy-MSGP approach for supplier evaluation and selection in food industry,” African J. Agric. Res., vol. 7, no. 5, Feb. 2012. doi: 10.5897/ajarx11.088. [Google Scholar] [CrossRef]
42. M. Tavana, M. Zareinejad, F. J. Santos-Arteaga, and M. A. Kaviani, “A conceptual analytic network model for evaluating and selecting third-party reverse logistics providers,” Int. J. Adv. Manuf. Technol., vol. 86, no. 5–8, pp. 1705–1721, Sep. 2016. doi: 10.1007/s00170-015-8208-6. [Google Scholar] [CrossRef]
43. S. Gourvénec, X. Capron, and D. L. Massart, “Genetic algorithms (GA) applied to the orthogonal projection approach (OPA) for variable selection,” Anal. Chim. Acta., vol. 519, no. 1, pp. 11–21, Aug. 2004. doi: 10.1016/j.aca.2004.05.023. [Google Scholar] [CrossRef]
44. B. H. Al-Kbodi, T. Rajeh, Y. Li, J. Zhao, T. Zhao and M. E. Zayed, “Heat extraction analyses and energy consumption characteristics of novel designs of geothermal borehole heat exchangers with elliptic and oval double U-tube structures,” Appl. Therm. Eng., vol. 235, pp. 121418, Nov. 2023. doi: 10.1016/J.APPLTHERMALENG.2023.121418. [Google Scholar] [CrossRef]
45. B. H. Al-Kbodi et al., “Transient heat transfer simulation, sensitivity analysis, and design optimization of shallow ground heat exchangers with hollow-finned structures for enhanced performance of ground-coupled heat pumps,” Energy Build, vol. 305, pp. 113870, Feb. 2024. doi: 10.1016/J.ENBUILD.2023.113870. [Google Scholar] [CrossRef]
46. F. Smarandache and S. Pramanik, “New trends in neutrosophic theory and applications volume II,” 2016. Accessed: Dec. 15, 2023. [Online]. Available: https://digitalrepository.unm.edu/math_fsp [Google Scholar]
47. N. P. Suh,“Axiomatic design theory for systems,” Res. Eng. Des., vol. 10, pp. 189–209, Dec. 1998. [Google Scholar]
48. A. Nasution and E. Supriyanto, “Current status and new geothermal development areas in Indonesia,” in Proc. 9th Asian Geotherm. Symp., Nov. 2011. [Google Scholar]
49. R. F. Asokawaty, D. P. Purba, D. W. Adityatama, F. Muhammad, and M. Umam, “Indonesia’s geothermal development compare to world top geothermal producers,” in Proc. 45th Workshop Geotherm. Reserv. Eng. Stanf. Univ., Feb. 2019, pp. 1–11. [Google Scholar]
50. A. Alinezhad and A. Amini, “Sensitivity analysis of TOPSIS technique: The results of change in the weight of one attribute on the final ranking of alternatives,” J. Optim. Ind. Eng., vol. 7, pp. 23–28, 2011. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF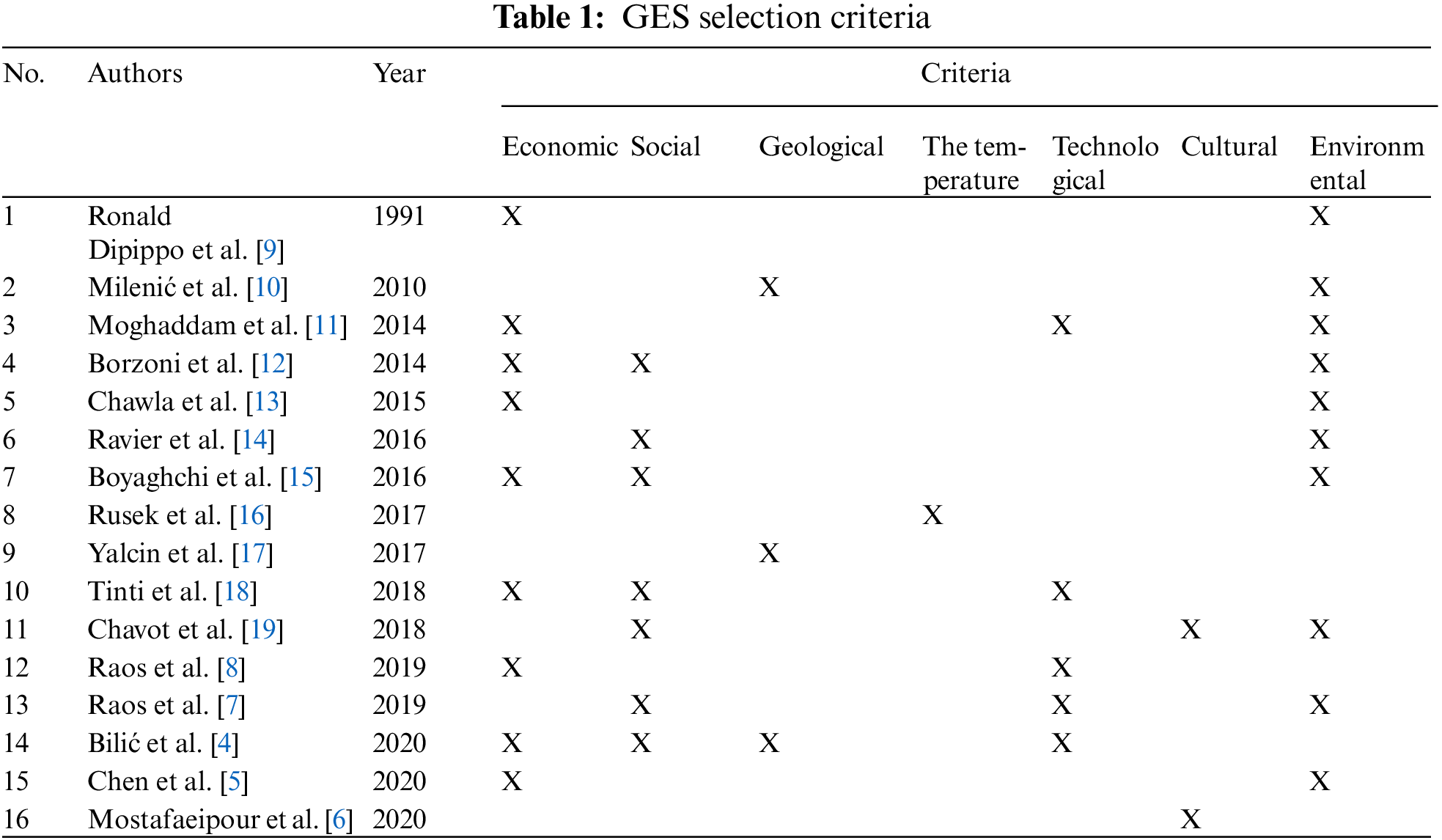
 Downloads
Downloads
 Citation Tools
Citation Tools