 Open Access
Open Access
REVIEW
Maximum Power Point Tracking Technology for PV Systems: Current Status and Perspectives
1 Faculty of Electric Power Engineering, Kunming University of Science and Technology, Kunming, 650500, China
2 Intelligent Electric Power Grid Key Laboratory of Sichuan Province, Chengdu, 610065, China
3 Foshan Graduate School of Innovation, Northeastern University, Foshan, 528311, China
4 College of Information Science and Engineering, Northeastern University, Shenyang, 110819, China
* Corresponding Author: Zhengxun Guo. Email:
Energy Engineering 2024, 121(8), 2009-2022. https://doi.org/10.32604/ee.2024.049423
Received 06 January 2024; Accepted 26 March 2024; Issue published 19 July 2024
Abstract
Maximum power point tracking (MPPT) technology plays a key role in improving the energy conversion efficiency of photovoltaic (PV) systems, especially when multiple local maximum power points (LMPPs) occur under partial shading conditions (PSC). It is necessary to modify the operating point efficiently and accurately with the help of MPPT technology to maximize the collected power. Even though a lot of research has been carried out and impressive progress achieved for MPPT technology, it still faces some challenges and dilemmas. Firstly, the mathematical model established for PV cells is not precise enough. Second, the existing algorithms are often optimized for specific conditions and lack comprehensive adaptability to the actual operating environment. Besides, a single algorithm may not be able to give full play to its advantages. In the end, the selection criteria for choosing the suitable MPPT algorithm/converter combination to achieve better performance in a given scenario is very limited. Therefore, this paper systematically discusses the current research status and challenges faced by PV MPPT technology around the three aspects of MPPT models, algorithms, and hardware implementation. Through in-depth thinking and discussion, it also puts forward positive perspectives on future development, and five forward-looking solutions to improve the performance of PV systems MPPT are suggested.Graphic Abstract
Keywords
Nomenclature
| I | PV system output current (A) |
| V | PV system output voltage (V) |
| P | PV system output power (W) |
| G | Instantaneous irradiance (W/m2) |
| T | Temperature (°C) |
| HIL | Hardware-in-loop |
Photovoltaic (PV) power is one of the most representative renewable energy resources, which is not only environmentally friendly but also sustainable and expandable [1–3]. The widespread application of this technology has driven the growth of renewable energy worldwide [4–6]. However, PV power generation systems often suffer from low power generation efficiency in practical applications. In particular, partial shading conditions (PSC) generally lead to multiple local maximum power points (LMPPs) in the system [7,8]. Therefore, it is crucial for PV systems to efficiently and accurately modify the operating point to maximize the power collection using maximum power point tracking (MPPT) technology [9].
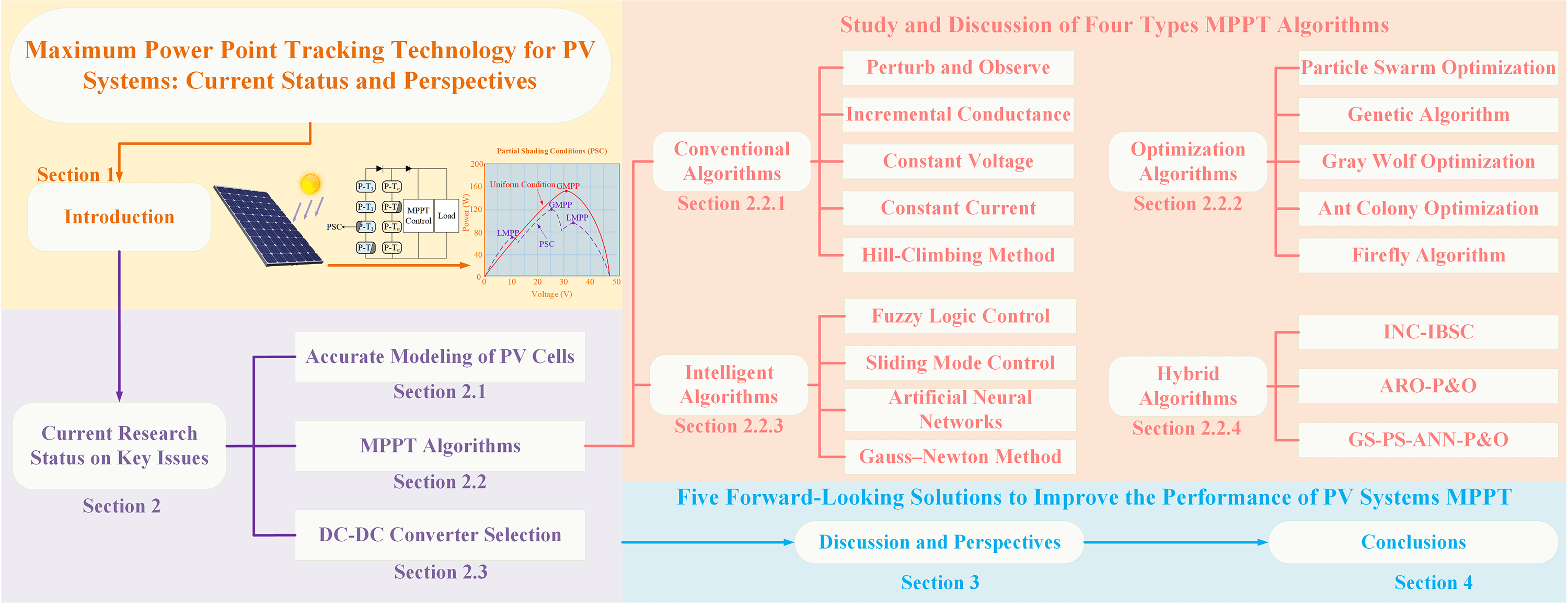
With the continuous progress of technology, it is worth noting that MPPT technology for PV systems still faces some challenges and dilemmas. First of all, under dynamic operating conditions, the nonlinear characteristics of PV systems become more complex. Over-idealized models such as single diode models (SDM) may not accurately capture the dynamic behavior of the system in real operation, pending optimization or transition to more accurate models. Second, despite the rich diversity of existing MPPT algorithms, most studies have only conducted simulation experiments. They also mainly optimize for specific conditions, lacking universality and comprehensive adaptability to the practical operating environment. Additionally, a single algorithm may not be sufficiently advantageous in the face of increasing demands and system complexity. How to efficiently combine algorithms under given conditions is also an issue worth discussing [10–12]. Finally, the selection criteria for choosing the suitable MPPT algorithm/converter combination to achieve better performance in a given scenario is very limited. This paper attempts to systematically discuss the current research status and challenges faced by MPPT technology around the above contents. By comparing SDM, double-diode model (DDM), and less applied triple-diode model (TMD) for PV systems, it was found that DDM had faster tracking speed and efficiency than SDM, which could be used as the best choice for more accurate modeling of PV systems MPPT. All four types of algorithms, traditional, intelligent, optimization, and hybrid, respectively, are studied and discussed. Two latest optimization algorithms that have not yet been applied to PV MPPT are also provided. The characteristics of the algorithms and the applicable scenarios are summarized. Besides, the tracking efficiency and conversion efficiency of different MPPT/non-isolated DC-DC converter combinations are analyzed. Through in-depth thinking and discussion, more forward-looking solutions to improve the performance of PV systems are suggested.
2 Current Research Status on Key Issues
2.1 Accurate Modeling of PV Cells
The accurate modeling is essential for the implementation of MPPT techniques in PV systems, several PV cell models have been proposed in previous literature [13–15], among which the most widely used models include the single-diode model (SDM) [16–18], DDM and TMD. Then connecting the models in series or in parallel to form PV arrays can be generalized to PV systems.
SDM simplifies the PV cell as a diode with forward voltage and output current. The light-induced electron-hole pair formation, voltage generation, and current flow are described. Since fewer unknown parameters need to be estimated in SDM, it is used to analyze the battery performance under static conditions in most. DDM considers the reverse saturation current. Whereas, TMD better considers effects like non-uniformity and temperature. While DDM has more parameters and higher computational complexity, it is closer to the actual situation and can more accurately describe the I-V and P-V characteristic curves of PV cells, especially under non-ideal conditions with better fitting ability.
References [19,20] conducted simulation studies for MPPT of SDM and DDM PV systems under various operating conditions. Reference [19] demonstrated that the root mean square error (RMSE) of DDM and SDM using the same MPPT algorithm is 8.97 * 10−4, and 9.0 * 10−4, respectively. The SDM-based MPPT algorithm also had the lowest RMSE of all the compared algorithms. Reference [21] extracted unknown parameters and tracked the MPP based on the DDM. Reference [22] adopted DDM for modeling PV systems closer to the real situation and implemented MPPT under partial shading and complex PSC. Reference [23] compared the performance of SDM and DDM in the MPPT technique. The experimental results showed that the DDM provided a more precise response to the physical behavior of the PV modules, which made the proposed MPPT technique faster and more accurate than other hybrid MPPT techniques. For example, the tracking speed and efficiency of the proposed MPPT algorithm based on DDM at an irradiance of 1000 W/m2 and a temperature of 25°C are 2 ms and 99.88%, respectively. Both were the best among all the compared algorithms, while the SDM-based one required 135 ms and the efficiency was only 98.70%. The comparison in Table 1 reveals that the increased accuracy will be accompanied by higher complexity and cost as the latter two models are based on the first model with an additional number of diodes. Furthermore, this will also increase the cost of hardware and software required to build and implement these models. Descriptions of all variables can be found in reference [11].
At present, the research and development of MPPT algorithms for PV systems mainly focus on several directions, including traditional algorithms, optimization algorithms, intelligent algorithms, and hybrid algorithms [29–31]. Reference [32] classified sixty-two MPPT algorithms for PV systems into seven categories in detail and provided a systematic introduction, comprehensive summary, and comparison of them. Reference [33] investigated the characteristics, implementation methods, advantages, and weaknesses of different MPPT algorithms under uniform environmental conditions (UEC) and PSC, as well as summarized their feasibility and bottlenecks under different environmental conditions.
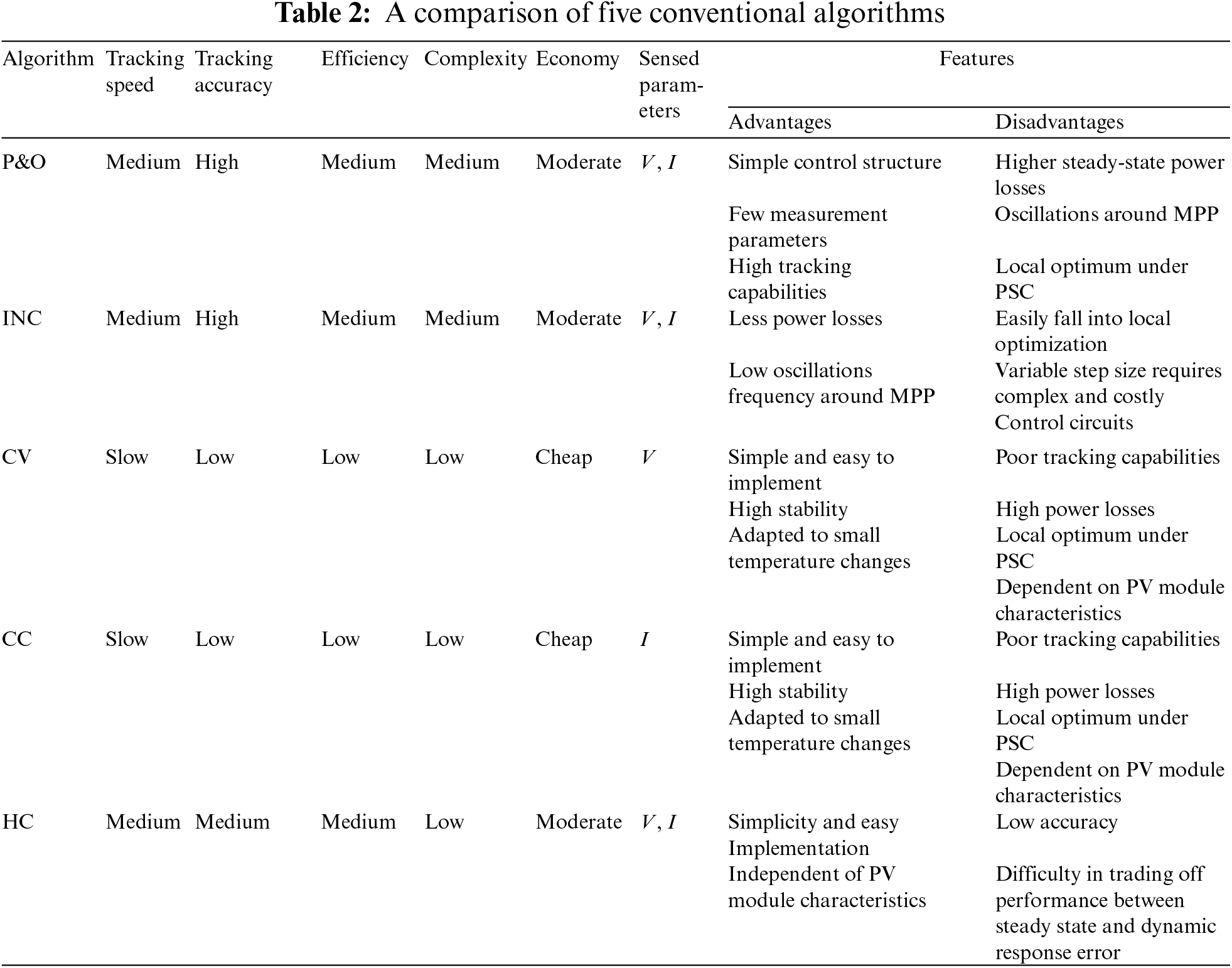
The conventional algorithms are more comprehensive in terms of basic research as well as simple and easy to implement. They are more efficient in the case of uniform irradiance. The most common conventional algorithms include perturb and observe (P&O) [34], incremental conductance (INC) [35], constant voltage (CV), constant current (CC) [36], and hill-climbing methods (HC) [37].
P&O and HC both determine the direction in which the optimal output power changes by introducing a perturbation. The only difference between them is the perturbation parameter. To track the MPP, the P&O senses and perturbs the voltage or current, while the HC disturbs the duty cycle. Moreover, the INC is used to determine the optimum operating point by detecting the ratio of conductance derivative to instantaneous conductance over time. CV uses a reference voltage or a value fixed under specific conditions to control the MPP voltage of the PV system. Similarly to CV, CC makes the system operate at a constant current state. The comparison of different conventional algorithms is shown in Table 2. Reference [38] developed an adaptive P&O MPPT algorithm that can track the power in 10.1 s that conventional P&O takes 13.8 s to track, achieving fast-tracking of the MPP with fewer steady-state oscillations. Reference [39] provided a more comprehensive comparison of 20 classical algorithms. By comparison, it can be found that conventional algorithms suffer from the problem of oscillations around the MPP, which can lead to power losses. The ability to adapt to dynamically changing operating conditions is poor, especially under PSC, they tend to fall into local optimization.
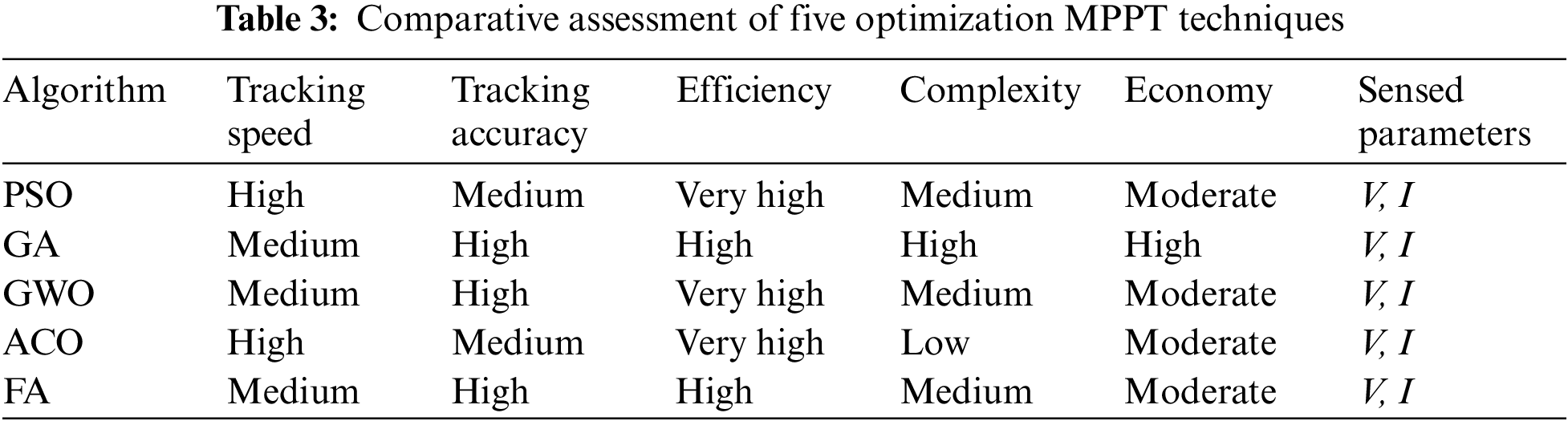
Optimization algorithms inspired by natural processes or behavioral patterns of biologists find the best solution to a problem from all possible alternatives. They are less likely to fall into a local optimum under dynamic operating conditions and can be more flexible in solving nonlinear problems [40,41]. Typical optimization algorithms include particle swarm optimization (PSO) [42], genetic algorithm (GA) [43], gray wolf optimization (GWO) [44], ant colony optimization (ACO) [45], and firefly algorithm (FA) [46]. Table 3 compares several of these algorithms [47]. Optimization algorithms have shown a trend of high number and rapid development due to their diverse sources of inspiration and simplicity of implementation. Two latest optimization algorithms that have not yet been applied to PV MPPT will be provided here, which are the puma optimizer (PO) [48] and crested porcupine optimizer (CPO) [49]. PO was inspired by the natural hunting behavior of cougars, where a male puma served as the optimal solution and a puma’s territory was the entire optimization space. The algorithm adopted a novel phase-change hyper-heuristic intelligence mechanism to vary the exploration and exploitation phases. CPO simulated four defense strategies used by crowned porcupines to protect themselves from predators: Sight, sound, odor, and physical attack. The results of the study showed that CPO demonstrated better performance than the comparison algorithms in terms of average fitness, convergence curve, and computational cost. When applying these two algorithms to PV MPPT, the stable power output can be directly considered as the corresponding fitness value of the achieved duty cycle (Dc). Individuals associated with larger values of fitness indicate that it has a better or higher quality solution. The fitness values for each control cycle will be determined by collecting the actual voltage and current.
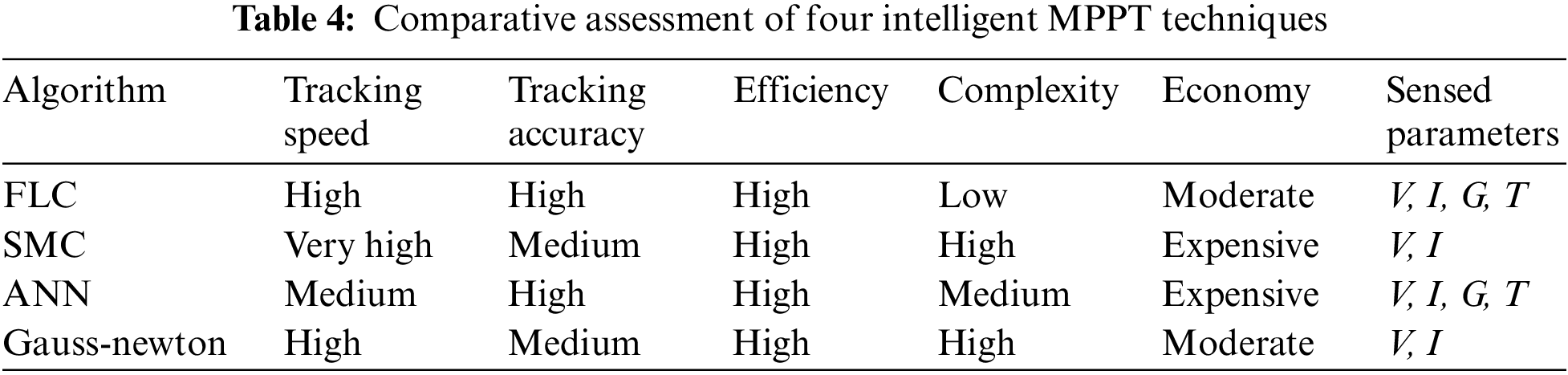
Intelligent algorithms have the potential to solve many of the problems associated with conventional MPPT methods without complex arithmetic or precise parameters, such as increasing tracking speed, reducing computation time, and minimizing power fluctuations near the GMPP. Widely used intelligent algorithms include fuzzy logic control (FLC) [50], sliding mode control (SMC) [51], artificial neural networks (ANN) [52,53], and Gauss–Newton method [54]. Table 4 compares the parameters of these four intelligent algorithms. FLC does not depend on the accurate modeling of the PV system. It has three main stages: Fuzzification, inference, and defuzzification. Simulation results in both references [50,55] demonstrated that FLC-based MPPT had faster convergence, higher stability and lower tracking error compared to P&O. The basic principle of SMC is controlling the DC-DC converter by detecting the DC link capacitor’s current. The SMC extracts the maximum power by activating an efficient sliding surface switching action. Reference [56] presented the double-integrated sliding mode controller (DISMC) with 99.10% efficiency and 0.035 s setting time compared to SMC and the single-integrated sliding mode controller (SISMC). The ANN learns the properties of the PV system by creating a nonlinear mapping between input and output nodes. It is continuously training based on the system data to achieve accurate prediction of the output power. Reference [57] innovatively developed a two-stage MPPT method to achieve improvement and optimization of the ANN. The results of the cases showed that this improved ANN not only had the shortest tracking time among the three cases but also achieved a tracking accuracy as high as 99.99%. Reference [58] categorized the existing intelligent algorithms and fully discussed their advantages and disadvantages.
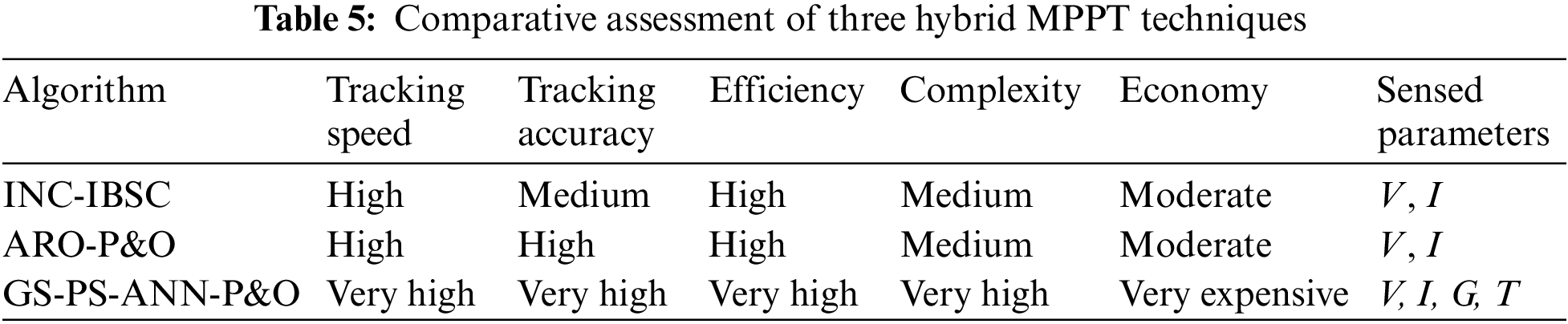
In the face of growing demands and system complexity, researchers have gradually realized that a single algorithm may not be able to give full play to its advantages. Therefore, hybrid algorithms have gradually become the mainstream trend, achieving more comprehensive and superior MPPT performance through the synergistic cooperation of different algorithms. There are three combinations of hybrid algorithms, which are traditional and traditional algorithms, traditional and intelligent or optimization algorithms, and intelligent and optimization algorithms. Reference [59] developed a hybrid approach consisting of the INC and integral back-stepping controller (IBSC), this method improved the operational efficiency of the PV system to 99.94%. Moreover, INC-IBSC was approximately 4 times faster than INC in tracking the maximum power. Reference [60] combined artificial rabbit optimization (ARO) and P&O to make MPPT more efficient and accurate under different environmental conditions. The results indicated that the algorithm has superior MPPT performance, with MPPT tracking efficiency and overall system efficiency as high as 96% and 99%, respectively. Reference [61] proposed a hybrid gravitational search (GS)-pattern search (PS)-artificial neural network (ANN)-P&O algorithm, which trained the ANN by hybrid GS-PS and P&O started working when the ANN could not recognize the MPP accurately. The MPPT accuracy of the proposed algorithm has been increased by 2–8% under different temperature and radiation conditions. Table 5 illustrates a brief comparison of the three hybrid algorithms described above. Reference [62] provided a more comprehensive overview of the three main types and about ninety hybrid MPPT algorithms.
DC-DC converter is one of the important hardware conditions for realizing MPPT in PV systems. MPPT algorithms generally work together with DC-DC converter to optimize the performance of PV systems and maximize the energy conversion efficiency under different operating conditions [63–65]. DC-DC converters applied to MPPT in PV systems are mainly non-isolated converters such as buck-boost [66], single-ended primary inductor converters (SEPIC), Zeta [67], and Cuk [68]. They are capable of generating higher or lower output signals to better realize the MPPT in the presence of variations in the external environmental conditions and connected loads.
Reference [12] explored the performance of each MPPT/converter combination consisting of four converters and three MPPT algorithms. The experimental results under the two arithmetic cases of constant temperature-irradiance change and fixed irradiance-temperature variation showed that the performance of the combination formed by the three algorithms with Cuk was outstanding. In particular, FLC/Cuk demonstrated the best MPPT performance in terms of tracking efficiency, with average MPPT efficiencies of 99.87% and 99.77%, respectively, and average converter conversion efficiencies of 89.43% and 89.51%, respectively. Besides, FLC/Zeta only required an average transient tracking time of 70.91 ms. Reference [69] applied P&O to four converters, buck-boost, Cuk, SEPIC, and Zeta, respectively. The average conversion efficiencies of these converters were 95.780%, 94.779%, 95.788%, and 95.787% at different temperatures, individually. The shortest average setting time was for buck-boost at 0.04 s, while Cuk had the longest at 0.065 s. In addition, a methodology for selecting the optimal converter for standalone PV systems is proposed. Reference [70] reviewed MPPT methods involving six non-isolated converters but did not give corresponding detailed data about MPPT performance. It concluded that the buck-boost converter was characterized by higher performance and lower power losses, making it the best choice for low-power loads.
MPPT technology for PV systems has made noteworthy progress in existing research, but still faces a series of challenges and opportunities:
a) High-precision modeling for PV systems will bring about high complexity and high-cost issues. In the future, a reasonable balance between model accuracy, cost, and system complexity should be considered. In addition, it was discovered during the discussion that the number of studies applying TMD to the PV systems MPPT was currently limited. This can be extended and explored more.
b) The conventional MPPT methods are simple in principle and hardware implementation, but they have low accuracy, slow speed, and tend to oscillate around the MPP. They are suitable for MPPT under uniform conditions. Intelligent algorithms do not require precise mathematical models and have high tracking efficiency. However, the realization cost is high and not widely used in PV MPPT. Optimization algorithms are applicable to complex nonlinear systems. Especially under PSC, it is the best choice to realize MPPT. However, they are highly stochastic and more dependent on the parameter settings. It will take a lot of time and effort to continuously tune the parameters.
c) Hybrid algorithms integrate the advantages of different algorithms, and their validation has been verified. Such algorithms suffer from the disadvantages of high complexity and long development cycles. With the help of deep learning, real-time data mining, multi-converter fusion, and other techniques, further exploration and research can be carried out on how to choose the right combination of algorithms for specific operating conditions.
d) Although many algorithms have been proposed to realize MPPT in PV systems, they only stay in the laboratory environment and simulation testing stage. When applied to large-scale PV systems, some algorithms might lead to fluctuations in the operating point, reducing system stability. Hardware-in-loop (HIL) is often used to evaluate the hardware implementation ability of a system. It puts part of the system hardware into the software simulation loop, which can compensate for the absolute idealization of purely digital simulation and improve the confidence of the whole model. By utilizing HIL, researchers are able to further validate the MPPT performance of various algorithms in real applications.
e) Despite many comparative studies on DC-DC converters and MPPT algorithms in the field of PV systems, the selection criterion that defines the selection of the suitable combination of MPPT algorithms/converters for PV systems to achieve better performance is very limited. That could be achieved by using a multi-objective optimization approach, which integrates evaluation metrics, e.g., the efficiency, stability, and response time of the PV systems. The fuzzy mathematics can be used to calculate the satisfaction of the Pareto optimal frontier solution and select the solution with the largest satisfaction as the compromise optimal solution. The weights are taken to obtain the final score of each combination. A potential advantage of multi-objective optimization is the ability to reveal interrelationships between different optimization objectives, such as trade-offs or conflicts that may exist between certain objectives.
This paper provides a systematic discussion of the current research status and challenges faced by PV MPPT technologies around the three aspects of MPPT models, algorithms, and hardware implementation. It also puts forward positive perspectives on future development. Specifically, the major conclusions claimed in this paper are as follows:
a) Improving the accuracy of PV systems models requires a reasonable balance between model complexity and economic cost, rather than blindly increasing accuracy. By comparing SDM, DDM, and TMD for PV systems, it was found that DDM had faster tracking speed and efficiency than SDM, which could be used as the best choice for more accurate modeling of PV systems MPPT.
b) Four types of algorithms are studied and discussed. Conventional MPPT algorithms are suitable for uniform conditions. Intelligent algorithms do not require accurate mathematical modeling and tracking efficiency is high. Optimization algorithms under PSC are the best choice to implement MPPT. Two latest optimization algorithms that have not yet been applied to PV MPPT are provided. Furthermore, hybrid algorithms are more effective in PSC and rapidly changing environmental conditions. Combining multiple algorithms builds on strengths and avoids weaknesses.
c) Various MPPT algorithms for PV systems have been developed, but most of them are only simulation experiments. Nevertheless, it is also necessary to compensate for the absolute idealization of purely digital simulations with the help of HIL experiments. Evaluate the hardware implementation ability of the system. Especially under dynamic operation and large-scale application conditions.
d) Hybrid algorithms have great potential to select the right combination of algorithms for specific operating conditions with the help of techniques such as deep learning, real-time data mining, and multi-converter fusion.
e) Non-isolated DC-DC converters still dominate. Buck-boost converters are characterized by high performance and low power losses, making them the best choice for low power loads. Besides, the FLC/Cuk combination always shows excellent efficiency performance, no matter how the irradiance, temperature, or load varies. This combination has great potential. By integrating the evaluation metrics of efficiency, stability, and response time of the PV systems using a multi-objective optimization approach. It is expected to help find the MPPT algorithms/DC-DC converters combination with optimal performance.
Acknowledgement: The authors would like to thank and acknowledge the Intelligent Electric Power Grid Key Laboratory of Sichuan Province.
Funding Statement: The authors received funding from the Open Fund Project of Intelligent Electric Power Grid Key Laboratory of Sichuan Province under Grant (2023-IEPGKLSP-KFYB03) and Yunnan Provincial Basic Research Project (202301AT070443).
Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, methodology, resources, validation: Bo Yang; investigation, data collection, writing-original draft and editing, analysis and interpretation of results: Rui Xie; visualization and contributed to the discussion of the topic: Zhengxun Guo. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data used in this study are available on request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. M. Mansoor, A. F. Mirza, and Q. Ling, “Harris hawk optimization-based MPPT control for PV systems under partial shading conditions,” J. Clean Prod., vol. 274, pp. 1–19, Nov. 2020. doi: 10.1016/j.jclepro.2020.122857. [Google Scholar] [CrossRef]
2. K. Obaideen et al., “Solar energy: Applications, trends analysis, bibliometric analysis and research contribution to sustainable development goals (SDGs),” Sustain., vol. 15, no. 2, pp. 1–34, Jan. 2023. doi: 10.3390/su15021418. [Google Scholar] [CrossRef]
3. B. Yang et al., “Salp swarm optimization algorithm based MPPT design for PV-TEG hybrid system under partial shading conditions,” Energy Conv. Manag., vol. 292, pp. 1–27, Sep. 2023. doi: 10.1016/j.enconman.2023.117410. [Google Scholar] [CrossRef]
4. B. Yang, R. Xie, J. H. Duan, and J. B. Wang, “State-of-the-art review of MPPT techniques for hybrid PV-TEG systems: Modeling, methodologies, and perspectives,” Glob. Energy Interconnect., vol. 6, no. 5, pp. 567–591, Oct. 2023. doi: 10.1016/j.gloei.2023.10.005. [Google Scholar] [CrossRef]
5. B. Yang et al., “A critical survey of technologies of large offshore wind farm integration: Summary, advances, and perspectives,” Prot. Control Mod. Power Syst., vol. 7, no. 1, pp. 1–32, Dec. 2022. doi: 10.1186/s41601-022-00239-w. [Google Scholar] [CrossRef]
6. B. Yang et al., “Comprehensive summary of solid oxide fuel cell control: A state-of-the-art review,” Prot. Control Mod. Power Syst., vol. 7, no. 1, pp. 1–31, Dec. 2022. doi: 10.1186/s41601-022-00251-0. [Google Scholar] [CrossRef]
7. S. Verma, S. Mohapatra, S. Chowdhury, and G. Dwivedi, “Cooling techniques of the PV module: A review,” Mater. Today Proc., vol. 38, pp. 253–258, Feb. 2021. doi: 10.1016/j.matpr.2020.07.130. [Google Scholar] [CrossRef]
8. M. A. Fin, D. Gharapetian, and M. Asgari, “Efficiency improvement of hybrid PV-TEG system based on an energy, exergy, energy-economic and environmental analysis; experimental, mathematical and numerical approaches,” Energy Conv. Manag., vol. 265, pp. 1–28, Aug. 2022. doi: 10.1016/j.enconman.2022.115767. [Google Scholar] [CrossRef]
9. S. Rezazadeh et al., “Photovoltaic array reconfiguration under partial shading conditions for maximum power extraction: A state-of-the-art review and new solution method,” Energy Conv. Manag., vol. 258, pp. 1–36, Apr. 2022. doi: 10.1016/j.enconman.2022.115468. [Google Scholar] [CrossRef]
10. A. K. Sharma et al., “Role of metaheuristic approaches for implementation of integrated MPPT-PV systems: A comprehensive study,” Mathematics, vol. 11, no. 2, pp. 1–48, Jan. 2023. doi: 10.3390/math11020269. [Google Scholar] [CrossRef]
11. B. Yang et al., “PV arrays reconfiguration for partial shading mitigation: Recent advances, challenges and perspectives,” Energy Conv. Manag., vol. 247, pp. 1–28, Nov. 2021. doi: 10.1016/j.enconman.2021.114738. [Google Scholar] [CrossRef]
12. J. L. Seguel, S. I. Seleme Jr, and L. M. F. Morais, “Comparative study of Buck-Boost, SEPIC, Cuk and Zeta DC-DC converters using different MPPT methods for photovoltaic applications,” Energies, vol. 15, no. 21, pp. 1–26, Nov. 2022. doi: 10.3390/en15217936. [Google Scholar] [CrossRef]
13. A. M. Humada, M. Hojabri, S. Mekhilef, and H. M. Hamada, “Solar cell parameters extraction based on single and double-diode models: A review,” Renew. Sust. Energ. Rev., vol. 56, pp. 494–509, Apr. 2016. doi: 10.1016/j.rser.2015.11.051. [Google Scholar] [CrossRef]
14. D. S. Pillai and N. Rajasekar, “Metaheuristic algorithms for PV parameter identification: A comprehensive review with an application to threshold setting for fault detection in PV systems,” Renew. Sust. Energ. Rev., vol. 82, pp. 3503–3525, Feb. 2018. doi: 10.1016/j.rser.2017.10.107. [Google Scholar] [CrossRef]
15. H. F. M. Romero, “Applications of artificial intelligence to photovoltaic systems: A review,” Appl. Sci., vol. 12, no. 19, pp. 1–31, Oct. 2022. doi: 10.3390/app121910056. [Google Scholar] [CrossRef]
16. Z. Kesilmiş, M. A. Karabacak, and M. Aksoy, “A novel MPPT method based on inflection voltages,” J. Clean Prod., vol. 266, pp. 1–12, Sep. 2020. doi: 10.1016/j.jclepro.2020.121473. [Google Scholar] [CrossRef]
17. A. F. Mirza, M. Mansoor, K. Zhan, and Q. Ling, “High-efficiency swarm intelligent maximum power point tracking control techniques for varying temperature and irradiance,” Energy, vol. 228, pp. 1–27, Aug. 2021. doi: 10.1016/j.energy.2021.120602. [Google Scholar] [CrossRef]
18. B. Yang et al., “Dynamic leader based collective intelligence for maximum power point tracking of PV systems affected by partial shading condition,” Energy Conv. Manag., vol. 179, pp. 286–303, Jan. 2019. doi: 10.1016/j.enconman.2018.10.074. [Google Scholar] [CrossRef]
19. L. Thangamuthu, J. R. Albert, K. Chinnanan, and B. Gnanavel, “Design and development of extract maximum power from single-double diode PV model for different environmental condition using BAT optimization algorithm,” J. Intell. Fuzzy Syst., vol. 43, no. 1, pp. 1091–1102, Jun. 2022. doi: 10.3233/JIFS-213241. [Google Scholar] [CrossRef]
20. K. Chennoufi, M. Ferfra, and M. Mokhlis, “Design and implementation of efficient MPPT controllers based on SDM and DDM using backstepping control and SEPIC converter,” presented at the 2021 9th Int. Renew. Sustain. Energ. Conf., Morocco, Nov. 23–27, 2021. [Google Scholar]
21. M. Leelavathi and V. S. Kumar, “Deep neural network algorithm for MPPT control of double diode equation based PV module,” Mater. Today Proc., vol. 62, pp. 4764–4771, Aug. 2022. doi: 10.1016/j.matpr.2022.03.340. [Google Scholar] [CrossRef]
22. M. H. Zafar, N. M. Khan, A. F. Mirza, and M. Mansoor, “Bio-inspired optimization algorithms based maximum power point tracking technique for photovoltaic systems under partial shading and complex partial shading conditions,” J. Clean Prod., vol. 309, pp. 1–18, Aug. 2021. doi: 10.1016/j.jclepro.2021.127279. [Google Scholar] [CrossRef]
23. M. C. Cavalcanti, F. Bradaschia, A. J. do Nascimento, G. M. S. Azevedo, and E. J. Barbosa, “Hybrid maximum power point tracking technique for PV modules based on a double-diode model,” IEEE Trans. Ind. Electron., vol. 68, no. 9, pp. 8169–8181, Sep. 2021. doi: 10.1109/TIE.2020.3009592. [Google Scholar] [CrossRef]
24. S. Senthilkumar, V. Mohan, S. P. Mangaiyarkarasi, and M. Karthikeyan, “Analysis of single-diode PV model and optimized MPPT model for different environmental conditions,” Int. Trans. Electr. Energy Syst., vol. 2022, pp. 1–17, Jan. 2022. doi: 10.1155/2022/4980843. [Google Scholar] [CrossRef]
25. E. J. Barbosa, M. C. Cavalcanti, G. M. S. Azevedo, R. C. Neto, E. A. O. Barbosa and F. Bradaschia, “Hybrid GMPPT technique for photovoltaic series based on fractional characteristic curve,” IEEE J. Photovolt., vol. 14, no. 1, pp. 170–177, Jan. 2024. doi: 10.1109/JPHOTOV.2023.3323774. [Google Scholar] [CrossRef]
26. N. Priyadarshi, P. Sanjeevikumar, M. S. Bhaskar, F. Azam, and S. M. Muyeen, “An improved standalone photovoltaic system with hybrid dual integral sliding mode and model predictive control for MPPT,” IET Renew. Power Gener., pp. 1–15, Sep. 2023. doi: 10.1049/rpg2.12665. [Google Scholar] [CrossRef]
27. E. J. Barbosa, M. C. Cavalcanti, G. M. D. Souza Azevedo, E. A. O. Barbosa, F. Bradaschia and L. R. Limongi, “Global hybrid maximum power point tracking for PV modules based on a double-diode model,” IEEE Access, vol. 9, pp. 158440–158455, Nov. 2021. doi: 10.1109/ACCESS.2021.3131096. [Google Scholar] [CrossRef]
28. P. A. Cotfas and D. T. Cotfas, “Comprehensive review of methods and instruments for photovoltaic-thermoelectric generator hybrid system characterization,” Energies, vol. 13, no. 22, pp. 1–32, Nov. 2020. doi: 10.3390/en13226045. [Google Scholar] [CrossRef]
29. B. Sangeetha, K. Manjunatha, P. T. Kumaran, A. Sheela, K. S. Yamuna and S. Sivakumar, “Performance optimization in photovoltaic systems: A review,” Arch. Comput. Method Eng., pp. 1–12, Nov. 2023. doi: 10.1007/s11831-023-10023-0. [Google Scholar] [CrossRef]
30. A. Mohapatra, B. Nayak, P. Das, and K. B. Mohanty, “A review on MPPT techniques of PV system under partial shading condition,” Renew. Sust. Energ. Rev., vol. 80, pp. 854–867, Dec. 2017. doi: 10.1016/j.rser.2017.05.083. [Google Scholar] [CrossRef]
31. R. B. Bollipo, S. Mikkili, and P. K. Bonthagorla, “Hybrid, optimal, intelligent and classical PV MPPT techniques: A review,” CSEE J. Power Energy, vol. 7, no. 1, pp. 9–33, Mar. 2021. doi: 10.17775/CSEEJPES.2019.02720. [Google Scholar] [CrossRef]
32. B. Yang et al., “Comprehensive overview of maximum power point tracking algorithms of PV systems under partial shading condition,” J. Clean Prod., vol. 268, pp. 1–24, Sep. 2020. doi: 10.1016/j.jclepro.2020.121983. [Google Scholar] [CrossRef]
33. J. L. Li, Y. W. Wu, S. L. Ma, M. X. Chen, B. P. Zhang and B. Jiang, “Analysis of photovoltaic array maximum power point tracking under uniform environment and partial shading condition: A review,” Energy Rep., vol. 8, pp. 13235–13252, Nov. 2022. doi: 10.1016/j.egyr.2022.09.192. [Google Scholar] [CrossRef]
34. R. Alik and A. Jusoh, “An enhanced P&O checking algorithm MPPT for high tracking efficiency of partially shaded PV module,” Sol. Energy, vol. 163, pp. 570–580, Mar. 2018. doi: 10.1016/j.solener.2017.12.050. [Google Scholar] [CrossRef]
35. I. Owusu-Nyarko, M. A. Elgenedy, I. Abdelsalam, and K. H. Ahmed, “Modified variable step-size incremental conductance MPPT technique for photovoltaic systems,” Electron., vol. 10, no. 19, pp. 1–18, Oct. 2021. doi: 10.3390/electronics10192331. [Google Scholar] [CrossRef]
36. H. Q. Wang, L. Vinayagam, H. Jiang, Z. Q. Cai, and H. Q. Li, “New MPPT solar generation implemented with constant-voltage constant-current DC/DC converte,” presented at the 2016 51st Int. Univ. Power Eng. Conf., Coimbra Inst Engn, Coimbra Inst Engn, Coimbra, Portugal, Sep. 6–9, 2016. [Google Scholar]
37. M. I. Bahari, P. Tarassodi, Y. M. Naeini, A. K. Khalilabad, and P. Shirazi, “Modeling and simulation of hill climbing MPPT algorithm for photovoltaic application,” presented at the 2016 Int. Symp. Power Electron., Electr. Drives, Autom. Motion, Capri, Italy, Jun. 22–24, 2016. [Google Scholar]
38. A. Mohapatra, B. Nayak, and C. Saiprakash, “Adaptive perturb & observe MPPT for PV system with experimental validation,” presented at the 2019 IEEE Int. Conf. Sustain. Energy Technol. Syst., Bhubaneswar, India, Feb. 26–Mar. 1, 2019. [Google Scholar]
39. M. Kumar, K. P. Panda, J. C. Rosas-Caro, A. Valderrabano-Gonzalez, and G. Panda, “Comprehensive review of conventional and emerging maximum power point tracking algorithms for uniformly and partially shaded solar photovoltaic systems,” IEEE Access, vol. 11, pp. 31778–31812, May 2023. doi: 10.1109/ACCESS.2023.3262502. [Google Scholar] [CrossRef]
40. B. Yang et al., “Novel bio-inspired memetic salp swarm algorithm and application to MPPT for PV systems considering partial shading condition,” J. Clean Prod., vol. 215, pp. 1203–1222, Apr. 2019. doi: 10.1016/j.jclepro.2019.01.150. [Google Scholar] [CrossRef]
41. D. Molina, J. Poyatos, J. D. Ser, S. García, A. Hussain and F. Herrera, “Comprehensive taxonomies of nature-and bio-inspired optimization: Inspiration versus algorithmic behavior, critical analysis recommendations,” Cogn. Comput., vol. 12, pp. 897–939, Sep. 2020. doi: 10.1007/s12559-020-09730-8. [Google Scholar] [CrossRef]
42. L. Q. Pan, Y. Zhao, and L. H. Li, “Neighborhood-based particle swarm optimization with discrete crossover for nonlinear equation systems,” Swarm Evol. Comput., vol. 69, pp. 1–11, Mar. 2022. doi: 10.1016/j.swevo.2021.101019. [Google Scholar] [CrossRef]
43. A. Hassan, O. Bass, and M. A. S. Masoum, “An improved genetic algorithm based fractional open circuit voltage MPPT for solar PV systems,” Energy Rep., vol. 9, pp. 1535–1548, Dec. 2023. doi: 10.1016/j.egyr.2022.12.088. [Google Scholar] [CrossRef]
44. K. Sekar, E. Arasan, and K. Chandrasekaran, “Grey wolf optimization and fed fast terminal sliding mode controllers based on interleaved boost converters for symmetric PV systems under asymmetric partial shading,” Symmetry, vol. 15, no. 7, pp. 1–14, Jul. 2023. doi: 10.3390/sym15071339. [Google Scholar] [CrossRef]
45. R. K. Phanden, L. Sharma, J. Chhabra, and H. I. Demir, “A novel modified ant colony optimization based maximum power point tracking controller for photovoltaic systems,” Mater. Today Proc., vol. 38, no. 15, pp. 89–93, Feb. 2021. doi: 10.1016/j.matpr.2020.06.020. [Google Scholar] [CrossRef]
46. R. B. Watanabe et al., “Implementation of the bio-inspired metaheuristic firefly algorithm (FA) applied to maximum power point tracking of photovoltaic systems,” Energies, vol. 15, no. 15, pp. 1–15, Aug. 2022. doi: 10.3390/en15155338. [Google Scholar] [CrossRef]
47. H. M. H. Farh, A. Fathy, A. A. Al-Shamma’a, S. Mekhilef, and A. M. Al-Shaalan, “Global research trends on photovoltaic maximum power extraction: Systematic and scientometric analysis,” Sustain. Energy Technol. Assess., vol. 61, pp. 1–20, Jan. 2024. doi: 10.1016/j.seta.2023.103585. [Google Scholar] [CrossRef]
48. B. Abdollahzadeh et al., “Puma optimizer (POA novel metaheuristic optimization algorithm and its application in machine learning,” Cluster Comput., pp. 1–49, Jan. 2024. doi: 10.1007/s10586-023-04221-5. [Google Scholar] [CrossRef]
49. M. Abdel-Basset, R. Mohamed, and M. Abouhawwash, “Crested porcupine optimizer: A new nature-inspired metaheuristic,” Knowl. Based Syst., vol. 284, pp. 1–42, Jan. 2024. doi: 10.1016/j.knosys.2023.111257. [Google Scholar] [CrossRef]
50. F. Yahiaoui et al., “Experimental validation and intelligent control of a stand-alone solar energy conversion system using dSPACE platform,” Front Energy Res., vol. 10, pp. 1–12, Aug. 2022. doi: 10.3389/fenrg.2022.971384. [Google Scholar] [CrossRef]
51. N. Priyadarshi, P. K. Maroti, and B. Khan, “An adaptive grid integrated photovoltaic system with perturb T-S fuzzy based sliding mode controller MPPT tracker: An experimental realization,” IET Renew. Power Gener., pp. 1–11, Jan. 2023. doi: 10.1049/rpg2.12738. [Google Scholar] [CrossRef]
52. M. Khan, M. A. Raza, T. A. Jumani, and S. Mirsaeidi, “Modeling of intelligent controllers for solar photovoltaic system under varying irradiation conditions,” Front Energy Res., vol. 11, pp. 1–15, Nov. 2023. doi: 10.3389/fenrg.2023.1288486. [Google Scholar] [CrossRef]
53. A. G. Olabi et al., “Artificial neural networks applications in partially shaded PV systems,” Therm. Sci. Eng. Prog., vol. 37, no. 1, pp. 1–23, Jan. 2023. doi: 10.1016/j.tsep.2022.101612. [Google Scholar] [CrossRef]
54. A. M. Farayola, A. N. Hasan, and A. Ali, “Efficient photovoltaic MPPT system using coarse Gaussian support vector machine and artificial neural network techniques,” Int. J. Innov. Comp. Inf. Control., vol. 14, no. 1, pp. 323–339, Feb. 2018. doi: 10.24507/ijicic.14.01.323. [Google Scholar] [CrossRef]
55. F. Tahiri, A. Harrouz, and I. Colak, “Analysis of the MPPT techniques used on the PV system in comparison, including the perturbation & observation approach, sliding mode control, and fuzzy logic control,” presented at the 2023 11th Int. Conf. Smart Grid, Paris, France, Jun. 4–7, 2023. [Google Scholar]
56. I. Rahul and R. Hariharan, “Enhancement of solar PV panel efficiency using double integral sliding mode MPPT control,” Tsinghua Sci. Technol., vol. 29, no. 1, pp. 271–283, Feb. 2024. doi: 10.26599/TST.2023.9010030. [Google Scholar] [CrossRef]
57. S. P. Ye, Y. H. Liu, H. Y. Pai, A. Sangwongwanich, and F. Blaabjerg, “A novel ANN-based GMPPT method for PV systems under complex partial shading conditions,” IEEE Trans. Sustain. Energy., vol. 15, no. 1, pp. 328–338, Jan. 2024. doi: 10.1109/TSTE.2023.3284866. [Google Scholar] [CrossRef]
58. H. Cheng, S. W. Li, Z. P. Fan, and L. W. Liu, “Intelligent MPPT control methods for photovoltaic system: A review,” presented at the 2021 33rd Chin. Control Decis. Conf., Kunming, China, May 22–24, 2021, pp. 22–24. [Google Scholar]
59. A. Harrison, N. H. Alombah, and J. D. N. Ndongmo, “A new hybrid MPPT based on incremental conductance-integral back stepping controller applied to a PV system under fast-changing operating conditions,” Int. J. Photoenergy, vol. 2023, pp. 1–17, Feb. 2023. doi: 10.1155/2023/9931481. [Google Scholar] [CrossRef]
60. G. G. S. Kumar and S. Titus, “Hybrid artificial rabbit optimization and perturb & observe MPPT for grid-connected PV system,” Electr. Power Compon. Syst., pp. 1–22, Aug. 2023. doi: 10.1080/15325008.2023.2249885. [Google Scholar] [CrossRef]
61. S. Alkhalaf, Z. M. Ali, and H. Oikawa, “A novel hybrid gravitational and pattern search algorithm based MPPT controller with ANN and perturb and observe for photovoltaic system,” Soft Comput., vol. 26, no. 15, pp. 7293–7315, Aug. 2022. doi: 10.1007/s00500-022-07139-z. [Google Scholar] [CrossRef]
62. H. M. Liu, M. Y. A. Khan, and X. L. Yuan, “Hybrid maximum power extraction methods for photovoltaic systems: A comprehensive review,” Energies, vol. 16, no. 15, pp. 1–64, Aug. 2023. doi: 10.3390/en16155665. [Google Scholar] [CrossRef]
63. W. H. Tan and J. Mohamad-Saleh, “Critical review on interrelationship of electro-devices in PV solar systems with their evolution and future prospects for MPPT applications,” Energies, vol. 16, no. 2, pp. 1–37, Jan. 2023. doi: 10.3390/en16020850. [Google Scholar] [CrossRef]
64. F. Mumtaz, N. Z. Yahaya, S. T. Meraj, B. Singh, R. Kannan and O. Ibrahim, “Review on non-isolated DC-DC converters and their control techniques for renewable energy applications,” Ain Shams Eng. J., vol. 12, no. 4, pp. 3747–3763, Dec. 2021. doi: 10.1016/j.asej.2021.03.022. [Google Scholar] [CrossRef]
65. A. Ba, C. O. Ehssein, M. E. M. O. M. Mahmoud, O. Hamdoun, and A. Elhassen, “Comparative study of different DC/DC power converter for optimal PV system using MPPT (P&O) method,” Appl. Sol. Energy., vol. 54, no. 4, pp. 235–245, Jul. 2018. doi: 10.3103/S0003701X18040047. [Google Scholar] [CrossRef]
66. D. F. Zaions, A. J. Balbino, C. L. Baratieri, and A. L. Stankiewicz, “Comparative analysis of buck and boost converters applied to different maximum power point tracking techniques for photovoltaic systems,” presented at the 2021 33rd Chin. Control Decis. Conf., Juiz de Fora, Brazil, Nov. 19–22, 2017. [Google Scholar]
67. A. Raj, S. R. Arya, and J. Gupta, “Solar PV array-based DC-DC converter with MPPT for low power applications,” Renew. Energ. Focus., vol. 34, pp. 109–119, Sep. 2020. doi: 10.1016/j.ref.2020.05.003. [Google Scholar] [CrossRef]
68. H. Gholizadeh, S. A. Gorji, E. Afjei, and D. Sera, “Design and implementation of a new Cuk-based step-up DC-DC converter,” Energies, vol. 14, no. 21, pp. 1–18, Nov. 2021. doi: 10.3390/en14216975. [Google Scholar] [CrossRef]
69. L. J. Jotham, C. A. Ooi, and J. Teh, “Non-isolated conventional DC-DC converter comparison for a photovoltaic system: A review,” J. Renew. Sustain. Energy., vol. 12, no. 1, pp. 1–22, Jan. 2020. doi: 10.1063/1.5095811. [Google Scholar] [CrossRef]
70. K. V. G. Raghavendra et al., “A comprehensive review of DC-DC converter topologies and modulation strategies with recent advances in solar photovoltaic systems,” Electronics, vol. 9, no. 1, pp. 1–41, Jan. 2020. doi: 10.3390/electronics9010031. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools