Fault Diagnosis Method of Energy Storage Unit of Circuit Breakers Based on EWT-ISSA-BP

1  Introduction

Low-voltage circuit breakers are essential control and protection equipment in low-voltage distribution systems, and their reliable operation is essential to the power system [1,2]. With the vigorous development of new energy, more and more wind farms are being established. In order to protect the electrical equipment inside the converter and wind turbine, the safe and reliable operation of low-voltage circuit breakers has become increasingly important. However, the circuit breaker is exposed to high loads and harsh environments for a long time, and its spring operating mechanism is prone to various failures. This will lead to the performance degradation of the internal mechanical components of the mechanism, making the equipment unable to operate normally. According to the investigation report of State Grid and CIGRE, it was found that the primary reason why circuit breakers refuse to move or not move is the failure of the operating mechanism [3,4]. Among them, the untimely detection of energy storage units is a significant cause of mechanical failure. In order to maintain stable operation of the power system, timely detection of faults is crucial. Traditional fault diagnosis methods are mainly based on threshold determination, regular inspection, manual judgment and other methods. These methods will reduce the service life of the equipment, cause a heavy burden on daily operations, and have low accuracy. Implementing maintenance is blind and costly, and it relies heavily on the experience of maintenance personnel. Based on this, non-invasive maintenance technology has developed rapidly in recent years.

2  Literature Review

The development of IoT-embedded technology and artificial intelligence algorithms has provided new ideas for non-invasive diagnosis of equipment. Various methods based on artificial intelligence algorithms have emerged in the field of fault diagnosis: methods based on expert systems [5,6], artificial neural Networks [7,8], fuzzy theory [9], support vector machine [10], probabilistic neural networks, Petri net and other methods. Among them, artificial neural networks and support vector machines show great potential in feature parameter identification and can obtain high diagnostic accuracy. Current research on diagnosing high-voltage circuit breaker (HVCB) operating mechanisms is mainly based on opening and closing coil current signals, contact stroke-time characteristic curves and vibration signals. Ye et al. [11] proposed a novel U-network for HVCB fault diagnosis based on CapsNet, which targets vibration signals and realizes the diagnosis of typical faults in circuit breaker electromagnets. Yang et al. [12] proposed a fault vibration signal enhancement method for circuit breakers based on WDCGAN. Sun et al. [13] used the ZFNet-DRN model to implement fault classification considering the randomness of the closing phase for the current signal of the opening and closing coil. Zhang et al. [14] proposed a fault diagnosis method for HVCB based on PCA-SSA-LVQ. Their research is based on the vibration signals of circuit breakers, achieving the diagnosis of typical faults during the opening process. Chmielewski et al. [15–17] conducted research on the modelling of circuit breakers and explored the relationship between fault characteristics and typical signals of circuit breakers. Huang et al. [18] used phase space reconstruction to extract vibration signal features based on the coil current and vibration signals. They realized the diagnosis of coil-plunger stuck, poor contact, latch stuck, insufficient power supply and other faults. Zhang et al. [19] proposed a circuit breaker fault diagnosis method that integrates circuit breaker vibration and coil current signals. This method solves the conflicts existing in multi-signal joint diagnosis. Wu et al. [20] proposed a circuit breaker fault diagnosis method based on a vibration signal envelope, which reduces software and hardware overhead. Rudsari et al. [21] proposed an efficient and accurate fault set production method by combining the coil current and contact stroke signals. Landry et al. [22–25] realized typical fault identification of circuit breakers based on the circuit breaker vibration signal. The above fault diagnosis research is mainly focused on high-voltage circuit breakers. There are few reports on online diagnostic technology for LVCBs. Until recently, few studies have been on the current signals of energy storage motors. The energy storage motor current signal directly reflects the energy storage state of the circuit breaker operating mechanism. Reasonable use of this signal can achieve rapid detection of the operating mechanism and then evaluate the operating status of the early warning circuit breaker in advance, providing support for the safe operation of the power grid.

In order to improve the accuracy and stability of fault diagnosis of the spring operating mechanism of LVCB, this article uses Empirical Wavelet Transform (EWT) to identify the motor current fault characteristic points. The Improve Sparrow Search Algorithm (ISSA) performs BPNN optimization. SSA simulates the foraging behavior of sparrows, searches on a global scale, and has strong convergence. SSA is applied in the training process of BPNN to enhance the network generalization ability and fault diagnosis accuracy. Based on the current signal of the energy storage motor, this paper realizes rapid diagnosis of six conditions: motor voltage increase, motor voltage decrease, energy storage spring stuck, transmission gear stuck, regular state, and energy storage spring not locked.

3  Methodology

3.1 Energy Storage Motor Signal Collection

Circuit breakers are divided into low-voltage, medium-voltage, high-voltage and extra-high voltage. Common types are oil circuit breakers, compressed air circuit breakers, SF6 circuit breakers and vacuum circuit breakers. Vacuum circuit breakers are widely used in medium and low-voltage fields. This paper takes the 1.5kV/4000A/75kA circuit breakers for wind turbines as the research object. The circuit breaker motor current signal is collected through the Hall coil current sensor; the sampling rate is 2 kHz, and the sampling length is 10 s. A fast mechanical switch repulsion mechanism control unit converts the collected current analogue signals into digital signals. The host computer software is written in QT and outputs the collected motor current signals. Fig. 1 is the circuit breaker energy storage motor current data acquisition system, in which ① is the auxiliary switch, ② is the opening spring, ③ is the closing spring, ④ is the closing electromagnet, ⑤ is the opening electromagnet, and ⑥ is the transmission gear. ⑦ is an energy storage motor. We set the fault by adjusting the voltage regulator, closing the spring, limit switch, and transmission gear.

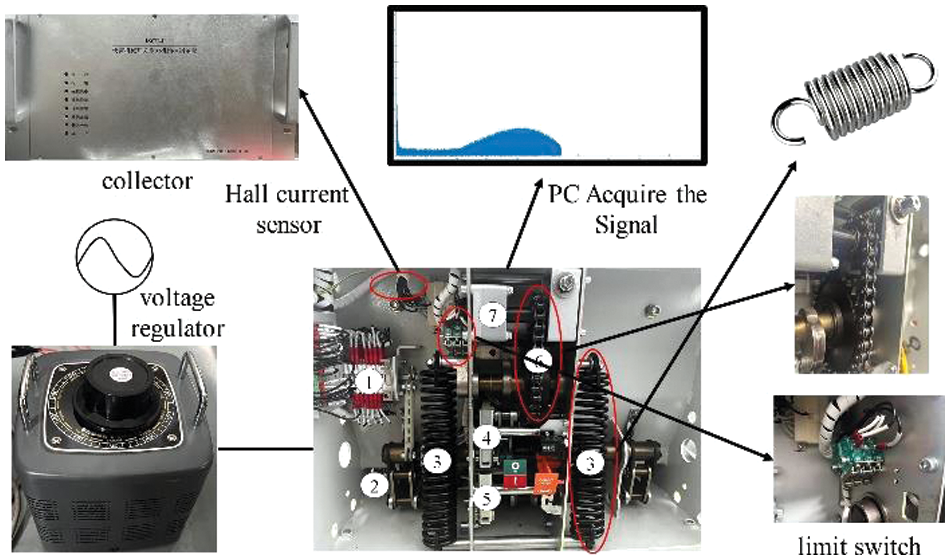
Figure 1: Circuit breaker energy storage motor current acquisition system

3.2 Energy Storage Motor Fault Feature Extraction

The action of the circuit breaker is divided into energy storage stage, opening stage and closing stage. The control system sends a closing signal; the energy storage motor releases the stored energy and the closing spring contracts. The opening spring stores energy, driving the contacts to close, and then the spring operating mechanism stretches the energy storage spring to the energy storage locking position through the energy storage motor. The control system sends an opening signal, and the opening spring releases energy to quickly separate the stored energy and complete the opening process. This article takes Taibang ZYJ220-66-106Z energy storage motor as an example to introduce the working principle. During the energy storage process of the energy storage motor, as the energy storage spring stretches, the load increases. During the smooth operation of the motor, multiple peaks appear in the current signal. In order to better extract the characteristics of the current signal, the envelope of the signal waveform needs to be extracted. The typical energy storage motor current envelope waveform is shown in Fig. 2. Among them, t1~t5 are essential features in the entire process when the circuit breaker receives the closing command and completes the closing action.

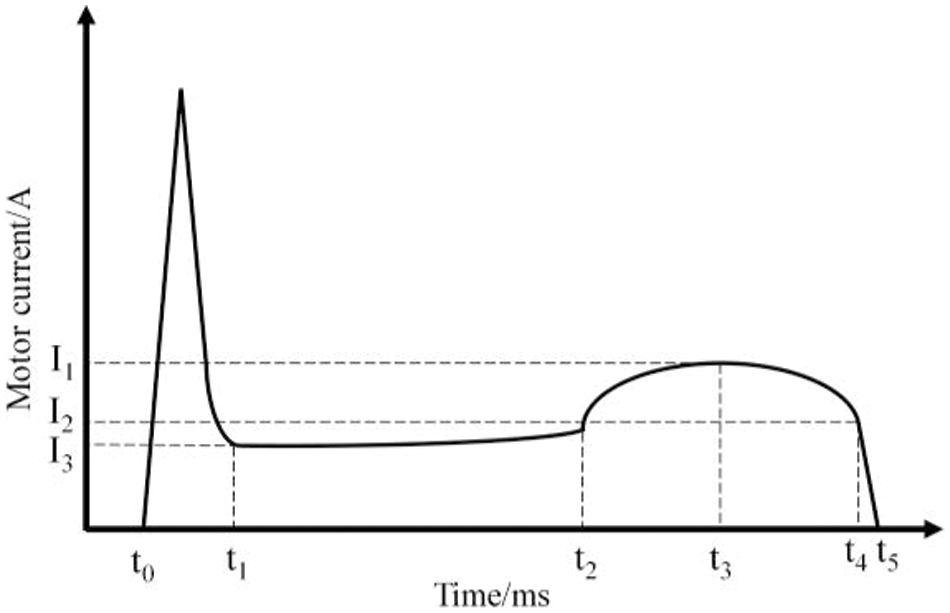
Figure 2: Typical energy storage motor current signal of circuit breaker

(a) From t0 to t1, the motor starts its action process. When the motor starts, the current is at its maximum, and the motor runs without load. The starting current amplitude is related to the motor loop resistance and starting voltage. The smaller the loop resistance, the greater the starting current. The higher the starting voltage, the greater the starting current.

(b) From t1 to t2, the motor runs with no load. At this time, the closing spring contracts to release energy, the circuit breaker closes, and the motor current tends to a stable value. This stable value is closely related to the starting voltage and motor loop resistance.

(c) From t2 to t4, the contact closing action is completed. The current of the energy storage motor increases, driving the closing spring to the energy storage locking position. At this stage, the spring jam will increase the energy storage motor load and the motor current. If the spring energy storage is not locked, I2 will increase accordingly. If the transmission gear is jammed, it will cause t2 to advance. If the motor voltage is too high or too low, t2 will advance or lag.

(d) From t4 to t5, the power supply of the energy storage motor is turned off, and the motor current gradually decreases to 0.

It can be seen from the ideal current curve of the energy storage motor. The turning points in the energy storage motor current waveform contain rich state information, and these turning points can reflect the health status of the circuit breaker energy storage unit to a certain extent. Therefore, we select the characteristic points in Table 1 as the characteristic points of this article. Imax and t2 can be used to reflect whether the energy storage motor voltage is over or undervoltage. t2 can reflect whether the circuit breaker transmission gear is stuck. I2 and t4 can reflect whether the circuit breaker is unlocked.

The energy storage motor used is an AC motor, and the rectified AC motor current signal is shown in Fig. 3a. In order to facilitate the extraction of feature quantities, we take the upper envelope surface of the energy storage motor current signal, and the envelope surface is shown in Fig. 3b. We can easily extract the required feature points according to the envelope waveform. Extract the maximum value from the envelope surface data to obtain Imax. Take the current value at the end of the envelope surface as I2. The sampling point corresponding to I2 is t4. There are many gear-like fluctuations on the envelope surface, and these fluctuations cannot be considered harmonic components. The gear-like fluctuation occurs because of the change in chain force value during the movement of the gear transmission chain. The existence of fluctuations makes it challenging to extract t2. In order to extract the feature point t2 more accurately, we decompose the signal.

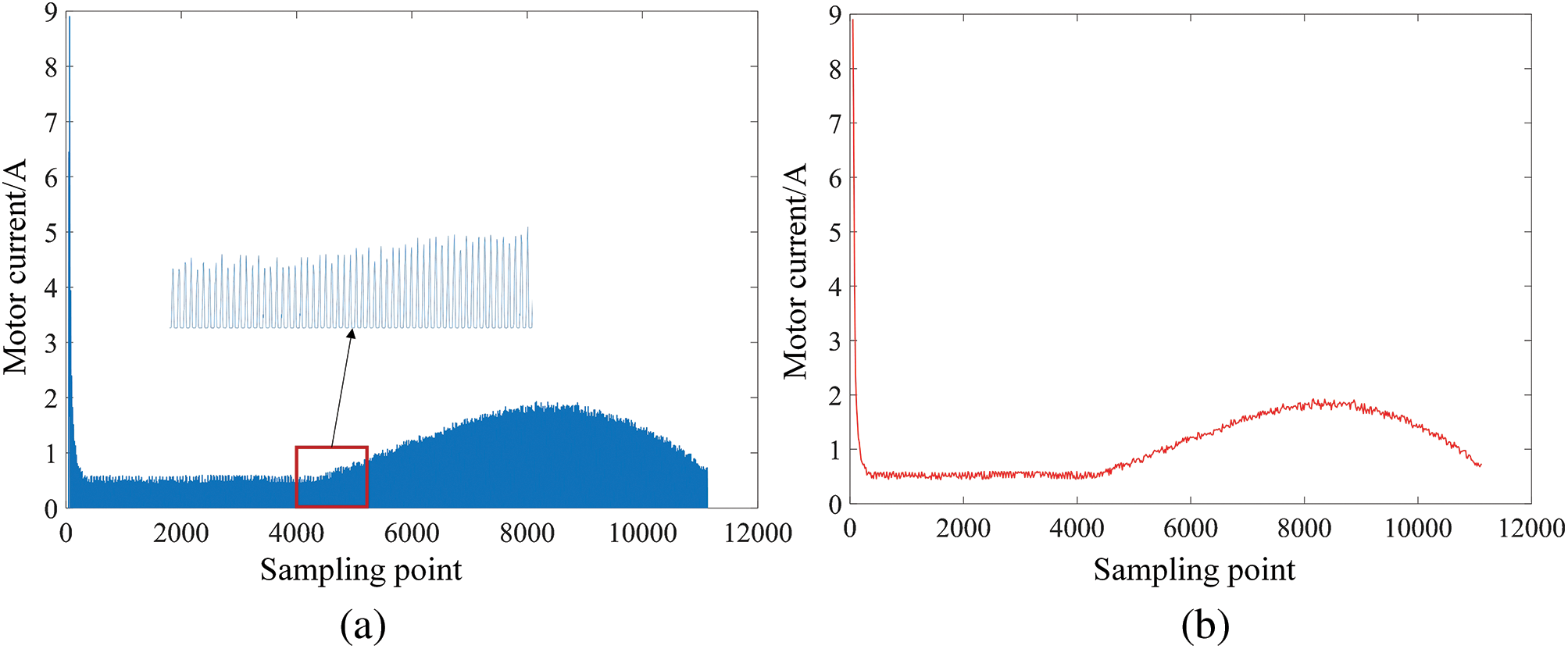
Figure 3: Collected energy storage motor current signal: (a) AC motor current signal after rectification; (b) Motor current signal envelope surface

Empirical Mode Decomposition (EMD) is often used to decompose signals, but its existence brings problems such as modal aliasing and endpoint effects. Ensemble Empirical Mode Decomposition (EEMD) adds auxiliary noise when performing EMD decomposition, improving the mode aliasing problem [26]. The Empirical Wavelet Transform (EWT) algorithm is not only based on the concept of “empirical” decomposition of the EMD algorithm but also includes the wavelet transform theoretical architecture [27]. It overcomes the shortcomings of the EMD algorithm’s lack of theory and is a processing method for adaptive time-frequency analysis of non-stationary signals. Fig. 4a shows the 10 IMF components after EEMD decomposition, and Fig. 4b shows the 10 IMF components after EWT decomposition. The red curve in the figure is the time domain waveform, and the blue curve is the frequency domain waveform. The IMF component after EEMD decomposition has a serious modal aliasing phenomenon. The EWT method spectrum decomposition is more reasonable, and the modal aliasing phenomenon is almost negligible. It can reflect the low-frequency component more effectively. Based on the decomposed low-frequency component, it can easily Extract feature point t2. 3-decomposition of the original signal can already meet the requirements. The time domain waveform after 3-decomposition is shown in Fig. 5. It is easier to extract the t2 component from the IMF component.

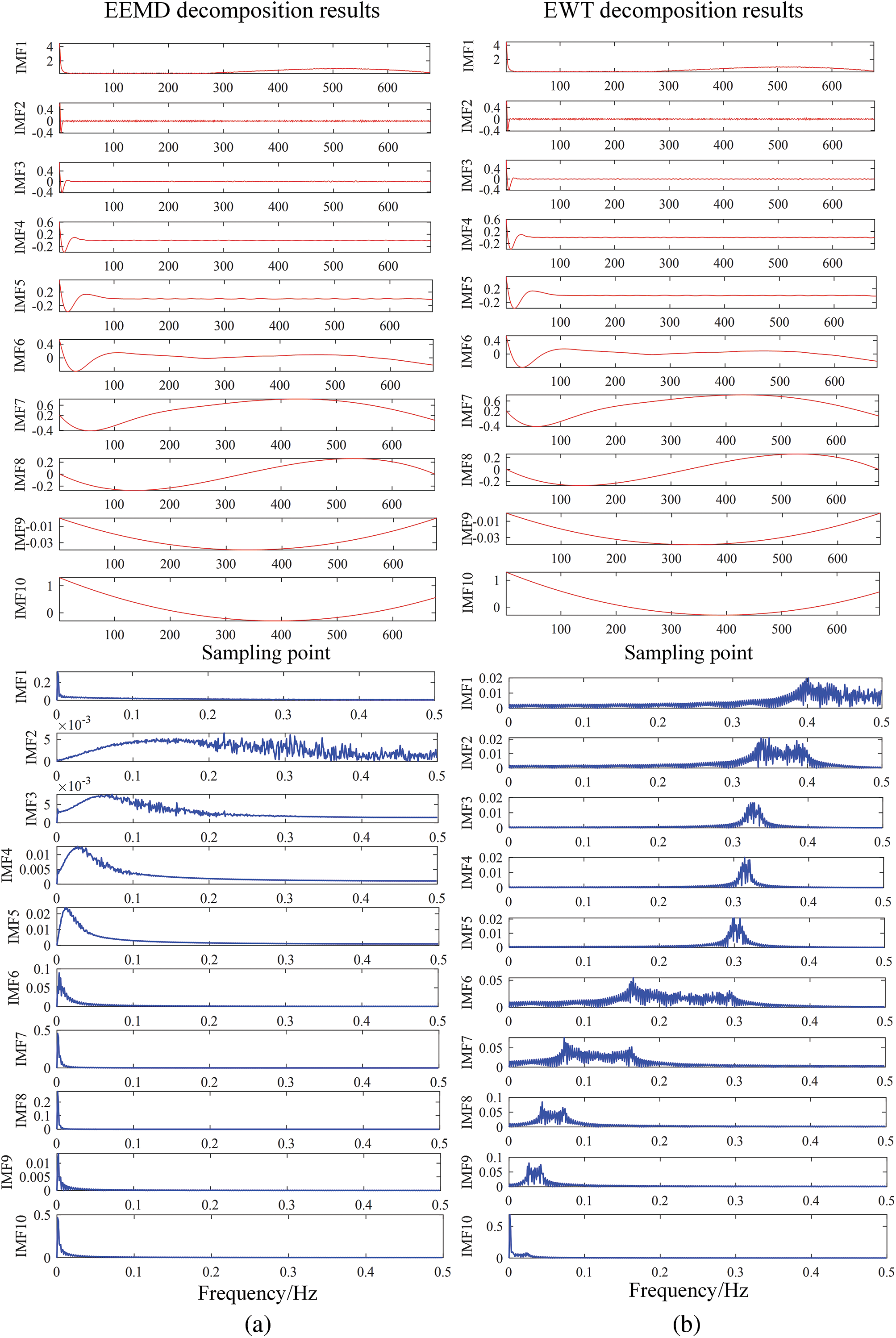
Figure 4: Waveform diagrams under different decomposition algorithms: (a) EEMD; (b) EWT

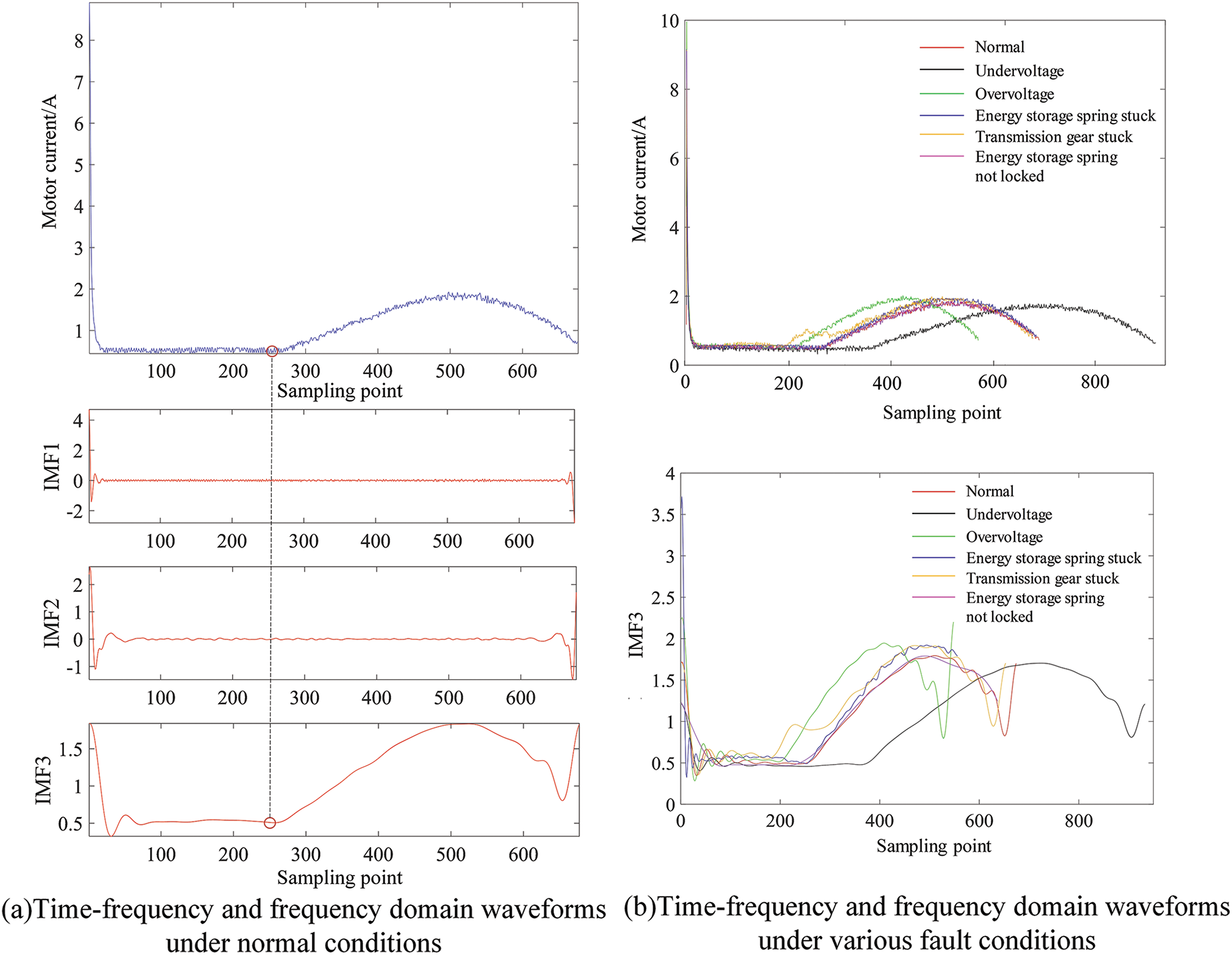
Figure 5: The time domain waveform after 3-decomposition

3.3 Fault Diagnosis Model Based on ISSA-BP

BP (Backpropagation) Neural Network is a commonly used artificial neural network model widely applied to classification and regression problems [28]. It is a feedforward artificial neural network that learns by adjusting weights and biases through the backpropagation algorithm, gradually reducing prediction errors for model optimization and fitting. However, it has drawbacks such as susceptibility to local optima and sensitivity to initial weights. In this paper, the initial weights and thresholds of BPNN are optimized by improved SSA, which in turn improves the diagnostic accuracy and model training rate.

3.3.1 BPNN

Artificial neural networks are conceptualized based on human brain-related biological activities [29], simulating intelligent processing of knowledge by mimicking the activity of human neurons. Currently, neural networks exhibit excellent performance in fault diagnosis, prediction, and various other fields. In artificial neural network models, the BPNN belongs to multi-layer feedforward networks. The training process of neural networks is based on the backpropagation algorithm. It consists of the input layer, hidden layer, and output layer. The basic structure of the BPNN is shown in Fig. 6.

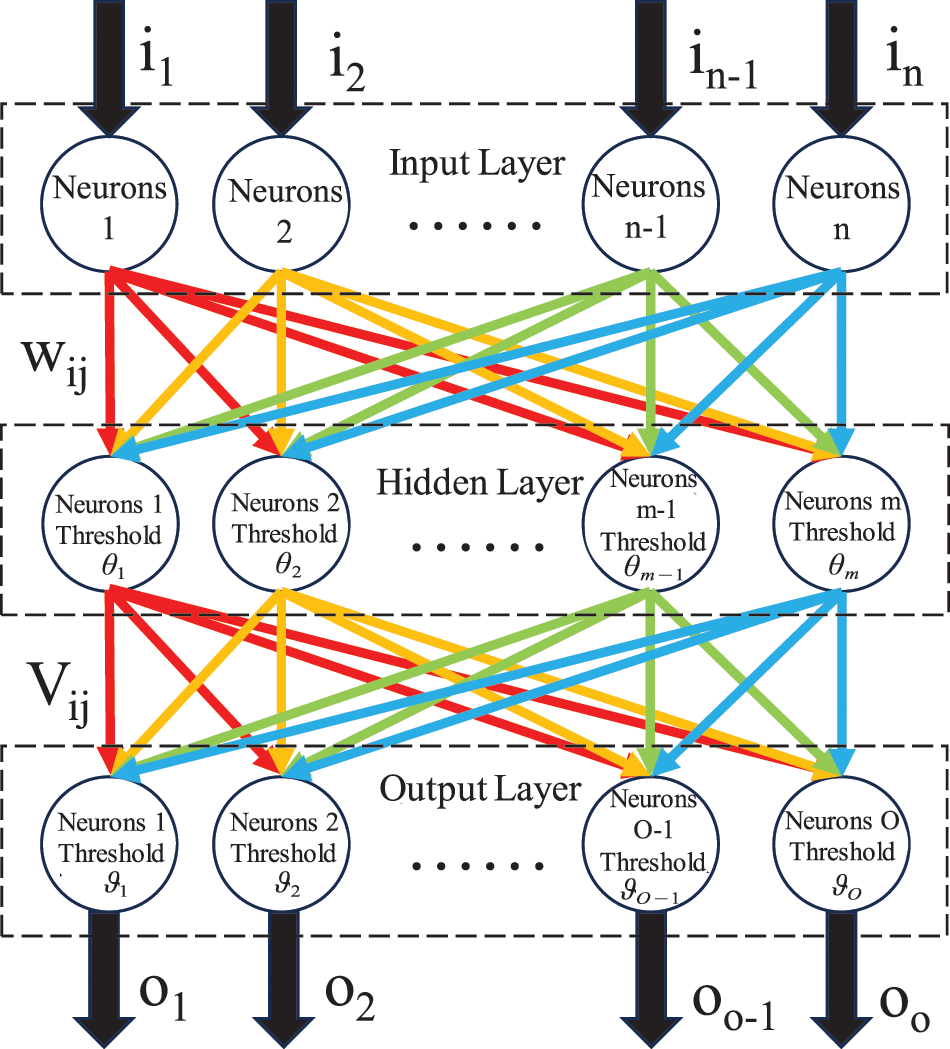
Figure 6: Basic structure of BPNN

The BP algorithm is crucial for BPNNs. It employs the backpropagation algorithm to update the network during the forward transmission of signals. The input signal I is represented as follows:

I=(i1,i2⋅⋅⋅in)(1)

The signal is transmitted from the input to the hidden layer, and the corresponding neuron output value mj is obtained based on the neuron threshold and activation function as:

mj=fm(∑i=1nωjiii−θj)(2)

where fm is the hidden layer activation function, ωji is the weight between the j-th hidden layer neuron and the i-th input layer neuron, and θj is the j-th hidden layer neuron threshold.

The output layer neuron output oj can be expressed as:

oj=fo(∑i=1mvjimi−ϑj)(3)

where fo is the output layer activation function, vji is the weight between the j-th output layer neuron and the i-th hidden layer neuron and ϑj is the j-th output layer neuron threshold.

The error function in forward propagation is defined as follows:

E=12∑i=1O(oi−yi)2(4)

where yi is the desired output, and o is the number of neurons in the initial layer.

In the backpropagation algorithm, the modification for each neuron’s threshold and corresponding connection weight in the BPNN is as follows:

vlj(n+1)=vlj(n)+Δvlj(n)

ϑlj(n+1)=ϑlj(n)+Δϑlj(n)

Δvlj(n)=−η∂E∂vlj

Δϑlj(n)=−η∂E∂ϑlj(5)

where η is the learning rate, the learning rate determines the step size at each parameter update. An excessively large or small learning rate can lead to training instability or slow convergence.

The learning process of the BPNN involves repeated cycles of forward signal transmission and backward error propagation. The network converges to reduce the error between actual and expected outputs by adjusting and correcting weights and thresholds. Therefore, BPNNs exhibit good nonlinear performance and are well suited for dealing with the simulation of nonlinear systems and the parallel processing of large amounts of information. However, during the network training process, BPNNs converge slowly and suffer from slow convergence and susceptibility to local optima during training. This paper uses ISSA to optimize the BPNN, which can enhance the fault diagnosis accuracy and training rate.

3.3.2 Improved Sparrow Search Algorithm

During the power grid operation, online diagnostic equipment is required to be simple, reliable and quickly identify faults. SSA [30] has a simple structure, easy implementation, fewer control parameters, and local solid search ability compared with other optimization algorithms. The solution process of SSA is to initialize the population of N sparrows and use the fitness function to calculate and rank the advantages and disadvantages of each sparrow’s position. However, SSA has shortcomings, such as easy premature convergence and low convergence accuracy. Therefore, this article improves SSA to improve the performance of the algorithm.

The initialization process of sparrow search is optimized, and chaotic initialization is introduced to increase the randomness of the initial weights of the neural network, which makes the neural network search in a broader range. Compared with Tent and Logistic chaos initialization, one-dimensional Sin chaos initialization has better chaotic characteristics. In this paper, one-dimensional Sin chaos is used for initialization:

{xn+1=sin⁡2xn,n=0,1...N−1⩽xn⩽1,xn≠0(6)

Based on the position update equations of the discoverers, the adaptive inertia weight ω is introduced to enhance the algorithm’s global optimization and local optimization ability, and the influence of the optimal position of the previous generation is considered in the position update process. The inertia weight ω and the discoverer update equations considering the influence of the optimal position of the previous generation are as follows:

ω=e2(1−t/itermax)−e−2(1−t/itermax)e2(1−t/itermax)+e−2(1−t/itermax)(7)

Xi,jt+1={(Xi,jt+ω(fj,gt−Xi,jt))⋅randR2<STXi,jt+QL,R2⩾ST(8)

where fj,gt is the j-th dimensional global optimum of the previous generation; Xi,jt stands for the position of the i-th sparrow in the j-th dimension at the t-th iteration; Q is a random number that obeys a normal distribution; L represents a matrix with 1 row and d columns and all elements are 1. R2 is a warning value, R2 ∈ (0, 1); ST is the safety value, ST ∈ (0.5, 1).

The strong disturbance ability of Cauchy mutation and the strong optimization ability of reverse learning are combined to update the optimal position of sparrow population. The probability function Ps is introduced for the alternate use of reverse learning and Cauchy mutation. The improved optimal position update formula is:

Xbest  ′(t)=Xbest(t)+cauchy(0,1)⊕Xbest(t)(9)

Xi,jt+1=Xbest  ′(t)+b1⊕(Xbest(t)−Xbest  ′(t))(10)

where Eq. (9) is the Cauchy mutation position update formula, Eq. (10) is the reverse learning position update formula, and the choice between the two depends on the probability function Ps. When rand < Ps, reverse learning is used for position update; otherwise, Cauchy mutation is used for position update, and the probability function Ps is as follows:

Ps=−e(1−1itermax)20+θ(11)

where θ is an adjustable parameter, generally 0.05.

The new position after Cauchy mutation or reverse learning is brought into the fitness function. When the fitness value of the new position is less than the fitness value corresponding to the current optimal position, the optimal position is updated.

3.3.3 Improved Sparrow Search Algorithm Optimizes BPNN

As mentioned earlier, traditional BP algorithms heavily depend on the initial weights and thresholds for training. Reasonable weights and thresholds can improve the training efficiency and diagnostic accuracy of BPNNs. SSA has global search ability and strong convergence. In this paper, the optimized SSA algorithm is used to optimize the initial weights and thresholds of BPNN to improve the diagnostic performance.

Fig. 7 shows the SSA-BP fault diagnosis steps.

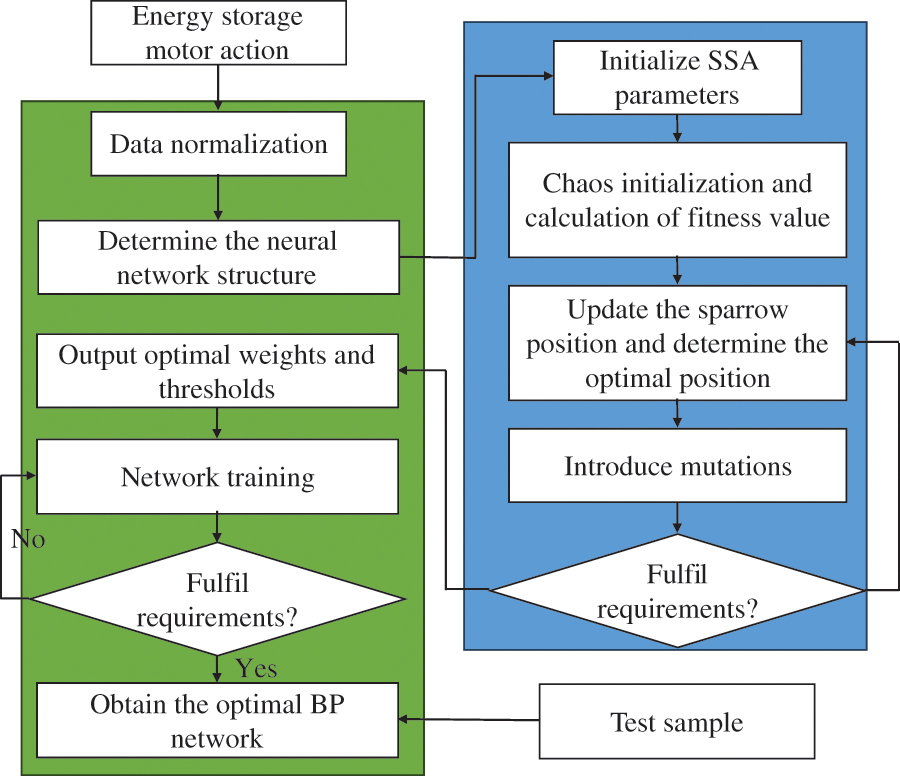
Figure 7: ISSA-BP fault diagnosis steps

(a) Normalize the input data to scale feature values to an appropriate range ([0, 1]) for improved model convergence, stability, and generalization.

The normalization formula is as follows:

y=x−maxmax−min(12)

(b) Determine the structure of the BPNN (including the number of nodes in the input layer, hidden layer and output layer). In this paper, it is proposed to diagnose the six conditions of normal state: gear jamming, spring jamming, motor voltage increase, motor voltage decrease and the energy storage spring unlatched, so the number of nodes in the output layer is set to be 6, and the output value of each node indicates the probability of the fault, the previous section selects five feature points as the feature quantity, so the number of nodes in the input layer of the BP network is 5. Determine the number of nodes in the hidden layer of the network through the empirical formula, M=5+6+8, α = 8.

(c) Set initial parameters of SSA: the number of sparrows (20), the maximum number of iterations (30), the dimension of positions (143), and the proportion of discoverers (20%). Sin Chaos initializes the initial position of the sparrow population.

(d) Define the fitness function, measuring the difference between the neural network’s predicted results and actual results. Cross-entropy is selected as the fitness function for its suitability in classification problems. The equation of cross entropy is as follows:

L=−1N∑i∑c=1Myiclog⁡(pic)(13)

where M is the category, yic is the sign function (taking 1 when the category of sample i is c and 0 for the rest), and pic is the predicted probability.

The optimal position and the worst position in the population are determined by updating the population fitness ranking matrix according to the cross-entropy equation.

(e) Update the sparrow position based on the position update equations, select the reverse learning strategy or Cauchy mutation method to generate a new solution based on the probabilistic Ps, and determine whether to update the position of the most optimal population.

(f) Determine whether to terminate the process based on termination conditions. If termination is reached, output the optimal solution and assign it to the BPNN. Set training parameters and train the network.

(g) Validate the diagnostic accuracy of the trained BPNN using a test set.

4  Results and Analysis

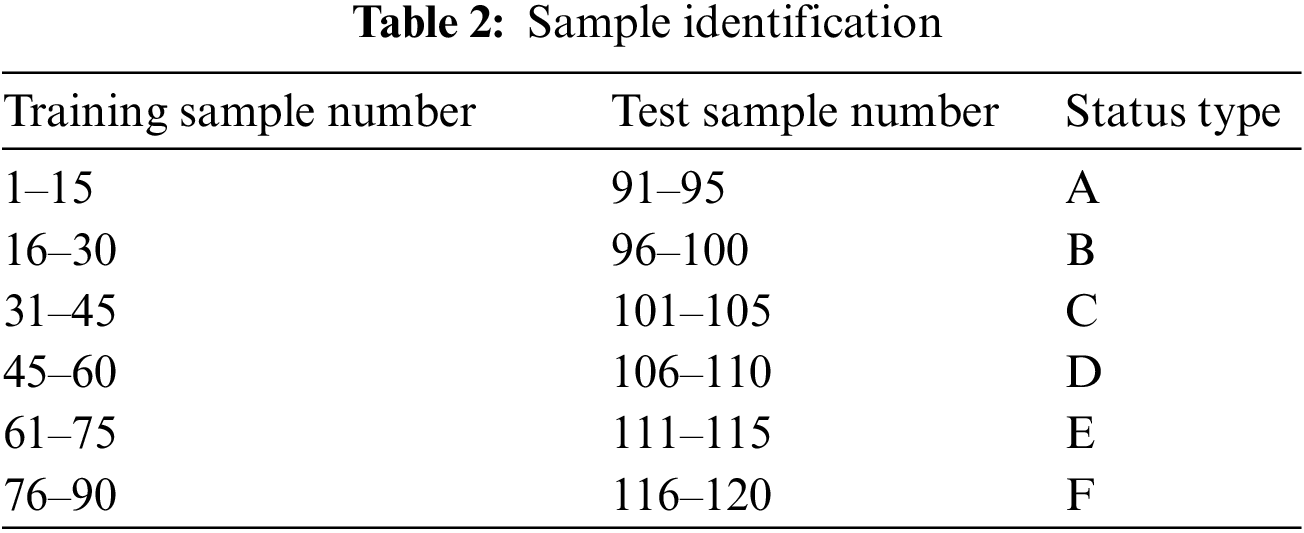
By consulting the circuit breaker manufacturer, we learned that in actual applications, the energy storage mechanism of the circuit breaker often suffers from mechanical failures such as transmission mechanism jamming, operating power supply failure, and closing spring jamming. Based on this we set up the following faults: Fault 1: Insufficient power supply to the energy storage motor. Set the power supply voltage of the energy storage motor to 154–198 V through the voltage regulator. Fault 2: The energy storage motor is overvoltage. Set the power supply voltage of the energy storage motor to 236–264 V. Fault 3: Place a hard object at the transmission gear to simulate the situation when the transmission gear is jammed. Fault 4: Simulate the energy storage spring by adding different elastic forces to the closing spring. Fault 5: Place objects of different thicknesses in front of the limit switch to simulate different degrees of unlatched springs. For algorithm training, select “A-Normal state of equipment”, “B-Motor voltage decrease”, “C-Motor voltage increase”, “D-Energy storage spring stuck”, “E-Transmission gear stuck” and “F-Energy storage spring is not locked”. There are 20 groups for each of the six types, 15 of which are used as BP neural network training sets, and the other 5 groups are used as subsequent test sets, as shown in Table 2.

After normalizing the feature points, a training set is created, and network training parameters are set, with a maximum iteration count of 10000, a learning rate of 0.01, and a neural network training error of 0.05. The softmax activation function is selected. The softmax function is particularly well suited for multi-categorization tasks, as it can convert raw scores into probabilities, making predictions more intuitive and easier to understand. SSA variables have lower bounds of −3, upper bounds of 1, and a safety value of 0.8. Input the training set into ISSA-BP, ISSA continuously updates the population position, and the optimal fitness is continuously updated. The improved sparrow search algorithm and the optimal individual fitness change curve of the improved sparrow search algorithm are shown in Fig. 8. It can be seen from the figure that as the number of evolutionary generations increases, the population continues to iterate. The optimal individual fitness gradually decreases, and ISSA-BP finds the optimal weights and thresholds around 25 generations. Since the chaotic initialization process of ISSA expands the optimization scope of SSA, it is necessary to find better weights and thresholds in the initial stage. SSA-BP falls into a local optimum during the iteration process. Therefore, the improved Sparrow search algorithm has faster convergence speed and accuracy, and the BPNN is trained with the optimal weights and thresholds found.

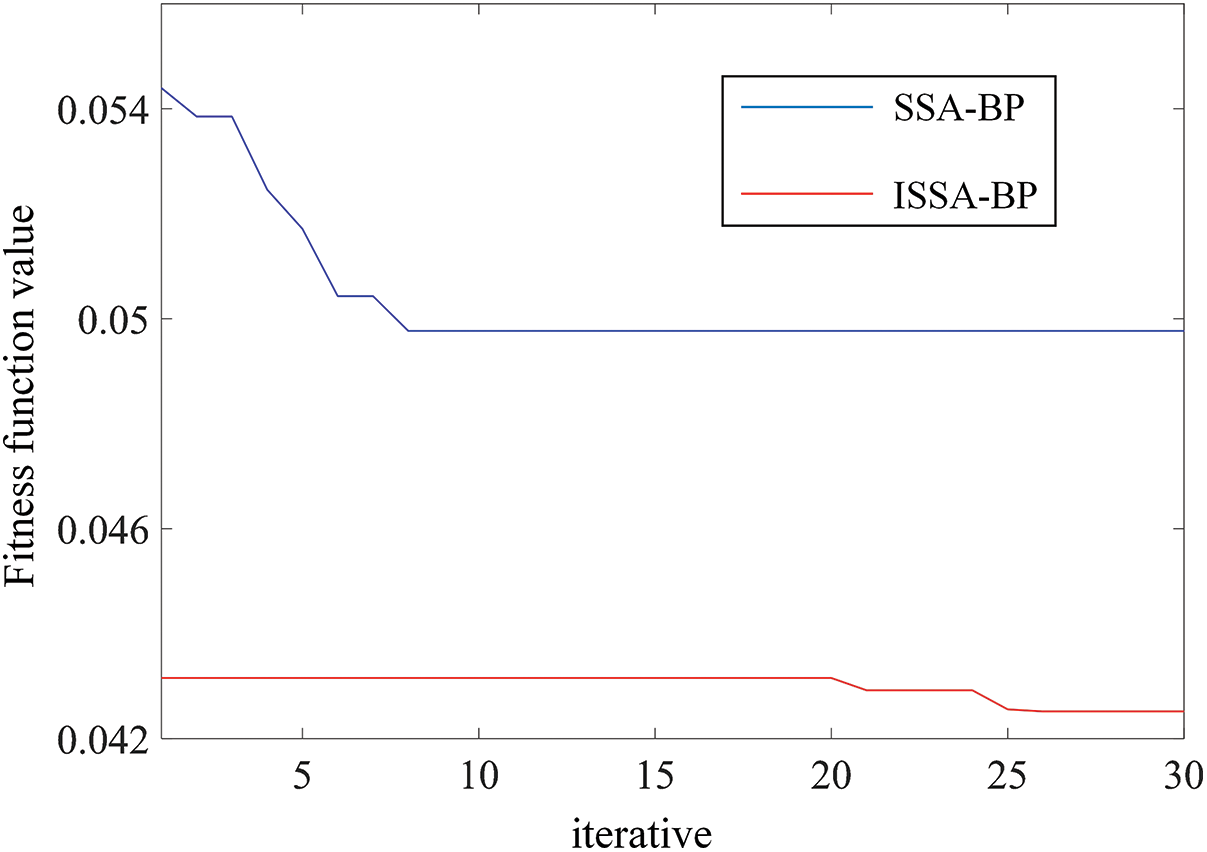
Figure 8: SSA-BP and ISSA-BP fitness decline curve

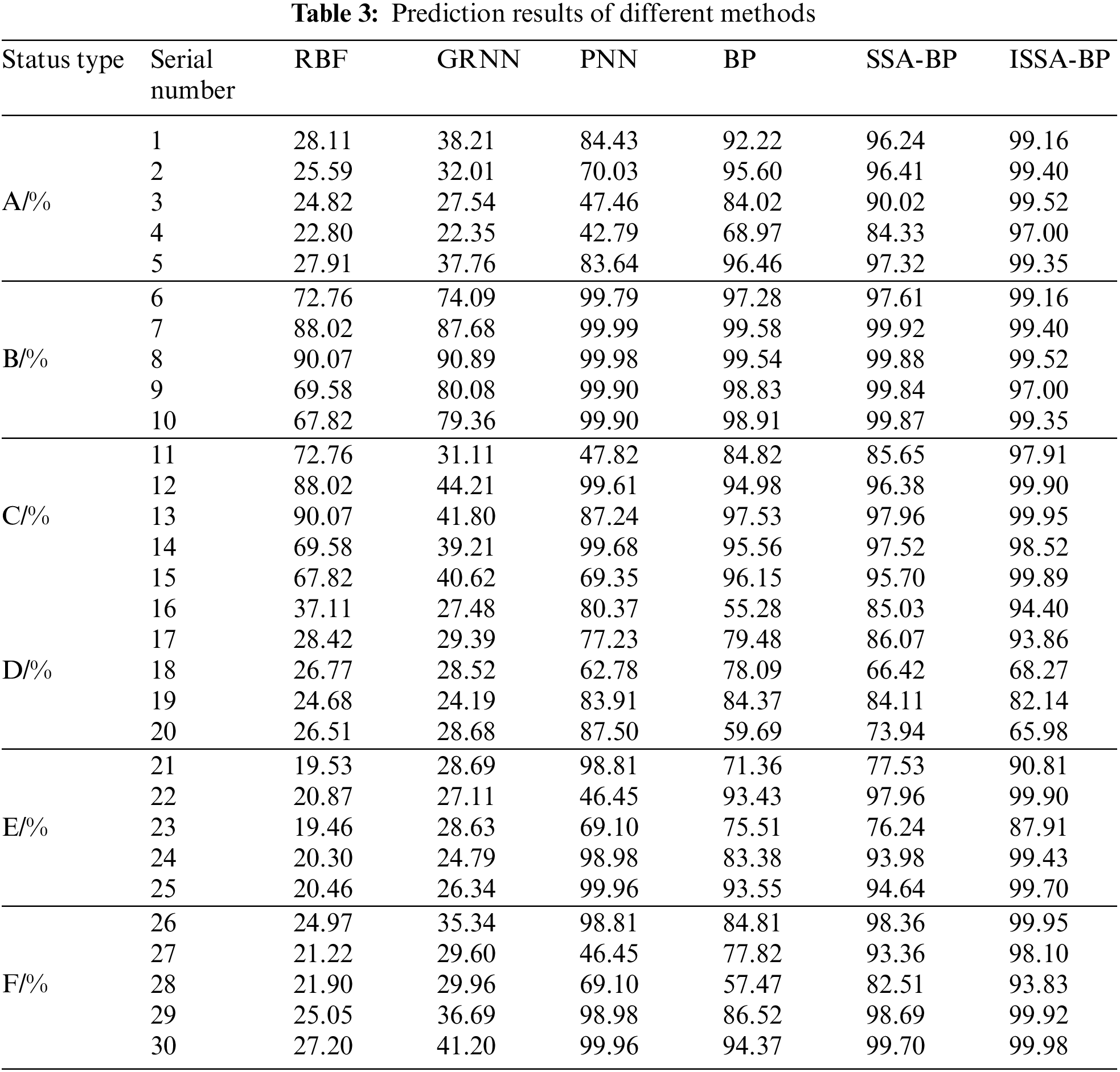
In order to test the effectiveness of ISSA optimized BP neural network, the proposed hybrid model was combined with basic a BP neural network model, SSA optimized BP neural network, Radial Basis Function neural network (RBF), Product-based Neural Network (PNN) and Generalized Regression Neural Network (GRNN) was compared. Table 3 shows the prediction results of different methods. Numbers 1–5 in the table correspond to “A-Normal state of equipment”, numbers 6–10 correspond to “B-motor voltage decreases”, numbers 11–15 correspond to “C-motor voltage rises”, numbers 16–20 correspond to “D-Energy storage spring is stuck”, numbers 21–25 correspond to “E-transmission gear is stuck”, numbers 25–30 correspond to “F-energy storage spring is not locked”. The mean probabilities of traditional BP for A-F are 87.45%, 98.83%, 93.81%, 71.38%, 83.45%, and 80.20%; the mean probabilities of SSA-BP for A-F are 92.86%, 99.42%, 94.64%, 79.11%, 88.07 %, and 94.52%.; the mean probability values of ISSA-BP for A-F are 98.89%, 99.90%, 99.23%, 80.93%, 95.55%, and 98.36%. Compared with other neural networks, ISSA-BP has a higher fault diagnosis accuracy rate, which verifies the algorithm’s effectiveness. Based on ISSA-BP, it can effectively distinguish between normal status and each fault.

5  Conclusion

This paper aims to achieve a non-invasive fault diagnosis of the spring operating mechanism of an LVCB by applying the Improved Sparrow Search Algorithm (ISSA) to optimize the BPNN. Taking the 1.5kV/4000A/75kA vacuum circuit breaker as an example, the motor current signal is collected during the energy storage process of the energy storage spring. The characteristics of the current signal are extracted based on empirical wavelet decomposition. ISSA is used to optimize the BPNN and find the optimal initial weights and thresholds, which speeds up the training rate of the BPNN and the accuracy of fault diagnosis. Research shows that the method proposed in this article can effectively identify energy storage motor overvoltage, energy storage motor Undervoltage, transmission gear stuck, energy storage spring stuck, and energy storage unlatched faults. The model’s recognition accuracy for energy storage spring stuck reaches more than 80%, and its recognition accuracy for other states reaches more than 95.55%. It can effectively identify faults in the energy storage unit of LVCB. The research results provide new ideas for the field of LVCB fault diagnosis and have broad application prospects. Based on our research, the diagnostic accuracy of energy storage spring stuck faults is lower than that of other faults. The energy storage spring stuck is a weak fault. A more efficient weak-fault feature extraction method will help future research. As the number of operations of the circuit breaker operating mechanism increases, wear and tear will cause insufficient lubrication of the mechanism or a weak energy storage spring. It may affect the characteristic curve of the circuit breaker operating mechanism, reducing the reliability of the model data training set. Therefore, studying a more reliable training set generation method is also a future work.

Acknowledgement: None.

Funding Statement: This research was funded by Sichuan Science and Technology Program (2023YFSY0013).

Author Contributions: Conceptualization, methodology, software: Tengfei Li; validation, formal analysis: Wenhui Zhang; data curation, visualization: Ke Mi; investigation: Qingming Lin; writing—original draft preparation: Shuangwei Zhao; writing—review and editing: Jiayi Song. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets and stimuli of this study are available upon reasonable request from the corresponding author.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Liu, L., Wang, B., Yang, L., Huang, Y. (2023). Early detection of health condition degradation of circuit breaker based on electrical quantity monitoring. Energies, 16(14), 5581. https://doi.org/10.3390/en16145581 [Google Scholar] [CrossRef]

2. Yang, Q., Hao, F. (2023). Deep auto-encoder network for mechanical fault diagnosis of high-voltage circuit breaker operating mechanism. Paladyn, 14(1), 20220096. https://doi.org/10.1515/pjbr-2022-0096 [Google Scholar] [CrossRef]

3. Janssen, A., Makareinis, D., Solver, C. E. (2014). International surveys on circuit-breaker reliability data for substation and system studies. IEEE Transactions on Power Delivery, 29(2), 808–214. https://doi.org/10.1109/TPWRD.2013.2274750 [Google Scholar] [CrossRef]

4. Li, X. F., Wu, S. J., Li, X. Y., Yuan, H., Zhao, D. (2020). Particle swarm optimization-support vector machine model for machinery fault diagnoses in high-voltage circuit breakers. Chinese Journal of Mechanical Engineering, 33(1), 104–113. https://doi.org/10.1186/s10033-019-0428-5 [Google Scholar] [CrossRef]

5. Zhang, D. (2002). Vehicle-fault diagnosis expert system based on integration of case-based and rule-based reasoning. Chinese Journal of Mechanical Engineering, 38(7), 91–95. [Google Scholar]

6. Yang, Z. L., Wang, B., Dong, X. H., Liu, H. (2012). Expert system of fault diagnosis for gear box in wind turbine. Systems Engineering Procedia, 4, 189–195. [Google Scholar]

7. Huang, Y. C. (2002). Abductive reasoning network based diagnosis system for fault section estimation in power systems. IEEE Transactions on Power Delivery, 17(2), 369–374. https://doi.org/10.1109/61.997901 [Google Scholar] [CrossRef]

8. Thukaram, D., Khincha, H. P., Vijaynarasimha, H. P. (2005). Artificial neural network and support vector machine approach for locating faults in radial distribution systems. IEEE Transactions on Power Delivery, 20(2), 710–721. https://doi.org/10.1109/TPWRD.2005.844307 [Google Scholar] [CrossRef]

9. Zhang, M., Wang, T., Tang, T., Benbouzid, M., Diallo, D. (2017). An imbalance fault detection method based on data normalization and EMD for marine current turbines. ISA Transactions, 68, 302–312. https://doi.org/10.1016/j.isatra.2017.02.011 [Google Scholar] [PubMed] [CrossRef]

10. Ao, H., Cheng, J., Zheng, J., Truong, T. K. (2015). Roller bearing fault diagnosis method based on chemical reaction optimization and support vector machine. Journal of Computing in Civil Engineering, 29(5), 4014077. https://doi.org/10.1061/(ASCE)CP.1943-5487.0000394 [Google Scholar] [CrossRef]

11. Ye, X., Yan, J., Wang, Y., Wang, J., Geng, Y. (2022). A novel U-Net and capsule network for few-shot high-voltage circuit breaker mechanical fault diagnosis. Measurement, 199, 111527. https://doi.org/10.1016/j.measurement.2022.111527 [Google Scholar] [CrossRef]

12. Yang, J., Zhang, G., Chen, B., Wang, Y. (2023). Vibration signal augmentation method for fault diagnosis of low-voltage circuit breaker based on W-CGAN. IEEE Transactions on Instrumentation and Measurement, 72, 1–11. https://doi.org/10.1109/TIM.2023.3240228 [Google Scholar] [CrossRef]

13. Sun, S., Sun, L., Wang, J., Gao, H. (2023). Fault diagnosis of conventional circuit breaker accessories based on grayscale image of current signal and improved ZFNet-DRN. IEEE Sensors Journal, 23(2), 1343–1356. https://doi.org/10.1109/JSEN.2022.3225189 [Google Scholar] [CrossRef]

14. Zhang, K., Chen, Z., Yang, L., Liang, Y. (2023). Principal component analysis (PCA) based sparrow search algorithm (SSA) for optimal learning vector quantized (LVQ) neural network for mechanical fault diagnosis of high voltage circuit breakers. Energy Reports, 9, 954–962. https://doi.org/10.1016/j.egyr.2022.11.118 [Google Scholar] [CrossRef]

15. Chmielewski, T., Oramus, P., Szewczyk, M., Kuczek, T., Piasecki, W. (2017). Circuit breaker models for simulations of short-circuit current breaking and slow-front overvoltages in HV systems. Electric Power Systems Research, 143, 174–181. https://doi.org/10.1016/j.epsr.2016.10.046 [Google Scholar] [CrossRef]

16. Huang, Y., Wang, J., Zhang, W., Al-Dweikat, M., Li, D. et al. (2013). A motor-drive-based operating mechanism for high-voltage circuit breaker. IEEE Transactions on Power Delivery, 28(4), 2602–2609. https://doi.org/10.1109/TPWRD.2013.2272741 [Google Scholar] [CrossRef]

17. Ji, T., Ye, X., Shi, M., Li, M., Wu, Q. H. (2020). Typical current modelling and feature extraction of high voltage circuit breaker towards condition analysis and fault diagnosis. IET Generation, Transmission & Distribution, 14(8), 1521–1527. https://doi.org/10.1049/iet-gtd.2018.5385 [Google Scholar] [CrossRef]

18. Huang, N., Chen, H., Cai, G., Fang, L., Wang, Y. (2016). Mechanical fault diagnosis of high voltage circuit breakers based on variational mode decomposition and multi-layer classifier. Sensors, 16(11), 1887. https://doi.org/10.3390/s16111887 [Google Scholar] [PubMed] [CrossRef]

19. Zhang, J., Wu, Y., Xu, Z., Din, Z., Chen, H. (2022). Fault diagnosis of high voltage circuit breaker based on multi-sensor information fusion with training weights. Measurement, 192, 110894. https://doi.org/10.1016/j.measurement.2022.110894 [Google Scholar] [CrossRef]

20. Wu, Y., Zhang, J., Yuan, Z., Chen, H. (2023). Fault diagnosis of medium voltage circuit breakers based on vibration signal envelope analysis. Sensors, 23(19), 8331. https://doi.org/10.3390/s23198331 [Google Scholar] [PubMed] [CrossRef]

21. Rudsari, F. N., Razi-Kazemi, A. A., Shoorehdeli, M. A. (2019). Fault analysis of high-voltage circuit breakers based on coil current and contact travel waveforms through modified SVM classifier. IEEE Transactions on Power Delivery, 34(4), 1608–1618. https://doi.org/10.1109/TPWRD.2019.2915110 [Google Scholar] [CrossRef]

22. Landry, M., Léonard, F., Landry, C., Beauchemin, R., Turcotte, O. et al. (2008). An improved vibration analysis algorithm as a diagnostic tool for detecting mechanical anomalies on power circuit breakers. IEEE Transactions on Power Delivery, 23(4), 1986–1994. https://doi.org/10.1109/TPWRD.2008.2002846 [Google Scholar] [CrossRef]

23. Wan, S., Dou, L., Liu, C., Wu, P., Liu, R. (2018). Study on on-line detection of characteristic parameters in high voltage circuit breaker opening process based on vibration signal. Electric Power Components and Systems, 46(18), 1969–1978. https://doi.org/10.1080/15325008.2018.1531328 [Google Scholar] [CrossRef]

24. Chen, L., Wan, S. (2021). Intelligent fault diagnosis of high-voltage circuit breakers using triangular global alignment kernel extreme learning machine. ISA Transactions, 109, 368–379. https://doi.org/10.1016/j.isatra.2020.10.018 [Google Scholar] [PubMed] [CrossRef]

25. Yang, Q., Ruan, J., Zhuang, Z., Huang, D. (2020). Fault identification for circuit breakers based on vibration measurements. IEEE Transactions on Instrumentation and Measurement, 69(7), 4154–4164. https://doi.org/10.1109/TIM.2019.2946470 [Google Scholar] [CrossRef]

26. Liu, X., Zhang, Y., Zhang, Q. (2022). Comparison of EEMD-ARIMA, EEMD-BP and EEMD-SVM algorithms for predicting the hourly urban water consumption. Journal of Hydroinformatics, 24(3), 535–558. https://doi.org/10.2166/hydro.2022.146 [Google Scholar] [CrossRef]

27. Chen, H., Kang, J., Chen, Y., Xu, D., Hu, Y. (2017). An improved time-frequency analysis method for hydrocarbon detection based on EWT and SET. Energies, 10(8), 1090. https://doi.org/10.3390/en10081090 [Google Scholar] [CrossRef]

28. Dai, Z., Shi, K., Zhu, Y., Zhang, X., Luo, Y. (2023). Intelligent prediction of transformer loss for low voltage recovery in distribution network with unbalanced load. Energies, 16(11), 4432. https://doi.org/10.3390/en16114432 [Google Scholar] [CrossRef]

29. Hopfield, J. J. (1988). Artificial neural networks. IEEE Circuits and Devices Magazine, 4(5), 3–10. [Google Scholar]

30. Xue, J., Shen, B. (2020). A novel swarm intelligence optimization approach: Sparrow search algorithm. Systems Science & Control Engineering, 8(1), 22–34. https://doi.org/10.1080/21642583.2019.1708830 [Google Scholar] [CrossRef]