Intelligent Power Grid Load Transferring Based on Safe Action-Correction Reinforcement Learning

1  Introduction

Power grids, especially distribution networks, are usually designed with different operating modes. In contrast to section switches, standby interconnection switches are normally turned on for emergency reserve transfer. When a line failure occurs, power load transfer must be conducted to cut off faulty equipment and restore the downstream power supply as soon as possible [1]. Enhancing the operating speed of load transfer is significant because it will reduce economic losses during power failure.

With the development of novel power systems, distribution networks have received an increasing amount of renewable power generation for the global carbon goal. Keeping the power balance becomes more difficult since the reduced capacities of conventional power units will not be able to support the power fluctuations of renewable power sources. In order to achieve a higher response speed of power balancing, the characteristics of load demands have been greatly changed considering demand side management. As a result, the difficulty of load transfer increases due to the changes in load demands. Moreover, the topology of distribution networks becomes more complex as the number of electricity consumers rises, increasing the difficulty of distribution network reconfiguration. Hence, the problem remains to develop advanced load transfer methods considering high-dimensional, strong-nonlinear input states of power grids, which is the motivation of this study.

The major methods used to solve the problems of load transfer and power grid reconfiguration can be categorized as mathematical programming, heuristics, and reinforcement learning [2,3]. For mathematical programming, the non-convex nonlinear optimization of power grid load transfer is generally converted into a second-order cone programming (SOCP) model. In reference [4], a robust optimization method is proposed for distribution network reconfiguration with wind power. In reference [5], the active and reactive power coordinated optimization is modeled as a mixed-integer SOCP problem. A reliability assessment method is proposed in reference [6] for post-fault reconstructed distribution networks, and the assessment is conducted by solving a mixed-integer linear model. In reference [7], a stochastic optimization problem for power grid economic scheduling is solved by the SOCP model. These mathematical programming methods usually achieve satisfactory optimal results, but their computational loads increase greatly when the network size increases [8]. The computational load cost may be unaffordable in the case of a line failure. Considering the category of heuristic methods, various algorithms have been developed. In reference [9], a modified crow search algorithm is proposed for multi-objective distribution network reconfiguration. Discrete particle swarm optimization is proposed in reference [10] for a similar reconfiguration task. Moreover, a hybrid heuristic-genetic algorithm [11], a jellyfish search algorithm [12], rain-fall optimization [13], and other heuristic methods [14,15] have proven feasible for distribution network optimization. These methods seek a balance between optimal results and computation loads by changing their hyper-parameters. However, the generalization of heuristic algorithms cannot be guaranteed, and it is difficult and tedious to determine the best algorithm for a specific task among the many available heuristic algorithms. With the development of artificial intelligence technologies, reinforcement learning has been introduced to power grid optimization tasks. The training process of reinforcement learning models is complex but can be conducted offline. After training, the reinforcement learning model is capable of making real-time load transfer decisions for post-fault power grids. Hence, the reinforcement learning method shows an apparent advantage in response speed when solving load transfer problems. Moreover, an artificial intelligence model such as a neural network can conveniently receive multiple input features, indicating the merit of handling high-dimensional, strong-nonlinear input states of power grids.

Due to the advantages of reinforcement learning, many reinforcement-learning-based power grid load transfer and network reconfiguration methods have been developed. In reference [16], a deep Q-network (DQN) is adopted to control the status of tie-switches for network reconfiguration. The DQN model is verified to be feasible in reference [17] for self-sufficient distribution networks with renewable energy sources. In reference [18], a noisy net is proposed to improve the performance of DQN by reducing voltage deviation and network loss. Based on a limited dataset of distribution network operation, a batch-constrained reinforcement learning method is proposed in reference [19]. In reference [20], a sequential reinforcement learning framework with two sub-models is established for unbalanced optimal grid operation. In reference [21], the DQN method is combined with probabilistic power flow estimation for load transfer. A multi-agent reinforcement learning framework is developed in reference [22] for AC/DC hybrid network reconfiguration. The aforementioned methods have exhibited promising performance and high operating speed. However, the reinforcement learning agent cannot account for the constraints of optimization problems, which may threaten the safety of power grid operation. Additionally, it is difficult to design manual action regulations for the reinforcement learning agent. Therefore, safe reinforcement learning methods need further research.

In terms of power grid scheduling studies based on safe reinforcement learning, a soft actor–critic with constraint layers is developed in [23,24] for Volt-VAR control. In reference [25], a safety layer is adopted to predict constrained states for distribution network control. In reference [26], a constrained policy optimization algorithm is proposed for power grid operation. Unfortunately, there are few other related studies, and the safe models developed for specific tasks may not apply to all power grid scheduling tasks. The research gaps of current load transfer studies are summarized as follows:

•   Research studies are currently pursuing reinforcement-learning-based methods to solve load transfer problems, since these methods are efficient in handling high-dimensional power grid states. However, the risk remains of using reinforcement learning to control power system operations, because the nonlinear neural networks are black-boxes. It should be further researched on how to improve the safety of reinforcement-learning-based power grid load transfer methods.

•   Although some load transfer studies have been developed based on safe reinforcement learning technologies, the security domain of power system operating and the correction amount of load transfer actions are usually measured in data-driven manners. The physical knowledge of power systems needs to be mined to enhance the reliability of safe reinforcement learning.

•   How to design the objective functions of reinforcement learning agents is a major difficulty for power grid load transfer problems. A balance should be always sought between the security and economy of load transfer results. The computation speed is also an important indicator to ensure the timely elimination of power grid faults.

In order to fill the aforementioned research gaps, the major contributions of this study are summarized as follows:

1.    A safe reinforcement learning method is newly proposed for the real-time power grid load transfer task. The load transfer problem is solved using a deep deterministic policy gradient (DDPG) model in which the load-shedding amount and the tie-switch status are both involved in the action space. The actions can be adaptively corrected in the method to enhance the safety of the power system operating.

2.    A safe action-correction framework is established in the proposed safe reinforcement learning method. In the framework, a sensitivity analysis method is developed to compute the sensitivity coefficients based on line-node power ratio matrixes. The method involves physical knowledge of power systems as the guidance for action corrections.

3.    Comparative studies reveal that the proposed method offers a promising computation speed for load transfer, indicating that the method can decrease the economic loss of a post-fault power grid. Meanwhile, the safety constraints of power grid load transfer can be always satisfied in the proposed method.

2  Modeling of Power Grid Load Transfer

The purpose of load transfer is to restore power supply when a line failure occurs. The interconnection switches and grid topology can be adjusted under load transfer control. In this case, power grid load transfer is modeled as an optimization problem, where the objective is to reduce the power load loss and the number of switch operations. The objective function is formulated as follows:

minPi,she,Aj,swCload(∑i=1NnodePi,org−∑i=1NnodePi,res)+Csw(Nsw,op)(1)

where Cload and Csw are the costs of power load loss and switch operations, respectively, and the costs are usually formulated as second-order polynomial functions, Pi,org is the original power load from the ith node, Pi,res is the restored power load, Nnode is the number of load nodes, Nsw,op is the number of operated switches, and Pi,she and Aj,sw are the control actions, denoting the amount of load shedding and the on-off of a switch, respectively:

Pi,she=Pi,org−Pi,res;i∈[1,Nnode],Pi,res≤Pi,org(2)

Aj,sw∈{0,1};0≤j≤Nsw,op≤Nsw(3)

where Nsw is the total number of interconnection switches in the power grid.

During load transfer, the constraints of power grid operation must be satisfied. Generally, node voltage and line power flow cannot exceed defined limits. The limits are formulated as:

Ui,min≤Ui≤Ui,max(4)

−Pij,max≤Pij≤Pij,max(5)

minPi,she,Aj,swCload(∑i=1NnodePi,org−∑i=1NnodePi,res)+Csw(Nsw,op)s.t.{Pi,she=Pi,org−Pi,resAj,sw∈{0,1}Ui,min≤Ui≤Ui,max−Pij,max≤Pij≤Pij,max(6)

According to the aforementioned optimization problem, the action space of load shedding amount is continuous and the space of tie-switch operations is discrete. A mixed integer programming method is needed for load transfer. The problem is also high-dimensional and strong-nonlinear since the number of network nodes is large and the computation of power loads is nonlinear. Therefore, this paper proposes a novel safe reinforcement learning method to enhance the computation speed of solving the load transfer problem. The principles and algorithms of the proposed method will be introduced in the following section.

3  Safe Action-Correction Reinforcement Learning Method

A key requirement of load transfer is a good computational rate of model solving, which affects the loss level of power line failure. Motivated by this, a reinforcement learning method is developed for quick and intelligent load transfer control. Considering that the reinforcement learning method cannot ensure safety constraints are satisfied, this study proposes an improved action-correction method for safe control. The algorithms are detailed in this section.

3.1 Load Transfer Agent Based on Reinforcement Learning

The core of reinforcement learning is to train an intelligent agent to choose actions according to the observed system states and reward rules. The agent proposed for power grid load transfer is presented in Fig. 1.

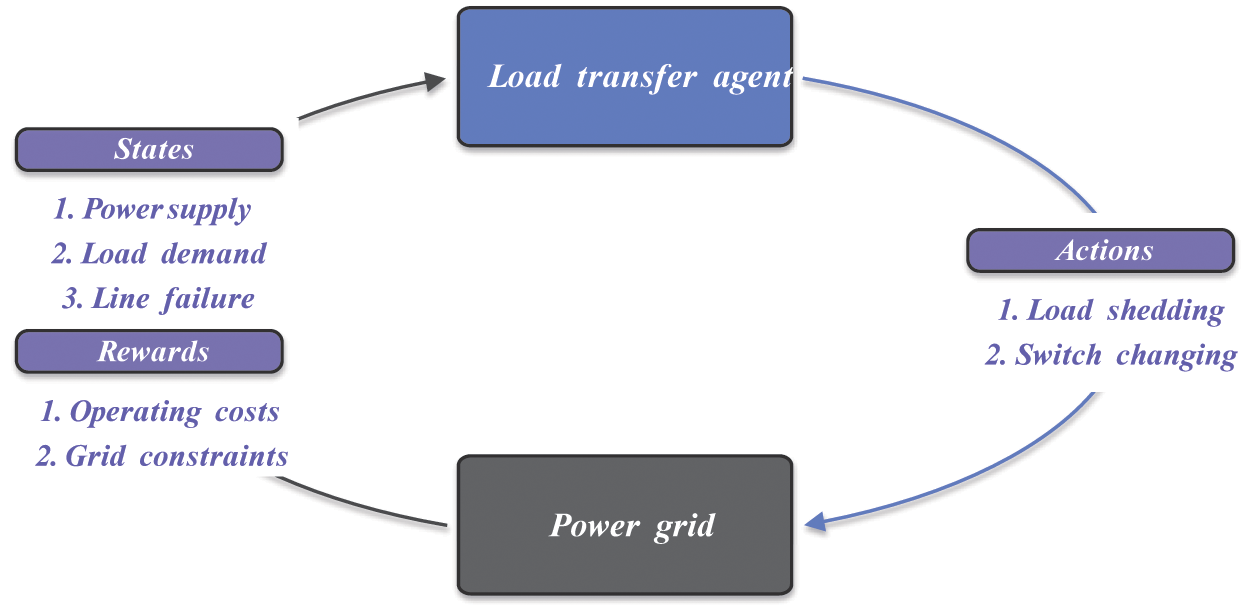
Figure 1: The intelligent agent for power grid load transfer

a) Actions

The actions of the agent include the load shedding amount and the on-off of switches, formulated as follows:

A={Pi,she,Aj,sw}(7)

where A is the action space of the agent, and Pi,she and Aj,sw are defined according to Eqs. (2) and (3), respectively. Specifically, the load-shedding amount is a continuous action, and the on-off of switches is a discrete action.

b) States

The real-time power grid states are the major inputs of the agent. When line failure occurs, the index of the faulty line should be provided. Thus, one-hot encoding is adopted for the state input of line failure, as follows:

Slf=[010⋯0]∈N1×Nline(8)

where Slf is the state input of line failure, and Nline is the total number of line branches in the power grid. A line is faulty if s=1(s∈Slf); otherwise, the line is operating normally. The original load demand Pi,org and power supply Gi,org of each node are also indispensable states for power flow computation. Therefore, the state space is defined as follows:

S=[Slf,Pi,org,Gi,org],i∈[1,Nnode](9)

c) Rewards

An agent prefers actions with higher rewards. Therefore, the reward function of load transfer is modified based on the objective defined in Eq. (1), as follows:

Rcost=1Cload(∑i=1NnodePi,org−∑i=1NnodePi,res)+Csw(Nsw,op)+ε(10)

where a higher reward Rcost can be achieved with lower operating costs, and ε is a very small value that prevents the function from being divided by zero. Moreover, a penalty is added to the reward function to punish the agent for breaking the constraints or failing to converge. The total reward is formulated as:

R=Rcost+Rpen(11)

where Rpen is a negative penalty term whose absolute value is larger than the maximum Rcost in training samples. Based on the previously defined action (A), state (S), and reward (R) functions, the intelligent agent can be established using reinforcement learning. Since the action space is continuous due to the load-shedding amount, the DDPG is adopted as the core agent model.

However, there is another difficulty in conventional reinforcement learning. Although the agent is unlikely to break the constraints due to the penalty term in Eq. (11), the punishment-based method cannot ensure that those constraints are always obeyed, so unsafe power grid operation may occur. To solve this problem, the safe action-correction method is proposed in this study.

3.2 Deep Deterministic Policy Gradient (DDPG)

The DDPG model is developed based on a deterministic policy gradient and actor-critic methods [27]. The deterministic policy gradient aims to train the agent model according to the gradient ascent direction of policy-value functions. The method is defined as:

∇θJ(πθ)=Es∼ρπ[∇θπθ(s)∇aQπ(s,a)|a=πθ(s)](12)

where θ is the set of trainable parameters in the agent, J is the accumulated reward, πθ is the policy function, s is the state, ρπ is the sampling space of states, Q is the action-value function, and a is the action. Based on the deterministic policy gradient method, DDPG builds an actor model to choose the deterministic policy and a critic model to evaluate the action-value function. Moreover, the actor and critic both have two copies in DDPG, namely the main and target models. The two model copies can update their trainable parameters asynchronously. The architecture of DDPG is shown in Fig. 2. The variables of action (a), state (s), and reward (r) in the architecture are defined as A, S, and R according to Eqs. (7)–(11).

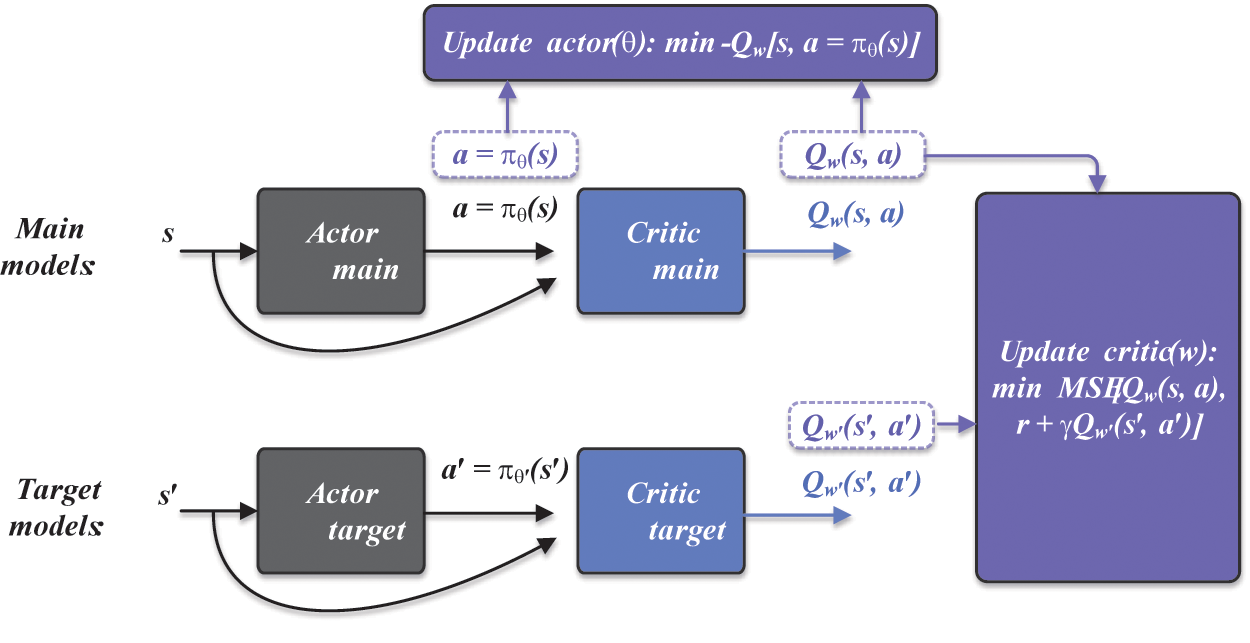
Figure 2: Architecture of the deep deterministic policy gradient (DDPG)

Based on the architecture, the actor determines the deterministic policy based on the state input, formulated as:

a=πθ(s)=MActor(s)(13)

where MActor is the main actor model and θ is its trainable parameter set. Based on the state input, the critic evaluates the value of the actor output, formulated as:

Qw(s,a)=MCritic(s,a)(14)

maxθ=Qw[s,a=πθ(s)](15)

The main critic parameters are solved by minimizing the evaluation error of action-value functions between the main and target models. This minimization objective is defined as:

minw=‖Qw(s,a)−(r+γQw′(s′,a′))‖22(16)

where s′ and a′ are the state and action for the target model, w and w′ are the parameters of the main and target models, respectively, r is the reward calculated based on Eq. (11), and γ is the constant for discounted rewards. Hence, the training of main models in DDPG can be conducted. For target models, the parameters are updated progressively under the following equations:

{θ′=τθ+(1−τ)θ′w′=τw+(1−τ)w′(17)

where 0<τ<1 is a weighting constant.

Based on the DDPG core models, an action-correction method is proposed to enhance the safety of power grid load transfer. The structure of the method is detailed in the following subsection.

3.3 Safe Action-Correction Based on Power System Sensitivity Analysis

According to the original DDPG-based load transfer method, the safety constraints cannot be guaranteed by using only a penalty reward on the agent. Compulsory measures must be developed to correct agent actions. Generally, line overload is the major threat during load transfer due to the line power flow limit, and load shedding is effective in handling the overload problem. It is also difficult to precisely measure the security domain of line overload. In this study, a safe action-correction method is proposed since the load-shedding amount Pi,she is one of the actions in the DDPG model. Moreover, the load shedding amount is measured under a sensitivity analysis method. The structure of the safe action-correction method is presented in Fig. 3. The procedures are as follows:

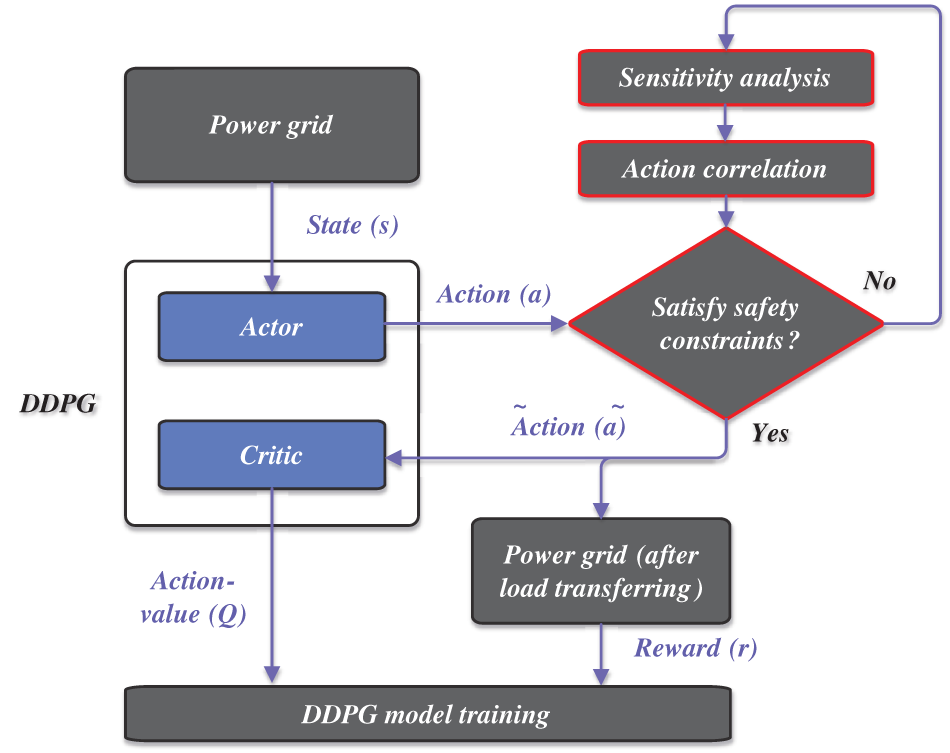
Figure 3: Structure of the proposed safe action-correction method

First, when a line failure occurs, states (s = S) of the power grid according to Eq. (9) are imported to the DDPG, and the original actions (a = A) according to Eq. (7) are computed under the actor model in DDPG.

Second, based on the original actions (a), the load transfer and power flow results are simulated to evaluate the safety constraints according to Eqs. (4) and (5).

Third, if the safety constraints cannot be satisfied, the actions are corrected using sensitivity analysis. The sensitivity analysis is conducted based on a line-node power ratio, formulated as [28]:

δk−i=λk−iUk,lineUi,node(cos⁡φk,linecos⁡φi,node+sin⁡φk,linesin⁡φi,node)(18)

where δk−i is the sensitivity coefficient between the kth branch line and ith node, Uk,line and φk,line are the voltage drop modulus and phase angle of the line head of the kth branch, respectively, Ui,node and φi,node are the voltage modulus and phase angle of the ith node, respectively, and λk−i is the line-node power ratio defined by:

λk−i∈Mλ=YlineAnodeTYnode−1∈RNline×Nnode(19)

where Mλ is the ratio matrix with a size of Nline lines and Nnode nodes, Yline is the line admittance matrix, Ynode is the node admittance matrix, and Anode is the node incidence matrix.

Fourth, based on the analysis results λk−i∈Mλ and the overload line, the node most sensitive to shed load demand is identified. Since the load shedding amount is the DDPG action, the action correction is formulated as:

P~i,she=Pi,she+αPi,org;P~i,she∈A,P~i,she≥Pi,she(20)

where A is the action space, P~i,she is the corrected action, and α is the shedding coefficient. A smaller value of α denotes a more precise correction, which will require a longer operating time.

Afterward, the sensitivity analysis and action correction can be repeated until the safety constraints in Eqs. (4) and (5) are satisfied. The corrected actions (a~) are thus obtained.

Finally, the corrected actions are used to update the DDPG parameters according to Eqs. (15) and (16). Specifically, the load-shedding amount during safe action correction will receive a larger punishment, modifying the reward function in Eq. (11) to the following form:

R~=12Cload(∑i=1NnodeP~i,she)−Cload(∑i=1NnodePi,she)+Csw(Nsw,op)+ε+Rpen(21)

where Pi,she is the original action from DDPG, and P~i,she is the corrected amount. Accordingly, the cost of load shedding from action correction is higher than that from the DDPG actor, preventing DDPG from frequently breaking the safety constraints. Moreover, since the constraints can always be satisfied after the proposed correction method, the penalty term Rpen is merely used to evaluate whether the load transfer has successfully converged.

As previously mentioned, conditional judgment can always ensure the constraints during DDPG-based load transfer, thus enhancing the safety of power grid operation. The proposed method is verified through comparative studies in the following section.

4  Results and Discussion

Experiments are conducted based on a distribution network case modified from the IEEE 33-bus system. The topology of the network is presented in Fig. 4 according to [29]. The power supply is provided on bus 1. The hourly solar photovoltaic forecasts and electricity load demand forecasts are both sampled from the real-world ISO-New dataset [30], and are then normalized to fit the unit values in the IEEE 33-bus case. Based on the dataset, real-time power grid load transfer is operated under one-hour intervals. The distribution networks contain five tie-switches for backup. The switches are normally off but can be turned on for load transfer under emergency conditions. The parameter configurations of experiments are determined as follows: the cost functions are Cload(P)=22×P2(p.u.) and Csw(N)=3×N2, the penalty term is Rpen=−5 for breaking safety constraints and Rpen=−10 for failing to converge, the weighting constant for DDPG training is τ=0.1, the load shedding coefficient of action-correction is α=0.02, and the discounted reward constant is γ=0.9. Under these configurations, the proposed load transfer agent is trained based on the real-world load dataset, where the line failure randomly occurs at one of the 32 branches, except for branches 1–2.

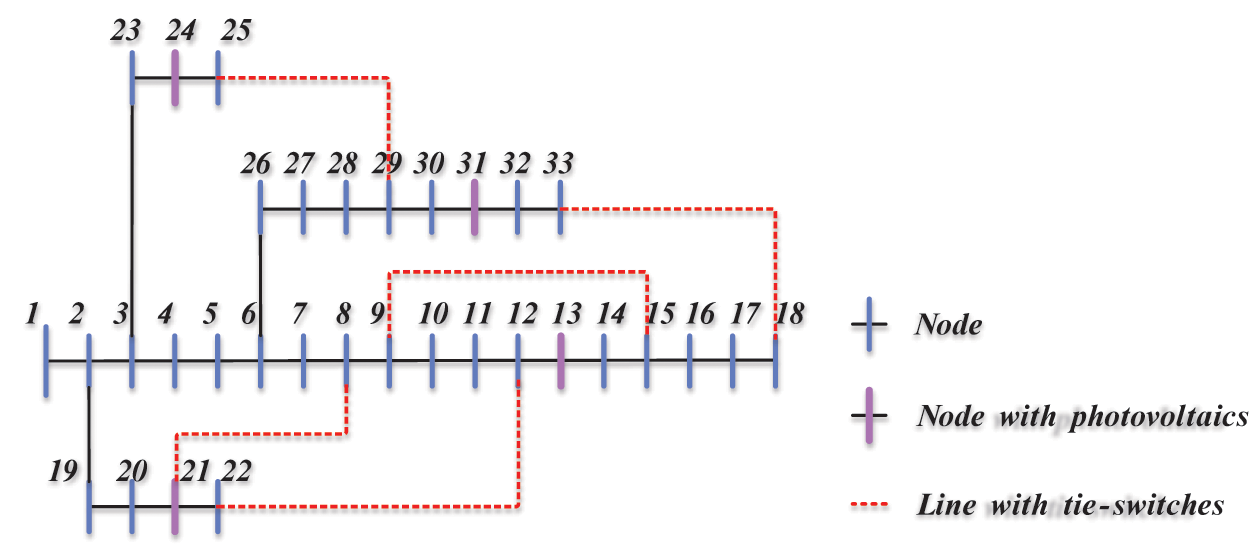
Figure 4: Topology of the IEEE 33-bus distribution network

4.1 Comparative Results

The proposed safe action correction is verified by comparison with two benchmark methods, including a genetic algorithm, which is a heuristic method, and a reinforcement learning agent without safe action correction. The two benchmarks both involve penalty terms to handle safety constraints. In Table 1, the results of actions and rewards for different methods are compared. The reward is computed using the function in Eq. (10) under several experimental trials. According to the comparisons of actions and rewards, the three methods have similar load-shedding ratios and total rewards. However, the genetic algorithm operates tie-switches more frequently compared with the two DDPG-based methods, usually performing 4 or 5 switch actions. As a result, the genetic algorithm obtains the lowest total reward (8.20 × 10−4) and is inferior to DDPG in this study. The comparison of rewards between the genetic algorithm and the proposed DDPG method is presented in Fig. 5. The distributions of rewards match the numerical results in Table 1, indicating that the proposed DDPG outperforms the genetic algorithm during load transfer due to higher rewards.

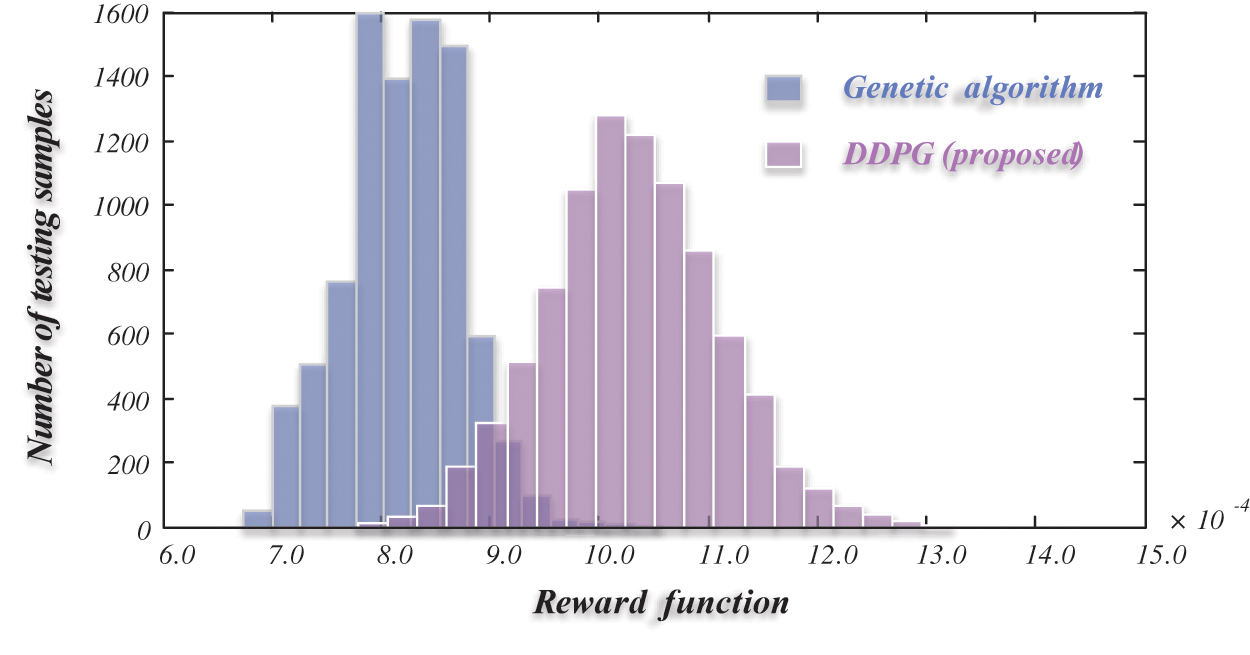
Figure 5: Comparison of rewards between the genetic algorithm and the proposed DDPG method

From the comparisons of actions and rewards, the DDPG methods with and without safe action correction achieve similar results, with both outperforming the genetic algorithm. Furthermore, the safety of each method is evaluated, and the results are shown in Table 2. Three metrics are adopted, including connecting the topology, converging successfully, and satisfying the safety constraints. Connecting the topology means that the tie-switches operate well and there is no isolated node in the distribution network with one line failure. Converging successfully indicates that the computation of load transfer has converged without fully considering the constraints. Satisfying the safety constraints requires that the agents do not break any constraints. On the testing samples, the two DDPG methods always connect the topology and converge successfully. However, the genetic algorithm merely achieves a 95.45% ratio in connecting the topology and a 92.50% ratio in converging successfully. The DDPG without action-correction can usually satisfy the safety constraints with a high probability of 98.13%, but the proposed method of DDPG with action-correction improves the probability to 100%, showing that the proposed method can always ensure the safety constraints are satisfied with just a slight decrease in rewards.

The computation times of the three methods are recorded and compared, and the results are shown in Table 3. The genetic algorithm requires large computation loads because it takes an average time of 587.24 s for the algorithm to solve each load transfer scenario. The DDPG method without safe action-correction takes an average of 0.18 s for power grid load transfer using a well-trained agent, which is the shortest computation time. Compared with the conventional DDPG method, the proposed method requires a longer decision-making time due to the loop of action-correction. However, the proposed method’s total decision-making time is still considerably shorter than that of the genetic algorithm. In fact, the proposed method is fast enough for the real-time load transfer applications of distribution networks.

4.2 Performance of the Proposed Method

The aforementioned study results indicate the superiority of the proposed method compared with benchmark methods. Therefore, the performance of the proposed method is tested on a detailed operating scenario. The net loads considering distributed photovoltaics in the scenario are provided in Fig. 6. The line failure occurs on the 29th branch between bus #29 and #30. In this case, the load transfer agent turns three tie-switches on, connecting the branches 25–29, 33–18, and 9–15. Due to overload, load shedding is conducted as shown in Fig. 6b. Buses #24, #25, and #30 decrease load demands to meet the safety constraints using the proposed method.

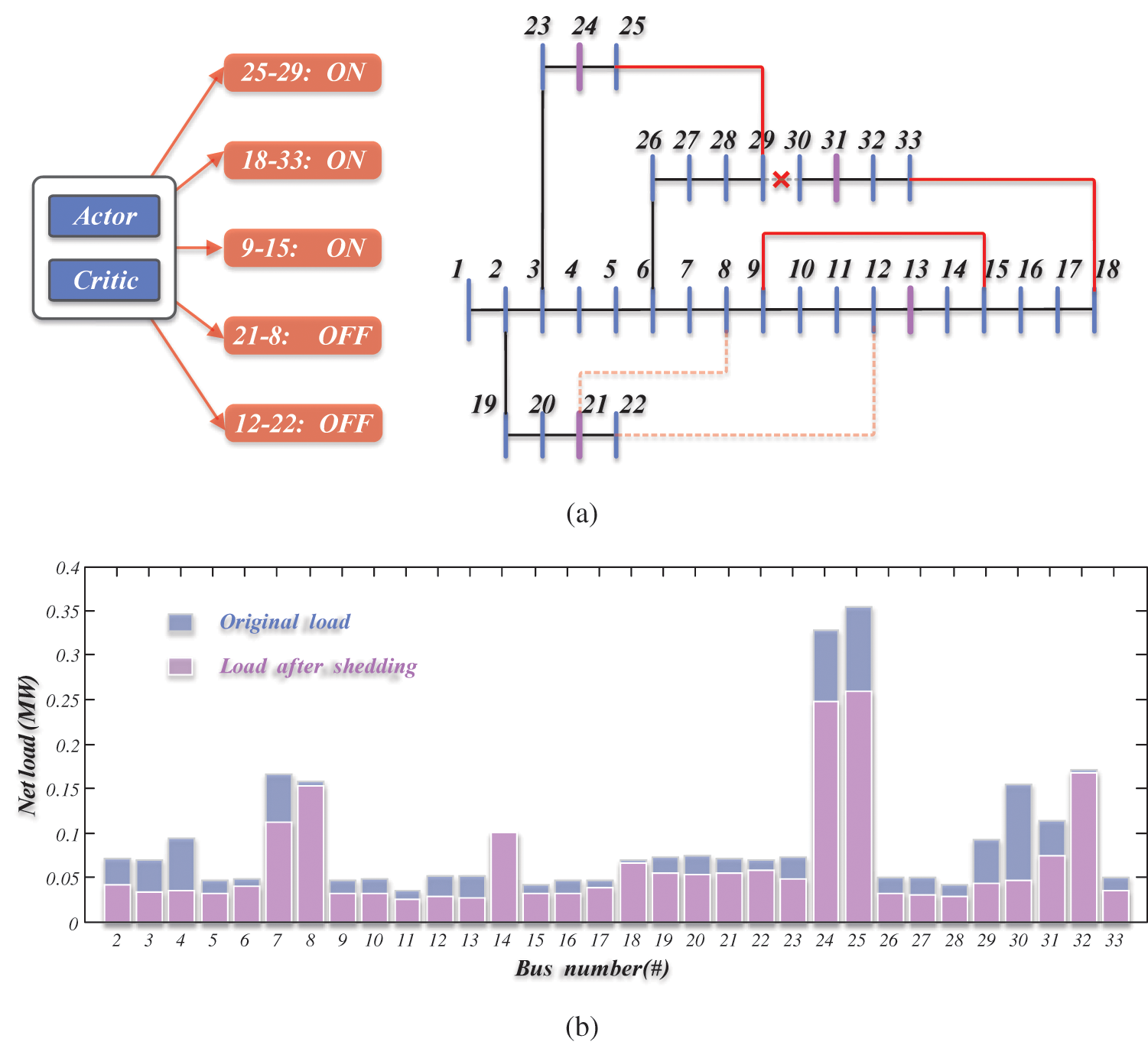
Figure 6: Intelligent load transfer results based on the proposed method. (a) Actions of tie-switches. (b) Actions of load shedding

4.3 Repetitive Experiments and Discussion

In addition to the case of the IEEE 33-bus system, cases of a 69-bus distribution system [31] and a 141-bus distribution system [32] are adopted for further comparative experiments between the conventional reinforcement learning method and the proposed safe action-correction method. Specifically, the 69-bus system is modified by adding tie-switches 11–43, 13–20, 15–46, 27–65, and 50–59. The 141-bus system is modified by adding tie-switches 5–86, 20–130, 32–82, 52–80, 59–66, 71–86, 94–104, 98–125, and 100–109. Since the training process of the reinforcement learning methods contains randomness, experiments are repeated ten times for all three distribution network cases. The experimental results are presented in Table 4.

The experimental results show that the probability of conventional DDPG satisfying the safety constraints drops slightly as the scale of the distribution system increases. The fluctuation of conventional DDPG solutions also rises according to the standard deviations of probabilities, since the training process becomes more complex with more network nodes. In contrast, the proposed method can always satisfy the safety constraints in the three system cases and the ten repetitive trials. According to all the experiments conducted in this study, the strengths and weaknesses of different reinforcement learning methods are summarized as follows:

•   Conventional reinforcement learning methods with penalty terms: The advantages of these methods are the convenient training process and the high decision-making speed, as indicated in Table 3. However, the weighting coefficients of rewards are difficult to configure. An unreasonable reward function may reduce the probability of satisfying the safety constraints.

•   The proposed safe action-correction reinforcement learning method: The merit of the proposed method is that the method can always ensure the safety constraints are satisfied based on manual action-corrections. However, the method is weak in computational speed due to the loop operations of discriminating constraints and correcting actions.

5  Conclusion

The real-time power grid load transfer task adjusts the ties-switches and the network topology during line failure to ensure stable power supplies. A high computation speed is required to minimize the net load loss. With the rapid development of artificial intelligence, reinforcement learning methods have been applied to load transfer, especially in distribution networks. Although reinforcement learning methods show satisfactory computation speed, these methods cannot ensure constraints are satisfied when solving optimization problems. This shortcoming of reinforcement learning increases the security risk of power grid operation.

In order to solve the shortcoming, this study proposes a safe action-correction method to improve the DDPG-based load transfer agents. The method is based on network sensitivity analysis and can modify the load shedding amount to always ensure the safe operation of power grids. The comparative results indicate that the proposed method outperforms the benchmark methods in handling safety constraints. The reward function and the computation time receive merely little degeneration compared with the conventional DDPG method.

Acknowledgement: The authors are grateful to the editors and reviewers’ great help on this paper. The authors also thank State Grid Jiangsu Corporation of China for the project funding.

Funding Statement: This work was supported by the Incubation Project of State Grid Jiangsu Corporation of China “Construction and Application of Intelligent Load Transferring Platform for Active Distribution Networks” (JF2023031).

Author Contributions: The authors confirm contribution to the paper as follows: draft manuscript preparation: Fuju Zhou; analysis and interpretation of results: Li Li and Tengfei Jia; data collection: Yongchang Yin, Aixiang Shi and Shengrong Xu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The availability of data and materials is cited in references.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Sobhani, M., Wang, P., Hong, T. (2023). Detecting load transfers. IEEE Transactions on Smart Grid, 14(2), 1367–1375. [Google Scholar]

2. Kundacina, O. B., Vidovic, P. M., Petkovic, M. R. (2022). Solving dynamic distribution network reconfiguration using deep reinforcement learning. Electrical Engineering, 104(3), 1487–1501. [Google Scholar]

3. Moura, A., Salvadorinho, J., Soares, B., Cordeiro, J. (2021). Comparative study of distribution networks reconfiguration problem approaches. RAIRO-Operations Research, 55, S2083–S2124. [Google Scholar]

4. Cui, Z. W., Bai, X. Q., Li, P. J., Li, B., Cheng, J. et al. (2020). Optimal strategies for distribution network reconfiguration considering uncertain wind power. CSEE Journal of Power and Energy Systems, 6(3), 662–671. [Google Scholar]

5. Li, C., Dai, Y., Wang, P., Xia, S. W. (2023). Active and reactive power coordinated optimization of active distribution networks considering dynamic reconfiguration and SOP. IET Renewable Power Generation. https://doi.org/10.1049/rpg2.12814 [Google Scholar] [CrossRef]

6. Li, Z. H., Wu, W. C., Zhang, B. M., Tai, X. (2020). Analytical reliability assessment method for complex distribution networks considering post-fault network reconfiguration. IEEE Transactions on Power System, 35(2), 1457–1467. [Google Scholar]

7. Sun, W. Q., Qiao, Y. K., Liu, W. (2022). Economic scheduling of mobile energy storage in distribution networks based on equivalent reconfiguration method. Sustainable Energy, Grids and Networks, 32, 100879. [Google Scholar]

8. Zhang, Y., Qian, T., Tang, W. H. (2022). Buildings-to-distribution-network integration considering power transformer loading capability and distribution network reconfiguration. Energy, 244, 123104. [Google Scholar]

9. Razavi, S. M., Momeni, H. R., Haghifam, M. R., Bolouki, S. (2022). Multi-objective optimization of distribution networks via daily reconfiguration. IEEE Transactions on Power Delivery, 37(2), 775–785. [Google Scholar]

10. Behbahani, M. R. P., Jalilian, A., Amini, M. (2020). Reconfiguration of distribution network using discrete particle swarm optimization to reduce voltage fluctuations. International Transactions on Electrical Energy Systems, 30(9), e12501. [Google Scholar]

11. Jakus, D., Cadenovic, R., Vasilj, J., Sarajcev, P. (2020). Optimal reconfiguration of distribution networks using hybrid heuristic-genetic algorithm. Energies, 13(7), 1544. [Google Scholar]

12. Shaheen, A., El-Sehiemy, R., Kamel, S., Selim, A. (2022). Optimal operational reliability and reconfiguration of electrical distribution network based on jellyfish search algorithm. Energies, 15(19), 6994. [Google Scholar]

13. Arulprakasam, S., Muthusamy, S. (2022). Reconfiguration of distribution networks using rain-fall optimization with non-dominated sorting. Applied Soft Computing, 115, 108200. [Google Scholar]

14. Tu, N. W., Fan, Z. H. (2023). IMODBO for optimal dynamic reconfiguration in active distribution networks. Processes, 11(6), 1827. [Google Scholar]

15. Kim, H. W., Ahn, S. J., Yun, S. Y., Choi, J. H. (2023). Loop-based encoding and decoding algorithms for distribution network reconfiguration. IEEE Transactions on Power Delivery, 38(4), 2573–2584. [Google Scholar]

16. Bui, V. H., Su, W. C. (2022). Real-time operation of distribution network: A deep reinforcement learning-based reconfiguration approach. Sustainable Energy Technologies and Assessments, 50, 101841. [Google Scholar]

17. Oh, S. H., Yoon, Y. T., Kim, S. W. (2020). Online reconfiguration scheme of self-sufficient distribution network based on a reinforcement learning approach. Applied Energy, 280, 115900. [Google Scholar]

18. Wang, B. B., Zhu, H., Xu, H. H., Bao, Y. Q., Di, H. F. (2021). Distribution network reconfiguration based on noisynet deep Q-learning network. IEEE Access, 9, 90358–90365. [Google Scholar]

19. Gao, Y. Q., Wang, W., Shi, J., Yu, N. P. (2020). Batch-constrained reinforcement learning for dynamic distribution network reconfiguration. IEEE Transactions on Smart Grid, 11(6), 5357–5369. [Google Scholar]

20. Yin, Z. Y., Wang, S. X., Zhao, Q. Y. (2023). Sequential reconfiguration of unbalanced distribution network with soft open points based on deep reinforcement learning. Journal of Modern Power Systems and Clean Energy, 11(1), 107–119. [Google Scholar]

21. Malekshah, S., Rasouli, A., Malekshah, Y., Ramezani, A., Malekshah, A. (2022). Reliability-driven distribution power network dynamic reconfiguration in presence of distributed generation by the deep reinforcement learning method. Alexandria Engineering Journal, 61(8), 6541–6556. [Google Scholar]

22. Wu, T., Wang, J. H., Lu, X. N., Du, Y. H. (2022). AC/DC hybrid distribution network reconfiguration with microgrid formation using multi-agent soft actor-critic. Applied Energy, 307, 118189. [Google Scholar]

23. Wang, W., Yu, N. P., Gao, Y. Q., Shi, J. (2020). Safe off-policy deep reinforcement learning algorithm for Volt-VAR control in power distribution systems. IEEE Transactions on Smart Grid, 11(4), 3008–3018. [Google Scholar]

24. Gao, Y. Q., Yu, N. P. (2022). Model-augmented safe reinforcement learning for Volt-VAR control in power distribution networks. Applied Energy, 313, 118762. [Google Scholar]

25. Kou, P., Liang, D. L., Wang, C., Wu, Z. H., Gao, L. (2020). Safe deep reinforcement learning-based constrained optimal control scheme for active distribution networks. Applied Energy, 264, 114772. [Google Scholar]

26. Li, H. P., He, H. B. (2022). Learning to operate distribution networks with safe deep reinforcement learning. IEEE Transactions on Smart Grid, 13(3), 1860–1872. [Google Scholar]

27. Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N. M. O., Erez, T. et al. (2015). Continuous control with deep reinforcement learning. International Conference on Learning Representations, San Diego, CA, USA. [Google Scholar]

28. Xu, Y., Zhi, J. (2015). A zone-divided emergency control strategy for overload lines based on power sensitivity. Transactions of China Electrotechnical Society, 30(15), 60–72. [Google Scholar]

29. Li, Y. Z., Hao, G. K., Liu, Y., Yu, Y. W., Ni, Z. X. et al. (2022). Many-objective distribution network reconfiguration via deep reinforcement learning assisted optimization algorithm. IEEE Transactions on Power Delivery, 37(3), 2230–2244. [Google Scholar]

30. Alhendi, A., Al-Sumaiti, A. S., Marzband, M., Kumar, R., Diab, A. A. Z. (2023). Short-term load and price forecasting using artificial neural network with enhanced Markov chain for ISO New England. Energy Reports, 9, 4799–4815. [Google Scholar]

31. Das, D. (2008). Optimal placement of capacitors in radial distribution system using a Fuzzy-GA method. International Journal of Electrical Power & Energy Systems, 30(6–7), 361–367. [Google Scholar]

32. Khodr, H. M., Olsina, F. G., de Oliveira-de Jesus, P. M., Yusta, J. M. (2008). Maximum savings approach for location and sizing of capacitors in distribution systems. Electric Power Systems Research, 78(7), 1192–1203. [Google Scholar]