 Open Access
Open Access
ARTICLE
Improved Unit Commitment with Accurate Dynamic Scenarios Clustering Based on Multi-Parametric Programming and Benders Decomposition
1 State Grid Corporation of China, Beijing, 100031, China
2 Central China Branch, State Grid Corporation of China, Wuhan, 430077, China
3 School of Electric and Electronic Engineering, Huazhong University of Science and Technology, Wuhan, 430074, China
4 China Electric Power Research Institute Co., Ltd., Beijing, 100192, China
* Corresponding Author: Mingyu Yan. Email:
Energy Engineering 2024, 121(6), 1557-1576. https://doi.org/10.32604/ee.2024.047401
Received 04 November 2023; Accepted 23 January 2024; Issue published 21 May 2024
Abstract
Stochastic unit commitment is one of the most powerful methods to address uncertainty. However, the existing scenario clustering technique for stochastic unit commitment cannot accurately select representative scenarios, which threatens the robustness of stochastic unit commitment and hinders its application. This paper provides a stochastic unit commitment with dynamic scenario clustering based on multi-parametric programming and Benders decomposition. The stochastic unit commitment is solved via the Benders decomposition, which decouples the primal problem into the master problem and two types of subproblems. In the master problem, the committed generator is determined, while the feasibility and optimality of generator output are checked in these two subproblems. Scenarios are dynamically clustered during the subproblem solution process through the multi-parametric programming with respect to the solution of the master problem. In other words, multiple scenarios are clustered into several representative scenarios after the subproblem is solved, and the Benders cut obtained by the representative scenario is generated for the master problem. Different from the conventional stochastic unit commitment, the proposed approach integrates scenario clustering into the Benders decomposition solution process. Such a clustering approach could accurately cluster representative scenarios that have impacts on the unit commitment. The proposed method is tested on a 6-bus system and the modified IEEE 118-bus system. Numerical results illustrate the effectiveness of the proposed method in clustering scenarios. Compared with the conventional clustering method, the proposed method can accurately select representative scenarios while mitigating computational burden, thus guaranteeing the robustness of unit commitment.Keywords
Nomenclature
| Indices and Sets | |
| i, j | Indices of gas nodes i and j |
| b | Indices of bus b |
| t | Index of the time period |
| Set of starting and ending buses of electric line l | |
| Parameters | |
| Minimum operation cost of generator i | |
| Probability of occurrence for scenario s | |
| Cost coefficient of generator i at segment q | |
| Cost coefficient of wind farm w | |
| Penalty factor for wind curtailment | |
| Forecast output of wind farm w at hour t in scenario s | |
| Capacity of line l | |
| Maximum output of generator i at segment q | |
| Minimum output of generator i | |
| The active power demand of load bus j at hour t in scenario s | |
| Elements of bus-branch and bus-generator matrices | |
| Elements of bus-wind farm and bus-generator matrices | |
| Up/down ramping limits of generator i | |
| Startup/shutdown ramping limits of generator i | |
| Startup/shutdown cost of generator i | |
| Minimum on/off time duration of generator i | |
| Initial on/off time of generator i | |
| Lagrangian multiplier used in the Benders decomposition | |
| An extremely small positive number | |
| Variables | |
| The active power output of generator i at hour t in scenario s | |
| The overall operation cost of the power system in scenario s | |
| Linear segment q for the active power output of generator i at hour t in scenario s | |
| Power flow of line l at hour t in scenario s | |
| Bus angle of bus b at hour t in scenario s | |
| State of generator i at hour t, 1 if on, otherwise 0 | |
| Startup/shutdown state of generator i at hour t, 1 if startup/shutdown, otherwise 0 | |
| Startup/shutdown cost of generator i at hour t | |
| Wind curtailment of wind farm w at hour t in scenario s | |
| Auxiliary variable | |
| Slack variables used in the Benders decomposition subproblem | |
| Constant matrix used in the compact form | |
| Constant matrix corresponding to active constraints | |
| Constant matrix corresponding to inactive constraints | |
| Constant matrix used in the compact form | |
| Set of binary and continuous variables used in the compact form | |
| Set of uncertain variables used in the compact form | |
Renewable energy is regarded as the silver bullet to replace conventional fossil energy and achieve carbon neutrality [1–3]. During the last decade, renewable energy has been rapidly developed [4–6]. However, the inherent intermittency and uncertainty of renewable energy bring significant operation challenges to the power system operator. How to accommodate the uncertain power output of renewable energy is recognized as a global problem.
The most popular method to address this challenge is the stochastic approach. In the stochastic approach, the uncertainty is described by multiple scenarios, and the stochastic programming obtains the optimal unit commitment considering these scenarios [7,8]. To simulate the uncertainty accurately, massive scenarios must be generated, which result in computational intractability [9]. The scenario clustering technique is thus proposed to mitigate the computational burden by reducing the scenarios [10]. More specifically, the scenario clustering technique aggregates similar scenarios into one scenario, which is known as a representative scenario. Accordingly, massive scenarios are converted into several representative scenarios. Stochastic programming only considers these representative scenarios rather than all scenarios [11]. The scalability of stochastic unit commitment is enhanced by using clustering techniques since fewer scenarios are considered.
The most famous clustering method is K-means, which clusters scenarios based on Euclidean distance [12]. The geographically-closed scenarios in algebraic space are clustered together as one representative scenario [13]. There are a lot of variant K-means methods like K-means++ and federated learning-based K-means [14–16]. The main problem with existing clustering techniques is that they cannot accurately select representative scenarios. This is because the power system schedule is highly nonlinear with respect to scenarios. More specifically, small changes in the scenarios could result in significant changes in the power system schedule [17]. Accordingly, the clustering technique should consider such highly nonlinear relationships between the power system schedule and input scenarios. Multi-parametric programming offers a powerful solution for reflecting the relationship between power system schedules and scenarios [18] and can thus be implemented in scenario clustering [19]. However, few studies focus on how to cluster scenarios using multi-parametric programming.
This paper provides the stochastic unit commitment with dynamic scenarios clustering based on multi-parametric programming. The major contributions of this paper as listed as follows:
1) The scenarios clustering method based on multi-parametric programming is proposed. Compared with conventional K-means or other unsupervised learning methods, the proposed clustering method adopts multi-parametric programming to specify critical regions and select representative scenarios considering the power system operation and network.
2) The dynamic clustering process consisting of multi-parametric programming and Benders decomposition for two-stage stochastic programming is provided. We innovatively embed the scenarios clustering process into the Benders decomposition solution process rather than the pre-solution stage. Therefore, the proposed dynamic clustering method can accurately reflect the impact of the scenario on the unit commitment schedule.
The rest of this paper is organized as follows: Section 2 introduces the mathematical formulation of the stochastic unit commitment based on Benders decomposition. Section 3 develops the proposed dynamic scenario clustering based on multi-parametric programming. Case studies are conducted in Section 4 to show the validity of the proposed method. Conclusion and further work are provided in Section 5.
2 Mathematical Formulation of Stochastic Unit Commitment
The two-stage stochastic unit commitment is adopted to accommodate the uncertain renewable energy. As shown in Fig. 1, the uncertain renewable energy is described using multiple scenarios. More specifically, each scenario represents one potential output. Since the number of scenarios is extremely large, scenarios are generally clustered into several representative scenarios. Stochastic unit commitment optimizes the state of unit commitment considering all representative scenarios. In the first stage, the unit commitment decision is determined to accommodate all scenarios. This decision should be robust enough since it cannot be changed at the second stage. In the second stage, the generator’s output is determined with respect to different scenarios under the unit commitment decision obtained in the first stage. The generator’s output could be different following different scenarios.
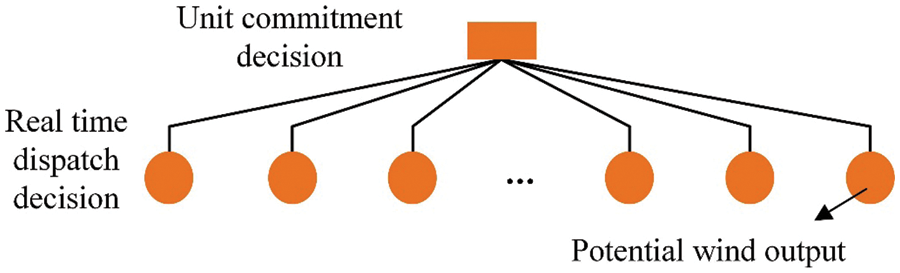
Figure 1: Framework of two-stage stochastic unit commitment
2.1 Stochastic Unit Commitment
The stochastic unit commitment mathematical formulation is shown as follows [20–22]:
Eqs. (1) and (2) represent the operation cost of unit commitment considering all possible representative scenarios. Owing to the well-known zero marginal cost characteristic of renewable energy, we set the operator cost of renewable energy as 0. Eqs. (3) and (4) enforce the generator’s output under each scenario. Eq. (5) represents power balance. Eq. (6) limits wind curtailment. Eq. (7) limits line flow. Eq. (8) enforces power flow using the DC power flow model [23,24]. Eqs. (9) and (10) represent the ramping limit of the generator. Eqs. (11) and (12) represent the startup/shutdown cost of the generator. Eqs. (13) and (14) limit the startup/shutdown state of the generator. Eqs. (15)–(17) enforce minimum on time, while Eqs. (18)–(20) enforce minimum off time.
The conventional stochastic unit commitment is generally solved via the Benders decomposition [25–27]. The Benders decomposition can decouple the primal stochastic unit commitment problem into the master problem and two subproblems. The master problem is the unit commitment problem, which determines the generator’s state. At the same time, two subproblems check the feasibility and optimality of the generator’s state, respectively. The flowchart of conventional Benders decomposition for stochastic unit commitment is shown in Fig. 2.
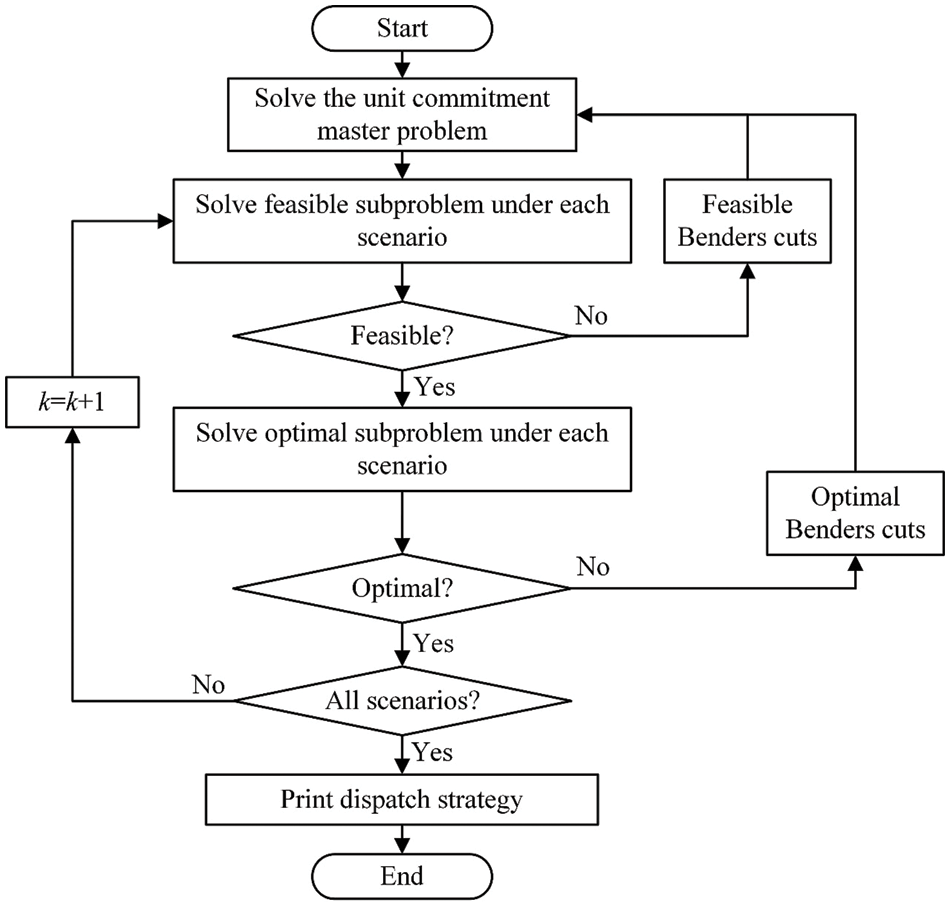
Figure 2: Flowchart of the conventional Benders decomposition for two-stage unit commitment
The master problem is listed as follows:
The feasible subproblem is applied to check whether the generator’s committed states can balance power balance under each scenario. The feasible subproblem is listed as follows:
The value of the objective is obtained by solving the subproblem. If the objective is positive, the unit commitment schedule cannot ensure load balance. Accordingly, the Benders cut Eq. (32) is generated to the master problem for revising the unit commitment schedule, which is listed as follows:
The optimal subproblem is applied after each feasible subproblem is satisfied. The optimal subproblem is to check whether generators’ committed states can balance power balance under each scenario in an economical manner. The optimal subproblem is listed as follows:
The value of the objective is obtained by solving the subproblem. If the objective does not satisfy criteria Eq. (40), the unit commitment schedule is not economically optimal. Accordingly, the Benders cut Eq. (41) is generated to the master problem for revising the unit commitment schedule, which is listed as follows:
3 Stochastic Unit Commitment Based on Dynamic Scenarios Clustering
3.1 Multi-Parametric Programming for Dynamic Scenarios Clustering
In practice, there are massive scenarios that result in the computational burden. In this section, we introduce the multi-parametric method to cluster the scenarios. The concept of scenario clustering method based on the conventional K-means method and multi-parametric method are shown in Figs. 3a and 3b, respectively. In the conventional K-means method, the scenarios are clustered based on Euclidean distance. More specifically, scenarios that are closed in Euclidean space are aggregated as one scenario. Some scenarios could be close in Euclidean space but have different impacts on the unit commitment schedule. These scenarios should not be clustered into one scenario. However, the K-means method could cluster into one scenario by mistake since they are close in Euclidean space. On the other hand, some scenarios could be far away in Euclidean space but have the same impact on the unit commitment schedule. The K-means method fails to cluster these scenarios since they are far away. In summary, the K-means method does not fully consider power system physical constraints and is thus inaccurate. Fig. 3b illustrates the proposed clustering method based on multi-parametric programming. In multi-parametric programming, the whole space will be divided into several critical regions (CRs). Scenarios in each critical region have the same impact on the power system schedule, i.e., unit commitment. Accordingly, scenarios are clustered based on power system physical constraints, which is thus more accurate than the conventional K-means method.
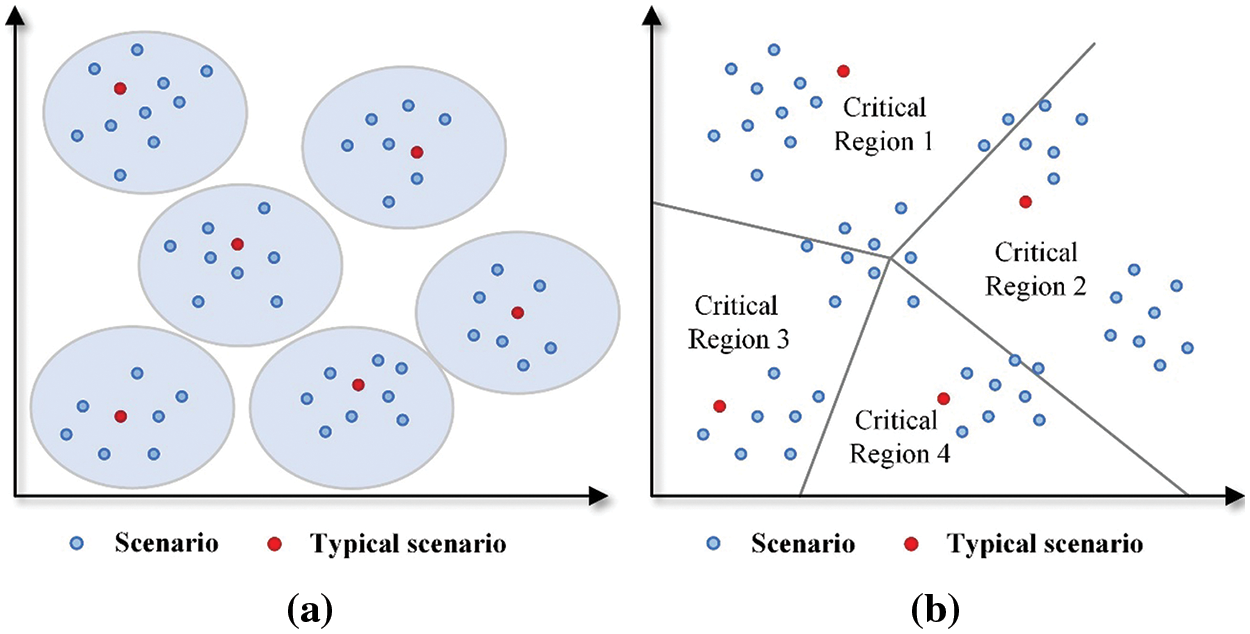
Figure 3: Illustration of scenario clustering based on (a) K-means method and (b) multi-parametric programming
Here, we use the optimal subproblem to illustrate how multi-parametric programming works. The major objective of multi-parametric programming is to obtain all CRs. Accordingly, scenarios in one CR can be aggregated as one representative scenario. The optimal subproblem is listed as follows:
After the optimal subproblem is solved, the constraint set in subproblem Eq. (43) can be categorized as active constraint set Eq. (44) and inactive constraint set Eq. (45). It is obvious that constraint Eq. (45) does not work since it is inactive. The optimal value of subproblem Eq. (43) is only enforced by constraint Eq. (44). Therefore, the optimal solution of P can be directly calculated using Eq. (44), which can be derived as Eq. (46). By replacing Eq. (46) with Eq. (45), constraint Eq. (47) can be obtained. Here, a conclusion is drawn: if the uncertain variable β is given a value like β0, P can be calculated using Eq. (46).
Furthermore, we can draw that for any β that satisfies Eq. (47), P* can be calculated using Eq. (46), indicating that β satisfying Eq. (47) has the same impact on I*. Therefore, Eq. (47) meets the definition of CR, so we can use Eq. (47) to calculate all CRs. It is obvious that scenarios belonging to one critical region can be aggregated as one representative scenario since their impacts on the unit commitment schedule are the same.
Then we introduce how to embed the clustering approach in the existing Benders decomposition. The Benders decomposition is the same as the master problem in Section 2, which is listed as follows:
Then, we first solve the following feasible problem under one scenario. After the optimal solution is obtained, we can use Eq. (50) to calculate the CR for this scenario. Then, all scenarios are screened to check whether they belong to this CR. Scenarios belonging to one CR would be aggregated as one scenario. These scenarios only generate one Benders cut and will not be solved, which mitigates the computational burden. All scenarios are clustered by repeating the above processes.
A similar process in the feasible subproblem will be repeated in the optimal subproblem for clustering scenarios. Then, we first solve the following optimal problem under one scenario. After the optimal solution is obtained, we can use Eq. (53) to calculate the CR for this scenario. Then, all scenarios are screened to check whether they belong to this CR. Scenarios belonging to one CR would be aggregated as one scenario. These scenarios only generate one Benders cut and will not be solved, which mitigates the computational burden. All scenarios are clustered by repeating the above processes.
Accordingly, dynamic scenarios cluster is applied in the existing stochastic unit commitment solve process. Meanwhile, these scenarios are accurately clustered. It should be mentioned that the proposed method can significantly reduce computational performance since in each subproblem, only calculation rather than optimization is required by using multi-parameter programming.
Overall, the flowchart of the proposed stochastic unit commitment with dynamic scenarios clustering is listed as follows:
1) Input relevant parameters.
2) Solve the master problem.
3) Select representative scenarios using multi-parametric programming. Solve the feasible subproblem under each scenario and generate corresponding Benders cut to the master problem.
4) Select representative scenarios using multi-parametric programming. Solve the optimal subproblem under each scenario and generate corresponding Benders cut to the master problem.
The flowchart of the proposed method is shown in Fig. 4.
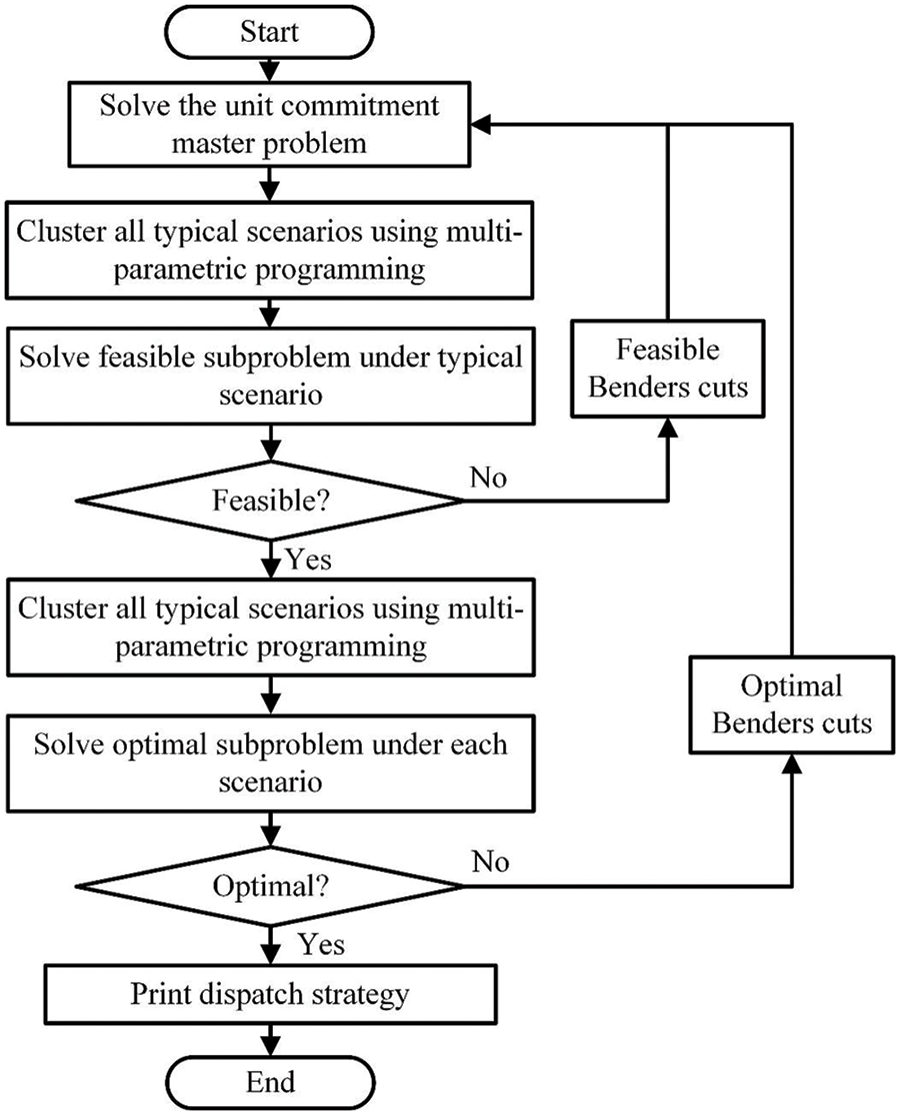
Figure 4: Flowchart of the proposed algorithm for proposed unit commitment
The proposed stochastic unit commitment with dynamic scenarios clustering is tested on a 6-bus system [28] and the modified IEEE 118-bus system. The proposed method aims to cluster scenarios in an accurate manner. Therefore, we compare the proposed method with the most popular clustering method (i.e., the K-means method). We also compare the proposed method with the method without clustering approach to illustrate the accuracy. Three cases are designed to illustrate the effectiveness of the proposed method:
Case I: The stochastic unit commitment with K-means scenarios clustering method.
Case II: The stochastic unit commitment without scenarios clustering method, i.e., 30 scenarios are considered.
Case III: The proposed stochastic unit commitment with dynamic scenarios clustering method based on multi-parametric programming.
The topology of the 6-bus system is shown in Fig. 5. This test system consists of six buses, three coal-fired generators, and two wind farms. We consider that the uncertain wind power satisfies the Gaussian distribution. The Monte Carlo method is adopted to generate 30 scenarios. Each scenario represents one potential power output of wind farm 1. These 30 scenarios are presented in Fig. 6 [29]. The K-means method cannot determine the number of clusters. In other words, we must first provide the initial number of clusters to the K-means method. Then, the K-means method is applied to cluster scenarios with the given initial number. We set the initial number of the K-means method as 5. Accordingly, after the K-means method is applied, thirty scenarios are clustered into five scenarios, which are depicted in Fig. 7. The stochastic unit commitment would determine the unit commitment schedule based on these 5 scenarios. The proposed method does not require a specific initial number of clusters. Alternatively, it clusters scenarios based on the CR. The clustered scenario during the first iteration is shown in Fig. 8. Only two scenarios rather than five scenarios can represent all these thirty scenarios at the first iteration. Therefore, the proposed method can more accurately select scenarios with respect to the system’s condition.
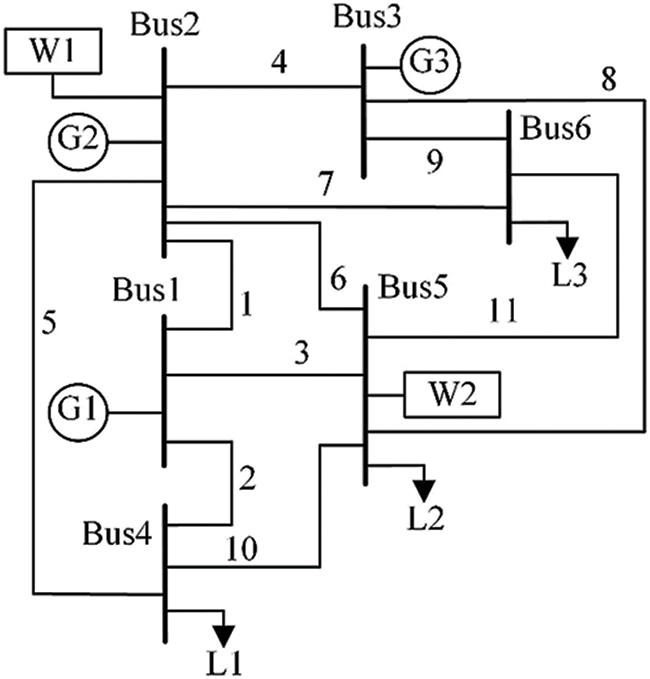
Figure 5: Topology of the 6-bus system
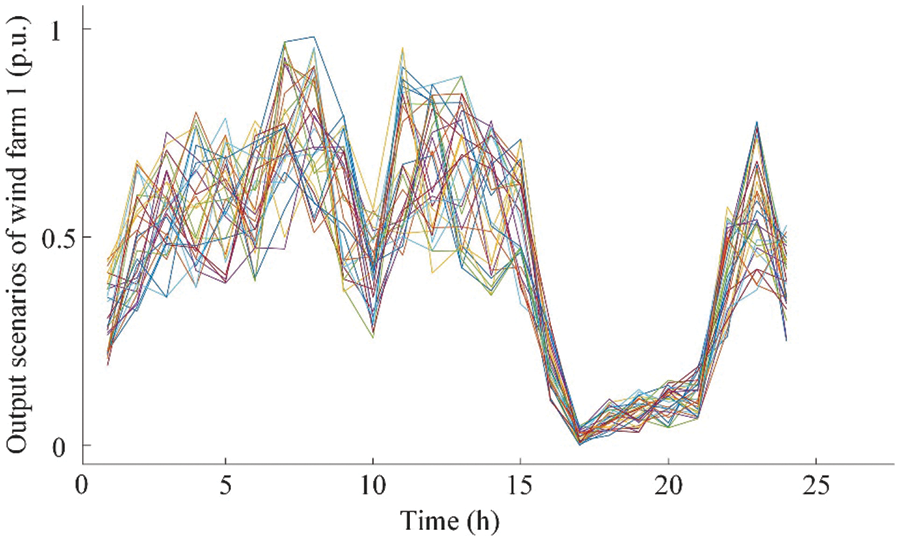
Figure 6: Scenarios of Wind Farm 1 for describing uncertain wind power output
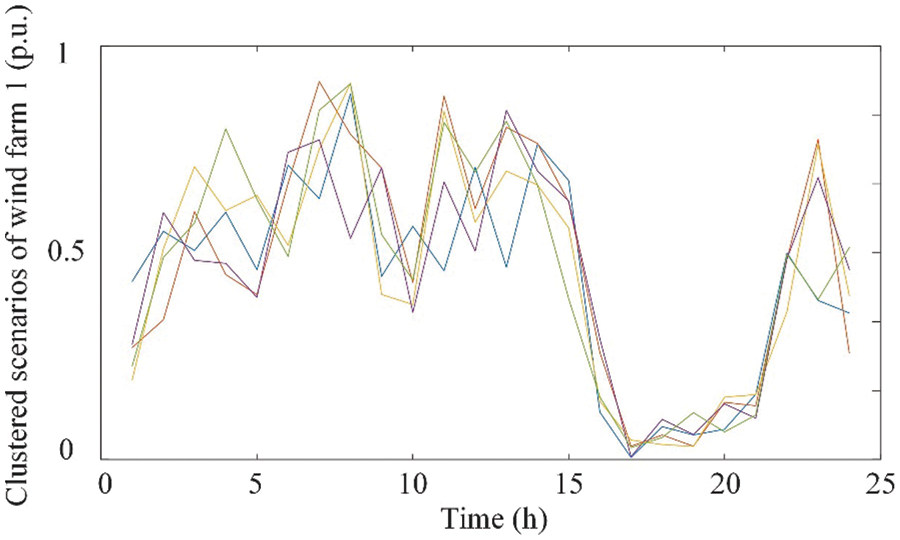
Figure 7: Clustered scenarios of Wind Farm 1 after employing the K-means method
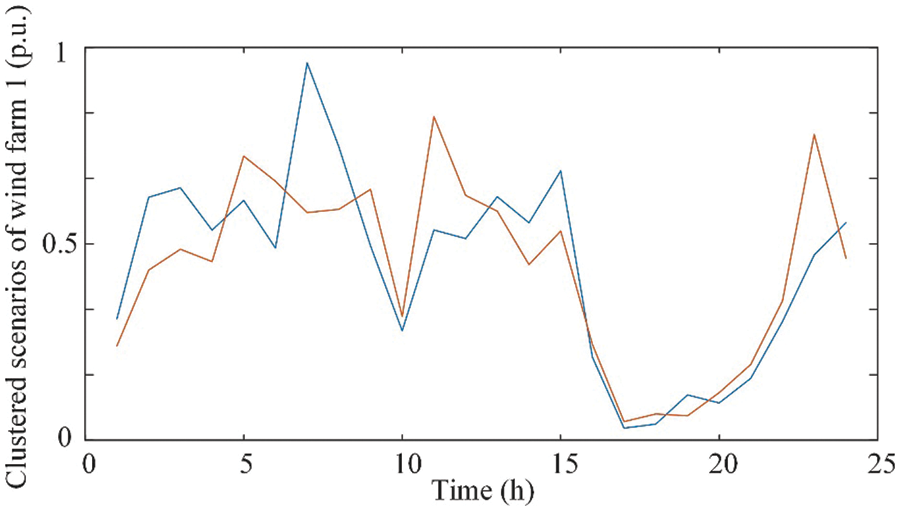
Figure 8: Clustered scenarios obtained by the proposed method
Table 1 compares the cost allocation in different cases. To check the robustness of these methods, we fix the first stage decision (generator’ state) using the value obtained in these three cases and check whether the first stage decision can balance the load in all thirty scenarios. If not, this scenario is labeled as an infeasible scenario. As Case I only considers five scenarios rather than all thirty scenarios, it has the lowest operation cost among these three cases. However, the clustering method in Case I cannot accurately aggregate and select all representative scenarios. Accordingly, the unit commitment schedule obtained in Case I is infeasible in seven scenarios. In Case II, all scenarios are considered, and the unit commitment is thus feasible in all scenarios. However, the robustness of Case II is achieved at the expense of the economy since the overall operation cost of the proposed method is larger than conventional stochastic unit commitment. Moreover, Case II has the worst computational performance since it considers the most number of scenarios. Case III relieves the computation burden compared with Case II as multi-parametric programming is applied to reduce the scenarios. Case III also achieves the same operation cost as that in Case II, and is feasible in all 30 scenarios, indicating that the proposed method can accurately cluster scenarios.
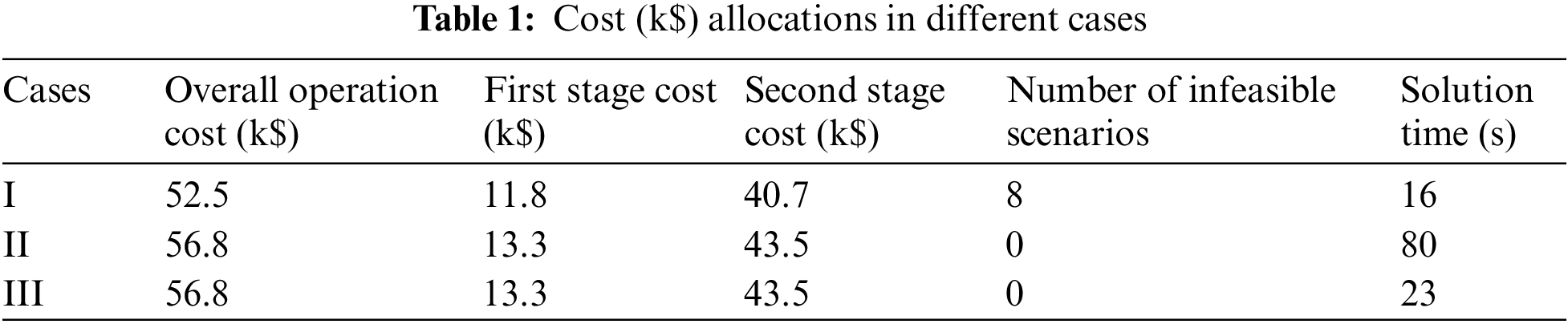
Table 2 compares the committed generators in different cases. In this test system, we assume that thirty scenarios are generated by the K-means method. Fewer generators are committed in Case I since fewer scenarios are considered by the K-means method. However, less committed generators cannot guarantee enough power supply when the wind power changes. In Case II, more generators are committed to ensuring power supply and accommodating renewable energy. Therefore, the robustness of system operation is maintained at the cost of committing extreme generators. However, thirty scenarios cannot accurately select enough representative scenarios, which could result in a power imbalance. Compared with Case II, more generators are committed in Case III owing to the accurate scenario clustering technique based on the multi-parametric method. The proposed method can select scenarios that have an impact on committed generators, thus resulting in the most accurate unit commitment schedule.

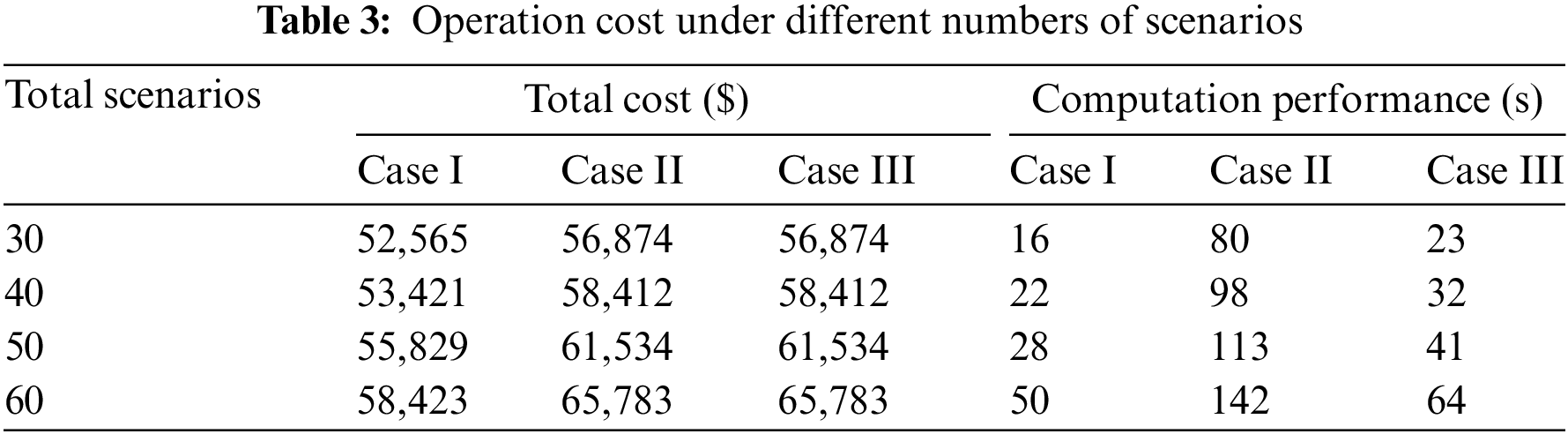
Table 3 compares the cost allocation with respect to a different number of scenarios. As the number of scenarios increases, the total costs of all three cases are increased. The total costs of Cases II and III are higher than those of Case I since more scenarios are considered. On the other hand, the computational time is increased when the number of infeasible scenarios is increased. The proposed method enhances computational performance in all cases.
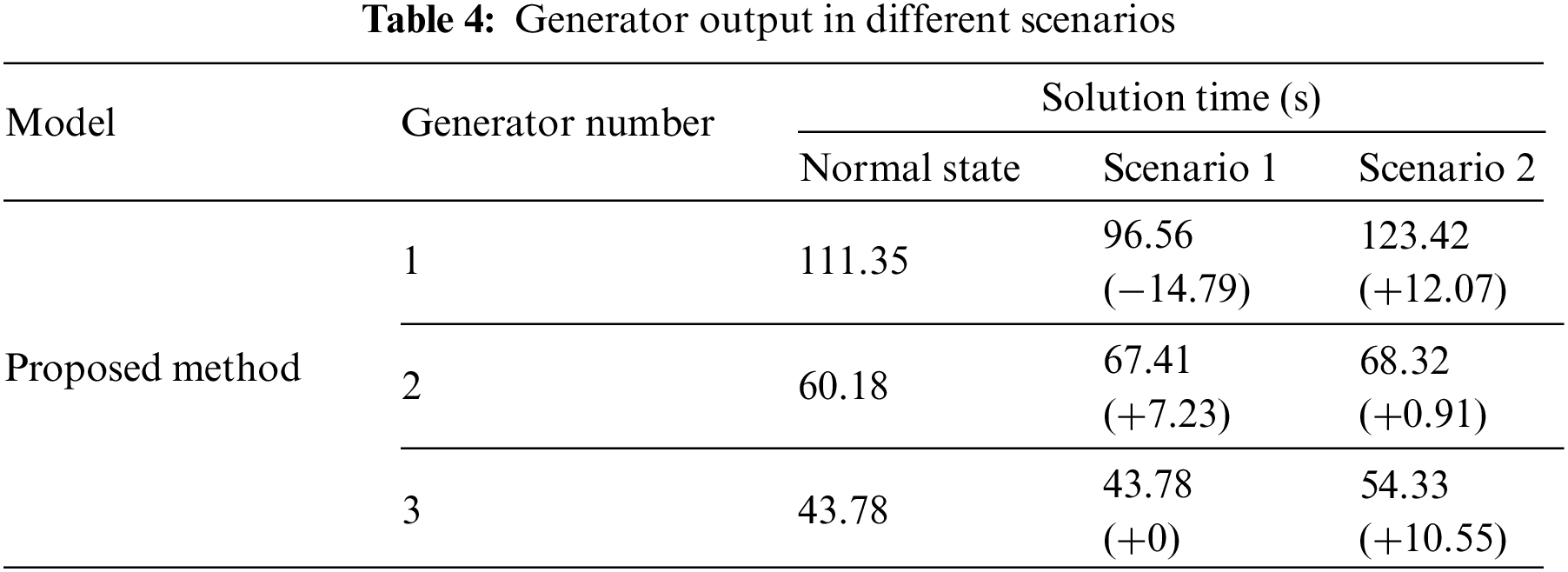
Consider that there are sixty scenarios, six scenarios are clustered by the proposed method. Table 4 provides the generator output in different scenarios. The generator is re-dispatched after each scenario to ensure the load balance in each scenario. In Scenario 1, the output of Generator 1 is reduced by 14.79 MW, while Generator 2’s output is increased by 7.23 MW. In Scenario 2, each generator output is re-dispatched again to accommodate variable wind power. For instance, the generator number in this case is increased rather than decreased in Scenario 1.
4.2 Modified IEEE 118-Bus System
The topology of the IEEE 118-bus system is presented in Fig. 9, which includes 118 buses, 186 transmission lines, and 54 generators. This system is modified by integrating 15 wind farms. The power generation of these wind farms is adopted from reference [30]. We first generate 500 scenarios and further use the K-means method and proposed method to cluster scenarios. One major drawback of the K-means method is that the K-means method cannot determine the number of clusters. In another word, we must first provide the initial number of clusters to the K-means method. Then, the K-means method is applied to cluster scenarios with the given initial number. Accordingly, the initial number is really important in stochastic unit commitment since a small initial number fails to represent all scenarios, while a large initial number could result in a computational burden. In this section, we want to illustrate that the proposed method cannot only determine the accurate cluster number but also accurately select representative scenarios. Therefore, we set the initial cluster number for the K-means method as 20, 50, and 80 scenarios, respectively, in Case II. The cost allocations of these three cases are shown in Table 5. It can be observed that as the number of scenarios in Case II increases, the overall operation cost increases. This is because the introduction of more scenarios increases the robustness of the power system schedule. As a result, the number of infeasible scenarios is reduced. However, such robustness is achieved at the cost of computational intractability. The solution time is significantly increased as the number of scenarios is increased.
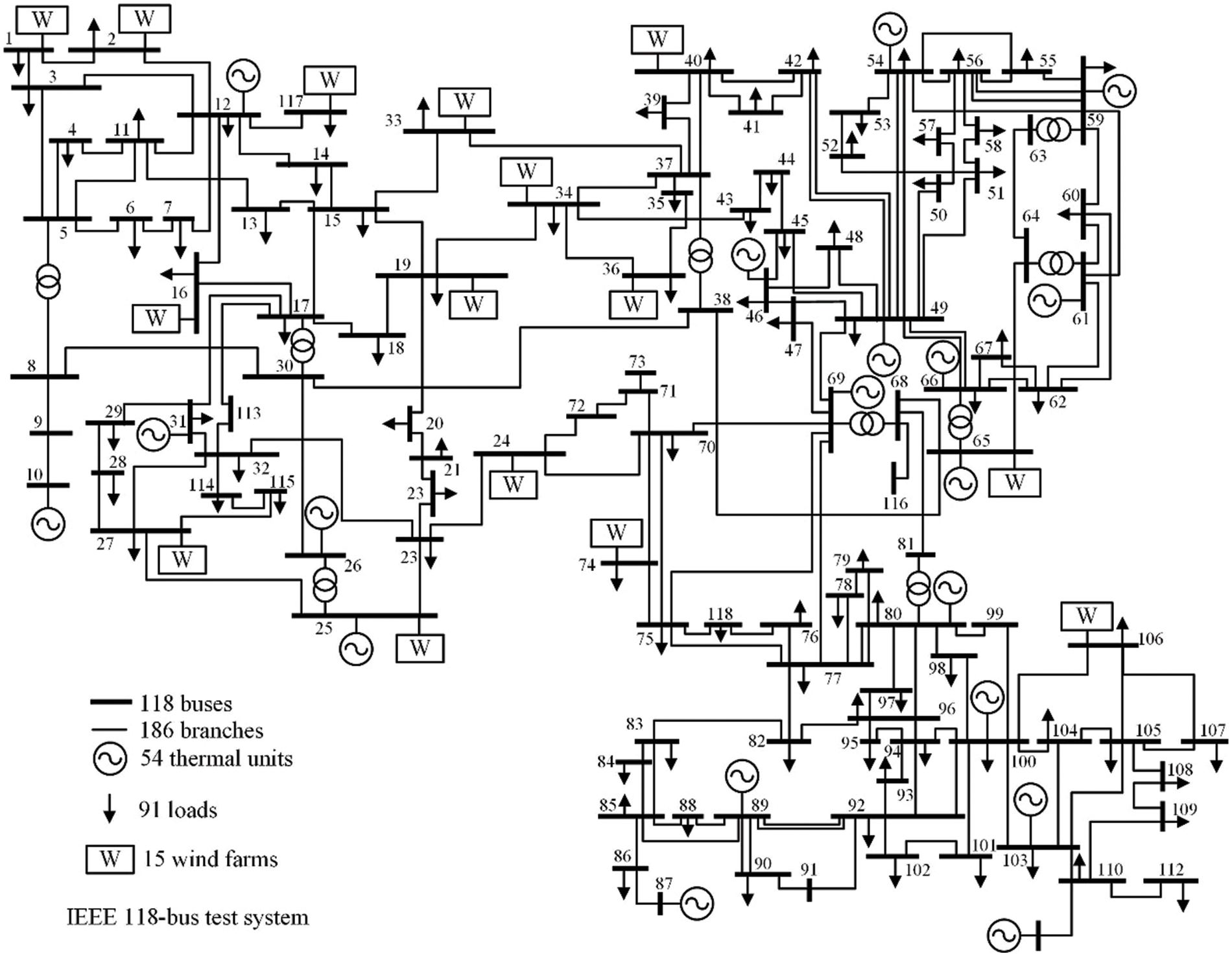
Figure 9: Topology of modified IEEE 118-bus system
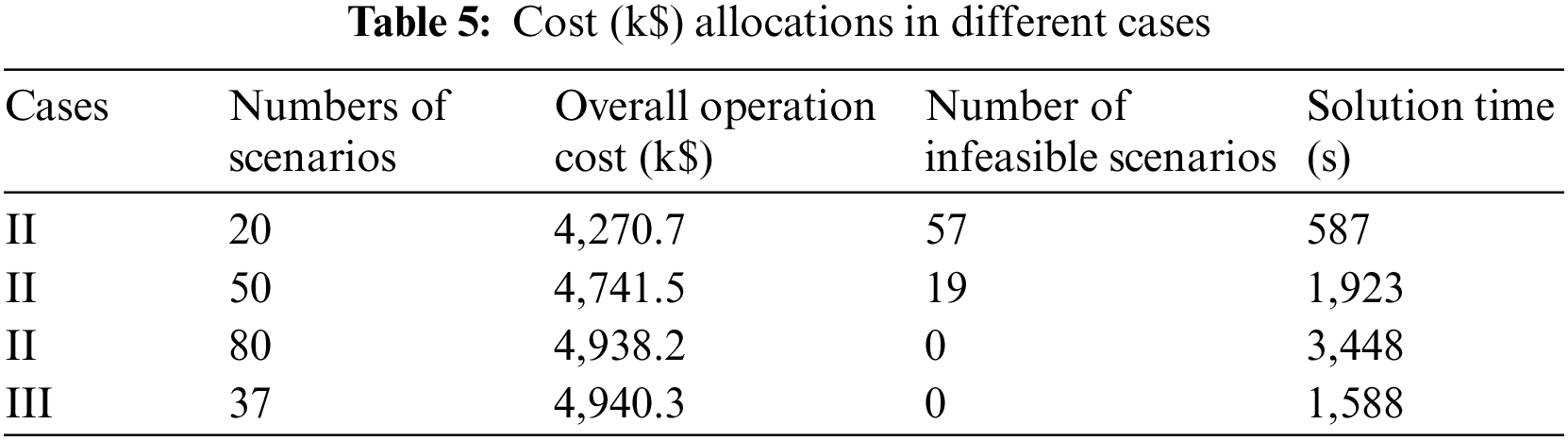
Case III adopted the proposed method to cluster all scenarios. The proposed method addresses the drawback of the K-means method since it clusters scenarios by finding CRs. The number of CRs is determined by solving the programming problem via multi-parametric programming. Therefore, the proposed method does not require the initial number of clusters. By applying the proposed method to cluster 500 scenarios, 37 scenarios are obtained. Case III achieves the same results as Case II with 80 scenarios, indicating that 37 scenarios rather than 80 scenarios are enough to represent all scenarios, thus reducing the computational burden. Moreover, the proposed method is more robust compared to the K-means method with 50 scenarios. This is because the K-means method fails to cluster those scenarios that have impacts on the unit commitment schedule. Additionally, some representative scenarios in the K-means have the same impact on the unit commitment schedule, and the K-means method fails to cluster these scenarios as one scenario.
Table 6 provides the number of hourly committed generator units in different cases. Similar numerical results are found in this test system. Fewer generators are committed in Case I since fewer scenarios are considered by the K-means method. In Case II, more generator units are committed to ensure system load balance. The committed generators in Cases II and III are the same, illustrating the effectiveness of the proposed method in enhancing system load.

In this paper, the stochastic unit commitment with dynamic scenario clustering based on multi-parametric programming and Benders decomposition is provided. First, similar to conventional two-stage unit commitment, the proposed stochastic unit commitment is solved via the Benders decomposition, which decouples the primal problem into the master problem and two types of subproblems. Then, we innovatively embed the scenario clustering approach in the Benders decomposition process using multi-parametric programming. The combination of Benders decomposition and multi-parametric programming clustering approach could accurately cluster scenarios that have the same impact on the unit commitment schedule. Therefore, the proposed method is more accurate than conventional cluster methods since they fail to consider the unit commitment schedule while clustering. Simulation results tested on the 6 bus-system and modified IEEE 118-bus system are conducted to illustrate the validity of the proposed method. Compared with the conventional clustering method, the proposed method can accurately select representative scenarios, thus guaranteeing the robustness of unit commitment. Moreover, compared with the conventional method, the proposed method could mitigate computational burden while maintaining the same robustness level. Our future work will consider stability constraints in the unit commitment and multi-stage robust unit commitment with an accurate scenarios clustering approach. Our future work will also focus on improving the scalability of the proposed method.
Acknowledgement: None.
Funding Statement: This paper was funded by the Science and Technology Project of State Grid Corporation of China, Grant Number 5108-202304065A-1-1-ZN.
Author Contributions: Conceptualization, Zhi Zhang and Haiyu Huang; Methodology, Wei Xiong; Software, Yijia Zhou; Validation, Mingyu Yan and Shaolian Xia; Writing—review and editing, Baofeng Jiang; Visualization, Renbin Su and Xichen Tian. All authors have read and agreed to the published version of the manuscript.
Availability of Data and Materials: Data supporting this study are included within the article.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Abdelghany, M. B., Al-Durra, A., Gao, F. (2024). A coordinated optimal operation of a grid-connected wind-solar microgrid incorporating hybrid energy storage management systems. IEEE Transactions on Sustainable Energy, 15(1), 39–51. https://doi.org/10.1109/TSTE.2023.3263540 [Google Scholar] [CrossRef]
2. Malekshah, S., Ansari, J. (2021). A novel decentralized method based on the system engineering concept for reliability-security constraint unit commitment in restructured power environment. International Journal of Energy Research, 45(1), 703–726. https://doi.org/10.1002/er.v45.1 [Google Scholar] [CrossRef]
3. Malekshah, S., Banihashemi, F., Daryabad, H., Yavarishad, N., Cuzner, R. (2022). A zonal optimization solution to reliability security constraint unit commitment with wind uncertainty. Computers and Electrical Engineering, 99, 107750. https://doi.org/10.1016/j.compeleceng.2022.107750 [Google Scholar] [CrossRef]
4. Ansari, J., Malekshah, S. (2019). A joint energy and reserve scheduling framework based on network reliability using smart grids applications. International Transactions on Electrical Energy Systems, 29(11), e12096. [Google Scholar]
5. Abomazid, A. M., El-Taweel, N. A., Farag, H. E. (2022). Optimal energy management of hydrogen energy facility using integrated battery energy storage and solar photovoltaic systems. IEEE Transactions on Sustainable Energy, 13(3), 1457–1468. https://doi.org/10.1109/TSTE.2022.3161891 [Google Scholar] [CrossRef]
6. Ma, R., Basumallik, S., Eftekharnejad, S. (2022). Controlled islanding resilience with high penetration of renewable energy resources. IEEE Transactions on Sustainable Energy, 14(2), 1312–1323. [Google Scholar]
7. Ding, T., Liu, S., Yuan, W., Bie, Z., Zeng, B. (2015). A two-stage robust reactive power optimization considering uncertain wind power integration in active distribution networks. IEEE Transactions on Sustainable Energy, 7(1), 301–311. [Google Scholar]
8. Malekshah, S., Malekshah, Y., Malekshah, A. (2021). A novel two-stage optimization method for the reliability based security constraints unit commitment in presence of wind units. Cleaner Engineering and Technology, 4, 100237. https://doi.org/10.1016/j.clet.2021.100237 [Google Scholar] [CrossRef]
9. Zhao, B., Bukenberger, J., Webster, M. (2021). Scenario partitioning methods for two-stage stochastic generation expansion under multi-scale uncertainty. IEEE Transactions on Power Systems, 37(3), 2371–2383. [Google Scholar]
10. Ziaee, O., Alizadeh-Mousavi, O., Choobineh, F. F. (2017). Co-optimization of transmission expansion planning and TCSC placement considering the correlation between wind and demand scenarios. IEEE Transactions on Power Systems, 33(1), 206–215. [Google Scholar]
11. Heitsch, H., Römisch, W. (2003). Scenario reduction algorithms in stochastic programming. Computational Optimization and Applications, 24, 187–206. https://doi.org/10.1023/A:1021805924152 [Google Scholar] [CrossRef]
12. Li, Z., Li, Z. (2016). Linear programming-based scenario reduction using transportation distance. Computers & Chemical Engineering, 88, 50–58. https://doi.org/10.1016/j.compchemeng.2016.02.005 [Google Scholar] [CrossRef]
13. Mei, F., Zhang, J., Lu, J., Lu, J., Jiang, Y. et al. (2021). Stochastic optimal operation model for a distributed integrated energy system based on multiple-scenario simulations. Energy, 219, 119629. https://doi.org/10.1016/j.energy.2020.119629 [Google Scholar] [CrossRef]
14. Davidov, S., Pantoš, M. (2017). Stochastic assessment of investment efficiency in a power system. Energy, 119, 1047–1056. https://doi.org/10.1016/j.energy.2016.11.036 [Google Scholar] [CrossRef]
15. Yu, J., Ryu, J. H., Lee, I. B. (2019). A stochastic optimization approach to the design and operation planning of a hybrid renewable energy system. Applied Energy, 247, 212–220. https://doi.org/10.1016/j.apenergy.2019.03.207 [Google Scholar] [CrossRef]
16. Li, S., Ma, H., Li, W. (2017). Typical solar radiation year construction using k-means clustering and discrete-time Markov chain. Applied Energy, 205, 720–731. https://doi.org/10.1016/j.apenergy.2017.08.067 [Google Scholar] [CrossRef]
17. Wang, Q., Wang, J., Guan, Y. (2012). Stochastic unit commitment with uncertain demand response. IEEE Transactions on Power Systems, 28(1), 562–563. [Google Scholar]
18. Gal, T., Nedoma, J. (1972). Multiparametric linear programming. Management Science, 18(7), 406–422. https://doi.org/10.1287/mnsc.18.7.406 [Google Scholar] [CrossRef]
19. Borrelli, F., Bemporad, A., Morari, M. (2003). Geometric algorithm for multiparametric linear programming. Journal of Optimization Theory and Applications, 118, 515–540. https://doi.org/10.1023/B:JOTA.0000004869.66331.5c [Google Scholar] [CrossRef]
20. Du, E., Zhang, N., Kang, C., Xia, Q. (2018). A high-efficiency network-constrained clustered unit commitment model for power system planning studies. IEEE Transactions on Power Systems, 34(4), 2498–2508. [Google Scholar]
21. Yan, M., Shahidehpour, M., Paaso, A., Zhang, L., Alabdulwahab, A. et al. (2020). Distribution system resilience in ice storms by optimal routing of mobile devices on congested roads. IEEE Transactions on Smart Grid, 12(2), 1314–1328. [Google Scholar]
22. Gan, W., Yan, M., Yao, W., Guo, J., Ai, X. et al. (2021). Decentralized computation method for robust operation of multi-area joint regional-district integrated energy systems with uncertain wind power. Applied Energy, 298, 117280. https://doi.org/10.1016/j.apenergy.2021.117280 [Google Scholar] [CrossRef]
23. Lv, J., Ding, T., Bie, Z., Wang, X. (2017). A novel linearization variant of reliability costs in the optimal scheduling model. IEEE Transactions on Power Systems, 32(5), 4140–4142. https://doi.org/10.1109/TPWRS.2017.2650783 [Google Scholar] [CrossRef]
24. Liu, B., Zhuo, F., Zhu, Y., Yi, H. (2014). System operation and energy management of a renewable energy-based DC micro-grid for high penetration depth application. IEEE Transactions on Smart Grid, 6(3), 1147–1155. [Google Scholar]
25. Zheng, Q. P., Wang, J., Liu, A. L. (2014). Stochastic optimization for unit commitment—a review. IEEE Transactions on Power Systems, 30(4), 1913–1924. [Google Scholar]
26. Zhao, C., Guan, Y. (2013). Unified stochastic and robust unit commitment. IEEE Transactions on Power Systems, 28(3), 3353–3361. https://doi.org/10.1109/TPWRS.59 [Google Scholar] [CrossRef]
27. Yan, M., Teng, F., Gan, W., Yao, W., Wen, J. (2023). Blockchain for secure decentralized energy management of multi-energy system using state machine replication. Applied Energy, 337, 120863. https://doi.org/10.1016/j.apenergy.2023.120863 [Google Scholar] [CrossRef]
28. Wen, Y., Guo, C., Pandžić, H., Kirschen, D. S. (2015). Enhanced security-constrained unit commitment with emerging utility-scale energy storage. IEEE Transactions on Power Systems, 31(1), 652–662. [Google Scholar]
29. Yan, M. (2023). 30 scenarios data. https://docs.google.com/spreadsheets/d/1NdfB4Iatbz4fyF7Cq7s78_xjddUH-AI3/edit?usp=sharing&ouid=105761789279000909209&rtpof=true&sd=true (accessed on 17/09/ 2023). [Google Scholar]
30. Jiang, H., Du, E., He, B., Zhang, N., Wang, P. et al. (2023). Analysis and modeling of seasonal characteristics of renewable energy generation. Renewable Energy, 219, 119414. https://doi.org/10.1016/j.renene.2023.119414 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools