Novel Static Security and Stability Control of Power Systems Based on Artificial Emotional Lazy Q-Learning

Nomenclature

1  Introduction

To respond positively to the global zero-carbon program, countries around the world are transforming and upgrading their industries in various fields [1]. In China, the government is taking the lead in building a novel power system based on renewable energy [2]. In recent years, the wind power and photovoltaic systems share in China has increased year by year, and hydroelectric power technology continues to develop [3]. The development and utilization of renewable energy can reduce pollution and save energy; however, renewable energy power generation brings volatility and strong uncertainty, which causes hidden dangers to the security and stability of the novel power system [4].

The novel power system security stabilization problems can be further classified into static, transient, and dynamic problems [5]. This study mainly focuses on static safety and stability control methods. Existing static security and stability control methods for novel power systems mainly include proportional-integral-derivative (PID) [6], PID control based on optimization algorithms [7], and reinforcement learning methods [8]. PID controllers are characterized by a simple structure, are easy to implement, and have fewer number of parameters.

When the control model is known, the parameters of the PID controller can be calculated accurately according to the requirements of system safety and stability [9]. However, in actual operation, because the parameters of the system model cannot be accurately measured and estimated, the accurate model of the actual power system is difficult to obtain, which leads to the low availability of the PID control parameters calculated according to the requirements of the system security and stability [10]. Based on the PID controller, the above problem of unavailability of PID parameters can be solved by adding the PID controller with an optimization algorithm. However, since the system structure and internal parameters are constantly changing, PID controllers based on optimization algorithms do not apply to systems where the parameters are constantly changing as the equipment is aging [11]. The reinforcement learning approach can effectively deal with the problem of unavailability of the parameters of the fluctuating system model because of the feature of not relying on the system model [12].

Existing reinforcement learning methods can be categorized into reinforcement learning and deep reinforcement learning methods. Compared with deep reinforcement learning methods, reinforcement learning methods represented by Q-learning methods are simple to be trained and rapid in operation, which can fulfill the requirements of static safe, stable, and rapid control of novel power systems [13]. Although Q-learning methods do not depend on the system model, the current Q-learning methods mainly have the following problems: (1) the curse of dimensionality of computer memory caused by excessively large action and state matrices [14]; (2) the problem of slow convergence and long training time during the training process because of the impossibility of filtering the high-quality data from the low-quality data. Existing deep reinforcement learning methods contain at least one deep neural network inside [15]. For example, the deep Q network contains one deep neural network; the doubled deep Q network contains two deep neural networks [16]; meanwhile, the deep deterministic policy gradient (DDPG) contains two deep neural networks [17]. The training process of deep neural networks has strong randomness and uncertainty. Moreover, the trained deep neural networks do not provide completely accurate control actions [18]. Therefore, this study mainly adopts the Q-learning method that can handle random inputs. Therefore, the deficiencies of the existing methods for the safety and stability control problem of the novel power system can be summarized as follows: (1) fixed-parameter PID methods are not capable of adapting to changes in system parameters; (2) inaccurate reinforcement learning leads to lower-performance control actions; (3) high-accuracy reinforcement learning leads to dimensional disasters and insufficient execution time; and (4) reinforcement learning methods that are not capable of selecting excellent actions for training lead to long convergence times and slow convergence speed.

The static security stability of the novel power system is required to fulfill the requirement of fast control, therefore the state matrix and action matrix of the Q-learning method adopted in this study will not be too large, which can avoid the curse of dimensionality [19]. To solve the problem that Q-learning methods cannot filter high-quality data and low-quality data, this study proposes lazy Q-learning methods. The proposed lazy Q-learning method can filter high-quality data, which can improve training efficiency [20]. The lazy Q-learning method can both determine the quality of the data and characterize the data dimensions from high to low dimensionality. After dimensionality reduction of high-quality data, intelligent agents based on this Q-learning method can provide accurate control actions for the safety and stability of novel power systems [21]. Therefore, the main contributions of this study can be summarized as follows:

(1) This study proposes a lazy Q-learning method to the static safety and stability control problem of a novel power system. The lazy Q-learning method is easier to converge to the optimal control action than the Q-learning method.

(2) This study applies lazy learning to filter and compress the data, which can characterize the relationship from high-dimensional data to low-dimensional data and can accelerate the convergence process of the algorithm.

(3) This study adopts the Q-learning method which can be updated online to deal with the static security stabilization problem of novel power systems and has a simple algorithmic process, requires less memory, and has fast computational speed.

The remaining sections of this paper are organized as follows. Section 2 analyzes the static security stabilization problem of a new type of power system. Section 3 proposes the lazy Q-learning method. Section 4 is the application of the proposed lazy Q-learning method to a specific problem. Section 5 is the conclusion and outlook of the paper.

2  Static Security Stability Analysis of a Novel Power System

2.1 Framework and Components of a Novel Power System

The static security and stability problems of novel power systems dominated by renewable energy sources are more prominent [22]. The novel power system is shown in Fig. 1.

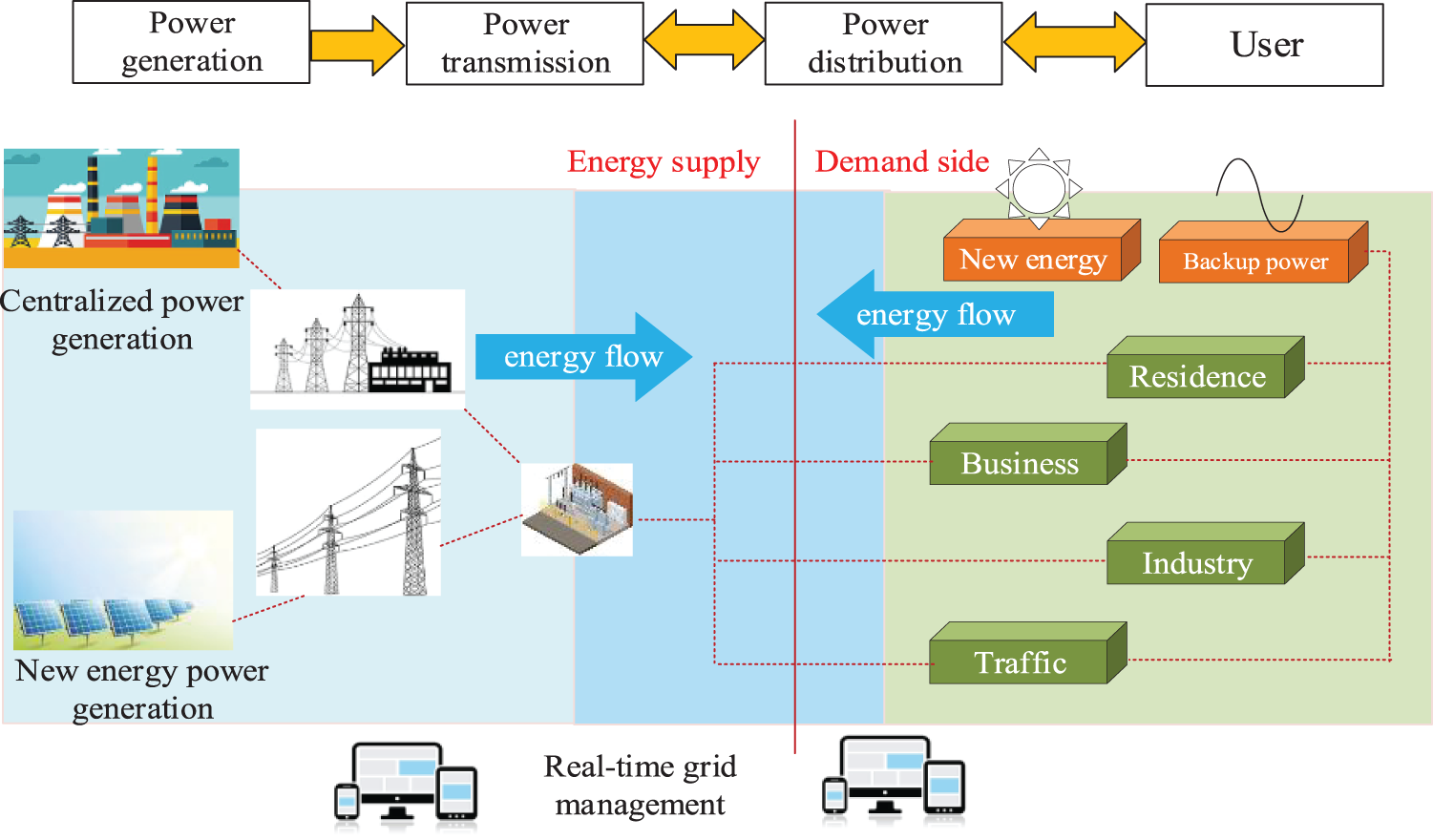
Figure 1: Novel power systems based on renewable energy sources

The control block diagram of the voltage stabilization actuator is shown in Fig. 2.

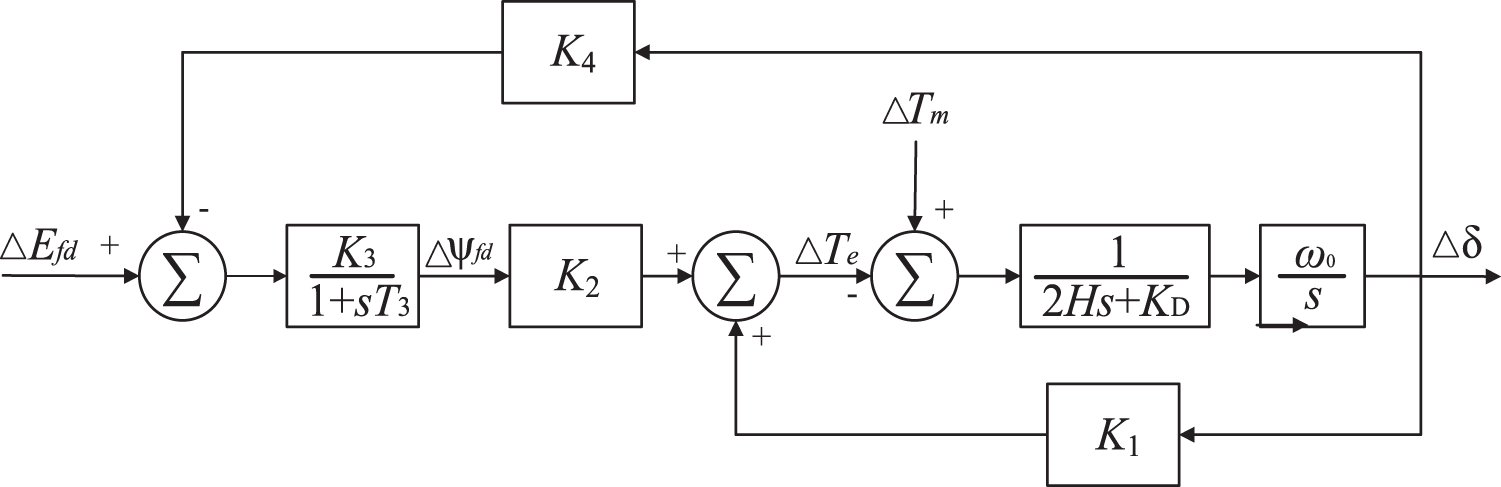
Figure 2: Control block diagram of voltage stabilization actuator

The self-inductance of the rotor circuit of a conventional motor is Lffd. The derivative operator p is replaced by the Laplace operator s as:

Δψfd=K31+sT3[ΔEfd−K4Δδ](1)

The contents of the parentheses in Eq. (1) can be rewritten as:

ψad0+Laqsid0=eq0+Raiq0+Xqsid0=Eq0(2)

ψaq0+Laqs′iq0=−Laqsiq0+Laqs′iq0=−(Xq−Xd′)iq0(3)

K1=EBEq0D×(RTsin⁡δ0+XTdcos⁡δ0)+EBiq0D(Xq−Xd′) ×(XTqsin⁡δ0−RTcos⁡δ0)(4)

Similarly, the other constants K2, K3, T3 and K4 are calculated as:

K2=LadsLads+Lfd[RTDEq0+(XTq(Xq−Xd′)D+1)iq0](5)

K3=Lads+LfdLadu11+XTqD(Xq−Xd′)(6)

T3=Td0s′XTq(Xq−Xd′)D+1(7)

K4=LaduLadsLads+LfdEBD(XTqsin⁡δ0−RTcos⁡δ0)(8)

If the effect of saturation is neglected, the constant K4 can be simplified to:

K4=EBD(Xd−Xd′)(XTqsin⁡δ0−RTcos⁡δ0)(9)

2.2 Modeling of Single-Machine Infinity Systems Considering Actuators and Automatic Voltage Regulation

The signal input to the automatic voltage actuator system is the machine terminal voltage Et. The Et can be represented by the state variables Δωr, Δδ and Δψfd. Therefore the Et can be calculated as:

Et2=ed2+eq2(10)

When the system is perturbed by small disturbances, the above equation can be rewritten as:

(Et0+ΔEt)2=(ed0+Δed)2+(eq0+Δeq)2(11)

When ignoring all second-order components of the perturbation signal, the above equation is rewritten as:

Et0ΔEt=ed0Δed+eq0Δeq(12)

therefore,

ΔEt=ed0Et0Δed+eq0Et0Δeq(13)

When the perturbation value is considered, the stator voltage equation can be written as:

Δed=−RaΔid+LlΔiq−Δψaq(14)

Δeq=−RaΔiq−LlΔid+Δψad(15)

Combining the above equations, the variation of machine terminal voltage ΔEt is:

ΔEt=K5Δδ+K6Δψfd(16)

where,

K5=ed0ΔEt0×[−Ram1+Lln1+Laqsn1]+eq0ΔEt0×[−Ran1−Llm1−Lads′m1](17)

K6=ed0ΔEt0×[−Ram2+Lln2+Laqsn2]+eq0ΔEt0×[−Ran2+Llm2+Lads′(1Lfd−m2)](18)

The model of the thyristor excitation system with automatic voltage regulation (AVR) is shown in Fig. 3, where EFMAX and EFMIN are the upper and lower limits of the excitation output voltage, respectively; TR is the time constant of the machine terminal voltage converter; Vref is the reference voltage of the system; and v1 is the output of the machine terminal voltage converter. Thyristor excitation systems contain only the links required for special systems and apply high-gain exciters. The limiting and protection circuits are omitted because the limiting and protection circuits do not affect the stability of small signals.

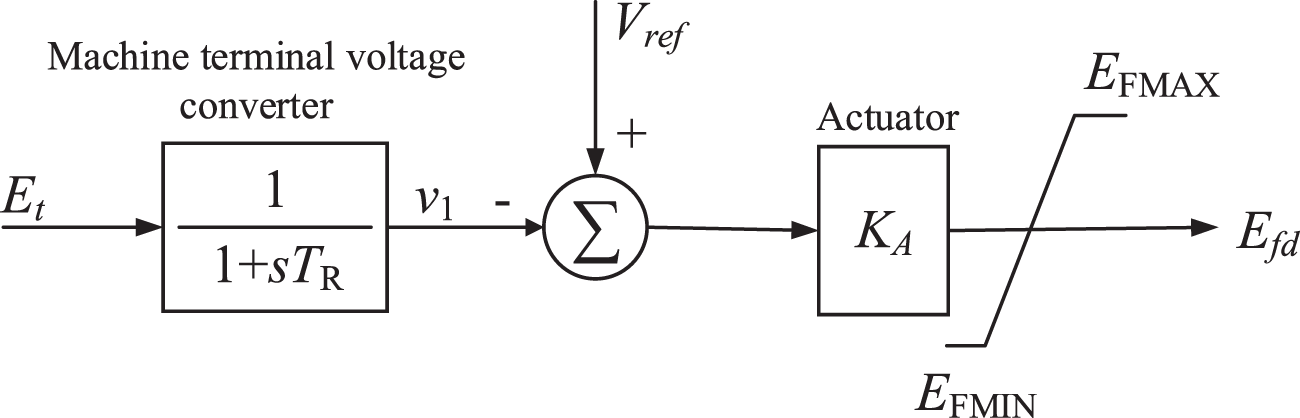
Figure 3: Thyristor excitation system with AVR

Adding disturbances to the terminal voltage converter, the variation of the output of the machine terminal voltage converter is calculated as:

Δv1=11+pTRΔEt(19)

therefore,

pΔv1=1TR(ΔEt−Δv1)(20)

The Eq. (20) is rewritten as:

pΔv1=K5TRΔδ+K6TRΔψfd−1TRΔv1(21)

The output of the system excitation voltage is:

Efd=KA(Vref−v1)(22)

The variation of excitation voltage is calculated as:

ΔEfd=KA(−Δv1)(23)

Considering the effect of the excitation system, the equation of the excitation circuit is:

pΔψfd=−ω0RfdLfdm1Lads′Δδ−ω0RfdLfdΔψfd×[1−Lads′Lfd+m2Lads′]−ω0RfdLaduKAΔv1(24)

Since the exciter is a first-order model, the order of the whole system is increased by one order from the original one, and the newly added state variables are [23]. Since pΔωr and pΔδ are not affected by the exciter, the entire state-space model of the power system is written in the form of the following vector matrix:

[Δω˙rΔδ˙Δψ˙fdΔv˙1]=[−KD2H−K12H−K22H0ω00000−ω0RfdLfdm1Lads′−ω0RfdLfd[1−Lads′Lfd+m2Lads′]−ω0RfdLaduKA0K5TRK6TR−1TR][ΔωrΔδΔψfdΔv1]+[b1000]ΔTm(25)

If the mechanical torque input is constant, ΔTm is 0. The system control framework including the voltage converter and AVR/exciter link is shown in Fig. 4, where Gex(s) is the transfer function of the AVR and the exciter. The Gex(s) applies to any type of exciter and can be expressed in terms of the constant KA as:

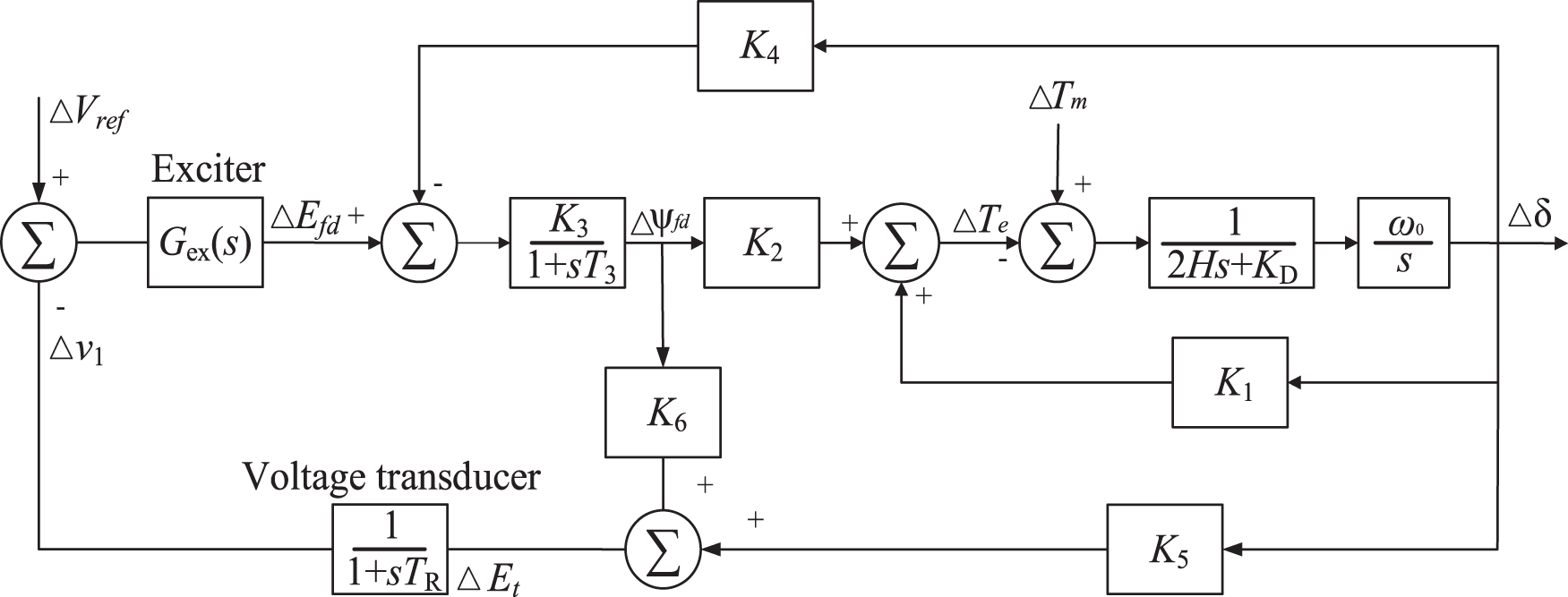
Figure 4: Block diagram of the control system with actuator and AVR

Gex(s)=KA(26)

The terminal voltage error signal at the input of the voltage converter is determined by the above equation.

2.3 System Model Combining Automatic Voltage Regulation and Power System Stabilizers

Power system stabilizers (PSS), which is an additional excitation control technique for suppressing low-frequency oscillations of synchronous generators by introducing additional feedback signals, have been applied to improve the stability of power systems [24]. The phase compensation link appropriately provides phase overrun characteristics to compensate for the phase lag between the exciter input and the generator air gap torque [25]. Since the signal link is a high-pass filter with a large time constant TW, the oscillating signal at frequency ωr does not change with the passage of the oscillating signal [26]. The stabilizer gain KSTAB determines the amount of damping generated by the PSS. The perturbation value is added to the signal filtering module as:

Δv2=pTw1+pTw(KSTABΔωr)(27)

pΔv2=KSTABpΔωr−1TwΔv2(28)

The component form of the state variable is adopted to express Eqs. (27) and (28) as:

pΔv2=a51Δωr+a52Δδ+a53Δψfd+a55Δv2+KSTAB2HΔTm(29)

where,

a51=KSTABa11(30)

a52=KSTABa12(31)

a53=KSTABa13(32)

a55=−1TW(33)

Similarly, the following equations can be obtained from the phase compensation link:

Δvs=Δv2(1+pT11+pT2)(34)

pΔvs=T1T2pΔv2+1T2Δv2−1T2Δvs(35)

pΔvs=a61Δωr+a62Δδ+a63Δψfd+a65Δv1+a66Δv2+a66Δvs+T1T2KSTAB2HΔTm(36)

a61=T1T2a51(37)

a62=T1T2a52(38)

a63=T1T2a53(39)

a65=T1T2a55+1T2(40)

a66=−1T2(41)

ΔEfd=KA(Δvs−Δv1)(42)

With the addition of the power system stabilizer, the actuator equation is:

pΔψfd=a32Δδ+a33Δψfd+a34Δv1+a36Δvs(43)

where,

a36=ω0RfdLaduKA(44)

When ΔTm=0, after adding a power system stabilizer, the state space model of the entire system is:

[Δω˙rΔδ˙Δψ˙fdΔv˙1Δv˙2Δv˙s]=[a11a12a13000a21000000a32a33a340a360a42a43a4400a51a52a530a550a61a62a630a65a66][ΔωrΔδΔψfdΔv1Δv2Δvs](45)

where,

a11=−KD2H(46)

a12=−K12H(47)

a13=−K22H(48)

a21=ω0(49)

a32=−ω0RfdLfdm1Lads′(50)

a33=−ω0RfdLfd[1−Lads′Lfd+m2Lads′](51)

a42=K5TR(52)

a43=K6TR(53)

a44=−1TR(54)

The control framework of the power system containing AVR and PSS is shown in Fig. 5. When the damping windings are neglected, the generator of the simplified system model is then shown in Fig. 6.

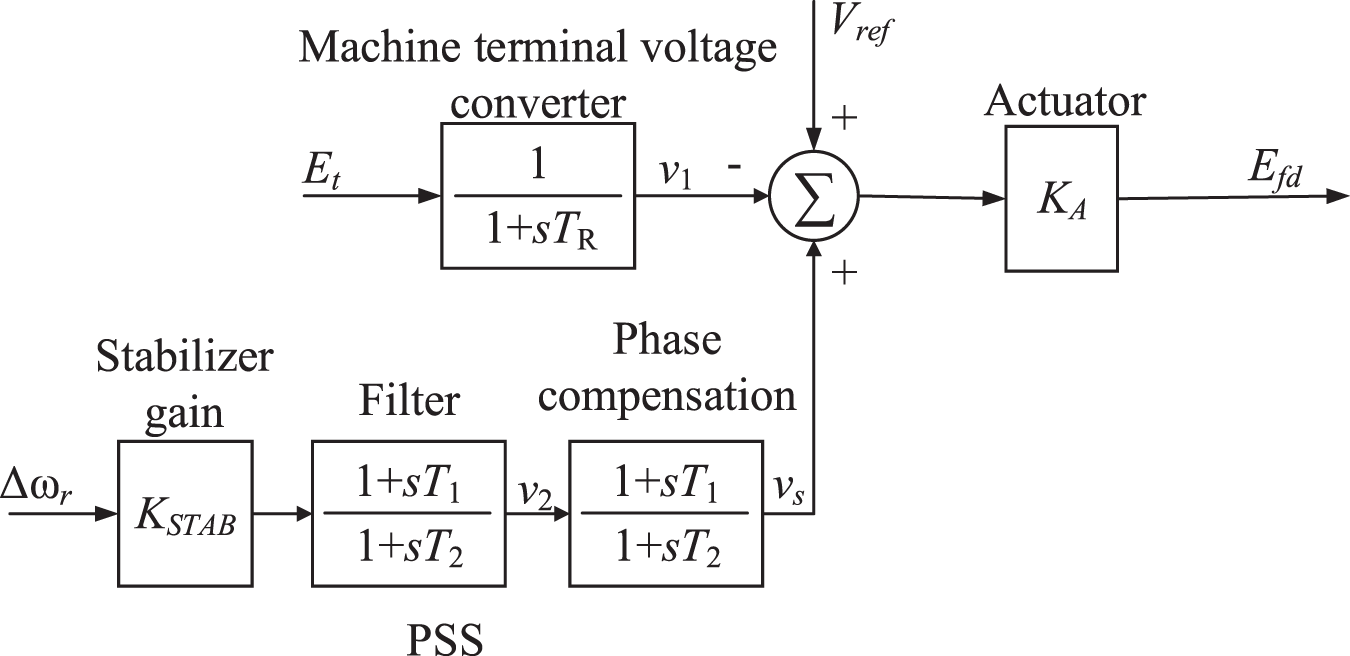
Figure 5: Thyristor excitation system including AVR and PSS

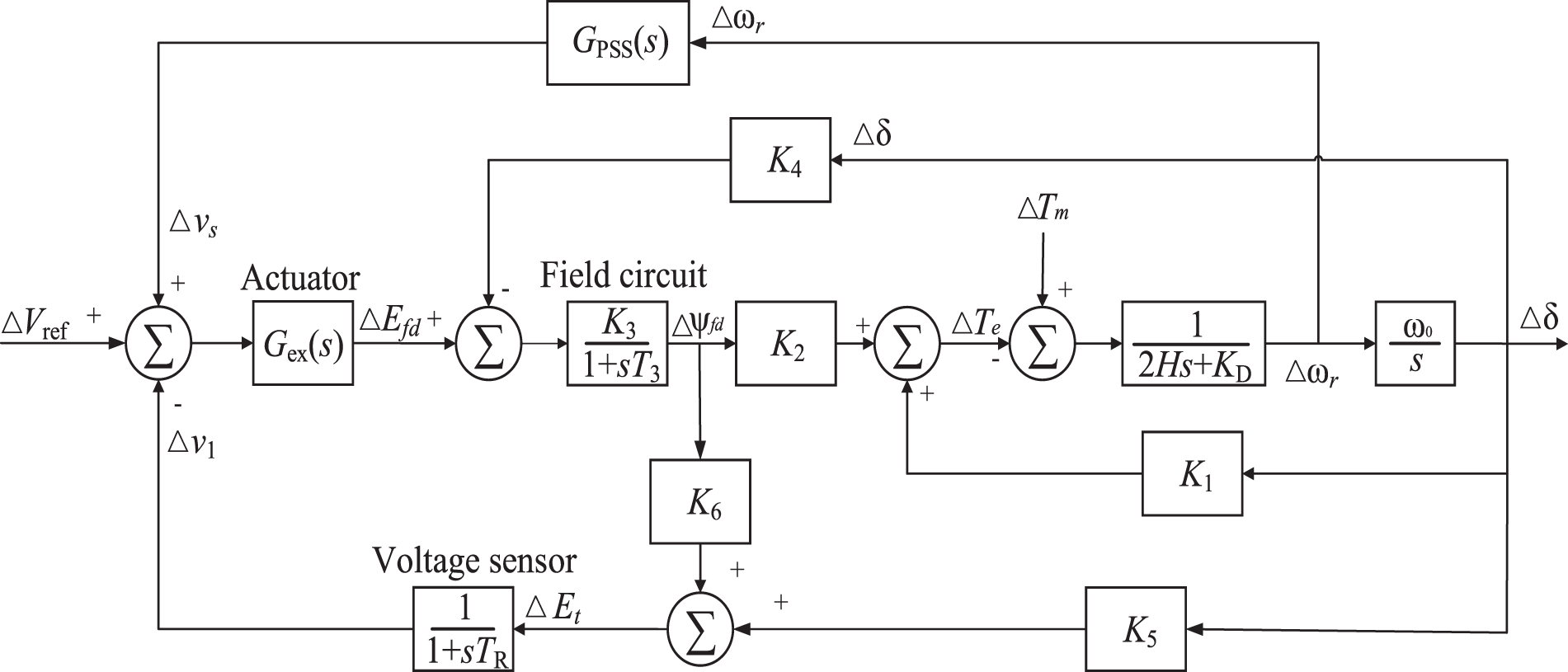
Figure 6: Generator model including AVR and PSS

In this study, the error integration criterion widely adopted in control science is applied as the evaluation index of static safety and stability control performance, i.e., Integral absolute error (IAE), Integral squared error (ISE), Integral time multiple absolute error (ITAE), Integral time multiple square error (ITSE), Integral squared time multiple absolute error (ISTAE), Integral squared time absolute error (ISTAE) and Integral squared time squared error (ISTSE). The specific expression is:

{IAE=∫0T|e(t)|dtISE=∫0Te2(t)dtITAE=∫0Tt|e(t)|dtITSE=∫0Tte2(t)dtISTAE=∫0Tt2|e(t)|dtISTSE=∫0Tt2e2(t)dt(55)

where e(t) is the control error. The smaller the value of the six control performance evaluation indexes in the error integration criterion, the smaller the error of the control process and the higher the control accuracy.

3  Artificial Emotional Lazy Q-Learning

The artificial emotional lazy Q-learning method proposed in this study consists of artificial emotion, lazy learning, and Q-learning.

The Q-learning algorithm has been almost synonymous with reinforcement algorithms since the first release of the Q-learning algorithm in 1989 by Chien et al. [27]. Q-learning belongs to the category of single-agent reinforcement learning algorithms, in which the agents validate the knowledge gained and update the optimal policy by searching for the optimal value in accordance with the environment online [28]. In the framework of Q-learning-based algorithms, the agent updates the value function according to the value of the reward function, which for Q-learning algorithms is the Q-function. Typically, the agent records and updates the Q-function in the form of a lookup table. Q-learning obtains reward values by continuously trying various action values in the environment and iterates the Q-function in the lookup table online according to the reward values [29]. Eventually, Q-learning will converge to the optimal policy. Based on Bellman’s equation, the updated formula for the Q(s(t),a(t)) matrix is:

Q(s(t),a(t))←Q(s(t),a(t))+α(r(t+1)+γmaxa∈AQ(s(t+1),a(t))−Q(s(t),a(t)))(56)

where Q(s(t),a(t)) is the Q-value of the execution action value a(t) in state s(t), Q(s(t),a(t)) is a matrix of size S×A, typically realized through a Lookup table; s(t) and a(t) are the current state value and action value of the system, respectively; s(t+1) is the next moment state; A is the set of actions, and the number of elements within A is finite to ensure that the Q-learning algorithm has a solution; α is the learning rate, taking values in the range 0<α<1, and α measures the level of trust between the retained part and the updated part; γ is the discount factor, which takes values in the range 0<γ<1, and γ reflects how much the Q-learning algorithm cares between the current reward value and the future reward value.

The Q-learning algorithm generally selects the optimal action value based on a greedy strategy [30], which means that the action value which can obtain the highest Q-value in the state s(t) at the current moment will always be selected. The specific formula is:

π∗(s(t))=arg⁡maxa∈AQ(s(t),a(t))(57)

where π∗(s(t)) is the optimal policy for the Q-learning algorithm. While the greedy strategy improves the convergence speed, after a certain number of iterations the agents in Q-learning may follow the same path to select the same action values and subsequently may miss the opportunity to select the better action values. Therefore, a probability updating strategy is required to be introduced to judge which action value is more likely to be selected in different states, and the probability updating formula is:

P(s(t),a(t))←{P(s(t),a(t))−β(1−P(s(t),a(t))),a(t+1)=a(t)P(s(t),a(t))(1−β),a(t+1)≠a(t)(58)

where P(s(t),a(t)) is the probability of selecting the action value a(t) in the state s(t); β is the probability distribution factor, which takes values in the range 0<β<1, and β can control the speed of action value search. While the matrix Q(s(t),a(t)) is being updated, the matrix P(s(t),a(t)) is updated simultaneously according to Eq. (58). As the number of iterations increases, the probability that an action value with a higher Q-value will be selected rises. Since the probability of other action values is always non-zero, the Q-learning algorithm can jump out of the local optimum.

In this study, the combined reward function is designed based on the high-frequency signal of the power angle deviation ΔδiH(t) and the integral of the power angle deviation ∫ΔδiH(t):

r(t)=−Kn(1−w)(ΔδiH(t))2−w(200−∫ΔδiH(t))2(59)

where Kn is a normalization constant which uniformly scales the values of ΔδiH(t) and ∫ΔδiH(t) to avoid large differences in magnitude. In this study, Kn=20000; (1−w) and w reflect the weights of ΔδiH(t) and ∫ΔδiH(t) in R(t), respectively.

In this study, the system power angle deviation is selected as the state value of the Q-learning algorithm:

s(t)∈{(−∞,−0.1],(−0.1,−0.0818],…,[0.1,+∞)}⏟13(60)

For the Q-learning algorithm, the magnitude of the power angle deviation corresponds to the state value s(t), and the adjustment command corresponds to the action value a(t) in the action set A. The size and range of the values s(t) significantly affect the setting of the action set A. The finite number of action values a(t) in the action set A are arranged in descending order:

A={a1(t),a2(t),⋯,ak(t)}(61)

where k is the number of action values.

When the number of action values a(t) is certain, a larger interval range of the action set A means that the probability of selecting the optimal action value will be reduced, which may result in over- or under-adjustment at a certain time. On the contrary, if the interval range of the action set A is too small, the agent will not traverse most of the state values s(t) of the power system, and the agent will be restricted in selecting the action values. However, if the state values input to the Q-learning algorithm are always stabilized within a small range, the range of the action set can be narrowed down and the accuracy of the action values can be improved.

After the interval range of the action set A is determined, the number of action values a(t) is required to be set. Generally, the number of action values in the action set A should not be set too high, because excessive action values will lead to a sharp increase in the number of elements in the matrix Q(s(t),a(t)) and P(s(t),a(t)) and result in the curse of dimensionality; On the contrary, too few action values will expand the degree of discretization of the action set A, which will weaken the ability of the agent to adapt to the random changes of the complex system. To reconcile this problem, inspired by the artificial emotional mechanism for continuous processing of action values, this study adopts the artificial emotional method to act on the action value output, i.e., summing the action value of the previous moment with the action value selected by the intelligent body at this moment to update the action value output at the current moment:

a(t)←a(t)+μa(t−1)(62)

where μ is the weight factor of the action value in the previous moment, which takes the value in the range of 0<μ≤1.

After improving the action value output method, the diagram of the artificial emotional Q-learning algorithm is shown in Fig. 7. The Q-learning method has two problems: (1) The output action of Q-learning is discrete. For more precise control, the ideal Q-learning action matrix should be set very large, thus exceeding the computer memory. (2) The agent chooses the action output corresponding to the largest probability every time will result in a greedy strategy, which may lead to actions with poor control performance being selected continuously. To avoid these two problems of the Q-learning method, the proposed artificial emotional lazy Q-learning adjusts the probability selection mechanism and the action output mechanism through the addition of emotions, and can output continuous control action values with a small number of action matrices, and can modify the probabilities based on the emotional values obtained by the agent, thus outputting control actions with higher control performances.

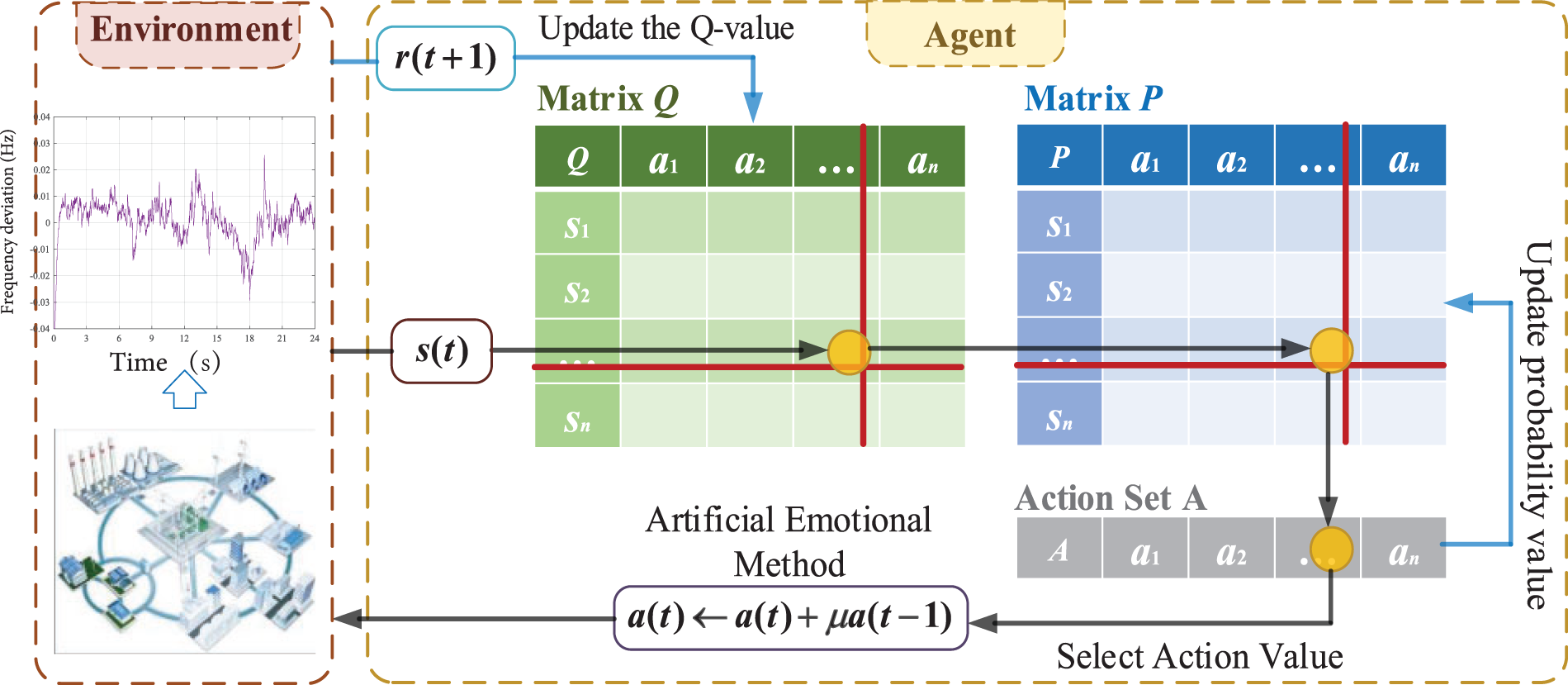
Figure 7: Artificial emotional Q-learning algorithm

The output method is to modify the action value based on the action value of the previous moment, to obtain more output values by the limited number of action values, and to adopt the updated action value as the output value of the Q-learning algorithm. Distinguished from the ordinary Q-learning algorithm which directly adopts the action value selected by the intelligent body as the output value, the improved action value output method weakens the adverse effect of randomness on the selection of the action value and enhances the continuity of the action value output as well. This method, although simple, reduces the number of action values and improves the running speed of the algorithm, while avoiding the problem of poor control performance because the output values are too discretized.

The lazy learning of the proposed artificial emotional lazy Q-learning method will predict the next system state. Therefore, the inputs of lazy learning are Δδi and ∫Δδi. In addition, lazy learning can predict the next state Δδi,(t+1)′ of the power system based on the set of actions A currently adopted by the power system. The inputs and outputs of the proposed artificial emotional lazy Q-learning method are shown in Table 1.

where the initial action set A is described as follows:

A=[a1,1a1,2⋯a1,ka2,1a2,2⋯a2,k⋮⋮⋱⋮aJi,1aJi,2⋯aJi,k](63)

where A has k-columns and each column of matrix A is a set of action vectors of regulation commands for the PSS. The predictions for the next state similarly have k-columns and each column corresponds to a prediction for each action vector. Therefore, Δδi,(t+1)′ is a k-column prediction matrix based on the predictions of all k-column action vectors.

Estimating the value of an unknown function employing the lazy learning method is similar to mapping g:ℜm→ℜ. The inputs and outputs of the lazy learning method can be obtained from the matrix Ф, described as follows:

{(φ1,y1),(φ2,y2),⋯,(φNlazy,yNlazy)}(64)

where φi is the matrix of size Nlazy × k, i=1,2,⋅⋅⋅,Nlazy; yi is a vector of size Nlazy × 1. The predicted value for the q-th query point can be calculated by the following equation:

yq^=φqT(ZTZ)−1ZTv(65)

where Z=Wϕ; v=Wy. W is a diagonal matrix. Wii=ωi, where ωi is the weight function of the distance d(φi,φq) from the query point φq to the point φi. Thereby, (ZTZ)β=ZT⋅v can be modeled as a locally weighted regression.

The selection process in the artificial emotional lazy Q-learning method can select the optimal state (the smallest |Δδi,(t+1)′|) from the next state (Δδi,(t+1)′).

The artificial emotional lazy Q-learning method in the artificial emotional Q-learning method can compute the total conditioning commands ΔPi, and assign ΔPi,j to the PSS in the i-th region, ΔPi=∑j=1JiΔPi,j. Q-learning is a model-free control algorithm. The controller based on Q-learning can update the control strategy online according to the environmental variations.

The relaxation operator of the artificial emotional lazy Q-learning method is similar to an operator performing constraint control on the output of a reinforcement network. Therefore, the constraints of the relaxation operator can be expressed as follows:

ΔPi,j←[ΔPi,j]∑j=1Ji([ΔPi,j])∑j=1Ji(ΔPi,j)(66)

where [ΔPi,j] is the constraint function with the following expression:

max{Pj,(t−1)−Pjdown,Pjmin}≤ΔPi,j≤min{Pj,(t−1)+Pjup,Pjmax}(67)

Traditional learning algorithms learn from all data acquired through parallel systems. However, employing such data for learning does not necessarily result in better control performance than the current real system. Therefore, the artificial emotional lazy Q-learning method approach proposed in this paper will filter those better data for learning. Specifically, when the state st at the time t is better than the state s(t+△t),1′ at the time t+Δt and worse than the state s(t+△t),2′ at time t+Δt, the algorithm will exclude the change process data from st to s(t+△t),1′, and will keep the change process data from st to s(t+△t),2′ for offline training.

Fig. 8 illustrates the steps of controller operation for the artificial emotional lazy Q-learning method under a parallel system. The environment and the agents adopt the artificial emotional lazy Q-learning method to find the optimal control strategy through interaction, and the fast control of the static security and stability of the novel power system is realized by updating the parameters of the system model.

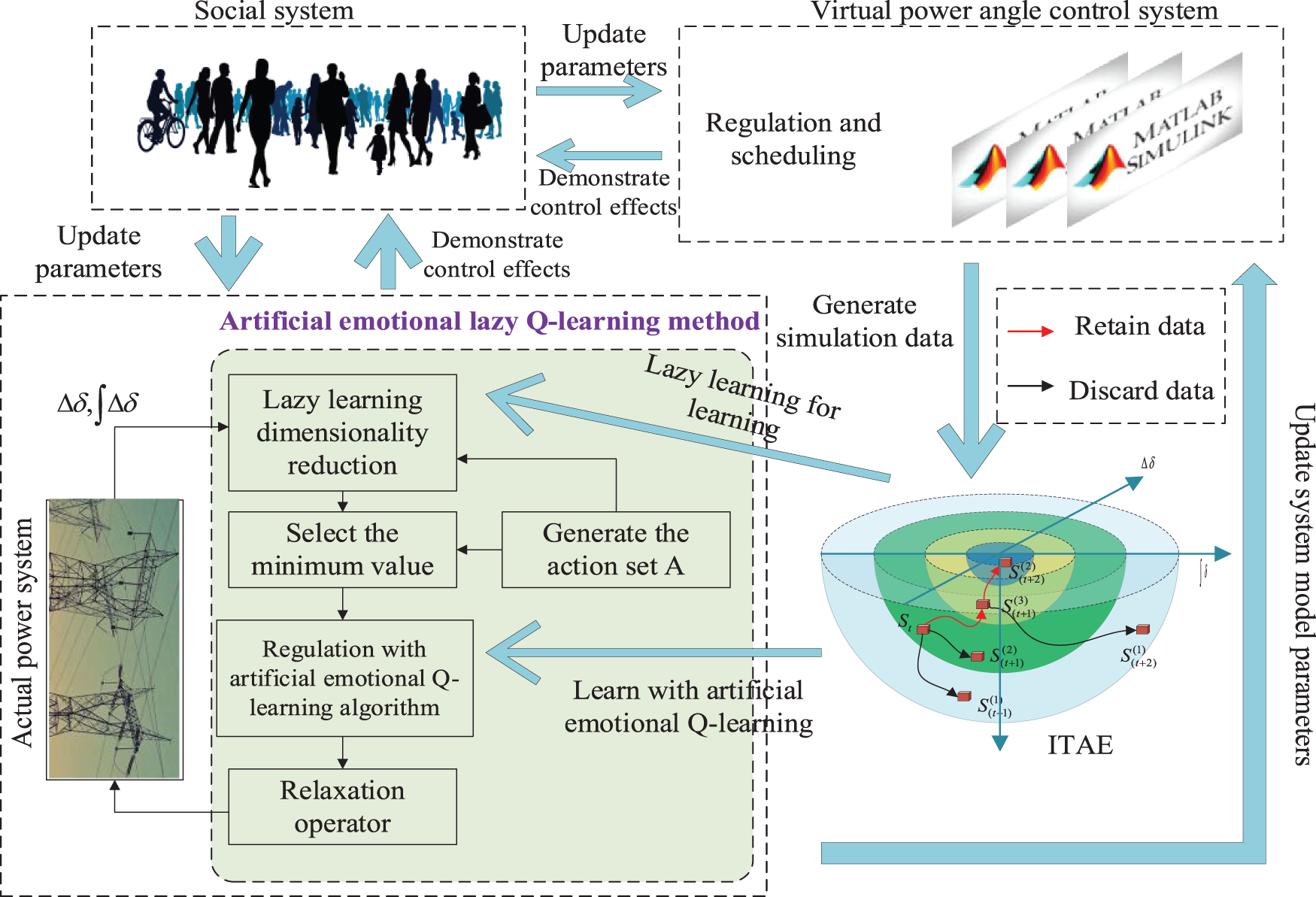
Figure 8: Flowchart of the artificial emotional lazy Q-learning algorithm in parallel systems

To quickly obtain accurate generation scheduling and control actions, numerous parallel safety stabilization systems are established in this paper as shown in Fig. 9. In the parallel power angle system, multiple virtual security stabilization systems are employed to continuously simulate the real security stabilization system. When the control effect of the virtual control power angle system is better than the real safety stabilization system, significant data of their power system stabilizers are exchanged between them. The virtual safety stabilizer system transfers important controller parameters to the real safety stabilizer system, while the real power angle system feeds the updated system model parameters back into the virtual safety stabilizer system. The social system in Figs. 8 and 9 mainly considers human and social characteristics, including human cognitive behavior, intention, and group perception. For the safety and stability control system of novel power systems in this study, the social system is the group of safety and stability control experts. These safety and stability control experts are equivalent to the human-in-the-loop control system. These fairly experienced safety and stability control experts continuously adjust the parameters of the virtual and actual systems, such as adjusting the learning rate and the emotion factor.

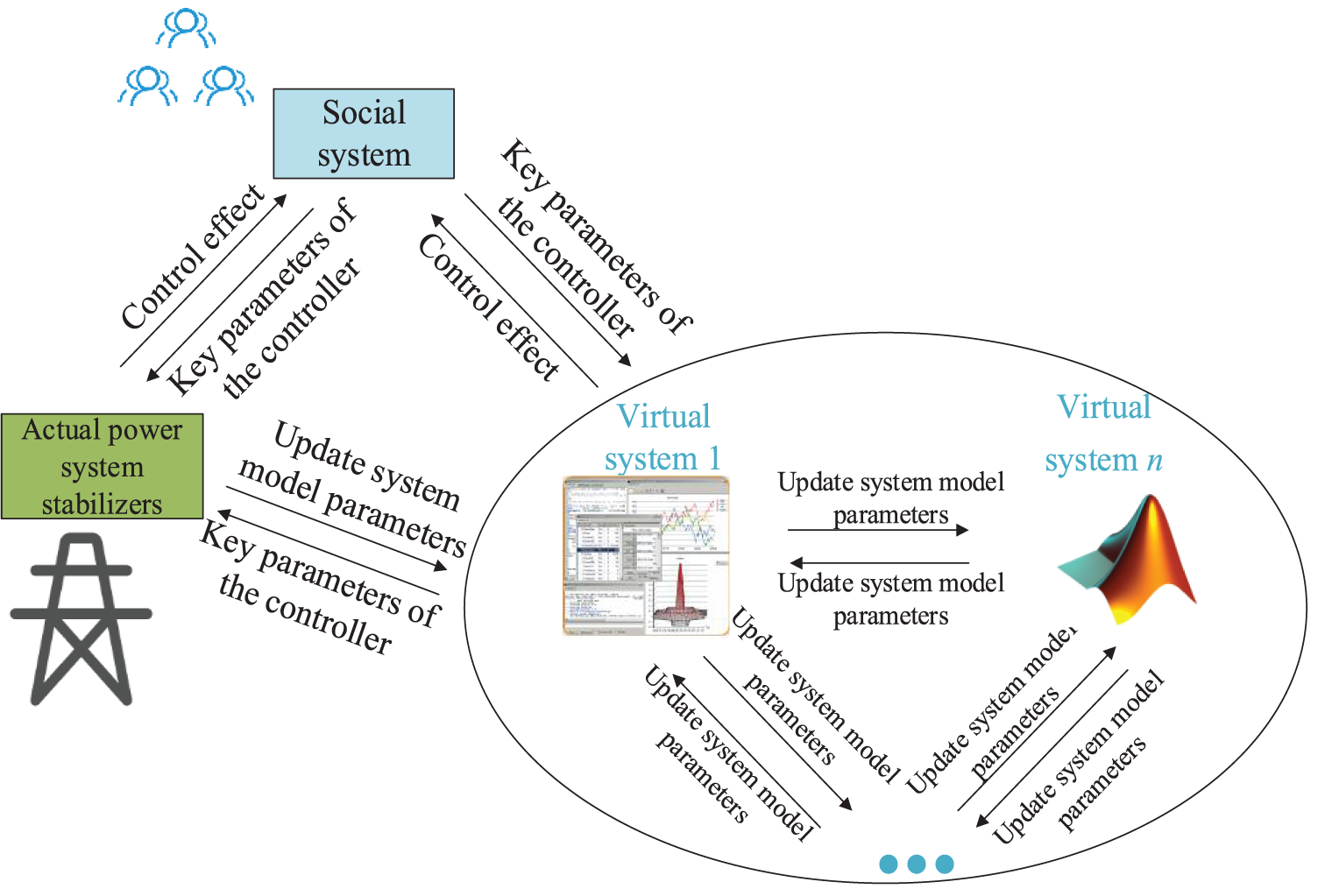
Figure 9: Parallel safety and stability control system

Because of the massive amount of data acquired through the parallel system, the training of the control algorithm learning will take much time if the traditional learning method is adopted. Therefore, a more efficient learning algorithm is required to learn the massive data as shown in Fig. 10. The artificial emotional lazy Q-learning method consists of four parts: lazy learning, selection operator, artificial emotional Q-learning, and relaxation operator. The proposed artificial emotion lazy Q-learning method can be designed as a secure and stable controller. In the proposed artificial emotional lazy Q-learning, the reinforcement network can output multiple power generation commands at the same time; the relaxation operation ensures that the output power generation commands will not exceed the upper and lower limits of the generator; and the lazy learning ensures that the states corresponding to sufficiently good control commands can be learned by the reinforcement network. The combination of the four modules in the proposed artificial emotional lazy Q-learning guarantees that the proposed method can output high-performance power generation control instructions that ensure system safety.

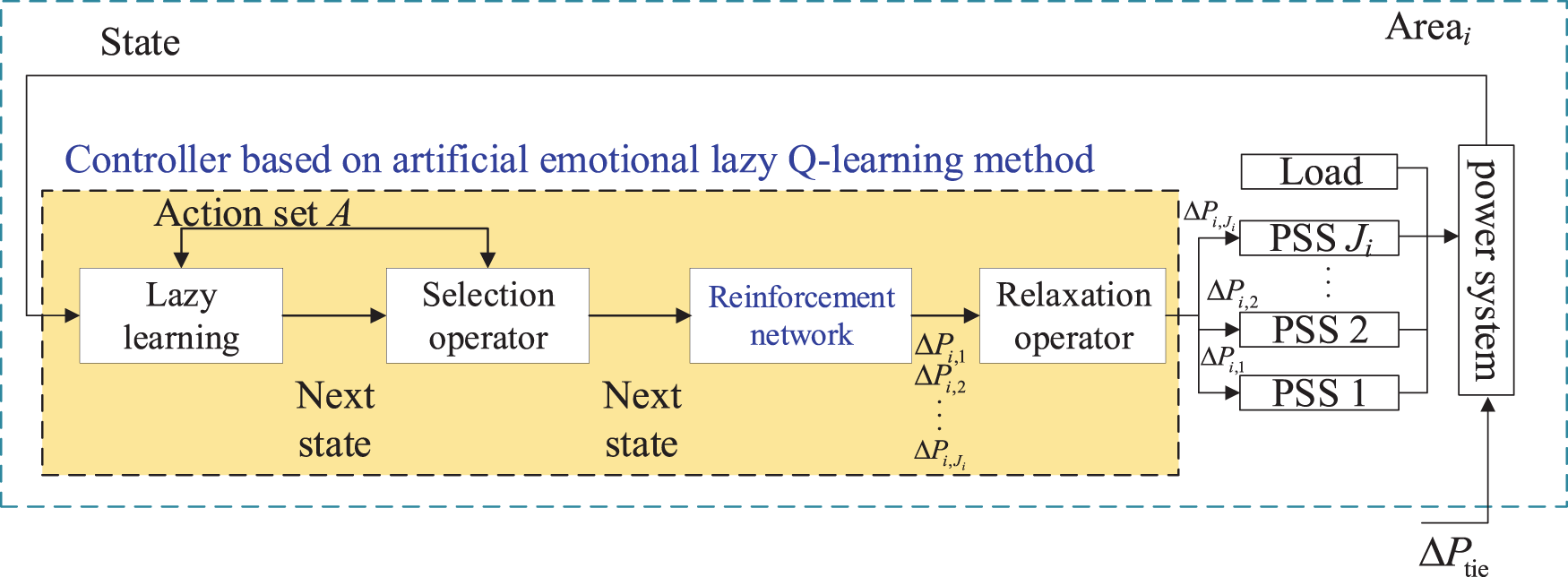
Figure 10: Secure and stable controller based on artificial emotional lazy Q-learning method

4  Case Studies

The experiments in this study are run on a Lenovo R900p2021h model computer (4.1 GHz CPU with 32 GB RAM) on MATLAB 2020B software.

In accordance with the single-machine infinity model presented in this study, three different input scenarios (Fig. 11) are designed to test the comparison algorithms. For a system, the voltage deviation must be maintained within a certain range; for example, the voltage deviation in China is required to be maintained within plus or minus 5%. Therefore, the voltage deviation close to 20% used in this study is employed to simulate the operation of the algorithm under extreme conditions. If the proposed method works well under extreme conditions, the proposed method has a very high safety and stability performances in the real system. For a fair comparison, this study adopted the same parameters for Q-learning and artificial emotional lazy Q-learning. The PID parameters in Table 2 are derived from the particle swarm algorithm seeking optimization with a population size and iteration number of 200. The comparison algorithms tested are the PID controller, the Q-learning controller, and the controller of the proposed artificial emotional lazy Q-learning method. The parameters of the comparison algorithms are shown in Table 2.

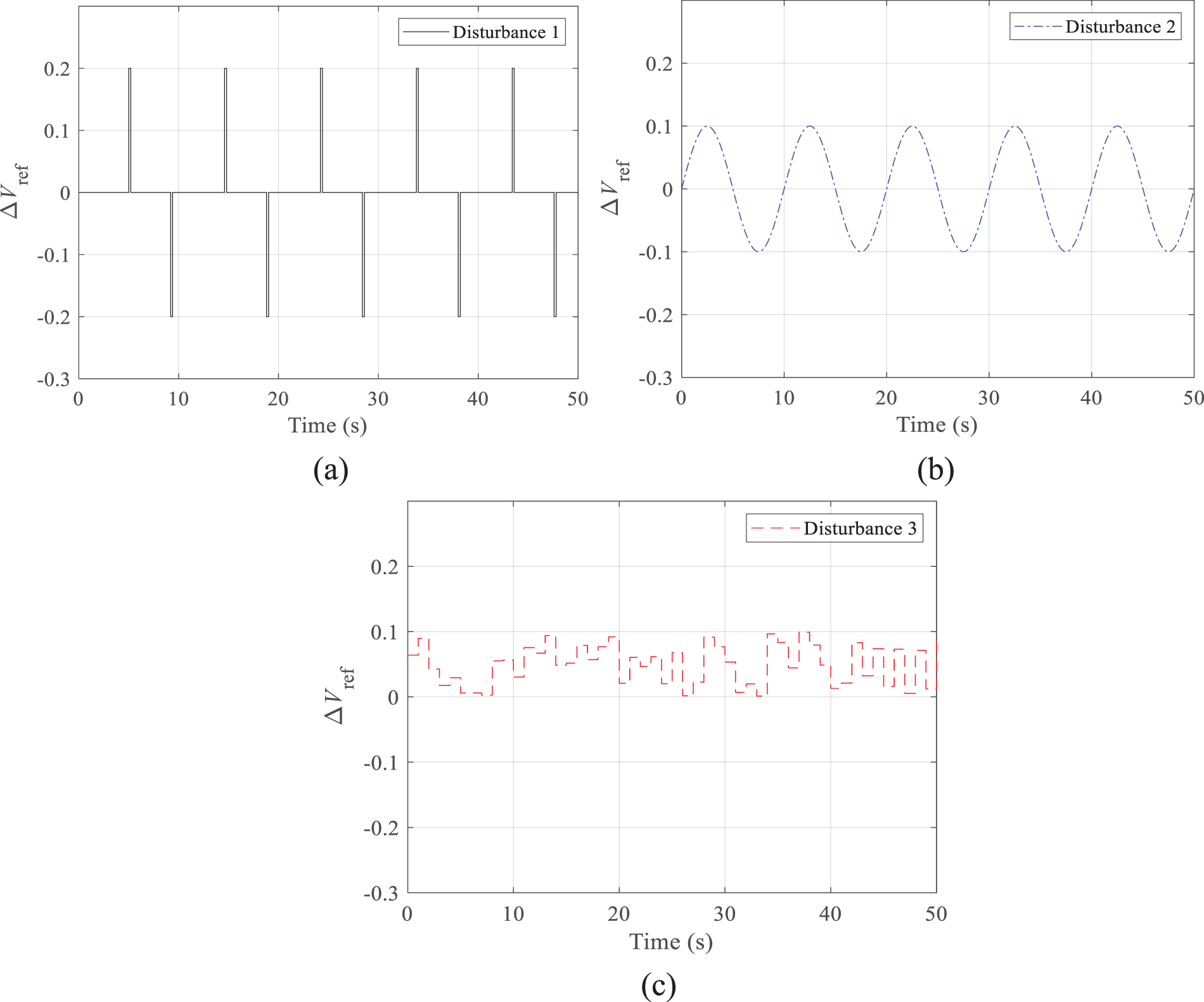
Figure 11: The three designed disturbance inputs: (a) Sudden voltage disturbance input; (b) Voltage sine disturbance input; (c) Voltage random step disturbance input

In the PID method, the larger the gain of the proportional part, the faster the system responds to the deviation, but too large a gain may cause the system to produce an excessive amount of overshoot. The larger the gain of the integral part, the stronger the ability of the system to eliminate the steady state error, but too large a gain may cause the system to generate too large an overshoot. The larger the gain of the differential part, the more sensitive the system is to changes in the input signal and the faster it responds, but too large a gain may cause the system to produce too large an overshoot.

In the Q-learning method, if the learning rate is set too large, Q-value updates may be too drastic, which may make the strategy unstable; if the learning rate is set too small, Q-value updates may be too slow, which makes the strategy learning time longer. If the discount factor is set small, then future rewards will have a greater impact on the strategy, which may make the strategy more cautious; if the discount factor is set large, then current rewards will have a greater impact on the strategy, which may make the strategy riskier. If the reward factor is set large, then rewards will have a greater impact on the strategy, which may make the strategy more inclined to adopt behaviors that will result in greater rewards; if the penalty factor is set large, then penalties will have a greater impact on the strategy, which may make the strategy more inclined to adopt behaviors that will result in avoiding penalties.

In the Q(λ) learning method, the larger the eligibility trace λ is set to indicate that the agent is more enabled to consider the effects from historical Q-values; however, a slow updating of Q-values can result if too large an eligibility trace is set.

The results obtained by the comparison algorithm in 3 different scenarios are shown in Figs. 12–14. The curves in Figs. 11–14 are plotted as data points obtained by sampling every 0.1 s.

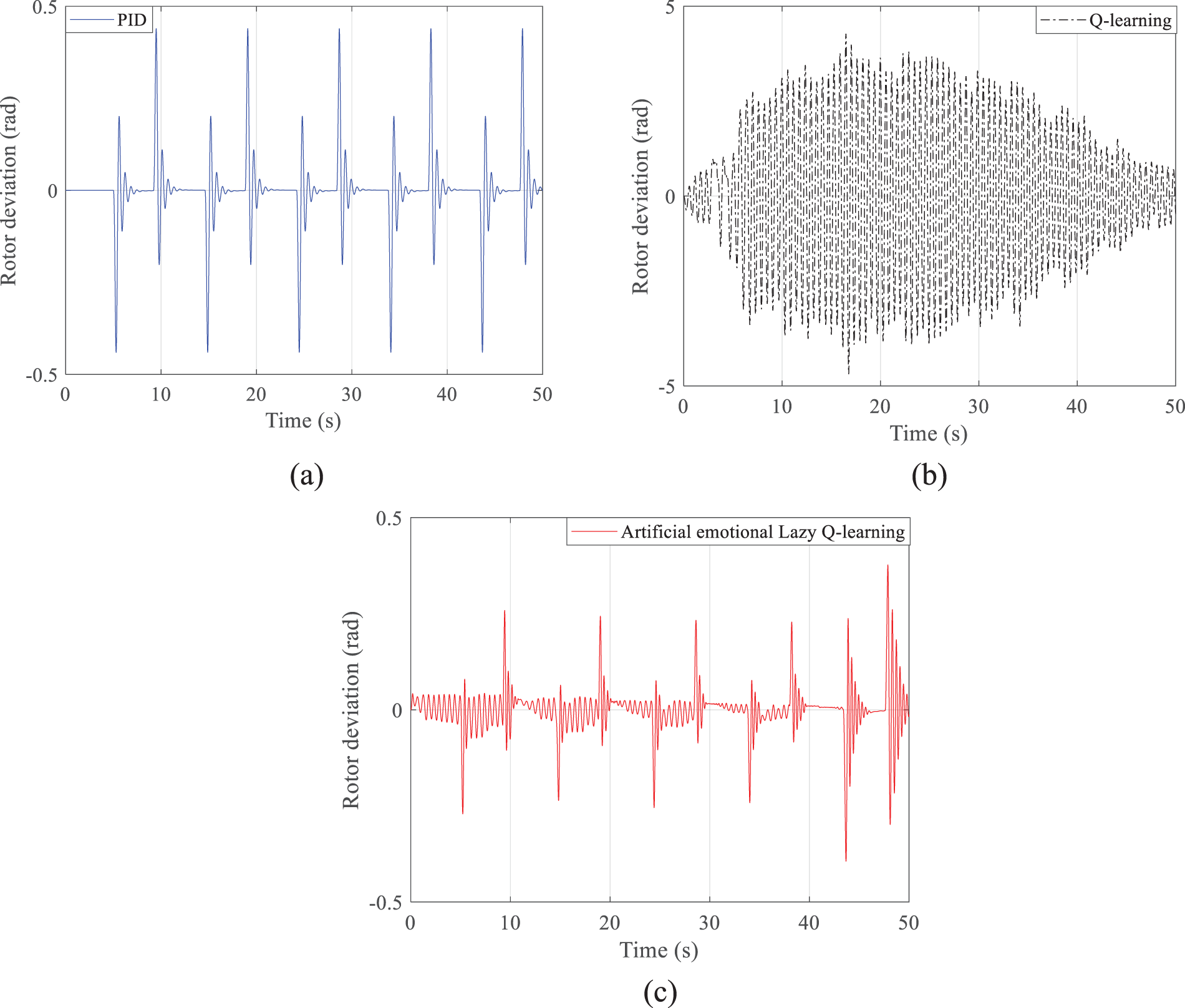
Figure 12: Power angle deviations obtained by the three methods in scenario 1: (a) PID; (b) Q-learning; (c) Artificial emotional lazy Q-learning

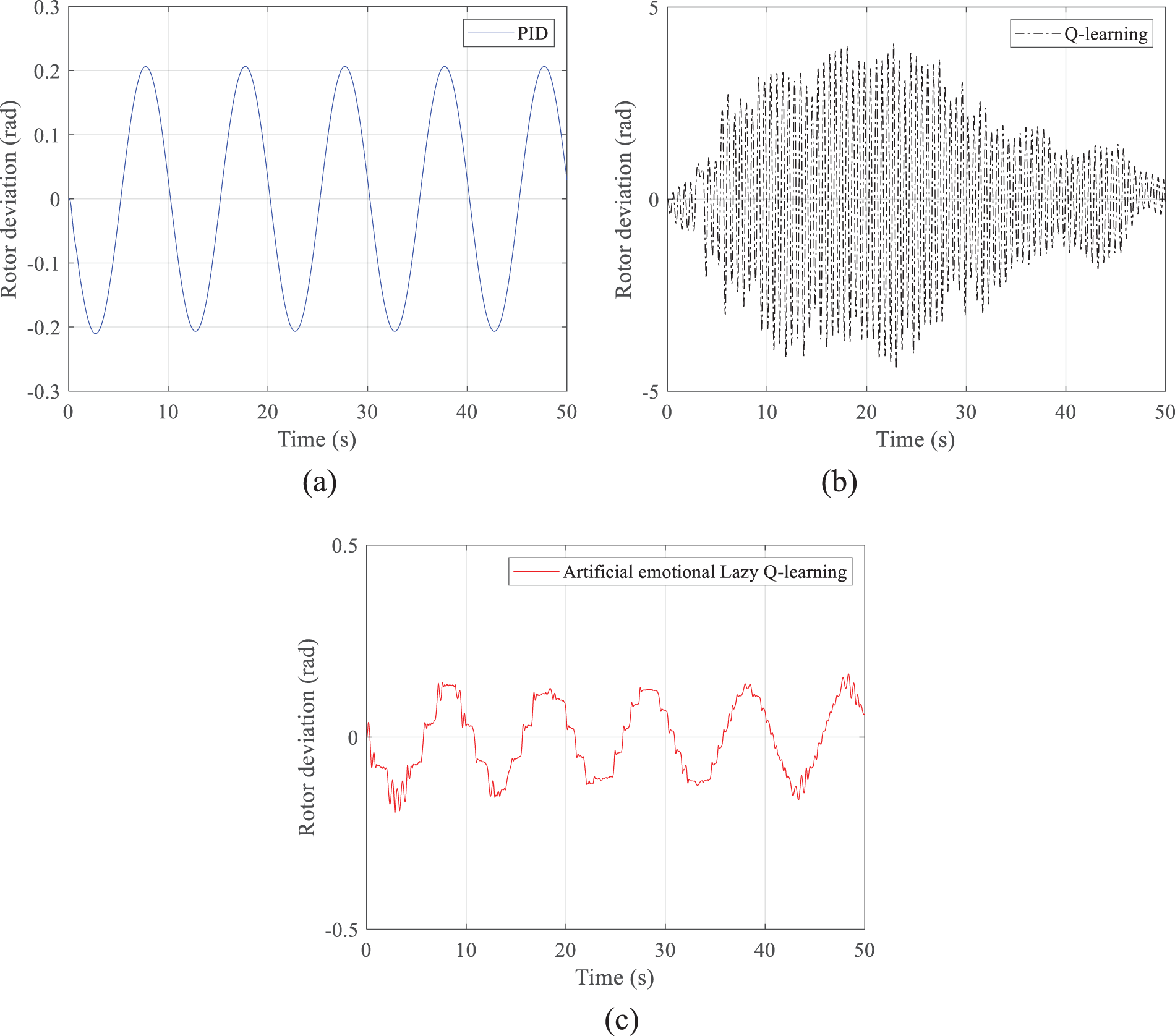
Figure 13: Power angle deviations obtained by the three methods in scenario 1: (a) PID; (b) Q-learning; (c) Artificial emotional lazy Q-learning

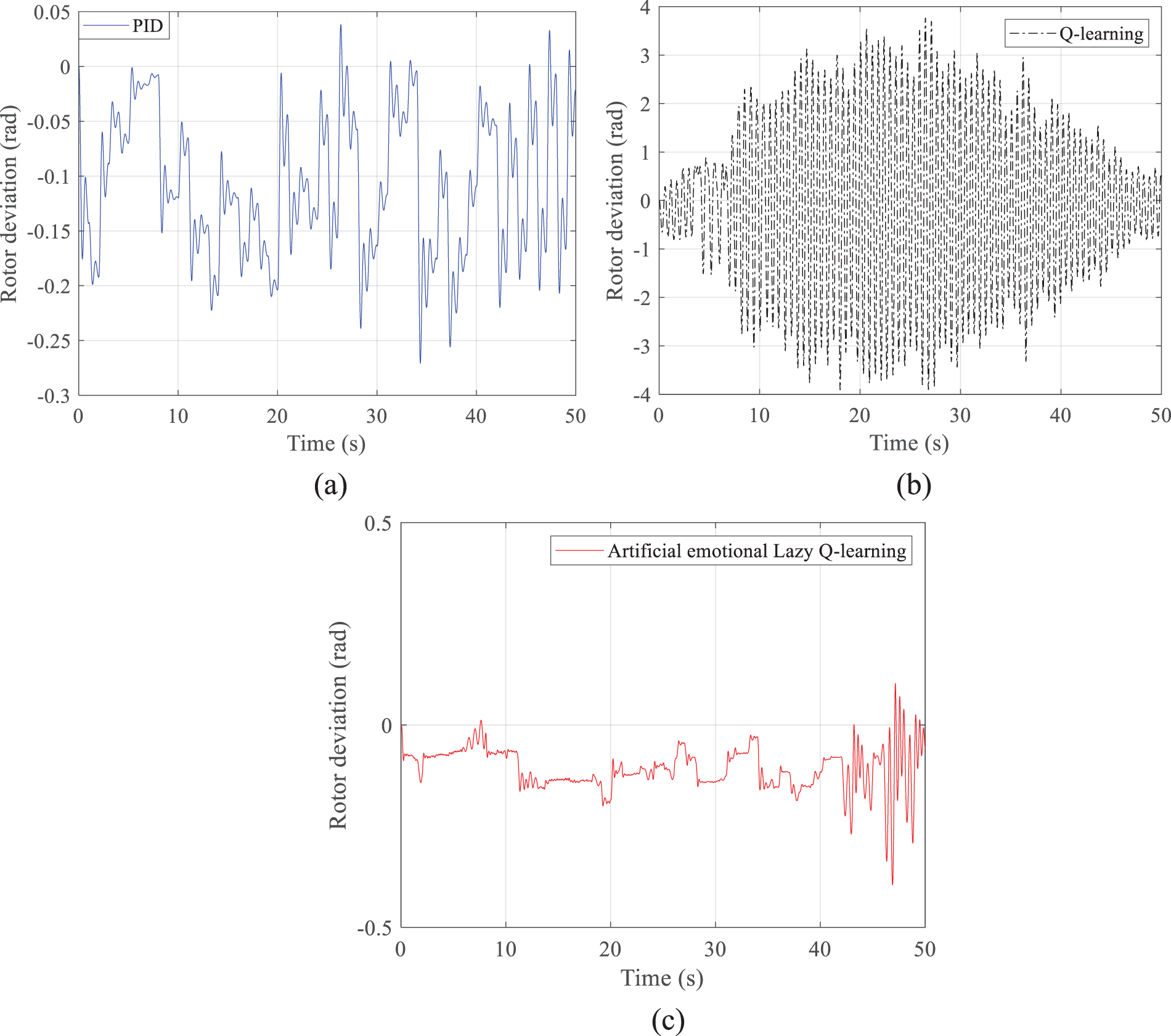
Figure 14: Power angle deviations obtained by the three methods in scenario 1: (a) PID; (b) Q-learning; (c) Artificial emotional lazy Q-learning

Figs. 12–14a show that the PID control changes more significantly with the disturbance and can track the input of the disturbance significantly quickly. Plots (b) of Figs. 12–14 show that the simple Q-learning algorithm is more randomized and less capable of tracking the perturbation completely. However, after a long period of time, the Q-learning algorithm can slowly achieve similar results as the PID control. At the same time, in Figs. 12–14b, the intermediate process is very jittery because all the Q-values in the initial condition are waiting to be updated, and the updating process relies on the probability matrix with randomized selection; although the probability matrix with randomized characteristics can increase the global optimization ability of the Q-learning method, but simultaneously brings a long training time, a slow convergence process, and a strong jittery result in the intermediate process. Figs. 12–14c show that the artificial emotional lazy Q-learning can predict in advance, and although the resulting power angle deviation curve is not as smooth as that of the PID method and has a similar jitter as the Q-learning algorithm, the overall value of the resulting power angle deviation curve is lower. First, Figs. 12–14 correspond to the results obtained in Figs. 11a–11c, respectively. All three figures simulate the case of successive drastic variations of the reference voltage; that is to say, Fig. 11 gives the performance of the control performance of these compared algorithms under harsh conditions.

The artificial emotion in the artificial emotional lazy Q-learning is still not as smooth as the PID control although the values of the actions given by the Q-learning are corrected. The results in Figs. 12–14 also serve to illustrate that the proposed artificial emotional lazy Q-learning method gives actions that, although with discrete characteristics, are still suitable for complex continuous control systems. Although the rotor deviation obtained by the PID method is smooth, the rotor deviation is still very large. Q-learning due to the presence of stochasticity leads to drastic variations that are not even as small as the rotor deviation obtained by the PID method. The proposed method can obtain smaller values of rotor deviation because of the incorporation of artificial emotion and lazy learning.

To verify the generalization of the control performance of the proposed method, this study further tests the proposed artificial emotional lazy Q-learning method with the existing related techniques in the step response case. The parameters of the compared algorithms are still shown in Table 2. The step input is shown in Fig. 15a. The response curves obtained from all the compared algorithms are shown in Fig. 15b.

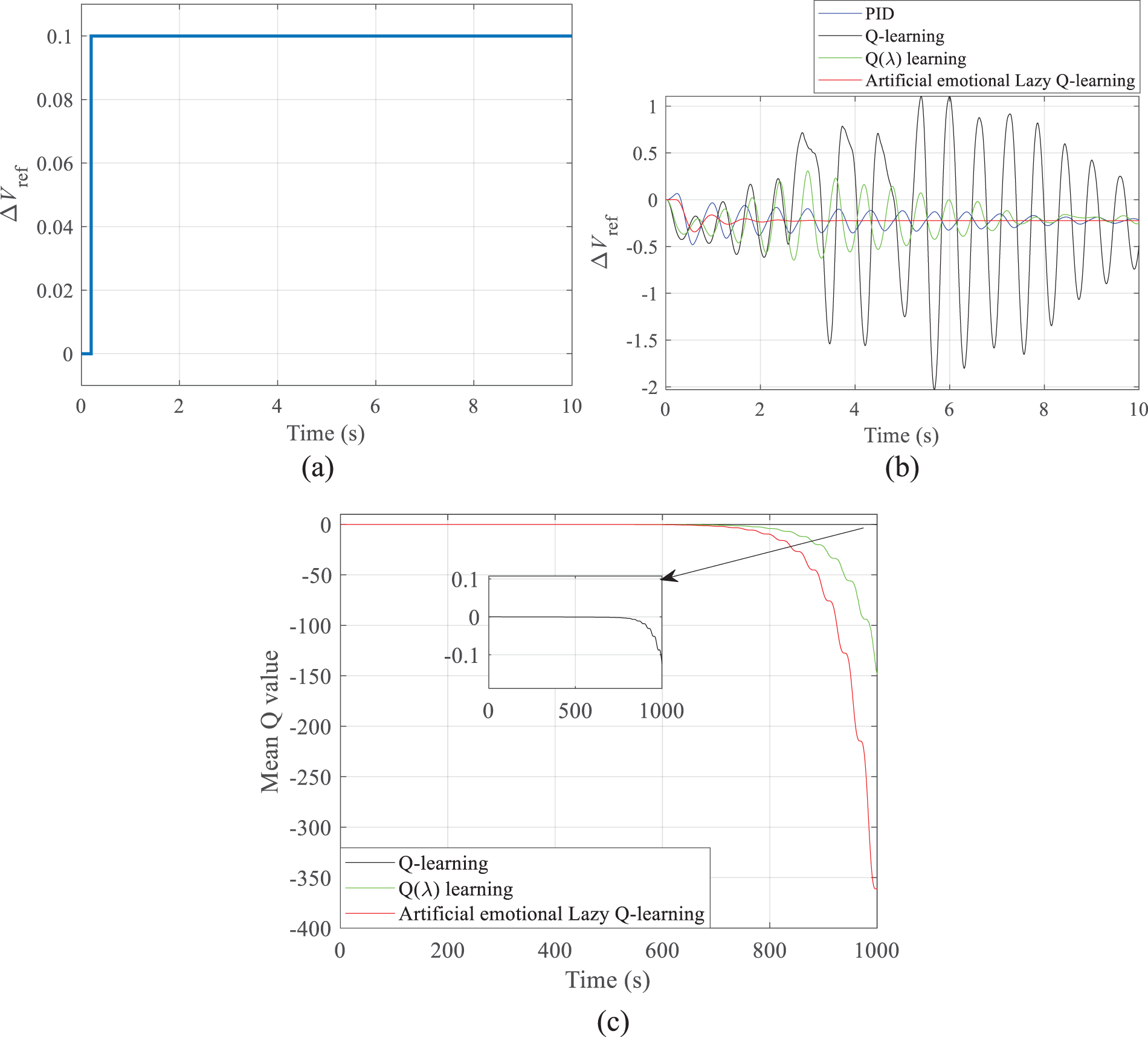
Figure 15: System inputs and outputs: (a) system inputs; (b) system outputs; (c) Q-value curves

Fig. 15b clearly illustrates that the proposed artificial emotional lazy Q-learning method has superior control performances and faster convergence speed. Since the reward value is set to a negative value, the Q-value is continuously reduced from the initialized state of zero; the faster the Q-value decreases indicates the faster update and convergence; therefore, the proposed method converges the fastest (Fig. 15c).

Although the proposed artificial emotional lazy Q-learning method can obtain better control performance metrics than the PID control and Q-learning methods, the artificial emotional lazy Q-learning method still suffers from the following deficiencies.

(1) While artificial emotions can improve the discrete characterization of actions given by Q learning to some extent, the gap still exists compared to continuous actions.

(2) Although lazy learning characterizes the information from high to low dimensions and filters high-quality data for Q-learning to learn, Q-learning methods may not understand how to give actions in non-high-quality cases of the system, and how to balance the comprehensive learning capability and high-quality learning capability of Q-learning methods still requires investigation.

(3) This study has fully considered the single-machine infinity system of the novel power system; however, the joint control problem of the security and stability control of the multi-region novel power system with multi-intelligence synergy has not been considered yet.

5  Conclusion and Prospect

For the problems of static safety and stability analysis of novel power systems, this study proposes an artificial emotional lazy Q-learning method with accelerated optimization search in parallel systems. The proposed method combines artificial emotion, lazy learning, and Q-learning. Compared with other methods, the proposed artificial emotional lazy Q-learning method can obtain better control performance in single-machine power systems with small disturbances. The main features of this study can be summarized as follows:

(1) Since lazy learning can simplify and filter the amount of data, the proposed artificial emotional lazy Q-learning method can quickly filter, sift, and learn the data of varying quality. Thereby, the proposed lazy Q-learning method can quickly learn numerous samples of a novel power system.

(2) Since the Q-learning method is a kind of reinforcement learning, which can control the system without a model online and can cope with the system that changes at any time, the proposed artificial emotional lazy Q-learning method can intelligently respond to the changes occurring in the system and give the optimal control strategy.

(3) In this study, a parallel system is adopted to construct multiple virtual novel power system static security analysis systems at the same time, and the proposed artificial emotional lazy Q-learning method is applied to search for the optimization at the same time. The adopted parallel system can prevent the emergence of the power system, further accelerate the convergence of the system, and quickly ensure the secure and stable operation of the novel power system.

Acknowledgement: The authors acknowledge the support of the China Southern Power Grid Digital Grid Research Institute Corporation.

Funding Statement: This research was funded by the Technology Project of China Southern Power Grid Digital Grid Research Institute Corporation, Ltd. (670000KK52220003) and the National Key R&D Program of China (2020YFB0906000).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Tao Bao, Xiyuan Ma; data collection: Zhuohuan Li, Duotong Yang; analysis and interpretation of results: Pengyu Wang, Changcheng Zhou; draft manuscript preparation: Tao Bao, Xiyuan Ma. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used or analysed during the current study are available from the corresponding author on reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Pamucar, D., Deveci, M., Canıtez, F., Paksoy, T., Lukovac, V. (2021). A novel methodology for prioritizing zero-carbon measures for sustainable transport. Sustainable Production and Consumption, 27, 1093–1112. https://doi.org/10.1016/j.spc.2021.02.016 [Google Scholar] [CrossRef]

2. Lan, L., Zhang, X., Zhang, Y. (2023). A collaborative generation-side clearing model for generation company in coupled energy, ancillary service and carbon emission trading market in China. Journal of Cleaner Production, 407, 137062. https://doi.org/10.1016/j.jclepro.2023.137062 [Google Scholar] [CrossRef]

3. Xiao, K., Yu, B., Cheng, L., Li, F., Fang, D. (2022). The effects of CCUS combined with renewable energy penetration under the carbon peak by an SD-CGE model: Evidence from China. Applied Energy, 321, 119396. https://doi.org/10.1016/j.apenergy.2022.119396 [Google Scholar] [CrossRef]

4. Shair, J., Li, H., Hu, J., Xie, X. (2021). Power system stability issues, classifications and research prospects in the context of high-penetration of renewables and power electronics. Renewable and Sustainable Energy Reviews, 145, 111111. https://doi.org/10.1016/j.rser.2021.111111 [Google Scholar] [CrossRef]

5. Hu, Z., Yao, W., Shi, Z., Shuai, H., Gan, W. et al. (2023). Intelligent and rapid event-based load shedding pre-determination for large-scale power systems: Knowledge-enhanced parallel branching dueling Q-network approach. Applied Energy, 347, 121468. https://doi.org/10.1016/j.apenergy.2023.121468 [Google Scholar] [CrossRef]

6. Singh, K. (2020). Load frequency regulation by de-loaded tidal turbine power plant units using fractional fuzzy based PID droop controller. Applied Soft Computing, 92, 106338. https://doi.org/10.1016/j.asoc.2020.106338 [Google Scholar] [CrossRef]

7. Xiang, Z., Shao, X., Wu, H., Ji, D., Yu, F. et al. (2020). An adaptive integral separated proportional-integral controller based strategy for particle swarm optimization. Knowledge-Based Systems, 195, 105696. https://doi.org/10.1016/j.knosys.2020.105696 [Google Scholar] [CrossRef]

8. Zhao, Y., Hu, W., Zhang, G., Huang, Q., Chen, Z. et al. (2023). Novel adaptive stability enhancement strategy for power systems based on deep reinforcement learning. International Journal of Electrical Power & Energy Systems, 152, 109215. https://doi.org/10.1016/j.ijepes.2023.109215 [Google Scholar] [CrossRef]

9. Yu, H., Guan, Z., Chen, T., Yamamoto, T. (2020). Design of data-driven PID controllers with adaptive updating rules. Automatica, 121, 109185. https://doi.org/10.1016/j.automatica.2020.109185 [Google Scholar] [CrossRef]

10. Khamies, M., Magdy, G., Ebeed, M., Kamel, S. (2021). A robust PID controller based on linear quadratic gaussian approach for improving frequency stability of power systems considering renewables. ISA Transactions, 117, 118–138. https://doi.org/10.1016/j.isatra.2021.01.052 [Google Scholar] [PubMed] [CrossRef]

11. Chen, Q., Wang, Y., Song, Y. (2021). Tracking control of self-restructuring systems: A low-complexity neuroadaptive PID approach with guaranteed performance. IEEE Transactions on Cybernetics, 53(5), 3176–3189. [Google Scholar]

12. Chen, C., Cui, M., Li, F., Yin, S., Wang, X. (2020). Model-free emergency frequency control based on reinforcement learning. IEEE Transactions on Industrial Informatics, 17(4), 2336–2346. [Google Scholar]

13. Zhao, F., Liu, Y., Zhu, N., Xu, T. (2023). A selection hyper-heuristic algorithm with Q-learning mechanism. Applied Soft Computing, 147, 110815. https://doi.org/10.1016/j.asoc.2023.110815 [Google Scholar] [CrossRef]

14. Wang, D., Fan, R., Li, Y., Sun, Q. (2023). Digital twin based multi-objective energy management strategy for energy internet. International Journal of Electrical Power & Energy Systems, 154, 109368. https://doi.org/10.1016/j.ijepes.2023.109368 [Google Scholar] [CrossRef]

15. Yang, T., Yu, X., Ma, N., Zhang, Y., Li, H. (2022). Deep representation-based transfer learning for deep neural networks. Knowledge-Based Systems, 253, 109526. https://doi.org/10.1016/j.knosys.2022.109526 [Google Scholar] [CrossRef]

16. Yan, H., Peng, Y., Shang, W., Kong, D. (2023). Open-circuit fault diagnosis in voltage source inverter for motor drive by using deep neural network. Engineering Applications of Artificial Intelligence, 120, 105866. https://doi.org/10.1016/j.engappai.2023.105866 [Google Scholar] [CrossRef]

17. Yan, Z., Xu, Y. (2020). A multi-agent deep reinforcement learning method for cooperative load frequency control of a multi-area power system. IEEE Transactions on Power Systems, 35(6), 4599–4608. https://doi.org/10.1109/TPWRS.59 [Google Scholar] [CrossRef]

18. Liu, M., Chen, L., Du, X., Jin, L., Shang, M. (2021). Activated gradients for deep neural networks. IEEE Transactions on Neural Networks and Learning Systems, 34(4), 2156–2168. [Google Scholar]

19. Ganesh, A. H., Xu, B. (2022). A review of reinforcement learning based energy management systems for electrified powertrains: Progress, challenge, and potential solution. Renewable and Sustainable Energy Reviews, 154, 111833. https://doi.org/10.1016/j.rser.2021.111833 [Google Scholar] [CrossRef]

20. Krouka, M., Elgabli, A., Issaid, C. B., Bennis, M. (2021). Communication-efficient and federated multi-agent reinforcement learning. IEEE Transactions on Cognitive Communications and Networking, 8(1), 311–320. [Google Scholar]

21. Yin, L., Li, S., Liu, H. (2020). Lazy reinforcement learning for real-time generation control of parallel cyber-physical–social energy systems. Engineering Applications of Artificial Intelligence, 88, 103380. https://doi.org/10.1016/j.engappai.2019.103380 [Google Scholar] [CrossRef]

22. Zhao, S., Li, K., Yang, Z., Xu, X., Zhang, N. (2022). A new power system active rescheduling method considering the dispatchable plug-in electric vehicles and intermittent renewable energies. Applied Energy, 314, 118715. https://doi.org/10.1016/j.apenergy.2022.118715 [Google Scholar] [CrossRef]

23. Huang, J., Zhang, Z., Han, J. (2021). Stability analysis of permanent magnet generator system with load current compensating method. IEEE Transactions on Smart Grid, 13(1), 58–70. [Google Scholar]

24. Guo, K., Qi, Y., Yu, J., Frey, D., Tang, Y. (2021). A converter-based power system stabilizer for stability enhancement of droop-controlled islanded microgrids. IEEE Transactions on Smart Grid, 12(6), 4616–4626. https://doi.org/10.1109/TSG.2021.3096638 [Google Scholar] [CrossRef]

25. Devito, G., Nuzzo, S., Barater, D., Franceschini, G. (2022). A simplified analytical approach for hybrid exciters of wound-field generators. IEEE Transactions on Transportation Electrification, 8(4), 4303–4312. https://doi.org/10.1109/TTE.2022.3167797 [Google Scholar] [CrossRef]

26. Deng, H., Fang, J., Qi, Y., Tang, Y., Debusschere, V. (2022). A generic voltage control for grid-forming converters with improved power loop dynamics. IEEE Transactions on Industrial Electronics, 70(4), 3933–3943. [Google Scholar]

27. Chien, C. F., Lan, Y. B. (2021). Agent-based approach integrating deep reinforcement learning and hybrid genetic algorithm for dynamic scheduling for Industry 3.5 smart production. Computers & Industrial Engineering, 162, 107782. https://doi.org/10.1016/j.cie.2021.107782 [Google Scholar] [CrossRef]

28. Li, H., He, H. (2022). Learning to operate distribution networks with safe deep reinforcement learning. IEEE Transactions on Smart Grid, 13(3), 1860–1872. https://doi.org/10.1109/TSG.2022.3142961 [Google Scholar] [CrossRef]

29. Yin, L., He, X. (2023). Artificial emotional deep Q learning for real-time smart voltage control of cyber-physical social power systems. Energy, 273, 127232. https://doi.org/10.1016/j.energy.2023.127232 [Google Scholar] [CrossRef]

30. Zou, Y., Yin, H., Zheng, Y., Dressler, F. (2023). Multi-agent reinforcement learning enabled link scheduling for next generation internet of things. Computer Communications, 205, 35–44. https://doi.org/10.1016/j.comcom.2023.04.006 [Google Scholar] [CrossRef]