Research on Carbon Emission for Preventive Maintenance of Wind Turbine Gearbox Based on Stochastic Differential Equation

1  Introduction

Wind power generation is one of the most mature technologies in renewable energy. However, wind farms are often situated in remote locations characterized by harsh working environments and elevated equipment heights, which significantly challenge the maintenance of wind turbine equipment. Wind turbines, as critical components of the wind power system, possess a complex structure and operate under demanding conditions. They are subject to various loads and environmental influences, leading to component degradation, faults, and failures. Particularly, gearboxes, as the components with the highest failure rate in wind turbines, frequently experience malfunctions and shutdowns. Consequently, reliability analysis is imperative to optimize maintenance strategies. Preventive maintenance is a pivotal method for ensuring equipment operates in a stable and efficient condition. It involves proactive equipment monitoring to identify early signs of failure and implementing maintenance activities to prevent equipment degradation, thus reducing downtime and maintenance losses. Traditional preventive maintenance strategies, such as time-based maintenance (TBM), often result in over or under-maintenance scenarios [1–3].

Condition-based maintenance (CBM) represents a more advanced approach, focusing on monitoring and diagnosing equipment conditions to detect abnormalities and tailor maintenance plans accordingly. This strategy has gained widespread application in wind farms. In preventive maintenance models for wind turbines, the Weibull model is frequently employed to depict the reliability changes of wind turbines. Service age regression and failure rate increment factors are used to represent the failure recovery rate and change rate post-maintenance, respectively [4]. This approach is particularly advantageous in the maintenance strategy of units under unique offshore environmental conditions, optimizing maintenance scope primarily based on system performance. The impact of maintenance on reliability, including the correlation between lifecycle reliability and the timing of maintenance and failure, has been studied through simulation in reference [5]. A proportional hazard model, describing the relationship between the operating status of a gearbox and its failure rate, has been utilized to predict the maintenance interval of gearboxes, with reliability as the core maintenance objective [6]. Therefore, the operating status of a gearbox is crucial in determining the optimal inspection time. Su et al. explored the operation and reliability of gearboxes under preventive maintenance, considering both TBM and CBM, by establishing a unified maintenance model based on stochastic process theory [7–9].

Previous literature has focused on predicting gearbox maintenance intervals with reliability as the primary objective. However, it often overlooks the environmental impacts on gearbox condition and the associated carbon emissions throughout the gearbox’s lifecycle. Prolonged operation of wind equipment not only increases preventive maintenance costs but also leads to performance deterioration. The operation of wind turbines is inherently linked with escalated energy consumption, operating costs, and carbon emissions. Thus, implementing appropriate maintenance decisions can significantly reduce both carbon emissions and operational costs. Maintenance decisions, as opposed to technological advancements, present a more feasible approach for reducing carbon emissions.

Franciosi et al. integrated the concept of circular economy into the regular preventive maintenance model, highlighting the importance of considering sustainability factors in daily maintenance activities for sustainable development [10]. A joint optimization model for maintenance and production plans, considering carbon emissions, was developed to determine the optimal maintenance and production strategy, factoring in energy consumption per unit of equipment and resultant carbon emissions [11]. Afrinaldi et al. proposed a model for determining optimal preventive replacements to minimize economic and environmental impacts [12]. A maintenance optimization model that considers carbon emissions was introduced in reference [13], incorporating improvement factors into the equipment failure rate and carbon emissions model to highlight maintenance imperfections. Subsequently, a multi-objective decision model was developed to minimize both carbon emissions and cost rates. Liu et al. proposed an opportunistic maintenance strategy for wind turbines, accounting for structural and random correlations, as well as carbon emissions. This strategy involves introducing service age regression factors and failure rate increasing factors into the failure rate and carbon emissions models to depict incomplete maintenance. Through case analysis, the optimal opportunistic maintenance timing was determined, elucidating the correlation coefficient and sensitivity of carbon emissions [14]. Although these studies consider carbon emissions during equipment maintenance and introduce factors to describe maintenance imperfections, they often neglect the impact of random minor factors on equipment condition.

There is a discernible relationship between equipment maintenance activities and carbon emissions. The assessment of equipment condition directly influences the choice of maintenance strategies. In conducting preventive maintenance, timely adjustment of maintenance schedules is essential to safeguard environmental benefits and minimize carbon emissions. Therefore, this article focuses on the wind turbine gearbox, considering the impact of external random disturbances on equipment state and the reduction in equipment failure and emission rates due to maintenance activities. Additionally, the role of equipment recycling in emission reduction is examined. By optimizing the preventive maintenance plan for gearboxes, the environmental benefits of the equipment are balanced, and the model’s effectiveness is demonstrated through numerical examples.

2  Mathematical Model and Solution

2.1 Description of Gearbox Model

Current equipment state models primarily utilize ordinary differential equations, which are based on fault rates but often neglect the impact of external disturbances during operation. Given that wind turbine equipment operation is influenced by random factors such as environmental conditions, weather changes, and routine inspections, it is essential to consider these aspects in equipment state modeling. Accordingly, to account for non-homogeneous random disturbances acting on the equipment, the Ito-type stochastic differential equation (SDE) is employed to construct the state change model. In this model, a random function X(t) represents the health state of the gearbox at time t. The evolution of X(t) reflects the state changes over the lifespan of the wind turbine gearbox. The external random interference experienced by the gearbox during operation is denoted by {B(t)}, a standard Brownian motion, and X(t) undergoes a random differential over the interval [0, t].

The state transition model for the wind power gearbox is represented by:

dX(t)=λ(X(t),t)dt+μ(X(t),t)dB(t)(1)

μ(X(t),t)=kX(t)(2)

wherein, λ(X(t),t) represents the equipment’s failure rate function, μ(X(t),t) denotes the random disturbance coefficient, and k is the state fluctuation parameter, referred to as the equipment state fluctuation rate. This model is based on the following assumptions:

Assumption 1: The maintenance of the gearbox is instantaneously completed, with the expected random disturbance value being zero.

Assumption 2: λ(X(t),t), μ(X(t),t) are B[0,t]×Bt measurable functions defined on [0,t]×Rt, if λ(X(t),t) and μ≤N and all t≤T meet the following conditions:

|λ(x,t)−λ(y,t)|+|μ(x,t)−μ(y,t)|<K|x−y|(3)

|λ(x,t)|+|μ(x,t)|<KT(1+|x|)(4)

Under these assumptions, the solution to the stochastic differential equation possesses a unique strong solution.

In life data analysis, the Weibull distribution is extensively used due to its ability to fit a wide range of sample data by adjusting its shape, scale, and position parameters. The variability in its shape parameters enables the description of diverse data trends, including decline, stability, and growth. The degradation of gearboxes aligns with the Weibull distribution, effectively characterizing the life distribution of wind turbine gearboxes. Based on this, the gearbox model assumes failure through component fatigue, with its shape parameters offering considerable flexibility in data fitting. Therefore, the fundamental failure rate model for gearboxes can be formulated as:

λ0(t)=βη(tη)β−1(5)

wherein, β is a shape parameter, and η is a proportion parameter.

The changes in the state of the wind turbine gearbox are influenced by a combination of the inherent degradation of the gearbox and external factors. The failure rate of the wind turbine gearbox is a continuous function, representing the basic failure rate. Consequently, the comprehensive failure rate of the wind power gearbox can be determined by incorporating the state fluctuation rate [15].

λ(t)=βη(tη)β−111+α⋅x(t)(6)

The reliability function of the gearbox is denoted by Eq. (7):

R(X(t),t)=exp⁡[−∫0tλ(X(t),t)dt]=exp⁡[−(tη)β11+α⋅x(t)](7)

The ζ-th preventive maintenance interval of the gearbox is denoted by Tζ. Therefore, [T1,T2,⋯,Tζ] is used to represent each preventive maintenance interval within the lifecycle of the gearbox.

Consequently, the number of preventive maintenance interventions can be expressed as:

NC=∑i=1ςλ(t)dt(8)

2.2 Model Analysis

Based on the failure rate model for the wind power gearbox, the likelihood function is formulated using Eq. (7) in conjunction with the failure density function f(x(t),t)=λ(x(t),t)×R(x(t),t) as follows:

L(β,η,α)=∏i=1rλ(x(ti),ti)∏j=1NR(x(ti),ti)=∏i=1rβη(tiη)β−111−α⋅x(ti)⋅∏j=1Nexp⁡[−(tjη)β11−α⋅x(tj)](9)

The logarithmic Likelihood function is then derived, as illustrated in Eq. (10):

ln⁡L(β,η,α)=rln⁡βη+∑i=1r[(β−1)ln⁡(tiη)−ln⁡(1−αx(ti))]−∑j=1N[(tjη)β11−α⋅x(tj)](10)

The Newton-Raphson iteration method is employed to develop the following iteration formula:

M=[∂ln⁡L∂β∂ln⁡L∂η∂ln⁡L∂α](11)

P=[∂2ln⁡L∂β2∂2ln⁡L∂β∂η∂2ln⁡L∂β∂α∂2ln⁡L∂η∂β∂2ln⁡L∂η2∂2ln⁡L∂η∂α∂2ln⁡L∂α∂β∂2ln⁡L∂α∂η∂2ln⁡L∂α2](12)

This yields:

[βηα]g+1=[βηα]g−Pg−1Mg(13)

By solving Eq. (13), the parameter estimation values for the above fault rate model can be determined. The maintenance timing for CBM is deduced based on a reliability threshold. It is assumed that at time t, the reliability of the gearbox equipment either reaches or falls below a threshold, denoted as R=Rref, When this occurs, maintenance is required to ensure that the condition of the gearbox remains within the normal operating range. Herein, Rref represents the reliability threshold of the device.

2.2.1 TBM Analysis

TBM assumes a consistent expected sample in each cycle [16]. An ordinary differential equation (ODE) is utilized to construct the state transition model for the wind power gearbox, as delineated below:

dE(X(t))=E[λ(E(X(t)),t)dt]=λE(X(t))dt(14)

The state transition model, developed using ODE, is:

dX(t)=λ(X(t),t)dt=βη(tη)β−1exp⁡(δ⋅x(t))dt(15)

wherein, δ represents the regression coefficient. Since X^(t) is the average expected value of X(t), the maximum likelihood estimation method is then applied to solve Eq. (15).

3  Carbon Emission Model

Throughout the lifecycle of wind turbines, environmental impacts primarily involve carbon emissions resulting from energy consumption during use and recycling. Recycling is recognized as a means to reduce carbon emissions. The need for maintenance is primarily due to the continuous degradation and performance deterioration of wind turbines during operation [17].

In operation, the gearbox transmits power from the wind to the generator. The rotor’s low speed in the wind turbine must be accelerated by the gearbox to achieve the necessary speed for power generation. To ensure braking capacity, braking devices are installed at both the input and output ends of the gearbox. These work in conjunction with the braking system to halt the wind turbine drive system. Consequently, during operation, forced lubrication of gears and bearings is critical for safety. This lubrication system comprises an oil supply device, a filtration system, an oil/air cooling device, and connecting pipelines. The energy consumption of this lubrication system is a contributor to carbon emissions. The primary objectives of lubricating the gearbox are to reduce friction and provide cooling, thereby ensuring efficient operation and extending the service life of the gearbox [18].

As such, the gearbox consumes energy during operation, leading to carbon emissions. For every 1 kWh of electricity consumed, carbon emissions amount to 0.272 kg, and carbon dioxide emissions are 0.997 kg.

When sudden malfunctions occur in a wind turbine’s gearbox, minor repairs are undertaken to maintain normal operation. However, these repairs neither alter the gearbox’s failure rate nor its carbon emissions; they simply restore operational health. Increasing the frequency of preventive maintenance enhances the duration of reliable gearbox operation, reducing the likelihood of failures and the need for minor maintenance.

Prolonging the operation of the wind gearbox escalates energy consumption and environmental impact, accompanied by operational performance degradation. Throughout the gearbox’s lifecycle, increasing the frequency of preventive maintenance for wind turbine equipment reduces the probability of unexpected gearbox failures and accordingly diminishes the frequency of fault maintenance. However, excessive preventive maintenance within a cycle can lead to unnecessary resource waste and an increase in carbon emissions during that cycle, as illustrated in Fig. 1 [14].

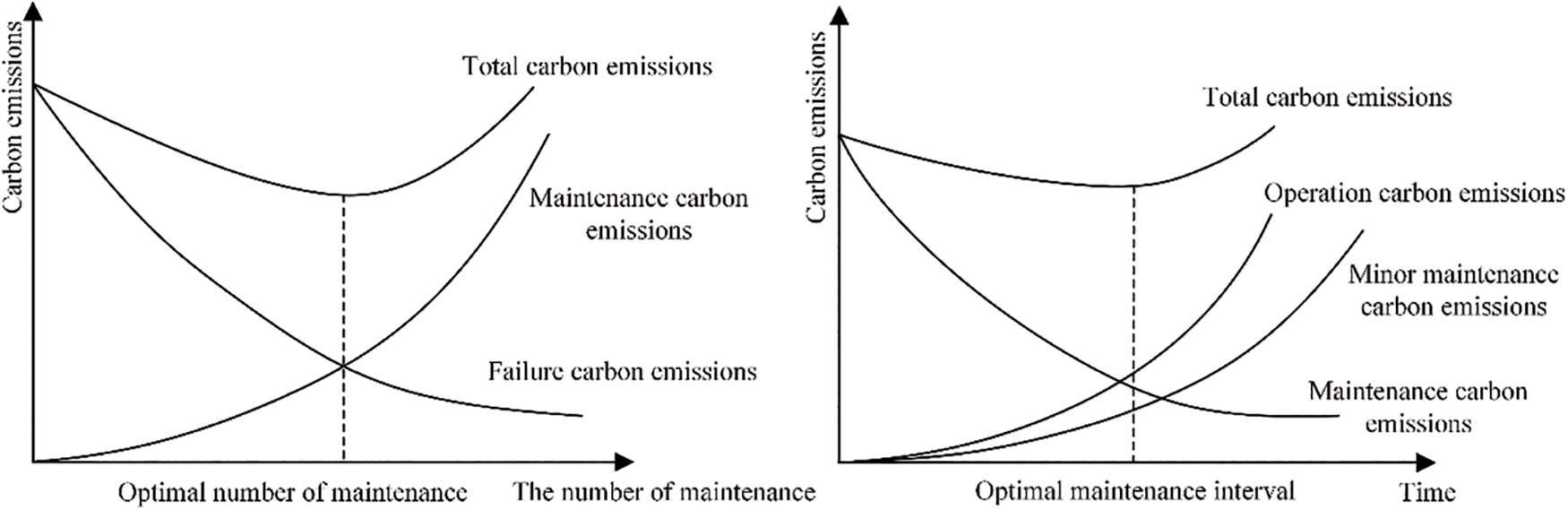
Figure 1: Variation in carbon emissions relative to the number of preventive maintenance interventions and preventive maintenance intervals

During the operational phase of a wind power project, which is the most prolonged phase of the entire project lifecycle, activities predominantly involve replacing equipment and materials and consuming energy resources. The carbon emissions during the gearbox’s lifespan are mainly due to energy used in operation, maintenance, construction, installation, and retirement of the wind turbine equipment [14].

CO2 emissions and energy consumption of wind farms are largely concentrated in the production and transportation stage of wind turbines, accounting for 89.62% of the total CO2 emissions and 113.95% of the total energy consumption. CO2 emissions and energy consumption in the infrastructure and operation and maintenance stages are the second and third highest, respectively. Recycling in the waste disposal stage results in CO2 emissions and energy consumption accounting for 46.24% and −88.72% of the total in the gearbox retirement stage, respectively [19]. Fig. 2 shows the distribution of CO2 emissions and energy consumption across these four stages.

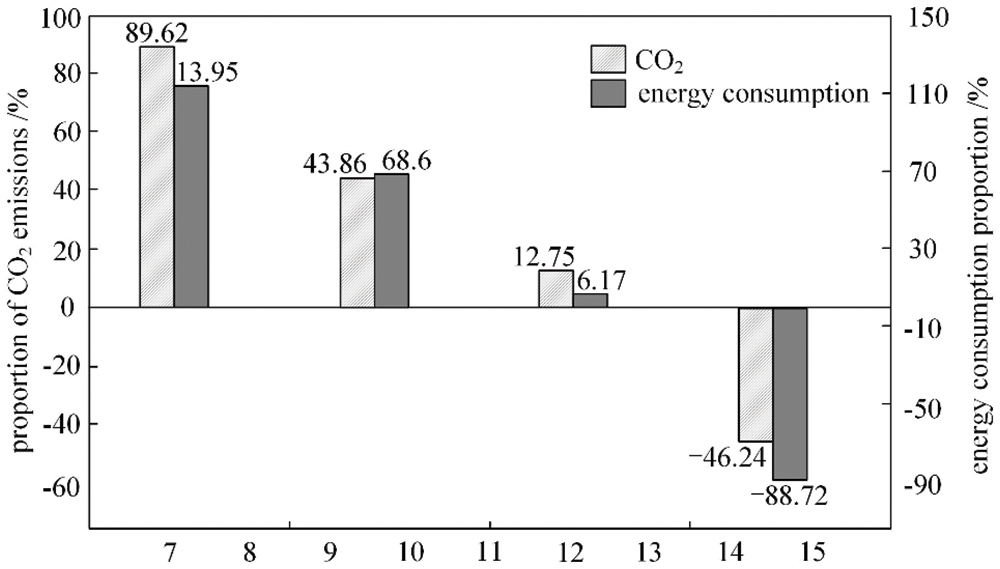
Figure 2: Ratio of CO2 emissions and energy consumption in each stage of the wind farm

The carbon emissions over the lifespan of gearboxes are divided into three parts: emissions generated during the operation phase, emissions during the maintenance phase, emissions during the production phase, and emissions recovered during the retirement phase.

Therefore, the carbon emissions GT over the lifespan of the gearbox are represented by:

GT=G1+G2+G3(16)

wherein G1 denotes the carbon emissions generated during the operation phase of the gearbox, equivalent to the total energy consumption during operation. This is expressed as:

G1=GuseH(17)

Guse-Carbon emissions per unit of energy consumed;

H-Total energy consumption during equipment operation.

G2 represents the carbon emissions produced during the gearbox’s maintenance phase, calculated as the total number of maintenance occurrences multiplied by the carbon emissions from a single maintenance event.

G2=ζGm(18)

ζ-The total number of maintenance times within the gearbox’s lifecycle;

Gm-The carbon emissions generated by a single gearbox maintenance activity.

Furthermore, G3 refers to the carbon emissions generated during the production phase and the carbon emissions recovered during the retirement phase. As the carbon emissions recovered during the retirement phase are considered a reduction in total emissions, the carbon emissions for the production and retirement phases are calculated as the emissions generated during production minus the emissions recovered during retirement.

G3=GP−εGP(19)

ε-Recovery coefficient;

Gp-Carbon emissions generated by manufacturing the device.

From the analysis above, it can be concluded that:

GT=GuseH+ζGm+GP−εGP(20)

The energy consumption function of the gearbox during operation is represented by:

hn(t)=at+b(21)

wherein, a and b are parameters of the device energy consumption function. Maintenance activities not only restore the equipment’s performance but also impact its carbon emissions. The relationship between the energy consumption functions of the gearbox, before and after the n-th preventive maintenance, is expressed as:

hn+1(t)=∏e=1nξehn(t)=∏e=1nξe(at+b)(22)

where, ξe represents the rate of change in the gearbox failure rate following the e-th preventive maintenance.

The total energy consumption of the gearbox during operation is calculated as:

H=∫0T1h1(t)dt+∫0T2h2(t)dt+⋯+∫0Tζhζ(t)dt=∑n=1ζ∫0Tnhn(t)dt(23)

The unit time carbon emissions over the gearbox’s lifecycle can be represented as:

GWP=GT∑n=1ζTn=GuseH+ζGm+GP−εGP∑n=1ζTn=Guse(∑n=1ζ∫0Tnhn(t)dt)+ζGm+GP−εGP∑n=1ζTn(24)

4  Example Analysis

4.1 Instance Validation

The state monitoring methods for wind power gearboxes typically include vibration monitoring, acoustic monitoring, oil grinding monitoring, and temperature monitoring, with both offline and online monitoring approaches. Under fault conditions, the vibration signal of a wind power gearbox is generally nonlinear and non-stationary [20]. Therefore, amplitude data is selected as the condition monitoring data and fault data for the wind power gearbox. This paper utilizes the actual fault monitoring data from a wind farm unit’s gearbox for simulation. The specified service life for this type of wind turbine is 15 years, with the vibration monitoring data presented in Table 1 and some fault data shown in Table 2.

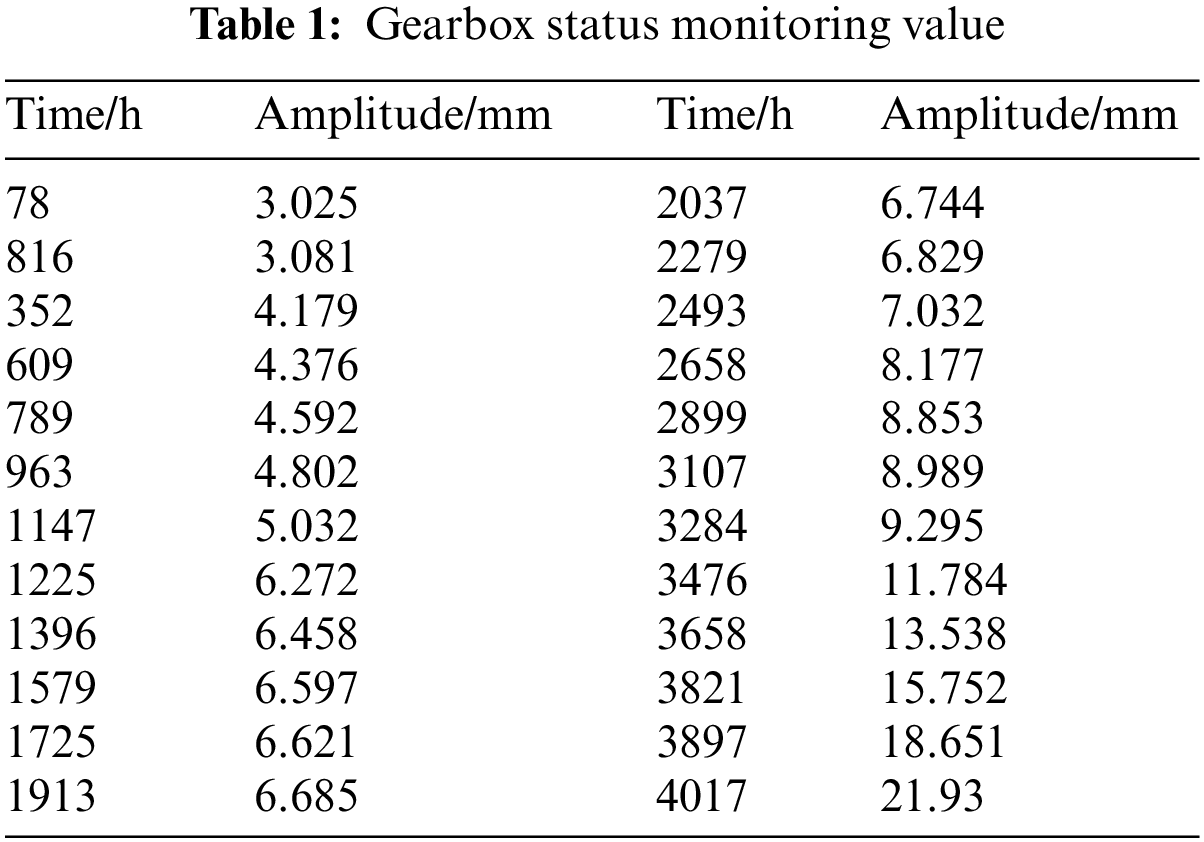
Based on the state monitoring data and the Newton-Raphson model parameter solving method, the following can be deduced: β=2.46,η=733.68,α=−0.335.

Consequently, the state transition model of the gearbox is formulated as follows:

dX(t)=[2.46733.68(t733.68)1.46⋅11−0.335⋅x(t)]dt+0.00127⋅x(t)dB(t)(25)

R[t,X(t)]=exp⁡[−(t733.68)2.46⋅11−0.335⋅x(t)](26)

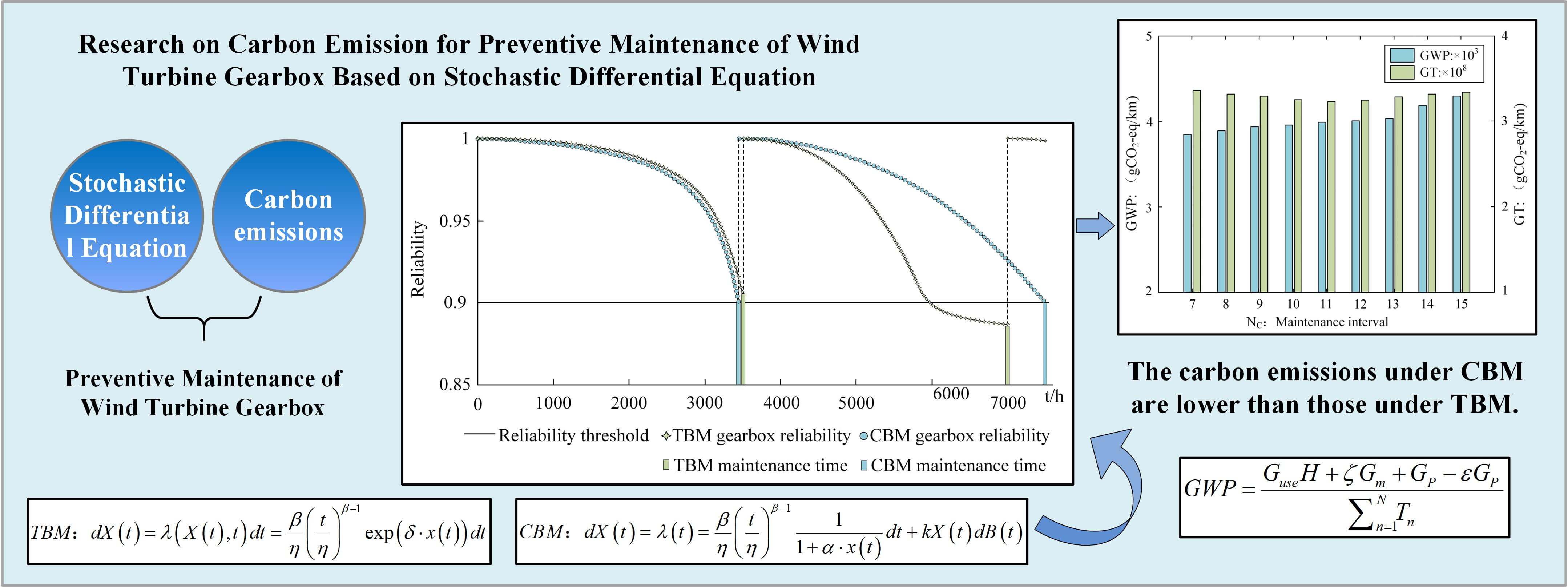
The state transition model of a wind power gearbox under Time-Based Maintenance (TBM) and Condition-Based Maintenance (CBM) is simulated and validated using MATLAB. Changes in transmission status and reliability over time are depicted in Fig. 3.

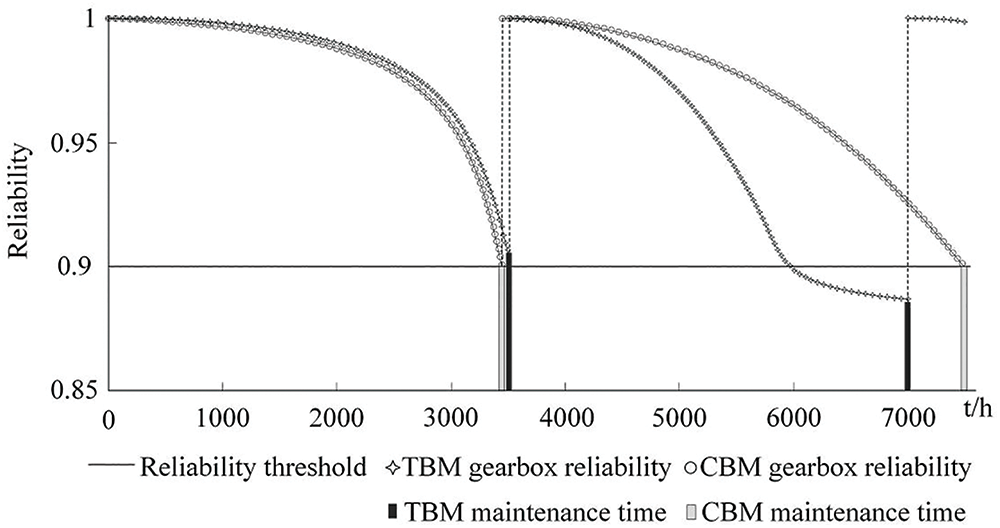
Figure 3: Gearbox reliability variation diagram under TBM and CBM

It is observed that both the operating status and reliability of the gearbox diminish over time. According to the reliability requirements for normal operation of the wind power gearbox, set at 0.9, maintenance is initiated when the reliability falls below this threshold. State-Based Maintenance (SBM) is contingent on the current health status of the wind power gearbox, with maintenance timing being variable. Upon reaching the maintenance threshold, the gearbox enters a new maintenance cycle.

In contrast, Time-Based Maintenance is executed after a predetermined number of operational hours. It is noted that during the first maintenance cycle, the gearbox’s reliability did not reach the threshold before maintenance, leading to over-maintenance. Conversely, during the second cycle, the gearbox’s reliability had already fallen below the threshold, indicative of insufficient maintenance.

4.2 Carbon Emission Analysis

4.2.1 Carbon Emission Analysis during TBM Maintenance

Carbon emission analysis is performed on the gearbox during Time-Based Maintenance (TBM). As derived from Eq. (18), ζ represents the number of preventive maintenance interventions for the gearbox during TBM.

Namely ζ=NT. Given that TBM schedules and intervals are fixed, the number of preventive maintenance cycles required over the gearbox’s lifecycle is constant. With a TBM interval of 3500 h and a gearbox lifespan of 15 years, operating 300 days annually for an average of 13 h per day, the number of TBM maintenance cycles for the gearbox totals 17. Namely NT=17,Guse=2720,H=108155 Gm=11450,Gp=8×107.

From Eq. (24), it can be inferred that:

GWP=GT∑n=1ζTn=2720×108155+17×11450+0.2×8×107∑n=1ζTn=5216.4

Hence, during TBM maintenance of the gearbox, the Global Warming Potential (GWP) of the gearbox is calculated to be 5216.4 g.

4.2.2 Carbon Emission Analysis during CBM Maintenance

For CBM maintenance of the gearbox, the number of preventive repairs ζ=NC, during the gearbox’s lifecycle, can be determined using Eqs. (8) and (24). It is found that the GWP per unit energy consumption of the gearbox is 4236.8 g, with NC = 11. As the number of preventive repairs varies, the GWP by the gearbox also changes correspondingly. The overall trend observed is an initial decrease followed by an increase.

Fig. 4 illustrates the trend of carbon emissions GT and GWP of the gearbox over its lifespan as a function of the number of preventive repairs.

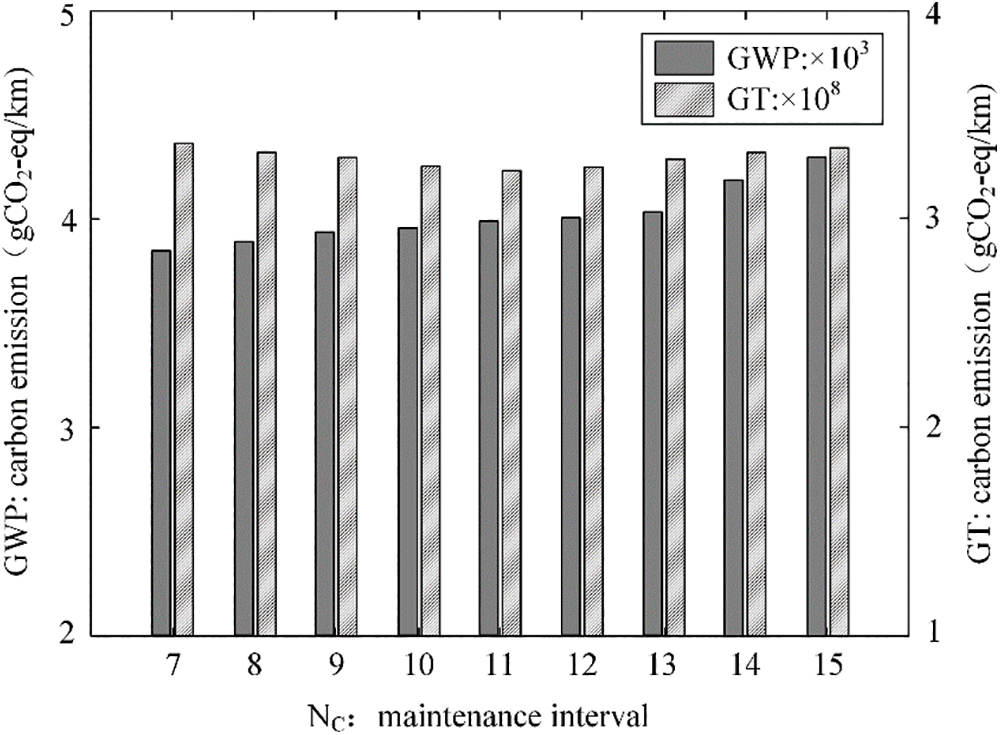
Figure 4: Changes in GWP and GT under CBM

The carbon emission model results for the wind turbine gearbox reveal that the minimum GWP value, 4236.8 g, is achieved when NC = 11.

4.3 Sensitivity Analysis

Given the complexity of factors influencing carbon emissions and the inherent uncertainty in the CBM process, it is crucial to understand how various impact factors may vary throughout the entire lifecycle of the equipment. This paper conducts a sensitivity analysis of three key parameters: carbon emissions per unit of energy consumption of gearboxes Guse, carbon emissions generated by maintenance activities of wind power gearboxes Gm, and carbon emissions generated during the manufacturing of a gearbox Gp.

(1) Carbon emissions per unit of energy consumed, Guse.

Variations in Guse directly influence the GWP of the gearbox.

As depicted in Fig. 5, when Guse is set at 3720, the minimum GWP value is achieved at NC = 10; conversely, when Guse is 1720, the optimal number of preventive maintenance interventions for minimizing GWP is NC = 14.

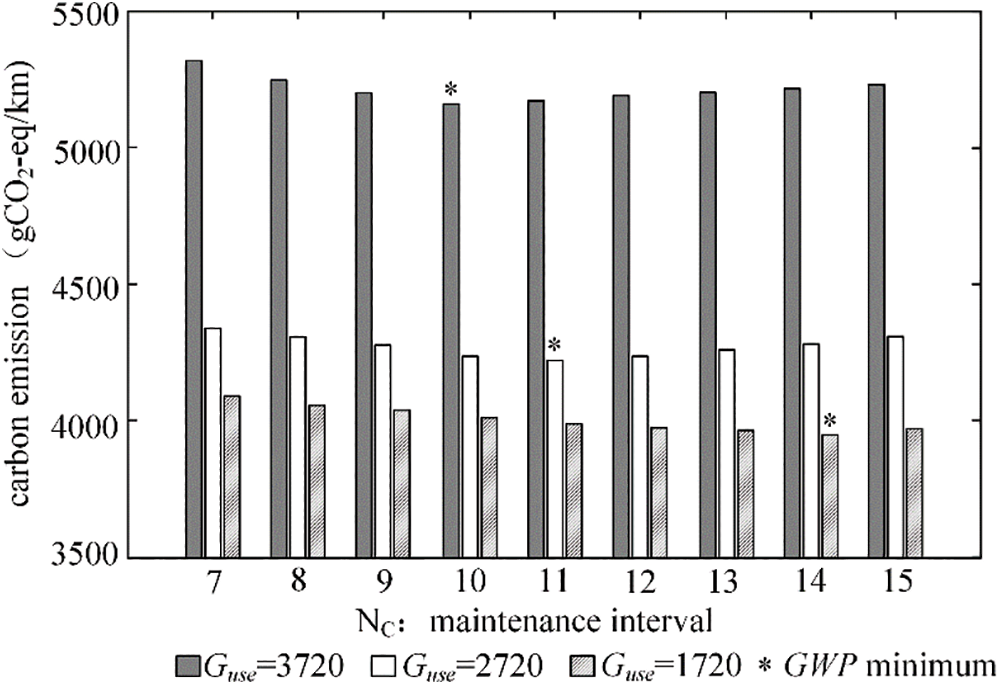
Figure 5: GWP varies with changes in Guse

An increase in Guse escalates the GWP of the gearbox, leading to higher carbon emissions during normal operation. Hence, adjusting the number of preventive maintenance sessions for the gearbox is a viable strategy for reducing its carbon emissions. As shown in Fig. 5, a decrease in Guse value makes the number of preventive maintenance times more sensitive to changes.

(2) Carbon emissions generated by a single maintenance activity Gm.

When the values of the parameter Gm are set at 7450, 11450, and 15450, respectively, the GWP value remains constant. Notably, when the minimum preventive maintenance frequency for optimal GWP is NC = 11, the variation in carbon emissions per unit operation of the gearbox is depicted in Fig. 6. It is evident that the carbon emissions associated with the gearbox’s unit energy consumption are not significantly affected by variations in Gm.

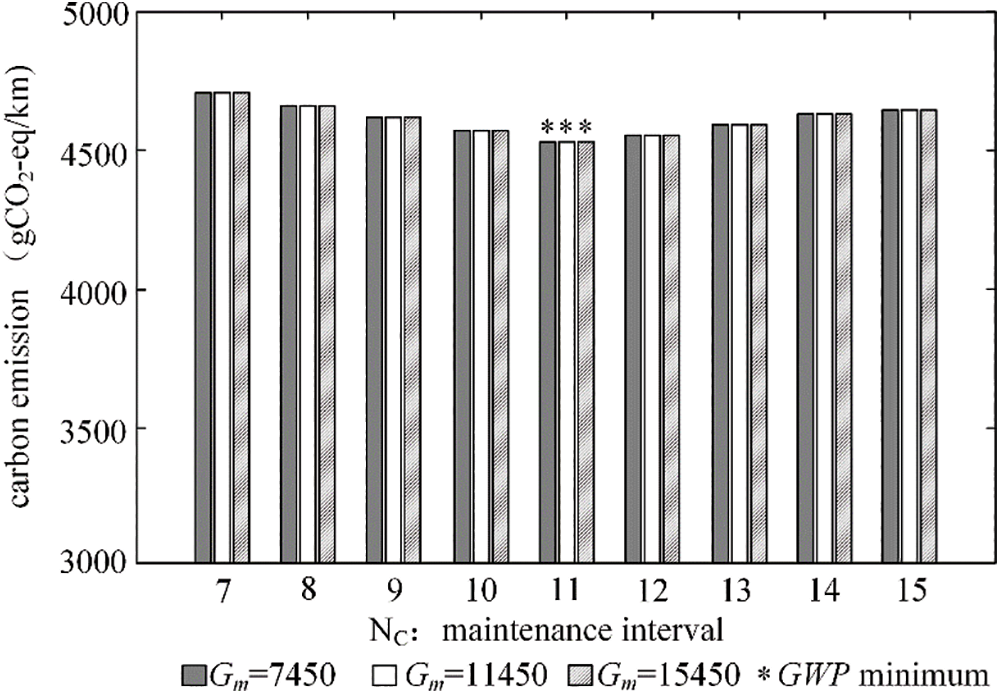
Figure 6: GWP variation with changes in Gm

(3) The carbon emissions Gp generated by manufacturing a device.

The GWP responds to changes in the parameter Gp value. When Gp values are set at 1.6 × 108, 8 × 107 and 7 × 107, the preventive maintenance frequencies NC required for the gearbox to achieve the minimum GWP value are 13, 11, and 10, respectively. As illustrated in Fig. 7, an increase in the Gp value leads to a more pronounced sensitivity in GWP fluctuations.

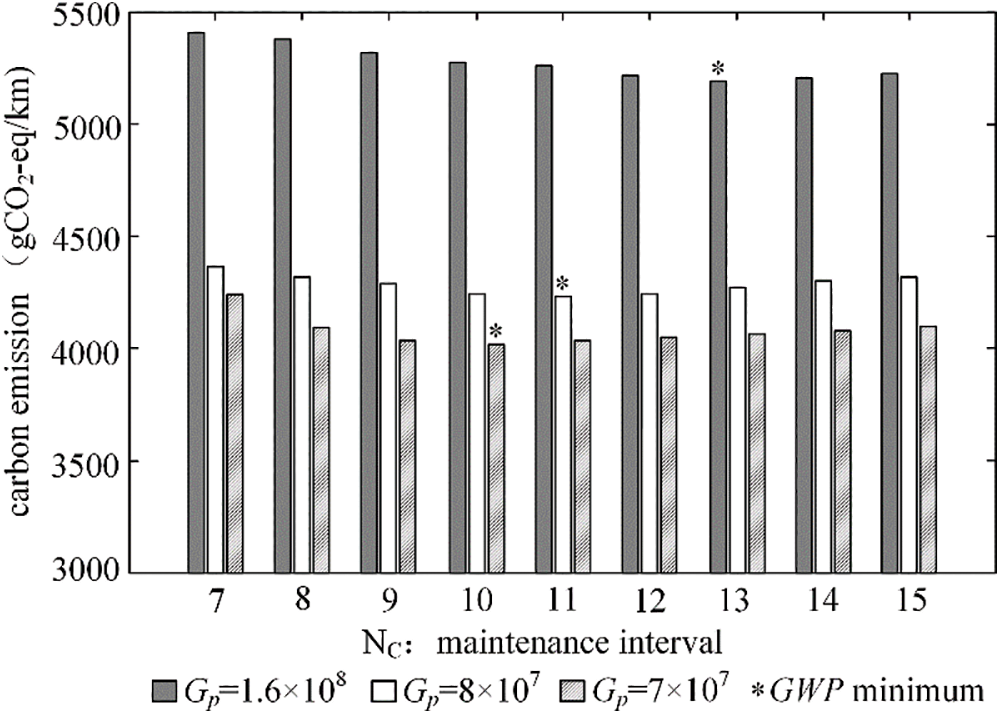
Figure 7: GWP variation with changes in Gp

In the carbon emission model of the wind turbine gearbox, adjusting the number of preventive maintenance sessions proves to be an effective strategy for reducing carbon emissions per unit of operation. By modulating the frequency of preventive maintenance, either by increasing or decreasing it, the gearbox’s carbon footprint can be optimized. This approach facilitates a balance between operational efficiency and environmental impact, highlighting the importance of strategic maintenance planning in reducing ecological footprints.

5  Conclusions

(1) This research demonstrates that compared to traditional TBM utilizing ODE, CBM employing SDE can more accurately track and simulate the state changes of wind power gearboxes, offering enhanced real-time accuracy.

(2) The carbon emissions model, when applied to both CBM with SDE-based and TBM with ODE-based approaches, reveals that carbon emissions under CBM are generally lower than those under TBM. However, over the long term, the carbon emissions from both methodologies are expected to converge, as TBM represents the expected outcome of CBM.

(3) The research findings indicate that the stochastic differential equation model is adept at incorporating the effects of daily inspections, maintenance, and environmental factors on the gearbox, thereby better ensuring the reliable operation of wind turbine equipment. The carbon emission models are capable of calculating the carbon emissions under both TBM and CBM. Utilizing these models for carbon emission assessments allows for timely adjustments to the preventive maintenance schedules of gearboxes, thereby reducing carbon emissions while ensuring their reliable operation.

(4) The results show that carbon emissions under CBM are generally lower than those under TBM. Sensitivity analysis of carbon emissions arising from energy consumption factors, such as Guse (carbon emissions per unit of energy consumed), Gm (carbon emissions from a maintenance activity), and Gp (carbon emissions from manufacturing a device), suggests that a decrease in the Guse value and an increase in the Gp value make the carbon emissions per unit of energy consumption in the gearbox more responsive to changes.

Acknowledgement: The authors would like to express our sincere appreciation to the anonymous referees for providing valuable suggestions and comments that have significantly contributed to the improvement of our manuscript.

Funding Statement: This research was supported by Basic Science Research Program through the National Natural Science Foundation of China (Grant No. 61867003) and Key Project of Science and Technology Research and Development Plan of China Railway Co., Ltd. (N2022X009).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Hongsheng Su, Lixia Dong, Xiaoying Yu; data collection: Lixia Dong, Kai Liu; analysis and interpretation of results: Lixia Dong, Hongsheng Su, Xiaoying Yu, Kai Liu; draft manuscript preparation: Hongsheng Su, Lixia Dong, Xiaoying Yu, Kai Liu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Márquez, G. P. F., Tobias, M. A., Pérez, P. M. J., Papaelias, M. (2012). Condition monitoring of wind turbines: Techniques and methods. Renewable Energy, 46, 169–178. [Google Scholar]

2. Tchakoua, P., Wamkeue, R., Ouhrouche, M., Hasnaoui, S. F., Tameghe, A. T. et al. (2014). Wind turbine condition monitoring: State-of-the-art review, new trends, and future challenges. Energies, 7(4), 2595–2630. [Google Scholar]

3. Song, T. X., Tan, T. Y., Han, G. C. (2022). Research on preventive maintenance strategies and systems for in-service ship equipment. Polish Maritime Research, 29(1), 85–96. [Google Scholar]

4. Joel, L., Kazem, A., Keld, H., Christopher, D. (2015). Effect of preventive maintenance intervals on reliability and maintenance costs of wind turbine gearboxes. Wind Energy, 18(11), 2013–2024. [Google Scholar]

5. Chan, D., Mo, J. (2017). Life cycle reliability and maintenance analyses of wind turbines. Energy Procedia, 110, 328–333. [Google Scholar]

6. Ling, M. H., So, H. Y., Balakrishnan, N. (2016). Likelihood inference under proportional hazards model for one-shot device testing. IEEE Transactions on Reliability, 65(1), 446–458. [Google Scholar]

7. Kang, Y., Su, H. S. (2015). Reliability analysis and control strategy design on preventive maintenance of repairable equipment. International Journal Control Automation and Systems, 8, 59–80. [Google Scholar]

8. Su, H. S. (2016). Stochastic model analysis and control strategy design on preventive maintenance based on condition. International Journal Control Automation and Systems, 9(3), 194–214. [Google Scholar]

9. Su, H. S. (2014). Preventive maintenance model analysis based on condition. International Journal of Security Applications, 8(4), 353–366. [Google Scholar]

10. Franciosi, C., Lambiase, A., Miranda, S. (2017). Sustainable maintenance: A periodic preventive maintenance model with sustainable spare parts management. IFAC-PapersOnLine. https://www.sciencedirect.com/science/article/pii/S2405896317334584 (accessed on 15/11/2023). [Google Scholar]

11. Zied, H., Nidhal, R., Ali, G. (2020). Maintenance on leasing sales strategies for manufacturing/remanufacturing system with increasing failure rate and carbon emission. International Journal of Production Research, 58(21), 6616–6637. [Google Scholar]

12. Afrinaldi, F., Taufik., Tasman, M. A., Zhang, H. C., Hasan, A. (2016). Minimizing economic and environmental impacts through an optimal preventive replacement schedule: Model and application. Journal of Cleaner Production, 143, 882–893. [Google Scholar]

13. Wang, Y. T., Liu, Q. M., Wu, B. S. (2023). Research on optimization of preventive maintenance of equipment considering carbon emissions. Industrial Engineering and Management, 28(3), 43–51 (In Chinese). [Google Scholar]

14. Liu, Q. M., Li, Z. N., Xia, T. B., Minchih, H., Li, J. X. (2022). Integrated structural dependence and stochastic dependence for opportunistic maintenance of wind turbines by considering carbon emissions. Energies, 39(1), 127–136. [Google Scholar]

15. Su, H. S., Wang, D. T., Duan, X. P. (2020). Condition maintenance decision of wind turbine gearbox based on stochastic differential equation. Energies, 13(17), 138–159. [Google Scholar]

16. Chen, L., Su, H. S., Huangfu, L. L. (2022). Preventive maintenance model analysis on wind-turbine gearbox under stochastic disturbance. Energy Reports, 8(Supplement 1), 224–231. [Google Scholar]

17. Bi, X. T., Yang, J., Yang, S. Y. (2021). LCA-based regional distribution and transference of carbon emissions from wind farms in China. Energies, 15(1), 198. [Google Scholar]

18. Silvia, M., Samuel, S. (2022). Practical example of modification of a gearbox lubrication system. Lubricants, 10(6), 110. [Google Scholar]

19. Xu, L., Yu, J. H., Chen, Y. (2020). Carbon emission and energy consumption accounting analysis of wind farm operation. Journal of Dalian Polytechnic University, 39(4), 281–288 (In Chinese). [Google Scholar]

20. Qian, P., Ma, X., Cross, P. (2017). Integrated data-driven model-based approach to condition monitoring of the wind turbine gearbox. IET Renewable Power Generation, 11(9), 1177–1185. [Google Scholar]