 Open Access
Open Access
ARTICLE
A Predictive Energy Management Strategies for Mining Dump Trucks
College of Mechanical and Electrical Engineering, Qingdao University, Qingdao, 266071, China
* Corresponding Author: Yulin Wang. Email:
Energy Engineering 2024, 121(3), 769-788. https://doi.org/10.32604/ee.2023.044042
Received 07 July 2023; Accepted 13 October 2023; Issue published 27 February 2024
Abstract
The plug-in hybrid vehicles (PHEV) technology can effectively address the issues of poor dynamics and higher energy consumption commonly found in traditional mining dump trucks. Meanwhile, plug-in hybrid electric trucks can achieve excellent fuel economy through efficient energy management strategies (EMS). Therefore, a series hybrid system is constructed based on a 100-ton mining dump truck in this paper. And inspired by the dynamic programming (DP) algorithm, a predictive equivalent consumption minimization strategy (P-ECMS) based on the DP optimization result is proposed. Based on the optimal control manifold and the SOC reference trajectory obtained by the DP algorithm, the P-ECMS strategy performs real-time stage parameter optimization to obtain the optimal equivalent factor (EF). Finally, applying the equivalent consumption minimization strategy (ECMS) realizes real-time control. The simulation results show that the equivalent fuel consumption of the P-ECMS strategy under the experimentally collected mining cycle conditions is 150.8 L/100 km, which is 10.9% less than that of the common CDCS strategy (169.3 L/100 km), and achieves 99.47% of the fuel saving effect of the DP strategy(150 L/100 km).Keywords
Nomenclature
| Engine torque, engine speed, engine efficiency | |
| Fuel consumption rate | |
| Battery pack efficiency | |
| Generator set output power | |
| Engine output power | |
| Traction motor demand power | |
| Battery pack output power | |
| Battery open circuit voltage | |
| Battery pack capacity | |
| Gravitational acceleration | |
| Vehicle speed | |
| Coefficient of inertia | |
| Vehicle acceleration | |
| Traction motor torque | |
| Drive shaft and gearbox transmission efficiency | |
| Main reducer ratio | |
| Tire rolling radius | |
| Vehicle demand power | |
| Traction motor output power | |
| Road resistance power consumption | |
| Air resistance power consumption | |
| Acceleration resistance power consumption | |
| Battery voltage vs. SOC | |
| Battery resistance vs. SOC | |
| Engine fuel consumption | |
| Battery equivalent fuel consumption | |
| Equivalent factor |
Recently, the energy consumption of conventional mining dump trucks has received increased attention as energy and environmental issues have become more prominent. Conventional large mining dump trucks are typically used in open-pit mining with electric drive. The trucks do not have power batteries. Therefore, they rely on the main brake and retarder for downhill braking. The mechanical energy generated during braking is usually converted to heat energy and dissipated, resulting in wasted energy. In addition, when going uphill with a full load, mining dump trucks must reduce speed to increase torque due to increased power demand, resulting in increased fuel consumption. Studies have shown that approximately 30% of all energy used in mining is consumed by the fuel consumption of mining dump trucks [1]. The PHEV is an essential technical approach to achieve energy savings and emissions reductions by coordinating multiple power sources, such as engines and electric motors, to improve overall vehicle dynamics while reducing energy consumption. This provides a reference for the development of mining dump trucks.
The energy management strategy (EMS) is essential for PHEVs to achieve fuel savings targets [2]. Its essence is that, based on the vehicle’s current operating conditions and mode of operation, it rationally allocates power between the engine and battery. Rule-based and optimization-based strategies are the two main areas of recent research on EMS [3]. As a classical rule-based strategy, the Charge-Depleting, Charge-Sustaining (CDCS) strategy has been studied by many scholars [4–6] due to its simplicity of implementation. However, obtaining desired results in the face of high battery consumption and rapid depletion is difficult, such as adverse weather or bumpy roads. The designer’s experience often determines the performance of the rule-based strategy, which ignores the system’s dynamic characteristics [5]. It has outstanding fuel economy in specific and brief operational conditions but deteriorates with increasing travel. Therefore, obtaining the optimal solution using rule-based algorithms alone is challenging.
Optimization-based strategies aim to determine the best value for a control parameter of a constructed system model, by means of training or computation, in order to attain system optimization. These strategies can be categorized into two groups: those based on intelligent algorithms, and those based on optimization theory. Optimization methods used for optimization-based strategies can be divided into classical, metaheuristic, and dynamic optimization methods. Classical optimization methods are mainly based on mathematical theories and principles and are generally applicable to problems where the parameters of the problem are certain and well-defined. This approach relies on mathematical derivations and proofs and can usually provide an exact optimization solution, but often cannot be applied when the problem is complex or the parameters are not certain. Metaheuristic optimization methods are mainly derived from the concept of natural heuristics and have the advantage of being able to deal with problems with a large search space, the existence of local optimal solutions and complex constraints [7,8]. However, since these methods are based on probabilities, the results obtained are often approximate rather than theoretically optimal solutions. Dynamic optimization methods are a class of optimization methods that deal with decisions that change over time. Typical examples are dynamic programming algorithms. Meta-heuristics and dynamic optimization methods are introduced in the following pages as common optimization methods in optimization-based strategies.
Intelligent algorithm-based optimization strategies obtain optimal or near-optimal solutions from model training results. Kong et al. [9] proposed an action dependent heuristic dynamic programming (ADHDP) algorithm employing a neural network to approximate the optimal control trajectory and cost function through multiple iterations. Similar approaches include Reinforcement Learning (RL) [10,11], Particle Swarm Optimization (PSO) [12], Genetic algorithms [13], etc. Usually, it relies on optimal data obtained jointly by numerous computational methods [14]. This requires sufficient forward-looking information, a high level of computation, and ample storage memory, which is difficult to achieve in real applications.
The other approach is an optimization strategy based on optimal control theory, including global and transient optimization algorithms. One representative global optimization strategy is the DP algorithm, references [15–18] described the relevant research. To reduce the difficulty of implementing DP algorithms, Sundstrom et al. [15] proposed a general DP algorithm for solving discrete optimal control problems. This algorithm was implemented using Matlab functions and has been widely used in studying EMS for PHEV. With the development of information technology, DP-based EMS can optimize fuel consumption by using GPS, GIS, ITS, and other technologies to obtain previously inaccessible forward-looking information. Zhao et al. [18] used the information fusion and prediction models of historical and real-time traffic data to identify the path characteristics and predict the path parameters using the traffic flow prediction model. However, in practice, due to the significant computational demands of the DP algorithm, so is usually implemented offline and used as a benchmark for evaluating other strategies [19,20]. The most representative transient optimization algorithm is the ECMS algorithm. Studies on the ECMS algorithm are available in references [21–24]. Chen et al. [24] used traffic data to generate simplified velocity profiles to obtain the desired SOC trajectory by solving the set optimization problem within the set time. The EF is adjusted according to the difference between the current SOC and the desired SOC. The advent of adaptive ECMS algorithms allows the EF to adaptively adjust to changes in operating conditions [25–28]. Zeng et al. [28] proposed an optimization-oriented A-ECMS by introducing an ILF-based multistep predictor to achieve ephemeral demand power prediction, and the optimal EF is periodically updated through local optimization based on the prediction. The EF obtained using intelligent algorithms after model training can achieve short-term optimality in the prediction range. However, the enormous computational burden and prediction errors make it difficult to implement in practice.
Incorporating the PHEV-equipped hybrid power system into the mining dump truck’s structure, its multiple power sources can improve vehicle dynamics. The existence of the Rechargeable Energy Storage System (REESS) can replace the retarder for auxiliary braking and realize braking energy recovery, and this can also help the engine work for a longer time in the high efficiency zone, improving fuel utilization efficiency. The design of a reasonable and efficient EMS to further minimize fuel consumption and improve the fuel economy of mining dump trucks has become the focus of existing research. EMS applied to mining dump trucks must prioritize safety issues. Existing studies typically use EMS to passively constrain battery SOC and adjust it through a compensation mechanism when battery SOC exceeds upper and lower limits, which can have serious consequences in practical applications. For example, in the long downhill process, the vehicle performs the brake energy recovery according to the set process, and the SOC gradually increases to reach the set upper limit, at which time the compensation mechanism in the control strategy is triggered to adjust the battery SOC, but the vehicle is likely to be unable to continue the brake energy recovery because the battery is full, thus losing the auxiliary brake function, which is very dangerous in the long downhill process. To meet safety requirements, active control constraints on battery SOC are needed. Therefore, the EMS must be designed with global planning of battery SOC in advance as a strong constraint for the following optimization process, and real-time vehicle control in the final stage. Among the EMS discussed above, the intelligent algorithm-based EMS is still in the initial research stage, and its substantial computational burden makes practical applications difficult. The CDCS strategy, as a common EMS in mining dump trucks, often does not perform well in the face of special conditions (e.g., extreme weather); The ECMS algorithm, as a transient optimization strategy, selecting the appropriate EF can achieve near-optimal results. However, mining operating conditions vary greatly during the same work cycle (e.g., uphill and downhill, no load and full load), and achieving the desired performance with a fixed EF is difficult.
To bridge the foregoing research gaps, this paper proposes a predictive equivalent consumption minimization strategy (P-ECMS), the core content of which includes global planning and stage parameter optimization, and the optimization results are used to realize the control of the vehicle using the ECMS algorithm, so that mining dump trucks can obtain the optimal EF under the current operating stage, and the EF can be changed with the change of working conditions, to meet the demand for energy saving and emission reduction, reduce fuel consumption. The details of the P-ECMS strategy are shown below:
The predictive equivalent consumption minimization strategy is proposed. The global planning is carried out for the cyclic conditions of the mine, and the optimal control manifold and the reference trajectory of the battery SOC are obtained by the DP algorithm. Apply the above SOC reference trajectory to guide the current SOC in the following real-time stage parameter optimization process and obtain the EF required by the ECMS algorithm in the current stage. Then the ECMS algorithm is used to achieve real-time control of mining dump trucks. The map information is used to construct the mining conditions for simulation experiments. The results show that the proposed P-ECMS strategy outperforms the common CDCS strategy in terms of fuel economy and is very close to the optimal solution under the DP strategy.
The rest of the article is organized as follows. Section 2 presents the mining dump truck powertrain model. Section 3 offers and analyzes the ECMS algorithm and DP algorithm. Then, Section 4 proposes the P-ECMS strategy. Section 5 analyzes the simulation results, and conclusions are drawn in Section 6.
This paper focuses on a 100-ton mining dump truck and develops a series of hybrid systems to improve its power and fuel economy. The series hybrid structure is shown in Fig. 1. The traction motor provides traction for the truck, while the generator set consists of an engine and a generator, which provides power to the traction motor. The battery pack regulates electrical power by receiving excess energy generated by the generator and energy recovered by the traction motor during braking. The main vehicle parameters are shown in Table 1.
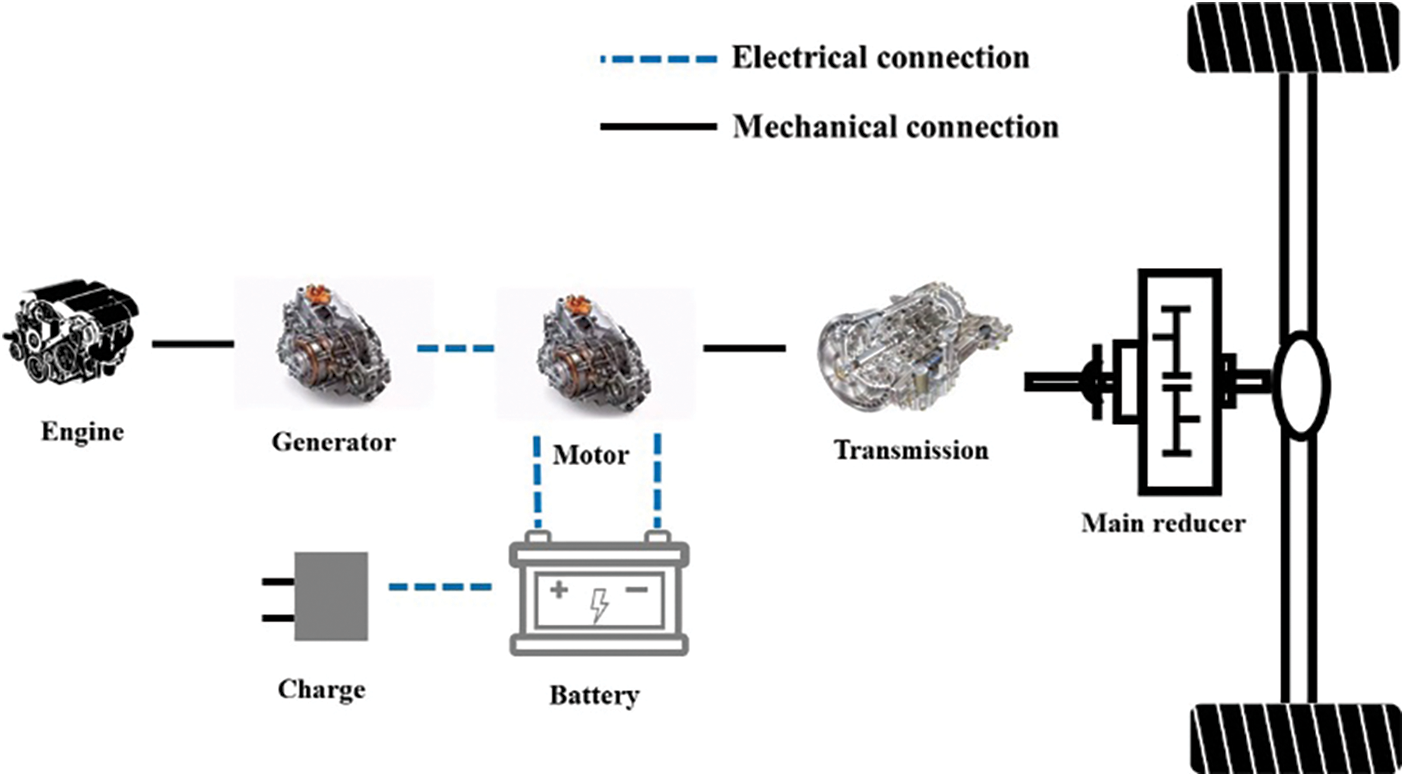
Figure 1: Structural diagram of the series hybrid system

Without considering the dynamic characteristics of the engine, the engine model is simplified to a static model with fuel consumption rate and efficiency defined as Eqs. (1) and (2):
The engine power should be satisfied as Eq. (3):
The main engine parameters are shown in Table 2. According to the engine bench test, the fuel consumption rate of the engine is measured, as shown in Fig. 2.
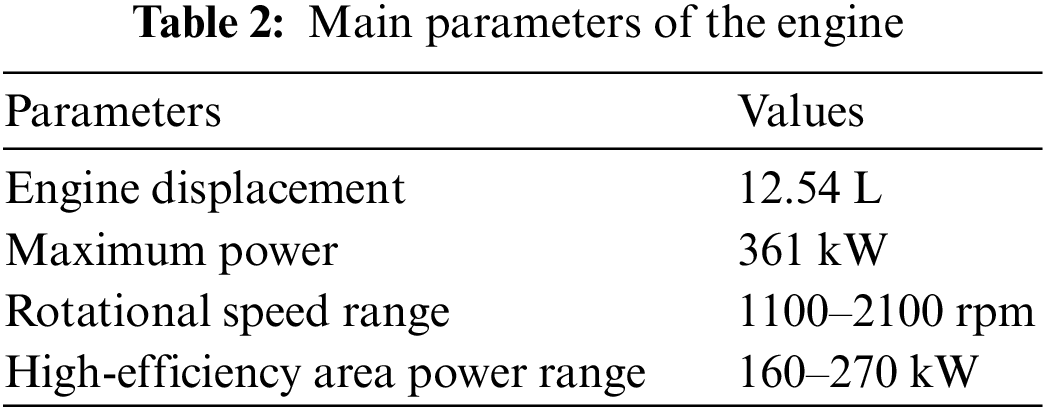
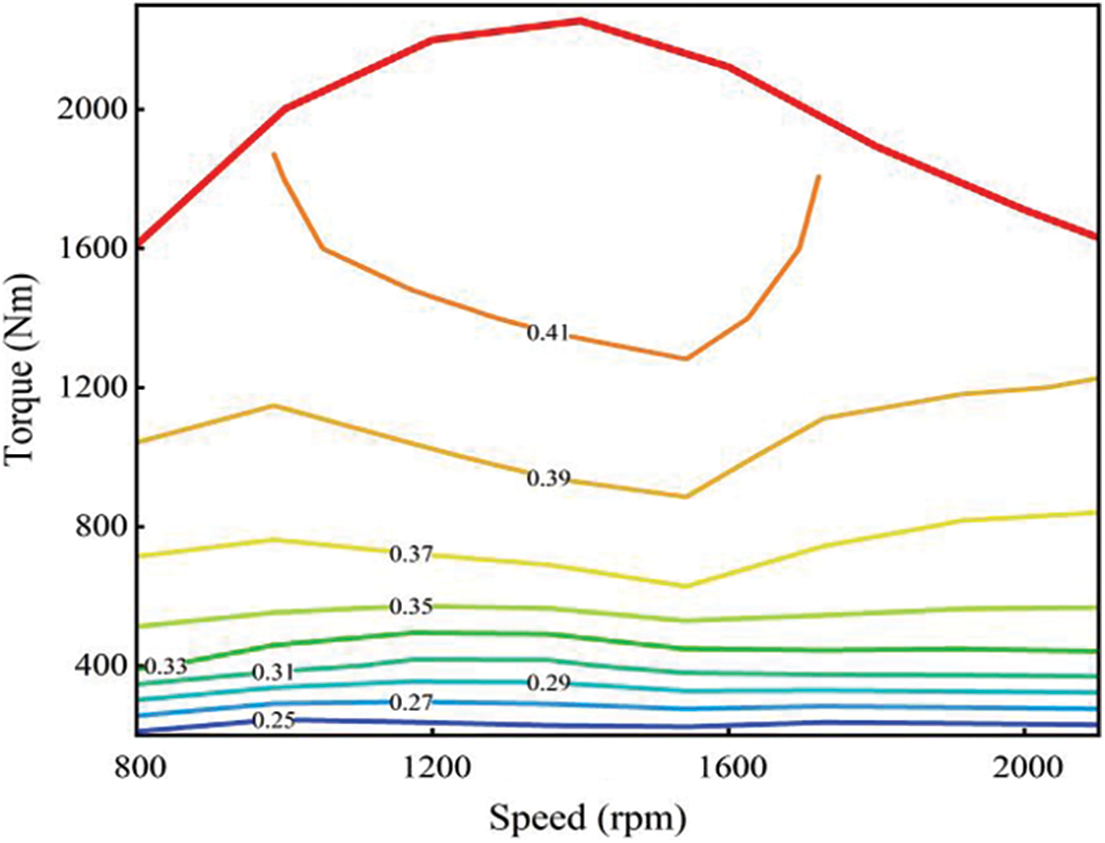
Figure 2: Engine efficiency map
2.2 The Traction Motor and Generator Model
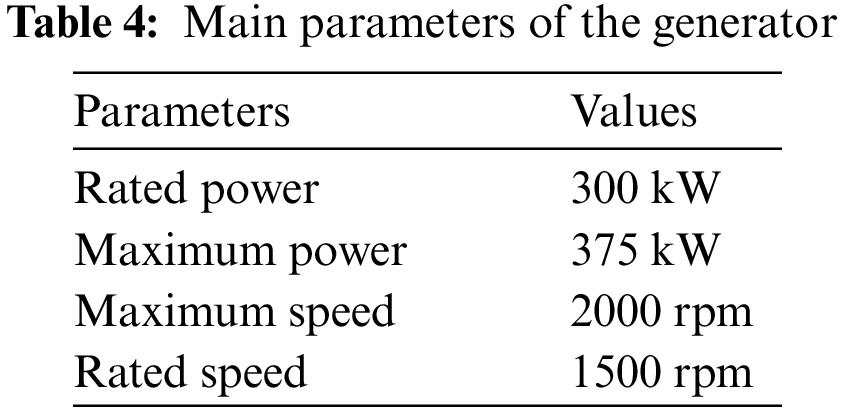
This paper selects two permanent magnet synchronous motors to drive the vehicle in series, with their main performance parameters listed in Table 3. Positive and negative values indicate different operating modes: positive value means that the traction motor consumes electrical energy to drive the vehicle, and negative value means that the vehicle brakes to recover braking energy and charge the battery pack. Motor data is obtained through bench testing. The generator’s structure is similar to the traction motor’s, with its main parameters shown in Table 4.

Lithium iron phosphate batteries, with their high power and energy density, safety, and long service life, are selected as the battery pack for the hybrid power system. A simple and effective internal resistance battery model is established [29], as shown below in Eq. (4):
In the formula:
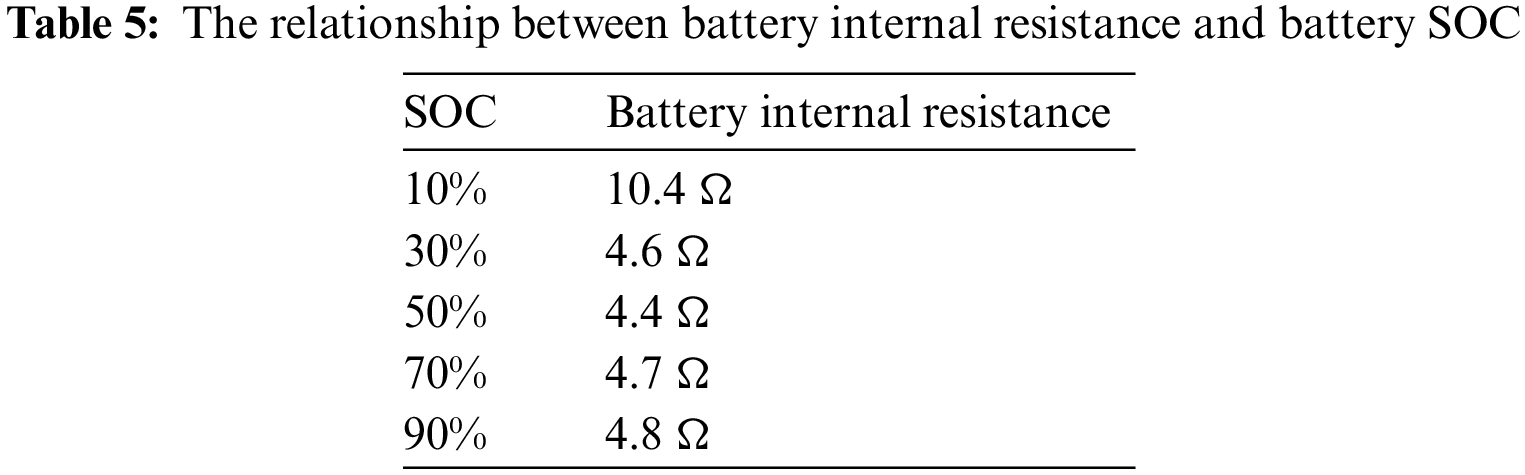

2.4 The Vehicle Power Demand Model
The road resistance, air resistance, and acceleration resistance when the hybrid mining dump truck is running on a road with a slope with a full load are shown as Eq. (5):
The driving force provided by the traction motor to the vehicle can be expressed as Eq. (6):
The power balance equation is shown as Eq. (7):
3 Brief Description of the Algorithm
To provide a better comprehension of the P-ECMS strategy, this chapter explains two algorithms employed for it, the ECMS algorithm and the DP algorithm, in detail in the following two sections.
The ECMS algorithm is a transient optimization algorithm that aims to minimize equivalent fuel consumption while satisfying the driver’s demand. The objective function as Eq. (8):
Subject to the physical constraints of
In the formula:
The DP algorithm is based on the Bellman optimality principle. In solving the optimal control problem, the DP algorithm divides the control problem into several periods. In each period, the optimal solution in the current state is calculated by combining the optimal solution of the previous period to obtain the optimal control manifold.
The equation of state for an optimal control problem can be expressed as Eq. (10):
Its cost function is
In the formula:
The optimal control problem is solved by controlling the variables u to minimize or maximize
The cumulative cost function at step k is shown as Eq. (12):
After the above backpropagation procedure, the optimal cost function of the whole trip
4 The Predictive Equivalent Consumption Minimization Strategy
To obtain good fuel economy and solve the common problems of mining dump trucks, this paper proposes a predictive equivalent consumption minimization strategy based on the DP optimization results, P-ECMS, to improve fuel economy. Given the single repetition of the mining dump truck’s working cycle and the significant differences between stages, the process can be divided into different stages. The optimal EF for each stage can be calculated in real time to achieve global optimization.
First, geographic information data is collected through real vehicle tests and processed to construct the mining site map. Since mining dump trucks operate under single-repetition working conditions, the collected driving data can be used to create typical cycle working conditions corresponding to the map. Then, the optimal global results for these typical cycle working conditions are solved offline using the DP algorithm. Segmentation points are determined based on characteristic points of the typical cycle condition (such as speed, slope, and load change points). By performing the stage parameter optimization based on the map information and the current SOC, the current optimal EF is obtained and applied to the ECMS algorithm, the realization of real-time control based on this optimal EF. The P-ECMS flow chart is shown in Fig. 3.
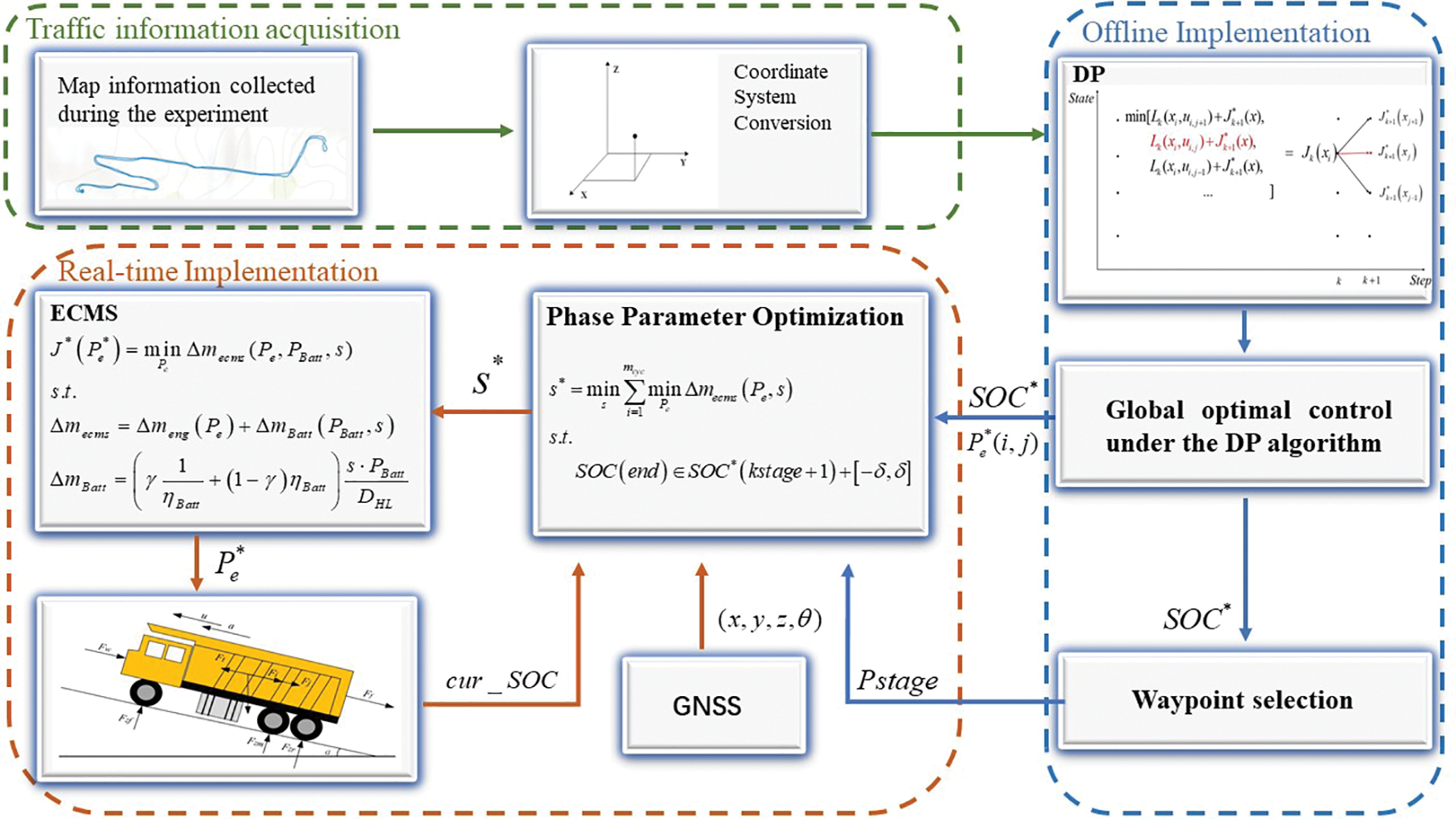
Figure 3: The P-ECMS strategy flow chart
4.1 Global Optimal Control Based on the Dynamic Programming Strategy
The P-ECMS strategy comprises global planning based on the DP algorithm, stage parameter optimization, and control implementation using the ECMS algorithm. This section describes global planning using the DP algorithm in the offline state to determine the optimal control manifold and the optimal reference trajectory of the battery SOC.
For the energy management problem of a series hybrid mining dump truck, the battery SOC is taken as the state variable, and the
In the formula:
The optimal control problem is expressed as Eq. (15):
In the formula:
The DP algorithm is utilized to solve the above problem. First, time is discretized in 1-second steps, battery SOC in 1%, and generator set output power in 10 kW steps. The variable grid is obtained and solved in two steps in the next process. For the case where the state variables are not in the grid, it is generally solved by linear interpolation to finally obtain the optimal control manifold
The inverse derivation process in the DP algorithm is shown below:
(1) Initialization: The state variable battery SOC is discretized over time into N steps, at each moment into
(2) Solve the optimization subproblem.
(3) If k = 2, the inverse solution process is finished; otherwise let k = k–1 and go to step (2).
The forward derivation process in the DP algorithm is shown below:
(1) Initialization: Initial value of battery SOC
(2) Apply the interpolation method to calculate the k-step optimal control variables.
(3) Calculate the k step forward cumulative generation value.
(4) Calculate the state variables at step k + 1.
(5) If k = N-1, end the process; otherwise let k = k + 1 and go to step (2).
4.2 Implementation of the P-ECMS Stage Parameter Optimization Algorithm
This section divides the whole trip into stages and obtains the optimal EFs for each stage by optimizing stage parameters with the optimal control manifold and the optimal reference trajectory of the battery SOC obtained in the previous section.
In ECMS algorithm, operating condition changes can affect the EF’s optimization effects. To adaptively adjust the EF, commonly used methods include real-time feedback based on battery SOC, offline optimization coupled with online identification, and regulation based on predictive information.
The cycle conditions of mining dump truck operation are relatively fixed, and the road information is relatively unique. Therefore, typical mining cycle conditions established by condition information collected through multiple cycle operations can be used as the real global conditions for predicting vehicle operations. The cycle is segmented and each stage is optimized separately due to the large variability of working conditions at different stages within the cycle.
First, the global segmentation process is performed based on the working condition information and the segmentation points determined in the offline state, which is divided into Pstage stages. The target battery SOC of the current stage is determined based on the current position determined by the Global Navigation Satellite System (GNSS) and the SOC trajectory obtained by the DP algorithm, which will be used as a constraint for participation in the next stage of the optimization sub-problem solution process and obtain the optimal EF. When positioning to the following stage, the EF of the next stage is calculated again using the above method with the current SOC and the corresponding target SOC.
The stage parameter optimization algorithm follows the steps below:
(1) Initialization: Load the map information and load the optimal control manifold Pe*(i, j), i = 1, … , Mx obtained by the DP algorithm, where mcyc is the time step under the current stage. Load segment mileage S(k) = 1, … , Pstage + 1. Set cur_kstage = 1. Set the allowable deviation value of stage target SOC
(2) Coordinate transformation: Get the current coordinates
(3) Stage update: If cur_kstage = kstage, then return to step (2). Otherwise, make cur_kstage = kstage and go to step (5).
(4) Get the current battery SOC information, which is recorded as cur_SOC.
(5) Determine the stage target power. According to the result of the DP algorithm, the stage target power SOC* (kstage + 1) is obtained as Eq. (20):
(6) Solve the stage parameter optimization subproblem.
(7) Output the optimal EF
4.3 Application of the ECMS Algorithm for Real-Time Control
This section utilizes the optimum EF, which was obtained from the stage parameter optimization algorithm discussed earlier, to implement the ECMS algorithm. The aim is to achieve the best power distribution between the genset and the batteries and to obtain optimal fuel economy.
The objective function of the series hybrid system when applying the ECMS algorithm can be expressed as Eq. (22):
In the formula:
In the formula:
In the formula:
The EF determines the performance of the ECMS algorithm. By applying the optimal EF
5 Simulation Results and Discussions
5.1 Driving Conditions Analysis
In this paper, an open-pit mining was selected as the test site, and the line-cycle test method was chosen for geographic data collection, considering the cost, cycle time, test conditions, and representativeness of geographic information. During the test, the driver was required to drive skillfully along a pre-planned test route, following the traffic flow during the working day for data collection and driving smoothly without overtaking or deliberately slowing down.
The driving condition of a mining dump truck in a mining are relatively fixed. After loading in the mining area, it travels uphill at a slower speed, then during the unloading area at a higher speed on flat roads, and finally returns empty to complete a cycle. In summary, the driving conditions of a mining dump truck mainly consist of four processes: full-load uphill, full-load flat road, empty-load downhill, and empty-load flat road. Fig. 4 is an illustration of the flow of a mining dump truck through a work cycle. The collected data is filtered, converted into appropriate units, and slope calculations are performed to obtain the actual circulation data of the mining, as shown in Fig. 5.
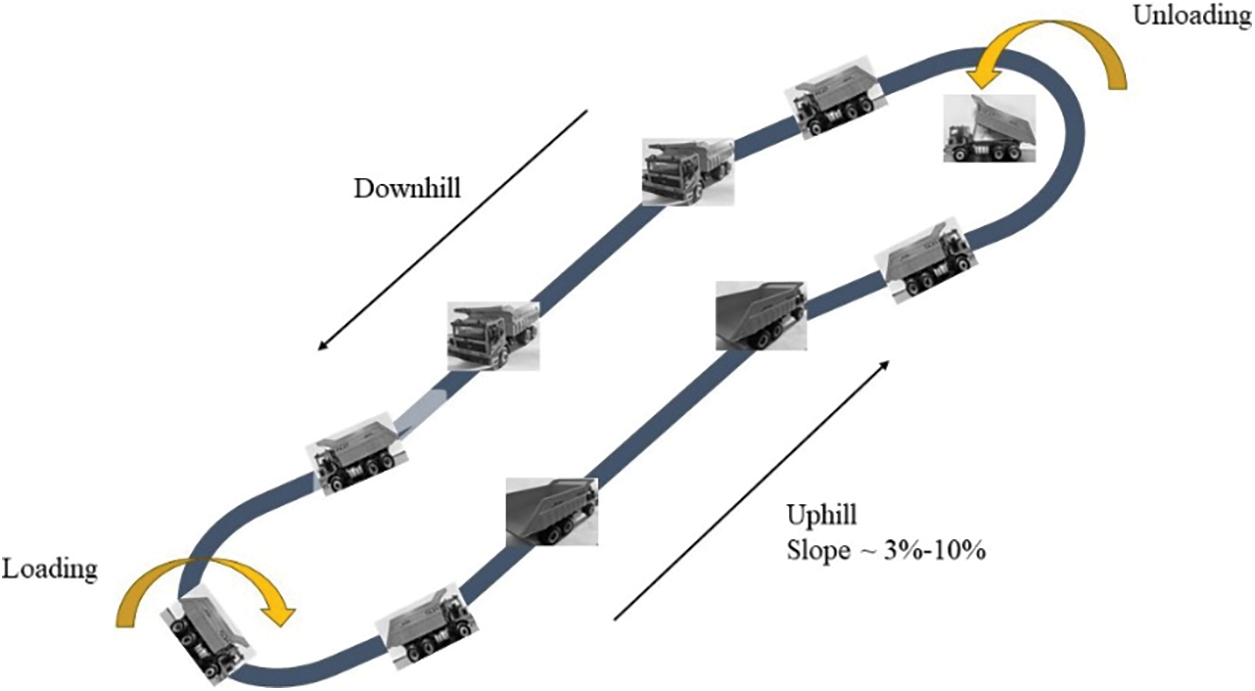
Figure 4: Mining cycle working conditions diagram
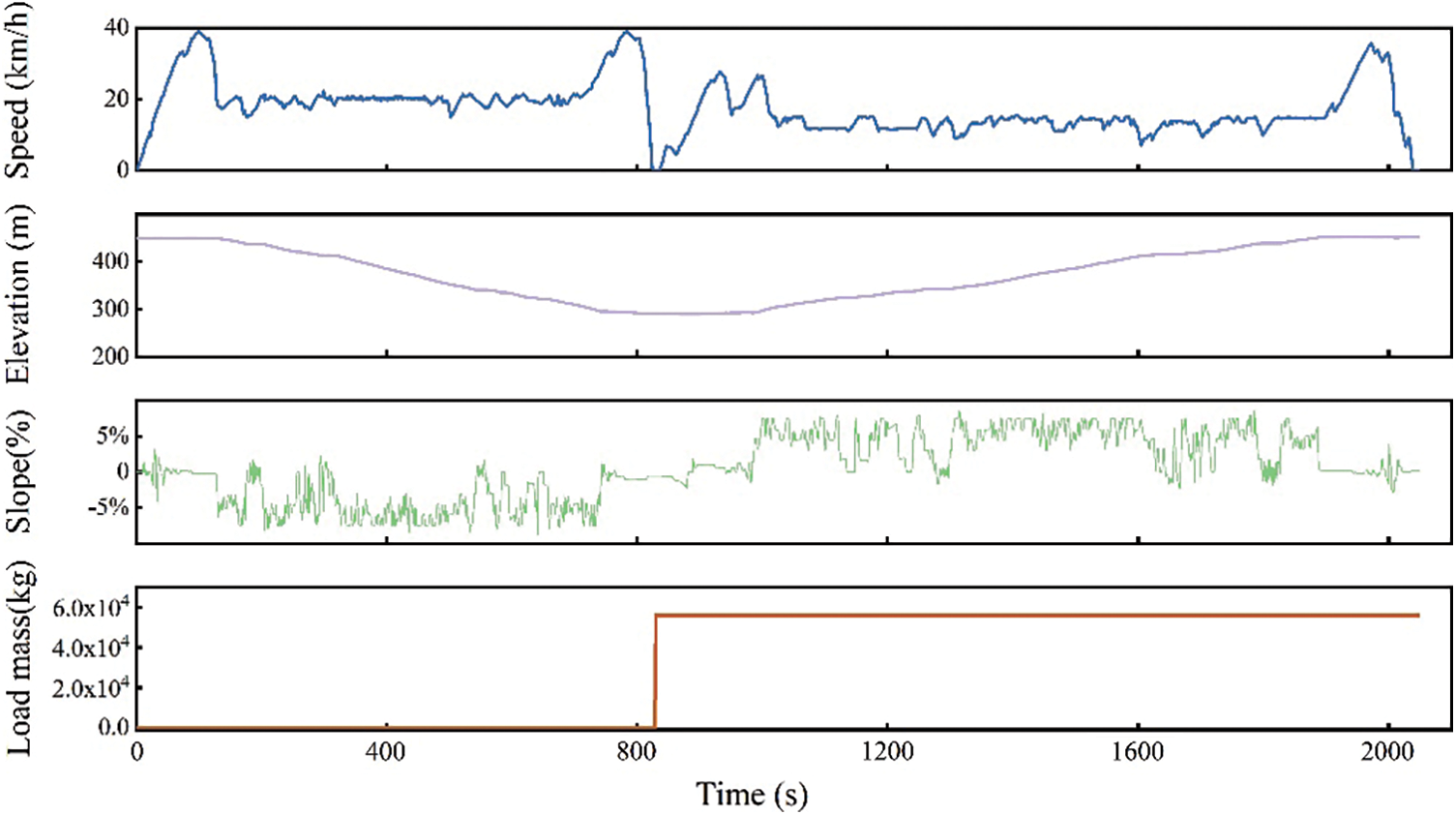
Figure 5: Actual cycle conditions of the mining
5.2 Analysis of Simulation Results
To verify the proposed P-ECMS, using the above cycle conditions, simulations were conducted using ADVISOR and Matlab based on the system model established in Chapter 2. Taking into account the realities of the mine site, the
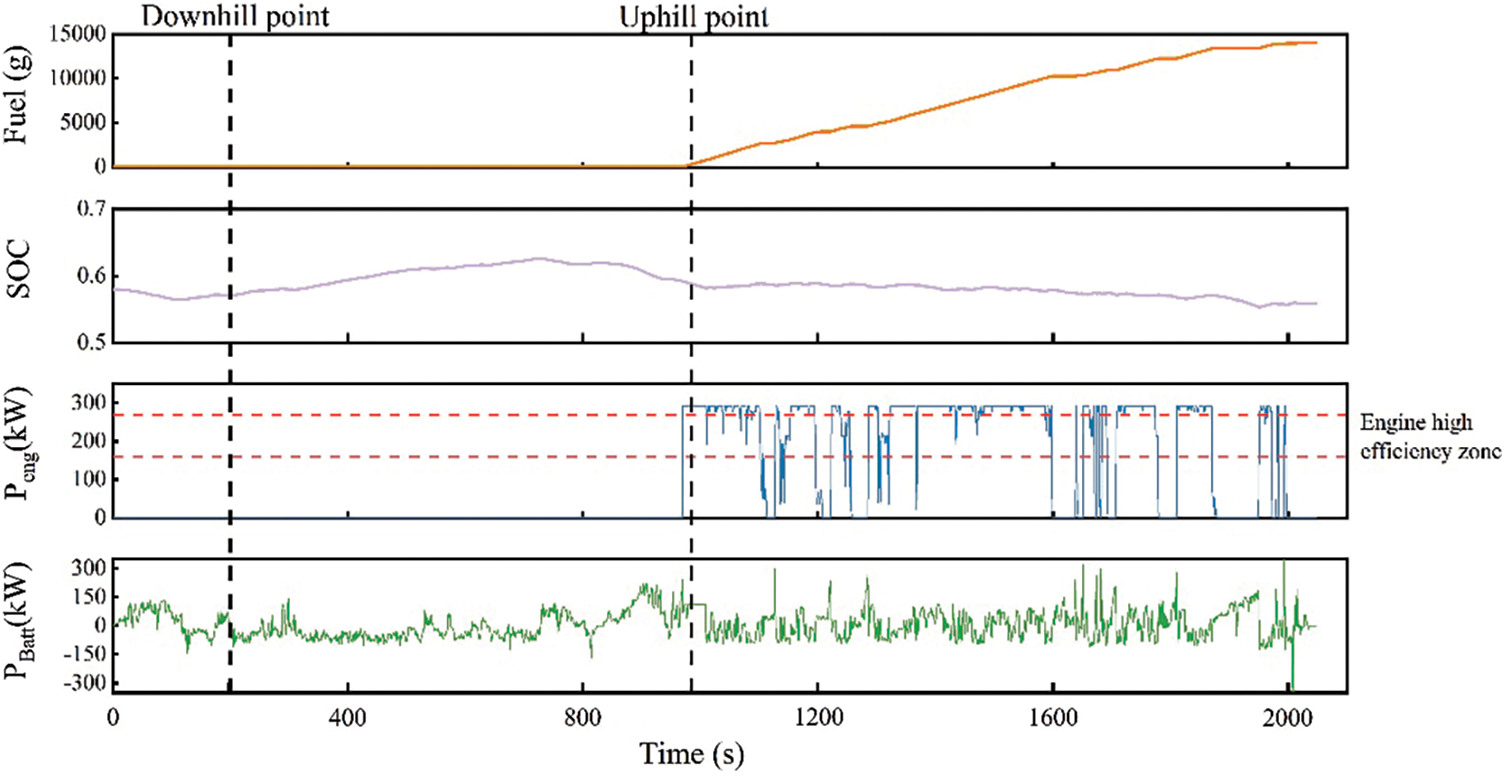
Figure 6: The CDCS strategy simulation results
The diagram shows that during the empty-load flat road phase before the downhill phase, the truck operates in the electric mode, and the generator set is inactive. During the empty-load downhill phase, the generator set remains off, the truck recovers braking energy, and the traction motor reverses to recharge the battery pack. After the downhill stage, the truck is loaded, and in the full-load flat road phase, it is again driven in the electric mode, only the battery pack providing power to the traction motor. As the truck enters the full-load uphill phase, the power demand increases and the generator set is activated. During this stage, the generator set provides power to the traction motor and charges the battery pack. After the climb, the truck’s power demand decreases, and it is driven in the electric mode during the full-load flat road phase. During the full-load uphill phase, the engine cannot operate efficiently for long periods, as seen from the generator set output, resulting in more fuel being consumed.
For the cycle conditions of the mining, the DP strategy results are shown in Fig. 7. Unlike the CDCS strategy, in the DP strategy, the generator set charges the battery pack during the empty-load flat road phase before the downhill phase when the engine power is also lower due to the lower power demand. During the empty-load downhill phase, the truck recovers braking energy, and the generator set does not operate. During the next full-load flat road phase, the generator set is activated to power the truck and simultaneously charge the battery pack, increasing the battery SOC. Fig. 7 shows that during full load operation, the engine is continuously running in its high efficiency zone.
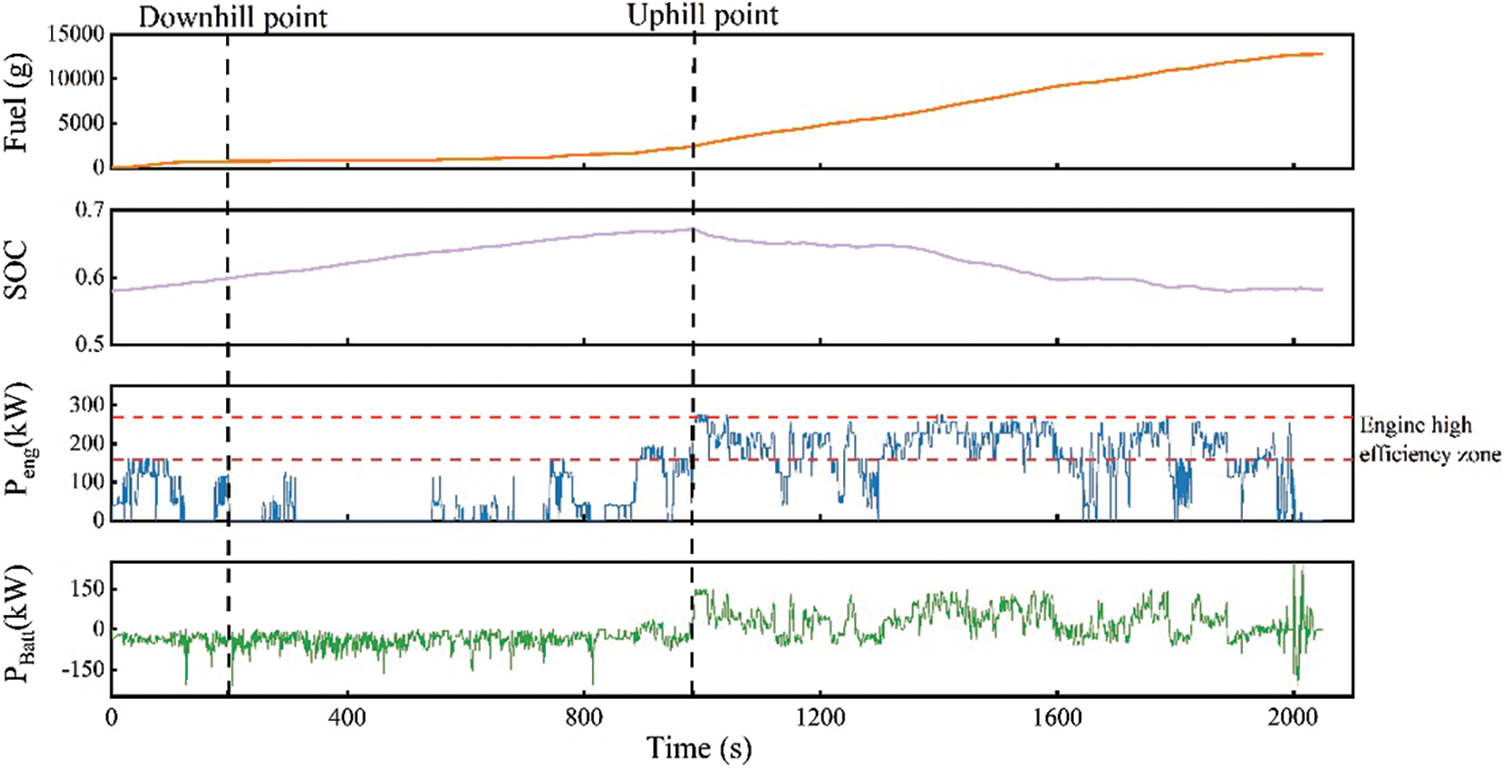
Figure 7: The DP strategy simulation results
The DP results show that the battery SOC should be high before the mining truck goes uphill. This allows the engine operating point to be adjusted to work in the high efficiency zone while meeting the power demand, thus reducing fuel consumption.
Based on information about working conditions, such as mining site slope changes, vehicle load changes, and vehicle speed, the working conditions can be divided into 16 stages. Simulation results under the P-ECMS strategy when operating in CS mode are shown in Fig. 8.
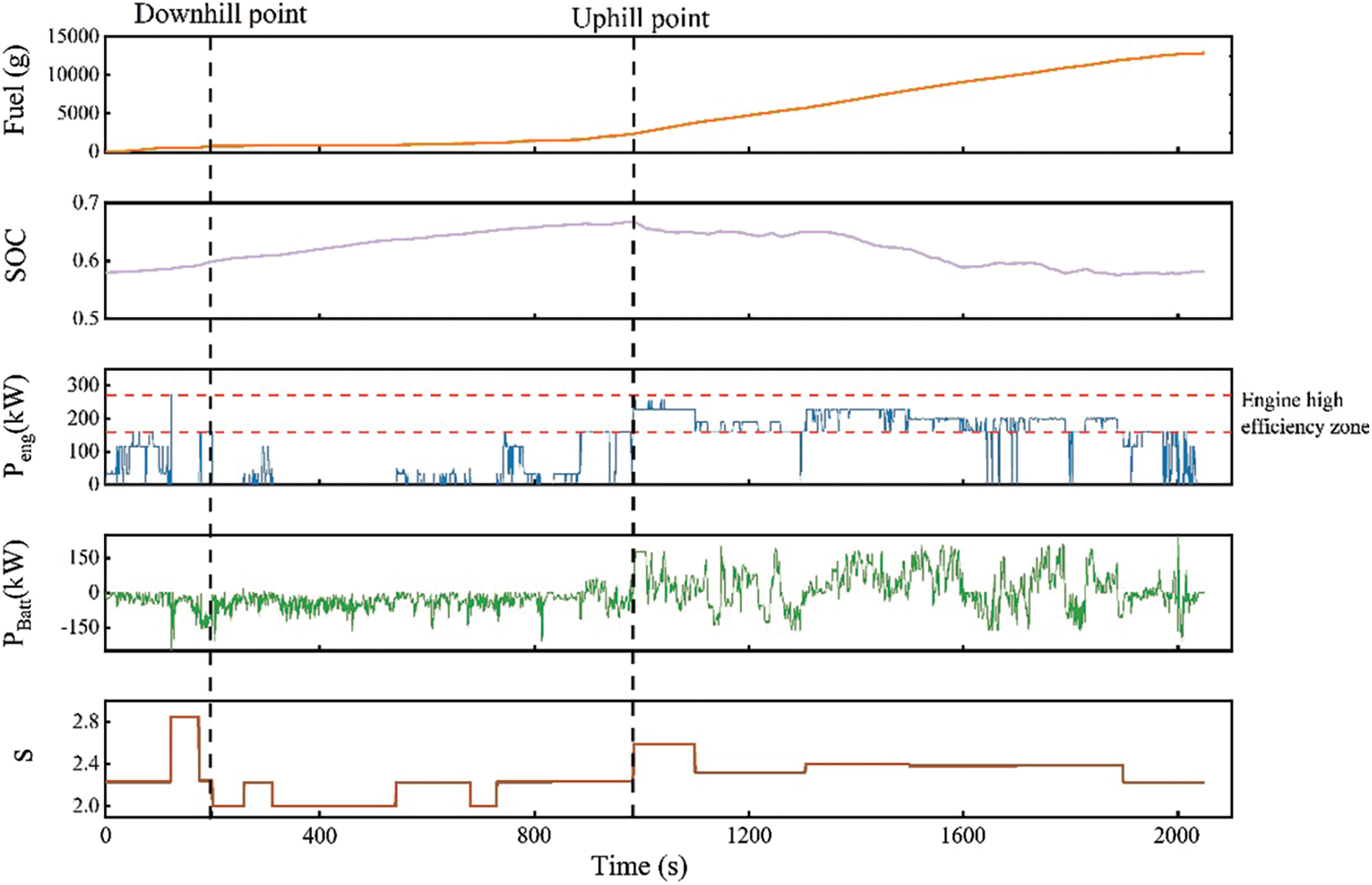
Figure 8: The P-ECMS strategy simulation results in CS mode
The EF for each stage is obtained using the stage parameter optimization algorithm. Combined with the change of this factor and considering the whole power demand, the truck can reach the desired target SOC as much as possible when operating in different stages, achieving optimal power allocation in each stage. For the whole range of conditions, the truck operation mode under the P-ECMS strategy is similar to that under the DP strategy, the generator set operating during the empty-load flat road phase and the full-load flat road phase to maintain a higher battery SOC enables the battery pack to provide sufficient power during uphill. However, compared to the DP strategy, during uphill operation, the generator set output power is lower, and the battery pack output power is higher, the engine operating time in the high efficiency zone is shorter compared to the operating time in the DP strategy, resulting in slightly higher fuel consumption.
When sufficient charging time is available, the plug-in hybrid mining dump trucks can operate in Charge-Depleting (CD) mode for improved fuel economy. Assuming a 12-hour operation in CD mode, we set the initial SOC at 0.8 and the minimum SOC throughout the operation at 0.3. The changes in fuel consumption and battery SOC during the operation under the P-ECMS strategy are shown in Fig. 9. After the CD mode concluded, the mining dump truck can continue to work before recharging and maintain the battery SOC near 0.3.
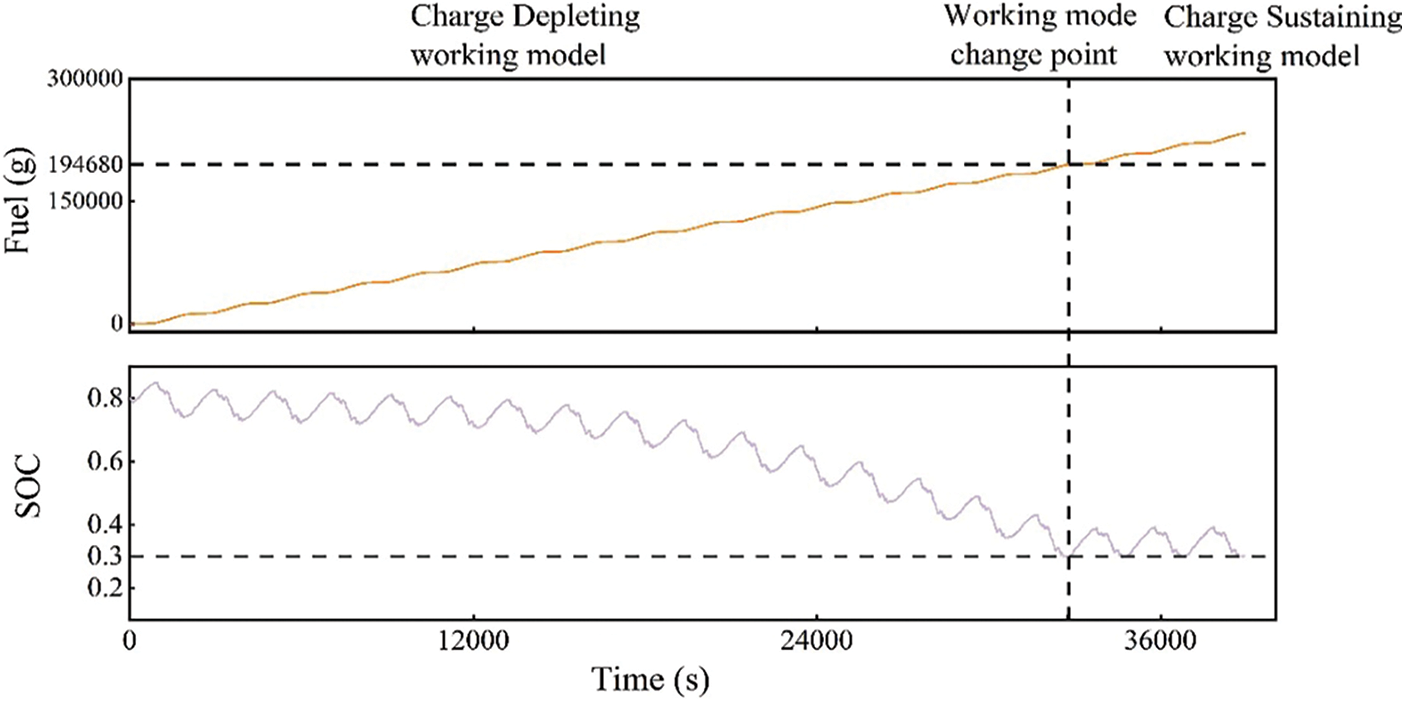
Figure 9: The P-ECMS strategy simulation results in CD mode
5.3 Comparison of Simulation Results
The results of the CDCS strategy, the DP strategy, and the P-ECMS strategy are shown in Table 7.

Although both in the DP strategy and in the P-ECMS strategy, the generator set operates during the empty-load flat road phase and the full-load flat road phase, the fuel consumption results are lower than those of the electric mode under the CDCS strategy. Under the P-ECMS strategy, the equivalent fuel consumption is 150.8 L/100 km, 10.9% lower than the CDCS strategy (169.3 L/100 km) and 0.53% higher than the DP strategy(150 L/100 km). The battery SOC of the P-ECMS strategy under typical mining cycle conditions compared to the DP strategy is shown in Fig. 10. The SOC trajectory of the P-ECMS strategy is more consistent with the globally optimized SOC trajectory of the DP strategy, demonstrating good follow-through. When operating in CD mode under the P-ECMS strategy control, the average fuel consumption is 143 L/100 km, representing a 5.2% reduction compared to CS mode.
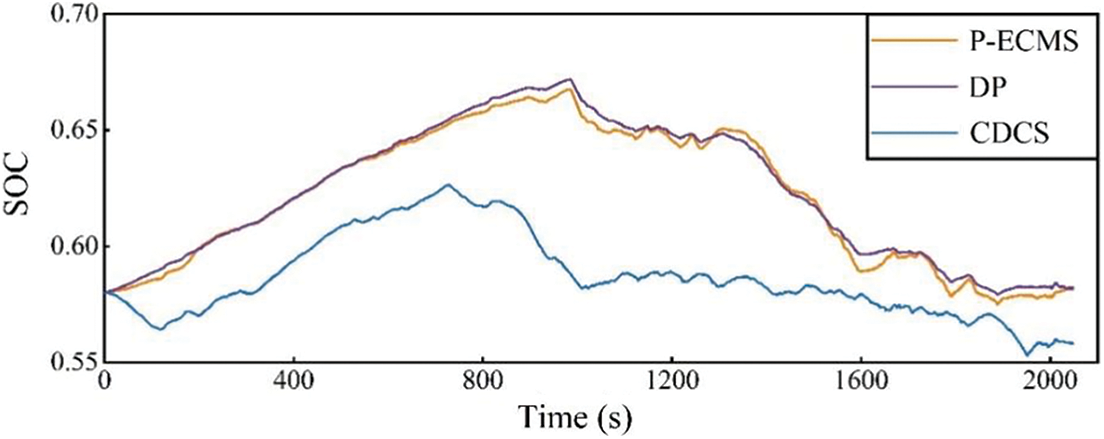
Figure 10: Battery SOC comparison
In summary, the P-ECMS strategy designed in this paper can more reasonably allocate power between the generator set and battery pack through real-time control, enabling the engine to operate more efficiently and reduce fuel consumption. It also has good power maintenance characteristics, reducing the frequency of stopping and charging for hybrid mining dump trucks, which improves transportation efficiency.
This paper proposes a predictive equivalent consumption minimization strategy based on the DP optimization results, P-ECMS. Based on a 100-ton conventional mining dump truck, a series hybrid system is constructed. Then, the collected driving data can be used to create typical cycle working conditions. We use the DP algorithm offline to perform global planning for the mining site cycle working conditions to obtain the optimal control manifold and the SOC reference trajectory. The SOC reference trajectory is then applied to guide the battery SOC in the subsequent real-time stage parameter optimization process to obtain the EF in the current stage and applied to the ECMS algorithm, the realization of real-time control based on this optimal EF.
(1) The CDCS strategy prioritizes driving the truck in electric mode, which results in a lower battery SOC when the mining truck is driving uphill. This increases the power output of the generator set. In contrast, although the engine block of the mining dump truck under the P-ECMS strategy is always in operation during the empty-load flat road phase and the full-load flat road phase, the output power is lower, and it keeps the battery SOC higher when starting to uphill, which the battery can provide enough power to regulate the engine operating range, reduce fuel consumption.
(2) Compared to the DP strategy, the P-ECMS strategy achieves near-optimal fuel economy. It also has the capability of real-time online control.
(3) Under mining conditions, the equivalent fuel consumption of the P-ECMS strategy is 150.8 L/100 km, which is 10.9% lower than the CDCS strategy (169.3 L/100 km). It is 99.47% of the fuel-saving effect of the DP strategy (150 L/100 km), achieving near-optimal fuel savings.
(4) The DP and P-ECMS strategies can distribute the power of the generator set and the power battery more rationally than the CDCS strategy, so the engine works more in its high efficiency zone and reduces fuel consumption.
(5) The P-ECMS strategy can enhance the fuel economy of plug-in hybrid mining dump trucks when running in CD mode, but only if there is sufficient time for charging and adequate charging equipment.
In view of the effectiveness of the P-ECMS strategy, the following research focuses on considering robustness, e.g., changes in gradient, temperature, etc., to improve the fuel economy of the strategy further.
Acknowledgement: Thanks are due to the editors and reviewers for their valuable opinions, which are of great help to improve the quality of this paper.
Funding Statement: The author received no specific funding for this study.
Author Contributions: Study conception and design: Yu Yixuan, Wang Yulin; data collection: Yu Yixuan, Li Qingcheng; analysis and interpretation of results: Yu Yixuan, Wang Yulin, Jiao Bowen; draft manuscript preparation: Yu Yixuan. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Siami-Irdemoosa, E., Dindarloo, S. R. (2015). Prediction of fuel consumption of mining dump trucks: A neural networks approach. Applied Energy, 151, 77–84. [Google Scholar]
2. Li, P., Jiao, X., Li, Y. (2021). Adaptive real-time energy management control strategy based on fuzzy inference system for plug-in hybrid electric vehicles. Control Engineering Practice, 107, 104703. [Google Scholar]
3. Onori, S., Serrao, L., Rizzoni, G. (2016). Hybrid electric vehicles: Energy management strategies. UK: Springer. [Google Scholar]
4. Peng, J., He, H., Xiong, R. (2017). Rule based energy management strategy for a series-parallel plug-in hybrid electric bus optimized by dynamic programming. Applied Energy, 185, 1633–1643. [Google Scholar]
5. Rezaei, A., Burl, J. B., Rezaei, M., Zhou, B. (2018). Catch energy saving opportunity in charge-depletion mode, a real-time controller for plug-in hybrid electric vehicles. IEEE Transactions on Vehicular Technology, 67(11), 11234–11237. [Google Scholar]
6. Gong, Q., Li, Y., Peng, Z. R. (2008). Trip-based optimal power management of plug-in hybrid electric vehicles. IEEE Transactions on Vehicular Technology, 57(6), 3393–3401. [Google Scholar]
7. Fausto, F., Reyna-Orta, A., Cuevas, E., Andrade, Á.G., Perez-Cisneros, M. (2020). From ants to whales: Metaheuristics for all tastes. Artificial Intelligence Review, 53, 753–810. [Google Scholar]
8. Eid, H. F., Mansour, R. F., Cuevas, E. (2022). A modified variant of coyote optimization algorithm for solving ordinary differential equations and oscillatory mechanical problems. Simulation, 98(12), 1161–1178. [Google Scholar]
9. Kong, Y., Xu, N., Liu, Q., Sui, Y., Yue, F. (2023). A data-driven energy management method for parallel PHEVs based on action dependent heuristic dynamic programming (ADHDP) model. Energy, 265, 126306. [Google Scholar]
10. Hu, X., Liu, T., Qi, X., Barth, M. (2019). Reinforcement learning for hybrid and plug-in hybrid electric vehicle energy management: Recent advances and prospects. IEEE Industrial Electronics Magazine, 13(3), 16–25. [Google Scholar]
11. Chen, Z., Hu, H., Wu, Y., Zhang, Y., Li, G. et al. (2020). Stochastic model predictive control for energy management of power-split plug-in hybrid electric vehicles based on reinforcement learning. Energy, 211, 118931. [Google Scholar]
12. Chen, S. Y., Wu, C. H., Hung, Y. H., Chung, C. T. (2018). Optimal strategies of energy management integrated with transmission control for a hybrid electric vehicle using dynamic particle swarm optimization. Energy, 160, 154–170. [Google Scholar]
13. Chen, Z., Mi, C. C., Xiong, R., Xu, J., You, C. (2014). Energy management of a power-split plug-in hybrid electric vehicle based on genetic algorithm and quadratic programming. Journal of Power Sources, 248, 416–426. [Google Scholar]
14. Liu, Y., Li, J., Lei, Z., Li, W., Qin, D. et al. (2019). An adaptive equivalent consumption minimization strategy for plug-in hybrid electric vehicles based on energy balance principle. IEEE Access, 7, 67589–67601. [Google Scholar]
15. Sundstrom, O., Guzzella, L. (2009). A generic dynamic programming Matlab function. 2009 IEEE Control Applications, (CCA) & Intelligent Control, (ISIC), pp. 1625–1630. St. Petersburg, Russia. [Google Scholar]
16. Zhou, W., Yang, L., Cai, Y., Ying, T. (2018). Dynamic programming for new energy vehicles based on their work modes part I: Electric vehicles and hybrid electric vehicles. Journal of Power Sources, 406, 151–166. [Google Scholar]
17. Gong, Q., Li, Y., Peng, Z. R. (2007). Optimal power management of plug-in HEV with intelligent transportation system. 2007 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, pp. 1–6. Zurich, Switzerland. [Google Scholar]
18. Zhao, Y., Cai, Y., Song, Q. (2018). Energy control of plug-in hybrid electric vehicles using model predictive control with route preview. IEEE/CAA Journal of Automatica Sinica, 8(12), 1948–4854. [Google Scholar]
19. Anselma, P. G., Biswas, A., Belingardi, G., Emadi, A. (2020). Rapid assessment of the fuel economy capability of parallel and series-parallel hybrid electric vehicles. Applied Energy, 275, 115319. [Google Scholar]
20. Powell, W. B. (2007). Approximate dynamic programming: Solving the curses of dimensionality. USA: John Wiley & Sons. [Google Scholar]
21. Han, J., Park, Y., Kum, D. (2014). Optimal adaptation of equivalent factor of equivalent consumption minimization strategy for fuel cell hybrid electric vehicles under active state inequality constraints. Journal of Power Sources, 267, 491–502. [Google Scholar]
22. Paganelli, G., Delprat, S., Guerra, T. M., Rimaux, J., Santin, J. J. (2002). Equivalent consumption minimization strategy for parallel hybrid powertrains. Vehicular Technology Conference. IEEE 55th Vehicular Technology Conference. VTC Spring 2002 (Cat. No. 02CH37367), pp. 2076–2081. Birmingham, USA. [Google Scholar]
23. Martinez, C. M., Hu, X., Cao, D., Velenis, E., Gao, B. et al. (2016). Energy management in plug-in hybrid electric vehicles: Recent progress and a connected vehicles perspective. IEEE Transactions on Vehicular Technology, 66(6), 4534–4549. [Google Scholar]
24. Chen, D., Kim, Y., Stefanopoulou, A. G. (2020). Predictive equivalent consumption minimization strategy with segmented traffic information. IEEE Transactions on Vehicular Technology, 69(12), 14377–14390. [Google Scholar]
25. Musardo, C., Rizzoni, G., Guezennec, Y., Staccia, B. (2005). A-ECMS: An adaptive algorithm for hybrid electric vehicle energy management. European Journal of Control, 11(4–5), 509–524. [Google Scholar]
26. Onori, S., Serrao, L., Rizzoni, G. (2010). Adaptive equivalent consumption minimization strategy for hybrid electric vehicles. Dynamic Systems and Control Conference, pp. 499–505. Cambridge, USA. [Google Scholar]
27. Choi, K., Byun, J., Lee, S., Jang, I. G. (2021). Adaptive equivalent consumption minimization strategy (A-ECMS) for the HEVs with a near-optimal equivalent factor considering driving conditions. IEEE Transactions on Vehicular Technology, 71(3), 2538–2549. [Google Scholar]
28. Zeng, T., Zhang, C., Zhang, Y., Deng, C., Hao, D. et al. (2021). Optimization-oriented adaptive equivalent consumption minimization strategy based on short-term demand power prediction for fuel cell hybrid vehicle. Energy, 227, 120305. [Google Scholar]
29. Sun, F., Xiong, R. (2015). A novel dual-scale cell state-of-charge estimation approach for series-connected battery pack used in electric vehicles. Journal of Power Sources, 274, 582–594. [Google Scholar]
30. Wang, R., Lukic, S. M. (2012). Dynamic programming technique in hybrid electric vehicle optimization. 2012 IEEE International Electric Vehicle Conference, pp. 1–8. Greenville, USA. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools