 Open Access
Open Access
ARTICLE
Enhanced Deep Reinforcement Learning Strategy for Energy Management in Plug-in Hybrid Electric Vehicles with Entropy Regularization and Prioritized Experience Replay
1 School of Computer Science and Engineering, Anhui University of Science & Technology, Huainan, 232001, China
2 School of Information Engineering, Huainan Union University, Huainan, 232001, China
* Corresponding Author: Li Wang. Email:
Energy Engineering 2024, 121(12), 3953-3979. https://doi.org/10.32604/ee.2024.056705
Received 29 July 2024; Accepted 26 September 2024; Issue published 22 November 2024
Abstract
Plug-in Hybrid Electric Vehicles (PHEVs) represent an innovative breed of transportation, harnessing diverse power sources for enhanced performance. Energy management strategies (EMSs) that coordinate and control different energy sources is a critical component of PHEV control technology, directly impacting overall vehicle performance. This study proposes an improved deep reinforcement learning (DRL)-based EMS that optimizes real-time energy allocation and coordinates the operation of multiple power sources. Conventional DRL algorithms struggle to effectively explore all possible state-action combinations within high-dimensional state and action spaces. They often fail to strike an optimal balance between exploration and exploitation, and their assumption of a static environment limits their ability to adapt to changing conditions. Moreover, these algorithms suffer from low sample efficiency. Collectively, these factors contribute to convergence difficulties, low learning efficiency, and instability. To address these challenges, the Deep Deterministic Policy Gradient (DDPG) algorithm is enhanced using entropy regularization and a summation tree-based Prioritized Experience Replay (PER) method, aiming to improve exploration performance and learning efficiency from experience samples. Additionally, the corresponding Markov Decision Process (MDP) is established. Finally, an EMS based on the improved DRL model is presented. Comparative simulation experiments are conducted against rule-based, optimization-based, and DRL-based EMSs. The proposed strategy exhibits minimal deviation from the optimal solution obtained by the dynamic programming (DP) strategy that requires global information. In the typical driving scenarios based on World Light Vehicle Test Cycle (WLTC) and New European Driving Cycle (NEDC), the proposed method achieved a fuel consumption of 2698.65 g and an Equivalent Fuel Consumption (EFC) of 2696.77 g. Compared to the DP strategy baseline, the proposed method improved the fuel efficiency variances (FEV) by 18.13%, 15.1%, and 8.37% over the Deep Q-Network (DQN), Double DRL (DDRL), and original DDPG methods, respectively. The observational outcomes demonstrate that the proposed EMS based on improved DRL framework possesses good real-time performance, stability, and reliability, effectively optimizing vehicle economy and fuel consumption.Keywords
Nomenclature
| Peng | PHEV engine power |
| ωeng | PHEV engine speed |
| Teng | PHEV engine torque |
| mf | Fuel consumption rate |
| ηeng | Engine efficiency |
| ηT | Mechanical transmission efficiency |
| Ff | Rolling resistance |
| Fi | Gradient resistance |
| SOC | Battery state of charge |
| Qmax | Battery maximum capacity |
| S | MDP state set |
| P | MDP state transition probabilities |
| Vmass | Vehicle mass |
| Varc | Air resistance coefficient |
| Pgearf | Front teeth number of the planetary gear |
| DMP | Motor maximum power |
| DMT | Motor maximum torque |
| Dmoi | Motor moment of inertia |
| π | Control strategy |
| π* | Optimal control strategy |
| θμ | Actor network parameters |
| θ′μ | Target actor network parameters |
| ρπ | State distribution under policy π |
| yt | Target Q-value |
| rt | Reward received at time step t |
| at | Action taken at time step t |
| EFC | Equivalent Fuel consumption |
| Fuel density | |
| Average efficiency in the engine power generation state | |
| Et | Energy consumption at time t |
| v | Vehicle velocity, considered as a state variable |
| Pele | PHEV motor power |
| ωele | PHEV motor speed |
| Teng | PHEV motor torque |
| ηele | PHEV motor efficiency |
| Pr | PHEV demanded power |
| ua | Longitudinal velocity |
| Fw | Air resistance |
| Ff | Acceleration resistance |
| Qin | Battery initial capacity |
| MDP | Markov decision process |
| A | MDP action set |
| R | MDP reward |
| Vradius | Tire radius |
| Vrrc | Rolling resistance coefficient |
| Pgearr | Rear teeth number of the planetary gear |
| EMP | Engine maximum power |
| EMT | Engine maximum torque |
| Emoi | Engine moment of inertia |
| γ | Discounting factor |
| Ts | Time interval |
| θQ | Critic network parameters |
| θ′Q | Target critic network parameters |
| L(θQ) | Loss function used to train the critic network |
| τ | Soft update coefficient |
| st | State at time step t |
| mt | Fuel consumption at time t |
| Electricity consumed under cyclic conditions | |
| Lower heating value of the fuel | |
| Mean efficiency in the motor power generation state | |
| Pi | Sampling probability of the i-th dataset in the experience pool |
| d | Vehicle travel distance, another state variable |
The automobile has made significant contributions to the development of human society. However, the emissions from traditional fuel-powered cars not only cause environmental pollution but also have adverse effects on human respiratory and cardiovascular health [1]. With the rising proliferation of automobiles, issues such as depletion of petroleum resources are receiving more and more attention. Therefore, the development of new energy vehicle technology is highly valued by the domestic and international automotive industry. Per the “Global Electric Vehicles (EV) Outlook 2022”, the present worldwide inventory of new energy vehicles exceeds 14 million and is expected to continue growing rapidly [2]. The new energy vehicle sector embarks on an accelerated developmental phase, infusing robust impetus into worldwide economic expansion. Simultaneously, it contributes to a reduction in greenhouse emissions, playing a pivotal role in confronting the challenges posed by climate change.
Emerging energy automobiles can be divided into electric vehicles (EVs), plug-in hybrid electric vehicles (PHEVs), and fuel cell vehicles (FCVs) [3]. Within the powertrain of EVs, rechargeable batteries serve as the sole energy source, converting electricity into kinetic energy to drive the vehicle. However, EVs are limited by their limited driving distance, extended charging duration, and battery safety issues. FCVs are based on fuel cell electric systems and have an additional rechargeable battery system, but the technology for fuel cell vehicles is not yet mature and involves expensive rare earth and precious metal materials, increasing production costs. PHEVs use two or more energy sources in their power systems, typically combining fuel and batteries with internal combustion engines and electric motors. PHEVs incorporate the strengths of EVs and hybrid electric vehicles (HEVs), allowing for pure electric and zero-emission driving in instances where the internal combustion engine falters in efficiency during slower speeds, and increasing the vehicle’s range through hybrid drive, on-board charging, and regenerative braking [4].
Energy management strategy (EMS), at the heart of PHEV technology, straightforwardly determines vehicle’s performance in terms of fuel economy, ride comfort, and overall power [5]. Its main task is to allocate power flow within the hybrid powertrain system (HPS) in a reasonable manner to keep the engine and motor operating in a more efficient range, achieving optimal fuel economy, and minimizing emissions. This ultimately results in the optimal driving condition for PHEVs. While meeting the system’s hard constraints, the EMS also needs to manage and maintain state of charge (SOC) of batteries throughout the entirety of the driving journey according to the actual driving conditions and the type of HPS.
Based on engineering practice and advanced research, EMSs for PHEVs can be delineated into three principal classifications: rule-based, optimization-based, and deep reinforcement learning (DRL)-based strategies. In engineering practice, rule-based EMSs have been widely used, which allocate power flow within the HPS based on real driving processes and engineering experience, using a set of predetermined rules [6]. In addition to rule-based strategies, fuzzy control methods are proposed to address systems with higher uncertainty or difficulties in mathematical modeling, such as PHEV energy management. However, both of these strategies depend on expert knowledge and fall short of achieving optimal control.
Strategies grounded in optimization enhance fuel efficiency and mitigate emissions by optimizing the energy allocation between the engine and motor. EMSs grounded in optimization principles can be segmented into global optimization and instantaneous optimization [7]. Global optimization can explore global optimal strategies but requires large computational resources, making it unsuitable for real-time problems. Instantaneous optimization methods have real-time capability but can be affected by the accuracy of the precise vehicle model or prediction of future driving states.
In recent times, amidst the swift evolution of artificial intelligence (AI), some studies have attempted to use DRL to address PHEV EMS problems and achieve optimal control. Various DRL algorithms have been developed, like Double Deep Q Network (DDQN), Double Deep Q-Learning (DDQL), and Deep Deterministic Policy Gradient (DDPG), which can treat energy management problems as continuous problems. DRL provides a new solution for decision-making problems in complex environments by continuously interacting with the environment, improving policies, and learning the best behavior.
Previous research on PHEV energy management has achieved certain results, but there are still limitations. Rule-based strategies rely on prior knowledge and their results are suboptimal. Global optimization strategies, represented by dynamic programming (DP), can obtain optimal solutions, but they require large computational resources and complete knowledge of driving conditions, making them unsuitable for real-time applications. Local optimization strategies, represented by model predictive control, have difficulty accurately predicting future vehicle conditions, which can reduce the accuracy of the strategy. Currently, research on EMSs based on DRL has made progress, but there are still some issues, such as difficulties in algorithm convergence, low learning efficiency, and instability. These issues become more evident in dynamic models like vehicle forward simulation, requiring algorithm improvements.
To address the aforementioned issues, this paper focuses on PHEVs and proposes an optimized EMS using an improved DRL framework. The proposed method combines entropy regularization and prioritized experience replay (PER). A forward simulation model is established for PHEV vehicles, and a Markov decision process (MDP) for energy management is created. The DDPG algorithm is applied for EMS. By introducing the output method of entropy regularization into the architecture of the DDPG algorithm, local optima of action selections from actor network are avoided, leading to better control results. The PER mechanism based on the sum tree structure is incorporated to enhance the learning efficacy of the experience samples.
The remaining parts of this paper are arranged in the subsequent manner. Section 2 provides a detailed overview of the research status of PHEVs and their EMSs, analyzing the problems and deficiencies of EMSs and defining the research direction. Section 3 introduces the system modeling and DRL algorithm. Section 4 proposes an EMS based on an improved DRL algorithm. Through entropy regularization and PER mechanism, DDPG is improved, and an MDP for PHEV energy management is established and applied. Section 5 conducts comparative experiments between the proposed improved DRL method, rule-based Charge Depletion-Charge Sustaining (CD-CS) and optimization-based DP strategies to verify its effectiveness and advancement. Finally, Section 6 summarizes the entire paper and presents future prospects.
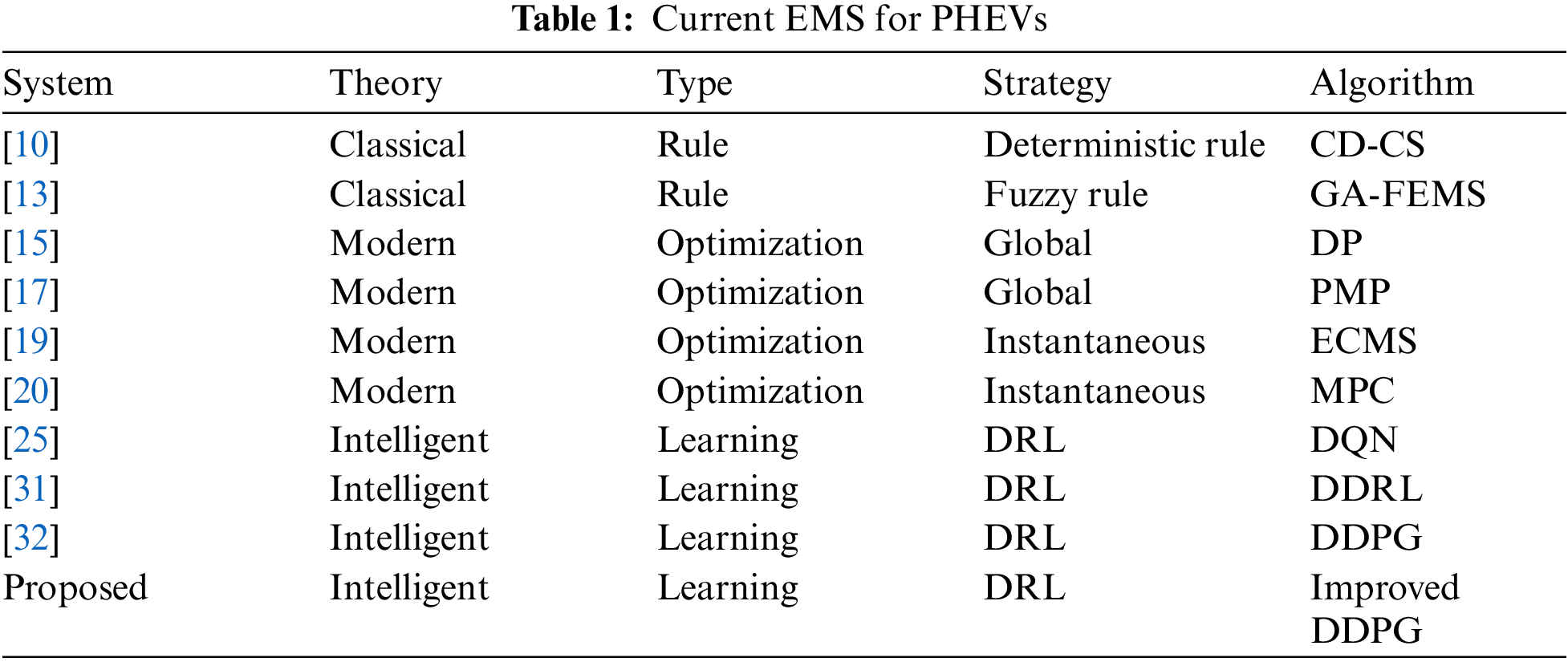
The research and development of PHEV powertrains includes configuration design, parameter alignment, and energy management. The goal is to select appropriate system structures and component types according to actual application scenarios and achieve the expected vehicle performance through EMSs that allocate power flow in HPSs [8]. Depending on the control algorithm used, research results of EMSs can be divided into three types: rule, optimization, and learning-based EMSs, as listed in Table 1.
Rule-based EMSs determine and output power source control quantities based on real-time information such as demanded power and battery SOC [9]. In the realm of rule-based strategies, we can categorize them into deterministic rules (DR) and fuzzy rules (FR). DR-based EMSs determine the output based on the throttle opening and its rate of change, combined with input state variables and logical threshold values. The most commonly used DR-based strategy is CD-CS [10], but it lacks flexibility for different driving cycles. Therefore, Peng et al. [11] recalibrated DR-based EMSs using DP and achieved good results. Fuzzy rules-based methods solve complex problems by establishing fuzzy rules that mimic human brain’s judgment and reasoning, offer higher flexibility and robustness. Chen et al. [12] combined DP with fuzzy logic rules, established fuzzy membership function rules based on the relationship between engine power and system power, along with vehicle velocity, acceleration, and battery SOC. Furthermore, the real-time fuzzy energy management mechanism is embedded into vehicle controller. Zhang et al. [13] proposed the Genetic Algorithm-Fuzzy EMS (GA-FEMS) method, which uses an improved genetic algorithm to address the constrained dual-objective optimization issue of fuzzy EMSs, designs rule library encoding, constraint handling, pruning, and maintenance operators to fine-tune the fuzzy rule library as well as membership function parameters, improving the performance of the EMS. The drawback of these methods is that designing a reasonable rule-based EMS requires a lot of expert experience and lacks adaptability to random driving environments during actual driving, making it unable to guarantee the optimal fuel economy under various driving conditions.
Optimization-based EMSs transform the power allocation problem of HPSs into an optimization problem of driving performance. By setting corresponding objective functions in advance and considering global and local constraints on the internal states of the HPS, the optimal power allocation sequence corresponding to the optimal objective function is solved in a given driving environment [14]. EMSs grounded in optimization principles can be segmented into global and instantaneous optimization approaches based on algorithm properties. Global optimization strategies aim to optimize torque distribution considering constraints, with the goal of vehicle fuel economy or emissions on a given driving condition. Currently used methods mainly include DP and Pontryagin’s Minimum Principle (PMP). Specifically, DP discretizes the state variables and solves them backward, so necessitates a comprehensive understanding of the complete driving scenario. He et al. [15] suggested a method for constructing real-time driving cycles on a global scale utilizing up-to-the-minute traffic information and applied DP to online energy management of PHEVs, achieving a 19.83% improvement in fuel efficiency compared to CD-CS. Li et al. [16] proposed a hierarchical adaptive EMS for PHEVs. They used a genetic algorithm belonging to global optimization to find globally optimal control sequences of driving environments and used the solution as the training data for deep learning (DL) model to achieve parameterized fitting of the optimal control strategy between input states and output actions using neural network parameters. Compared to the conventional CD-CS, the EMS enhances not just fuel efficiency, but also validates real-time operational capabilities and adaptability through Hardware-in-the-Loop (HIL) experiments. PMP transforms the complex global optimization challenge into a localized Hamiltonian minimization issue based on optimal control theory, so PMP has smaller computational requirements compared to DP. Zhang et al. [17] proposed an online coordinated optimization strategy based on PMP for single-axle series-parallel PHEVs. They integrated the high-fidelity capacity loss model of lithium iron phosphate batteries into the optimization framework, considering both cycle aging and calendar aging characteristics of the battery. Then, they controlled the SOC and ampere throughput of the battery in real-time based on the reference trajectory, aiming for online adaptive performance under different driving environments. Although global optimization control strategies can achieve global optimality in theory, they cannot be used for real-time control of HEV. This arises due to the necessity for pre-existing knowledge of the complete driving environment in global optimization. Acquiring precise information about future road conditions during actual vehicle operations is challenging. Additionally, the computational demands for global optimization are substantial.
EMSs based on instantaneous optimization, such as Equivalent Consumption Minimization Strategy (ECMS) and Model Predictive Control (MPC), are used to address the limitations of global optimization [18]. Instantaneous optimization refers to calculating fuel consumption of engines and electricity consumption of motors at each instant during vehicle operation, while meeting power and other prerequisites, and minimizing sum of the pair. In the literature [19], driving circumstances were segmented according to the specific geographical locations of bus stops. Particle swarm optimization was employed to fine-tune the Equivalent Factor (EF) for each segment under different initial SOC, resulting in the optimal instantaneous energy allocation for hybrid power system. MPC employs dynamic optimization principles as an advanced technique in process controls. It is widely applied in linear and nonlinear control systems due to its robustness, good control performance, and high stability. In the literature [20], the prediction of velocity was accomplished using the Markov Chain-based Monte Carlo approach in a multi-scale single-step prediction form. Post-processing techniques, including quadratic fitting and average filtering, were utilized to mitigate the fluctuation in the predicted outcomes. MPC was then utilized for energy management optimization. In the work of Tang et al. [21], the vehicle energy dataset (VED) dataset from Ann Arbor, Michigan was used as the training basis for the speed predictor. Different machine learning models are evaluated in terms of prediction efficiency and accuracy under different time domains. A PMP-MPC based multi-objective optimization strategy, considering battery temperature, was proposed for PHEV, striking a balance between fuel efficiency and overall driving cost. Ripaccioli et al. [22] proposed the application of stochastic model predictive control in EMS. The algorithm’s complexity was reduced through quadratic programming, improving its real-time applicability.
DRL combines the knowledge systems of DL and reinforcement learning (RL), capitalizing on the perceptual strengths of DL and the decision-making prowess of RL. By continuously interacting with the environment, it adapts its policies and learns the optimal behavior, providing new solutions for decision-making problems in complex environments [23]. DRL models sequential decision-making problems as adaptive DP problems. Among various types of DRL algorithms, model-free DRL is better suited for complex environments where modeling is difficult, making it applicable to PHEV energy management problems. In the work of Li et al. [24], an DDPG-based EMS was designed for PHEVs while taking terrain information into account. It constructed a mixed discrete-continuous action space and achieves more efficient training process by combining pre-training based on DP control results. Zou et al. [25] presented an online-updated EMS for fixed-line HEVs, merging MPC with Deep Q Network (DQN) algorithm. The immediate operational effectiveness and optimization efficiency of the implemented control approach are affirmed via HIL assessment. Sun et al. [26] designed a fast learning-based algorithm based on Q-learning and ECMS for energy managements of fuel cell/battery/ultracapacitor HEVs. Du et al. [27] proposed a fast Q-learning algorithm that achieves only 4.6% increase in terms of fuel usage in comparison to DP, but significantly reduced the computation time required. The real-time applicability of the algorithm was verified using HIL testing, demonstrating that the EMS has the capacity to enhance vehicle fuel efficiency and holds promise for applications requiring instantaneous response. Han et al. [28] addressed the over-optimization issue of deep Q network algorithm and proposed an EMS based on DDQN algorithm for HEVs, achieving 93.2% of the energy optimization results in comparison to DP.
While methods based on Deep Q-Learning (DQL) algorithm have achieved certain results, they are more suitable for discrete actions and lack effectiveness in continuous action applications. Therefore, Wang et al. [29] utilized the Actor-Critic algorithm, which is more suitable for continuous actions, to oversee the energy utilization of HEVs, leading to a decrease of 21.8% in energy usage in comparison to baseline models. DDPG algorithm, as an extension of the DQN algorithm, implements continuous action control using experience replay mechanism. Lian et al. [30] implemented DDPG to tackle the multi-faceted EMS challenges within an expansive control variable domain. Combining the strengths of DQN and DDPG algorithms, in the work of Li et al. [31], a Double DRL (DDRL) strategy is proposed for HEVs. DQN was used to optimize the shifting timing of the vehicle, while DDPG algorithm was applied to control the engine throttle. Wang et al. [32] introduced a multi-agent cooperative optimization framework based on DDPG. They decomposed the EMS problem into a collaborative task for multiple agents, incorporating interaction between the vehicle and EMS agents into the energy-saving strategy. Table 1 lists the representative EMS for PHEVs.
3 Vehicle Modeling and MDP Construction
The structure and control of power-split PHEVs are the most complex. The closed-loop forward simulation model (FSM) of PHEVs is built to replicate real driving processes and optimize EMSs. The FSM is commonly used in the complete design process of automobiles, as it can accurately replicate the vehicle’s actual operating conditions, enhancing the realism and reliability of simulations [33]. The structure of the FSM for PHEVs is shown in Fig. 1.
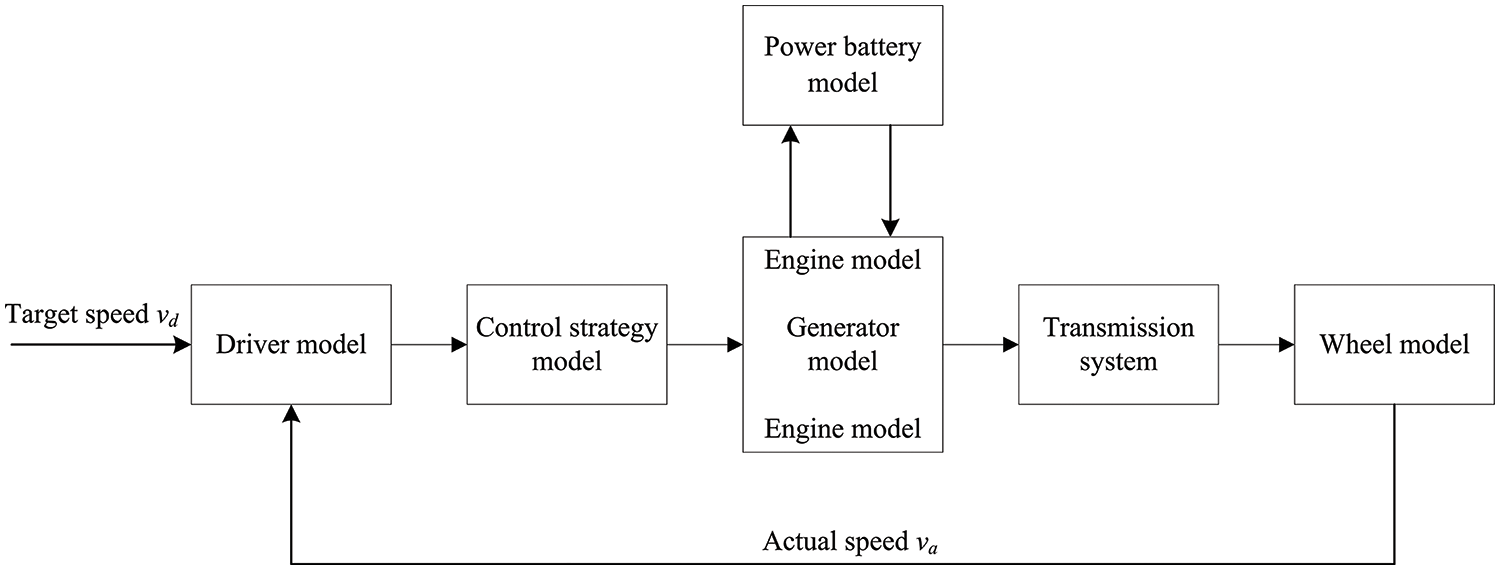
Figure 1: FSM structure for power-split PHEVs
Power-split PHEVs often employ planetary gear mechanisms as power coupling devices. Compared to series and parallel PHEVs with mechanical or electrical coupling, power-split PHEVs can flexibly tune the power output of both the engine and electric motor in accordance with operating conditions, thereby improving energy utilization [34]. Toyota introduced the third-generation Prius model in 2009, equipped with the THS-III hybrid system shown in Fig. 2 [35]. It utilizes a dual planetary gear arrangement with the front planetary gear set performing power splitting and the rear planetary gear set serving as a fixed-axis transmission. The engine links to the front planetary carrier via a torsional damper, while the small motor-generator (MG1) connects to the front sun gear, and the large motor (MG2) is linked to the rear sun gear. The rear planetary carrier is locked to the transmission case, and the front and rear planetary gear sets share the ring gear. This transmission is a typical power-split device where the engine output power is split once through the front planetary gear set, with the energy split between MG1 to MG2 or stored in the battery in the form of electricity, and the remaining mechanical energy is combined with the power generated by MG2 and transmitted to the output end.
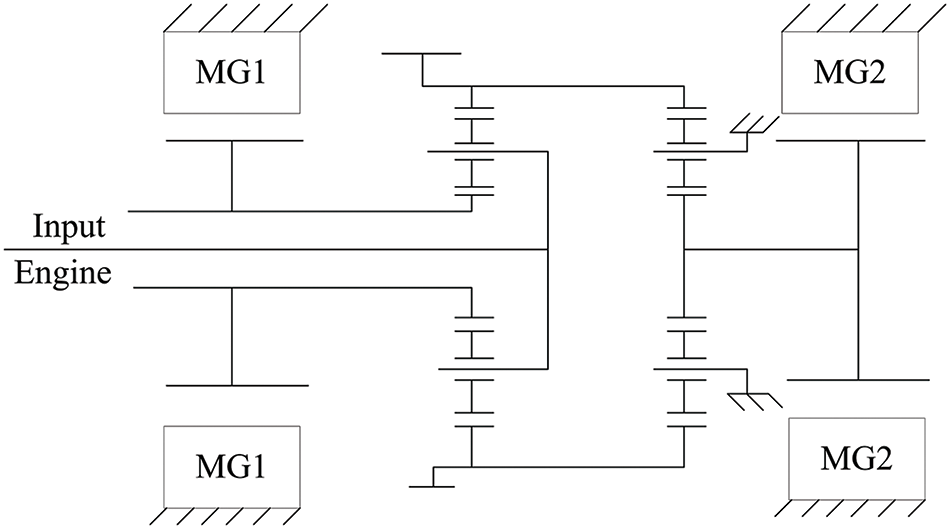
Figure 2: THS-III hybrid powertrain system. Adapted from Reference [35]
3.2 PHEV Modeling, Main Parameters and Constraint Conditions
The core of the forward PHEV modeling framework encompasses five essential components: the engine model, electric motor model, vehicle dynamics, power flow balance, and battery SOC equations. The engine model is designed to describe the fuel consumption and power output characteristics of the engine. The electric motor model provides details on the power output and efficiency characteristics of the motor. The vehicle dynamics model calculates the power demand during driving. The power flow balance describes the distribution of power between the engine, electric motor, and battery. The battery SOC model calculates and tracks the battery’s state of charge.
The integration of these five models forms a comprehensive framework for PHEV modeling, which covers the performance of power sources, power demand calculation, power distribution management, and battery energy state tracking. This comprehensive model accurately reflects the operation characteristics of a PHEV under various driving conditions, supporting simulation and optimization tasks. It aids in designing more efficient energy management strategies, ultimately enhancing vehicle performance and fuel economy.
The engine is an important power source for PHEVs and is currently the most common power source for vehicles, obtaining energy through fuel combustion. The engine is modeled using a Quasi-static Map [36]. Assuming the engine can achieve instantaneous response, by utilizing the torque and speed of the current operational state through the Map, one can derive real-time information on fuel consumption and efficiency. Fig. 3 illustrates the corresponding efficiency and fuel consumption Map graph for the engine. It uses a 2.2 L fuel-injected four-cylinder engine with a maximum power (MP) of 131 kW and a maximum torque (MT) of 221 N.m. The engine power Peng is determined by the engine speed ωeng and engine torque Teng:
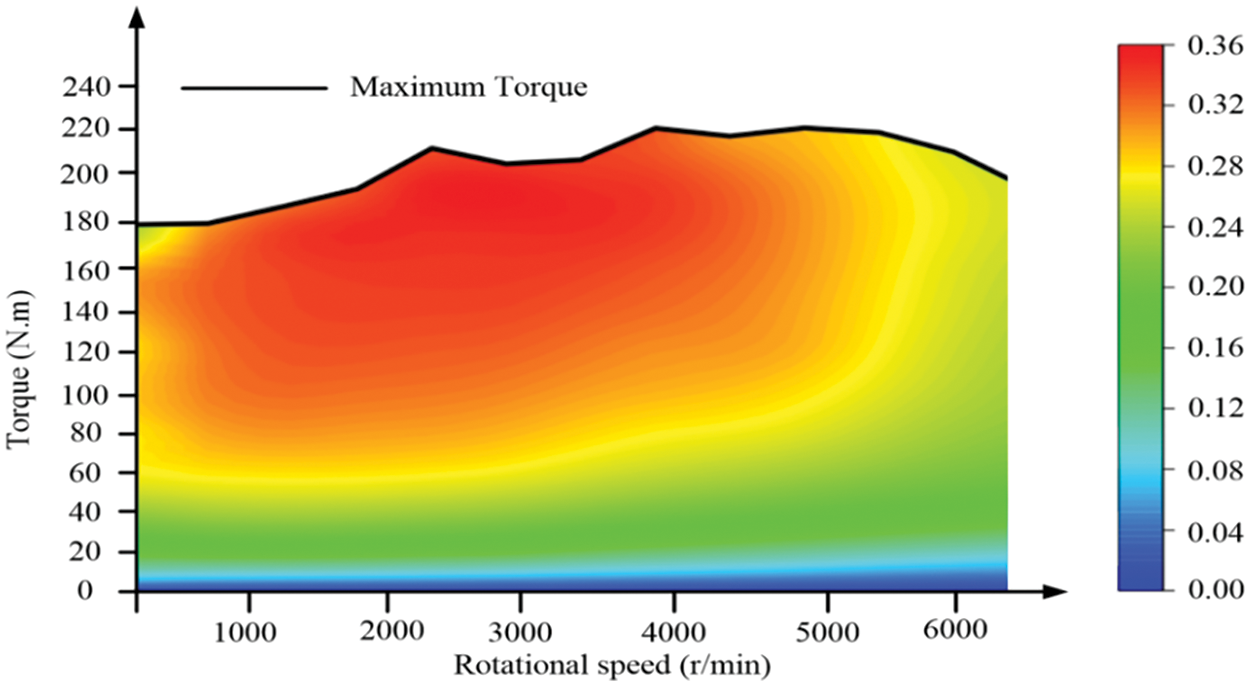
Figure 3: Engine fuel consumption and efficiency map
The engine model retrieves the fuel consumption rate mf and engine efficiency ηeng based on the current speed and torque through a lookup table:
where geng and feng are lookup functions used to obtain the fuel consumption rate and engine efficiency.
The electric motor provides auxiliary power to the PHEV and can achieve regenerative braking, playing a key role particularly during low-speed or acceleration. The motor’s efficiency and power output determine the performance of the electric drive. The electric motor power Pele is determined by the motor speed ωele and motor torque Tele:
Similarly, the electric motor is also modeled using a Quasi-static Map graph. The motor specifications are based on the permanent magnet motor used in the Toyota Prius, with an MP of 34 kW and an MT of 260 N.m. Fig. 4 shows the motor Map graph regarding operating efficiency. Then the electric motor efficiency ηele can be obtained through lookup functions:
where fele are lookup function used to obtain the electric motor efficiency.
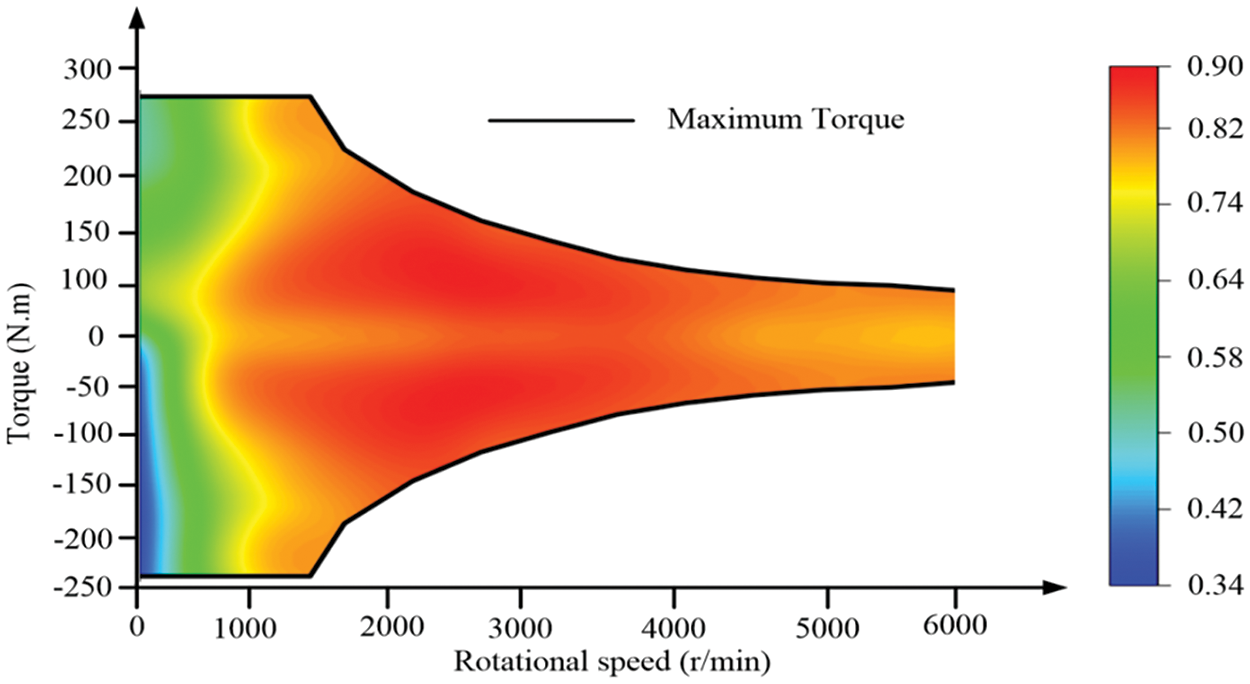
Figure 4: Motor efficiency map
The vehicle dynamics model describes the power demand during driving. This model considers various driving resistances (e.g., rolling resistance, air resistance) and calculates the total required power. This is crucial for designing and optimizing EMSs as it helps determine the required engine and motor power under different driving conditions. In the examination of the longitudinal dynamics of PHEVs, the demanded power can be calculated as:
where ηT represents the mechanical transmission efficiency. ua represents the longitudinal velocity. Ff is the rolling resistance, Fw is the air resistance. Fi denotes the gradient resistance, and Ff stands for the acceleration resistance.
The power flow balance equation ensures that power is distributed among the engine, electric motor, and battery, maintaining equilibrium within the system, and preventing power shortages or wastage. It helps manage the power flow within the system, ensuring that the engine and motor outputs are aligned with the battery’s charging and discharging states. The power flow balance equation satisfies:
SOC of the vehicle’s battery is a crucial indicator reflecting the remaining energy level and is a crucial parameter for energy management in HEVs. Accurate SOC calculation is vital for predicting the remaining battery energy, formulating charging strategies, and optimizing the overall vehicle performance. The ampere-hour integration technique can be used to obtain the amount of electricity already used by the battery [37]. The battery SOC calculation is given by:
where Qin represents the initial capacity of the battery. Qmax denotes the maximum capacity of the battery.
Table 2 presents the key characteristics of the PHEV. The vehicle mass Vmass directly influences the vehicle’s dynamic characteristics and energy consumption. The tire radius Vradius impacts the rolling resistance and the gear ratio of the drivetrain, subsequently influencing acceleration performance and fuel efficiency. The air resistance coefficient Varc determines the air resistance, affecting energy consumption at higher speeds, with a higher coefficient leading to increased energy loss. The rolling resistance coefficient Vrrc affects energy loss during driving, with a higher coefficient resulting in greater fuel consumption. The number of gears in the planetary gear system, Pgearf and Pgearr, determines the vehicle’s gear ratio, which influences the power output characteristics of the engine and electric motor and the overall transmission efficiency. The maximum power DMP of the electric motor affects the vehicle’s acceleration capability and top speed, while the maximum torque DMT determines acceleration performance under various driving conditions. The moment of inertia Dmoi of the electric motor influences its acceleration and deceleration characteristics. The maximum power EMP of the engine affects the overall power performance of the vehicle, and the maximum torque EMT determines the vehicle’s acceleration capability and response time. The engine’s moment of inertia Emoi affects its dynamic response characteristics, such as the speed of start-up and shut-down. These parameters collectively define the performance of the PHEV under different driving conditions, including power output, fuel efficiency, acceleration capability, and handling. In the modeling process, these parameters must be considered to accurately predict vehicle performance under various conditions and optimize its energy management strategy.

To streamline the vehicle model, we posit the ensuing assumptions, and potential impact factors that are neglected are clarified:
1) Neglecting energy consumption of additional loads, like air conditioning and onboard displays.
2) Disregarding the impact of ambient temperatures on the system components of hybrid powertrain system.
3) Not considering the specific efficiencies of each transmission component, setting the overall transmission efficiency between the wheels and the gearbox input to 90%.
4) Neglecting dynamic reactions to clutch switching and alterations in transmission ratios.
5) Not considering the actual dynamic characteristics of transmission components such as the gearbox, main reducer, and tires.
The EMS of HEVs can be reformulated as an optimal control challenge within a finite time domain, which can be viewed as MDP. An MDP refers to a system where the current state only depends on the previous state and actions. It can be represented as:
where S denotes the state set. A denotes the action set. P represents signifies state transition probabilities. R indicates rewards.
The optimal control strategy obtained from the EMS reflects the optimal objectives such as economic efficiency and comfort. Therefore, in a Markov environment, the optimal control strategy π* can be obtained through the maximization of the expected cumulative reward (CR):
where s0 denotes initial state. s(.) represents state value. a(.) represents the action value. r(.) represents reward value. N denotes the overall duration, and A denotes the action space. The time interval Ts = 1 s. Qπ(s, a), which assessing result of action a(t) under the control strategy π in state s(t), can be defined as:
where γ represents the discounting factor. It reflects the importance of future rewards. When γ = 0, it indicates a short-sighted focus only on current rewards.
If the optimal action a*(t) be chosen under state s(t), it will result in the maximum action value, which is the optimal action value:
Finally, the optimal control strategy π* can be represented as:
DRL fused the disciplines of DL and RL to solve complex control problems belonging to MDP. On one hand, DL has strong representation capabilities for policies and states, enabling it to simulate complex decision-making processes. On the other hand, RL empowers agents with self-supervised learning abilities, enabling them to interact with the environment autonomously and improve through trial and error.
RL framework consists of two main modules and three types of variables: the agent module, the environment module, state variables, action variables, and reward values. The agent takes the environment’s state as input and outputs an action based on the current control policy. After the environment executes the action, it transitions to a new state and generates a corresponding reward value. The agent calculates the loss function based on known parameters and updates the policy by solving gradient data.
DDPG algorithm draws inspiration from the DQN algorithm and employs the Actor-Critic framework to achieve policy output in continuous states. It also adopts the deterministic policy gradient (DPG) algorithm to transform the output actions from probabilistic to deterministic. Fig. 5 illustrates the principle structure of the DDPG algorithm.
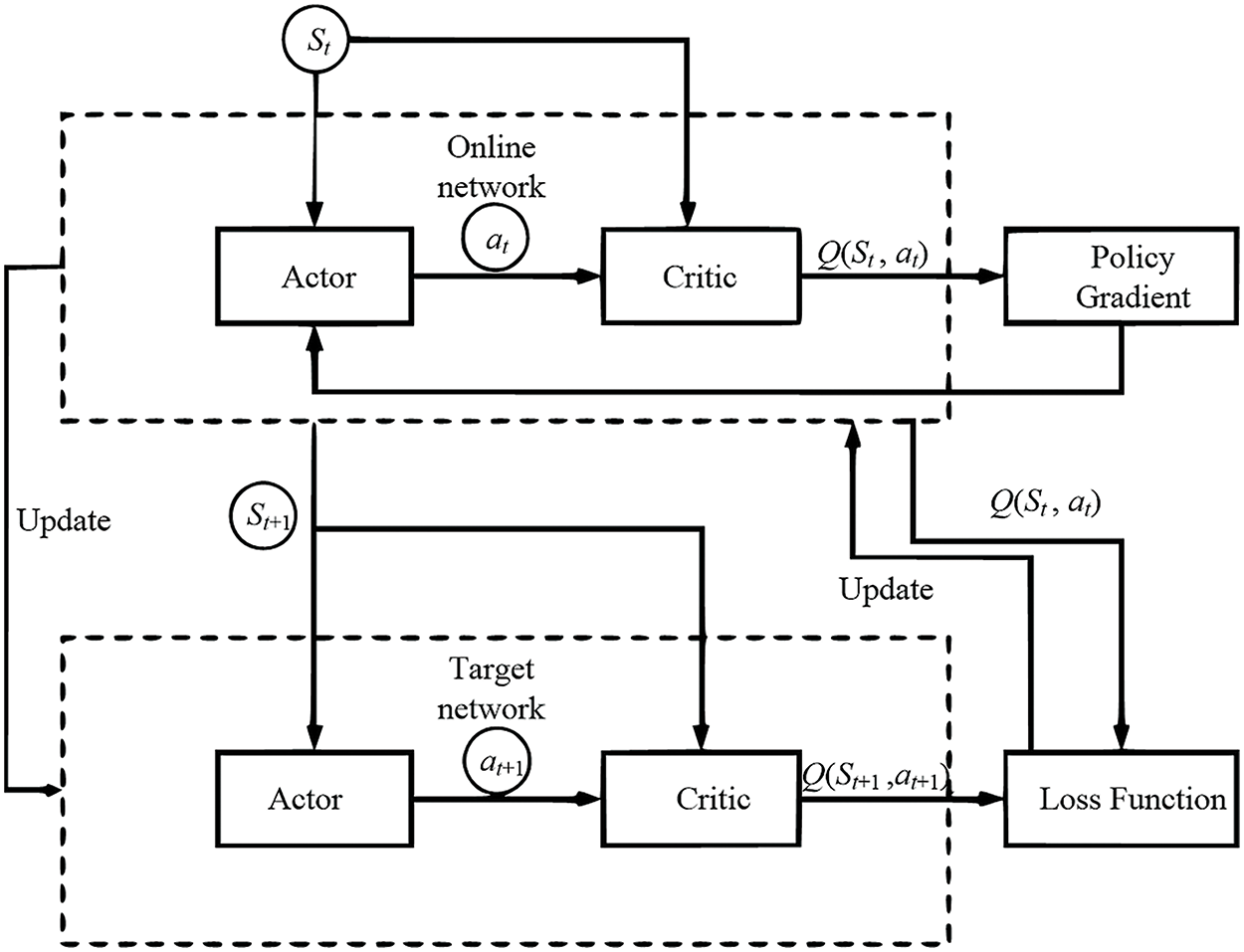
Figure 5: Structure of the DDPG
In the DDPG algorithm, there are two networks: actor and critic. The actor network approximates policy function, taking state s as input, and outputting action a. Since DDPG is deterministic, the policy gradient can be given by:
where
Critic network is employed to approximate the value function. Its input consists of state s and action a, and results in Q-value. The critic network utilizes the minimization of a loss function to update the network:
where
In DDPG, actor target network and critic target network are utilized to enhance the stability of training. Parameters in the target networks are optimized using soft updates:
where
In the EMS tasks of PHEVs, traditional DRL algorithms often suffer from slow convergence, low learning efficiency, and poor stability. These issues primarily arise due to the high dimensionality of both the state space and the action space in EMS applications, which significantly complicates the learning of effective strategies. The complexity of the high-dimensional space makes it difficult for traditional DRL algorithms to efficiently explore all possible state-action combinations. In such spaces, agents struggle to find reward signals, resulting in sparse reward distributions. Sparse rewards make the learning process more challenging, as the agent receives limited useful feedback in most scenarios.
Furthermore, while agents need to explore the environment to find the optimal strategy, excessive exploitation of currently known information can lead to suboptimal solutions. On the other hand, excessive exploration can result in inefficient learning, preventing the agent from converging quickly. In real-world EMS applications, the environment may change over time. Traditional DRL methods typically assume a static environment, causing the learned strategies to quickly become ineffective when the environment changes, rendering them unable to adapt to new situations.
Moreover, traditional DRL algorithms usually require a large number of samples to learn a satisfactory strategy. The high correlation between samples during the training process can lead to inefficiencies in sample utilization.
4 Improved DDPG-Based PHEV EMS
An improved DDPG method that incorporates entropy regularization and PER is proposed for the EMS task of PHEVs to address issues related to convergence, learning efficiency, and stability in traditional DRL algorithms. Specifically, to enhance exploration performance, entropy regularization introduces an entropy term into the reward function, encouraging the agent to maintain diversity in policy selection. This approach prevents the agent from prematurely converging to suboptimal policies, effectively avoiding early convergence and promoting higher-quality learning. Regarding sample efficiency, a sum-tree-based PER is employed to efficiently organize and retrieve experience samples with varying priorities. This not only enhances sample utilization but also significantly reduces sample correlation issues, thereby improving both the effectiveness and efficiency of learning. In terms of environmental adaptability, the introduction of entropy regularization enables the agent to maintain a moderate level of exploration in the face of environmental changes, allowing it to better adapt to dynamic environments. Additionally, entropy regularization mitigates the issue of high variance in policy gradient methods, resulting in smoother and more stable policy gradient estimates, which accelerates convergence. PER further ensures that the model focuses on key experience samples during training, reducing unnecessary computations and randomness in the training process, thereby making policy updates more stable and efficient.
The proposed PHEV framework built upon the improved DDPG is illustrated in Fig. 6. The actor-critic network feeds the state and policy output to the vehicle model, simulating the vehicle driving process. The reward function evaluates the policy and outputs the value function to the replay experience pool. The framework obtains the action at from the agent for scheduling and receives the reward value rt and state value at time t as feedback. The policy network stores the dataset Et = (st, at, rt, st+1) within the experience pool, and samples the dataset Eϕ = (sϕ, aϕ, rϕ, sϕ+1) as a mini-batch data to train the Actor and Criticnetworks. DDPG trains the Critic and Actor networks separately to obtain the optimal parameters in the networks. For the Critic network, the parameters are optimized through loss function
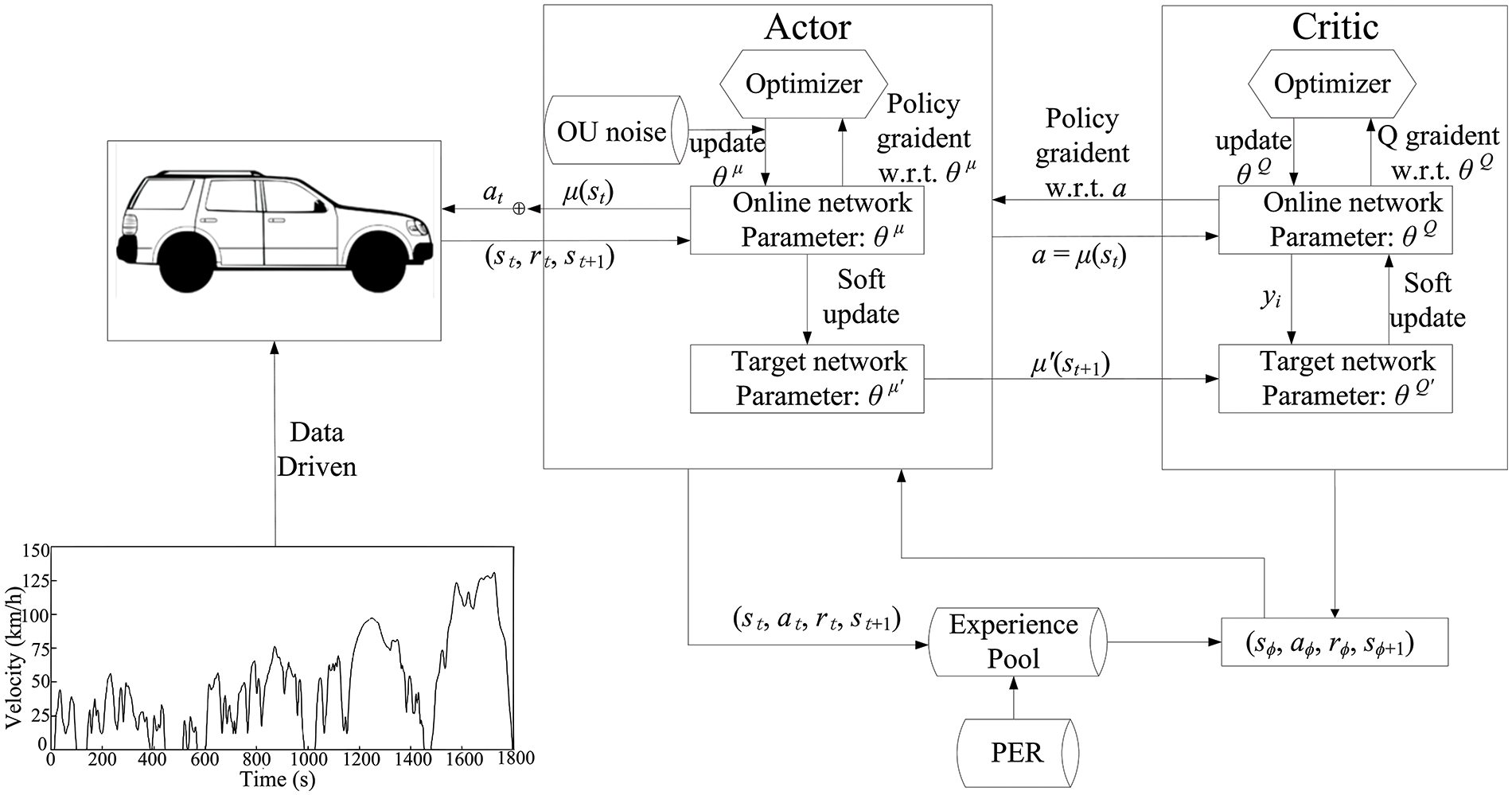
Figure 6: Proposed EMS framework based on improved DDPG
In practical learning control, the Actor network often selects actions with higher probabilities as its output, leading to a high level of certainty in the action output. This can result in complacency, reduced exploration capability, and a narrower range of selectable actions, ultimately preventing the attainment of the optimal solution. To improve the output of the Actor network, entropy regularization is employed to introduce greater uncertainty in the action output, increasing the diversity of selectable actions and avoiding local optimization, thereby facilitating the exploration of the optimal strategy.
Entropy regularization utilizes entropy to represent the probability of actions. In a set of n probability distributions, the entropy value can be calculated as:
A higher entropy value indicates a more uniform probability distribution and greater randomness in actions, as shown in Fig. 7a. On the other hand, a lower entropy value indicates a more concentrated probability distribution and less randomness in actions, as depicted in Fig. 7b.
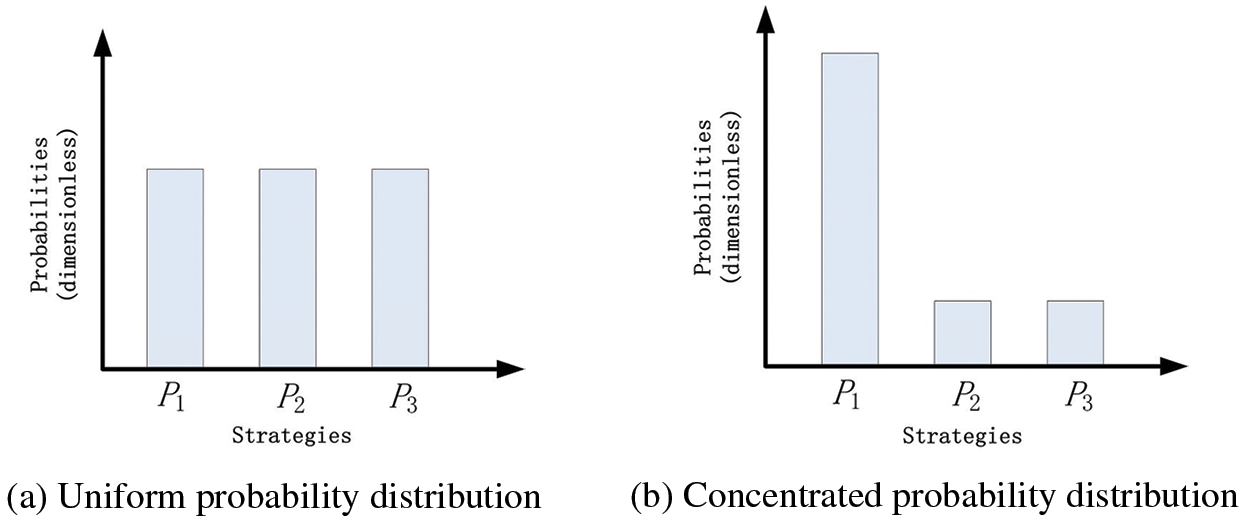
Figure 7: Probability distribution (The horizontal axis represents different strategies (P1, P2, P3, etc.), which are the selectable actions output by the Actor network. The vertical axis indicates the selection probability of each strategy (or action), without units, typically ranging from 0 to 1. This reflects the likelihood of different strategies being chosen in the Actor network’s output)
The actions output by the Actor network have different probability densities, and the set of action vectors A can be represented by its entropy value as:
where
When optimizing the Actor network parameters, it is necessary to consider the magnitude of entropy, so the entropy is set as a regularization term in the cost function:
where α is the weight coefficient.
The formula for gradient update with the new function is given by:
The core module of PER is to measure the priority of each sample, and a common method is to evaluate the importance of samples on the basis of temporal difference (TD) error. TD error expresses the difference between predicted and target values, and samples with larger TD errors contribute more to gradient learning, thus should be prioritized for sampling.
The dataset sampling probability can be defined as:
where K is the set of datasets in the experience pool.
where
Traditional PER often relies on simple priority sorting, which proves inefficient for sample selection and priority updates, particularly when managing large-scale experience buffers. Updating priorities may require reordering or maintaining the priority queue, a process fraught with complexity that slows down the update cycle. As a result, this inefficiency can lead to suboptimal utilization of information during the learning process, ultimately affecting performance outcomes. To address this, a sum-tree data structure is used to sample prioritized data. Sum-tree PER leverages a sum-tree data structure to manage priority samples more efficiently, enabling rapid insertion, deletion, and update operations. The inherent structure of the sum-tree allows for priority updates to be completed in logarithmic time. This efficiency in sample selection and priority updating ensures that critical samples are more swiftly replayed, significantly enhancing learning efficiency and stability in PHEV energy management, especially when handling large datasets and frequent updates.
Each leaf node in the sum-tree represents the priority value of each dataset, and the values of two nodes are continuously added up to form a binary tree, with the root value being the sum of all dataset priority values. Each sampling divides the root value into batch_size intervals with a length of ñ, which leads to the relationship shown as:
From each interval, a dataset Zt is uniformly sampled. The priority value of Zt is denoted as
1) Traverse the child nodes starting from the root node.
2) If the priority value of the left child node is greater than
3) If the priority value of the left child node is less than
4) Continue this process until reaching a leaf node, the dataset corresponding to the priority value of the leaf node is the data to be sampled.
By incorporating the PER mechanism into DDPG, the difficulty of training under fluctuating states can be addressed. It samples data (state and action quantities) that contribute to larger training error gradients, enhancing training accuracy and accurately training the optimal actions.
In terms of stability and convergence of the algorithm, only key states are selected, including power demand, state of charge, vehicle speed, and travel distance, represented as:
where v denotes the vehicle velocity. Ssoc denotes the state of charge. d is the vehicle travel distance. These state variables are considered as the current state value St. The action values taken by the Actor network are represented as at, which controls the pedal opening based on the driver model and calculates the current total power demand Pr by allocating Pr to the engine and motor based on
where η ∈ [0,1] is the power allocation coefficient. The reward value r evaluated by the Critic network is set to the negative sum of the total costs of fuel consumption and energy consumption within the time step. The reward value r(s, a) is represented as:
where mt represents fuel consumption at time t. pfuel represents the fuel price. Et represents energy consumption at time t. pele represents the electricity price. The next state value is St+1, and the online networks utilize the training sample data (St, St+1, rt, at) to perform EMS training. Each step’s result is independent and unrelated to the previous step. After collecting and updating the samples, the parameters are fed into the target networks, followed by the update process. The specific algorithm flow is as follows:
1. Build the Actor network with θQ as parameters and build the Critic network with θμ as parameters.
2. Initialize parameters θQ and θμ.
3. Feed θQ and θμ to the Actor and Critic target networks.
4. Based on the Actor online network, entropy regularization is employed to make the Actor network output an action at.
5. Perform at, obtain a reward rt, and acquire a new state st+1.
6. Save the tuple (st, at, rt, st+1) to R.
7. Based on the TD error of N tuples in R, sample a prioritized batch of tuples.
8. Update Critic network through loss function minimization with Eq. (15).
9. Perform Actor online updates, where the actions output by the Actor online network are related to the scores given by the Critic online network. Update the Actor to maximize the Q-value output using the policy gradient method, and introduce a regularization term with entropy value during the update.
10. Update the Target networks with Eqs. (16) and (17).
11. Finally, return to the Actor online network for sampling and continue the loop process.
DRL, as an AI algorithm, relies heavily on abundant data for its data-driven approach. Leveraging the characteristics of a forward simulation model, the input variables for the driver module are defined by the vehicle speed. Thus, the driving cycles can serve as the basis for data-driven EMSs using DRL method. The resulting trained control strategies are represented in the form of network parameters, reflecting the correlation between stochastic states and optimal actions mapping within the policy function. Initially, the control strategy undergoes offline training using operational data, after which the trained policy is downloaded into the controller for online learning.
In the training of the proposed improved DDPG method, the learning rate is set to 0.001, the discount factor to 0.99, and the initial exploration factor to 1. The experience replay buffer capacity is configured to hold 1,000,000 experiences, with a batch size of 64 for training. The maximum number of episodes is set to 100, and each episode is limited to 4200 time steps. The entropy regularization coefficient is set to 0.07. In the PER mechanism, the bias correction coefficient for importance sampling starts at 0.4 and is gradually increased to 1.0. In the experiments, five different random seeds (seed 42, seed 275, seed 399, seed 572, seed 873) were used to initialize various stochastic components of the model, including the initialization of neural network weights, the sampling of experiences from the replay buffer, and the injection of exploration noise. These seeds were selected arbitrarily but consistently across all experiments to ensure that the results are not dependent on a particular random initialization, thereby enhancing the robustness of the findings.
When conducting energy consumption tests for vehicles, adherence to specific standards is imperative. Currently, prevalent cyclic testing includes the New European Driving Cycle (NEDC), the American Federal Test Procedure (FTP) 75 cycle, the China Light Vehicle Test Cycle (CLTC), and the globally standardized World Light Vehicle Test Cycle (WLTC). In this study, WLTC and NEDC cycles are chosen as the test conditions for the vehicle.
The WLTC cycle, designed to comprehensively and objectively evaluate vehicle performance, comprises four stages [38]. The first stage, representing low-speed driving conditions to simulate urban commuting, spans from 0 to 589 s, covering a total distance of 3.095 km. The average speed during this phase is 18.91 km/h, with a maximum speed reaching 56.50 km/h. The second stage, focusing on medium-speed conditions to simulate suburban driving, occurs from 589 to 1022 s, covering a total distance of 4.756 km. The average speed increases to 39.54 km/h, approximately 35% higher than the low-speed stage. The third and fourth stages represent high-speed and super-high-speed conditions, simulating highway driving. The time span for these stages is from 1022 to 1800 s, with a combined total distance of 15.416 km, and speeds exceeding 130 km/h. The total duration of the WLTC cycle is 1800 s, covering a total distance of 23.26 km, as illustrated in Fig. 8.
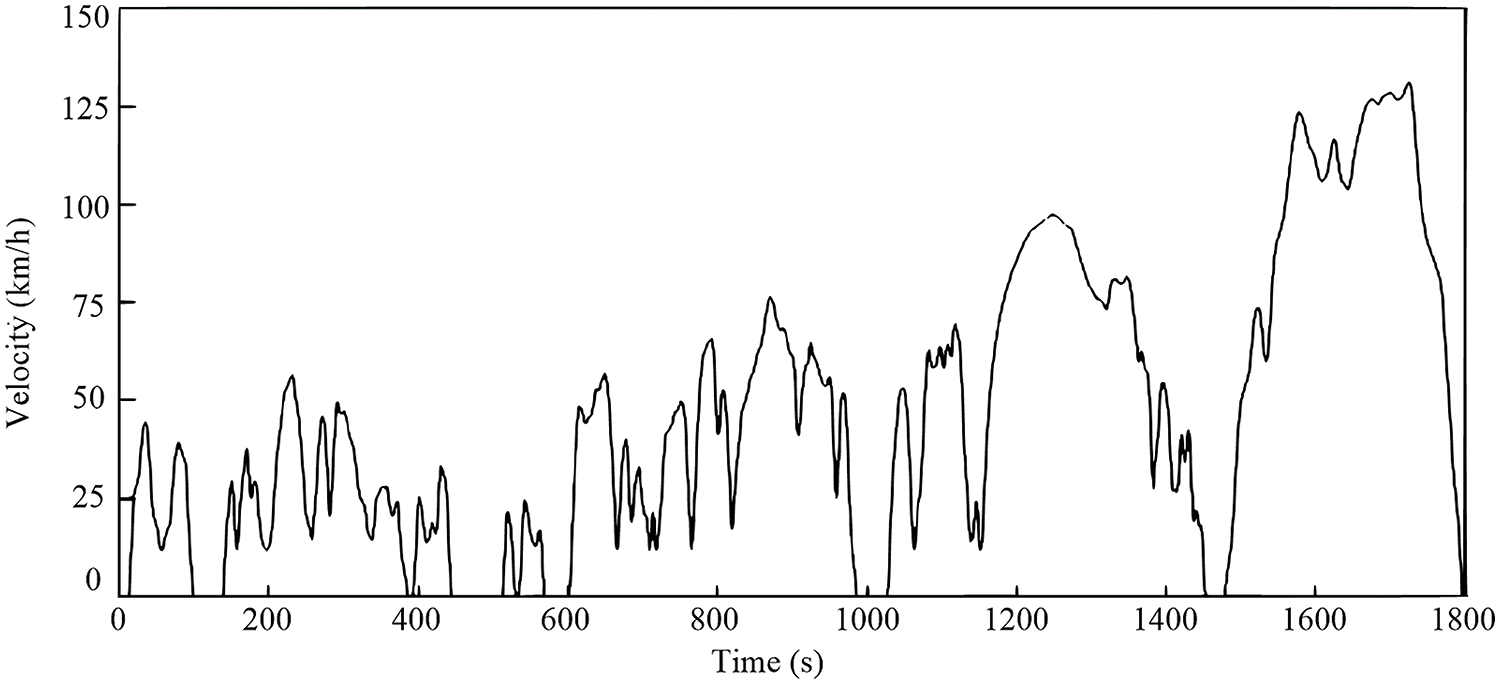
Figure 8: WLTC driving cycles
NEDC consists of two stages. In the first stage, designed to replicate urban conditions, a city driving scenario is repeated four times, spanning from 0 to 780 s [39]. The maximum speed for each city driving scenario is 50 km/h, resulting in a total simulated distance of 4.072 km. The second stage, simulating suburban and highway conditions, extends from 780 to 1180 s, with a maximum speed of 120 km/h and a total simulated distance of 6.955 km. The entire NEDC simulation lasts for 1180 s, covering a total distance of 11 km, as depicted in Fig. 9.
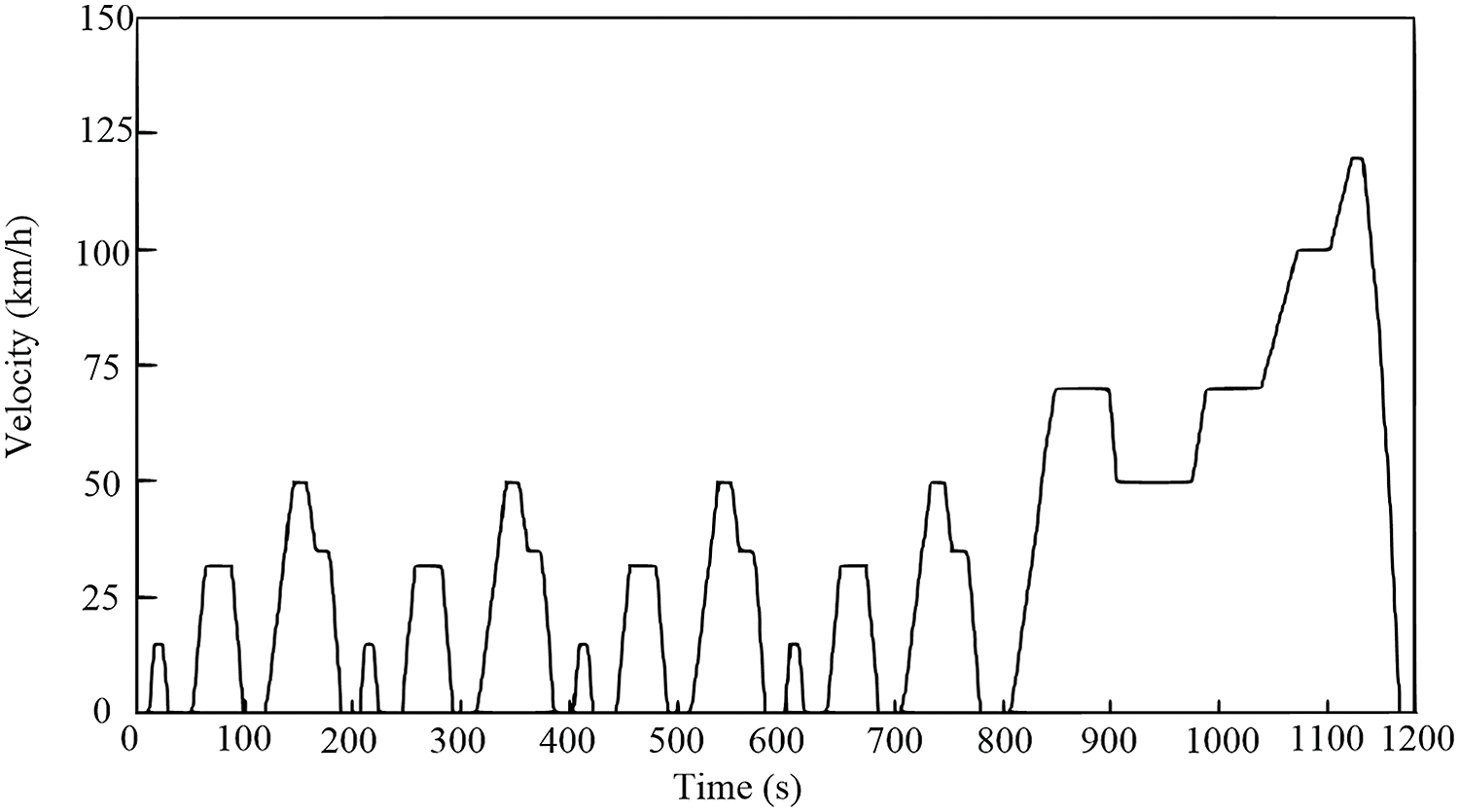
Figure 9: NEDC driving cycles
5.2 Equivalent Fuel Consumption (EFC)
Optimizing the parameters of the EMS and transmission ratio is undertaken within the constraints of meeting power performance design targets and various component performance requirements. This optimization aims to enhance the overall vehicle energy efficiency.
During operation under cyclic conditions, the vehicle consumes both fuel and electricity. Significant fluctuations in SOC of the power battery occur in the Charge-Deplete (CD) phase, while minor fluctuations occur in the Charge-Sustain (CS) phase. For simplicity, the energy consumption is converted into equivalent fuel consumption. The concept of EFC, encompassing the energy consumption of the power battery and engine fuel consumption, is proposed to assess the economic efficiency of the entire vehicle under cyclic conditions [40]. The formula for calculating energy consumption equivalent to fuel consumption is expressed as:
where
Fig. 10 illustrates the trajectory of the total CR changes, and the results are derived from the average of outcomes obtained using 5 different random seeds. As DRL algorithms aim to explore the optimal control strategy that achieves the maximum CR in the current environmental module, achieving a stable and convergent state in the total CR during the training phase indicates the success of the training. The results depicted in Fig. 10 effectively highlight the differences in the update principles between the improved network and the original DDPG. Although both trajectory curves exhibit a horizontal convergence state after approximately 75 rounds, the reward trajectory corresponding to the original DDPG algorithm shows more frequent and intense fluctuations. In contrast, the reward trajectory of the proposed algorithm appears smoother and more stable. This is because the latter maintains a slow and gradual progression of the current control strategy toward the optimal control strategy through a soft update approach. In other words, the original DDPG algorithm tends to oscillate around the optimal point, while the proposed algorithm progressively moves towards the optimal point.
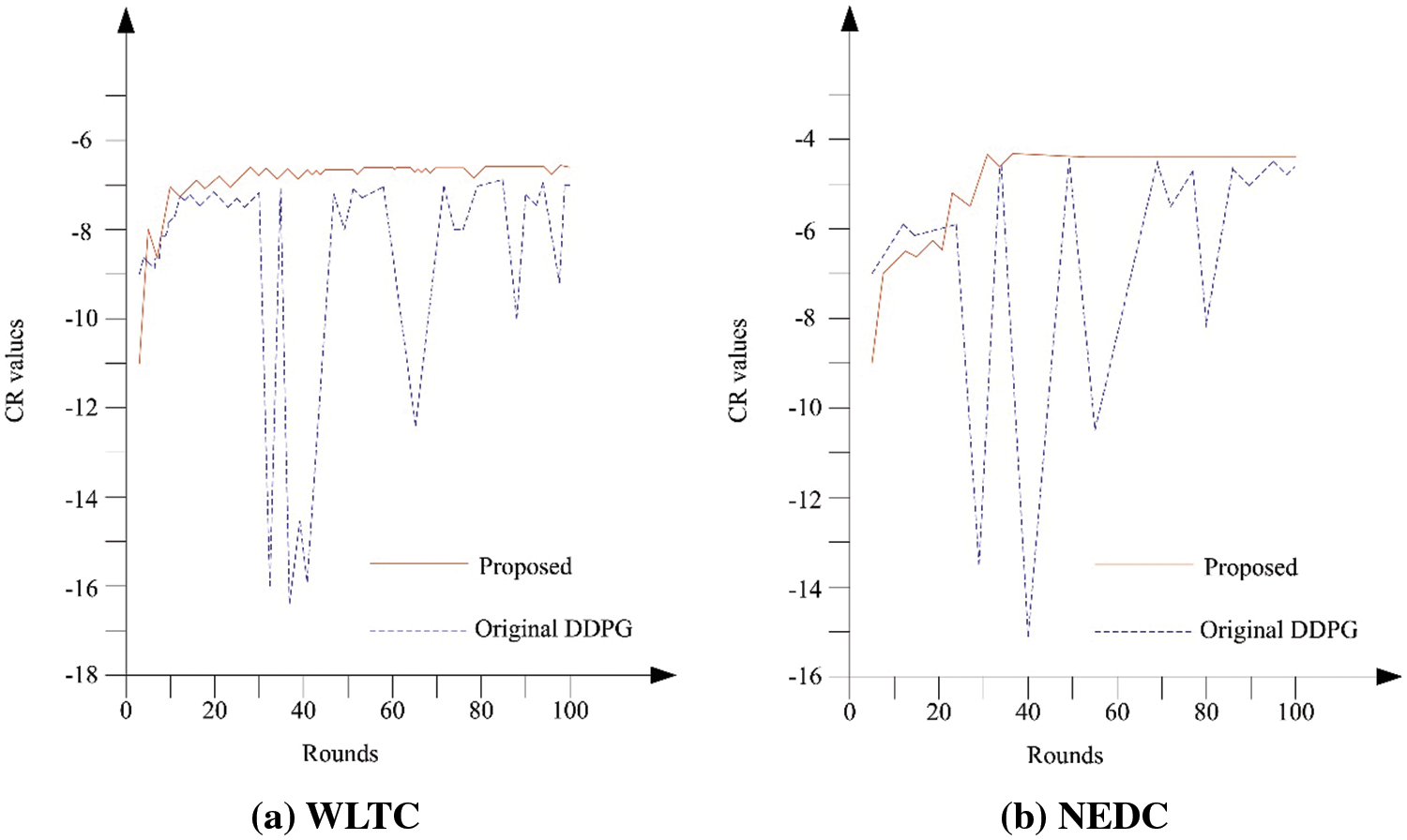
Figure 10: CR value comparison during training
In PHEVs, the variations in motor torque, power battery SOC, and engine operating characteristics are directly intertwined with energy consumption. SOC comparative analysis under WLTC cycle conditions is depicted in Fig. 11a. The results were taken from the mean value of 5 different random seeds. A smaller SOC deviation generally signifies that the energy management system excels in managing battery status, optimizing energy use, and improving system reliability. By narrowing the gap between SOC predictions and actual values, the EMS can effectively boost battery efficiency, prolong its lifespan, and enhance overall vehicle performance. The graph presents SOC variation curves for EMSs optimized by ECMS, DQL, DDPG, and the proposed algorithm. Starting with an initial SOC of 35%, during the testing cycle, DQN’s SOC fluctuates around the target SOC, with a variation of 1.74%, the highest among the four algorithms. ECMS’s SOC curve initially deviates from the target SOC but gradually approaches it at the end of the cycle, with a significant overall variation of 1.46%. DDPG’s SOC variation curve exhibits slightly smaller fluctuations compared to DQN and ECMS, with a variation of 1.3%, representing a 26% decrease compared to ECMS. The proposed algorithm demonstrates the smallest SOC fluctuations, with a variation of 1.2%, a 30% decrease compared to ECMS, and 5% decrease compared to the original DDPG. At the end of the cycle, the final SOC for different algorithms is close to the target SOC: DQN, ECMS, DDPG, and the proposed algorithm have final SOCs of 34.97%, 35.38%, 35.37%, and 34.96%, respectively. Fig. 11b illustrates the SOC variation curves for different DRL algorithms under NEDC cycle conditions, with an initial SOC of 35%. The proposed algorithm exhibits a maximum SOC variation of 0.67%, a 22% decrease compared to the original DDPG algorithm, and a final SOC of 34.95%, closer to the target SOC. In addition, the variation distribution of ECMS is confined solely below the target SOC, exhibiting the poorest performance in sustaining the sustainability of battery charge and discharge. In summary, the proposed algorithm achieves optimal performance in both cycle conditions.
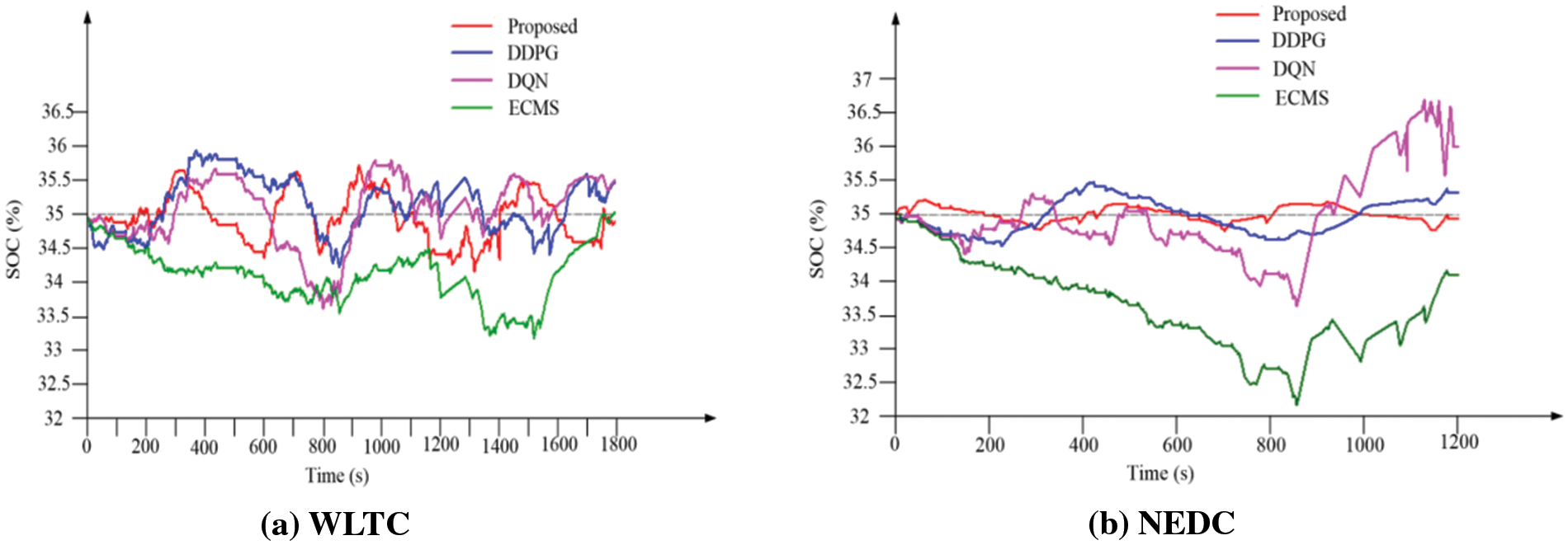
Figure 11: SOC functuation comparison among different DRL algorithms
Multiple representative driving scenarios were selected from two experimental datasets and arranged in ascending order based on their average speeds. After filtering, smoothing, and other processing steps, these scenarios were concatenated to construct a real-world road driving scenario with a total duration of 5400 s and a total milage around 70 km. The scenario includes 2700 s of urban driving, 1000 s of suburban driving, and 1700 s of highway driving. The characteristics of this typical scenario include frequent instantaneous speed changes, particularly evident in urban driving conditions. Additionally, it comprehensively covers urban, suburban, and highway driving segments, with a notable proportion of time dedicated to suburban and highway driving.
In the proposed enhancement to the DDPG method, the random seed determines the initial weights of the neural network model. Different initializations may lead to the model learning varied feature representations and strategies. Similarly, in PER, the sequence of sample sampling depends on the random seed. Table 3 presents the performance, mean, and standard deviation (SD) of the proposed method across different random seeds on the experimental dataset, with the initial SOC set at 60%. By employing multiple random seeds and averaging the results, fluctuations caused by random initialization and noise can be reduced. This approach enhances the consistency of model decisions under varying experimental conditions, ensuring the reliability of the energy management strategy. Furthermore, a stable model can better handle diverse driving conditions and energy demands in practical applications, thereby improving the system’s overall performance and reliability.
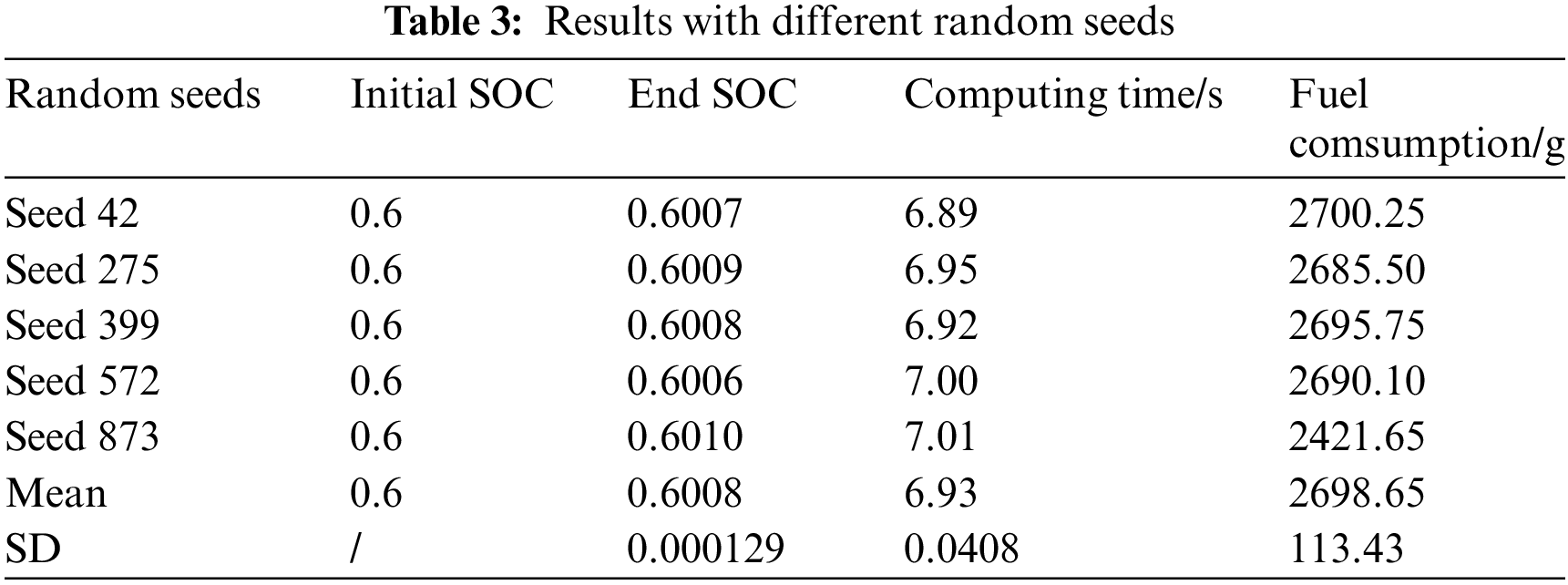
To validate the effectiveness and advancement of the proposed EMS under the aforementioned typical scenarios, EMS based on CD-CS, DP, and DRL models were individually tested. Comparative experiments were conducted to assess various strategies. Rule-based CD-CS, widely employed in the industry, holds significant reference value in the comparative experiments. DP-based EMS, while not suitable for real-time application on vehicles, provides optimal solutions that serve as benchmarks for comparing the effectiveness and advancement of other algorithms. DP, a branch of operations research, facilitates optimal decision-making in vehicle energy management but lacks real-time applicability, often serving as a benchmark for comparison with other strategies.
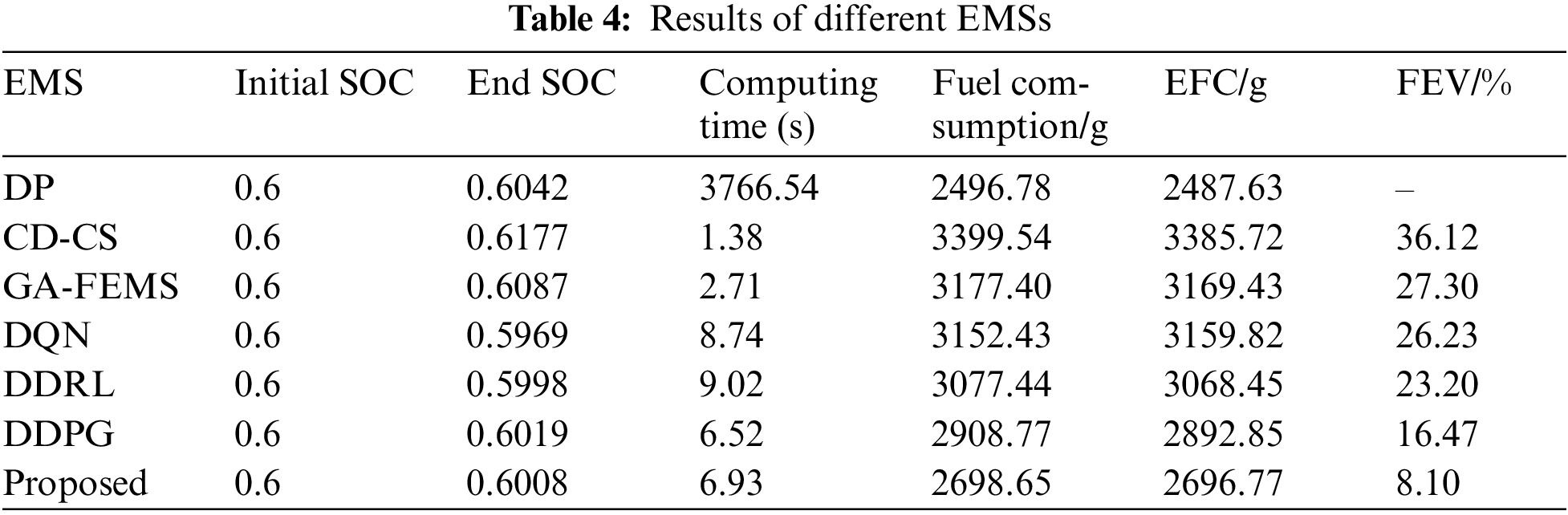
Table 4 provides a detailed breakdown of different EMSs, including SOC, fuel consumption, and computational efficiency. The results were taken from the mean value of 5 different random seeds. All control strategies maintain the same initial state, with an initial SOC of 60%, and achieve a final SOC around 60%. Among the methods compared, DP calculates the optimal policy by optimizing the total utility function. CD-CS optimizes the control strategy to minimize the clustering error of states. The loss function for GA-FEMS focuses on minimizing energy consumption. DQN employs a loss function in the form of mean squared error (MSE) for the Q-value function. For DDRL, DDPG, and the proposed method, the loss function includes MSE of the Critic network within the Actor-Critic framework, as shown in Eq. (15). In terms of computational time, CD-CS and GA-FEMS consume 1.38 s and 2.71 s, respectively. Compared to other optimization and learning-based EMSs, computational efficiency stands out as a significant advantage for rule-based control strategies. DP-based EMS, with higher variable dimensions and greater complexity, incurs a longer computational time of 3766.54 s. Although it yields the lowest fuel consumption, signifying optimal fuel efficiency, the time consumed indicates that global optimization algorithms are suitable only as comparative benchmarks in offline environments. Learning-based EMSs achieve control efficiency just below rule-based strategies. Therefore, in addressing complex, time-varying, high-dimensional control tasks, DRL demonstrates good control performance in terms of computational efficiency. Regarding fuel efficiency, DP achieves the lowest fuel consumption, totaling 2496.78 g for the entire journey. Two rule-based EMS, CD-CS and GA-FEMS, despite shorter computational times, result in fuel consumptions of 3399.54 g and 3177.40 g, respectively. Compared to the benchmark DP strategy, this leads to fuel efficiency variances (FEV) of 36.12% and 27.30%. It is noteworthy that the proposed method, through enhancements to the DDPG algorithm, significantly improves fuel efficiency. In the exact training environment, it saves 210.12 g of fuel compared to the original DDPG.
In this paper, a forward simulation vehicle model was constructed. By modeling the MDP process of vehicle energy management, improved DRL algorithm is applied to the hybrid powertrain of THS-III platform, yielding the following conclusions: 1) The introduction of entropy regularization strategy in DDPG not only enhances the agent’s exploration capability in the environment but also adjusts the exploration range based on environmental changes, facilitating improved action exploration. 2) The Priority Experience Replay (PER) mechanism effectively addresses issues like inefficient learning due to uniform sampling in the experience pool of DDPG. The addition of sum tree aids in enhancing the efficiency of searching for experiences, avoiding inefficiencies associated with greedy exploration of high-priority experiences in the pool. In the future, the plan involves employing a distributed DRL algorithm framework for learning EMS for PHEVs. By configuring each sub-agent module to share the same environmental model, the exploration efficiency of the global network for the optimal control solution in the current environmental module is enhanced.
Acknowledgement: The authors express their deep appreciation to the editorial team and reviewers for their invaluable contributions and dedication towards improving this work.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Li Wang and Xiaoyong Wang; data collection: Li Wang; analysis and interpretation of results: Li Wang and Xiaoyong Wang; draft manuscript preparation: Li Wang and Xiaoyong Wang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. R. R. Kumar and K. Alok, “Adoption of electric vehicle: A literature review and prospects for sustainability,” J. Clean. Prod., vol. 253, Apr. 2020, Art. no 119911. doi: 10.1016/j.jclepro.2019.119911. [Google Scholar] [CrossRef]
2. International Energy Agency, Global EV Outlook 2022: Securing Supplies for an Electric Future. OECD, Apr. 2022. doi: 10.1787/c83f815c-en. [Google Scholar] [CrossRef]
3. R. Stotts, O. G. Lopez-Jaramillo, S. Kelley, A. Krafft, and M. Kuby, “How drivers decide whether to get a fuel cell vehicle: An ethnographic decision model,” Int. J. Hydrogen Energy, vol. 46, no. 12, pp. 8736–8748, Feb. 2021. doi: 10.1016/j.ijhydene.2020.12.042. [Google Scholar] [CrossRef]
4. I. Veza, M. Z. Asy’ari, M. A. Idris, V. Epin, I. R. Fattah and M. Spraggon, “Electric vehicle (EV) and driving towards sustainability: Comparison between EV, HEV, PHEV, and ICE vehicles to achieve net zero emissions by 2050 from EV,” Alexandria Eng. J., vol. 82, pp. 459–467, Nov. 2023. doi: 10.1016/j.aej.2023.10.020. [Google Scholar] [CrossRef]
5. C. Yang, M. Zha, W. Wang, K. Liu, and X. Chen, “Efficient energy management strategy for hybrid electric vehicles/plug-in hybrid electric vehicles: Review and recent advances under intelligent transportation system,” IET Intell. Transp. Syst., vol. 14, no. 7, pp. 702–711, May 2020. doi: 10.1049/iet-its.2019.0606. [Google Scholar] [CrossRef]
6. H. Zhang et al., “Energy management strategy for plug-in hybrid electric vehicle integrated with vehicle-environment cooperation control,” Energy, vol. 197, Jun. 2020, Art. no. 117192. doi: 10.1016/j.energy.2020.117192. [Google Scholar] [CrossRef]
7. A. Meydani, H. Shahinzadeh, and H. Nafisi, “Optimum energy management strategies for the hybrid sources-powered electric vehicle settings,” in Proc. 28th Int. Electr. Power Distrib. Conf. (EPDC), 2024, pp. 1–19. [Google Scholar]
8. A. Urooj and A. Nasir, “Review of hybrid energy storage systems for hybrid electric vehicles,” World Electr. Veh. J., vol. 15, no. 8, Aug. 2024, Art. no. 342. doi: 10.3390/wevj1508342. [Google Scholar] [CrossRef]
9. P. Muthyala et al., “Comparative study of real-time A-ECMS and rule-based energy management strategies in long haul heavy-duty PHEVs,” Energy Convers. Manag.: X, vol. 100, no. 2, Jul. 2024, Art. no. 100679. doi: 10.1016/j.ecmx.2024.100679. [Google Scholar] [CrossRef]
10. M. Vajedi, A. Taghavipour, N. L. Azad, and J. McPhee, “A comparative analysis of route-based power management strategies for real-time application in plug-in hybrid electric vehicles,” in Proc. Am. Control Conf., 2014, pp. 2612–2617. [Google Scholar]
11. J. Peng, H. He, and R. Xiong, “Rule based energy management strategy for a series-parallel plug-in hybrid electric bus optimized by dynamic programming,” Appl. Energy., vol. 185, pp. 1633–1643, Jan. 2017. doi: 10.1016/j.apenergy.2015.12.031. [Google Scholar] [CrossRef]
12. Z. Chen and C. Mi, “An adaptive online energy management controller for power-split HEV based on dynamic programming and fuzzy logic,” in Proc. IEEE Veh. Power Propuls. Conf., 2009, pp. 335–339. [Google Scholar]
13. R. Zhang and J. Tao, “GA-based fuzzy energy management system for FC/SC-powered HEV considering H2 consumption and load variation,” IEEE Trans. Fuzzy Syst., vol. 26, no. 4, pp. 1833–1843, Aug. 2018. doi: 10.1109/tfuzz.2017.2779424. [Google Scholar] [CrossRef]
14. X. Lü et al., “Overview of improved dynamic programming algorithm for optimizing energy distribution of hybrid electric vehicles,” Electr Power Syst. Res., vol. 232, Jul. 2024, Art. no. 110372. doi: 10.1016/j.epsr.2024.110372. [Google Scholar] [CrossRef]
15. H. He, J. Guo, J. Peng, H. Tan, and C. Sun, “Real-time global driving cycle construction and the application to economy driving pro system in plug-in hybrid electric vehicles,” Energy, vol. 152, pp. 95–107, Jun. 2018. doi: 10.1016/j.energy.2018.03.061. [Google Scholar] [CrossRef]
16. Y. Li, H. He, A. Khajepour, H. Wang, and J. Peng, “Energy management for a power-split hybrid electric bus via deep reinforcement learning with terrain information,” Appl. Energy., vol. 255, Dec. 2019, Art. no. 113762. doi: 10.1016/j.apenergy.2019.113762. [Google Scholar] [CrossRef]
17. S. Zhang, X. Hu, S. Xie, Z. Song, L. Hu and H. Cong, “Adaptively coordinated optimization of battery aging and energy management in plug-in hybrid electric buses,” Appl. Energy., vol. 256, Dec. 2019, Art. no. 113891. doi: 10.1016/j.apenergy.2019.113891. [Google Scholar] [CrossRef]
18. N. Azim Mohseni, N. Bayati, and T. Ebel, “Energy management strategies of hybrid electric vehicles: A comparative review,” IET Smart Grid, vol. 7, no. 3, pp. 191–220, Jul. 2024. doi: 10.1049/stg2.12133. [Google Scholar] [CrossRef]
19. C. Yang, S. Du, L. Zhang, S. You, Y. Yang and Y. Zhao, “Adaptive real-time optimal energy management strategy based on equivalent factors optimization for plug-in hybrid electric vehicle,” Appl. Energy., vol. 203, pp. 883–896, Oct. 2017. doi: 10.1016/j.apenergy.2017.06.106. [Google Scholar] [CrossRef]
20. S. Xie, H. He, and J. Peng, “An energy management strategy based on stochastic model predictive control for plug-in hybrid electric buses,” Appl. Energy., vol. 196, pp. 279–288, Jun. 2017. doi: 10.1016/j.apenergy.2016.12.112. [Google Scholar] [CrossRef]
21. X. Tang, T. Jia, X. Hu, Y. Huang, Z. Deng and H. Pu, “Naturalistic data-driven predictive energy management for plug-in hybrid electric vehicles,” IEEE Trans. Transp. Electrification., vol. 7, no. 2, pp. 497–508, Jun. 2021. doi: 10.1109/TTE.2020.3025352. [Google Scholar] [CrossRef]
22. G. Ripaccioli, D. Bernardini, S. Di Cairano, A. Bemporad, and I. Kolmanovsky, “A stochastic model predictive control approach for series hybrid electric vehicle power management,” in Proc. Am. Control Conf., 2010, pp. 5844–5849. [Google Scholar]
23. J. J. Jui, M. A. Ahmad, M. M. I. Molla, and M. I. M. Rashid, “Optimal energy management strategies for hybrid electric vehicles: A recent survey of machine learning approaches,” J. Eng. Res., vol. 12, no. 3, pp. 454–467, Jan. 2024. doi: 10.1016/j.jer.2024.01.016. [Google Scholar] [CrossRef]
24. T. Li, X. Tang, H. Wang, H. Yu, and X. Hu, “Adaptive hierarchical energy management design for a plug-in hybrid electric vehicle,” IEEE Trans. Veh. Technol., vol. 68, no. 12, pp. 11513–11522, Dec. 2019. doi: 10.1109/TVT.2019.2926733. [Google Scholar] [CrossRef]
25. R. Zou, L. Fan, Y. Dong, S. Zheng, and C. Hu, “DQL energy management: An online-updated algorithm and its application in fix-line hybrid electric vehicle,” Energy, vol. 225, Jun. 2021, Art. no. 120174. doi: 10.1016/j.energy.2021.120174. [Google Scholar] [CrossRef]
26. H. Sun, Z. Fu, F. Tao, L. Zhu, and P. Si, “Data-driven reinforcement-learning-based hierarchical energy management strategy for fuel cell/battery/ultracapacitor hybrid electric vehicles,” J. Power Sources, vol. 455, Apr. 2020, Art. no. 227964. doi: 10.1016/j.jpowsour.2020.227964. [Google Scholar] [CrossRef]
27. G. Du, Y. Zou, X. Zhang, Z. Kong, J. Wu and D. He, “Intelligent energy management for hybrid electric tracked vehicles using online reinforcement learning,” Appl. Energy., vol. 251, Oct. 2019, Art. no. 113388. doi: 10.1016/j.apenergy.2019.113388. [Google Scholar] [CrossRef]
28. X. Han, H. He, J. Wu, J. Peng, and Y. Li, “Energy management based on reinforcement learning with double deep Q-learning for a hybrid electric tracked vehicle,” Appl. Energy., vol. 254, Nov. 2019, Art. no. 113708. doi: 10.1016/j.apenergy.2019.113708. [Google Scholar] [CrossRef]
29. P. Wang, Y. Li, S. Shekhar, and W. F. Northrop, “Actor-critic based deep reinforcement learning framework for energy management of extended range electric delivery vehicles,” in Proc. IEEE/ASME Int. Conf. Adv. Intell. Mechatron., 2019, pp. 1379–1384. [Google Scholar]
30. R. Lian, J. Peng, Y. Wu, H. Tan, and H. Zhang, “Rule-interposing deep reinforcement learning based energy management strategy for power-split hybrid electric vehicle,” Energy, vol. 197, Apr. 2020, Art. no. 117297. doi: 10.1016/j.energy.2020.117297. [Google Scholar] [CrossRef]
31. W. Li et al., “Deep reinforcement learning-based energy management of hybrid battery systems in electric vehicles,” J. Energy Storage, vol. 36, Apr. 2021, Art. no. 102355. doi: 10.1016/j.est.2021.102355. [Google Scholar] [CrossRef]
32. Y. Wang, Y. Wu, Y. Tang, Q. Li, and H. He, “Cooperative energy management and eco-driving of plug-in hybrid electric vehicle via multi-agent reinforcement learning,” Appl. Energy., vol. 332, Feb. 2023, Art. no. 120563. doi: 10.1016/j.apenergy.2022.120563. [Google Scholar] [CrossRef]
33. X. Sun et al., “An energy management strategy for plug-in hybrid electric vehicles based on deep learning and improved model predictive control,” Energy, vol. 269, Apr. 2023, Art. no. 126772. doi: 10.1016/j.energy.2023.126772. [Google Scholar] [CrossRef]
34. X. Yang, C. Jiang, M. Zhou, and H. Hu, “Bi-level energy management strategy for power-split plug-in hybrid electric vehicles: A reinforcement learning approach for prediction and control,” Front. Energy Res., vol. 11, Mar. 2023, Art. no. 1153390. doi: 10.3389/fenrg.2023.1153390. [Google Scholar] [CrossRef]
35. S. Wang, C. Yu, D. Shi, and X. Sun, “Research on speed optimization strategy of hybrid electric vehicle queue based on particle swarm optimization,” Math. Probl. Eng., vol. 2018, pp. 1–14, Oct. 2018. doi: 10.1155/2018/6483145. [Google Scholar] [CrossRef]
36. J. Kuchly et al., “Predictive energy management of a HEV considering engine torque dynamics,” in Proc. Eur. Control Conf., 2021, pp. 1367–1372. [Google Scholar]
37. X. Zhang, J. Hou, Z. Wang, and Y. Jiang, “Study of SOC estimation by the ampere-hour integral method with capacity correction based on LSTM,” Batteries, vol. 8, no. 10, Oct. 2022, Art. no. 170. doi: 10.3390/batteries8100170. [Google Scholar] [CrossRef]
38. A. T. Zachiotis and E. G. Giakoumis, “Methodology to estimate road grade effects on consumption and emissions from a light commercial vehicle running on the WLTC cycle,” J. Energy Eng., vol. 146, no. 5, Oct. 2020. doi: 10.1061/(ASCE)EY.1943-7897.0000694. [Google Scholar] [CrossRef]
39. F. Işıklı, A. Sürmen, and A. Gelen, “Modelling and performance analysis of an electric vehicle powered by a PEM fuel cell on the new European driving cycle (NEDC),” Arab J. Sci. Eng., vol. 46, pp. 7597–7609, Aug. 2021. doi: 10.1007/s13369-021-05469-y. [Google Scholar] [CrossRef]
40. X. Hu, X. Zhang, X. Tang, and X. Lin, “Model predictive control of hybrid electric vehicles for fuel economy, emission reductions, and inter-vehicle safety in car-following scenarios,” Energy, vol. 196, Apr. 2020, Art. no. 117101. doi: 10.1016/j.energy.2020.117101. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools