Malfunction Diagnosis of the GTCC System under All Operating Conditions Based on Exergy Analysis

Nomenclature

1  Introduction

Renewable energy is increasingly being used in power plants to reduce the effect of CO2 emissions on the climate [1,2]. However, renewable energy has the characteristics of intermittency and volatility, which can quickly impact the power grid [3,4]. The gas turbine combined cycle (GTCC) system has the characteristics of operational solid flexibility, low pollutant emission levels, and high energy utilization efficiency [5]. It can play a crucial role in maintaining the stability of the power grid. After long-term operation, the performance of components in the GTCC system decreases. If not kept in time, the power generation cost increases.

The thermal economic malfunction diagnosis method can identify the components affected by the malfunctions and quantify the effect of the malfunctions on fuel consumption [6]. The actual conditions (obtained through monitoring systems) are compared with reference conditions (“reference conditions” mean the design conditions or the condition of the system after maintenance). The reference condition can be obtained through software simulation, which can determine the operation performance of the GTCC system under actual conditions without malfunctions. The reference condition eliminates the effect of environmental factors such as LHV and temperature on fuel consumption.

Many scholars have conducted extensive research in the field of thermal economic diagnosis. Valero et al. [7] proposed a thermal economic method to diagnose the cause of heat consumption deviation in a 350 MW power plant. Royo et al. [8] introduced a new parameter called dissipative temperature to analyze the impact of inherent malfunctions on the efficiency of thermal system components. Torres et al. [9] introduced a thermal economic diagnosis method based on thermal economics and structural theory. The component malfunction was analyzed, and a mathematical formula was proposed to calculate the endogenous irreversible and exogenous malfunctions related to additional fuel consumption. Sliva et al. [10] developed a thermal economic diagnosis and prediction system for analyzing a GTCC power plant in Brazil. The system provided the thermodynamic condition of all components of the GTCC, as well as performance improvements that can be achieved by eliminating detected malfunction. Reference [11] conducted an advanced exergy analysis method in a GTCC system to determine the irreversibility caused by the interaction of components and to avoid irreversibility through technical improvements. The exergy analysis method divided exergy loss into avoidable loss and unavoidable loss. Lorenzoni et al. [12] evaluated the effect of different malfunctions in power systems and heat pumps. The fuel impact formula was used together with varying production diagrams for thermal economy diagnosis to quantify the impact of each malfunction on dissipative components. Wang et al. [13] proposed an advanced exergy analysis diagnostic method to demonstrate the process of component malfunction. The diagnostic process was illustrated through multiple component malfunction cases. The results indicated that this method can identify malfunction components and quantify malfunction degree.

Meanwhile, some scholars have also developed several diagnostic evaluation methods: data reconciliation method, characteristic curve method, eliminating induced effects method, fuel influence formula method, and further improved methods mentioned above. Zhang et al. [14] proposed a power plant diagnosis method based on structural and thermal economics theories. The method was applied to a 300 MW power plant, and the results showed that the thermal economic method was a promising diagnostic tool for complex energy systems. Valero et al. [15] described the possible malfunctions that may occur in components of a GTCC system. In addition, the fuel impact formula, which constitutes the thermal economic formula for quantifying the degree of malfunction, was discussed. Orozco et al. [16] proposed a diagnostic method for a GTCC system. The method used thermal economic methods and artificial neural networks to identify malfunctioning components and their effect on fuel. Zaleta-Aguilar et al. [17] proposed a data reconciliation method for energy system diagnosis. The results indicated that the method can detect and quantify the performance deviations of power plants. Meanwhile, power plants can provide irreversible maintenance recommendations for components.

Previous studies have focused on different diagnostic evaluation methods and analyzed the effects of different malfunctions on component efficiency and fuel consumption. However, these studies only focus on specific components or operating conditions, and little research on fuel impact and maintenance profits in power plants under overall operating conditions. Therefore, this paper uses dissipative temperature to quantify the malfunction conditions of different components in the GTCC system. Meanwhile, an overall operating conditions malfunction database for the GTCC system has been established. By analyzing the additional fuel consumption and maintenance costs caused by the malfunction condition and adjusting the maintenance coefficient of the GTCC under different malfunctions, reasonable maintenance decisions have been obtained.

2  Component Malfunction Diagnosis Method

The advanced exergy analysis method is introduced to quantify the effect of malfunction on the GTCC system under multiple malfunction conditions. Meanwhile, the dissipative temperature is proposed to locate the malfunction component. Combining dissipative temperature and the advanced exergy analysis method, malfunction identification and quantification are implemented.

2.1 Exergy Analysis Methods

2.1.1 Conventional Exergy Analysis Method

The exergy analysis method determines the degree and source of the thermodynamic efficiency reduction in the energy system [18].

Therefore, exergy destruction within the kth component is calculated by Eq. (1):

E˙D,k=E˙F,k−E˙P,k(1)

where the subscript F, P, and D are the fuel exergy, product exergy, and exergy destruction within the kth component.

The exergy balance of the system is as follows:

E˙F,tot=E˙P,tot+∑E˙D,k+E˙L,tot(2)

where E˙F,tot is the total fuel exergy within the system; E˙P,tot is the total product exergy within the system; E˙L,tot is the total exergy loss caused by interaction between the system and environment; E˙D,k is the exergy destruction within the kth component.

2.1.2 Advanced Exergy Analysis Method

The exergy destruction E˙D,k within the kth component, can be divided into endogenous exergy destruction E˙D,kEN and exogenous exergy destruction E˙D,kEX. The kth component operates with its actual efficiency, while others operate under theoretical conditions, and the E˙D,kEN can be calculated. The E˙D,kEX is caused by irreversibility in other components. Therefore, the E˙D,k can be represented as follows:

E˙D,k=E˙D,kEN+E˙D,kEX(3)

To calculate the E˙D,kEN within a component, the theoretical conditions are defined for all remaining component. For example, the isentropic and mechanical efficiency are set at 100%, while the heat exchange efficiency of the heat exchangers in the boiler is set at 100%.

2.2 Explanation and Quantification of Multiple Malfunctions

To better show the implementation process of various malfunctions diagnoses, a case of multiple malfunctions occurring in the GTCC system is introduced. Multiple malfunctions conditions often involve multiple malfunctions occurring on several different components.

The thermodynamic properties of the kth component are mainly determined by its performance parameter (αk). Meanwhile, the performance parameters of the kth component may be affected by other components. Therefore, the additional ΔE˙D,k is determined by the performance parameters (α1, α2…, αk, αk+1, …, αn).

E˙D,k=g(α1,α2…,αk…,αn,y)(4)

where the function g is the relationship between E˙D,k and (α1, α2…, αk, αk+1, …, αn) under operation conditions y, while the symbol n is the components number of the system.

The E˙D,kEN from reference condition to malfunction condition can be expressed as:

ΔE˙D,kEN=gk(αk,MAL,y)−gk(αk,REF,y)≈[∂gk∂αk]y(αk,MAL−αk,REF)(5)

The additional ΔE˙D,k can be described by its performance parameters as the difference between the reference condition and malfunction condition:

ΔE˙D,k=g(α1,α2…,αk,MAL,…,αn,y)−g(α1,α2…,αk,REF,…,αn,y)(6)

The additional ΔE˙D,kEX from the reference condition to the malfunction condition can also be obtained:

ΔE˙D,kEX=ΔE˙D,k−ΔE˙D,kEN(7)

I assume that after long-term operation, both component k and component l have reached malfunction conditions.

The malfunctions cause a variation of the E˙DEN within the component k and component l, while malfunctions in component k and component l can also cause a variation of the E˙DEX within the other components.

For component k and component l, a variation of the E˙DEX of the remaining components, in turn, results in a variation of the E˙DEX of component k and component l.

2.3 Dissipative Temperature for Malfunction Identification

Performance parameters are difficult to monitor in real-time, but the working medium parameters connected to component k are relatively easy to obtain. Generally, ∆αk is calculated by measuring the working medium’s thermodynamic parameters.

It is challenging to locate malfunctioning components and quantify the degree of malfunction.

The dissipative temperature ζ is defined:

ζk=(ein,k−eout,k)/(sin,k−sout,k)(8)

where sein,k is the inlet exergy of the kth component; eout,k is the outlet exergy of the kth component; sin,k is the inlet entropy of the kth component; sout,k is the outlet entropy of the kth component.

The dissipative temperature is the ratio between the given component’s exergy and entropy differences. In actual operation, if no malfunction occurs in a component, then the dissipative temperature of the kth component is equal to the reference value under the reference operating condition. However, if a malfunction occurs in the kth component, its irreversibility and entropy production increase, thereby causing the parameters to deviate from the reference conditions. Due to the irreversibility of the energy system, which mainly converts exergy into heat, the temperature of the related working medium changes. Therefore, the dissipative temperature reflects the changes in entropy production in the malfunction component.

Fig. 1 clearly illustrates how the dissipative temperature determines whether a malfunction occurs in a given component. It describes the analytical process of the working medium flowing through the kth component from reference conditions (indicated by dashed lines) to different malfunction conditions.

(1) When a malfunction (a) occurs in the k component, the inlet condition remains unchanged. Still, the increase in additional endogenous exergy destruction causes the dissipative temperature to change from ζk to ζ’k, resulting in the outlet condition of the k component deviating from a certain point on the solid line a.

(2) When a malfunction (b) occurs in other components, the inlet condition of component k deviates from the point into a point in‘, and the outlet condition deviates from point out to point out‘. The dissipative temperature remains unchanged, so line b parallels the reference operating condition (dashed line).

(3) When the malfunctions (a, b) occur simultaneously on the kth component and other components, the inlet and outlet conditions deviate to points in‘‘ and out‘‘, respectively.

In summary, since only the values of exergy and entropy are required, the dissipative temperature can quickly locate malfunction components and apply them to multiple malfunction conditions.

Figure 1: The variation in the working medium of component k from reference conditions to different malfunction conditions

3  System Description and Malfunction Description

Ebsilon software established the GTCC system model. The GTCC system comprises a gas turbine (GT), HRSG, steam turbine (ST), and other components. The system flowchart is shown in Fig. 2.

Figure 2: Flowchart of the GTCC system

3.1 Description of the GTCC System

The overall operating condition model of the GTCC system is established using Ebsilon software.

3.1.1 Compressor Modeling

The reference provides the compressor characteristic curve [19]. A calculation model for the compressor’s overall operating condition has been established.

3.1.2 Combustion Chamber Modeling

The combustion chamber calculation model only considers energy balance [19].

(1+βL)×(hg3−hg1)=(hf2−hf1)+βL(ha2−ha1)+ηcc×LHV(9)

where β is the excess air coefficient; L is the theoretical air volume, kg/kg; h is the specific enthalpy, kJ/kg; η is the efficiency; LHV is the fuel lower heating value; The superscript/subscript: a means air; cc means combustion chamber; f means fuel; g means gas; 1 means compressor inlet; 2 means compressor outlet; 3 means combustion chamber outlet.

3.1.3 Gas Turbine Modeling

The mass flow rate and cooling air volume under design conditions are referenced [20]. The cooling air volume under off-design operating conditions is corrected, and the pressure loss is calculated using the method in Reference [20]. The efficiency of each gas turbine stage under off-design operating conditions is corrected by the formula in Reference [20].

The gas turbine’s inlet temperature, pressure, and mass under off-design operating conditions should meet the Flugel formula [20].

km⋅TA⋅p=const(10)

where k is a constant; A is the inlet area of the turbine, m2.

3.1.4 HRSG Modeling

The calculation process of off-design conditions, energy conservation, and heat exchange balance are ensured for each heat exchange surface of the HRSG [21].

Among them, the equilibrium equations of endothermic, exothermic, and heat transfer are as follows:

mgcp(Tg1−Tg2)=ms(hs2−hs1)=(UA)p△T(11)

△T=[(Tg1−Ts2)−(Tg2−Ts1)]/ln[(Tg1−Ts2)−(Tg2−Ts1)](12)

where mg is the gas mass flow, kg/s; ms is the steam/water mass flow, kg/s; cp is the average heat capacity of flue gas, kJ/(kg·K); ΔT is the logarithmic heat transfer temperature difference, K; (UA)p is the overall heat transfer coefficient of the heating surface; The superscript/subscript: 1 means inlet; 2 means outlet.

3.2 Flowchart of System Condition Maintenance Based on Exergy Analysis

The degree of component malfunction and the components’ additional fuel consumption is obtained by monitoring the thermodynamic parameters of the GTCC system in real-time and comparing the dissipative temperature with the GTCC system malfunction database. I compared the actual gas consumption of the GTCC system with the reference gas consumption and analyzed whether the GTCC system needed maintenance. I was simultaneously adjusting the maintenance coefficient of the GTCC under different malfunctions to obtain more accurate maintenance time. The flowchart for maintenance of the GTCC system is shown in Fig. 3.

Figure 3: GTCC system overall operation condition malfunction diagnosis logic diagram

3.3 System Malfunction Description

The experimental results of the GTCC system before maintenance showed that the system’s output power at 100% power load was 371.5 MW, which is 24.3 MW lower than the design value of 395.8 MW. The GTCC system malfunction simulation result is 1) the isentropic efficiency of high, medium, and low-pressure compressor components has decreased by 3%; 2) the combustion efficiency of the combustion chamber has decreased by 1%; 3) the isentropic efficiency of high, medium, and low-pressure turbine components has decreased by 3%, 4) the isentropic efficiency of high, medium, and low-pressure steam turbines has decreased by 3%, and 5) the thermal efficiency of each heat exchanger of the HRSG has decreased by 3%.

Table 1 provides a detailed description of common malfunctions related to specific performance parameters for different components in the GTCC system.

Table 2 lists the assumed reference condition and theoretical condition of all components. The definition of theoretical condition follows the literature [14].

4  Result and Discussion

4.1 Endogenous and Exogenous Exergy Destruction under Design Condition

To better demonstrate the E˙DEN caused by the irreversibility of the component and the E˙DEX caused by other components, the difference between the E˙DEN and the E˙DEX in the GTCC system is shown in Fig. 4.

Figure 4: Exergy destruction of different components in the GTCC system. (a) Compressor, Combustion chamber, Gas turbine, Steam turbine. (b) Heat exchanger of HRSG

For most components, the endogenous exergy destruction ratio reaches over 80%, indicating that their performance is mainly determined by themselves. The combustion chamber has the highest exergy destruction, reaching 161.9 MW. The high-pressure superheater/reheater, high-pressure evaporator, high-pressure economizer, and low-pressure economizer have a large proportion of exogenous exergy destruction, indicating that the performance of these components is significantly affected by other elements.

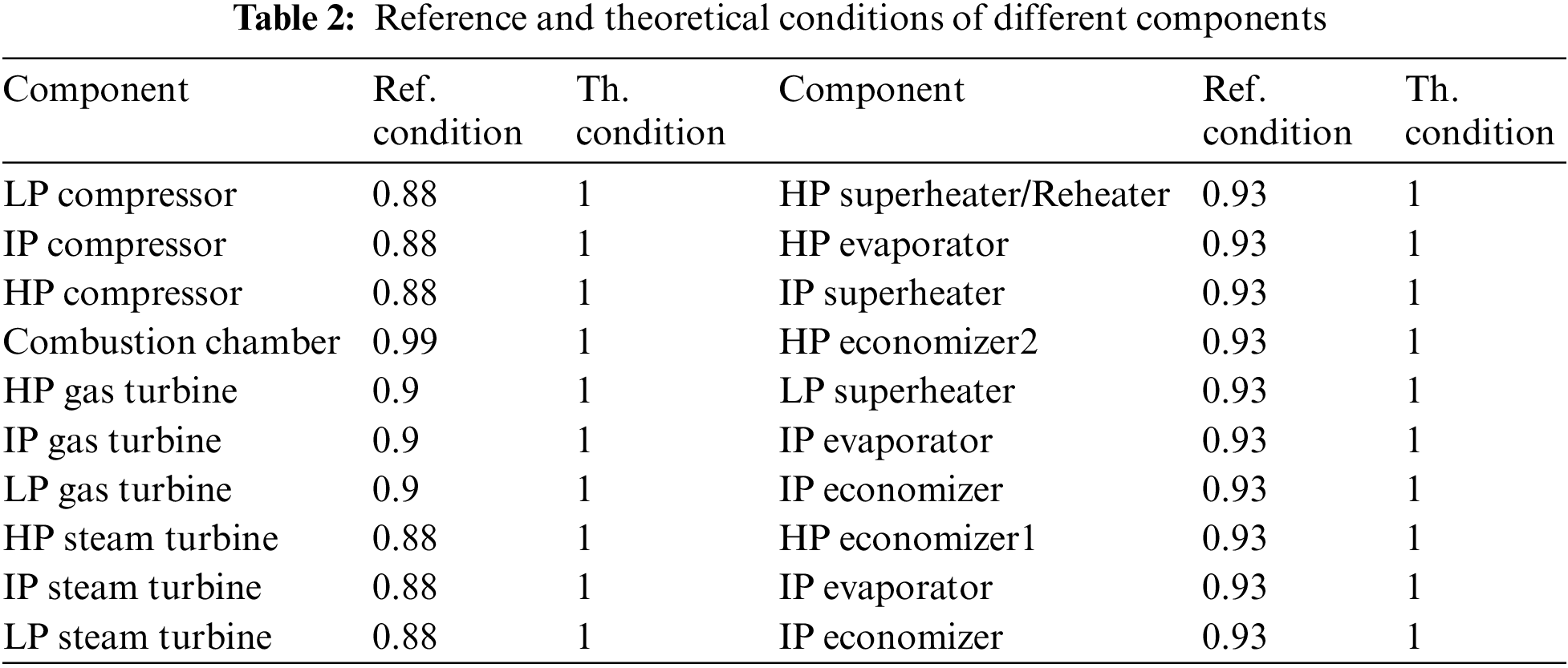
4.2 The GTCC System’s Overall Operating Condition Component Malfunction Database

A component malfunction database of the GTCC system’s overall operating condition is established to locate the malfunction degree of different components quickly.

The isentropic efficiency of the low-pressure compressor is reduced by 0%–10%. When the power load is 100%, the dissipative temperature of the low-pressure compressor significantly decreases from 2957.45 to 1518.01, and the exergy destruction increases from 7.03 to 13.06 MW; when the power load is 60%, the dissipative temperature of the low-pressure compressor significantly decreases from 2663.56 to 1348.35, while the total exergy loss increases from 3.252 to 6.11 MW.

The isentropic efficiency of the high-pressure turbine is reduced by 0%–10%. When the power load is 100%, the dissipative temperature of the high-pressure turbine significantly decreases from −11998.41 to −5548.86, and the exergy destruction increases from 14.95 to 19.44 MW; when the power load is 60%, the dissipative temperature of the high-pressure turbine decreases significantly from −11640.42 to −5388.3, and the exergy destruction increases from 10.28 to 12.49 MW.

The thermal efficiency of the high-pressure evaporator is reduced by 0%–10%. When the power load is 100%, the dissipative temperature of the high-pressure evaporator increases from 408.92 to 411.5, and the exergy destruction increases from 2.67 to 7.08 MW; when the power load is 60%, the dissipative temperature of the high-pressure evaporator rises from 417.25 to 422.26, and the exergy destruction increases from 3.51 to 7.81 MW.

Fig. 5 analyzes the dissipative temperature and exergy destruction of the compressor, gas turbine, and HRSG, respectively. The results indicate that the dissipative temperature is sensitive enough to characterize the degree of component malfunction. Meanwhile, the database of overall operating condition component malfunctions helps to locate the degree of component malfunction in real-time.

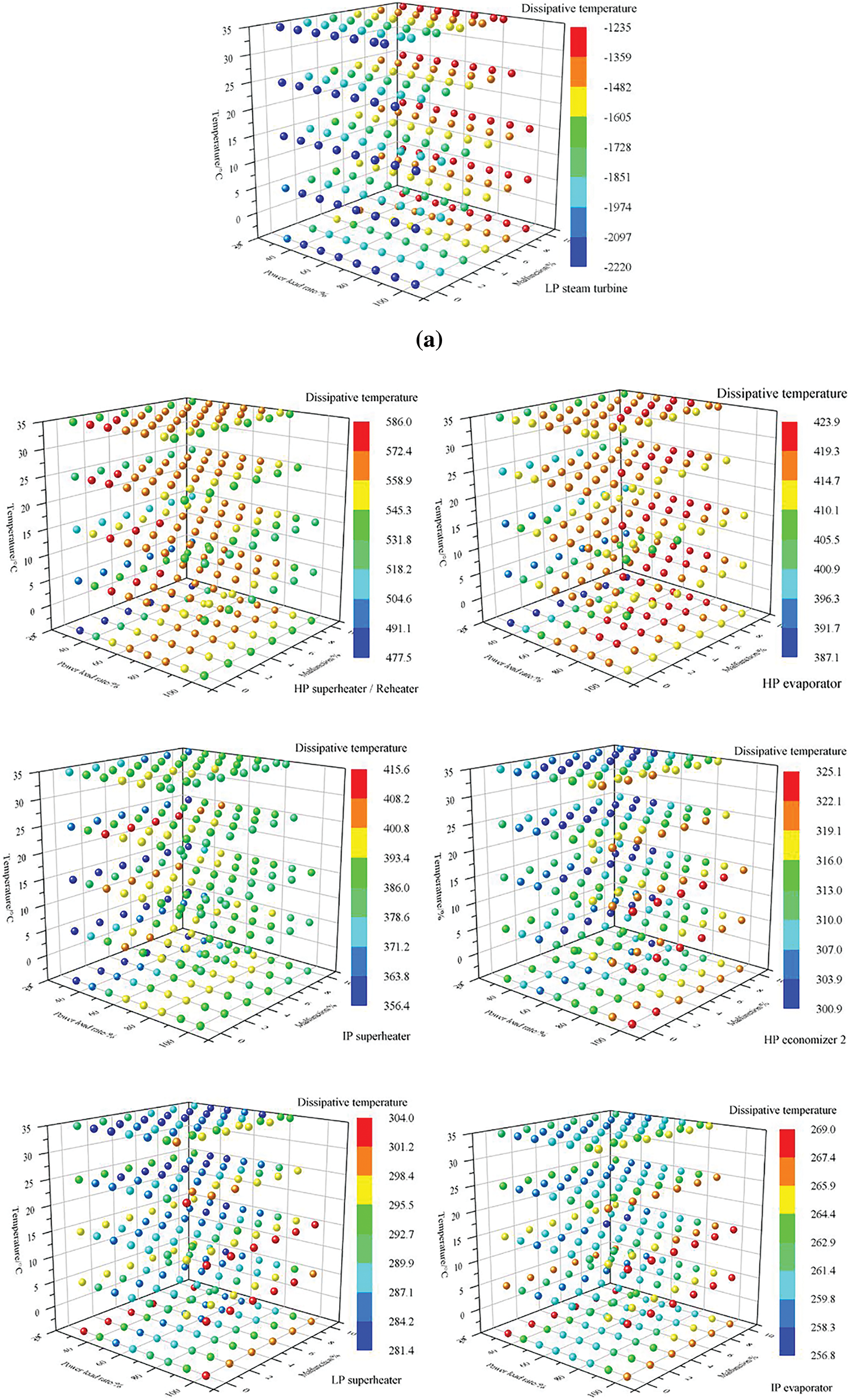
Figure 5: Malfunction database of different components in the GTCC system. (a) Dissipative temperature of compressors, turbines, and steam turbines. (b) Dissipative temperature of heat exchanger in HRSG. (c) Exergy destruction of compressors, turbines, steam turbines, combustion chamber. (d) Exergy destruction of heat exchanger in HRSG

4.3 The GTCC System Flowchart under Malfunction Condition

Fig. 6 clearly shows the changes in dissipative temperature and exergy destruction within each component in the GTCC system under reference or malfunction conditions.

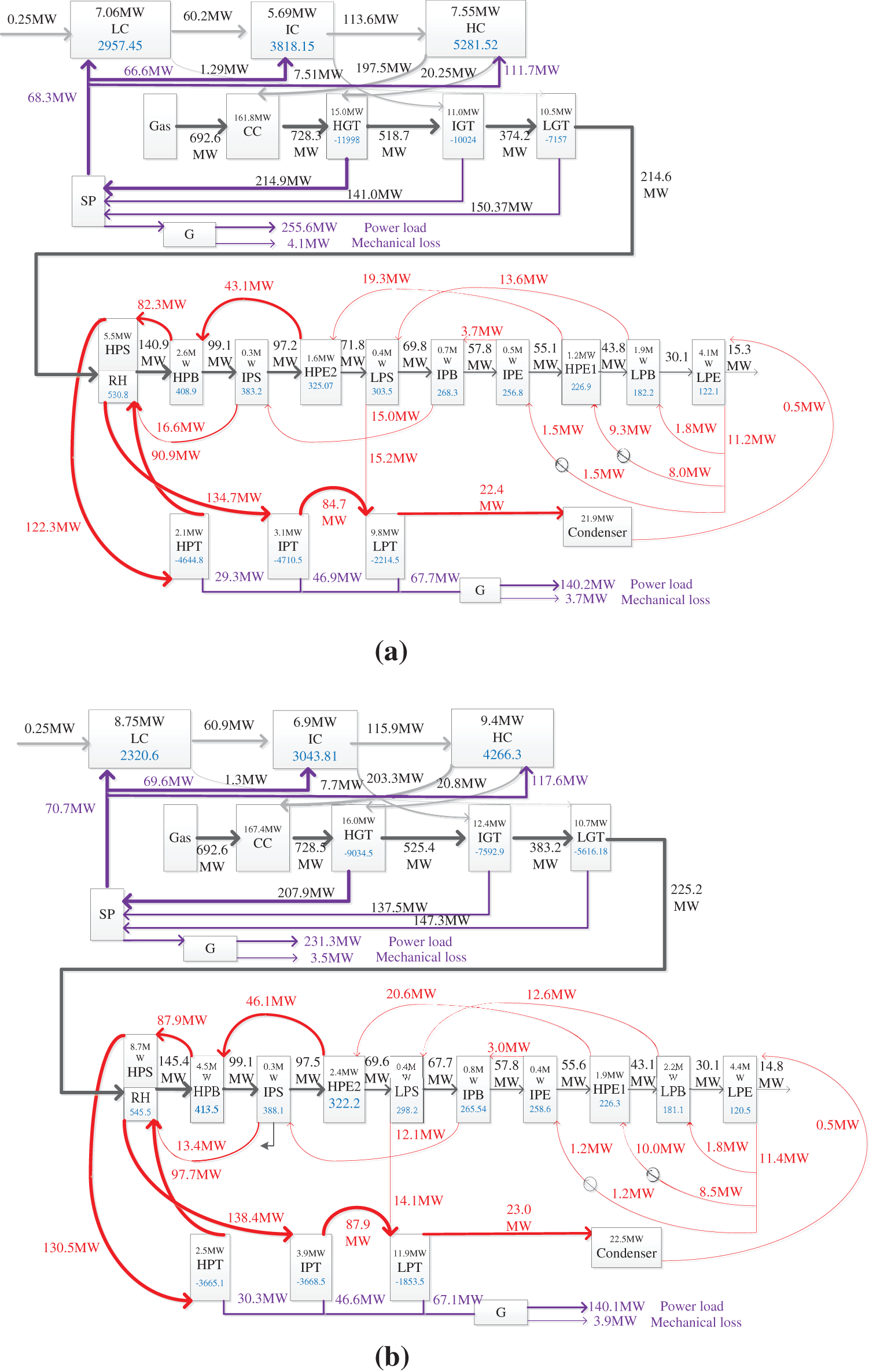
Figure 6: Flowchart of the exergy and dissipative temperature for the GTCC system. (a) Exergy and dissipative temperature of different components in the GTCC system under reference condition. (b) Exergy and dissipative temperature of different components in the GTCC system under malfunction condition

Under reference conditions, the dissipative temperature of the low-pressure compressor is 2957.446. When the isentropic efficiency of the low-pressure compressor decreases by 3%, the dissipative temperature is 2320.6. According to the malfunction database under overall operating conditions, when the isentropic efficiency of the low-pressure compressor decreases by 2%–4%, the dissipative temperature is 2441.2 and 2109.1, respectively. Therefore, the isentropic efficiency of the low-pressure compressor has been determined to decrease by 3%.

Under reference conditions, the high-pressure turbine’s dissipative temperature is −11998. When the isentropic efficiency decreases by 3%, the dissipative temperature is −9034.5. According to the malfunction database under overall operating conditions, when the isentropic efficiency decreases by 2%–4%, the dissipative temperature is −9850 and −8316.4, respectively. Therefore, the isentropic efficiency of the high-pressure turbine has been determined to decrease by 3%.

Under reference conditions, the dissipative temperature of the high-pressure evaporator is 408.9. When the thermal efficiency of the high-pressure evaporator decreases by 3%, the dissipative temperature is 413.5. According to the malfunction database under overall operating conditions, when the isentropic efficiency of the high-pressure evaporator decreases by 2%–4%, the dissipative temperatures are 413.15 and 413.72, respectively. Therefore, the thermal efficiency of the high-pressure evaporator has been determined to decrease by 3%.

In the case of multiple malfunctions, the dissipative temperature can quickly locate the malfunctioning components and degree of malfunction in the GTCC system.

4.4 Economic Changes in GTCC System under Malfunction Condition

To accurately decide the GTCC system’s maintenance time, this paper uses a specific power supply characteristic day as an example to provide the gas consumption rate and economic changes of the GTCC system under reference conditions and malfunction conditions. Meanwhile, the economic parameters and formulas for maintenance are provided. The economic parameters of the GTCC system maintenance are listed in Table 3.

CHM1=Am/(Pe∗PT∗N∗X)(13)

CHM2=24∗Tm∗D/(PT∗N)(14)

PHM=Np∗bb(15)

bb=(ΔED˙/ef)/(P/ep)(16)

where CHM1 is a direct cost of kilowatt hour maintenance, $/kW·h; CHM2 is a cost of maintenance and generation loss for kilowatt hour of electricity, $/kW·h; PHM is maintenance profit, $/kW·h; Am are maintenance costs,104 $; Pe is power, kW; PT is maintenance interval, year; N are annual operating hours; X is power load rate; Tm is maintenance time; D is electricity price, $/kW·h; Np is natural gas price, $/Nm3; bb is additional gas consumption of power generation, Nm3/kW·h; ef is fuel specific exergy, kJ/kW·h; ep is particular power exergy, kJ/kW·h.

At 7 o’clock, the power generation consumption rate of the GTCC system under reference condition and malfunction condition is 0.17717 and 0.18863 Nm3/kWh, respectively, with an additional power generation consumption rate of 0.01146 Nm3/kWh. At 11 o’clock, the power generation consumption rate of the GTCC system under reference condition and malfunction condition is 0.17337 and 0.1843 Nm3/kWh, respectively, with an additional power generation consumption rate of 0.01093 Nm3/kWh. At 17 o’clock, the power generation consumption rate of the GTCC system under reference condition and malfunction condition is 0.19547 and 0.20505 Nm3/kWh, respectively, with an additional power generation consumption rate of 0.00958 Nm3/kWh.

According to Fig. 7, the power generation maintenance profit is 6.07 $/MWh, and the maintenance expense is 5.83 $/MWh. Since the maintenance profit exceeds the maintenance expense, the GTCC system should be maintained immediately.

Figure 7: Performance parameter changes of the GTCC system before and after maintenance. (a) Characteristic daily power supply curve of the GTCC system. (b) Natural gas power consumption rate of GTCC system under reference and malfunction condition. (c) Maintenance revenue and maintenance cost of the GTCC system

The GTCC system’s maintenance time is determined by maintenance profit and expense. External factors quickly affect maintenance costs, electricity prices, and gas prices. Therefore, the impact of these changes on maintenance profit should be analyzed.

The Fig. 8a shows that as the gas price increases, the maintenance profit of the GTCC system increases. When the gas price is 0.548 $/Nm3, the maintenance expense and maintenance profit reach a balance point.

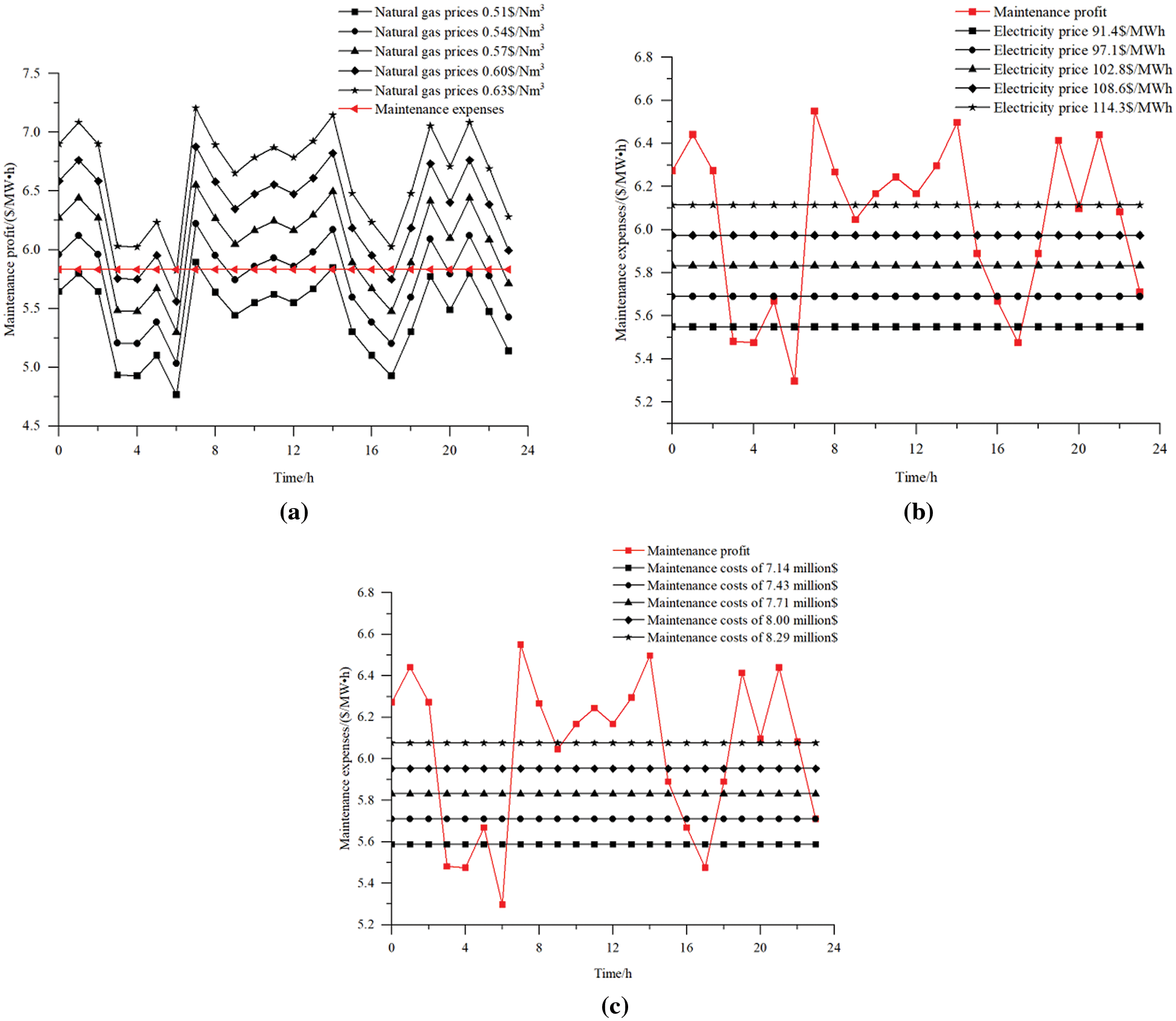
Figure 8: The impact of changes in economic parameters on maintenance profit and expense. (a) The impact of changes in natural gas prices on maintenance profit. (b) The impact of electricity price changes on maintenance expense. (c) The impact of changes in maintenance costs on maintenance expense

The Fig. 8b shows that as the electricity price increases, the maintenance expense of the GTCC system increases. The maintenance expense and profit are balanced when the electricity price is 112.3 $/MWh.

The Fig. 8c shows that as the maintenance costs increase, the maintenance expense of the GTCC system rises. When the maintenance cost is 8.265 × 106 $, the maintenance expense and maintenance profit reach a balance point.

Therefore, when making maintenance decisions, it is necessary to analyze the degree of component malfunction and additional fuel consumption and comprehensively consider maintenance costs, electricity prices, and gas prices.

4.5 Reliability Changes in GTCC System under Malfunction Condition

The life of the heated components of a gas turbine mainly depends on its operating temperature. During the operation period, the power load of the gas turbine determines its operating temperature. Therefore, the maintenance coefficient is corrected by the power load of the gas turbine. When gas turbine component malfunctions occur, the same fuel can cause a decrease in gas turbine power load. Therefore, this article analyzes the changes in the gas turbine maintenance coefficient under different component malfunctions.

During the operation period, T3 represents the operating temperature of the heated components. Under off-design conditions, the gas turbine adopts a T3–T4 regulation mode. As shown in Fig. 9, as the gas turbine’s power load rate decreases, T3 first remains constant and then decreases. T3 decreases more significantly under the same power load as the temperature decreases.

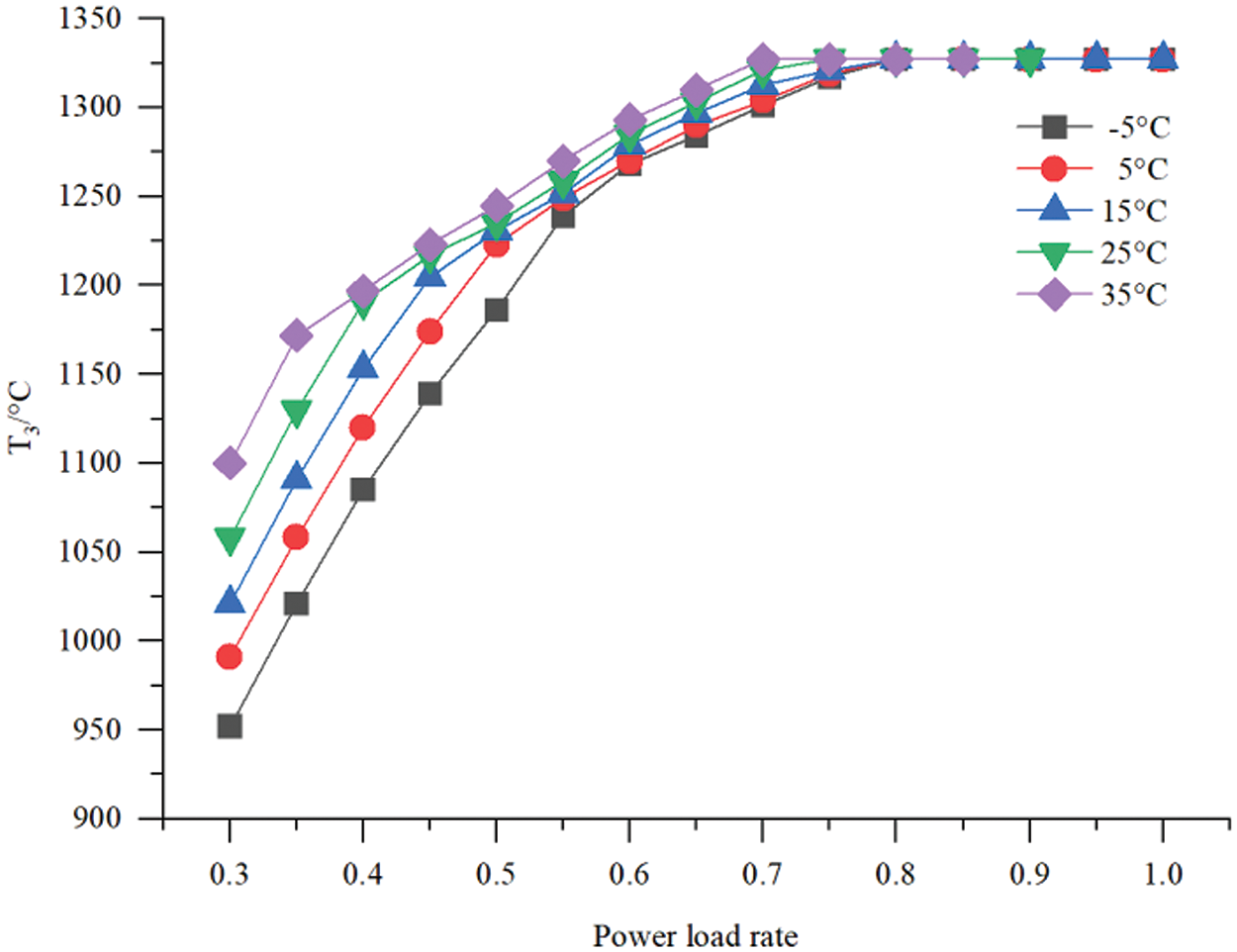
Figure 9: T3 variation under different power load rates and ambient temperature

When gas turbine component malfunctions occur, the output power of the gas turbine decreases. The performance of different components decreased by 1%, and the change in output power of the gas turbine is analyzed. As shown in Fig. 10, the malfunction of the combustion chamber significantly impacts the gas turbine by reducing it by 3.8 MW. The output power reduction of the turbine is more significant than the compressor’s. When the high-pressure turbine and high-pressure compressor malfunction occur, the output power reduction of the gas turbine is 1.6 and 0.8 MW, respectively. Meanwhile, the power load rate of the high-pressure turbine decreased from 1 to 0.6, resulting in output power reduction of 1.6 and 1.13 MW, respectively.

Figure 10: Power variation of a gas turbine with a 1% decrease in component performance

During the T3 regulation stage, T3 remains unchanged. In this T4 regulation stage, the impact of component malfunction on T3 is studied. As shown in Fig. 11, the compressor’s isentropic efficiency decreases, the compressor’s power consumption increases, the compressor’s outlet gas temperature increases, and T3 increases. The combustion efficiency of the combustion chamber decreases by 1%, the heat of the flue gas decreases, and T3 significantly decreases.

Figure 11: T3 variation of a gas turbine with a 1% decrease in component performance

The malfunction of gas turbine components causes a decrease in the output power of the gas turbine. Under the same power load, the fuel consumption of the gas turbine in the malfunction condition increases, T3 increases, and the maintenance coefficient changes. As shown in Fig. 12, when the health condition power load rate is higher than 0.8, the maintenance coefficient is 1.3, while the given malfunction condition power load rate is higher than 0.76, the maintenance coefficient is 1.3.

Figure 12: Maintenance coefficient under component malfunction

5  Conclusion

This paper analyses the malfunction degree of components in the GTCC system before maintenance based on the exergy analysis and formulates a reasonable maintenance time.

Firstly, the dissipative temperature is proposed to identify multiple malfunctions in the system quickly. The advanced exergy analysis method is adopted to analyze the E˙DEN and E˙DEX of the GTCC system components. The malfunction database of the GTCC system components has been established. Taking a GTCC system under malfunctions as an example, the exergy destruction of components under malfunctions is obtained, and the reliability of dissipative temperature in malfunction identification is verified. The economic performance of the GTCC system under reference or malfunction conditions is analyzed during the power supply characteristic period. And the maintenance coefficient of the gas turbine is adjusted. The main conclusions are as follows:

1. The proportion of E˙DEN in most components accounts for more than 80% of the total exergy destruction, with the combustion chamber being the most significant exergy destruction component.

2. Taking the GTCC system under malfunctions as an example, the overall operating condition component malfunction database of the GTCC system identifies the malfunction degree of the GTCC system components. It obtains the exergy destruction of the GTCC system components. Meanwhile, the reliability of dissipative temperature in determining the GTCC system malfunctions has been verified.

3. Taking the power supply characteristic day as an example, the GTCC system’s power generation maintenance profit is 6.07 $/MWh, and the maintenance expense is 5.83 $/MWh. Meanwhile, the GTCC system maintenance should be arranged immediately. Maintenance expenses increase when maintenance costs and electricity prices increase; while gas prices rise, maintenance profit increases.

4. The compressor, combustion chamber and turbine malfunction reduces the gas turbine’s output power. Under the same power load, the operating temperature increases. The compressor’s isentropic efficiency decreases, and the operating temperature increases. The combustion efficiency of the combustion chamber decreases, and the operating temperature decreases.

Acknowledgement: None.

Funding Statement: This work was partly supported by the China Postdoctoral Science Foundation (Grant number: 370140).

Author Contributions: Conceptualization, Xinwei Wang, Ming Li, Hankun Bing; methodology, Xinwei Wang; software, Xinwei Wang; validation, Xinwei Wang, Dongxing Zhang, Yuanshu Zhang; formal analysis, Xinwei Wang; investigation, Xinwei Wang; resources, Xinwei Wang; data curation, Xinwei Wang; writing—original draft preparation, Xinwei Wang; writing—review and editing, Xinwei Wang; visualization, Xinwei Wang; supervision, Xinwei Wang; project administration, Xinwei Wang; funding acquisition, Xinwei Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Xu, Y. Chen, J. Wang, P. D. Lude, and D. Wang, “Ideal scheme selection of an integrated conventional and renewable energy system combining multi-objective optimization and matching performance analysis,” Energy Convers. Manage., vol. 251, Jan. 2022, Art. no. 114989. doi: 10.1016/j.enconman.2021.114989. [Google Scholar] [CrossRef]

2. Y. Chen, J. Xu, J. Wang, P. D. Lude, and D. Wang, “Configuration optimization and selection of a photovoltaic-gas integrated energy system considering renewable energy penetration in power grid,” Energy Convers. Manage., vol. 254, no. 4, Feb. 2022, Art. no. 115260. doi: 10.1016/j.enconman.2022.115260. [Google Scholar] [CrossRef]

3. B. Zhang et al., “Rapid load transition for integrated solid oxide fuel cell–Gas turbine (SOFC-GT) energy systems: A demonstration of the potential for grid response,” Energy Convers. Manage., vol. 258, Apr. 2022, Art. no. 115544. doi: 10.1016/j.enconman.2022.115544. [Google Scholar] [CrossRef]

4. Y. Zhang, P. Johansson, and A. Kalagasidis, “Feasibilities of utilizing thermal inertia of district heating networks to improve system flexibility,” Appl. Therm. Eng., vol. 97, no. 5, pp. 70–77, Aug. 2022. doi: 10.1016/j.applthermaleng.2022.118813. [Google Scholar] [CrossRef]

5. G. Fan et al., “Comparative analysis on design and off-design performance of novel cascade CO2 combined cycles for gas turbine waste heat utilization,” Energy, vol. 254, no. 6, Sep. 2022, Art. no. 124222. doi: 10.1016/j.energy.2022.124222. [Google Scholar] [CrossRef]

6. V. Verda, “Accuracy level in thermoeconomic diagnosis of energy systems,” Energy, vol. 31, no. 22, pp. 3248–3260, Dec. 2006. doi: 10.1016/j.energy.2006.03.022. [Google Scholar] [CrossRef]

7. A. Valero, M. A. Lozano, and J. L. Bartolomé, “On-line monitoring of power-plant performance, using exergetic cost techniques,” Appl. Therm. Eng., vol. 16, no. 5, pp. 933–948, Dec. 1996. doi: 10.1016/1359-4311(95)00092-5. [Google Scholar] [CrossRef]

8. J. Royo, A. Valero, and A. Zaleta-Aguilar, “The dissipation temperature: A tool for the analysis of malfunctions in thermomechanical systems,” Energy Convers. Manage., vol. 38, no. 8, pp. 1557–1566, Nov. 1997. doi: 10.1016/S0196-8904(96)00217-8. [Google Scholar] [CrossRef]

9. C. Torres, A. Valero, L. Serra, and J. Royo, “Structural theory and thermoeconomic diagnosis Part I. On malfunction and dysfunction analysis,” Energy Convers. Manage., vol. 43, no. 8, pp. 1503–1518, Aug. 2002. doi: 10.1016/S0196-8904(02)00032-8. [Google Scholar] [CrossRef]

10. J. A. M. Silva, O. J. Venturini, E. E. S. Lora, A. F. Pinho, and J. J. C. S. Santos, “Thermodynamic information system for diagnosis and prognosis of power plant operation condition,” Energy, vol. 36, no. 40, pp. 4072–4079, Jul. 2011. doi: 10.1016/j.energy.2011.04.040. [Google Scholar] [CrossRef]

11. F. Petrakopoulou, G. Tsatsaronis, T. Morosuk, and A. Carassai, “Conventional and advanced exergetic analyses applied to a combined cycle power plant,” Energy, vol. 41, no. 28, pp. 146–152, May 2012. doi: 10.1016/j.energy.2011.05.028. [Google Scholar] [CrossRef]

12. R. A. Lorenzoni, J. J. C. S. Santos, A. B. Lourenço, and J. L. M. Donatelli, “On the accuracy improvement of thermoeconomic diagnosis through exergy disaggregation and dissipative equipment isolation,” Energy, vol. 194, no. 1, Mar. 2020, Art. no. 116834. doi: 10.1016/j.energy.2019.116834. [Google Scholar] [CrossRef]

13. L. Wang, P. Fu, N. Wang, T. Morosuk, Y. Yang and G. Tsatsaronis, “Malfunction diagnosis of thermal power plants based on advanced exergy analysis: The case with multiple malfunctions occurring simultaneously,” Energy Convers. Manage., vol. 148, no. 86, pp. 1453–1467, Sep. 2017. doi: 10.1016/j.enconman.2017.06.086. [Google Scholar] [CrossRef]

14. C. Zhang, S. Chen, C. Zheng, and X. Lou, “Thermoeconomic diagnosis of a coal fired power plant,” Energy Convers. Manage., vol. 48, no. 1, pp. 405–419, Feb. 2007. doi: 10.1016/j.enconman.2006.07.001. [Google Scholar] [CrossRef]

15. A. Valero et al., “On the thermoeconomic approach to the diagnosis of energy system malfunctions: Part 2. Malfunction definitions and assessment,” Energy, vol. 29, no. 8, pp. 1889–1907, Dec. 2004. doi: 10.1016/j.energy.2004.03.008. [Google Scholar] [CrossRef]

16. D. J. R. Orozco, O. J. Venturini, J. C. Escobar Palacio, and O. A. del Olmo, “A new methodology of thermodynamic diagnosis, using the thermos-economic method together with an artificial neural network (ANNA case study of an externally fired gas turbine (EFGT),” Energy, vol. 123, no. 99, pp. 20–35, Mar. 2017. doi: 10.1016/j.energy.2016.12.099. [Google Scholar] [CrossRef]

17. A. Zaleta-Aguilar, A. Olivares-Arriaga, S. Cano-Andrade, and D. A. Rodriguez-Alejandro, “β-characterization by irreversibility analysis: A thermoeconomic diagnosis method,” Energy, vol. 111, no. 12, pp. 850–858, Sep. 2016. doi: 10.1016/j.energy.2016.06.012. [Google Scholar] [CrossRef]

18. S. Kelly, G. Tsatsaronis, and T. Morosuk, “Advanced exergetic analysis: Approaches for splitting the exergy destruction into endogenous and exogenous parts,” Energy, vol. 34, no. 7, pp. 384–391, Mar. 2009. doi: 10.1016/j.energy.2008.12.007. [Google Scholar] [CrossRef]

19. X. Wang, L. Duan, and Z. Zhu, “Peak regulation performance study of GTCC based CHP system with compressor inlet air heating method,” Energy, vol. 262, no. 6–7, Jan. 2023, Art. no. 125366. doi: 10.1016/j.energy.2022.125366. [Google Scholar] [CrossRef]

20. X. Wang and L. Duan, “Peak regulation performance study of the gas turbine combined cycle based combined heating and power system with gas turbine interstage extraction gas method,” Energy Convers. Manage., vol. 269, no. 2, Oct. 2022, Art. no. 116103. doi: 10.1016/j.enconman.2022.116103. [Google Scholar] [CrossRef]

21. X. Wang and L. Duan, “Comparative study of multiple-mode collaborative operation strategy and traditional heat and power decoupling technologies for cogeneration system based on GTCC,” Case Stud. Therm. Eng., vol. 49, no. 8–9, Sep. 2023, Art. no. 103213. doi: 10.1016/j.csite.2023.103213. [Google Scholar] [CrossRef]