 Open Access
Open Access
REVIEW
Research Progress of Photovoltaic Power Prediction Technology Based on Artificial Intelligence Methods
1 College of Energy and Power Engineering, Inner Mongolia University of Technology, Hohhot, 010051, China
2 College of Electric Power, Inner Mongolia University of Technology, Hohhot, 010080, China
* Corresponding Author: Yan Jia. Email:
Energy Engineering 2024, 121(12), 3573-3616. https://doi.org/10.32604/ee.2024.055853
Received 08 July 2024; Accepted 12 September 2024; Issue published 22 November 2024
Abstract
With the increasing proportion of renewable energy in China’s energy structure, among which photovoltaic power generation is also developing rapidly. As the photovoltaic (PV) power output is highly unstable and subject to a variety of factors, it brings great challenges to the stable operation and dispatch of the power grid. Therefore, accurate short-term PV power prediction is of great significance to ensure the safe grid connection of PV energy. Currently, the short-term prediction of PV power has received extensive attention and research, but the accuracy and precision of the prediction have to be further improved. Therefore, this paper reviews the PV power prediction methods from five aspects: influencing factors, evaluation indexes, prediction status, difficulties and future trends. Then summarizes the current difficulties in prediction based on an in-depth analysis of the current research status of physical methods based on the classification of model features, statistical methods, artificial intelligence methods, and combined methods of prediction. Finally, the development trend of PV power generation prediction technology and possible future research directions are envisioned.Graphic Abstract
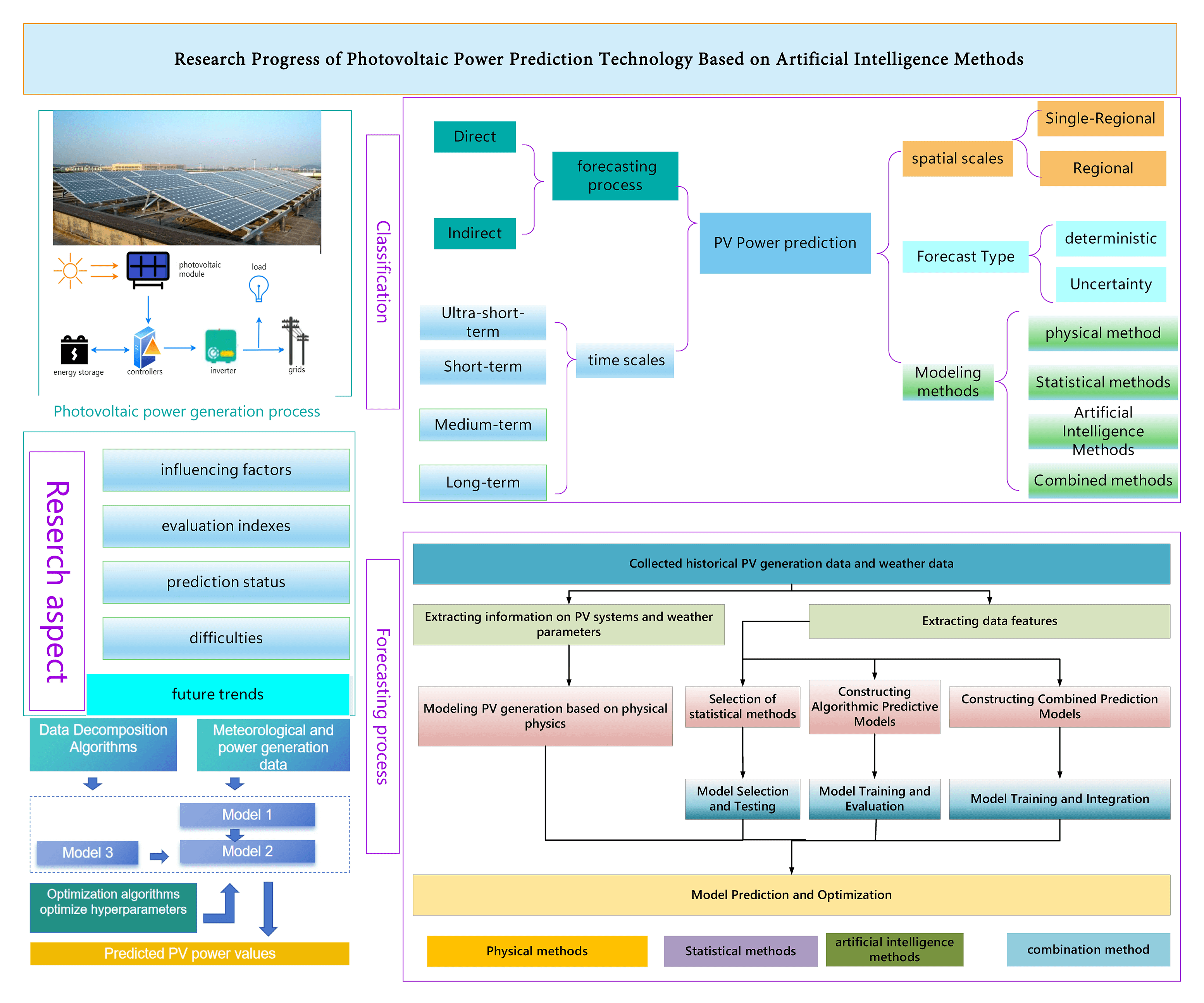
Keywords
Amidst sustained economic growth and the escalating depletion of traditional non-renewable energy resources, the issue of energy scarcity is becoming increasingly prominent. Concurrently, the continuous exploitation and consumption of fossil fuels lead to significant emissions of harmful pollutants into the atmosphere, resulting in severe environmental degradation. Consequently, addressing environmental pollution issues has become urgent. Reducing pollutant emissions and conserving energy have gained widespread global attention. To address these challenges, gradually reducing reliance on traditional non-renewable energy sources while increasing the proportion of renewable energy usage has become a critical measure and a significant undertaking [1,2].
Solar energy, compared to other energy sources, possesses distinct characteristics such as widespread availability, ease of use, and high cost-effectiveness. Moreover, it does not emit pollutants, making it a highly efficient and promote-worthy renewable resource. As a result, solar energy is receiving increasing global attention. Data published by the International Energy Agency (IEA) in 2024 indicates that photovoltaic (PV) power generation has been increasingly recognized in recent years, with a rapid increase in installed capacity. In 2023, the newly added PV capacity surpassed that of other renewable energy sources, accounting for 75% of the global new renewable energy installations. As shown in Fig. 1, the newly added PV capacity in 2023 was 374.9 GW. Future growth is expected to continue at a relatively fast pace.

Figure 1: PV capacity additions by technology and segment, 2016–2028. Reprinted from Reference [3]
According to the report Snapshot of Global PV Markets 2024 published by IEA [4], as shown in Fig. 2, the global PV industry has achieved significant growth between 2022 and 2023. According to statistics, the global cumulative installed PV capacity increases rapidly from 1.2 TW in 2022 to 1.6 TW in 2023. Among them, China’s installed PV capacity accounts for more than 60% of the global new installed capacity, and its annual capacity in 2023 accounts for more than 15% of the global cumulative capacity. The global solar market is growing exponentially, Solar Power Europe [5] forecasts that global solar will more than double to 2.3 TW by 2025.

Figure 2: Evolution of cumulative PV installations
At the same time, due to China’s robust manufacturing capacity, the production of PV modules has increased dramatically, leading to a global supply exceeding demand, Consequently, the cost of modules is rapidly declining, with prices reaching record lows. The market growth rate is remarkable, with the market outside of China growing at a rate of 30%, while China’s own domestic growth rate exceeds 120%. The number of countries with theoretical penetration rates exceeding 10% has doubled from last year to 18 countries. Solar energy plays a crucial role in reducing carbon dioxide emissions in the electricity sector. According to the latest statistics, new renewable energy installations accounted for over 75% of the market share, with this new capacity contributing nearly 60% to total electricity generation. These figures not only highlight the significant contribution of the PV market to the transition of the energy structure but also demonstrate its vast potential and growth rate in the global energy market.
As the proportion of PV power generation continues to grow within the energy mix, the power industry faces a series of new challenges. The intermittency and uncertainty of PV power generation impose higher requirements on higher grid operation and management. Accurate forecasting of PV output power becomes crucial for load balancing, reserve resource allocation, and the maintenance of system stability [6–8]. The PV power forecast is a key component of the grid’s reserve allocation and stability. Accurate PV power generation forecasting is critical for power production companies and system operators, enabling them to plan operational strategies more effectively and ensure that power supply matches load demand. By optimizing generation scheduling, they can prevent issues related to power shortages or surpluses caused by mismatches between supply and demand [9,10]. The PV power forecast is a key element of the PV power distribution strategy.
In addition, efficient scheduling strategies and accurate PV power forecasts are important for achieving supply-demand balance and optimizing reserve allocation [11,12]. By accurately predicting the PV power output, the supply and demand relationship of the grid can be more effectively managed, allowing for the rational arrangement of power generation and load. This reduces unnecessary energy waste, facilitates the expansion of PV power generation scale, enhances its economic and social benefits, and improves the operational efficiency of the grid [13,14].
The power output of a PV system is influenced by a variety of factors that interact to cause fluctuations [15,16]. Among these factors, solar irradiance is the most significant, and temperature also plays a considerable role. In the actual operation of PV systems, a variety of meteorological elements such as cloud migration, wind and wind direction changes, and relative air humidity can affect the light conditions and module temperature to different degrees [17]. The temperature of the module can be affected to varying degrees. In addition, there are several long-term factors that should not be ignored, including the aging of PV panels, the mismatch of performance between modules, and the decay of efficiency loss due to dust accumulation and coverage. The efficiency and electricity production of PV systems are influenced by a combination of various meteorological factors, such as cloud cover, seasonal variations, and weather patterns, which lead to significant volatility and instability in output power [18–21]. Short-term fluctuations in PV power generation may lead to voltage fluctuations in distribution feeders, affecting the normal operation of the grid [22].
Comprehensive analysis shows that the power output characteristics of PV systems are the result of interactions among multiple factors, which often exhibit significant non-linearity and uncertainty due to their dynamic changes and mutual influences. As a consequence, the power output of PV systems demonstrates pronounced non-linear behavior. This makes it challenging to achieve accurate predictions relying solely on traditional simplified models.
Through the collection of historical PV power forecasting research review data in the Web of Science (WoS) database, various keywords were used for searches, including combinations of terms such as “machine learning,” “artificial intelligence,” “photovoltaic power generation,” and “performance prediction.” Table 1 is a list of representative reviews from recent years, including the authors, publication year, and main research content.
As can be seen from the Table 1. Existing reviews on PV power forecasting have primarily focused on the introduction and comparison of single traditional models, often emphasizing the advantages of different statistical and machine learning methods. However, as research in this field advances, there has been a shift toward reduced usage of conventional machine learning models, with researchers increasingly adopting deep learning models that exhibit superior learning capabilities. Previous literature reviews have not adequately covered these deep learning models. Another emerging trend is the move away from focusing solely on the improvement of individual predictive models and algorithms, towards a more comprehensive approach that includes data preprocessing, weather type classification, and model parameter optimization.
This review bridges the gaps by offering a comprehensive overview of both traditional physical and statistical methods, as well as the currently trends machine learning and deep learning models used in PV power forecasting. The review also evaluates the strengths and weaknesses of various algorithms and their predictive accuracy, visually represented through graphs to highlight differences. Furthermore, the review delves into recent advances in combined methods, including data decomposition, model parameter optimization, clustering techniques, and a comparative analysis of commonly used ensemble models.
This article’s structure is as follows:
This paper commences with an introduction to the evaluation metrics used to assess the forecasting capability of PV power generation. Subsequently, we present the classification methods and criteria for PV power forecasting. We then conduct a comprehensive review and analysis of the current state of research based on the selection of different prediction models. With the surge in artificial intelligence, data-driven and machine learning-based models have achieved higher prediction accuracies. Although traditional physical and statistical methods are less frequently used nowadays, they can enhance prediction capabilities when combined with machine learning models. Therefore, this paper provides a brief introduction and analysis of both physical and statistical methods. Subsequently, we detail the application of artificial intelligence methods in PV forecasting, specifically comparing the widely used machine learning and deep learning models and summarizing their respective advantages and disadvantages. Lastly, we introduce the more recent combined methods that have gained significant attention and usage, such as data decomposition, clustering algorithms, intelligent optimization methods, and combinations of multiple deep learning models. Through an analysis of the most recent findings published over the past 3 years, we summarize the current level of research and discuss future prospects for PV power forecasting, offering insights to guide subsequent research endeavors.
The contribution of this paper is as follows:
1. The current developments in the field of PV power generation as well as its future potential are described, and the impact of PV power fluctuations on the power system is illustrated. Various factors contributing to the instability of PV power output are analyzed. The importance and significance of research to improve the level of PV power prediction is discussed.
2. The deficiencies and limitations of the currently available review articles in the field were analyzed, and the technical articles issued in the field in recent years were counted and analyzed.
3. The evaluation indexes and classification methods of power prediction are introduced in detail, and the current status of the research is explained and discussed in detail based on four different prediction methods, and the advantages and disadvantages of each technical method are compared and analyzed.
4. The artificial intelligence methods and combined methods currently widely used in this field are highlighted and compared, while the application of data decomposition, weather clustering, and optimization algorithms in PV power prediction are studied and discussed.
5. Summarizes the current research results in the field of photovoltaic power prediction and discusses the future direction of the development of this field.
2 Projected Evaluation Indicators
When assessing the performance of PV power forecasting models, researchers commonly adopt a suite of metrics to facilitate a comprehensive analysis and evaluation. These metrics are intended to collectively reflect the accuracy, stability, and generalization ability of the models, thus providing a scientific foundation for model optimization and selection. They mainly include Mean Absolute Error (MAE), Normalization Error (MSE), Mean Absolute Percentage Error (MAPE), Root Mean Square Error (RMSE), Normalized Root Mean Square Error (NRMSE), Coefficient of Determination (R²). The formula for calculating the evaluation indicators is shown in the Table 2.
The advantage of MAE is its intuitive nature, which is easy to understand as it directly reflects the mean of the errors in the original units of the data. However, it is not suitable for cross-data set comparisons because it is affected by the size and units of the data.
MAPE, as a percentage representation of error, provides scale- and unit-independent metrics that facilitate comparisons across datasets. However, it can be biased against small values, small absolute errors can lead to high percentage errors in the case of small values, and the MAPE metric can be so large that the ability to assess it fails when there are 0 values in the dataset [35]. MSE is a statistical measure used to evaluate the precision of forecasting models by calculating the squared differences between predicted values and actual observations. However, MSE is highly sensitive to outliers within the dataset. The presence of outliers can cause a significant increase in the MSE value, potentially leading to a biased assessment of model performance and impacting the fairness of the evaluation results [36]. RMSE provides a measure of error in the same units as the original data while reducing the impact of outliers, and is a metric that balances the magnitude and frequency of errors [37]. The NRMSE normalizes the RMSE, enabling fair comparisons of RMSE across different datasets and forecasting models. Precision measurement is primarily evaluated using the R² metric, which quantifies the goodness of fit between predicted and actual values. The R² value intuitively reflects the accuracy of the model’s predictions. Ranging from 0 to 1, a value closer to 1 indicates higher prediction accuracy, while a value closer to 0 suggests lower accuracy. The R² can also be presented as a percentage. At the same time, R² carries the risk of overfitting, so careful consideration needs to be given to the model’s generalization ability when relying on R² as a performance metric.
In summary, the selection of appropriate evaluation metrics is critical to accurately measure and compare model performance.
3 Classification of Power Prediction Methods
PV power forecasting can be categorized using various approaches, with each classification scales corresponding to distinct predictive methodologies. In this paper, we focus on five primary scales of the prediction process, prediction time scale, prediction space scale, prediction type, and prediction using the model to summarize the classification of PV power prediction. The basis and results of the classification are illustrated in Fig. 3.

Figure 3: Classification of PV power prediction
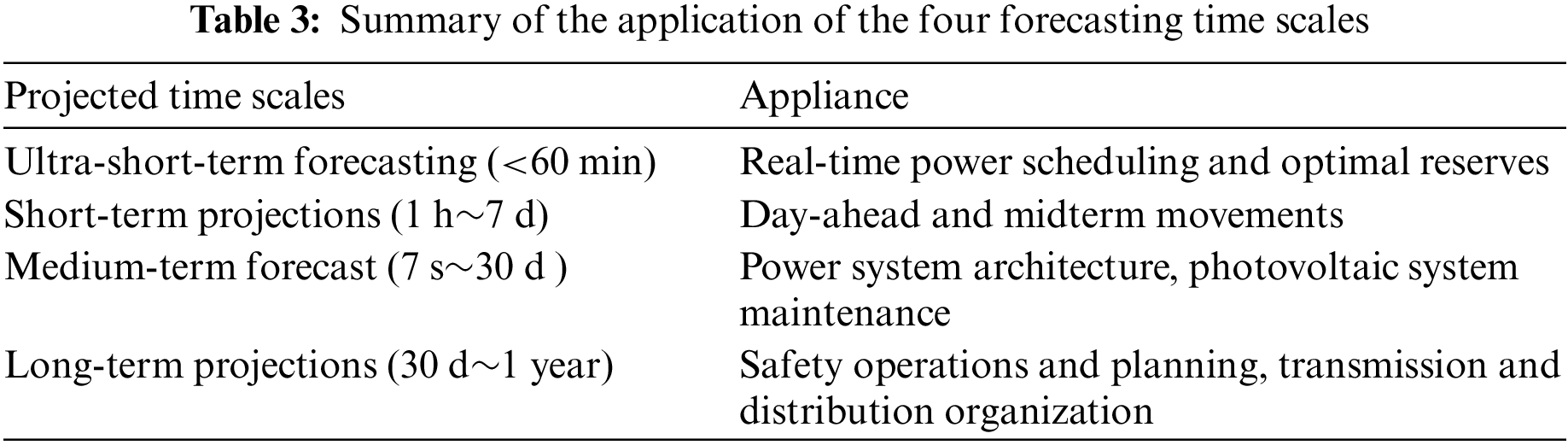
Direct prediction refers to the direct output of predicted power values based on historical sample power data [39]. Indirect prediction means that the received solar radiation value is first predicted and then the power prediction is calculated by the system power characteristic modeling [40]. Depending on different forecasting needs, different time scales can be selected. The time scales for forecasting are primarily divided into four categories: ultra-short-term, short-term, medium-term, and long-term. Table 3 outlines the main applications for each time scale [41]. The performance of a forecasting model can significantly vary with the selection of different prediction time scales. Presently, the preponderance of research is concentrated on short-term and ultra-short-term photovoltaic power forecasting. When selecting a prediction time scale, it is crucial to make a reasonable choice based on different application scenarios and to choose a model that is well-suited to the chosen time scale.
Prediction spatial scales can be categorized into single-regional prediction and regional prediction. Predictions for the power generation of a single site are referred to as single-regional predictions, while regional prediction involves forecasting the power generation of multiple sites within a region [42]. Forecasting can be categorized by the type of forecasting into deterministic forecasting (point forecasting) and uncertainty forecasting. Deterministic forecasts provide exact values at a particular forecast moment. Uncertainty forecasting is further subdivided into two forms: interval forecasting and probabilistic forecasting.
According to the difference in the characteristics of the models used in the power prediction process, they can be categorized into physical methods, statistical methods, artificial intelligence methods, and combined methods [43]. As shown in Fig. 4, the PV power prediction process based on the use of different model features is given. The physical method obtains the predicted power value by inputting the collected historical data of PV power generation and meteorological parameters into the equations established based on physical principles. Statistical methods obtain the predicted power values based on mathematical principles by selecting specific statistical methods to characterize the historical data. Artificial intelligence methods involve constructing predictive models using machine learning algorithms or deep learning algorithms. These models are trained on preprocessed data, and once trained, they are used to make predictions. Combined methods predict PV power by studying and combining the use of multiple models.

Figure 4: PV power prediction process using different models
The main contents of physical, statistical, artificial intelligence, and combinatorial methods based on different models are shown in Fig. 5. Statistical methods mainly contain Autoregressive Moving Average (ARMA), Autoregressive Integrated Moving Average (ARIMA), Exponential Smoothing, and Regression, artificial intelligence methods mainly include models such as SVM, ANN, and related variants of ANN models, and combinatorial methods are introduced for Signal Decomposition, clustering algorithm, Combined DL algorithm, optimization algorithm, etc., are introduced.

Figure 5: Main methods of classification based on different models
Physical methods encompass the modeling of the physical principles of PV power generation, including the process of receiving solar radiation and converting it into electrical energy. By mathematically modeling the geographical location of the photovoltaic system in the prediction area, along with the received meteorological parameters and solar radiation values, these methods simulate the PV panels receiving solar radiation and converting it into electrical energy [44]. Physical methods are usually categorized into three types: numerical weather prediction (NWP), ground-based cloud maps or satellite cloud observations, and sky imaging.
The input information of the physical model contains three kinds of dynamic meteorological data, the measured data of the model power output statistics (Model Output Statistics, MOS) of the PV system, and the system information of the PV plant. As shown in Fig. 6, the physical method is more demanding in terms of input data. It has a simpler modeling process.

Figure 6: Physical methods
Zhang et al. [45] calculated the correlation coefficient between the weather forecast data of the day to be tested and historical days. They selected historical days with high correlation coefficients as the weather forecast data for the day to be tested. Based on NWP data as input, they obtained the power generation value for the day to be tested. Wolff et al. [46] tested and evaluated multiple NWP parameters. They input different NWP data and conducted power forecasting, validating the impact of NWP parameter values on PV power generation. Jiang et al. [47] proposed a novel irradiance ramp conversion technique based on the NWP method, which can utilize the NWP data more effectively. Zhang et al. [48] used sky imaging data, and by combining with artificial intelligence algorithms, it was found that the prediction results were better in the ultrashort-term prediction. Dong et al. [49] corrected ground-based cloud map predictions using NWP to accurately predict the degree of ground irradiance reduction caused by cloud shading in the ultra-short-term. To effectively utilize satellite cloud observation data, Ye et al. [50] established a ultra-short-term PV power prediction model based on cloud image features. They used CNN to extract features from satellite cloud images, effectively improving the input data.
Physical methods forecast PV power output by conducting precise simulation of the physical processes involved. However, these models encounter significant challenges in practical applications. When using physical methods for prediction, a comprehensive understanding of solar radiation equations and detailed parameters of photovoltaic components is required, which is often challenging to attain in practice. Additionally, physical models react sluggishly to data fluctuations and, particularly when dealing with complex meteorological conditions, experience a significant decrease in prediction accuracy. They lack adaptability to variable environmental factors. Physical models exhibit insufficient robustness against data noise and external disturbances, limiting their generalization capabilities in changing environments. In the current field of photovoltaic power forecasting, physical methods are used less frequently, and their prediction accuracy is generally low, with accuracy notably lower than other methods.
Statistical methods construct models based on historical data and probability statistical theory. By selecting statistical theories, they analyze historical data of photovoltaic power generation to identify statistical relationships among the data. By examining the historical time series of power output and the associated data characteristics of photovoltaic systems, they recognize statistical associations with meteorological parameters. Subsequently, these associations are utilized to build models that predict future power generation [51].
As shown in Fig. 7, which take meteorological parameter information, PV power, and other data as inputs, and establish a model by selecting appropriate statistical methods, through which the output value of PV power is predicted. Statistical methods mainly include the time series method [52] and the regression analysis method [53], Among them, the time series method is widely used in the prediction of photovoltaic power generation.

Figure 7: Statistical methods
Within the domain of time series forecasting, linear regression, exponential smoothing, and the ARIMA model are commonly used analytical tools. While linear regression and exponential smoothing models, based on straightforward mathematical formulations, perform well with data exhibiting clear linear or exponential growth trends, they may not adequately capture the nonlinear patterns and long-term dependencies present in time series with complex dynamic characteristics. This limitation restricts their predictive accuracy. In contrast, the ARIMA model, by combining autoregression, differencing for stationarity, and moving averages, can more effectively handle the volatility and seasonal variations in time series, thereby offering greater reliability in terms of predictive accuracy. The Seasonal Autoregressive Integrated Moving Average (SARIMA) model, as an enhancement of the classic ARIMA model, is specifically designed for analyzing time series data with seasonal fluctuations. In PV power forecasting, seasonal changes—such as variations in daylight hours and seasonal shifts in sun angles—have a profound impact on the output power of PV systems. The SARIMA model, by incorporating seasonal differencing and seasonal autoregressive and moving average components, not only accurately captures these cyclical variations but also provides higher prediction accuracy and stronger adaptability compared to traditional ARIMA models. This significantly enhances the reliability of the forecasting results.
Alsharif et al. [54] used the ARIMA model to predict daily solar radiation in Seoul, South Korea, and found that ARIMA has good power prediction accuracy. Kushwaha et al. [55] used SARIMA for ultra-short-term power forecasting and found that the model performs well under clear sky conditions but shows a significant decline in performance during rapidly changing cloudy weather. To overcome this limitation, SARIMA can be combined with various models to compensate for the shortcomings in unpredictable weather conditions. Vrettos et al. [56] combined SARIMA with the machine learning model ANN for forecasting. The improved prediction model exhibits higher prediction accuracy.
Statistical methods have an easier modeling process than physical methods. However, they tend to be more susceptible to interference, exhibit slower responsiveness to data changes, and may achieve lower accuracy in predictions. The statistical methods cannot be applied to newly established field stations that lack historical PV processing data [57]. Statistical methods are mainly applied at higher time scales, and the predictive accuracy of statistical models decreases with increasing predictive time scales [58].
4.3 Artificial Intelligence Methods
Compared to conventional techniques, artificial intelligence technologies demonstrate superior adaptability and fitting performance when dealing with high-dimensional, nonlinear datasets. Particularly in fluctuating meteorological conditions, AI methods provide more accurate prediction outcomes. Currently, the academic community is gradually shifting from traditional statistical analysis methods to utilizing AI algorithms for research. These algorithms are favored for their ability to deeply mine underlying patterns within historical data and refine their prediction models through ongoing learning processes. With data-driven learning strategies, AI models can effectively predict new datasets and make decisions, which is particularly evident in the application scenario of photovoltaic power forecasting, where they exhibit high accuracy and adaptability to environmental changes.
Artificial intelligence methods applied to photovoltaic power forecasting can primarily be categorized into machine learning algorithms and deep learning algorithms. The artificial intelligence methods as shown in Fig. 8. Firstly, the historical data are subjected to data preprocessing, and this process usually includes data cleaning, correlation analysis, data normalization, and other operations. Abnormal data and missing data are removed and interpolated through data cleaning to avoid the impact of data anomalies on the training of the model. The correlation analysis operation filters out the meteorological parameters with a strong correlation with the power value for input, and the normalization operation removes the scale by mapping the values of each variable into the same scale. It helps to reduce the amount of computation and shorten the training time of the model.

Figure 8: Artificial intelligence methods
After going through the data preprocessing operations, the processed data is then divided into a training set, testing set, and validation set. The training set is used for model training, by selecting the appropriate machine model for feature extraction and training on the input data, to find out the connection and law between the data.
The predictive ability of the trained model is then validated and performance is evaluated using the validation set.
Finally, the validation set data is fed into the trained model to obtain the final PV power prediction values.
Machine learning stands as a pivotal branch of artificial intelligence, focusing on the analysis and processing of extensive historical datasets to enable models to identify patterns and trends. In the realm of PV power generation, the application of machine learning technology is particularly crucial. It can construct highly adaptive non-linear models that dynamically adjust their internal parameters and weights based on the characteristics of the input data. Compared to traditional linear prediction methods, machine learning models offer a considerable advantage over traditional linear forecasting methods, particularly in handling complex non-linear relationships. They can capture subtle changes in the data and predict the output power of photovoltaic systems under different environmental conditions. This adaptability allows machine learning models to provide more accurate and reliable prediction results when faced with variable meteorological conditions and system operating states [59].
The widely used ML algorithms can primarily be categorized into three types: SVM, ensemble learning methods, and ANN.
SVM are an efficient supervised learning algorithm. The basic strategy of SVM involves finding an optimal hyperplane in a high-dimensional feature space that not only clearly separates data points of different classes but also maximizes the margin between the data points and the hyperplane. As shown in Fig. 9, this figure intuitively illustrates the working principle of SVM. Through this margin-maximization approach, SVM can significantly improve the model’s prediction accuracy on new data, enhancing its generalization performance and ensuring the reliability of the prediction results.

Figure 9: SVM schematic diagram
In regression analysis, SVM introduces the concept of an ε-insensitive zone to implement Support Vector Regression (SVR), allowing the model to make predictions within a predefined error threshold, thereby enhancing its robustness in the face of data fluctuations. Additionally, SVM effectively controls the model’s complexity through appropriate regularization terms, avoiding the risk of overfitting and ensuring the model’s generalization capability on unseen data. This balance between model complexity and prediction accuracy enables SVM to demonstrate strong application potential in a wide range of data science problems.
Although SVM excel at addressing issues of prediction bias and local optima, the accuracy of their predictions is heavily influenced by the choice of kernel function parameters and the penalty factor [60]. Particularly in cases where the number of features far exceeds the number of samples, SVM’s predictive performance may be suboptimal, making it more suitable for smaller-scale datasets. Traditional parameter selection methods based on empirical rules often fail to achieve optimal prediction results. The performance of SVM is highly dependent on the choice of kernel function and the setting of the penalty factor, both of which directly affect the model’s generalization ability and prediction accuracy. The selection of the kernel function determines how SVM maps data in a high-dimensional feature space, while the penalty factor regulates the model’s tolerance for classification errors. Incorrect parameter choices can lead to overfitting or underfitting, affecting the accuracy and stability of the model in practical applications. Therefore, carefully tuning these parameters is crucial for optimizing the performance of SVM models. In practice, systematic methods such as cross-validation are typically employed to finely tune parameters in search of the best configuration, aiming to achieve more accurate predictions on unknown data. This approach helps enhance the model’s generalization capability, ensuring optimal predictive performance on new datasets.
Chen et al. [61] optimized the parameters of the constructed SVM PV power prediction model using and particle swarm algorithm (PSO), which effectively improved the accuracy of the SVM prediction model. Wang et al. [62] established a prediction model by considering cloud variations, using SVM for cloud image classification and further integrating ground-based cloud images with the physical method in the prediction model.
Decision tree algorithms represent a widely-used supervised learning technique that recursively divides data clusters into finer subgroups through a series of logical questions. As shown in Fig. 10, the algorithm constructs its decision path by continuously evaluating the data’s features and identifying the optimal splitting points until a predefined stopping criterion is met. Decision trees are favored due to their intuitive structure and ease of interpretation, rendering them adaptable to diverse array of datasets.

Figure 10: Block diagram of decision tree
The construction of a decision tree not only depends on feature selection but also on how the contribution of features to the split effectiveness is quantified. In practice, decision tree algorithms select features and splitting points by minimizing information loss or maximizing homogeneity, ensuring that each subset has high consistency on specific features.
To enhance the generalization performance and improve the predictive accuracy of decision trees, researchers employ various optimization techniques. These include pruning techniques, which reduce model complexity by trimming branches that contribute little to overall prediction, thus alleviating overfitting. Additionally, ensemble learning strategies, such as RF and Gradient Boosting Decision Trees (GBDT), integrate predictions from multiple decision trees, enhancing model robustness and resistance to outliers. Feature selection techniques further optimize model performance by screening out the most critical features for the prediction task, excluding those that are irrelevant or provide redundant information, thus streamlining the model and improving its efficiency. Through these methods, decision trees can focus more effectively on the most informative features for learning and prediction.
The synergistic application of these strategies can markedly enhance a model’s performance on unseen data and bolster its interpretability. Pruning not only reduces model depth but also removes noisy features that could lead to overfitting. Ensemble learning injects diversity into the model, reducing sensitivity to fluctuations in individual decision tree performance. Feature selection ensures that the model focuses only on the most critical information during its construction phase.
The integrated application of these optimization methods offers a more nuanced and systematic approach to enhancing decision tree models, enabling them to make more precise and stable predictions when handling complex datasets. However, each strategy has its applicable scenarios and potential limitations, so they need to be flexibly selected and adjusted according to specific problems and data characteristics in practical applications.
The RF algorithm is known for its robust generalization capabilities and robustness. Zhang et al. [63] used the RF algorithm for prediction and compared its results with those of Backpropagation (BP), Radial Basis Function (RBF), and MLP models. They found that the RF algorithm exhibited higher fitting accuracy and prediction precision. Lahouar et al. [64] leveraged the characteristics of RF, including its resilience to irrelevant input variables, good generalization ability, and the ability to measure the importance of input features. Based on these properties, they proposed an RF-based predictor for day-ahead power forecasting.
In recent years, ANN have become a focal point of research and application due to their unique advantages. These networks are renowned for their outstanding parallel processing capabilities, powerful nonlinear modeling abilities, and excellent fault-tolerance mechanisms, particularly demonstrating their broad applicability in analyzing nonlinear and non-stationary datasets [65]. However, traditional shallow neural networks may have limitations in capturing the complex mapping relationships between inputs and outputs, which can sometimes constrain their predictive accuracy [66].
As shown in Fig. 11, its composition mainly consists of an input layer, a number of hidden layers, and an output layer.

Figure 11: Neural network block diagram
When constructing the input layer, variables that have a significant impact on PV power output are typically selected as input parameters. The number of nodes in the hidden layer is usually determined using a trial-and-error adjustment method. Initially, an empirical formula is used to estimate an appropriate number of nodes, followed by fine-tuning based on the training results. As for the output layer, it corresponds to the power prediction value.
Nespoli et al. [67,68] constructed an ANN model for PV power prediction. Their results showed that the ANN predictions were accurate; however, there was some uncertainty when considering terrain and weather features and quantifying predictions.
Back Propagation (BP) neural networks have also received considerable attention. These networks belong to a class of single-direction information transmission with a multi-layer feedforward structure. However, neural networks have inherent drawbacks, such as the possibility of getting stuck in local optima and slower convergence processes, which can limit the overall predictive performance of the model. Li et al. [69] combined wavelet transform and Incremental Adaptive Generalized Autoregressive (IAGA) with BP neural networks to address these limitations in neural network predictions.
Jebli et al. [70] used Linear Regression (LR), RF, SVR, and ANN to perform solar energy forecasting using data from the Moroccan region. The computed results are shown in Table 4. From the prediction results, it can be seen that all models exhibit higher prediction accuracy in real-time forecasting compared to daily forecasting. Real-time forecasting requires longer training times. Among the models, the ANN outperforms the others in both real-time and daily forecasting, demonstrating superior prediction results. Therefore, the ANN model appears to be more suitable for long-term solar energy prediction.
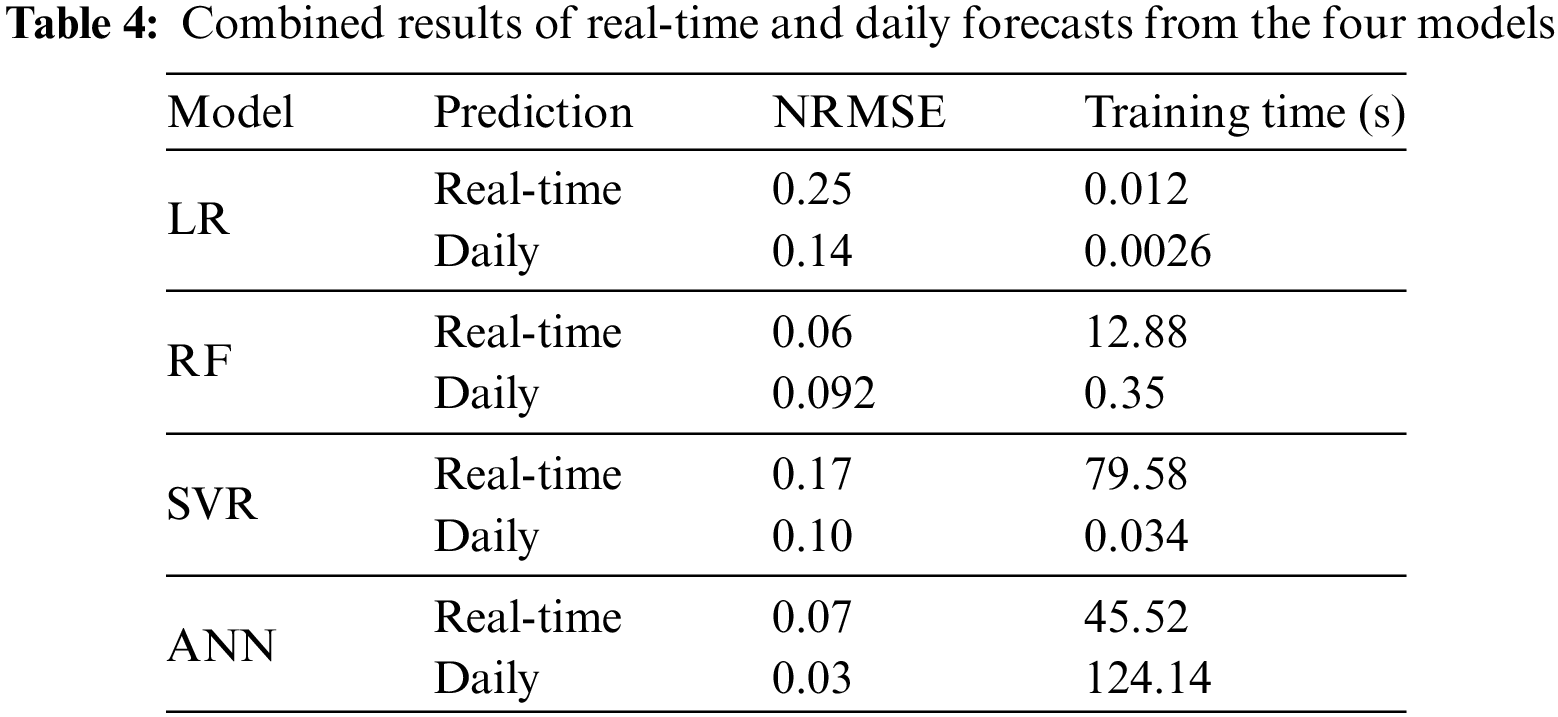
RF and ANN have superior capabilities in solving complex nonlinear problems, and they typically outperform LR and SVR in real-time solar forecasting tasks. ANN outperforms other models in predicting daily power generation, largely due to its deep computational architecture and multi-learning layer design, as well as its ability to analyze comprehensive data in depth. ANN’s strengths in accuracy and error control make it an ideal tool in the field of forecasting.
Asiedu et al. [71] used both single and hybrid machine learning models to predict photovoltaic power generation at different time scales. Experimental results show that RF, Extreme Gradient Boosting (XGBoost), and ANN exhibit significantly lower errors compared to other models, with ANN standing out as the most prominent. Although RF performs slightly better in MAE, ANN excels in the comprehensive evaluation system. Meanwhile, traditional linear regression and its variants, Ridge and Lasso, show poorer prediction results, confirming that machine learning methods outperform statistical methods in terms of predictive capability. Furthermore, models built by integrating multiple machine learning techniques have even lower errors, which are calculated as shown in Fig. 12, which confirms that model ensembling can significantly improve prediction accuracy.

Figure 12: Comparison of single and hybrid model predictions
Traditional machine learning techniques, such as decision trees and SVM, typically rely on shallow model structures that often require researchers to preselect and extract features. This process can be laborious and is potentially constrained by the researcher’s experience and domain knowledge. Conversely, deep learning models adopt complex network structures composed of multiple layers of nonlinear processing units. These models can automatically learn and extract features directly from raw data without human intervention. The core advantage of deep learning lies in its ability to automatically perform feature learning through deep neural network architectures. These networks can capture complex patterns and hierarchical information in the data. Each layer of neurons transforms the output of the previous layer through nonlinear transformations, gradually building more abstract feature representations. This bottom-up feature learning process enables deep learning models to demonstrate exceptional performance in many fields.
Commonly used DL models for PV power forecasting include Convolutional Neural Networks (CNN) and Recurrent Neural Networks (RNN). In addition, attention mechanisms and Temporal Convolutional Networks (TCN) have recently gained significant attention from researchers.
1. CNN
CNN can be used to process time series-type data. In PV power prediction, CNN can be used to extract spatial features in meteorological data or for feature extraction in multivariate time series, which can effectively improve prediction accuracy. In general, CNN-based classification models consist of four types of layers namely the convolutional layer, pooling layer, fully connected layer, and logistic regression layer. As shown in Fig. 13.

Figure 13: The structure of CNN. Reprinted from Reference [72]
The convolutional layers utilize convolution kernels to capture spatial features and latent information from the input data. Subsequently, pooling layers perform downsampling operations, such as max pooling or average pooling, on the feature maps. This process refines the features by reducing their dimensionality and decreasing computational load. Subsequently, fully connected layers map these features into a high-dimensional space to facilitate further analysis and inference. Finally, a logistic regression layer serves as the output layer, applying a logistic function to generate the final prediction result.
2.RNN
RNN is a structure designed for sequence data and is suitable for processing time series information such as photovoltaic power generation and meteorological data. Since long sequences can lead to gradient problems, including gradient vanishing or explosion, LSTM, as an extension of RNN, is able to efficiently capture and maintain long-term dependencies in sequential data by introducing forgetting gates, input and output gates, and memory units, and thus performs much better in dealing with long-term dependency problems [73].
Currently, LSTM is widely used and concerned with PV power prediction. The structure of LSTM is shown in Fig. 14.

Figure 14: Neural modules of LSTM. Reprinted from Reference [74]
Sharadga et al. [75] proposed that accurate and transferable prediction models can be achieved through the use of publicly available datasets, even in the absence of solar radiation measurements and other weather parameters. Wang et al. [76] conducted a prediction study using LSTM, CNN, and CLSTM for solar power generation over a single day in a region of Australia in 2019. They found that the choice of input sequence length is very important and has a significant impact on prediction accuracy. Zhou et al. [77] Used time series integration methods for forecasting and found that the built-in attention mechanism of LSTM enables it to adaptively focus on the important features for each forecast time period. However, LSTM also has the characteristic of handling overly long time series, which can lead to the loss of important information and difficulty in mining the inherent patterns of the data.
Perera et al. [78] used CNN to predict daily power generation in a specific region and found that CNN had good predictive capabilities, yielding accurate results. Wang et al. [79] proposed a PV power prediction model that integrates a Solar Radiation Model (SRM), CNN, and LSTM. Compared to other methods, this model produced superior prediction results. Wang et al. [80] proposed a weather classification-based method and used a CNN-LSTM model to predict power generation for PV stations in a regional area. For each station, separate convolutional and pooling layers were established to extract features specific to each station as well as inter-station features, which were then fed into the LSTM for prediction.
3. Attention Mechanisms (AM)
When processing long sequential data, the RNN may gradually decrease the weight of information from earlier time points in the neuron state over time. This phenomenon can cause the network to have difficulty in capturing features from earlier time points, which can lead to the problem of information forgetting [81]. The AM draws on how the human brain focuses its attention, and by increasing the focus on important information during the training process, it enhances the impact of that information, which in turn improves the accuracy of the model overall. It assigns differential importance weights to input features, enabling the model to identify and focus on the information segments that are critical for the prediction task. This approach endows the model with a functionality akin to human visual attention, allowing it to automatically discover and emphasize the features that have the greatest impact on the output results.
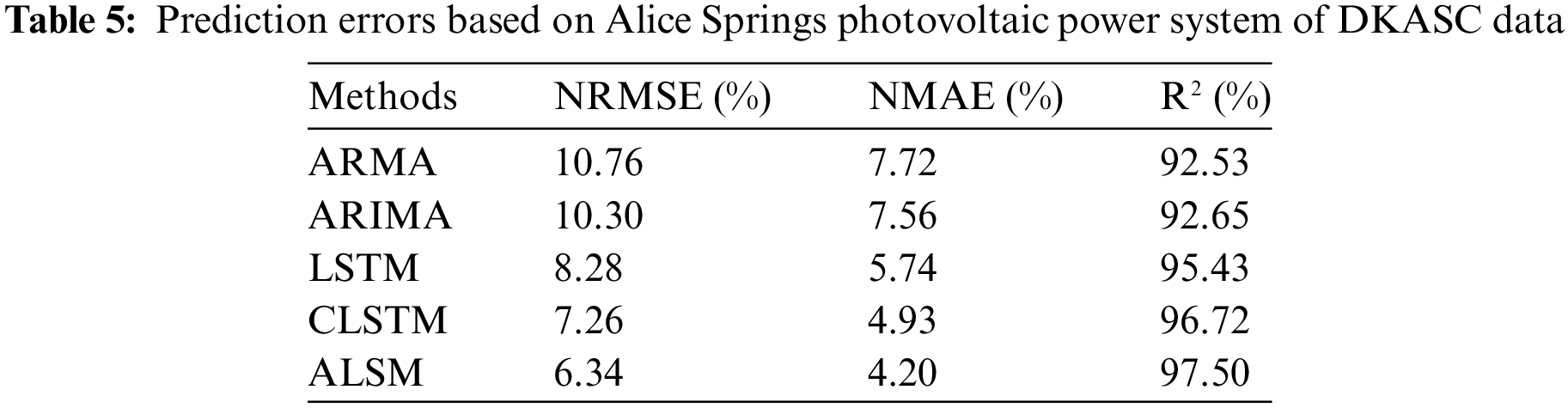
Li et al. [82] introduced an evolutionary attention learning method in LSTM, where the AM can assign importance weights for each specific time step, effectively addressing the issue of attention dispersion in traditional LSTM models. CNN network has good feature extraction ability for time series, and LSTM network time series have good prediction accuracy when they are predicted. Qu et al. [83] combined CNN, LSTM, and AM to propose the ALSM model. They used the ALSM model to predict photovoltaic power for the next hour and compared the prediction results with the errors of single models, as shown in Table 5. The ALSM model demonstrated improved prediction accuracy compared to single models, indicating that the AM can enhance model performance to a certain extent. However, they also found that the ALSM model has certain limitations, such as being suitable only for a specific range of prediction spans. It performed well for hourly predictions on a day-ahead basis, but its prediction accuracy was limited when applied to longer time scales.
4. TCN
Traditional RNN models such as LSTM also cannot parallelize operations and suffer from long training times and slow convergence speeds [84]. TCN introduces mechanisms such as causal convolution, dilation convolution, and residual module, which effectively remedies the difficulties of traditional RNN in long sequence feature extraction. The core task of TCN is to extract the significant spatial features in the input data and pre-process them appropriately. The network structure consists of a series of dilated and causal one-dimensional convolutional layers [85], that keep the input and output lengths of these layers consistent. The structure is shown in Fig. 15, The design of the expanding convolutional layer allows the network to adjust the amount of historical information it receives on demand, which allows the network to dig deeper into the intrinsic characteristics of the PV power data. The TCN also integrates a residual network module, a design that helps to prevent gradient explosion and gradient vanishing problems and ensures the ability to maintain long-term dependence on the information during the training process. The structure of the residual module is shown in Fig. 16. When the input and output dimensions of the residual module are different, the nonlinear mapping function can downsize the high-dimensional data to optimize the performance and efficiency of the network.

Figure 15: Dilated causal convolution. Reprinted from Reference [86]

Figure 16: TCN residual module. Reprinted from Reference [87]
Zhang et al. [88,89] utilized TCN for PV power prediction and enhanced the TCN neural network’s ability to extract features from time series signals by introducing different attention mechanisms. They further reweighted the TCN results to compensate for missing and overlooked information, thereby improving the neural network’s prediction accuracy and generalization capability.
Combined methods combine two or more algorithms for prediction by comparing and integrating multiple prediction methods or models and fully exploiting the advantages of different prediction methods or models [90]. Predicting PV power output is a sophisticated process, influenced by a multitude of factors such as meteorological conditions, seasonal variations, and equipment performance. Conventional single-model prediction approaches may not adequately capture these complex dynamics, leading to significant deviations in predictions under certain conditions. To surmount this challenge, researchers are increasingly turning to combined methods. By developing a hybrid model that incorporates a variety of prediction techniques, the unique advantages of each model can be harnessed while mitigating the weaknesses inherent to any single model. This approach enhances overall predictive accuracy. Combined methods can balance and complement the shortcomings of individual models, reducing prediction errors caused by model limitations.
Combined prediction is improved by using methods such as data decomposition and model optimization, or by assigning weights to the predictions of different models by using weighted fusion to finalize the prediction. as shown in Fig. 17.
Figure 17: Power prediction of PV based on combined methods
In recent years, more researchers have started using ensemble methods for prediction, combining multiple algorithms to avoid the problem of significant bias in single-model predictions. Artificial intelligence algorithms are employed in various stages of model construction to achieve optimal prediction schemes. As shown in Table 6, researchers use various data decomposition algorithms to preprocess the prediction dataset, reducing noise and extracting features to improve the reliability of the dataset. Ensemble prediction models are constructed by combining multiple algorithms, enabling complementary strengths among the models, such as the popular CNN, LSTM, and AM combination model, which can maximize the predictive capabilities and achieve high prediction accuracy.
Furthermore, for the issue of parameter selection in prediction models, which was traditionally based on experience, more researchers are now using intelligent optimization algorithms to optimize the hyperparameters of the prediction models. Intelligent optimization algorithms have good solving capabilities for complex problems, and using optimized hyperparameters for prediction can significantly improve the reliability and robustness of the models.
Additionally, due to the impact of weather, season, and other factors on photovoltaic power generation, researchers use weather clustering algorithms to categorize different weather and seasonal types. Separate models are then constructed and trained for each category, effectively reducing the impact of seasonal and weather changes on the models.
(1) Data decomposition algorithm
Noise interference is a major challenge throughout the data acquisition process for solar power generation. At the same time, the variability and unpredictability of weather introduce uncertainty factors that may have an impact on the continuity and reliability of solar power generation [99].
Decomposition algorithms divide time series data into different sub-signals and apply prediction models to forecast PV power for each subsequence. On one hand, decomposing the original data amplifies the small samples in power data, thereby obtaining more predictive features. On the other hand, decomposing the original data can reduce the impact of noise on prediction accuracy.
The methods usually used for time series decomposition of PV power data are Wavelet Transform (WT) [100], Empirical Modal Decomposition (EMD) [101], Integrated Empirical Modal Decomposition (EEMD) [102] Complementary Empirical Emotional Modal Decomposition (CEEMD) [103], CEEMDAN [104], VMD [105], etc.
WT requires manual setting of its basis functions, which reduces its adaptability. VMD has good robustness against noise. However, when using VD, one needs to specify the number of modal components K and the penalty factor
EMD suffers from issues such as poor robustness and mode mixing. However, Ensemble EEMD can effectively address these problems by adding Gaussian white noise to the original signal before performing EMD. The reconstructed Intrinsic Mode Functions (IMFs) generate new data samples after EEMD decomposition and denoising. This improves the correlation among the data and mitigates the effect of noise pollution on the prediction of PV power generation data in historical datasets. Traditional signal decomposition algorithms also face issues like mode aliasing, pseudo-modes, and residual noise [107].
VMD has good robustness against noise, which can effectively reduce the impact of noise. For a given sequence, there should be an appropriate set of VMD parameters to achieve optimal decomposition results. Boucetta et al. [108] combined the VMD algorithm with a CNN-LSTM model for short-term PV solar power forecasting, predicting PV power for future intervals of 15, 30, and 60 min. The VMD-CNN-LSTM model showed significantly lower errors compared to other single models. Jia et al. [109] determined VMD parameters by calculating the correlation coefficient between the VMD residual and the PV power series. They then fed the decomposed sub-sequences and the residual sequence into an ISSA-GRU model for forecasting. This approach achieved better prediction results than manually setting the parameters, although the obtained parameters might not be the optimal ones. Tao et al. [110] used GA optimization for the VMD parameters and LSTM for prediction. The RMSE of the VMD-LSTM model was approximately 29.14% lower and the MAE was about 26.64% lower compared to the LSTM model alone. When comparing the VMD-LSTM model with the VMD-GA-LSTM model, the latter reduced the RMSE by about 0.16% and the MAE by 7.36%.
Liu et al. [111] employed WT, CEEMD, and VMD to decompose the original data into more predictable components. They then aggregated the prediction results of each component and averaged them to obtain the final prediction, effectively improving the accuracy of the prediction model.
(2) Intelligent optimization algorithm
Among DL methods, RNN and LSTM networks are widely used to analyze the temporal correlations in PV data due to their advantages in handling time series data. At the same time, CNN play a significant role in analyzing the spatial features of PV data with their superior feature extraction capabilities [112]. However, these models require the specification of certain parameters, such as the learning rate, number of convolutional kernels, number of iterations, and number of neurons. The choice of these parameters determines the quality of the model’s prediction results and requires hyperparameter tuning, which is typically done using bio-inspired optimization algorithms to identify the optimal hyperparameters for the model [113].
Metaheuristic algorithms are often used to optimize the parameters of predictive models, such as Genetic Algorithms (GA) [114], Particle Swarm Optimization (PSO) [115], and Multi-Objective Grey Wolf Optimizer (GWO) [116]. The Crested Porcupine Optimizer (CPO) can also significantly improve the prediction performance of time series data.
Li et al. [117] optimized Bi-LSTM prediction model using PSO technique. Zhang et al. [118] optimized the weights and thresholds of Outlier Robust Extreme Learning Machine (ORELM) using Improved Atom Search Optimization (IASO). Fu et al. [119] proposed the use of Improved Nelder-Mead Grey Wolf Optimization (INGO) to optimize the two hyperparameters of the Shared Weight Gated Memory Network (SWGMN) wind speed prediction model, finding the optimal parameter combination.
Wang et al. [98] constructed a MISO-CNN-BiLSTM prediction model and introduced Improved Snake Optimization (MISO) to optimize the hyperparameters of BiLSTM. They set up multiple control groups for comparison and found that the proposed model had higher prediction accuracy under various weather conditions. The Fig. 18 shows the prediction accuracy in cloudy weather.

Figure 18: Comparison of models for cloudy weather. Reprinted from Reference [98]
Herrera et al. [97] used BOA to optimally adjust the hyperparameters of the LSTM model and then used the optimized model for day-ahead PV power prediction. They compared the results with those of GRU and MLP models. The results are shown in Tables 7 and 8.
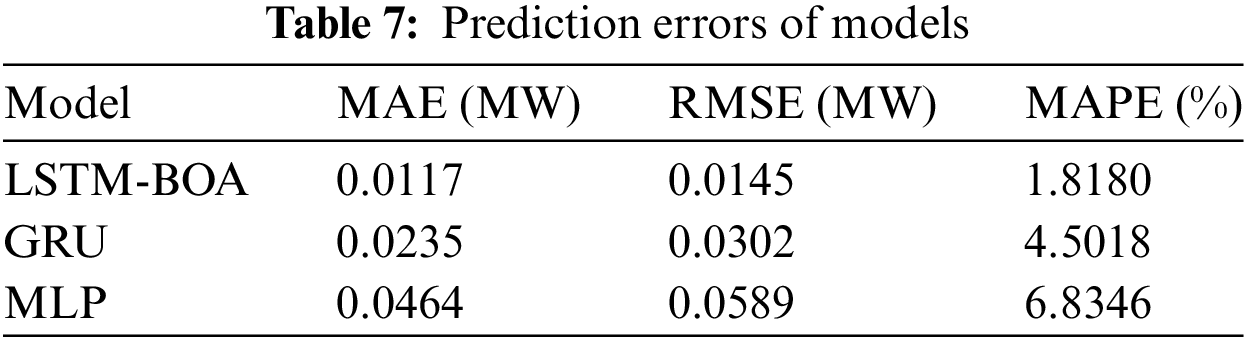

As shown in Tables 7 and 8, the model with hyperparameters optimized using BOA exhibits lower error values and better fitting performance compared to single models. However, the introduction of optimization algorithms increases the complexity of the model and prolongs the training time. Although metaheuristic algorithms such as PSO and GWO demonstrate strong global convergence, they have limitations in terms of generalizability and fault tolerance. Therefore, most researchers are dedicated to improving optimization strategies to enhance the convergence and optimization capabilities of the algorithms.
(3) Clustering algorithm
To address the intricacies of weather patterns and mitigate the impact of randomness on photovoltaic power generation forecasting, scholars incorporated clustering techniques within their predictive methodologies. The frequently used clustering methods are the K-means algorithm [120] and the Fuzzy C Means algorithm.
1) K-means algorithm
The K-means algorithm is an unsupervised clustering technique based on inter-sample distances, which determines the cluster affiliation of each sample by calculating the Euclidean distance from the sample point to the cluster center. In this process, the samples are automatically assigned to the nearest clusters based on their distances from the cluster centers without the need to pre-label the samples. The K-means++ algorithm, as a derivative of K-means, has a core improvement in the optimization of the initialization process of the cluster centers. Compared with the K-means algorithm, K-means++ selects the initial clustering centers by a new strategy that avoids the problems that may be caused by the completely random selection of clustering centers in the K-means algorithm.
The advantage of the K-means algorithm is its ability to adapt to data sets of different sizes, and its operating principle is intuitive and easy to understand. The algorithm improves the robustness and stability of clustering by optimizing the location of the cluster centers and using a distance metric to select the optimal center of mass for each cluster. However, a major limitation of the technique is that the number of clusters must be pre-specified, which is difficult to determine in some cases. In the K-means process, the goal of the algorithm is to minimize the Euclidean distance between observations and their respective cluster centers as a way to achieve efficient grouping of data points [121].
The K-means++ algorithm is improved using a strategy where the distance between the initial clustering centers should be as far as possible. This algorithm starts by randomly selecting a sample point as the starting clustering center [122]. Subsequently, each sample point calculates the probability of becoming the next clustering center based on its distance from the current clustering center, and the farther away the sample point is, the higher the probability that it will be selected as the clustering center. In this way, the K-means++ algorithm can determine all the clustering centers step by step. The advantage of K-means++ over the basic K-means algorithm is that it can improve the quality of the clusters without relying on the random selection of cluster centers, thus enhancing the accuracy and efficiency of the algorithm [123].
2) Fuzzy C Means algorithm (FCM)
The FCM algorithm iteratively calculates the affiliation of the sample points by optimizing the objective function to achieve automatic classification of the sample data. Through its concept of affiliation, it can deal with fuzzy boundaries of sample points between multiple categories. FCM continuously adjusts the affiliation of sample points through an iterative process until convergence and finally determines the category that each sample point belongs to [124,125].
The specific steps of FCM are as follows:
Design the number of clusters as well as the hyperparameter m. Initialize the affiliation matrix
1) Update the clustering center as shown in Eq. (1).
2) The updated affiliation matrix is shown in Eq. (2).
3) Determine whether the iteration termination condition is satisfied or not, under the premise of not exceeding the maximum number of iterations, the iteration termination condition is shown in Eq. (3).
Fuzzy C Means also suffers from several obvious limitations. The FCM algorithm relies on the Euclidean distance to measure the similarity between sample points, which may not be sufficient to accurately reflect the complex interactions between variables. In addition, the FCM algorithm usually assumes that all meteorological factors have an equal impact on PV power generation, which may ignore the actual weights and dynamics of different factors. To overcome these limitations, future research needs to explore more advanced methods to enhance the accuracy and applicability of FCM algorithms when dealing with complex systems [126].
A large number of published research results have shown that the accuracy of PV power prediction can be significantly improved by using clustering. Due to the strong correlation between PV power and solar radiation intensity, the However, PV power is affected by multiple meteorological factors at the same time. Lin et al. [127] calculated the correlations between various parameters and power generation, finding that photovoltaic power generation is related to multiple meteorological factors. They used multiple meteorological parameters for clustering and as predictive features to jointly determine the final power prediction value. Lin et al. [126] calculated the correlations between various parameters and power generation, finding that photovoltaic power generation is related to multiple meteorological factors. They used multiple meteorological parameters for clustering and as predictive features to jointly determine the final power prediction value.
Selecting a single solar radiation intensity for clustering can lead to a large bias, so it is more effective to use multiple meteorological variables with high correlation as clustering features.
With the increased use of combined methods, this section facilitates the reader to understand the prediction accuracy of combinatorial methods by introducing the most commonly used models by researchers, and the corresponding prediction process, and comparing the prediction accuracy of the combinatorial models used in the literature with that of other single prediction models, so as to facilitate the reader’s intuitive understanding of the model construction process of the combinatorial methods, and the specific use of the methods of data decomposition, parameter optimization, and clustering. The methods of data decomposition, parameter optimization, clustering, and other methods are also given. At the same time, the error value of the specific model after using the combination of methods is given.
Sun et al. [95] proposed a WTEEMD-FCM-IGWO-LSTM method. They used EEMD to denoise and reconstruct meteorological data, improving the signal-to-noise ratio. After decomposition and denoising with EEMD, Wavelet Transform Decomposition (WTD) was used to handle residual white noise in the decomposed signals. Considering the uncertainty and randomness of meteorological factors, FCM clustering algorithm was utilized to classify the data. An Improved Grey Wolf Optimizer (IGWO) was then used to optimize the hyperparameters of the LSTM model. Finally, the LSTM model was applied to predict photovoltaic power for three different meteorological conditions. Compared to the control group’s errors, the adopted method achieved significant improvements in error control, as shown in the Fig. 19.

Figure 19: Error comparison. Reprinted from Reference [95]
As can be seen from Fig. 19, the WTEEMD-FCM-IGWO-LSTM model used in the study can significantly reduce prediction errors, demonstrating lower RMSE and MAE values across different weather conditions. Whether used individually or in combination, data decomposition algorithms, clustering algorithms, and intelligent optimization algorithms can all contribute to reducing the error of the prediction model to some extent.
Dai et al. [128] proposed a hybrid ensemble-optimized BiGRU prediction model. The model integrates one-dimensional CNN to perform convolution operations for feature extraction. The Attention Mechanism is used to assign weight coefficients to features, thus enhancing the focus on salient information. Additionally, stacking BiGRU layers deepens the model architecture, enhancing its feature extraction capabilities. The BiGRU model undergoes a hybrid optimization process.
The prediction results were compared with those of single models, as shown in the Fig. 20, including Support SVM, XGBoost, TCN, BiLSTM, and BiGRU, as well as ensemble models that include optimized BiLSTM and BiGRU prediction models. Comparison results show that the hybrid ensemble-optimized BiGRU model has the highest fit with actual data and superior fitting performance. Other ensemble models also exhibit satisfactory prediction accuracy, albeit lower than the hybrid BiGRU model. In contrast, single models such as BiLSTM, BiGRU, XGBoost, and SVM show poorer fit with actual data and larger prediction errors. This confirms the view that integrating multiple models through ensemble methods can significantly improve prediction outcomes.
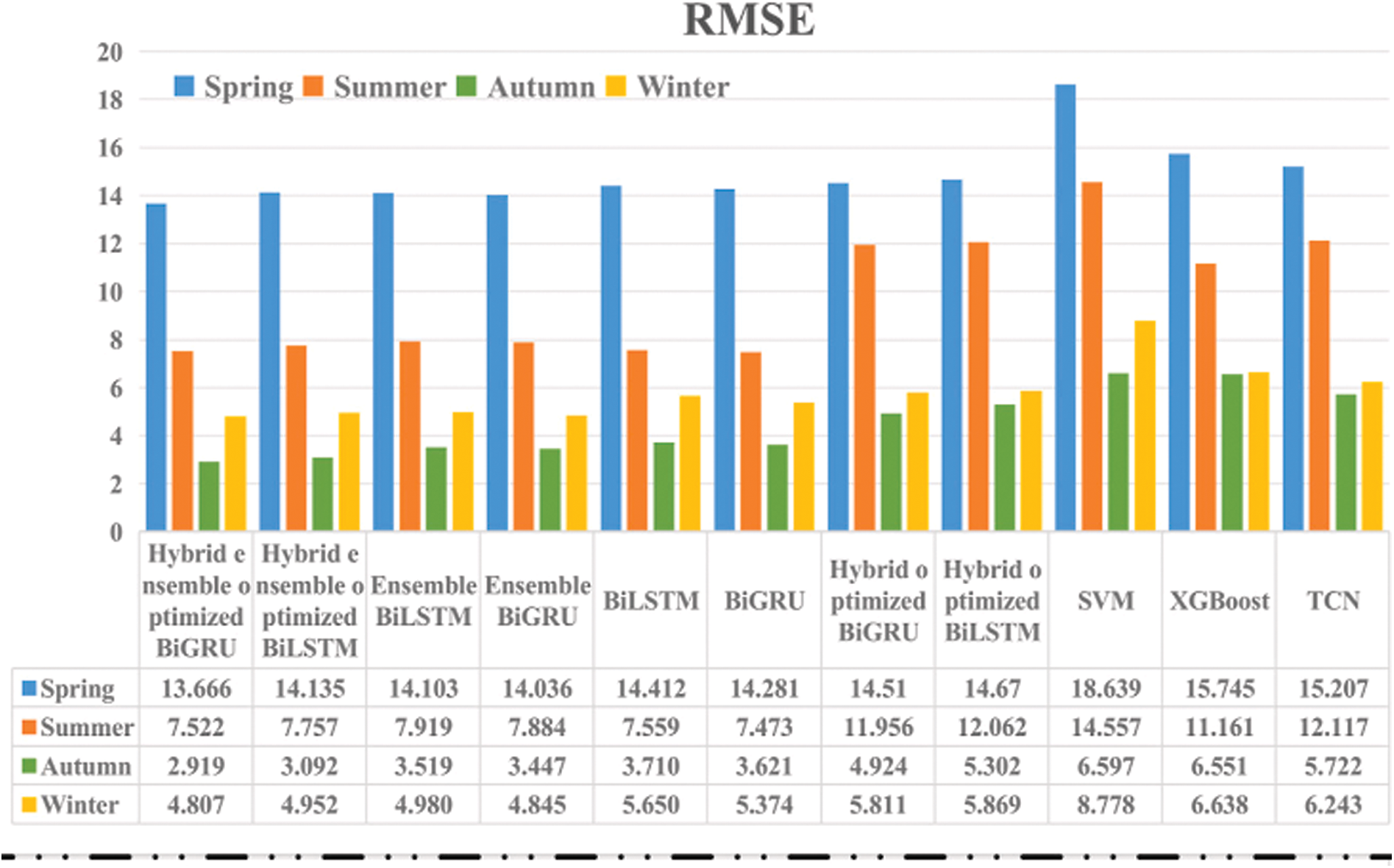

Figure 20: Comparison of predicted results. Reprinted from Reference [128]
Zang et al. [129] proposed two novel CNN models, Residual Network (ResNet) and Dense Convolutional Network (DenseNet), as prediction models. They compared the prediction results of the proposed models with those of traditional machine learning models such as SVM and MLP, as well as conventional CNN models. The prediction results are shown in the Fig. 21.

Figure 21: Comparison between different variants of CNN and ML models. Reprinted from Reference [129]
They found that CNNs perform well in spatial data and static pattern recognition, while RNNs, LSTM, and GRU are more suitable for predicting time series that contain temporal relationships. Compared to RNN, LSTM, and GRU, variants of CNNs, such as TCN, DenseNets, and ResNets, demonstrate superior performance. Therefore, future research could further investigate deeper neural networks, and selecting better deep learning models could help improve the accuracy of photovoltaic power predictions.
5 Conclusion and Future Perspective
This paper offers a comprehensive overview of the field of PV power prediction, introducing and summarizing four distinct methods based on various model classifications for comparative analysis. Physical methods, which do not require the training of prediction models to forecast PV power, However, their effectiveness is highly dependent on the obtained PV meteorological data, which is less commonly used in practice. Statistical methods, despite their relatively simple model structures, but the prediction accuracy has room for improvement, mostly applied to short-term prediction scenarios. Artificial intelligence technology with its flexibility, robustness, and high prediction accuracy, in the field of PV prediction advantage, but this method needs to be trained through many iterations to optimize the model, while the data requirements are high, and there is a risk of overfitting, mainly used in ultra-short-term and short-term PV power generation prediction. The combination of diverse algorithms can integrate the strengths of each algorithm, and can be complementary to the advantages of the algorithm model, from multiple perspectives, all aspects of the algorithm to improve the prediction ability, are now widely used and attention.
In machine learning prediction methods, among SVM, RF, XGBoost, and ANN, the prediction accuracy of the ANN model is significantly higher than that of other traditional models, especially ANN has the most outstanding performance. With the continuous development and advancement of artificial intelligence technology, deep learning models are characterized by their intricate hierarchical structure and formidable capability for feature extraction and learning. Models with multi-layer nonlinear neural network structure CNN, RNN, GAN, and other models and related improved models are proposed, these models can automatically learn multi-level abstract features from the original input data, have better prediction ability for data with time series features. Their prediction accuracy significantly outperforms that of physical methods, statistical methods, and traditional machine learning methods. Concurrently, recognizing the distinct strengths and capabilities of different models, in recent years more researchers have taken to build a combination of prediction models for PV power prediction, such as by combining deep learning models such as CNN, LSTM, AM, etc., CNN is used for feature extraction, LSTM is used for time series prediction, and AM is used for focusing on more important features to ensure the robustness of the system. Combining the prediction models can take advantage of the strengths of multiple models, complement the shortcomings, and give the best prediction effect.
Furthermore, to enhance the predictive performance, more researchers use the combination method for prediction, they are leveraging data decomposition techniques for noise reduction, optimizing prediction model parameters, and employing weather clustering, all of which contribute to bolstering the model’s robustness and mitigating the effects of abnormal noise. This paper delves into data decomposition algorithms, intelligent optimization algorithms, and clustering methods, which have become staples in PV power prediction, it provides a detailed discussion and introduction to these methods, comparing and analyzing their respective strengths and weaknesses, offering valuable insights for future research endeavors. Finally, the paper examines typical combination of prediction methods and the achievable prediction accuracies, presenting a reference for further improvement of prediction accuracy in the future.
Upon reviewing the content of this paper, it is evident that PV power prediction has achieved significant predictive capabilities and accuracy through ongoing advancements. However, it also has certain limitations, indicating that there is ample scope for further enhancement. We believe that the following points can also be studied and breakthroughs:
(1) The current study has less research on extreme weather conditions, and the prediction model has a large deviation. Many extreme weather phenomena have not yet been taken into account, such as heavy rain, blizzards, sandstorms, haze and so on. Future research should be carried out on PV power prediction under severe weather conditions.
(2) The current predictive performance in unstable meteorological conditions, such as cloudy and rainy weather, remains inadequate and warrants further investigation. Most existing studies take the division of weather types, and model construction and training according to different weather types. However, the correlation method and model research on forecast day and historical data are still insufficient, and numerical weather prediction and cloud cover change modelling can be applied in the future to reduce the impact of its uncertainty.
(3) Seasonal changes also have a certain impact on the PV power output, showing a relatively stable and predictable pattern. By making reasonable use of surface solar radiation intensity data and constructing independent sub-prediction models according to the characteristics of different seasons, the impact of seasonal variations on the prediction results of PV power generation can be effectively compensated.
(4) Current research is increasingly focusing on optimizing the entire PV power prediction process, including data pre-processing, model construction, result analysis and other stages, and artificial intelligence algorithms and decomposition algorithms are widely used in each process to improve the accuracy of model prediction. However, many algorithms face inherent limitations. For instance, optimization algorithms may exhibit slow convergence rates when solving target problems, and their robustness can be insufficient. The clustering algorithm has more influencing factors and poorer clustering effect, and the research and improvement of various algorithms should be increased in the future. Looking for algorithms with better features and prediction ability for PV power sequence features to further improve the accuracy of prediction.
(5) Currently, the focus of PV power prediction is predominantly on centralized photovoltaic power generation systems, yet there is a pressing need for further exploration in the realm of distributed PV power prediction. The variability and randomness of distributed PV power output are more significant, and the influencing factors include not only traditional meteorological data such as temperature, wind speed and cloudiness, but also geographic conditions such as topography and geomorphology. These factors significantly influence the accuracy of predictions.
Acknowledgement: Not applicable.
Funding Statement: This paper is supported in part by the Inner Mongolia Autonomous Region Science and Technology Project Fund (2021GG0336) and Inner Mongolia Natural Science Fund (2023ZD20).
Author Contributions: The authors acknowledge their contributions to this article as follows: study conception and design: Daixuan Zhou, Yan Jia; data collection: Xu Wang; Literature search and organization: Fuxing Wang; analyzing and interpreting the results: Daixuan Zhou, Yujin Liu, Yan Jia; manuscript writing: Daixuan Zhou, Yujin Liu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. F. Rodríguez, A. Galarza, J. C. Vasquez, and J. M. Guerrero, “Using deep learning and meteorological parameters to forecast the photovoltaic generators intra-hour output power interval for smart grid control,” Energy, vol. 239, 2022, Art. no. 122116. doi: 10.1016/j.energy.2021.122116. [Google Scholar] [CrossRef]
2. J. Liu, W. Fang, X. Zhang, and C. Yang, “An improved photovoltaic power forecasting model with the assistance of aerosol index data,” IEEE Trans. Sustain. Energy, vol. 6, no. 2, pp. 434–442, 2015. doi: 10.1109/TSTE.2014.2381224. [Google Scholar] [CrossRef]
3. IEA, “Renewable electricity capacity additions by technology and segment, 2016–2028, IEA, Paris,” Licence: CC BY 4.0. 2024. Accessed: Aug. 03, 2023. [Online]. Available: https://www.iea.org/data-and-statistics/charts/renewable-electricity-capacity-additions-by-technology-and-segment-2016-2028 [Google Scholar]
4. I. E. Agency, “Snapshot of Global PV Markets 2024,” 2024. Accessed: Aug. 10, 2023. [Online]. Available: https://iea-pvps.org/snapshot-reports/snapshot-2024/ [Google Scholar]
5. S. Europe, “Global Market Outlook 2022–2026 and discover,” 2022. Accessed: Aug. 06, 2023. [Online]. Available: https://www.solarpowereurope.org/insights/market-outlooks/global-market-outlook-for-solar-power-2022 [Google Scholar]
6. B. -M. Hodge, C. Brancucci Martinez-Anido, Q. Wang, E. Chartan, A. Florita and J. Kiviluoma, “The combined value of wind and solar power forecasting improvements and electricity storage,” Appl. Energy, vol. 214, pp. 1–15, 2018. doi: 10.1016/j.apenergy.2017.12.120. [Google Scholar] [CrossRef]
7. J. Tong, L. Xie, S. Fang, W. Yang, and K. Zhang, “Hourly solar irradiance forecasting based on encoder–decoder model using series decomposition and dynamic error compensation,” Energy Convers. Manag., vol. 270, 2022, Art. no. 116049. doi: 10.1016/j.enconman.2022.116049. [Google Scholar] [CrossRef]
8. S. Impram, S. Varbak Nese, and B. Oral, “Challenges of renewable energy penetration on power system flexibility: A survey,” Energy Strategy Rev., vol. 31, 2020, Art no. 100539. doi: 10.1016/j.esr.2020.100539. [Google Scholar] [CrossRef]
9. A. Woyte, V. V. Thong, R. Belmans, and J. Nijs, “Voltage fluctuations on distribution level introduced by photovoltaic systems,” IEEE Trans. Energy Convers., vol. 21, no. 1, pp. 202–209, 2006. doi: 10.1109/TEC.2005.845454. [Google Scholar] [CrossRef]
10. A. Dolara, S. Leva, and G. Manzolini, “Comparison of different physical models for PV power output prediction,” Sol. Energy, vol. 119, pp. 83–99, 2015. doi: 10.1016/j.solener.2015.06.017. [Google Scholar] [CrossRef]
11. D. Sampath Kumar, O. Gandhi, C. D. Rodríguez-Gallegos, and D. Srinivasan, “Review of power system impacts at high PV penetration Part II: Potential solutions and the way forward,” Sol. Energy, vol. 210, pp. 202–221, 2020. doi: 10.1016/j.solener.2020.08.047. [Google Scholar] [CrossRef]
12. P. Lin, Z. Peng, Y. Lai, S. Cheng, Z. Chen and L. Wu, “Short-term power prediction for photovoltaic power plants using a hybrid improved Kmeans-GRA-Elman model based on multivariate meteorological factors and historical power datasets,” Energy Convers. Manag., vol. 177, pp. 704–717, 2018. doi: 10.1016/j.enconman.2018.10.015. [Google Scholar] [CrossRef]
13. D. W. van der Meer, J. Widén, and J. Munkhammar, “Review on probabilistic forecasting of photovoltaic power production and electricity consumption,” Renew. Sustain. Energ. Rev., vol. 81, pp. 1484–1512, 2018. doi: 10.1016/j.rser.2017.05.212. [Google Scholar] [CrossRef]
14. X. Wang, Y. Sun, D. Luo, and J. Peng, “Comparative study of machine learning approaches for predicting short-term photovoltaic power output based on weather type classification,” Energy, vol. 240, 2022, Art no. 122733. doi: 10.1016/j.energy.2021.122733. [Google Scholar] [CrossRef]
15. G. T. Chala and S. M. Al Alshaikh, “Solar photovoltaic energy as a promising enhanced share of clean energy sources in the future—A comprehensive review,” Energies, vol. 16, no. 24, 2023, Art. no. 7919. doi: 10.3390/en16247919. [Google Scholar] [CrossRef]
16. G. F. Al-Doori, R. A. Mahmood, A. Al-Janabi, A. M. Hassan, and T. G. Chala, “Impact of surface temperature of a photovoltaic solar panel on voltage production,” Energ. Environ. Tropics, pp. 81–93, 2023. doi: 10.1007/978-981-19-6688-0_6. [Google Scholar] [CrossRef]
17. S. Wu, “A review of research on power prediction methods for photovoltaic power generation systems,” (in ChineseThermal Eng., vol. 36, no. 8, pp. 1–7, 2021. doi: 10.16146/j.cnki.rndlgc.2021.08.001. [Google Scholar] [CrossRef]
18. S. Ferlito, G. Adinolfi, and G. Graditi, “Comparative analysis of data-driven methods online and offline trained to the forecasting of grid-connected photovoltaic plant production,” Appl. Energy, vol. 205, pp. 116–129, 2017. doi: 10.1016/j.apenergy.2017.07.124. [Google Scholar] [CrossRef]
19. E. Skoplaki and J. A. Palyvos, “On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations,” Sol. Energy, vol. 83, no. 5, pp. 614–624, 2009. doi: 10.1016/j.solener.2008.10.008. [Google Scholar] [CrossRef]
20. S. A. Sulaiman, A. K. Singh, M. M. M. Mokhtar, and M. A. Bou-Rabee, “Influence of dirt accumulation on performance of PV panels,” Energy Proc., vol. 50, pp. 50–56, 2014. doi: 10.1016/j.egypro.2014.06.006. [Google Scholar] [CrossRef]
21. Z. Zhen, Z. Xuan, F. Wang, R. Sun, N. Duić and T. Jin, “Image phase shift invariance based multi-transform-fusion method for cloud motion displacement calculation using sky images,” Energy Convers. Manag., vol. 197, 2019, Art. no. 111853. doi: 10.1016/j.enconman.2019.111853. [Google Scholar] [CrossRef]
22. Y. Wang, N. Zhang, C. Kang, M. Miao, R. Shi and Q. Xia, “An efficient approach to power system uncertainty analysis with high-dimensional dependencies,” IEEE Trans. Power Syst., vol. 33, no. 3, pp. 2984–2994, 2018. doi: 10.1109/TPWRS.2017.2755698. [Google Scholar] [CrossRef]
23. M. Jobayer, M. A. Shaikat, M. N. Rashid, and M. R. Hasan, “A systematic review on predicting PV system parameters using machine learning,” Heliyon, vol. 9, no. 6, 2023, Art. no. e16815. doi: 10.1016/j.heliyon.2023.e16815. [Google Scholar] [PubMed] [CrossRef]
24. M. N. Akhter, S. Mekhilef, H. Mokhlis, and N. M. Shah, “Review on forecasting of photovoltaic power generation based on machine learning and metaheuristic techniques,” IET Renew. Pow. Gen., vol. 13, no. 7, pp. 1009–1023, 2019. doi: 10.1049/iet-rpg.2018.5649. [Google Scholar] [CrossRef]
25. B. D. Dimd, S. Voller, U. Cali, and O. M. Midtgard, “A review of machine learning-based photovoltaic output power forecasting: Nordic context,” IEEE Access, vol. 10, pp. 26404–26425, 2022. doi: 10.1109/ACCESS.2022.3156942. [Google Scholar] [CrossRef]
26. R. Ahmed, V. Sreeram, Y. Mishra, and M. D. Arif, “A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization,” Renew. Sustain. Energ. Rev., vol. 124, 2020, Art. no. 109792. doi: 10.1016/j.rser.2020.109792. [Google Scholar] [CrossRef]
27. A. Kumar, A. Kumar, D. I. S. Ramírez, A. M. del Rio, and F. P. G. Márquez, “A review and analysis of forecasting of photovoltaic power generation using machine learning,” in Proc. Sixteenth Int. Conf. Manag. Sci. Eng. Manag.–Vol. 1, 2022, pp. 492–505. doi: 10.1007/978-3-031-10388-9_36. [Google Scholar] [CrossRef]
28. F. Pandzic and T. Capuder, “Advances in short-term solar forecasting: A review and benchmark of machine learning methods and relevant data sources,” Energies, vol. 17, no. 1, 2024, Art. no. 97. doi: 10.3390/en17010097. [Google Scholar] [CrossRef]
29. J. F. Gaviria, G. Narvaez, C. Guillen, L. F. Giraldo, and M. Bressan, “Machine learning in photovoltaic systems: A review,” Renew. Energy, vol. 196, pp. 298–318, 2022. doi: 10.1016/j.renene.2022.06.105. [Google Scholar] [CrossRef]
30. E. Engel and N. Engel, “A review on machine learning applications for solar plants,” Sensors, vol. 22, no. 23, 2022, Art. no. 9060. doi: 10.3390/s22239060. [Google Scholar] [PubMed] [CrossRef]
31. K. J. Iheanetu, “Solar photovoltaic power forecasting: A review,” Sustainability, vol. 14, no. 24, 2022, Art no. 17005. doi: 10.3390/su142417005. [Google Scholar] [CrossRef]
32. J. Tian, R. Ooka, and D. Y. Lee, “Multi-scale solar radiation and photovoltaic power forecasting with machine learning algorithms in urban environment: A state-of-the-art review,” J. Clean. Prod., vol. 426, 2023, Art. no. 139040. doi: 10.1016/j.jclepro.2023.139040. [Google Scholar] [CrossRef]
33. V. Prema, M. S. Bhaskar, D. Almakhles, N. Gowtham, and K. U. Rao, “Critical review of data, models and performance metrics for wind and solar power forecast,” IEEE Access, vol. 10, pp. 667–688, 2022. doi: 10.1109/ACCESS.2021.3137419. [Google Scholar] [CrossRef]
34. R. Asghar, F. R. Fulginei, M. Quercio, and A. Mahrouch, “Artificial neural networks for photovoltaic power forecasting: A review of five promising models,” IEEE Access, vol. 12, pp. 90461–90485, 2024. doi: 10.1109/ACCESS.2024.3420693. [Google Scholar] [CrossRef]
35. S. Kim and H. Kim, “A new metric of absolute percentage error for intermittent demand forecasts,” Int. J. Forecast, vol. 32, no. 3, pp. 669–679, 2016. doi: 10.1016/j.ijforecast.2015.12.003. [Google Scholar] [CrossRef]
36. T. O. Hodson, “Root-mean-square error (RMSE) or mean absolute error (MAEWhen to use them or not,” Geosci. Model Dev., vol. 15, no. 14, pp. 5481–5487, 2022. doi: 10.5194/gmd-15-5481-2022. [Google Scholar] [CrossRef]
37. M. Ćalasan, S. H. E. Abdel Aleem, and A. F. Zobaa, “On the root mean square error (RMSE) calculation for parameter estimation of photovoltaic models: A novel exact analytical solution based on Lambert W function,” Energy Convers. Manag., vol. 210, 2020, Art. no. 112716. doi: 10.1016/j.enconman.2020.112716. [Google Scholar] [CrossRef]
38. M. Husein, E. J. Gago, B. Hasan, and M. C. Pegalajar, “Towards energy efficiency: A comprehensive review of deep learning-based photovoltaic power forecasting strategies,” Heliyon, vol. 10, no. 13, 2024, Art. no. e33419. doi: 10.1016/j.heliyon.2024.e33419. [Google Scholar] [PubMed] [CrossRef]
39. D. Boruah and S. S. Chandel, “Challenges in the operational performance of six 15–19 kWp photovoltaic mini-grid power plants in the Jharkhand State of India,” Energy Sustain. Dev., vol. 73, pp. 326–339, 2023. doi: 10.1016/j.esd.2023.02.013. [Google Scholar] [CrossRef]
40. J. Antonanzas, N. Osorio, R. Escobar, R. Urraca, F. J. Martinez-de-Pison and F. Antonanzas-Torres, “Review of photovoltaic power forecasting,” Sol. Energy, vol. 136, pp. 78–111, 2016. doi: 10.1016/j.solener.2016.06.069. [Google Scholar] [CrossRef]
41. A. Alcañiz, D. Grzebyk, H. Ziar, and O. Isabella, “Trends and gaps in photovoltaic power forecasting with machine learning,” Energy Rep., vol. 9, pp. 447–471, 2023. doi: 10.1016/j.egyr.2022.11.208. [Google Scholar] [CrossRef]
42. Y. Y. Yang, X. J. Meng, G. Feng, H. Y. Wang, and X. Y. Cheng, “A two-layer artificial neural network-based method for regional photovoltaic power prediction in multiple time scales,” (in ChineseJ. North China Elect. Power Univ.: Nat. Sci. Ed., vol. 48, no. 2, pp. 55–63, 2021. [Google Scholar]
43. N. M. Sabri and M. El Hassouni, “Accurate photovoltaic power prediction models based on deep convolutional neural networks and gated recurrent units,” Energ. Sources, Part A: Recov., Utiliz., Environ. Effects, vol. 44, no. 3, pp. 6303–6320, 2022. doi: 10.1080/15567036.2022.2097751. [Google Scholar] [CrossRef]
44. U. K. Das, K. S. Tey, M. Seyedmahmoudian, S. Mekhilef, M. Y. I. Idris and W. Van Deventer, “Forecasting of photovoltaic power generation and model optimization: A review,” Renew. Sustain. Energ. Rev., vol. 81, pp. 912–928, 2018. doi: 10.1016/j.rser.2017.08.017. [Google Scholar] [CrossRef]
45. S. Zhang, D. Lei, D. Y. Ji, Y. Hao, and X. F. Zhang, “Ultra-short-term PV power prediction based on NWP similarity analysis,” J. Solar Energ., vol. 43, no. 4, pp. 142–147, 2022. doi: 10.19912/j.0254-0096.tynxb.2020-0717. [Google Scholar] [CrossRef]
46. B. Wolff, O. Kramer, and D. Heinemann, “Selection of numerical weather forecast features for PV power predictions with random forests,” in Int. Work. Data Analy. Renew. Energy Integ., 2016, pp. 78–91. doi: 10.1007/978-3-319-50947-1_8. [Google Scholar] [CrossRef]
47. W. L. Jiang et al., “PV power prediction method based on NWP irradiance ramp conversion,” (in ChineseJ. Shandong Univ. (Eng. Ed.), vol. 51, no. 5, pp. 114–121, 2021. [Google Scholar]
48. Y. Zhang, K. Meng, W. Kong, and Z. Y. Dong, “Collaborative filtering-based electricity plan recommender system,” IEEE Trans. Ind. Inform., vol. 15, no. 3, pp. 1393–1404, 2019. doi: 10.1109/TII.2018.2856842. [Google Scholar] [CrossRef]
49. M. Dong, X. F. Li, Z. Yang, Y. Chang, M. Ren and C. X. Zhang, “Research progress on data-driven distributed photovoltaic power prediction methods,” (in ChineseGrid Clean Energ., vol. 40, no. 1, pp. 8–17+28, 2024. [Google Scholar]
50. C. Ye, D. Liu, and K. Cao, “Ultra-short-term photovoltaic power prediction model based on cloud features,” (in ChineseGrid Clean Energ., vol. 39, no. 10, pp. 70–79, 2023. [Google Scholar]
51. D. Lee, J. -W. Jeong, and G. Choi, “Short term prediction of pv power output generation using hierarchical probabilistic model,” Energies, vol. 14, no. 10, 2021, Art. no. 2822. doi: 10.3390/en14102822. [Google Scholar] [CrossRef]
52. J. Zhang, Z. Liu, and T. Chen, “Interval prediction of ultra-short-term photovoltaic power based on a hybrid model,” Elect. Power Syst. Res., vol. 216, 2023, Art. no. 109035. doi: 10.1016/j.epsr.2022.109035. [Google Scholar] [CrossRef]
53. G. Sahin, G. Isik, and W. G. J. H. M. van Sark, “Predictive modeling of PV solar power plant efficiency considering weather conditions: A comparative analysis of artificial neural networks and multiple linear regression,” Energy Rep., vol. 10, pp. 2837–2849, 2023. doi: 10.1016/j.egyr.2023.09.097. [Google Scholar] [CrossRef]
54. M. H. Alsharif, M. K. Younes, and J. Kim, “Time series ARIMA model for prediction of daily and monthly average global solar radiation: The case study of Seoul, South Korea,” Symmetry, vol. 11, no. 2, pp. 240, 2019. doi: 10.3390/sym11020240. [Google Scholar] [CrossRef]
55. V. Kushwaha and N. M. Pindoriya, “Very short-term solar PV generation forecast using SARIMA model: A case study,” in 2017 7th Int. Conf. Power Syst. (ICPS), Pune, India, 2017, pp. 430–435. doi: 10.1109/ICPES.2017.8387332. [Google Scholar] [CrossRef]
56. E. Vrettos and C. Gehbauer, “A hybrid approach for short-term PV power forecasting in predictive control applications,” in 2019 IEEE Milan PowerTech., Milan, Italy, Jun. 23–27, 2019, pp. 1–6. doi: 10.1109/PTC.2019.8810672. [Google Scholar] [CrossRef]
57. M. Q. Raza, M. Nadarajah, and C. Ekanayake, “On recent advances in PV output power forecast,” Sol. Energy, vol. 136, pp. 125–144, 2016. doi: 10.1016/j.solener.2016.06.073. [Google Scholar] [CrossRef]
58. H. Wang et al., “Taxonomy research of artificial intelligence for deterministic solar power forecasting,” Energy Convers. Manag., vol. 214, 2020, Art. no. 112909. doi: 10.1016/j.enconman.2020.112909. [Google Scholar] [CrossRef]
59. S. Huang, Q. Zhou, J. Shen, H. Zhou, and B. Yong, “Multistage spatio-temporal attention network based on NODE for short-term PV power forecasting,” Energy, vol. 290, 2024, Art. no. 130308. doi: 10.1016/j.energy.2024.130308. [Google Scholar] [CrossRef]
60. Q. K. Lang, X. X. Wang, Y. X. Wang, and Q. Wu, “Research on PV power output prediction based on GBDT and SVM,” (in ChineseJ. Shanghai Elect. Pow. Univ., vol. 39, no. 3, pp. 275–280, 2023. [Google Scholar]
61. Y. F. Chen, X. Y. Ma, K. cheng, T. Bao, Y. S. Chen and C. Z. Zhou, “Ultra-short-term power prediction of new energy based on meteorological feature quantity selection and SVM model parameter optimisation,” (in ChineseJ. Solar Energ., vol. 44, no. 12, pp. 568–576, 2023. doi: 10.19912/j.0254-0096.tynxb.2022-1401. [Google Scholar] [CrossRef]
62. Y. Wang, X. Wang, D. Hao, Y. Sang, H. Xue and Y. Mi, “Combined ultra-short-term prediction method of PV power considering ground-based cloud images and chaotic characteristics,” Sol. Energy, vol. 274, 2024, Art. no. 112597. doi: 10.1016/j.solener.2024.112597. [Google Scholar] [CrossRef]
63. C. K. Zhang, H. D. Liu, Y. N. Zhu, F. Jia, H. Q. Guo and J. L. Zhang, “Random forest ultra-short-term photovoltaic power prediction based on multiple feature analysis extraction,” (in ChineseDemand Side Manag., vol. 25, no. 06, pp. 50–56, 2023. [Google Scholar]
64. A. Lahouar, A. Mejri, and J. B. H. Slama, “Importance based selection method for day-ahead photovoltaic power forecast using random forests,” in 2017 Int. Conf. Green Energy Convers. Syst. (GECS), 2017, pp. 1–7. doi: 10.1109/GECS.2017.8066171. [Google Scholar] [CrossRef]
65. Y. Liu, “Short-term prediction method of solar photovoltaic power generation based on machine learning in smart grid,” Math. Probl. Eng., vol. 2022, no. 1, 2022, Art. no. 8478790. doi: 10.1155/2022/8478790. [Google Scholar] [CrossRef]
66. K. P. Marish, S. Rengaraj, K. Alagar, and M. Vinayagam, “Artificial neural network-based output power prediction of grid-connected semitransparent photovoltaic system,” Environ. Sci. Pollut. Res., vol. 29, no. 7, pp. 10173–10182, 2022. doi: 10.1007/s11356-021-16398-6. [Google Scholar] [PubMed] [CrossRef]
67. A. Nespoli et al., “Day-ahead photovoltaic forecasting: A comparison of the most effective techniques,” Energies, vol. 12, no. 9, 2019, Art. no. 1621. doi: 10.3390/en12091621. [Google Scholar] [CrossRef]
68. S. Al-Dahidi, O. Ayadi, M. Alrbai, and J. Adeeb, “Ensemble approach of optimized artificial neural networks for solar photovoltaic power prediction,” IEEE Access, vol. 7, pp. 81741–81758, 2019. doi: 10.1109/ACCESS.2019.2923905. [Google Scholar] [CrossRef]
69. Z. Li, R. S. Xu, X. Cao, X. R. Luo, and H. X. Sun, “Short-term prediction of photovoltaic power based on wavelet transform and IAGA-BP neural network,” Renew. Energ., vol. 41, no. 7, pp. 883–890, 2023. doi: 10.13941/j.cnki.21-1469/tk.2023.07.003. [Google Scholar] [CrossRef]
70. I. Jebli, F. -Z. Belouadha, M. I. Kabbaj, and A. Tilioua, “Prediction of solar energy guided by pearson correlation using machine learning,” Energy, vol. 224, 2021, Art. no. 120109. doi: 10.1016/j.energy.2021.120109. [Google Scholar] [CrossRef]
71. S. T. Asiedu, F. K. A. Nyarko, S. Boahen, F. B. Effah, and B. A. Asaaga, “Machine learning forecasting of solar PV production using single and hybrid models over different time horizons,” Heliyon, vol. 10, no. 7, 2024, Art. no. e28898. doi: 10.1016/j.heliyon.2024.e28898. [Google Scholar] [PubMed] [CrossRef]
72. F. Wang et al., “Generative adversarial networks and convolutional neural networks based weather classification model for day ahead short-term photovoltaic power forecasting,” Energy Convers. Manag., vol. 181, pp. 443–462, 2019. doi: 10.1016/j.enconman.2018.11.074. [Google Scholar] [CrossRef]
73. L. Y. Jia, S. N. Yun, Z. N. Zhao, H. L. L, S. Y. Wan and L. Yang, “Progress in applied research on neural network short-term photovoltaic power forecasting,” (in ChineseJ. Solar Energ., vol. 43, no. 12, pp. 88–97, 2022. doi: 10.19912/j.0254-0096.tynxb.2021-0501. [Google Scholar] [CrossRef]
74. J. Yue et al., “Runoff simulation in data-scarce alpine regions: Comparative analysis based on LSTM and physically based models,” Water, vol. 16, no. 15, 2024, Art. no. 2161. doi: 10.3390/w16152161. [Google Scholar] [CrossRef]
75. H. Sharadga, S. Hajimirza, and R. S. Balog, “Time series forecasting of solar power generation for large-scale photovoltaic plants,” Renew. Energy, vol. 150, pp. 797–807, 2019. [Google Scholar]
76. G. Wang, Y. Su, and L. Shu, “One-day-ahead daily power forecasting of photovoltaic systems based on partial functional linear regression models,” Renew. Energy, vol. 96, pp. 469–478, 2016. doi: 10.1016/j.renene.2016.04.089. [Google Scholar] [CrossRef]
77. H. Zhou, Y. Zhang, L. Yang, Q. Liu, and Y. Du, “Short-term photovoltaic power forecasting based on long short term memory neural network and attention mechanism,” IEEE Access, vol. 7, no. 99, pp. 78063–78074, 2019. doi: 10.1109/ACCESS.2019.2923006. [Google Scholar] [CrossRef]
78. M. Perera, J. De Hoog, K. Bandara, D. Senanayake, and S. Halgamuge, “Day-ahead regional solar power forecasting with hierarchical temporal convolutional neural networks using historical power generation and weather data,” Appl. Energy, vol. 361, 2024, Art. no. 122971. doi: 10.1016/j.apenergy.2024.122971. [Google Scholar] [CrossRef]
79. D. F. Wang, J. Liu, Y. Huang, B. T. Shi, and M. Y. Jin, “Research on PV power prediction method combining solar radiation calculation and CNN-LSTM combination,” J. Solar Energ., vol. 45, no. 2, pp. 443–450, 2024. doi: 10.19912/j.0254-0096.tynxb.2022-1542. [Google Scholar] [CrossRef]
80. S. Y. Wang, W. X. sheng, K. Y. Liu, and D. L. Jia, “Improved CNN-LSTM regional photovoltaic power single-value and probabilistic prediction method based on weather classification,” (in ChineseNew Power Syst., vol. 1, no. 3, pp. 283–292, 2023. doi: 10.20121/j.2097-2784.ntps.230042. [Google Scholar] [CrossRef]
81. H. Y. Li and B. P. Gao, “Short-term PV power prediction based on improved VMD and SNS-Attention-GRU,” (in ChineseJ. Solar Energ., vol. 44, no. 8, pp. 292–300, 2023. doi: 10.19912/j.0254-0096.tynxb.2022-0581. [Google Scholar] [CrossRef]
82. Y. Li, Z. Zhu, D. Kong, H. Han, and Y. Zhao, “EA-LSTM: Evolutionary attention-based LSTM for time series prediction,” Knowl. Based Syst., vol. 181, 2019, Art. no. 104785. doi: 10.1016/j.knosys.2019.05.028. [Google Scholar] [CrossRef]
83. J. Qu, Z. Qian, and Y. Pei, “Day-ahead hourly photovoltaic power forecasting using attention-based CNN-LSTM neural network embedded with multiple relevant and target variables prediction pattern,” Energy, vol. 232, 2021, Art. no. 120996. doi: 10.1016/j.energy.2021.120996. [Google Scholar] [CrossRef]
84. J. G. Cui, F. Wang, Z. F. Ye, Z. J. Zhu, and G. W. Yan, “PV power interval prediction based on QD and causal attention TCNs,” J. Solar Energ., vol. 45, no. 3, pp. 488–495, 2024. doi: 10.19912/j.0254-0096.tynxb.2022-1730. [Google Scholar] [CrossRef]
85. C. Hu, Y. Zhao, H. Jiang, M. Jiang, F. You and Q. Liu, “Prediction of ultra-short-term wind power based on CEEMDAN-LSTM-TCN,” Energy Rep., vol. 8, pp. 483–492, 2022. doi: 10.1016/j.egyr.2022.09.171. [Google Scholar] [CrossRef]
86. F. Li, W. Zuo, K. Zhou, Q. Li, Y. Huang and G. Zhang, “State-of-charge estimation of lithium-ion battery based on second order resistor-capacitance circuit-PSO-TCN model,” Energy, vol. 289, 2024, Art. no. 130025. doi: 10.1016/j.energy.2023.130025. [Google Scholar] [CrossRef]
87. N. He, Q. Yan, R. X. Li, L. Q. Liu, L. J. Zhang and C. Qian, “Short-term forecasting of air-conditioning electrical loads based on CEEMDAN and TCN-GRU-MLR models,” (in ChineseControl Eng., pp. 1–10, 2023. doi: 10.14107/j.cnki.kzgc.20230938. [Google Scholar] [CrossRef]
88. H. T. Zhang, W. J. Li, X. F. Li, C. Q. Xie, Q. H. Zhu and C. Y. Xiang, “Power prediction of photovoltaic power generation based on variational modal decomposition and temporal attention mechanism TCN network,” (in ChineseElect. Measur. Instrument., pp. 1–8, 2024. [Google Scholar]
89. C. Xing and Z. B. Zhang, “Short-term photovoltaic output probability prediction method based on improved time-convolutional network,” J. Solar Energ., vol. 44, no. 2, pp. 373–380, 2023. doi: 10.19912/j.0254-0096.tynxb.2021-1033. [Google Scholar] [CrossRef]
90. F. Zhou, Z. Huang, and C. Zhang, “Carbon price forecasting based on CEEMDAN and LSTM,” Appl. Energy, vol. 311, 2022, Art. no. 118601. doi: 10.1016/j.apenergy.2022.118601. [Google Scholar] [CrossRef]
91. X. Lu, Y. Guan, J. Liu, W. Yang, J. Sun and J. Dai, “Research on real-time prediction method of photovoltaic power time series utilizing improved grey wolf optimization and long short-term memory neural network,” Processes, vol. 12, no. 8, 2024. doi: 10.3390/pr12081578. [Google Scholar] [CrossRef]
92. J. Zhang, Y. Hao, R. Fan, and Z. Wang, “An ultra-short-term PV power forecasting method for changeable weather based on clustering and signal decomposition,” Energies, vol. 16, no. 7, 2023. doi: 10.3390/en16073092. [Google Scholar] [CrossRef]
93. Y. Fan, Z. Ma, W. Tang, J. Liang, and P. Xu, “Using crested porcupine optimizer algorithm and CNN-LSTM-attention model combined with deep learning methods to enhance short-term power forecasting in PV generation,” Energies, vol. 17, no. 14, 2024, Art. no. 3435. doi: 10.3390/en17143435. [Google Scholar] [CrossRef]
94. R. Wang, L. Zhang, and J. Lu, “Short term photovoltaic power prediction based on new similar day selection and VMD-NGO-BiGRU,” (in ChineseJ. Hunan Univ. Natural Sci., vol. 51, no. 2, pp. 68–80, 2024. [Google Scholar]
95. F. Sun, L. Li, D. Bian, H. Ji, N. Li and S. Wang, “Short-term PV power data prediction based on improved FCM with WTEEMD and adaptive weather weights,” J. Build. Eng., vol. 90, 2024, Art. no. 109408. doi: 10.1016/j.jobe.2024.109408. [Google Scholar] [CrossRef]
96. W. Liu, Q. Liu, and Y. Li, “Ultra-short-term photovoltaic power prediction based on modal reconstruction and BiLSTM-CNN-Attention model,” Earth Sci. Inform., vol. 17, no. 3, pp. 2711–2725, 2024. doi: 10.1007/s12145-024-01308-4. [Google Scholar] [CrossRef]
97. R. Herrera Casanova and A. Conde, “Enhancement of LSTM models based on data pre-processing and optimization of Bayesian hyperparameters for day-ahead photovoltaic generation prediction,” Comput. Elect. Eng., vol. 116, 2024, Art. no. 109162. doi: 10.1016/j.compeleceng.2024.109162. [Google Scholar] [CrossRef]
98. Y. Wang, Y. Yao, Q. Zou, K. Zhao, and Y. Hao, “Forecasting a short-term photovoltaic power model based on improved snake optimization, convolutional neural network, and bidirectional long short-term memory network,” Sensors, vol. 24, no. 12, 2024, Art. no. 3897. doi: 10.3390/s24123897. [Google Scholar] [PubMed] [CrossRef]
99. Z. Wang, Y. Wang, S. Cao, S. Fan, Y. Zhang and Y. Liu, “A robust spatial-temporal prediction model for photovoltaic power generation based on deep learning,” Comput. Elect. Eng., vol. 110, 2023, Art. no. 108784. doi: 10.1016/j.compeleceng.2023.108784. [Google Scholar] [CrossRef]
100. H. Wang et al., “Deterministic and probabilistic forecasting of photovoltaic power based on deep convolutional neural network,” Energy Convers. Manag., vol. 153, pp. 409–422, 2017. doi: 10.1016/j.enconman.2017.10.008. [Google Scholar] [CrossRef]
101. Z. Xiong, J. Yao, Y. Huang, Z. Yu, and Y. Liu, “A wind speed forecasting method based on EMD-MGM with switching QR loss function and novel subsequence superposition,” Appl. Energy, vol. 353, 2024, Art. no. 122248. doi: 10.1016/j.apenergy.2023.122248. [Google Scholar] [CrossRef]
102. F. Li et al., “Improving the accuracy of multi-step prediction of building energy consumption based on EEMD-PSO-Informer and long-time series,” Comput. Elect. Eng., vol. 110, 2023, Art. no. 108845. doi: 10.1016/j.compeleceng.2023.108845. [Google Scholar] [CrossRef]
103. Y. Ding, Z. Chen, H. Zhang, X. Wang, and Y. Guo, “A short-term wind power prediction model based on CEEMD and WOA-KELM,” Renew. Energy, vol. 189, pp. 188–198, 2022. doi: 10.1016/j.renene.2022.02.108. [Google Scholar] [CrossRef]
104. Y. Lin, Z. Lin, Y. Liao, Y. Li, J. Xu and Y. Yan, “Forecasting the realized volatility of stock price index: A hybrid model integrating CEEMDAN and LSTM,” Expert. Syst. Appl., vol. 206, 2022. Art. no. 117736. doi: 10.1016/j.eswa.2022.117736. [Google Scholar] [CrossRef]
105. Y. Wen, S. Pan, X. Li, and Z. Li, “Highly fluctuating short-term load forecasting based on improved secondary decomposition and optimized VMD,” Sustain. Energy, Grids and Netw., vol. 37, 2024, Art. no. 101270. doi: 10.1016/j.segan.2023.101270. [Google Scholar] [CrossRef]
106. A. Kumar, Y. Zhou, and J. Xiang, “Optimization of VMD using kernel-based mutual information for the extraction of weak features to detect bearing defects,” Measurement, vol. 168, 2021, Art. no. 108402. doi: 10.1016/j.measurement.2020.108402. [Google Scholar] [CrossRef]
107. Y. Zhao, K. H. Adjallah, A. Sava, and Z. Wang, “Influence of sampling frequency ratio on mode mixing alleviation performance: A comparative study of four noise-assisted empirical mode decomposition algorithms,” Machines, vol. 9, no. 12, 2021, Art. no. 315. doi: 10.3390/machines9120315. [Google Scholar] [CrossRef]
108. L. N. Boucetta, Y. Amrane, A. Chouder, S. Arezki, and S. Kichou, “Enhanced forecasting accuracy of a grid-connected photovoltaic power plant: A novel approach using hybrid variational mode decomposition and a CNN-LSTM model,” Energies, vol. 17, no. 7, 2024, Art. no. 1781. doi: 10.3390/en17071781. [Google Scholar] [CrossRef]
109. P. Jia, H. Zhang, X. Liu, and X. Gong, “Short-term photovoltaic power forecasting based on VMD and ISSA-GRU,” IEEE Access, vol. 9, pp. 105939–105950, 2021. doi: 10.1109/ACCESS.2021.3099169. [Google Scholar] [CrossRef]
110. K. Tao, J. Zhao, N. Wang, Y. Tao, and Y. Tian, “Short-term photovoltaic power forecasting using parameter-optimized variational mode decomposition and attention-based neural network,” Energ. Sources, Part A: Rec., Utiliz. Environ. Effects, vol. 46, no. 1, pp. 3807–3824, 2024. doi: 10.1080/15567036.2024.2323158. [Google Scholar] [CrossRef]
111. S. Z. Liu and C. Ma, “Short-term photovoltaic power prediction based on wavelet transform and hybrid deep learning,” (in ChineseRenew. Energy, vol. 41, no. 6, pp. 744–749, 2023. [Google Scholar]
112. A. Agga, A. Abbou, M. Labbadi, and Y. El Houm, “Short-term self consumption PV plant power production forecasts based on hybrid CNN-LSTM, ConvLSTM models,” Renew. Energy, vol. 177, pp. 101–112, 2021. doi: 10.1016/j.renene.2021.05.095. [Google Scholar] [CrossRef]
113. C. D. Iweh and E. R. Akupan, “Control and optimization of a hybrid solar PV–Hydro power system for off-grid applications using particle swarm optimization (PSO) and differential evolution (DE),” Energy Rep., vol. 10, pp. 4253–4270, 2023. doi: 10.1016/j.egyr.2023.10.080. [Google Scholar] [CrossRef]
114. T. H. T. Nguyen and Q. B. Phan, “Hourly day ahead wind speed forecasting based on a hybrid model of EEMD, CNN-Bi-LSTM embedded with GA optimization,” Energy Rep., vol. 8, pp. 53–60, 2022. doi: 10.1016/j.egyr.2022.05.110. [Google Scholar] [CrossRef]
115. D. He et al., “Application of PSO-RBF neural network to predict the thermal and electrical performance of solar PV/T systems,” (in ChineseRenew. Energy, no. 4, pp. 455–463, 2024. doi: 10.13941/j.cnki.21-1469/tk.2024.04.005. [Google Scholar] [CrossRef]
116. Y. Zhuo, H. Ni, and P. F. Xiao, “Single-parameter time series prediction method for thermal systems based on GWO-VMD-LSTM,” (in ChineseThermal Eng., vol. 39, no. 6, pp. 80–88, 2024. doi: 10.16146/j.cnki.rndlgc.2024.06.010. [Google Scholar] [CrossRef]
117. J. Li, Z. Song, X. Wang, Y. Wang, and Y. Jia, “A novel offshore wind farm typhoon wind speed prediction model based on PSO-Bi-LSTM improved by VMD,” Energy, vol. 251, 2022, Art. no. 123848. doi: 10.1016/j.energy.2022.123848. [Google Scholar] [CrossRef]
118. C. Zhang, L. Hua, C. Ji, M. Shahzad Nazir, and T. Peng, “An evolutionary robust solar radiation prediction model based on WT-CEEMDAN and IASO-optimized outlier robust extreme learning machine,” Appl. Energy, vol. 322, 2022, Art. no. 119518. doi: 10.1016/j.apenergy.2022.119518. [Google Scholar] [CrossRef]
119. W. L. Fu, X. R. Zhang, H. R. Zhang, Y. C. Fu, and X. T. Liu, “Ultra-short-term wind speed prediction study based on INGO-SWGMN hybrid model,” (in ChineseJ. Solar Energ., vol. 45, no. 5, pp. 133–143, 2024. doi: 10.19912/j.0254-0096.tynxb.2022-1975. [Google Scholar] [CrossRef]
120. T. R. Ayodele, A. S. O. Ogunjuyigbe, A. Amedu, and J. L. Munda, “Prediction of global solar irradiation using hybridized k-means and support vector regression algorithms,” Renew. Energy Focus, vol. 29, pp. 78–93, 2019. doi: 10.1016/j.ref.2019.03.003. [Google Scholar] [CrossRef]
121. S. Singh et al., “Optimum power forecasting technique for hybrid renewable energy systems using deep learning,” Elect. Power Compon. Syst., pp. 1–18. doi: 10.1080/15325008.2024.2316251. [Google Scholar] [CrossRef]
122. X. Y. Wang and Y. P. Bai, “The global Minmax k-means algorithm,” SpringerPlus, vol. 5, 2016, Art. no. 1665, 2024. doi: 10.1186/s40064-016-3329-4. [Google Scholar] [PubMed] [CrossRef]
123. S. Z. Guan, Y. B. Tang, Z. Cai, L. T. Wu, H. B. Zheng, and T. F. Qin, “Ultra-short-term prediction of solar irradiance based on Kmeans++-Bi-LSTM,” J. Solar Energy, vol. 44, no. 12, pp. 170–174, 2023. doi: 10.19912/j.0254-0096.tynxb.2022-1294. [Google Scholar] [CrossRef]
124. Q. Zhao, S. Shao, L. Lu, X. Liu, and H. Zhu, “A new PV array fault diagnosis method using fuzzy c-mean clustering and fuzzy membership algorithm,” Energies, vol. 11, no. 1, 2018, Art. no. 238. doi: 10.3390/en11010238. [Google Scholar] [CrossRef]
125. R. Krishnapuram and J. M. Keller, “A possibilistic approach to clustering,” IEEE Trans. Fuzzy Syst., vol. 1, no. 2, pp. 98–110, 1993. doi: 10.1109/91.227387. [Google Scholar] [CrossRef]
126. A. E. Ezugwu et al., “A comprehensive survey of clustering algorithms: State-of-the-art machine learning applications, taxonomy, challenges, and future research prospects,” Eng. Appl. Artif. Intell., vol. 110, 2022, Art. no. 104743. doi: 10.1016/j.engappai.2022.104743. [Google Scholar] [CrossRef]
127. N. Li, L. Li, F. Huang, X. Liu, and S. Wang, “Photovoltaic power prediction method for zero energy consumption buildings based on multi-feature fuzzy clustering and MAOA-ESN,” J. Build. Eng., vol. 75, 2023, Art. no. 106922. doi: 10.1016/j.jobe.2023.106922. [Google Scholar] [CrossRef]
128. Y. Dai, W. Yu, and M. Leng, “A hybrid ensemble optimized BiGRU method for short-term photovoltaic generation forecasting,” Energy, vol. 299, 2024, Art. no. 131458. doi: 10.1016/j.energy.2024.131458. [Google Scholar] [CrossRef]
129. H. Zang, L. Cheng, T. Ding, K. W. Cheung, Z. Wei and G. Sun, “Day-ahead photovoltaic power forecasting approach based on deep convolutional neural networks and meta learning,” Int. J. Elect. Pow. Energy Syst., vol. 118, 2020, Art. no. 105790. doi: 10.1016/j.ijepes.2019.105790. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF


 Downloads
Downloads
 Citation Tools
Citation Tools