 Open Access
Open Access
REVIEW
A Critical Review of Active Distribution Network Reconfiguration: Concepts, Development, and Perspectives
1 Faculty of Electric Power Engineering, Kunming University of Science and Technology, Kunming, 650500, China
2China Southern Power Grid Honghe Power Supply Bureau, Mengzi, 661100, China
3 Faculty of Science, Kunming University of Science and Technology, Kunming, 650500, China
4China Southern Power Grid Yuxi Power Supply Bureau, Yuxi, 653100, China
5 Yunnan Electric Power Grid Co., Ltd., Kunming, 650000, China
6 College of Electrical Engineering, Shanghai University of Electric Power, Shanghai, 200090, China
7 College of Information Science and Engineering, Northeastern University, Shenyang, 110819, China
8 Foshan Graduate School of Innovation, Northeastern University, Foshan, 528311, China
* Corresponding Author: Zhengxun Guo. Email:
Energy Engineering 2024, 121(12), 3487-3547. https://doi.org/10.32604/ee.2024.054662
Received 04 June 2024; Accepted 02 September 2024; Issue published 22 November 2024
Abstract
In recent years, the large-scale grid connection of various distributed power sources has made the planning and operation of distribution grids increasingly complex. Consequently, a large number of active distribution network reconfiguration techniques have emerged to reduce system losses, improve system safety, and enhance power quality via switching switches to change the system topology while ensuring the radial structure of the network. While scholars have previously reviewed these methods, they all have obvious shortcomings, such as a lack of systematic integration of methods, vague classification, lack of constructive suggestions for future study, etc. Therefore, this paper attempts to provide a comprehensive and profound review of 52 methods and applications of active distribution network reconfiguration through systematic method classification and enumeration. Specifically, these methods are classified into five categories, i.e., traditional methods, mathematical methods, meta-heuristic algorithms, machine learning methods, and hybrid methods. A thorough comparison of the various methods is also scored in terms of their practicality, complexity, number of switching actions, performance improvement, advantages, and disadvantages. Finally, four summaries and four future research prospects are presented. In summary, this paper aims to provide an up-to-date and well-rounded manual for subsequent researchers and scholars engaged in related fields.Keywords
Nomenclature
| ABC | Artificial bee colony |
| ACO | Ant colony optimization |
| ADN | Active distribution network |
| BA | Bat algorithm |
| BEM | Branch exchange method |
| CSA | Cuckoo search algorithm |
| DABC | Discrete artificial bee colony |
| DN | Distributed network |
| DG | Distributed generation |
| DL | Deep learning |
| DMA | Discrete monkey algorithm |
| ESS | Energy storage system |
| EOA | Equilibrium optimizer algorithm |
| FA | Firework algorithm |
| HAS | Harmony search algorithm |
| ICSA | Improve cuckoo search algorithm |
| IWO | Invasive weed optimization |
| IAICA | Improved adaptive imperialist competitive algorithm |
| ISFLA | Improved shuffled frog leaping algorithm |
| GA | Genetic algorithm |
| LCM | Loop cutting method |
| LRA | Lagrange relaxation approach |
| MABC | Multi-object artificial bee colony |
| MPGSA | Modified plant growth simulation algorithm |
| MWOA | Modified whale optimization algorithm |
| N.P. | No proposed |
| OPF | Optimal flow pattern |
| PDN | Passive distribution network |
| RL | Reinforcement learning |
| SMA | Slime mold algorithm |
| TSA | Tabu search algorithm |
| Active power loss of the network, kW | |
| l | Number of the branch |
| Total number of branches | |
| Branch impedance, Ω | |
| Opened and closed state of the branch | |
| Average annual outage time of load node i, s | |
| Number of users at load node i | |
| Average load at load node i, kW | |
| Actual values of distribution network node voltages, kV | |
| Conductance between nodes i and j, S | |
| Phase angle difference between nodes i and j, ° | |
| Flexible load, kW | |
| Current velocity of the ith particle | |
| Active power flowing through the branch l, kW | |
| Reactive power flowing through the branch l, kVar | |
| Voltage at the end node of the branch l, kV | |
| Capacity of branch l, kW | |
| Total number of nodes | |
| Average voltage of all nodes, kV | |
| K | Total number of line switches in the network |
| Rated values of distribution network node voltages, kV | |
| Current position of the ith particle in search space | |
| W | Inertia weight |
| r1, r2 | Two random numbers |
| Average failure rate of load node i | |
| C1 C2 | Acceleration coefficients |
| Ld Ud | Upper and lower limits of the search space |
As the last link in the power supply system [1], the distribution network directly distributes electric energy to end-users to ensure a reliable power supply [2]. For the safety of the grid, the structure of distribution networks often is shifted from a mesh topology to a radial one [3]. Note that the planning of closed-loop distribution grids and the characteristics of open-loop operation provide the groundwork for such changes [4]. Furthermore, the maturation of power electronics [5], artificial intelligence [6], communication engineering [7], and other technologies, coupled with the widespread implementation of distributed power sources [8], energy storage [9], and demand-side response [10] accelerate the development of active distribution networks (ADN) but introduce increasing complexity to the network structure [11].
Active distribution network reconfiguration (ADNR), as a crucial technology for smart grid development [12], offers several benefits such as reducing network losses [13], eliminating overloads [14], improving power quality [15], and increasing the capacity for distributed generation (DG) grid connection [16]. It can be viewed as a multi-objective and multi-constraint problem. Currently, various methods for ADNR have been proposed. Merlin and Back first formulated the distributed system reconfiguration (DSR) method as a mixed-integer nonlinear optimization problem to minimize energy loss [17]. Based on the typical daily load and output prediction of DG, Reference [18] utilized an improved optimal fuzzy C-mean clustering method to address the dynamic reconfiguration problem for minimizing feeder losses. To enhance the security and cost-effectiveness of distribution network operations, another study [19] employed the limit scenario method to robustly optimize ADN and system reactive voltage, which resolved the volatility issues associated with integrating distributed energy sources. Meanwhile, more studies focus on ADNR models. Literature [20] proposed a robust model considering generation and load uncertainty, thus effectively incorporating uncertain load demand, and fluctuating generation of DG into the reconstruction framework, and enhancing the accuracy of the reconstruction model. The study [21] provided the radial constraints applicable to different reconstruction methods from the perspective of reconstruction model solution accuracy and solution speed.
In the past few decades, a large number of ADNR methods have been proposed. To provide a comprehensive overview of the existing research methods for ADNR, this paper undertook an overall statistic on relevant literatures published from 2013 to September 2023. Furthermore, Fig. 1 depicts the statistics results, which reveal an increasing research interest in ADNR, thus indicating its emergence as a prominent and popular research topic.
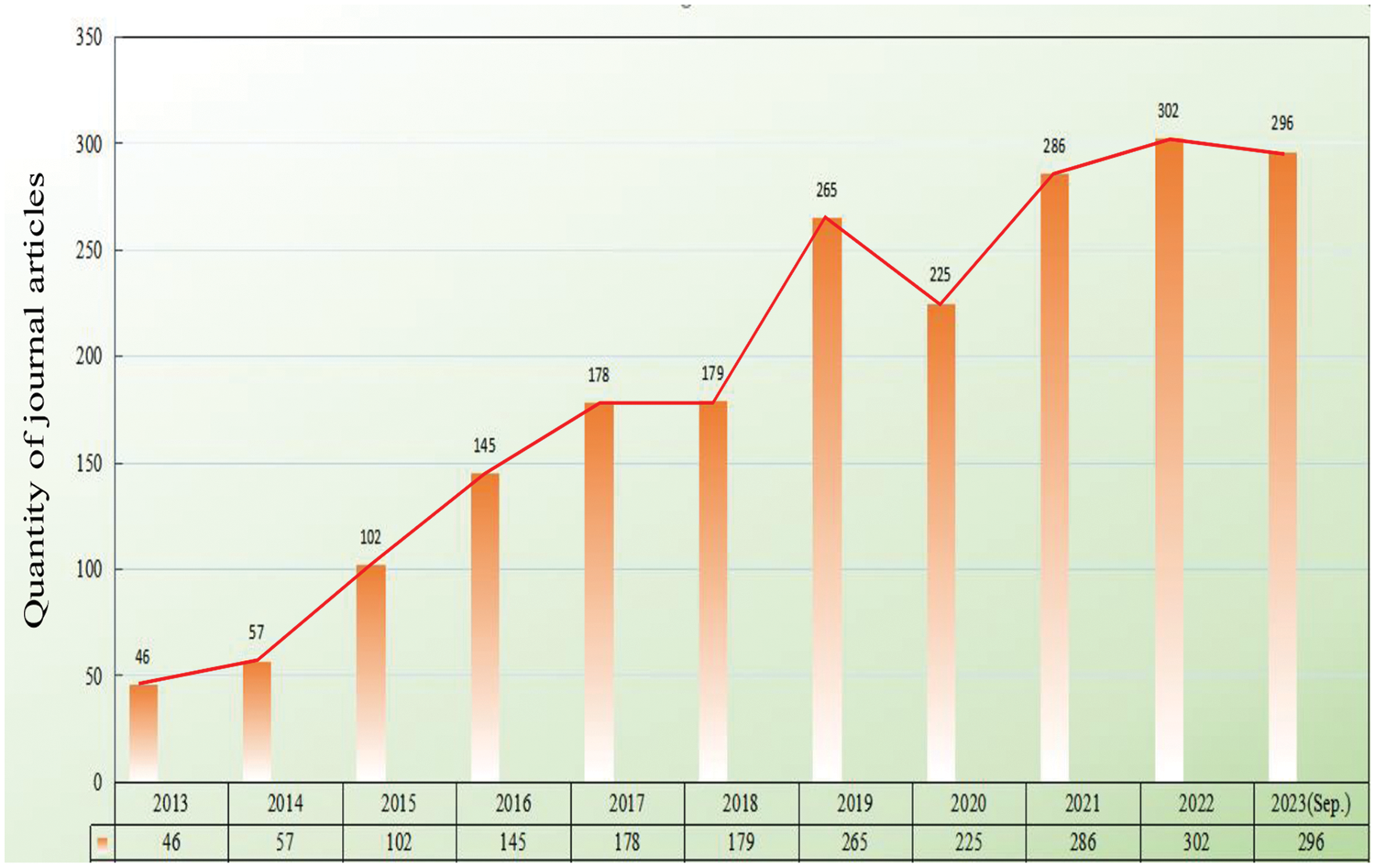
Figure 1: Statistic results of ADNR methods from 2013 to September 2023
Thus far, several reviews on ADNR have been published. However, they did not provide a comprehensive and systematic summary of modeling technology, constraint condition, test system, and evaluation criteria, especially the key indicators, discussion of the targeted application, and research recommendations for ADNR. Therefore, this paper aims to provide a fully comprehensive and integrated review of the various methods used in ADNR. Specifically, the paper seeks to systematically analyze and compare different methods and develop a detailed evaluation of each method to give a comprehensive reference guide for future in-depth research in related fields. Specifically, Table 1 demonstrates the highlights and limitations of existing reviews.
For the sake of overcoming these gaps addressed in Table 1, this paper aims to provide a fully comprehensive and integrated review of the various methods used in ADNR. Specifically, each method will be systematically compared, analyzed, and evaluated to formulate a reliable reference guide for future in-depth research in related fields. Fig. 2 illustrates the tackled problems and main goals.
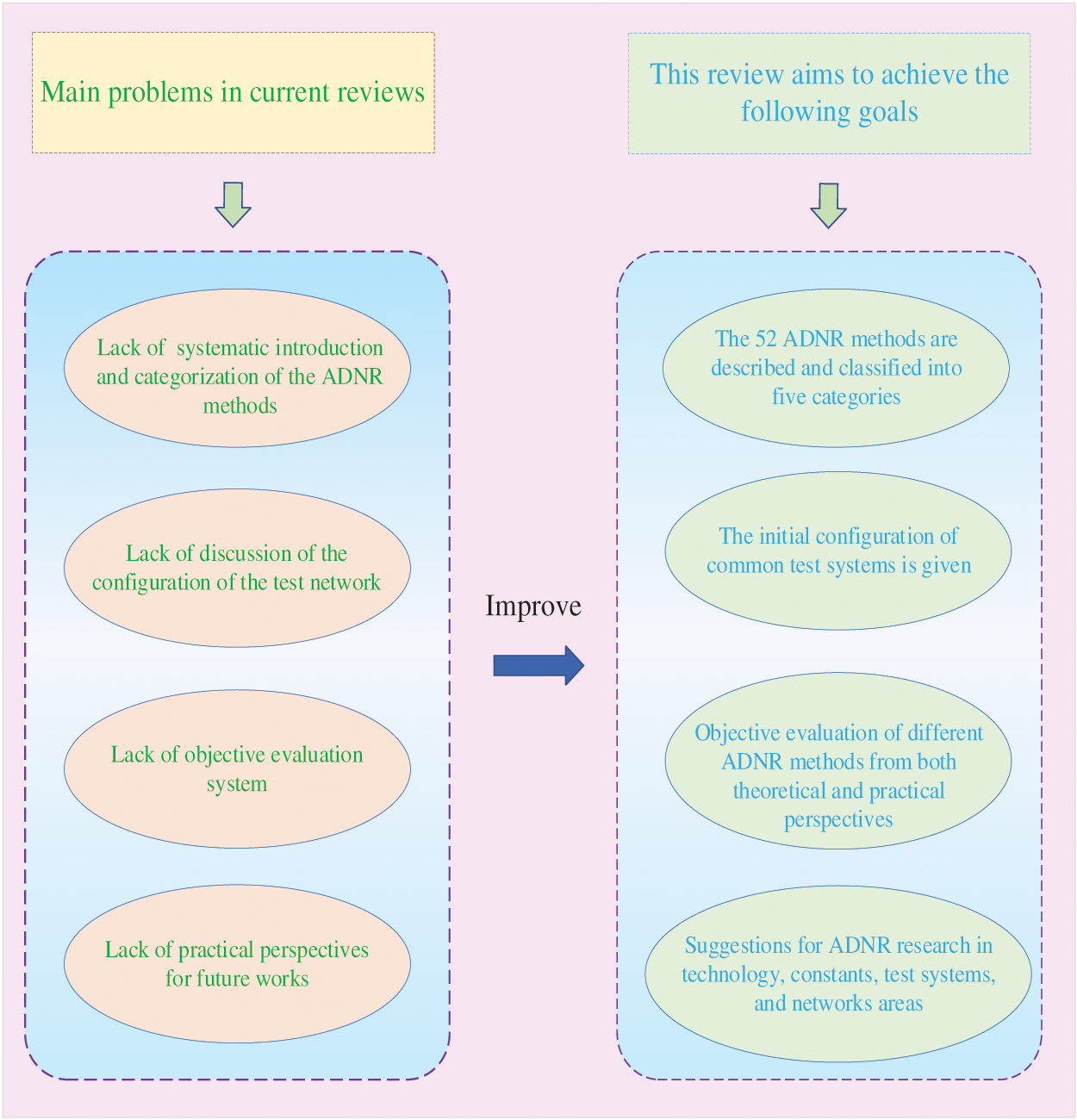
Figure 2: Tackled problems and main goals of this paper
Therefore, this paper aims to provide a fully comprehensive and integrated review of the various methods used in ADNR. Specifically, the paper seeks to systematically analyze and compare different methods and develop a detailed evaluation of each method to provide a comprehensive reference guide for future in-depth research in related fields. The main contributions of this paper are as follows:
• A comprehensive review of existing algorithms for ADNR is given, which are classified into five categories, i.e., traditional, mathematical, meta-heuristic, machine learning based method, and hybrid algorithm. Besides, the specific optimization structures and strengths and weaknesses of each algorithm are detailly introduced and analyzed.
• A set of systematic scoring guidelines based on theoretical and practical aspects are developed to analyze and evaluate various methods profoundly and objectively. Which theoretical index incorporates optimization objective algorithm structure, and hyperparameter while the practical one includes economic cost, power and voltage loss, and practical application.
• Insightful suggestions/recommendations are proposed for further improvements of ADNR from four different aspects, i.e., technology, constant, testing system, and network.
The remainder of this paper is organized as follows: Section 2 provides the technical background of ADNR, summarizes the mathematical modeling of the ADNR process, provides detailed objective/constraint formulations, and summaries the initial state of the network configuration. Section 3 reviews 52 methods for ADNR, classified into five categories, and analyzes and compares the theoretical properties of each method, such as complexity, practicality, number of switching actions, and reconfiguration effectiveness. Section 4 provides a discussion of this literature. Finally, Section 5 offers a thorough analysis, summary, suggestions, and outlooks for future research in this area.
2 Active Distribution Network Reconfiguration
The ADN is designed as a closed-loop system with an open-loop operation, and it has a radial structure [28]. During normal operating conditions, the sectional switch is closed and the contact switch is disconnected, which allows the network to operate in a radial configuration [29]. In this state, network reconfiguration can be implemented to achieve load balancing, eliminate overloads, reduce network loss, improve voltage quality, and enhance the overall economic performance of the system.
2.1.1 Passive Distribution Network
Due to the safe power supply development concept, the operation, control, and management modes of traditional distribution networks are passive, also referred to as passive distribution networks (PDNs) [30], as depicted in Fig. 3. Electric energy is primarily generated by large power plants, transmitted through the transmission grid, and ultimately distributed to consumers via the distribution network [31]. In PDNs, electric energy flows from the grid to the load, which leads to the consideration of one-way energy flow characteristics in various aspects such as line selection [32], equipment selection, relay protection, power flow control, and metering [33]. The natural distribution of load demand in PDNs cannot be automatically adjusted, and abnormal operating states and faults cannot be controlled in advance [34], making it difficult to ensure the quality of power supply in all directions and achieve optimal economic operation of the entire distribution system [35].
Figure 3: Passive distribution network architecture
The connection of DG to the distribution network will have a significant impact on power flow direction and magnitude [36], short-circuit current direction and magnitude [37], equipment capacity and selection [38], voltage and reactive power distribution [39], power factor and harmonics, protection coordination, and settings, automation settings and management, fault restoration, and other factors [40]. Therefore, to achieve the intelligent transformation of traditional distribution networks [41], it is crucial to establish an ADN with active control and management functions [42,43].
2.1.2 Active Distribution Network
ADN can actively control various DGs [44] via advanced technologies such as information [45], communication, and power electronics to manage power flow based on flexible network topology [46], as shown in Fig. 4. Its control purpose is to increase the capacity of acceptable renewable energy, enhance the utilization rate of distribution network assets, delay the investment in upgrading [47], and improve the quality and reliability of power supply for users [48].

Figure 4: Distribution network architecture
Compared to the ADN, which actively controls and manages distributed energy devices in different areas through a flexible network topology [49], the traditional distribution network is based on the one-way power distribution network between grid power supply and user power consumption [50,51]. The traditional distribution network does not participate in system frequency regulation, voltage, and reactive power control, and does not provide ancillary services to the system [52].
The ADN is characterized by high penetration of distributed power sources [53] and flexible network topology [54]. These characteristics can have an impact on the magnitude of supply voltage, network loss [55], voltage distribution, and frequency range of unit operation in the power system [56]. As a result, the ADN requires cooperation with demand-side response, to enable the integration of distributed power, such as DG [57], ESS, and other distributed resources [58].
Demand-side response (DSR) is a strategy used to manage the balance between the supply and demand of the power system. When there is an imbalance between supply and demand [59], DSR involves customers taking an active role in adjusting their regular power consumption patterns in response to price incentives from the power company. This may involve reducing or shifting their load during a certain period to improve the operational efficiency of the power system [60]. DSR aims to improve the reliability and stability of the power system by matching supply and demand in real-time [61].
Demand-side response measures can be classified into two types: price-based demand-side response and incentive-based demand-side response [62]. Price-based demand-side response refers to customers arranging and adjusting their electricity consumption time [63] and mode based on targeted tariffs set by power supply companies [64,65]. Incentive-based demand-side [66] response means that power supply companies use economic incentives [67] or compensation mechanisms to motivate customers to adjust or cut their loads during peak hours based on load availability [68].
The price-based demand-side response includes three types of tariffs:
• Time-sharing tariff: This tariff divides electricity into three prices (peak, flat, and valley) based on the user’s electricity consumption time.
• Real-time tariffs: This tariff fluctuates in real-time according to the cost of electricity purchased in the market and can effectively reflect the supply and demand of electricity.
• Peak tariff: This tariff sets a high price during emergencies to encourage users to use electricity at off-peak times or reduce consumption.
Moreover, the incentive-based demand-side response includes several measures:
• Direct load control: The power supply company adjusts or shuts down the customer’s electricity consumption equipment remotely during peak or emergency times and compensates the customer.
• Interruptible load: After the customer signs a contract with the power supply company, the company informs the customer in advance of the outage time, capacity, and compensation method. If the customer defaults on the contract, they will be punished.
• Demand-side bidding: The customer participates in market bidding and, after a consensus is reached between supply and demand, cuts the load value.
Consequently, demand-side response can promote the transformation of traditional distribution networks while ensuring the safe and efficient operation of ADNs. It can also enable distributed power supply, achieve large-scale access to distributed power supply, and optimally allocate resources on both the supply and demand sides [69].
2.3 Distribution Network Switch
As a large number of distributed power sources and ESSs are put into operation, the distribution network experiences spatial and temporal differences in load [70], uneven distribution of tidal currents, and large network losses [71]. In such cases, the topology of the distribution network must be changed by altering the opening and closing states of switches [72]. Faulty branches can be isolated by closing some normally open switches [73], while faulty loads can be transferred to other feeders by breaking some normally closed switches [74]. Reconfiguration of the ADN is achieved by changing the topology of the network by switching the state of switches in the distribution network [75]. This balances the load [76], eliminates overload [77], balances current, and reduces network loss [78].
(1) Reduction of power loss
Network loss reduction [79,80] is the most common objective of distribution network reconfiguration [81,82], and its objective function expression is as follows:
where the control vector
(2) Balanced load
The more balanced the load is, the higher the stability margin of the distribution network is [83]. The index describing the degree of load balance is not unique [84], and the load balance coefficient [85] is usually used as the measurement standard:
where
The formula that describes the balanced load by maximizing the minimum margin over all lines is as follows:
(3) Power distribution reliability
System reliability indicators [86] considered in distribution network reconfiguration mainly include the average number of system outages [87], system average outage duration, and customer average outage demand [88], etc.:
where R is the set of load nodes;
(4) Voltage quality improvement
Usually, the range of node voltage fluctuation is one of the constraints of distribution network reconfiguration [89], and some studies also take it as the optimized objective of reconfiguration [90], expressed by:
where
Similarly, the formula for measuring the range of node voltage fluctuation is not unique. The formula for calculating the range of node voltage fluctuation concerning the margins is as follows:
where
(5) Switch operation times
Frequent changes in the opening and closing state of the switch will reduce the service life of the switch. To extend the service life of the switch, the number of switch operations should be reduced as much as possible [91].
where K indicates the total number of line switches in the network;
(6) Voltage offset index
Node voltage offset size is an important indicator to measure whether the voltage quality is qualified [92], and the minimum node voltage offset can ensure the safe and stable operation of the system [93].
where M is the number of distribution network nodes;
2.5 Reconfiguration Constraints
(1) Node voltage constraints
where
(2) Bus voltage constraints
(3) Considering the constraint of the power flow equation of distributed power supply
where
(4) Thermal capacity of distribution lines constraints
where
(5) Active power outputs of DG units
where
(6) Power factors of DG units
where
2.5.2 Discreteness Constraints
(1) Network topology constraints
The topology of the distribution network in the reconfiguration process is radial and must not create loops or islands.
where
(2) Current safety constraints
where
2.6 The Initial State of the Network Configuration
Most of the tests related to ADNR are based on the standard IEEE 33 bus and IEEE 69 bus systems, with flexible configurations for various hybrid energy sources such as wind, photovoltaic, fuel cells, and energy storage, depending on the research context. Additionally, a small number of studies have explored the feasibility of field testing methods. In this paper, we have selected systems with promising performance for illustration.
(1) Initial state of the standard IEEE33-bus radial distribution system:
The IEEE 33 bus radial distribution system comprises 33 buses with 32 lines and 5 interconnection switches that are normally open: 33, 34, 35, 36, and 37. The initial data for the 33-bus radial distribution system is provided in Table A1. In Reference [94], the initial total active power was set at 3715 kW, the total reactive power at 2300 kvar, and the total active losses were 202.676 kW. In comparison, in Reference [95], considering the presence of a comprehensive energy system, with the total active/reactive power of the system unchanged, the active power loss was 211 kW.
(2) Initial state of the standard IEEE69-bus radial distribution system:
The IEEE 69 bus radial distribution system consists of 69 buses with 68 lines and 5 interconnection switches that are normally open: 69, 70, 71, 72, and 73. The initial data for the 69-bus radial distribution system is provided in Table A2. In Reference [94] the system was set to have total power losses of 229.73 kW under rated load conditions. In the Reference [96], the system’s total active load was set at 3802 kW, and total reactive load at 2694 kvar, with initial active losses of 225 kW, and reactive losses of 102.16 kvar.
(3) The initial state of the actual network test system:
Reference [97] conducted experiments on an actual 47-bus distribution network to validate the effectiveness of their proposed algorithm. This network comprised 47 buses and 42 branches, and received power from a 132 kV transmission system. Notably, four key substations were connected to Buses 2, 17, 34, and 39. Additionally, there were seven tie switches facilitating alterations to the system’s configuration in response to unforeseen events or contingencies. For a comprehensive overview of the system’s bus details, please refer to Table A3.
3 Research Methods and Evaluation
3.1 Methods Evaluation Criteria
This paper presents a comprehensive evaluation of each reconfiguration method, focusing on both theoretical and practical aspects. The theoretical evaluation mainly considers the complexity of reconfiguration methods, with a particular emphasis on the complexity of meta-heuristic algorithms, which is largely dependent on the algorithm design. The evaluation indicators used for this evaluation include (a) multi-objective optimization, (b) hyper-parameters, and (c) operational mechanism. The application evaluation aims to assess the testing process and practical effectiveness of the reconfiguration methods, which is scored based on three aspects: (a) test system, (b) optimization indicators, and (c) social indicators. The complexity and applicability of reconfiguration methods increase with the accumulation of the above evaluation indicators. Thus, the overall score of each ADNR method can be calculated by:
where
The proportions of each indicator and the detailed evaluation criteria are presented in Fig. 5.
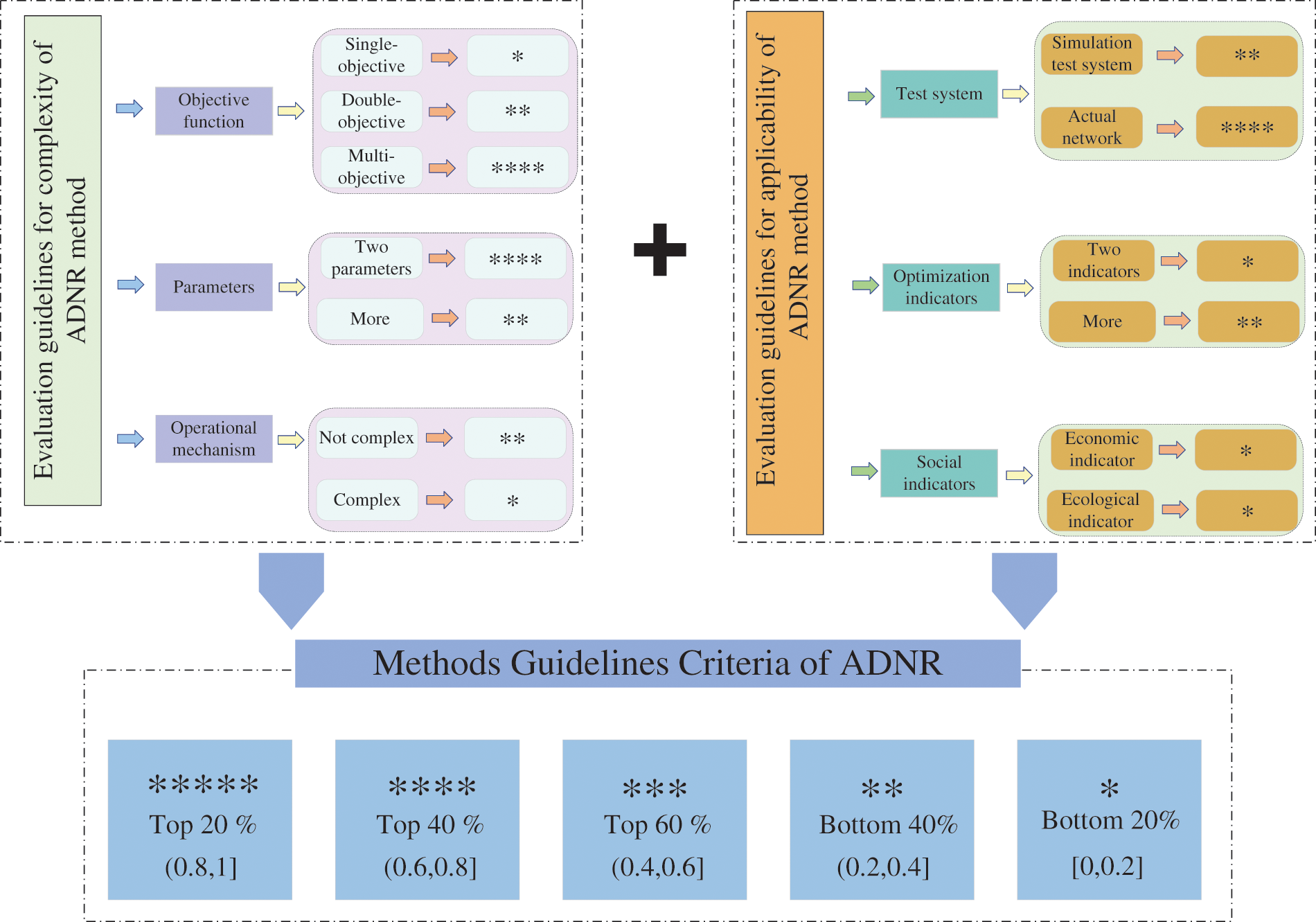
Figure 5: The methods evaluation criteria
3.2 Research Methods and Evaluation
Up to now, many researchers have conducted research on ADNR. In this chapter, we will divide the existing research methods into five categories: traditional methods, mathematical methods, meta-heuristic methods, machine learning methods, and hybrid methods. Next, a detailed introduction of each method will be offered.
The LCM was proposed by Darish Shrimohammad in 1989 [98]. It created multiple loops by closing all the connection switches in the system and then switches the distribution network system to a weak grid state and ignoring the OFP of the system branch reactance calculation network [99]. Finally, the distribution system was restored to radial structure operation by turning on the switch with the minimum current under the optimal flow mode [100].
Although the LCM has low requirements on the network structure of the distribution system, its calculation efficiency is low, and it cannot be applied to medium and large network structures. Moreover, it is prone to producing the “island” effect in network reconfiguration [101].
Compared to the LCM, the BEM started from the radial distribution network and calculated the power flow distribution and network loss of the distribution network [102]. The distribution network formed a loop network by closing the connection switch. Therefore, another switch needed to be opened to restore the network to a radial structure, to balance the load and reduce the network loss. The process would stop when the system network loss couldn’t be further reduced [103]. The BEM had the advantage of fast solution speed, but it heavily depended on the initial network structure [104].
3.2.2 Mathematical Programming Method
Mathematical programming methods have not received much attention due to their complex operation mechanism. In this paper, we review the mathematical methods that have been proposed so far, the summary of mathematical programming methods is tabulated in Table 2.
The LRA is capable of transforming difficult constraints into a part of the objective function to maintain linearity. This method yields a superior lower bound and is equivalent to transforming the (0,1) integer variable into a continuous variable ranging from 0 to 1. The Lagrange multiplier, which reflects duality information, is obtained as a result of Lagrange relaxation, as illustrated in Fig. 6. The method further decomposes the coupled variables in the constraint and simplifies them into independent sub-problems [105].
Figure 6: Schematic diagram of LRA
In the Reference [106], the minimum active power loss of the network was taken as the objective function, and the distribution network reconfiguration was formulated as a mixed integer linear programming (MILP) problem. The Lagrange relaxation method was used for dynamic distribution network reconfiguration. The operational constraints were relaxed, and the Lagrange duality problem was subsequently decoupled into several independent sub-problems. The solution of the Lagrange dual problem was then used for heuristic search. The algorithm was tested using two examples, a 15-bus test benchmark and a 1021-bus real test system, and the results showed that the algorithm was robust and scalability, making it suitable for large-scale distribution networks.
The Standard Newton method is an iterative derivative algorithm, that utilizes the first and second derivatives of the objective function at the current iteration point, xk, to approximate the function and determine the minimum point of the quadratic model as the next iteration point. This process is repeated until the minimum value meets the required accuracy, and the method is known for its fast-solving speed and high precision.
In Reference [107], the Standard Newton method was applied to calculate the distribution of branch current in an integer search, which was then used to guide the status of switches in the distribution network to search for the global optimal value. While this approach can solve the power flow calculation with only one iteration, it may be susceptible to local minima.
The simplex method, proposed by George Dantzig in 1947, is an optimization method for multi-variable functions. It first finds a basic feasible solution and then determines whether it is the optimal solution. If not, it finds another solution and continues iterating until it either finds the optimal solution or determines that it is unbounded [108]. In Reference [109], an improved simplex algorithm for minimizing distribution network losses based on linear programming was proposed. This algorithm determined the infeasibility of a given problem during the initialization of the linear programming solution. By ignoring the voltage constraint and considering line capacity, this algorithm generated a radial system configuration that ensures the minimum system loss under the line capacity constraint.
In recent years, the rapid development of bionics and computer technology has led to wide attention and application of meta-heuristic algorithms due to their high efficiency, accuracy, and relative simplicity. Meta-heuristic algorithms can effectively balance the exploration of the local and full-domain equilibrium when dealing with optimization problems, enabling them to quickly find the full-domain optimal solution. As a result, many meta-heuristic algorithms and their variants have been applied to ADNR.
3.2.3 Meta-Heuristic Algorithm
Reference [117] employed the SA method to find the optimal switching strategy for DNR to minimize power losses and balance loads. However, this method is time-consuming due to the repeated power flow calculations during the solving process. To address this limitation, Reference [118] proposed a highly efficient and accurate approach for power flow solution. It ensures both high-speed and high-precision power flow solutions. By incorporating the network connectivity checking matrix and the criterion for imposing radiality constraint suggested by Lavorato et al., it utilizes the SA algorithm to determine the radial structure that reduces active power losses.
Reference [119], to minimize power losses, applied the Tabu Search (TS) method to solve ADNR with distributed generation (DG). Despite demonstrating that the TS method has superior computational speed and solution accuracy compared to Simulated Annealing (SA), the global search capability of the TS algorithm heavily depends on the length of the tabu list. Reference [120] modified the size of the tabu list with an adaptive strategy. Additionally, it employed a ‘random multiplicative move’ to achieve a global optimum for ADNR. Reference [121] proposed an adaptive TS method. Compared to the traditional TS method, this method eliminated the concept of a list of prohibited attributes and aspiration criteria, and restarted the search from the existing solutions, avoiding the paths formed by revisiting candidate solutions. This method was tested on 33, 84, 118, and 136 nodes, and the test results verified its effectiveness.
In the Reference [122], the impact of DG and electric vehicle grid-connection’s volatility and intermittence on the system was considered. A genetic algorithm was adopted to solve the network distribution network reconfiguration problem, using network loss, voltage deviation, and voltage stability as the objective function. To improve the PV carrying capacity (PVCC) of a distribution system with harmonic pollution, the Reference [123] proposed distribution network reconfiguration and employed the NSGA-II algorithm to find a Pareto-front candidate solution set for the grid-connection problem of many photovoltaic generating units. Reference [124] aimed to minimize the economic losses of operators under fault conditions. It used a combination of GA and mathematical optimization for a comprehensive analysis of the power system through nonlinear programming and discontinuous derivatives. The method was validated on IEEE 9 bus and 30 bus systems and was evaluated for its effectiveness in reducing network losses and economic losses. The flowchart of GA applied to ADNR is shown in Fig. 7.
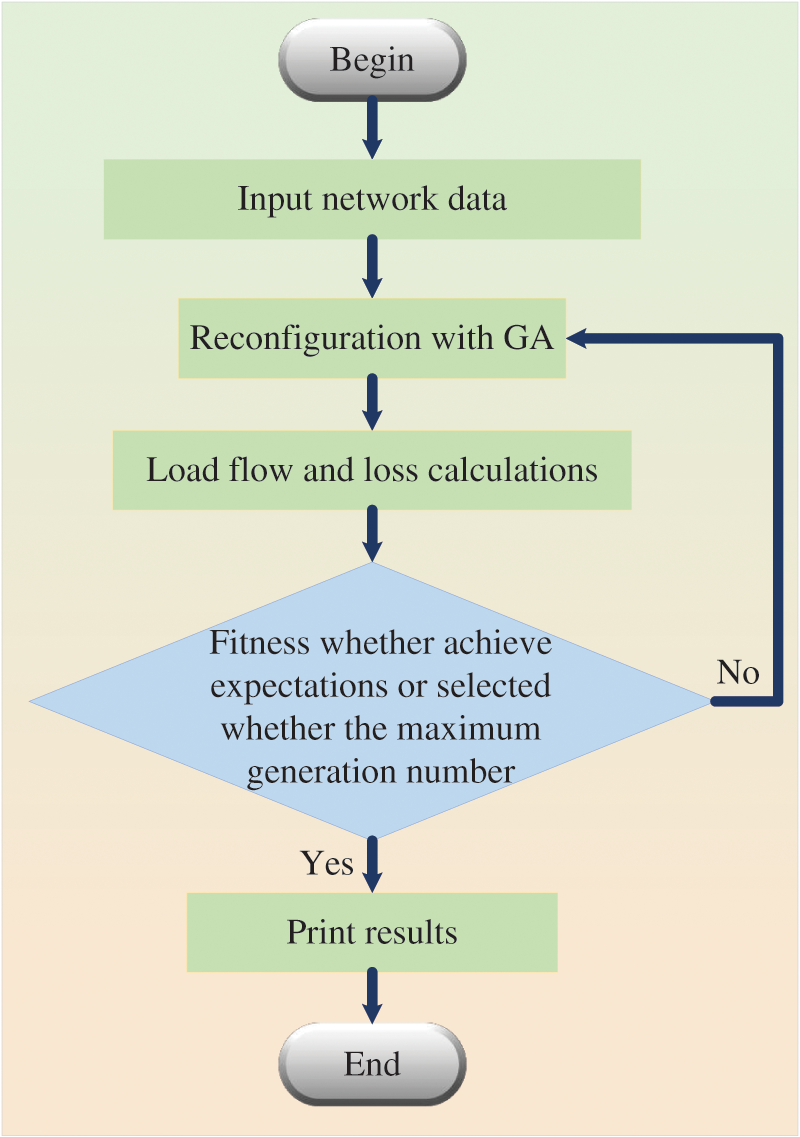
Figure 7: The flowchart of GA applied to ADNR
Reference [125] established a dynamic reconfiguration model to minimize network losses and switch operations in the short term. They optimized the model using Ant Colony Optimization (ACO) and validated the feasibility of this method under the variable characteristics of DG output. The flowchart of ACO addressing ADNR with DGs is depicted in Fig. 8. The traditional ACO suffers from slow search speed, low flexibility, and a tendency to fall into local optima. Literature [126] addressed these shortcomings by proposing an improved differential evolution ACO. This novel approach integrated an enhanced differential evolution algorithm with linearly decreasing weight into the ACO for the reconfiguration of the IEEE 33 bus system with DGs. Simulation results demonstrated that this method not only achieved faster convergence and avoided local optima but also offered significantly higher flexibility.
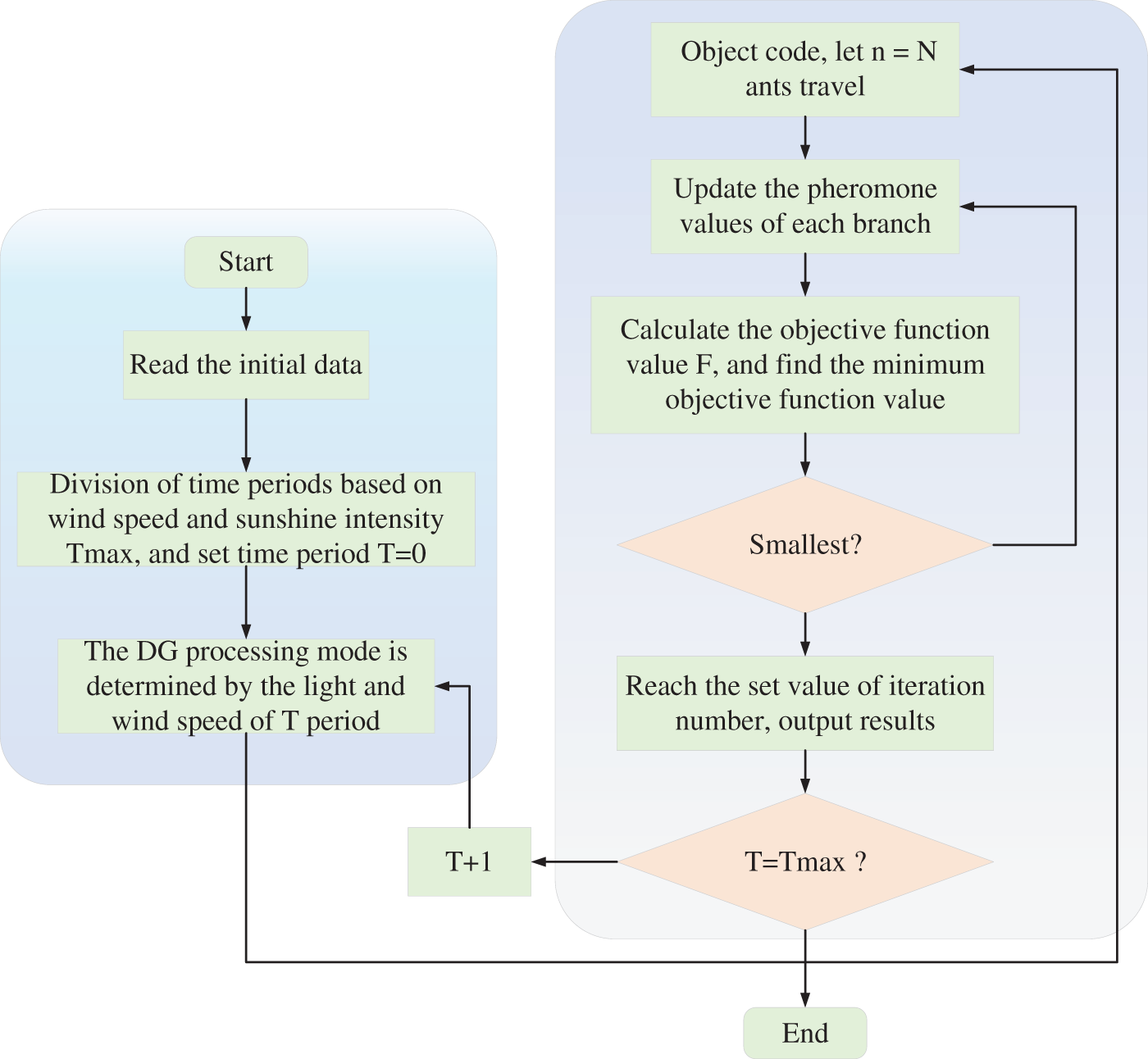
Figure 8: The flowchart of ACO addressing ADNR with DGs
Reference [127] achieved significant improvements in network losses and voltage distribution balance by simultaneously implementing hierarchical reconfiguration, DG integration, and low-voltage distribution allocation. This demonstrated that the Particle Swarm Optimization (PSO) algorithm can effectively provide solutions for segmenting switches and sizing DG units. However, the performance of the PSO algorithm largely depends on the initial data selection. Additionally, a considerable amount of parameter tuning is required during the reconfiguration process to achieve optimal results. The Hybrid Particle Swarm Optimization (HPSO) proposed in the Reference [128] improved the particle position update formula. By balancing local and global searches in later stages, the results tended towards the optimal particles in the population, ultimately converging to the global optimum particle. Compared to the approach in Reference [128], which only improved the particle position update formula, the Improved Particle Swarm Optimization Approach proposed in Reference [129] employed a chaos-oriented inertia weight and crossover operation mechanism. This method enhanced the particle velocity update, particle position update, and linearly varying inertia weight. It required fewer control parameters, needing only the inertia coefficient to be set, and its superiority was validated on the IEEE 69 bus system. Reference [94] introduced evolutionary particle swarm optimization, effectively addressing the problem of poor convergence caused by inaccurate parameter settings such as inertia weight (w), cognitive constant (c1), and social constant (c2). The process of applying PSO to ADNR is illustrated in Fig. 9, and the summary of PSO algorithms is tabulated in Table 3.
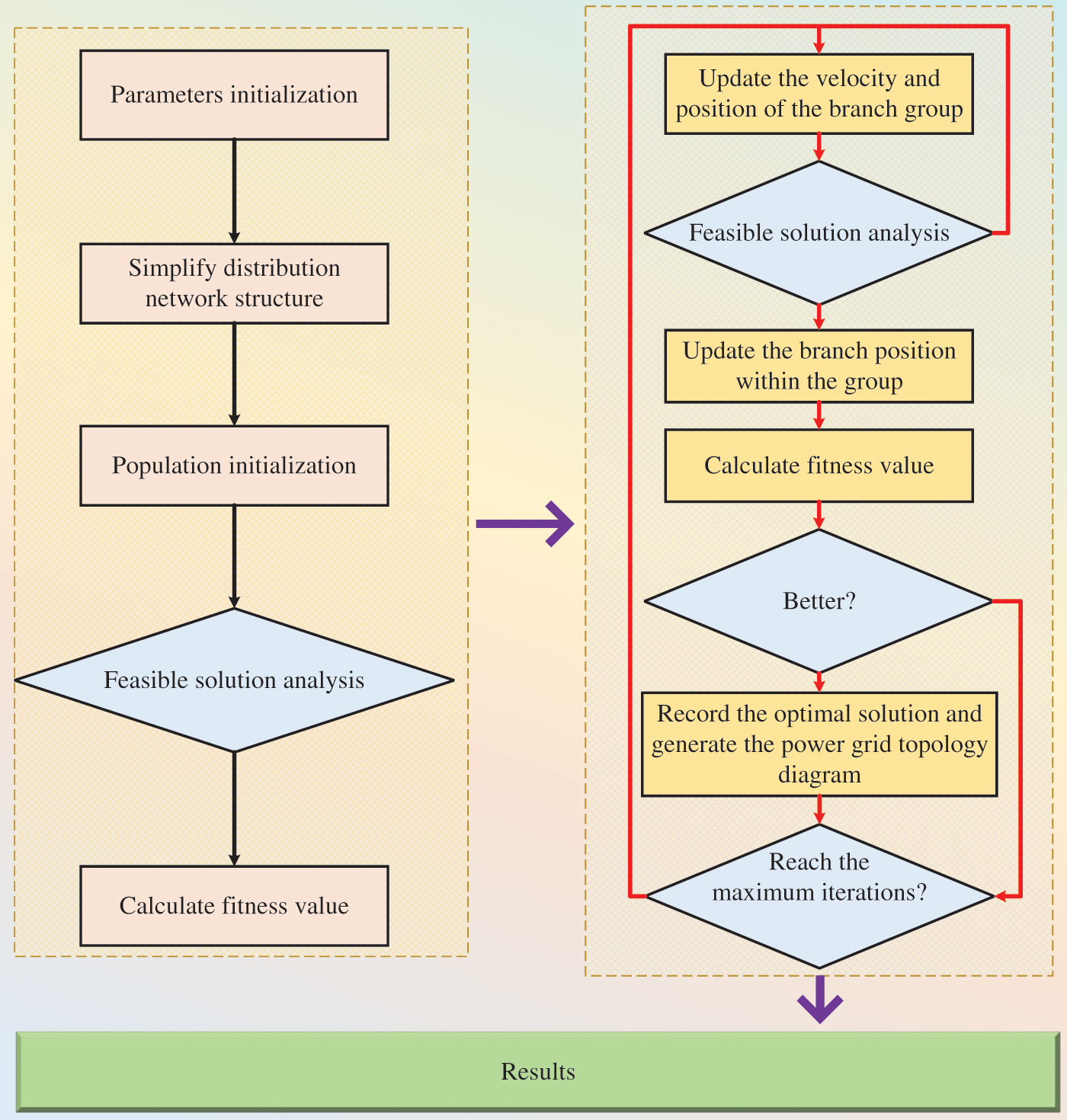
Figure 9: Flow chart of PSO applied to ADNR
In Reference [135], the Harmony Search Algorithm (HSA) was used to solve the distribution network reconfiguration problem. However, due to the large amount of data in the large-scale distribution network reconfiguration, the algorithm was prone to falling into the local minimum and unable to find the global optimal solution. Based on this, an improved HSA was proposed in Reference [96] to optimize the algorithm by enhancing the PAR and BW parameters in the iteration process of optimization. The process of solving ADNR with IHSA is illustrated in Fig. 10. Additionally, Reference [136] proposed a self-adaptive HSA that provides better accuracy and convergence. The performance of HSA for ADNR is shown in Table 4.
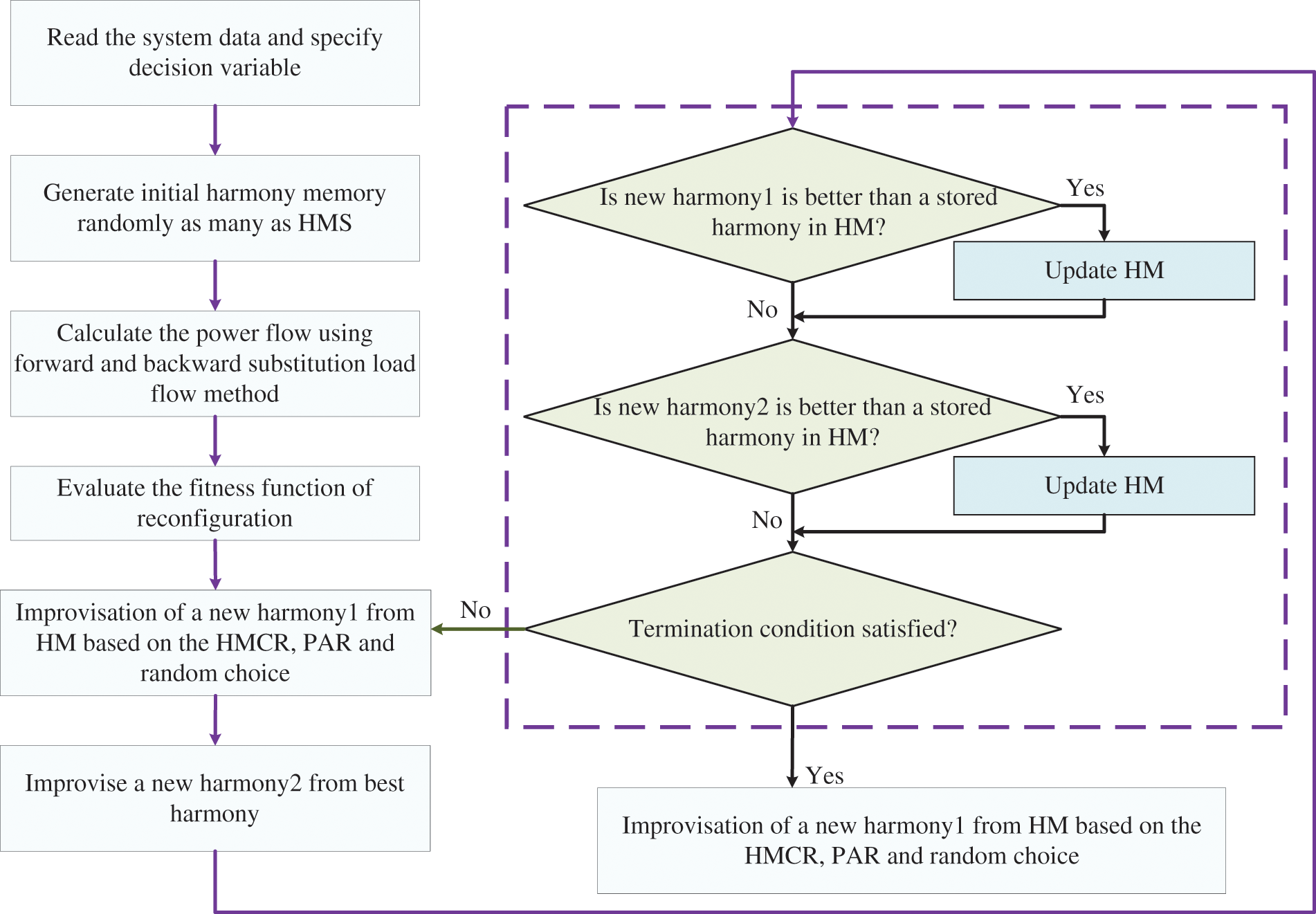
Figure 10: Flow chart of IHSA for solving ADNR
To improve the convergence of the algorithm, the discrete artificial bee colony (DABC) [138] was proposed to continuously search for the new food source location in memory. Furthermore, Reference [95] proposed the multi-objective artificial bee colony (MABC) to enrich the search process for optimal solutions by using archived solutions. The specific evaluation is shown in Table 5. The flowchart of the artificial bee colony based ADNR is depicted in Fig. 11.
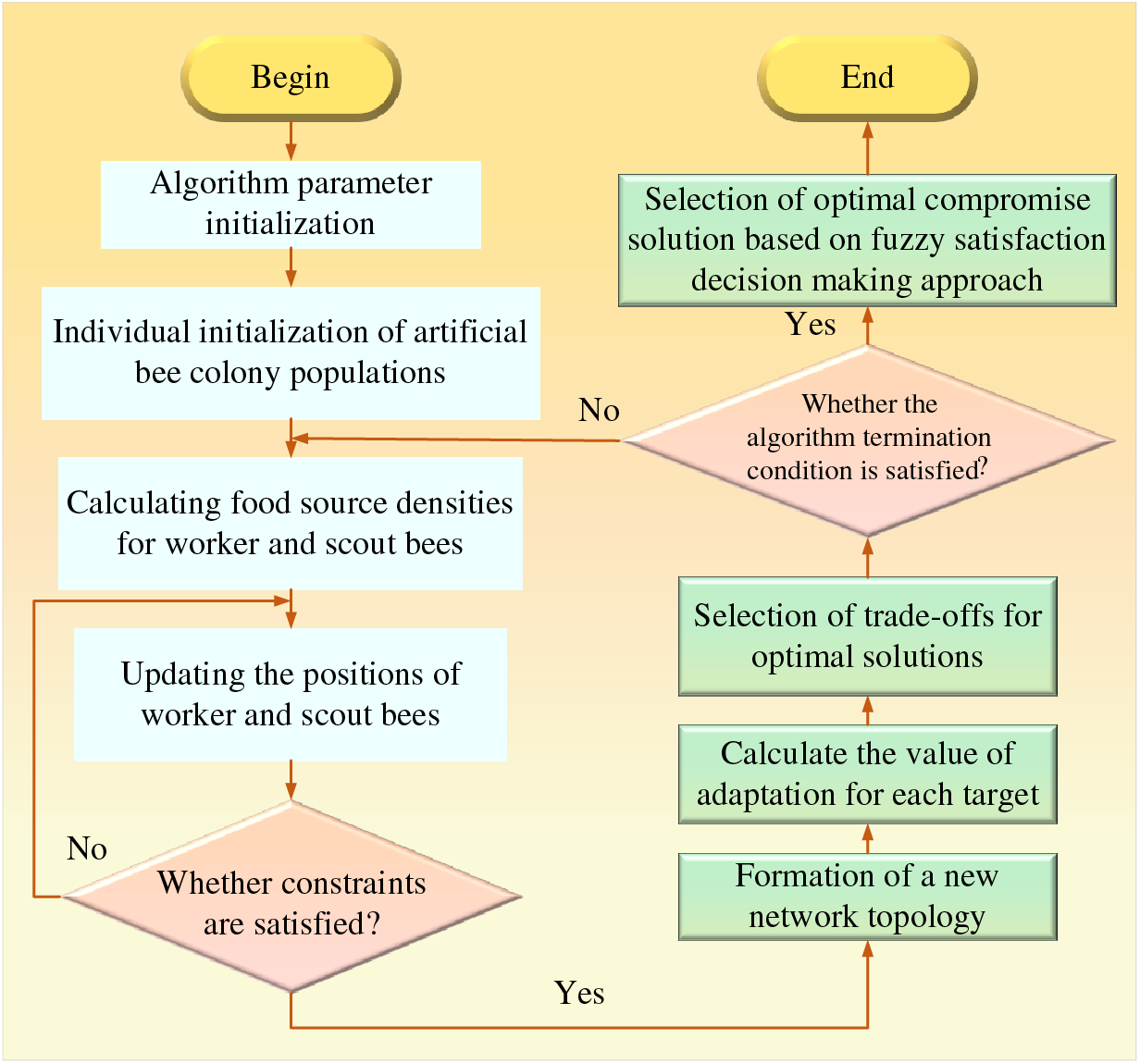
Figure 11: Principle of ABC applied to ADNR
The original cuckoo search algorithm (CSA) can only solve the simple continuous optimization problem. Therefore, Reference [140] introduced the variable radix operation and incorporated the concept of quantum bits to construct an improved CSA for ADNR. Additionally, the hybrid algorithm of CSA and simulated annealing was developed to effectively improve the convergence speed and solution quality of ADNR [117]. The specific performance of the above methods is tabulated in Table 6. The flowchart of CSA is given in Fig. 12.
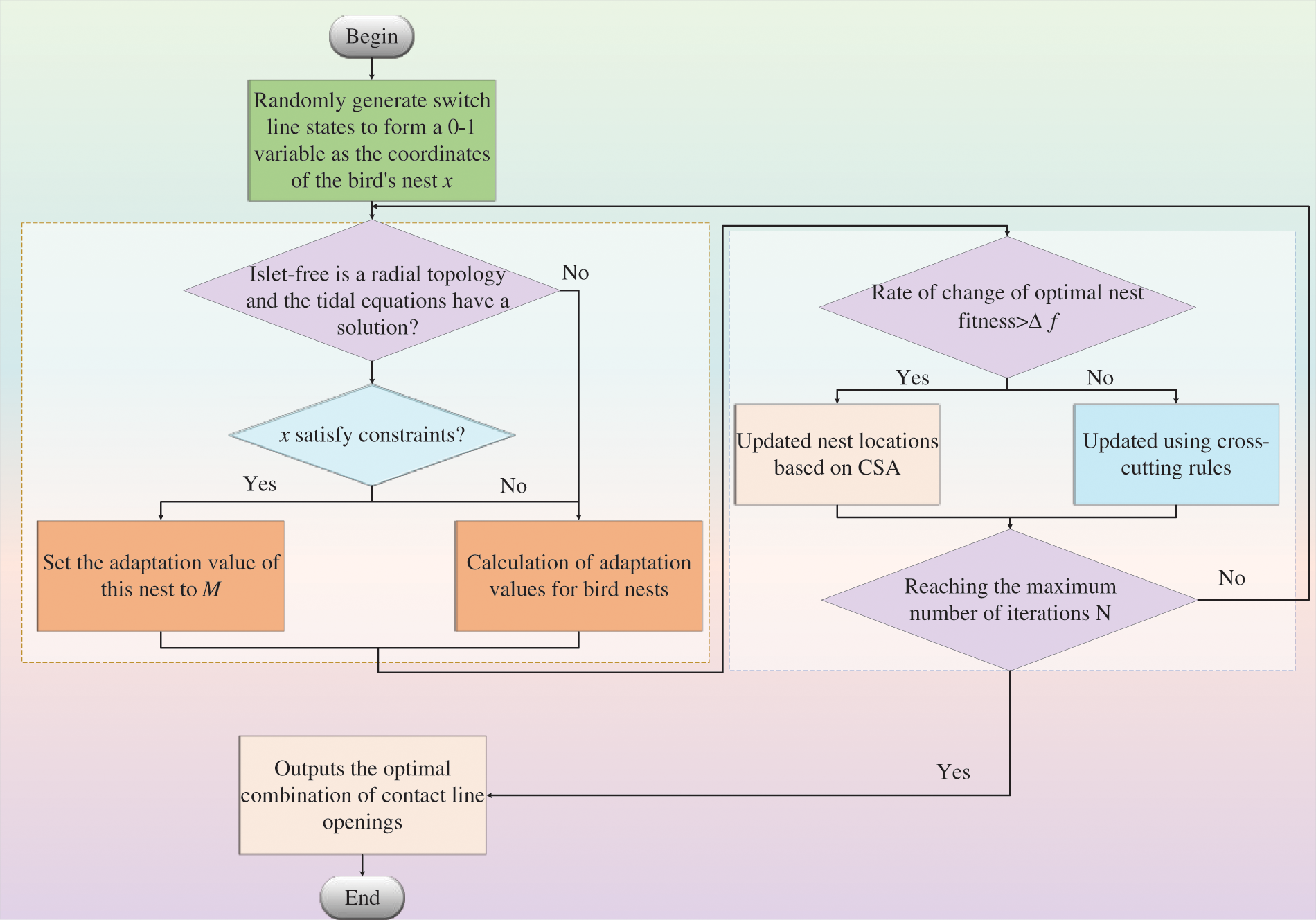
Figure 12: Flow chart of CSA
Inspired by the diffusion and foraging behavior of slime molds, the SMA optimizes the changing process of vein morphology and systolic patterns during foraging. With the change of food odor concentration in the air, slime molds constantly change their movement position and speed [142].
However, SMA is slow to converge, has low computational efficiency, and is prone to falling into local optima. In Reference [143], a parallel slime mold algorithm based on packet communication strategy and inertia weights was proposed to improve its convergence. Additionally, a multi-group flight slime mold algorithm based on packet communication and Levy flight was proposed in the Reference [144]. The flow chart of SMA to solve the problem of DNR with DG is shown in Fig. 13. Specific parameters are shown in Table 7.
Figure 13: Flow chart of SMA applied to ADNR

Overall, genetic algorithm (GA), particle swarm optimization (PSO), and Tabu search (TS) are the most commonly used meta-heuristic algorithms for ADNR. However, with the increasing scale of grid-connected distributed power supply and ESSs, as well as the demand for more intelligent and reliable power supply in the distribution network, the reconfiguration of ADN has become increasingly complex. As a result, meta-heuristic algorithms with stronger search capabilities and higher optimization efficiency are being increasingly applied in the reconfiguration of ADNs, summary of other meta-heuristic methods applications is demonstrated in Table 8.
3.2.4 Machine Learning Based Method
Machine learning exhibits powerful parallel information processing capabilities through self-adaptation and self-learning. Machine learning based ADNR methods are summarized in Table 9.
Reinforcement Learning Approach
RL is a machine learning method where agents act based on feedback from environmental characteristics. By continuously observing the environment and through repeated trial-and-error, agents accumulate experience and ultimately achieve goal optimization. The principle of RL based ADNR is shown in Fig. 14. The model-free multi-agent deep reinforcement learning (MDRL) proposed by the Reference [157], used multi agents to control the operations of the branch switches in the network. Through centralized training and distributed execution, this training framework reconstructed the network. Reference [158] developed a data-driven batch-constrained reinforcement learning (RL) algorithm for the dynamic ADNR problem, which learned the network reconfiguration control policy from a finite historical operational dataset without interacting with the distribution network.
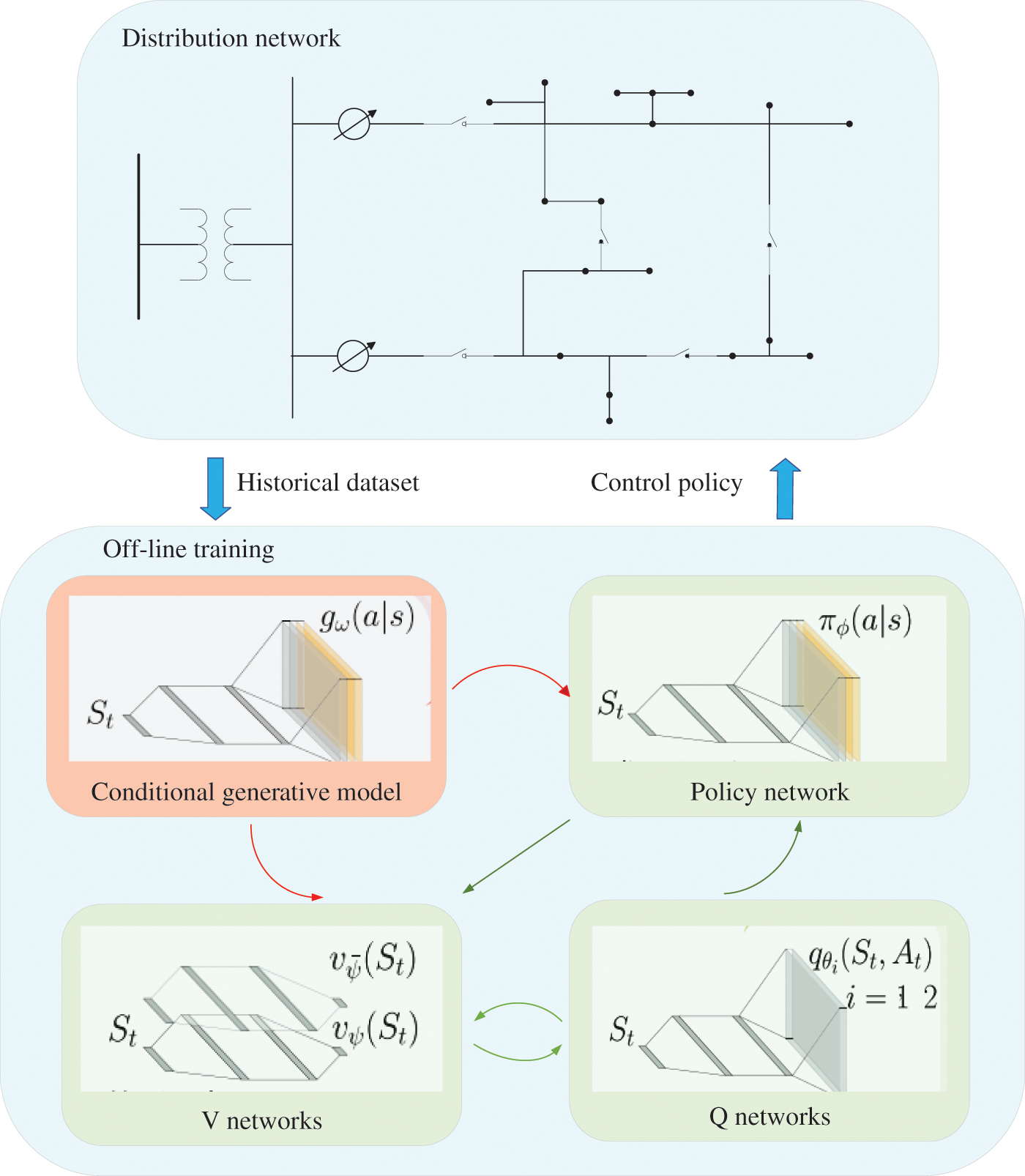
Figure 14: Reinforcement learning principles
Reference [159] proposed an ADNR method based on Efficient Deep Learning (EDL), which is based on deep convolutional neural network (CNN) to design the short-term voltage stability assessment network, and selected historical data to train it. The STVS platform calculated the indices under all topologies and gradually filters out the topologies that meet the requirements. The large number of computations leads to poor robustness of the algorithm, which is difficult to cope with the challenges of ADN. Reference [160] combined DL with robust optimization: based on deep neural networks adaptively constructing the uncertainty set of DG and load from the historical dataset of the distribution network, robust ADNR was considered as a two-stage mixed-integer quadratic programming problem, and solved the ADNR configuration by using column generation method and constraint generation method. The flowchart for solving ADNR by DL is shown in Fig. 15.
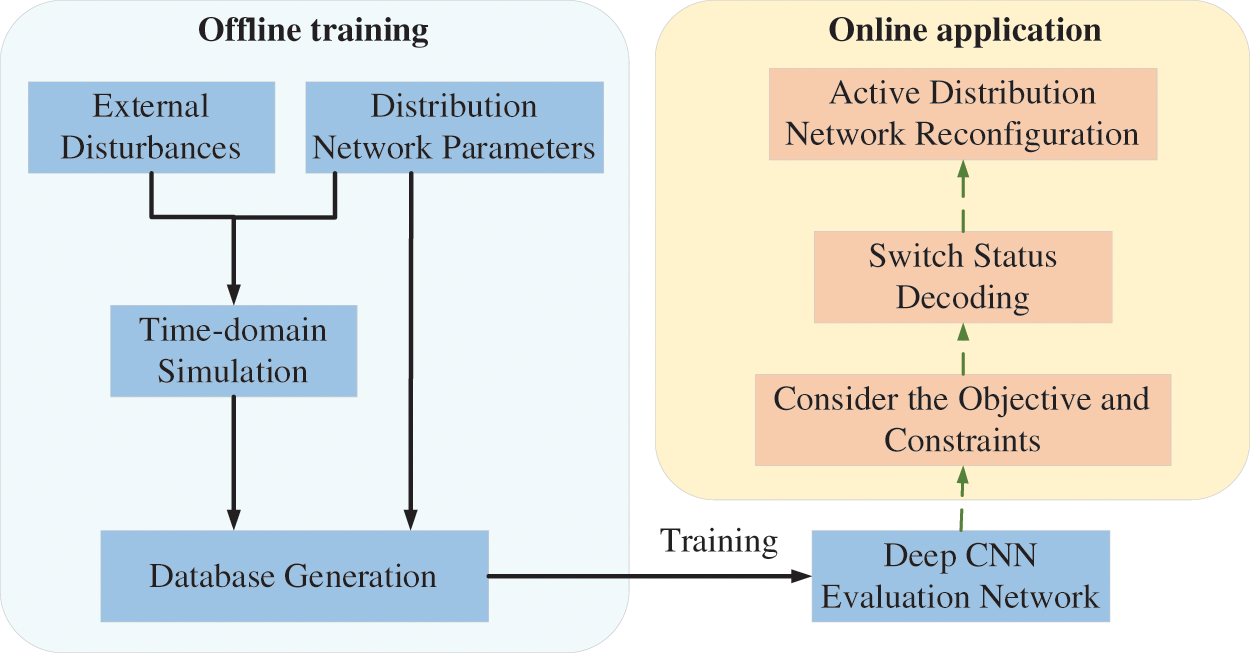
Figure 15: The flowchart for solving ADNR by DL
As ESS and DG become more widely connected to the grid, DSR to incentive measures such as time-of-use and real-time pricing are causing tidal changes in the power system, resulting in voltage fluctuations, and increasing system complexity. Many scholars have attempted to mix meta-heuristic algorithms to ensure global optimal results, The summary of hybrid algorithm is shown in Table 10.

The paper provides a comprehensive review of numerous existing methods for ADNR, which focuses on both theoretical and practical aspects, aiming to emphasize the operational mechanisms, testing systems, optimization objectives, complexities, strengths, weaknesses, and limitations of each method to facilitate a more comprehensive and practical comparison. Tables 2–10 offer detailed summaries of the 52 ADNR methods mentioned in this paper, categorized by application years, sub-methods, and experimental data.
Based on the recently proposed ADNR methods, two constructive discussions are conducted to illustrate the current research status and existing issues, as follows:
a) Photovoltaic, wind power and other renewable energy sources exhibit strong randomness and significant fluctuations. The integration of a large amount of renewable energy into the distribution network can lead to issues such as poor power quality, excessive voltage fluctuations, uneven load distribution, and high network losses. To address these difficult and complex issues, each type of method goes its way, as follows:
Mathematical programming methods (e.g., linear programming and nonlinear programming) mainly consider the impact of renewable energy sources on the power loss of the active distribution network. In particular, the Lagrange relaxation divides the network into smaller regions via dual decomposition, which converts this MINLP problem into a simpler MILP one. Then coordinating node solutions can be obtained to minimize overall network loss. The Standard Newton method transforms the objective into an unconstrained problem using Lagrange multipliers or penalty functions, making it ideal for large-scale reconfiguration under renewable energy integration. The Simplex algorithm, while ignoring the capacity limits of transmission lines, converts the minimum network loss problem into a linear programming problem. However, when a significant number of renewable energy sources are integrated into the system, it significantly increases the complexity and difficulty of computation. Therefore, the effectiveness of this method may decline substantially.
Unlike mathematical programming methods that only consider a single objective, i.e., power loss, and ignore mitigating the impact of renewable energy sources on the distribution network, Meta-heuristic algorithms effectively and flexibly handle large-scale nonlinear optimization problems e.g., minimizing power losses, maximizing renewable energy utilization, minimizing voltage fluctuations, etc. They enable decision-making on variables such as capacity, location, output power of renewable energy sources, and load adjustments, which exhibit good global exploration capabilities. Furthermore, their stochastic elements can effectively address the uncertainty of renewable energy sources.
By leveraging data-driven insights, Machine Learning methods establish models that accurately describe the operation status, load demands, and power quality of distribution networks containing renewable energy sources. Through training these models and addressing multi-objective optimization problems like minimizing power losses, maximizing renewable utilization, and minimizing voltage fluctuations, rational reconfiguration solutions are obtained. Subsequently, their adaptive learning capabilities are applied to adapt the reconfiguration strategies dynamically, aligning with the output stochastic nature of renewable energy sources. Moreover, Machine Learning methods can accurately predict the energy supply and demand relationship, effectively overcoming uncertainty and fluctuations in the distribution network.
b) The applicable electrical network scenarios of each ADNR method are different due to their mechanism differences, as follows:
The traditional method has the advantages of simple modeling and fast solving speed, but it is only suitable for small and medium-sized distribution networks. When facing more complex networks, it is unable to handle intricate typologies and multiple constraints, and may get stuck in local optimal solutions;
The Mathematical programming method can accurately establish mathematical models and is suitable for small and medium-sized distribution network reconfiguration. As the distribution network scales up, the Mathematical programming method needs to consider complex linear and nonlinear constraints, making the model establishment and solving process more complicated and resulting in longer reconfiguration times;
Meta-heuristic algorithms are currently widely applied in medium to large-scale active distribution network reconfiguration. By utilizing diverse searching strategies, they have the opportunity to find global optimal solutions. However, due to the need for multiple iterations and searches, as well as their susceptibility to initial solutions, they tend to have longer run times and may lead to sub-optimal reconfiguration results;
Machine learning based methods can leverage the advantages of data-driven approaches to adapt to the environment and requirements of distribution networks while possessing strong predictive and optimization capabilities. With the development of big data and artificial intelligence technologies, machine learning based methods are expected to gain even more applications in the future;
Hybrid algorithms make full use of the strengths of different methods, considering various problems and requirements, and utilize diverse and global search strategies to obtain more optimal solutions. However, when dealing with large-scale distribution network reconfiguration, the design and implementation of the algorithm can be more complex.
c) The distribution networks studied in this paper are all tree structures, so in most cases, there is no loop. Complex loop problems need to be unlooped and tested, and each node is verified to be out of bounds through simulation, which in turn calculates the loop.
Overall, Table 11 tabulates a comprehensive and systematic summary and analysis.

Lastly, Fig. 16a systematically summarizes the major benefits and limitations of each method. Based on the summary of the major benefits and limitations of each method in Fig. 16a, a 6-axis radar chart is used in Fig. 16b to visually compare the performance of five types of ADNR methods across six indicators: objective function, social indicator, hyperparameters, optimization indicators, operational mechanism, and test system. The scoring system used in the radar chart rates methods according to their relative performance: the best-performing method in each indicator receives 5 points, the second-best receives 4 points, the average method receives 3 points, and the worst receives 1 point.
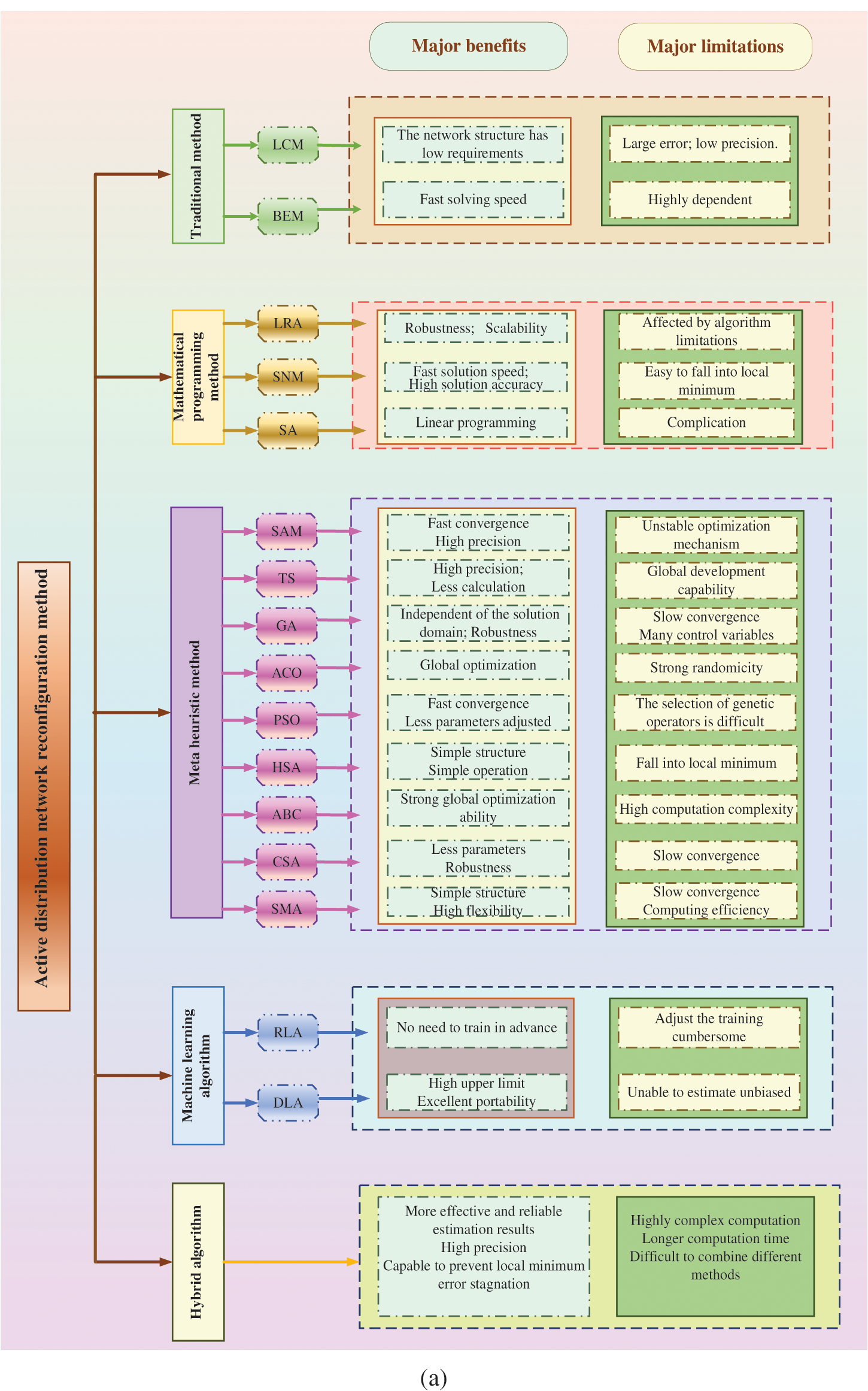
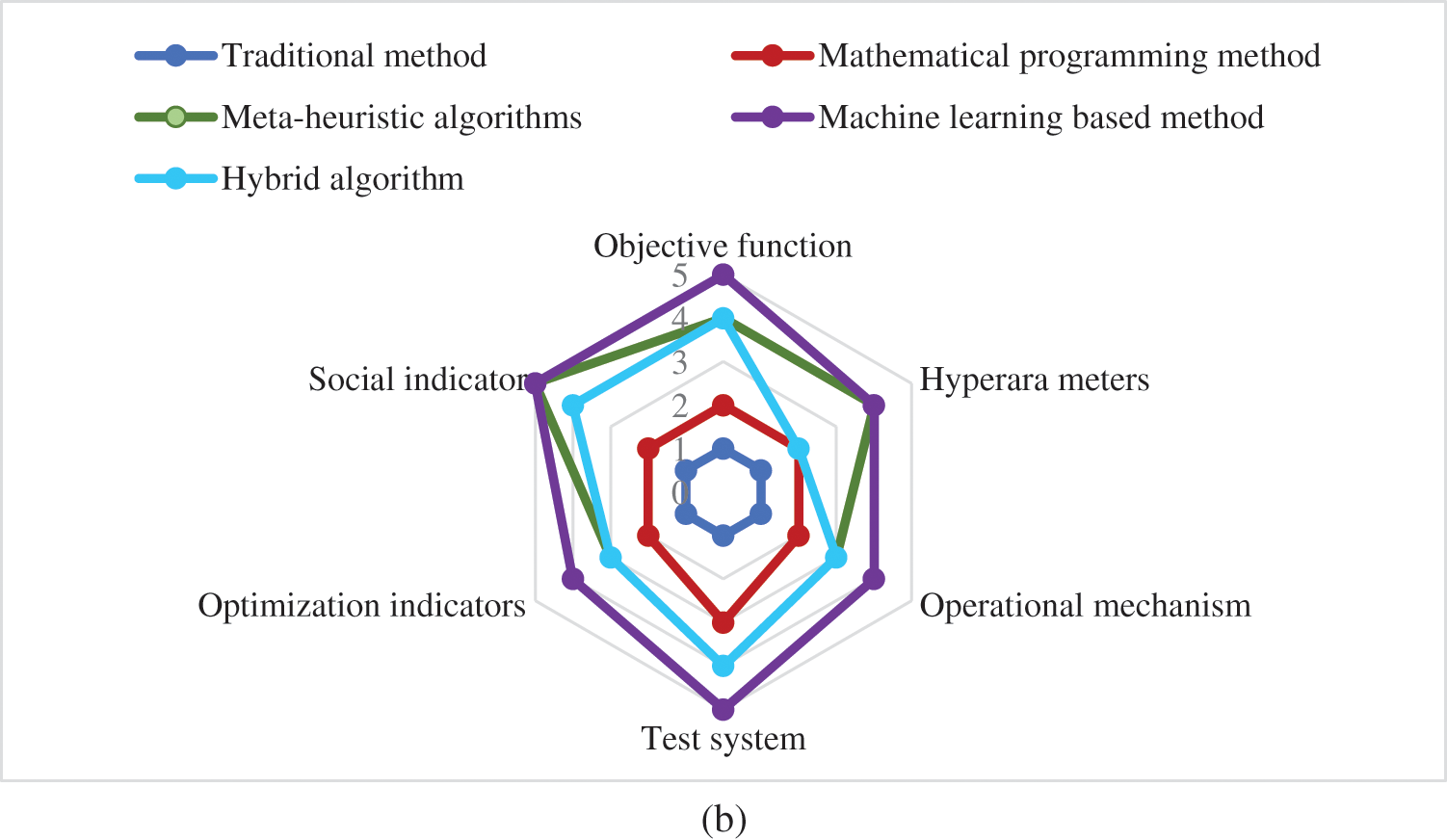
Figure 16: Comprehensive evaluation of ADNR methods (a) Summary and comparison of all algorithms (b) Comprehensive comparison
This paper profoundly summarizes and analyzes active distribution network reconfiguration methods, which endeavors to offer future researchers comprehensive and systematic references and guidelines. Here, several conclusions are stated as follows:
a) A total of 52 methods are summarized and counted in this paper, which are categorized into five major categories, i.e., traditional (2 methods), mathematics-based (3 methods), meta-heuristic (32 methods), hybrid (3 methods), and machine learning based (2 methods).
b) Given the uniqueness of ADNR methods and their impact on the network, a comprehensive evaluation system is carefully established considering complexity and applicability. Specifically, complexity is determined by three indicators: (a) multi-objective optimization, (b) hyperparameters, and (c) operational mechanism. Meanwhile, the applicability is scored according to three aspects: (a) test system, (b) optimization indicators, and (c) social indicators.
c) 32 meta-heuristic algorithms are widely used in ADNR thanks to their fast convergence speed and independence for models. However, due to their inherent randomness, it is challenging to balance the relationship between local and global optimization. Many scholars have attempted to mix meta-heuristic algorithms to ensure global optimal results.
On this basis, the paper provides the following recommendations for future research:
a) Reconfiguration technology improvement: Heuristic algorithms such as PSO [131,133], GA [132], and HSA [96,136] were heavily used in ADNR, and the feasibility of the algorithms was verified in small-scale simulation test networks, e.g., IEEE 33-bus system and IEEE 69-bus system. Compared with heuristic algorithms, machine learning algorithms such as DL [160], RL [162,163], etc., acquired more satisfactory performance on actual 123-node networks, Modified CIGRE 14-bus network actual networks. Hence, RL and DL with strong stability, adaptability, portability, and drivability seem to be promising tools for large-scale ADNR in the future.
b) Reconfiguration constraint improvement: The introduction of numerous ESSs, DGs, and DR complexifies the topology of the grid. Additionally, DRs based on incentives such as time-sharing tariffs and real-time tariffs can change power flow and cause voltage fluctuations. Unfortunately, DRs are usually ignored in ADNR, which contradicts reality and application. Thus, more complex constraints of flexible power sources and the influence of DRs ought to be covered when implementing ADNR.
c) Reconfiguration test system improvement: Test systems of ADNR are mainly small-scale, e.g., the IEEE 14 bus system [137], IEEE16 bus system [156], and IEEE32 bus system [145]. The small-scale test network cannot effectively reflect the real situation of power grids, especially integrated ESSs and DGs. Therefore, larger-scale systems with real nodes are recommended to validate the proposed ADNR methods.
d) Reconfiguration network improvement: More significant consideration should be given to the unified whole of the heat network, gas network, and grid, and the reconfiguration problem should be approached from the perspective of energy integration and synergy.
Acknowledgement: The authors would like to acknowledge the Science and Technology Commission of Shanghai Municipality.
Funding Statement: The authors received funding from the National Natural Science Foundation of China (62263014), Yunnan Provincial Basic Research Project (202401AT070344, 202301AT070443) and Science and Technology Commission of Shanghai Municipality (STCSM) Sailing Program (22YF1414400).
Author Contributions: The authors confirm contribution to the paper as follows: Funding acquisition, supervision, resources: Bo Yang; investigation, data collection, writing—original draft and editing, analysis and interpretation of results: Rui Zhang; validation: Jie Zhang; supervision: Jiale Li; formal analysis: Yimin Zhou; visualization: Yuanweiji Hu; data collection: Bin He; analysis and interpretation of results: Xianlong Cheng; investigation: Gongshuai Zhang; formal analysis: Xiuping Du; visualization: Si Ji; funding acquisition: Yiyan Sang; visualization and contributed to the discussion of the topic: Zhengxun Guo. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data used in this study are available on request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. M. R. Dar and S. Ganguly, “Dual-Stage model predictive control with reduced model framework for voltage control in active distribution networks,” J. Mod. Power Syst. Clean Energy, pp. 1–12, Jun. 2024. doi: 10.35833/MPCE.2024.000394. [Google Scholar] [CrossRef]
2. P. K. Kesavan, U. Subramaniam, D. J. Almakhles, and S. Selvam, “Modelling and coordinated control of grid connected photovoltaic, wind turbine driven PMSG, and energy storage device for a hybrid DC/AC microgrid,” Prot. Control Mod. Power Syst., vol. 9, no. 1, pp. 154–167, Jan. 2024. doi: 10.23919/PCMP.2023.000272. [Google Scholar] [CrossRef]
3. J. X. Gong, Y. L. Xu, J. Zhang, and C. H. Xu, “Research on the network structure of new power system distribution network,” (in ChineseShandong Electr. Power, vol. 51, no. 1, pp. 45–51, Jan. 2024. doi: 10.20097/j.cnki.issn1007-9904.2024.01.005. [Google Scholar] [CrossRef]
4. L. Q. Bai, T. Jiang, F. X. Li, H. H. Chen, and X. Li, “Distributed energy storage planning in soft open point based active distribution networks incorporating network reconfiguration and DG reactive power capability,” Appl. Energy, vol. 210, no. 15, pp. 1082–1091, Jan. 2018. doi: 10.1016/j.apenergy.2017.07.004. [Google Scholar] [CrossRef]
5. Q. Chen, S. Bu, and C. Y. Chung, “Small-Signal stability criteria in power electronics-dominated power systems: A comparative review,” J. Mod. Power Syst. Clean Energy, vol. 12, no. 4, pp. 1–16, Dec. 2023. doi: 10.35833/MPCE.2023.000526. [Google Scholar] [CrossRef]
6. B. Yang et al., “Recent advances in fault diagnosis techniques for photovoltaic systems: A critical review,” Prot. Control Mod. Power Syst., vol. 9, no. 3, pp. 36–59, May 2024. doi: 10.23919/PCMP.2023.000583. [Google Scholar] [CrossRef]
7. H. C. Wang, H. Y. Song, and J. Yu, “Research on optimization scheme for new power system terminal communication network,” (in ChineseShandong Electr. Power, vol. 51, no. 2, pp. 56–66, Feb. 2024. doi: 10.20097/j.cnki.issn1007-9904.2024.02.006. [Google Scholar] [CrossRef]
8. A. Saxena and R. Shankar, “An interactive operating demand response approach for hybrid power systems integrating renewable energy sources,” Prot. Control Mod. Power Syst., vol. 9, no. 3, pp. 174–194, May 2024. doi: 10.23919/PCMP.2023.000282. [Google Scholar] [CrossRef]
9. S. A. Arefifar, M. S. Alam, and A. Hamadi, “A review on self-healing in modern power distribution systems,” J. Mod. Power Syst. Clean Energy, vol. 11, no. 6, pp. 1719–1733, Nov. 2023. doi: 10.35833/MPCE.2022.000032. [Google Scholar] [CrossRef]
10. H. Wang, L. Wang, and Q. Yao, “Research on the safety assessment of operation of distribution network based on the timing characteristics,” in 2018 Chin. Automat. Congress (CAC), Xi’an, China, 2018, pp. 47–52. [Google Scholar]
11. T. Ahmad et al., “Artificial intelligence in sustainable energy industry: Status quo, challenges and opportunities,” J. Clean. Prod., vol. 289, Mar. 2021, Art. no. 125834. doi: 10.1016/j.jclepro.2021.125834. [Google Scholar] [CrossRef]
12. X. Zhao, Q. Xu, and Y. Yang, “Service restoration of distribution system considering novel battery charging and swapping station, repair crews, and network reconfigurations,” J. Mod. Power Syst. Clean Energy, pp. 1–13, Jun. 2024. doi: 10.35833/MPCE.2024.000010. [Google Scholar] [CrossRef]
13. S. Repo, F. Ponci, and D. D. Giustina, “Holistic view of active distribution network and evolution of distribution automation,” in IEEE PES Innov. Smart Grid Technol., Istanbul, Turkey, 2014, pp. 1–6. [Google Scholar]
14. X. X. Gong, B. Gu, and Z. S. Wu, “Research on dynamic reconfiguration of active distribution network,” (in ChineseElectr. Technol., vol. 12, pp. 52–60, Dec. 2014. doi: 10.3969/j.issn.1673-3800.2014.12.013. [Google Scholar] [CrossRef]
15. B. Yang, T. Yu, H. C. Shu, J. Dong, and L. Jiang, “Robust sliding-mode control of wind energy conversion systems for optimal power extraction via nonlinear perturbation observers,” Appl. Energy, vol. 210, pp. 711–723, Jan. 2018. doi: 10.1016/j.apenergy.2017.08.027. [Google Scholar] [CrossRef]
16. X. Z. Dong, Z. R. Wu, L. M. Chen, Z. W. Liu, and X. L. Xu, “Distribution network reconfiguration method with distributed generators based on an improved shuffled frog leaping algorithm,” in 2018 IEEE PES/IAS Power Africa, Cape Town, South Africa, 2018, pp. 102–107. [Google Scholar]
17. A. Merlin and H. Back, “Search for a minimal loss operating spanning tree configuration in an urban power distribution system,” in Proc. 5th Power Syst. Comput. Conf., Cambridge, UK, 1975, pp. 1–18. [Google Scholar]
18. Z. Dong and L. Lin, “Dynamic reconfiguration strategy based on partition of time intervals with improved fuzzy C-means clustering,” in 2018 China Int. Conf. Electr. Distrib., Tianjin, China, 2018, pp. 398–404. [Google Scholar]
19. I. Diaaeldin, S. Abdel Aleem, A. El-Rafei, A. Abdelaziz, and A. F. Zobaa, “Optimal network reconfiguration in active distribution networks with soft open points and distributed generation,” Energies, vol. 12, no. 21, Sep. 2019, Art. no. 4172. doi: 10.3390/en12214172. [Google Scholar] [CrossRef]
20. M. Mahdavi, K. Schmitt, and F. Jurado, “Robust distribution network reconfiguration in the presence of distributed generation under uncertainty in demand and load variations,” IEEE Trans. Power Deliv., vol. 38, no. 5, pp. 3480–3495, Oct. 2023. doi: 10.1109/TPWRD.2023.3277816. [Google Scholar] [CrossRef]
21. M. Mahdavi, H. H. Alhelou, P. Gopi, and N. Hosseinzadeh, “Importance of radiality constraints formulation in reconfiguration problems,” IEEE Syst. J., vol. 2015, pp. 1–14, Jul. 2023. doi: 10.1109/JSYST.2023.3283970. [Google Scholar] [CrossRef]
22. B. Sultana, M. W. Mustafa, U. Sultana, and A. R. Bhatti, “Review on reliability improvement and power loss reduction in distribution system via network reconfiguration,” Renew. Sustain. Energ. Rev., vol. 66, pp. 297–310, Dec. 2016. doi: 10.1016/j.rser.2016.08.011. [Google Scholar] [CrossRef]
23. S. Mishra, D. Das, and S. Paul, “A comprehensive review on power distribution network reconfiguration,” Energy Syst., vol. 8, pp. 227–284, Mar. 2017. doi: 10.1007/s12667-016-0195-7. [Google Scholar] [CrossRef]
24. O. Badran, S. Mekhilef, H. Mokhlis, and W. Dahalan, “Optimal reconfiguration of distribution system connected with distributed generations: A review of different methodologies,” Renew. Sustain. Energy Rev., vol. 73, pp. 854–867, Jun. 2017. doi: 10.1016/j.rser.2017.02.010. [Google Scholar] [CrossRef]
25. I. G. Guimaraes, D. P. Bernardon, V. J. Garcia, M. Schmitz, and L. L. Pfitscher, “A decomposition heuristic algorithm for dynamic reconfiguration after contingency situations in distribution systems considering island operations,” Elect. Power Syst. Res., vol. 192, Mar. 2021. Art. no. 106969. doi: 10.1016/j.epsr.2020.106969. [Google Scholar] [CrossRef]
26. M. Mahdavi, H. H. Alhelou, and N. D. Hatziargyriou, “Reconfiguration of electric power distribution systems: Comprehensive reconfiguration of electric power distribution systems: Comprehensive review and classification,” IEEE Access, vol. 9, pp. 118502–118527, Aug. 2021. doi: 10.1109/ACCESS.2021.3107475. [Google Scholar] [CrossRef]
27. M. Mahdavi, H. H. Alhelou, A. Bagheri, S. Z. Djokic, and R. A. V. Ramos, “A comprehensive review of metaheuristic methods for the reconfiguration of electric power distribution systems and comparison with a novel approach based on efficient genetic algorithm,” Access, vol. 9, pp. 122872–122906, Aug. 2021. doi: 10.1109/ACCESS.2021.3109247. [Google Scholar] [CrossRef]
28. G. B. He et al., “Optimal location and sizing of distributed generator via improved multi-objective particle swarm optimization in active distribution network considering multi-resource,” Energy Eng., vol. 120, no. 9, pp. 2133–2154, Aug. 2023. doi: 10.32604/ee.2023.029007. [Google Scholar] [CrossRef]
29. C. X. Tao, S. Z. Yang, and T. G. Li, “Application of DSAPSO algorithm in distribution network reconfiguration with distributed generation,” Energy Eng., vol. 121, no. 1, pp. 187–201, Dec. 2023. doi: 10.32604/ee.2023.042421. [Google Scholar] [CrossRef]
30. S. T. Xi, N. Liu, Y. Wang, Y. Liu, and F. Jing, “Exploration of traditional distribution network optimization construction scheme,” (in ChineseElectric Age, vol. 9, pp. 48–50, Sep. 2019. doi: 10.1186/s42162-024-00368-6. [Google Scholar] [CrossRef]
31. G. Bratati, K. C. Ajoy, and R. B. Arup, “Reliability and efficiency enhancement of a radial distribution system through value-based auto-recloser placement and network remodeling,” Prot. Control Mod. Power Syst., vol. 8, no. 1, pp. 1–14, Jan. 2023. doi: 10.1186/s41601-022-00274-7. [Google Scholar] [CrossRef]
32. B. Chen, K. Xiang, L. Yang, Q. M. Su, D. S. Huang and T. Huang, “Theoretical line loss calculation of distribution network based on the integrated electricity and line loss management system,” in 2018 China Int. Conf. Electr. Distrib. (CICED), Tianjin, China, 2018, pp. 2531–2535. [Google Scholar]
33. L. Lan et al., “Distribution network planning method using demand response resources,” in 2018 China Int. Conf. Electr. Distrib. (CICED), Tianjin, China, 2018, pp. 2641–2644. [Google Scholar]
34. K. Liu and Y. Y. Li, “Study on solutions for active distribution network protection,” (in ChineseProc. CSEE, vol. 34, no. 16, pp. 2584–2590, Jun. 2014. doi: 10.13334/j.0258-8013.pcsee.2014.16.008. [Google Scholar] [CrossRef]
35. Y. Yu, Z. G. Zhu, C. Huang, and K. Deng, “Fault trend judgment for distribution network based on big data analysis,” (in ChineseAutom. Today, vol. 42, no. 1, pp. 132–146, Jan. 2018. doi: 10.3969/j.issn.1002-087X.2018.01.039. [Google Scholar] [CrossRef]
36. K. H. Wu et al., “Research on voltage stability of active distribution network with distributed generations,” in 2018 China Int. Conf. Electr. Distrib. (CICED), Tianjin, China, 2018, pp. 78–83. [Google Scholar]
37. S. Qi, X. Wang, Q. Huang, and C. Shao, “Analysis on voltage fluctuation of active distribution network containing wind-solar hybrid distributed generation,” in China Int. Conf. Electr. Distrib. (CICED), Tianjin, China, 2018, pp. 168–173. [Google Scholar]
38. C. L. Li, W. Han, L. L. Zhou, and X. J. Li, “Coordinated control strategy of distributed generation based on active distribution network under multi-time scales,” in Int. Conf. Smart City Syst. Eng. (ICSCSE), Hunan, China, 2016, pp. 417–420. [Google Scholar]
39. E. Luo, H. Lu, P. Cong, and Y. H. Li, “Multi-stage coordinated optimization of active distribution network with adjustable load and distributed generation,” in 2019 6th Int. Conf. Inf. Sci. Control Eng. (ICISCE), Shanghai, China, 2019, pp. 793–797. [Google Scholar]
40. W. X. Liu, T. Ma, and Y. H. Xu, “Cooperative optimisation strategy of comprehensive vulnerability of active distribution network considering information interrupted,” IET Renew. Power Gener., vol. 14, no. 11, pp. 1978–1987, Jul. 2020. doi: 10.1049/iet-rpg.2019.0742. [Google Scholar] [CrossRef]
41. X. Q. Fu, X. P. Wu, C. Y. Zhang, S. Q. Fan, and N. Liu, “Planning of distributed renewable energy systems under uncertainty based on statistical machine learning,” Prot. Control Mod. Power Syst., vol. 7, no. 4, pp. 619–645, Oct. 2022. doi: 10.1186/s41601-022-00262-x. [Google Scholar] [CrossRef]
42. Y. J. Chen et al., “Dynamic reconfiguration for TEG systems under heterogeneous temperature distribution via adaptive coordinated seeker,” Prot. Control Mod. Power Syst., vol. 7, no. 3, pp. 567–585, Oct. 2022. doi: 10.1186/s41601-022-00259-6. [Google Scholar] [CrossRef]
43. B. Xu et al., “Reactive power optimization of a distribution network with high-penetration of wind and solar renewable energy and electric vehicles,” Prot. Control Mod. Power Syst., vol. 7, no. 4, pp. 801–813, Oct. 2022. doi: 10.1186/s41601-022-00271-w. [Google Scholar] [CrossRef]
44. W. Wang et al., “Partitioning calculation method of short-circuit current for high proportion DG access to distribution network,” Energy Eng., vol. 121, no. 9, pp. 2569–2584, Aug. 2024. doi: 10.32604/ee.2024.051409. [Google Scholar] [CrossRef]
45. G. Dai, Z. J. Wu, J. Xu, and X. L. Dou, “Study of FTU optimal placement in the active distribution network,” Power Syst. Prot. Control, vol. 44, no. 23, pp. 86–93, Dec. 2016. doi: 10.7667/PSPC152089. [Google Scholar] [CrossRef]
46. H. Xiao, X. Ge, and Z. Zhao, “Day-ahead active distribution network optimal schedule with EV penetration,” in Int. Conf. Electr. Utility Deregul. Restruct. Power Technol. (DRPT), Changsha, China, 2015, pp. 2695–2699. [Google Scholar]
47. J. H. Li et al., “Two-stage planning of distributed power supply and energy storage capacity considering hierarchical partition control of distribution network with source-load-storage,” Energy Eng., vol. 121, no. 9, pp. 2389–2408, Aug. 2024. doi: 10.32604/ee.2024.050239. [Google Scholar] [CrossRef]
48. G. F. Wang et al., “Dynamic economic scheduling with self-adaptive uncertainty in distribution network based on deep reinforcement learning,” Energy Eng., vol. 121, no. 6, pp. 1671–1695, May 2024. doi: 10.32604/ee.2024.047794. [Google Scholar] [CrossRef]
49. Y. Jia, L. Yang, and Z. Wang, “Impact of the active management and active control on the survivability of distribution network structure,” in 2015 5th Int. Conf. Electr. Utility Deregul. Restruct. Power Technol. (DRPT), Changsha, China, 2015, pp. 1250–1254. [Google Scholar]
50. B. Yang et al., “A critical survey of technologies of large offshore wind farm integration: Summary, advances, and perspectives,” Prot. Control Mod. Power Syst., vol. 7, no. 2, pp. 233–264, May 2022. doi: 10.1186/s41601-022-00239-w. [Google Scholar] [CrossRef]
51. W. Lu, W. X. Li, W. H. Du, and P. Zhang, “Design and application of integrated energy management system for active distribution network,” (in ChineseAutom. Electr. Power Syst., vol. 40, no. 8, pp. 133–139, Apr. 2016. [Google Scholar]
52. X. L. Fang, Q. Yang, and W. J. Yan, “Power generation maximization of distributed photovoltaic systems using dynamic topology reconfiguration,” Prot. Control Mod. Power Syst., vol. 7, no. 3, pp. 508–522, Jul. 2022. doi: 10.1186/s41601-022-00254-x. [Google Scholar] [CrossRef]
53. D. Zhang and J. Wang, “Research on construction and development trend of micro-grid in China,” (in ChinesePower Syst. Technol., vol. 40, no. 2, p. 8, Dec. 2015. doi: 10.13335/j.1000-3673.pst.2016.02.017. [Google Scholar] [CrossRef]
54. X. Shen and M. Cao, “Research on the influence of distributed power grid for distribution network,” (in ChineseTrans. China Electr. Soc., vol. 30, pp. 346–351, Sep. 2015. [Google Scholar]
55. H. Mehrjerdi and R. Hemmati, “Modeling and optimal scheduling of battery energy storage systems in electric power distribution networks,” J. Clean. Prod., vol. 234, pp. 810–821, Oct. 2019. doi: 10.1016/j.jclepro.2019.06.195. [Google Scholar] [CrossRef]
56. S. T. Meraj, S. S. Yu, M. S. Rahman, K. Hasan, M. S. H. Lipu and H. Trinh, “Energy management schemes, challenges and impacts of emerging inverter technology for renewable energy integration towards grid decarbonization,” J. Clean. Prod., vol. 405, Jun. 2023. Art. no. 137002. doi: 10.1016/j.jclepro.2023.137002. [Google Scholar] [CrossRef]
57. X. L. Li, G. F. Geng, Y. Q. Ji, and L. Z. Lu, “Integrated optimal planning of energy storage and demand side response in active power distribution network,” (in ChinesePower Syst. Technol., vol. 40, no. 12, pp. 3803–3810, Dec. 2016. doi: 10.13335/j.1000-3673.pst.2016.12.024. [Google Scholar] [CrossRef]
58. G. A. Di, F. Liberati, and A. Lanna, “Electric energy storage systems integration in distribution grids,” in 2015 IEEE 15th Int. Conf. Environ. Electr. Eng. (EEEIC), Rome, Italy, 2015, pp. 1279–1284. [Google Scholar]
59. S. Han, X. Yan, L. Qin, X. Q. Lin, and B. Zeng, “Research on electricity market operation mechanism and its benefit of demand side participation,” IOP Conf. Series: Earth Environ. Sci., vol. 81, Apr. 2017, Art. no. 012180. doi: 10.1088/1755-1315/81/1/012180. [Google Scholar] [CrossRef]
60. H. G. Yan, S. S. Chen, M. Zhong, and L. M. Jiang, “Research and design of demand side energy efficiency management and demand response system,” (in ChinesePower Syst. Technol., vol. 39, no. 1, pp. 42–47, Jan. 2015. doi: 10.13335/j.1000-3673.pst.2015.01.007. [Google Scholar] [CrossRef]
61. B. Yang et al., “Comprehensive summary of solid oxide fuel cell control: A state-of-the-art review,” Prot. Control Mod. Power Syst., vol. 7, no. 3, pp. 523–553, Sep. 2022. doi: 10.1186/s41601-022-00251-0. [Google Scholar] [CrossRef]
62. L. Gelazanskas and K. A. A. Gamage, “Demand side management in smart grid: A review and proposals for future direction,” Sustain. Cities Soc., vol. 11, pp. 22–30, 2014. doi: 10.1016/j.scs.2013.11.001. [Google Scholar] [CrossRef]
63. S. Wen, W. Xiong, J. Tan, S. W. Chen, and Q. Li, “Blockchain enhanced price incentive demand response for building user energy network in sustainable society,” Sustain. Cities Soc., vol. 68, May 2021, Art. no. 102748. doi: 10.1016/j.scs.2021.102748. [Google Scholar] [CrossRef]
64. J. Ma, K. L. Di, and R. Li, “Hierarchical optimization method for price incentive demand response to improve the consumption rate of microgrid PV,” (in ChineseElectr. Power, vol. 49, no. 8, pp. 99–105, Aug. 2016. doi: 10.11930/j.issn.1004-9649.2016.08.099.07. [Google Scholar] [CrossRef]
65. H. Hou, Y. Wang, C. Xie, B. Y. Xiong, Q. Y. Zhang and L. Huang, “A dispatching strategy for electric vehicle aggregator combined price and incentive demand response,” IET Energy Syst. Integr., vol. 3, no. 4, pp. 508–519, Aug. 2021. doi: 10.1049/esi2.12042. [Google Scholar] [CrossRef]
66. P. P. Wang, Y. J. Sun, and Y. Li, “Application of uncertainty demand response modeling to power credit incentive decisions,” (in ChineseAutom. Electr. Power Syst., vol. 39, no. 10, pp. 93–99, May 2015. doi: 10.7500/AEPS20140705006. [Google Scholar] [CrossRef]
67. X. Gong, Y. Su, X. F. Zhang, and X. J. Huang, “Optimal charging scheduling for electric vehicle aggregator considering incentive demand response,” (in ChineseMod. Electr. Power, vol. 36, no. 6, pp. 16–22, Dec. 2019. doi: 10.19725/j.cnki.1007-2322.2019.06.003. [Google Scholar] [CrossRef]
68. B. Y. Tian, H. Q. Xu, X. Y. Zhang, X. Q. Chang, and T. Ma, “Day-ahead optimal dispatching method of microgrid considering electricity price incentive demand response,” (in ChinesePower Demand Side Manag., vol. 22, no. 6, pp. 45–50, Nov. 2020. doi: 10.3969/j.issn.1009-1831.2020.06.010. [Google Scholar] [CrossRef]
69. L. Zhang and Y. Xia, “Optimal scheduling strategy for active distribution network considering demand side response,” in 2018 2nd IEEE Conf. Energy Internet Energy Syst. Integr. (EI2), Beijing, China, 2018, pp. 1–6. [Google Scholar]
70. D. Swaminathan and A. Rajagopalan, “Multi-objective golden flower optimization algorithm for sustainable reconfiguration of power distribution network with decentralized generation,” Axioms, vol. 12, no. 1, Jan. 2023, Art. no. 70. doi: 10.3390/axioms12010070. [Google Scholar] [CrossRef]
71. V. F. S. Júnior, R. S. F. Ferraz, R. S. F. Ferraz, and A. C. Rueda-Medina, “Network reconfiguration and distributed generators allocation and sizing using multi-objective optimization algorithms,” in 2023 15th Seminar Power Electr. Control (SEPOC), Santa Maria, Brazil, 2023, pp. 1–6. [Google Scholar]
72. B. S. K. Patnam and N. M. Pindoriya, “Centralized stochastic energy management framework of an aggregator in active distribution network,” IEEE Trans. Ind. Inform., vol. 15, no. 3, pp. 1350–1360, Mar. 2019. doi: 10.1109/TII.2018.2854744. [Google Scholar] [CrossRef]
73. D. S. Rani, N. Subrahmanyam, and M. Sydulu, “Multi-objective invasive weed optimization-an application to optimal network reconfiguration in radial distribution systems,” Int. J. Electr. Power Energy Syst., vol. 73, pp. 932–942, Dec. 2015. doi: 10.1016/j.ijepes.2015.06.020. [Google Scholar] [CrossRef]
74. F. Capitanescu, L. F. Ochoa, H. Margossian, and N. D. Hatziargyriou, “Assesing the potential of network reconfiguration to improve distributed generation hosting capacity in active distribution systems,” IEEE Trans. Power Syst., vol. 30, no. 1, pp. 346–356, May 2014. doi: 10.1109/TPWRS.2014.2320895. [Google Scholar] [CrossRef]
75. B. Katanchi, A. A. Shojaei, and M. Yaghoobi, “Distribution network reconfiguration in effective presence of dgs, evcss and drp: A novel multi-objective approach,” Electr. Power Components Syst., pp. 1–17, Apr. 2024. doi: 10.1080/15325008.2024.2342009. [Google Scholar] [CrossRef]
76. N. W. Tu and Z. H. Fan, “IMODBO for optimal dynamic reconfiguration in active distribution networks,” Processes, vol. 11, no. 6, Jun. 2023, Art. no. 1827. doi: 10.3390/pr11061827. [Google Scholar] [CrossRef]
77. W. Huang and S. Q. Ji, “Fast loss reduction reconfiguration method of distribution network based on feeder couple,” (in ChinesePower Syst. Autom., vol. 39, no. 5, pp. 75–80, Mar. 2015. doi: 10.7500/AEPS20140513002. [Google Scholar] [CrossRef]
78. A. Asrari, S. Lotfifard, and M. S. Payam, “Pareto dominance-based multiobjective optimization method for distribution network reconfiguration,” IEEE Trans. Smart Grid, vol. 7, no. 3, pp. 1401–1410, May 2016. doi: 10.1109/TSG.2015.2468683. [Google Scholar] [CrossRef]
79. A. Azizi, B. Vahidi, and A. F. Nematollahi, “Reconfiguration of active distribution networks equipped with soft open points considering protection constraints,” J. Mod. Power Syst. Clean Energy, vol. 11, no. 1, pp. 212–222, Jan. 2023. doi: 10.35833/MPCE.2022.000425. [Google Scholar] [CrossRef]
80. M. B. Shafik, H. Chen, G. I. Rashed, R. A. El-Sehiemy, M. R. Elkadeem and S. R. Wang, “Adequate topology for efficient energy resources utilization of active distribution networks equipped with soft open points,” IEEE Access, vol. 7, pp. 99003–99016, Jul. 2019. doi: 10.1109/ACCESS.2019.2930631. [Google Scholar] [CrossRef]
81. H. Yu, S. Niu, Y. Shang, Z. Y. Shao, Y. W. Jia and L. N. Jian, “Electric vehicles integration and vehicle-to-grid operation in active distribution grids: A comprehensive review on power architectures, grid connection standards and typical applications,” Renew. Sustain. Energ. Rev., vol. 168, Oct. 2022, Art. no. 112812. doi: 10.1016/j.rser.2022.112812. [Google Scholar] [CrossRef]
82. S. A. A. Matin, S. A. Mansouri, M. Bayat, A. R. Jordehi, and P. Radmehr, “A multi-objective bi-level optimization framework for dynamic maintenance planning of active distribution networks in the presence of energy storage systems,” J. Energy Storage, vol. 52, Aug. 2022, Art. no. 104762. doi: 10.1016/j.est.2022.104762. [Google Scholar] [CrossRef]
83. V. Janamala, K. Radha Rani, P. Sobha Rani, A. N. Venkateswarlu, and S. Ram, “Optimal switching operations of soft open points in active distribution network for handling variable penetration of photovoltaic and electric vehicles using artificial rabbits optimization,” Process Integr. Optim. Sustain., vol. 7, no. 1, pp. 419–437, Jul. 2023. doi: 10.1007/s41660-022-00304-9. [Google Scholar] [CrossRef]
84. Y. Xu, M. Zhao, H. Wu, S. Xiang, and Y. Yuan, “Coordination of network reconfiguration and mobile energy storage system fleets to facilitate active distribution network restoration under forecast uncertainty,” Front. Energy Res., vol. 10, Jan. 2023, Art. no. 1024282. doi: 10.3389/fenrg.2022.1024282. [Google Scholar] [CrossRef]
85. A. Saber, H. H. Zeineldin, T. H. El-Fouly, and A. Al-Durra, “Overcurrent protection coordination with flexible partitioning of active distribution systems into multiple microgrids,” Int. J. Electr. Power Energy Syst., vol. 151, Sep. 2023, Art. no. 109205. doi: 10.1016/j.ijepes.2023.109205. [Google Scholar] [CrossRef]
86. W. Jin, S. Zhang, and J. Li, “Robust planning of distributed generators in active distribution network considering network reconfiguration,” Appl. Sci., vol. 13, no. 13, Apr. 2023, Art. no. 7747. doi: 10.3390/app13137747. [Google Scholar] [CrossRef]
87. M. A. Mejia, L. H. Macedo, G. Muñoz-Delgado, J. Contreras, and A. Padilha-Feltrin, “Active distribution system planning considering non-utility-owned electric vehicle charging stations and network reconfiguration,” Sustain. Energy, Grids Netw., Sep. 2023, Art. no. 101101. doi: 10.1016/j.segan.2023.101101. [Google Scholar] [CrossRef]
88. X. Xu, D. Niu, L. Peng, S. P. Zheng, and J. P. Qiu, “Hierarchical multi-objective optimal planning model of active distribution network considering distributed generation and demand-side response,” Sustain. Energy Technol. Assess., vol. 53, Oct. 2022, Art. no. 102438. doi: 10.1016/j.seta.2022.102438. [Google Scholar] [CrossRef]
89. M. Ehsanbakhsh and M. S. Sepasian, “Simultaneous siting and sizing of soft open points and the allocation of tie switches in active distribution network considering network reconfiguration,” IET Gener., Transm. Distrib., vol. 17, no. 1, pp. 263–280, Nov. 2023. doi: 10.1049/gtd2.12683. [Google Scholar] [CrossRef]
90. S. Rasheed and A. R. Abhyankar, “Efficient operational planning of active distribution network by embedding uncertainties and network reconfiguration,” Elect. Power Syst. Res., vol. 216, Mar. 2023, Art. no. 109036. doi: 10.1016/j.epsr.2022.109036. [Google Scholar] [CrossRef]
91. Q. Shi et al., “Network reconfiguration and distributed energy resource scheduling for improved distribution system resilience,” Int. J. Electr. Power Energy Syst., vol. 124, Jan. 2021, Art. no. 106355. doi: 10.1016/j.ijepes.2020.106355. [Google Scholar] [CrossRef]
92. L. Jun, Y. Fan, Z. Y. Song, and X. K. Liu, “Research on multi-objective distribution network reconfiguration considering power supply reliability,” in 2019 4th Int. Conf. Power Renew. Energy, Chengdu, China, 2019, pp. 61–64. [Google Scholar]
93. C. Ma, Q. Duan, H. Wang, and Y. Mu, “Multi-objective dynamic network reconstruction method for active distribution network including distributed generation and electric vehicles,” in 2022 5th Int. Conf. Energy, Electr. Power Eng. (CEEPE), Chongqing, China, 2022, pp. 612–617. [Google Scholar]
94. N. F. Napis, A. F. A. Kadir, T. Khatib, T. Khatib, E. E. Hassan and M. F. Sulaima, “An improved method for reconfiguring and optimizing electrical active distribution network using evolutionary particle swarm optimization,” Appl. Sci., vol. 8, no. 5, p. 804, Apr. 2018. doi: 10.3390/app8050804. [Google Scholar] [CrossRef]
95. H. Nasiraghdam and S. Jadid, “Optimal hybrid PV/WT/FC sizing and distribution system reconfiguration using multi-objective artificial bee colony (MOABC) algorithm,” Sol. Energy, vol. 86, no. 10, pp. 3057–3071, Oct. 2012. doi: 10.1016/j.solener.2012.07.014. [Google Scholar] [CrossRef]
96. D. Sudha, N. Subrahmanyam, and M. Sydulu, “Self adaptive harmony search algorithm for optimal network reconfiguration,” in 2014 Power Energy Conf. Illinois (PECI), Champaign, IL, USA, 2014, pp. 1–6. [Google Scholar]
97. H. Shareef, A. A. Ibrahim, N. Salman, A. Mohamed, and W. L. Ai, “Power quality and reliability enhancement in distribution systems via optimum network reconfiguration by using quantum firefly algorithm,” Int. J. Electr. Power Energy Syst., vol. 58, pp. 160–169, Jun. 2014. doi: 10.1016/j.ijepes.2014.01.013. [Google Scholar] [CrossRef]
98. H. W. Hong and D. Shirmohammadi, “Reconfiguration of electric distribution networks for resistive line losses reduction,” Trans. Power Deliv., vol. 4, no. 2, pp. 1492–1498, Apr. 1989. doi: 10.1109/61.25637. [Google Scholar] [CrossRef]
99. F. V. Gomes, S. Carneiro, J. L. R. Pereira, M. P. Vinagre, P. A. N. Garcia and L. R. D. Araujo, “A new distribution system reconfiguration approach using optimum power flow and sensitivity analysis for loss reduction,” IEEE Trans. Power Syst., vol. 21, no. 4, pp. 1616–1623, Oct. 2006. doi: 10.1109/TPWRS.2006.879290. [Google Scholar] [CrossRef]
100. X. K. Feng, W. W. Shen, C. Y. Dong, J. L. Zeng, J. D. Shi and D. J. Wang, “Study on fundamental principles and methodologies of distribution network reconfiguration,” TELKOMNIKA Indonesian J. Electr. Eng., vol. 12, no. 3, pp. 1695–1700, Mar. 2014. doi: 10.11591/telkomnika.v12i3.4564. [Google Scholar] [CrossRef]
101. H. M. Khodr, M. A. Matos, and J. Pereira, “Distribution optimal power flow,” in IEEE Lausanne Power Tech, Lausanne, Switzerland, 2007, pp. 1441–1446. doi: 10.1109/PCT.2007.4538527. [Google Scholar] [CrossRef]
102. N. Gupta, A. Swarnkar, and K. R. Niazi, “A modified branch-exchange heuristic algorithm for large-scale distribution networks reconfiguration,” in 2012 IEEE Power Energy Soc. Gen. Meet., San Diego, CA, USA, 2012, pp. 1–7. [Google Scholar]
103. A. Dejamkhooy, Y. F. Khaneghah, and H. Shayeghi, “Modified branch exchange reconfiguration of active distributed network for simultaneous loss reduction and power quality improvement,” Int. Trans. Electr. Energy Syst., vol. 29, no. 10, Jun. 2019, Art. no. 12065. doi: 10.1002/2050-7038.12065. [Google Scholar] [CrossRef]
104. E. C. Pereira, C. H. N. R. Barbosa, and J. A. Vasconcelos, “Distribution network reconfiguration using iterative branch exchange and clustering technique,” Energies, vol. 16, no. 5, Mar. 2023, Art. no. 2395. doi: 10.3390/en16052395. [Google Scholar] [CrossRef]
105. M. L. Fisher, “The Lagrangian relaxation method for solving integer programming problems,” Manage. Sci., vol. 27, no. 1, pp. 1–18, Jan. 1981. doi: 10.1287/mnsc.27.1.1. [Google Scholar] [CrossRef]
106. N. V. Kovački, P. M. Vidović, and A. T. Sarić, “Scalable algorithm for the dynamic reconfiguration of the distribution network using the Lagrange relaxation approach,” Int. J. Electr. Power Energy Syst., vol. 94, pp. 188–202, Jan. 2018. doi: 10.1016/j.ijepes.2017.07.005. [Google Scholar] [CrossRef]
107. H. P. Schmidt, N. Ida, N. Kagan, and J. C. Guaraldo, “Fast reconfiguration of distribution systems considering loss minimization,” in IEEE Trans. Power Syst., London, UK, 2005, pp. 1311–1319. [Google Scholar]
108. F. Gao and L. Han, “Implementing the Nelder-Mead simplex algorithm with adaptive parameters,” Comput. Optim. Appl., vol. 51, no. 1, pp. 259–277, May 2010. doi: 10.1007/s10589-010-9329-3. [Google Scholar] [CrossRef]
109. A. Abur, “A modified linear programming method for distribution system reconfiguration,” Int. J. Electr. Power Energy Syst., vol. 18, no. 7, pp. 469–474, Oct. 1996. doi: 10.1016/0142-0615(96)00005-1. [Google Scholar] [CrossRef]
110. J. A. Taylor and F. S. Hover, “Convex models of distribution system reconfiguration,” IEEE Trans. Power Syst., vol. 27, no. 3, pp. 1407–1413, Feb. 2012. doi: 10.1109/TPWRS.2012.2184307. [Google Scholar] [CrossRef]
111. R. A. Jabr, R. Singh, and B. C. Pal, “Minimum loss network reconfiguration using mixed-integer convex programming,” IEEE Trans. Power Syst., vol. 27, no. 2, pp. 1106–1115, May 2012. doi: 10.1109/TPWRS.2011.2180406. [Google Scholar] [CrossRef]
112. J. F. Franco, M. J. Rider, M. Lavorato, and R. Romero, “A mixed-integer LP model for the reconfiguration of radial electric distribution systems considering distributed generation,” Electr. Power Syst. Res., vol. 97, pp. 51–60, Apr. 2013. doi: 10.1016/j.epsr.2012.12.005. [Google Scholar] [CrossRef]
113. A. S. Deese, “Comparative study of accuracy and computation time for optimal network reconfiguration techniques via simulation,” Int. J. Electr. Power Energy Syst., vol. 63, pp. 394–400, Dec. 2014. doi: 10.1016/j.ijepes.2014.05.030. [Google Scholar] [CrossRef]
114. H. F. Zhai, M. Yang, B. Chen, and N. Kang, “Dynamic reconfiguration of three-phase unbalanced distribution networks,” Int. J. Electr. Power Energy Syst., vol. 99, pp. 1–10, Jul. 2018. doi: 10.1016/j.ijepes.2017.12.027. [Google Scholar] [CrossRef]
115. L. H. Macedo, J. M. Home-Ortiz, R. Vargas, J. Mantovani, R. Romero and J. P. S. Catalão, “Short-circuit constrained distribution network reconfiguration considering closed-loop operation,” Sustain. Energy Grids Netw., vol. 32, Dec. 2022, Art. no. 100937. doi: 10.1016/j.segan.2022.100937. [Google Scholar] [CrossRef]
116. S. Chen, Y. Yang, M. Qin, and Q. S. Xu, “Coordinated multiobjective optimization of the integrated energy distribution system considering network reconfiguration and the impact of price fluctuation in the gas market,” Int. J. Electr. Power Energy Syst., vol. 138, Jun. 2022, Art. no. 107776. doi: 10.1016/j.ijepes.2021.107776. [Google Scholar] [CrossRef]
117. X. Q. Xiao, W. Bo, and S. Z. Hong, “Reconfiguration of two-voltage distribution network based on cuckoo search and simulated annealing algorithm,” (in ChinesePower Syst. Prot. Control, vol. 48, pp. 84–91, May 2020. doi: 10.19783/j.cnki.pspc.190949. [Google Scholar] [CrossRef]
118. B. Stojanović and T. Rajić, “Novel approach to reconfiguration power loss reduction problem by simulated annealing technique,” Int. Trans. Electr. Energy Syst., vol. 27, no. 12, Nov. 2017, Art. no. 2464. doi: 10.1002/etep.2464. [Google Scholar] [CrossRef]
119. Y. Mishima, K. Nara, T. Satoh, T. Ito, and H. Kaneda, “Method for minimum-loss reconfiguration of distribution system by tabu search,” Elect. Eng. Jpn., vol. 152, no. 2, pp. 18–25, May 2005. doi: 10.1002/eej.20086. [Google Scholar] [CrossRef]
120. A. Y. Abdelaziz, F. M. Mohamed, S. F. Mekhamer, and M. A. L. Badr, “Distribution system reconfiguration using a modified Tabu Search algorithm,” Elect. Power Syst. Res., vol. 80, no. 8, pp. 943–953, Aug. 2010. doi: 10.1016/j.epsr.2010.01.001. [Google Scholar] [CrossRef]
121. R. Y. Yamamoto, T. Pinto, R. Romero, and L. H. Macedo, “Reformulated adaptive tabu search algorithm applied to the reconfiguration of radial distribution systems,” Available at SSRN, Jun. 2024, Art. no. 4871994. doi: 10.2139/ssrn.4871994. [Google Scholar] [CrossRef]
122. R. Chidanandappa, T. Ananthapadmanabha, and H. C. Ranjith, “Genetic algorithm based network reconfiguration in distribution systems with multiple DGs for time varying loads,” Procedia Technol., vol. 21, pp. 460–467, Oct. 2015. doi: 10.1016/j.protcy.2015.10.023. [Google Scholar] [CrossRef]
123. E. Kazemi-Robati, M. S. Sepasian, H. Hafezi, and H. Arasteh, “PV-hosting-capacity enhancement and power-quality improvement through multiobjective reconfiguration of harmonic-polluted distribution systems,” Int. J. Electr. Power Energy Syst., vol. 140, Sep. 2022, Art. no. 107972. doi: 10.1016/j.ijepes.2022.107972. [Google Scholar] [CrossRef]
124. G. A. D. Vargas, D. J. Mosquera, and E. R. Trujillo, “Optimization of topological reconfiguration in electric power systems using genetic algorithm and nonlinear programming with discontinuous derivatives,” Electronics, vol. 13, no. 3, p. 616, Feb. 2024. doi: 10.3390/electronics13030616. [Google Scholar] [CrossRef]
125. Y. K. Wu, C. Y. Lee, L. C. Liu, and S. H. Tsai, “Study of reconfiguration for the distribution system with distributed generators,” IEEE Trans. Power Deliv., vol. 25, no. 3, pp. 1678–1685, Jul. 2010. doi: 10.1109/TPWRD.2010.2046339. [Google Scholar] [CrossRef]
126. C. Qian and A. Y. Wang, “Distribution network reconfiguration based on improved differential evolution ant colony algorithm,” in 2022 3rd Int. Conf. Big Data, Artif. Intell. Internet Things Eng. (ICBAIE), Xi’an, China, 2022, pp. 234–240. [Google Scholar]
127. K. S. Sambaiah and T. Jayabarathi, “Loss minimization techniques for optimal operation and planning of distribution systems: A review of different methodologies,” Int. Trans. Electr. Energy Syst., vol. 30, no. 2, Nov. 2019, Art. no. e12230. doi: 10.1002/2050-7038.12230. [Google Scholar] [CrossRef]
128. C. Ma, C. Li, X. Zhang, G. X. Li, and Y. G. Han, “Reconfiguration of distribution networks with distributed generation using a dual hybrid particle swarm optimization algorithm,” Math. Probl. Eng., vol. 2017, no. 2, pp. 1–10, Aug. 2017. doi: 10.1155/2017/1517435. [Google Scholar] [CrossRef]
129. A. Alanazi and T. I. Alanazi, “Multi-objective framework for optimal placement of distributed generations and switches in reconfigurable distribution networks: An improved particle swarm optimization approach,” Sustainability, vol. 15, no. 11, May 2023, Art. no. 9034. doi: 10.3390/su15119034. [Google Scholar] [CrossRef]
130. L. Li and F. C. Xue, “Distribution network reconfiguration based on niche binary particle swarm optimization algorithm,” Energy Proc., vol. 17, pp. 178–182, 2012. doi: 10.1016/j.egypro.2012.02.080. [Google Scholar] [CrossRef]
131. F. Zhao, J. Si, and J. Wang, “Research on optimal schedule strategy for active distribution network using particle swarm optimization combined with bacterial foraging algorithm,” Int. J. Electr. Power Energy Syst., vol. 78, pp. 637–646, Jun. 2016. doi: 10.1016/j.ijepes.2015.11.112. [Google Scholar] [CrossRef]
132. B. Vasudevan and A. K. Sinha, “Reliability improvement of reconfigurable distribution system using GA and PSO,” Elect. Eng., vol. 100, pp. 1263–1275, Jun. 2018. doi: 10.1007/s00202-017-0580-9. [Google Scholar] [CrossRef]
133. M. B. Shafik, G. I. Rashed, H. Chen, M. R. Elkadeem, and S. R. Wang, “Reconfiguration strategy for active distribution networks with soft open points,” in 2019 14th IEEE Conf. Ind. Electr. Appl., Xi’an, China, 2019, pp. 330–334. [Google Scholar]
134. A. Rezaee Jordehi, “Particle swarm optimisation with opposition learning-based strategy: An efficient optimisation algorithm for day-ahead scheduling and reconfiguration in active distribution systems,” Soft Comput., vol. 24, no. 24, pp. 18573–18590, Jun. 2020. doi: 10.1007/s00500-020-05093-2. [Google Scholar] [CrossRef]
135. M. H. Shariatkhah, M. R. Haghifam, J. Salehi, and A. Moser, “Duration based reconfiguration of electric distribution networks using dynamic programming and harmony search algorithm,” Int. J. Electr. Power Energy Syst., vol. 41, no. 1, pp. 1–10, Oct. 2012. doi: 10.1016/j.ijepes.2011.12.014. [Google Scholar] [CrossRef]
136. M. V. Santos, G. A. Brigatto, and L. P. Garcés, “Methodology of solution for the distribution network reconfiguration problem based on improved harmony search algorithm,” IET Gener., Trans. Distrib., vol. 14, no. 26, pp. 6526–6533, Feb. 2021. doi: 10.1049/iet-gtd.2020.0917. [Google Scholar] [CrossRef]
137. S. J. Dias, F. Marques, N. L. P. Garcés, and G. A. A. A. Brigatto, “A novel solution method for the distribution network reconfiguration problem based on a search mechanism enhancement of the improved harmony search algorithm,” Energies, vol. 15, no. 6, Feb. 2022, Art. no. 2083. doi: 10.3390/en15062083. [Google Scholar] [CrossRef]
138. M. M. Aman, G. B. Jasmon, A. H. A. Bakar, and H. Mokhlis, “Optimum network reconfiguration based on maximization of system loadability using continuation power flow theorem,” Int. J. Electr. Power Energy Syst., vol. 54, pp. 123–133, Jan. 2014. doi: 10.1016/j.ijepes.2013.06.026. [Google Scholar] [CrossRef]
139. K. D. Choton, B. Octavian, K. Ganesh, T. S. Mahmoud, and D. Habibi, “Optimal placement of distributed energy storage systems in distribution networks using artificial bee colony algorithm,” Appl. Energy, vol. 232, pp. 212–228, Dec. 2018. doi: 10.1016/j.apenergy.2018.07.100. [Google Scholar] [CrossRef]
140. C. Gao, A. Q. Yu, and Y. Ding, “Reconfiguration of three-phase unbalanced active distribution network based on improved cuckoo search algorithm,” (in ChineseJ Power syst. Automati., vol. 32, no. 9, pp. 143–150, Nov. 2019. doi: 10.19635/j.cnki.csu-epsa.000367. [Google Scholar] [CrossRef]
141. T. T. Nguyen, A. V. Truong, and T. A. Phung, “A novel method based on adaptive cuckoo search for optimal network reconfiguration and distributed generation allocation in distribution network,” Int. J. Electr. Power Energy Syst., vol. 78, pp. 801–815, Jun. 2016. doi: 10.1016/j.ijepes.2015.12.030. [Google Scholar] [CrossRef]
142. A. M. Othman and A. A. El-Fergany, “Optimal dynamic operation and modeling of parallel connected multi-stacks fuel cells with improved slime mould algorithm,” Renew. Energy, vol. 175, pp. 770–782, Sep. 2021. doi: 10.1016/j.renene.2021.04.148. [Google Scholar] [CrossRef]
143. H. J. Wang, J. S. Pan, T. T. Nguyen, and S. W. Weng, “Distribution network reconfiguration with distributed generation based on parallel slime mould algorithm,” Energy, vol. 244, Apr. 2022, Art. no. 123011. doi: 10.1016/j.energy.2021.123011. [Google Scholar] [CrossRef]
144. J. S. Pan, H. J. Wang, T. T. Nguyen, F. M. Zou, and S. C. Chu, “Dynamic reconfiguration of distribution network based on dynamic optimal period division and multi-group flight slime mould algorithm,” Elect. Power Syst. Res., vol. 208, Jul. 2022, Art. no. 107925. doi: 10.1016/j.epsr.2022.107925. [Google Scholar] [CrossRef]
145. A. Kavousi-Fard and T. Niknam, “Multi-objective stochastic distribution feeder reconfiguration from the reliability point of view,” Energy, vol. 64, pp. 342–354, Jan. 2014. doi: 10.1016/j.energy.2013.08.060. [Google Scholar] [CrossRef]
146. S. H. Mirhoseini, S. M. Hosseini, M. Ghanbari, and M. Ahmadi, “A new improved adaptive imperialist competitive algorithm to solve the reconfiguration problem of distribution systems for loss reduction and voltage profile improvement,” Int. J. Electr. Power Energy Syst., vol. 55, pp. 128–143, Feb. 2014. doi: 10.1016/j.ijepes.2013.08.028. [Google Scholar] [CrossRef]
147. A. Kavousi-Fard and M. R. Akbari-Zadeh, “Reliability enhancement using optimal distribution feeder reconfiguration,” Neurocomputing, vol. 106, pp. 1–11, Apr. 2013. doi: 10.1016/j.neucom.2012.08.033. [Google Scholar] [CrossRef]
148. R. Rajaram, K. S. Kumar, and N. Rajasekar, “Power system reconfiguration in a radial distribution network for reducing losses and to improve voltage profile using modified plant growth simulation algorithm with distributed generation (DG),” Energy Rep., vol. 1, pp. 116–122, Nov. 2015. doi: 10.1016/j.egyr.2015.03.002. [Google Scholar] [CrossRef]
149. S. Naveen, K. S. Kumar, and K. Rajalakshmi, “Distribution system reconfiguration for loss minimization using modified bacterial foraging optimization algorithm,” Int. J. Electr. Power Energy Syst., vol. 69, pp. 90–97, Jul. 2015. doi: 10.1016/j.ijepes.2014.12.090. [Google Scholar] [CrossRef]
150. H. Li, W. Mao, A. Zhang, and C. Li, “An improved distribution network reconfiguration method based on minimum spanning tree algorithm and heuristic rules,” Int. J. Electr. Power Energy Syst., vol. 82, pp. 466–473, Nov. 2016. doi: 10.1016/j.ijepes.2016.04.017. [Google Scholar] [CrossRef]
151. A. Uniyal and S. Sarangi, “Optimal network reconfiguration and DG allocation using adaptive modified whale optimization algorithm considering probabilistic load flow,” Elect. Power Syst. Res., vol. 192, Mar. 2021, Art. no. 106909. doi: 10.1016/j.epsr.2020.106909. [Google Scholar] [CrossRef]
152. E. Azad-Farsani, I. G. Sardou, and S. Abedini, “Distribution network reconfiguration based on LMP at DG connected busses using game theory and self-adaptive FWA,” Energy, vol. 215, Jan. 2021, Art. no. 119146. doi: 10.1016/j.energy.2020.119146. [Google Scholar] [CrossRef]
153. D. Anteneh, B. Khan, O. P. Mahela, H. H. Alhelou, and J. M. Guerrero, “Distribution network reliability enhancement and power loss reduction by optimal network reconfiguration,” Comput. Electr. Eng., vol. 96, Dec. 2021, Art. no. 107518. doi: 10.1016/j.compeleceng.2021.107518. [Google Scholar] [CrossRef]
154. Y. Li, B. Sun, Y. Zeng, S. M. Dong, S. Q. Ma and X. Zhang, “Active distribution network active and reactive power coordinated dispatching method based on discrete monkey algorithm,” Int. J. Electr. Power Energy Syst., vol. 143, Dec. 2022, Art. no. 108425. doi: 10.1016/j.ijepes.2022.108425. [Google Scholar] [CrossRef]
155. L. L. Li, J. L. Xiong, M. L. Tseng, Z. Yan, and M. K. Lim, “Using multi-objective sparrow search algorithm to establish active distribution network dynamic reconfiguration integrated optimization,” Expert Syst. Appl., vol. 193, May 2022, Art. no. 116445. doi: 10.1016/j.eswa.2021.116445. [Google Scholar] [CrossRef]
156. M. Cikan and B. Kekezoglu, “Comparison of metaheuristic optimization techniques including equilibrium optimizer algorithm in power distribution network reconfiguration,” Alex. Eng. J., vol. 61, no. 2, pp. 991–1031, 2022. doi: 10.1016/j.aej.2021.06.079. [Google Scholar] [CrossRef]
157. Z. Lin, C. X. Jiang, Y. J. Lu, and C. X. Liu, “Active distribution network reconfiguration with renewable energy based on multi-agent deep reinforcement learning,” in 2023 6th Int. Conf. Energy, Electr. Power Eng. (CEEPE), Guangzhou, China, 2023, pp. 535–542. [Google Scholar]
158. Y. Gao, W. Wang, J. Shi, and N. P. Yu, “Batch-constrained reinforcement learning for dynamic distribution network reconfiguration,” IEEE Trans. Smart Grid, vol. 11, no. 6, pp. 5357–5369, Jun. 2020. doi: 10.1109/TSG.2020.3005270. [Google Scholar] [CrossRef]
159. W. Huang, W. Zheng, and D. J. Hill, “Distribution network reconfiguration for short-term voltage stability enhancement: An efficient deep learning approach,” IEEE Trans. Smart Grid, vol. 12, no. 6, pp. 5385–5395, Jul. 2021. doi: 10.1109/TSG.2021.3097330. [Google Scholar] [CrossRef]
160. W. Zheng, W. Huang, and D. J. Hill, “A deep learning-based general robust method for network reconfiguration in three-phase unbalanced active distribution networks,” Int. J. Electr. Power Energy Syst., vol. 120, Sep. 2020, Art. no. 105982. doi: 10.1016/j.ijepes.2020.105982. [Google Scholar] [CrossRef]
161. S. H. Oh, Y. T. Yoon, and S. W. Kim, “Online reconfiguration scheme of self-sufficient distribution network based on a reinforcement learning approach,” Appl. Energy, vol. 280, Dec. 2020, Art. no. 115900. doi: 10.1016/j.apenergy.2020.115900. [Google Scholar] [CrossRef]
162. V. H. Bui and W. Su, “Real-time operation of distribution network: A deep reinforcement learning-based reconfiguration approach,” Sustain. Energy Technol. Assess., vol. 50, Mar. 2022, Art. no. 101841. doi: 10.1016/j.seta.2021.101841. [Google Scholar] [CrossRef]
163. S. Malekshah, A. Rasouli, Y. Malekshah, A. Ramezani, and A. Malekshah, “Reliability-driven distribution power network dynamic reconfiguration in presence of distributed generation by the deep reinforcement learning method,” Alex. Eng. J., vol. 61, no. 8, pp. 6541–6556, Aug. 2022. doi: 10.1016/j.aej.2021.12.012. [Google Scholar] [CrossRef]
Appendix A

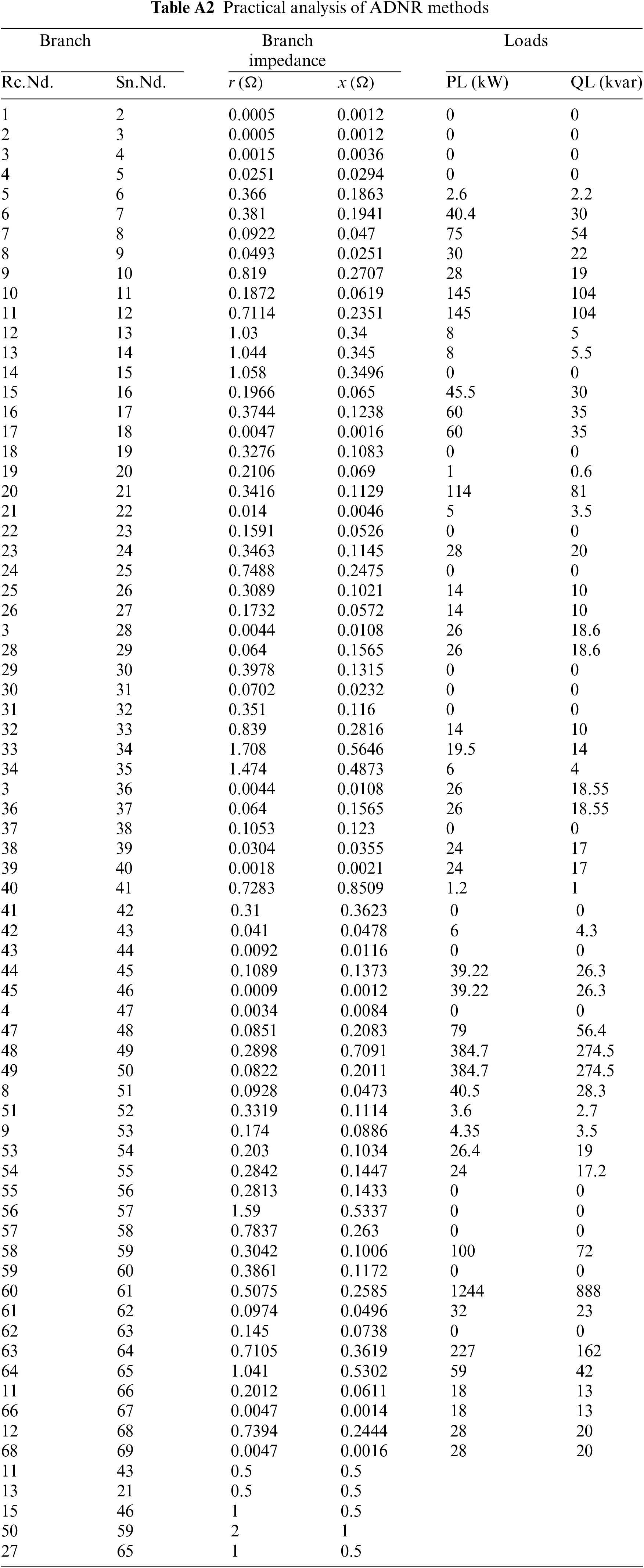
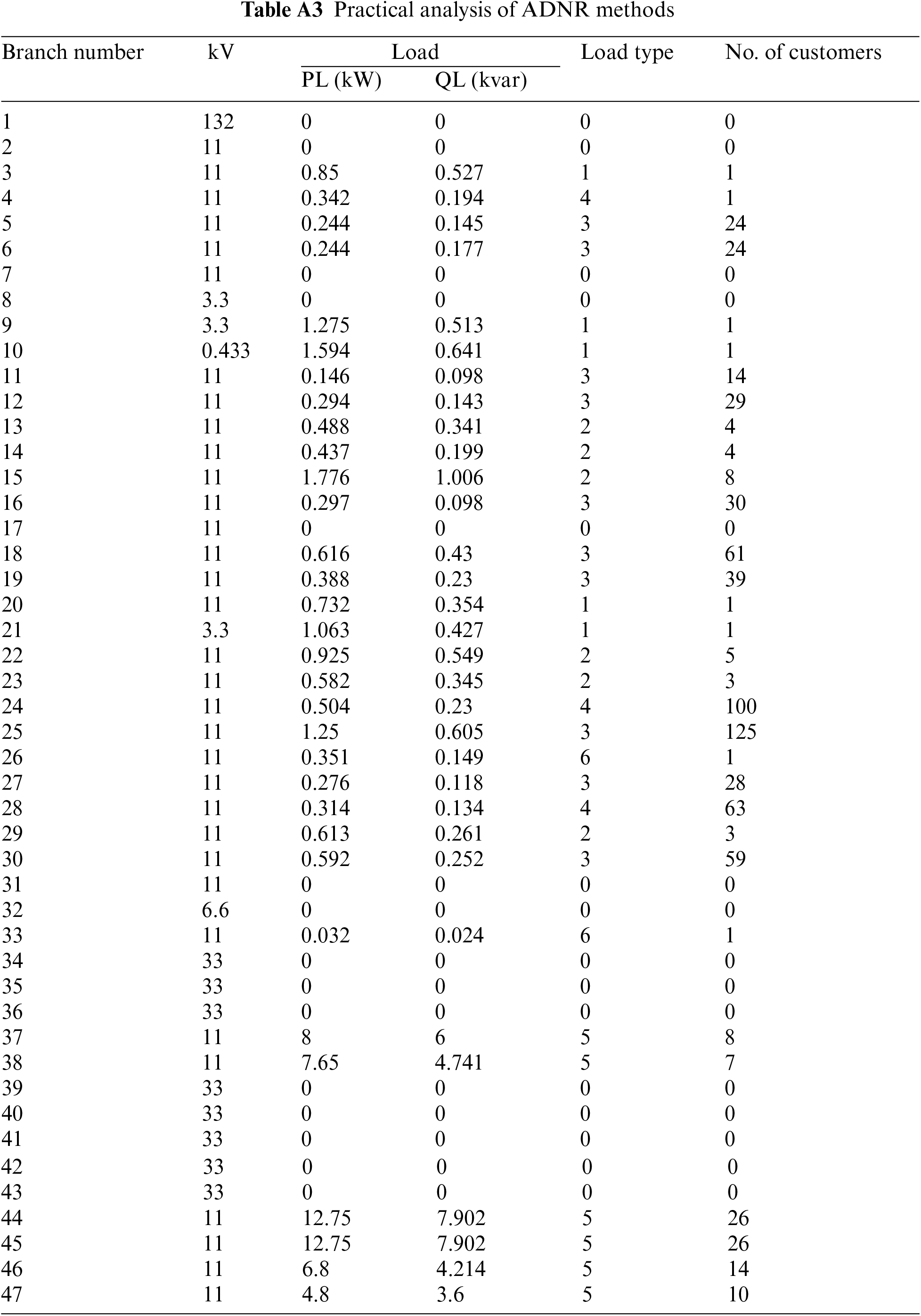
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF





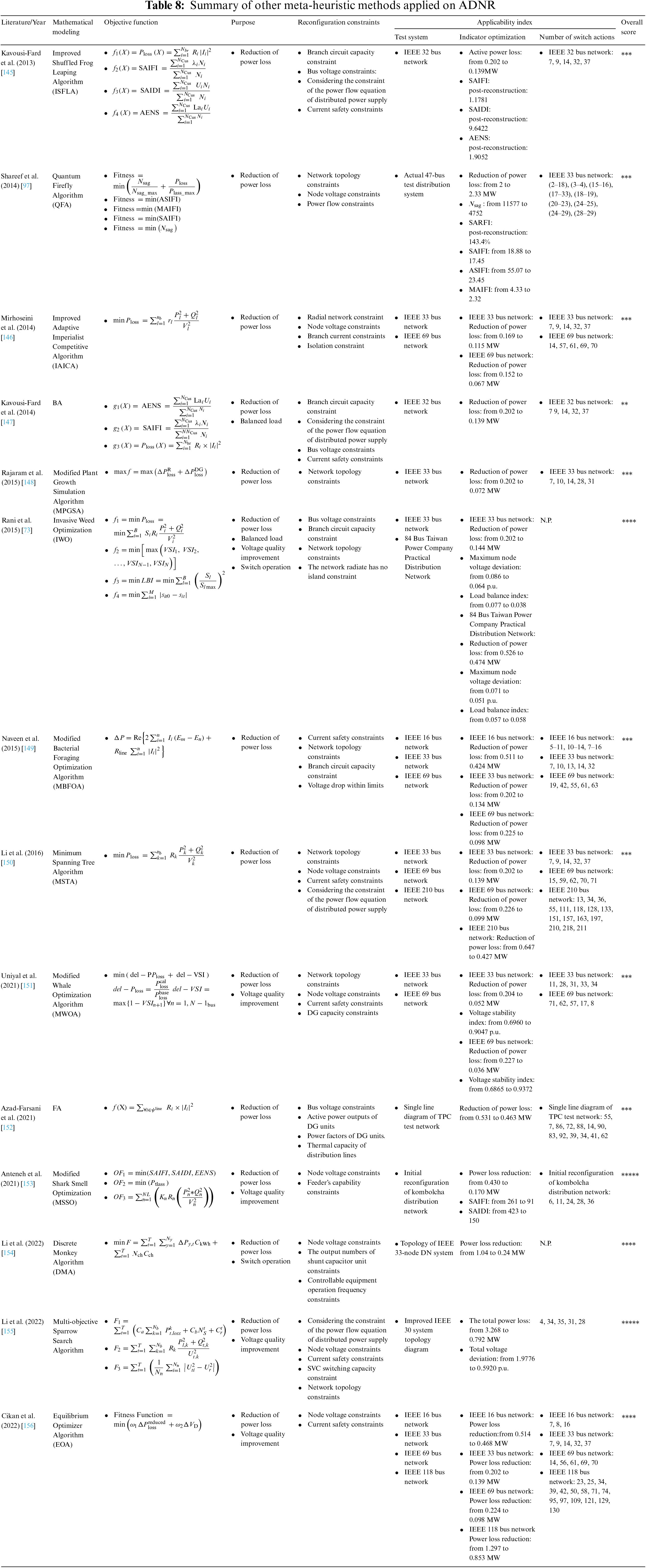
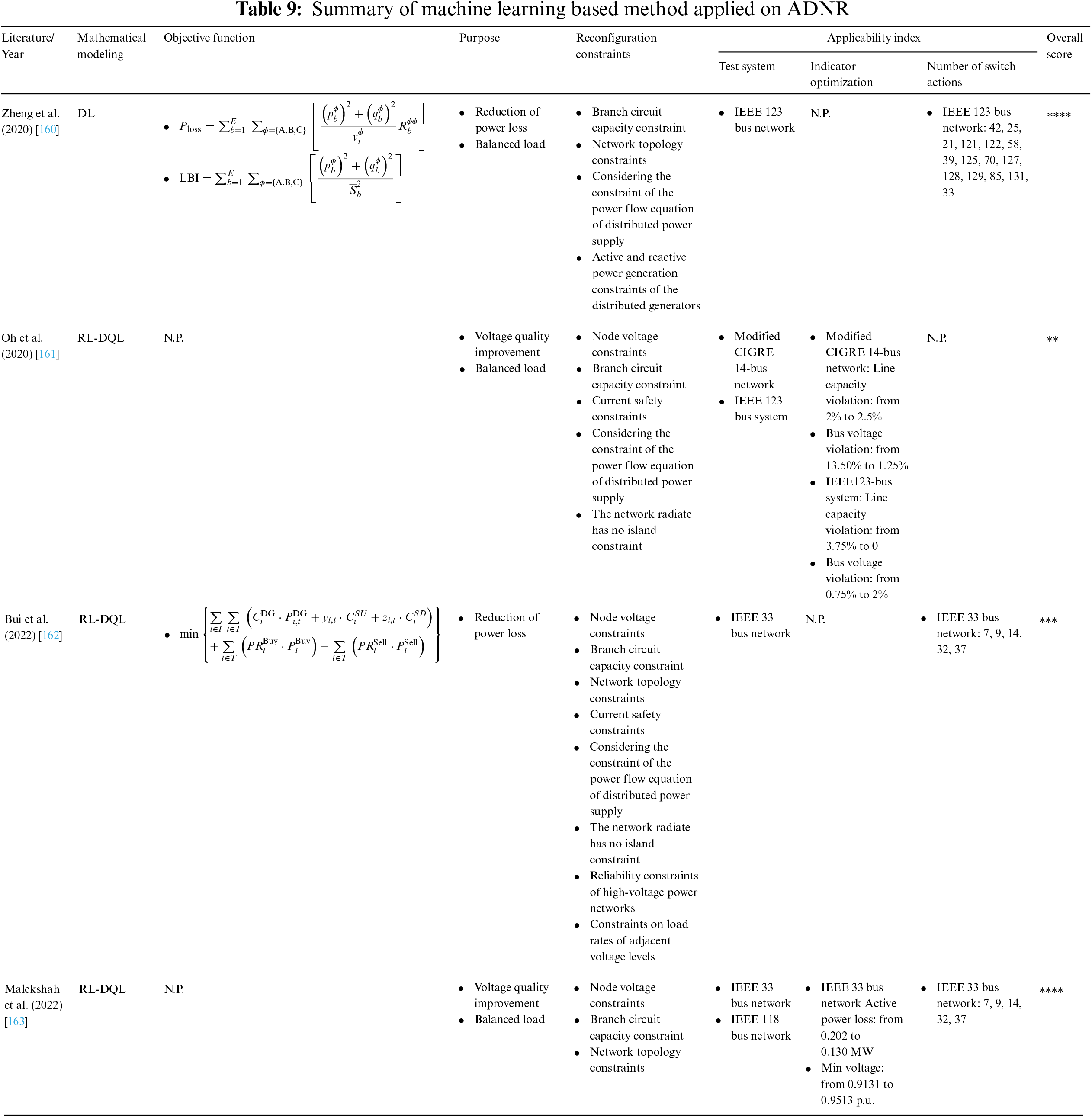
 Downloads
Downloads
 Citation Tools
Citation Tools