Distributed Robust Scheduling Optimization of Wind-Thermal-Storage System Based on Hybrid Carbon Trading and Wasserstein Fuzzy Set

1  Introduction

In recent years, the combined pressure of environmental degradation and energy scarcity have spurred rapid advancements in new energy power generation, particularly in wind power [1]. Anticipated by 2030, China’s installed wind power capacity is forecasted to surpass 1.2 billion kilowatts, constituting well over half of the nation’s overall energy capacity. Additionally, the country aims to reduce its carbon dioxide emissions per unit of gross domestic product by over 65% relative to 2005 levels. Furthermore, the consumption of non-fossil energy in primary energy is expected to reach approximately 25%, while forest stock volume is set to increase by 6 billion cubic meters compared to 2005 figures. Lastly, the combined installed capacity of wind and solar power is targeted to exceed 1.2 billion kilowatts [2]. However, as wind power generation grows, its unpredictability poses challenges to the power supply’s flexible regulation capacity, complicating the adjustment to dynamic load changes. The current predominant approach is the multi-energy complementary mode, primarily comprising storage, fire, and water [3]. Pumping and storage stand out as the most effective control modes for developing new energy systems now and in the future. Nevertheless, the urgent issue to address under the coordination of a multisource power grid is how to mitigate the unpredictability of wind power output effectively while simultaneously considering the low-carbon economy [4].

Research on new energy integrated power generation systems characterized by high permeability has been extensively conducted domestically and internationally [5]. Jiang et al. [6] quantitatively outlined the flexibility requirements of these systems, using quantiles to ascertain the probabilistic distribution intervals of the output from wind-solar power station clusters. Xu et al. [7–9] devised two types of system optimization models with the aim of maximizing the integration of wind and solar power while minimizing overall system costs. These models consider transmission factors and incorporate demand response strategies within the northwest region. Li et al. [10] delved into the power control methods of wind turbines, considering their potential role in power system frequency modulation; they also explored reserve power regulation strategies for units under variable wind speeds, presuming the use of a 5 MW unit model. Hou et al. [11] introduced a frequency response model that considers renewable energy penetration, governor dead zones, and generation rate limits and proposed a refined version of this model. Zhu et al. [12] quantitatively optimized the capacity and control parameters of the energy storage system using a third-order virtual synchronous machine control technique, thereby improving the system’s ability to handle power imbalances at various levels of wind power penetration.

A novel hybrid stochastic/interval optimization technique for combined heat and power day-ahead scheduling was proposed in [13]. Li et al. [14] proposed a paradigm for optimal day-ahead scheduling. A dynamic power regulation margin model, which accounts for adjacent time periods and is based on anti-peak regulation, was presented. Zhang et al. [15] detailed the construction of a similar model considering inverse peak regulation. Furthermore, this study introduced a model that integrates a battery energy storage system with a wind turbine termed wind turbine and battery energy storage system and proposed a unique rolling optimization framework for the two-stage generation planning market. Zhang et al. [16] proposed the distributed robust chance constraint model. Currently, the primary goal of the adjustable power supply side, such as multi-energy systems, is to stabilize the fluctuations and abrupt changes in wind power. A critical challenge is to mitigate further the uncertainty of wind power in the electrical grid while leveraging its low-carbon advantages.

Concurrently, the incorporation of carbon trading mechanisms within new scenery-based power systems has become a focal point of contemporary research. Lei et al. [17] devised a framework for operating photothermal power plants and wind power systems that integrate carbon trading, melding low-carbon approaches with market mechanisms. Jiao et al. [18] incorporated a stepped carbon trading mechanism into the operational and scheduling phases of the system, applying a two-stage robust optimization method to enhance output. Furthermore, Lu et al. [19] constructed a regional virtual power plant that accommodated the green certificate-carbon trading mechanism and executed a two-stage distributed resilient optimization schedule, informed by a stepwise carbon trading mechanism within the ambit of a quota system.

Bhavsar et al. [20] developed an integrated source-load-storage optimization model incorporating a carbon trading mechanism aimed at minimizing the system’s operational costs. Additionally, they introduced an optimization method that considers the implications of carbon trading. Leng et al. [21] proposed an integrated energy co-optimization model that leverages a stepped carbon trading mechanism and multi-energy demand response, encompassing cooling, heating, electricity, and gas. Wei et al. [22] proposed a pricing model for electric vehicle agents within parking facilities, designed in consideration of the carbon trading scheme.

The research underscores that the deployment of a carbon trading mechanism can effectively reduce the carbon emissions of the joint system. However, carbon trading presents certain challenges, such as the difficulty in assigning responsibility for carbon emissions and the limited eagerness among stakeholders to participate in carbon emissions reduction. As a solution, this study proposes a distributed robust optimal scheduling approach, predicated on a hybrid carbon trading mechanism, for wind-thermal-storage systems.

Considering the issues discussed, the study first constructs a hybrid step-by-step carbon trading mechanism, targeting the dual objectives of minimizing costs and carbon emissions. This mechanism integrates short-term and long-term carbon trading strategies. Subsequently, the study proposes an advanced distributed robust optimization scheduling model, employing the Wasserstein metric to establish a fuzzy set. The research culminates with an analysis of the effects of the distributed robust scheduling approach and the hybrid carbon trading mechanism on the power system’s operational costs, providing insights for reducing carbon emissions while ensuring system stability.

This review paper is structured as follows: Section 2 introduces the framework of a wind–fire storage system considering a carbon trading mechanism. Section 3 presents a model for optimizing the portfolio of wind turbines considering the uncertainty of their output power. Section 4 presents a distributional robust optimization model based on the Wasserstein metric, Section 5 provides case simulations and analyses, and Section 6 contains conclusions and future trends.

2  Framework for Wind–Fire Storage Systems Considering Carbon Trading Mechanisms

2.1 Framework Structure for Wind–Fire Storage Systems

Realizing low-carbon goals within wind-thermal-storage ecosystems is possible by meticulously orchestrating the operational timetable of energy components. Comprising thermal generators, storage mechanisms, and wind energy converters, the wind-thermal-storage configuration is illustrated in Fig. 1. Through engagement with the broader market, this system integrates seamlessly with the power grid and the carbon exchange market.

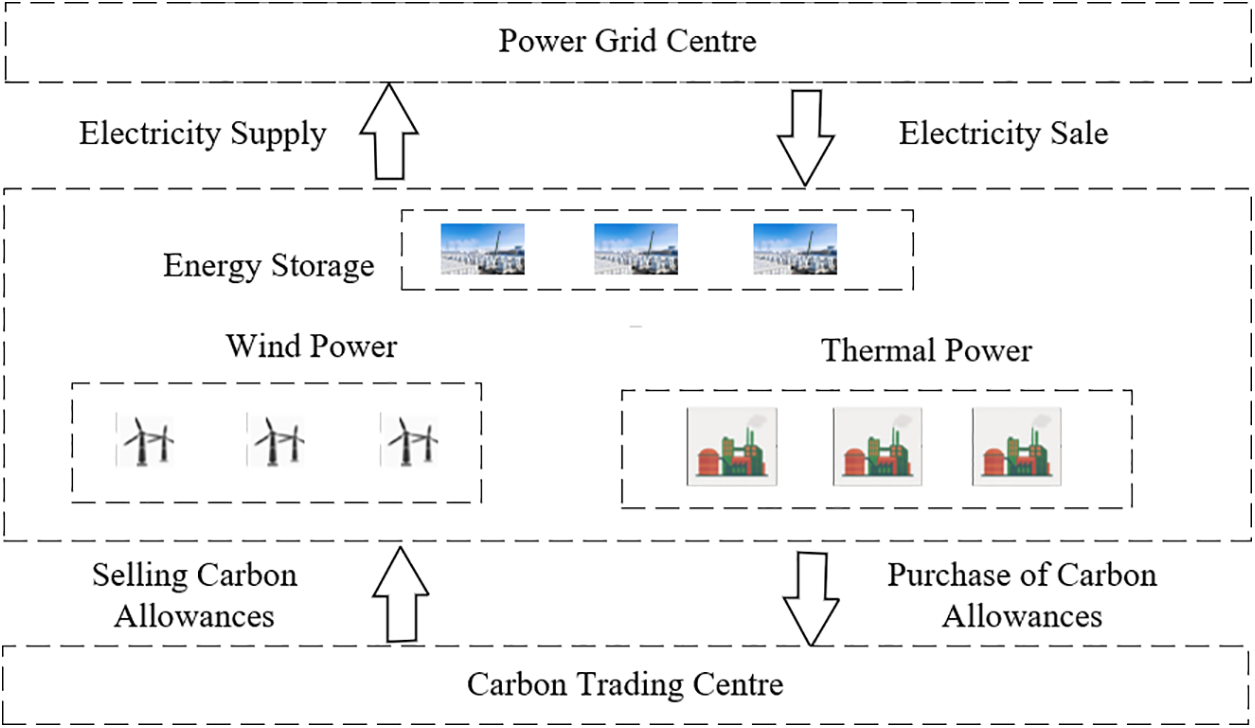
Figure 1: System architecture diagram

2.2 Reward and Punishment for Carbon Emission in Wind–Fire Storage Systems

In pursuit of the wind-thermal-storage system’s low-carbon targets, this research delves into the system’s carbon emission incentive and disincentive framework, evaluating it within immediate and extended timeframes.

2.2.1 Short-Term Reward and Punishment Mechanism

This research embraces a carbon trading schema based on emission permits. With the maturation of the carbon allowance market, electricity users are gradually integrated into it. Authorities commonly employ a gratuitous approach to allocate initial carbon allowances to microgrids and additional energy systems. Calculations of actual carbon emissions are inferred from established emission factors. By utilizing emission permits issued by the government, the framework enables the enactment of immediate and extended incentives and penalties to regulate carbon emissions. Within this context, the wind-thermal-storage system functions as a singular entity in the carbon marketplace [23,24]. Formulas to compute the carbon emissions and allowances for this system hinge on factors, such as the power generation and consumption of thermal units.

Etr(Etbuy)=τtcEtbuy(1)

Etc(Etbuy,EtW)=ηbuyEtbuy+ηreEtW(2)

Etbuy=max(∑i∈N(Ei,tbuy−Ei,tsell−PpESS),0)(3)

where τtc represents the carbon emissions per unit of purchased electricity; Etr and Etc denote the carbon emissions and carbon emission allowances of wind-thermal-storage systems, respectively; Etbuy represents the purchased electricity of wind–fire storage systems; EtW is electricity generated by wind turbines; ηbuy and ηre are the allocation of carbon emission allowances, determined on a per-unit basis for renewable energy generation and the purchasing of electricity; Ei,tbuy and Ei,tsell are carbon emission allowances per unit of renewable electricity generation and per unit of purchased electricity; PpESS is purchased and sold electricity per unit, charging and discharging power of storage equipment; and N indicates the number of wind–fire storage systems.

This study employs a step-type carbon emissions trading model to delineate the cost implications associated with carbon trading, as detailed below:

Ftc={−λtcEtr,Etr<0λtcEtr,0≤Etr<Lλtc(1+α)(Etr−L)+λtcL,L≤Etr<2Lλtc(1+2α)(Etr−2L)+λtc(2+α)L,2L≤Etr<3Lλtc(1+3α)(Etr−3L)+λtc(3+3α)L,3L≤Etr<4Lλtc(1+4α)(Etr−4L)+λtc(4+6α)L,4L<Etr(4)

where Ftc is the expression for the cost of carbon trading; λtc is the base price of carbon trading; L is the length of the carbon emission interval for carbon trading; and a is the growth rate of the carbon trading interval. Eq. (4) represents the carbon trading cost of the wind–fire storage system. It shows that a large amount of carbon emissions leads to high carbon trading costs [25–27].

2.2.2 Long-Term Incentive and Penalty Mechanisms

Given that the cost associated with the short-term carbon trading mechanism is relatively invariant, it lacks appeal for certain carbon-emitting enterprises over the long haul. Consequently, this study introduces a long-term incentive and disincentive framework, which is predicated upon the assessment of carbon emission reductions achieved by the wind-thermal-storage system, setting forth a corresponding incentive and disincentive structure. Illustratively, adopting a daily cycle for carbon assessment, this mechanism is scrutinized while keeping other parameters constant. Thus, within this carbon assessment framework, the reduction of carbon emissions constitutes a dynamic process of adjustment. Generally, curtailing carbon emissions is conducive to power trading, heightening the emphasis on the cost of carbon emissions.

The wind-thermal-storage system’s cumulative carbon emissions during each evaluation period serve as the metric for assessment. By leveraging the consumption and generation data of the system, the carbon emissions can be scrutinized. Should the assessment metrics align with the anticipated benchmarks within a given cycle, the subsequent cycle sees a decrement in the external selling price and an increment in the purchasing price. By contrast, failing to meet the assessment standards leads to noncompliance with the external trading prices. This engenders a long-term incentive and disincentive regime for the carbon emissions of the wind-thermal-storage system, fostering a balance between economic considerations and carbon emissions. The formula for adjusting the external purchase and sale prices in the wind-thermal-storage system is delineated as follows:

λts=λts,0−εsΔλt(γDireal−γexpect),t∈Di(5)

λtb=λtb,0−εbΔλt(γDireal−γexpect),t∈Di(6)

γDireal=∑t∈DiEtr(Etbuy)(7)

Δλt=λts,0−λtb,0(8)

where λts and λtb are the adjusted external purchase and sale price, respectively; λts,0 and λtb,0 are the unadjusted external purchase and sale price, respectively; εs and εb are tariff incentive and penalty factor, respectively; Δλt is the difference between unadjusted external tariffs; γDireal and γexpect are the actual and expected levels of the assessment indicator; Di is carbon emission assessment period. Eqs. (5) and (6) guarantee the adjustment of external sales and external purchase prices of the grid company, respectively; Eq. (7) defines the practical evaluation indexes of the wind–fire storage system; and Eq. (8) expresses the difference between the unadjusted external sales price and the external purchase price.

3  Optimization Model Accounting for Uncertainty in Wind Turbine Outputs

3.1 Wind Turbine Output Uncertainty Analysis

When the modeling procedure’s grid uncertainty is exclusively linked to the variance in the wind turbine’s output capacity, this power discrepancy’s associated uncertainty dataset can be symbolized as δ={δ1,δ2,⋯,δK}. The quantifiable connection among the wind turbine’s actual output, the intended output, and the turbine’s output deviation is expressed as follows:

{δw,t=pw,trea−pw,tplaδw,t∈{δ1,δ2,⋯,δK}.(9)

In this context, K represents the quantity of power deviation samples originating from the wind turbine generator (WTG) output. At time t, the actual power output of the wth WTG is denoted as pw,trea, whereas the anticipated power output is referred to as pw,tpla. The difference between these two, known as the output deviation power, is expressed as δw,t.

3.2 Modeling of Unit Combinations Considering Wind Power Uncertainties

3.2.1 Objective Function

The goal function integrates the predicted performance of thermal power plants, energy storage systems (accounting for negative output during charging), and flexible loads over a 24-h period, treating these as continuous choice variables. The daily operational state of thermal units is symbolized by a binary decision variable, with the aim to minimize overall expenses under severe scenarios, thereby creating a model adaptable to the fluctuations in wind turbine generation [28,29]. This model unfolds in a dual-stage approach: at first, stage one determines the actual power yield from wind turbines according to initial scheduling plans. Afterward, stage two revolves around revising the dispatch plan for thermal plants, storage units, and interruptible loads, considering the realized wind power output, seamlessly integrating carbon trading aspects into the dispatch strategy. The all-encompassing objective is captured in Eq. (10).

min{F(x)+supp∈FEP[f(x,δ)]+Ftc_all}(10)

where F(x) signifies the initial-stage operational expense of the system, embodying the aggregate cost in the absence of wind turbine variability considerations. By contrast, f(x,δ) symbolizes the secondary stage scheduling cost, reflecting the readjustment costs incurred due to unpredictability in wind turbine operations. P denotes the authentic probability distribution of wind power forecast deviations, while F represents the fuzzy set associated with the probabilistic distribution of these deviations. Long-term and short-term carbon trading costs are indicated by Ftc_all.

a)   Total cost of the first stage

F(x)=fthe+fcut+fbat(11)

Eq. (11) represents the cost of the first phase of the system, In the formula, fthe, fcut, and fbat are the total costs of heat engine, interruptible load, and energy storage, respectively.

fthe=∑h = 1H∑t = 1T[Ch,t(Ph,t)+Ch,tO+Ch,tS](12)

Ch,t(Ph,t)=aiPh,t2+biPh,t+ci(13)

Eqs. (12) and (13) are the expression of the total cost of thermal power units. In the formula, Ch,t(Ph,t) is the operating cost of the hth heat unit at time t, which can be fitted as a quadratic function of Ph,t; Ph,t is the operating power of the hth thermal unit at time t. ai, bi, and ci are cost coefficients. Ch,tO and Ch,tS represent start-up and shut-down costs, respectively.

fcut=∑n = 1N∑t = 1TCn,tPn,t(14)

Cn,t=anλt(15)

Eqs. (14) and (15) are the total cost expression of interruptible load. In the formula, Pn,t is the load shedding amount of the nth bus at time t, Cn,t is the load shedding compensation price, an is the compensation coefficient, and λt is the time-varying electricity price.

fbat=∑m = 1M∑t = 1T(Km,tchPm,tchη−Km,tdisPm,tdis/η)(16)

Eq. (16) is the total cost expression of energy storage. In the formula, Pm,tdis and Pm,tch are the discharge and charging power of the mth energy storage system at time t, Km,tch is the charging cost coefficient, Km,tdis is the discharge income coefficient, and η is the charging and discharging efficiency of the energy storage system.

b)   Total cost of the second stage

supP∈FEP[f(x,δ)]=ftheδ+fcutδ+fbatδ(17)

Eq. (17) is the second stage cost of the system. In the formula, ftheδ, fcutδ, and fbatδ are the rescheduling costs of thermal power units, interruptible loads, and energy storage in extreme cases, respectively.

Ftc_all=Ftc(Etc,Etr)+Ft−2c(18)

Ft−2c=(γDireal−γexpect)Elongreal(19)

Eqs. (18) and (19) are the long-term and short-term carbon transaction costs in the second stage of the system cost. Ft−2c represents the long-term carbon trading price. Elongreal represents actual carbon emissions over the period of long-term carbon trading.

An examination into the carbon evaluation scheme is conducted, contemplating a single day as the evaluative period, with all other variables held constant. The modified external electricity price resulting from this mechanism leads to a significant decrease in electricity trading costs, suggesting that prior carbon emissions were interconnected with energy sharing advantages. However, compromising on carbon reduction efforts can yield greater economic gains. Consequently, within the carbon assessment framework, carbon mitigation unfolds as a dynamic adjustment procedure. In summary, lowering carbon emissions proves advantageous to power trading, prompting increased awareness of carbon expenses and more financial support to the generation sector.

3.2.2 Constraints

In the defined model, the following constraints should be met:

Power balance constraint

∑h = 1HPh,t+∑w = 1WPw,tpla=∑n = 1N(Pn,tload−Pn,t)+∑m = 1M(Pm,tch−Pm,tdis)(20)

where Pw,tpla is the operating power of the hth WTG at time t, Pn,tload is the load power.

Thermal power unit constraints

xh,tuPh,min≤Ph,t≤xh,tuPh,max(21)

∑h = 1H(xh,tuPh,max−Ph,t)≥ρ∑n = 1NPn,tload(22)

where Ph,max and Ph,min are the maximum and minimum output power, respectively. ρ is the hot-readiness factor. The binary variable of the thermal turbine is expressed in vector form as x=(xh,tu,xh,to,xh,ts)T. Thermal power unit states, startups, and shutdowns are denoted by xh,tu, xh,to, and xh,ts, respectively. xh,tu=1 denotes that the system is in operating state, and xh,tu=0 denotes that the system is in nonoperating state.

Wind turbine output power constraints

0≤Pw,trea≤Pwmax(23)

where Pw,trea is the actual output power of the unit, Pwmax is the maximum output power.

Interruptible load constraint

0≤Pn,t≤Pn,tmax(24)

where Pn,tmax is the maximum overload power of the nth node at moment t.

Energy storage constraints

0≤Pm,tdis≤Pm,tmax(25)

0≤Pm,tch≤Pm,tmax(26)

η∑t = 1TPm,tch−1η∑t = 1TPm,tdis=0(27)

where Pm,tmax is the upper limit of charging and discharging power, η is the charging and discharging efficiency of the energy storage system.

Power flow security constraints

Plmin≤Pl,t≤Plmax(28)

Plmin≤∑h = 1HGl−hPh,t+∑w = 1WGl−wPw,trea+∑m = 1MGl−m(Pm,tch−Pm,tdis)−∑n = 1NGl−n(Pn,tload−Pn,t)≤Plmax(29)

where Pl,t is the line power of branch I at time t; Plmax and Plmin are the upper and lower limits of the line power, respectively; Gl−h, Gl−w, Gl−m, and Gl−n are line-to-thermal, line-to-wind, line-to-storage, and line-to-load electricity transfer allocation factors.

4  Distributed Robust Optimization Model Based on Wasserstein Metrics

The construction of fuzzy sets is central to the efficacy of the distributed robust optimization (DRO) method, integral for the mathematical restructuring, resolution of the DRO model, and the preservation of result conservatism. Utilizing Wasserstein metrics, these fuzzy sets aim to diminish the discrepancy between dual probability distributions, thus allowing the empirical distribution, inferred from historical data, to reflect the true probability distribution P more accurately—an objective difficult to attain through mere historical data scrutiny. The model’s conceptual framework is illustrated in Fig. 2.

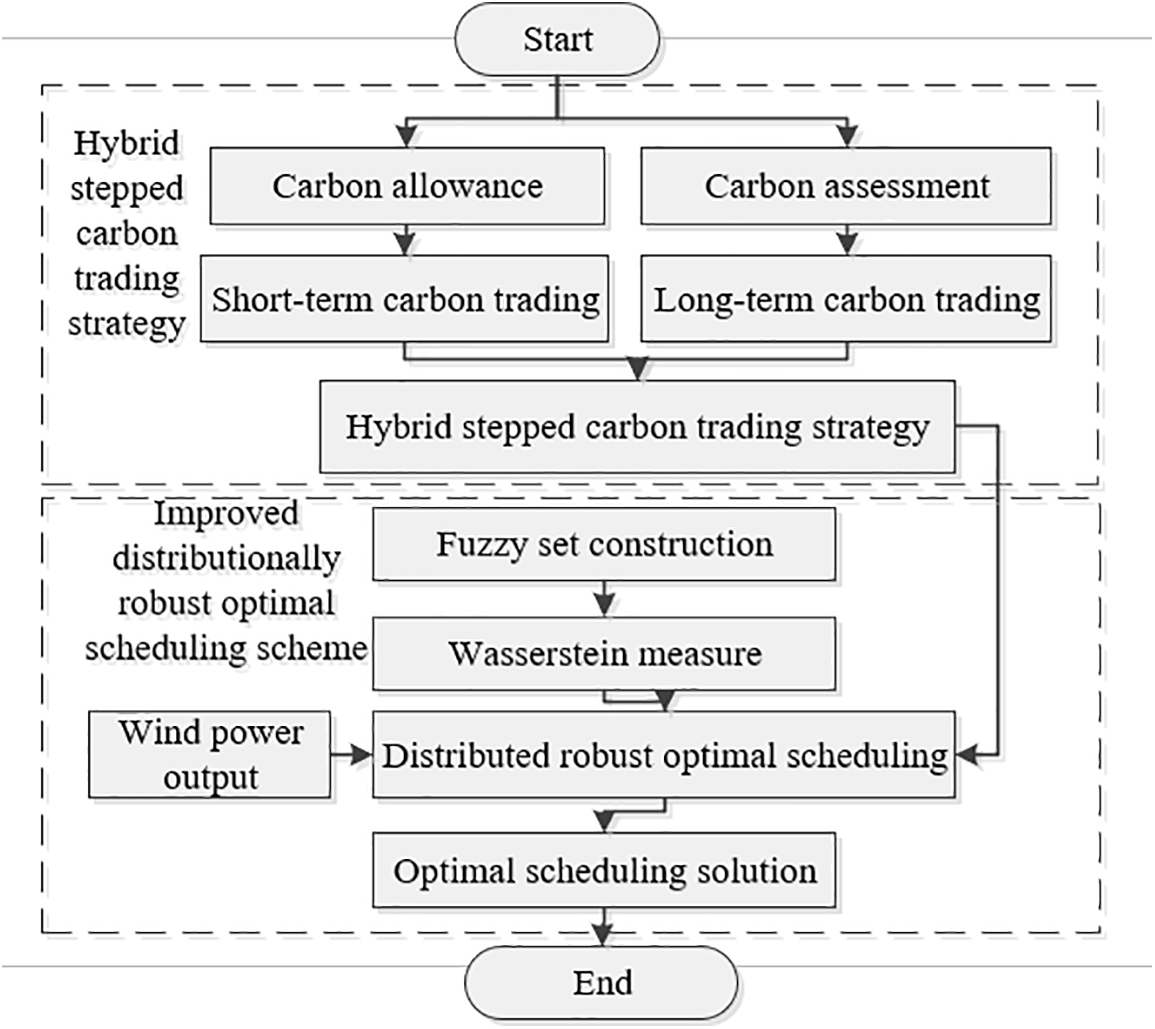
Figure 2: Flowchart of the proposed scheme

4.1 Data-Driven Preprocessing Method for Fuzzy Sets

Consider set δ={δ1,δ2,⋯,δK} as the sample collection. Set P0(δ) represents the ensemble of comprehensive probability distributions pertaining to wind power forecasting errors. Function gr(δ) is described as a segmented linear function, while γr denotes a segmented constant.

⟨P∈P0(δ)δw,t∈δEP(δ)=0P(δmin≤δw,t≤δmax)=1EP[gr(δ)]≤γr⟩(30)

gr(δ) denotes a piecewise linear function that refines each component of the uncertainty set through division into segments. Essentially, this function serves to expand the initial uncertainty set F, simplifying the computational task of determining the actual deviation of the wind turbine’s output power within these segmented intervals. As a result, it enables the retrieval of data that more accurately reflects the true probability distribution, thereby reducing the conservativeness in the calculations. Consequently, the fourth term in Eq. (30) can be rephrased as Eq. (31).

EP[gr(δ)]=EP[max(δw,t,r−Cw,t,r,0)]≤γr(31)

Given that r signifies the quantity of partitions, r=3, and Cw,t,r denotes the segment division constant; an ancillary variable gr(δ) is introduced to serve as the maximum limit for σ, simplifying the computation of gr(δ). Consequently, the initial fuzzy set F undergoes extension, giving rise to the augmented fuzzy set Q.

Q={PC∈P0(δ,σ):(δw,t,r,σw,t,r)∈δ×σEPc(δ)=0PC[(δw,t,r,σw,t,r)∈S]=1EPC(σw,t,r)≤γr}(32)

S={(δ,σ)∈(δ,σ):P(δmin≤δw,t≤δmax)=1gr(δw,t,r)≤σw,t,rσw,t,r≤maxδw,t,r∈δgr(δw,t,r)}(33)

Eqs. (32) and (33) denote extended fuzzy sets and two-dimensional sets, respectively. In this context, Q defines a set of joint probability distributions of δ and σ, denoted by PC. The two-dimensional set S illustrates the boundary of the two-dimensional variable (δw,t,r,σw,t,r) and the relationship between δw,t,r and σw,t,r. Each variable will correspond to the corresponding constraints.

4.2 Fuzzy Set Construction Based on Wasserstein Measure

To begin with, in engineering practice, δ cannot accurately derive the output by calculation. However, the empirical distribution PK can be expressed from δ={δ1,δ2,⋯,δK}, as illustrated in Eq. (34).

PK=1K∑k=1Kdk(34)

where dk is the Dirichlet process of δK. This process pertains to K instances where wind power bias is observed, with Q’s centroid being PK. The objective is for Q to encompass P to the greatest extent possible. The dissimilarity between P and PK is assessed with the Wasserstein metric, under the condition that P and PK must fulfill a specific association.

limK→∞PK=P(35)

The definition of Wasserstein distance is as follows:

W(PK,P)=inf∏{∫‖ξK−ξ‖∏(dξK,dξ)}.(36)

The fuzzy set Wδ based on the Wasserstein measure can be expressed as

{Wδ={P∈Q:W(PK,P)≤R1(K)}limK→∞R1(K)=0(37)

In the context where the fuzzy set Wδ, defined by the Wasserstein metric, serves as a conceptual center with parameter PK and a radius denoted as R(K), integrating a confidence level of 1/4 enables regulation of the conservativeness in the optimization outcomes of the DRO model.

4.3 Strongly Dual Transformation

Reformulating the objective function for optimization necessitates the application of a robust binary conversion to effectively restructure the distributionally robust segment. This transition is articulated in Eq. (38), subsequently facilitating its integration with the broader minimization strategy to address the problem with optimal efficiency.

EP[f(x,δ)]={infλ≥0[λ⋅R1(K)+1K∑k = 1Kvks.t.{f(x,δmax)−λ⋅(δmax−δk)≤vkf(x,δmin)+λ⋅(δmin−δk)≤vkf(x,δk)≤vk(38)

The quadratic constraints within Eq. (38), established through robust dyadic transformations of the objective function, exhibit constraints when faced with a substantial sample size. vk and the quadratic constraints increase with K, resulting in substantial computational expenses when dealing with large sample sizes. The following mathematical strategy is employed in the study to address this issue:

{infλ∈R[λ⋅R1(K)+1K∑k=1Kf(x,δk)]s.t.{f′(x,δmax)≤λ−f′(x,δmin)≤λ(39)

Eqs. (38) and (39) satisfy the following relationship:

infλ≥0[λ⋅R1(K)+1K∑k = 1Kvk]≈infλ∈R[λ⋅R1(K)+1K∑k = 1Kf(x,δk)](40)

Here, f′(x,δmax) represents the derivative of f with respect to δ. Eqs. (40) and (39) provide an approximate upper limit for Eq. (38). Notably, Eq. (39) maintains a stable number of quadratic constraints without increase in vk, even as the value of K grows, rendering the computational process efficient and yielding consistent optimization outcomes.

5  Case Simulation and Analysis

5.1 Base Data

The upgraded IEEE 6 bus system was utilized as the experimental platform to authenticate the DRO strategy for unit commitment, with an emphasis on the unpredictability of wind turbine generation. Fig. 3 depicts the layout of the upgraded IEEE 6 bus system.

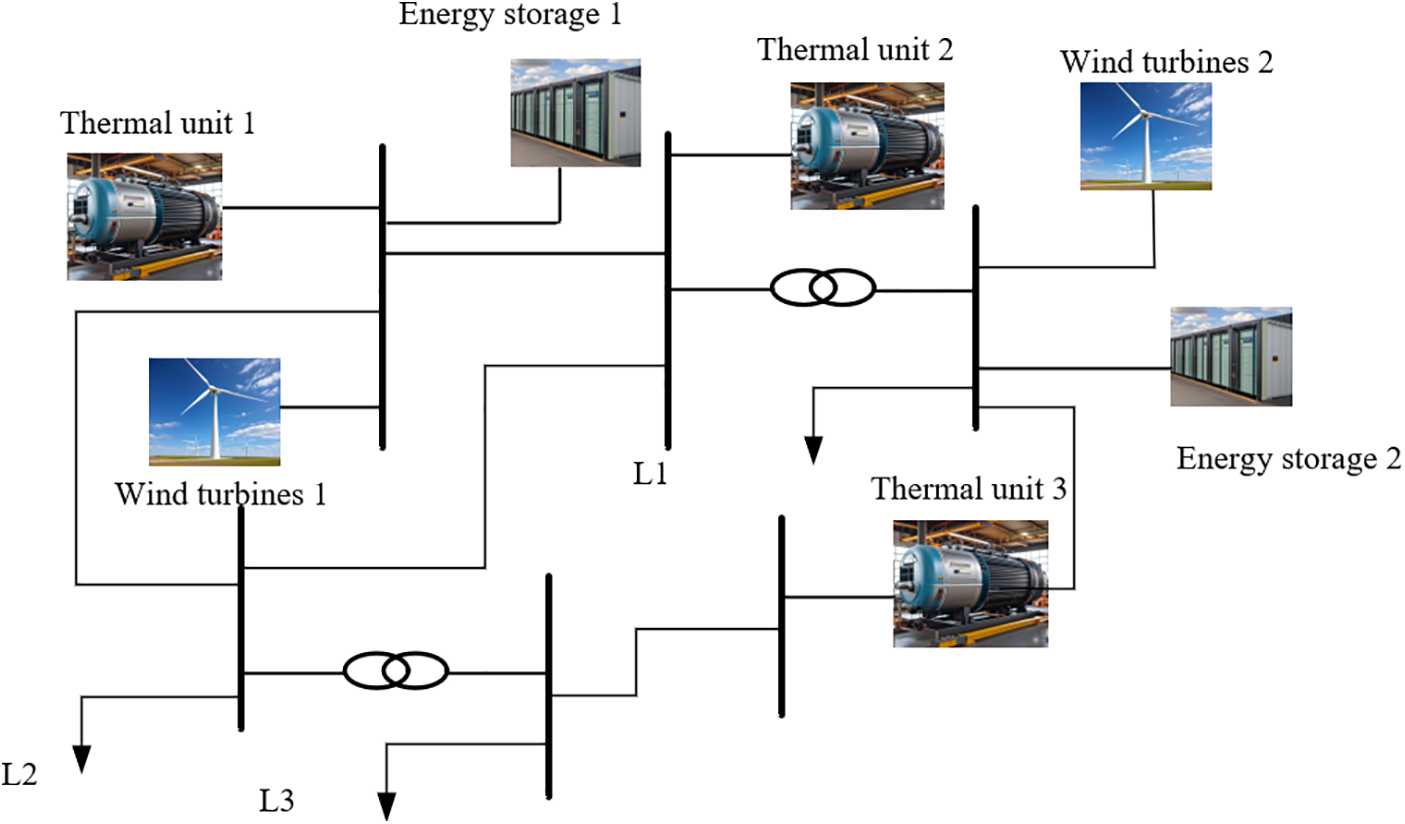
Figure 3: Improved IEEE 6 bus system

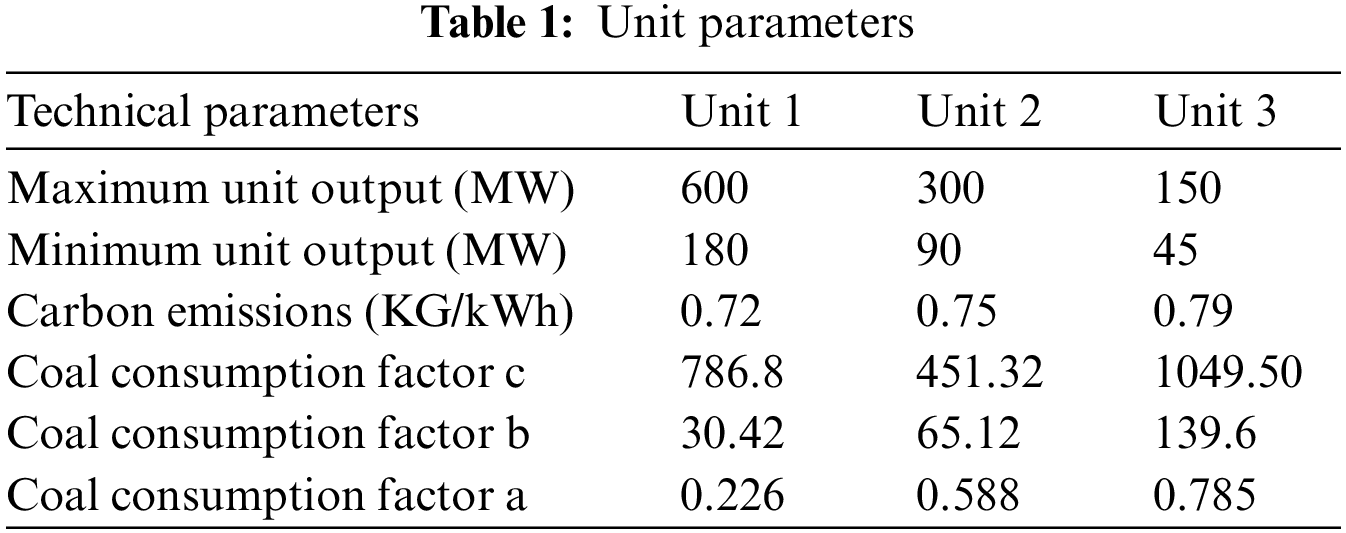
The system is designed for a 24-h dispatch cycle with hourly sectionalization and consists of six buses and seven spurs. Bus 1 is designated as the balancing bus, and three thermal units are assigned to buses 1, 2, and 6, the first of which serves as the main generator and the last two as standby generators. The specific parameters of these units are listed in Tables 1 and 2. The system also has two wind turbines on buses 1 and 3. At the same time, energy storage units are strategically deployed on the same buses to complement each turbine, ensuring that each turbine has a dedicated standby energy storage unit. The parameters are obtained by capacity optimization configuration. This configuration minimizes wind energy wastage and reduces overall system expenditure by providing auxiliary power during thermal turbine downtime for maintenance.

5.2 Scenario Selection

In anticipation of the forthcoming day’s load conditions and guided by the optimization objectives, the scheduling algorithm and model are designed to facilitate scheduling optimization through the modulation of each unit’s output. This entails calibrating the output levels of thermal and wind power units, along with energy storage devices, to align with the subsequent day’s load requirements and fulfill the optimization goals. Subsequently, forecasts for the next day’s load and wind power are generated, acknowledging the time-varying and cyclical patterns of power loads and the unpredictable nature of wind power. Leveraging the predicted load profile and optimization objectives for the next day, the scheduling algorithm and model adeptly orchestrate scheduling optimization by fine-tuning the outputs of the respective units. Such adjustments are calibrated to cater to the imminent day’s load demands while striving to meet the optimization objectives.

5.2.1 Power Load Forecasting

In this study, the PSO-RNN method is used to forecast the power load. Before establishing the PSO-RNN prediction model, some historical data must be processed in advance to filter out some errors and abnormal data so as not to affect the accuracy of the power load prediction.

The power load data of a power company in Liaoning from September 2020 to September 2021 are selected as the historical data needed for prediction, and the real historical data from 1 September 2020 to 31 August 2021 is used as the training set, the data in September 2021 are used as the test set, and PSO-RNN is used to predict the load size. A neural network is used to predict the load size; the inertia factor and learning parameter are set to 0.7 and 0.08, respectively; the initial number of particle swarms is 100; the maximum number of iterations of particle swarms is 1000; and simulation and training are conducted on the historical data.

5.2.2 Prediction of Wind Power Generation Power

Renewable wind energy offers pollution-free, limitless, and cost-effective attributes, making it an appealing resource. Its expansion, with more wind turbines installed, aims to enhance forecasting for better power scheduling. The PSO-RNN method continues to play a role in wind power prediction. This section employs actual hourly average wind power generation data from a wind farm in the Liaoning region, spanning from 1 September 2020 to 31 August 2021, as the training dataset, while September 2021 data serves as the testing set. Training iterations are capped at 3000, with a learning rate of 0.015 and a precision level of 0.00001.

Figs. 4 and 5 reveal that for WTGs, during the period of 0:00–6:00, when the wind power is large, the power system load is small; during the period of 8:00–12:00, when the power system load is large, the wind power is low, indicating that WTGs have a strong anti-peak shunting. This result shows that wind turbines have strong anti-peaking characteristics.

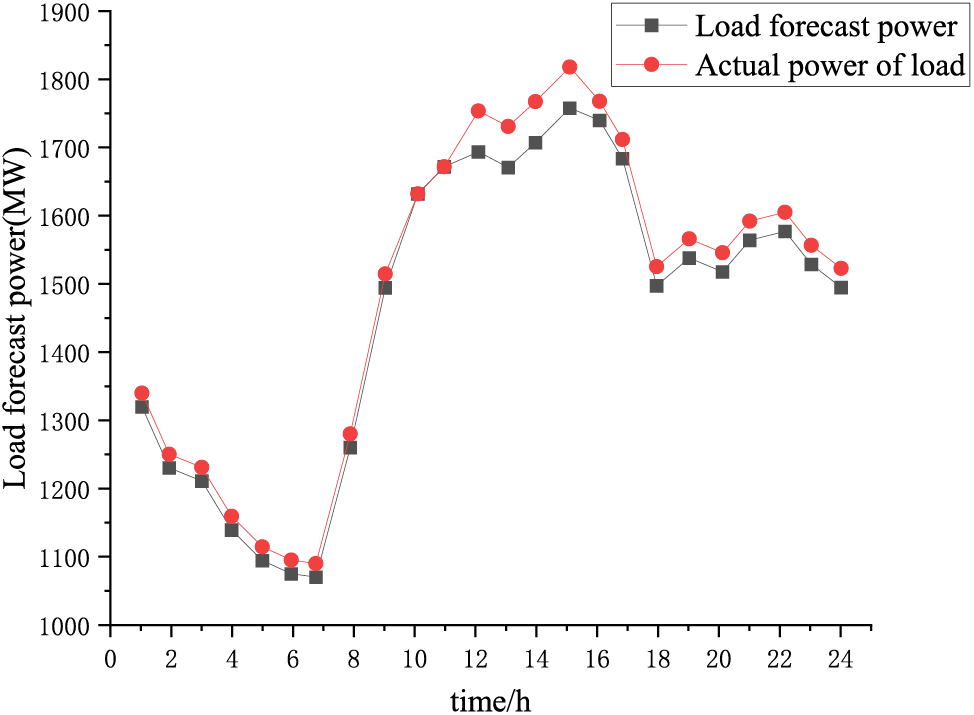
Figure 4: Forecasted electricity load consumption profile

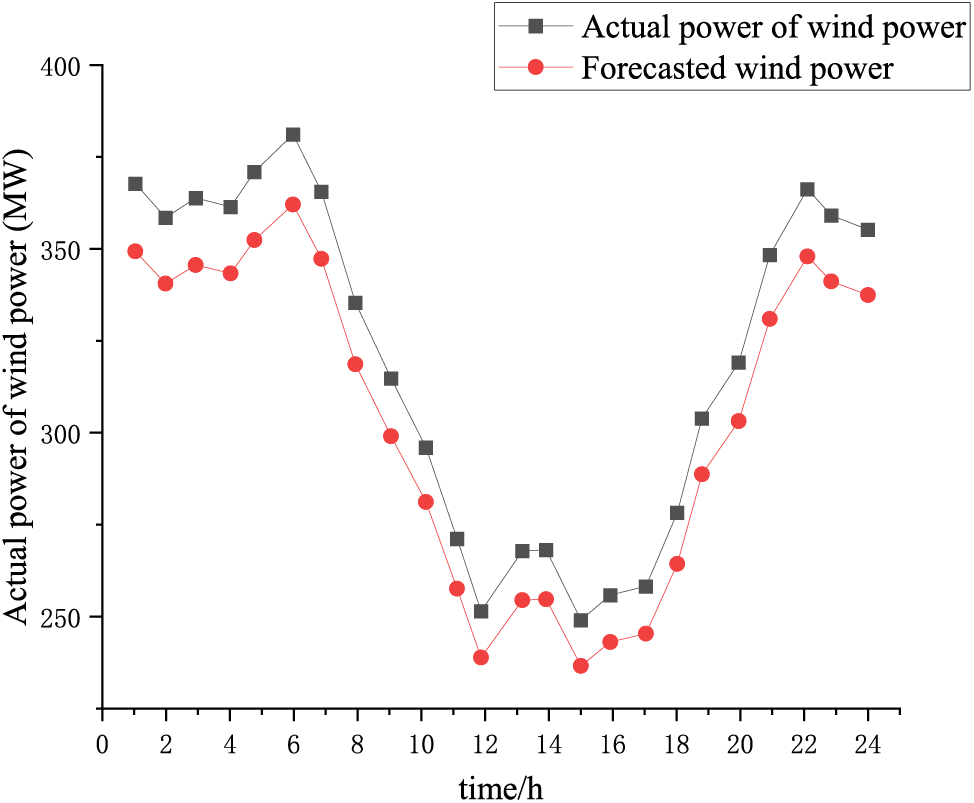
Figure 5: Predicted wind power curve

5.3 Analysis of Simulation Results

The confidence level for the fuzzy set within the distributionally robust optimization framework is established at 0.95 to ascertain the benefits of integrating a carbon trading mechanism and to evaluate the impact of uncertain parameter volatility on the overall cost. Four different scenarios are delineated as in Table 3.

Following optimization calculations, the system’s capacity is judiciously determined by modeling security constraints under extreme conditions during the dispatch process, leveraging enhanced distribution robust optimization techniques. Conversely, given that thermal power units exhibit more stable output than wind power units, the inherent volatility of wind power precludes the use of static scheduling methods. Consequently, energy storage devices are implemented to comply with the operational security constraints of the system. With the minimization of generation costs serving as the objective function and factoring in the cost of generation for each unit aligned with the daily load curve, the results of the system’s optimization scheduling are delineated below:

Figs. 6–9 show the output optimization results of the system for each of the four different scenarios. The figure illustrates that Scenario 1 experiences considerable wind abandonment between 0:00 and 9:00. Conversely, Scenario 4, as proposed in this study, achieves a substantial decrease in wind abandonment, concurrently adhering to the system’s security constraints. The findings indicate that the robust optimization scheduling approach for the wind–fire storage system, which incorporates a hybrid carbon trading mechanism, is secure and cost effective. Given that the system dispatch employs a refined optimization method, which considers the most adverse conditions of wind power fluctuation, it can handle all projected system scenarios. Consequently, altering additional parameters is not needed, with adjustments confined solely to the output of thermal units and wind power generation.

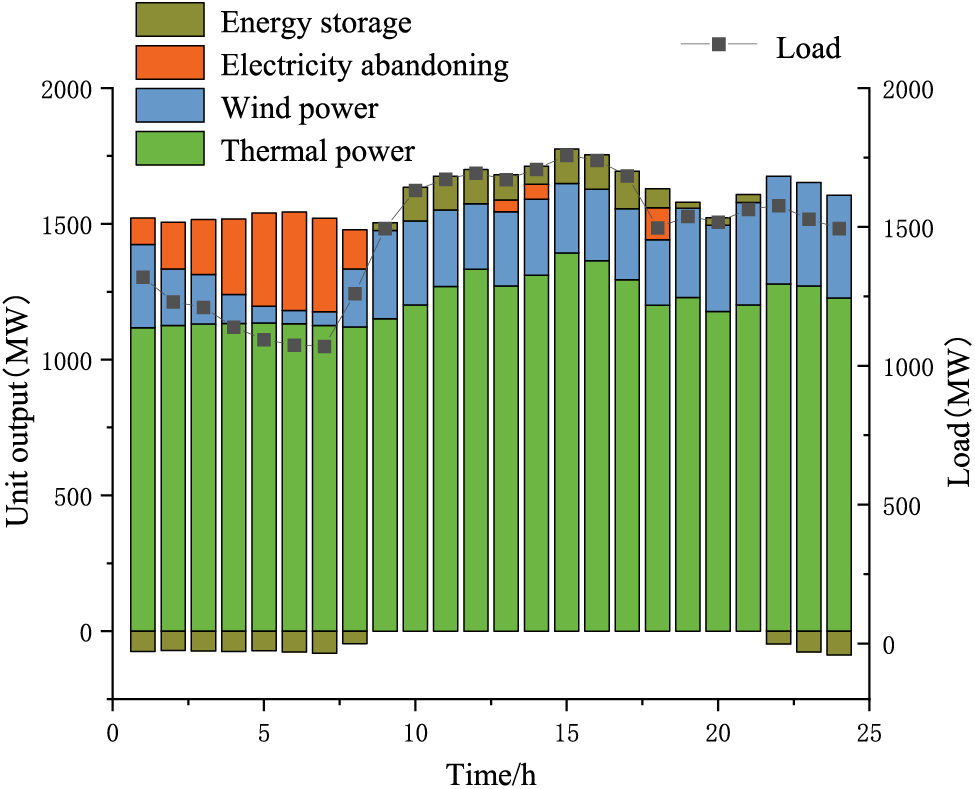
Figure 6: Scenario 1 unit output optimization results

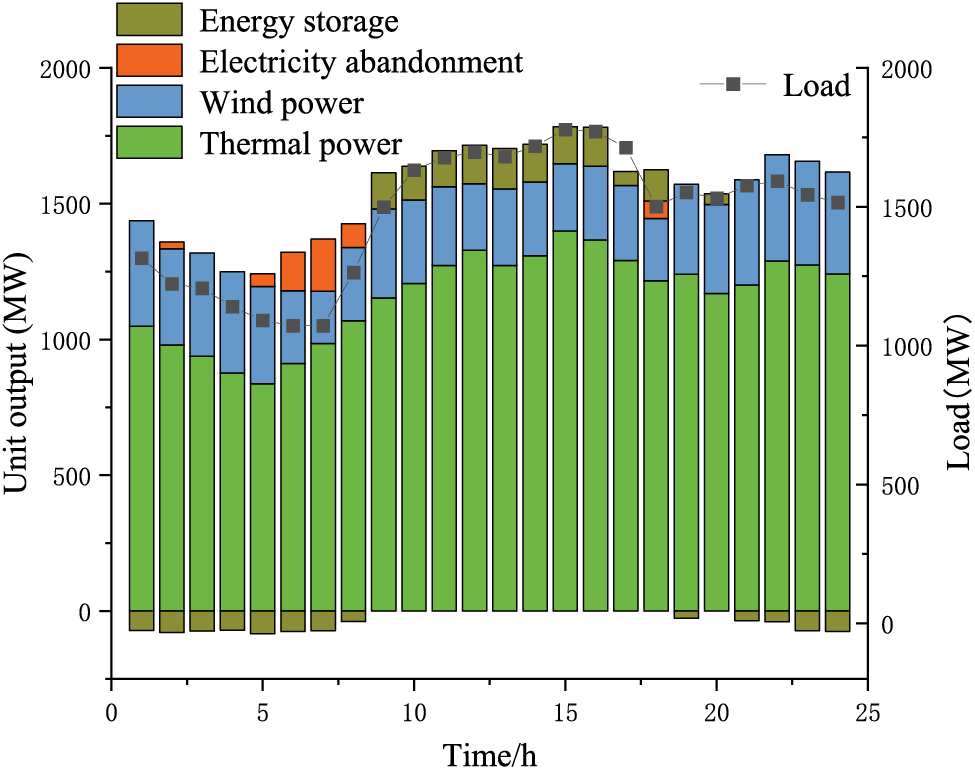
Figure 7: Scenario 2 unit output optimization results

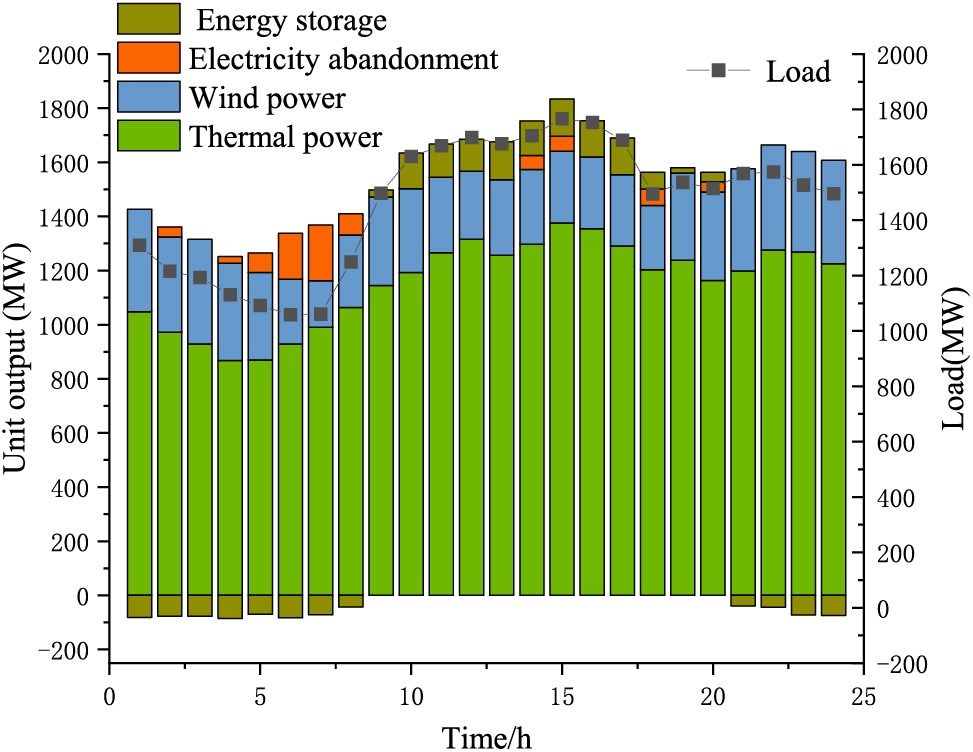
Figure 8: Scenario 3 unit output optimization results

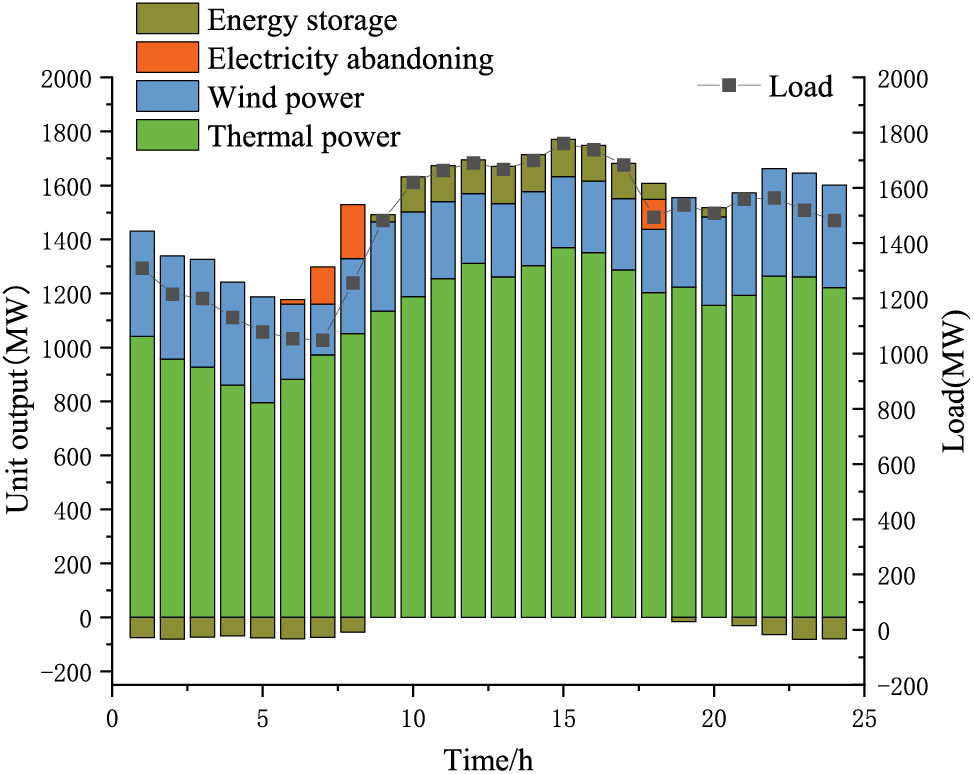
Figure 9: Scenario 4 unit output optimization results

5.4 Analysis of Different Scenarios

The emission reduction benefits of different scenarios are compared and analyzed by constructing scenario simulations under four scenarios, in which the carbon transaction cost is used as a measure of low carbon. The cost of each of its parameters for different scenarios is shown in Table 4.

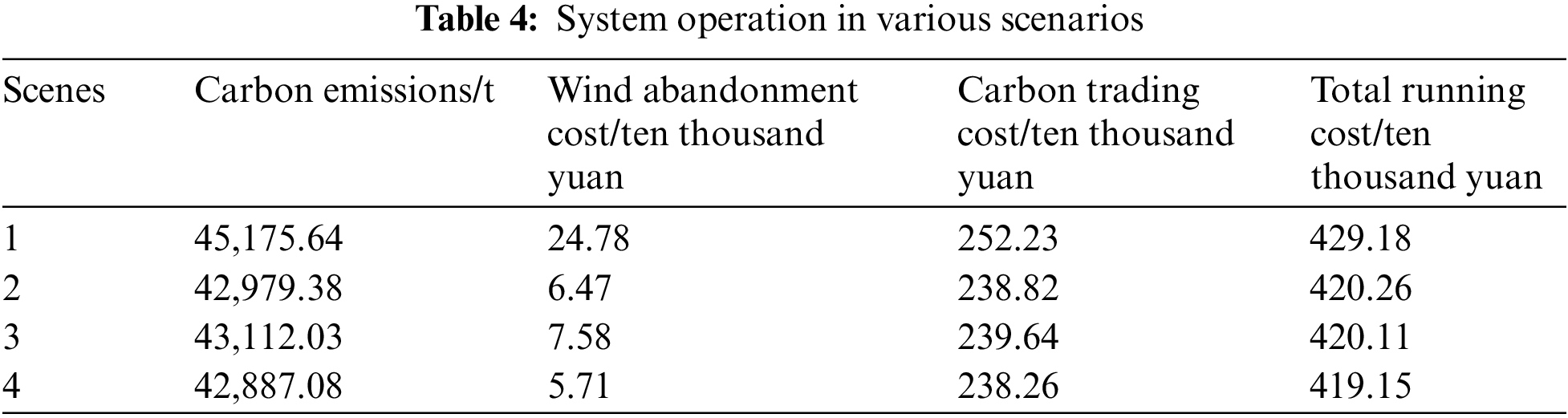
Neglecting the cost of energy storage while pursuing the low-carbon goal, Scenario 4 of this study further introduces DRO based on stepped carbon trading, achieving a considerable reduction in carbon emissions by 5.15% compared with Scenario 2, showing the remarkable efficacy of stepped carbon trading in reducing emissions. In terms of enhancing the efficiency of new energy use, Scenario 4 reduces the wind abandonment cost by RMB 18,700 compared with Scenario 3 and by RMB 191,000 compared with Scenario 1 while considering stepped carbon trading, thus remarkably enhancing the utilization rate of wind power generation; in terms of the overall economic operating cost of the system, Scenario 4 reduces the cost of wind power generation by 6.38% compared with Scenario 1 and by 6.24% compared with Scenario 2. 6.24% of the cost. Overall, the above results verify the remarkable effectiveness of the hybrid carbon trading mechanism proposed in this study and the improved distributional robust optimal scheduling in the practice of low-carbon economic scheduling.

6  Conclusion

In this paper, a distributed robust low-carbon scheduling model of a wind-thermal-storage system considering the influence of carbon trading mechanism is proposed. The main innovations include a hybrid carbon trading mechanism and a distributed robust scheduling model with improved fuzzy set representation. Through simulation verification, the following conclusions are drawn:

(1) Introducing hybrid long-term and short-term carbon trading reduces the operating cost of the wind-thermal storage system and the amount of wind curtailment.

(2) Compared with the traditional method to solve the uncertainty problem, the improved distributionally robust optimal scheduling in this paper considers both economy and stability.

(3) Through simulation verification, the fuzzy set preprocessing method proposed in this paper can obtain more economical optimization results with a smaller sample size and larger space to reduce conservatism.

Acknowledgement: None.

Funding Statement: This work was supported by Liaoning Provincial Doctoral Research Initiation Fund Project (2022-BS-225); Liaoning Provincial Department of Education Scientific Research Project (LJKZ1091).

Author Contributions: Yuedong Wu: writing the original draft; Gang Wang: writing review & editing, supervision; Xiaoyi Qian and Yi Zhao: writing-review & editing, co-supervision. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. G. R. Yu, T. X. Hao, and J. X. Zhu, “Discussion on China’s carbon peaking and carbon neutrality action strategy,” (in Chinese), Bull. Chin. Acad. Sci., vol. 37, pp. 423–434, 2022. [Google Scholar]

2. Q. Hassan et al., “The renewable energy role in the global energy transformations,” Renew. Energy Focus, vol. 48, pp. 100545, Mar. 2024. doi: 10.1016/j.ref.2024.100545. [Google Scholar] [CrossRef]

3. F. Wei et al., “A Bi-level optimization model of integrated energy system considering wind power uncertainty,” Renew. Energy, vol. 202, no. 1, pp. 973–991, Jan. 2023. doi: 10.1016/j.renene.2022.12.007. [Google Scholar] [CrossRef]

4. J. C. Guo, D. Wu, Y. Y. Wang, L. M. Wang, and H. Y. Guo, “Co-optimization method research and comprehensive benefits analysis of regional integrated energy system,” Appl. Energy, vol. 340, pp. 121034, Jul. 2023. doi: 10.1016/j.apenergy.2023.121034. [Google Scholar] [CrossRef]

5. H. Xiao, F. Y. Long, L. J. Zeng, W. Q. Zhao, J. Wang and Y. H. Li, “Optimal scheduling of regional integrated energy system considering multiple uncertainties and integrated demand response,” Electric Power Syst. Res., vol. 217, pp. 109169, 2023. doi: 10.1016/j.epsr.2023.109169. [Google Scholar] [CrossRef]

6. W. Y. Jiang, Y. Q. Liu, G. H. Fang, and Z. Y. Ding, “Research on short-term optimal scheduling of hydro-wind-solar multi-energy power system based on deep reinforcement learning,” J. Clean. Prod., vol. 385, pp. 135704, Apr. 2023. doi: 10.1016/j.jclepro.2022.135704. [Google Scholar] [CrossRef]

7. H. Y. Xu, Y. Q. Chang, Y. Zhao, and F. L. Wang, “A new multi-timescale optimal scheduling model considering wind power uncertainty and demand response,” Int. J. Electric. Power Energy Syst., vol. 147, pp. 108832, May 2023. doi: 10.1016/j.ijepes.2022.108832. [Google Scholar] [CrossRef]

8. Q. S. Zheng, Y. J. Gu, Y. H. Liu, J. W. Ma, and M. F. Peng, “Chaotic particle swarm algorithm-based optimal scheduling of integrated energy systems,” Elect. Power Syst. Res., vol. 216, pp. 108979, Apr. 2023. doi: 10.1016/j.epsr.2022.108979. [Google Scholar] [CrossRef]

9. M. Yang, Y. Cui, and J. X. Wang, “Multi-objective optimal scheduling of island microgrids considering the uncertainty of renewable energy output,” Int. J. Electric. Power Energy Syst., vol. 144, pp. 108619, Jan. 2023. doi: 10.1016/j.ijepes.2022.108619. [Google Scholar] [CrossRef]

10. J. F. Li, X. T. He, W. D. Li, M. Z. Zhang, and J. Wu, “Low-carbon optimal learning scheduling of the power system based on carbon capture system and carbon emission flow theory,” Elect. Power Syst. Res., vol. 218, pp. 109215, May 2023. doi: 10.1016/j.epsr.2023.109215. [Google Scholar] [CrossRef]

11. J. M. Hou, W. J. Yu, Z. H. Xu, Q. B. Ge, Z. Li and Y. Meng, “Multi-time scale optimization scheduling of microgrid considering source and load uncertainty,” Elect. Power Syst. Res., vol. 216, pp. 109037, Mar. 2023. doi: 10.1016/j.epsr.2022.109037. [Google Scholar] [CrossRef]

12. G. Zhu and Y. Gao, “Multi-objective optimal scheduling of an integrated energy system under the multi-time scale ladder-type carbon trading mechanism,” J. Clean. Prod., vol. 417, pp. 137922, Sep. 2023. doi: 10.1016/j.jclepro.2023.137922. [Google Scholar] [CrossRef]

13. H. Wang, H. J. Xing, Y. F. Luo, and W. B. Zhang, “Optimal scheduling of micro-energy grid with integrated demand response based on chance-constrained programing,” Int. J. Electric. Power Energy Syst., vol. 144, pp. 108602, Jan. 2023. doi: 10.1016/j.ijepes.2022.108602. [Google Scholar] [CrossRef]

14. Q. Li, X. K. Xiao, Y. C. Pu, S. Y. Luo, H. Liu and W. R. Chen, “Hierarchical optimal scheduling method for regional integrated energy systems considering electricity-hydrogen shared energy,” Appl. Energy, vol. 349, pp. 121670, Nov. 2023. doi: 10.1016/j.apenergy.2023.121670. [Google Scholar] [CrossRef]

15. J. L. Zhang, X. F. Kong, J. Shen, and L. Sun, “Day-ahead optimal scheduling of a standalone solar-wind-gas based integrated energy system with and without considering thermal inertia and user comfort,” J. Energy Storage, vol. 57, pp. 106187, Jan. 2023. doi: 10.1016/j.est.2022.106187. [Google Scholar] [CrossRef]

16. L. Zhang, D. Y. Liu, G. W. Cai, L. L. Yu, L. H. Koh and T. S. Wang, “An optimal dispatch model for virtual power plant that incorporates carbon trading and green certificate trading,” Int. J. Electric. Power Energy Syst., vol. 144, pp. 108558, Jan. 2023. doi: 10.1016/j.ijepes.2022.108558. [Google Scholar] [CrossRef]

17. D. Y. Lei, Z. H. Zhang, Z. J. Wang, L. Zhang, and W. Liao, “Long-term, multi-stage low-carbon planning model of electricity-gas-heat integrated energy system considering ladder-type carbon trading mechanism and CCS,” Energy, vol. 280, pp. 128113, Oct. 2023. doi: 10.1016/j.energy.2023.128113. [Google Scholar] [CrossRef]

18. P. H. Jiao, X. Cai, L. L. Wang, J. J. Chen, Y. L. Zhao and Y. F. Cao, “Flexibility operation for integrated energy system considering hydrogen energy under inertia characteristics and stepped carbon trading mechanism,” Sustain. Cities Soc., vol. 98, pp. 104809, Nov. 2023. doi: 10.1016/j.scs.2023.104809. [Google Scholar] [CrossRef]

19. Q. Lu, Q. S. Guo, and W. Zeng, “Optimal dispatch of community integrated energy system based on Stackelberg game and integrated demand response under carbon trading mechanism,” Appl. Therm. Eng., vol. 219, pp. 119508, Jan. 2023. doi: 10.1016/j.applthermaleng.2022.119508. [Google Scholar] [CrossRef]

20. S. Bhavsar, R. Pitchumani, J. Maack, I. Satkauskas, M. Reynolds and W. Jones, “Stochastic economic dispatch of wind power under uncertainty using clustering-based extreme scenarios,” Elect. Power Syst. Res., vol. 229, pp. 110158, Jan. 2024. doi: 10.1016/j.epsr.2024.110158. [Google Scholar] [CrossRef]

21. C. M. Leng, H. Yang, Y. K. Song, Z. T. Yu, and C. Shen, “Expected value model of microgrid economic dispatching considering wind power uncertainty,” Energy Rep., vol. 9, no. 10, pp. 291–298, Oct. 2023. doi: 10.1016/j.egyr.2023.05.092. [Google Scholar] [CrossRef]

22. H. Wei, W. S. Wang, and X. X. Kao, “A novel approach to hybrid dynamic environmental-economic dispatch of multi-energy complementary virtual power plant considering renewable energy generation uncertainty and demand response,” Renew. Energy, vol. 219, pp. 119406, Dec. 2023. doi: 10.1016/j.renene.2023.119406. [Google Scholar] [CrossRef]

23. H. P. Chen, H. Wu, T. Y. Kan, J. H. Zhang, and H. L. Li, “Low-carbon economic dispatch of integrated energy system containing electric hydrogen production based on VMD-GRU short-term wind power prediction,” Int. J. Electric. Power Energy Syst., vol. 154, pp. 109420, Dec. 2023. doi: 10.1016/j.ijepes.2023.109420. [Google Scholar] [CrossRef]

24. S. Bhavsar, R. Pitchumani, M. A. Ortega-Vazquez, and N. Costilla-Enriquez, “A hybrid data-driven and model-based approach for computationally efficient stochastic unit commitment and economic dispatch under wind and solar uncertainty,” Int. J. Electric. Power Energy Syst., vol. 151, pp. 109144, Sep. 2023. doi: 10.1016/j.ijepes.2023.109144. [Google Scholar] [CrossRef]

25. N. Houben et al., “Optimal dispatch of a multi-energy system microgrid under uncertainty: A renewable energy community in Austria,” Appl. Energy, vol. 337, pp. 120913, May 2023. doi: 10.1016/j.apenergy.2023.120913. [Google Scholar] [CrossRef]

26. R. J. Liu, Z. J. Bao, and Z. Z. Lin, “Collaborative low-carbon economic dispatch of source-network-load distribution considering a two-tier reward-punishment carbon trading mechanism,” Power Syst. Autom., vol. 48, pp. 1–22, 2024 (In Chinese). [Google Scholar]

27. Z. P. Zhang, Z. T. Liu, and J. F. Zhu, “Measuring the utility of China’s carbon trading policy to promote low-carbon technological innovation–An empirical study based on a multi-temporal double-difference method,” Sci. Technol. Progress Countermeasures, pp. 1–12, 2024 (In Chinese). [Google Scholar]

28. Z. Y. Zhao and X. Y. Li, “Low-carbon economic dispatch of carbon capture power plant-electricity-to-gas virtual power plant based on ladder carbon trading,” Power Gen. Technol., vol. 44, pp. 769–780, 2023 (In Chinese). [Google Scholar]

29. J. Y. Guo et al., “A robust economic dispatch model for a multi-energy microgrid day-ahead considering wind power uncertainty and carbon trading cost,” Electrotechnology, vol. 20, pp. 86–91, 2023 (In Chinese). [Google Scholar]