 Open Access
Open Access
ARTICLE
Short-Term Prediction of Photovoltaic Power Based on DBSCAN-SVM Data Cleaning and PSO-LSTM Model
1 School of Energy and Power Engineering, Inner Mongolia University of Technology, Hohhot, 010051, China
2 Key Laboratory of Wind Energy and Solar Energy Utilization Technology, Ministry of Education, Hohhot, 010051, China
3 Production Management Department, Inner Mongolia Energy Power Generation Investment Group Co., Ltd., Hohhot, 010051, China
* Corresponding Author: Yan Jia. Email:
Energy Engineering 2024, 121(10), 3019-3035. https://doi.org/10.32604/ee.2024.052594
Received 08 April 2024; Accepted 03 June 2024; Issue published 11 September 2024
Abstract
Accurate short-term photovoltaic (PV) power prediction helps to improve the economic efficiency of power stations and is of great significance to the arrangement of grid scheduling plans. In order to improve the accuracy of PV power prediction further, this paper proposes a data cleaning method combining density clustering and support vector machine. It constructs a short-term PV power prediction model based on particle swarm optimization (PSO) optimized Long Short-Term Memory (LSTM) network. Firstly, the input features are determined using Pearson’s correlation coefficient. The feature information is clustered using density-based spatial clustering of applications with noise (DBSCAN), and then, the data in each cluster is cleaned using support vector machines (SVM). Secondly, the PSO is used to optimize the hyperparameters of the LSTM network to obtain the optimal network structure. Finally, different power prediction models are established, and the PV power generation prediction results are obtained. The results show that the data methods used are effective and that the PSO-LSTM power prediction model based on DBSCAN-SVM data cleaning outperforms existing typical methods, especially under non-sunny days, and that the model effectively improves the accuracy of short-term PV power prediction.Keywords
Nomenclature
| PV | Photovoltaic |
| LSTM | Long Short-Term Memory |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| PSO | Particle Swarm Optimization |
| WPE | Weather Prediction Error |
| SVM | Support Vector Machine |
| ANN | Artificial Neural Network |
| MLR | Multiple Linear Regression |
| PL | Power Law |
| RPL | Rational Power Law |
| NARXNN | Nonlinear Auto-Regressive Neural Networks with Exogenous Input |
| LightGBM | Light Gradient Boosting Machine |
| XGBoost | Extreme Gradient Boosting |
| BP | Back Propagation |
| IGWD | Improved Grey Wolf Algorithm |
| ADASYN | Adaptive Synthetic |
| GHI | Global Horizontal Irradiance |
| DNI | Direct Normal Irradiance |
| TEMP | Temperature |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
In recent years, the global energy transition has placed a significant emphasis on the development and utilization of solar energy, with PV power generation entering a phase of large-scale expansion [1]. Various factors, such as solar radiation intensity, temperature, and air pressure, influence PV power generation, leading to noticeable fluctuations, randomness, and instability in the power grid [2,3]. The reliable and accurate prediction of PV power generation plays a crucial role in enhancing operational coordination between solar energy and power systems. This, in turn, ensures a stable energy supply, facilitates the efficient power scheduling of energy companies, optimizes the allocation of power resources, and ultimately improves economic efficiency [4–6].
PV power prediction methods usually include direct and indirect methods. Among the indirect methods, deep learning algorithms are widely used for PV power prediction due to their superior ability to exhibit strong robustness and accuracy. These network architectures can dig deeper into the evolutionary features of the time series to obtain more accurate predictions [7]. However, the performance of a single model is still limited. Therefore, many scholars have improved the model structure or introduced new mechanisms to enhance its performance, adaptive capability, and generalization.
Bâra et al. [8] improved model prediction accuracy by embedding weather prediction errors into a deep learning-enhanced stacked regressor approach, especially for off-grid inverters and large-scale industrial PV plants, showing higher applicability and improvement, with MAE reductions ranging from 10% to 23%. In addition, the study proposes adjustment factors based on feature engineering and WPE to further optimize the prediction model to obtain more stable daily deviation ratios. Zhang et al. [9] proposed a short-term power prediction method for distributed PV systems based on Attention-LSTM and transfer learning. Migration learning enhances the generalization ability of the Attention-LSTM model, which makes the proposed Attention-LSTM model still able to predict the power effectively in the case of limited data. Yu et al. [10] proposed a new time-frequency integrated converter for day-ahead photovoltaic power prediction. The model integrates four key components of temporal attention, frequency attention, Fourier attention, and weather embedding for in-depth analysis of PV power time series. Abdelhak et al. [11] used ANN and regression analysis to predict the power output of PV modules and considered the effect of ambient conditions and operating temperatures on the predicted outputs. The ANN model was able to accurately predict the power output of the PV modules during the test period, and the MLR model failed to capture system nonlinearities with lower accuracy; however, the nonlinear regression RPL and PL models provided significantly better accuracy in predicting module power output. Gao et al. [12] proposed NARX-LSTM-LightGBM forecasting framework is effective for short-term PV power forecasting. The combined model showed significant improvement in prediction accuracy under different weather conditions compared to the separate models. Tan et al. [13] introduced a short-term PV power prediction method that integrates the XGBoost model with the LSTM network model. Experimental findings indicate that the combined XGBoost-LSTM model enhances prediction accuracy compared to using a standalone model. Luo et al. [14] proposed a physically constrained LSTM network to predict PV power accurately. The results show that the proposed PC-LSTM model has stronger prediction capability and is more robust than the standard LSTM model for PV power prediction for sparse data. The results show that the prediction performance of the hybrid model is better than the single prediction model. Chen et al. [15] proposed a short-term PV power generation prediction model based on adaptive K-means and LSTM by clustering the PV power generation of the original training set and the prediction day using adaptive K-means, training the LSTM for each type of data of the original training set, and training the LSTM for the trained PV power generation of the original training set. LSTM, and combining the trained LSTMs. In the work by Ding et al. [16], an innovative fusion model was introduced, amalgamating the wavelet decomposition technique with a LSTM. The approach employs the wavelet decomposition technique to analyze historical energy sequence data. Subsequently, the processed energy feature data is merged with weather data, facilitating the incorporation of the LSTM learning model for feature-level fusion. Experimental outcomes demonstrate the proposed model’s superior performance compared to both the BPNN and LSTM across diverse seasonal and weather conditions. Xue et al. [17] proposed an IGWO based on an improved adaptation coefficient as an elite backpropagation strategy to optimize the LSTM forecasting model. Using IGWO to optimize the parameters of the fully connected layer of the LSTM, an IGWO-LSTM combined model with better convergence speed solution efficiency and effective avoidance of locally optimal solutions was built to predict solar power generation.
However, the attention to data processing in the above studies may be obscure, and good data quality helps the prediction model to be more stable and improve the prediction accuracy. Ye et al. [18] proposed a combined identification method for multiple anomalous data. Example analyses show that the proposed method can be applied to detect a higher proportion of anomalous data and effectively identify both continuous and discrete anomalous data, thus significantly improving the linear correlation between irradiance and PV power generation. Ling et al. [19] used the ADASYN algorithm to effectively reduce the imbalance problem caused by extreme meteorological features in small sample sizes by rebalancing the dataset. The stability of the model prediction results after ADASYN sampling is much higher than that before over-sampling, and the coefficient of variation of the RMSE is significantly reduced, which indicates that the robustness of the model to extreme meteorological features has been enhanced.
In summary, this paper adopts a new data processing method, combining DBSCAN clustering and SVM detection of outliers for data processing, obtaining the optimal network structure and finding the optimal hyper-parameters of the LSTM network through the global search capability of PSO, and establishing the PSO-LSTM prediction model, which improves its training effect and generalization capability. Finally, the results of different models are analyzed to verify the feasibility and superiority of the proposed model.
2.1 Pearson Correlation Analysis
PV power output is primarily influenced by weather factors, and data obtained from PV power stations often contain multiple meteorological features, some of which have a significant impact on PV power output (e.g., solar irradiance). In contrast, others have a small impact on PV output power output (e.g., wind direction, barometric pressure, etc.), Therefore, meteorological factors that have a significant impact on the PV power forecasting model were selected as inputs through Pearson’s correlation coefficient.
Pearson’s correlation coefficient [20], first proposed by the statistician Carl Pearson, is a statistical indicator used to measure the degree of linear correlation between two (groups of) variables, x and y, whose values are within the interval [−1, 1] with the following formula:
where n is the total number of samples; xi is the meteorological parameter at the ith time;
After Pearson correlation analysis, as shown in Fig. 1, the GHI, DNI, and TEMP were selected as inputs to the prediction model.

Figure 1: Heat map of correlation coefficients between meteorological data and PV power
The experimental data in this paper is obtained from the DKASC website in Australia, and the selected data is from 1 January to 28 February 2019, as shown in Fig. 2. Since PV power generation is intermittent, the period of the data selected in this paper is from 7:00 am to 19:00. The time interval of data collection is 5 min, with a total of 133 data points per day, totaling 59 days and 8555 pieces of data, of which 39 days are sunny days and 20 days are non-sunny days.

Figure 2: Input feature data
2.2 DBSCAN-SVM Based Outlier Detection
In this paper, DBSCAN-SVM method is used to identify and detect abnormal data, as shown in Fig. 3. DBSCAN [21] belongs to the density clustering algorithm, which defines the class as the largest collection of density-connected objects, and the clustering is completed by constantly searching for high-density core samples and expanding to get the largest collection in the sample space, The main steps of DBSCAN are as follows:

Figure 3: DBSCAN-SVM outlier detection flow
(1) Define the neighborhood radius eps and the number of samples threshold min samples.
(2) Draw a sample p from the sample space that has not been visited yet;
(3) If sample p is a core sample, go to step 4; otherwise mark it as a noise sample or a boundary sample of a class according to the actual situation and return to step 2; and
(4) Find all the density connected samples starting from sample p, constitute a cluster Cp (the boundary samples of this cluster are all non-core samples), and mark these samples as visited;
(5) If all samples have been visited, the algorithm ends; otherwise return to step 2.
The clustering results are shown in Fig. 4.

Figure 4: Plot of DBSCAN clustering result
Then, the obtained clusters are input to the SVM for outlier detection, OneClassSVM belongs to a class of Support Vector Machines, which is robust to the presence of noise or outliers in the detection of data, and is able to effectively detect outliers. The basic idea of OneClassSVM is to expect to minimize the volume of the hypersphere and thus minimize the effect of the anomaly data. Fig. 5 shows the outlier detection results.

Figure 5: Graph of outlier detection result
To handle the variations in the size range and unit of measurement of collected data such as power, solar radiance, and temperature from the PV power plant, data normalization is essential to ensure that these characteristic data share a consistent metric scale and prevent the impact of differing scales. In this study, the maximum-minimum normalization method is employed, effectively mapping the original data into the [0, 1] value domain [22–23]. The calculation formula for this normalization method is as follows:
where
2.4 Indicators for Model Evaluation
This study employs two widely recognized metrics: the root mean square error (RMSE) and the mean absolute error (MAE) to ensure a rigorous and objective evaluation of the prediction model. These metrics are quantitative measures to assess the prediction model’s accuracy by quantifying the errors between predicted and actual values [24]. The calculations are as follows:
where
3 Principles of PSO-LSTM Prediction Modeling
PSO algorithm is inspired by the collective intelligence exhibited by birds in nature, and its optimization search is implemented by simulating the foraging process of birds. As shown in Fig. 6, During foraging, each bird lacks precise knowledge of the food’s location and can only perceive the distance between the food and itself. However, individuals in the flock can share location information. Birds employ a feeding strategy of first locating the nearest individual to the food within the flock and then searching for possible food locations in its vicinity.

Figure 6: Particle swarm algorithm illustrated
Suppose there is a population of m particles in a D-dimensional search space. Let the characteristic information [25] at moment t be:
where
Then the velocity and position information of the particle at the moment t+1 is updated:
where i denotes the particle number; d denotes the dimension of the solution problem; k is the current number of iterations; w is the inertia weight, regulating the search range of the solution space; c1 and c2 are the learning factors, regulating the step size of the direction of flying to its own and the global best position, respectively; r1 and r2 are random numbers uniformly distributed between [0, 1].
3.2 Leong and Short-Term Memory Networks
The Long Short-Term Memory (LSTM) is employed as an optimized recurrent neural network, featuring a connected subnetwork within each neural module. Each subnetwork represents a storage cell known as the LSTM cell, as depicted in Fig. 7. The LSTM cell comprises three gate units: an input gate, a forget gate, and an output gate [26]. These gate units offer continuous read, write, and reset operations to the memory cell, allowing it to dynamically adjust between different gates. This functionality serves the purpose of maintaining both long-term and short-term memory of the input data sequence.

Figure 7: LSTM unit neural module [29]
The forgetting gate governs the impact of the previous moment’s cell state, c(t-1), on the current moment’s cell state, c(t), deciding which information is retained and which is forgotten. In contrast, input gates play a role in assimilating the current moment’s input, x(t), into the cell state c(t), determining the incorporation of new information. The output gate oversees the influence of the cell state, c(t), on the current output, h(t), in the LSTM network, regulating the extent to which the cell state is transferred to the output. The computational procedure [27–28] is as follows:
In this context, let xt represent the input and ht denote the output. More specifically, ht corresponds to the output of the input gate, ft signifies the output of the oblivion gate, ct denotes the state of the cell at the current time point (t), and ot represents the output of the output gate. The parameter matrices and bias terms associated with these processes are denoted by W and b, respectively.
In the present research, the experimental platform employed is Jupyter Notebook, while TensorFlow is chosen as the deep learning framework. The study focuses on developing the PSO-LSTM prediction model, built upon the LSTM network model—a renowned architecture acknowledged for its efficacy in time series analysis. To enhance the performance of the LSTM network, the study harnesses the global search capabilities inherent in the particle swarm algorithm to identify optimal hyperparameters. This approach ensures a thorough exploration of the parameter space, contributing to the refinement of the LSTM model. Furthermore, the learning process is facilitated by the Adam optimization algorithm, chosen to enhance both the convergence speed and stability of grid learning. The strategic use of Adam optimization aims to optimize the training dynamics, improving efficiency and reliability in the learning process. As shown in Fig. 8, the algorithm flow of the PSO-LSTM model is as follows:
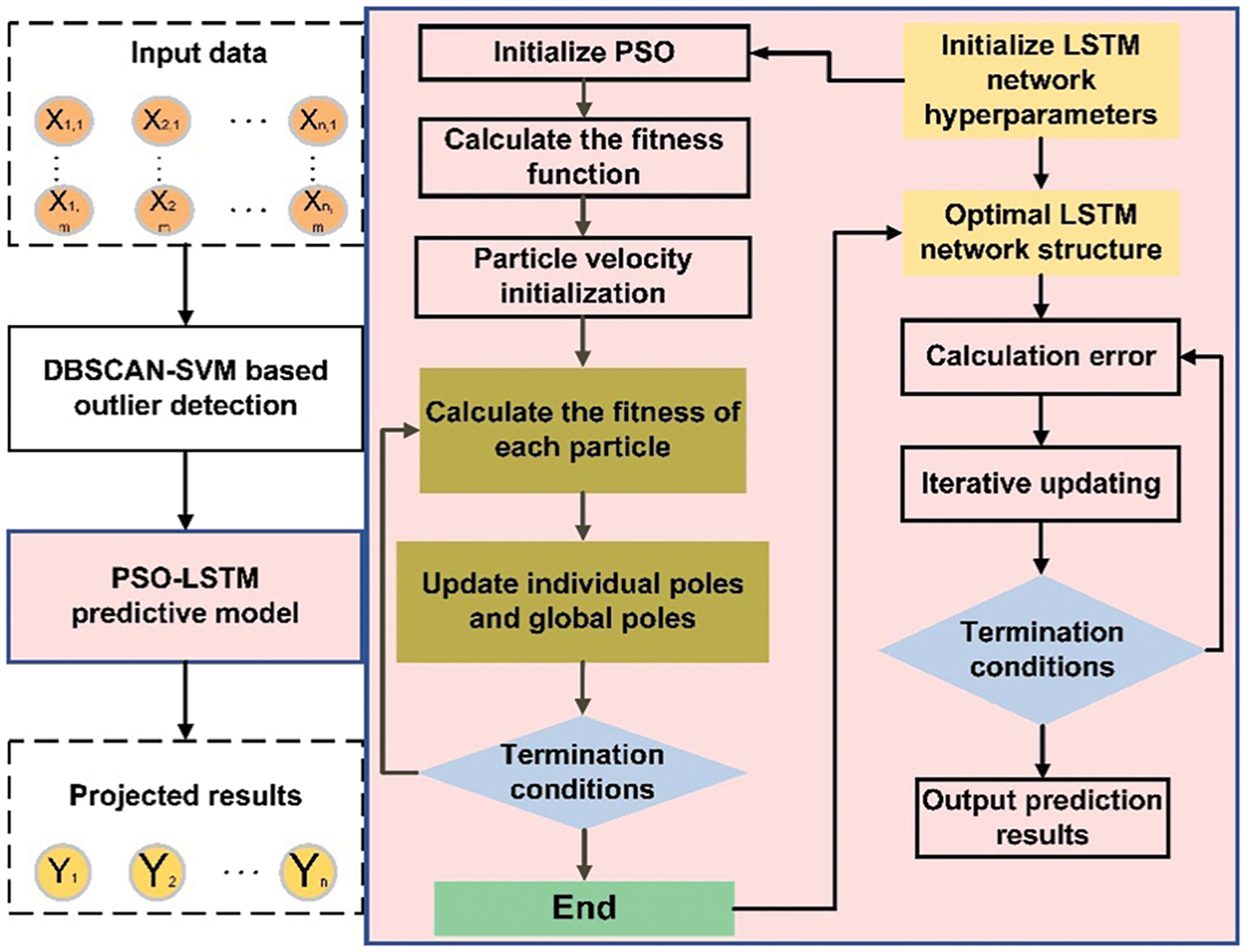
Figure 8: Flowchart of PSO-LSTM model algorithm
Step 1: Input historical PV power, solar irradiance, and temperature data.
Step 2: Data preprocessing.
Step 3: Divide the experimental data into training data, validation data and test data.
Step 4: Initialize the PSO algorithm by taking the time window size in the LSTM model as the optimization object.
Step 5: PSO iteration; in each PSO iteration, perform the following steps for each particle:
1) Apply the sliding time window corresponding to the particle to the training data and use the LSTM model for training and validation.
2) Determine the RMSE value of the fitness function to evaluate the performance of the LSTM model within the present sliding time window.
3) Update the individual best position (best time window) and global best position (global best time window).
4) Update the velocity and position of the particles to find a better time window in the search space.
Step 6: After the PSO algorithm converges, select the global optimal time window as the optimal parameter.
Step 7: Re-training the LSTM model using the optimal time window and output of PV power prediction results.
4 Calculated Case Validation Analysis
This study develops three prediction models: the BP neural network, the LSTM network, and the PSO-LSTM network. This division is applied separately to sunny and non-sunny day data. Such a distribution strategy ensures a balanced representation of the dataset across these sets, enabling robust training, effective validation, and reliable testing of the models under diverse weather conditions. Finally, the superiority of each model is assessed by comparing the RMSE and MAE of the predicted and actual values. The model with lower RMSE and MAE values is considered superior. The model parameter settings are shown in Table 1.

4.1 Data-Processing Impact Analysis
Based on the above proposed data processing method, it is introduced into the BP and LSTM models for validation, and the validation results show the effectiveness of the data processing, as shown in Fig. 9, the data processing reduces the RMSE of the models. Compared with the BP, the RMSE of the DBSCAN-SVM-BP is reduced by 33.58% under sunny day and 26.46% under non-sunny day; compared to LSTM, the RMSE of DBSCAN-SVM-LSTM is reduced by 18.24% in sunny day and 2.88% in non-sunny day.

Figure 9: Impact on the model after data processing
4.2 Non-Sunny Day Prediction Results
The non-sunny day dataset was systematically employed to train three distinct models. Subsequently, the RMSE and MAE metrics were computed to assess the disparities between the predicted values and their corresponding actual counterparts for each model. The prediction results are shown in Figs. 10 and 11.

Figure 10: Plot of non-sunny day predictions vs. actual values for the four models

Figure 11: Plot of predicted vs. actual values for non-sunny day 13:30–18:00 for the four models
In Fig. 10, the LSTM prediction model’s prediction results align with the trend of the actual values. However, the predicted values of the fluctuating segment are lower than the actual values under non-sunny day. The RMSE is calculated to be 6.76% and the MAE to be 4.86%. The difference between the prediction results of the PSO-LSTM prediction model and the actual values is reduced, and the predicted values of the fluctuating segment are closer to the actual values, showing specific stability. The predicted value of the PSO-LSTM prediction model is closer to the actual value and shows some stability. The RMSE is calculated to be 6.44%, and the MAE is 3.39%. Finally, the predicted values of the PSO-LSTM prediction model after DBSCAN-SVM data processing are closer to the actual values, and the stability is improved. The calculated RMSE is 5.96%, and MAE is 3.26%. From 13:30 to 17:00, Fig. 11 shows that the DBSCAN-SVM-PSO-LSTM prediction model outperforms the other two prediction models and shows some stability.
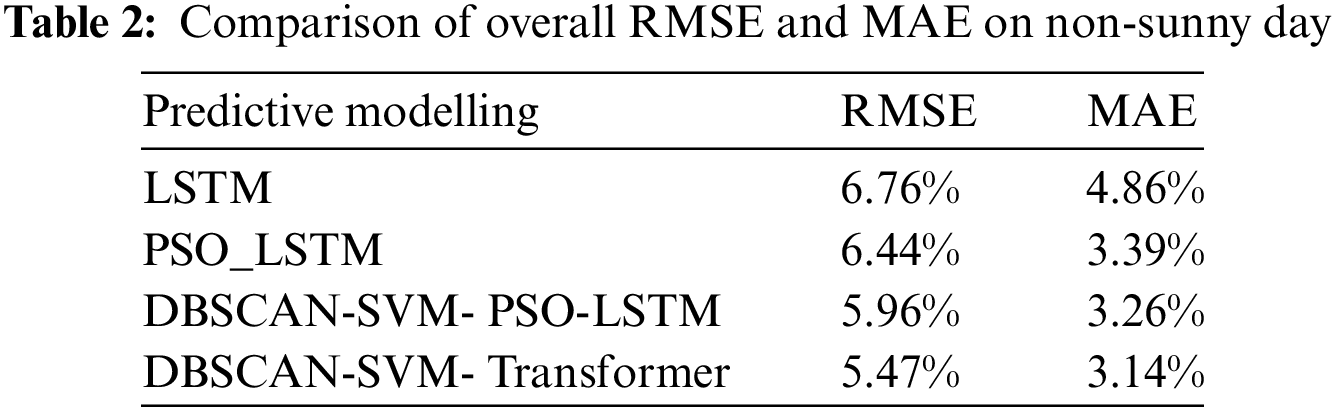
Table 2 is a comprehensive comparison table of RMSE and MAE for non-sunny day. The results indicate that, under non-sunny conditions, compared to the LSTM network predictions, the PSO-LSTM network exhibited a 3.45% decrease in RMSE and a 30.25% decrease in MAE. The results also showed that the data was processed by DBSCAN-SVM and then trained again using the PSO-LSTM model, which resulted in an improvement of 7.45% in RMSE and 3.83% in MAE. In addition, the model was also compared with Transformer.
4.3 Results of Sunny Day Prediction
Figs. 12 and 13 show the differences exhibited between the various models under sunny day. The PSO-LSTM model predictions are closer to the real values, and the data are processed by DBSCAN-SVM, which further improves the PSO-LSTM model outputs. The calculated RMSE and MAE are shown in Table 3.

Figure 12: Plot of sunny day predictions vs. actual values for the four models
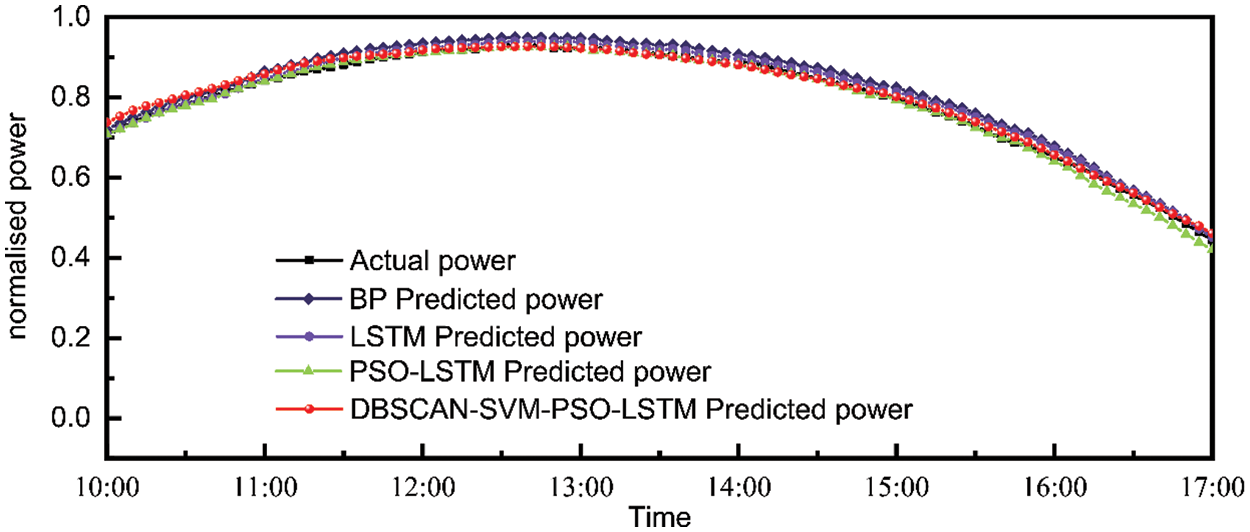
Figure 13: Plot of predicted vs. actual values for sunny day 10:00–17:00 for the four models
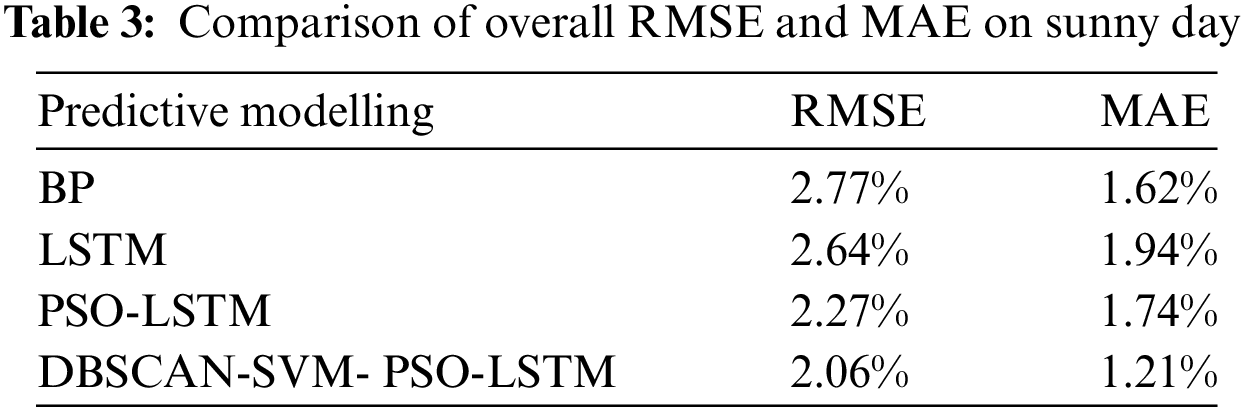
Table 3 presents the RMSE and MAE of the three prediction models for sunny day. Compared to the LSTM network predictions, the PSO-LSTM network demonstrates a 14.01% decrease in RMSE and a 10.3% decrease in MAE. Notably, the PSO-LSTM prediction model exhibits a relatively modest improvement compared to the LSTM model under favorable weather conditions.
The results also showed that the data was processed by DBSCAN-SVM and then trained again using the PSO-LSTM model, which improved RMSE by 9.25% and MAE by 30.4%.
The effectiveness of the PSO-LSTM prediction model is evaluated through comparative analysis with the Inner Mongolia PV plant model. Fig. 14 compares the error part of the model prediction results with the prediction results of the actual on-site power plant, and the comparison results show that the PSO-LSTM prediction model has excellent stability. The effectiveness of the PSO-LSTM prediction model is evaluated through comparative analysis with the Inner Mongolia PV plant model.

Figure 14: Comparison of the error component of the model prediction results with the actual site prediction results
In this study, a PSO-LSTM PV power prediction model based on DBSCAN-SVM is developed. The model’s vulnerability to anomalies is mitigated by DBSCAN-SVM data preprocessing, which proves that good data quality impacts the model. In addition, the global search capability of particle swarm optimization is utilized to optimize the hyperparameters of LSTM, which improves the accuracy of the LSTM prediction model. The main conclusions are as follows:
(1) The method of data processing was applied to the BP and LSTM models for validation, and the accuracy of the models was improved after data processing, proving the effectiveness of data processing.
(2) The rapid fluctuation of solar irradiance during non-sunny days leads to significant changes in PV power generation, and the proposed PSO-LSTM power prediction model has superior stability performance and higher prediction accuracy. Secondly, the DBSCAN-SVM processed data are fed into the model for training, and the prediction results are improved, with the RMSE reduced by 7.45% and the MAE reduced by 3.83%. The PSO-LSTM power prediction model shows better stability when the PV power generation remains stable on a sunny day. The data processed by DBSCAN-SVM improves the prediction accuracy of the model, with a reduction of 9.25% in RMSE and 30.4% in MAE.
(3) The prediction accuracy of the model developed in this paper is improved when compared to existing prediction models for actual field sites.
In the future research, we will continue to improve the DBSCAN-SVM data processing method and continue to optimize the proposed PSO-LSTM prediction model for comparison with advanced model algorithms. Considering the actual situation of PV power fields, meteorological factors such as PV panel temperature and cloudiness can be subsequently introduced into the model to further improve the accuracy of PV power prediction.
Acknowledgement: None.
Funding Statement: This paper is supported in part by the Inner Mongolia Autonomous Region Science and Technology Project Fund (2021GG0336) and Inner Mongolia Natural Science Fund (2023ZD20).
Author Contributions: The authors acknowledge their contributions to this article as follows: study conception and design: Yujin Liu, Yan Jia; data collection, analyzing and interpreting the results, analyzing and interpreting the results: Yujin Liu, Yan Jia; manuscript writing: Yujin Liu; data exemplification: Weihua Yin, Zhifeng Liu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The source of the data is the PV dataset from the Data Centre for Photovoltaics and Imagery in Australia (DKASC). Participants in this study did not consent to the disclosure of the site validation data and therefore were unable to provide supporting data.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. S. Zhong, X. Wang, B. Xu, H. Wu, and M. Ding, “Hybrid network model based on data enhancement for short-term power prediction of new PV plants,” J. Mod. Power Syst. Clean Energy, vol. 12, no. 1, pp. 77–88, Jan. 2024. doi: 10.35833/MPCE.2022.000759. [Google Scholar] [CrossRef]
2. H. Y. Xu and Q. Zhang, “Photovoltaic Power generation prediction technology based on digital twin and improved LSTM,” J. Eng. Therm. Energy Power, vol. 38, no. 2, pp. 84–91, Jul. 2023. [Google Scholar]
3. X. Y. Liu, J. Wang, and T. C. Yao, “Ultra short-term distributed photovoltaic power prediction based on satellite remote sensing,” (in Chinese), Trans. China Electr. Soc., vol. 37, no. 7, pp. 1800–1809, 2022. [Google Scholar]
4. S. O. Vasilica and B. Adela, “On-grid and off-grid photovoltaic systems forecasting using a hybrid meta-learning method,” Knowl. Inf. Syst., vol. 66, no. 4, pp. 2575–2606, Jan. 2024. doi: 10.1007/s10115-023-02037-8. [Google Scholar] [CrossRef]
5. Y. Q. Wang, F. Xu, and Z. J. Liu, “Ultra-short-term power forecasting of distributed photovoltaic based on dynamic correlation characterization and graph network modeling,” Autom. Electr. Power Syst., vol. 47, no. 20, pp. 72–82, 2023. [Google Scholar]
6. H. Z. Li, J. T. Feng, and P. C. Wang, “Research on photovoltaic power generation prediction model based on TDE-SO-AWM-GRU,” (in Chinese), Electr. Power, pp. 1–10, 2024. [Google Scholar]
7. L. Y. Jia, S. N. Yun, Z. N. Zhao, H. L. Li, S. Y. Wang and L. Yang, “Recent progress of short-term forecasting of photovoltaic generation based on artificial neural networks,” Acta Energiae Solaris Sinica, vol. 43, no. 12, pp. 88–97, Dec. 2022. [Google Scholar]
8. A. Bâra and S. -V. Oprea, “Embedding the weather prediction errors (WPE) into the photovoltaic (PV) forecasting method using deep learning,” J. Forecast., pp. 1–26, Dec. 2023. [Google Scholar]
9. J. Zhang, L. Hong, S. N. Ibrahim, and Y. He, “Short-term prediction of behind-the-meter PV power based on attention-LSTM and transfer learning,” IET Renew. Power Gener., vol. 18, no. 3, pp. 321–330, Feb. 2024. doi: 10.1049/rpg2.12829. [Google Scholar] [CrossRef]
10. C. M. Yu, J. Qiao, C. Chen, C. Yu, and X. Mi, “TFEformer: A new temporal frequency ensemble transformer for day-ahead photovoltaic power prediction,” J. Clean. Prod., vol. 448, pp. 141690, Apr. 2024. doi: 10.1016/j.jclepro.2024.141690. [Google Scholar] [CrossRef]
11. K. Abdelhak and I. Razika, “Solar photovoltaic power prediction using artificial neural network and multiple regression considering ambient and operating conditions,” Energy Convers. Manag., vol. 288, pp. 15, Jul. 2023. [Google Scholar]
12. H. Gao et al., “Short-term prediction of PV power based on combined modal decomposition and NARX-LSTM-LightGBM,” Sustainability, vol. 15, no. 10, pp. 8266–8266, May 2023. doi: 10.3390/su15108266. [Google Scholar] [CrossRef]
13. H. W. Tan, Q. L. Yang, J. C. Xing, K. F. Huang, and S. Zhao, “Photovoltaic power prediction based on combined XGBoost-LSTM model,” Acta Energiae Solaris Sinica, vol. 43, no. 8, pp. 75–81, Mar. 2022. [Google Scholar]
14. X. Luo, D. X. Zhang, and X. Zhu, “Deep learning based forecasting of photovoltaic power generation by incorporating domain knowledge,” (in Chinese), Energy, vol. 225, no. 12040, pp. 120240, Jun. 2021. doi: 10.1016/j.energy.2021.120240. [Google Scholar] [CrossRef]
15. Y. Chen and X. Y. Chen, “Prediction of short-term photovoltaic power generation based on adaptive Kmeans and LSTM,” (in Chinese), Electr. Meas. Instrum., vol. 60, no. 7, pp. : 94–99, Jul. 2023. [Google Scholar]
16. Q. Ding, F. Yan, W. Xia, J. Hu, and L. Shen, “Multi-source data fusion based on wavelet decomposition and LSTM for distributed photovoltaic power prediction,” in 2022 IEEE 8th Int. Conf. Comput. Commun. (ICCC), Chengdu, China, 2022, pp. 2246–2250. [Google Scholar]
17. Y. Xue, Y. Yan, W. Jia, Y. Heng, S. Zhang and Y. Qin, “Photovoltaic power prediction model based on IGWO-LSTM,” Acta Energiae Solaris Sinica, vol. 44, no. 7, pp. 207–213, Jul. 2023. [Google Scholar]
18. L. Ye, B. D. Cui, Z. Li, Y. Zhao, and P. Lu, “Combined identification method for high proportion of abnormal operation data in photovoltaic power station,” (in Chinese), Autom. Electr. Power Syst., vol. 46, no. 20, pp. 74–82, Oct. 2022. [Google Scholar]
19. X. Ling, X. G. Zhou, and W. Z. Chen, “Research on photovoltaic output prediction based on ADASYN-XGBoost algorithm,” (in Chinese), China Rural Water Hydropower, no. 6, pp. 1–9, May 2024. doi: 10.12396/znsd.231785. [Google Scholar] [CrossRef]
20. Y. Xue, J. X. Li, J. T. Yang, Q. Li, and K. Ding, “Short-term prediction of photovoltaic power based on similar day analysis and improved whale algorithm to optimize LSTM network model,” (in Chinese), South. Power Syst. Technol., vol. 17, pp. 1–9, Nov. 2023. [Google Scholar]
21. Q. B. Li, X. Y. Lu, and P. J. Lin, “Photovoltaic power prediction based on DBSCAN-PCA and improved self-attention mechanism,” (in Chinese), Electr. Switch, vol. 62, no. 1, pp. 6–12, Mar. 2024. [Google Scholar]
22. C. Y. Wang, L. Y. Zhang, Z. Liu, J. Tan, and S. Xu, “Feature mining based indRNN photovoltaic power generation prediction,” (in Chinese), Proc. CSU-EPSA, vol. 33, no. 4, pp. 17–22, Apr. 2021. [Google Scholar]
23. T. Wang, X. Wang, Y. Xu, and W. Li, “Study on LSTM photovoltaic model considering similar days,” Acta Energiae Solaris Sinica, vol. 44, no. 8, pp. 316–323, Aug. 2023. [Google Scholar]
24. Y. J. Chen, X. Y. Ma, and K. Cheng, “Ultra-short-term power prediction of new energy based on meteorological feature quantity selection and SVM model parameter optimization,” Acta Energiae Solaris Sinica, vol. 44, no. 12, pp. 568–576, Dec. 2023. [Google Scholar]
25. J. H. Yuan, B. B. Xie, and B. L. He, “Short term forecasting method of photovoltaic output based on DTW-VMD-PSO-BP,” (in Chinese), Acta Energiae Solaris Sinica, vol. 43, no. 8, pp. 58–66, Jun. 2022. doi: 10.1007/s00202-023-01883-7. [Google Scholar] [CrossRef]
26. X. Zheng, X. G. Liu, H. Y. Zhang, and Q. Wang, “An enhanced feature extraction based long short-term memory neural network for wind power forecasting via considering the missing data reconstruction,” Energy Rep., vol. 11, no. 11, pp. 97–144, Jun. 2024. doi: 10.1016/j.egyr.2023.11.040. [Google Scholar] [CrossRef]
27. B. Chen, Z. Li, S. Li, Q. Zhao, and X. Liu, “A wind power prediction framework for distributed power grids,” Energ. Eng., vol. 121, no. 5, pp. 1291–1307, Apr. 2024. doi: 10.32604/ee.2024.046374 [Google Scholar] [CrossRef]
28. Z. Garip, E. Ekinci, and A. Alan, “Day-ahead solar photovoltaic energy forecasting based on weather data using LSTM networks: A comparative study for photovoltaic (PV) panels in turkey,” Electr. Eng., vol. 105, no. 5, pp. 3329–3345, Oct. 2023. [Google Scholar]
29. Y. C. Zhou, T. Xiao, and Q. Y. Xie, “Clustering-based lustering-based HPO-BILSTM short-term prediction of PV power,” (in Chinese), Acta Energiae Solaris Sinica, vol. 45, no. 4, pp. 512–518, Apr. 2024. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools