Source-Load Coordinated Optimal Scheduling Considering the High Energy Load of Electrofused Magnesium and Wind Power Uncertainty

1  Introduction

Numerous nations are actively pursuing new energy generation, which is driving up the size of new energy sources in order to create a new kind of electrical grid defined by cleaner energy sources [1]. For example, China will have 440 million kilowatts of installed wind and 610 million kilowatts of installed solar power by the end of 2023. By 2025, the combined installed capacity of solar and wind energy is expected to surpass 1.2 billion kilowatts. However, power supply is unpredictable since wind energy has anti-peaking and stochastic properties [2]. The phenomenon of power abandonment takes place when the power of wind energy sources is not efficiently released during peak hours, which greatly challenges the flexibility of the electrical network [3,4].

Demand-side load resources are growing more and more vital to scheduling [5]. Integrating conventional units and controllable load side resources into optimal power grid dispatching is a novel approach to addressing the issue of wind and solar energy losing power [6]. At home and abroad, some achievements have been made in the aspect of demand side load participating in optimal dispatching of power grid together with conventional units to absorb new energy. Reference [7] proposes to address the carbon capture plant constraints by engaging the resources of the demand-side response and to improve the low carbon system performance by coordinating and optimizing the supply and demand resources. High energy load also belongs to demand-side response load. Reference [8] considers the optimal wind power consumption scheduling model for the multi-timescale demand response of the involved high-energy loads, and applies an improved bionic model incorporating particle swarm optimization to minimize the system operation and wind abandonment costs and to find the optimal energy allocation within the system. Reference [9] proposes load response scheduling priority and hierarchical tariff strategy, and constructed a blockchain-based trading structure for a load aggregator, wind energy, and high power consuming enterprises, which can guarantee the return of the loop accumulator effectively and increase the level of wind energy dissipation. Reference [10] proposes a method for optimized source-load coherent dispatch that takes into account the high energetic loading of wind energy and the unpredictability of a conventional source of power. Reference [11] considers the adjustment of electrofused magnesium high energy-carrying loads to minimize fluctuations in wind generation. The approach involves combining electrofused magnesium loads with the fossil fuel power plant to allow for optimal network regulation.

The high share of new energies has become a feature in modern electricity system. The discontinuity and volatility of wind energy have brought significant uncertainty to the power system, greatly increasing the risk of stable operation of the electric system [12]. The literature primarily focusing on the uncertainty of new energy in scheduling includes the following: Reference [13] proposes an improved method to increase wind energy utilization by response load; simultaneously optimizing wind power energy consumption and system operating cost by a multi-objective differential evolution method. The response loads are classified into two categories based on the response characteristics, and the stochastic nature of wind energy is considered. The suggested method can maximize the wind energy utilization and reduce system operation cost more effectively. Reference [14] proposes a parameter simplification method to cope with the uncertainty of renewable energy by introducing a normally distributed probability distribution function and a reserve capacity allocation cost. Reference [15] proposed a critical time scale selection algorithm for real-time scheduling of high percentage of renewable energy based on temporal aggregation features, and the results of the study help to adapt to the uncertainty of renewable energy day-before-power prediction mistakes and to maintain the safe network operation. Reference [16] proposes an opportunity-constrained stochastic market design that generates robust competitive equilibria and internalizes the uncertainty in the price formation process for renewable resources. Reference [17] proposed a robust two-stage optimal scheduling method, and the proposed scheduling model can increase the profit of the operator and reduce the energy cost of the consumer. Reference [18] proposes a two-tier multi-temporal coordination methodology that reduces the impact of uncertainty in renewable energy sources, loads, and stochastic component failures on power balance, operating costs, and system reliability. Reference [19] proposes a pre-day economic scheduling approach for wind power generation taking into account the extreme cases of wind power generation based on a uncertainty set.

The above research has coordinated and cooperated with the new energy consumption system on both sides of the energy sources and loads and provided a theoretical basis for the research method of considering the uncertainty of wind power, but there are still the following shortcomings: the existing research mostly incorporates the high energy-carrying loads on the load side into the power grid, which in turn regulates the consumption of new energy sources, but it has not yet carried out an in-depth research on the participation of electrofusion magnesium high-load load in the grid scheduling problem. The second-order cone approximation algorithm of wind power uncertainty is not considered to reduce the scheduling error of units, which is too biased towards load regulation and optimization. Therefore, the high capacity load of electro-melting of magnesium is included in the system regulation and control, and participates in the grid optimum dispatching in cooperation with fossil generating units. In this paper, a double-layer optimization model of source and load is constructed, which has the largest consumption of wind energy generation and the lowest operating cost of the system. In the upper model, the blocked wind power is regulated by the high energy load of fused magnesium. The lower layer model adopts the second-order cone approximation algorithm to address the issue of high deviation of electricity power brought about by wind power unpredictability, and then realizes the economical dispatching of the network. Finally, a numerical example is calculated by Gurobi, and the results show that the model is effective and reasonable in practice.

2  Principles of Wind Power Consumption by High Energy Loads

2.1 High Energy Load Operating Characteristics

High energy load is characterized by a significant proportion of energy value in its output value, which has a large demand, such as large industrial enterprises, and its load demand far exceeds that of ordinary families or small enterprises. These loads have a large power capacity and adjustable characteristics [20]. It consumes a lot of energy, and the high energy load needs a lot of electricity to meet the production or operation needs. The high energy load is relatively concentrated, and its production plan is flexible and has good regulation performance. The typical discrete high-energy regulating load is fused magnesium load. Magnesium oxide is a kind of heat-resistant and refractory material widely used in cement, chemical industry, aviation, electronics and other fields. There are a large number of magnesia resources in central Liaoning Province, which can obtain high-purity magnesium oxide crystals.

2.2 Operational Characteristics of Wind Energy

The trend in power development for systems is the grid integration of a considerable amount of wind electricity. However, the intermittent, fluctuating and anti-peak characteristics of wind energy can not be ignored. and the high proportion of wind energy access makes the uncertainty of power supply enhanced [21–23]. The uncertainty associated with the large number of wind energy connections to the grid adversely affects grid dispatch. As shown in Fig. 1, the range of wind speeds and the rate of change are uneven, resulting in wind farm output that may vary substantially between rated output and zero output, and wind power that may also vary substantially over two consecutive days when the total wind resource is close.

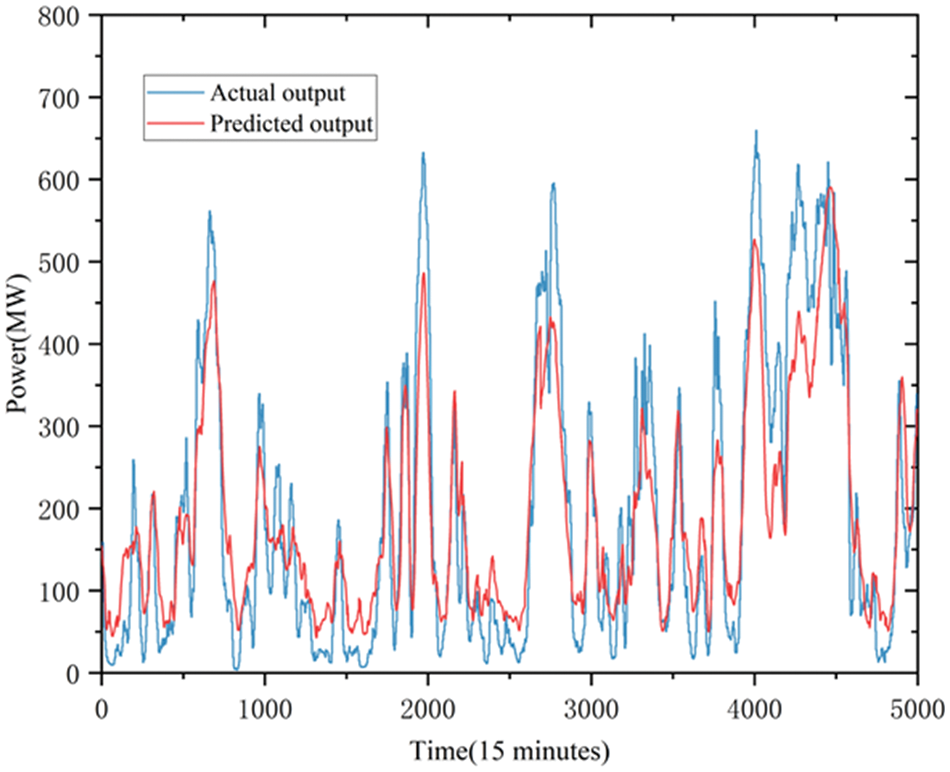
Figure 1: Schematic diagram of wind power dissipation by electrofusion magnesium loads

2.3 Principle Analysis of Wind Power Dissipation by Electrofused Magnesium Loads

The rising integration of large-scale renewable energy sources into the power grid has heightened the need for enhanced regulation capabilities from traditional units within the system. To effectively mitigate the fluctuations associated with new energy generation, this study suggests the inclusion of electrofused magnesium high energy-carrying loads in the dispatch of the network. Considering the close proximity between new energy sources and high-energy loads, along with their complementary demand, utilizing high-energy loads with substantial adjustable capacity and rapid response times can effectively address wind power fluctuations. This approach facilitates swift adjustments to promote wind power consumption and minimize system inefficiencies caused by unused air volume.

At time t, the net system load of wind energy is

PC,t=PL,t−PW,t(1)

In the above equation: PC,t shows the net load, PL,t presents the system load, PW,t is the total wind farms result.

Fig. 2 shows that net load curve of the system is at the lower limit of the minimum output of the unit from time T1 to T2. Due to the insufficient regulating ability of the thermal power unit, it can only resort to wind abandonment and limitation to ensure system safety. The system experiences its highest level of abandoned wind volume in the absence of high-energy load regulation. However, when the high-energy load is involved in system dispatching, the rate of abandoned air within the system decreases. If the regulation capacity of the high-energy load is large enough, new energy can be completely absorbed. Therefore, including high energy-carrying loads in system scheduling and regulation effectively reduces system wind power abandonment and enhance the ability of the grid system to consume wind energy.

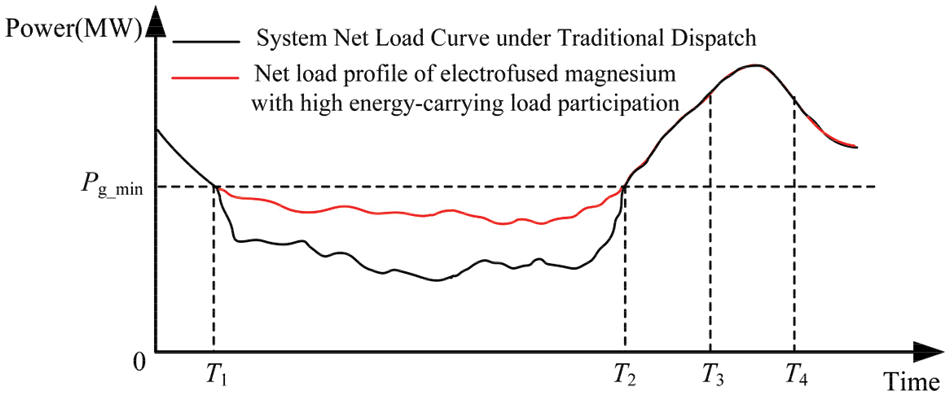
Figure 2: Schematic diagram of wind power dissipation by electrofusion magnesium loads

3  Two-Layer Optimization Model

Two-layer optimization, a form of nested optimization, comprises two hierarchical optimization tasks. The higher layer determines the strategy that the lower layer uses to maximize its own objective function. As shown in Fig. 3, a two-layer optimization model is used to study the problem of source-load coordination and optimal scheduling, and the models top and lower layers are connected by the output and power balance of conventional units. The upper and lower layers of the model are linked by conventional unit output and power balance. The top layer model is designed to get the regulatory power of the high energy-carrying load of electrofused magnesium, wind power consumption, and overall output of conventional units while maximizing system wind power consumption. The lower model was optimized in order to reduce the traditional units in the operating cost of the system. Based on the combined output of all conventional units and wind power output, it solves the output curve of each conventional unit as well as the system running cost.

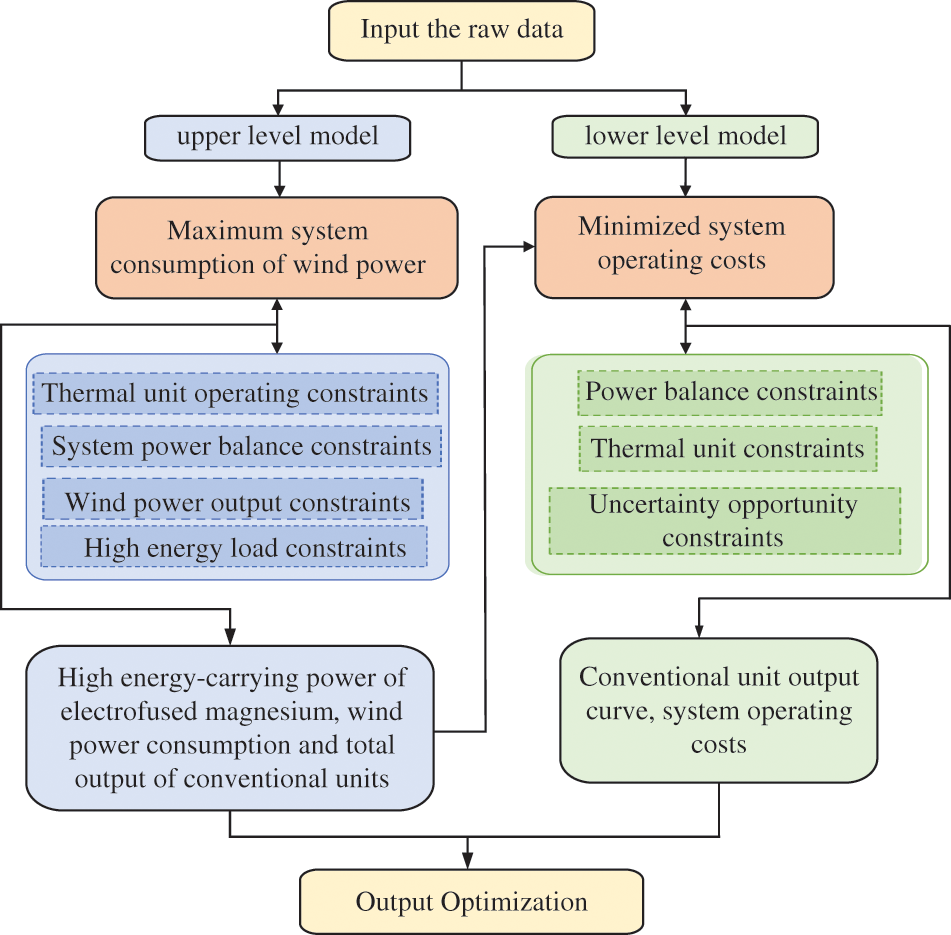
Figure 3: Flowchart for solving two-layer optimization model

3.1 Upper Level Optimization Model

With the aim of maximizing wind power consumption and taking into account a number of constraints, including thermal power units, wind power, and load, the upper optimization model optimizes the total output of thermal power units, the output of wind power, and the regulated power of fused magnesium with high energy load.

maxPwind=∑t=1T∑i=1NWPwind,itΔT(2)

In the above equation: Pwind is the output force for wind power dispatching. NW equals the total number of wind turbines. Pwind,it the result from the wind plantation i at the given time, and ΔT notes the length of the time period.

The constraints include those related to power balance, wind power output, thermal power unit operation, and power regulation for high energy carrying loads of electrofused magnesium.

(1)   Power balance constraints

Pwind,it+PGt=PLoadt+∑k=1NmgΔPmg,kt(3)

In the above equation: PGt is the total active power of the heating plants at a given time t. PLoadt is the active predicted power of the regular load of the network at time t. Nmg is the number of electric magnesium melting furnace. ΔPmg,kt is the electrical magnesium melted furnace during the period of t regulating power.

(2)   Wind power output constraints

0≤Pwind,it≤Pwind,i,foret(4)

In the above equation: Pwind,i,foret is the predicted value of active output of wind farm i at time t.

(3)   Operating restrictions for thermal units

Higher and Lesser Limit Constraints on Input Power:

PGmin≤PGt≤PGmax(5)

Climbing Speed Constraint:

{PGt−PGt−1≤PGupPGt−1−PGt≤PGdown (6)

In the above equation: PGmin and PGmax are the higher and lesser limit constraints on input power, respectively. PGup and PGdown  are the upward and downward creep rates of the thermal unit, respectively.

(4)   Power constraints for high energy load regulation of electrofused magnesium

Regulating Power Constraints:

Pup≤∑k = 1NmgΔPmg,kt≤Pdown(7)

Pmin+Pmg,baset+∑k=1NmgΔPmg,kt≤Pmax(8)

In the above equation: Pmin and Pmax are the lesser and maximum limits of the electrofused magnesium load, respectively. Pup and Pdown are the lesser and maximum limits of the regulated amount of electrofused magnesium load, respectively.

Adjustment number constraints:

0≤∑t=1T|STt−STt−1|≤M(9)

In the above equation: STt and STt−1 are the amount of regulation of the electrofused magnesium high energy load at the period t as well as t–1, respectively. STt = 0 means that the electrofused magnesium high energy load at time t is not involved in regulation, and STt = 1 means that it is involved in regulation.

In order to have sufficient regulation range for the thermal units in the lower tier that take into account the uncertainty of wind power, the regulation power of the high energy-carrying loads of electrofused magnesium needs to be satisfied:

PLoadt+∑k=1NmgΔPmg,kt≥PGmin+Pwind,it+ω(10)

In the above equation: ω is the historical production error of wind energy.

From the upper optimization, you may obtain the complete thermal electricity unit production, the maximum wind power consumption, and the electric fusion magnesium load regulation power, the net load curve for:

PGt=PLoadt+∑k=1NmgΔPmg,kt−∑i=1NwPwind,it(11)

3.2 Lower Level Optimization Model

3.2.1 Modeling without Wind Energy Uncertainty

On the basis of realizing the optimal scheduling scheme of maximum wind power consumption, considering the minimization of coal consumption cost, wind abandonment penalty cost and carbon emission cost of heating power generators, the system operation cost is optimized, and its mathematical model is as follows:

minF=FTH+FQT+FRP(12)

FTH=∑t=1T∑x=1nUxt[ax(Pxt)2+bxPxt+cx]ΔT(13)

FQT=∑t=1T∑i=1NWρi(Pwind,i,foret−Pwind,it)ΔT(14)

FRP=∑t=1T∑x=1nfPxtΔT(15)

In the above equation: FTH is the cost of coal used by electric utilities. FQT is the financial cost of wind quitting the network. FRP is the carbon emission cost of the thermal power unit. ax,bx,cx are the coal consumption coefficients of the heating generator x. Pxt is the result of the heat energy x at time t. Uxt the switching on and off state of the heating generator x in time period t, with 1 denoting the switching on and 0 denoting the switching off. T is the total amount of scheduling intervals for the dates. n the number of units of the heating generator. ρi is the unit penalty cost of the wind power farm i. If the wind power is fully consumed, then Pwind,i,foret=Pwind,it. fx is the carbon dioxide emission penalty depending on the amount of electrical energy for heating generator x.

minF=∑t=1T∑x=1n[Uxt(ax(Pxt)2+bxPxt+cx)+ρi(Pwind,i,foret−Pwind,it)+fPxt]ΔT(16)

The thermal power unit power balancing, the creep limitation on the thermal power unit, and the final power restriction on the thermal power source are some of the system restrictions.

(1)   Power balance constraints for thermal units:

∑t=1T∑x=1nPxt=∑t=1TPGt(17)

(2)   Climbing constraints for thermal units:

{UxtPxt−Uxt−1Pxt−1≤Px,upUxt−1Pxt−1−UxtPxt≤Px,down(18)

In the above equation: Px,up and Px,down are the maximum upward and downward creeping outputs of thermal unit x.

(3)   Output power constraints for thermal power units:

UxtPx,min≤Px≤UxtPx,max(19)

In the above equation: Px,min and Px,max are the lower and maximum output power limits of heating unit x.

3.2.2 Optimization Model Considering Wind Power Uncertainty Opportunity Constraints

Differences between expected and reality wind energy output levels are frequently caused by the unpredictability and volatility of wind energy. Historical probability error data can be used to calculate this discrepancy. The stability and economy of the electricity grid are greatly impacted by the uncertainty surrounding renewable energy. Because of this, the source-load optimal dispatch method which considers wind power uncertainty is extremely important [18].

(1)   Confusion in wind energy characterisation

Assuming that the actual value of the new energy plant output at a certain moment t is

Pw,fact=Pw,fore+ω(20)

In the above equation: Pw,fore is the anticipated amount of active electricity produced by a wind plantation.

All conventional units must deal with the uncertainty of wind power before making adjustments in order to maintain the real-time power balance of the system. This means that all conventional units must adjust the wind power prediction error. The active output of the conventional units is as follows after accounting for the unpredictability of wind power:

Pω,x=Px−αxω(21)

In the above equation: Px is effective production of the conventional component x when the wind energy produced is Pω, when the prediction error equals 0. Pω,x is the traditional unit x actual power production modified to account for wind power variability. αx equals the weight that conventional unit x bears for the deviation of wind energy production, then

{∑x=1nαx=10≤αx≤1(22)

(2)   General form of opportunity constraints

Different generator sets cannot simultaneously surpass the lowest and highest output limits of a particular traditional generator set while the power system is operating normally. The general form of opportunity constraint can be expressed by bilateral opportunity constraint as follows:

{Pr{Pxt−αxtω−Px¯≥0}≤1−εPr{Px_−Pxt+αxtω≥0}≤1−ε(23)

In the above equation: Px_ and Px¯ are the lesser and maximum output power limits of heating power generator x. ε means the confidence level of the interval.

In the previous section we obtained the objective function for the operating cost of heating power generators. When wind power uncertainty is introduced, the model uses the system minimum operating cost expectation as the optimization objective function. This function is represented by the next equation is as follows:

minE[F]=[∑t=1T∑x=1nUxt(ax(Pxt)2+bxPxt+cx)+ρi(Pwind,i,foret−Pwind,it)+fPxt]ΔT(24)

{∑x=1nPω,xt=PLt−PRt−ωt∑x=1nPxt=PLt−PRtPRt={PWt−Pabont=0PWt−Pabont≠0Pω,xt=Pxt−αxtωt(25)

{Pr{Px¯−Pω,xt≥0}≥εPr{Pω,xt−Px_≥0}≥ε∑x=1nαxt=1Pω,xt≥0,0≤αxt≤1(26)

In the above equation: PLt is the numerical value of the burden prior to time t. PRt is the forecasted consumption value of wind energy at time t before the day. Pabont is the amount of wind rejected.

The difference between the net load value for the day ahead with the real net burden value at moment t is ω, which is jointly regulated by n thermal units, and the regulation of thermal unit x at that moment is αxtωt.

(3)   Chance constraint approximation based on second-order cone programming

Define a generalized set of distributionally robust chance constraints as follows [24]:

Z:={x:P∈PinfP[|a(x)Tω*+b(x)|≤T]≥1−ε(27)

In the above equation: ω∗ is a random perturbation vector, E[ω∗]=0 and Var[ω∗]=δ2, rewrite Eq. (26) above as a general bilateral constraint:

ZA(ε)=(x:P∈PinfP[|a(x)Tω*+b(x)|≤T]≥1−εinfP∈PP[|a(x)Tω*+b(x)|≥−T]≥1−ε)(28)

Then Eq. (28) above can be equated to the general second order cone form:

ZA(ε)=(x:b(x)+1−εεa(x)δ2a(x)≤T−b(x)+1−εεa(x)δ2a(x)≤T)(29)

According to (23), let

{a(x)=−αxb(x)=Px−Px¯+Px_2T=Px¯−Px_2(30)

Bringing Eq. (30) into (29), (29) can be equated as:

{Px−Px¯+Px_2+αxδε1−ε≤Px¯−Px_2−Px+Px¯+Px_2+αxδε1−ε≤Px¯−Px_2(31)

Assuming that ω satisfies the normal distribution, ω∼N(μ,δ2) and μ=E[ω], δ2=Var[ω]. Eq. (24) indicate E[F]=E[FTH]+E[FQT]+E[FRP]. It expands in the form of (for convenience, t is omitted from the following equations, such as Px for Pxt):

E[αxPω,x]=αxE[(Px−αxω)2]

=αxE[Px2−2αxωPx+αx2ω2](32)

=αx[Px2−2αxμPx+αx2(δ2+μ2]

E[bxPω,x]=bxE[Px−αxω]=bx(Px−αxμ)(33)

Then the original objective function (24) can be transformed into the following form:

minF=∑t=1T∑x=1n[ax[Px2−2αxμPx+αx2(δ2+μ2)]+bx(Px−αxμ)+cx+ρi(Pwind,i,fore)+f(Px−αxμ)]ΔT(34)

{Px−Px¯+Px_2+αxδε1−ε≤Px¯−Px_2−Px+Px¯+Px_2+αxδε1−ε≤Px¯−Px_2(35)

{∑x=1nPx=PL−PRPx≥00≤αx≤0∑x=1nαx=1(36)

By using the opportunity constraint condition, the model establishes a relationship between the operational expenses of the electrical grid and the uncertainty of wind energy production. It then converts the opportunity constraint economically feasible problem into a problem of optimization where the goal is to find the minimum expectation of the system objective function.

4  Case

4.1 Cases and Parameters

Verifying the efficacy and fairness of the optimization model in this work, we conduct simulation verification of the constructed model. Using a typical day load in Northeast China as an example, the thermal energy plants have a total capacity of 2300 MW and are composed of 7 units. The maximum and minimum generated by heating units are displayed in Table 1, together with the factors related to running costs. The total installed wind power capacity is 900 MW. A day with significant variations in wind power output characteristics is selected as the baseline data, with a unit penalty cost for wind abandonment set at 49.02 $/(MWh). The rated power of the electrofused magnesium high energy-carrying load is 600 MW. It can be adjusted upward by 20% and downward by 15% of the rated power, with a scheduling cost of 11.20 $/(MWh). The system scheduling cycle is 24 h with a sampling time of 15 min.

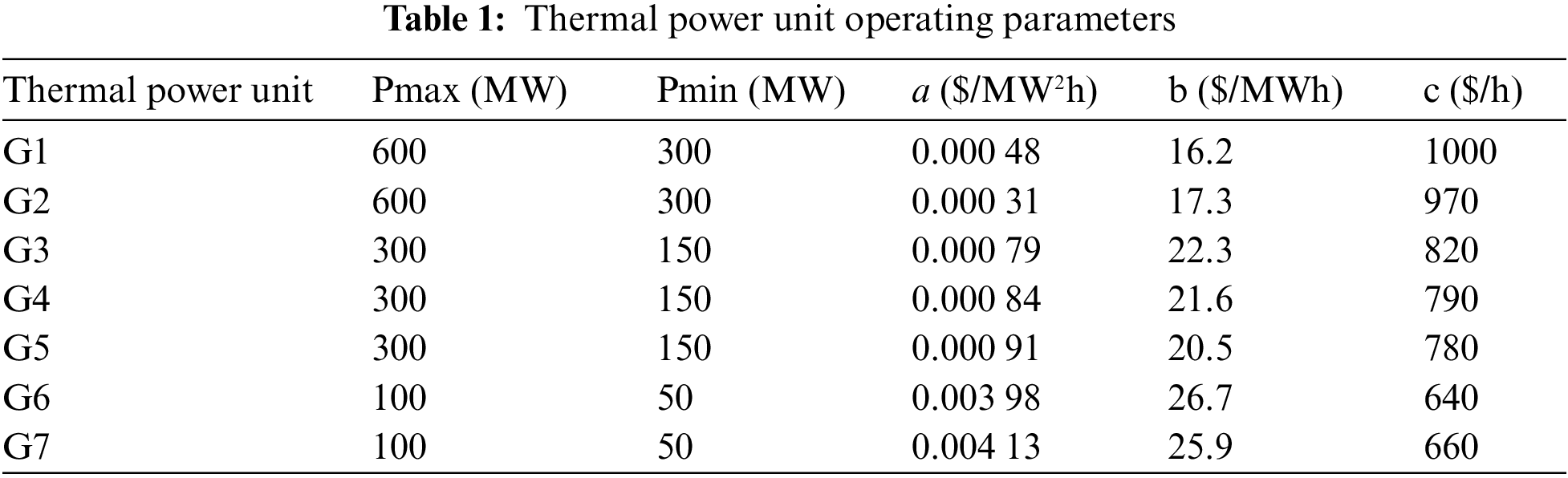
Fig. 4 illustrates the daily conventional load, which exhibits a double peak pattern, with the highest load occurring between 17–19 h and the lowest load between 2–6 h. Wind power output shows an inverse pattern to the conventional load, with its peak occurring between 0–7 h and lower output between 8–20 h, reaching its lowest point between 9–12 h. In the period of low peak load, wind power is at the peak stage, which shows that wind energy has obvious features associated with anti-peak regulation. This will lead to serious wind abandonment in the system and increase the regulating pressure of heating power generators.

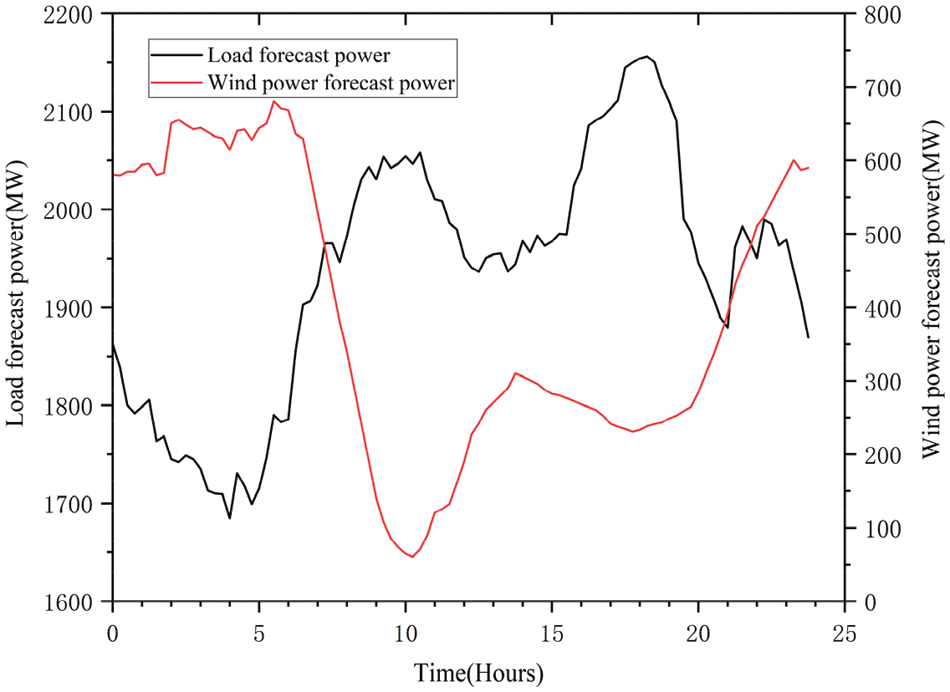
Figure 4: Load forecasted power and wind forecasted power curves

4.2 Analysis of Results

In order to confirm the validity of the proposed optimization model, we have compared the three schemes:

Scenario 1: Traditional dispatching, in which the thermal power unit on the power supply side participates in the system regulation, and the high-energy load on the load side does not take part in system regulation;

Scenario 2: Coordinated source and load scheduling, wherein a high-energy demand of fused magnesium on the demand side and the thermal power unit on the energy supply side both contribute to system management;

Scenario 3: Source-load coordination optimization model scheduling considering uncertainties about wind power, and uncertainties about wind power is considered on the basis of Scenario 2.

The forecast data of load and wind energy is used to derive the emission of a heating generator for Scenarios 1, 2, and 3, as illustrated in Figs. 5–7.

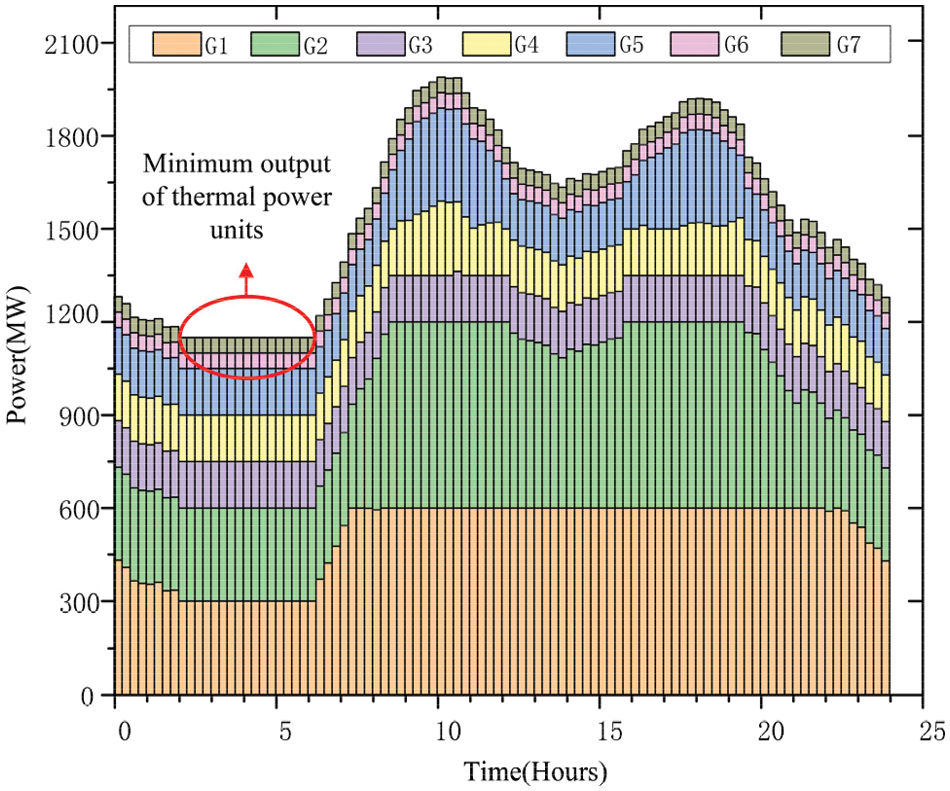
Figure 5: Scenario 1 each unit contributing

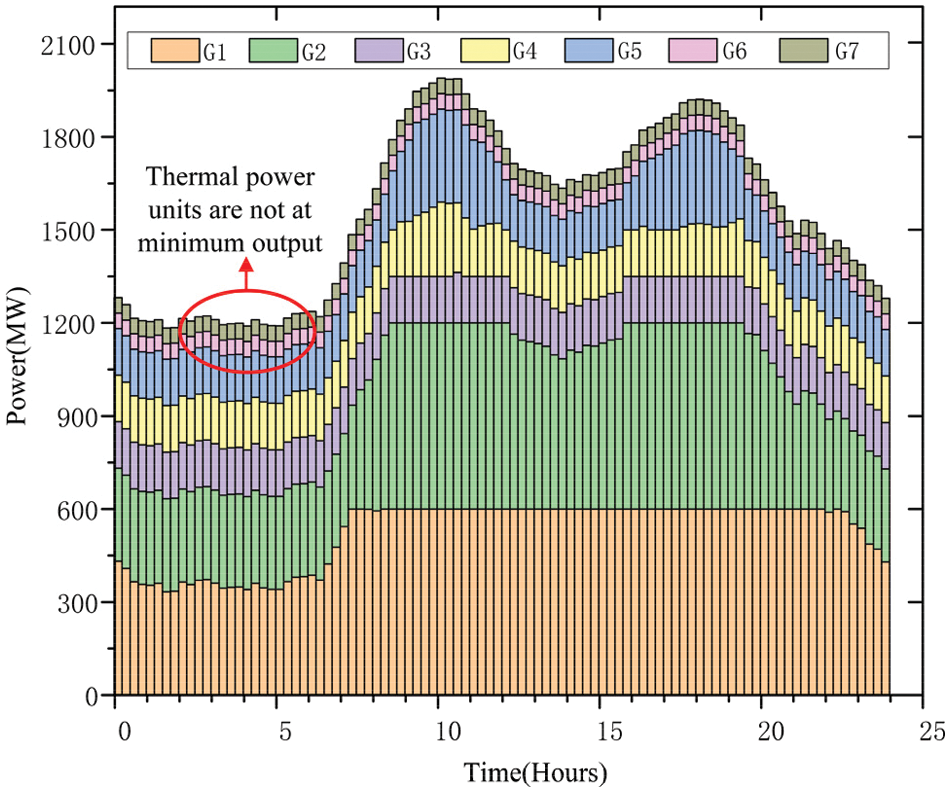
Figure 6: Scenario 2 each unit contributing

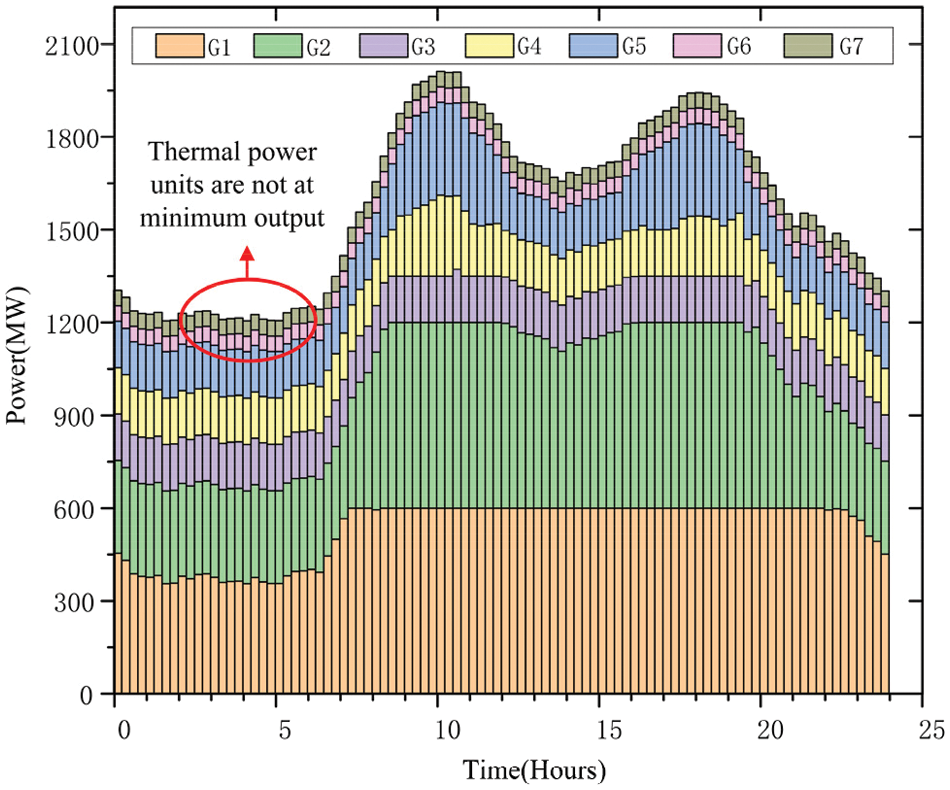
Figure 7: Scenario 3 each unit contributing

Fig. 5 illustrates the emission of a heating generators over different time periods in Scenario 1. The units of thermal energy operate at the minimum output level for 17 hourly segments. During the 17th hourly segment, the thermal power unit operates at its lowest level. Due to the need to maintain system balance, the excess wind power generation cannot be absorbed, resulting in wind power curtailment. Figs. 6 and 7 depict emission of a heating generators for Scenario 2 and Scenario 3, respectively, on an hourly basis. It is evident that after regulating the high energy-carrying load of electro-melting magnesium, the excess curtailed wind energy is utilized, and the thermal power units do not operate at the minimum output level.

Fig. 8 shows the online load profile and wind curtailment for Scenario 1. Fig. 8 shows the net load curve of Scenario 1, and the blue part is the abandoned air volume. In the traditional dispatching, wind power has anti-peak oversight, so when the amount of wind power generated is at its highest and the load power is at its lowest, the system will cut off the wind, which is not good for using wind power.

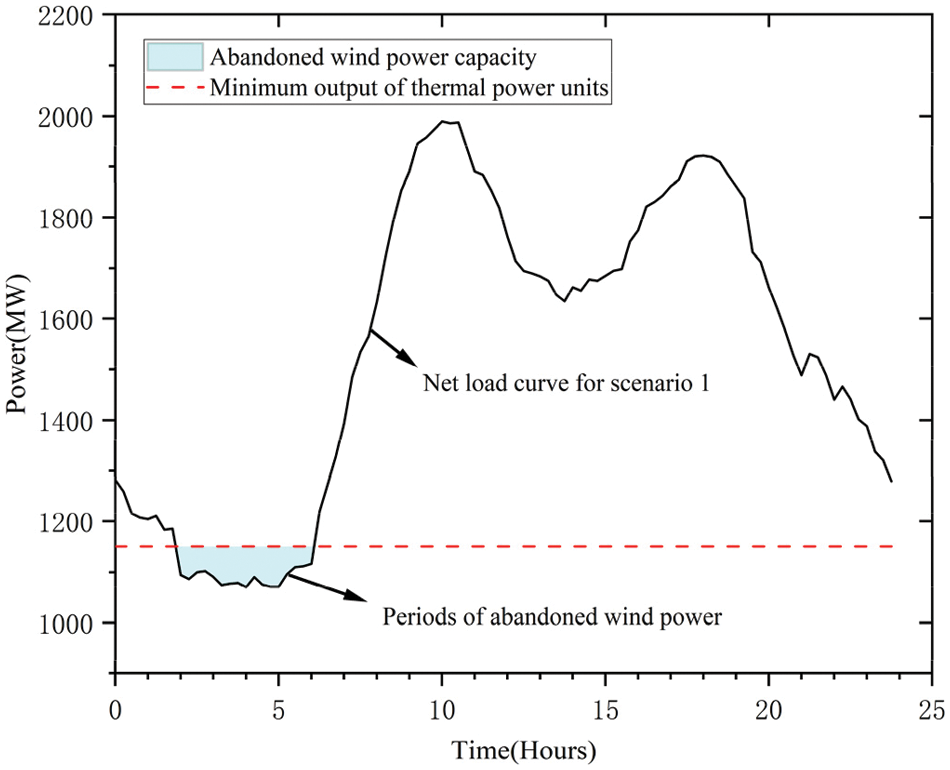
Figure 8: Scenario 1 net load curve

The power curves of high energy load and net load of fused magnesium are shown in Fig. 9. In Scenario 1, during the period of 2–6, the generator of thermal energy was was operating at its lowest possible capacity, and the load side prohibited from engaging in network management, which significantly increased the regulation pressure of the generator of thermal energy and the system abandoned the wind. In Scenario 2, the high-energy load of fused magnesium on the load side participates in the network adjustment to increase the power, which maximizes the consumption of wind energy and is beneficial to the consumption of wind energy. In Scenario 3, in the same period of large wind power treatment and small load, due to the unpredictability of wind energy, the high energy load of fused magnesium participates in the system regulation more, which is more conducive to the absorption of wind energy.

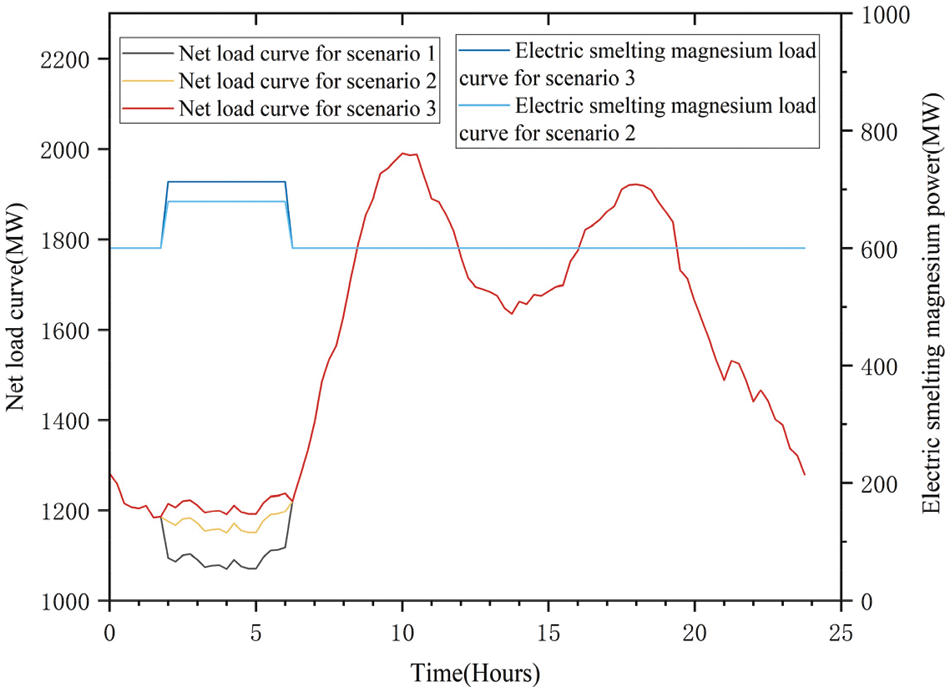
Figure 9: High energy load and net load power curves for electrofused magnesium

In Fig. 10, the actual overall output of the thermal energy units is compared with the total generated by heating power units taking wind power unpredictability into consideration and not.

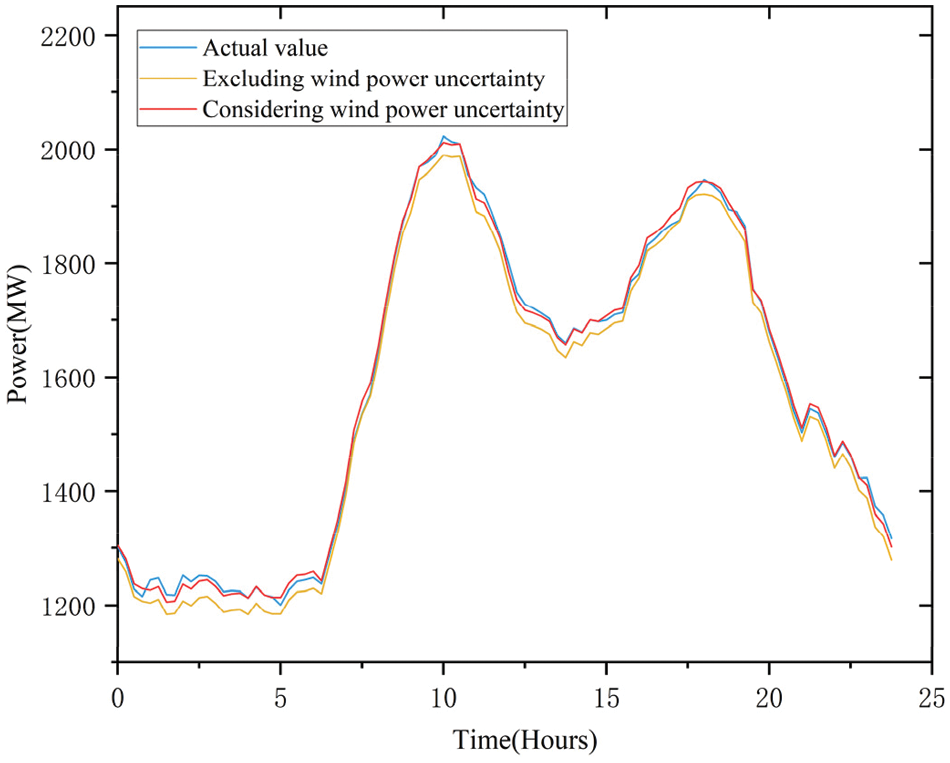
Figure 10: Comparison of total output curves of thermal power units

Both Scenarios 2 and 3 involve high energy-carrying loads of electrofused magnesium in system regulation. The difference is that Scenario 2 does not consider the effect of wind energy uncertainty, while Scenario 3 does. Fig. 10 shows the yellow curve as the unit output without considering wind power uncertainty, the red curve with wind power uncertainty considered, and the blue line as the actual unit output. When wind power uncertainty is not considered, the real result of the blue curve differs slightly from the anticipated outcome of the yellow curve. When wind power uncertainty is considered, the real result of the blue curve and the anticipated result of the red curve still differ from one another, but the red curve is closer to the actual output than the yellow curve. It can be seen that the two-layer optimal scheduling proposed can more accurately predict unit output, considering wind power uncertainty.

Comparison of the total export error of thermal units with and without wind energy unpredictability, as shown in Fig. 11, the blue part is the output error of units without wind power uncertainty, and the red part is considered. The red part is obviously smaller than the blue part, so it can be seen that the double-layer optimal scheduling considering wind power uncertainty proposed in this paper can reduce the output error of heating power generators.

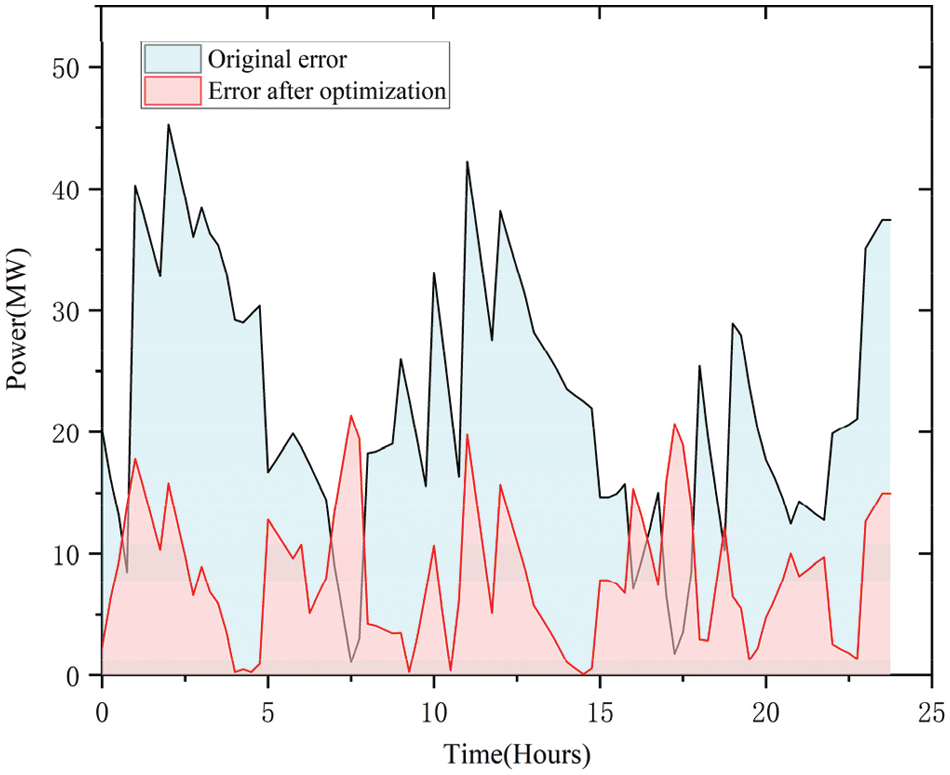
Figure 11: Comparison of total output curves of thermal power units

The analysis focuses on thermal unit 1 output. Fig. 12 displays the output curves of thermal unit 1 without and with consideration of wind power uncertainty.

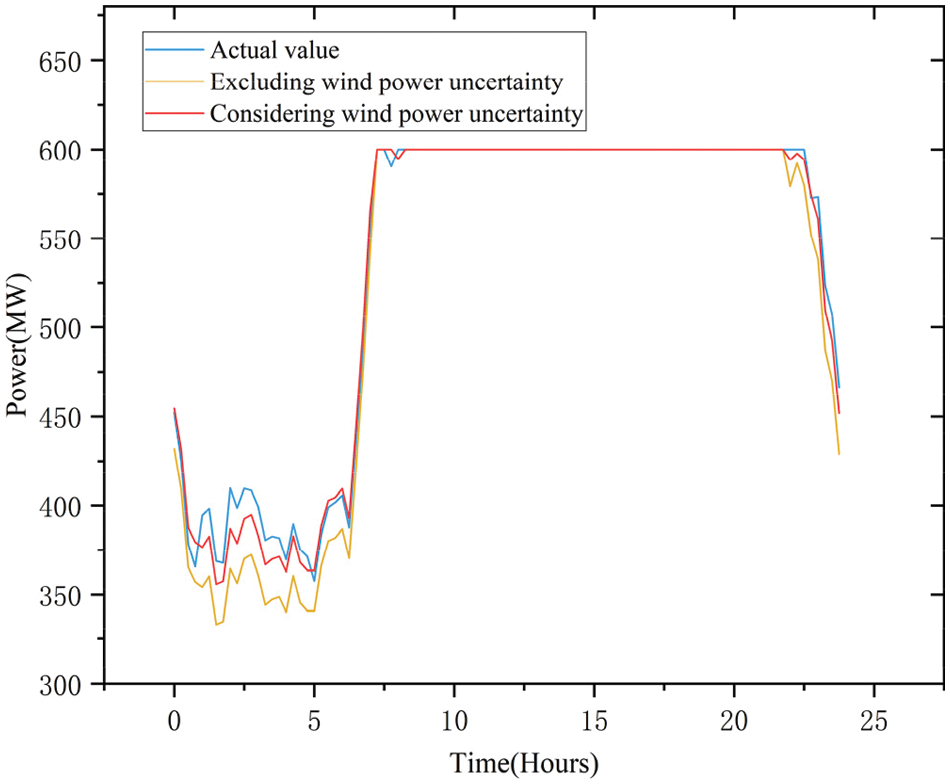
Figure 12: Comparison of thermal unit 1 output curves

Fig. 12 illustrates that thermal unit 1 is closer to the actual output value in Scenario 3, considering wind power uncertainty, compared to scenario 2, which does not consider wind power uncertainty. This results in a reduction of thermal unit 1 output error.

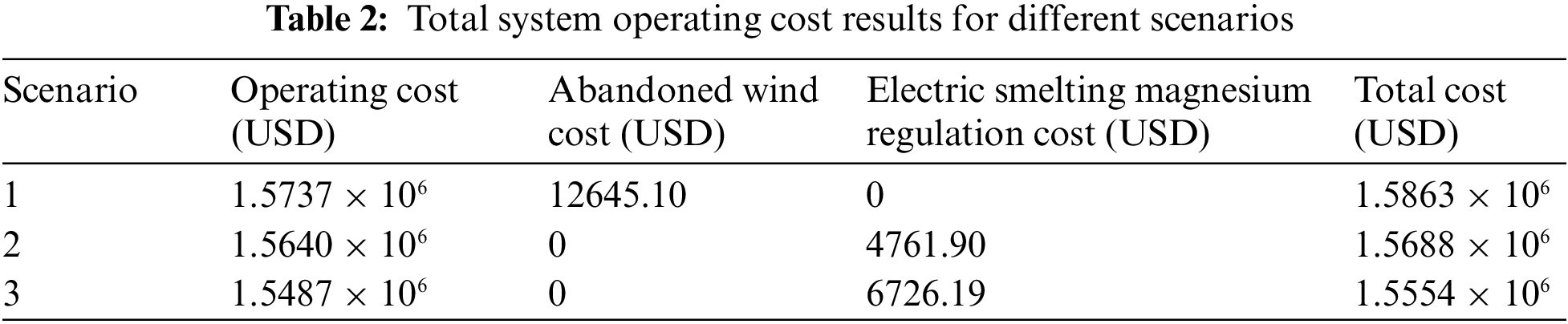
The system cost of the proposed optimization model and the traditional scheduling model is present Table 2 shows that the operation cost and wind abandonment cost of heating power generators in Scenarios 2 and 3 are lower than those in Scenario 1. In Scenario 1, wind power abandonment is 257.96 MW, with an abandonment rate of 0.28%. In Scenarios 2 and 3, system wind abandonment is significantly reduced due to the participation of high energy-carrying loads of electrofused magnesium in system regulation. Compared to Scenario 1, the overall cost of system operating is decreased by 1.10% in Scenario 2 and by 1.95% in Scenario 3. The use of electrofused magnesium high carrying capacity load regulation in system scheduling has resulted in substantial economic benefits while utilizing obstructed wind power.

5  Conclusion

This paper addresses the challenges of wind energy consumption obstruction, inadequate regulation capacity of heating power generators, and uncertainty of wind energy output. It incorporates demand-side electric fusion magnesium high energy-carrying loads into the regulation framework. In order to achieve the greatest wind power consumption and lower system maintenance costs, the article presents a two-layer model for source-load coordination. Furthermore, it constructs an opportunity constraint optimization model considering wind power uncertainty. Through case simulations, the outcomes that follow are reached:

(1)   In scenarios involving massive amounts connected to the grid wind electricity and insufficient regulation capacity of heating power generators, integrating the high energy-carrying load of electro-melting magnesium into the system scheduling optimization and regulation results in reducing the wind abandonment rate from 0.28% to 0%. This integration also reduces the restricted time period of wind power to 0, permitting total reliance on wind energy. The strategy of optimization raises the rate of wind power use and increases wind power generation consumption in an efficient manner.

(2)   This paper presents a source-load two-tier model of efficiency that considers the uncertainty of wind energy generation. This model aims to align the net load curve more closely with the actual value, enabling thermal power units to reduce output errors and approach the real output.

(3)   By adopting the source-load two-layer model of efficiency, which considers maximum system consumption and minimum system operation cost, the relationship between wind power consumption and system economy can be effectively addressed, leading to improved accuracy in day-ahead scheduling.

Acknowledgement: This paper was completed with the hard help of every author.

Funding Statement: This research was funded by the National Key R&D Program of China, Grant Number 2019YFB1505400.

Author Contributions: Conceptualization, Tingting Xu, Yi Gu; methodology, Tingting Xu, Guoliang Bian; software, Chuang Liu; validation, Juan Li, Chuang Liu, Tingting Xu; formal analysis, Guoliang Bian; writing—original draft preparation, Tingting Xu; writing—review and editing, Juan Li, Chuang Liu; supervision, Juan Li; funding acquisition, Yi Gu, Guiping Zhou. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The wind, load profiles, unit parameters and other data used in this paper have been given in the paper.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. Zou et al., “The role of new energy in carbon neutral,” Pet. Explor. Dev., vol. 48, no. 2, pp. 480–491, Apr. 2021. doi: 10.1016/S1876-3804(21)60039-3. [Google Scholar] [CrossRef]

2. J. Zhu et al., “Survey on modeling of temporally and spatially interdependent uncertainties in renewable power systems,” Energies, vol. 16, no. 16, pp. 5938, Aug. 2023. doi: 10.3390/en16165938. [Google Scholar] [CrossRef]

3. S. R. Sinsel, R. L. Riemke, and V. H. Hoffmann, “Challenges and solution technologies for the integration of variable renewable energy sources—A review,” Renew. Energy, Rev., vol. 145, pp. 2271–2285, Jan. 2020. doi: 10.1016/j.renene.2019.06.147. [Google Scholar] [CrossRef]

4. S. D. Ahmed, F. S. M. Al-Ismail, M. Shafiullah, F. A. Al-Sulaiman, and I. M. El-Amin, “Grid integration challenges of wind energy: A review,” IEEE Access, vol. 8, pp. 10857–10878, 2020. doi: 10.1109/access.2020.2964896. [Google Scholar] [CrossRef]

5. X. Lu, K. Zhou, X. Zhang, and S. Yang, “A systematic review of supply and demand side optimal load scheduling in a smart grid environment,” J. Clean. Prod., vol. 203, pp. 757–768, Dec. 1, 2018. doi: 10.1016/j.jclepro.2018.08.301. [Google Scholar] [CrossRef]

6. B. Li, J. Shen, X. Wang, and C. Jiang, “From controllable loads to generalized demand-side resources: A review on developments of demand-side resources,” Renew. Sustain. Energy Rev., vol. 53, pp. 936–944, Jan. 2016. doi: 10.1016/j.rser.2015.09.064. [Google Scholar] [CrossRef]

7. H. Sun, H. Zou, J. Wen, W. Ke, and L. Kou, “Optimal scheduling considering carbon capture and demand response under uncertain output scenarios for wind energy,” Sustainability, vol. 16, no. 3, pp. 970, 2024. doi: 10.3390/su16030970. [Google Scholar] [CrossRef]

8. S. W. Su et al., “Multi-time scale coordinated optimization of new energy high permeability power system considering flexibility requirements,” J. Electric. Eng. Technol., vol. 18, no. 2, pp. 815–828, Mar. 2023. doi: 10.1007/s42835-022-01244-7. [Google Scholar] [CrossRef]

9. X. B. Zhu, Y. Liu, Y. Cao, and Z. Jiao, “Demand response scheduling based on blockchain considering the priority of high load energy enterprises,” Energy Rep., vol. 9, pp. 992–1000, Sep. 2023. doi: 10.1016/j.egyr.2023.05.044. [Google Scholar] [CrossRef]

10. P. Zhao, Y. X. Zhang, Q. Z. Hua, H. P. Li, and Z. Wen, “Bio-inspired optimal dispatching of wind power consumption considering multi-time scale demand response and high-energy load participation,” Comput. Model. Eng. Sci., vol. 134, no. 2, pp. 957–979, 2023. doi: 10.32604/cmes.2022.021783 [Google Scholar] [CrossRef]

11. X. Zhao et al., “Low carbon scheduling method of electric power system considering energy-intensive load regulation of electrofused magnesium and wind powerfluctuation stabilization,” Appl. Energy, vol. 357, pp. 122573, 2024. doi: 10.1016/j.apenergy.2023.122573. [Google Scholar] [CrossRef]

12. Z. F. Liu et al., “Improving the economic and environmental benefits of the energy system: A novel hybrid economic emission dispatch considering clean energy power uncertainty,” Energy, vol. 285, pp. 128668, Dec. 2023. doi: 10.1016/j.energy.2023.128668. [Google Scholar] [CrossRef]

13. Q. Xu, Y. Lv, D. Wang, and P. Du, “A bilateral tradeoff decision model for wind power utilization with extensive load scheduling,” Appl. Sci., vol. 9, no. 9, pp. 1777, 2019. doi: 10.3390/app9091777. [Google Scholar] [CrossRef]

14. H. L. Xu, Z. Y. Meng, and Y. S. Wang, “Economic dispatching of microgrid considering renewable energy uncertainty and demand side response,” Energy Rep., vol. 6, pp. 196–204, Dec. 2020. doi: 10.1016/j.egyr.2020.11.261. [Google Scholar] [CrossRef]

15. Y. Chen et al., “Selection of a critical time scale of real-time dispatching for power systems with high proportion renewable power sources,” IEEE Access, vol. 8, pp. 52257–52267, 2020. doi: 10.1109/ACCESS.2020.2980253. [Google Scholar] [CrossRef]

16. Y. Dvorkin, “A chance-constrained stochastic electricity market,” IEEE Trans. Power Syst., vol. 35, no. 4, pp. 2993–3003, Jul. 2020. doi: 10.1109/TPWRS.2019.2961231. [Google Scholar] [CrossRef]

17. P. M. Wang, L. Q. Zheng, T. Y. Diao, S. Q. Huang, and X. Q. Bai, “Robust bilevel optimal dispatch of park integrated energy system considering renewable energy uncertainty,” Energies, vol. 16, no. 21, pp. 7302, Nov. 2023. doi: 10.3390/en16217302. [Google Scholar] [CrossRef]

18. X. Lei, T. Huang, Y. Yang, Y. Fang, and P. Wang, “A bi-layer multi-time coordination method for optimal generation and reserve schedule and dispatch of a grid-connected microgrid,” IEEE Access, vol. 7, pp. 44010–44020, 2019. doi: 10.1109/ACCESS.2019.2899915. [Google Scholar] [CrossRef]

19. J. Xu et al., “A day-ahead economic dispatch method considering extreme scenarios based on wind power uncertainty,” CSEE J. Power Energy Syst., vol. 5, no. 2, pp. 224–233, Jun. 2019. doi: 10.17775/CSEEJPES.2016.00620. [Google Scholar] [CrossRef]

20. K. Tang, S. Fang, G. H. Chen, and T. Niu, “Unit maintenance strategy considering the uncertainty of energy intensive load and wind power under the carbon peak and carbon neutral target,” IEEE Access, vol. 11, pp. 38819–38827, 2023. doi: 10.1109/ACCESS.2023.3267274. [Google Scholar] [CrossRef]

21. Y. Teng, Q. Hui, Y. Li, O. Leng, and Z. Chen, “Availability estimation of wind power forecasting and optimization of day-ahead unit commitment,” J. Mod. Power Syst. Clean Energy, vol. 7, no. 6, pp. 1675–1683, Nov. 2019. doi: 10.1007/s40565-019-00571-5. [Google Scholar] [CrossRef]

22. J. Ding et al., “Mixed aleatory-epistemic uncertainty modeling of wind power forecast errors in operation reliability evaluation of power systems,” J. Mod. Power Syst. Clean Energy, vol. 10, no. 5, pp. 1174–1183, Sep. 2022. doi: 10.35833/MPCE.2020.000861. [Google Scholar] [CrossRef]

23. Y. Dvorkin, M. Lubin, S. Backhaus, and M. Chertkov, “Uncertainty sets for wind power generation,” IEEE Trans. Power Syst., vol. 31, no. 4, pp. 3326–3327, Jul. 2016. doi: 10.1109/TPWRS.2015.2476664. [Google Scholar] [CrossRef]

24. D. Bienstock, M. Chertkov, and S. Harnett, “Chance-constrained optimal power flow: Risk-aware network control under uncertainty,” SIAM Rev., vol. 56, no. 3, pp. 461–495, 2014. doi: 10.1137/130910312. [Google Scholar] [CrossRef]