Application of DSAPSO Algorithm in Distribution Network Reconfiguration with Distributed Generation

Nomenclature

1  Introduction

In recent years, the substantial consumption of traditional fossil fuel resources and the continuous growth of energy demand have made distributed generation an indispensable part of the power system [1]. However, the output of distributed energy sources is characterized by volatility and randomness, which significantly increases the uncertainty and complexity of the grid after integration, thereby exerting a significant impact on power losses, node voltages, and power flow direction in the distribution network [2].

Scientific and rational distribution network restructuring (DNR) can reduce the active power losses of the entire distribution network system, avoid node voltage violations, and thus improve the quality of electrical energy. The increasing number of scholars researching distribution network restructuring has led to the consideration of numerous factors, resulting in the proliferation of internal functions. As a consequence, the optimization problem becomes non-convex, non-linear, high-dimensional, and subject to multiple constraints, greatly limiting the applicability of mathematical methods and heuristic algorithms [3]. In recent years, distribution network restructuring methods based on intelligent optimization algorithms have garnered significant attention from researchers. In a previous work [4], an improved grey wolf algorithm was proposed, which introduced a wolf named GAMMA to enhance population diversity. However, the addition of new dimension values to the original algorithm hinders the resolution of complex problems. To address the issue of easily falling into local optima during the computational process of intelligent algorithms, a modified Teaching-Learning-Based Optimization (TLBO) algorithm was proposed in reference [5]. This improved algorithm incorporated an adaptive teaching factor and introduced a “self-learning” phase to enhance optimization efficiency. In reference [6], the method of undetermined coefficients was employed to transform the dual-objective problem of network loss and voltage deviation into a single-objective function for comprehensive optimization. Although this approach provides a more comprehensive comparison to single-objective optimization results, the use of manually set weighting coefficients cannot achieve unbiased selection of reconstruction results. In reference [7], the Analytic Hierarchy Process (AHP) and the Linear Weighting Method (LWM) were introduced to determine the weights of various indicators and achieve the transformation from multi-objective functions to a single-objective function. Despite the simplicity and computational efficiency of transforming multi-objective problems into single-objective problems, the subjectivity of these methods hinders the achievement of fully unbiased optimization for each objective.

This paper proposes a dynamic simulated annealing particle swarm optimization algorithm (DSAPSO) that combines the advantages of simulated annealing (SA) and particle swarm optimization (PSO) algorithms. By applying the Metropolis principle of the simulated annealing algorithm to restrict the generation of local optima, and improving the velocity update method of the population, the optimization process is balanced with different emphases in the earlier and later stages, leading to enhanced optimization speed.

With network loss and node voltage deviation as objective functions, the Pareto principle is employed in combination with fuzzy membership functions to achieve unbiased selection of multi-objective reconstruction results. The IEEE-33 distribution system and IEEE-69 distribution system are used as examples to demonstrate the effectiveness of the DSAPSO algorithm in the presence of distributed power generation. The simulation results show that the DSAPSO algorithm exhibits good convergence speed, avoids getting trapped in local optima, and possesses good generality.

2  Model Building

2.1 Objective Function

References [8,9] indicated that the fundamental concept of distribution network reconfiguration involves altering the network topology through modifications to sectionalizing switches and tie switches. The objective is to optimize network performance indicators. The objective functions typically include minimizing active power loss, maximizing load balancing, and reducing the number of switch operations. This paper focuses on minimizing active power loss and node voltage deviation as the objective functions.

{ F1=min​Ploss=∑k=1 mβkRkPk2+Qk2Uk2F2=min Utotal=∑k=1m∣1−Uk'∣(1)

In the formula: m for the total number of branches in the distribution network, βk for the branch contact switch or the opening and closing state of the segment switch, closed or broken corresponding to 1 or 0, respectively; Rk and Uk are the kth branch resistance value and terminal voltage; Pk, Qk are the kth branch active and reactive power. Uk‘ denotes the per unit value of the terminal voltage for the kth branch.

For a multi-objective minimization problem,

{ minF=[ f1(x),f2(x),…,fn(x) ]s.t.gi(x)=0i=1,2,…,Khj(x)≤0j=1,2,…,R(2)

In a multi-objective minimization problem, x denotes the solution vector in the solution space, F represents the objective function vector, n is the number of objective functions, gi(x) represents the general form of equality constraints, and hi(x) represents the general form of inequality constraints. K and R denote the number of equality and inequality constraints, respectively.

In the solution space, comprising all feasible reconstruction plans, if for any two feasible solutions a and x, each sub-objective function value of a is not inferior to the corresponding value of x, i.e., fi(x)≤fi(a) (for i=1,2,…,n), and there exists i0 (i0∈{1,2,…,K}) such that fi(x)≤fi(a), then solution a dominates solution x. If there is no feasible solution in the solution space that dominates a, then solution a is regarded as a non-dominated solution of the multi-objective programming problem, and all non-dominated solutions constitute the Pareto front of the problem’s solution set.

After obtaining the set of Pareto optimal solutions, we employ fuzzy membership degrees to express the satisfaction of each Pareto solution with respect to the objectives. Furthermore, we utilize these satisfaction values to identify the final set of compromise solutions. The function for determining fuzzy membership degrees is presented below:

μi={ 1,fi<fiminfimax−fifimax−fimin,fimin⩽fi⩽fimax0,fimax<fi(3)

In the equation, μi represents the fuzzy membership degree corresponding to the i-th objective function, while fimin and fimax represent the lower and upper bounds of the i-th objective function, respectively.

2.2 Conditions of Constraint

(1) The node voltage constraint is shown in Eq. (4):

Vimin⩽Vi⩽Vimax(4)

Vi is the voltage of the node i; Vimax and Vimin are the upper and lower voltage limits of the node i.

(2) The tidal current constraint is shown in Eq. (5):

Pi+PDGi=PLi+Vi∑i=1nVj(Gijcosδij+Bijsinδij)Qi+QDGi=QLi+Vi∑j=1nVj(Gijsinδij−Bijcosδij)(5)

PDGi is the distributed power access the active power of the node i; PLi is the active power of the load in the node i; QDGi is the distributed power access node reactive power in the node i; QLi is the reactive power of the load in the node i; Vi and Vj correspond to the voltage of the node i and node j; Gij and Bij correspond to the real and imaginary parts of the conductance between the node i and node j; and δij are the phase difference angle of the voltage between the node i and node j.

(3) The branch circuit capacity constraint is shown in Eq. (6):

Pi2+Qi2⩽Sk.max(6)

Pi and Qi are the active and reactive power of the load at the branch i; Sk.max is the maximum value of the accessible capacity on the branch.

(4) The power constraint of the Distributed Generation (DG) is expressed as Eq. (7):

{ PDGmin<PDGi<PDGmaxQDGmin<QDGi<QDGmax(7)

The variables PDGmin and PDGmax represent the minimum and maximum active power, respectively, of the distributed generation (DG) connected to node i. Similarly, the variables QDGmin and QDGmax indicate the minimum and maximum reactive power, respectively, of the distributed generation (DG) connected to node i.

(5) Network topology constraints

gk∈G(8)

In the reconstructed network structure, gk represents the network that satisfies the radial requirements, while G represents the collection of all such networks. During the reconstruction process, the network structure must maintain a radial connected state, with the removal of loops and isolated islands.

3  Algorithm of Reconfiguration

3.1 Particle Swarm Algorithm

Particle swarm algorithm as a heuristic intelligence algorithm is commonly applied to solve multi-constrained optimization problems, and its main idea is to iterate through particles cooperating and competing on the basis of mutual information sharing, and according to their respective velocities v. The population as a whole searches in the solution space by referring to the position of the current optimal particle, and the individual particles are updated using the individual optimal position and the global optimal position in reference [10]. Each particle corresponds to a solution and an optimization result. In one iteration, the particle completes the position and velocity update by Eqs. (9) and (10):

vik+1=ωvik+c1r1(Pbestk−xik)+c2r2(Gbestk−xik)(9)

xik+1=xik+vik+1(10)

In the formula, w is the inertia parameter; c1 and c2 are the individual learning factor, group learning factor, respectively; r1 and r2 is the uniformly distributed pseudo-random number in the interval [0,1]; xik is the position of the particle i which is at the moment of k; vik is the velocity of the particle iwhich is at the moment of k, and Pbestk is the historical optimal position at the moment of k for the particle i; Gbestk is the optimal position at the moment of k for all particles.

3.2 Dynamic Simulated Annealing Particle Swarm Algorithm

The simulated annealing algorithm is an algorithm proposed by Mitropolis’ research on the solid-state annealing process, which requires setting an initial temperature according to the initial state of the population in the initial stage of the iteration, and its optimization-seeking step is an iterative process of alternating linear cooling and seeking new solutions. The core of this algorithm lies in the Mitropolis criterion, which not only accepts the current optimal value in the solution process, but also moves in the direction of the worse value with a certain probability, thus enhancing the ability to jump out of the local optimal solution in the optimization search process [11,12]. Its expression is as follows:

pi(k)={ 1,exp(−Ei(k)−EgTk)Ei(k)⩾Eg,Ei(k)<Eg(11)

T(k)={ E(Gbest)/log(0.2),T(k−1)μ,k=1k≥1(12)

In the formula, Ei(k) denotes the ith particle’s internal energy at the kth iteration (the fitness of the current particle); Eg denotes the internal energy of the current population optimum; Tk denotes the current temperature of the kth iteration.

To address the problem that the particle swarm converges too fast in the early stage, the traversal of the optimization space is not strong and thus it is easy to fall into the local optimum, and the search accuracy is not high in the later stage. First, referring to the dynamic inertia weighting strategy in reference [13]. The following improvements are made to the particle swarm algorithm:

c1=c1max−k(c1max−c1min)​/kmaxc2=c2min−k(c2min−c2max)​/kmax(13)

c1max, c1min and c2max, c2min correspond to the maximum and minimum values of the individual learning factor and the group learning factor, respectively. The parameters are set as c1max=2.50, c1min=1.25, c2max=2.50, c2min=1.25. As the number of iterations increases, the individual learning factor and the group learning factor decrease and increase respectively, which corresponds to the gradual shift of the focus of the algorithm search from the overall traversal search to improving the local refinement from the early to the late stage of the optimization search process.

Also introduce the nonlinear time-varying inertia weights with logistic mapping in reference [14], the expressions are as follows:

r(k)={ r(0)=rand    (0,1),k=1r(k)=4r(k−1)(1−r(k−1)),k>1(14)

w(t)=r(k)wmin+(wmax−wmin)kKmax(15)

In the formula, r(0)≠{0,0.25,0.75,1}; the r(t) is the random number generated by the iteration. wmax=0.9, and wmin=0.4.

To improve the particle swarm algorithm, the Mitropolis criterion of the simulated annealing algorithm is introduced into the update of particles as follows:

Step 1: Generate an initial population and set parameters, such as the maximum iteration count, search space, and search speed limits.

Step 2: Randomly assign initial positions and velocities to each particle.

Step 3: Update the values of c1, c2, and w using Eqs. (13)–(15).

Step 4: Iterate through particles using Eqs. (9) and (10) to optimize and record their fitness and the swarm’s best position.

Step 5: Update the temperature based on the current iteration count using Eqs. (11) and (12). Compare the current particle’s internal energy with the swarm’s best particle’s internal energy to determine whether to accept the current best solution.

Step 6: Identify non-dominated solutions and store them in the Pareto solution set.

Step 7: Update the Pareto optimal solution set and select the particle with the highest satisfaction degree as the global best particle using fuzzy membership degrees.

Step 8: Check if the maximum iteration count has been reached. If so, output the current best particle; otherwise, return to Step 3.

The flow chart of DSAPSO algorithm is shown in Fig. 1.

Figure 1: Flow chart of DSAPSO algorithm

4  Experimental Setup

4.1 Parameter Setting

The effectiveness and efficiency of the proposed algorithm in this paper are evaluated through MATLAB simulation using the IEEE 33-node system. Fig. 2 illustrates the topology diagram of the IEEE 33-node system, comprising 32 closed sectionalizing switches and 5 open tie switches. The specific system parameters are as follows: the base voltage is 12.66 kV, the active power load is 3.715 MW, the reactive power load is 2.3 Mvar, and the base capacity is defined as 10 MVA. In the DSAPSO algorithm, the population size is set to 30, the maximum number of iterations is 50, and the individual learning factor and swarm learning factor have maximum values of 2.5 and minimum values of 1.25, respectively. The cooling coefficient is set to 0.95, while the inertia weight w has maximum and minimum values of 0.9 and 0.4, respectively.

Figure 2: Topology diagram of the IEEE 33-node system

4.2 Validation of Algorithm Effectiveness

To verify the effectiveness of the proposed improved algorithm in solving the problem of minimizing network loss, distribution network reconfiguration (DNR) is performed in the IEEE 33-node system. Two scenarios are considered: one with the integration of distributed generation (DG) of the same type, and another with DGs of different types. Table 1 presents the parameters for DGs integration, while Table 2 displays the results of the network reconfiguration. Fig. 3 illustrates the convergence characteristics of different algorithms when DGs of the same type are integrated, while Fig. 4 shows the node voltage distribution after the integration of multiple DGs.

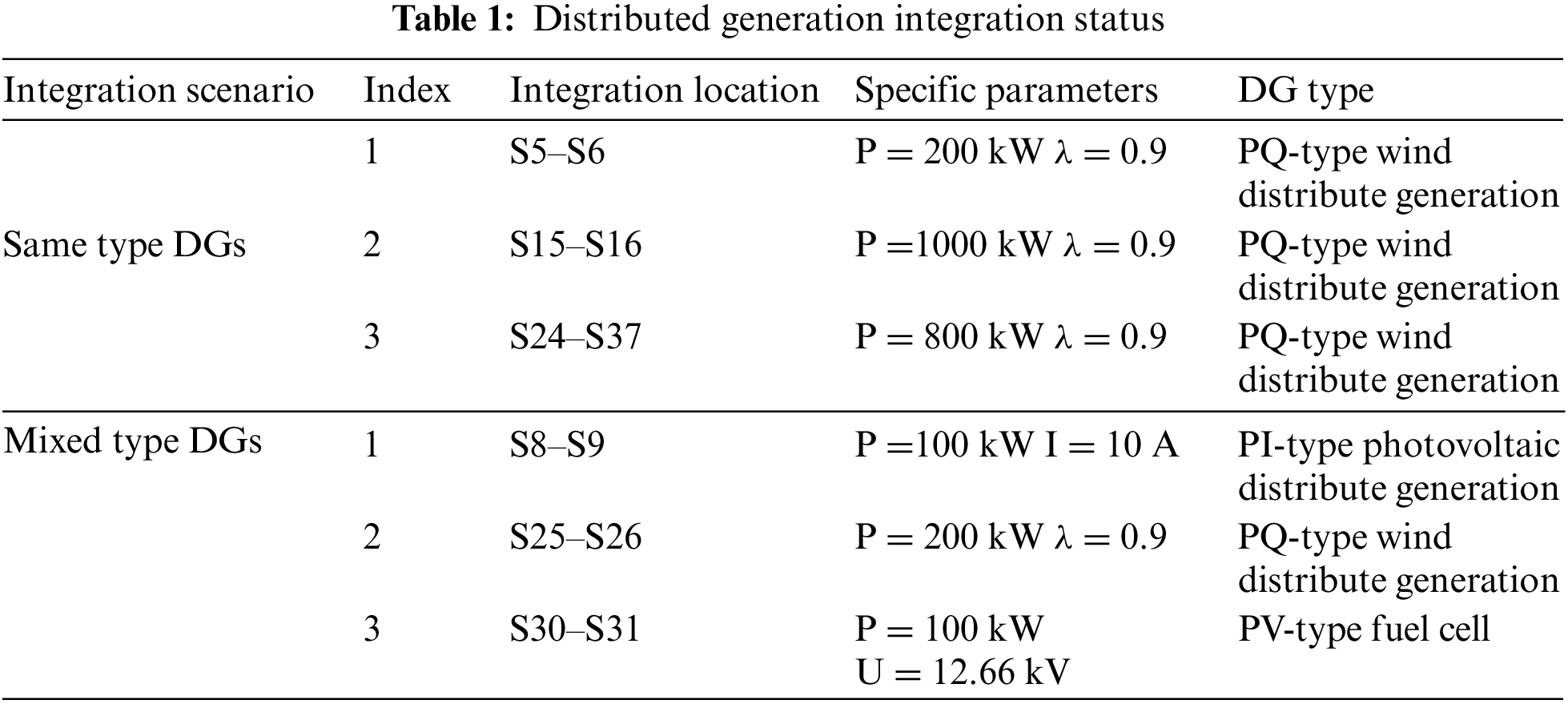
Figure 3: The convergence characteristics curves of different algorithms

Figure 4: Comparative analysis of convergence iterations for different algorithms over 30 runs

According to Table 2, when integrating the same type of distributed power generation, the reconstructed and optimized system exhibits an increase in the minimum node voltage. The EP-PSO algorithm proposed in reference [15] results in active power losses of 92.46 kW, while the MPSO algorithm proposed in reference [16] yields 96.88 kW and the DSAPSO algorithm proposed in this paper achieves 89.43 kW. Fig. 3 illustrates the convergence characteristics curves of the three algorithms in the context of integrating the same type of distributed power generation. The algorithm proposed in this paper converges after 12 iterations, whereas the MPSO algorithm in reference [16] and the EP-PSO algorithm in reference [15] require 19 and 16 iterations, respectively. Given the complexity of the solution space and computational workload in the integration of distributed power generation into the distribution grid restructuring problem, there is a risk of encountering local optima during the optimization process. The algorithm proposed in this paper enhances its ability to escape local optima by restricting the movement direction of the population using the Metropolis Principle, resulting in lower fitness values.

After running for 30 iterations, Fig. 4 depicts the comparison of iteration performance among three algorithms. In this study, our proposed algorithm achieved lower iteration counts in 25 out of 30 runs compared to the other two particle swarm optimization (PSO) algorithms. Our algorithm had an average iteration count of 15, whereas the other two algorithms had average iteration counts of 19 and 21. These results demonstrate a significant improvement of 21.05% and 28.57% in average convergence iterations compared to the other PSO algorithms, attributed to the dynamic learning factor control strategy used in our algorithm, consequently enabling faster convergence to the desired state.

Based on the data presented in Fig. 5, it is evident that integrating multiple types of DG units has significantly improved the system’s overall voltage level. However, Table 2 reveals that despite these improvements, the active power loss remains at 169.29 kW, indicating an insufficient enhancement. Therefore, network reconfiguration is still necessary. By utilizing the GA-QPSO algorithm proposed in Reference [17], the active power loss is reduced to 113.55 kW after reconfiguration, resulting in a loss reduction rate of 32.92%. The lowest node voltage is measured at 0.9337 p.u. Implementing the algorithm from this paper for reconfiguration leads to a decrease in network loss from 169.29 to 111.83 kW, with a loss reduction rate of 33.94%. The lowest node voltage measures 0.9407 p.u. Consequently, the performance of the proposed algorithm is superior. Additionally, as depicted in Fig. 5, both reconfiguration algorithms significantly enhance node voltage. Notably, the method presented in this paper not only improves the lowest node voltage but also ensures a more uniform voltage distribution throughout the system.

Figure 5: Voltage profile for IEEE-33 system before and after DNR with multiple DG accessing

4.3 Verification of Algorithm Efficiency

The performance of the Dynamic Simulated Annealing Particle Swarm Optimization (DSAPSO) algorithm in addressing the multi-objective reconfiguration problem of the distribution network, considering the presence of various types of distributed generation sources, is verified. Four different types of distributed generation sources are selected and integrated into the IEEE-33 node model based on the parameters provided in reference [18]. The objective functions for the distribution network reconfiguration aim to minimize active power loss and node voltage deviation. Table 3 presents the parameters and characteristics of the integrated distributed generation sources. The reconfiguration results are shown in Table 4, while the node voltage profiles are depicted in Fig. 6.

Figure 6: Voltage profile for IEEE-33 system before and after DNR with multiple DG accessing

The results presented in Table 4 indicate that the system’s network losses have reduced to 64.39 kW, achieving a reduction of 42.77% compared to the original network. Furthermore, the overall node voltage deviation has decreased from 1.6670 to 0.7043, representing a reduction of 57.7%. In comparison to the HDQPSO algorithm’s results obtained in reference [18], the algorithm proposed in this paper exhibits significant advantages in terms of network losses and node voltage deviation. Additionally, Fig. 6 illustrates that the proposed algorithm for network restructuring effectively improves the minimum node voltage from 0.9341 to 0.9680 p.u., enhancing not only the overall node voltage level but also the uniformity of voltage distribution, resulting in improved voltage stability.

4.4 Verification of Algorithm Generality

To evaluate the DSAPSO algorithm’s effectiveness in addressing network restructuring issues in distribution systems, simulations were performed using the IEEE 69-node system. The distribution system, depicted in Fig. 7, comprises a total of 73 branches, including 5 tie lines, with a rated voltage of 12.66 kV. The system’s active power load is 3802.2 kW, while the reactive power load is 2694.6 kVar. Within the DSAPSO algorithm, the population size was set at 30, with a maximum iteration count of 50. The individual and social learning factors were assigned maximum and minimum values of 2.5 and 1.25, respectively. Additionally, a cooling coefficient of 0.95 was employed, alongside an inertia weight (w) range of 0.9 to 0.4. Table 5 provides a comprehensive overview of the network restructuring outcomes, presenting relevant comparisons with similar findings from other scholarly sources.

Figure 7: Topology of IEEE-69 node network

Based on the data presented in Table 5, the implementation of the algorithm proposed in this paper resulted in a significant reduction in the network losses of the system, decreasing from 224.14 to 99.75 kW. Furthermore, this algorithm effectively decreased the voltage deviation at the nodes from 2.872 to 1.948, and increased the lowest node voltage from 0.910 to 0.942. In contrast, in the study referenced as reference [19], an improved harmony search algorithm was employed for the reconstruction of the IEEE-69 node system. A comparative analysis between these approaches demonstrates the algorithm proposed in this paper’s successful optimization of the network restructuring problem within the IEEE-69 node system. Therefore, it exhibits a high level of universality.

5  Conclusions

This paper addresses the problem of distribution network restructuring considering the integration of distributed energy resources. A combined optimization algorithm based on Simulated Annealing (SA) and Particle Swarm Optimization (PSO) is proposed. To overcome the issue of PSO getting stuck in local optima, the Metropolis criterion is introduced to allow particles to move towards poorer solutions with a certain probability, thereby enhancing their ability to escape local optima during the optimization process. Additionally, an improved dynamic learning factor is employed to enhance the global convergence speed of the optimization.

Furthermore, inspired by Pareto principles, a fuzzy membership function is used to combine the network losses and voltage deviations as objective functions. The results are then selected without discrimination. The effectiveness, efficiency, and universality of the proposed DSAPSO algorithm are validated through case studies conducted on the IEEE-33 and IEEE-69 distribution network systems. The findings demonstrate that the DSAPSO algorithm can efficiently obtain the optimal network topology in a shorter time, reducing network losses and improving overall node voltage levels.

Acknowledgement: During the preparation of this academic paper, I would like to express my special gratitude to Baosheng Xing and Wenbo Wang for their invaluable assistance. Their professional knowledge and experience have played a crucial role in my research work. Firstly, I would like to extend my appreciation to Baosheng Xing for his selfless guidance and support throughout the research process. His profound thoughts and unique insights have been immensely beneficial to me. He offered valuable suggestions regarding my research questions and provided an extensive collection of literature materials for my reference. Secondly, I would like to thank Wenbo Wang for his important guidance in experimental design and data analysis. His vast experience and expertise have enabled me to better understand and apply relevant theories and methodologies.

Funding Statement: This research is supported by the Science and Technology Program of Gansu Province (No. 23JRRA880).

Author Contributions: All authors reviewed the results and approved the final version of the manuscript. Data collection: Caixia Tao and Taiguo Li; analysis and interpretation of results and draft manuscript preparation: Shize Yang.

Availability of Data and Materials: Data supporting this study are included within the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Si, K. (2020). Research on distribution network reconstruction considering distributed power access (Master Thesis). College of Electrical Engineering, Shandong University, China. [Google Scholar]

2. Wang, W., Cui, X., Ma, X., Wang, Y., Liu, H. (2015). Multi-objective reactive power optimization considering multiple wind turbines connected to distribution networks. Power System Technology, 39(7), 1860–1865. [Google Scholar]

3. Zhou, M. (2021). Research on distribution network reconstruction with distributed generation of renewable energy (Master Thesis). School of Electrical Engineering and Automation, Hefei University of Technology, China. [Google Scholar]

4. Wang, L., Cheng, J., Wang, W. (2022). Research on distribution network reconstruction with distributed power sources based on improved grey wolf algorithm. Modern Electric Power, 39(1), 56–63. [Google Scholar]

5. Pan, B., Wang, H., Zhang, Y., Gui, X., Wan, Y. (2020). Research on active distribution network reconstruction strategy with distributed power sources. Power System Protection and Control, 48(15), 102–107. [Google Scholar]

6. Wu, Y., Cheng, X., Liu, J. (2023). Optimization and reconstruction of distribution network with distributed power sources based on SA-CS algorithm. Science Technology and Engineering, 23(2), 626. [Google Scholar]

7. Li, M., Wang, L., Liu, X. (2019). Research on multi-objective active reconstruction of distribution network based on genetic algorithm with gated communities. Power System Protection and Control, 47(7), 30–38. [Google Scholar]

8. Li, Y., Chang, Y., Liang, X. (2021). Research on optimal reconstruction method for distribution network with new energy sources connected. Control Engineering, 28(5), 931–937. [Google Scholar]

9. Wei, E., Yang, H., Xue, R. (2023). Multi-objective distribution network reconstruction method based on discrete monkey algorithm. Proceedings of the CSEE, 35(1), 30–35. [Google Scholar]

10. Zhang, L., Le, J., Li, H. (2022). Reconstruction method for distribution network with ZIP load considering mixed integer linear programming. Power System Protection and Control, 50(8), 25–32. [Google Scholar]

11. Chen, K., Xian, S., Guo, P. (2021). Adaptive simulated annealing algorithm for solving traveling salesman problem. Control Theory and Applications, 38(2), 245–254. [Google Scholar]

12. Zang, Y., Xu, Z., Huang, A. (2021). Distribution of nonuniform combustion field reconstruction based on improved simulated annealing algorithm. Acta Physica Sinica, 70(13), 229–240. [Google Scholar]

13. Zhang, C., Zou, D., Shen, X. (2021). Application of improved particle swarm algorithm in power economic dispatch. Manufacturing Automation, 43(1), 53–57+64. [Google Scholar]

14. Zheng, Y., Li, S., Lu, L. (2023). Transformer fault diagnosis based on multi-strategy ISOA optimized SVM. Smart Grid, 51(2), 38–44. [Google Scholar]

15. Olamaei, J., Niknam, T., Gharehpetian, G. (2008). Application of particle swarm optimization for distribution feeder reconfiguration considering distributed generators. Applied Mathematics and Computation, 201(1), 575–586. [Google Scholar]

16. Arya, A., Kumar, Y., Dubey, M. (2011). Reconfiguration of electric distribution network using modified particle swarm optimization. International Journal of Computer Applications, 34(6), 54–62. [Google Scholar]

17. Chen, K., Pan, L. (2022). Optimization and reconstruction design of distribution network with distributed power sources based on GA-QPSO algorithm. Experimental Research and Exploration, 41(2), 111–115+120. [Google Scholar]

18. Xu, L. (2017). Research on distribution network reconstruction with distributed power sources (Master Thesis). School of Information Engineering, Nanchang Hangkong University, China. [Google Scholar]

19. Liang, S., Mao, Y., Liu, X. (2017). Application of improved harmony search algorithm in distribution network reconstruction. Proceedings of the CSEE, 29(3), 90–95. [Google Scholar]