Research on Coordinated Development and Optimization of Distribution Networks at All Levels in Distributed Power Energy Engineering

1  Introduction

Under the continuous deepening of energy technology energy policy and electricity marketization, the distribution network must adapt to the requirements of renewable resources. The dynamic distribution network has become a way of distribution network distributed energy planning. It enables active management of large-scale distribution networks. The relatively complete grid-connected control technologies for a single distributed power source mainly include PQ control, PV control and droop control. These can not meet the dynamic control requirements of the power system. Currently, many main problems of internal combustion engines, including fluid flow, combustion, internal combustion engine performance calculation, component heat transfer and temperature field calculation, lubrication, cooling system calculation, etc., have mature software available. And these local problem models can be directly used. Scholars at home and abroad have researched distribution network planning, including distributed energy sources or charging stations. Some scholars have planned and analyzed the investment cost, active power loss and reliability of the distribution network with distributed energy sources. Reference [1] used fuzzy variables to represent load and distributed generation uncertainty. Scholars aim to minimize the unclear expected value and establish a fuzzy optimal programming model. Reference [2] applied the improved particle swarm algorithm to the problem of location and volume determination of distributed energy sources. Scholars verified the effectiveness of the model and algorithm through simulation analysis. Reference [3] studied the optimal installation location and capacity of distributed energy sources considering stochastic uncertainty.

Some scholars have established a charging station planning model considering charging characteristics, charging behavior, urban planning, transportation and power network, etc. Reference [4] proposed the optimal location and constant capacity model of wind power and photovoltaics for grid-connected electric vehicles and then uses Monte Carlo simulation to simulate. Reference [5] established a distribution network planning model considering the optimization of charging station layout but did not consider the uncertainty of renewable energy. Reference [6] thought constraints such as setting and discharging efficiency and power balance of electric vehicle swapping stations and proposed a unit combination optimization model but did not consider factors such as the environment. Reference [7] takes the minimization of system cost and pollution discharge as the optimization goal. The author fully considers demand response, energy storage, wind power, and photovoltaic-related links to establish a "source-grid-load-storage" coordination scheduling model. It adopts a multiobjective particle swarm optimization algorithm to solve it. Reference [8] comprehensively considered distributed energy, energy storage, and flexible loads to establish a multiobjective optimal scheduling model related to renewable energy utilization, network loss, and user satisfaction. The improved particle swarm algorithm is used for centralized optimization. Reference [9] analyzed the feasibility and economy of connecting electric vehicles to the grid and optimized the optimal charging and discharging of electric vehicles. This allows more EVs to be plugged into the grid, which can be charged at a lower cost. Reference [10] integrated the load into the dispatching scope into a hybrid control system for the wind and solar output accommodation problem. Scholars take optimal economic dispatch as the objective function and combine intelligent optimization algorithms to solve the objective function. It solves the random fluctuation problem of photovoltaic and wind power output. This constitutes an independently controlled device. The system can meet both the demand for electricity and the grid’s needs. First, the micro-energy dispatching network’s controllability refers to the power grid’s overall single controllability. The control area of the entire network must be carried out in a relatively dense area. The system lacks flexibility. Secondly, the management of the micro-energy dispatching network pays more attention to autonomous administration in the control area, which requires a higher-level network management organization to realize the optimal operation of the access network. In addition, each micro-energy dispatching network requires a separate energy management unit.

In this way, the needs of large-scale distribution networks can be well met, thereby improving the overall utilization efficiency of the power market. This paper presents a dynamic energy optimization method for distributed generation energy. This paper focuses on the optimal closed-loop control performance in an optimization period in the future and introduces feedback correction. The method proposed in this paper can timely and effectively correct the deviation of optimal scheduling results caused by forecast errors and random factors. The manner in this paper can improve the precision of optimal control. The experimental results in this paper achieve the goal of “multi-level coordination, level-by-level refinement, feedback correction" and maximum consumption of intermittent distributed power. Finally, this paper uses examples and simulation methods to test the technology proposed in this paper.

2  Active and Reactive Power Coordination Scheduling Architecture Based on Distributed Power Sources

This paper divides the dynamic programming problem of multi-time-scale emotionally distributed generation energy into several epoch problems. The coordination relationship between each step is shown in Fig. 1.

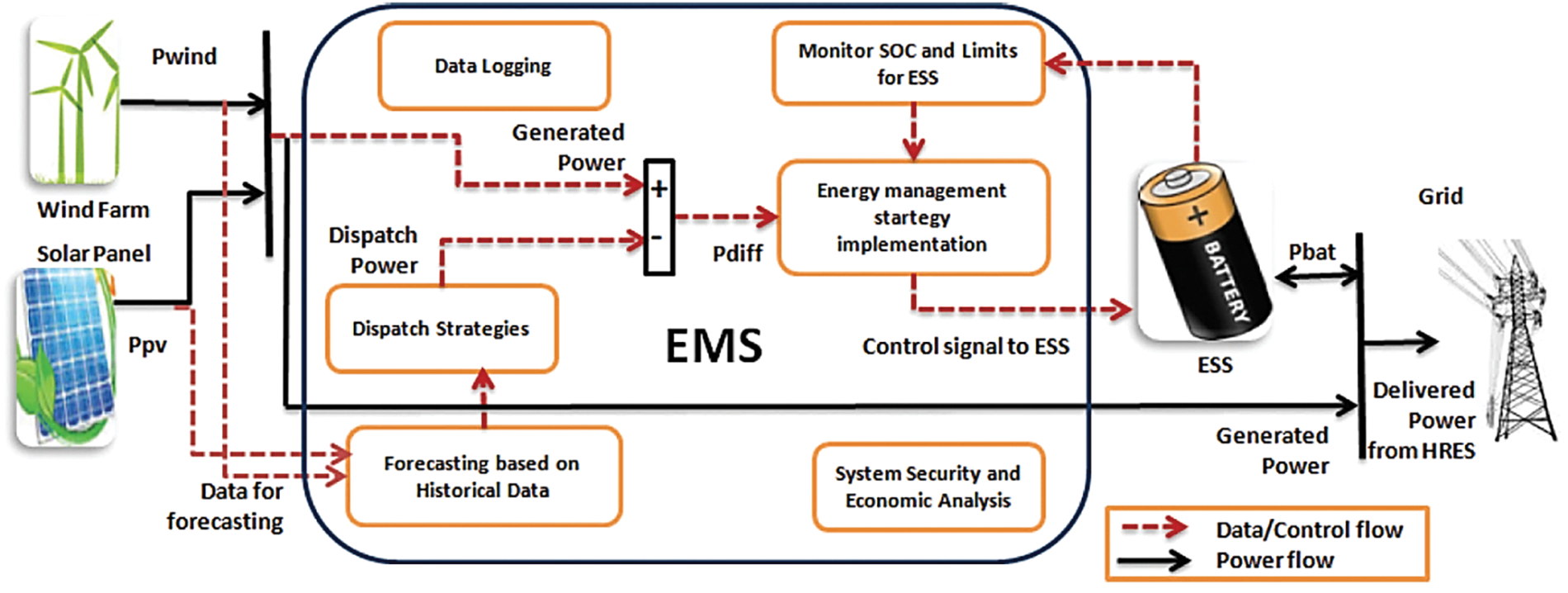
Figure 1: Peak shaving optimization structure of distributed power energy based on distributed energy

1) Day-ahead optimal allocation: According to the forecast of day-ahead load and renewable energy, the optimal dispatch of active and reactive power of distributed generation energy is carried out. The optimal scheduling for the previous day is to determine the operating conditions and activities of the low-speed power units in the system for the next day. Low-speed dynamic devices mainly include power load regulators (OLTCs), compensation capacitors, and interruptible loads. Restricted by the production process and the device’s service life, the combination of power on-load voltage regulation and capacitor components leads to the micro-energy grid’s limited feeding rate and daily feeding quantity. Customers must be informed in advance to avoid unnecessary loss of power supply when implementing interruptible loads. The warning period is usually 2 to 1 working day. Such adjustable devices have a limited rate of adjustment. This method is not suitable for short-term scrolling and real-time feedback correction.

2) Daytime rolling optimal scheduling: Due to the extensive forecast time range, the instability factor of sustainable development and the considerable uncertainty of load forecasting, the forecast accuracy gradually decreases. The former scheduling scheme is difficult to adapt to the requirements of power balance. In the daily short-cycle rolling optimization, each cycle ΔT begins to forecast the power generation and load of renewable energy in cycle MΔT. The system optimizes the optimal control of this period and adjusts the power allocation scheme of resources other than the low-speed power plant. In this process the system only completes the output of each regulating resource controlled once. At the next point t0+ΔT, the system reverses the time window by one step and performs the above steps. The sustainable energy and load vary greatly in rolling optimization, which is calculated more accurately than the least squares method.

3) Immediate correction: Although the fluctuation of renewable energy has a specific reduction in the load load of distributed power sources, it is still the optimal scheduling method for an open loop. In the smaller period Δt(Δt<ΔT), the daytime immediate feedback correction step is the sampling step. Perform ultra-short-term and ultra-short-term forecasts on each sampling time’s current power and load conditions. The system uses the active and reactive power of each adjustment mode in the present time as the initial value and takes it as the optimal index. The system adjusts the output of each adjustment method to the maximum through the optimal strategy. The plan establishes a closed-loop optimal controller based on the latest ultra-short-term forecast error. It corrects the scheduling results caused by forecast errors and improves the dynamic optimization of the system. For the sequence, start-up period and solution in the above periods, the system must be based on the space-time difference of each control system in the distribution network. The system needs to be adjusted appropriately according to its adjustment rate and other relevant operating characteristics. This enables the coordination between each control system and each optimal link and ensures the optimal state of the system.

3  Global Optimal Control Strategy in Long Time Scale

Based on the load forecast of the following dispatch period and the power forecast of intermittent power, this paper uses the best optimal power algorithm to obtain the best allocation scheme of each controlled system. This method requires much information, a complicated algorithm, and much computation. It is suitable for overall optimal control of large volumes. This paper proposes an optimal design method based on dynamic programming for the overall operation of distributed power sources. The purpose is:

minK=∑t=1δ(Dk(t)ξk(t)ΔT+∑i=1nDi(t)ξDM−i(t)ΔT)(1)

K is the optimal output power value. δ is the level of units that can be split throughout the scheduling period. The number of individual distributed power outputs, energy storage unit outputs and loads can be considered the same. ΔT is the duration of each work phase. Dk(t) and ξk(t) refer to the node electricity cost and the production of the feeder at the t time. n is a controlled distributed power source. Di(t) and ξDM−i(t) are the first to control the power and power output of the distributed power supply at i nodes.

Each new renewable resource is considered to use Maximum Power Point Tracking (MPPT). Under the assumed conditions, the system can ignore the benefits of saving and reducing energy consumption, reducing costs. This indicator aims to consider and optimize the power supply demand of distributed power sources. In this way, the purpose of total power consumption of distributed power sources is achieved [7]. At the same time, because the grid price at peak time is higher than that at valley time, more power output is allocated to the feeder than at peak time. This method can improve the performance of the system. The optimal power flow constraints of distributed power sources are as follows: On the premise that the power supply lines cannot be transmitted in reverse, the conditions are:

{ξMi(t)−ξNi(t)=Ui(t)∑j=1n[Uj(t)⋅(Mijcos⁡(αij(t))+Aijsin⁡(αij(t)))]i∈YAψMi(t)−ψNi(t)=Ui(t)∑j=1n[Uj(t)⋅(Aijcos⁡(αij(t))+Mijsin⁡(αij(t)))]i∈YAξ_Mi≤ξMi(t)≤ξ¯Mii∈YMψ_φi≤ψφi(t)≤ψ¯φii∈YφU_i≤Ui(t)≤U¯ii∈YA|Ii(t)|≤|I¯i|i∈YλU1(t)≤Ubus(t)(2)

YA is all nodes of a set. YM is a controlled set of decentralized electrical energy supplies. Yφ is the total non-energy source. Yλ is the general name for the branch. E is the power distribution of the distributed power source i. ξ_Mi and ξ¯Mi are its lower and upper limits. There are many kinds of distributed power, and each active power’s upper and lower limits are very different [8]. The upper and lower limits of the active power output of the battery pack depend on the grid-connected inverter capability, as well as the selection of the battery pack. Other micro-energy dispatching networks, such as gas turbines, fuel cells, etc. are relatively stable under the state of charge (SOC) during operation. ψφi(t) is the reactive output of reactive power source i. ψ_φi and ψ¯φi are its lower and upper bounds. Ui(t) is the voltage at the junction. U_i and U¯i are their upper and lower limits. |I¯i| is the maximum value of the branch flow Ii. U1 and Ubus are the voltage amplitudes at the end of the feeder and at the end of the substation. The first two formulas in Eq. (2) satisfy the equality constraints of power balance, and the third formula ensures no reverse transmission of power supply.

4  Regional Autonomous Control Strategy on Short Time Scale

The external conditions and load requirements of distributed power sources are constantly changing. In this paper, a method of local autonomy is adopted for the dynamic characteristics of distributed power sources to realize the emotional response of dynamic attributes of active distributed power sources. At the same time, the system recognizes dynamic adjustment of dynamic load and dynamic characteristics of intermittent power supply. Assuming the optimal power flow optimized by the active distribution network, the target power ξk∗ at which the equalizer injects energy into the feeder can be calculated in this paper. At the same time, this paper can obtain the target value ξg∗ of g autonomous regions input energy to the feeder. ξk is the real power that the substation is converging to the feeder. ξg is the value of work injected into feeder g.

Δξk represents the deviation of the actual value of the substation’s total power input feeder from the overall optimal target. Δξg represents the deviation of the true value of the energy input into the feeder from the autonomous region. Expressed explicitly by (3) and (4).

Δξk=ξk−ξk∗(3)

Δξg=ξg−ξg∗(4)

Through Eqs. (3) and (4), the regional autonomous control strategy in the short term can be expressed as:

δgΔξk−Δξg=0(5)

δg is the power synergy factor that the region g participates in. All autonomous regions δg on the feeder are reasonably configured according to the remaining capacity of the distributed power resources within each independent subregion. In this control mode, the disturbance will be shared by the respective autonomous area and equalization unit when the power disturbance occurs in the feeder. The characteristics of this cooperative distribution method in the power disturbance in autonomous and non-autonomous regions are entirely different. When the power disturbance D occurs in the involuntary zone of the transmission line, it can be obtained:

Δξ=Δξk+∑Δξg(6)

From Eq. (6), it can be seen that after the autonomous control of each area is stabilized, if there is Δξg=δgΔξk, then it can be obtained:

Δξk=Δξ1+∑δg(7)

Δξi=δgΔξ1+∑δg(8)

It is assumed that the power disturbance Δξ>0 occurs on the feeder, that is, the load increases or the intermittent energy decreases in the involuntary area to achieve power balance. This results in an increase in the power of the substation to the feeder by Δξ. The value on the left side of Eq. (5) corresponding to the corresponding independent region is greater than 0. Each autonomous zone increases the output of each decentralized power source in the zone, thereby increasing the power Δξg injected into the feeder by each autonomous zone, while Δξk gradually decreases until Eq. (5) is reached. Finally, this power disturbance is shared by the substation assembly and all autonomous regions. Likewise, when the power disturbance Δξ<0 occurs in the involuntary area of the feeder. The load in the unintended area is reduced or the intermittent energy is increased to achieve power balance. This results in a reduction in the power Δξ collected by the substation to the feeder, whereby the value on the left side of Eq. (5) for the corresponding independent zone will be lower than zero. Thus the power output of each decentralized power supply in the area of each autonomous region reduces the power Δξg injected into the feeder. This allows Δξk to gradually increase until the requirements of Eq. (5) are reached. And when the feeder power disturbance occurs in the autonomous area, that is, Δξ=0, each autonomous area will manage itself. This ensures that they inject power into the feeder. Fig. 2 shows the principle of regional autonomous control of the active distribution network on a short time scale [9].

Figure 2: The principle of regional autonomous control

DeadBand shown in Fig. 3 is a deadband processing component used to mask small disturbances and prevent frequent control changes [10]. 1/(1+sTg) is a simulation for signal delaying the sampling loop. K(1+1/(sT)) is a constrained proportional-integrated controller. It is used to close-loop control and constrain the power regulation of each autonomous zone. Its upper limits Δξlimupp and Δξlimlow may be determined by the adjustment capability of all controllable distributed power sources in the independent area. Δξg1,Δξg2,…,Δξgn is the optimal power adjustment of the optimal target corresponding to each independent system [11].

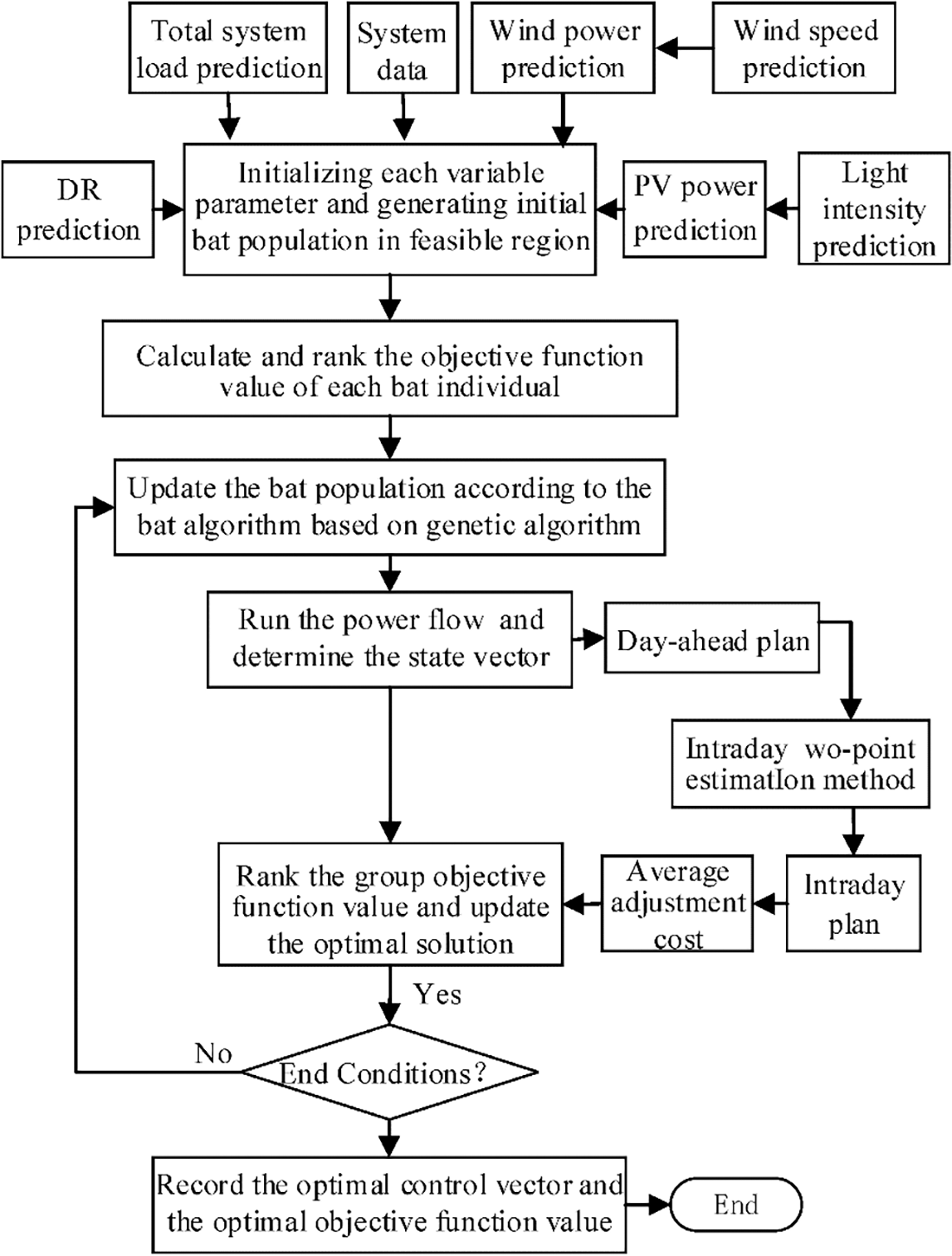
Figure 3: Short time scale active power optimization scheduling flow chart

5  Instance Simulation

Based on the IEEE3311 kV distribution network specification, this paper simulates and analyzes it. In the example, this paper proposes two kinds of dynamic power systems: the slow change of wind and photovoltaic; the sudden shift in wind and photovoltaic. Take 15 min as the maximum number of steps on a larger scale. This paper uses the original dual interior point method to optimize the power distribution and announces a new dynamic distribution system power distribution scheme after 1 h [12,13]. This article is based on the power output over the corresponding time interval [14,15]. At the same time, this paper uses M = N = 3 to carry out a rolling forecast to calculate the power of load, wind power and photovoltaic power generation within 15 min. In this paper, the continuous quadratic programming method is adopted, and the output power of the power system, such as load, wind and solar energy, is used as the input variable. In this paper, the gain of the dynamic output power of the system is obtained by the quadratic programming method. At the same time, the author adjusted the power of the long-term distributed power system so that the system’s short-term output power and long-term power output changed the most (Fig. 3) [16,17].

This article has re-planned the simulation example in Fig. 4. Fig. 4 shows the planned output value of active work on a long-term scale. The experimental condition is an economic dispatch model with the minimum operating power dispatch cost in the functional distribution network. Fig. 5 is a simulation diagram of short-term dynamic power output planning value. The model is short-time-scale optimal scheduling to minimize scheduling costs [18]. The short-time scale optimal scheduling takes the current actual active output of the system as the initial value of a new round of optimal rolling scheduling and forms a closed-loop control. This model overcomes the uncertainty of the system and wind power and photovoltaic. This way, the forecast value of the new round of active output is more realistic. Short-time-scale optimal scheduling takes the minimization of scheduling cost as the goal. This article has added this paragraph to the final draft. Fig. 6 shows the output value of each controllable distributed power source on a short time scale [19].

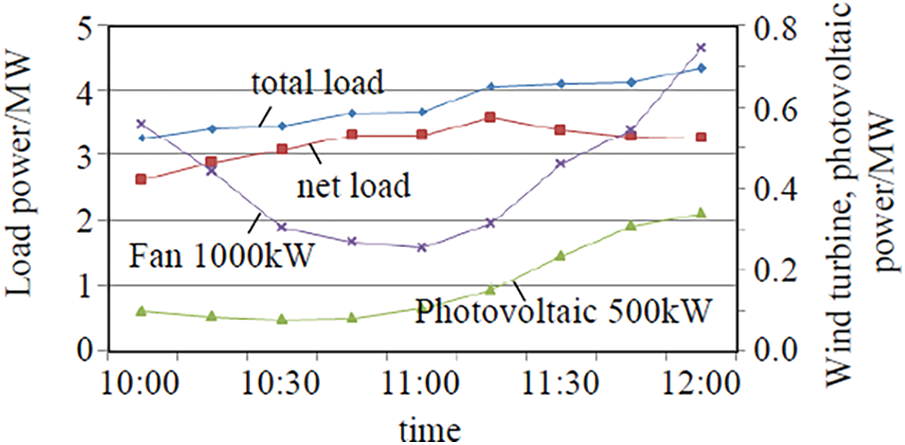
Figure 4: Load, wind and PV forecast data

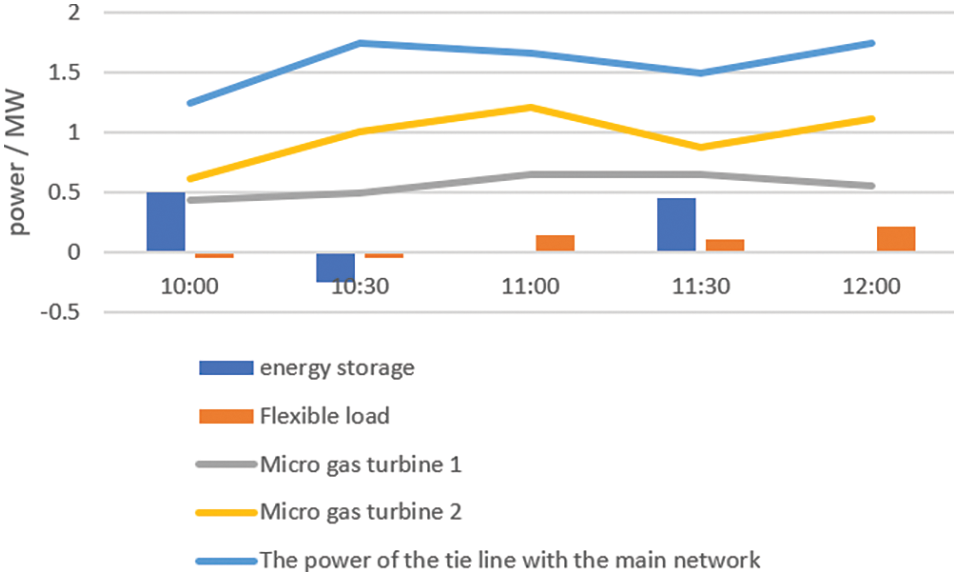
Figure 5: The planned value of active power output of each distributed power generation on a long-term scale

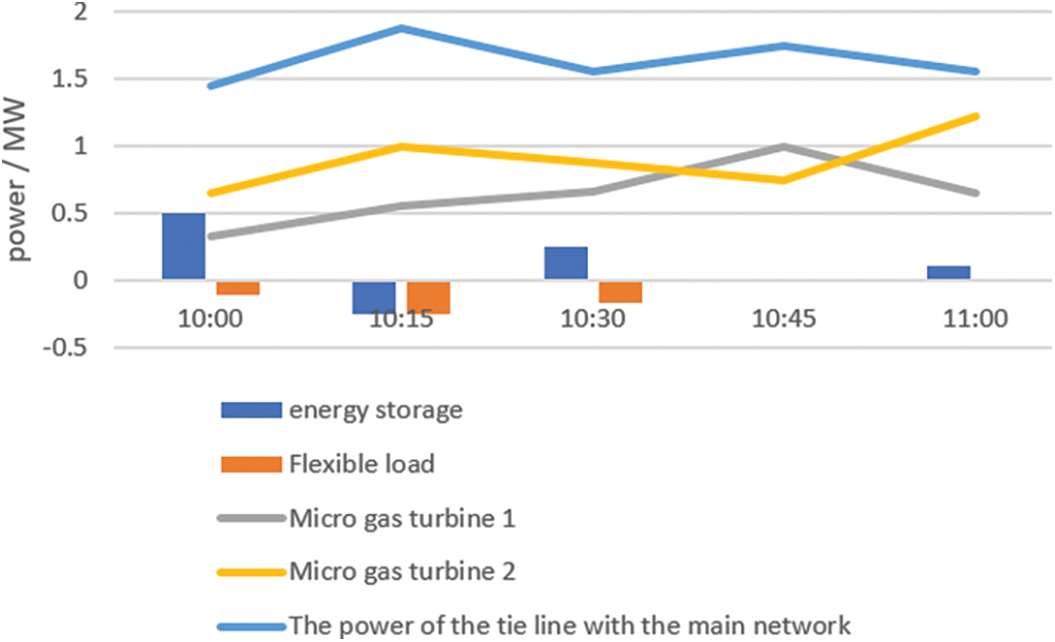
Figure 6: Active power output of each distributed power source on the short time scale

The conventional open-loop optimization algorithm can optimally estimate the load, wind power and photovoltaic power generation in the optimal period at one time. The system allocates them optimally. Figs. 7a–7c compared the optimal sorting methods combining conventional open-loop and distributed energy [20–23]. A conclusion is drawn through simulation and analysis: this paper uses the optimal scheduling of distributed generation energy. Its power variation law is consistent with the power variation generated by the conventional open-loop optimal power flow algorithm, and the optimization effect is similar. However, different from the traditional open-loop optimal power flow allocation method, the rolling optimization scheme of power resources based on distributed generation takes the change of power output power as its parameter [24,25]. The system realizes the rolling optimization scheduling based on distributed power supply energy by feedback correction through real-time measurement data. Its running process is more stable. It can effectively resolve the fluctuations and uncertainties brought about by emergencies. The system ensures the stability of its output power, reduces its mechanical loss and increases the life of the distributed power supply.

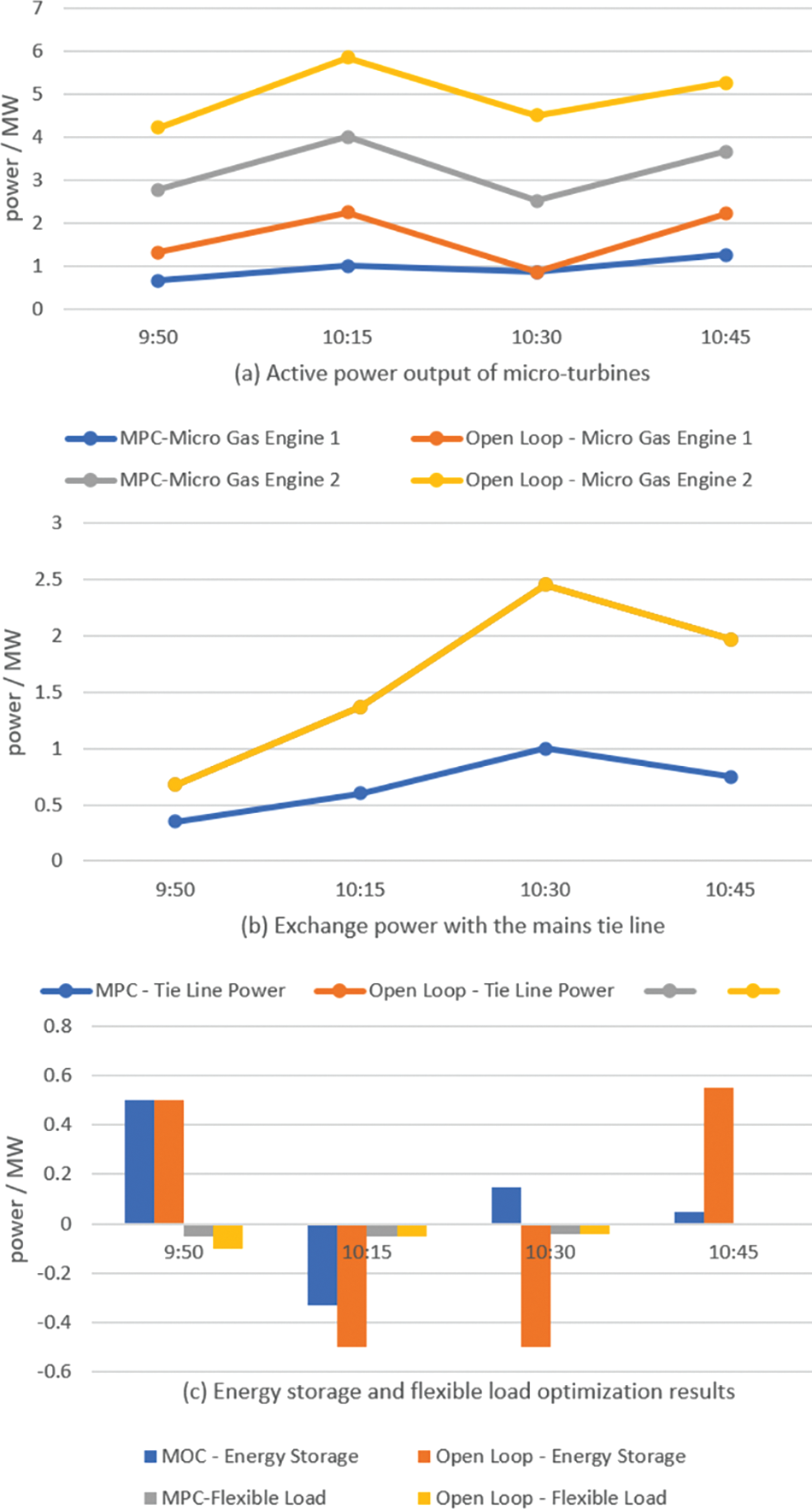
Figure 7: Comparison of optimized scheduling results

6  Conclusion

This paper mainly studies the power load distribution problem in distributed power sources. It proposes a long-term optimal power flow based on the active power output of distributed power sources as the benchmark for the control scheme. This paper analyzes the power output of each controllable DG energy source using a multi-stage rolling optimization method. The example calculation shows that it is feasible to use this method to adjust the active power of distributed power sources. The dynamic energy optimization method of distributed power sources proposed in this paper can be extended and applied to distributed energy generation in microgrids and distribution planning and construction of electric vehicle charging piles. There are still contents that can be further deepened in the current research. Although the unit combination optimization model is discussed in this paper, factors such as the environment are not considered. Because the output of intermittent distributed power is greatly affected by natural elements, there is a significant prediction deviation in the existing prediction methods. At the same time, this paper fails to carry out comprehensive, coordinated planning for the distribution network, including distributed power generation and charging stations. This article only plans from the perspective of distributed power supply. The starting point of the article has certain limitations. The difference between the distributed power supply and the charging station planning scheme will also affect the construction and transformation of the distribution grid. One step can build a more accurate rolling forecast model for load, wind power and photovoltaic in model predictive control. This way, the rolling optimization process is based on more precise input information to obtain a more realistic active power output value.

In the future, it is necessary to deeply analyze the timing characteristics, frequency domain characteristics, structural characteristics and supply and demand characteristics of participating objects. At the same time, it is necessary to establish a comprehensive “source-network-load-storage" coordination and dispatching model. When doing research on load aggregation modeling, this paper needs to deeply study the coordination characteristics within the aggregator and establish a two-layer interactive aggregation model. The regional scale should be fully evaluated when choosing an active distribution network dispatch framework. At the same time, choose a more reasonable coordination scheduling architecture.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Alatshan, M. S., Alhamrouni, I., Sutikno, T., Jusoh, A. (2020). Application of static synchronous compensator and energy storage system for power system stability enhancement. Bulletin of Electrical Engineering and Informatics, 9(6), 2222–2234. https://doi.org/10.11591/eei.v9i6.2319 [Google Scholar] [CrossRef]

2. Li, Y., Bai, X., Meng, J., Zheng, L. (2022). Multi-level refined power system operation mode analysis: A data-driven approach. IET Generation, Transmission & Distribution, 16(13), 2654–2680. https://doi.org/10.1049/gtd2.12481 [Google Scholar] [CrossRef]

3. Dong, Y., Shan, X., Yan, Y., Leng, X., Wang, Y. (2022). Architecture, key technologies and applications of load dispatching in China power grid. Journal of Modern Power Systems and Clean Energy, 10(2), 316–327. https://doi.org/10.35833/MPCE.2021.000685 [Google Scholar] [CrossRef]

4. Balsamo, F., de Falco, P., Mottola, F., Pagano, M. (2020). Power flow approach for modeling shipboard power system in presence of energy storage and energy management systems. IEEE Transactions on Energy Conversion, 35(4), 1944–1953. https://doi.org/10.1109/TEC.2020.2997307 [Google Scholar] [CrossRef]

5. Zhang, H., Ma, S., Ding, T., Lin, Y., Shahidehpour, M. (2020). Multi-stage multi-zone defender-attacker-defender model for optimal resilience strategy with distribution line hardening and energy storage system deployment. IEEE Transactions on Smart Grid, 12(2), 1194–1205. https://doi.org/10.1109/TSG.2020.3027767 [Google Scholar] [CrossRef]

6. Pan, E., Liu, S., Liu, J., Qi, Q., Guo, Z. (2020). The state grid corporation of China’s practice and outlook for promoting new energy development. Energy Conversion and Economics, 1(2), 71–80. https://doi.org/10.1049/enc2.12007 [Google Scholar] [CrossRef]

7. Anees, H. M., Kazmi, S. A. A., Naqvi, M., Naqvi, S. R., Dastgeer, F. et al. (2021). A mathematical model-based approach for DC multi-microgrid performance evaluations considering intermittent distributed energy resources, energy storage, multiple load classes, and system components variations. Energy Science & Engineering, 9(10), 1919–1934. https://doi.org/10.1002/ese3.901 [Google Scholar] [CrossRef]

8. Dai, R., Esmaeilbeigi, R., Charkhgard, H. (2021). The utilization of shared energy storage in energy systems: A comprehensive review. IEEE Transactions on Smart Grid, 12(4), 3163–3174. https://doi.org/10.1109/TSG.2021.3061619 [Google Scholar] [CrossRef]

9. Zhu, H., Zhang, Y., Liu, F., Wei, W. (2020). Effect of excess hydrogen on hydrogen fueled internal combustion engine under full load. International Journal of Hydrogen Energy, 45(39), 20419–20425. https://doi.org/10.1016/j.ijhydene.2019.12.022 [Google Scholar] [CrossRef]

10. Pla, B., de la Morena, J., Bares, P., Jiménez, I. (2020). Cycle-to-cycle combustion variability modelling in spark ignited engines for control purposes. International Journal of Engine Research, 21(8), 1398–1411. https://doi.org/10.1177/1468087419885754 [Google Scholar] [CrossRef]

11. Wang, X., Sun, B. G., Luo, Q. H. (2019). Energy and exergy analysis of a turbocharged hydrogen internal combustion engine. International Journal of Hydrogen Energy, 44(11), 5551–5563. https://doi.org/10.1016/j.ijhydene.2018.10.047 [Google Scholar] [CrossRef]

12. Malé, Q., Staffelbach, G., Vermorel, O., Misdariis, A., Ravet, F. et al. (2019). Large eddy simulation of pre-chamber ignition in an internal combustion engine. Flow, Turbulence and Combustion, 103(2), 465–483. https://doi.org/10.1007/s10494-019-00026-y [Google Scholar] [CrossRef]

13. Li, Y., Gao, W., Zhang, P., Ye, Y., Wei, Z. (2019). Effects study of injection strategies on hydrogen-air formation and performance of hydrogen direct injection internal combustion engine. International Journal of Hydrogen Energy, 44(47), 26000–26011. https://doi.org/10.1016/j.ijhydene.2019.08.055 [Google Scholar] [CrossRef]

14. Gainey, B., Longtin, J. P., Lawler, B. (2019). A guide to uncertainty quantification for experimental engine research and heat release analysis. SAE International Journal of Engines, 12(5), 509–290. https://doi.org/10.4271/03-12-05-0033 [Google Scholar] [CrossRef]

15. Thawko, A., Yadav, H., Eyal, A., Shapiro, M., Tartakovsky, L. (2019). Particle emissions of direct injection internal combustion engine fed with a hydrogen-rich reformate. International Journal of Hydrogen Energy, 44(52), 28342–28356. https://doi.org/10.1016/j.ijhydene.2019.09.062 [Google Scholar] [CrossRef]

16. Wang, L., Dubey, A., Gebremedhin, A. H., Srivastava, A. K., Schulz, N. (2022). MPC-based decentralized voltage control in power distribution systems with EV and PV coordination. IEEE Transactions on Smart Grid, 13(4), 2908–2919. https://doi.org/10.1109/TSG.2022.3156115 [Google Scholar] [CrossRef]

17. Li, B., Chen, Y., Wei, W., Wang, Z., Mei, S. (2022). Online coordination of LNG tube trailer dispatch and resilience restoration of integrated power-gas distribution systems. IEEE Transactions on Smart Grid, 13(3), 1938–1951. https://doi.org/10.1109/TSG.2022.3141548 [Google Scholar] [CrossRef]

18. Pereira, K., Pereira, B. R., Contreras, J., Mantovani, J. R. (2018). A multiobjective optimization technique to develop protection systems of distribution networks with distributed generation. IEEE Transactions on Power Systems, 33(6), 7064–7075. https://doi.org/10.1109/TPWRS.2018.2842648 [Google Scholar] [CrossRef]

19. Lei, S., Chen, C., Zhou, H., Hou, Y. (2018). Routing and scheduling of mobile power sources for distribution system resilience enhancement. IEEE Transactions on Smart Grid, 10(5), 5650–5662. https://doi.org/10.1109/TSG.2018.2889347 [Google Scholar] [CrossRef]

20. Wenzhi, S., Zhang, H., Tseng, M. L., Weipeng, Z., Xinyang, L. (2022). Hierarchical energy optimization management of active distribution network with multi-microgrid system. Journal of Industrial and Production Engineering, 39(3), 210–229. https://doi.org/10.1080/21681015.2021.1972478 [Google Scholar] [CrossRef]

21. Zhang, W., Xu, Y. (2018). Distributed optimal control for multiple microgrids in a distribution network. IEEE Transactions on Smart Grid, 10(4), 3765–3779. https://doi.org/10.1109/TSG.2018.2834921 [Google Scholar] [CrossRef]

22. Luo, F., Dong, Z. Y., Liang, G., Murata, J., Xu, Z. (2018). A distributed electricity trading system in active distribution networks based on multi-agent coalition and blockchain. IEEE Transactions on Power Systems, 34(5), 4097–4108. https://doi.org/10.1109/TPWRS.2018.2876612 [Google Scholar] [CrossRef]

23. Ehsan, A., Yang, Q. (2018). Coordinated investment planning of distributed multi-type stochastic generation and battery storage in active distribution networks. IEEE Transactions on Sustainable Energy, 10(4), 1813–1822. https://doi.org/10.1109/TSTE.2018.2873370 [Google Scholar] [CrossRef]

24. Yousaf, M., Jalilian, A., Muttaqi, K. M., Sutanto, D. (2022). An adaptive overcurrent protection scheme for dual-setting directional recloser and fuse coordination in unbalanced distribution networks with distributed generation. IEEE Transactions on Industry Applications, 58(2), 1831–1842. https://doi.org/10.1109/TIA.2022.3146095 [Google Scholar] [CrossRef]

25. Dashtpeyma, M., Ghodsi, R. (2022). Resilient electricity distribution network: Exploring research and managerial implications. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 46(1), 1–14. https://doi.org/10.1007/s40998-021-00453-6 [Google Scholar] [CrossRef]